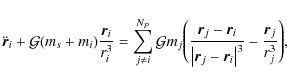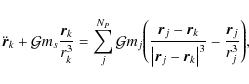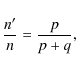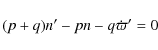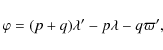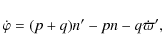| Issue |
A&A
Volume 508, Number 2, December III 2009
|
|
|---|---|---|
| Page(s) | 1021 - 1030 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200911943 | |
| Published online | 08 October 2009 | |
A&A 508, 1021-1030 (2009)
Neptune Trojans and Plutinos: colors, sizes, dynamics, and their possible collisions![[*]](/icons/foot_motif.png)
A. J. C. Almeida1,2 - N. Peixinho3,4 - A. C. M. Correia1,5
1 - Departamento de Física, Universidade de Aveiro, Campus de Santiago,
3810-193 Aveiro, Portugal
2 -
Instituto de Telecomunicações, IT - Aveiro, Campus de Santiago,
3810-193 Aveiro, Portugal
3 -
Centro de Física Computacional, Universidade de Coimbra, 3004-516 Coimbra, Portugal
4 -
Observatório Astronómico da Universidade de Coimbra, 3040-004 Coimbra, Portugal
5 -
Astronomie et Systèmes Dynamiques, IMCCE-CNRS UMR8028,
77 Av. Denfert-Rochereau, 75014 Paris, France
Received 24 February 2009 / Accepted 23 September 2009
Abstract
Neptune Trojans and Plutinos are two subpopulations of trans-Neptunian objects
located in the 1:1 and the 3:2 mean motion resonances with Neptune, respectively, and
therefore protected from close encounters with the planet.
However, the orbits of these two kinds of objects may cross very often, allowing
a higher collisional rate between them than with other kinds of trans-Neptunian
objects, and a consequent size distribution modification of the two subpopulations.
Observational colors and absolute magnitudes of Neptune Trojans and Plutinos show that i) there are no intrinsically bright (large) Plutinos at small inclinations; ii) there is an apparent excess of blue and intrinsically faint (small) Plutinos; and iii) Neptune Trojans possess the same blue colors as Plutinos within the same (estimated) size range do.
For the present subpopulations we analyzed the most favorable conditions for close encounters/collisions and address any link there could be between those encounters and the sizes and/or colors of Plutinos and Neptune Trojans. We also performed a simultaneous numerical simulation of the outer Solar System over 1 Gyr for all these bodies in order to estimate their collisional rate.
We conclude that orbital overlap between Neptune Trojans and Plutinos is favored for Plutinos with large libration amplitudes, high eccentricities, and small inclinations. Additionally, with the assumption that the collisions can be disruptive creating smaller objects not necessarily with similar colors, the present high concentration of small Plutinos with small inclinations can thus be a consequence of a collisional interaction with Neptune Trojans and such hypothesis should be further analyzed.
Key words: methods: N-body simulations - solar system: formation - techniques: photometric - celestial mechanics - Kuiper Belt - minor planets, asteroids
1 Introduction
Trans-Neptunian objects (TNOs), also known as Kuiper belt objects (KBOs), are a population of small and primitive icy bodies orbiting (mostly) beyond Neptune. Studying them is one of the most significant ways to obtain information on the early ages of the Solar System.
Based on some distinct dynamical properties, the TNOs can be subdivided into several different subpopulations, often also called families or groups. Subdividing them as a function of their physical properties seems to be far more complex. TNOs have surface colors so diverse that they can go from blue/neutral (i.e. solar-like) to extremely red. A possible explanation for the wide variety of colors was originally proposed by Luu & Jewitt (1996) with the collisional resurfacing model. In this model, the competition between surface reddening, due to cosmic-ray bombardment, and a resurfacing with frozen material (assumed to be bluer) withdrawn from beneath its crust by impact collisions could be responsible for the observed wide range of surface colors. Once the model seemed to fail, at least in its simple form, more complex forms were proposed, namely, collisional resurfacing combined with cometary activity (Delsanti et al. 2004), and collisional resurfacing with layered reddening and even re-bluing by cosmic rays (Gil-Hutton 2002).
An alternate idea proposes that surface colors are primordial (Tegler et al. 2003b, and references therein). More recently, Grundy (2009) has shown that an object could lose its redness simply by ice sublimation (without resurfacing). This could explain the lack of red colors among TNOs that evolved into Jupiter-family comets due to their closeness to the Sun; yet, as the aforementioned work acknowledges, the existence of the blue/neutral TNOs at heliocentric distances where ices do not sublimate suggests the existence of other coloring mechanisms. Our understanding on the origin and eventual alteration of TNOs colors is still very limited and, up to the present, none of these approaches has led to a fully consistent explanation for the color diversity (for a review see Doressoundiram et al. 2008).
Among the TNOs, two subpopulations caught our attention: the Neptune Trojans and the Plutinos.
Neptune Trojans are small bodies trapped in a 1:1 mean motion orbital resonance with Neptune, also
with orbital eccentricities smaller than 0.1. Roughly they co-orbit with Neptune
concentrated
![]() ahead and
ahead and
![]() behind Neptune's position.
Chiang & Lithwick (2005) propose that Neptune Trojans formed by in-situ accretion from small-sized debris
once Neptune's migration has stopped.
On the other hand, other works indicate they can survive planetary migration
(Nesvorný & Dones 2002; Kortenkamp et al. 2004) and, more recently, thanks to
the discovery of some high-inclined Neptune Trojans, Nesvorný & Vokrouhlický (2009)
sustain they were captured during planetary migration.
Compared to TNOs, Neptune Trojans seem to be quite small in
size (diameters D<100 km) and also slightly blue.
At the time of our analysis 6 Neptune Trojans were known
behind Neptune's position.
Chiang & Lithwick (2005) propose that Neptune Trojans formed by in-situ accretion from small-sized debris
once Neptune's migration has stopped.
On the other hand, other works indicate they can survive planetary migration
(Nesvorný & Dones 2002; Kortenkamp et al. 2004) and, more recently, thanks to
the discovery of some high-inclined Neptune Trojans, Nesvorný & Vokrouhlický (2009)
sustain they were captured during planetary migration.
Compared to TNOs, Neptune Trojans seem to be quite small in
size (diameters D<100 km) and also slightly blue.
At the time of our analysis 6 Neptune Trojans were known![]() , all of them librating around the Lagrangian
point L4.
, all of them librating around the Lagrangian
point L4.
Plutinos are those trapped in a 3:2 mean motion orbital resonance with Neptune, with eccentricity values ranging between 0.1 and 0.3. Unlike Trojans, the colors of Plutinos vary from the blue/neutral to the very red, and their sizes range from a few tens of km to a few thousands (note that Pluto is a Plutino). Roughly, Plutinos possess semi-major axes within 39 < a < 40.5 AU. Through long-term dynamical evolution studies Lykawka & Mukai (2007) identified 98 Plutinos and that will be our reference. Being locked at the 3:2 resonance, Plutinos can periodically cross the orbit of Neptune without colliding with it. However, this protection from collisions is not possible for Neptune Trojans and Plutinos. A first look at the geometry of these two populations suggests that they might even collide frequently.
The analysis of the collisional resurfacing model by Thébault & Doressoundiram (2003) and Thébault (2003) found that Plutinos were significantly more affected by collisions than other TNOs. Since, observationally, Plutinos did not exhibit bluer colors than all other TNOs taken as a whole, the aforementioned work strongly argued against the collisional resurfacing model, at least as major cause for the color diversity of TNOs. Neptune Trojans were not included in Thébault & Doressoundiram's simulations, though, since they were not known at the time. Notwithstanding the arguments against it, the collisional resurfacing that was analyzed was a very simple model. For instance, the possibility of collisional disruption of differentiated bodies producing fragments or ruble-piles with surface colors distinct from those of the parent bodies has not been taken into account in the collisional resurfacing models yet. Naturally, the possible outcomes of this scenario would be far more complex and our understanding of the physics of collisional processes between the icy TNOs is still limited (see review by Leinhardt et al. 2008). Nonetheless, both a collisional family of TNOs associated with (136108) Haumea and a collisional system of satellites associated with Pluto have been detected (Canup 2005; Brown et al. 2007; Stern et al. 2006).
Surveys show a power-law for the size distribution of TNOs with slope change at
![]() km (Bernstein et al. 2004), which is most consistent with TNOs being gravity dominated
bodies with negligible material strength. Objects larger than
km (Bernstein et al. 2004), which is most consistent with TNOs being gravity dominated
bodies with negligible material strength. Objects larger than ![]() 100 km are difficult to
disrupt, hence likely primordial, and objects smaller than this are expected to be shattered due to
disruptive collisional evolution (Kenyon et al. 2008; Pan & Sari 2005).
de Elía et al. (2008) studied
the collisional evolution of Plutinos considering only Plutino-Plutino collisions.
They inferred that any eventual slope change at
100 km are difficult to
disrupt, hence likely primordial, and objects smaller than this are expected to be shattered due to
disruptive collisional evolution (Kenyon et al. 2008; Pan & Sari 2005).
de Elía et al. (2008) studied
the collisional evolution of Plutinos considering only Plutino-Plutino collisions.
They inferred that any eventual slope change at
![]() km on the power-law
size distribution of Plutinos should be primordial and not of collisional
origin. Yet, they found that
collisional populations may form from the breakup of objects larger than 100 km, and if those populations form
with small inclinations their fragments will likely stay in the resonance.
km on the power-law
size distribution of Plutinos should be primordial and not of collisional
origin. Yet, they found that
collisional populations may form from the breakup of objects larger than 100 km, and if those populations form
with small inclinations their fragments will likely stay in the resonance.
On Sect. 2 we will analyze the observational data relative to Neptune Trojans and Plutinos. We will discuss two particular observational properties: 1) there is an apparent ``excess'' of small blue Plutinos and these happen to be also in the same size range and to possess the same colors as the known Neptune Trojans; and 2) there is a concentration of small Plutinos, and absence of large ones, with small orbital inclinations. The eventual collisional interaction between Plutinos and Neptune Trojans has not been analyzed in previous works. Since their geometry points to the existence of mutual collisions, the existence of an eventual link between the colors and sizes of Neptune Trojans and Plutinos and their interactions/collisions motivated us to this work. On Sect. 3 we will study the dynamics of Neptune Trojans and Plutinos, separately, focusing on their orbits around the Lagrangian point L4. On Sect. 4 we will discuss the possibility of collisions between Neptune Trojans and Plutinos and the best conditions for this to happen. Finally, on Sect. 5 we will present our conclusions.
2 Observational results and discussion
In Table A.1 we summarize the orbital elements, B-R colors, and R-filter absolute magnitudes (HR) for 4 Neptune Trojans (from Sheppard & Trujillo 2006) and 41 Plutinos (see references on the table). In Fig. 1 we plot the orbital inclination vs orbital eccentricity of all these objects, together with their B-R colors, indexed on a color palette on the right hand side of the figure, and in which objects are plotted proportionally to their estimated diameter also indexed on the top of the figure.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11943f1.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg17.png)
|
Figure 1: Orbital inclination vs. eccentricity, estimated size, and color of Neptune Trojans and Plutinos for which those properties have been measured. |
| Open with DEXTER | |
The diameters of these objects (in kilometers) are estimated from the absolute magnitudes using the formula
(Russell 1916):
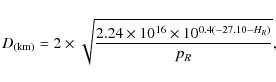
|
(1) |
where HR is the R-filter absolute magnitude, and the R-filter albedo is taken as pR=0.09(Brown & Trujillo 2004). A size estimation exception is made for Pluto which is represented with D=2390 km. A vertical dashed line separates Neptune Trojans, located on the left side of the figure, from Plutinos, located on the right side.
A first look at Fig. 1 shows that:
- (i)
- all Trojans are blue
![[*]](/icons/foot_motif.png) ,
small (D<100 km)
compared to the size distribution of Plutinos, and possess small eccentricities;
,
small (D<100 km)
compared to the size distribution of Plutinos, and possess small eccentricities;
- (ii)
- there is an apparent concentration of small Plutinos with small inclination values and a concentration of large Plutinos at high inclinations;
- (iii)
- Plutinos have higher eccentricity values than Trojans, and their colors range from blue to red appearing randomly distributed in inclination and eccentricity;
- (iv)
- all Plutinos within the same (estimated) size range as Neptune Trojans possess blue colors.
Based on these properties we decide to explore two possible scenarios:
- (1)
- could the equally blue colors of the equally sized Plutinos and Neptune Trojans be the result of some collisional interaction between both populations?
- (2)
- could the concentration of small Plutinos with small inclinations be the result of some collisional interaction between them and Neptune Trojans?
Therefore, since the possible effects of a significant number of Neptune Trojans were not considered in the aforementioned simulations, in this work we explore if and how these Trojans could be the major cause of the non-homogeneity of surface properties observed among Plutinos and the (apparent) homogeneity of surface properties observed for Neptune Trojans.
Let us grasp scenario (1). The members of the collisional families associated with (136108) Haumea possess very similar bluish colors (Brown et al. 2007). It is reasonable to hypothesize that if Neptune Trojans collided heavily with part of the Plutino population the collision outcomes could be similar in color. Considering that assumption, for this scenario to be possible we need to find a similar collision rate between Trojans and Plutinos independent of the eccentricity and/or inclination values of Plutinos since the small (D<100 km) and blue Plutinos are homogeneously scattered both in eccentricity and inclination.
As to scenario (2), we are considering a less strict hypothesis in which the collision outcomes of Neptune Trojans and part of the Plutino population are not necessarily equal in color. The Pluto system has, presumably, a collisional origin, however, while Charon, Nix, and Hydra possess similar colors, Pluto is quite distinct (e.g. Stern 2009). Let us assume that the disruption of large layered TNOs could generate several objects with distinct colors either from fragments coming from different layers with different colors or from re-accretion of different parts of a heterogeneous cloud of debris. Hence, collisions would generate both blue and red, small and medium objects (D<300 km). For this scenario to be possible we need to find a much higher collision rate between Trojans and the Plutinos with small inclination values than with the Plutinos at high inclinations. Also, given that we do not see neither red nor mid/large-sized Neptune Trojans, whereas we see it among Plutinos in the presumable region of collisions, the primordial size and color distributions of Trojans and Plutinos should not have been similar.
Note that even though resonant objects are known to possess large variations of their eccentricity and/or inclination values,
Nesvorný & Roig (2000) showed the existence of two dynamical populations of Plutinos, separating at
![]() ,
which do not seem to easily mix. Consequently, any different
collisional/surface evolution that both populations might have had in
the past should still be detectable today.
,
which do not seem to easily mix. Consequently, any different
collisional/surface evolution that both populations might have had in
the past should still be detectable today.
In order to test if the low-inclined Plutinos are indeed smaller than the other ones we use the
Kolmogorov-Smirnov test (Press et al. 1992; Kolmogorov 1933; Smirnov 1939).
We successively compare the absolute magnitude HR distribution of our 41 Plutinos (with measured B-R colors) having i<ic with those
having ![]() ,
varying ic from
,
varying ic from ![]() to
to
![]() in increments of
in increments of
![]() .
Two
significant solutions exist: a) Plutinos with
.
Two
significant solutions exist: a) Plutinos with
![]() are intrinsically fainter, and assumed to be
smaller, than those above
are intrinsically fainter, and assumed to be
smaller, than those above ![]() with a (one-tailed) significance p=0.0024; b) Plutinos with
with a (one-tailed) significance p=0.0024; b) Plutinos with
![]() are intrinsically fainter than those above
are intrinsically fainter than those above
![]() with a significance p=0.0030. Even
though we do not obtain an unique solution for the best inclination value that separates the larger
(brighter) from the smaller (fainter) Plutinos, we can conclude that the low-inclined ones are in fact
smaller. Figure 2 shows the cumulative distribution functions of absolute magnitudes
for the higher inclined and lower inclined Plutinos in both solutions.
with a significance p=0.0030. Even
though we do not obtain an unique solution for the best inclination value that separates the larger
(brighter) from the smaller (fainter) Plutinos, we can conclude that the low-inclined ones are in fact
smaller. Figure 2 shows the cumulative distribution functions of absolute magnitudes
for the higher inclined and lower inclined Plutinos in both solutions.
![\begin{figure}
\par\includegraphics[width=8cm]{11943f2.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg27.png)
|
Figure 2:
Cumulative distribution function of absolute magnitudes HR for Plutinos above and below |
| Open with DEXTER | |
We will proceed with the study of the dynamics of Plutinos and Neptune Trojans and investigate their possible collisions.
3 Dynamical evolution
In previous section we discussed the possible relations between the colors of Plutinos and Neptune Trojans, and the eventual collisions between them. It is now our goal to test the possibility of collisions numerically. For that purpose we will simulate the outer Solar System evolution, where the TNOs are considered massless. This hypothesis is essential to speed up the integrations. The equation of motion for the planets is given bywhere
For TNOs, since they are assumed massless, the equation of motion is given by
where
In our simulations we will use the symplectic integrator from Laskar & Robutel (2001), with an integration step-size of 0.1 yr. The system is composed of 5 planets (Table A.2), 6 Trojans (Table A.3) and 98 Plutinos (Table A.4).
3.1 Resonant motion
Since both Trojans and Plutinos are resonant objects we will briefly recall here the bases of resonant motion, following Murray & Dermott (1999). Consider then a TNO in some resonance with Neptune. We assume, for simplicity, that Neptune is in a circular orbit and that all motion takes place in the plane of its orbit. We also ignore any perturbations between the two bodies as we are only interested in how resonant relationships lead to repeated encounters.We can examine the geometry of resonance for a general case by first considering
two bodies moving around the Sun, in circular and
coplanar orbits. So, let us assume that
where n and n' are the mean motions of Neptune and the TNO, respectively (for Trojans p = 1 and q = 0, while for Plutinos p = 2and q = 1). If the two bodies are in conjunction at time t=0, the next conjunction will occur when
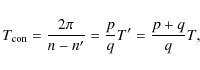
|
(5) |
where T and T' are the orbital periods of the two bodies.
Now consider the case when e=0, ![]() ,
and
,
and
![]() ,
where e denotes the eccentricity for Neptune and e' and
,
where e denotes the eccentricity for Neptune and e' and ![]() denotes the eccentricity and longitude of pericentre of
the TNO respectively. If the resonant relation
denotes the eccentricity and longitude of pericentre of
the TNO respectively. If the resonant relation
is satisfied, then we can rewrite Eq. (4) as
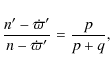
|
(7) |
where
where
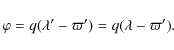
|
(9) |
Thus,
and
Along with the orbital parameters of the Trojans and Plutinos that we used in our simulations, in Tables A.3 and A.4, respectively, we provide the equilibrium libration angle, the main libration period and amplitude of each TNO obtained over the next 250 kyr.
3.2 Trojans
Neptune Trojans are resonant objects in a 1:1 mean motion resonance with Neptune. In our model we computed the motion of the six Neptune Trojans listed in Table A.3. In Fig. 3, we show the behavior of all known Trojans, along time, in a co-rotating frame with Neptune for 100 Myr. Each dot shows the position of the TNO every 10 kyr.
As expected, we see in Fig. 3 that all Trojans orbit around the
Lagrangian point L4, and execute tadpole-type orbits.
This kind of orbits represents stable oscillations
in the vicinity of the Lagrangian equilibrium point
(e.g. Giuliatti Winter et al. 2007).
The differences between the shape of their orbits depend
on the libration amplitude but also on their orbital eccentricity
and inclination values. Trojan 2007VL305, that execute the most
scattered orbit, also presents the highest eccentricity and inclination
(e = 0.062 and
![]() ).
On the other hand, for small values of these two orbital parameters, the
TNOs remain roughly in the path of Neptune's orbit, only changing its
relative position to the planet due to libration.
).
On the other hand, for small values of these two orbital parameters, the
TNOs remain roughly in the path of Neptune's orbit, only changing its
relative position to the planet due to libration.
![\begin{figure}
\par$
\begin{array}{cc}
\includegraphics[scale=0.25, angle=0]{119...
...} &
\includegraphics[scale=0.25, angle=0]{11943f3f.ps}\end{array}$
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg56.png)
|
Figure 3: Orbital evolution of the Neptune Trojans (in green) listed in Table A.3 over 100 Myr in the co-rotating frame of Neptune (in blue). Each panel shows the projection of the TNO position every 10 kyr in the orbital plane of Neptune. x and y are spatial coordinates centered on the star and rotating with Neptune, normalized by the Neptune-Sun distance. All Trojans orbit around the Lagrangian point L4 and execute tadpole-type orbits. More scattered orbits correspond to higher values of the eccentricity and inclination, while distance to the L4 point depend on the libration amplitude. |
| Open with DEXTER | |
In Table A.3 we provide the libration amplitude and period for all Trojans.
While amplitudes can vary from only ![]() to
to ![]() ,
the periods of
libration remain around 9 kyr for all objects.
Trojan 2001QR322 presents the largest libration amplitude and therefore moves
further away of the equilibrium point L4.
As a consequence, its orbit will be more susceptible of being destabilized by
gravitational perturbations from the planets and other bodies in the system.
Indeed, in our long-term numerical simulations (Sect. 4.1) this TNO will
abandon the Trojan orbit after 112 Myr and become an ordinary Kuiper belt object.
,
the periods of
libration remain around 9 kyr for all objects.
Trojan 2001QR322 presents the largest libration amplitude and therefore moves
further away of the equilibrium point L4.
As a consequence, its orbit will be more susceptible of being destabilized by
gravitational perturbations from the planets and other bodies in the system.
Indeed, in our long-term numerical simulations (Sect. 4.1) this TNO will
abandon the Trojan orbit after 112 Myr and become an ordinary Kuiper belt object.
3.3 Plutinos
Plutinos are resonant TNOs in a 3:2 mean motion resonance with Neptune. Thus, like Trojans, although they can cross the orbit of Neptune, they are protected from possible encounters with this planet. In Fig. 4 we have drawn the typical path of a Plutino in the co-rotating frame of Neptune, for three different values of the eccentricity (e = 0.1, 0.2 and 0.3).
| Figure 4: Typical path of a Plutino (dotted line) in the rotating frame of Neptune (full line) for different eccentricity values (e = 0.1, 0.2 and 0.3). Only high eccentricity values (e > 0.2) allow the Plutino to cross the orbit of Neptune. Due to the 3:2 mean motion resonance the trajectories are repeated every two orbits of the TNO around the Sun. |
|
| Open with DEXTER | |
These plots are drawn assuming that the Plutino is at exact resonance (
![]() ), which is not true, because the orbit is librating
around an equilibrium position
), which is not true, because the orbit is librating
around an equilibrium position ![]() (Eq. (8)).
As a consequence, in a more realistic situation we will observe an oscillation of
those paths as the one represented in Fig. 5.
In Table A.4 we provide the libration amplitude and period for all Plutinos.
The equilibrium libration angle for them all is
(Eq. (8)).
As a consequence, in a more realistic situation we will observe an oscillation of
those paths as the one represented in Fig. 5.
In Table A.4 we provide the libration amplitude and period for all Plutinos.
The equilibrium libration angle for them all is
![]() ,
but the amplitudes of libration can be as low as
,
but the amplitudes of libration can be as low as ![]() for Plutino
1996TQ66 or as large as
for Plutino
1996TQ66 or as large as ![]() for Plutinos 1995QY9 and 2001KN77.
The libration periods,
for Plutinos 1995QY9 and 2001KN77.
The libration periods,
![]() ,
vary between 14.5 and 26.6 kyr, the average
being around 20 kyr.
For comparison, the values for Pluto are
,
vary between 14.5 and 26.6 kyr, the average
being around 20 kyr.
For comparison, the values for Pluto are
![]() and
and
![]() kyr.
kyr.
![\begin{figure}
\par\includegraphics[width=7cm]{11943f5.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg66.png)
|
Figure 5: Libration motion of the orbit of a Plutino. |
| Open with DEXTER | |
In our model we computed the motion of about 100 Plutinos, whose orbital
parameters are listed in Table A.4.
All objects present moderate eccentricities and inclinations, (
![]() and
and
![]() ).
According to Malhotra (1995) these values can be a consequence of the
resonant mechanism of capture, during the residual planetesimal cleaning in the
vicinity of the young giant planets. Due to Neptune's migration, the
eccentricity and inclination of the Plutinos are pumped after capture in
resonance.
).
According to Malhotra (1995) these values can be a consequence of the
resonant mechanism of capture, during the residual planetesimal cleaning in the
vicinity of the young giant planets. Due to Neptune's migration, the
eccentricity and inclination of the Plutinos are pumped after capture in
resonance.
In Fig. 6 we show the behavior of six Plutinos, along time, in a co-rotating frame with Neptune for 100 Myr, each dot showing the position of the object every 10 kyr. Because Plutinos are much more numerous than Trojans, we can only represent a small fraction of them. We have chosen the most representative cases, namely, the Plutino with the lowest and largest libration (1996TP66 and 2001KN77, respectively), the Plutinos with smallest and highest eccentricity (2003VS2 and 2005GE187, respectively), and the Plutinos with smallest and highest inclination (2002VX130 and 2005TV189, respectively).
![\begin{figure}
\par$
\begin{array}{cc}
\includegraphics[scale=0.25, angle=0]{119...
...s} &
\includegraphics[scale=0.25, angle=0]{11943f6f.ps}\end{array}$
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg69.png)
|
Figure 6:
Orbital evolution of some Plutinos (in red) taken from
Table A.4 over 100 Myr in the co-rotating frame of Neptune (in
blue). Each panel shows the projection of the TNO position every 10 kyr in
the orbital plane of Neptune. x and y are
spatial coordinates centered on the star and rotating with Neptune, normalized
by the Neptune-Sun distance.
We have chosen the most representative cases, namely, Plutino 1996TP66, with
the lowest libration amplitude (
|
| Open with DEXTER | |
As expected, depending on the eccentricity values, the orbits of the Plutinos are all in good agreement with the paths shown in Fig. 4. Because of the libration motion of the orbits (Fig. 5) their trajectories approach or cross the Lagrangian points L4 and L5, that is, the Plutinos orbits share the same spatial zone as the Neptune Trojans.
4 Numerical simulations
In Sect. 2 we have shown that, although Neptune Trojans and Plutinos appear to have different origins, some of their properties indicate that the two types are quite identical, suggesting that there must be some sort of communication between them. Indeed, in the previous section we saw that due to the libration motion of the orbits there is a wide zone of spatial overlap around the Lagrangian point L4 of Neptune. As a consequence, we may expect close encounters and collisions between the two kinds of TNOs to occur at a higher rate than in the remaining Kuiper belt, resulting in a change of the size distributions of the two populations.
In order to test this possibility we simulated the long-term future evolution of the outer Solar System for 1 Gyr. The orbits of the outer planets, the Neptune Trojans and the Plutinos are integrated simultaneously according to the model described in the beginning of Sect. 3.
4.1 Stability of the Neptune Trojans
The stability of the Neptune Trojans orbits is an important issue on the
dynamics of the outer Solar System.
According to Dvorak et al. (2007) Trojans with low-inclined orbits are
less stable.
The stability area around L4 and L5 disappears after about 108 yr for
small inclinations, while this stability zone is still present for about
109 yr for high inclinations.
More precisely, it was concluded that there exists a region (
![]() )
of larger stability for the Neptune Trojans, although only two
have presently been found in this region (Table A.3).
)
of larger stability for the Neptune Trojans, although only two
have presently been found in this region (Table A.3).
During our numerical simulations all Trojans remained stable within the limits
shown in Fig. 3 during 1 Gyr, except
Trojan 2001QR322, which escapes
from the Lagrangian L4 point after about 112 Myr.
This last observation was somehow unexpected, since Chiang et al. (2003)
concluded that this same Neptune Trojan was stable over 1 Gyr.
This difference of behaviors is a consequence of a modification in the initial
conditions (Table A.3), obtained with new observational data.
This event is more or less in agreement with the results from
Dvorak et al. (2007), because Trojan 2001QR322 is the one with smallest
inclination (
![]() ).
Although other Trojans with identical inclination values remained stable,
we notice that Trojan 2001QR322 also has the largest libration amplitude (
).
Although other Trojans with identical inclination values remained stable,
we notice that Trojan 2001QR322 also has the largest libration amplitude (
![]() )
and its orbit is therefore more susceptible of being
disturbed by planetary perturbations.
This suggests that the stability of the Trojans is smaller for low-inclined
orbits, but also for large libration amplitudes.
)
and its orbit is therefore more susceptible of being
disturbed by planetary perturbations.
This suggests that the stability of the Trojans is smaller for low-inclined
orbits, but also for large libration amplitudes.
In Fig. 7 we plot the long-term evolution of the orbital period and the eccentricity of the Trojan 2001QR322. The behavior of this object is extremely regular, until it undergoes a sudden increment of the eccentricity, which removes it from the 1:1 mean motion resonance with Neptune. Interestingly, just after escaping the resonance, the semi-major axis of this TNO is temporarily stabilized near the 3:2 resonance with Neptune, i.e., its orbit becomes very close to the Plutinos' orbits. However, contrary to regular Plutinos, the eccentricity undergoes important chaotic variations from nearly zero up to 0.3. This regime lasts for about 300 Myr, time after which the eccentricity grows to almost 0.8. As a consequence, close encounters with the planets become possible and the TNO leaves the area near to the 3:2 mean motion resonance. Later on, the same TNO seems to be captured in a 9:2 mean motion resonance with Neptune, and stays there for about 100 Myr. Finally, the orbit is again destabilized and the eccentricity grows to extreme values, and the TNO turns into a comet.
![\begin{figure}
\par\includegraphics[scale=0.35, angle=-90]{11943f7a.ps}\\
\includegraphics[scale=0.35, angle=-90]{11943f7b.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg72.png)
|
Figure 7: Long-term evolution of the orbital period (over Neptune's orbital period) and the eccentricity of Trojan 2001QR322 for 525 Myr. Initially a Trojan, the orbit of this TNO is not stable and quits the 1:1 mean motion resonance after about 112 Myr. Then it jumps to different configurations until it becomes a comet and eventually collides with a planet or the Sun. In this simulation it is ejected from the Solar System after 525 Myr. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[scale=0.35, angle=-90]{11943f8a.ps}\\
\includegraphics[scale=0.35, angle=-90]{11943f8b.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg73.png)
|
Figure 8: Long-term evolution of the orbital period (over Neptune's orbital period) and the eccentricity for Plutino 2000FV53 for 150 Myr. Initially a Plutino, the orbit of this TNO is not stable and quits the 3:2 mean motion resonance just after about 69 Myr. Its eccentricity then increases progressively and the TNO becomes a short-period comet that eventually collides with a planet or the Sun. In this simulation it is ejected from the Solar System after 150 Myr. |
| Open with DEXTER | |
4.2 Stability of the Plutinos
The orbits of the Plutinos are believed to be stable as long as
the libration amplitudes are smaller than ![]() (Nesvorný & Roig 2000).
For larger libration widths, the planetary perturbations will
remove the TNO from its orbit in short time intervals.
The same phenomena was observed for Trojans.
(Nesvorný & Roig 2000).
For larger libration widths, the planetary perturbations will
remove the TNO from its orbit in short time intervals.
The same phenomena was observed for Trojans.
During our numerical simulations over 1 Gyr, 10 Plutinos over 98
quit their orbits (about 10%).
In Table 1 we list all these bodies, as well as their libration
width (Table A.4).
Contrary to expectations, we observe that only two Plutinos present libration
amplitudes around ![]() .
The minimum libration width observed is around
.
The minimum libration width observed is around ![]() .
A possible explanation is that because Plutinos are not alone in their orbits and,
according to Yu & Tremaine (1999) and Nesvorný et al. (2000), some Plutinos may be pushed out of the
resonance by Pluto into close encounters with Neptune.
Indeed, stability maps by Nesvorný & Roig (2000) only take into account the effect of
the four giant planets.
.
A possible explanation is that because Plutinos are not alone in their orbits and,
according to Yu & Tremaine (1999) and Nesvorný et al. (2000), some Plutinos may be pushed out of the
resonance by Pluto into close encounters with Neptune.
Indeed, stability maps by Nesvorný & Roig (2000) only take into account the effect of
the four giant planets.
Table 1: List of all unstable Plutinos during 1 Gyr.
In Fig. 8 we plot the long-term evolution of the orbital period and the eccentricity of TNO 2000FV53. The initial 3:2 resonant configuration is abandoned just after 69 Myr, time after which the eccentricity increases progressively. The TNO then undergoes close encounters with the planets, which will increase the eccentricity even more, until it can reaches very high values. The Plutino 2000FV53 then becomes a short-period comet and eventually collides with a planet or the Sun. This mechanism has already been described as the responsible for the provision of short period comets into the inner Solar System (e.g. Morbidelli 1997). In our simulation the aforementioned TNO is ejected from the Solar System after only 150 Myr.
4.3 Orbital overlap between Trojans and Plutinos
In Sect. 3.3 we saw that because of libration the Plutinos' orbits can approach the Lagrangian point L4. In order to check the extent of the orbital overlap between Neptune Trojans and Plutinos, in Fig. 9 we plotted simultaneously their orbits in a co-rotating frame with Neptune. We used the Trojan 2007VL305 for all representations, since it has the most scattered orbit, maximizing the possibility of orbital merging with a Plutino. For the Plutinos we used the same bodies as in Sect. 3.3, which correspond to the extreme cases of libration, eccentricity, and inclination. The only exception is that Plutino 1996TP66 (with the lowest libration width) has been replaced by Pluto, since a low libration amplitude does not allow the Plutino to flyby the Lagrangian points.
![\begin{figure}
\par$
\begin{array}{cc cc}
\includegraphics[width=1.7in]{11943f9a...
...43f9k.ps} &
\includegraphics[width=1.7in]{11943f9l.ps}\end{array}$
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg76.png)
|
Figure 9: Orbital evolution of the Trojan 2007VL305 (in green) and Pluto plus most of the Plutinos in Fig. 6 (in red), over 1 Gyr in the co-rotating frame of Neptune (in blue). Left panel a) shows the projection of the TNO position every 100 kyr in the orbital plane of Neptune, while right panels b) shows the projection of the TNO in the orbital plane of Neptune every 10 kyr, only when the distance to this plane is smaller than 10-3 AU. We observe that orbital overlap is favored for Plutinos with large libration amplitudes, high eccentricity values and low-inclined orbits. |
| Open with DEXTER | |
Since the TNOs are not necessarily in the same orbital plane as Neptune (especially for those having high inclination values), two types of plots have been made: one where we plotted the projection of the TNO position in the orbital plane of Neptune (Fig. 9a), and another where we plotted the projection of the TNO in the orbital plane of Neptune, only when the distance to this plane is smaller than 10-3 AU (Fig. 9b), that is, less than 150 000 km, half of the Earth-Moon distance. Indeed, most of our Trojans have small inclinations and therefore lie close to Neptune's orbital plane most of the time. As a consequence, near this plane close encounters with Plutinos are maximized.
The importance of plotting the two situations is clearly illustrated by the behavior of Pluto (Fig. 9). At first glance, looking only to the projection on Neptune's orbital plane, we observe a large zone shared by the orbits of the two kinds of TNOs, suggesting that close encounters may be a regular possibility. However, when we restrain the plot only to Neptune's orbital plane, we observe that Pluto is never on this plane when it approaches L4, preventing any close encounter with Trojans.
From the analysis of Fig. 9, we can conclude that Plutinos with large libration amplitudes (e.g. 2001KN77) maximize the chances of intercepting Trojans. This behavior was expected, as their orbits invade a large zone around the Lagrangian point L4.
On the other hand, Plutinos with small eccentricity values (
![]() ;
e.g.
2003VS2), always avoid Trojans independently of its
libration amplitude or orbital inclination, since the small eccentricity
prevents them from crossing Neptune's orbit.
According to Fig. 4, this result could also be expected, because for small
eccentricity there is no interception of the Plutino and Neptune's orbits.
;
e.g.
2003VS2), always avoid Trojans independently of its
libration amplitude or orbital inclination, since the small eccentricity
prevents them from crossing Neptune's orbit.
According to Fig. 4, this result could also be expected, because for small
eccentricity there is no interception of the Plutino and Neptune's orbits.
Finally, when comparing the behavior of Plutinos in low-inclined orbits (2001KN77 and 2002VX130) with high-inclined ones (Pluto, 2003VS2, 2005GE187 and 2005TV189) we conclude that high orbital inclination decreases the chances of close encounters because the Plutino is never close to Neptune's orbital plane when it crosses the orbit of the planet. The fact that Plutinos with small inclination share the Trojan space was expectable, as both TNOs remain close to the same orbital plane. However, Plutinos with high inclination could also approach the orbital plane of Neptune at the moment they are close to the Lagrangian points, which is not really observed.
From the above analysis (and also for the remaining 5 Trojans and 92 Plutinos), we empirically conclude that orbital overlap between Trojans and Plutinos is favored for Plutinos with large libration amplitudes, high eccentricities and small inclinations.
4.4 Collisions between Neptune Trojans and Plutinos
In order to directly check if close encounters between the Neptune Trojans and Plutinos can occur, and how often during 1 Gyr of numerical simulations, we computed the distance between all bodies after each step-size.
For that purpose we arbitrarily selected two critical distances, one
![]() AU (
AU (![]() 3000 km), for which we assume that the two
TNOs effectively collide, and a second
3000 km), for which we assume that the two
TNOs effectively collide, and a second
![]() AU
(
AU
(![]() 300 000 km), for which the two bodies do not collide but become closer
than the Earth-Moon distance.
The value of d2
is equivalent to the radius of the Hill sphere of a body
with 0.01% of Pluto's mass at the same distance from the Sun as
Neptune.
This second situation is very important, because the orbits of the TNOs
will be significantly perturbed by their mutual gravity and our model
described in
Sect. 3 will no longer apply.
We assume that TNOs undergoing such close encounters may effectively
collide, or deviate considerably from their initial orbits and quit the resonant
configuration with Neptune.
300 000 km), for which the two bodies do not collide but become closer
than the Earth-Moon distance.
The value of d2
is equivalent to the radius of the Hill sphere of a body
with 0.01% of Pluto's mass at the same distance from the Sun as
Neptune.
This second situation is very important, because the orbits of the TNOs
will be significantly perturbed by their mutual gravity and our model
described in
Sect. 3 will no longer apply.
We assume that TNOs undergoing such close encounters may effectively
collide, or deviate considerably from their initial orbits and quit the resonant
configuration with Neptune.
After 1 Gyr of simulations we did not observe any event for which the
minimal distance between two bodies,
![]() ,
is lower than d1, and
registered only 14 close encounters for which
,
is lower than d1, and
registered only 14 close encounters for which
![]() .
The results are listed in Table 2.
However, these results cannot be seen as definitive but rather as minimal
estimations of close encounters.
Indeed, since our step-size is 0.1 yr, in a circular orbit a Trojan will travel
about 0.1 AU per step-size.
As a consequence, two TNOs may effectively collide between two step-sizes
and our program is unable to detect it.
The results listed in Table 2 must then be seen as indicative
of the possibility of collisions and not as conclusive.
.
The results are listed in Table 2.
However, these results cannot be seen as definitive but rather as minimal
estimations of close encounters.
Indeed, since our step-size is 0.1 yr, in a circular orbit a Trojan will travel
about 0.1 AU per step-size.
As a consequence, two TNOs may effectively collide between two step-sizes
and our program is unable to detect it.
The results listed in Table 2 must then be seen as indicative
of the possibility of collisions and not as conclusive.
Table 2:
Close encounters between TNOs during 1 Gyr (
![]() ).
).
Assuming a constant speed for TNOs and a uniform distribution of their
relative minimal distances,
we roughly estimate the real number of close encounters
![]() to be
50 times more frequent than those listed in Table 2
(0.1 AU
/ d2 = 50).
Effective collisions (
to be
50 times more frequent than those listed in Table 2
(0.1 AU
/ d2 = 50).
Effective collisions (
![]() )
should also be more frequent in the
same proportion.
Thus, since
d1 = 10-2 d2, the results showed in Table 2 for
)
should also be more frequent in the
same proportion.
Thus, since
d1 = 10-2 d2, the results showed in Table 2 for
![]() can be seen as a rough indicator of the real number
of effective collisions occurring between Neptune Trojans and Plutinos.
can be seen as a rough indicator of the real number
of effective collisions occurring between Neptune Trojans and Plutinos.
Among the 14 ``collisions'' listed in Table 2, two were between
Trojans, two between a Trojan and a Plutino, and the remaining ten between Plutinos.
It is not a surprise that Trojans or Plutinos also undergo close
encounters between each other,
because of the libration of their orbits (Fig. 5).
The two Plutinos that encounter Trojans are 1995HM5 (e = 0.26,
![]() ,
,
![]() )
and 2002VU130 (e = 0.21,
)
and 2002VU130 (e = 0.21,
![]() ,
,
![]() ), both having small orbital
inclinations and high values for the eccentricity and libration amplitude.
This confirms our predictions from Sect. 4.3, that collisions between
Trojans and Plutinos are favored for Plutinos with
large libration amplitudes, high eccentricities and small inclinations.
), both having small orbital
inclinations and high values for the eccentricity and libration amplitude.
This confirms our predictions from Sect. 4.3, that collisions between
Trojans and Plutinos are favored for Plutinos with
large libration amplitudes, high eccentricities and small inclinations.
The fact that we count more close encounters between two Plutinos than between a Trojan and a Plutino cannot be seen as an indicator that this last kind of encounter is less frequent. Indeed, in our simulations the number of Trojans (6) is about 16 times smaller than the number of Plutinos (98). Therefore, there are roughly 16 times more chances of observing an encounter between two Plutinos. If our simulations had as much Trojans as it has Plutinos, we could then probably expect to observe about 32 Trojan-Plutino encounters. As a consequence, from the results listed in Table 2 we infer that this kind of encounter is roughly 3 times more frequent than a Plutino-Plutino one. The same applies to the encounters between Trojans. In our simulation they are also about 16 times less probable than a Trojan-Plutino encounter and we infer that they should be about 50 times more frequent than encounters between Plutinos. Only adopting a model with an identical initial number of Trojan and Plutinos would allow us to determine the exact proportions for each kind of encounter.
5 Conclusions
In this work we aimed to verify if both Plutino and Neptune Trojan populations can collide, and how frequently does that occur, and examine if there could be a connection between such possibility and the observed properties of the two (sub)populations of TNOs in question. We analyzed the available colors and absolute magnitudes of Plutinos and Neptune Trojans. The nonexistence of significant albedo diversity among the large majority of these objects is assumed, hence we interpreted absolute magnitudes as an equivalent to the object size. We find that:
- (i)
- there are no intrinsically bright (large) Plutinos at small inclinations;
- (ii)
- there is an apparent excess of blue and intrinsically faint (small) Plutinos;
- (iii)
- Neptune Trojans possess the same blue colors as Plutinos within the same (estimated) size range do.
In order to differentiate between these two scenarios we performed a numerical simulation over 1 Gyr of the future evolution of the outer Solar System composed by 5 planets, 6 Neptune Trojans, and 98 Plutinos.
By plotting simultaneously the orbits of the Neptune Trojans and Plutinos in a co-rotating frame with Neptune, it becomes clear that there is a large overlap of the orbits of the two kinds of TNOs. A more detailed analysis revealed, however, that close encounters with the Neptune Trojans are favored for Plutinos with large libration amplitudes, high eccentricities, and small inclinations. Tables A.3 and A.4 show the libration amplitudes and periods computed for all these objects.
After 1 Gyr of numerical simulations we registered 2 Trojan-Plutino, 2 Trojan-Trojan, and
10 Plutino-Plutino close approaches, i.e. less than ![]() 300 000 km.
Since we have used the currently known objects, Trojans are much less numerous
than Plutinos in our simulation. If the number of objects among each population
were similar, we roughly infer that Trojan-Plutino and Trojan-Trojan
``collisions'' should be about three and fifty times more frequent,
respectively, than Plutino-Plutino collisions.
300 000 km.
Since we have used the currently known objects, Trojans are much less numerous
than Plutinos in our simulation. If the number of objects among each population
were similar, we roughly infer that Trojan-Plutino and Trojan-Trojan
``collisions'' should be about three and fifty times more frequent,
respectively, than Plutino-Plutino collisions.
The collision rates between Neptune Trojans and between Neptune Trojans and Plutinos might explain both why we observe a small number of Neptune Trojans and why there is an absence of large Neptune Trojans: a strong collisional evolution possibly played an important role by shattering and/or depleting Neptune Trojans.
Our results also show that Plutinos in
low-inclined orbits have more chances of colliding
with Neptune Trojans. This result gives no support for a (mutual) collisional
origin of the equal-sized and equal-colored Neptune Trojans and small Plutinos,
as the latter are equally spread in inclination (see Sect. 2, scenario #1). On the other hand, it
gives plausibility to the origin of the concentration of small Plutinos with
![]() as being a consequence of
some collisional interaction with Neptune Trojans (see Sect. 2, scenario #2).
as being a consequence of
some collisional interaction with Neptune Trojans (see Sect. 2, scenario #2).
During our numerical simulations we also observed that the orbit of Trojan 2001QR322 became unstable as well as the orbits of 10 more Plutinos. The stability of Neptune Trojans appears to be enhanced for high inclination values (Dvorak et al. 2007), and also for low libration amplitudes. On the other hand, Plutinos seem to be essentially pushed out of their resonance by Pluto, in conformity with the results of Yu & Tremaine (1999) and Nesvorný et al. (2000).
This work's results were derived for objects considered as test particles (except for Pluto) and the number of ``collisions'' were extrapolated from the amount of close encounters after each integration step-size. Accurate estimations for the amount of collisions between Neptune Trojans and Plutinos can only be made with the inclusion of mutual gravitational interactions between all objects, and using a representative spatial and size distribution.
Nonetheless, our sketchy analysis indicates that under certain assumptions, which have parallel in what has been inferred for other TNOs, shattering collisions involving Neptune Trojans might have played a crucial role on the creation of the size-inclination asymmetries observed among Plutinos. We recall that we have disregarded the possibility that these asymmetries might have been created by collisional interaction with some other subpopulation of TNOs than the Neptune Trojans in view of the results obtained by Thébault & Doressoundiram (2003) and Thébault (2003). If those works come to be revealed as inadequate approximations of the relative collision rates suffered by TNOs our inference on a possible cause for the size-inclination distribution of Plutinos looses its ground. Further, if Neptune Trojans and low-inclined Plutinos do not possess identical spin rate versus size distributions, which should be distinct from the higher inclined Plutinos, then our suggestions cannot hold either (e.g. Farinella et al. 1981). More detailed studies on the interaction between Neptune Trojans and Plutinos should be attempted.
AcknowledgementsThe authors thank the referee D. Nesvorný for his comments that helped to improve this document and to M. H. M. Morais for discussions. This work was supported by the Fundação para a Ciência e a Tecnologia (Portugal).
References
- Barucci, M. A., Doressoundiram, A., Tholen, D., Fulchignoni, M., & Lazzarin, M. 1999, Icarus, 142, 476 [NASA ADS] [CrossRef]
- Bernstein, G. M., Trilling, D. E., Allen, R. L., et al. 2004, AJ, 128, 1364 [NASA ADS] [CrossRef]
- Boehnhardt, H., Delsanti, A., Barucci, A., et al. 2002, A&A, 395, 297 [NASA ADS] [EDP Sciences] [CrossRef]
- Brown, M. E., & Trujillo, C. A. 2004, AJ, 127, 2413 [NASA ADS] [CrossRef]
- Brown, M. E., Barkume, K. M., Ragozzine, D., & Schaller, E. L. 2007, Nature, 446, 294 [NASA ADS] [CrossRef]
- Canup, R. M. 2005, Science, 307, 546 [NASA ADS] [CrossRef]
- Chiang, E. I., & Lithwick, Y. 2005, ApJ, 628, 520 [NASA ADS] [CrossRef]
- Chiang, E. I., Jordan, A. B., Millis, R. L., et al. 2003, AJ, 126, 430 [NASA ADS] [CrossRef]
- de Elía, G. C., Brunini, A., & Di Sistro, R. P. 2008, A&A, submitted
- Delsanti, A. C., Boehnhardt, H., Barrera, L., et al. 2001, A&A, 380, 347 [NASA ADS] [EDP Sciences] [CrossRef]
- Delsanti, A., Hainaut, O., Jourdeuil, E., et al. 2004, A&A, 417, 1145 [NASA ADS] [EDP Sciences] [CrossRef]
- Doressoundiram, A., Peixinho, N., de Bergh, C., et al. 2002, AJ, 124, 2279 [NASA ADS] [CrossRef]
- Doressoundiram, A., Peixinho, N., Doucet, C., et al. 2005, Icarus, 174, 90 [NASA ADS] [CrossRef]
- Doressoundiram, A., Boehnhardt, H., Tegler, S. C., & Trujillo, C. 2008, Color Properties and Trends of the Transneptunian Objects (The Solar System Beyond Neptune), 91
- Dvorak, R., Schwarz, R., Süli, Á., & Kotoulas, T. 2007, MNRAS, 382, 1324 [NASA ADS]
- Farinella, P., Paolicchi, P., & Zappala, V. 1981, A&A, 104, 159 [NASA ADS]
- Gil-Hutton, R. 2002, Planet. Space Sci., 50, 57 [NASA ADS] [CrossRef]
- Gil-Hutton, R., & Licandro, J. 2001, Icarus, 152, 246 [NASA ADS] [CrossRef]
- Giuliatti Winter, S. M., Winter, O. C., & Mourão, D. C. 2007, Physica D Nonlinear Phenomena, 225, 112 [NASA ADS] [CrossRef]
- Grundy, W. M. 2009, Icarus, 199, 560 [NASA ADS] [CrossRef]
- Hainaut, O. R., & Delsanti, A. C. 2002, A&A, 389, 641 [NASA ADS] [EDP Sciences] [CrossRef]
- Jewitt, D. C., & Luu, J. X. 2001, AJ, 122, 2099 [NASA ADS] [CrossRef]
- Kenyon, S. J., Bromley, B. C., O'Brien, D. P., & Davis, D. R. 2008, Formation and Collisional Evolution of Kuiper Belt Objects (The Solar System Beyond Neptune), 293
- Kolmogorov, A. N. 1933, Giornale dell' Istituto Italiano degli Attuari, 4, 83 (in Italian)
- Kortenkamp, S. J., Malhotra, R., & Michtchenko, T. 2004, Icarus, 167, 347 [NASA ADS] [CrossRef]
- Laskar, J., & Robutel, P. 2001, Celest. Mech. Dyn. Astron., 80, 39 [NASA ADS] [CrossRef]
- Leinhardt, Z. M., Stewart, S. T., & Schultz, P. H. 2008, Physical Effects of Collisions in the Kuiper Belt ed. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, & A. Morbidelli, 195
- Luu, J., & Jewitt, D. 1996, AJ, 112, 2310 [NASA ADS] [CrossRef]
- Lykawka, P. S., & Mukai, T. 2007, Icarus, 189, 213 [NASA ADS] [CrossRef]
- Malhotra, R. 1995, AJ, 110, 420 [NASA ADS] [CrossRef]
- Morbidelli, A. 1997, Icarus, 127, 1 [NASA ADS] [CrossRef]
- Murray, C. D., & Dernott, S. F. 1999, Solar System dynamics (Cambridge University press)
- Nesvorný, D., & Dones, L. 2002, Icarus, 160, 271 [NASA ADS] [CrossRef]
- Nesvorný, D., & Roig, F. 2000, Icarus, 148, 282 [NASA ADS] [CrossRef]
- Nesvorný, D., & Vokrouhlický, D. 2009, AJ, 137, 5003 [NASA ADS] [CrossRef]
- Nesvorný, D., Roig, F., & Ferraz-Mello, S. 2000, AJ, 119, 953 [NASA ADS] [CrossRef]
- Pan, M., & Sari, R. 2005, Icarus, 173, 342 [NASA ADS] [CrossRef]
- Peixinho, N., Boehnhardt, H., Belskaya, I., et al. 2004, Icarus, 170, 153 [NASA ADS] [CrossRef]
- Press, W., Teukolsky, S., Vetterling, W., & Flannery, B. 1992, Numerical Recipes in FORTRAN (UK: Cambridge University Press)
- Romanishin, W., & Tegler, S. C. 1999, Nature, 398, 129 [NASA ADS] [CrossRef]
- Russell, H. N. 1916, ApJ, 43, 173 [NASA ADS] [CrossRef]
- Sheppard, S. S., & Trujillo, C. A. 2006, Science, 313, 511 [NASA ADS] [CrossRef]
- Smirnov, N. V. 1939, Bull. Moscow Univ., 2, 3 (in Russian)
- Stern, S. A. 2009, Icarus, 199, 571 [NASA ADS] [CrossRef]
- Stern, S. A., Weaver, H. A., Steffl, A. J., et al. 2006, Nature, 439, 946 [NASA ADS] [CrossRef]
- Tegler, S. C., & Romanishin, W. 1998, Nature, 392, 49 [NASA ADS] [CrossRef]
- Tegler, S. C., & Romanishin, W. 2000, Nature, 407, 979 [NASA ADS] [CrossRef]
- Tegler, S. C., & Romanishin, W. 2003, Icarus, 161, 181 [NASA ADS] [CrossRef]
- Tegler, S. C., Romanishin, W., & Consolmagno, G. J. 2003a, ApJ, 599, L49 [NASA ADS] [CrossRef]
- Tegler, S. C., Romanishin, W., & Consolmagno, S. J. 2003b, ApJ, 599, L49 [NASA ADS] [CrossRef]
- Thébault, P. 2003, Earth Moon and Planets, 92, 233 [NASA ADS] [CrossRef]
- Thébault, P., & Doressoundiram, A. 2003, Icarus, 162, 27 [NASA ADS] [CrossRef]
- Yu, Q., & Tremaine, S. 1999, AJ, 118, 1873 [NASA ADS] [CrossRef]
Online Material
Appendix A: Additional tables
Table A.1: Data relative to Trojans and Plutinos.
Table A.2: Orbital data for the Giant Planets and Pluto at JD 2 454 200.50 (http://ssd.jpl.nasa.gov/horizons.cgi).
Table A.3: Orbital data for the Neptune Trojans at JD 2 454 200.50 (ftp://ftp.lowell.edu/pub/elgb/astorb.html).
Table A.4: Orbital data for the Plutinos at JD 2 454 200.50 (ftp://ftp.lowell.edu/pub/elgb/astorb.html).
Footnotes
- ... collisions
![[*]](/icons/foot_motif.png)
- Appendix A is olny available in electronic form at http://www.aanda.org
- ... known
![[*]](/icons/foot_motif.png)
- See http://cfa-www.harvard.edu/iau/lists/NeptuneTrojans.html
- ... blue
![[*]](/icons/foot_motif.png)
- For simplicity throughout this work we will call an object
blue
when B-R<1.5 and red when
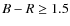 .
The B-R color of the
Sun is 1.03.
.
The B-R color of the
Sun is 1.03.
All Tables
Table 1: List of all unstable Plutinos during 1 Gyr.
Table 2:
Close encounters between TNOs during 1 Gyr (
![]() ).
).
Table A.1: Data relative to Trojans and Plutinos.
Table A.2: Orbital data for the Giant Planets and Pluto at JD 2 454 200.50 (http://ssd.jpl.nasa.gov/horizons.cgi).
Table A.3: Orbital data for the Neptune Trojans at JD 2 454 200.50 (ftp://ftp.lowell.edu/pub/elgb/astorb.html).
Table A.4: Orbital data for the Plutinos at JD 2 454 200.50 (ftp://ftp.lowell.edu/pub/elgb/astorb.html).
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11943f1.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg17.png)
|
Figure 1: Orbital inclination vs. eccentricity, estimated size, and color of Neptune Trojans and Plutinos for which those properties have been measured. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11943f2.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg27.png)
|
Figure 2:
Cumulative distribution function of absolute magnitudes HR for Plutinos above and below |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par$
\begin{array}{cc}
\includegraphics[scale=0.25, angle=0]{119...
...} &
\includegraphics[scale=0.25, angle=0]{11943f3f.ps}\end{array}$
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg56.png)
|
Figure 3: Orbital evolution of the Neptune Trojans (in green) listed in Table A.3 over 100 Myr in the co-rotating frame of Neptune (in blue). Each panel shows the projection of the TNO position every 10 kyr in the orbital plane of Neptune. x and y are spatial coordinates centered on the star and rotating with Neptune, normalized by the Neptune-Sun distance. All Trojans orbit around the Lagrangian point L4 and execute tadpole-type orbits. More scattered orbits correspond to higher values of the eccentricity and inclination, while distance to the L4 point depend on the libration amplitude. |
| Open with DEXTER | |
| In the text | |
| |
Figure 4: Typical path of a Plutino (dotted line) in the rotating frame of Neptune (full line) for different eccentricity values (e = 0.1, 0.2 and 0.3). Only high eccentricity values (e > 0.2) allow the Plutino to cross the orbit of Neptune. Due to the 3:2 mean motion resonance the trajectories are repeated every two orbits of the TNO around the Sun. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm]{11943f5.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg66.png)
|
Figure 5: Libration motion of the orbit of a Plutino. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par$
\begin{array}{cc}
\includegraphics[scale=0.25, angle=0]{119...
...s} &
\includegraphics[scale=0.25, angle=0]{11943f6f.ps}\end{array}$
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg69.png)
|
Figure 6:
Orbital evolution of some Plutinos (in red) taken from
Table A.4 over 100 Myr in the co-rotating frame of Neptune (in
blue). Each panel shows the projection of the TNO position every 10 kyr in
the orbital plane of Neptune. x and y are
spatial coordinates centered on the star and rotating with Neptune, normalized
by the Neptune-Sun distance.
We have chosen the most representative cases, namely, Plutino 1996TP66, with
the lowest libration amplitude (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.35, angle=-90]{11943f7a.ps}\\
\includegraphics[scale=0.35, angle=-90]{11943f7b.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg72.png)
|
Figure 7: Long-term evolution of the orbital period (over Neptune's orbital period) and the eccentricity of Trojan 2001QR322 for 525 Myr. Initially a Trojan, the orbit of this TNO is not stable and quits the 1:1 mean motion resonance after about 112 Myr. Then it jumps to different configurations until it becomes a comet and eventually collides with a planet or the Sun. In this simulation it is ejected from the Solar System after 525 Myr. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.35, angle=-90]{11943f8a.ps}\\
\includegraphics[scale=0.35, angle=-90]{11943f8b.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg73.png)
|
Figure 8: Long-term evolution of the orbital period (over Neptune's orbital period) and the eccentricity for Plutino 2000FV53 for 150 Myr. Initially a Plutino, the orbit of this TNO is not stable and quits the 3:2 mean motion resonance just after about 69 Myr. Its eccentricity then increases progressively and the TNO becomes a short-period comet that eventually collides with a planet or the Sun. In this simulation it is ejected from the Solar System after 150 Myr. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par$
\begin{array}{cc cc}
\includegraphics[width=1.7in]{11943f9a...
...43f9k.ps} &
\includegraphics[width=1.7in]{11943f9l.ps}\end{array}$
\end{figure}](/articles/aa/full_html/2009/47/aa11943-09/Timg76.png)
|
Figure 9: Orbital evolution of the Trojan 2007VL305 (in green) and Pluto plus most of the Plutinos in Fig. 6 (in red), over 1 Gyr in the co-rotating frame of Neptune (in blue). Left panel a) shows the projection of the TNO position every 100 kyr in the orbital plane of Neptune, while right panels b) shows the projection of the TNO in the orbital plane of Neptune every 10 kyr, only when the distance to this plane is smaller than 10-3 AU. We observe that orbital overlap is favored for Plutinos with large libration amplitudes, high eccentricity values and low-inclined orbits. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.