A hot white dwarf luminosity function from the Sloan Digital Sky Survey

J. Krzesinski; S. J. Kleinman; A. Nitta; S. Hügelmeyer; S. Dreizler; J. Liebert; H. Harris

doi:10.1051/0004-6361/200912094

Free Access

Issue		A&A Volume 508, Number 1, December II 2009


Page(s)		339 - 344
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/200912094
Published online		01 October 2009

A&A 508, 339-344 (2009)

A hot white dwarf luminosity function from the Sloan Digital Sky Survey

J. Krzesinski^1,2 - S. J. Kleinman³ - A. Nitta³ - S. Hügelmeyer⁴ - S. Dreizler⁴ - J. Liebert⁵ - H. Harris⁶

1 - Mt. Suhora Observatory, Cracow Pedagogical University, ul. Podchorazych 2, 30-084 Cracow, Poland
2 - Apache Point Observatory, PO Box 59, Sunspot, NM 88349, USA
3 - Gemini Observatory, 670 N. A'Ohoku Place, Hilo, HI 96720, USA
4 - Institut für Astrophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
5 - Steward Observatory, University of Arizona, Tucson, AZ 85726, USA
6 - US Naval Observatory, PO Box 1149, Flagstaff, AZ 86002-1149, USA

Received 17 March 2009 / Accepted 9 September 2009

Abstract
Aims. We present a hot white dwarf (WD) luminosity function (LF) using data taken from the Sloan Digital Sky Survey (SDSS) Data Release 4. We present and discuss a combined LF, along with separate DA and non-DA as LFs. We explore the completeness of our LFs and interpret a sudden drop in the non-DA LF near 2 $M_{\rm bol}$ as a transition of the non-DA WD atmosphere into the DA one during WD evolution. Our LF extends roughly between $-0.5 < M_{\rm bol} < 7$ or equivalently, ${\sim} 120~000~{\rm K} > T_{\rm eff} > {\sim}25~000$ K. Our LF should now be useful for estimates of recent star formation and for studies of neutrino and other potential particle emission losses in hot WDs.
Methods. To create a sample whose completeness can be characterized fully, we used stars whose spectra were obtained via the SDSS's ``hot standard'' target selection criteria. The hot standard stars were purposefully targeted to a high level of completeness by the SDSS for calibration purposes. We are fortunate that many of them are hot white dwarfs stars. We further limited the sample to stars with fitted temperatures exceeding 23 500 K and $\log{g} > 7.0$ . We determined stellar distances for our sample based on their absolute SDSS g filter magnitudes, derived from WD stellar atmosphere model fits to the SDSS stellar spectra.
Results. We compared our LF with those of other researchers where overlap occurs; however, our LFs are unique in their extension to the most luminous/hottest WDs. The cool end of our LF connects with the hot end of previously determined SDSS WD LFs and agreement here is quite good. It is also good with previous non-SDSS WD LFs. We note distinct differences between the DA and non-DA LFs and discuss the reliability of the DA LF at its hot end. We have extended the range of luminosities covered in the most recent WD LFs. The SDSS sample is understood quite well and its exploration should contribute to a number of new insights into early white dwarf evolution.

Key words: stars: luminosity function, mass function - white dwarfs

1 Introduction

The luminosity function (LF) and space density of WDs provide constraints on the local star formation rate and history of the Galactic disk in the Solar neighborhood. They can also be used to help determine the role of weakly interacting particles in WD cooling (Irsen et al. 2008) and thus their ages. A large WD sample of known completeness is required to determine a precise LF to address these questions. Luckily, the Sloan Digital Sky Survey (SDSS) (Pier 2003; Gunn et al. 2006; Stoughton et al. 2002; Gunn et al. 1998; Tucker et al. 2006; York et al. 2000) provides the perfect sample for this effort. Although primarily designed as an extra-Galactic survey, the SDSS is an extremely rich source of stellar (and in particular, white dwarf) spectra. Eisenstein et al. (2006a) published a catalog of spectroscopically confirmed white dwarf stars from the SDSS Data Release 4 (DR4: Adelman-McCarthy et al. 2006). Their catalog contained 9316 WDs, nearly 3.6 times the number of WDs found in the first SDSS WD catalog (Kleinman et al. 2004) based on DR1 (Abazajian et al. 2003) data, consistent with the ratio of spectroscopic sky coverage (4783 / 1360 square degrees) in DR4 vs. DR1.

Harris et al. (2006) have constructed a reduced proper-motion based WD LF using the photometric sample from SDSS DR3 (Abazajian et al. 2005) and proper motions from Monet et al. (2003). The large data set available from SDSS enabled them to sample the LF within a magnitude range of ${\sim}7<M_{\rm bol}<14$ using 0.5 mag bins, with each bin containing hundreds of stars for quite excellent statistics. Hu et al. (2007) also calculated a DA WD LF based on the much smaller SDSS DR1 WD sample, but extending to $M_{\rm bol}=4$ at its blue end. These LFs compare well with that of Liebert et al. (2005), which is based on DAs from the Palomar Green survey (Green et al. 1986). Most recently, DeGennaro et al. (2008) have presented a DA WD LF also based on SDSS DR4 data, using statistical arguments and a comparison to the Harris et al. (2006) LF to estimate sample completeness. The agreements and disagreements between the two LFs are fairly well understood, although their cutoff at $M_{\rm bol} \sim 6$ offers only a small chance of comparision to our own LF, which extends to much hotter stars. Prior to the flurry of new SDSS-based WD LFs, WD LFs were constructed by for example Flemming et al. (1986) and Vennes et al. (2002). There were also attempts to estimate the local non-DA WDs space density dating back to 1985 (Wesemael et al. 1985). None, however, extend below $M_{\rm bol}=4$ mag, while our new LF extends to below $M_{\rm bol}=-0.5$ mag.

Traditionally, distances in WD LFs have been calculated using a statistical proper motion method (e.g. Oswalt et al. 1996; Liebert et al. 1988; Evans 1992, and others). For our relatively bright, therefore distant stars, this approach is less likely to work, since many are simply too far away to have measurable proper motions. We therefore calculated bolometric magnitudes derived from fitting theoretical atmosphere model to the SDSS spectra and compared them to the observed SDSS g filter (SDSS filters: Fukugita et al. 1996) magnitudes to obtain distances to each of our objects. Unlike all the other WDLFs, ours is based solely on spectroscopically-confirmed WDs from the SDSS spectroscopic sample and covers a $M_{\rm bol}$ range from -0.75-7.0.

2 Our hot white dwarf sample

The SDSS ``hot_std'' category targets bright (g<19), isolated, hot stars for calibration purposes. In short, the following criteria define the hot_stds, where the subscript $\circ$ indicates a fully-dereddened magnitude:

g > 14
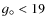
$g_\circ < 19$
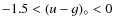
$-1.5 < (u-g)_\circ < 0$
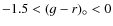$-1.5 < (g-r)_\circ < 0$ .

Because of the relative rarity of these objects in the sky and their importance in calibration, the SDSS gave hot standard stars the highest priority in assigning fibers (Blanton et al. 2003). In theory, then, WDs within the color selection range of the hot_std targets could be 100% complete within the SDSS database. However, because the hot_stds are used for calibration some fairly severe additional non-photometric requirements are placed on them in order that the photometry and spectroscopy can be completely trusted. These additional constraints require the targets to have no interpolated pixels and to be unblended and far from CCD edges. Eisenstein et al. (2006a) estimated that these additional constraints lower the spectroscopic completeness of the photometrically-specified sample to below 77%, contrary to the earlier statements of Krzesinski et al. (2004). Nonetheless, the hot_stds are still among the most complete of all stars spectroscopically observed by the SDSS and their incompleteness is calculable (see Sect. 3.2). Since the Eisenstein et al. (2006a) WD catalog does not state which of their WDs were targeted as hot_stds, we supplemented their catalog with SDSS DR4 database queries for all objects targeted as hot_stds.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12094fg1.eps} \end{figure}$	Figure 1: The photometric $(g-r)_\circ$ and $(u-g)_\circ$ (small and large symbols respectively) vs. fit temperatures for our hot_std sub-sample of the DR4 WD stars from Eisenstein et al. (2006a). Only DA (solid squares) and DB (open circles) WDs with $T_{\rm eff} > 20~000$ K are shown. The dashed line shows our additional $T_{\rm eff}$ sample cut at 23 500 K.
Open with DEXTER

Figure 1 is a plot of hot DAs and DBs from Eisenstein et al. (2006a) along with the hot_std $(u-g)_\circ$ and $(g-r)_\circ$ color cuts. The $(u-g)_\circ <0.0$ color selection ends up cutting out DAs at cooler temperatures than the DBs. Objects above the horizontal line (some DAs cooler than 23 500 K) are not targeted as hot_std stars, thereby introducing some incompleteness in our sample below that temperature. We therefore imposed an additional cut on our sample of $T_{\rm eff}>23~500$ (the vertical line in Fig. 1), so the temperature selection of DAs and non-DAs in our sample is unaffected by the DAs higher (u-g) values.

3 Luminosity function

Once our white dwarf sample was well-defined, we determined their distances and absolute bolometric magnitudes. Next, we calculated the sample's completeness and volume corrections before forming our final luminosity functions.

3.1 The atmospheric models and distances

We used the Eisenstein et al. (2006a) fit $T_{\rm eff}$ and $\log{g}$ parameters for the pure DA and DB stars in our sample. Unfortunately, Eisenstein et al. (2006a) do not include any predicted absolute photometric magnitudes in their output, so we needed additional work to convert the $T_{\rm eff}$ and $\log{g}$ fits into an absolute magnitude which we could use to calculate distances. Bergeron (2001, private communication) calculated a grid of $\log{g}$ , $T_{\rm eff}$ vs. $M_{\rm bol}$ and absolute SDSS u, g, r, i, z filters magnitudes for pure DA and DB WDs. Eisenstein et al. (2006a) demonstrated that their models (from Detlev Koester; published in Finley et al. 1997) are in good agreement with Bergeron's, so we can use the $T_{\rm eff}$ and $\log{g}$ fits from their Koester model fits to obtain absolute SDSS filter magnitudes from the Bergeron grid. We used these absolute magnitudes to compare with the observed magnitudes and obtain distances to all our objects.

For the non DA/DB stars, we used other spectral models and fits accordingly: Rauch & Deetjen (2003) non-LTE H+He models for the DAOs and Hügelmeyer et al. (2006) models for DO and PG1159 spectra. We used stellar radii taken from evolutionary models of Wood (1995) with thick and thin hydrogen layers for DAO and DO WDs and Bloecker (1995), Schoenberner (1983) and Wood & Faulkner (1986) models for PG1159 stars. DAB (3 stars) and DBA (1 star) WDs were treated in the same way as DA and DB WDs, respectively. For magnetic or binary DAs and DBs the fit parameters were taken from the Eisenstein et al. (2006a) DR4 WD catalog; for binary DOs, from Hügelmeyer et al. (2006). Finally we calculated two LFs, one for all WDs including magnetic and binary WDs, and one without them. The LFs with and without the magnetic and binary WDs are not significantly different from each other, so we therefore continue with these objects included in our further analysis.

In general, an absolute SDSS filter magnitude $M_{\rm flt}$ can be obtained by implementing the modified Girardi et al. (2002) formula (Eq. (2)):

$\begin{eqnarray*}M_{\rm flt} &=&~ 2.5 \log\left(3631\times10^{-23}\right) +2.5 ... ...bda )~{\rm d}\lambda \right) \\ &+&~ {\rm zeropoint}({\rm flt}) \end{eqnarray*}$

where:

flt	one of u, g, r, i, z SDSS filters,
$3631 \times 10^{-23}$ [erg/cm²/s/cm]	AB system zero magnitude for
	a SDSS filter
	Oke & Gunn (1983),
c	speed of light in cm/s,
A2 cm	Angstrom to cm conversion,
$pc=3.0857 \times 10^{18}\rm ~[cm]$	1 parsec,
$R_{\odot}$	solar radius in cm,
$\rm Flux\cdot \pi~[erg/cm^2/s/cm]$	flux density from the model,
Filter $(\lambda)$	SDSS filter transmission within
	the wavelength range $\lambda_{1}$ - $\lambda_{2}$ ,
$\lambda ~[\AA]$	wavelength in Angstroms,
$R_{\star}~[R_{\odot}]$	stellar radius taken from
	evolutionary models
zeropoint(flt) [mag]	SDSS photometric zero point.

Here zeropoint(u) = -0.04, zeropoint(g) = zeropoint(r) = 0.00, zeropoint(i) = 0.015 and zeropoint(z) = 0.03. The SDSS magnitude system (photometric system: Hogg 2001; Ivezic et al. 2004; Smith et al. 2002) is close to being on the AB system Oke & Gunn (1983), but not quite, so the above zero points are needed (Abazajian et al. 2004; Eisenstein et al. 2006b).

We used the Girardi et al. (2002) equations, above, to obtain absolute SDSS g filter magnitudes for all WDs in our sample. For most of them, we calculated absolute bolometric magnitudes (by extending the wavelength range in the equation from 0 to infinity). For some of the DOs and PG1159 stars in the sample, however, we do not have complete enough models to estimate a total stellar flux, so in those cases we used the standard equation, below, to obtain absolute bolometric magnitudes:

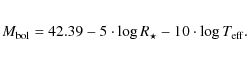
$\begin{eqnarray*}M_{\rm bol} = 42.39 - 5\cdot \log R_{\star}-10\cdot \log T_{\rm eff}. \end{eqnarray*}$

We compared results using this equation with the absolute magnitudes determined by our model grids and found the answers to be in good agreement ( $\sim$ 0.3 mag on average).

We do not have models for the hottest DBs in our sample those between about 30 000 K and 42 500 K, the so-called ``DB gap'' region (Eisenstein et al. 2006a,b). For these objects, therefore, we extended the Bergeron grid using the DO models from Hügelmeyer et al. (2006) as a guide. However, this procedure likely introduces magnitude errors of approximately 0.5 mag.

Finally, we had to apply a reddening correction to our calculated absolute and observed magnitudes in order to obtain distances to our objects. Since we don't know how much of the measured interstellar reddening is really between us and our individual target stars, we employed the same iterative reddening approach as described in Harris et al. (2006), assuming zero reddening at 100 pc and full reddening at 250 pc.

3.2 Completeness

To normalize our LF, we employed the standard ( $1/V_{\max}$ ) method as introduced by Schmidt (1998). The quantity $V_{\max}$ describes the maximum volume in which a star can contribute to the LF:

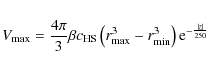
$\begin{eqnarray*}V_{\max}= \frac{4\pi}{3} \beta c_{\rm HS} \left( r_{\max}^3 - r_{\min}^3 \right) {\rm e}^{-\frac{\vert z \vert}{250}} \end{eqnarray*}$

where, $\beta$ is the ratio of the SDSS DR4 spectral observation coverage of the sky (4783 degrees; Adelman-McCarthy et al. 2006) to the total sky surface. We accommodate the hot_std incompleteness by introducing the $c_{\rm HS}$ factor. Finally, the e $^{-\frac{\vert z \vert}{250}}$ factor takes into account the exponentially decreasing WD density with distance z (in parsecs) from the Galactic plane, assuming a Galactic scale height of 250 pc as in Harris et al. (2006).

Table 1: SDSS DR4 spectroscopic hot_std sample incompleteness map.

The $c_{\rm HS}$ incompleteness factor is not a constant number for all WDs in our sampled due to the additional isolation criteria placed on hot_stds. The hot_std incompleteness is a function of both Galactic latitude, b and object brightness, g. At lower b, the increased number of stars will make the hot_std unblended criteria harder to meet, thereby increasing the incompleteness. Similarly, brighter objects cover more pixels on the CCD, and thus are more likely to be thrown out of the hot_std category due to the blending or edge criteria. Eisenstein et al. (2006a) estimates that hot_std incompleteness varies from 0.55 to 0.60 for 30 < b < 40 and from 0.60 to 0.63 when $40 \leq b < 70$ , then from 0.40 to 0.55 for g magnitudes 15 < g< 17, and from 0.55 to 0.63 for $17 \leq g < 19.5$ mag.

Because we need to know the incompleteness as both b and g vary, we queried the SDSS database to obtain a full two-dimensional incompleteness map. We formed a $6\times18$ grid with g varying from 14-19 in 1 mag bins and b varying from -90 to +90 in 10 degree bins. Our method was to determine the ratio of hot_stds observed spectroscopically to the total number of potential hot_stds that passed the photometric criteria, but not the isolation requirements for each of our (g, b) cells. The SDSS software pipeline separates blended objects into a parent (deblended) object and its constituent children. We allowed the parent object in our search, but not the children. We also removed all moving objects (e.g., asteroids) and objects too close to the edge of the CCD chips to make sure that the photometry was properly determined. Table 1 shows the results of our $c_{\rm HS}(g,b)$ calculations. Values in cells are given in $[\%]$ and ``-'' denotes cells with no spectroscopic hot_stds in them. Magnitude bins are 1.0 mag wide in g starting from given magnitudes in the first column. Latitude bins are 10 degrees wide extending from the values in the first row.

Altogether we found 5778 photometric (PH) hot_standards and 1984 spectroscopically (SP) observed objects formally classified by the pipeline as a hot_std. The incompleteness factors of spectroscopic hot_stds for each cell can be calculated as:

$\begin{eqnarray*}c_{{\rm HS}_{i}} = \frac{SP_{i}}{PH_{i}}\cdot {\rm footprint} \cdot 100\% \end{eqnarray*}$

where footprint ( $\sim$ 1.39) is the photometric to spectroscopic coverage ratio of the sky surface in SDSS DR4. A detailed map of hot_std incompleteness for SDSS survey is provided in Table 1. The dash signs in the table denotes cells where no spectroscopic hot_stds were found, which does not necessarily mean that there are no photometric hot_stds in those bins.

3.3 Results

Using the incompleteness map given in Table 1, we calculated our LF for $M_{\rm bol}$ bins of 0.5 mag width. The resulting luminosity function is presented in Fig. 2 along with that of Harris et al. (2006). It covers an absolute bolometric magnitude range between -0.75 and 7.25 and provides some overlap with the cooler LF of Harris et al. (2006).

To determine exactly which bins were affected by our temperature cut, we calculated the LF for two different cutoff temperatures, our nominal 23 500 K and one at 20 000 K, as discussed in Sect. 2. The two LFs converge at $M_{\rm bol} \sim 6.75$ , which we therefore take as the coolest complete bin in our LF. There appears to be general agreement with Harris et al. (2006), although there aren't any complete bins in common.

Note the plateau seen in our LF between $M_{\rm bol} \sim 0.5 {-} 3.75$ ( $T_{\rm eff} \sim 50~000{-} 100~000$ K). Eisenstein et al. (2006a) point out a systematic overestimation of $T_{\rm eff}$ in their model fits for the hottest WDs, starting for DAs around $T_{\rm eff}\sim30~000$ K. At $T_{\rm eff}\sim50~000$ K, approximately $M_{\rm bol}=4.0$ , this overestimate is a roughly 10% effect. Furthermore, at these temperatures, non-LTE (NLTE) effects become important whereas the Eisenstein et al. (2006a) fits were based only on LTE models. To correct for these two mis-estimates, we applied a parabolic temperature correction determined by the Eisenstein et al. (2006a) comparisons to existing literature fits and NLTE corrections from Napiwotzki et al. (1999). The resulting LF is shown in Fig. 3. As expected, the cool end of this corrected LF remains largely the same, but the hot end changes considerably, the parabolic temperature adjustments having the biggest effect.

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg2.eps} \end{figure}$

Figure 2:

Our primary WD LFs. The solid line includes all stars in our sample while the dotted line excludes the more uncertain magnetic and binary WDs. The two dashed lines show the effect of different temperature cuts: our preferred cut at 23 500 K and one cut further at 20 000 K to provide more overlap with the Harris et al. (2006) sample, shown as the solid line with open circles. The top axis shows the approximate effective temperature in kilo-Kelvin corresponding to plotted x-axis, $M_{\rm bol}$ .

Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg3.eps} \end{figure}$	Figure 3: The same as Fig. 2 but with $T_{\rm eff}$ and NLTE corrections applied.
Open with DEXTER

Table 2: Number of all types of WDs per magnitude bin.

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg4.eps} \end{figure}$	Figure 4: Our WD LF as in Fig. 3, but with 1.0 mag bins.
Open with DEXTER

With these corrections included, 41 stars' temperatures dropped to below our 23 500 K cutoff. Table 2 lists the LF bin values both before and after these corrections (as shown in Figs. 2 and 3). Columns 2 and 3 list the number of DAs in each bin before and after the corrections. Since the corrections to the DAO, DB, DO, and PG 1159 stars were not needed, they are listed separately in Cols. 4 through 7, respectively. Finally, Col. 8 lists the total number of WDs of all types in each bin.

As Fig. 3 shows, the plateau seen in Fig. 2 narrows, but remains even after the NLTE and fit temperature corrections were applied. Figure 4 repeats the LFs shown in Fig. 2, but with 1.0 mag bins to increase the signal in each bin; again the plateau remains. While there are still problems with the hottest DA WDs temperature determination (see conclusions), a glance at Table 2 shows that the DAs start appearing at $M_{\rm bol}\sim2.0$ , precisely where our plateau begins. It appears we are seeing the emergence of the non-DAs into the LF.

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg5.eps} \end{figure}$

Figure 5:

DA (solid circles) and non-DA (open squares) LFs plotted with the PG survey DA LF (open circles) of Liebert et al. (2005). The magnitude bin width is 1.0 and the bins are centered on integer magnitudes. Thinner line right below SDSS DA LF is the DA LF without magnetic DAs and binary DA+M systems. In case of non-DA LF removing magnetic and binary DB+M systems from the WD sample affects the LF near $M_{\rm bol} = 7$ and the rest of the thin line overlaps with the thick one. The top axis shows the approximate effective temperature in kilo-Kelvin corresponding to plotted x-axis, $M_{\rm bol}$ .

Open with DEXTER

4 DA and non-DA luminosity functions

Table 2 shows that the hot end of our LF is made up entirely of non-DA WDs. We therefore divided our main LF into two LFs, one with only DAs and one for non-DAs. We kept the 23 500 K $T_{\rm eff}$ cutoff for the DA-only LF, but were able to decrease the temperature cutoff to 16 000 K for the non-DA LF. Using bins of 1.0 mag centered on half integer and integer magnitudes, we plot the resulting new LFs in Figs. 5 and 6, respectively. We also compare to the DA LF of Liebert et al. (2005), after converting it from M_V into $M_{\rm bol}$ space densities.

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg6.eps} \end{figure}$	Figure 6: The same as in Fig. 5 but bins are centered on half integer magnitudes. In both plots, we can see the appearance of the first DAs affect a dip in the non-DA LF.
Open with DEXTER

The first thing to notice is that our new DA LF and that of Liebert et al. (2005) are in very good agreement. The hot end of the non-DA LF has an interesting shape, with a sudden drop in the LF near $M_{\rm bol}=2$ . $M_{\rm bol}=2$ , however, this is precisely where the DAs start appearing. If we follow the initial slope of the non-DA LF and extend it before the drop-off to $M_{\rm bol}=2$ , it leads directly to the start of the DA LF. Thus, it seems this drop off is simply due to the appearance of DAs. These luminosity functions represent the first time this separation of the WD population has been seen. Table 3 provides the numbers behind the separate DA and non-DA LFs as shown in Fig. 6. The last DA and non-DA bins (marked with asterisks) are incomplete due to our temperature cutoffs at 23 500 K and 16 000 K respectively.

Table 3: DA and non-DA WD distribution per magnitude bin.

5 Conclusions

As shown, our WD LF agrees very well with previous efforts, but extends to significantly hotter stars and shows clear emergence of DAs and non-DAs in the general WD cooling curve. However, due to the problems with hot DA WD temperature determination the DA and non-DA space densities cannot be compared directly at the hot end of these LFs. Although the systematic DA $T_{\rm eff}$ overestimation of Eisenstein et al. (2006a) WD catalog data has been corrected and the pure hydrogen NLTE vectors have been applied, yet there are more severe problems affecting the hottest DA WD temperature and $\log{g}$ determination. These include lower spectra quality of the fainter HSs or the presence of metals in the hot DA WD atmosphere visible as the onset of the Balmer line problem (Vennes 1999) in the spectra. Barstow et al. (2003) and Vennes et al. (2005) investigated the effect of metallicity influence on the hot DA WD (above 50 000 K) temperature determination. They have shown that, due to heavy elements present in the DA atmosphere, in some cases the hot DA temperatures can be overestimated by at least $20\%$ , which translates to $\sim$ 1 $M_{\rm bol}$ more luminous WDs. In such circumstances the space density of the DA WDs seems reasonably well established for $M_{\rm bol} > 3$ mag and is not certain for the more luminous part of the DA LF. In that regard, the non-DA LF is likely the most reliable out of both our LFs. It covers -0.5 to 9.5 bolometric magnitude range and shows the drop off near $M_{\rm bol}=2$ which we interpret as the non-DA to DA atmosphere conversion (Figs. 5, 6). We can see that in the DB gap temperature range, 30 000-43 000 K ( $M_{\rm bol}{:}~ 5 {-} 6$ ), our non-DA LF has only a slight space density decrease, suggesting the number of recently discovered hot DB stars (Eisenstein et al. 2006a,b) has nearly, if not completely, filled the ``gap''.

Note that the error bars presented in the figures are formal errors, calculated as a sum of $1/(V_{\max})^2$ for each luminosity bin, and they do not take observed or absolute bolometric magnitude error determinations into account. In fact the $V_{\max}$ method underestimates LF error bars by a factor of 10 (Geijo et al. 2006) near the 9-7 $M_{\rm bol}$ magnitude range where our LF has its cool end, and in that regard the agreement between our LF and others can have larger tolerance. In their theoretical work Geijo et al. (2006) did not make any LF error estimations for the hotter regions our LF covers, so we cannot determine the error quality in that range, but we can expect the ones we present are also underestimated.

In short, we have calculated a new WD LF with an extended range of luminosities based on the well-understood and explored SDSS WD data set. However, to improve the quality of the LF at its hot end, new follow up observations of low signal to noise spectra are necessary as well as careful analysis of the metal content in the WD spectra. Further exploration of our LF should contribute a number of new insights into early white dwarf evolution.

Acknowledgements

Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/.
The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh,University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.

References

Abazajian, K., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2003, AJ, 126, 2081 [NASA ADS] [CrossRef]
Abazajian, K., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2004, AJ, 128, 502 [NASA ADS] [CrossRef]
Abazajian, K., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2005, AJ, 129, 1755 [NASA ADS] [CrossRef]
Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2006, ApJS, 162, 38 [NASA ADS] [CrossRef]
Barstow, M. A., Good, S. A., Burleigh, M. R., et al. 2003, MNRAS, 344, 562 [NASA ADS] [CrossRef]
Blanton, M. R., Lin, H., Lupton, R. H., et al. 2003, AJ, 125, 2276 [NASA ADS] [CrossRef]
Bloecker, T. 1995, A&A, 299, 755 [NASA ADS]
DeGennaro, S., Hippel, T., Winget, D. E., et al. 2008, AJ, 135, 1 [NASA ADS] [CrossRef]
Eisenstein, D. J., Liebert, J., Harris, H. C., et al. 2006a, ApJ, 167, 40 [NASA ADS] [CrossRef]
Eisenstein, D. J., Liebert, J., Koester, D., et al. 2006b, AJ, 132, 676 [NASA ADS] [CrossRef]
Evans, D. W. 1992, MNRAS, 255, 521 [NASA ADS]
Finley, D. S., Koester, D., & Basri, G. 1997, ApJ, 488, 375 [NASA ADS] [CrossRef]
Fleming, T. A., Liebert, J., & Green, R. F. 1986, ApJ, 308, 176 [NASA ADS] [CrossRef]
Fukugita, M., Ichikawa, T., Gunn, J.E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef]
Geijo, E. M., Torres, S., Isern, J., & Garcia-Berro, E., MNRAS, in preparation
Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences]
Green, R. F., Schmidt, M., & Liebert, J. 1986, ApJS, 61, 305 [NASA ADS] [CrossRef]
Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef]
Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef]
Harris, H. C., Munn, J. A., Kilic, M., et al. 2006, AJ, 131, 571 [NASA ADS] [CrossRef]
Hogg, D. W., Finkbeiner, D. P., Schlegel, D. J., & Gunn, J. E. 2001, AJ, 122, 2129 [NASA ADS] [CrossRef]
Hu, Q., Wu, C., & Wu, X.-B. 2007, A&A, 466, 627 [NASA ADS] [CrossRef] [EDP Sciences]
Hügelmeyer, S. D., Dreizler, S., Homeier, D., et al. 2006, A&A, 454, 617 [NASA ADS] [CrossRef] [EDP Sciences]
Isern, J., Garcia-Berro, E., Torres, S., & Catalan, S. 2008, ApJ, 682, L109 [NASA ADS] [CrossRef]
Ivezic, Z., Lupton, R. H., Schlegel, D., et al. 2004, Astron. Nachrichten, 325, 583 [NASA ADS] [CrossRef]
Kleinman, S. J., Harris, H. C., Eisenstein, D. J., et al. 2004, AJ, 607, 426 [NASA ADS] [CrossRef]
Krzesinski, J., Nitta, A., Kleinman, S. J., et al. 2004, A&A, 417, 1093 [NASA ADS] [CrossRef] [EDP Sciences]
Liebert, J., Dahn, C. C., & Monet, D. G. 1988, ApJ, 332, 891 [NASA ADS] [CrossRef]
Liebert, J., Bergeron, P., & Holberg, J. B. 2005, ApJS, 156, 47 [NASA ADS] [CrossRef]
Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef]
Napiwotzki, R., Green, P. J., & Saffer, R. A. 1999, ApJ, 517, 399 [NASA ADS] [CrossRef]
O'Brien, M. S., & Kawaler, S. D. 2000, ApJ, 539, 372 [NASA ADS] [CrossRef]
Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef]
Oswalt, T. D., Smith, J. A., Wood, M. A., & Hintzen, P. 1996, Nature, 382, 692 [NASA ADS] [CrossRef]
Pier, J. R., Munn, J. A., Hindsley, R. B., et al. 2003, AJ, 125, 1559 [NASA ADS] [CrossRef]
Rauch, T., & Deetjen, J. L. 2003, Stellar Atmosphere Modeling, 288, 103 [NASA ADS]
Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef]
Schoenberner, D. 1983, ApJ, 272, 708 [NASA ADS] [CrossRef]
Smith, J. A., Tucker, D. L., Kent, S., et al. 2002, AJ, 123, 2121 [NASA ADS] [CrossRef]
Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef]
Tucker, D., Kent, S., Richmond, M. W., et al. 2006, Astron. Nachrichten, 327, 821 [NASA ADS] [CrossRef]
Vennes, S. 1999, ApJ, 525, 995 [NASA ADS] [CrossRef]
Vennes, S., Smith, R. J., Boyle, B. J., et al. 2002, MNRAS, 335, 673 [NASA ADS] [CrossRef]
Vennes, S., Chayer, P., Dupuis, J., & Lanz, T. 2005, ASPC, 334, 1985
Wesemael, F., Green, R. F., & Liebert, J. 1985, ApJS, 307, 65
Wood, M. A. 1995, in White Dwarfs, Proc. of the 9th European Workshop on White Dwarfs ed. D. Koester, & K. Werner (Berlin, Heidelberg, New York: Springer-Verlag), Lecture Notes in Physics, 443, 41
Wood, P. R., & Faulkner, D. J. 1986, ApJ, 307, 65 [CrossRef]
York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef]

All Tables

Table 1: SDSS DR4 spectroscopic hot_std sample incompleteness map.

Table 2: Number of all types of WDs per magnitude bin.

Table 3: DA and non-DA WD distribution per magnitude bin.

All Figures

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12094fg1.eps} \end{figure}$	Figure 1: The photometric $(g-r)_\circ$ and $(u-g)_\circ$ (small and large symbols respectively) vs. fit temperatures for our hot_std sub-sample of the DR4 WD stars from Eisenstein et al. (2006a). Only DA (solid squares) and DB (open circles) WDs with $T_{\rm eff} > 20~000$ K are shown. The dashed line shows our additional $T_{\rm eff}$ sample cut at 23 500 K.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg2.eps} \end{figure}$	Figure 2: Our primary WD LFs. The solid line includes all stars in our sample while the dotted line excludes the more uncertain magnetic and binary WDs. The two dashed lines show the effect of different temperature cuts: our preferred cut at 23 500 K and one cut further at 20 000 K to provide more overlap with the Harris et al. (2006) sample, shown as the solid line with open circles. The top axis shows the approximate effective temperature in kilo-Kelvin corresponding to plotted x-axis, $M_{\rm bol}$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg3.eps} \end{figure}$	Figure 3: The same as Fig. 2 but with $T_{\rm eff}$ and NLTE corrections applied.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg4.eps} \end{figure}$	Figure 4: Our WD LF as in Fig. 3, but with 1.0 mag bins.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg5.eps} \end{figure}$	Figure 5: DA (solid circles) and non-DA (open squares) LFs plotted with the PG survey DA LF (open circles) of Liebert et al. (2005). The magnitude bin width is 1.0 and the bins are centered on integer magnitudes. Thinner line right below SDSS DA LF is the DA LF without magnetic DAs and binary DA+M systems. In case of non-DA LF removing magnetic and binary DB+M systems from the WD sample affects the LF near $M_{\rm bol} = 7$ and the rest of the thin line overlaps with the thick one. The top axis shows the approximate effective temperature in kilo-Kelvin corresponding to plotted x-axis, $M_{\rm bol}$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.1cm,clip]{12094fg6.eps} \end{figure}$	Figure 6: The same as in Fig. 5 but bins are centered on half integer magnitudes. In both plots, we can see the appearance of the first DAs affect a dip in the non-DA LF.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.