| Issue |
A&A
Volume 508, Number 1, December II 2009
|
|
|---|---|---|
| Page(s) | 355 - 369 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200912093 | |
| Published online | 15 October 2009 | |
A&A 508, 355-369 (2009)
Scaled solar tracks and isochrones in a large region of the Z-Y plane
II. From 2.5 to 20 M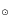 stars
stars![[*]](/icons/foot_motif.png)
G. Bertelli1 - E. Nasi1 - L. Girardi1 - P. Marigo2
1 - INAF - Padova Astronomical Observatory, Vicolo
dell'Osservatorio 5, 35122 Padova, Italy
2 - Astronomy Department, Padova University,
Vicolo dell'Osservatorio 3, 35122 Padova, Italy
Received 17 March 2009 / Accepted 17 September 2009
Abstract
We extend our theoretical computations for low-mass stars to
intermediate-mass and massive stars, for which few databases exist in the
literature. Evolutionary tracks and isochrones are computed
for initial masses
![]() for a
grid of 37 chemical compositions with metal content Z between
0.0001 and 0.070 and helium content Y between 0.23 and 0.40 to enable users
to obtain isochrones for ages as young as about 107 years and to simulate
stellar populations with different helium-to-metal enrichment laws.
The Padova stellar evolution code is identical to that used in the first
paper of this series. Synthetic TP-AGB
models allow stellar tracks and isochrones to be extended until the end of
the thermal pulses along the AGB. We provide software tools for the
bidimensional interpolation (in Y and Z) of the isochrones
from very old ages down to about 107 years. This lower limit
depends on chemical composition.
The extension of the blue loops and the instability strip of Cepheid stars are
compared and the Cepheid mass-discrepancy is discussed. The location of red
supergiants in the H-R diagram is in good agreement with the evolutionary
tracks for masses from 10 to
for a
grid of 37 chemical compositions with metal content Z between
0.0001 and 0.070 and helium content Y between 0.23 and 0.40 to enable users
to obtain isochrones for ages as young as about 107 years and to simulate
stellar populations with different helium-to-metal enrichment laws.
The Padova stellar evolution code is identical to that used in the first
paper of this series. Synthetic TP-AGB
models allow stellar tracks and isochrones to be extended until the end of
the thermal pulses along the AGB. We provide software tools for the
bidimensional interpolation (in Y and Z) of the isochrones
from very old ages down to about 107 years. This lower limit
depends on chemical composition.
The extension of the blue loops and the instability strip of Cepheid stars are
compared and the Cepheid mass-discrepancy is discussed. The location of red
supergiants in the H-R diagram is in good agreement with the evolutionary
tracks for masses from 10 to
![]() .
Tracks and isochrones are available in tabular form for the
adopted grid of chemical compositions in the extended plane Z-Y in three
photometric systems. An interactive web interface allows users to obtain
isochrones of any chemical composition inside the provided Z-Y range
and also to simulate stellar populations with different Y(Z) helium-to-metal
enrichment laws.
.
Tracks and isochrones are available in tabular form for the
adopted grid of chemical compositions in the extended plane Z-Y in three
photometric systems. An interactive web interface allows users to obtain
isochrones of any chemical composition inside the provided Z-Y range
and also to simulate stellar populations with different Y(Z) helium-to-metal
enrichment laws.
Key words: stars: evolution - Cepheids
1 Introduction
In general, the helium content of stellar populations is poorly known. For super-solar metallicities, the helium content is unconstrained, and has usually been derived from simple reasoning, based on naive chemical evolution models of galaxies, rather than observational grounds.
The most popular assumption in evolutionary models of stars is that Y increases linearly with Z. This assumption is inaccurate for old globular clusters, some of which contain multiple stellar populations with evidence of significant helium enrichment (Piotto et al. 2007; Piotto 2009). Even the solar initial content of helium has been debated, since the values derived from helioseismology depend on the assumed efficiency of helium diffusion (Guzik et al. 2005, 2006; Basu & Antia 2008), whereas on the other hand helioseismology has been challenged by the debate about the oxygen abundance (Montalban et al. 2004; Scott et al. 2009). For these reasons it is likely that the helium content of stellar evolutionary models will in the future be revised many times. An alternative approach, followed in this paper, is that of computing stellar models for a significant range of the Z - Y plane, so that interpolations in the grid allow us to consider many possible Y(Z) relations.
A large amount of theoretical investigation has been devoted to the evolution of low-mass stars populating old galactic globular clusters, since rich stellar clusters provide us with the opportunity to test the results of stellar evolution theories. The increasing amount of data for young populous clusters in both of the Magellanic Clouds encourages us to pay special attention to the evolutionary behaviour of more massive stars presently evolving in those clusters. However, not so much theoretical computation has been addressed to the implementation of existing stellar model databases for more massive stars, as done for low masses.
The Padova and Geneva groups originally compiled grids of stellar
models with overshooting up to
![]() for several chemical
compositions (Bressan et al.
1993; Fagotto et al. 1994a,b; and relative isochrones in Bertelli et al. 1994;
Schaller et al. 1992; Schaerer et al. 1993a,b; Charbonnel et al. 1993; Meynet
et al. 1994).
Girardi et al. (2000) computed a new set of low- and intermediate-mass stellar
models with updated opacities and equation of state.
Bono et al. (2000) presented intermediate-mass standard models with different
helium and metal content (
for several chemical
compositions (Bressan et al.
1993; Fagotto et al. 1994a,b; and relative isochrones in Bertelli et al. 1994;
Schaller et al. 1992; Schaerer et al. 1993a,b; Charbonnel et al. 1993; Meynet
et al. 1994).
Girardi et al. (2000) computed a new set of low- and intermediate-mass stellar
models with updated opacities and equation of state.
Bono et al. (2000) presented intermediate-mass standard models with different
helium and metal content (
![]() ), and Pietrinferni et al.
(2004, 2006) database makes available stellar models and isochrones
for scaled-solar and
), and Pietrinferni et al.
(2004, 2006) database makes available stellar models and isochrones
for scaled-solar and ![]() -enhanced metal distributions in the mass range
between 0.5 and
-enhanced metal distributions in the mass range
between 0.5 and
![]() with and without overshooting.
with and without overshooting.
Following the first release of the new stellar evolution models of the Padova
database for low-mass stars in a large region of the Z-Y plane by Bertelli
et al. (2008, hereinafter Paper I), in this paper we present models for stars
from 2.5 to
![]() with the same range of chemical compositions as
in Paper I. Among the astrophysical problems of interest in this
range of mass, we discuss whether observations of Cepheids in the Magellanic
Clouds (MCs) and the Galaxy can be reproduced by
these new models. Massive red supergiants in the Galaxy and in MCs with newly
derived physical parameters by Levesque et al. (2005, 2006) are compared
with our models from 10 to
with the same range of chemical compositions as
in Paper I. Among the astrophysical problems of interest in this
range of mass, we discuss whether observations of Cepheids in the Magellanic
Clouds (MCs) and the Galaxy can be reproduced by
these new models. Massive red supergiants in the Galaxy and in MCs with newly
derived physical parameters by Levesque et al. (2005, 2006) are compared
with our models from 10 to
![]() ,
evaluating the adequacy of
stellar models in this mass range.
,
evaluating the adequacy of
stellar models in this mass range.
A neglected process in our massive stellar models is stellar rotation. Significant advances have been made in this field (e.g., Heger & Langer 2000; Meynet & Maeder 2000), which demonstrated that the evolutionary paths of rapidly rotating massive stars can differ from those of non-rotating stars. A book by Maeder (2009) on the physics, formation, and evolution of rotating stars presents a very detailed description of the effects of rotation on stellar evolution. Rapid rotation can trigger strong mixing inside massive stars, extend the core hydrogen-burning lifetime, significantly increase the luminosity, and change the chemical composition at the stellar surface with time. Regardless of the success of rotating stellar models in explaining a variety of stellar phenomena, rotational mixing is still a matter of debate (de Mink et al. 2009).
Our choice of neglecting stellar rotation in this set of models has two main motivations, namely:
- 1.
- not all stars begin their life with the same rotational velocity;
- 2.
- stars have rotational axes that are not all oriented in the same direction.
The present paper is organized as follows. In Sect. 2, we summarize the main input physics and in Sect. 3, TP-AGB models are described. In Sect. 4, stellar tracks are presented with a description of tables indicating changes in surface chemical composition after the first and the second dredge-up. Isochrones and relative tables are described in Sect. 5, in addition to the interpolation scheme allowing to obtain isochrones and to simulate stellar populations in a large region of the Z-Y plane. Cepheids and the problem of the mass discrepancy are discussed in Sect. 6. Section 7 deals with massive red supergiants in the Galaxy and the Magellanic Clouds, and Sect. 8 presents the concluding remarks.
2 Input physics and coverage of the Z-Y plane
The stellar evolution code adopted in this work is the same
as in Bertelli et al. (2008, hereinafter Paper I ).
The masses described in this paper are between 2.5 and
![]() ,
to ensure that we have a complete stellar model database from
0.15 to
,
to ensure that we have a complete stellar model database from
0.15 to
![]() .
In the following, we summarize the input physics described in Paper I.
.
In the following, we summarize the input physics described in Paper I.
2.1 Initial masses and chemical compositions
Table 1: Combinations of Z and Y of the computed tracks.
The first release of the new evolutionary models was presented in Paper I for masses from 0.15 to2.2 The choice of scaled-solar abundances
For each value of Z, the fractions of different metals follow a scaled solar distribution, as compiled by Grevesse & Noels (1993), and adopted in the OPAL opacity tables. The ratio of abundances of different isotopes is assumed to be identical to Anders & Grevesse (1989).
In this regard, we note that both the solar composition, and what is referred to as the alpha-enhanced distribution of metals have changed, by factors of up to 0.3 dex, in the past few years. Moreover, there is also an increasing perception that neither scaled solar, nor alpha-enhanced compositions are universal: they apply only to particular regions of spiral galaxies that are similar to our own. For instance, there are documented cases of slightly alpha-depleted composition in some areas of the LMC (e.g., Pompéia et al. 2008). For nearby dwarf galaxies, the modern observational picture is that their populations are in general slightly alpha-depleted for [Fe/H]>-1.0, becoming alpha-enhanced only at very low metallicities (see Fig. 11 in Tolstoy et al. 2009, and references therein). On the high-metallicity end, although it is generally believed that the most massive ellipticals are metal-rich and alpha-enhanced, there is no guarantee that they follow the same distribution of alpha-elements as nearby halo stars.
The above-mentioned observations of dwarf galaxies demonstrate that low-metallicity models with scaled solar compositions are useful and, in many cases, appropriate, to the study of nearby galaxies. Since the observational view of a ``typical alpha-enhanced composition'' continues to change, we prefer to be conservative and begin the modelling from the most well studied case, the scaled solar one, which is reasonably well-known, apart from the solar oxygen abundance. We will explore a few possible cases of alpha-enhancement in future papers.This approach is consistent with our choice of scaled solar abundances and the rules introduced by Salaris et al. (1993) to approximate low-Z alpha-enhanced isochrones using scaled solar ones (which can be applied to the Milky Way halo, metal-poor globular clusters, and the metal-poorest stars in dwarf galaxies).
As far as the use of ``old solar abundances'' is concerned (Grevesse & Noels 1993), we note the following:
- Some more recent studies (e.g., Caffau et al. 2008, and references therein) confirm the high O abundances typical of older compilations of solar abundances, rather than the low values claimed by Asplund et al. (2004). Solar models computed with low heavy-element abundances also strongly disagree with the constraints from helioseismology (see Basu & Antia 2008, and references therein).
- We computed a few sequences of stellar tracks using several solar compositions. The difference between the models computed at the same mass, metallicity, and mixing length parameter was found to be negligible (as discussed in Sect. 4.3.1).
2.3 Opacities
The radiative opacities for scaled solar mixtures are assumed to be those of
the OPAL group (Iglesias & Rogers 1996) for temperatures higher than
![]() ,
and the molecular opacities are those of Alexander & Ferguson (1994) for
,
and the molecular opacities are those of Alexander & Ferguson (1994) for
![]() as in Salasnich et al. (2000).
For very high temperatures (
as in Salasnich et al. (2000).
For very high temperatures (
![]() ), we use the
opacities of Weiss et al. (1990).
), we use the
opacities of Weiss et al. (1990).
The conductive opacities of electron-degenerate matter are taken from Itoh
et al. (1983). For the
interpolation within the opacity tables grids in both papers, we
used the two-dimensional bi-rational cubic damped-spline algorithm
(see Schlattl & Weiss 1998; Salasnich et al. 2000; and Weiss &
Schlattl 2000). In general, evolutionary models of low-mass stars differ very
little by changing the opacity interpolation scheme. The model predictions for
massive stars (
![]() )
are far more sensitive to the interpolation algorithm as
discussed in Salasnich et al. (2000)
)
are far more sensitive to the interpolation algorithm as
discussed in Salasnich et al. (2000)
2.4 Equation of state
The equation of state (EOS) for temperatures higher than 107 K is
that of a fully-ionized gas, including electron degeneracy in the way
described by Kippenhahn et al. (1967). The effect of Coulomb
interactions between the gas particles at high densities is taken into
account as described in Girardi et al. (1996).
For temperatures lower than 107 K, the detailed ``MHD'' EOS of
Mihalas et al. (1990, and references therein) is adopted.
We note that the MHD EOS is critical only for stellar models of
mass lower than 0.7 ![]() during their main sequence evolution.
during their main sequence evolution.
2.5 Reaction rates and neutrino losses
The reaction rates are taken from the compilation of Caughlan & Fowler
(1988, hereinafter CF88), apart from
![]() and
and
![]() ,
for which we use the determinations by
Landré et al. (1990). The
uncertain 12C(
,
for which we use the determinations by
Landré et al. (1990). The
uncertain 12C(
![]() )16O rate was set to be 1.7 times
the values given by Caughlan & Fowler (1988), as indicated by the
study of Weaver & Woosley (1993) of the nucleosynthesis by massive
stars. The electron screening factors for all reactions are those
from Graboske et al. (1973).
The abundances of the various elements are evaluated with the aid of a
semi-implicit extrapolation scheme, as described in Marigo et al. (2001).
The energy losses by neutrinos are from Haft et al. (1994).
)16O rate was set to be 1.7 times
the values given by Caughlan & Fowler (1988), as indicated by the
study of Weaver & Woosley (1993) of the nucleosynthesis by massive
stars. The electron screening factors for all reactions are those
from Graboske et al. (1973).
The abundances of the various elements are evaluated with the aid of a
semi-implicit extrapolation scheme, as described in Marigo et al. (2001).
The energy losses by neutrinos are from Haft et al. (1994).
In Sect. 4.3.2 we discuss the effects on stellar models of
measurements of the
![]() reaction rate by
the LUNA experiment (Formicola et al. 2004).
reaction rate by
the LUNA experiment (Formicola et al. 2004).
2.6 Convection
The most important physical process for mixing in stars is convection, but at
present convection remains a main source of uncertainty in stellar models
computations.
In our stellar models, convection is treated with the Schwarzschild
criterion for stability.
Usually energy transport in the outer convection zone of stars is described
according to the mixing-length theory (MLT) of Böhm-Vitense (1958).
We adopt the same value as in Paper I for the MLT parameter (
![]() ),
calibrated by means of the solar model.
),
calibrated by means of the solar model.
2.6.1 Overshoot
The extension of the convective regions in stellar models takes into account overshooting from the borders of both core and envelope convective zones (Bressan et al. 1981; Alongi et al. 1991; Girardi et al. 2000). In the following, we adopt the formulation by Bressan et al. (1981) in which the boundary of the convective core is defined to be the layer where the velocity (rather than the acceleration) of convective elements vanishes. This non-local treatment of convection requires the use of a free parameter related to the mean free path l of convective elements defined to beWe adopt the same prescription as in Paper I (Bertelli et al. 2008) and in
Girardi et al. (2000) for the parameter
![]() for H- and He-burning
stages.
Overshooting at the lower boundary of convective envelopes is also considered.
For
for H- and He-burning
stages.
Overshooting at the lower boundary of convective envelopes is also considered.
For
![]() ,
a value of
,
a value of
![]() was assumed, as in
Bertelli et al. (1994) and Girardi et al. (2000).
was assumed, as in
Bertelli et al. (1994) and Girardi et al. (2000).
2.6.2 Hydrogen semiconvection
During the core H-burning phase of massive stars, radiation pressure and electron scattering opacity produce a large convective core surrounded by an H-rich region, which is potentially unstable to convection if the original gradient in chemical abundance remains, but stable if suitable mixing is allowed to occur. This region of the star is assumed in theoretical models to undergo sufficient mixing until the condition of neutrality is restored, to transport negligible energy flux. The Schwarzschild condition produces smoother chemical profiles and, in some cases, a fully intermediate convective layer. Similar instability also occurs during the early shell H-burning phase. Taking into account mass loss from massive stars, the extension of semiconvection and/or intermediate full convection at the top of the H-burning shell is much smaller than in constant-mass stellar models. The effects of H-semiconvection on the evolution of massive stars were summarized by Chiosi & Maeder (1986).2.6.3 Helium semiconvection
As He-burning proceeds in the convective core of low-mass stars during the early stages of the horizontal branch (HB), the size of the convective core increases. Once the central value of helium falls below2.7 Mass loss
Mass loss has a crucial impact on the evolution of massive stars, affecting
evolutionary tracks, lifetimes, and surface abundances.
The role of radiation pressure in driving mass loss from massive stars has
been firmly accepted by theoretical astrophysics since the pioneering studies
by Lucy & Solomon (1970), and Castor et al. (1975). A relevant review on the
evolution of massive stars with mass loss was given by Chiosi & Maeder (1986), while
Kudritzki & Puls (2000) exhaustively describe winds from hot stars.
The metallicity dependence of mass loss rates is usually included using the
formula:
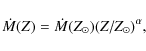
where the exponent
In this paper, we adopt the mass loss rates from stellar winds driven by
radiation pressure according to
de Jager et al. (1988) for all evolutionary stages starting from the main
sequence and from about ![]() 6-7 to
6-7 to
![]() (the upper mass limit to this evolutionary track release).
The rates incorporate the dependence on metallicity given by
Kudritzki et al. (1989)
(the upper mass limit to this evolutionary track release).
The rates incorporate the dependence on metallicity given by
Kudritzki et al. (1989)
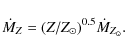
In a future paper dealing with the evolution of massive stars, for the mass-loss rates we will adopt relationships based on more recent observations and/or determinations.
3 Synthetic TP-AGB models
An important update of the database of evolutionary tracks is the extension
of stellar models and isochrones until the end of the thermal pulses along
the asymptotic giant branch (TP-AGB) for all masses up to ![]()
![]() .
The evolution from the first thermal pulse to the complete ejection of
the stellar envelope is computed with the synthetic code described in Marigo
& Girardi (2007, and references therein), to whom we refer for all details.
It is important to mention that these TP-AGB tracks have been updated
in many aspects, describing for instance the transition to the C-star phase
by means of the third dredge-up event, the prevention of this transition for
the
most massive tracks because of hot bottom burning, the proper effective
temperatures
of carbon stars, and suitable mass-loss rates of the M and C-type stars.
Although the models are not calibrated in the same way as Marigo & Girardi
(2007)
tracks (i.e., present models might not reproduce the luminosity functions and
lifetimes of carbon stars in the Magellanic Clouds), they represent a
significant improvement to the simple way the TP-AGB tracks were included
in many previous sets of isochrones.
.
The evolution from the first thermal pulse to the complete ejection of
the stellar envelope is computed with the synthetic code described in Marigo
& Girardi (2007, and references therein), to whom we refer for all details.
It is important to mention that these TP-AGB tracks have been updated
in many aspects, describing for instance the transition to the C-star phase
by means of the third dredge-up event, the prevention of this transition for
the
most massive tracks because of hot bottom burning, the proper effective
temperatures
of carbon stars, and suitable mass-loss rates of the M and C-type stars.
Although the models are not calibrated in the same way as Marigo & Girardi
(2007)
tracks (i.e., present models might not reproduce the luminosity functions and
lifetimes of carbon stars in the Magellanic Clouds), they represent a
significant improvement to the simple way the TP-AGB tracks were included
in many previous sets of isochrones.
4 Stellar tracks
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12093fig1.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg41.png)
|
Figure 1: Evolutionary tracks in the HR diagram for the composition Z=0.001, Y=0.23 (dot-dashed line) and Z=0.001, Y=0.40 (solid line). |
| Open with DEXTER | |
4.1 Evolutionary stages and mass ranges
We consider that stellar models are on the zero age main-sequence (ZAMS) when chemically homogeneous stars begin their H-burning and the gravitational energy production is less than about 1% of the total energy. Our models are evolved from the ZAMS, and the evolution is followed in detail through the entire H- and He-burning phases. The tracks are stopped at the beginning of the TP-AGB phase (bTP-AGB) in intermediate-mass stars, or at the carbon ignition in our more massive models. Stellar models and isochrones are extended until the end of the thermal pulses along the AGB with the synthetic TP-AGB models by Marigo & Girardi (2007).
4.2 Tracks in the HR diagram
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{12093fig2.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg42.png)
|
Figure 2: Evolutionary tracks in the HR diagram for the composition Z=0.040, Y=0.26 (dot-dashed line) and Z=0.040, Y=0.40 (solid line). |
| Open with DEXTER | |
We display
only some examples of the sets of computed evolutionary tracks
(i.e., Z=0.001 for Y=0.23 and Y=0.40,
and Z=0.040 for Y=0.26 and Y=0.40) for masses between 2.5 and
![]() from the ZAMS to the beginning of either the TP-AGB, or
carbon burning.
Figures 1 and 2 illustrate the range of
temperatures and
luminosities involved for the boundary values of helium content at a given
metallicity in the theoretical HR diagram. These figures also illustrate the
dependences of the extension of blue loops on both metallicity and helium
content, which are significant at low metallicity, and practically absent for
higher metal content (
from the ZAMS to the beginning of either the TP-AGB, or
carbon burning.
Figures 1 and 2 illustrate the range of
temperatures and
luminosities involved for the boundary values of helium content at a given
metallicity in the theoretical HR diagram. These figures also illustrate the
dependences of the extension of blue loops on both metallicity and helium
content, which are significant at low metallicity, and practically absent for
higher metal content (
![]() ).
The extension of blue loops requires a detailed discussion since there are
observations that are not easily reproduced by stellar models, such as
Cepheids,
and this topic is dealt with in Sect. 6. The location of red supergiants (RSG)
on the H-R diagram did not always agree with the predictions of stellar
evolutionary models, previousy appearing to be too cool and too luminous to
coincide with the position of the evolutionary tracks. New effective
temperatures and luminosities for the RSG populations of galaxies by Levesque
et al. (2005, 2006) greatly improved the agreement between the RSGs and the
evolutionary models, as is evident in Sect. 7 from the comparison with our new
moderate massive models.
The data tables for the present evolutionary tracks are available only
in electronic format
).
The extension of blue loops requires a detailed discussion since there are
observations that are not easily reproduced by stellar models, such as
Cepheids,
and this topic is dealt with in Sect. 6. The location of red supergiants (RSG)
on the H-R diagram did not always agree with the predictions of stellar
evolutionary models, previousy appearing to be too cool and too luminous to
coincide with the position of the evolutionary tracks. New effective
temperatures and luminosities for the RSG populations of galaxies by Levesque
et al. (2005, 2006) greatly improved the agreement between the RSGs and the
evolutionary models, as is evident in Sect. 7 from the comparison with our new
moderate massive models.
The data tables for the present evolutionary tracks are available only
in electronic format![]() .
.
4.3 Testing the effects of different input physics
We computed a few sequences for different initial chemical compositions, opacities, and for nuclear reaction rates from the LUNA experiment, obtaining very modest changes in the tracks, as discussed in the following.
4.3.1 Initial chemical composition and opacities
Updating both the chemical mixture (EOS) and the low-temperature opacities (determined with the AESOPUS code by Marigo & Aringer 2009), we computed a few sequences of stellar tracks using the distribution of element abundances of the solar chemical composition according to a) Grevesse & Noels (1993), b) Grevesse & Sauval (1998), and c) Grevesse et al. (2007). The differences between the models for the same Z are negligible. To complete additional comparison, we also used the opacity tables by Alexander & Ferguson (1994), with reference to the Grevesse (1991) solar composition. We found that the differences between the models, computed at the same mass, metallicity and mixing-length parameter, are completely negligible. In particular, the corresponding giant branches in the H-R diagram practically overlap, the typical separation at fixed luminosity being of the order of 0.002 dex or less throughout their extension.
4.3.2 Nuclear reaction rates
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{12093fig3.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg44.png)
|
Figure 3:
Evolutionary tracks in the HR diagram for the composition
Z=0.004,
Y=0.26 computed with the new LUNA rate for the
|
| Open with DEXTER | |
In our models, we tested the effect of measurements of the
![]() reaction rate by the LUNA
experiment (Formicola et al. 2004) and from the NACRE compilation (Angulo et al. 1999). The tracks obtained with the CF88 rate
practically coincide with those obtained with the NACRE
rate, as shown by Imbriani et al. (2004).
The LUNA rate was simulated by simply multiplying that of
Caughlan & Fowler by a factor of 0.6 (LUNA Collaboration, Bemmerer et al.
2006; Imbriani et al. 2005; Lemut et al. 2006).
The results are shown in Fig. 3 for Z=0.004 and Y=0.26, and in
Fig. 4 for Z=0.017 and Y=0.26 for the masses indicated in the
figures. Additional tracks for Z=0.008 were computed, but are not shown for
conciseness. From these tracks, we conclude that:
reaction rate by the LUNA
experiment (Formicola et al. 2004) and from the NACRE compilation (Angulo et al. 1999). The tracks obtained with the CF88 rate
practically coincide with those obtained with the NACRE
rate, as shown by Imbriani et al. (2004).
The LUNA rate was simulated by simply multiplying that of
Caughlan & Fowler by a factor of 0.6 (LUNA Collaboration, Bemmerer et al.
2006; Imbriani et al. 2005; Lemut et al. 2006).
The results are shown in Fig. 3 for Z=0.004 and Y=0.26, and in
Fig. 4 for Z=0.017 and Y=0.26 for the masses indicated in the
figures. Additional tracks for Z=0.008 were computed, but are not shown for
conciseness. From these tracks, we conclude that:
- the MS becomes slightly bluer and slightly more luminous in models with
a LUNA rate, as
a consequence of the H-burning lifetimes becoming shorter by about 1.5%.
This is in general agreement with the results by Weiss et al. (2005);
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{12093fig4.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg45.png)
Figure 4: Evolutionary tracks in the HR diagram for the composition Z=0.017, Y=0.26 computed with the new LUNA rate for the
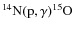 nuclear reaction (dot-dashed line)
and with the rate according to Caughlan & Fowler (1988) (solid line).
nuclear reaction (dot-dashed line)
and with the rate according to Caughlan & Fowler (1988) (solid line).
Open with DEXTER - the He-burning lifetimes do not change. He-burning loops have their
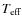 extension practically unchanged for Z=0.004 and 0.008, whereas for
Z=0.017 the loops become more extended with LUNA rates. This effect is
surprising, and goes in the opposite sense to the results described in Weiss
et al. (2005).
extension practically unchanged for Z=0.004 and 0.008, whereas for
Z=0.017 the loops become more extended with LUNA rates. This effect is
surprising, and goes in the opposite sense to the results described in Weiss
et al. (2005).
4.4 Changes in surface chemical composition
The surface chemical composition of the stellar models is affected by
two defined dredge-up events. The first occurs on
the first ascent of the RGB for all stellar models (except for
the very-low mass ones which do not evolve beyond the main
sequence). The second dredge-up is found after the core
He-exhaustion, being remarkable only in models with
![]() and
and
![]() .
For masses higher than
.
For masses higher than
![]() ,
the second dredge-up occurs in concomitance with
the carbon ignition at the core, so that the exposition of He-enriched
material at the surface is too short-lived to be of interest, and
not followed in detail by the present calculations.
We provide tables with the
surface chemical composition of H, 3He, 4He, and main CNO isotopes,
before and after the first dredge-up, and after the second dredge-up.
As an example, Table 2 shows the surface abundances for
the chemical composition Z=0.008 and Y=0.26.
,
the second dredge-up occurs in concomitance with
the carbon ignition at the core, so that the exposition of He-enriched
material at the surface is too short-lived to be of interest, and
not followed in detail by the present calculations.
We provide tables with the
surface chemical composition of H, 3He, 4He, and main CNO isotopes,
before and after the first dredge-up, and after the second dredge-up.
As an example, Table 2 shows the surface abundances for
the chemical composition Z=0.008 and Y=0.26.
Table 2: Surface chemical composition (by mass fraction) of [Z=0.008, Y=0.26] models.
5 Isochrones
From the tracks presented in this paper, we constructed isochrones
as in Paper I, with the algorithm of ``equivalent evolutionary points''
used in Bertelli et al. (1994) and Girardi et al. (2000).
The initial point of each isochrone is the
![]() model in the
lower main sequence. The terminal stage of the isochrone is
the tip of the TP-AGB or the beginning of carbon burning.
We note that there are usually small
differences in the logarithm of the effective temperature between the last
model of the track at the beginning of the TP-AGB and the starting point
of the synthetic TP-AGB model of the corresponding mass. Constructing the
isochrones, we removed these small discontinuities with a suitable shift.
model in the
lower main sequence. The terminal stage of the isochrone is
the tip of the TP-AGB or the beginning of carbon burning.
We note that there are usually small
differences in the logarithm of the effective temperature between the last
model of the track at the beginning of the TP-AGB and the starting point
of the synthetic TP-AGB model of the corresponding mass. Constructing the
isochrones, we removed these small discontinuities with a suitable shift.
A comparison of isochrones with the same metallicity (Z=0.001) and
different helium content (Y=0.23 and Y=0.40) can be found in
Fig. 5 showing the range of variations in luminosity and
temperature for some isochrones (
![]() ).
The extension to the end of the TP-AGB phase is also shown for each isochrone.
An increase in the helium content at the same metallicity in stellar
models causes a decrease in the mean opacity and an increase in the
mean molecular weight of the envelope (Vemury & Stothers 1978), and
in turn higher luminosities, hotter effective temperatures and shorter
hydrogen and helium lifetimes of stellar models.
In apparently conflict with the previous statement about
higher luminosity for a helium increase in evolutionary tracks, the evolved
portion of the isochrones with lower helium are more luminous, as shown in
Fig. 5 where we plot isochrones with Z=0.001 for Y=0.23 and
Y=0.40. This effect is related to the
interplay between the increase in luminosity and the decrease in lifetime
of stellar models with higher helium content (at the same mass and
metallicity).
).
The extension to the end of the TP-AGB phase is also shown for each isochrone.
An increase in the helium content at the same metallicity in stellar
models causes a decrease in the mean opacity and an increase in the
mean molecular weight of the envelope (Vemury & Stothers 1978), and
in turn higher luminosities, hotter effective temperatures and shorter
hydrogen and helium lifetimes of stellar models.
In apparently conflict with the previous statement about
higher luminosity for a helium increase in evolutionary tracks, the evolved
portion of the isochrones with lower helium are more luminous, as shown in
Fig. 5 where we plot isochrones with Z=0.001 for Y=0.23 and
Y=0.40. This effect is related to the
interplay between the increase in luminosity and the decrease in lifetime
of stellar models with higher helium content (at the same mass and
metallicity).
5.1 Reliability of the interpolation
The program YZVAR is used to both obtain isochrones and simulate stellar populations. The method of interpolation has been described in detail in Paper I. In the database, there are 37 sets of stellar tracks covering a large region of the Z-Y plain and users can obtain either isochrones for whichever Z-Ycombination inside the provided range, or stellar populations with the required Y(Z) enrichment law.
Most of the problems about the reliability of the interpolation originate
from the extension of the loops during the central He-burning, which varies
significantly from low to high metal content for the considered range of mass.
For example, if we consider the two subsequent values of Z of our grid,
Z=0.017 and Z=0.040, we have extended loops for the first one (starting
from a mass that increases with helium content Y). No loops are present
for the upper mass
![]() for Y > 0.26.
In the case of Z=0.040, for all Y values and masses, no loops are
present, as shown in Fig. 2.
In this case, we cannot expect the extension of the loops to have a linear
behaviour
as a function of the metal content in the interpolation for intermediate
chemical compositions. We analysed the interpolation for Z=0.0285 and two
intermediate cases, namely Y=0.28 and Y=0.37.
for Y > 0.26.
In the case of Z=0.040, for all Y values and masses, no loops are
present, as shown in Fig. 2.
In this case, we cannot expect the extension of the loops to have a linear
behaviour
as a function of the metal content in the interpolation for intermediate
chemical compositions. We analysed the interpolation for Z=0.0285 and two
intermediate cases, namely Y=0.28 and Y=0.37.
In the case of
Z=0.0285, Y=0.28 the loops obtained by interpolation are
significantly less extended and/or less luminous than those of tracks
computed for the same
chemical composition at 7 and
![]() .
In contrast, the
interpolated tracks of 15 and
.
In contrast, the
interpolated tracks of 15 and
![]() exhibit significant loops, while
in the computed ones there are no loops.
In Fig. 6 the solid green lines represent the
computed tracks, and the red dotted lines represent the interpolated tracks.
exhibit significant loops, while
in the computed ones there are no loops.
In Fig. 6 the solid green lines represent the
computed tracks, and the red dotted lines represent the interpolated tracks.
To improve the interpolation for this range of metal content, we computed new
tracks with Z=0.030,
Y=0.26, 0.30, 0.34, and 0.40 for
![]() .
In this, way the results of the interpolation become far more reliable, as
evident in Fig. 6, where the blue line shows the result of the
interpolation after taking into account this new set for masses greater than
.
In this, way the results of the interpolation become far more reliable, as
evident in Fig. 6, where the blue line shows the result of the
interpolation after taking into account this new set for masses greater than
![]() .
The comparison of the lifetimes of the computed and the
interpolated tracks infers differences of lower than
.
The comparison of the lifetimes of the computed and the
interpolated tracks infers differences of lower than ![]() .
The interpolation is also superior in the case of Z=0.0285 and
Y=0.37, when taking into account the new tracks computed for the intermediate
metal content Z=0.030.
.
The interpolation is also superior in the case of Z=0.0285 and
Y=0.37, when taking into account the new tracks computed for the intermediate
metal content Z=0.030.
Another critical region of the interpolation is at
low metallicities (of Z between 0.0004 and 0.001 for high values of Y)
owing to the different morphological behaviour of the involved tracks.
A computed set of tracks (
![]() )
with Z=0.0007 and
Y=0.35 was compared with a corresponding interpolated set and the
results are shown in Fig. 7, where the green lines represent the
computed tracks and the red dotted lines the interpolated ones. There are
some differences in the red region, which is reached for the first time after
the central
hydrogen exhaustion for the 7 and
)
with Z=0.0007 and
Y=0.35 was compared with a corresponding interpolated set and the
results are shown in Fig. 7, where the green lines represent the
computed tracks and the red dotted lines the interpolated ones. There are
some differences in the red region, which is reached for the first time after
the central
hydrogen exhaustion for the 7 and
![]() .
If we check the lifetime
of the phases at variance with the computed tracks (see Fig. 8), the
differences are negligible with respect to the total He-burning lifetime.
.
If we check the lifetime
of the phases at variance with the computed tracks (see Fig. 8), the
differences are negligible with respect to the total He-burning lifetime.
In all other cases, the comparisons are satisfactory.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig5.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg57.png)
|
Figure 5: Comparison of isochrones for the same Z=0.001 and different helium content. Blue solid lines correspond to Y=0.40 (the related AGB is in black), and red dot-dashed ones to Y=0.23 (the related AGB is in green). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig6.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg58.png)
|
Figure 6: Comparison between interpolated and computed tracks with Z=0.0285, Y=0.28. The red dotted lines are the interpolated tracks between Z=0.017 and Z=0.040, while the green solid lines are the computed ones for the specific Z. The blue lines are the interpolated tracks taking into account the new set computed for Z=0.030 and various Y. Taking into account the new set, the interpolation is in closer agreement with the actual computed tracks. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig7.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg59.png)
|
Figure 7:
Comparison between interpolated and computed tracks with
Z=0.0007, Y=0.35.
The red dotted lines are the interpolated tracks for masses between 5 and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig8.eps}\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg60.png)
|
Figure 8: Differences between the lifetime spent by the interpolated track (red solid line) and that of the computed track (green dashed line) are insignificant. The chemical composition is as in Fig. 7. |
| Open with DEXTER | |
5.2 Bolometric corrections
The present isochrones are provided in the Johnson-Cousins-Glass system as defined by Bessell (1990) and Bessell & Brett (1988), in the Vegamag systems of ACS onboard HST (cf. Sirianni et al. 2005), and in the SDSS system. The formalism that we follow to derive bolometric corrections in these systems is described in Girardi et al. (2002). The definition of zeropoints was revised as described in a paper by Girardi et al. (2008), a description that is not repeated here.
Suffice it to say that the bolometric correction tables are based
on an updated and extended library of stellar spectral fluxes. The core
of the library now consists of the ``ODFNEW'' ATLAS9 spectral fluxes
from Castelli & Kurucz (2003), for
![]() of between 3500 and
50 000 K,
of between 3500 and
50 000 K, ![]() of between -2 and 5, and scaled-solar metallicities
[M/H] of between -2.5 and +0.5. This library is extended to
high
of between -2 and 5, and scaled-solar metallicities
[M/H] of between -2.5 and +0.5. This library is extended to
high
![]() by using pure black-body spectra.
For lower
by using pure black-body spectra.
For lower
![]() ,
the library is completed
with spectral fluxes for M, L, and T dwarfs from Allard et al. (2000), M giants from Fluks et al. (1994), and finally C star
spectra from Loidl et al. (2001). Details about the implementation of
this library, and in particular about the C star spectra, are provided
in Marigo et al. (2008) and Girardi et al. (2008).
,
the library is completed
with spectral fluxes for M, L, and T dwarfs from Allard et al. (2000), M giants from Fluks et al. (1994), and finally C star
spectra from Loidl et al. (2001). Details about the implementation of
this library, and in particular about the C star spectra, are provided
in Marigo et al. (2008) and Girardi et al. (2008).
We note that in the isochrones we apply the
bolometric corrections derived from this library without making any
correction for the enhanced He content. As demonstrated in Girardi et al. (2007), for a given metal content, an enhancement of He
as high as
![]() produces changes in the bolometric corrections of only a
few thousandths of magnitude. Just in some particular situations,
for instance at low
produces changes in the bolometric corrections of only a
few thousandths of magnitude. Just in some particular situations,
for instance at low
![]() and for blue passbands, the
He-enhancement can produce more sizeable effects on BCs; these situations,
however, correspond to cases where the emitted stellar flux would
in all cases be very small, and therefore are of little interest.
and for blue passbands, the
He-enhancement can produce more sizeable effects on BCs; these situations,
however, correspond to cases where the emitted stellar flux would
in all cases be very small, and therefore are of little interest.
5.3 Description of isochrone tables
Complete tables with the isochrones can be obtained through our web site![]() interactive services.
interactive services.
The user must select the chemical composition, the
![]() spacing
between contiguous isochrones, and the photometric system.
The following photometric systems are available:
spacing
between contiguous isochrones, and the photometric system.
The following photometric systems are available:
- UBVRIJHK absolute magnitudes in the Johnson-Cousins-Glass photometric system.
- ACS-WFC photometric system (bolometric corrections from Girardi et al. 2008). In the tables, the absolute magnitudes for the following 12 filters are listed: F435W, F475W, F550M, F555W, F606W, F625W, F658N, F660N, FF775W, F814W, F850LP, F892N.
- ACS-HRC photometric system (see Girardi et al. 2008). The absolute magnitudes listed in the tables are for the following 16 filters: F220W, F250W, F330W, F344N, F435W, F475W, F550M, F555W, F606W, F625W, F658N, F660N, F775W, F814W, F850LP, F892N.
1. logAge: logarithm of the age in years;2. log(L/Lo): logarithm of surface luminosity (in solar units);3. logTef: logarithm of effective temperature (in K);4. logG: logarithm of surface gravity (in cgs units);5. Mi: initial mass in solar masses;6. Mcur: actual stellar mass in solar masses;7. FLUM: indefinite integral over the initial mass M of the Salpeter initial mass function by number;8. - 15.: UBVRIJHK absolute magnitudes in the Johnson-Cousins-Glass system;16. C/Othe surface C/O ratio;17. C.P.: index marking the presence of a characteristic point, when different from zero.
We note that the
initial mass is the useful quantity for population synthesis calculations,
since together with the initial mass function it determines the relative
number of stars in different sections of the isochrones.
In Col. 7, the
indefinite integral evaluated over the initial mass M of the initial mass
function (IMF) by number, i.e.,
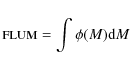
|
(1) |
is presented, for the case of the Salpeter IMF,
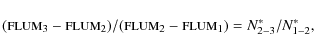
where the terms have their usual meaning.
We remark that the
Salpeter (1955) IMF is not valid for masses lower than about
![]() .
The user can easily derive FLUM relations for alternative choices of
the IMF, by using the values of the initial mass that we present in Col. 5 of
the isochrone tables.
Finally, the last column may signal the presence of a characteristic
evolutionary point. Values of 1 refer to points from the ZAMS to the early
AGB phase, and values of 2 represent the TP-AGB phase. Along the TP-AGB, we
mark its beginning, its end, and the point where C/O increases above unity,
corresponding to the transition from M to carbon stars, if present. The
presence of only one characteristic point of type 2 indicates a very short
TP-AGB phase.
.
The user can easily derive FLUM relations for alternative choices of
the IMF, by using the values of the initial mass that we present in Col. 5 of
the isochrone tables.
Finally, the last column may signal the presence of a characteristic
evolutionary point. Values of 1 refer to points from the ZAMS to the early
AGB phase, and values of 2 represent the TP-AGB phase. Along the TP-AGB, we
mark its beginning, its end, and the point where C/O increases above unity,
corresponding to the transition from M to carbon stars, if present. The
presence of only one characteristic point of type 2 indicates a very short
TP-AGB phase.
6 Cepheids
From an evolutionary perspective, Cepheids are post-red giant
stars crossing the instability strip on so-called blue loops following the
onset of core He-burning. Obviously the extension of the loop and the
distribution of the lifetime along it determines the appearance and the
distribution of the Cepheids in the HR diagram. Many factors can modify the
loops, including all those able to change the relative contribution
to the total luminosity from the H-burning shell and the central He-burning
core. In this respect, a crucial effect is produced by the physical treatment
of the central and envelope convection and related uncertainties.
For the intermediate-mass stars, appreciable core overshooting during the
main sequence
causes a smaller loop, while envelope overshooting during
the RGB phase tends to favour more extended loops.
The parameters characterizing the core and envelope overshoot in
Padova models were calibrated with observational constraints (Alongi
et al. 1991, 1993 and ref. therein).
In Figs. 9-11, we present
tracks for
2.5, 3, 4, 5, 6, 7, 8, and
![]() for values of the metallicity Z=0.002, Z=0.004, and Z=0.008.
To compare the extension of the loops,
in the same figures we plotted the corresponding tracks computed
by the Teramo group (TE04, Pietrinferni et al. 2004). These TE04 stellar models
have an upper mass limit of
for values of the metallicity Z=0.002, Z=0.004, and Z=0.008.
To compare the extension of the loops,
in the same figures we plotted the corresponding tracks computed
by the Teramo group (TE04, Pietrinferni et al. 2004). These TE04 stellar models
have an upper mass limit of
![]() in their database.
The main-sequence phases and the contraction towards the Hayashi limit
are very similar for the two evolutionary grids. Our red giant phase
appears slightly redder because of a different
choice of mixing length parameter. The loops have different extensions,
but this is normal because of the sensitivity of the loops to many of the
input parameters.
in their database.
The main-sequence phases and the contraction towards the Hayashi limit
are very similar for the two evolutionary grids. Our red giant phase
appears slightly redder because of a different
choice of mixing length parameter. The loops have different extensions,
but this is normal because of the sensitivity of the loops to many of the
input parameters.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig9.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg71.png)
|
Figure 9:
PD09 evolutionary tracks with
Z=0.002, Y=0.23 for masses between 2.5 and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig10.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg72.png)
|
Figure 10:
PD09 evolutionary tracks with
Z=0.004, Y=0.26 for masses between 2.5 and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig11.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg73.png)
|
Figure 11:
PD09 evolutionary tracks with
Z=0.008, Y=0.26 for masses between 2.5 and
|
| Open with DEXTER | |
The only true and puzzling difference is that related to the absence of loops in TE04 tracks at lower mass in the case Z=0.004. Our tracks illustrate a typical behaviour, in the sense that the minimum mass exhibiting a significant loop (able to intercept the instability strip of Cepheids) tends to increase with the metal content Z (and with the helium content Y at fixed metallicity). This prediction is confirmed by all the chemical compositions considered in our computations.
In contrast, the case Z=0.004 of TE04 appears to contradict this pattern,
since only the
![]() model exhibits an extended loop, while for
Z=0.002 and Z=0.008 loops are present at lower masses.
This is at variance with the period (mass) distribution of Cepheids in the
SMC, for which the metal content Z=0.004 is usually adopted.
model exhibits an extended loop, while for
Z=0.002 and Z=0.008 loops are present at lower masses.
This is at variance with the period (mass) distribution of Cepheids in the
SMC, for which the metal content Z=0.004 is usually adopted.
A similar difference was already shown by evolutionary tracks
of intermediate-mass stars with no convective overshooting discussed in
Castellani et al. (1990). They explained the decrease in the extension of
the blue loop for masses around 5 ![]() and the intermediate metal
content Z=0.006 and Y=0.23, connected with the occurrence of the
first dredge-up. It is not obvious why this feature is not present for
higher Y values and/or different Z, as would be expected.
and the intermediate metal
content Z=0.006 and Y=0.23, connected with the occurrence of the
first dredge-up. It is not obvious why this feature is not present for
higher Y values and/or different Z, as would be expected.
6.1 Comparison with the observations: SMC, LMC, Milky Way
Cordier et al. (2003) explored the distribution of SMC Cepheids in the HR diagram in relation to the extension of the loops of the evolutionary tracks. They showed that the blue loops are sufficiently extended only if the metallicity is substantially lower than the usually adopted value for the SMC. They found that tracks with metallicity Z=0.001 correctly reproduce the boundary of the Cepheids towards lower luminosity. According to Cordier et al. (2003), Cepheids populating the faint bottom of the instability strip are likely to be metal-poor stars, while variables distributed throughout the instability strip should belong to populations of various metal contents.
Romaniello et al. (2008) derived direct measurements of the iron abundances of Galactic and Magellanic Cepheids from FEROS and UVES high-resolution and high signal-to noise spectra. The mean iron abundance ([Fe/H]) was found to be about solar for the Galactic sample, with a range of values between -0.18 dex and +0.25 dex. For the LMC sample, the mean value is about -0.33 dex with a range of values between -0.62 dex and -0.10 dex. For the SMC sample, the mean value is about -0.75 dex with a range of values between -0.87 and -0.63 dex.
If the behaviour of the loops in the evolutionary models is correct (i.e., the increase of the minimum mass that intercepts the instability strip with Z and Y), this means that the lower limit to data for Cepheids in the HR diagram is determined by the stars of lower metal content Z. In Figs. 12-14 we checked whether our models can reproduce the lower boundaries of the instability strip compatibly with the dispersion in Z found by Romaniello et al. (2008) for SMC, LMC, and MW respectively.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig12.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg75.png)
|
Figure 12:
PD09 isochrones with
Z=0.002, Y=0.24 for ages in the range
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig13.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg77.png)
|
Figure 13:
PD09 isochrones with
Z=0.006, Y=0.25 for ages in the range
|
| Open with DEXTER | |
In Fig. 12 we show the loops of isochrones with ages in the range
![]() (the separation between the isochrones is
(the separation between the isochrones is
![]() )
and
chemical composition Z=0.002, Y=0.24. The blue and red
long dashed lines represent, respectively, the blue and red edges of the
theoretical instability strip as obtained by Eqs. (1a) and (2a) in
Caputo et al. (2004),
where we adopt the mass-luminosity relation calibrated in our models.
The black thick line represents the lower boundary of the instability strip
from Fig. 7 of the paper on the SMC Cepheids by Sandage et al. (2009).
The blue and red dotted lines are the experimental
boundaries of the strip shown in the same Fig. 7 of Sandage et al.
We note that:
)
and
chemical composition Z=0.002, Y=0.24. The blue and red
long dashed lines represent, respectively, the blue and red edges of the
theoretical instability strip as obtained by Eqs. (1a) and (2a) in
Caputo et al. (2004),
where we adopt the mass-luminosity relation calibrated in our models.
The black thick line represents the lower boundary of the instability strip
from Fig. 7 of the paper on the SMC Cepheids by Sandage et al. (2009).
The blue and red dotted lines are the experimental
boundaries of the strip shown in the same Fig. 7 of Sandage et al.
We note that:
- the observed instability strip is narrower than the theoretical one;
- the slope of the lower boundary for observed stars coincides with the slope of the faint envelope of the loops;
- the masses of the stars developing loops close to the
observed lower boundary are in the range
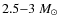 ;
;
- the observed lower limit could be recovered by models by adopting a slightly lower metal content than the assumed Z=0.002 (as given by Romaniello et al. 2008).
- in the case of the LMC, the observed strip is also narrower than the theoretical one (the red edges differ significantly in position but not in slope);
- the ages of the loops shown are in the interval
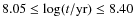 (with
(with
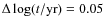 )
and the masses of models with
loops close to the observed bottom are in the range
)
and the masses of models with
loops close to the observed bottom are in the range
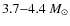 ;
;
- the chemical composition adopted in our analysis (Z=0.006) that can
reproduce the observations is
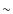
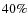 higher than the lower
limit indicated by Romaniello et al. (Z=0.004) and
higher than the lower
limit indicated by Romaniello et al. (Z=0.004) and 
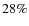 lower than
the mean value (Z=0.008), which is usually adopted for the LMC.
lower than
the mean value (Z=0.008), which is usually adopted for the LMC.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig14.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg85.png)
|
Figure 14:
PD09 isochrones with
Z=0.010, Y=0.26 for ages in the range
|
| Open with DEXTER | |
6.2 Mass discrepancy
A long-standing open question is given by the
discrepancy between the pulsation and the evolutionary mass of
the Cepheids (for a brief review see Keller 2008).
Caputo et al. (2005) considered 34 Cepheids in the Milky Way
with solar-like metal content previously studied by Storm et al. (2004).
They determined the pulsation mass ![]() from the predicted PLC relations
and the evolutionary one
from the predicted PLC relations
and the evolutionary one ![]() from the mass-period-luminosity (MPL) or
the mass-color-luminosity (MCL) relations adopting
the canonical
from the mass-period-luminosity (MPL) or
the mass-color-luminosity (MCL) relations adopting
the canonical![]() relation mass-luminosity (ML).
The comparison between the two determinations of the mass showed that
the
relation mass-luminosity (ML).
The comparison between the two determinations of the mass showed that
the
![]() ratio is correlated with the Cepheid period, ranging
from
ratio is correlated with the Cepheid period, ranging
from ![]() at
at
![]() to
to ![]() 1 at
1 at
![]() .
In other words, the discrepancy between the pulsation
and the evolutionary mass decreases when moving from lower to higher mass
Cepheids and disappears for masses around
.
In other words, the discrepancy between the pulsation
and the evolutionary mass decreases when moving from lower to higher mass
Cepheids and disappears for masses around
![]() .
The authors
interpreted this discrepancy as an effect of mass loss occurring during
and before the central He-burning phase. However, the data would imply
a mass-loss efficiency that decreases with increasing Cepheid initial
mass; this mass-loss is at odds with empirical estimates
where the mass loss increases with stellar luminosity
and radius (Schroeder & Cuntz 2007).
Another plausible solution of the Cepheid mass discrepancy is given
by extra convective mixing; in this case, the relation ML is modified
because the luminosity of the He-burning phase is higher than in the
canonical case and increases with an increasing amount of extra mixing.
Chiosi et al. (1992a,b) discussed the mass discrepancy of Cepheids by comparing
models incorporating either semiconvection or overshoot and determining
the pulsation mass from Cepheid models (Chiosi et al. 1993).
In the case of models with overshoot, the discrepancy no longer exists for the
considered Cepheids in the young rich LMC cluster NGC 2157.
.
The authors
interpreted this discrepancy as an effect of mass loss occurring during
and before the central He-burning phase. However, the data would imply
a mass-loss efficiency that decreases with increasing Cepheid initial
mass; this mass-loss is at odds with empirical estimates
where the mass loss increases with stellar luminosity
and radius (Schroeder & Cuntz 2007).
Another plausible solution of the Cepheid mass discrepancy is given
by extra convective mixing; in this case, the relation ML is modified
because the luminosity of the He-burning phase is higher than in the
canonical case and increases with an increasing amount of extra mixing.
Chiosi et al. (1992a,b) discussed the mass discrepancy of Cepheids by comparing
models incorporating either semiconvection or overshoot and determining
the pulsation mass from Cepheid models (Chiosi et al. 1993).
In the case of models with overshoot, the discrepancy no longer exists for the
considered Cepheids in the young rich LMC cluster NGC 2157.
On the one side, mass loss, in an ad-hoc manner at least, offers a mechanism capable of modifying the M-L relation by directly reducing the mass of a Cepheid. On the other side, according to a discussion by Neilson & Lester (2008, 2009), considering winds driven not only by radiation, but including momentum input from pulsation and shocks generated in the atmosphere, the calculated mass-loss rate for Cepheids is enhanced and helps us to illuminate the issue of infrared excess and the mass discrepancy,
After reanalysing the results of Caputo et al. (2005), Keller (2008) rejects the mass loss hypothesis and reaches the conclusion that an increased internal mixing remains the most likely cause of the Cepheids mass discrepancy.
As an exercise, we considered the same sample of Cepheids used
in Fig. 14 (Cepheids in open clusters of Table 3 of Tammann et al.
2003). For a solar chemical composition (Z=0.017, Y=0.27) we computed
a dense grid of isochrones (
![]() ), then
for each point (Cepheid) of the plane
MV-(MV-MI), we obtained the
minimum distance from the points which describe the totality of the
isochrones. This minimum singles out the age and the evolutionary mass
), then
for each point (Cepheid) of the plane
MV-(MV-MI), we obtained the
minimum distance from the points which describe the totality of the
isochrones. This minimum singles out the age and the evolutionary mass
![]() of
the Cepheid under consideration (with an uncertainty related to the
ranging of isochrones). The corresponding pulsation mass
of
the Cepheid under consideration (with an uncertainty related to the
ranging of isochrones). The corresponding pulsation mass ![]() was computed using the mass-dependent PLC relation for fundamental
pulsators (employing the observed quantities MI and (MV-MI) of Table 2
in Caputo et al. 2005). The estimated pulsation and evolutionary masses are
presented in Fig. 15. In the same figure, the open symbols
represent the pulsation masses computed with the PLC relation by Chiosi et al.
(1993) (we point out that the opacity tables used in Chiosi et al.
differ from those of Caputo et al. and those of the present paper).
was computed using the mass-dependent PLC relation for fundamental
pulsators (employing the observed quantities MI and (MV-MI) of Table 2
in Caputo et al. 2005). The estimated pulsation and evolutionary masses are
presented in Fig. 15. In the same figure, the open symbols
represent the pulsation masses computed with the PLC relation by Chiosi et al.
(1993) (we point out that the opacity tables used in Chiosi et al.
differ from those of Caputo et al. and those of the present paper).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig15.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg93.png)
|
Figure 15: Cepheids in open clusters and associations (from the paper by Tammann et al. 2003) are plotted with the pulsation and the evolutionary mass determined as described in the text. Solid dots are pulsation masses determined according to the PLC relation by Caputo et al. (2005) and open circles according to the PLC relation by Chiosi et al. (1993). |
| Open with DEXTER | |
Independently from the formulation used to obtain ![]() ,
the data plotted
in this figure show that for stars of mass lower than
,
the data plotted
in this figure show that for stars of mass lower than ![]()
![]() ,
the
evolutionary mass is higher than the pulsation one (
,
the
evolutionary mass is higher than the pulsation one (
![]() ),
while for stars more massive than
),
while for stars more massive than
![]() the pulsation mass is higher
than the evolutionary one (
the pulsation mass is higher
than the evolutionary one (
![]() ).
In the range
).
In the range
![]() ,
the parametrization
,
the parametrization
![]() could be
satisfactory. We could interpret this by suggesting that the parameter
could be
satisfactory. We could interpret this by suggesting that the parameter
![]() ,
which determines the efficiency of the extramixing, must be a
function of the mass of the star. In other words,
,
which determines the efficiency of the extramixing, must be a
function of the mass of the star. In other words,
![]() should
decrease with increasing stellar mass, assuming values close to
should
decrease with increasing stellar mass, assuming values close to
![]() in the
range
in the
range
![]() .
This should be taken as a suggestion and not a firm
result because the number of stars in the sample is very limited; the
values of the absolute magnitudes of the Cepheids are significantly different
depending on the different estimates.
.
This should be taken as a suggestion and not a firm
result because the number of stars in the sample is very limited; the
values of the absolute magnitudes of the Cepheids are significantly different
depending on the different estimates.
From our sample, we excluded GY Sge and S Vul because their ![]() was >
was >
![]() (i.e., beyond the validity range of theoretical
relations), and EV Sct because it is probably a binary.
The differences between
the results of Keller and ours are mainly caused by
Keller proposing an additional internal mixing, parametrized by
(i.e., beyond the validity range of theoretical
relations), and EV Sct because it is probably a binary.
The differences between
the results of Keller and ours are mainly caused by
Keller proposing an additional internal mixing, parametrized by
![]() for the whole mass range, and us suggesting an extra
mixing that decreases with the stellar mass, but with
for the whole mass range, and us suggesting an extra
mixing that decreases with the stellar mass, but with
![]() in the range
in the range
![]() .
.
7 Massive red supergiants
Red supergiants (RSGs) are a He-burning phase in the evolution of moderately
high mass stars (
![]() ). The evolution of these stars, particularly
at low metallicities, is still poorly understood. The latest-type RSGs in the
Magellanic Clouds are cooler than the current evolutionary tracks allow,
occupying the region to the right of the Hayashi limit where stars are no
longer in hydrostaic equilibrium.
Until recently, the location of Galactic red supergiants (RSGs) in the
Hertzsprung-Russell (H-R) diagram was poorly matched by stellar evolutionary
tracks, evolutionary theory being unable to produce stars as cool and luminous
as those observed (Massey 2003). Many possible explanations might
contribute to this discrepancy: there is poor knowledge of RSG molecular
opacities, the near-sonic velocities of the convective layers invalidate
simplifications of mixing length theory, and the highly extended atmospheres
of these stars differ from the plane-parallel geometry assumption adopted by
evolutionary models (Levesque et al. 2006). A similar problem was evident for
RSGs in the Magellanic Clouds (MCs) as shown by the data of Massey & Olsen
(2003) with the more robust available calibration at that time.
). The evolution of these stars, particularly
at low metallicities, is still poorly understood. The latest-type RSGs in the
Magellanic Clouds are cooler than the current evolutionary tracks allow,
occupying the region to the right of the Hayashi limit where stars are no
longer in hydrostaic equilibrium.
Until recently, the location of Galactic red supergiants (RSGs) in the
Hertzsprung-Russell (H-R) diagram was poorly matched by stellar evolutionary
tracks, evolutionary theory being unable to produce stars as cool and luminous
as those observed (Massey 2003). Many possible explanations might
contribute to this discrepancy: there is poor knowledge of RSG molecular
opacities, the near-sonic velocities of the convective layers invalidate
simplifications of mixing length theory, and the highly extended atmospheres
of these stars differ from the plane-parallel geometry assumption adopted by
evolutionary models (Levesque et al. 2006). A similar problem was evident for
RSGs in the Magellanic Clouds (MCs) as shown by the data of Massey & Olsen
(2003) with the more robust available calibration at that time.
Afterwards Levesque et al. (2005, 2006) used moderate-resolution
optical spectrophotometry and the new MARCS stellar atmosphere models (Plez
2003; Gustafsson et al. 2003) to determine the physical properties of RSGs in
both the Milky Way and the MCs for the comparison with the evolutionary models.
They derived a new effective temperature scale significantly warmer than those
in the literature, showing that the newly derived temperatures and bolometric
corrections provide closer agreement with stellar evolutionary tracks.
The comparison of Galactic RSGs was with the Geneva evolutionary tracks of
solar metallicity (Meynet & Maeder 2003) spanning a range of initial
rotational velocities from 0 to 300 km s-1.
Levesque et al. (2006) extended their study to Magellanic Cloud red
supergiants to test the effects of metallicity and found evidence of
significant visual extinction because of circumstellar dust. The effective
temperatures of K supergiants are about the same in the SMC, LMC and
Milky Way but the lower abundance of TiO leads to effective temperatures
that are lower for M supergiants of the same spectral subtype.
On average, RSGs in the Magellanic Clouds are not as cool as Galactic RSGs, in
agreement with the shifting of the rightmost extension (the Hayashi limit)
of the evolutionary tracks to warmer effective temperatures at lower
metallicities. The observed average spectral subtypes of RSGs in these galaxies
shifts from M2 I in the Milky Way to M1 I in the LMC and K5-K7 I in the
SMC.
The newly derived physical parameters by Levesque et al. (2005, 2006) brought
the location of the RSGs into
much closer agreement with the predictions of stellar evolutionary theory.
There is now excellent agreement between Milky Way supergiants and the
evolutionary tracks, accurately reproducing this stage of massive star
evolution in the Milky Way. Figures 16-18 show our more
massive tracks from 10 to 20 ![]() displaying also the data from Levesque
et al. (2005, 2006) of RSGs in the Milky Way, LMC, and SMC.
displaying also the data from Levesque
et al. (2005, 2006) of RSGs in the Milky Way, LMC, and SMC.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig16.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg101.png)
|
Figure 16:
Evolutionary tracks in the HR diagram, for the composition
Z=0.017,
Y=0.30 for masses
10, 12, 15, and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig17.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg102.png)
|
Figure 17:
Evolutionary tracks in the HR diagram, for the composition
Z=0.008,
Y=0.26 for masses
10, 12, 15, and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig18.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg103.png)
|
Figure 18:
Evolutionary tracks in the HR diagram, for the composition
Z=0.004,
Y=0.26 for masses
10, 12, 15, and
|
| Open with DEXTER | |
8 Concluding remarks
Observations of some globular clusters in the Galaxy and the LMC provide evidence of multiple populations and/or significant variations in the helium content, in contrast to traditional scenarios in which globular clusters are simple stellar populations of uniform age and chemical composition. The current database of Padova tracks allows the computation of isochrone sets covering a wide range of ages and enables users to analyse stellar populations (star clusters or galaxies) with different helium enrichment laws, given the extended Z-Y region of the evolutionary models.
The scaled solar database of models and isochrones, presented in Paper I, has
been extended in mass to include stellar evolutionary computations from
2.5 to
![]() for the same large region of the Z-Y plane.
An important update of this database is the extension of stellar models and
isochrones until the end of the TP-AGB phase by means of synthetic models,
using the same relations as in Marigo & Girardi (2007).
Revised bolometric corrections by Girardi et al. (2008) are employed to
transform Padova isochrones into UBVRIJHK and ACS photometric systems.
for the same large region of the Z-Y plane.
An important update of this database is the extension of stellar models and
isochrones until the end of the TP-AGB phase by means of synthetic models,
using the same relations as in Marigo & Girardi (2007).
Revised bolometric corrections by Girardi et al. (2008) are employed to
transform Padova isochrones into UBVRIJHK and ACS photometric systems.
In the range of more massive stars presented in this Paper II, our models can be tested in at least two interesting astrophysical problems: 1) Cepheids and the mass-discrepancy problem; 2) massive red supergiants and the problems of their effective temperature (Massey 2003).
Considering the observations of Cepheids in the Galaxy and the Magellanic Clouds (Tamman et al. 2003; Sandage et al. 2004, 2009), we show that the observed instability strip is narrower than the theoretical one, and that the slope of the lower boundary of observed stars coincides with the slope of the faint envelope connecting each of the loops of the theoretical tracks for the chemical composition of the MCs. Because of the small number of Cepheids in open clusters and associations of the Milky Way, we cannot draw the lower boundary of the observed strip as we did for the MCs, but in this case, the loops of the theoretical models can also indicate the location of MW Cepheids in the HR-diagram.
The long-standing open question about the discrepancy between the pulsation and
the evolutionary mass of Cepheid stars is considered, by determining the
evolutionary mass of Cepheids in MW open clusters (Tamman et al. 2003) from
our models (isochrones) and the pulsation mass from the mass dependent PLC
relation for fundamental pulsators. The evolutionary mass is found to be higher
than the pulsation mass for stars of mass lower than ![]()
![]() ,
while
for stars more massive than 10
,
while
for stars more massive than 10 ![]() the pulsation mass is higher than the
evolutionary one. If we consider extra convective mixing as a plausible
solution of the Cepheid mass discrepancy, the parameter that determines the
efficiency of the extra mixing should decrease with increasing stellar mass.
the pulsation mass is higher than the
evolutionary one. If we consider extra convective mixing as a plausible
solution of the Cepheid mass discrepancy, the parameter that determines the
efficiency of the extra mixing should decrease with increasing stellar mass.
Red supergiants in both the Galaxy and the Magellanic Clouds were too cool and
luminous compared with evolutionary tracks (Massey 2003; Massey &
Olsen 2003) until when Levesque et al. (2005, 2006) derived a new effective
temperature scale and new bolometric corrections, producing far closer
agreement with stellar evolutionary tracks. Our tracks from 10 to 20 ![]() for the appropriate chemical composition can reproduce the
location in the H-R diagram of red supergiants in the MW and the MCs as given
by Levesque et al. (2005, 2006).
for the appropriate chemical composition can reproduce the
location in the H-R diagram of red supergiants in the MW and the MCs as given
by Levesque et al. (2005, 2006).
A web site has been dedicated to make available the entire database to the scientific community.
In the section YZVAR of the static databases at http://stev.oapd.inaf.it users can find:
- data files with the information relative to each evolutionary track;
- isochrone files from Paper I
with the chemical composition of the computed grids in
the Z-Y plane, and age interval in the range
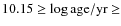
 9.00.
9.00.
We point out that older isochrones (Paper I) are available in both the static database and the interactive service, while younger isochrones only interactively. All isochrones (old and young) are available through the interactive service for the chosen photometric system (see Sect. 5.3).
In the future, a web interactive interface will provide data of stellar populations in terms of SFR, IMF, chemical composition, and mass loss during the RGB phase.
AcknowledgementsWe acknowledge our referee's useful comments and suggestions that helped to improve the presentation of our results. We thank C. Chiosi for his continuous interest and support to stellar evolution computations. We thank A. Weiss and B. Salasnich for help with opacity tables, G. Bono and A. Bressan for useful discussions. We acknowledge financial support from INAF COFIN 2005 ``A Theoretical lab for stellar population studies'' and from Padova University (Progetto di Ricerca di Ateneo CPDA 052212).
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef]
- Allard, F., et al. 2000, in From giant planets to cool stars, ed. C. A. Griffith, & M. S. Marley, ASP Conf. Ser., 212, 127
- Alongi, M., Bertelli, G., Bressan, A., & Chiosi, C. 1991, A&A, 244, 95 [NASA ADS]
- Alongi, M., Bertelli, G., Bressan, A., et al. 1993, A&AS, 97, 851 [NASA ADS]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 19 [CrossRef]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef]
- Asplund, M., Grevesse, N., Sauval, A. J., et al. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences]
- Basu, S., & Antia, H. M. 2008, Phys. Rep., 457, 217 [NASA ADS] [CrossRef]
- Bemmerer, D., et al. (LUNA Collaboration) 2006, Nucl. Phys. A, 779, 297
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I)
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [NASA ADS]
- Bono, G., Caputo, F., Cassisi, S., et al. 2000, ApJ, 543, 955 [NASA ADS] [CrossRef]
- Bressan, A., Bertelli, G., & Chiosi, C. 1981, A&A, 102, 25 [NASA ADS]
- Bressan, A., Fagotto, F., Bertelli, G., & Chiosi, C. 1993, A&AS, 100, 647 [NASA ADS]
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2008, A&A, 488, 1031 [NASA ADS] [CrossRef] [EDP Sciences]
- Caputo, F., Castellani, V., Degl'Innocenti, S., Fiorentino, G., & Marconi, M. 2004, A&A, 424, 927 [NASA ADS] [CrossRef] [EDP Sciences]
- Caputo, F., Bono, G., Fiorentino, G., Marconi, M., & Musella, I. 2005, A&A, 629, 1021 [NASA ADS]
- Castellani, V., Chieffi, A., Tornambe, A., & Pulone, L. 1985, ApJ, 296, 204 [NASA ADS] [CrossRef]
- Castellani, V., Chieffi, A., & Straniero, O. 1990, ApJS, 74, 463 [NASA ADS] [CrossRef]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, ed. N. E. Piskunov et al. (San Francisco: ASP) IAU Symp., 210, 20
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef]
- Caughlan, G. R., & Fowler, W. A. 1988, Atom. Data Nucl. Data Tables, 40, 283 [NASA ADS] [CrossRef]
- Charbonnel, C., Meynet, G., Maeder, A., et al. 1993, A&A, 101, 415 [NASA ADS]
- Chiosi, C., & Maeder, A. 1986, ARA&A, 24, 239 [NASA ADS] [CrossRef]
- Chiosi, C., Bertelli, G., & Bressan, A. 1992a, ARA&A, 30, 305 [NASA ADS] [CrossRef]
- Chiosi, C., Wood, P. R., Bertelli, G., Bressan, A., & Mateo, M. 1992b, ApJ, 385, 205 [NASA ADS] [CrossRef]
- Chiosi, C., Wood, P. R., & Capitanio, N. 1993, ApJS, 86, 541 [NASA ADS] [CrossRef]
- Cordier, D., Goupil, M. J., & Lebreton, Y. 2003, A&A, 409, 491 [NASA ADS] [CrossRef] [EDP Sciences]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. 1988, A&AS, 72, 295 [NASA ADS]
- de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] 489, 685
- Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994a, A&AS, 104, 365 [NASA ADS]
- Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994b, A&AS, 105, 29 [NASA ADS]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef]
- Formicola, A., et al. (LUNA Collaboration) 2004, Phys. Lett. B, 591, 61
- Fluks, M. A., Plez, B., The, P. S., de Winter, D., et al. 1994, A&AS, 105, 311 [NASA ADS]
- Girardi, L., Bressan, A., Chiosi, C., Bertelli, G., & Nasi, E. 1996, A&AS, 117, 113 [NASA ADS] [CrossRef] [EDP Sciences]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences]
- Girardi, L., Castelli, F., Bertelli, G., & Nasi, E. 2007, A&A, 468, 657 [NASA ADS] [CrossRef] [EDP Sciences]
- Girardi, L., Dalcanton, J., Williams, B., et al. 2008, PASP, 120, 583 [NASA ADS] [CrossRef]
- Graboske, H. C., de Witt, H. E., Grossman, A. S., & Cooper, M. S. 1973, ApJ, 181, 457 [NASA ADS] [CrossRef]
- Grevesse, N. 1991, J. Phys. IV, 1, 181 [CrossRef]
- Grevesse, N., & Noels, A. 1993, Phys. Scr. T, 47, 133 [NASA ADS] [CrossRef]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [NASA ADS] [CrossRef]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2003, in Stellar Atmosphere Modeling, ed. I. Hubeny et al., ASP Conf. Ser., 288, 331
- Guzik, J. A., Watson, L. S., Cox, A. N., et al. 2005, ApJ, 627, 1049 [NASA ADS] [CrossRef]
- Guzik, J. A., Watson, L. S., & Cox, A. N. 2006, MSAIt, 77, 389 [NASA ADS]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef]
- Holtzman, J. A., Burrows, C. J., Casertano, S., et al. 1995, PASP, 107, 1065 [NASA ADS] [CrossRef]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2004, A&A, 420, 625 [NASA ADS] [CrossRef] [EDP Sciences]
- Imbriani, G., et al. (LUNA Collaboration) 2005, EPJ A, 25, 455
- Itoh, N., Mitake, S., Iyetomi, H., & Ichimara, S. 1983, ApJ, 273, 774 [NASA ADS] [CrossRef]
- Keller, S. C. 2008, ApJ, 677, 483 [NASA ADS] [CrossRef]
- Kippenhahn, R., Weigert, A., & Hofmeister, E. 1967, in Methods in Computational Physics, ed. B. Alder, S. Fernbach, & M. Rotenberg (New York: Academic Press), 7, 129
- Kudritzki, R. P. 2002, ApJ, 577, 389 [NASA ADS] [CrossRef]
- Kudritzki, R. P., & Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] [CrossRef]
- Kudritzki, R. P., Gabler, A., Gabler, R., Groth, H. G., & Pauldrach, A. W. A. 1989, IAU Coll., 113, 67 [NASA ADS]
- Landré, V., Prantzos, N., Aguer, P., et al. 1990, A&A, 240, 85 [NASA ADS]
- Lemut, A., et al. (LUNA Collaboration) 2006, Phys. Lett, B, 634, 483
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2005, ApJ, 628, 973 [NASA ADS] [CrossRef]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2006, ApJ, 645, 1102 [NASA ADS] [CrossRef]
- Loidl, R., Lancon, A., & Jorgensen, U. G. 2001, A&A, 371, 1065 [NASA ADS] [CrossRef] [EDP Sciences]
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin, Heidelberg: Springer)
- Marigo, P., & Aringer, B. 2009, A&A, in press [arXiv:0907.3248]
- Marigo, P., & Girardi, L. 2007, A&A, 469, 239 [NASA ADS] [CrossRef] [EDP Sciences]
- Marigo, P., Girardi, L., Chiosi, C., & Wood, P. R. 2001, A&A, 371, 152 [NASA ADS] [CrossRef] [EDP Sciences]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences]
- Massey, P. 2003, ARA&A, 41, 15 [NASA ADS] [CrossRef]
- Massey, P., & Olsen, K. A. G. 2003, AJ, 126, 2867 [NASA ADS] [CrossRef]
- Massey, P., Levesque, E. M., Plez, B., & Olsen, K. A. G. 2008, in Proc. IAU Symp. 250, 97
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS]
- Meynet, G., Maeder, A., Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97 [NASA ADS]
- Mihalas, D., Hummer, D. G., Mihalas, B. W., & Däppen, W. 1990, ApJ, 350, 300 [NASA ADS] [CrossRef]
- Mokiem, M. R., de Koter, A., Vink, J. S., et al. 2007, A&A, 473, 603 [NASA ADS] [CrossRef] [EDP Sciences]
- Montalban, J., Miglio, A., Noels, A., Grevesse, N., & di Mauro, M. P. 2004, ESA SP-559, 574
- Neilson, H. R., & Lester, J. B. 2008, ApJ, 684, 569 [NASA ADS] [CrossRef]
- Neilson, H. R., & Lester, J. B. 2009, ApJ, 690, 1829 [NASA ADS] [CrossRef]
- Pompéia, L., Hill, V., Spite, M., et al. 2008, A&A, 480, 379 [NASA ADS] [CrossRef] [EDP Sciences]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef]
- Piotto, G. 2009, in The Ages of Stars, IAU Symp., 258, 233
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef]
- Plez, B. 2003, in GAIA Spectroscopy: Science and Technology, ed. U. Munari, ASP Conf. Ser., 298, 189
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef]
- Romaniello, M., Primas, F., Mottini, M., et al. 2008, A&A, 488, 731 [NASA ADS] [CrossRef] [EDP Sciences]
- Salaris, M., Chieffi, A., & Straniero, O. 1993, ApJ, 414, 580 [NASA ADS] [CrossRef]
- Salasnich, B., Girardi, L., Weiss, A., & Chiosi, C. 2000, A&A, 361, 1023 [NASA ADS]
- Salpeter, E. E. 1955, ApJ, 121,161
- Sandage, A., Tammann, G. A., & Reindl, B. 2004, A&A, 424, 43 [NASA ADS] [CrossRef] [EDP Sciences]
- Sandage, A., Tammann, G. A., & Reindl, B. 2009, A&A, 493, 471 [NASA ADS] [CrossRef] [EDP Sciences]
- Schaerer, D., Meynet, G., Maeder, A., & Schaller, G. 1993a, A&AS, 98, 523 [NASA ADS]
- Schaerer, D., Charbonnel, C., Meynet, G., Maeder, A., & Schaller, G. 1993b, A&AS, 102, 339 [NASA ADS]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [NASA ADS]
- Schlattl, H., & Weiss, A. 1998, in Proc. Neutrino Astrophysics, Ringberg Castle, Germany, Oct. 1997, ed. M. Altmann, W. Hillebrandt et al.
- Schroder, K. P., & Cuntz, M. 2007, A&A, 465, 593 [NASA ADS] [CrossRef] [EDP Sciences]
- Scott, P., Asplund, M., Grevesse, N., & Sauval, A. J. 2009, ApJ, 691, L119 [NASA ADS] [CrossRef]
- Sirianni, M., Jee, M. J., Benítez, N., et al. 2005, PASP, 117, 1049 [NASA ADS] [CrossRef]
- Storm, J., Carney, B. W., Gieren, W. P., et al. 2004, A&A, 415, 531 [NASA ADS] [CrossRef] [EDP Sciences]
- Tammann, G. A., Sandage, A., & Reindl, B. 2003, A&A, 404, 423 [NASA ADS] [CrossRef] [EDP Sciences]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [CrossRef]
- Vemury, S. K., & Stothers, R. 1978, ApJ, 225, 939 [NASA ADS] [CrossRef]
- Villanova, S., Piotto, G., King, I., et al. 2007, ApJ, 663, 296 [NASA ADS] [CrossRef]
- Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences]
- Weaver, T. A., & Woosley, S. E. 1993, Phys. Rep., 227, 65 [NASA ADS] [CrossRef]
- Weiss, A., & Schlattl, H. 2000, A&AS, 144, 487 [NASA ADS] [CrossRef] [EDP Sciences]
- Weiss, A., Keady, J. J., & Magee, N. H. Jr. 1990, Atom. Data Nucl. Data Tables, 45, 209 [NASA ADS] [CrossRef]
- Weiss, A., Serenelli, A., Kitsikis, A., et al. 2005, A&A, 441, 1129 [NASA ADS] [CrossRef] [EDP Sciences]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef]
Footnotes
- ... stars
![[*]](/icons/foot_motif.png)
- Isochrone tables are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/508/355
- ... format
![[*]](/icons/foot_motif.png)
- A website with the complete data-base (including additional data and future extensions) will be maintained at http://stev.oapd.inaf.it/YZVAR with suitable information on electronic tables (the same as in Paper I).
- ... site
![[*]](/icons/foot_motif.png)
- http://stev.oapd.inaf.it/YZVAR
- ... canonical
![[*]](/icons/foot_motif.png)
- By this term, we mean without overshooting from the convective core.
All Tables
Table 1: Combinations of Z and Y of the computed tracks.
Table 2: Surface chemical composition (by mass fraction) of [Z=0.008, Y=0.26] models.
All Figures
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12093fig1.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg41.png)
|
Figure 1: Evolutionary tracks in the HR diagram for the composition Z=0.001, Y=0.23 (dot-dashed line) and Z=0.001, Y=0.40 (solid line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{12093fig2.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg42.png)
|
Figure 2: Evolutionary tracks in the HR diagram for the composition Z=0.040, Y=0.26 (dot-dashed line) and Z=0.040, Y=0.40 (solid line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{12093fig3.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg44.png)
|
Figure 3:
Evolutionary tracks in the HR diagram for the composition
Z=0.004,
Y=0.26 computed with the new LUNA rate for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{12093fig4.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg45.png)
|
Figure 4:
Evolutionary tracks in the HR diagram for the composition
Z=0.017,
Y=0.26 computed with the new LUNA rate for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig5.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg57.png)
|
Figure 5: Comparison of isochrones for the same Z=0.001 and different helium content. Blue solid lines correspond to Y=0.40 (the related AGB is in black), and red dot-dashed ones to Y=0.23 (the related AGB is in green). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig6.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg58.png)
|
Figure 6: Comparison between interpolated and computed tracks with Z=0.0285, Y=0.28. The red dotted lines are the interpolated tracks between Z=0.017 and Z=0.040, while the green solid lines are the computed ones for the specific Z. The blue lines are the interpolated tracks taking into account the new set computed for Z=0.030 and various Y. Taking into account the new set, the interpolation is in closer agreement with the actual computed tracks. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig7.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg59.png)
|
Figure 7:
Comparison between interpolated and computed tracks with
Z=0.0007, Y=0.35.
The red dotted lines are the interpolated tracks for masses between 5 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig8.eps}\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg60.png)
|
Figure 8: Differences between the lifetime spent by the interpolated track (red solid line) and that of the computed track (green dashed line) are insignificant. The chemical composition is as in Fig. 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig9.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg71.png)
|
Figure 9:
PD09 evolutionary tracks with
Z=0.002, Y=0.23 for masses between 2.5 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig10.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg72.png)
|
Figure 10:
PD09 evolutionary tracks with
Z=0.004, Y=0.26 for masses between 2.5 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig11.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg73.png)
|
Figure 11:
PD09 evolutionary tracks with
Z=0.008, Y=0.26 for masses between 2.5 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig12.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg75.png)
|
Figure 12:
PD09 isochrones with
Z=0.002, Y=0.24 for ages in the range
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig13.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg77.png)
|
Figure 13:
PD09 isochrones with
Z=0.006, Y=0.25 for ages in the range
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig14.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg85.png)
|
Figure 14:
PD09 isochrones with
Z=0.010, Y=0.26 for ages in the range
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig15.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg93.png)
|
Figure 15: Cepheids in open clusters and associations (from the paper by Tammann et al. 2003) are plotted with the pulsation and the evolutionary mass determined as described in the text. Solid dots are pulsation masses determined according to the PLC relation by Caputo et al. (2005) and open circles according to the PLC relation by Chiosi et al. (1993). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig16.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg101.png)
|
Figure 16:
Evolutionary tracks in the HR diagram, for the composition
Z=0.017,
Y=0.30 for masses
10, 12, 15, and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig17.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg102.png)
|
Figure 17:
Evolutionary tracks in the HR diagram, for the composition
Z=0.008,
Y=0.26 for masses
10, 12, 15, and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12093fig18.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12093-09/Timg103.png)
|
Figure 18:
Evolutionary tracks in the HR diagram, for the composition
Z=0.004,
Y=0.26 for masses
10, 12, 15, and
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


