| Issue |
A&A
Volume 508, Number 1, December II 2009
|
|
|---|---|---|
| Page(s) | 451 - 455 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200911970 | |
| Published online | 21 October 2009 | |
A&A 508, 451-455 (2009)
Rotations and densities of trans-Neptunian objects![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png) (Research Note)
(Research Note)
D. Perna1,2,3 - E. Dotto3 - M. A. Barucci1 - A. Rossi4 - S. Fornasier1,5 - C. de Bergh1
1 - LESIA, Observatoire de Paris, 5 place Jules Janssen, 92195 Meudon Principal Cedex, France
2 - Università di Roma Tor Vergata, Italy
3 - INAF - Osservatorio Astronomico di Roma, Italy
4 - ISTI-CNR, Pisa, Italy
5 - Université Paris Diderot - Paris 7, France
Received 28 February 2009 / Accepted 12 July 2009
Abstract
Context. Trans-Neptunian objects (TNOs) represent a new
frontier in the study of our Solar System. In particular, the
investigation of their rotational properties can provide important
hints about their internal structure and collisional evolution.
Aims. We expand the limited sample of TNOs with known rotation
rates, and improve the knowledge of the physical nature of these
bodies.
Methods. We carried out photometric observations of 5 TNOs (144897 2004 UX10, 145451 2005 RM43, 145453 2005 RR43, 2003 UZ117, and 2003 UZ413) using the New Technology Telescope of the European Southern Observatory.
Results. We determined the spin rates of four targets, while only an estimation of the period was possible for 2003 UZ117.
Conclusions. From the computed rotational periods and the
obtained light curve amplitudes of four TNOs, we derived the lower
limit to their axis ratio a/b, and hence estimated
their density. Combining our new results with literature data, we
investigated the density statistics of the small bodies of the outer
Solar System.
Key words: Kuiper Belt - techniques: photometric
1 Introduction
The study of trans-Neptunian objects (TNOs) represents one of the most outstanding subjects in planetary science, since these distant and icy bodies are considered to be the remnants of the planetesimals in the outer Solar System and to retain the most pristine (least altered) material that can presently be observed. Their investigation can help us to cast light on the origin and early evolution of our own Solar System, as well as to understand how the same processes work in extra-solar protoplanetary disks and planetary systems.
In particular, it is possible to extract information about the
collisional history of TNOs by analysing their rotational rate
distribution with size, since the current spin properties of TNOs are
supposed to have been strongly affected by the mutual collisions
experienced by these bodies.
The majority of larger TNOs should rotate with quite primordial angular
momentums, while most of the smaller ones are probably fragments
generated by disruptive collisions (Davis & Farinella 1997). Sheppard et al. (2008) suggested that an intermediate population of radii 50 ![]() 100 km should have been gravitationally stable to catastrophic
break-up, but with spin properties highly altered over the age of the
Solar System.
100 km should have been gravitationally stable to catastrophic
break-up, but with spin properties highly altered over the age of the
Solar System.
A very powerful tool for retrieving information about these distant bodies is the analysis of their photometric light curves, which are functions of the rotational period, spin axis orientation, shape, and large-scale surface structure of the observed objects. Their densities are also constrained by rotational stability considerations, hence the analysis of light curves allows us to obtain hints about the internal structure of the investigated bodies.
To increase the still rather limited sample of TNOs with known rotational properties (few tens of objects, for a review see Sheppard et al. 2008), we carried out two observing runs at the New Technology Telescope (NTT) of the European Southern Observatory (ESO), in the framework of the Large Programme 178.C-0036 (P.I. Barucci). The results obtained from the first run for 5 TNOs and 2 Centaurs were published in Dotto et al. (2008). In this paper, we present the data collected during the second observing run studying 5 additional TNOs (144897 2004 UX10, 145451 2005 RM43, 145453 2005 RR43, 2003 UZ117, and 2003 UZ413).
2 Observations and data reduction
The data presented in this work were obtained on three nights
(December 4-6, 2007) at the ESO-NTT (La Silla, Chile)
using the EMMI instrument, equipped with a 2 ![]() 1 mosaic of 2048
1 mosaic of 2048 ![]() 4096 MIT/LL CCD with square 15
4096 MIT/LL CCD with square 15 ![]() m pixels. Photometric observations were performed in RILD mode, with a binning of 2
m pixels. Photometric observations were performed in RILD mode, with a binning of 2 ![]() 2, yielding a resolution of 0.33 arcsec/pixel. We used the R filter (centered on 641.0 nm), adjusting the exposure time according to the object magnitude and sky conditions.
2, yielding a resolution of 0.33 arcsec/pixel. We used the R filter (centered on 641.0 nm), adjusting the exposure time according to the object magnitude and sky conditions.
The images were reduced using standard procedures with the MIDAS software package: after subtraction of the bias from the raw data and flat-field correction, the instrumental magnitudes were measured with aperture photometry. Because of the non-photometric sky conditions, an absolute calibration of the magnitudes, by means of observing standard stars, was impossible. Therefore, we performed differential photometry with bright (to minimize random errors) field stars, typically using three of them within each image. By visual inspection and radial profile analysis of the images, we searched for possible signatures of a faint coma around the observed TNOs, but none were found.
The obtained (light-time corrected) single-night light curves are presented in Fig. 1.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{11970fg1.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg4.png)
|
Figure 1: Single-night light curves of the observed TNOs. The name of the target and the night of observation (with respect to 0 UT) are reported above each plot. |
| Open with DEXTER | |
3 Data analysis and results
We performed a Fourier analysis of the light curves following the method developed by Harris et al. (1989). For 4 out of the 5 observed TNOs, we obtained the synodic rotational period, while the quality of the data points was not good enough to find an unambiguous solution for 2003 UZ117, the faintest of our targets. The composite light curves are shown in Figs. 2-5.
Assuming that the observed light curve amplitudes are due only to the
bodies' shapes, with negligible albedo variations on their surfaces, we
estimated a lower limit to the axis ratio a/b from the relation
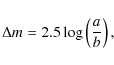
|
(1) |
where
A lower limit to the density of each observed object, below which
centrifugal break-up would occur, was derived by means of the equation

|
(2) |
where P is the rotational period (expressed in hours) and the resulting density is expressed in g cm-3. This formula is obtained by equating the centrifugal acceleration at the equator of a rotating prolate spheroid with its acceleration of gravity at the surface (Pravec & Harris 2000).
Furthermore, we estimated possible density ranges using the Chandrasekhar (1987) table for rotationally stable Jacobi ellipsoids. Minimum and maximum values of the density were obtained by inputing into the above-mentioned table the computed a/b lower limit and a/b=2.31 (more elongated ellipsoids are unstable to rotational fission, Jeans 1919), respectively.
We note that both these derivations of the density assume a
cohesionless and strengthless body, i.e., a body with no
tensile nor pressure-dependent strength. In other words, they assume a
fluid body. It was shown that while cohesion does not play a role
in determining the permissible spin
(for objects of diameter larger than about 10 km, which is
the case for the bodies we are dealing with), any granular material
(e.g., dry sand) can withstand considerable shear stress depending
on the confining pressure, as a consequence of the interlocking of the
granular particles (Holsapple 2001, 2004, 2007). This shear stress can be parameterized by the so-called angle of friction (![]() ). Typical values of the angle of friction in solid bodies are around
). Typical values of the angle of friction in solid bodies are around ![]() ,
while the fluid assumption implies that
,
while the fluid assumption implies that ![]() .
Ice acts as a viscous fluid over timescales of years, so an icy
body would relax to a fluid shape as described by Chandrasekhar (1987). In our analysis we made this simplifying assumption. Nonetheless, we emphasize that Holsapple showed
how a ``granular model'', with non-zero
.
Ice acts as a viscous fluid over timescales of years, so an icy
body would relax to a fluid shape as described by Chandrasekhar (1987). In our analysis we made this simplifying assumption. Nonetheless, we emphasize that Holsapple showed
how a ``granular model'', with non-zero ![]() ,
could describe such a body without constraining its shape to be a
Maclaurin or Jacobi ellipsoid. This should be taken into account,
especially in
cases where extremely low (e.g.,
,
could describe such a body without constraining its shape to be a
Maclaurin or Jacobi ellipsoid. This should be taken into account,
especially in
cases where extremely low (e.g.,
![]() g cm-3) or extremely high (e.g.,
g cm-3) or extremely high (e.g.,
![]() g cm-3) densities are derived within a strenghtless scenario.
g cm-3) densities are derived within a strenghtless scenario.
The outcome of the above-quoted analysis on the observed TNOs is presented below.
144897 2004 UX10:
we observed this target during three nights (December 4-6) for about 12 h. The composite light curve (Fig. 2) exhibits a double peaked periodicity of 7.58145451 2005 RM43:
its double peaked composite light curve (Fig. 3), of amplitude145453 2005 RR43:
from the analysis of the light curve (15 h of observations during three nights) a double peaked periodicity of 5.082003 UZ117:
we observed this object for about 10.5 h during two nights (December 4, 6). Although the light curve periodicity seems to be compatible with a rotational period of about 6 h, no clear solutions were found and different values are plausible.2003 UZ413:
the data we collected in about 14.5 h of observing time during three nights suggest, for this resonant (2:3) TNO, a double peaked periodicity of 4.13Table 1: Derived results.
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg2.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg35.png)
|
Figure 2: Composite light curve of 144897 2004 UX10, obtained with a synodic period of P=7.58 h. The zeropoint is at 0 UT on December 5th, 2007. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg3.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg36.png)
|
Figure 3: Composite light curve of 145451 2005 RM43, obtained with a synodic period of P=9.00 h. The zeropoint is at 0 UT on December 5th, 2007. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg4.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg37.png)
|
Figure 4: Composite light curve of 145453 2005 RR43, obtained with a synodic period of P=5.08 h. The zeropoint is at 0 UT on December 5th, 2007. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg5.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg38.png)
|
Figure 5: Composite light curve of 2003 UZ413, obtained with a synodic period of P=4.13 h. The zeropoint is at 0 UT on December 5th, 2007. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg6.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg39.png)
|
Figure 6: Estimated density ranges of TNOs as a function of their absolute magnitude H. Data from this work (asterisks, last column of Table 1), Dotto et al. (2008; open squares, including Centaur 95626 2002 GZ32), and Sheppard et al. (2008) and references therein (filled circles). |
| Open with DEXTER | |
4 Discussion
For each observed object, Table 1 reports the dynamical classification (according to Gladman et al. 2008), the absolute magnitude H (reported by the Minor Planet Center),
the computed rotational period, the light curve amplitude, the lower limit to the axis ratio a/b(from Eq. (1)), the lower limit to the density (from Eq. (2)), and the density range obtained
from the Chandrasekhar (1987) table for rotationally stable Jacobi ellipsoids. In Fig. 6, these latter density values are plotted versus H, together with literature data (Dotto et al. 2008; Sheppard et al. 2008, and references therein). Only objects with absolute magnitude ![]() (i.e., radius
(i.e., radius ![]() 100 km assuming moderate albedos) are taken into account.
100 km assuming moderate albedos) are taken into account.
Sheppard et al. (2008)
proposed the existence of a dimension/density trend, with larger
(brighter) TNOs being denser than smaller (fainter) ones, suggesting
that it could be caused by different
porosity and/or rock/ice mass fraction for bodies of different sizes.
We investigated this potential relationship on the basis of our new
results. Employing the entire sample (19 objects) shown in
Fig. 6, we computed the Pearson correlation coefficient between densities and absolute
magnitudes, deriving a value of r=-0.46. The probability that 19 measurements of two uncorrelated variables would yield
![]() is about 4.8% (see, for example, Taylor 1997),
so the trend can be considered statistically significant.
Nevertheless, it is evident that the sample includes several objects
with similar absolute magnitudes but very different estimated
densities. This may be due to dissimilar internal structures of TNOs
with comparable dimensions, or alternatively to differences in size
among TNOs of similar absolute magnitude. The small sample of TNO
albedo measurements presently available in the literature does not
allow us to solve the ambiguity between
brightness and dimensions, but the latter case is unlikely since
albedos and sizes of TNOs seem to be correlated, with larger bodies
having higher albedos (Stansberry et al. 2008).
The hypothesized dimension/density relationship is also strongly
influenced by a single object, 136108 Haumea: disregarding this, the
correlation coefficient drops to -0.29. Improving the TNO density
statistics is therefore indispensable to confirm or reject any
relationship between density and size.
is about 4.8% (see, for example, Taylor 1997),
so the trend can be considered statistically significant.
Nevertheless, it is evident that the sample includes several objects
with similar absolute magnitudes but very different estimated
densities. This may be due to dissimilar internal structures of TNOs
with comparable dimensions, or alternatively to differences in size
among TNOs of similar absolute magnitude. The small sample of TNO
albedo measurements presently available in the literature does not
allow us to solve the ambiguity between
brightness and dimensions, but the latter case is unlikely since
albedos and sizes of TNOs seem to be correlated, with larger bodies
having higher albedos (Stansberry et al. 2008).
The hypothesized dimension/density relationship is also strongly
influenced by a single object, 136108 Haumea: disregarding this, the
correlation coefficient drops to -0.29. Improving the TNO density
statistics is therefore indispensable to confirm or reject any
relationship between density and size.
5 Conclusions
In the framework of the ESO Large Programme 178.C-0036 (P.I. Barucci), we performed photometric observations of 5 TNOs. None of them were found to exhibit a coma. From the analysis of the rotational light curves, we computed the spin rate of 4 targets (a rotational period of about 6 h was found to be plausible for 2003 UZ117, but alternative solutions cannot be excluded) and, from the derived lower limit to the axis ratio a/b, we estimated the object density. 2003 UZ413 emerged as quite peculiar: it is presently the second most rapid rotator among TNOs, after 136108 Haumea, and further observations would be extremely useful.
We investigated the density/dimension relationship for TNOs suggested by Sheppard et al. (2008), by adding our new results to literature data. Although the trend could be considered statistically significant, the limited sample and the presence of objects of similar absolute magnitude with completely different estimated densities prevent us from assessing its validity.
Increasing the available sample of reliable albedo measurements (to reduce the ambiguity between brightness and size) and, especially, of density estimations, seem to be necessary to investigate the existence of a relationship between TNO densities and dimensions. As pointed out in Sect. 3, TNO density estimations, although reasonable given the current knowledge and understanding of the physical nature of these bodies, should be improved by replacing the fluid assumption with a more complex picture including internal stresses. We are currently working in this direction.
References
- Binzel, R. P., Farinella, P., Zappalà, V., et al. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson: Univ. of Arizona Press), 416
- Chandrasekhar, S. 1987, Ellipsoidal Figures of Equilibrium (New York: Dover)
- Davis, D., & Farinella, P. 1997, Icarus, 125, 50 [NASA ADS] [CrossRef]
- Dotto, E., Perna, D., Barucci, M. A., et al. 2008, A&A, 490, 829 [NASA ADS] [CrossRef] [EDP Sciences]
- Gladman, B., Marsden, B. G., & VanLaerhoven, C. 2008, in The Solar System Beyond Neptune, ed. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, & A. Morbidelli (Tucson: Univ. of Arizona Press), 43
- Harris, A. W., Young, J. W., Bowell, E., et al. 1989, Icarus, 77, 171 [NASA ADS] [CrossRef]
- Holsapple, K. A. 2001, Icarus, 154, 432 [NASA ADS] [CrossRef]
- Holsapple, K. A. 2004, Icarus, 172, 272 [NASA ADS] [CrossRef]
- Holsapple, K. A. 2007, Icarus, 187, 500 [NASA ADS] [CrossRef]
- Jeans, J. 1919, Problems of cosmogony and stellar dynamics (Cambridge: Cambridge Univ. Press)
- Pravec, P., & Harris, A. W. 2000, Icarus, 148, 12 [NASA ADS] [CrossRef]
- Sheppard, S. S., Lacerda, P., & Ortiz, J. L. 2008, in The Solar System Beyond Neptune, ed. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, & A. Morbidelli (Tucson: Univ. of Arizona Press), 129
- Stansberry, J., Grundy, W., Brown, M., et al. 2008, in The Solar System Beyond Neptune, ed. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, & A. Morbidelli (Tucson: Univ. of Arizona Press), 161
- Taylor, J. R. 1997, An introduction to error analysis - 2nd edn. (Sausalito, California: University Science Books)
Footnotes
- ... objects
![[*]](/icons/foot_motif.png)
- Based on observations carried out at the European SouthernObservatory (ESO), La Silla, Chile. ESO Large Programme 178.C-0036.
- ...
![[*]](/icons/foot_motif.png)
- Photometric light curves are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/508/451
All Tables
Table 1: Derived results.
All Figures
![\begin{figure}
\par\includegraphics[width=18cm,clip]{11970fg1.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg4.png)
|
Figure 1: Single-night light curves of the observed TNOs. The name of the target and the night of observation (with respect to 0 UT) are reported above each plot. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg2.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg35.png)
|
Figure 2: Composite light curve of 144897 2004 UX10, obtained with a synodic period of P=7.58 h. The zeropoint is at 0 UT on December 5th, 2007. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg3.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg36.png)
|
Figure 3: Composite light curve of 145451 2005 RM43, obtained with a synodic period of P=9.00 h. The zeropoint is at 0 UT on December 5th, 2007. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg4.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg37.png)
|
Figure 4: Composite light curve of 145453 2005 RR43, obtained with a synodic period of P=5.08 h. The zeropoint is at 0 UT on December 5th, 2007. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg5.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg38.png)
|
Figure 5: Composite light curve of 2003 UZ413, obtained with a synodic period of P=4.13 h. The zeropoint is at 0 UT on December 5th, 2007. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{11970fg6.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa11970-09/Timg39.png)
|
Figure 6: Estimated density ranges of TNOs as a function of their absolute magnitude H. Data from this work (asterisks, last column of Table 1), Dotto et al. (2008; open squares, including Centaur 95626 2002 GZ32), and Sheppard et al. (2008) and references therein (filled circles). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


