| Issue |
A&A
Volume 508, Number 1, December II 2009
|
|
|---|---|---|
| Page(s) | 133 - 140 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200811541 | |
| Published online | 15 October 2009 | |
A&A 508, 133-140 (2009)
Damped and sub-damped Lyman-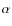 absorbers in z > 4 QSOs
absorbers in z > 4 QSOs![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
R. Guimarães1 - P. Petitjean2 - R. R. de Carvalho3 - S. G. Djorgovski4 - P. Noterdaeme5 - S. Castro6 - P. C. da R. Poppe1 - A. Aghaee7,8
1 - Universidade Estadual de Feira de Santana, Av. Transnordestina,
s/n, 40036-900, Feira de Santana, BA, Brasil
2 - UPMC Paris 6, Institut d'Astrophysique de Paris, CNRS, 98bis
boulevard Arago, 75014 Paris, France
3 - Instituto Nacional de Pesquisas Espaciais - INPE, Av. dos
Astronautas 1758, 12227-010 S. J. dos Campos, SP, Brasil
4 - California Institute of Technology, MS 105-24, Pasadena, CA 91125,
USA
5 - Inter-University Centre for Astonomy and Astrophysics, Post Bag 4,
Ganeshkhind, Pune 411 007, India
6 - Europeen Southern Observatory, Karl-Schwarzschild Strasse 2,
Garching, Germany
7 - Department of Physics, University of Sistan and Baluchestan, 98135
Zahedan, Iran
8 - School of Astronomy and Astrophysics, Institute for Research in
Fundamental Sciences (IPM), PO Box 193595-5531, Tehran, Iran
Received 17 December 2008 / Accepted 7 September 2009
Abstract
We present the results of a survey of damped (DLA, ![]() H I)>20.3)
and sub-damped Lyman-
H I)>20.3)
and sub-damped Lyman-![]() systems (
systems (
![]() H I)<20.3)
at z>2.55 along the lines-of-sight to 77
quasars with emission redshifts in the range
H I)<20.3)
at z>2.55 along the lines-of-sight to 77
quasars with emission redshifts in the range ![]() .
Intermediate resolution (
.
Intermediate resolution (![]() )
spectra were obtained with the Echellette Spectrograph and Imager (ESI)
mounted on the Keck telescope. A total of 100 systems with
)
spectra were obtained with the Echellette Spectrograph and Imager (ESI)
mounted on the Keck telescope. A total of 100 systems with ![]() H I)>19.5
were detected of which 40 systems
are damped Lyman-
H I)>19.5
were detected of which 40 systems
are damped Lyman-![]() systems for an absorption length of
systems for an absorption length of ![]() .
About half of the lines of sight of this homogeneous survey have never
been investigated for DLAs.
We study the evolution with redshift of the cosmological density of the
neutral gas and
find, consistent with previous studies at similar resolution, that
.
About half of the lines of sight of this homogeneous survey have never
been investigated for DLAs.
We study the evolution with redshift of the cosmological density of the
neutral gas and
find, consistent with previous studies at similar resolution, that ![]() decreases at z>3.5. The overall cosmological
evolution of
decreases at z>3.5. The overall cosmological
evolution of ![]() shows a peak around this redshift. The H I column
density distribution for
shows a peak around this redshift. The H I column
density distribution for ![]() H
I
H
I![]() is fitted, consistent with previous surveys, with a single power-law of
index
is fitted, consistent with previous surveys, with a single power-law of
index ![]() .
This power-law overpredicts data at the high-end
and a second, much steeper, power-law (or a gamma function) is needed.
There is a flattening of the function at lower H I column
densities with an index of
.
This power-law overpredicts data at the high-end
and a second, much steeper, power-law (or a gamma function) is needed.
There is a flattening of the function at lower H I column
densities with an index of ![]() for the column density range
for the column density range ![]() H I
)=19.5-21. The fraction of
H I mass in sub-DLAs is
of the order of 30%. The H I column
density distribution does not evolve strongly from
H I
)=19.5-21. The fraction of
H I mass in sub-DLAs is
of the order of 30%. The H I column
density distribution does not evolve strongly from ![]() to
to ![]() .
.
Key words: Galaxy: evolution - Galaxy: formation - quasars: absorption lines - intergalactic medium - cosmology: observations
1 Introduction
The amount of neutral gas in the Universe is an important ingredient of galaxy formation scenarios because the neutral phase of the intergalactic medium is the reservoir for star-formation activity in the densest places of the universe where galaxies are to be formed. It is therefore very important to make a census of the mass in this phase and to determine its cosmological evolution (see e.g. Péroux et al. 2001).
The gas with highest H I column
density is detected through damped Lyman-![]() absorptions
in the spectra of remote quasars. Although damped wings are seen for
column densities of the order of log N(H
I)
absorptions
in the spectra of remote quasars. Although damped wings are seen for
column densities of the order of log N(H
I) ![]() 18, the neutral phase corresponds to
log N(H I)
18, the neutral phase corresponds to
log N(H I) ![]() 19.5
(Viegas 1995).
The column density defining the so-called damped Lyman-
19.5
(Viegas 1995).
The column density defining the so-called damped Lyman-![]() (DLA) systems has been taken to be log N(H
I)
(DLA) systems has been taken to be log N(H
I) ![]() 20.3 because this
corresponds to the critical mass surface density limit for star
formation (Wolfe et al. 1986)
but also because the equivalent width of the corresponding absorption
is appropriate for a search for these systems in low resolution
spectra. Therefore several definitions have been introduced.
20.3 because this
corresponds to the critical mass surface density limit for star
formation (Wolfe et al. 1986)
but also because the equivalent width of the corresponding absorption
is appropriate for a search for these systems in low resolution
spectra. Therefore several definitions have been introduced. ![]() is the mass density of baryons in DLA systems, defined arbitrarily as
systems with log N(H I)
is the mass density of baryons in DLA systems, defined arbitrarily as
systems with log N(H I) ![]() 20.3.
20.3.
![]() is
the mass density of neutral hydrogen in all systems: DLAs, Lyman limit
systems (LLS) and the Lyman-
is
the mass density of neutral hydrogen in all systems: DLAs, Lyman limit
systems (LLS) and the Lyman-![]() forest. The mass density of H I in
the Lyman-
forest. The mass density of H I in
the Lyman-![]() forest is negligible because the slope of the H I column
density distribution is larger than -2 (
forest is negligible because the slope of the H I column
density distribution is larger than -2 (![]() -1.5; the gas is highly ionized). It is more
difficult to estimate the contribution of LLS as the column density of
these systems is very difficult to derive directly because the Lyman-
-1.5; the gas is highly ionized). It is more
difficult to estimate the contribution of LLS as the column density of
these systems is very difficult to derive directly because the Lyman-![]() line lies in the logarithmic regime of the curve of growth.
line lies in the logarithmic regime of the curve of growth.
However, ![]() is not easily related to physical quantities as
the LLS with log N < 19.5
are at least partly ionized when the ones with log N > 19.5
are not
(see e.g. Meiring et al. 2008). On the
contrary, as emphasized by Prochaska et al. (2005),
hereafter PHW05, the mass density of the neutral phase,
is not easily related to physical quantities as
the LLS with log N < 19.5
are at least partly ionized when the ones with log N > 19.5
are not
(see e.g. Meiring et al. 2008). On the
contrary, as emphasized by Prochaska et al. (2005),
hereafter PHW05, the mass density of the neutral phase, ![]() ,
is a good indicator of the mass available for star-formation and should
be used instead. Note that
,
is a good indicator of the mass available for star-formation and should
be used instead. Note that ![]() is not equal to
is not equal to ![]() .
The column density limit at which the gas is mostly neutral cannot be
defined
precisely but should lie between log N(H
I) = 19 and 19.5. A
conservative position is to consider that all systems above 19.5 are
neutral (see also O'Meara et al. 2007).
.
The column density limit at which the gas is mostly neutral cannot be
defined
precisely but should lie between log N(H
I) = 19 and 19.5. A
conservative position is to consider that all systems above 19.5 are
neutral (see also O'Meara et al. 2007).
Whether or not the mass of the neutral gas in the systems with
19.5 < log N(H
I) < 20.3
(the so-called sub-DLAs or super-LLS) is negligible has been the source
of intense discussions in recent years.
Note that these discussions are related to the mass in the neutral
phase only. Indeed, it is
known (e.g. Petitjean et al. 1993) that
the total mass associated with the
Lyman limit systems is greater than that of DLAs. Indeed the gas in the
LLS phase is mostly ionized
and located in extended halos whereas DLAs are located in dense and
compact regions. Péroux et al. (2003), hereafter
PMSI03, were the first to consider the sub-DLAs as an important
reservoir of neutral gas. They claim that at z>3.5,
DLAs could contain only 50% of the neutral
gas, the rest being found in sub-DLAs. When correcting for this, they
find that
the comoving mass density shows no evidence for a decrease above z=2.
PHW05 questioned this estimate. They use the Sloan Digital Sky Survey
to measure the mass density of predominantly neutral gas ![]() .
They find that DLAs contribute >80% of
.
They find that DLAs contribute >80% of ![]() at all redshift. Uncertainties are very large however and the same
authors estimate that the systems with log N(H
I) > 19 (the
super-LLS) could contribute 20-50% of
at all redshift. Uncertainties are very large however and the same
authors estimate that the systems with log N(H
I) > 19 (the
super-LLS) could contribute 20-50% of
![]() .
Therefore, the question of the contribution of super-LLS to
.
Therefore, the question of the contribution of super-LLS to ![]() is
not settled yet.
is
not settled yet.
In addition, the evolution of ![]() at the very high redshift, z>4,
is not known. PHW05 claim that there is no evolution of
at the very high redshift, z>4,
is not known. PHW05 claim that there is no evolution of ![]() for z>3.5 but they caution the reader that
results for z>4 should be confirmed with
higher resolution data. The reason is that the Lyman-
for z>3.5 but they caution the reader that
results for z>4 should be confirmed with
higher resolution data. The reason is that the Lyman-![]() forest is so dense
at these redshifts that it is very easy to misidentify a strong blend
of lines
with a DLA. Therefore
forest is so dense
at these redshifts that it is very easy to misidentify a strong blend
of lines
with a DLA. Therefore ![]() can be easily overestimated.
can be easily overestimated.
In this paper we present the result of a survey for DLAs and
sub-DLAs at high redshift (z>2.55)
using intermediate resolution data. We identify a total of 100 systems
with log N(H I) ![]() 19.5
of which 40 are DLAs over the redshift range
19.5
of which 40 are DLAs over the redshift range ![]() along 77 lines of sight towards
quasars with emission redshift 4
along 77 lines of sight towards
quasars with emission redshift 4 ![]()
![]()
![]() 6.3.
The sample and data reduction are presented in Sect. 2. In
Sect. 3 we describe the procedures used to select the
absorption systems. Section 4 analyses statistical
quantitities characterizing the evolution of DLAs and sub-DLAs and
discusses the cosmological evolution of the neutral gas mass density.
Conclusions are summarized in Sect. 5. Throughout the paper,
we adopt
6.3.
The sample and data reduction are presented in Sect. 2. In
Sect. 3 we describe the procedures used to select the
absorption systems. Section 4 analyses statistical
quantitities characterizing the evolution of DLAs and sub-DLAs and
discusses the cosmological evolution of the neutral gas mass density.
Conclusions are summarized in Sect. 5. Throughout the paper,
we adopt ![]() ,
,
![]() and
H0 = 72 km s-1.
and
H0 = 72 km s-1.
2 Observation and data reduction
Medium resolution (
![]() )
spectra of all z > 3 quasars
discovered in the course of the DPOSS
survey (Digital Palomar Observatory Sky Survey; see, e.g., Kennefick
et al. 1995;
Djorgovski et al. 1999,
and the complete listing of QSOs available at
http://www.astro.caltech.edu/ george/z4.qsos) were obtained
with the Echellette Spectrograph and Imager (ESI, Sheinis
et al. 2002)
mounted on the KECK II 10 m telescope. In total, 99 quasars
were observed, 57 of which have already reported in the literature (see
Table 1
for details). In Table 1
we provide a summary of the observation log for the 99 quasars.
Columns 1 to 8 give, respectively, the quasar's name,
the emission redshift, the apparent R magnitude,
the J2000 quasar coordinates, the date of observation, the exposure
time and the notes.
)
spectra of all z > 3 quasars
discovered in the course of the DPOSS
survey (Digital Palomar Observatory Sky Survey; see, e.g., Kennefick
et al. 1995;
Djorgovski et al. 1999,
and the complete listing of QSOs available at
http://www.astro.caltech.edu/ george/z4.qsos) were obtained
with the Echellette Spectrograph and Imager (ESI, Sheinis
et al. 2002)
mounted on the KECK II 10 m telescope. In total, 99 quasars
were observed, 57 of which have already reported in the literature (see
Table 1
for details). In Table 1
we provide a summary of the observation log for the 99 quasars.
Columns 1 to 8 give, respectively, the quasar's name,
the emission redshift, the apparent R magnitude,
the J2000 quasar coordinates, the date of observation, the exposure
time and the notes.
The echelle mode allows us to cover the full wavelength range
from 3900 Å to 10 900 Å in ten orders with ![]() 300 Å
overlap between two adjacent orders.
The instrument has a spectral dispersion of about
11.4 km s-1 pixel-1
and a pixel size ranging from 0.16 Å pixel-1
in the blue to 0.38 Å pixel-1
in the red. The 1 arcsec wide slit is projected onto
6.5 pixels, resulting in a
300 Å
overlap between two adjacent orders.
The instrument has a spectral dispersion of about
11.4 km s-1 pixel-1
and a pixel size ranging from 0.16 Å pixel-1
in the blue to 0.38 Å pixel-1
in the red. The 1 arcsec wide slit is projected onto
6.5 pixels, resulting in a ![]() spectral resolution.
spectral resolution.
Data reduction followed standard procedures using IRAF for 70% of the sample and the programme makee for the remaining data. For the IRAF reduction, the procedure was as follows. The images were overscan corrected for the dual-amplifier mode. Each amplifier has a different baseline value and different gain which were corrected for by using a script adapted from LRIS called esibias. Then all the images were bias subtracted and corrected for bad pixels. The images were divided by a normalized two-dimensional flat-field image to remove individual pixel sensitivity variations. The flat-field image was normalized by fitting its intensity along the dispersion direction using a high order polynomial fit, while setting all points outside the order aperture to unity. The echelle orders were traced using the spectrum of a bright star. Cosmic rays were removed from all two-dimensional images. For each exposure the quasar spectrum was optimally extracted and background subtracted. The task apall in the IRAF package echelle was used to do this. The CuAr lamps were individually extracted using the quasar's apertures. Lines were identified in the arc lamp spectra by using the task ecidentify and a polynomial was fitted to the line positions resulting in a dispersion solution with a mean rms of 0.09 Å. The dispersion solution computed on the lamp was then assigned to the object spectra by using the task dispcor. Wavelengths and redshifts were computed in the heliocentric restframe. The different orders of the spectra were combined using the task scombine in the IRAF package. It is important to note that the signal-to-noise ratio drops sharply at the edges of the orders. We have therefore carefully controlled this procedure to avoid any spurious feature.
The signal-to-noise ratio (SNR) per pixel was obtained in the
regions of the Lyman-![]() forest that are free of absorption and the mean SNR value, averaged
between the Lyman-
forest that are free of absorption and the mean SNR value, averaged
between the Lyman-![]() and Lyman-
and Lyman-![]() QSO emission lines, was computed. We used only spectra with mean SNR
QSO emission lines, was computed. We used only spectra with mean SNR ![]() .
For simplicity, we excluded from our analysis broad absorption line
(BAL) quasars. We therefore used 77 lines-of-sight out of the 99
available to us.
.
For simplicity, we excluded from our analysis broad absorption line
(BAL) quasars. We therefore used 77 lines-of-sight out of the 99
available to us.
The continuum was automatically fitted (Aracil et al.
2004;
Guimarães et al. 2007)
and the spectra were normalized. We checked the normalization for all
lines-of-sight and manually corrected for
local defects especially in the vicinity of the Lyman-![]() emission lines and when the Lyman-
emission lines and when the Lyman-![]() forest is strongly blended.
forest is strongly blended.
Metallicities measured for twelve z>3 DLAs observed along five lines-of-sight of this sample have been published by Prochaska et al. (2003b); see also Prochaska et al. (2003a).
3
Identification of damped and sub-damped Lyman-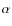 systems
systems
We used an automatic version of the Voigt profile fitting routine VPFIT
(Carswell et al. 1987)
to decompose the Lyman-![]() forest of the spectra in individual components. As usual, we
restricted our search to beyond of 3000 km s-1
from the QSO emission redshift. This is to
avoid contamination of the study by proximate effects such as the
presence of overdensities
around quasars (e.g. Rollinde et al. 2005;
Guimarães et al. 2007).
forest of the spectra in individual components. As usual, we
restricted our search to beyond of 3000 km s-1
from the QSO emission redshift. This is to
avoid contamination of the study by proximate effects such as the
presence of overdensities
around quasars (e.g. Rollinde et al. 2005;
Guimarães et al. 2007).
From this fit we could identify the candidates with
log N(H I) - error ![]() 19.5.
We then carefully inspected each of these candidates individually with
special attention to
the following characteristics of DLA absorption lines:
19.5.
We then carefully inspected each of these candidates individually with
special attention to
the following characteristics of DLA absorption lines:
- the wavelength range over which the line is going to zero;
- the presence of damped wings;
- the identification of associated metal lines when possible.
The metal lines have been searched for using a search list of the strongest atomic transitions given in Table 4. The corresponding absorptions have been fitted using the package VPFIT. A full account of this metallic column densities and the corresponding abundances is out of the scope of this paper and will be presented elsewhere (Guimarães et al., in preparation).
Table 3: QSOs without detected DLAs and/or sub-DLAs.
Table 4: Principal absorption metal lines most frequently detectedassociated with high column density absorption systems.
4 Analysis
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig1.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg38.png)
|
Figure 1: Solid curve shows the redshift sensitivity function of our survey for all lines-of-sight, the filled grey histogram is only for unpublished lines-of-sight. Dashed curve shows the redshift sensitivity function of previous surveys computed by PMSI03. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig2.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg39.png)
|
Figure 2:
Histogram of the H I column
densities measured for the 100 DLAs and sub-DLAs with
log N(H I) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig3.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg40.png)
|
Figure 3: The logarithm of the H I column density measured in our unpublished systems (circles) is plotted versus the redshift. The data points of Péroux et al. (2001) are shown for comparison with crosses. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig4.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg41.png)
|
Figure 4: The H I column density difference between our measurements and those by either Péroux et al. (2005) (triangles) or Prochaska & Wolfe (2009) (squares) in systems common to different surveys versus redshift. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig5.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg42.png)
|
Figure 5: Frequency distribution function over the redshift range z = 2.55-5.03. The dashed green, solid black and dotted blue lines are, respectively, a power-law, a double power-law and a gamma function fits to the data. The solid red and dashed black lines are, power-law and gamma function fits to the data obtained by PHW05. |
| Open with DEXTER | |
To give a global overview of the survey, we plot in
Fig. 3,
log N(H I)
versus ![]() for the 65 unpublished damped/sub-DLA absorption systems. In the same
figure we show for comparison the data points from the Péroux
et al. (2001)
survey.
for the 65 unpublished damped/sub-DLA absorption systems. In the same
figure we show for comparison the data points from the Péroux
et al. (2001)
survey.
In Fig. 4, we plot for comparison, as a function of redshift, the difference between the H I column densities measured for the same systems by us and by either Péroux et al. (2005) from high-resolution data or Prochaska & Wolfe (2009) from SDSS data. The measurements are consistent within errors.
Table 5: Frequency distribution fitting parameters.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11541fig6.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg49.png)
|
Figure 6:
H I frequency
distribution, |
| Open with DEXTER | |
4.1 Column density distribution function
The H I absorption system
frequency distribution function is defined as:
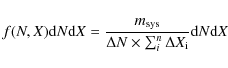
|
(1) |
where
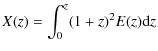
|
(2) |
where
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig7.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg61.png)
|
Figure 7:
Number density of absorbers vs. redshift. Red circles and inverse
triangles are from this work
for DLAs and sub-DLAs, respectively. The values obtained by PWH05 (blue
inverse triangles) and PDDKM05 (green squares) for DLAs are
overplotted. The green diamonds are the values obtained for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig8.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg62.png)
|
Figure 8:
Cosmological evolution of the H I mass
density. For DLAs: red squares are the results of this work, green
squares are from PDDKM05, blue inverse triangles from PHW05 and black
triangles from Rao et al. (2005). For sub-DLAs: red circles
are this work (for systems with column densities |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig9.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg63.png)
|
Figure 9:
|
| Open with DEXTER | |
A power-law, a gamma function and/or a double power-law are usually
used to fit the frequency distribution. It is apparent from
Fig. 5
that a power-law (of the form ![]() )
fits the function closely over the column density range
19.5 < log N(H
I) < 21. The index
of this power spectrum (see Table 5) is higher (
)
fits the function closely over the column density range
19.5 < log N(H
I) < 21. The index
of this power spectrum (see Table 5) is higher (
![]() )
than what is found by PHW05 but over a smaller column density range
log N(H I) > 20.3.
The discrepancy is apparently due to the difference in the column
density ranges
considered by both studies. If we restrict our fit to the same range as
PHW05 we find an index of
)
than what is found by PHW05 but over a smaller column density range
log N(H I) > 20.3.
The discrepancy is apparently due to the difference in the column
density ranges
considered by both studies. If we restrict our fit to the same range as
PHW05 we find an index of ![]() which is consistent with the results of PHW05.
We note that PDDKM05 already mentioned that the low end of the column
density
distribution is flatter than
which is consistent with the results of PHW05.
We note that PDDKM05 already mentioned that the low end of the column
density
distribution is flatter than ![]() .
.
There is a large deficit of high column density systems in our
survey compared to what
would be expected from the single power-law fit. This has been noted
before and discussed
in detail by PHW05. A double power-law was used to fit our full sample
with better results
(see Table 5).
However, the sharp break in the function at log N(H
I) ![]() 21 suggests a gamma function of the
form
21 suggests a gamma function of the
form ![]() (Pei & Fall 1995)
should better describe the data.
(Pei & Fall 1995)
should better describe the data.
We have calculated the frequency distribution function, f(N,X),
in different
redshift bins of equal distance path: 2.55-3.40; 3.40-3.83 and
3.83-5.03.
Results are shown in Fig. 6.
The functions are fitted as described above and
fit results are given in Table 5. We find that
the function do not evolve much with redshift.
This is consistent with the finding by PHW05 that the global
characteristics of the function do not
change much with time. There is however a tendancy for a flattening of
the function which may indicate
that the number of sub-DLAs relatively to other systems is larger at
lower redshift.
Although we do not think this is the case because we have used a
conservative
approach, part of this evolution at the highest redshift could possibly
be a consequence of losing the sub-DLAs in the strongly blended Lyman-![]() forest at z>4.
We note also a slight decrease of the number of systems with
log N(H I) > 20.5
at the highest redshifts. This is consistent with the finding by
PDDKM05 that
the relative number of high column density DLAs decreases with
redshift.
forest at z>4.
We note also a slight decrease of the number of systems with
log N(H I) > 20.5
at the highest redshifts. This is consistent with the finding by
PDDKM05 that
the relative number of high column density DLAs decreases with
redshift.
Another way to look at these variations is to compute
the redshift evolution of the number of (sub)DLAs per unit path length.
The observed density of systems is defined as
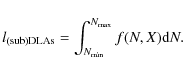
|
(3) |
Results obtained during the present survey together with those of PWH05 and PDDKM05 are plotted in Fig. 7. The important feature of this plot is that the number density of DLAs peaks at
Table 6: Absorption distance path - Data for Fig. 8.
4.2
Neutral hydrogen cosmological mass density, 
The comoving mass density of neutral gas is given by
where the density is in units of the current critical density
Results from PHW05 and PDDKM05 are also plotted in
Fig. 8.
It can be seen that we confirm the decrease of ![]() for z>3 that was noticed by
PDDKM05. The measurement from the SDSS in this redshift range is
higher. However, our survey is of higher spectral resolution and should
in principle be more reliable in this redshift range.
It seems that the evolution of
for z>3 that was noticed by
PDDKM05. The measurement from the SDSS in this redshift range is
higher. However, our survey is of higher spectral resolution and should
in principle be more reliable in this redshift range.
It seems that the evolution of ![]() is a steep increase from z=2 to z=3
and then a slightly flatter decrease up to z=5. The
inclusion of
the sub-DLAs does not change this picture as sub-DLAs contribute to a
maximum of about 30%
to the total H I mass.
The contribution by sub-DLAs is better seen in Fig. 9
where we plot the cumulative density versus the maximum H I column
density considered. As noted already by numerous authors, the
discrepancy of measurements at z<1.5 is
still a problem.
is a steep increase from z=2 to z=3
and then a slightly flatter decrease up to z=5. The
inclusion of
the sub-DLAs does not change this picture as sub-DLAs contribute to a
maximum of about 30%
to the total H I mass.
The contribution by sub-DLAs is better seen in Fig. 9
where we plot the cumulative density versus the maximum H I column
density considered. As noted already by numerous authors, the
discrepancy of measurements at z<1.5 is
still a problem.
It also can be seen from Fig. 8 that ![]() are lower than
are lower than ![]() ,
the mass density in stars in local galaxies. We find for the ratio of
the peak value of
,
the mass density in stars in local galaxies. We find for the ratio of
the peak value of ![]() to
to ![]() for this work has
for this work has ![]() .
Previous surveys, PDDKM05 and PHW05, have found 0.37
and 0.40 for the ratio.
.
Previous surveys, PDDKM05 and PHW05, have found 0.37
and 0.40 for the ratio.
5 Discussion
We have presented the results of a survey for damped and sub-damped
Lyman-![]() systems (logN(H I)
systems (logN(H I) ![]() 19.5)
at
19.5)
at ![]() along the lines of sight to 77 quasars with emission redshifts in the
range
along the lines of sight to 77 quasars with emission redshifts in the
range ![]() .
In total 99 quasars were observed but 22 lines of sight were not used
because of poor SNR and/or because of
the presence of broad absorption lines.
Intermediate resolution (
.
In total 99 quasars were observed but 22 lines of sight were not used
because of poor SNR and/or because of
the presence of broad absorption lines.
Intermediate resolution (![]() )
spectra were obtained with the Echellette Spectrograph and Imager (ESI)
mounted on the Keck telescope. The damped Lyman-
)
spectra were obtained with the Echellette Spectrograph and Imager (ESI)
mounted on the Keck telescope. The damped Lyman-![]() absorptions were identified on the basis of
(i) the width of the saturated absorption; (ii) the
presence of damped wings and (iii) the presence
of metals at the corresponding redshift. The detection was run
automatically but all lines
were verified visually. A total of 100 systems with
absorptions were identified on the basis of
(i) the width of the saturated absorption; (ii) the
presence of damped wings and (iii) the presence
of metals at the corresponding redshift. The detection was run
automatically but all lines
were verified visually. A total of 100 systems with ![]() (H
I)
(H
I) ![]() 19.5 were detected
of which 40 systems
are Damped Lyman-
19.5 were detected
of which 40 systems
are Damped Lyman-![]() systems (log N(H I)
systems (log N(H I) ![]() 20.3)
for an absorption
length of
20.3)
for an absorption
length of ![]() .
Spectra are shown in Appendix B.
.
Spectra are shown in Appendix B.
PHW05 derived from SDSS data that the cosmological density of
the neutral gas increases strongly by a factor close to two from ![]() to
to ![]() .
Beyond this redshift, measurements are more difficult because the Lyman-
.
Beyond this redshift, measurements are more difficult because the Lyman-![]() forest is dense. Our measurements should be more reliable because of
better spectral resolution.
We show, consistent with the findings of PDDKM05, that the cosmological
density of the neutral gas decreases at z>3.5.
The overall cosmological evolution seems therefore to have a peak at
this redshift.
forest is dense. Our measurements should be more reliable because of
better spectral resolution.
We show, consistent with the findings of PDDKM05, that the cosmological
density of the neutral gas decreases at z>3.5.
The overall cosmological evolution seems therefore to have a peak at
this redshift.
We find that the H I column
density distribution does not evolve strongly from
![]() to
to ![]() .
The one power-law fit in the range log N(H
I) > 20.3
gives an index of
.
The one power-law fit in the range log N(H
I) > 20.3
gives an index of ![]() = -1.80
= -1.80![]() 0.25,
consistent with previous determinations.
However, we find that the fit over the column density range
log N(H I) = 19.5-21
is quite flat (
0.25,
consistent with previous determinations.
However, we find that the fit over the column density range
log N(H I) = 19.5-21
is quite flat (![]()
![]() 1.4).
This probably indicates that the slope at the low end
is much flatter than -2. This power law overpredicts data at the high
end
and a second much steeper power law (or a gamma function) is needed.
The fraction
of H I mass in sub-DLAs
is of the order of 30%. Our data do not support
the claim by PDDKM05 that the incidence of low column density systems
is higher at high redshift. The number density of sub-DLAs seems to
peak at
1.4).
This probably indicates that the slope at the low end
is much flatter than -2. This power law overpredicts data at the high
end
and a second much steeper power law (or a gamma function) is needed.
The fraction
of H I mass in sub-DLAs
is of the order of 30%. Our data do not support
the claim by PDDKM05 that the incidence of low column density systems
is higher at high redshift. The number density of sub-DLAs seems to
peak at
![]() as well.
as well.
It is apparent that statistical errors are still large in our survey. It therefore would be of importance to enlarge the sample of (sub)DLAs at high redshift. For this we need to observe fainter quasars. The advent of X-shooter, a new generation spectrograph at the VLT with a spectral resolution of R=6700 in the optical, should allow this to be done in a reasonable amount of observing time.
AcknowledgementsS.G.D. is supported by the NSF grant AST-0407448, and the Ajax Foundation. Cataloguing of DPOSS and discovery of PSS QSOs was supported by the Norris Foundation and other private donors. We thank E. Thiébaut, and D. Munro for freely distributing his yorick programming language (available at ftp://ftp-icf.llnl.gov:/pub/Yorick), which we used to implement our analysis. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaian community. We are most fortunate to have the opportunity to conduct observations from this mountain. We acknowledge the Keck support staff for their efforts in performing these observations.
References
- Aracil, B., Petitjean, P., Pichon, C., & Bergeron, J. 2004, A&A, 419, 811 [NASA ADS] [CrossRef] [EDP Sciences]
- Carswell, R. F., Webb, J. K., Baldwin, J. A., & Atwood, B. 1987, ApJ, 319, 709 [NASA ADS] [CrossRef]
- Dessauges-Zavadsky, M., Péroux, C., Kim, T.-S., D'Odorico, S., & McMahon, R. G. 2003, MNRAS, 345, 447 [NASA ADS] [CrossRef]
- Djorgovski, S. G., Odewahn, S. C., Gal, R. R., Brunner, R. J., & de Carvalho, R. R. 1999, in Photometric Redshifts and the Detection of High Redshift Galaxies, ed. R. J. Weymann, L. J. Storrie-Lombardi, M. Sawicki, & R. J. Brunner, Astron. Soc. Pac., San Francisco, ASP Conf. Ser., 191, 179
- Fukugita, M., Hogan, C. J., & Peebles, P. J. E. 1998, ApJ, 503, 518 [NASA ADS] [CrossRef]
- Guimarães, R., Petitjean, P., Rollinde, E., et al. 2007, MNRAS, 377, 657 [NASA ADS] [CrossRef]
- Kennefick, J. D., Djorgovski, S. G., & de Carvalho, R. R. 1995, AJ, 110, 2553 [NASA ADS] [CrossRef]
- Meiring, J. D., Kulkarni, V. P., Lauroesch, J. T., et al. 2008, MNRAS, 384, 1015 [NASA ADS] [CrossRef]
- O'Meara, J. M., Prochaska, J. X., Burles, S., et al. 2007, ApJ, 656, 666 [NASA ADS] [CrossRef]
- Pei, Y. C., & Fall, S. M. 1995, ApJ, 454, 69 [NASA ADS] [CrossRef]
- Péroux, C., Storrie-Lombardi, L. J., McMahon, R. G., Irwin, M., & Hook, I. M. 2001, AJ, 121, 1799 [NASA ADS] [CrossRef]
- Péroux, C., McMahon, R. G., Storrie-Lombardi, L. J., & Irwin, M. J. 2003, MNRAS, 346, 1103 [NASA ADS] [CrossRef] (PMSI03)
- Péroux, C., Dessauges-Zavadsky, M., D'Odorico, S., Sun Kim, T., & McMahon, R. G. 2005, MNRAS, 363, 479 [NASA ADS] (PDDKM05)
- Petitjean, P., Webb, J. K., Rauch, M., Carswell, R. F., & Lanzetta, K. 1993, MNRAS, 262, 499 [NASA ADS]
- Prochaska, J. X., & Wolfe, A. M. 2009, ApJ, 696, 1543 [NASA ADS] [CrossRef]
- Prochaska, J. X., Castro, S., & Djorgovski, S. G. 2003a, ApJS, 148, 317 [NASA ADS] [CrossRef]
- Prochaska, J. X., Gawiser, E., Wolfe, A. M., Castro, S., & Djorgovski, S. G. 2003b, ApJ, 595, L9 [NASA ADS] [CrossRef]
- Prochaska, J. X., Herbert-Fort, S., & Wolfe, A. M. 2005, ApJ, 635, 123 [NASA ADS] [CrossRef] (PHW05)
- Rao, S. M., Turnshek, D. A., & Nestor, D. B. 2006, ApJ, 636, 610 [NASA ADS] [CrossRef]
- Rollinde, E., Srianand, R., Theuns, T., Petitjean, P., & Chand, H. 2005, MNRAS, 361, 1015 [NASA ADS] [CrossRef]
- Sheinis, A. I., Bolte, M., Epps, H. W., et al. 2002, PASP, 114, 851 [NASA ADS] [CrossRef]
- Storrie-Lombardi, L. J., & Wolfe, A. M. 2000, ApJ, 543, 552 [NASA ADS] [CrossRef]
- Viegas, S. M. 1995, MNRAS, 276, 268 [NASA ADS]
- Wolfe, A. M., Turnshek, D. A., Smith, H. E., & Cohen, R. D. 1986, ApJS, 61, 249 [NASA ADS] [CrossRef]
Online Material
Appendix A: Notes on individual systems
In this Appendix we discuss systems where we note differences between our measurements and measurements by others.
- 1.
- PSS 0131+0633 (
 ). Péroux et al. (2001) report two
sub-DLA candidates at
). Péroux et al. (2001) report two
sub-DLA candidates at  = 3.17 and
3.61 with log N(H I)
= 19.9 and 19.8 respectively.
For the second system however, Péroux et al. (2001) give in
Table 5 a redshift of
= 3.17 and
3.61 with log N(H I)
= 19.9 and 19.8 respectively.
For the second system however, Péroux et al. (2001) give in
Table 5 a redshift of  = 3.61
for the H I line and
= 3.61
for the H I line and  = 3.609
for the metal lines but a redshift of
= 3.609
for the metal lines but a redshift of  = 3.69
and
log N(H I)
= 19.5 in their Sect. 8 namely, ``Notes on Individual
Objects''. We also detect the first sub-DLA at
= 3.69
and
log N(H I)
= 19.5 in their Sect. 8 namely, ``Notes on Individual
Objects''. We also detect the first sub-DLA at  = 3.173
with
= 3.173
with 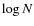 (H
I) = 19.95
(H
I) = 19.95  0.10. Metal lines at that redshift are detected in the red part of the
spectrum. For the second DLA candidate, we confirm the presence of the
0.10. Metal lines at that redshift are detected in the red part of the
spectrum. For the second DLA candidate, we confirm the presence of the  = 3.689
absorption with log N(H I)
= 19.50
= 3.689
absorption with log N(H I)
= 19.50  0.10 in agreement with the sub-DLA candidate reported in
Sect. 8 of Peroux et al. (2001). Metal
lines at that redshift are also observed in the red part of the
spectrum.
0.10 in agreement with the sub-DLA candidate reported in
Sect. 8 of Peroux et al. (2001). Metal
lines at that redshift are also observed in the red part of the
spectrum.
- 2.
- PSS0747+4434 (
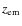 = 4.435).
Péroux et al. (2001)
report two DLA candidates at zrm
abs = 3.76 and 4.02 with
log N(H I)
= 20.3 and 20.6 respectively, which are confirmed by our observations.
We measure log N(H I)
= 20.00
= 4.435).
Péroux et al. (2001)
report two DLA candidates at zrm
abs = 3.76 and 4.02 with
log N(H I)
= 20.3 and 20.6 respectively, which are confirmed by our observations.
We measure log N(H I)
= 20.00  0.20
at
0.20
at  = 3.762 and
log N(H I)
= 21.10
= 3.762 and
log N(H I)
= 21.10  0.15
at
0.15
at  = 4.019. No
metal lines at
= 4.019. No
metal lines at  = 3.76
are observed in both surveys. We remind the reader that our data are of
higher spectral resolution.
= 3.76
are observed in both surveys. We remind the reader that our data are of
higher spectral resolution.
- 3.
- SDSS 0756+4104 (
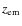 = 5.09). We
detect a sub-DLA candidate at
= 5.09). We
detect a sub-DLA candidate at  = 4.360
with log N(H I)
= 20.15
= 4.360
with log N(H I)
= 20.15  0.10.
Although no Lyman series and metals are detected for this system, the
spectrum has a high enough SNR to fit the H I line
well and to ascertain that this aborber is highly likely to be damped.
0.10.
Although no Lyman series and metals are detected for this system, the
spectrum has a high enough SNR to fit the H I line
well and to ascertain that this aborber is highly likely to be damped.
- 4.
- BR 0951-450 (
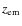 = 4.35).
PMSI03 report the detection of two DLA candidates at
= 4.35).
PMSI03 report the detection of two DLA candidates at  = 3.8580
and 4.2028 with log N(H I)
= 20.6 and 20.4 respectively, which are confirmed by our observations.
We measure log N(H I)
= 20.70
= 3.8580
and 4.2028 with log N(H I)
= 20.6 and 20.4 respectively, which are confirmed by our observations.
We measure log N(H I)
= 20.70  0.20
at
0.20
at  = 3.856 and
log N(H I)
= 20.35
= 3.856 and
log N(H I)
= 20.35  0.15
at
0.15
at  = 4.202. We
discover an additional damped candidate at
= 4.202. We
discover an additional damped candidate at  = 3.235
with log N(H I)
= 20.25
= 3.235
with log N(H I)
= 20.25  0.10.
We believe that this system is not included in the statistical sample
of PMSI03, because it falls below the threshold of log N(H
I) = 20.30. Metal lines at that redshift
are observed in the red part of the spectrum.
0.10.
We believe that this system is not included in the statistical sample
of PMSI03, because it falls below the threshold of log N(H
I) = 20.30. Metal lines at that redshift
are observed in the red part of the spectrum.
- 5.
- BRI 1013+0035 (
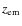 = 4.38).
PMSI03 report one DLA candidate at
= 4.38).
PMSI03 report one DLA candidate at  = 3.103
with log N(H I)
= 21.1. This system is not included in our sample since its redshift is
smaller than the minimum redshift beyond which a DLA/sub-DLA could be
detected in our spectrum. One damped candidate was discovered at
= 3.103
with log N(H I)
= 21.1. This system is not included in our sample since its redshift is
smaller than the minimum redshift beyond which a DLA/sub-DLA could be
detected in our spectrum. One damped candidate was discovered at  = 3.738
with log N(H I)
= 20.15
= 3.738
with log N(H I)
= 20.15  0.20.
We believe that this system is not included in the statistical sample
of PMSI03 because it falls below the threshold of log N(H
I) = 20.30. Although no Lyman series and
metals are detected for this system, the SNR in the spectrum is high
enough to ascertain that this absorber is highly likely to be damped.
0.20.
We believe that this system is not included in the statistical sample
of PMSI03 because it falls below the threshold of log N(H
I) = 20.30. Although no Lyman series and
metals are detected for this system, the SNR in the spectrum is high
enough to ascertain that this absorber is highly likely to be damped.
- 6.
- PSS 1057+4555 (
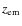 = 4.126).
Péroux et al. (2001)
report three DLA candidates at
= 4.126).
Péroux et al. (2001)
report three DLA candidates at  = 2.90,
3.05 and 3.32 with log N(H I)
= 20.1, 20.3 and 20.2 respectively, which are confirmed by our
observations. We measure log N(H I)
= 20.05
= 2.90,
3.05 and 3.32 with log N(H I)
= 20.1, 20.3 and 20.2 respectively, which are confirmed by our
observations. We measure log N(H I)
= 20.05  0.10
at
0.10
at  = 2.909,
log N(H I)
= 19.80
= 2.909,
log N(H I)
= 19.80  0.15
at
0.15
at  = 3.058 and
log N(H I)
= 20.15
= 3.058 and
log N(H I)
= 20.15  0.10
at
0.10
at  = 3.317.
Metal lines at all three redshifts are observed in the red part of the
spectrum. We report a new sub-DLA at
= 3.317.
Metal lines at all three redshifts are observed in the red part of the
spectrum. We report a new sub-DLA at  = 3.164
with log N(H I)
= 19.50
= 3.164
with log N(H I)
= 19.50  0.20.
Several metal lines are detected for this sytem.
0.20.
Several metal lines are detected for this sytem.
- 7.
- PSS 1253-0228 (
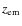 = 4.007).
Péroux et al. (2001)
report two DLA candidates at
= 4.007).
Péroux et al. (2001)
report two DLA candidates at  = 2.78
and 3.60 with log N(H I)
= 21.4 and 19.7, respectively. The system at
= 2.78
and 3.60 with log N(H I)
= 21.4 and 19.7, respectively. The system at  =
2.78 is not included in our sample because its redshift falls below the
minimum redshift beyond which DLA/sub-DLA could be detected in our
spectrum. We measure log N(H I)
= 19.95
=
2.78 is not included in our sample because its redshift falls below the
minimum redshift beyond which DLA/sub-DLA could be detected in our
spectrum. We measure log N(H I)
= 19.95  0.10
at
0.10
at  = 3.608.
Several metal lines are detected for this sytem.
= 3.608.
Several metal lines are detected for this sytem.
- 8.
- J 1325+1123 (
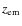 = 4.400).
We have discovered two sub-DLA candidates at
= 4.400).
We have discovered two sub-DLA candidates at  = 3.723
and 4.133 with log N(H I)
= 19.50
= 3.723
and 4.133 with log N(H I)
= 19.50  0.20
and 19.50
0.20
and 19.50  0.20,
respectively. C IV metal lines
are detected at
0.20,
respectively. C IV metal lines
are detected at  = 3.723.
These two sub-DLAs can be found in the list of SDSS DR5 systems
= 3.723.
These two sub-DLAs can be found in the list of SDSS DR5 systems ![[*]](/icons/foot_motif.png) .
.
- 9.
- PSS 1633+1411 (
zrm
em = 4.349). Péroux
et al. (2001)
report one sub-DLA candidate at
 = 3.90
with log N(H I)
= 19.8. Here, we measure log N(H I)
= 19.0
= 3.90
with log N(H I)
= 19.8. Here, we measure log N(H I)
= 19.0  0.20
at
0.20
at  = 3.909.
We report a new DLA at
= 3.909.
We report a new DLA at  = 2.880
with log N(H I)
= 20.30
= 2.880
with log N(H I)
= 20.30  0.15.
Several metal lines are detected for this sytem.
0.15.
Several metal lines are detected for this sytem.
- 10.
- PSS 1646+5514 (
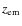 = 4.084).
No DLA candidate is detected by Péroux et al. (2001) along this
line
of sight. We report here two sub-DLA candidates at
= 4.084).
No DLA candidate is detected by Péroux et al. (2001) along this
line
of sight. We report here two sub-DLA candidates at  =
2.932 and 4.029 with log N(H I)
= 19.50
=
2.932 and 4.029 with log N(H I)
= 19.50  0.10
and 19.80
0.10
and 19.80  0.15,
respectively. No metals are seen
over the available wavelength coverage.
0.15,
respectively. No metals are seen
over the available wavelength coverage.
- 11.
- PSS 2122-0014 (
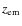 = 4.084).
Péroux et al. (2001)
report two candidates at
= 4.084).
Péroux et al. (2001)
report two candidates at  = 3.20
and 4.00 with log N(H I)
= 20.3 and 20.1, respectively. Here, we measure log N(H
I) = 20.20
= 3.20
and 4.00 with log N(H I)
= 20.3 and 20.1, respectively. Here, we measure log N(H
I) = 20.20  0.10
and 20.15
0.10
and 20.15  0.15
at
0.15
at  = 3.207
and 4.001. Several metal lines are detected for both systems. We report
a new sub-DLA candidate at
= 3.207
and 4.001. Several metal lines are detected for both systems. We report
a new sub-DLA candidate at  = 3.264
with log N(H I)
= 19.90
= 3.264
with log N(H I)
= 19.90  0.15.
Several metal lines also are detected for this system.
0.15.
Several metal lines also are detected for this system.
- 12.
- PSS 2154+0335 (
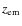 = 4.359).
Péroux et al. (2001)
report two candidates at
= 4.359).
Péroux et al. (2001)
report two candidates at  = 3.61
and 3.79 with log N(H I)
= 20.4 and 19.70, respectively. No candidate with log N(H
I) > 19.50 is
detected in our spectrum.
= 3.61
and 3.79 with log N(H I)
= 20.4 and 19.70, respectively. No candidate with log N(H
I) > 19.50 is
detected in our spectrum.
- 13.
- PSS 2155+1358 (
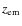 = 4.256). Péroux
et al. (2001)
report one DLA at
= 4.256). Péroux
et al. (2001)
report one DLA at  = 3.32
with log N(H I)
= 21.10. Dessauges et al. (2003) report
three sub-DLAs at
= 3.32
with log N(H I)
= 21.10. Dessauges et al. (2003) report
three sub-DLAs at  = 3.142,
3.565 and 4.212 with log N(H I)
= 19.94, 19.37 and 19.61. Here, we measure log N(H
I) = 19.90
= 3.142,
3.565 and 4.212 with log N(H I)
= 19.94, 19.37 and 19.61. Here, we measure log N(H
I) = 19.90  0.20,
20.75
0.20,
20.75  0.20
and 20.00
0.20
and 20.00  0.10
at zrm
abs = 3.143, 3.318 and 4.211,
respectively. Several metal lines are detected for these systems.
0.10
at zrm
abs = 3.143, 3.318 and 4.211,
respectively. Several metal lines are detected for these systems.
- 14.
- PSS2344+0342 (
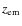 = 4.340).
Péroux et al. (2001)
report two DLAs at
= 4.340).
Péroux et al. (2001)
report two DLAs at  = 2.68
and 3.21 with log N(H I)
= 21.10 and 20.9. The first system is not included in our sample
because
its redshift falls below the minimum redshift beyond which a
DLA/sub-DLA could be detected in our spectrum. We measure log N(H
I) = 21.20
= 2.68
and 3.21 with log N(H I)
= 21.10 and 20.9. The first system is not included in our sample
because
its redshift falls below the minimum redshift beyond which a
DLA/sub-DLA could be detected in our spectrum. We measure log N(H
I) = 21.20  0.10
at
0.10
at  = 3.220.
Dessauges et al. (2003)
report one sub-DLA at
= 3.220.
Dessauges et al. (2003)
report one sub-DLA at  =
3.882 with log N(H I)
= 19.50. We measure log N(H I)
= 19.80
=
3.882 with log N(H I)
= 19.50. We measure log N(H I)
= 19.80  0.10
at
0.10
at  = 3.884.
= 3.884.
Appendix B: List of figures
![\begin{figure}
\includegraphics[width=17cm,height=18.5cm,clip]{11541fig10.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg94.png)
|
Figure B.1:
Spectra of the 100 confirmed Lyman- |
| Open with DEXTER | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig11.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg95.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig12.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg96.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig13.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg97.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig14.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg98.png)
|
Figure B.1: cintinued. |
| Open with DEXTER | |
![\begin{figure}
\addtocounter{figure}{-1}
\par\includegraphics[width=17cm,clip]{11541fig15.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg99.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig16.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg100.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig17.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg101.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=11cm,clip]{11541fig18.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg102.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
Table 1: Summary of observations.
Table 2: List of DLA-subDLAs.
Footnotes
- ... QSOs
![[*]](/icons/foot_motif.png)
- The observations reported here were obtained with the W. M. Keck Observatory, which is operated by the California Association for Research in Astronomy, a scientific partnership among the California Institute of Technology, the University of California, and the National Aeronautics and Space Administration.
- ...
![[*]](/icons/foot_motif.png)
- Tables 1, 2 and Appendices are only available in electronic form at http://www.aanda.org
- ... systems
![[*]](/icons/foot_motif.png)
- http://www.ucolick.org/ xavier/SDSSDLA/tab_dr5.html
All Tables
Table 3: QSOs without detected DLAs and/or sub-DLAs.
Table 4: Principal absorption metal lines most frequently detectedassociated with high column density absorption systems.
Table 5: Frequency distribution fitting parameters.
Table 6: Absorption distance path - Data for Fig. 8.
Table 1: Summary of observations.
Table 2: List of DLA-subDLAs.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig1.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg38.png)
|
Figure 1: Solid curve shows the redshift sensitivity function of our survey for all lines-of-sight, the filled grey histogram is only for unpublished lines-of-sight. Dashed curve shows the redshift sensitivity function of previous surveys computed by PMSI03. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig2.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg39.png)
|
Figure 2:
Histogram of the H I column
densities measured for the 100 DLAs and sub-DLAs with
log N(H I) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig3.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg40.png)
|
Figure 3: The logarithm of the H I column density measured in our unpublished systems (circles) is plotted versus the redshift. The data points of Péroux et al. (2001) are shown for comparison with crosses. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig4.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg41.png)
|
Figure 4: The H I column density difference between our measurements and those by either Péroux et al. (2005) (triangles) or Prochaska & Wolfe (2009) (squares) in systems common to different surveys versus redshift. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig5.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg42.png)
|
Figure 5: Frequency distribution function over the redshift range z = 2.55-5.03. The dashed green, solid black and dotted blue lines are, respectively, a power-law, a double power-law and a gamma function fits to the data. The solid red and dashed black lines are, power-law and gamma function fits to the data obtained by PHW05. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11541fig6.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg49.png)
|
Figure 6:
H I frequency
distribution, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig7.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg61.png)
|
Figure 7:
Number density of absorbers vs. redshift. Red circles and inverse
triangles are from this work
for DLAs and sub-DLAs, respectively. The values obtained by PWH05 (blue
inverse triangles) and PDDKM05 (green squares) for DLAs are
overplotted. The green diamonds are the values obtained for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig8.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg62.png)
|
Figure 8:
Cosmological evolution of the H I mass
density. For DLAs: red squares are the results of this work, green
squares are from PDDKM05, blue inverse triangles from PHW05 and black
triangles from Rao et al. (2005). For sub-DLAs: red circles
are this work (for systems with column densities |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11541fig9.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg63.png)
|
Figure 9:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=17cm,height=18.5cm,clip]{11541fig10.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg94.png)
|
Figure B.1:
Spectra of the 100 confirmed Lyman- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig11.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg95.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig12.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg96.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig13.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg97.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig14.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg98.png)
|
Figure B.1: cintinued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\addtocounter{figure}{-1}
\par\includegraphics[width=17cm,clip]{11541fig15.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg99.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig16.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg100.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=17cm,clip]{11541fig17.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg101.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\addtocounter{figure}{-1}
\includegraphics[width=11cm,clip]{11541fig18.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa11541-08/Timg102.png)
|
Figure B.1: continued. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.