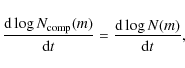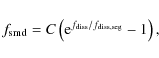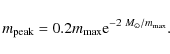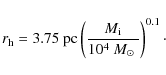| Issue |
A&A
Volume 507, Number 3, December I 2009
|
|
|---|---|---|
| Page(s) | 1409 - 1423 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200913325 | |
| Published online | 04 November 2009 | |
A&A 507, 1409-1423 (2009)
The evolution of the stellar mass function in star clusters![[*]](/icons/foot_motif.png)
J. M. D. Kruijssen1,2
1 - Astronomical Institute, Utrecht University,
PO Box 80000, 3508TA Utrecht, The Netherlands
2 -
Leiden Observatory, Leiden University,
PO Box 9513, 2300RA Leiden, The Netherlands
Received 20 September 2009 / Accepted 23 October 2009
Abstract
Context. The dynamical escape of stars from star clusters
affects the shape of the stellar mass function (MF) in these clusters,
because the escape probability of a star depends on its mass. This is
found in N-body simulations and has been approximated in
analytical cluster models by fitting the evolution of the MF. Both
approaches are naturally restricted to the set of boundary conditions
for which the simulations were performed.
Aims. The objective of this paper is to provide and to apply a
simple physical model for the evolution of the MF in star clusters for
a large range of the parameter space. It should also offer a new
perspective on the results from N-body simulations.
Methods. A simple, physically self-contained model for the
evolution of the stellar MF in star clusters is derived from the basic
principles of two-body encounters and energy considerations. It is
independent of the adopted mass loss rate or initial mass function
(IMF), and contains stellar evolution, stellar remnant retention,
dynamical dissolution in a tidal field, and mass segregation.
Results. The MF evolution in star clusters depends on the
disruption time, remnant retention fraction, initial-final stellar mass
relation, and IMF. Low-mass stars are preferentially ejected after ![]() Myr.
Before that time, masses around 15-20% of the maximum stellar mass are
lost due to their rapid two-body relaxation with the massive stars that
still exist at young ages. The degree of low-mass star depletion grows
for increasing disruption times, but can be quenched when the retained
fraction of massive remnants is large. The highly depleted MFs of
certain Galactic globular clusters are explained by the enhanced
low-mass star depletion that occurs for low remnant retention
fractions. Unless the retention fraction is exceptionally large,
dynamical evolution always decreases the mass-to-light ratio. The
retention of black holes reduces the fraction of the cluster mass in
remnants because white dwarfs and neutron stars have masses that are
efficiently ejected by black holes.
Myr.
Before that time, masses around 15-20% of the maximum stellar mass are
lost due to their rapid two-body relaxation with the massive stars that
still exist at young ages. The degree of low-mass star depletion grows
for increasing disruption times, but can be quenched when the retained
fraction of massive remnants is large. The highly depleted MFs of
certain Galactic globular clusters are explained by the enhanced
low-mass star depletion that occurs for low remnant retention
fractions. Unless the retention fraction is exceptionally large,
dynamical evolution always decreases the mass-to-light ratio. The
retention of black holes reduces the fraction of the cluster mass in
remnants because white dwarfs and neutron stars have masses that are
efficiently ejected by black holes.
Conclusions. The modeled evolution of the MF is consistent with N-body simulations when adopting identical boundary conditions. However, it is found that the results from N-body
simulations only hold for their specific boundary conditions and should
not be generalised to all clusters. It is concluded that the model
provides an efficient method to understand the evolution of the stellar
MF in star clusters under widely varying conditions.
Key words: stellar dynamics - stars: kinematics - Galaxy: globular clusters: general - galaxies: star clusters - Galaxy: open clusters and associations: general - galaxies: stellar content
1 Introduction
The evaporation of star clusters is known to change the shape of the underlying stellar mass functionThe existing parameterised cluster models that incorporate a description of low-mass star depletion are restricted by the physically self-contained models on which they are based. Some studies (Kruijssen & Lamers 2008; Lamers et al. 2006) assume an increasing lower stellar mass limit to account for the evolving MF, others (Anders et al. 2009) fit a changing MF slope to N-body simulations. In both cases, the models are accurate for a certain range of boundary conditions, but they do not include a physical model and are therefore lacking flexibility. While N-body simulations do include the appropriate physics, they are very time-consuming. As a result, only a limited number of clusters can be simulated and the applicability of the simulations is thus restricted to the specific set of boundary conditions for which they have been run.
It would be desirable to obtain a simple physical model for the evolution of the MF, which would have a short runtime and could be used independently of N-body simulations. Forty years ago, a pioneering first approach to such a model was made by Hénon (1969), who considered the stellar mass-dependent escape rate of stars from star clusters. However, the applicability of his model was limited due to a number of assumptions that influenced the results. First of all, Hénon (1969) assumed that the clusters exist in isolation and neglected the tidal field. As a consequence, the escape of a star could only occur by a single, close encounter and the repeated effect of two-body relaxation was not included. Secondly, the distribution of stars was independent of stellar mass, i.e. mass segregation was not included. Both mass segregation and the influence of a tidal field are observed in real clusters, and can be expected to affect the evolution of the MF.
The aim of this paper is to derive a physical description of the evolution of the stellar MF in star clusters, alleviating the assumptions that were made by Hénon (1969). This should explain the results found in N-body simulations and observations, while providing the required flexibility to explore the properties of star clusters with simple, physically self-contained models. The outline of this paper is as follows. In Sect. 2, total mass evolution of star clusters is discussed. A recipe for the evolution of the MF is derived in Sect. 3, covering stellar evolution, the retain of stellar remnants, dynamical dissolution and mass segregation. The model is compared to N-body simulations in Sect. 4. In Sect. 5, the model is applied to assess the evolution of the MF for different disruption times and remnant retention fractions. The consequences for other cluster properties are also considered. This paper is concluded with a discussion of the results and their implications.
2 The mass evolution of star clusters
The mass of star clusters decreases due to stellar evolution and dynamical dissolution. This is expressed mathematically aswith M the cluster mass, and the subscripts ``ev'' and ``dis'' denoting stellar evolution and dynamical dissolution. The contribution of stellar evolution to the mass loss is derived from the decrease of the maximum stellar mass with time and depends on the adopted stellar evolution model.
The dynamical evaporation of star clusters is increasingly well
understood. Over the past years it has become clear that clusters lose
mass on a disruption timescale
![]() that is proportional to a combination of the half-mass relaxation time
that is proportional to a combination of the half-mass relaxation time
![]() and the crossing time
and the crossing time
![]() as
as
![]() (e.g. Gieles & Baumgardt 2008; Baumgardt & Makino 2003; Baumgardt 2001). It is found that x=0.75-0.80, depending on the concentration (
(e.g. Gieles & Baumgardt 2008; Baumgardt & Makino 2003; Baumgardt 2001). It is found that x=0.75-0.80, depending on the concentration (
![]() )
or King parameter (W0) of the cluster (Baumgardt & Makino 2003). This proportionality leads to a disruption timescale that scales with the present day mass as (Lamers et al. 2005):
)
or King parameter (W0) of the cluster (Baumgardt & Makino 2003). This proportionality leads to a disruption timescale that scales with the present day mass as (Lamers et al. 2005):
with M the cluster mass, t0 the dissolution timescale parameter which sets the rapidity of dissolution and depends on the cluster environment, and
which can be integrated for the mass evolution of the cluster due to dynamical dissolution.
The above formulation of the cluster mass evolution was extended to include stellar remnants, photometric cluster evolution, and a simple description of the MF in the SPACE cluster models (Kruijssen & Lamers 2008). Stellar remnants were accounted for by assuming initial-final mass relations (similar to Sect. 3.1 of the present paper), while the photometric evolution was computed by integrating stellar isochrones from the Padova group (Bertelli et al. 1994; Girardi et al. 2000). The description of low-mass star depletion followed the simple model from Lamers et al. (2006) in which the minimum stellar mass of the MF increases with time.
The present study provides a new description of the evolution of the MF which is based on fundamental principles, and does not depend on the above prescription for the total mass evolution. In addition, the latest Padova models (Marigo et al. 2008) are incorporated to calculate the photometric cluster evolution. These improvements update the SPACE cluster models.
3 The evolution of the stellar mass function
To describe the evolution of the MF, the effects of stellar evolution, stellar remnant production, and dynamical dissolution need to be included. While the focus of this paper lies with the effects of dissolution, a proper treatment of stellar evolution is essential. This is described first, before presenting a model for cluster dissolution3.1 Stellar evolution
The influence of stellar evolution on the MF is twofold. First of all, the maximum stellar mass decreases, because at any time during cluster evolution the most massive stars reach the end of their lives. Secondly, the stellar remnants that are created upon the death of these massive stars constitute a part of the MF that can only be lost from the cluster by dynamical mechanisms.The maximum stellar mass in the cluster as a function of its age is taken from the Padova 2008 isochrones (Marigo et al. 2008) for metallicities in the range Z=0.0001-0.03. The stellar remnant masses
![]() are computed from their progenitor stellar mass m using initial-final mass relations. Following Kruijssen & Lamers (2008), for white dwarfs (
are computed from their progenitor stellar mass m using initial-final mass relations. Following Kruijssen & Lamers (2008), for white dwarfs (
![]() )
the relation from Kalirai et al. (2008) is adopted:
)
the relation from Kalirai et al. (2008) is adopted:
which holds for all ages that are covered by the Padova isochrones. For neutron stars (
while for black holes (
With these relations, the remnant MF is computed from conservation of numbers as
with
For a given velocity dispersion of remnants, the retention fraction of each remnant type depends on the local escape velocity
![]() ,
which is related to the potential
,
which is related to the potential ![]() as
as
![]() .
Stellar remnants are predominantly produced in the cluster centre in
the case of mass segregation, which is reached most rapidly for massive
stars (see Sect. 3.2). For a Plummer (1911, also see Eq. (9)# potential this implies that upon remnant production
.
Stellar remnants are predominantly produced in the cluster centre in
the case of mass segregation, which is reached most rapidly for massive
stars (see Sect. 3.2). For a Plummer (1911, also see Eq. (9)# potential this implies that upon remnant production
![]() ,
with G the gravitational constant and r0 the Plummer radius. Adopting a Maxwellian distribution of velocities that is truncated at
,
with G the gravitational constant and r0 the Plummer radius. Adopting a Maxwellian distribution of velocities that is truncated at
![]() ,
it is straightforward to show that
,
it is straightforward to show that
where A is a normalisation constant to account for the truncation of the velocity distribution and
Typical values of the kick velocity dispersion
![]() are given in literature. White dwarf kicks have recently been proposed to be of order
are given in literature. White dwarf kicks have recently been proposed to be of order
![]() km s-1 (Davis et al. 2008; Fregeau et al. 2009). For neutron stars
km s-1 (Davis et al. 2008; Fregeau et al. 2009). For neutron stars
![]() km s-1
is adopted, which is a somewhat conservative estimate with respect to
theory, but it agrees reasonably well with observed neutron star
numbers in globular clusters and represents a compromise between single
star and binary channels (for estimates of the retention fraction and
discussions of the ``neutron star retention problem'' see Drukier 1996; Arzoumanian et al. 2002; Lyne & Lorimer 1994; Pfahl et al. 2002). Gravitational wave recoils are thought to exert black hole kicks of order
km s-1
is adopted, which is a somewhat conservative estimate with respect to
theory, but it agrees reasonably well with observed neutron star
numbers in globular clusters and represents a compromise between single
star and binary channels (for estimates of the retention fraction and
discussions of the ``neutron star retention problem'' see Drukier 1996; Arzoumanian et al. 2002; Lyne & Lorimer 1994; Pfahl et al. 2002). Gravitational wave recoils are thought to exert black hole kicks of order
![]() km s-1 (Moody & Sigurdsson 2009). This value depends on metallicity, but for simplicity I assume a single, typical value here.
km s-1 (Moody & Sigurdsson 2009). This value depends on metallicity, but for simplicity I assume a single, typical value here.
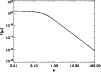
The retention fractions following from Eq. (8) are shown as a function of cluster mass per unit Plummer radius in Fig. 1. This quantity best reflects the retention fraction because
![]() in Eq. (8). Open clusters (with initial masses
in Eq. (8). Open clusters (with initial masses ![]() such that typically
such that typically
![]() ,
Larsen 2004) do not retain any neutron stars or black holes, while globular clusters (
,
Larsen 2004) do not retain any neutron stars or black holes, while globular clusters (
![]() -
-
![]() ,
Harris 1996) retain 0.1-4% of the neutron
stars and 0.3-7% of the black holes. These values are in excellent
agreement with other studies (e.g. Moody & Sigurdsson 2009; Pfahl et al. 2002),
but are still lower than the large observed number of neutron stars in
a number of globular clusters (the aforementioned ``retention
problem'').
,
Harris 1996) retain 0.1-4% of the neutron
stars and 0.3-7% of the black holes. These values are in excellent
agreement with other studies (e.g. Moody & Sigurdsson 2009; Pfahl et al. 2002),
but are still lower than the large observed number of neutron stars in
a number of globular clusters (the aforementioned ``retention
problem'').
3.2 Dissolution and the evolution of the mass function
Dissolution alters the shape of the stellar MF in star clusters due to the effects of two-body relaxation and energy equipartition. In a pioneering paper, Hénon (1969) derived the escape rate of stars of different masses from an isolated cluster. The cluster was represented by a Plummer (1911) gravitational potential:where r0 denotes the Plummer radius setting the concentration of the cluster and
with N(m) the MF, m the stellar mass, E the total energy of the cluster, and
This approaches the power law

|
Figure 1: Retention fraction of stellar remnants as a function of cluster mass per unit Plummer radius M/r0, for black holes (solid), neutron stars (dashed) and white dwarfs (dotted). |
| Open with DEXTER | |
|
Figure 2:
Hénon function |
| Open with DEXTER | |
The total mass loss rate corresponding to Eq. (10) conflicts with N-body simulations (as was already noted by Wielen 1971) because only ejections by single, close encounters are included. This restriction implies that the disruption timescale
![]() is proportional to the half-mass relaxation time
is proportional to the half-mass relaxation time
![]() times the Coulomb logarithm
times the Coulomb logarithm
![]() (
(
![]() ), while N-body simulations show that it scales with a combination of the half-mass relaxation time and the crossing time (
), while N-body simulations show that it scales with a combination of the half-mass relaxation time and the crossing time (
![]() )
due to two-body relaxation, i.e. the repeated effect of soft encounters (e.g. Fukushige & Heggie 2000; Baumgardt & Makino 2003). Nonetheless, the escape rate from Hénon (1969)
does accurately describe what happens if two stars interact and can
therefore be used as a starting point for a more complete description
of the evolution of the MF. For that purpose, it is convenient to scale
Eq. (10) to the mass loss rate found in N-body simulations and only use the relative or `differential' stellar mass dependence from Hénon (1969). This is allowed if the ratio
)
due to two-body relaxation, i.e. the repeated effect of soft encounters (e.g. Fukushige & Heggie 2000; Baumgardt & Makino 2003). Nonetheless, the escape rate from Hénon (1969)
does accurately describe what happens if two stars interact and can
therefore be used as a starting point for a more complete description
of the evolution of the MF. For that purpose, it is convenient to scale
Eq. (10) to the mass loss rate found in N-body simulations and only use the relative or `differential' stellar mass dependence from Hénon (1969). This is allowed if the ratio
![]() only depends on global cluster properties. It is straightforward to show (e.g. Spitzer 1987; Heggie & Hut 2003) that indeed this is the case as
only depends on global cluster properties. It is straightforward to show (e.g. Spitzer 1987; Heggie & Hut 2003) that indeed this is the case as
![]() .
As such, one can write
.
As such, one can write
with
where
![]() represents a correction factor to account for additional physics (see
below). The numerator reflects the escape rate, while the denominator
is proportional to the mass loss rate.
represents a correction factor to account for additional physics (see
below). The numerator reflects the escape rate, while the denominator
is proportional to the mass loss rate.
For mathematical simplicity![]() Hénon (1969) made the following assumptions in the derivation of Eq. (10).
Hénon (1969) made the following assumptions in the derivation of Eq. (10).
- (1)
- The cluster exists in isolation and the tidal field is neglected. Therefore, escape can only occur by a single, close encounter and the repeated effect of soft encounters (two-body relaxation) is not accounted for. This underestimates the escape rate of massive stars;
- (2)
- The distribution of stars is independent of stellar mass, i.e. mass segregation is not included. Depending on the balance between their encounter rate and their proximity to the escape energy, this over- or underestimates the escape rate of low-mass stars from Hénon (1969). Considering the results from Baumgardt & Makino (2003), the latter seems to be the case.
Let us assume that the distribution of stars over radius and velocity
space is initially independent of their mass. This implies that mass
segregation is dynamically created and not primordial, which is
discussed in Sect. 6. For such an initial distribution, the separation from the escape energy ![]() is independent of mass. As the cluster evolves, energy equipartition is
reached between the stars and the radius, velocity and proximity to the
escape energy become a function of stellar mass. I first consider this
effect on the escape rate before including the timescale on which
two-body relaxation occurs for different stellar masses. Please note
that the formulation of Eq. (13) with
is independent of mass. As the cluster evolves, energy equipartition is
reached between the stars and the radius, velocity and proximity to the
escape energy become a function of stellar mass. I first consider this
effect on the escape rate before including the timescale on which
two-body relaxation occurs for different stellar masses. Please note
that the formulation of Eq. (13) with
![]() appearing in the numerator and the denominator implies that only the proportionality of
appearing in the numerator and the denominator implies that only the proportionality of
![]() is important. Its exact value is determined by constants that drop out when substituting in Eq. (13).
is important. Its exact value is determined by constants that drop out when substituting in Eq. (13).
It is intuitive to express the dependence of the escape rate on the energy needed for escape as
![]() .
The energy that is required for escape
.
The energy that is required for escape ![]() is related to the position and velocity of the star
is related to the position and velocity of the star![]() . For the potential in Eq. (9) it is given by
. For the potential in Eq. (9) it is given by
with r and v the radial position and velocity of the star, and
with
where r0 represents the typical radius of the system, in this case the Plummer radius. This relation assumes that there is no particular stellar mass which dominates the mass spectrum. The decrease of radial position with stellar mass implied by Eq. (16) is a direct consequence of the energy loss endured by massive stars
with
By comparing the models to N-body simulations (provided by Gieles, private communication) with different IMF power law slopes ![]() and a ratio between the maximum and minimum mass of 10, the approximate relation
and a ratio between the maximum and minimum mass of 10, the approximate relation
![]() is found
is found![]() for a MF
for a MF
![]() .
Fitting the Kroupa IMF with a single power law in the mass range 0.08-
.
Fitting the Kroupa IMF with a single power law in the mass range 0.08-
![]() (as used by Baumgardt & Makino 2003) yields
(as used by Baumgardt & Makino 2003) yields
![]() ,
resulting in c1=0.020 as mentioned earlier
,
resulting in c1=0.020 as mentioned earlier![]() . The comparison with N-body simulations also showed that a single value of c1 suffices to determine the MF evolution, even though it does not remain constant over the full cluster lifetime.
. The comparison with N-body simulations also showed that a single value of c1 suffices to determine the MF evolution, even though it does not remain constant over the full cluster lifetime.
Because
![]() ,
Eq. (17)
indicates that the escape rate of low-mass stars is increased if a
cluster is in complete energy equipartition. However, the timescale on
which two-body relaxation occurs between different stellar masses has
not yet been considered. For a cluster starting with a stellar
mass-independent distribution of radial positions and velocities, the
equipartition timescale
,
Eq. (17)
indicates that the escape rate of low-mass stars is increased if a
cluster is in complete energy equipartition. However, the timescale on
which two-body relaxation occurs between different stellar masses has
not yet been considered. For a cluster starting with a stellar
mass-independent distribution of radial positions and velocities, the
equipartition timescale ![]() scales as
scales as
for equipartition between stars of masses m and m' (Heggie & Hut 2003). This is a modified version of the relaxation timescale, which shows a very similar proportionality (
The correction factor for the escape rate
![]() that appears in the integrals of Eq. 13 now follows from Eqs. (17) and (18) as
that appears in the integrals of Eq. 13 now follows from Eqs. (17) and (18) as
It was mentioned before that the proportionalities of
The influence of the tidal field is now included in two ways. First of all, the escape of stars no longer occurs by a single, close encounter but arises due to two-body relaxation on the equipartition timescale, representing the repeated effect of soft encounters. Secondly, the above derivation of the separation from the escape energy assumes a potential which approximates tidally limited clusters. As a result, the escape rate of massive stars is increased with respect to clusters in the model of Hénon (1969), which was derived for an isolated cluster. On the other hand, the effect of mass segregation is included by introducing a stellar mass-dependence for the energy needed by stars to reach the escape velocity. Low-mass stars are closer to the tidal radius than massive stars, leading to a lower energy that is needed for escape and an increased escape rate. It depends on the shape of the MF which mechanism dominates.
The evolution of the MF of various cluster components is obtained from Eqs. (12), (13) and (19) by writing
where the MFs of stars, white dwarfs, neutron stars and black holes are represented by
If stellar evolution is included, the resulting mass loss causes an
expansion of the cluster, during which stars are lost independently of
their masses. This delays the onset of mass segregation and the stellar
mass-dependent mass loss that is described above. The moment of
transition to stellar mass-dependent mass loss can be characterised by
a certain fraction of the initial cluster mass that has been lost by
dissolution
![]() .
It is assumed that the fraction
.
It is assumed that the fraction
![]() of the mass loss for which the escape rate depends on the stellar mass grows exponentially
of the mass loss for which the escape rate depends on the stellar mass grows exponentially![]() between 0 and 1 as
between 0 and 1 as
where the subscript ``smd'' denotes ``stellar mass-dependent'',
for a King parameter of W0=5, with the dissolution timescale parameter at the solar galactocentric radius

|
Figure 3:
MF slope change
|
| Open with DEXTER | |
The modeled MF slope change
![]() in the mass range m=0.1-
in the mass range m=0.1-
![]() is shown in Fig. 3 for different IMFs covering m=0.1-
is shown in Fig. 3 for different IMFs covering m=0.1-
![]() .
Evidently,
.
Evidently,
![]() is a function of the remaining mass fraction and is insensitive to the
slope of the IMF, as long as that the ratio between the maximum and
minimum mass is kept fixed and stellar evolution is excluded. This is
an interesting observation in view of the MF evolution of globular
clusters, in which
is a function of the remaining mass fraction and is insensitive to the
slope of the IMF, as long as that the ratio between the maximum and
minimum mass is kept fixed and stellar evolution is excluded. This is
an interesting observation in view of the MF evolution of globular
clusters, in which
![]() -
-
![]() and stellar evolution only plays a minor role. Figure 3
shows that the slope of the MF in globular clusters could be a
possible indicator for the mass fraction that has been lost due to
dissolution, provided that the IMF does not vary and the remnant
retention fractions were not substantially dissimilar during the early
evolution of different globular clusters (see Sect. 5.2 and Fig. 19).
and stellar evolution only plays a minor role. Figure 3
shows that the slope of the MF in globular clusters could be a
possible indicator for the mass fraction that has been lost due to
dissolution, provided that the IMF does not vary and the remnant
retention fractions were not substantially dissimilar during the early
evolution of different globular clusters (see Sect. 5.2 and Fig. 19).

|
Figure 4:
Relative escape rate
|
| Open with DEXTER | |

|
Figure 5:
Mass of the highest relative escape rate
|
| Open with DEXTER | |
Even though its quantitative properties only hold for a Kroupa MF, the variation of the relative escape rate with the maximum mass of the MF has several implications for star cluster evolution. The change of
4 Comparison to N-body simulations
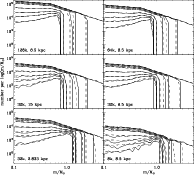
|
Figure 6:
Comparison of the evolution of the stellar MF from the models (dashed) to the N-body runs from Baumgardt & Makino (2003, solid)
for the exact same boundary conditions. The initial number of particles
and the galactocentric radius are indicated in the bottom-left corner
of each panel. From top to bottom, the subsequent MFs in each panel are shown for the times at which the remaining cluster mass fraction equals
|
| Open with DEXTER | |
The model described in Sect. 3 can be easily verified by running it for the exact same boundary conditions as the N-body simulations![]() by Baumgardt & Makino (2003)
and comparing the results. They conducted simulations of Roche
lobe-filling clusters between 8k and 128k particles, which were evolved
in the Galactic tidal field at galactocentric radii in the range
2.833-15 kpc. The boundary conditions for the N-body runs of Baumgardt & Makino (2003) differ from those described in Sect. 3 by neglecting kick velocities and defining the Kroupa stellar IMF between 0.1 and 15
by Baumgardt & Makino (2003)
and comparing the results. They conducted simulations of Roche
lobe-filling clusters between 8k and 128k particles, which were evolved
in the Galactic tidal field at galactocentric radii in the range
2.833-15 kpc. The boundary conditions for the N-body runs of Baumgardt & Makino (2003) differ from those described in Sect. 3 by neglecting kick velocities and defining the Kroupa stellar IMF between 0.1 and 15
![]() ,
thereby excluding black holes. For this particular comparison, the same
IMF, stellar evolution prescription, and initial-final mass relation
for stellar remnants are used in the model that is presented in this
paper.
,
thereby excluding black holes. For this particular comparison, the same
IMF, stellar evolution prescription, and initial-final mass relation
for stellar remnants are used in the model that is presented in this
paper.
In Fig. 6, the modeled evolution of the (luminous) stellar MF is compared to the N-body runs with King parameter W0=5
for a range of cluster masses and total disruption times. As time
progresses, the maximum stellar mass decreases due to stellar evolution
and the MF is lowered due to the dynamical dissolution of the star
cluster. The slope of the MF changes due to the preferential escape of
low-mass stars, which have energies closer to their escape energies,
even to the extent that it dominates over their relatively slow
two-body relaxation. For both the models and the N-body simulations, the MF develops a slight bend at
![]() when approaching total disruption. The bend arises as an optimum
between on the one hand high energies but slow relaxation for the
lowest stellar masses, and on the other hand quick relaxation but low
energies for the highest stellar masses (see the discussion at the end
of Sect. 3).
when approaching total disruption. The bend arises as an optimum
between on the one hand high energies but slow relaxation for the
lowest stellar masses, and on the other hand quick relaxation but low
energies for the highest stellar masses (see the discussion at the end
of Sect. 3).
In all cases, the resemblance of the models and the N-body simulations is striking. The models reproduce all key aspects of the N-body runs, such as the amount of low-mass star depletion, the changing slope at
![]() for clusters close to dissolution, the survival of the Kroupa bend at
for clusters close to dissolution, the survival of the Kroupa bend at
![]() ,
and the dependence of the low-mass depletion on the total lifetime of
the cluster (compare the three 32k runs). The only difference
occurs at the high-mass end of the MF, where the maximum stellar masses
do not match at young ages. This is due to a minor dissimilarity of the
total mass evolution (also see Kruijssen & Lamers 2008; Lamers et al. 2005).
Because the maximum stellar mass only depends on the age of the
cluster, this causes a difference in maximum stellar mass when showing
the MFs at fixed remaining cluster mass fractions. The contrast is
clearest at young ages, since there the maximum stellar mass most
rapidly decreases.
,
and the dependence of the low-mass depletion on the total lifetime of
the cluster (compare the three 32k runs). The only difference
occurs at the high-mass end of the MF, where the maximum stellar masses
do not match at young ages. This is due to a minor dissimilarity of the
total mass evolution (also see Kruijssen & Lamers 2008; Lamers et al. 2005).
Because the maximum stellar mass only depends on the age of the
cluster, this causes a difference in maximum stellar mass when showing
the MFs at fixed remaining cluster mass fractions. The contrast is
clearest at young ages, since there the maximum stellar mass most
rapidly decreases.
In the description of the model in Sect. 3, two constants have been determined from the N-body simulations by Baumgardt & Makino (2003). These constants are the ratio of the mean speed squared to the central escape velocity squared (c1, see Eq. (17)) and the proportionality constant for the relation marking the transition to stellar mass-dependent mass loss (c2, see Eq. (22)). As mentioned in Sect. 3, for a Kroupa IMF and King parameter W0=5 one obtains c1=0.020 and c2=0.25. To illustrate the robustness of the models, in Fig. 7 they are compared to a 64k N-body run with W0=7. For such a cluster with a higher concentration, the early mass segregation implies c2=0.15. Again, the model and the simulation are in excellent agreement.

|
Figure 7:
Comparison of the evolution of the stellar MF from the models (dashed) to the N-body run from Baumgardt & Makino (2003, solid) with W0=7
for the exact same boundary conditions. From top to bottom, the
subsequent MFs are shown for the times at which the remaining
cluster mass fraction equals
|
| Open with DEXTER | |
The dependence of the MF evolution on both constants is considered in Fig. 8. For c1, the dependence of the evolution of the MF on its value is shown in the upper panel of Fig. 8, while for c2 it is shown in the bottom panel of Fig. 8. Both panels show the evolution of the MF for the 64k cluster in Fig. 6 for different values of c1 and c2.

|
Figure 8:
Influence of the constants c1 and c2 on the evolution of the stellar MF. From top to bottom, the subsequent MFs in each panel are shown for the times at which the remaining cluster mass fraction equals
|
| Open with DEXTER | |
The ratio of the mean speed squared to the central escape velocity squared c1 affects the escape probability of the stars with the lowest masses. Because these stars are closest to their escape energies in a mass-segregated cluster, they are most strongly influenced by the value of c1. For higher c1, the MF gets more depleted in low-mass stars due to their closer proximity to the escape energy, while for lower c1 more low-mass stars are retained as the balance between close proximity to the escape energy and slow relaxation shifts to the latter.
The proportionality constant for the transition to stellar mass-dependent dissolution c2 in Eq. (22) affects the MF as a whole. For lower c2, the transition occurs earlier and more low-mass stars are lost, while for higher c2
the onset of the depletion is delayed and the slope of the MF remains
closer to its initial value. If one were to assume a constant
![]() ,
which is contrary to the adopted relation with cluster mass in Eq. (22),
this would therefore yield a stellar MF in massive clusters that is
underpopulated in low-mass stars, and a MF in low-mass clusters that is
overabundant in low-mass stars.
,
which is contrary to the adopted relation with cluster mass in Eq. (22),
this would therefore yield a stellar MF in massive clusters that is
underpopulated in low-mass stars, and a MF in low-mass clusters that is
overabundant in low-mass stars.
5 Star cluster evolution
In this section, the described model is applied to compute the evolution of clusters for a variety of boundary conditions. The stellar content as well as integrated photometry are addressed, using the boundary conditions from Sect. 3 instead of those that were adopted to compare the model to N-body simulations in Sect. 4. The most important differences are the mass range of the IMF, the inclusion of remnant kick velocities, and the initial-final mass relation.The model that will be referred to as the ``standard model'' uses a metallicity Z=0.004 (which is typical of globular clusters), a King parameter![]() of W0=7 (corresponding to
of W0=7 (corresponding to
![]() in Eq. (2)), a dissolution timescale parameter t0=1 Myr, and a Kroupa IMF between
in Eq. (2)), a dissolution timescale parameter t0=1 Myr, and a Kroupa IMF between
![]() and the maximum stellar mass given by the Padova isochrones at
and the maximum stellar mass given by the Padova isochrones at
![]() ,
which is typically
,
which is typically
![]() .
For the computation of the retained remnant fraction (see Eq. (8)), the Plummer radius r0 is related to the half-mass radius
.
For the computation of the retained remnant fraction (see Eq. (8)), the Plummer radius r0 is related to the half-mass radius ![]() as
as
![]() .
The half-mass radius is assumed to remain constant during the cluster lifetime (e.g. Aarseth & Heggie 1998). For the relation between
.
The half-mass radius is assumed to remain constant during the cluster lifetime (e.g. Aarseth & Heggie 1998). For the relation between ![]() and initial cluster mass
and initial cluster mass ![]() the expression from Larsen (2004) is adopted:
the expression from Larsen (2004) is adopted:
The models that are used in this section are computed from 107 yr to
5.1 The influence of the disruption time
The disruption time of a cluster affects the evolution of the MF and of the integrated photometric properties. To assess the influence of the disruption time on cluster evolution, clusters with low and high remnant retention fractions should be treated separately, because the presence of massive remnants also has a pronounced effect on the results (see Sect. 5.2). As shown in Fig. 1, for a given kick velocity dispersion the remnant retention fraction is set by the cluster mass. This means that the division between low and high remnant retention fractions can be made by making a cut in initial cluster mass.

|
Figure 9:
Influence of the disruption time on the evolution of the stellar MF for a cluster with a low remnant retention fraction (
|
| Open with DEXTER | |
A quantifiable way to look at the evolution of the stellar MF in star clusters is to consider the slope of the MF
![]() in certain mass intervals (De Marchi & Pulone 2007; Vesperini et al. 2009; De Marchi et al. 2007; Richer et al. 1991). For the commonly used mass intervals
in certain mass intervals (De Marchi & Pulone 2007; Vesperini et al. 2009; De Marchi et al. 2007; Richer et al. 1991). For the commonly used mass intervals
![]() (
(![]() )
and
)
and
![]() (
(![]() ), Fig. 10 shows the evolution of the slope
), Fig. 10 shows the evolution of the slope ![]() for the same clusters as before. Like Fig. 9,
this illustrates that for short disruption times the slope steepens as
the cluster dissolves, while for long disruption times the slope
flattens with time. The presented models and other model runs indicate
that
for the same clusters as before. Like Fig. 9,
this illustrates that for short disruption times the slope steepens as
the cluster dissolves, while for long disruption times the slope
flattens with time. The presented models and other model runs indicate
that ![]() increases with time for
increases with time for
![]() Gyr and decreases for
Gyr and decreases for
![]() Gyr.
For total disruption times in between these values, the slope first
increases and then decreases. The slope in the second mass interval
Gyr.
For total disruption times in between these values, the slope first
increases and then decreases. The slope in the second mass interval ![]() shows the same behaviour. It increases for
shows the same behaviour. It increases for
![]() Gyr and decreases for
Gyr and decreases for
![]() Gyr.
Gyr.
The mass-to-light (M/L) ratio evolution of star clusters is affected by the evolution of the MF due to the large variations in M/L ratio between stars of different masses. Massive stars have lower M/L ratios than low-mass stars, implying that a cluster with a MF that is depleted in low-mass stars will have a reduced M/L ratio (Kruijssen 2008; Kruijssen & Lamers 2008; Baumgardt & Makino 2003). As such, one would also expect a correlation between the slope of the MF and M/L ratio.
In Fig. 11, the evolution of the ratio of the V-band M/LV to the mass-to-light ratio due to stellar evolution
![]() is shown for the same clusters as in Figs. 9 and 10. This quantity reflects the relative M/LV ratio
change induced by dynamical evolution with respect to evolutionary
fading only. If the escape rate would be independent of stellar mass,
the evolution would follow a horizontal line at
is shown for the same clusters as in Figs. 9 and 10. This quantity reflects the relative M/LV ratio
change induced by dynamical evolution with respect to evolutionary
fading only. If the escape rate would be independent of stellar mass,
the evolution would follow a horizontal line at
![]() .
However, when accounting for dynamical evolution, the
M/L ratio is always smaller than that for stellar
evolution only. Somewhat surprisingly, this is also the case for
clusters for which the slope of the MF increases (see Fig. 10). This is explained by looking at the evolution of the entire MF in Fig. 9.
Even though the slope at low masses increases for short disruption
times due to the escape of intermediate-mass stars, the most massive
stars that dominate the cluster light are still retained. Because stars
of intermediate masses are lost instead, the M/L ratio decreases.
.
However, when accounting for dynamical evolution, the
M/L ratio is always smaller than that for stellar
evolution only. Somewhat surprisingly, this is also the case for
clusters for which the slope of the MF increases (see Fig. 10). This is explained by looking at the evolution of the entire MF in Fig. 9.
Even though the slope at low masses increases for short disruption
times due to the escape of intermediate-mass stars, the most massive
stars that dominate the cluster light are still retained. Because stars
of intermediate masses are lost instead, the M/L ratio decreases.
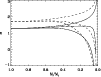
|
Figure 10:
Influence of the disruption time on the stellar MF slope |
| Open with DEXTER | |
Because the slope of the stellar MF either increases or decreases at masses
![]() ,
the decrease of the M/L ratio implies a large range of MF slopes that can occur at low
M/L ratios. This is shown in Fig. 12, where the relation between
,
the decrease of the M/L ratio implies a large range of MF slopes that can occur at low
M/L ratios. This is shown in Fig. 12, where the relation between ![]() and the M/L ratio drop is presented. The slope of the stellar MF in a certain mass range does not necessarily reflect the M/L ratio of the entire cluster. Considering the aforementioned rule of thumb stating that for total disruption times
and the M/L ratio drop is presented. The slope of the stellar MF in a certain mass range does not necessarily reflect the M/L ratio of the entire cluster. Considering the aforementioned rule of thumb stating that for total disruption times
![]() Gyr the depletion of the MF occurs around 15-20% of the mass of the most massive star
Gyr the depletion of the MF occurs around 15-20% of the mass of the most massive star
![]() ,
it is useful to define the slope in a mass range that is related to
,
it is useful to define the slope in a mass range that is related to
![]() .
In Fig. 12, the relation between slope and M/L ratio is also shown for the slope in the stellar mass range
.
In Fig. 12, the relation between slope and M/L ratio is also shown for the slope in the stellar mass range
![]() .
In such a relative mass range, the slope follows a much narrower relation with M/L ratio. The range between 30% and 80% of
.
In such a relative mass range, the slope follows a much narrower relation with M/L ratio. The range between 30% and 80% of
![]() was chosen to maximise this effect.
was chosen to maximise this effect.
For the slopes in the fixed stellar mass ranges (![]() and
and ![]() ,
see above), the relation with the M/L ratio becomes better defined for long-lived clusters. It is shown in Figs. 10-12 that both the slope and the M/L ratio
decrease for clusters with long disruption times, indicating that both
quantities are more clearly related for globular cluster-like
lifetimes.
,
see above), the relation with the M/L ratio becomes better defined for long-lived clusters. It is shown in Figs. 10-12 that both the slope and the M/L ratio
decrease for clusters with long disruption times, indicating that both
quantities are more clearly related for globular cluster-like
lifetimes.
The colour of star clusters is also influenced by the evolution
of the MF, due to the colour differences between stars of different
masses. The V-I magnitude difference
![]() with respect to the V-I value that a cluster would have if dynamical evolution were neglected is shown in Fig. 13. As the clusters dissolve, their colours become redder due to the escape of main sequence stars. The magnitude difference in V-I exceeds
with respect to the V-I value that a cluster would have if dynamical evolution were neglected is shown in Fig. 13. As the clusters dissolve, their colours become redder due to the escape of main sequence stars. The magnitude difference in V-I exceeds
![]() mag for total disruption times
mag for total disruption times ![]() 1.5 Gyr. In redder passbands (e.g. the V-K colour),
the difference grows to several tenths of magnitudes. For longer total
disruption times only stars of the lowest masses are ejected (see
Fig. 9), which hardly contribute to the cluster light and colour, implying that the colours are only marginally affected.
1.5 Gyr. In redder passbands (e.g. the V-K colour),
the difference grows to several tenths of magnitudes. For longer total
disruption times only stars of the lowest masses are ejected (see
Fig. 9), which hardly contribute to the cluster light and colour, implying that the colours are only marginally affected.

|
Figure 11:
Influence of the disruption time on the M/LV ratio evolution for a cluster with a low remnant retention fraction (
|
| Open with DEXTER | |

|
Figure 12:
Influence of the disruption time on the combined evolution of the MF slope |
| Open with DEXTER | |
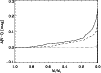
|
Figure 13:
Influence of the disruption time on the V-I colour for a cluster with a low remnant retention fraction (
|
| Open with DEXTER | |
5.2 The influence of the remnant retention fraction
The formation of stellar remnants introduces massive bodies in the MF that do not end their lives due to stellar evolution like massive stars do. Depending on their kick velocities, stellar remnants can be retained in (massive) clusters. If they are retained, they keep affecting the evolution of the stellar MF until the cluster is disrupted. Especially black holes can have a pronounced effect on cluster evolution.
The remnant retention fraction arises from the cluster mass, radius and the kick velocity dispersion (see Eq. (8)). In this section, the mass-radius relation from Eq. (24) is used. Although the results will differ for other relations, it has been verified that for commonly used alternatives![]() ,
the change is only marginal and does not affect the nature of the
conclusions. To separate the effect of remnant retention from that of
the disruption time, a fixed initial cluster mass of
,
the change is only marginal and does not affect the nature of the
conclusions. To separate the effect of remnant retention from that of
the disruption time, a fixed initial cluster mass of
![]() is assumed while independently varying the velocity dispersion of the
remnant kick velocities and the disruption time. The corresponding
evolution of the stellar MF is shown in Fig. 14, for the standard model (see the beginning of this section) with black hole kick velocity dispersions
is assumed while independently varying the velocity dispersion of the
remnant kick velocities and the disruption time. The corresponding
evolution of the stellar MF is shown in Fig. 14, for the standard model (see the beginning of this section) with black hole kick velocity dispersions
![]() km s-1, equivalent to
km s-1, equivalent to
![]() for a
for a
![]() cluster, and for dissolution timescale parameters
cluster, and for dissolution timescale parameters
![]() Myr, which for a
Myr, which for a
![]() cluster implies
cluster implies
![]() Gyr. Assuming an age of 12 Gyr, the present-day mass in the case of t0=1 Myr is about
Gyr. Assuming an age of 12 Gyr, the present-day mass in the case of t0=1 Myr is about
![]() ,
comparable to globular clusters. The remaining fraction of the initial mass is
,
comparable to globular clusters. The remaining fraction of the initial mass is
![]() .
.

|
Figure 14:
Influence of the black hole kick velocity dispersion and disruption
time on the evolution of the stellar MF for an initial cluster mass
|
| Open with DEXTER | |
If the velocity dispersion of black hole kicks is low and a relatively large fraction of black holes is retained, then the escape rate of massive stars is increased with respect to high kick velocity dispersions. This arises due to the quick two-body relaxation between the massive stars and the black holes, which will have masses larger than the most massive stars after a few Myr of stellar evolution. As a result, the escape rate of low-mass stars is largest in clusters containing only few black holes. This happens for clusters with either long or short disruption times, but the effect is largest for long-lived clusters (the solid lines in Fig. 14). In these clusters the maximum stellar mass is more strongly decreased by stellar evolution than in short-lived clusters, implying that the black hole masses are larger compared to the most massive stars in these clusters. For long disruption times, the presence of massive remnants therefore has a more pronounced effect on the escape rate of massive stars than for short disruption times. If these long-lived clusters retain a sufficiently large fraction of the stellar remnants, their stellar MF may even become depleted in massive stars.
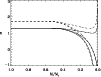
The top panel of Fig. 14 also shows that for a cluster with a high remnant retention fraction, the impact of the disruption time on the MF evolution is similar to that of clusters with low retention fractions (see Fig. 9). However, the influence of the disruption time becomes smaller when more remnants are retained. This explains why Baumgardt & Makino (2003) only found a very weak dependence of the evolution of the MF on the disruption time (also see Fig. 6), since they neglected remnant kick velocities and retained all remnants in their simulations.
|
Figure 15:
Influence of the black hole retention fraction on the stellar MF slope |
| Open with DEXTER | |
Analogous to Fig. 10 in Sect. 5.1, the evolution of the MF slope in different mass ranges is shown in Fig. 15 for the clusters with t0=1 Myr from Fig. 14![]() .
The kick velocity dispersion has an effect on the MF that is more
uniform than the consequences of variations in the disruption time,
leading to very similar slope evolutions in the two different stellar
mass ranges. Independent of the mass range, an increase in remnant
retention fraction is reflected by an increase of
.
The kick velocity dispersion has an effect on the MF that is more
uniform than the consequences of variations in the disruption time,
leading to very similar slope evolutions in the two different stellar
mass ranges. Independent of the mass range, an increase in remnant
retention fraction is reflected by an increase of ![]() .
The model that is displayed for
.
The model that is displayed for
![]() km s-1, t0=1 Myr, and
km s-1, t0=1 Myr, and
![]() (the upper dashed and solid lines in Fig. 15) marks the transition between an increase or decrease of the MF slope by dynamical evolution. For an initial
(the upper dashed and solid lines in Fig. 15) marks the transition between an increase or decrease of the MF slope by dynamical evolution. For an initial
![]() ,
low-mass stars are preferentially ejected during most of the cluster lifetime, while for
,
low-mass stars are preferentially ejected during most of the cluster lifetime, while for
![]() mainly the massive stars escape. For shorter disruption times, the
transition is located at a smaller black hole retention fraction.
mainly the massive stars escape. For shorter disruption times, the
transition is located at a smaller black hole retention fraction.
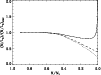
Because the black hole retention fraction affects the overall slope of the stellar MF, the changes in ![]() are matched by corresponding changes in the M/L ratio. In Fig. 16, the relative M/LV ratio change due to dynamical evolution is shown for same clusters as in Fig. 15. Contrary to the clusters with low remnant retention fractions in Sect. 5.1, the M/L ratio of the clusters in Fig. 16
does not monotonously decrease. Close to total disruption, the massive
remnants are the last bodies to be ejected. During that short phase of
cluster evolution, the M/L ratio is increased by dynamical evolution and exceeds the value it would have due to stellar evolution alone.
are matched by corresponding changes in the M/L ratio. In Fig. 16, the relative M/LV ratio change due to dynamical evolution is shown for same clusters as in Fig. 15. Contrary to the clusters with low remnant retention fractions in Sect. 5.1, the M/L ratio of the clusters in Fig. 16
does not monotonously decrease. Close to total disruption, the massive
remnants are the last bodies to be ejected. During that short phase of
cluster evolution, the M/L ratio is increased by dynamical evolution and exceeds the value it would have due to stellar evolution alone.
|
Figure 16:
Influence of the black hole retention fraction on the M/LV ratio evolution for an initial cluster mass
|
| Open with DEXTER | |
The behaviour of M/L ratio for different black hole
kick velocity dispersions has interesting implications for the relation
between stellar MF slope and M/L ratio, which is shown in Fig. 17. In combination with Fig. 12
(note the different axes), it shows possible evolutionary tracks of
star clusters in this plane, indicating that nearly every location may
be reached. However, when limiting ourselves to long-lived clusters,
Fig. 17 illustrates that these clusters will follow a trend of decreasing slope with decreasing M/L ratio, albeit with excursions to high M/L ratios and slightly higher ![]() close to their total disruption. This explains the trend that was found by Kruijssen & Mieske (2009), who considered the relation between the observed MF slopes and M/L ratios of Galactic globular clusters.
close to their total disruption. This explains the trend that was found by Kruijssen & Mieske (2009), who considered the relation between the observed MF slopes and M/L ratios of Galactic globular clusters.

|
Figure 17:
Influence of the black hole retention fraction on the combined evolution of the MF slope |
| Open with DEXTER | |
The colour change due to dynamical evolution is only very small for clusters with
![]() Gyr (see Sect. 5.1).
Because clusters in which remnants are retained are massive, their
lifetimes are correspondingly long. As a result, the colour evolution
is largely unaffected for the clusters in which the remnant retention
fraction could play a role (
Gyr (see Sect. 5.1).
Because clusters in which remnants are retained are massive, their
lifetimes are correspondingly long. As a result, the colour evolution
is largely unaffected for the clusters in which the remnant retention
fraction could play a role (
![]() mag).
The colour change is even smaller if more massive remnants are
retained, because then the stellar MF more closely resembles its
initial form (see the upper panel of Fig. 14). Long-lived clusters generally appear
mag).
The colour change is even smaller if more massive remnants are
retained, because then the stellar MF more closely resembles its
initial form (see the upper panel of Fig. 14). Long-lived clusters generally appear ![]() 0.005 mag bluer in V-I due to dynamical evolution during the last
0.005 mag bluer in V-I due to dynamical evolution during the last ![]() 3-20%
of their lifetimes and reach a similar reddening upon their total
disruption, which is well within observational errors. The colours of
old clusters are thus only marginally affected by dynamical evolution.
3-20%
of their lifetimes and reach a similar reddening upon their total
disruption, which is well within observational errors. The colours of
old clusters are thus only marginally affected by dynamical evolution.
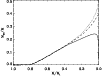
The evolution of the total remnant mass fraction is shown in Fig. 18
for different black hole kick velocity dispersions. The seemingly
counterintuitive result is that the fraction of the cluster mass that
is constituted by remnants is smaller when more black holes are
retained. As shown in Fig. 14,
the retention of black holes suppresses the depletion of the low-mass
end of the MF due to the ``sweet spot'' escape (see Sect. 3) of massive (![]()
![]() )
stars by the black holes. After
)
stars by the black holes. After ![]() 1 Gyr,
white dwarfs and neutron stars have masses that are similar to those of
the massive stars, implying that their escape rate is also increased
when more black holes are retained. Because the total mass constituted
by white dwarfs and neutron stars is larger than the combined mass of
all black holes, the fraction of the total cluster mass that is
constituted by remnants decreases if these low-mass remnants are
ejected by the more massive black holes.
1 Gyr,
white dwarfs and neutron stars have masses that are similar to those of
the massive stars, implying that their escape rate is also increased
when more black holes are retained. Because the total mass constituted
by white dwarfs and neutron stars is larger than the combined mass of
all black holes, the fraction of the total cluster mass that is
constituted by remnants decreases if these low-mass remnants are
ejected by the more massive black holes.
|
Figure 18: Influence of the black
hole retention fraction on the total remnant mass fraction. Shown is
the ratio of the total mass in stellar remnants
|
| Open with DEXTER | |
6 Discussion and applications
The results of this paper show that the stellar MFs in star clusters differ strongly from their initial forms due to dynamical cluster evolution. The specific kinds of these differences depend on the properties of the star clusters and their tidal environment, most importantly on the disruption time, remnant retention fraction, and IMFA physical model for the evolution of the stellar MF is presented in
which two-body relaxation leads to a stellar mass dependence of the
escape rate. For any particular stellar mass, the escape rate is
determined by the typical proximity of that mass to the escape energy
and by the timescale on which the two-body relaxation with the other
stars takes place. Combined with a prescription for stellar evolution,
stellar remnant production, and remnant retention using kick velocity
dispersions, this provides a description for the total evolution of
the MF. This description is independent of the adopted total mass evolution.
The model shows that the slope of the mass function is a possible
indicator for the mass fraction that has been lost due to dissolution,
provided that the IMF does not vary and the remnant retention fraction
has been fairly similar for young globular clusters![]() .
.
For the exact same initial conditions, the model shows excellent agreement with N-body simulations of the evolving MF by Baumgardt & Makino (2003). However, an important advantage of the presented model compared to the (more accurate) N-body simulations is its short runtime and corresponding flexibility. It can be easily applied to compute the evolution of clusters for a large range of initial conditions. The results can then be used to identify interesting cases for more detailed and less simplified calculations with N-body or Monte Carlo models.
The most important simplification of the model is neglecting the effect
of binary encounters on the stellar mass dependence of the escape rate.
To incorporate binaries, a conclusive census of the binary population
in star clusters would be required, which is not yet available.
Nonetheless, it is possible to make a qualitative estimate for the
effect of binaries. The encounter rate of binaries would typically be
higher than that of individual stars, because the cross section of
binaries is larger. This would increase the relative escape rate at the
stellar mass for which the binary fraction![]() peaks. This binary fraction is found to increase with primary mass (see e.g. Kouwenhoven et al. 2009).
Because massive stars are removed by stellar evolution, this implies
that the binary fraction decreases with age, which is in agreement with
the low binary fraction observed in globular clusters (
peaks. This binary fraction is found to increase with primary mass (see e.g. Kouwenhoven et al. 2009).
Because massive stars are removed by stellar evolution, this implies
that the binary fraction decreases with age, which is in agreement with
the low binary fraction observed in globular clusters (![]()
![]() ,
e.g. Richer et al. 2004).
The effect of binaries on the evolution of the mass function would thus
be most notable if the majority of the dynamical mass loss occurs at
ages <50 Myr (the typical lifetime of an
,
e.g. Richer et al. 2004).
The effect of binaries on the evolution of the mass function would thus
be most notable if the majority of the dynamical mass loss occurs at
ages <50 Myr (the typical lifetime of an
![]() star),
in which case it would somewhat enhance the relative escape rate of the
most massive stars. The influence is expected to be small, since the
presence of binaries mainly affects ejections by hard encounters and
leaves the overall evaporation rate largely unchanged (Küpper et al. 2008).
On the other hand, neglecting binary encounters of massive remnants
such as black holes could underestimate their escape rate for times
beyond 50 Myr. This would imply that the model overestimates the impact
of the black hole retention fraction on the evolution of the MF.
star),
in which case it would somewhat enhance the relative escape rate of the
most massive stars. The influence is expected to be small, since the
presence of binaries mainly affects ejections by hard encounters and
leaves the overall evaporation rate largely unchanged (Küpper et al. 2008).
On the other hand, neglecting binary encounters of massive remnants
such as black holes could underestimate their escape rate for times
beyond 50 Myr. This would imply that the model overestimates the impact
of the black hole retention fraction on the evolution of the MF.
The model is applied to investigate the influence of the
disruption time and remnant retention on the evolution of the MF and
integrated photometric properties of star clusters. For total
disruption times
![]() Gyr,
the modeled relative escape rate is highest at a certain ``sweet spot''
mass that is typically 15-20% of the mass of the most massive objects
in the cluster. For longer lifetimes, the evolution of the MF is
dominated by low-mass star depletion, unless the retention fraction of
massive stellar remnants is larger than 0.25. Only in the
particular case of such a high retention fraction, the M/L ratio is increased by dynamical evolution when the cluster approaches total disruption. In all other scenarios, the M/L ratio decreases because the most massive (luminous) stars are kept
Gyr,
the modeled relative escape rate is highest at a certain ``sweet spot''
mass that is typically 15-20% of the mass of the most massive objects
in the cluster. For longer lifetimes, the evolution of the MF is
dominated by low-mass star depletion, unless the retention fraction of
massive stellar remnants is larger than 0.25. Only in the
particular case of such a high retention fraction, the M/L ratio is increased by dynamical evolution when the cluster approaches total disruption. In all other scenarios, the M/L ratio decreases because the most massive (luminous) stars are kept![]() .
When defining the slope of the MF in the range 30-80% of the maximum
stellar mass, this gives a clear relation between the MF slope and the M/L ratio. For slopes that are defined in fixed mass ranges, there is not necessarily a correlation between slope and M/L ratio if
.
When defining the slope of the MF in the range 30-80% of the maximum
stellar mass, this gives a clear relation between the MF slope and the M/L ratio. For slopes that are defined in fixed mass ranges, there is not necessarily a correlation between slope and M/L ratio if
![]() Gyr.
In clusters with a longer total disruption time, both quantities are
related. Dynamical cluster evolution is found to induce some reddening
of the integrated cluster colours, amounting up to 0.1-0.2 mag in V-I for total disruption times
Gyr.
In clusters with a longer total disruption time, both quantities are
related. Dynamical cluster evolution is found to induce some reddening
of the integrated cluster colours, amounting up to 0.1-0.2 mag in V-I for total disruption times
![]() Gyr.
The fraction of the cluster mass that is constituted by remnants
surprisingly decreases if more black holes are retained, because the
black holes preferentially eject bodies around the masses of white
dwarfs and neutron stars, which contain most of the total remnant mass.
Gyr.
The fraction of the cluster mass that is constituted by remnants
surprisingly decreases if more black holes are retained, because the
black holes preferentially eject bodies around the masses of white
dwarfs and neutron stars, which contain most of the total remnant mass.

|
Figure 19: MF slope versus
remaining lifetime (assuming a globular cluster age of 12 Gyr).
Diamonds represent the observed values from De Marchi et al. (2007), with typical errors as shown by the error bar in the lower right corner. The remaining lifetimes are taken from Baumgardt et al. (2008). Dotted curves represent the model evolutionary tracks of clusters with
|
| Open with DEXTER | |
Contrary to what is suggested by other studies (e.g. Anders et al. 2009; Baumgardt & Makino 2003), the evolution of the MF is not homologous. The reason that these studies concluded that its evolution is very similar for all clusters (also see Figs. 6 and 7), is that they assumed that all remnants were retained. It is illustrated in Fig. 14 that the differences between clusters with dissimilar disruption times disappear when the retention fraction increases. For realistic retention fractions, differences do arise. If two clusters with different initial masses have the same total disruption time, their MF evolution will be dissimilar due to their different remnant retention fractions and the impact of the retained remnants on the dynamical cluster evolution. Alternatively, if two clusters have equal initial masses but different total disruption times, for instance due to differences in their galactic location or environment, their MF evolution will be dissimilar due to the dynamical impact of the evolution of the maximum stellar mass.
The larger variation of MF evolution that is found with presented model may also be able to explain observations of globular clusters in which the MF cannot be characterised by a single power law (De Marchi et al. 2000). If the evolution of the MF were homologous, these features would likely be primordial (Baumgardt & Makino 2003), but this is not necessarily the case when using realistic retention fractions. Most other differences between the results presented in Sect. 5 and those from Baumgardt & Makino (2003) are also due to their assumption of full remnant retention. For example, their M/L ratio evolution shows a smaller decrease than in Fig. 11. This is explained in Fig. 16, where it is shown that dynamical evolution reduces the M/L ratio by a smaller amount if the retention fraction is larger.
Studies on the fractal nature of cluster formation show that star clusters are initially substructured (Elmegreen 2000; Bonnell et al. 2003). Even though this substructure is typically erased on a crossing time, it can induce primordial mass segregation in star clusters (McMillan et al. 2007; Allison et al. 2009). The influence of primordial mass segregation on the evolution of the MF has recently been investigated by Baumgardt et al. (2008) and Vesperini et al. (2009). While Baumgardt et al. (2008) do not include stellar evolution and concentrate on two-body relaxation, Vesperini et al. (2009) do include stellar evolution. They show that for some degrees of primordial mass segregation, the mass loss by stellar evolution can induce additional dynamical mass loss that strongly decreases the total disruption time. For clusters that survive for a Hubble time, the MF evolution in the case of primordial mass segregation is very similar to an initially unsegregated cluster. Vesperini et al. (2009) conclude that the evolution of the MF is only affected by primordial mass segregation for clusters in which the total disruption time is sufficiently decreased by the induced mass loss. In that case, the slope of the MF remains much closer to its initial value than it would in clusters without primordial mass segregation. Their conclusion is consistent with the model presented in this paper, because the evolution of the MF is determined by the most massive stars at the time when the largest mass loss occurs (see Figs. 4 and 9). This induced mass loss enters the model in terms of the absolute mass loss rate in Eq. (3), not in the stellar mass-dependent escape rate per unit mass loss rate of Eq. (13).
A change in total mass loss rate is not the only consequence of primordial mass segregation. Baumgardt et al. (2008)
have shown that low-mass star depletion is enhanced for clusters
without stellar evolution that are primordially mass-segregated. This
occurs because energy equipartition is reached on a shorter timescale
and because of their use of a fixed (
![]() )
maximum stellar mass. As a result, there are no massive bodies to
increase the escape rate of intermediate mass stars (see Fig. 5),
implying that only the low-mass stars are preferentially lost. In the
present paper, mass segregation is assumed to arise dynamically, but
the model could in principle be adapted to cover primordial mass
segregation by setting c2=0 and adjusting c1 to the initial velocity distribution until it is erased by dynamical evolution (see Eq. (22)), after which the values from Sect. 3 can be used
)
maximum stellar mass. As a result, there are no massive bodies to
increase the escape rate of intermediate mass stars (see Fig. 5),
implying that only the low-mass stars are preferentially lost. In the
present paper, mass segregation is assumed to arise dynamically, but
the model could in principle be adapted to cover primordial mass
segregation by setting c2=0 and adjusting c1 to the initial velocity distribution until it is erased by dynamical evolution (see Eq. (22)), after which the values from Sect. 3 can be used![]() . This does not necessarily yield enhanced low-mass star depletion for clusters with a complete IMF (including masses
. This does not necessarily yield enhanced low-mass star depletion for clusters with a complete IMF (including masses
![]() )
because of the presence of massive stars or remnants.
)
because of the presence of massive stars or remnants.
The presented model can be applied to the MFs of Galactic globular clusters that are observed by De Marchi et al. (2007). These MFs are more strongly depleted than is found in the N-body simulations by Baumgardt & Makino (2003), which has been attributed to primordial mass segregation (Baumgardt et al. 2008).
However, the observations can also very accurately be explained with
the realistic remnant retention fractions that are used in the present
paper. This is shown in Fig. 19, where the observed MF slopes and remaining lifetimes of the globular clusters from De Marchi et al. (2007) are compared with the globular cluster-like models from Sect. 5.2 (t0=1 Myr). The models are in much better agreement with the data than the N-body runs with complete remnant retention from Baumgardt & Makino (2003). Deviations to other values of ![]() can occur due to variations in disruption time and remnant retention fractions, as is also shown in Fig. 19.
For example, a variation of the remnant kick velocity with metallicity
in combination with the known variation of the disruption time (see
e.g. Kruijssen & Portegies Zwart 2009; Kruijssen & Mieske 2009) should be sufficient to cover the observed scatter.
can occur due to variations in disruption time and remnant retention fractions, as is also shown in Fig. 19.
For example, a variation of the remnant kick velocity with metallicity
in combination with the known variation of the disruption time (see
e.g. Kruijssen & Portegies Zwart 2009; Kruijssen & Mieske 2009) should be sufficient to cover the observed scatter.
The above line of reasoning provides an explanation for the the depleted MFs in Fig. 19 that is consistent with the simulations by Vesperini et al. (2009), who showed that the effects of primordial mass segregation are in fact suppressed in long-lived clusters due to the expansion caused by stellar evolution. This increases the relaxation time and yields an evolution of the MF that is very similar to the initially unsegregated scenario, indicating that primordial mass segregation is not a likely explanation for strongly depleted MFs. Observations of the remnant composition of these globular clusters could reveal a definitive answer as to whether the depleted MFs are explained by primordial mass segregation or by dynamical evolution with a realistic remnant retention fraction.
Dynamical cluster evolution does not appear to have a large
effect on the colours of old (globular) clusters. The only way in which
the colours could be affected beyond typical observational errors, is
if globular clusters have lost substantial fractions of their masses
during the first ![]() Gyr
after their formation. In that case, the dynamical evolution of the
stellar MF in globular clusters may have implications for studies of
colour bimodality (e.g. Larsen et al. 2001) or the blue tilt (e.g. Harris et al. 2006). It could then also possibly explain the trend of increasing V-K colour with decreasing M/LV ratio found by Strader et al. (2009) for globular clusters in M 31, because quickly dissolving clusters generally become redder and have reduced M/L ratios.
More research is needed to determine the role of the changing MF in the
above properties of globular cluster systems.
Gyr
after their formation. In that case, the dynamical evolution of the
stellar MF in globular clusters may have implications for studies of
colour bimodality (e.g. Larsen et al. 2001) or the blue tilt (e.g. Harris et al. 2006). It could then also possibly explain the trend of increasing V-K colour with decreasing M/LV ratio found by Strader et al. (2009) for globular clusters in M 31, because quickly dissolving clusters generally become redder and have reduced M/L ratios.
More research is needed to determine the role of the changing MF in the
above properties of globular cluster systems.
It can be concluded that the evolution of the stellar MF in star clusters is not as similar for all clusters as previously thought. Its precise evolution is determined by cluster characteristics like the disruption time, the remnant retention fraction, initial-final stellar mass relation, and the IMF. In order to decipher the evolution of observed star clusters, it is essential to record these characteristics and to relate them to possible scenarios for the internal evolution of clusters. That way, observables like the slope of the MF, the M/L ratio, the broadband colours, and the mass fraction in remnants can be better understood.
AcknowledgementsI thank Henny Lamers and Simon Portegies Zwart for support, advice and constructive comments on the manuscript. I also thank Douglas Heggie for inspiring suggestions during the KITP conference on globular clusters in Santa Barbara and for commenting on the manuscript. Holger Baumgardt is acknowledged for interesting discussions and for kindly providing the data from Baumgardt & Makino (2003) and Baumgardt et al. (2008). I would like to thank Nate Bastian, Mark Gieles and Peter Kruijssen for constructive comments on the manuscript. I am indebted to Mark Gieles for kindly providing N-body runs for different IMFs. The referee, Thijs Kouwenhoven, is thanked for thoughtful comments. The Institute of Astronomy in Cambridge is gratefully acknowledged for their kind hospitality during my visit, when a large part of this work was carried out. This research is supported by a TopTalent fellowshipfrom the Netherlands Organisation for Scientific Research (NWO), grant number 021.001.038.
References
- Aarseth, S. J. 1999, PASP, 111, 1333 [NASA ADS] [CrossRef]
- Aarseth, S. J., & Heggie, D. C. 1998, MNRAS, 297, 794 [NASA ADS] [CrossRef]
- Allison, R. J., Goodwin, S. P., Parker, R. J., et al. 2009, ApJ, 700, L99 [NASA ADS] [CrossRef]
- Anders, P., Lamers, H. J. G. L. M., & Baumgardt, H. 2009, A&A, 502, 817 [NASA ADS] [CrossRef] [EDP Sciences]
- Arzoumanian, Z., Chernoff, D. F., & Cordes, J. M. 2002, ApJ, 568, 289 [NASA ADS] [CrossRef]
- Baumgardt, H. 2001, MNRAS, 325, 1323 [NASA ADS] [CrossRef]
- Baumgardt, H., & Makino, J. 2003, MNRAS, 340, 227 [NASA ADS] [CrossRef]
- Baumgardt, H., De Marchi, G., & Kroupa, P. 2008, ApJ, 685, 247 [NASA ADS] [CrossRef]
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS]
- Boily, C. M., Fleck, J.-J., Lançon, A., & Renaud, F. 2009, Ap&SS, 110
- Bonnell, I. A., Bate, M. R., & Vine, S. G. 2003, MNRAS, 343, 413 [NASA ADS] [CrossRef]
- Chernoff, D. F., & Weinberg, M. D. 1990, ApJ, 351, 121 [NASA ADS] [CrossRef]
- Davis, D. S., Richer, H. B., King, I. R., et al. 2008, MNRAS, 383, L20 [NASA ADS]
- De Marchi, G., & Pulone, L. 2007, A&A, 467, 107 [NASA ADS] [CrossRef] [EDP Sciences]
- De Marchi, G., Paresce, F., & Pulone, L. 2000, ApJ, 530, 342 [NASA ADS] [CrossRef]
- De Marchi, G., Paresce, F., & Pulone, L. 2007, ApJ, 656, L65 [NASA ADS] [CrossRef]
- Drukier, G. A. 1996, MNRAS, 280, 498 [NASA ADS]
- Elmegreen, B. G. 2000, ApJ, 530, 277 [NASA ADS] [CrossRef]
- Fregeau, J. M., Richer, H. B., Rasio, F. A., & Hurley, J. R. 2009, ApJ, 695, L20 [NASA ADS] [CrossRef]
- Fryer, C. L., & Kalogera, V. 2001, ApJ, 554, 548 [NASA ADS] [CrossRef]
- Fukushige, T., & Heggie, D. C. 2000, MNRAS, 318, 753 [NASA ADS] [CrossRef]
- Gieles, M., & Baumgardt, H. 2008, MNRAS, 389, L28 [NASA ADS]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef]
- Harris, W. E., Whitmore, B. C., Karakla, D., et al. 2006, ApJ, 636, 90 [NASA ADS] [CrossRef]
- Heggie, D., & Hut, P. 2003, The Gravitational Million-Body Problem: A Multidisciplinary Approach to Star Cluster Dynamics (Cambridge University Press), 372
- Hénon, M. 1960, Annales d'Astrophysique, 23, 668 [NASA ADS]
- Hénon, M. 1969, A&A, 2, 151 [NASA ADS]
- Kalirai, J. S., Hansen, B. M. S., Kelson, D. D., et al. 2008, ApJ, 676, 594 [NASA ADS] [CrossRef]
- King, I. R. 1966, AJ, 71, 64 [NASA ADS] [CrossRef]
- Kouwenhoven, M. B. N., Brown, A. G. A., Goodwin, S. P., Portegies Zwart, S. F., & Kaper, L. 2009, A&A, 493, 979 [NASA ADS] [CrossRef] [EDP Sciences]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef]
- Kruijssen, J. M. D. 2008, A&A, 486, L21 [NASA ADS] [CrossRef] [EDP Sciences]
- Kruijssen, J. M. D., & Lamers, H. J. G. L. M. 2008, A&A, 490, 151 [NASA ADS] [CrossRef] [EDP Sciences]
- Kruijssen, J. M. D., & Mieske, S. 2009, A&A, 500, 785 [NASA ADS] [CrossRef] [EDP Sciences]
- Kruijssen, J. M. D., & Portegies Zwart, S. F. 2009, ApJ, 698, L158 [NASA ADS] [CrossRef]
- Küpper, A. H. W., Kroupa, P., & Baumgardt, H. 2008, MNRAS, 389, 889 [NASA ADS] [CrossRef]
- Lamers, H. J. G. L. M., Anders, P., & De Grijs, R. 2006, A&A, 452, 131 [NASA ADS] [CrossRef] [EDP Sciences]
- Lamers, H. J. G. L. M., Gieles, M., & Baumgardt, H. 2009, A&A, to be submitted
- Lamers, H. J. G. L. M., Gieles, M., Bastian, N., et al. 2005, A&A, 441, 117 [NASA ADS] [CrossRef] [EDP Sciences]
- Larsen, S. S. 2004, A&A, 416, 537 [NASA ADS] [CrossRef] [EDP Sciences]
- Larsen, S. S., Brodie, J. P., Huchra, J. P., Forbes, D. A., & Grillmair, C. J. 2001, AJ, 121, 2974 [NASA ADS] [CrossRef]
- Lyne, A. G., & Lorimer, D. R. 1994, Nature, 369, 127 [NASA ADS] [CrossRef]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences]
- McMillan, S. L. W., Vesperini, E., & Portegies Zwart, S. F. 2007, ApJ, 655, L45 [NASA ADS] [CrossRef]
- Moody, K., & Sigurdsson, S. 2009, ApJ, 690, 1370 [NASA ADS] [CrossRef]
- Nomoto, K., Shigeyama, T., & Hashimoto, M. 1988, in Supernovae, Remnants, Active Galaxies, Cosmology, ed. G. Boerner, 34
- Pfahl, E., Rappaport, S., Podsiadlowski, P., & Spruit, H. 2002, ApJ, 574, 364 [NASA ADS] [CrossRef]
- Plummer, H. C. 1911, MNRAS, 71, 460 [NASA ADS]
- Portegies Zwart, S. F., McMillan, S. L. W., Hut, P., & Makino, J. 2001, MNRAS, 321, 199 [NASA ADS] [CrossRef]
- Richer, H. B., Fahlman, G. G., Buonanno, R., et al. 1991, ApJ, 381, 147 [NASA ADS] [CrossRef]
- Richer, H. B., Fahlman, G. G., Brewer, J., et al. 2004, AJ, 127, 2771 [NASA ADS] [CrossRef]
- Salpeter, E. E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef]
- Spitzer, L. 1987, Dynamical evolution of globular clusters (Princeton, NJ: Princeton University Press),191
- Strader, J., Smith, G. H., Larsen, S., Brodie, J. P., & Huchra, J. P. 2009, AJ, 138, 547 [NASA ADS] [CrossRef]
- Takahashi, K., & Portegies Zwart, S. F. 2000, ApJ, 535, 759 [NASA ADS] [CrossRef]
- Vesperini, E., & Heggie, D. C. 1997, MNRAS, 289, 898 [NASA ADS]
- Vesperini, E., McMillan, S. L. W., & Portegies Zwart, S. 2009, ApJ, 698, 615 [NASA ADS] [CrossRef]
- Wielen, R. 1971, A&A, 13, 309 [NASA ADS]
Footnotes
- ... clusters
![[*]](/icons/foot_motif.png)
- Tables of models are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/507/1409
- ... function
![[*]](/icons/foot_motif.png)
- Hereafter, ``mass function'' is referred to as ``MF''.
- ... dissolution
![[*]](/icons/foot_motif.png)
- The model presented in this paper is independent of the
mass loss rate and of the form of the IMF
 ,
but for explanatory purposes a Kroupa
(2001) IMF is adopted later on.
,
but for explanatory purposes a Kroupa
(2001) IMF is adopted later on.
- ... found
![[*]](/icons/foot_motif.png)
- This prescription for c1
implies that the condition for the stars in the cluster to be
physically bound
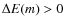 is satisfied for all
is satisfied for all 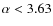 .
.
- ... earlier
![[*]](/icons/foot_motif.png)
- Nonetheless, the relation for c1 should be expected to exhibit some variation for different mass ranges.
- ... simplicity
![[*]](/icons/foot_motif.png)
- And because this is the only way to obtain an analytical solution as in Eq. (10).
- ... star
![[*]](/icons/foot_motif.png)
- The energy difference
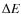 that is discussed here concerns the energy that needs to be added to
reach the escape energy. As such, it differs from the separation from
the escape energy in Fukushige
& Heggie (2000) and Baumgardt
(2001), who are considering the excess
energy of stars and its relation to the escape time, resulting in the
aformentioned relation
that is discussed here concerns the energy that needs to be added to
reach the escape energy. As such, it differs from the separation from
the escape energy in Fukushige
& Heggie (2000) and Baumgardt
(2001), who are considering the excess
energy of stars and its relation to the escape time, resulting in the
aformentioned relation
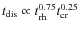 .
.
- ... stars
![[*]](/icons/foot_motif.png)
- And the energy gain experienced by low-mass stars.
- ... exponentially
![[*]](/icons/foot_motif.png)
- This form assumes that the increase of the fraction of the mass loss that is stellar mass-dependent scales with the total dynamical mass loss, which is a compromise between a step function and a linear increase.
- ... simulations
![[*]](/icons/foot_motif.png)
- These were performed using NBODY4 (Aarseth 1999).
- ... parameter
![[*]](/icons/foot_motif.png)
- For W0=5, or
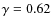 ,
the results vary only marginally.
,
the results vary only marginally.
- ... fractions
![[*]](/icons/foot_motif.png)
- High remnant retention fractions will be treated in the discussion of the influence of the retention fraction in Sect. 5.2.
- ... alternatives
![[*]](/icons/foot_motif.png)
- Such as a constant radius or density.
- ...
![[*]](/icons/foot_motif.png)
- For the clusters with relatively long disruption times that are considered in this section, the variable stellar mass range that was introduced in Sect. 5.1 to trace the relation between MF slope and M/L ratio gives an evolution of the slope that is comparable that for the fixed mass ranges. It is omitted from the figures in this section to improve their clarity.
- ... clusters
![[*]](/icons/foot_motif.png)
- Any variability of the retention fraction would induce substantial scatter, see Sect. 5.2 and Fig. 19.
- ... IMF
![[*]](/icons/foot_motif.png)
- Although not specifically shown in this paper (but not surprisingly), the differences also depend on the initial-final stellar mass relation.
- ... fraction
![[*]](/icons/foot_motif.png)
- The fraction of stars residing in binary or multiple systems.
- ... kept
![[*]](/icons/foot_motif.png)
- This process differs from a possible variability of the proportionality between the velocity dispersion and the cluster mass, which concerns a much shorter timescale (e.g. Boily et al. 2009).
- ... used
![[*]](/icons/foot_motif.png)
- As explained in Sect. 3, c1 represents the ratio of the mean speed squared to the central escape velocity squared that depends on the degree of mass segregation (and thus on the IMF). On the other hand, c2 is a proportionality constant in the expression for the onset of the stellar mass-dependent escape of stars, which depends on the concentration or King parameter.
All Figures

|
Figure 1: Retention fraction of stellar remnants as a function of cluster mass per unit Plummer radius M/r0, for black holes (solid), neutron stars (dashed) and white dwarfs (dotted). |
| Open with DEXTER | |
| In the text | |

|
Figure 2:
Hénon function |
| Open with DEXTER | |
| In the text | |

|
Figure 3:
MF slope change
|
| Open with DEXTER | |
| In the text | |

|
Figure 4:
Relative escape rate
|
| Open with DEXTER | |
| In the text | |

|
Figure 5:
Mass of the highest relative escape rate
|
| Open with DEXTER | |
| In the text | |

|
Figure 6:
Comparison of the evolution of the stellar MF from the models (dashed) to the N-body runs from Baumgardt & Makino (2003, solid)
for the exact same boundary conditions. The initial number of particles
and the galactocentric radius are indicated in the bottom-left corner
of each panel. From top to bottom, the subsequent MFs in each panel are shown for the times at which the remaining cluster mass fraction equals
|
| Open with DEXTER | |
| In the text | |

|
Figure 7:
Comparison of the evolution of the stellar MF from the models (dashed) to the N-body run from Baumgardt & Makino (2003, solid) with W0=7
for the exact same boundary conditions. From top to bottom, the
subsequent MFs are shown for the times at which the remaining
cluster mass fraction equals
|
| Open with DEXTER | |
| In the text | |

|
Figure 8:
Influence of the constants c1 and c2 on the evolution of the stellar MF. From top to bottom, the subsequent MFs in each panel are shown for the times at which the remaining cluster mass fraction equals
|
| Open with DEXTER | |
| In the text | |

|
Figure 9:
Influence of the disruption time on the evolution of the stellar MF for a cluster with a low remnant retention fraction (
|
| Open with DEXTER | |
| In the text | |

|
Figure 10:
Influence of the disruption time on the stellar MF slope |
| Open with DEXTER | |
| In the text | |

|
Figure 11:
Influence of the disruption time on the M/LV ratio evolution for a cluster with a low remnant retention fraction (
|
| Open with DEXTER | |
| In the text | |

|
Figure 12:
Influence of the disruption time on the combined evolution of the MF slope |
| Open with DEXTER | |
| In the text | |

|
Figure 13:
Influence of the disruption time on the V-I colour for a cluster with a low remnant retention fraction (
|
| Open with DEXTER | |
| In the text | |

|
Figure 14:
Influence of the black hole kick velocity dispersion and disruption
time on the evolution of the stellar MF for an initial cluster mass
|
| Open with DEXTER | |
| In the text | |

|
Figure 15:
Influence of the black hole retention fraction on the stellar MF slope |
| Open with DEXTER | |
| In the text | |

|
Figure 16:
Influence of the black hole retention fraction on the M/LV ratio evolution for an initial cluster mass
|
| Open with DEXTER | |
| In the text | |

|
Figure 17:
Influence of the black hole retention fraction on the combined evolution of the MF slope |
| Open with DEXTER | |
| In the text | |

|
Figure 18: Influence of the black
hole retention fraction on the total remnant mass fraction. Shown is
the ratio of the total mass in stellar remnants
|
| Open with DEXTER | |
| In the text | |

|
Figure 19: MF slope versus
remaining lifetime (assuming a globular cluster age of 12 Gyr).
Diamonds represent the observed values from De Marchi et al. (2007), with typical errors as shown by the error bar in the lower right corner. The remaining lifetimes are taken from Baumgardt et al. (2008). Dotted curves represent the model evolutionary tracks of clusters with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



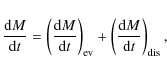
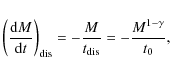
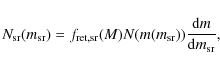
![\begin{displaymath}
f_{\rm ret,sr}(x)=A\left[{\rm erf}\left(\frac{x}{\sqrt{2}}\right)-\sqrt{\frac{2}{\pi}}x{\rm e}^{-x^2/2}\right] ,
\end{displaymath}](/articles/aa/full_html/2009/45/aa13325-09/img68.png)
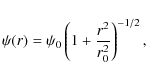
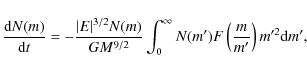
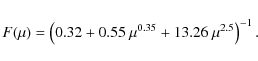
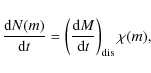
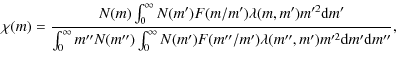
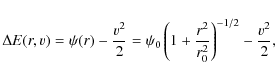
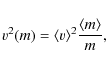
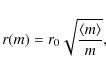
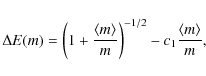
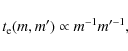
![$\displaystyle mm'\left[\left(1+\frac{\langle m\rangle}{m}\right)^{-1/2}-c_1\frac{\langle m\rangle}{m}\right]^{-1} \cdot$](/articles/aa/full_html/2009/45/aa13325-09/img127.png)