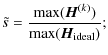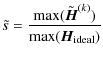Strehl-constrained iterative blind deconvolution for post-adaptive-optics data

G. Desiderà; M. Carbillet

doi:10.1051/0004-6361/200912913

Free Access

Issue		A&A Volume 507, Number 3, December I 2009


Page(s)		1759 - 1762
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361/200912913
Published online		08 October 2009

A&A 507, 1759-1762 (2009)

Strehl-constrained iterative blind deconvolution for post-adaptive-optics data

G. Desiderà^1,2 - M. Carbillet²

1 - DISI, Università di Genova, Via Dodecaneso 35, 16146 Genova, Italy
2 - UMR 6525 H. Fizeau, Université de Nice Sophia Antipolis/CNRS/Observatoire de la Côte d'Azur, Parc Valrose, 06108 Nice Cedex 2, France

Received 17 July 2009 / Accepted 4 September 2009

Abstract
Aims. We aim to improve blind deconvolution applied to post-adaptive-optics (AO) data by taking into account one of their basic characteristics, resulting from the necessarily partial AO correction: the Strehl ratio.
Methods. We apply a Strehl constraint in the framework of iterative blind deconvolution (IBD) of post-AO near-infrared images simulated in a detailed end-to-end manner and considering a case that is as realistic as possible.
Results. The results obtained clearly show the advantage of using such a constraint, from the point of view of both performance and stability, especially for poorly AO-corrected data. The proposed algorithm has been implemented in the freely-distributed and CAOS-based Software Package AIRY.

Key words: methods: data analysis - methods: numerical - techniques: image processing

1 Introduction

Blind deconvolution is well suited for post-adaptive-optics (AO) data when the associated point-spread function (PSF) is poorly known, hence not permitting a satisfactory deconvolution and a subsequent optimal astrophysical interpretation from the reconstructed object. To improve PSF reconstruction (and hence the whole blind deconvolution process in order to obtain better reconstructed objects), one possibility is to use a priori information about the physical features of the PSF (Bertero & Boccacci 1998). For this purpose we propose to simply consider one of the basic characteristic of modern optical telescope data, which is the Strehl ratio (SR, Strehl 1902), as a new constraint applied during PSF reconstruction. The SR is nowadays used in optical astronomy in order to characterize the image quality that is obtained after AO correction of the images (the higher the SR, the closer to the ideal PSF), and an estimation of it is commonly delivered together with the data obtained at suitably equipped telescopes.

In a previous paper (Desiderà et al. 2006), we developed iterative blind deconvolution (IBD) of multiple images with application to the Fizeau interferometer of the Large Binocular Telescope (LBT). The corresponding code has also been integrated within the Software Package AIRY (Astronomical Image Reconstruction in interferometrY, see Correia et al. 2002, and http://www.airyproject.eu), which can be used to reconstruct either Fizeau interferometric multiple images (Carbillet et al. 2002; Anconelli et al. 2005a,b, 2006a,b, 2007; La Camera et al. 2007) or standard mono-pupil data (Habart et al. 2004; Domiciano et al. 2008).

In this paper, we propose a Strehl constraint to extend the IBD algorithm and apply this method to the reconstruction of 8m-class telescope images, which represents a current and generic case. Nevertheless, and in order to consider data that is as realistic as possible, we consider, as an example, the precise case of LUCIFER (Lbt near-infrared spectroscopic Utility with Camera and Integral-Field unit for Extragalactic Research) images, with a detailed end-to-end numerical simulation of the associated AO system.

The paper is organized as follows. In Sect. 2 we briefly describe the structure of the IBD used in our simulations and its implementation. In Sect. 3 we describe the motivations behind the introduction of the SR constraint and its integration within the IBD algorithm. Then we give the results of our numerical experiments, involving a detailed modeling of the AO system, in Sect. 4. Finally Sect. 5 consists of a discussion of the method proposed and the results obtained.

2 IBD structure and limitations

2.1 IBD structure

As described in Desiderà et al. (2006), the IBD method used in this study restores the object and the PSF separately in an iterative form: within each global iteration, which we will call a ``cycle'', either the object or the PSF is kept fixed while the other is updated. Therefore the output of each cycle updates both the object (within the so-called object box) and the PSF (within the PSF box), as provided by the previous one. Both in the object box and in the PSF box we use the Richardson-Lucy (RL) algorithm to perform the reconstruction. To briefly formalize the problem we use bold letters to denote $N \times N$ arrays, whose pixels are indexed by a multi-index n = {n₁,n₂}, and we consider the following model of image formation (Snyder et al. 1993):

$\begin{displaymath} {\vec {g}}({\vec n}) = ({\vec H} * {\vec f})({\vec n}) + {\vec b}({\vec n}) + {\vec w}({\vec n}), \end{displaymath}$

(1)

where ${\vec g}$ is the detected image, ${\vec H}$ the corresponding PSF, ${\vec f}$ is the object array, ${\vec b}$ is the background, and $\vec w$ represents the noise term including read-out noise (RON). Moreover, we assume that the PSF is normalized to unit volume. The data of the problem are then g and b, and the goal is to obtain an estimate of both H and f.

We introduce an index k characterizing the IBD global cycles. If $\{{\vec H}^{(k-1)} ; {\vec f}^{(k-1)}\}$ is the output of the cycle k-1 (or the initial estimate in the case k=1), then for each cycle k the function of both the PSF box and the object box consists of the application of the reconstruction algorithm to provide the updates ${\vec f}^{(k)}$ and ${\vec H}^{(k)}$ of the object and the PSF, respectively.

Regarding the reconstruction algorithm, since the index k is used to characterize the IDB cycle, a different index, let us say l, will be used for the iterations of RL internal to the object box or the PSF box. Accordingly, the result of the lth iteration of RL inside the cycle k will be denoted by ${\vec f}^{(k,l)}$ and ${\vec H}^{(k,l)}$ . Note that the maximum number of iterations is a priori different for the object and the PSF reconstructions ( $l_{\rm obj} \neq l_{\rm psf}$ ).

Inside the object box the processing step consists of the following instructions:

-

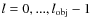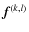For $l=0,...,l_{\rm obj}-1$ , given ${\vec f}^{(k,l)}$ , compute:

		$\displaystyle \tilde{\vec f}^{(k,l+1)}={\vec f}^{(k,l)} [{\vec H}^{(k-1)}]^T* \frac{{\vec g}}{{\vec H}^{(k-1)}*{\vec f}^{(k,l)}+{\vec b}},$	(2)
		$\displaystyle \tilde{c}^{(k,l+1)}=\sum_{\vec n} {{\tilde{\vec f}}^{(k,l+1)}({\vec n})}.$

-

Set:

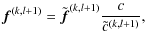
$\displaystyle {\vec f}^{(k,l+1)}=\tilde{\vec f}^{(k,l+1)}\frac{c}{\tilde{c}^{(k,l+1)}},$

(3)

where $c=\sum_{{\vec n}}\left \{{\vec g}({\vec n})-{\vec b}({\vec n}) \right \}$ represents the estimated flux of the object and $l_{\rm obj}$ is the number of RL iterations. The output of this box is the array ${\vec f}^{(k)}={\vec f}^{(k,l_{\rm obj})}$ , part of the output of the global cycle.

Analogously, for the PSF box we only need to exchange f and H within the previous equations, with $l_{\rm psf}$ the number of RL iterations, and where the normalization of the solution is calculated to obtain a PSF with a unit volume.

We use a pure IBD without any kind of additional constraint but that on the SR, in order to study here the gain due to the proposed method.

2.2 IBD limitations

IBD contains several parameters the choice of which can be critical for the final object reconstruction, such as the number of iterations within the object and PSF boxes ( $l_{\rm obj}$ and $l_{\rm psf}$ respectively), and also the total number of IBD cycles to be performed ( $k_{\rm max}$ ). In particular, a bad choice for $l_{\rm obj}$ or $l_{\rm psf}$ can compromise the result of the deconvolution for both the object and the PSF. For example, for what concerns $l_{\rm psf}$ , performing too many iterations can overfit the peak of the reconstructed PSF with respect to that of the unknown one. On the other hand, choosing a too small number of iterations could be insufficient to improve the reconstructed PSF.

3 The Strehl constraint

$\begin{figure} \par {\includegraphics[width=8.2cm,clip]{12913f1.eps} }\end{figure}$	Figure 1: General structure of the Strehl-constrained IBD.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{New-Figs/12913f2.eps}\hspace*{9mm} \includegraphics[width=8.2cm,clip]{New-Figs/12913f2b.eps}\par \end{figure}$	Figure 2: Left: final error on the reconstruction of the PSF. Right: final error on the reconstruction of the object. Both plots are made as a function of the SR of the image data and comparing the simple IBD (rhombuses) to the Strehl-constrained IBD (asterisks). A gain of up to a factor $\sim$ 10 is achieved for the poorer SR.
Open with DEXTER

In particular, in order to circumvent the risk of choosing too high a value for $l_{\rm psf}$ , we introduce a new constraint on the PSF reconstruction with the idea of taking into account the main physical feature of the PSF to be reconstructed, namely its SR. We will see that with this constraint the IBD is much less sensible to the value of $l_{\rm psf}$ . The constraint is applied to the output of the PSF box ${\vec H}^{(k)}$ and essentially consists of blurring it when its SR exceeds the estimated one s, in order to reach the desired SR. The blurring process is performed in an iterative manner with a Gaussian function ${\vec G}$ , with a small rms $\sigma$ in order to make the peak of the PSF lower by following a slower process. ${\vec G}$ being normalized to the unit volume, the result of the convolution with ${\vec H}^{(k)}$ preserves the unit volume itself, while the band remains essentially the same. The processing steps to perform after the PSF box are then:

-

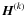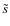initialize with ${\vec H}^{(k)}$ and compute its SR $\tilde{s}$ :

$\displaystyle \tilde{s}=\frac{\max({\vec H}^{(k)})}{\max({\vec H}_{\rm ideal})};$

(4)

-

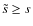while $\tilde{s} \ge s$ compute:

	$\displaystyle \tilde{\vec H}^{(k)}={\vec G}*\tilde{\vec H}^{(k)};$	(5)
	$\displaystyle \tilde{s}=\frac{\max(\tilde{\vec H}^{(k)})}{\max({\vec H}_{\rm ideal})}$	(6)

-

set:

$\displaystyle {\vec H}^{(k)}=\tilde{\vec H}^{(k)}~~$

(7)

where the output of the PSF box is ${\vec H}^{(k)}={\vec H}^{(k,l_{\rm psf})}$ , the update of the PSF provided by the cycle k. A pictorial representation of the general structure of the Strehl-constrained IBD is given in Fig. 1.

4 Numerical experiments

$\begin{figure} \par\mbox{\includegraphics[width=4.4cm,clip]{12913f3a.eps}\hspace... ...s}\hspace*{3mm} \includegraphics[width=4.4cm,clip]{12913f3d.eps} }\end{figure}$	Figure 3: Final error map (relative to the case of ${\rm SR}=0.27$ ) as a function of the iterations within the object box and the PSF box. Left: PSF reconstruction. Right: object reconstruction. Top: simple IBD. Bottom: Strehl-constrained IBD.
Open with DEXTER

In our numerical experiments we consider objects represented by $256 \times 256$ pixels arrays and we assume that they are observed in H band ( $\lambda=1.65~\mu$ m) with a pixel size of 15 mas. Since we are interested in studying the behaviour of the IBD introducing the SR constraint, we consider a set of different AO-corrected PSFs with increasing SR. The five PSFs used here (with SR from 0.17 to 0.68) have been obtained by means of the Software Package CAOS (Carbillet et al. 2005), according to a precise model of the first-light AO system of LBT and the near-infrared camera LUCIFER described in a previous paper (Carbillet et al. 2004b). The main parameters associated with these simulations are reported in Table 1.

Table 1: Main parameters describing the PSF simulation.

For the object, we have chosen a binary system, since it represents the elementary object to be reconstructed. We assume that the two components are of magnitude 12 and the angular separation is 285 mas (19 pixels), i.e. $\sim$ 7 times larger than the diffraction limit ( $\sim$ 40 mas). For each PSF, the images have been simulated according to Eq. (1), using a time exposure of 1200 s, with a total transmission of 0.3 and considering a CCD RON of 10 e^- rms.

In order to test the performance of the Strehl constraint, we have designed and run a large number of IBD simulations using a different number of iterations to be used within the object and PSF boxes. $l_{\rm obj}$ and $l_{\rm psf}$ range from 1 to 30 while the total number of cycles remain the same, fixed to 100 iterations. In this way, for each set of PSFs we computed $30 \times 30$ IBD projects with and without application of the Strehl constraint. For each project and for each PSF we then computed the error on the reconstructed PSF and on the collected flux (on $3\times3$ pixels which roughly correspond to $\lambda/D$ ) of the two stars at each global iteration. Doing so, we can give the behaviour of the minimum error achievable with respect to the asymmetry of the IBD.

Figure 2 shows the error on both the PSF reconstruction and the object reconstruction as a function of the SR characterizing the data processed, with and without the Strehl constraint. The improvement is clear if we compare the behaviour of the error in the two cases, behavior which becomes remarkably low, and moreover flat, with the application of the Strehl constraint. Figure 3 also shows the corresponding maps as a function of the iterations within the object box and the PSF box. We can observe here how it can be important to choose the right number of iterations in order to avoid a high divergence in the reconstruction process, in the case of a standard IBD. On the contrary, this limitation vanishes when considering the use of the Strehl-constrained IBD. In addition, the errors remain contained in a smaller range, which is reassuring with respect to the choice of the right iteration numbers for a given reconstruction.

$\begin{figure} \par {\includegraphics[width=9cm]{12913f4.eps} }\end{figure}$	Figure 4: From top to bottom and from left to right: observed image (SR = 0.27), reconstructed object with the simple IBD, reconstructed object with the Strehl-constrained IBD, PSF corresponding to the observed image, reconstructed PSF with the simple IBD, reconstructed PSF with the Strehl-constrained IBD. A logarithmic scale is used.
Open with DEXTER

5 Conclusions

In this paper, we introduced a new constraint on the reconstructed PSF in order to circumvent the well-know limitations of an IBD algorithm. The constraint forces the reconstructed PSF to fit the SR as much as possible, a feature which is strictly related to the observation conditions.

IBD algorithms (such as the one described in this paper) mainly suffer from the asymmetry between the iteration numbers adopted in the two reconstruction boxes (the so-called PSF box and object box). This limitation makes it difficult to calibrate all the parameters in order to obtain the best results. The application of the Strehl constraint seems to regularize the blind algorithm making it more robust, even in the case of a non-optimal choice of the parameters. In addition, the solutions themselves are characterized by a smaller error with respect to the standard IBD.

The gain of the proposed method essentially concerns the photometry of the object to be reconstructed, an example is givenin Fig. 4 in which both the reconstructed object and the reconstructed PSF, using the Strehl constraint or not, are shown. The improvement obtained in the reconstructed PSF reflects an optimized reconstruction of the object, in which it is possible to collect the flux closer to the real position of the two unknown spots.

The mathematical application of the constraint, which can be seen as a projection in the set of the admissible PSFs, is easy to use. The constraint is applied before the reconstruction algorithm used to update the PSF, so that it can be used together with others constraints (an example is the constraint on the Fourier support of the PSF given in Desiderà et al. 2006) and/or within different kind of blind deconvolution algorithms (Jefferies & Christou 1993; Ayers 1988; Holmes 1992; Tsumuraya et al. 1994; Fisch et al. 1995; Biggs & Andrews 1998).

The implementation of the proposed algorithm is included in the ad hoc module CBD (Constrained Blind Deconvolution) of the freely-distributed and CAOS-based Software Package AIRY.

Acknowledgements

The authors would like to thank Prof. Mario Bertero and Prof. Henri Lanteri for interesting discussions on the subject.

References

Anconelli, B., Bertero, M., Boccacci, P., et al. 2005a, A&A, 430, 731 [NASA ADS] [CrossRef] [EDP Sciences]
Anconelli, B., Bertero, M., Boccacci, P., & Carbillet, M. 2005b, A&A, 431, 747 [NASA ADS] [CrossRef] [EDP Sciences]
Anconelli, B., Bertero, M., Boccacci, P., et al. 2006a, A&A, 448, 1217 [NASA ADS] [CrossRef] [EDP Sciences]
Anconelli, B., Bertero, M., Boccacci, P., et al. 2006b, A&A, 460, 349 [NASA ADS] [CrossRef] [EDP Sciences]
Anconelli, B., Bertero, M., Boccacci, P., et al. 2007, J. Comp. Appl. Math., 198, 321 [NASA ADS] [CrossRef]
Ayers, G. R., & Dainty, J. C. 1988, Opt. Lett., 13, 547 [NASA ADS] [CrossRef]
Bertero, M., & Boccacci, P. 1998, in Introduction to Inverse Problems in Imaging (Bristol: IOP Publishing)
Biggs D. S. C., & Andrews, M. 1998, SPIE Proc., 3461, 33
Carbillet, M., Correia, S., Boccacci, P., et al. 2002, A&A, 387, 743 [CrossRef]
Carbillet, M. C., Vérinaud, C., Guarracino, M., et al. 2004a, SPIE Proc., 5490, 550
Carbillet, M., Riccardi, A., & Esposito, S. 2004b, SPIE Proc., 5490, 721 [NASA ADS]
Carbillet, M., Vérinaud, C., Femenía, B., et al. 2005, MNRAS, 356, 1263 [NASA ADS] [CrossRef]
Correia, S., Carbillet, M., Boccacci, P., et al. 2002, A&A, 387, 733 [NASA ADS] [CrossRef] [EDP Sciences]
Desiderà, G., Anconelli, B., Bertero, M., et al. 2006, A&A, 452, 727 [NASA ADS] [CrossRef] [EDP Sciences]
Domiciano de Souza, A., Kervella, P., Bendjoya, Ph., & Niccolini, G. 2008, A&A, 480, L29 [NASA ADS] [CrossRef] [EDP Sciences]
Fish D. A., Brinicombe, A. M., & Pike, E. R. 1995, JOSA A, 12, 58 [NASA ADS] [CrossRef]
Habart, É., Testi, L., Natta, A., & Carbillet, M. 2004, ApJ, 614, L129 [NASA ADS] [CrossRef]
Holmes, T. J. 1992, JOSA, A9, 1052 [NASA ADS]
Jefferies, S. M., & Christou, J. C. 1993, ApJ, 415, 862 [NASA ADS] [CrossRef]
La Camera, A., Desiderà, G., Arcidiacono, C., et al. 2007, A&A, 471, 1091 [NASA ADS] [CrossRef] [EDP Sciences]
Snyder, D. L., Hammoud, A. M., & White, R. L. 1993, J. Opt. Soc. Am. A, 10, 1014 [NASA ADS] [CrossRef]
Strehl, K. 1902, Zeit. Instrumenkde, 22, 213
Tsumuraya, F., Miura, N., & Baba, N. 1994, A&A, 282, 699 [NASA ADS]

Footnotes

...http://www.airyproject.eu): Implemented within the CAOS (Code for Adaptive Optics Systems) problem-solving environment (see Carbillet et al. 2004a, and http://fizeau.unice.fr/caos).
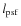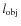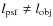... asymmetry: I.e. the fact that optimal values of $l_{\rm psf}$ and $l_{\rm obj}$ will be a priori such that $l_{\rm psf} \ne l_{\rm obj}$ .

All Tables

Table 1: Main parameters describing the PSF simulation.

All Figures

$\begin{figure} \par {\includegraphics[width=8.2cm,clip]{12913f1.eps} }\end{figure}$	Figure 1: General structure of the Strehl-constrained IBD.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{New-Figs/12913f2.eps}\hspace*{9mm} \includegraphics[width=8.2cm,clip]{New-Figs/12913f2b.eps}\par \end{figure}$	Figure 2: Left: final error on the reconstruction of the PSF. Right: final error on the reconstruction of the object. Both plots are made as a function of the SR of the image data and comparing the simple IBD (rhombuses) to the Strehl-constrained IBD (asterisks). A gain of up to a factor $\sim$ 10 is achieved for the poorer SR.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=4.4cm,clip]{12913f3a.eps}\hspace... ...s}\hspace*{3mm} \includegraphics[width=4.4cm,clip]{12913f3d.eps} }\end{figure}$	Figure 3: Final error map (relative to the case of ${\rm SR}=0.27$ ) as a function of the iterations within the object box and the PSF box. Left: PSF reconstruction. Right: object reconstruction. Top: simple IBD. Bottom: Strehl-constrained IBD.
Open with DEXTER
In the text

$\begin{figure} \par {\includegraphics[width=9cm]{12913f4.eps} }\end{figure}$	Figure 4: From top to bottom and from left to right: observed image (SR = 0.27), reconstructed object with the simple IBD, reconstructed object with the Strehl-constrained IBD, PSF corresponding to the observed image, reconstructed PSF with the simple IBD, reconstructed PSF with the Strehl-constrained IBD. A logarithmic scale is used.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.