Very low-mass white dwarfs with a C–O core

P. G. Prada Moroni; O. Straniero

doi:10.1051/0004-6361/200912847

Home

All issues

Volume 507 / No 3 (December I 2009)

A&A, 507 3 (2009) 1575-1583

Full HTML

Free Access

Issue		A&A Volume 507, Number 3, December I 2009


Page(s)		1575 - 1583
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/200912847
Published online		01 October 2009

A&A 507, 1575-1583 (2009)

Very low-mass white dwarfs with a C-O core

P. G. Prada Moroni^1,2 - O. Straniero³

1 - Physics Department ``E. Fermi'', University of Pisa, largo B. Pontecorvo 3, 56127 Pisa, Italy
2 - INFN, largo B. Pontecorvo 3, 56127 Pisa, Italy
3 - INAF - Osservatorio Astronomico di Collurania, via Maggini, 64100 Teramo, Italy

Received 8 July 2009 / Accepted 9 September 2009

Abstract
Context. The lower limit for the mass of white dwarfs (WDs) with a C-O core is commonly assumed to be roughly 0.5 $M_{\odot }$ . As a consequence, WDs of lower masses are usually identified as He-core remnants.
Aims. When the initial mass of the progenitor star is between 1.8 and 3 $M_{\odot }$ , which corresponds to the so-called red giant (RGB) phase transition, the mass of the H-exhausted core at the tip of the RGB is 0.3 < $M_{\rm H}/M_{\odot}$ < 0.5. Prompted by this well known result of stellar evolution theory, we investigate the possibility to form C-O WDs with mass M < 0.5 $M_{\odot }$ .
Methods. The pre-WD evolution of stars was computed with initial mass of about 2.3 $M_{\odot }$ , undergoing anomalous mass-loss episodes during the RGB phase and leading to the formation of WDs with He-rich or CO-rich cores. The cooling sequences of the resulting WDs are also described.
Results. We show that the minimum mass for a C-O WD is about 0.33 $M_{\odot }$ , so that both He and C-O core WDs can exist in the mass range 0.33-0.5 $M_{\odot }$ . The models computed for the present paper provide the theoretical tools for indentifying the observational counterpart of very low-mass remnants with a C-O core among those commonly ascribed to the He-core WD population in the progressively growing sample of observed WDs of low mass. Moreover, we show that the central He-burning phase of the stripped progeny of the 2.3 $M_{\odot }$ star lasts longer and longer as the total mass decreases. In particular, the $M= 0.33~M_{\odot}$ model takes about 800 Myr to exhaust its central helium, which is more than three times longer than the value for the standard 2.3 $M_{\odot }$ star: it is, by far, the longest core-He burning lifetime. Finally, we find the occurrence of gravonuclear instabilities during the He-burning shell phase.

Key words: stars: evolution - stars: white dwarfs - stars: horizontal-branch - stars: interiors - stars: oscillations

1 Introduction

The value for the minimum mass of white dwarfs (WDs) with a carbon-oxygen (C-O) core is commonly agreed to be around 0.5 $M_{\odot }$ (Weideman 2000; Meng et al. 2008). The main reason for such a belief is a firm result of the theory of stellar evolution and can be easily understood by looking at Fig. 1, which shows the mass of the hydrogen-exhausted core $M_{\rm H}$ at the first thermal pulse on the asymptotic giant (AGB) and at the tip of the red giant branch (RGB tip) as a function of their initial mass. As is well known, for initial masses lower than 3 $M_{\odot }$ , the value of $M_{\rm H}$ at the first thermal pulse is nearly constant around 0.55 $M_{\odot }$ , the exact value depending on the chemical composition. This value represents the minimum mass for C-O WDs produced by the evolution of single, low-, or intermediate-mass stars undergoing normal mass-loss during the pre-AGB evolution. Nonetheless, anomalous mass-loss episodes occurring on the RGB or during the core He-burning phase, as caused by either Roche-lobe overflow in close-binary evolution or tidal stripping in close encounters between stars in high-density environments, could interrupt or change the stellar evolution, leading to the production of a smaller remnant. Actually, slightly smaller C-O WDs result from the evolution of a low-mass star (M < 1.5-1.7 $M_{\odot }$ , and the exact value depends on the composition), which loses its envelope before the onsent of the AGB, the so-called AGB-manqué (Sweigart et al. 1974; Caloi 1989; Greggio & Renzini 1990; Castellani & Tornambé 1991; Dorman et al. 1993). Examples of these objects are the extreme horizontal branch stars (EHB) in globular clusters (GCs) and the field subdwarf B stars, which are core He-burning stars with extremely thin H-envelopes that eventually become C-O core WDs with low mass (Castellani & Castellani 1993; Castellani et al. 1994; D'Cruz et al. 1996; Brown et al. 2001; Han et al. 2002; Han et al. 2003; Castellani et al. 2006; Han 2008). But even in such a case, the theory of stellar evolution predicts a lower limit, since the mass of the H-exhausted core at the He ignition is slightly lower than 0.5 $M_{\odot }$ for these low-mass stars (Castellani et al. 1992; Dominguez et al. 1999; Girardi 1999; Castellani et al. 2000). In practice, if the mass of the electron-degenerate He-rich core were lower, the cooling processes, i.e. the electronic thermal conduction and the plasma neutrino emission, would prevail on the heating caused by the release of gravitational energy, the He burning would be skipped and an He-core WD would be produced.

The scenario described above explains why WDs whose mass is lower than 0.5 $M_{\odot }$ are commonly believed to have an He-rich core, but this is not the whole story. In fact, stars with initial mass in the range 1.8 to 3 $M_{\odot }$ , which undergo intense and rapid mass-loss episodes, could produce both CO- or He- rich WDs with mass lower than 0.5 $M_{\odot }$ . In these stars, the degree of electron degeneracy and, in turn the cooling processes, in the core developed during the RGB are weaker and the He ignition occurs when its mass is lower (see e.g. Fig. 1). As early as 1985 in a very instructive paper, Iben & Tutukov showed that a star with an initial mass of 3 $M_{\odot }$ evolving in a close-binary system can produce a remnant of 0.4 $M_{\odot }$ with a sizeable C-O core. More recently, Han et al. (2000), obtained a similar result by computing the evolution of close binary systems by selecting different initial parameters. They show, in particular, that a star with an initial mass M₁ = 2.51 $M_{\odot }$ , belonging to a binary with mass ratio q=M₁/M₂=2 and initial period P=2.559 d, eventually succeeds in igniting the He-burning, even if they did not follow the evolution up to the formation of the C-O WD, since their code met numerical problems when the primary star was as low as 0.33 $M_{\odot }$ with a C-O core of 0.11 $M_{\odot }$ .

In this framework and by means of detailed computations performed with a full Henyey code able to consistently follow the evolution of stars from the pre-main sequence to the final cooling phase of WDs, we have investigated possible evolutionary scenarios leading to the production of very low-mass C-O WDs (VLMWDs), that is, with mass lower than ${<}0.5~M_{\odot}$ . The peculiar features of the corresponding cooling evolution will be also discussed.

2 The red giant phase transition

The stellar models shown in the present work were computed with an updated version of FRANEC (Prada Moroni & Straniero 2002; Degl'Innocenti et al. 2008), a full Henyey evolutionary code. We adopted a metallicity Z=0.04 and an initial helium abundance of Y=0.32 suitable for the very metal-rich stars belonging to some open galactic cluster, such as NGC 6791. A simple way of understanding the findings by Iben & Tutukov (1985) and Han et al. (2000) is to analyze Fig. 1, which shows the dependence of $M_{\rm H}$ at the first thermal pulse and at the RGB tip on the initial mass for isolated-single stars. At the beginning of the thermally pulsing AGB phase, $M_{\rm H}$ is almost constant, around 0.55 $M_{\odot }$ , for initial masses lower than 3 $M_{\odot }$ , but at the tip of RGB it presents a deep minimum around 2.3 $M_{\odot }$ for this particular chemical composition (Sweigart et al. 1990; Castellani et al. 1992; Bono et al. 1997b). Such behavior is the consequence of the physical conditions occurring in the He-core at the ignition of the 3 $\alpha$ nuclear reaction.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f1.eps} \end{figure}$	Figure 1: Mass of the H-exhausted core $M_{\rm H}$ at the first thermal pulse on the AGB (circles and solid line) and at the tip of the RGB (diamond and dashed line) as a function of the initial mass for stars with Z=0.04, Y=0.32.
Open with DEXTER

For initial mass lower than 1.5-1.7 $M_{\odot }$ , a regime of strong electron-degeneracy develops in the He-core at the beginning of the red giant phase, and the ignition of the 3 $\alpha$ occurs in a violent nuclear runaway, the so-called He-flash (Hoyle & Schwarzschild 1955) when $M_{\rm H}$ approaches about 0.46 $M_{\odot }$ , for metal-rich stars, and 0.50 $M_{\odot }$ , for metal-poor stars. The first ignition point is off center, and it is followed by a series of weaker and more central flashes, until a quiescent He burning takes place in the center.

From this point on, the higher the initial mass, the weaker the electron-degeneracy of the core in the red giant phase. Consequently, the mass of the H-exhausted core required for the 3 $\alpha$ ignition is lower and lower. When the initial mass is as high as about 2.3 $M_{\odot }$ , the He-burning ignites almost quiescently, through a single and central weak flash. For higher masses, the core in the red giant phase is not degenerate any more. Nevertheless, for stars with initial mass greater than about 2.3 $M_{\odot }$ , the larger the initial mass, the higher the $M_{\rm H}$ at the tip of the RGB. In these stars, indeed, the He in the core is mainly produced during the central H-burning phase, which occurs in a convective core whose mass extension is a growing function of the initial total mass. Such a variation in the physical conditions at the He ignition, gives rise to a minimum $M_{\rm H}$ at the RGB tip that marks the transition between low and intermediate mass stars (the so-called RGB phase transition, after Renzini & Buzzoni 1983).

For the present composition (Z=0.04 Y=0.32), such a minimum occurs for M = 2.3 $M_{\odot }$ and $M_{\rm H}$ = 0.315 $M_{\odot }$ . The RGB phase transition occurs at higher masses as the initial He abundance decreases or the initial metallicity increases. Moreover, the value of the minimum $M_{\rm H}$ at the RGB tip depends slightly on chemical composition (see e.g. Sweigart et al. 1989). Notice that, as previously stated, this minimum disappears at the first thermal pulse (see the upper curve in Fig. 1). The reason is that the H-burning shell continues to process H during the core He-burning and moves further outward. Moreover, it is a well-established result of the theory of stellar evolution that the lower the mass of the H-exhausted core at the onset of the 3 $\alpha$ , the fainter the star and the longer the central He-burning phase. Thus, the H-burning shell will work for a longer time for stars belonging to the RGB phase transition. This is the reason stars with initial mass lower than 3 $M_{\odot }$ enter the AGB phase with nearly the same $M_{\rm H}$ (Dominguez et al. 1999). Since Iben (1967), who provided the first detailed study of the evolutionary characteristics of stars belonging to the RGB phase transition, many studies have been focused on this particular range of stellar mass (see e.g. Sweigart et al. 1989, 1990; Castellani et al. 1992), but only a few have dicussed the possible compact remnants of these evolutionary sequences.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f2.eps} \end{figure}$	Figure 2: Mass of the H-exhausted core as a function of the age for a star of M = 2.3 $M_{\odot }$ , Z=0.04, Y=0.32.
Open with DEXTER

Figure 2 illustrates the temporal evolution of the mass of the H-exhausted core $M_{\rm H}$ for a star with initial mass 2.3 $M_{\odot }$ . The four circles mark the following evolutionary phases: the central H exhaustion, the base and the tip of the RGB, respectively, and the central He exhaustion. As one can easily see, when the star exhausts its central H, the mass of the core is already 0.225 $M_{\odot }$ , which is more than the 70% of the value at the RGB tip. In fact, a sizeable convective core was developed during the previous main sequence phase, which was supported by the H-burning through the CNO cycle. When the star reaches the base of the RGB, the mass of the core is 0.254 $M_{\odot }$ , which is about the 80% of the mass at the He ignition, namely 0.315 $M_{\odot }$ .

This means that, since a large fraction of the He-core required for the ignition of the He-burning is already developed at the beginning of the red giant, a star with mass of about 2.3 $M_{\odot }$ , which undergoes a strong mass-loss episode during or immediately after the red giant phase can easily experience the core He-burning phase and produce a C-O VLMWD, that is a C-O WD with a mass substantially lower than 0.5 $M_{\odot }$ , provided that the residual total mass after the anomalous mass loss episode is higher than about 0.32 $M_{\odot }$ .

3 Evolution of the stripped progeny of the 2.3 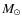$M_{\odot }$ star

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{12847f3a.eps}\hspace{1.5c... ...ps}\hspace{1.5cm} \includegraphics[width=7.8cm,clip]{12847f3h.eps} \end{figure}$	Figure 3: Evolutionary tracks after the rapid mass-loss episode occurred during the RGB of the models described in the text. The labeled masses are final massess or, more specfically, the residual mass after the mass-loss episode. In all the cases illustrated here, the progenitor is a star with M = 2.3 $M_{\odot }$ and Z=0.04.
Open with DEXTER

To check this working hypothesis and provide models of C-O WDs with mass lower than 0.5 $M_{\odot }$ , we computed the evolution at constant mass of a star with M = 2.3 $M_{\odot }$ until the red giant phase. Then at about $\log L/L_{\odot}$ = 1.34, when $M_{\rm H}$ = 0.257 $M_{\odot }$ , we switched on a mass-loss regime at constant rate, namely: 10 $^{-7}~M_{\odot}$ yr^-1. Then, we stopped this regime once the required stellar masses were obtained, and we followed the next evolution until the final cooling phase. This numerical recipe allowed us to compute a series of starting models of stars that underwent an intense mass-loss episode on a time scale much shorter than the evolutionary time scale, as happens during the Roche-lobe overflow in interacting binary stars or during the tidal stripping caused by close encounters between stars in crowded environment. The details of the rapid mass-loss phase are not relevant for the following evolution. We also checked that the overall evolution of the remnant is not sensitive to the luminosity at which the mass-loss episode occurs, with the only exception of the smallest model, namely that of M = 0.33 $M_{\odot }$ .

Figure 3 shows the evolutionary tracks in the HR-diagram for different values of the final mass, from 0.5 $M_{\odot }$ to 0.33 $M_{\odot }$ , from the red giant to the final WD phase. All the models shown in this figure, except for the one in the bottom-left panel (i.e. panel g), succeed to ignite He and become WDs with a C-O core. The evolutionary tracks of the first three models (those whose remnant masses are 0.5, 0.48, and 0.461 $M_{\odot }$ ) are quite similar. Once the mass loss has been switched off, the star continues to climb the red giant branch until the 3 $\alpha$ reaction starts in the center. The He ignition occurs through a mild flash, which is much weaker than those found in lower mass stars (those developing high-degeneracy conditions), but stronger than a normal 2.3 $M_{\odot }$ star (no anomalous mass-loss episodes). The flash is stronger for the smallest remnant. A few million years after the flash, a quiescent central He-burning phase takes place in a convective core, while, as usual, the H-burning continues in a surrounding shell. The star moves toward higher effective temperatures until the energy contribution of the 3 $\alpha$ nuclear reaction to the total luminosity has reached its relative maximum, then it turns back to the red. The central He exhaustion is followed by the onset of the He-burning in shell. At this point, the residual H-rich outer layer is thin, of the order of 0.06 and 0.03 $M_{\odot }$ , for the models of 0.5 and 0.461 $M_{\odot }$ , respectively. The former model attempts to climb the AGB until the thickness of the outer envelope is reduced to approximately 0.01 $M_{\odot }$ , when it starts to quickly move toward the blue. The latter model, which starts the He-shell burning phase with a much thinner H-rich envelope, leaves the red side of the HR diagram immediately after the end of the core He-burning. All 3 models finally approach their WD tracks, where they cool down as a C-O WDs.

A general feature emerges from the analysis of these models, which also holds for the models described in the rest of the paper: the lower the mass of the remnant, the lower the mass fraction of the C-O core with respect to the total final mass. Consequently, the thickness of the He-rich zone grows as the mass of the WD decreases. The core of the 0.5 $M_{\odot }$ WD is about 91% of the total mass, while those of the 0.48 and 0.461 $M_{\odot }$ are 89% and 85%, respectively.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{12847f4a.eps}\hspace*{1cm} \includegraphics[width=8.5cm,clip]{12847f4b.eps} \vspace*{5mm} \end{figure}$

Figure 4:

Model of 0.43 $M_{\odot }$ , whose progenitor of M = 2.3 $M_{\odot }$ underwent a strong mass-loss episode during the red giant phase. Left panel: evolutionary track in the HR diagram from the RGB phase to the end of the He-thermal pulses. Upper-right panel: evolution of the total luminosity during the thermal pulse phase. Bottom-right panel: contributions to the total luminosity of the shell-H burning (dashed line) and the shell-He burning (solid line).

Open with DEXTER

The evolution becomes much more complex and difficult to compute for lower masses, as shown by the looping tracks of the models with remnant masses of 0.43, 0.4, and 0.38 $M_{\odot }$ plotted in Fig. 3 (panels d-f). The evolution of the 0.43 $M_{\odot }$ star looks like those described above until the central-He exhaustion, when the model begins to move toward higher effective temperatures. At that point, after four pre-pulses marked by the small zigzag in the HR diagram, the model experiences a series of 20 He-shell thermal pulses, where the star describes a loop in the HR diagram during each flash. This series of thermally pulsing loops lasts about 10 Myr. Figure 4 shows the evolutionary track of the 0.43 $M_{\odot }$ in the HR diagram, zoomed around this phase, and the evolution as a function of time of the total luminosity and the relative contributions of the shell-H burning and of the shell He-burning. After the last of these thermal pulses, the model experiences a couple of post-pulses, again producing small zigzags in the evolutionary track, followed by a quiescent phase during which the shell He-burning provides most of the energy, after an initial short period during which the H shell dominated. In the meantime, the model moves toward higher effective temperatures approaching the cooling track, where it experiences three strong H-shell flashes. During these episodes, the residual H-rich envelope is progressively eroded, until the star can cool down as a WD with a C-O core, whose mass is 79% of the total mass.

The evolution of the model with 0.4 $M_{\odot }$ follows the same path of the 0.43 $M_{\odot }$ star qualitatively, with the difference that, after the thermally pulsing phase with its characteristic loops in the HR diagram, it experiences a late thermal pulse when the model is already approaching the cooling sequence, as shown in Fig. 3 (panel e). Finally, the star again approaches the cooling track and experiences a few strong H-shell flashes. The remnant is a WD with a C-O core whose mass is 70% of the total mass.

$\begin{figure} \par\includegraphics[width=8.45cm,clip]{12847f5a.eps}\hspace*{1cm} \includegraphics[width=8.5cm,clip]{12847f5b.eps} \end{figure}$	Figure 5: Same as in Fig. 4 but for the model of 0.38 $M_{\odot }$ . The He-flash (point a), the beginning (point b) and the end (point c) of the quiescent He-burning in the convective core, the first of the two main He-thermal pulses (point d) are marked.
Open with DEXTER

The evolution of the model with 0.38 $M_{\odot }$ , shown in Fig. 5, presents some peculiarities. The ignition of the 3 $\alpha$ reaction occurs through a flash, when the star was already leaving the red giant branch (point a in Fig. 5, left-panel). Although substantially milder than occurs in low-mass stars, this He-flash is stronger than those found for the models described so far. The peak of the 3 $\alpha$ luminosity is about 8.75 $\times$ $10^5~L_{\odot}$ , to be compared to what is found in the normal 2.3 $M_{\odot }$ evolution (3.46 $\times$ $10^5~L_{\odot}$ ) or in the case of the model producing a remnant mass of 0.48 $M_{\odot }$ (5.24 $\times$ $10^5~L_{\odot}$ ). The quiescent central He-burning evolution began after about 5 Myr and proceeds in a convective core for 380 Myr (points b and c in Fig. 5).

We are witnessing here an important feature of these peculiar objects, which we discuss later in more detail: the quiescent central He-burning lasts significantly longer than all other models. Point d in the figure marks the onset of the first of two main He-thermal pulses, followed by a series of 38 thermal pulses lasting 46 Myr. Once again, during each of these pulses, the model describes a loop in the HR diagram. The He-thermal pulses we show above are not the same as what occur in standard AGB stars. In fact, in that case the thermal instability is the consequence of the accumulation of a critical mass of He accreted by the quiescent H-burning shell, while in this case the compression stems from the contraction of the core, which follows the exhaustion of central He.

To the best of our knowledge, Iben et al. (1986) were the first to show and describe these oscillations following the evolution of a remnant of 0.378 $M_{\odot }$ with a progenitor of 3 $M_{\odot }$ . Subsequently, in a couple of papers devoted to computating evolutionary and pulsational models of metal-rich stars, Bono et al. (1997a,b) have shown that the evolution after the central He exhaustion of models with reduced envelope is characterized by loops in the HR diagram, which they call gravonuclear loops. Since these authors already fully and clearly describe these gravonuclear instabilities, we only focus on the their main features. As understood early in the pioneering study by Schwarzschild & Harm (1965), the ignition of a nuclear reaction (i.e. the 3 $\alpha$ ), whose efficiency is sensitive to temperature, in a shell characterized by a steep temperature profile leads to a thermal instability, because the rate at which nuclear energy is released is higher than that at which is dissipated by radiative transfer or converted in work to expand the outer layers. As a consequence the temperature in the burning shell increases, so that the rate of nuclear energy release is further enhanced and a runaway onsets. This is the physical reason behind both the standard and well-known, thermal pulses in AGB stars, and the peculiar, less-known, gravonuclear instabilities.

On the other hand, what triggers the instability, i.e. the cause of the compression of the He-shell and the consequent exceeding of the treshold temperature for the nuclear reaction ignition, is different: the accumulation of fresh He produced by the H-burning shell in normal thermally pulsing AGB stars and the contraction of the core after the central He exhaustion in the present gravonuclear oscillations. Moreover, at variance with standard thermal pulses, during the loop evolution the H- and He-shell never get near each other and, eventually, the He-burning shell is quenched by the expansion of the envelope. Figure 6 shows the time evolution of the central density (upper panel) and the central temperature (bottom panel) of the 0.38 $M_{\odot }$ model during the gravonuclear oscillations. As shown by Iben et al. (1986) and Bono et al. (1997a,b), at variance with standard thermally pulsing phase in normal AGB stars, these pulses affect the entire star, with large oscillations in the central quantities, of the order of 40% in density and 20% in temperature. After the last of these thermal pulses, the model approaches the WD sequence, where it experiences four strong H-flashes and, finally, cools down as WD, whose C-O core is only 50% of the total mass.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f6.eps} \end{figure}$	Figure 6: Model of 0.38 $M_{\odot }$ . Evolution of the central density (in g/cm³, upper panel) and of the central temperature (in K, lower-panel) during the thermal pulse phase.
Open with DEXTER

Figure 3 (panels g and h) shows two different evolutionary tracks, corresponding to the same final mass (M = 0.33 $M_{\odot }$ ), but leading to the formation of WDs with different composition. In the former case (panel g of Fig. 3), the rapid mass-loss episode starts at the same point of the RGB evolution as in all previous cases. This model fails to ignite He in the core and becomes a He WD. In the second model, the rapid mass-loss episode on the RGB has been turned on later, when the mass of the H-exhausted core is $\approx$ 1% more massive than in all previous cases. In such a case, the star enters the core-He burning phase (panel h of Fig. 3). When the star is already leaving the RGB, the He ignition occurs through a mild flash. During the flash, an extended convective core (about 80% of the total mass) suddenly appears. Notice the quick decrease in the surface luminosity, due to the temporary stop of the H-burning shell caused by the expansion and the consequent cooling powered by the energetic outcome of the He burning. Then, for a certain time, oscillation of the He-burning luminosity takes place, correlated to oscillation of the extension of the convective core and anti-correlated to oscillation of the gravitational energy release. Meanwhile, the evolutionary track describes small loops in the HR diagram. Later on, a long lasting quiescent He-burning sets in a convective core, whose maximum mass is about 0.1 $M_{\odot }$ . Once the central He is nearly exhausted, the H-burning shell resumes and becomes the dominant energy source. Approaching the WD sequence, the model experiences three strong H flashes, corresponding to the large loops in the HR diagram. Finally, the star cools down as a WD with a C-O core of about 53% of the total mass. This is the lowest C-O WD we have managed to produce for this chemical composition, since models with mass lower than 0.33 $M_{\odot }$ do not ignite the 3 $\alpha$ reactions and terminate their evolution as He-core WDs.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f7.eps} \end{figure}$	Figure 7: Helium burning lifetime (in Myr) as a function of the total mass (in $M_{\odot }$ ).
Open with DEXTER

Let us stress two peculiar properties of the C-O VLMWDs. Figure 7 shows the duration of the central He-burning $t_{\rm He}$ as a function of the total mass of the remnant obtained by stripping part of the envelope mass along the RGB of a progenitor star with initial mass 2.3 $M_{\odot }$ , whose evolution has been discussed above. As already noted, the lower the remnant mass the longer the time spent by the models in the central He-burning phase. Such an increase is quite smooth and shallow for remnant mass over 0.5 $M_{\odot }$ , but becomes very steep for lower masses. The smallest models that succeeds to ignite He-burning, that is, M = 0.33 $M_{\odot }$ , takes about 800 Myr to exhaust its central He, which is more than three time longer than for the standard 2.3 $M_{\odot }$ star. For this peculiar star, the core He-burning lasts longer than the central-H burning of the progenitor ( $t_{\rm H}$ $\approx$ 613 Myr). It is, by far, the longest core-He burning lifetime. As previously recalled, the He-burning lifetime depends on the stellar luminosity, which is lower for a star with smaller H-exhausted core at the He ignition. Thus, looking at the core masses plotted in Fig. 1, the longest He-burning lifetime for standard models is attained by the star with about 2.3 $M_{\odot }$ , the one corresponding to the minimum of the RGB fase transition (Castellani et al. 1992, 2000; Dominguez et al. 1999; Girardi 1999). Table 1 lists the mass of the H-exhausted core $M_{\rm H}$ , taken at the time when the central He abundance decreased 0.001 from the initial value, for models of different total mass M. As one can see, at the He ignition, all the models presented here have, more or less, the same core mass of the standard 2.3 $M_{\odot }$ model. Nonetheless, the substantial erosion of the H-rich envelope causes a depression of the shell-H burning that is more evident for models producing smaller remnants. As a consequence, the rate of growth of the $M_{\rm H}$ core during the central He-burning, hence the luminosity evolution and the length of this phase, is quite different in remnants with different envelope thicknesses. The lower the mass of the remnant, the less efficient the H-burning shell and the slower the increase in the $M_{\rm H}$ core. In the extreme case of the 0.33 $M_{\odot }$ model, the mass of the H-exhausted core remains almost constant during the entire central He-burning, as the H-shell is pratically turned off. This explains the steep growth of the central He-burning lifetime $t_{\rm He}$ as the mass of the remnants decreases below 0.5 $M_{\odot }$ . Due to the very long He-burning lifetime, the age of the 0.33 $M_{\odot }$ model at the beginning of the cooling sequence is 1.5 Gyr, to be compared with the 0.9 Gyr of the standard 2.3 $M_{\odot }$ model, which is expected to produce a C-O WD of about 0.6 $M_{\odot }$ .

Table 1: He-burning ignition.

Another interesting feature of the C-O VLMWDs concerns their internal composition. Figure 8 shows the chemical abundance profiles of ⁴He, ¹²C, and ¹⁶O of the C-O WD of 0.33 $M_{\odot }$ . As previously stated, the lower the mass of the remnant, the lower the fraction of the total mass confined in the C-O core or, equivalently, the greater the fraction of mass confined in the He-rich external layer. In the case of the 0.33 $M_{\odot }$ model, the He-rich layer is about the 50% of the total mass, which is very different from the value found for the more massive (normal) C-O WDs, namely 1-2%.

4 Cooling evolution

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f8.eps} \end{figure}$	Figure 8: Internal mass fraction of helium (solid line), carbon (dashed line), and oxygen (dot-dashed line) as a function of the mass coordinate for the C-O WD with M = 0.33 $M_{\odot }$ .
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f9.eps} \end{figure}$	Figure 9: Comparison between the cooling curves, $\log L/L_{\odot}$ vs. time, of the two WDs of 0.33 $M_{\odot }$ , that with the He-core (dashed line) and with C-O core (solid line).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f10.eps} \end{figure}$	Figure 10: Radius vs. effective temperature of the two WDs of 0.33 $M_{\odot }$ , that with the He-core (dashed line) and with C-O core (solid line).
Open with DEXTER

The present evolutionary computations confirm that it is possible to have C-O WDs with mass as low as 0.33 $M_{\odot }$ , significantly lower than 0.5 $M_{\odot }$ , the classical and commonly accepted lower limit. This means that both He and C-O core WDs can exist in the mass range 0.33-0.5 $M_{\odot }$ . We focus on comparing the structure and evolution of the two remnants of 0.33 $M_{\odot }$ with different core compositions.

The thickness of the H-rich outermost layer of the two models of 0.33 $M_{\odot }$ is practically the same, namely M = 0.0014 $M_{\rm WD}$ for the He WD and M = 0.0015 $M_{\rm WD}$ for the C-O WD. Figure 9 shows the comparison between the cooling curves of the He-core WD and the C-O core one. As expected (see the detailed discussion by Panei et al. 2007), the remnant with the He-rich core cools more slowly than with a C-O core, because of its higher specific heat, so that the thermal content of the He WD is larger than for the C-O one with the same total mass. Such a difference in the cooling times is partially counterbalanced at $\log L/L_{\odot}$ $\approx$ -4, when the C-O core begins to crystallize.

Figure 10 shows the comparison between the radii as a function of the effective temperature for the two WDs of 0.33 $M_{\odot }$ . For a given effective temperature, the He-core WD is more expanded than the other one, the difference being non negligible at the beginning of the cooling ( $\sim$ 8.5%). In principle, this difference in the radii at a given effective temperature offers the possibility of distinguishing the core composition of WDs in the mass range 0.33-0.5 $M_{\odot }$ . Since the C-O VLMWDs are the result of nonstandard evolutionary channels, it might be interesting to compare their main characteristics to those of the C-O WDs produced by the evolution of noninteracting-single stars (i.e. WD with mass M $\ge$ 0.5 $M_{\odot }$ ). Figures 11 and 12 show the comparison between the tracks in the HR diagram and the cooling curves, respectively, of the lowest C-O core WD we managed to build, that of 0.33 $M_{\odot }$ , with the more standard 0.5 and 0.6 $M_{\odot }$ remnants. As expected, the evolutionary tracks of the low-mass C-O WD is redder than those of the more massive objects and marks the reddest frontier of the C-O WD loci. The tracks of these peculiar objects overlap the region of the HR diagram occupied by the He WDs. For the comparison among the cooling curves, as shown in Fig. 12, the luminosity evolutions look quite similar, although not identical, down to $\log L/L_{\odot}$ $\approx$ -4.4. Then, at fainter magnitudes or for cooling ages over $\approx$ 9 Gyr, the evolution of the standard WDs speeds up and their luminosity drop more quickly than does the 0.33 $M_{\odot }$ model. When the cooling age is 14 Gyr, the 0.6 $M_{\odot }$ WD reaches $\log L/L_{\odot}$ $\approx$ -5.4, while the 0.33 $M_{\odot }$ one is still at -4.9. The reason for this behavior is that the solid core of the VLMWD is less dense than those of the other two objects, an occurrence causing a delay in the onset of the Debye-cooling regime. This difference in the luminosity becomes even greater when the longer lifetime of the progenitors of the VLMWDs is taken into account.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f11.eps} \end{figure}$	Figure 11: Comparison between the cooling tracks of C-O core WDs of masses: 0.33 $M_{\odot }$ (solid line), 0.5 $M_{\odot }$ (dotted line), 0.6 $M_{\odot }$ (dot-dashed line).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f12.eps} \end{figure}$	Figure 12: Comparison between the cooling curves, $\log L/L_{\odot}$ vs. time, of C-O core WDs of masses: 0.33 $M_{\odot }$ (solid line), 0.5 $M_{\odot }$ (dotted line), 0.6 $M_{\odot }$ (dot-dashed line).
Open with DEXTER

5 Summary and conclusions

By means of fully consistent evolutionary computations, we have proved that the minimum mass for a C-O WD is much lower than the commonly agreed 0.5 $M_{\odot }$ . In fact, we described the evolutionary paths leading to the production of C-O WDs with mass as low as 0.33 $M_{\odot }$ , nearly the value of the minimum $M_{\rm H}$ required for the He ignition in nondegenerate conditions, which depends only slightly on the chemical composition. These VLMWDs with a C-O core might result from the evolution of a star with initial mass around 2.3 $M_{\odot }$ , which undergoes a considerable mass loss along the red giant phase.

As a consequence, both He and C-O core WDs can exist in the mass range 0.33-0.5 $M_{\odot }$ . As expected and already shown by the detailed analysis of Panei et al. (2007), the cooling times of these two classes of WDs are quite different, because the He-core remnants are significantly slower than the C-O ones. Furthermore, we showed also that the He WDs are more expanded than their C-O counterparts at any given effective temperature. In principle, such an occurrence would allow one to distinguish between WDs with an He-core and those with a C-O-core in the mass range where both remnants exist, namely 0.33-0.5 $M_{\odot }$ .

Large samples of observed VLMWDs (M < 0.5 $M_{\odot }$ ), belonging to the field (Liebert et al. 2005; Maxted et al. 2005; Eisenstein et al. 2006) or to stellar clusters (Bedin et al. 2005; Monelli et al. 2005; Kalirai et al. 2007; Bedin et al. 2008; Calamida et al. 2008) are now available. In the near future, based on the models discussed here, it should be possible to identify the observational counterpart of very low-mass remnants with a C-O core among those commonly ascribed to the He-core WD population.

Computation of the evolution of the stripped progeny of the 2.3 $M_{\odot }$ also provided the evidence for the longest lasting central He-burning stellar objects. In fact, we showed that the lower the remnant mass, the longer the central He-burning phase. Such an increase becomes very steep for masses lower than 0.5 $M_{\odot }$ and reaches the maximum for the M = 0.33 $M_{\odot }$ model, which takes about 800 Myr to exhaust its central He, which is more than three times longer than the time required by the longest lasting He-burning standard star, i.e. the 2.3 $M_{\odot }$ . Thus, the M = 0.33 $M_{\odot }$ model attains the longest core He-burning lifetime.

Acknowledgements

It's a pleasure to thank Giuseppe Bono and Scilla Degl'Innocenti, who kindly read the paper, for the many useful and pleasant discussions, and to thank the referee (Han Zhanwen) for the positive and useful report. P.G.P.M. has been supported by PRIN-MIUR 2007 (Multiple stellar populations in globular clusters: census, characterizations and origin, PI G. Piotto), and O.S. by the PRIN-INAF program 2008.

References

Bedin, L. R., Salaris, M., Piotto, G., et al. 2005, ApJ, 624, L45 [NASA ADS] [CrossRef]
Bedin, L. R., King, I. R., Anderson, J., et al. 2008, ApJ, 678, 1279 [NASA ADS] [CrossRef]
Bono, G., Caputo, F., Cassisi, S., Castellani, V., & Marconi, M. 1997a, ApJ, 479, 279 [NASA ADS] [CrossRef]
Bono, G., Caputo, F., Cassisi, S., Castellani, V., & Marconi, M. 1997b, ApJ, 489, 822 [NASA ADS] [CrossRef]
Brown, T. M., Sweigart, A. V., Lanz, T., Landsman, W. B., & Hubeny, I. 2001, ApJ, 562, 368 [NASA ADS] [CrossRef]
Calamida, A., Corsi, C. E., Bono, G., et al. 2008, ApJ, 673, L29 [NASA ADS] [CrossRef]
Caloi, V. 1989, A&A, 221, 27 [NASA ADS]
Castellani, M., & Castellani, V. 1993, ApJ, 407, 649 [NASA ADS] [CrossRef]
Castellani, M., & Tornambé, A. 1991, ApJ, 381, 393 [NASA ADS] [CrossRef]
Castellani, V., Chieffi, S., & Straniero, O. 1992, ApJS, 78, 517 [NASA ADS] [CrossRef]
Castellani, V., Luridiana, V., & Romaniello, M. 1994, ApJ, 428, 633 [NASA ADS] [CrossRef]
Castellani, V., Degl'Innocenti, S., Girardi, L., et al. 2000, A&A, 354, 150 [NASA ADS]
Castellani, M., Castellani, V., & Prada Moroni, P. G. 2006, A&A, 457, 569 [NASA ADS] [CrossRef] [EDP Sciences]
Catalan, S., Isern, J., Garcia-Berro, E., & Ribas, I. 2008, MNRAS, 387, 1693 [NASA ADS] [CrossRef]
D'Cruz, N. L., Dorman, B., Rood, R. T., & O'Connell, R. W. 1996, ApJ, 466, 359 [NASA ADS] [CrossRef]
Degl'Innocenti, S., Prada Moroni, P. G., Marconi, M., & Ruoppo, A. 2008, Ap&SS, 316, 25 [NASA ADS] [CrossRef]
Dominguez, I., Chieffi, A., Limongi, M., & Straniero, O. 1999, ApJ, 524, 226 [NASA ADS] [CrossRef]
Dorman, B., Rood, R. T., & O'Connell, R. W. 1993, ApJ, 419, 596 [NASA ADS] [CrossRef]
Eisenstein, D. J., Liebert, J., Harris, H. C., et al. 2006, ApJS, 167, 40 [NASA ADS] [CrossRef]
Girardi, L. 1999, MNRAS, 308, 818 [NASA ADS] [CrossRef]
Greggio, L., & Renzini, A. 1990, ApJ, 364, 35 [NASA ADS] [CrossRef]
Han, Z. 2008, A&A, 484, L31 [NASA ADS] [CrossRef] [EDP Sciences]
Han, Z., Tout, C. A., & Eggleton, P. P. 2000, MNRAS, 319, 215 [NASA ADS] [CrossRef]
Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef]
Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef]
Hoyle, F., & Schwarzschild, M. 1955, ApJS, 2, 1 [NASA ADS] [CrossRef]
Iben, I. Jr 1967, ApJ, 147, 650 [NASA ADS] [CrossRef]
Iben, I. Jr, & Tutukov, A. V. 1985, ApJS, 58, 661 [NASA ADS] [CrossRef]
Iben, I. Jr, Fujimoto, M. Y., Sugimoto, D., & Miyaji, S. 1986, ApJ, 304, 217 [NASA ADS] [CrossRef]
Kalirai, J. S., Bergeron, P., Hansen, B. M. S., et al. 2007, ApJ, 671, 748 [NASA ADS] [CrossRef]
Liebert, J., Bergeron, P., & Holberg, J. B. 2005, ApJS, 156, 47 [NASA ADS] [CrossRef]
Maxted, P. F. L., Marsh, T. R., & Moran, C. K. J. 2005, MNRAS, 319, 305 [NASA ADS] [CrossRef]
Meng, X., Cheng, X., & Han, Z. 2008, A&A, 487, 625 [NASA ADS] [CrossRef] [EDP Sciences]
Monelli, M., Corsi, C. E., Castellani, V., et al. 2005, ApJ, 621, L117 [NASA ADS] [CrossRef]
Panei, J. A., Althaus, L. G., Chen, X., & Han, Z. 2007, MNRAS, 382, 779 [NASA ADS] [CrossRef]
Prada Moroni, P. G., & Straniero, O. 2002, ApJ, 581, 585 [NASA ADS] [CrossRef]
Prada Moroni, P. G., & Straniero, O. 2007, A&A, 466, 1043 [NASA ADS] [CrossRef] [EDP Sciences]
Renzini, A., & Buzzoni, A. 1983, memSAIT, 54, 739
Schwarzschild, M., & Harm, R. 1965, ApJ, 142, 855 [NASA ADS] [CrossRef]
Sweigart, A. W., Mengel, J. G., & Demarque, P. 1974, A&A, 30, 13 [NASA ADS]
Sweigart, A. W., Greggio, L., & Renzini, A. 1989, ApJS, 69, 911 [NASA ADS] [CrossRef]
Sweigart, A. W., Greggio, L., & Renzini, A. 1990, ApJ, 364, 527 [NASA ADS] [CrossRef]
Weidemann, V. 2000, A&A, 363, 647 [NASA ADS]

Footnotes

... normal: E.g. a Reimers like mass-loss rate during the RGB phase.
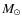
... $M_{\odot }$: The exact value depending on the chemical composition: from 0.46 to 0.50 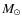$M_{\odot }$ for Z=0.04 to Z=0.0001.
... mass: We define the C-O core as the region where the helium mass fraction is lower than than 0.5.
... objects: The central density of the 0.6 WD is 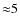${\approx}5$ times higher than that of the 0.33 WD.

All Tables

Table 1: He-burning ignition.

All Figures

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f1.eps} \end{figure}$	Figure 1: Mass of the H-exhausted core $M_{\rm H}$ at the first thermal pulse on the AGB (circles and solid line) and at the tip of the RGB (diamond and dashed line) as a function of the initial mass for stars with Z=0.04, Y=0.32.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f2.eps} \end{figure}$	Figure 2: Mass of the H-exhausted core as a function of the age for a star of M = 2.3 $M_{\odot }$ , Z=0.04, Y=0.32.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{12847f3a.eps}\hspace{1.5c... ...ps}\hspace{1.5cm} \includegraphics[width=7.8cm,clip]{12847f3h.eps} \end{figure}$	Figure 3: Evolutionary tracks after the rapid mass-loss episode occurred during the RGB of the models described in the text. The labeled masses are final massess or, more specfically, the residual mass after the mass-loss episode. In all the cases illustrated here, the progenitor is a star with M = 2.3 $M_{\odot }$ and Z=0.04.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{12847f4a.eps}\hspace{1cm} \includegraphics[width=8.5cm,clip]{12847f4b.eps} \vspace{5mm} \end{figure}$	Figure 4: Model of 0.43 $M_{\odot }$ , whose progenitor of M = 2.3 $M_{\odot }$ underwent a strong mass-loss episode during the red giant phase. Left panel: evolutionary track in the HR diagram from the RGB phase to the end of the He-thermal pulses. Upper-right panel: evolution of the total luminosity during the thermal pulse phase. Bottom-right panel: contributions to the total luminosity of the shell-H burning (dashed line) and the shell-He burning (solid line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.45cm,clip]{12847f5a.eps}\hspace*{1cm} \includegraphics[width=8.5cm,clip]{12847f5b.eps} \end{figure}$	Figure 5: Same as in Fig. 4 but for the model of 0.38 $M_{\odot }$ . The He-flash (point a), the beginning (point b) and the end (point c) of the quiescent He-burning in the convective core, the first of the two main He-thermal pulses (point d) are marked.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f6.eps} \end{figure}$	Figure 6: Model of 0.38 $M_{\odot }$ . Evolution of the central density (in g/cm³, upper panel) and of the central temperature (in K, lower-panel) during the thermal pulse phase.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f7.eps} \end{figure}$	Figure 7: Helium burning lifetime (in Myr) as a function of the total mass (in $M_{\odot }$ ).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f8.eps} \end{figure}$	Figure 8: Internal mass fraction of helium (solid line), carbon (dashed line), and oxygen (dot-dashed line) as a function of the mass coordinate for the C-O WD with M = 0.33 $M_{\odot }$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f9.eps} \end{figure}$	Figure 9: Comparison between the cooling curves, $\log L/L_{\odot}$ vs. time, of the two WDs of 0.33 $M_{\odot }$ , that with the He-core (dashed line) and with C-O core (solid line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f10.eps} \end{figure}$	Figure 10: Radius vs. effective temperature of the two WDs of 0.33 $M_{\odot }$ , that with the He-core (dashed line) and with C-O core (solid line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f11.eps} \end{figure}$	Figure 11: Comparison between the cooling tracks of C-O core WDs of masses: 0.33 $M_{\odot }$ (solid line), 0.5 $M_{\odot }$ (dotted line), 0.6 $M_{\odot }$ (dot-dashed line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12847f12.eps} \end{figure}$	Figure 12: Comparison between the cooling curves, $\log L/L_{\odot}$ vs. time, of C-O core WDs of masses: 0.33 $M_{\odot }$ (solid line), 0.5 $M_{\odot }$ (dotted line), 0.6 $M_{\odot }$ (dot-dashed line).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.