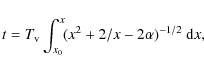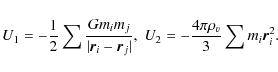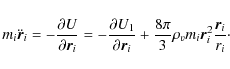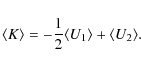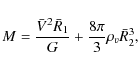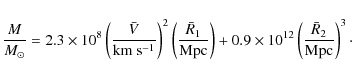Local dark matter and dark energy as estimated on a scale of ~1 Mpc in a self-consistent way

A. D. Chernin; P. Teerikorpi; M. J. Valtonen; V. P. Dolgachev; L. M. Domozhilova; G. G. Byrd

doi:10.1051/0004-6361/200912762

Free Access

Issue		A&A Volume 507, Number 3, December I 2009


Page(s)		1271 - 1276
Section		Cosmology (including clusters of galaxies)
DOI		https://doi.org/10.1051/0004-6361/200912762
Published online		01 October 2009

A&A 507, 1271-1276 (2009)

Local dark matter and dark energy as estimated on a scale of $\sim$ 1 Mpc in a self-consistent way

A. D. Chernin^1,2 - P. Teerikorpi¹ - M. J. Valtonen¹ - V. P. Dolgachev² - L. M. Domozhilova² - G. G. Byrd³

1 - Tuorla Observatory, Department of Physics and Astronomy, University of Turku, 21500 Piikkiö, Finland
2 - Sternberg Astronomical Institute, Moscow University, Moscow 119899, Russia
3 - University of Alabama, Tuscaloosa, AL 35487-0324, USA

Received 24 June 2009 / Accepted 14 September 2009

Abstract
Context. Dark energy was first detected from large distances on gigaparsec scales. If it is vacuum energy (or Einstein's $\Lambda$ ), it should also exist in very local space. Here we discuss its measurement on megaparsec scales of the Local Group.
Aims. We combine the modified Kahn-Woltjer method for the Milky Way-M 31 binary and the HST observations of the expansion flow around the Local Group in order to study in a self-consistent way and simultaneously the local density of dark energy and the dark matter mass contained within the Local Group.
Methods. A theoretical model is used that accounts for the dynamical effects of dark energy on a scale of $\sim$ 1 Mpc.
Results. The local dark energy density is put into the range $0.8{-}3.7\rho_{\rm v}$ ( $\rho _{\rm v}$ is the globally measured density), and the Local Group mass lies within $3.1{-}5.8 \times 10^{12}~M_{\odot}$ . The lower limit of the local dark energy density, about $4/5 \times$ the global value, is determined by the natural binding condition for the group binary and the maximal zero-gravity radius. The near coincidence of two values measured with independent methods on scales differing by $\sim$ 1000 times is remarkable. The mass $\sim$ $4~ \times~ 10^{12}~M_{\odot}$ and the local dark energy density $\sim$ $\rho _{\rm v}$ are also consistent with the expansion flow close to the Local Group, within the standard cosmological model.
Conclusions. One should take into account the dark energy in dynamical mass estimation methods for galaxy groups, including the virial theorem. Our analysis gives new strong evidence in favor of Einstein's idea of the universal antigravity described by the cosmological constant.

Key words: galaxies: Local Group - cosmology: dark matter - cosmology: cosmological parameters

1 Introduction

Regardless of its microscopic structure and physical nature, dark energy is not currently assumed to cluster. If dark energy is described macroscopically by Einstein's cosmological constant $\Lambda$ , the dark energy density is the same in all space. It does not change with time, and it has the same value in any reference frame. This interpretation is adopted in the currently standard $\Lambda$ cold dark matter ( $\Lambda$ CDM) cosmology, where dark energy is treated as a medium with positive constant density and negative pressure ( $\rho_{\rm v} > 0$ , $p_{\rm v} < 0$ ). It is characterized by the equation of state $\rho_{\rm v} = - p_{\rm v}$ (c =1), like that of a vacuum. According to the equations of general relativity, gravity depends on pressure, as well as density: the effective gravitating density $\rho_{\rm eff} = \rho + 3 p$ is negative for a vacuum (= $-2 \rho_{\rm v}$ ), and this leads to repulsion (antigravity). Since all galaxies and galaxy systems are embedded in a perfectly uniform and static dark energy background, their motions in space are affected by its antigravity. The antigravity is so strong that it accelerates the cosmological recession. This acceleration was observationally discovered at $\sim$ 1000 Mpc horizon-scale distances (Riess et al. 1998; Perlmutter et al. 1999).

1.1 The very local environment

Dark matter antigravity can also affect galaxy motions in our near environment in a volume several Mpc across, as first mentioned by Chernin et al. (2000). The region is dominated by our Milky Way and its sister galaxy M 31 at 0.7 Mpc from us, approaching each other with a relative velocity $\simeq$ 120 km s^-1. Together with the Magellanic Clouds, the Triangulum galaxy, and four dozen other dwarf galaxies, these two major galaxies form the Local Group occupying a spherical volume of $\le$ 1.2 Mpc in radius. Around the group, two dozen neighboring dwarf galaxies are seen at distances 1.6-3 Mpc from the group barycenter, moving away from the group. Their motion is the local part of the expansion flow discovered in 1929 by Hubble. The Local Group and the flow may be viewed as an isolated system with a common origin and evolutionary history (the local ``Hubble cell''). Systems of this kind are typical in the local universe.

Galaxies in the Local Group and in the neighboring flow have been systematically observed with the HST during more than 200 orbital periods (Karachentsev 2005; Karachentsev et al. 2003-2009). From these and other observations, high-precision radial velocities and distances are known for about 200 galaxies of the Local Group and neighbors within 7 Mpc from the group center.

The two major physical parameters of the local Hubble cell are the total gravitating (dark and baryonic) mass of the Local Group and the local density of the dark energy. The total mass of the group has been determined with a number of empirical methods including the classic model of Kahn & Woltjer (1959; see also Einasto & Lynden-Bell 1982), the virial theorem (see a review by van den Bergh 1999), and the zero-velocity estimate (cf. a recent paper by Karachentsev et al. 2009 and references therein). The results are in the interval $(2{-}5.6) \times 10^{12}~M_{\odot}$ .

1.2 Dark energy, the mass, and the ``lost gravity'' effect

If dark energy is identified with Einstein' constant $\Lambda$ , the local dark energy density must be identical to that measured in the global observations (Riess et al. 1998; Perlmutter et al. 1999). From recent CMB studies (Spergel et al. 2007), $\rho_{\rm v} \approx 7 \times 10^{-30}$ g cm^-1. In earlier studies, using the HST observations of the local Hubble cell (Karachentsev 2005; Karachentsev et al. 2003-2009), we found that the density of dark energy can be studied independently of the global measurements (Chernin 2001; Chernin et al. 2006; Teerikorpi et al. 2008). We concluded that a local dark energy density of the global value $\rho _{\rm v}$ and a group mass from the literature are consistent with the local Hubble cell $\sim$ 1 Mpc dynamics.

In the present paper, we make the next step using the Hubble cell data. In contrast to our earlier study, we derive the Local Group mass and the local dark energy density from the Hubble cell data in a self-consistent manner within a common framework.

We show first (Sects. 2, 3) that the true mass of the group can only be found if the dark energy is included in the procedure. Indeed, galaxies and their systems ``lose'' a part of their gravity due to the antigravity of the dark energy within their volumes. So, dynamical mass estimation should take into account this ``lost-gravity'' effect - otherwise the mass would be systematically underestimated. As a result, the value of the mass determined with the dynamical methods depends on the assumed value of the local density of the dark energy.

Secondly, we introduce in Sect. 4 a mass-density diagram for the local Hubble cell which displays this dependence explicitly. The HST data enable us to localize the area in the diagram which contains the allowed values of the local density of the dark energy density and the gravitating mass of the group. Significantly, the new approach is entirely independent of virial considerations or zero-velocity estimates. The Kahn-Woltjer model modified to include the dark energy and a simple model of the cell show the basis of the framework. In Sect. 5, we show that our discussion of the inner parts of the local Hubble cell is consistent with the observed outflow of the dwarf galaxies beyond the zero-gravity radius. Finally, in Sect. 6, we summarize the results and their significance for local and global cosmology. In the Appendix we consider the lost-gravity effect in the virial theorem and its significance for virial mass determination in groups and clusters of galaxies.

2 Modified Kahn-Woltjer (MKW) model

Fifty years ago, Kahn & Woltjer (1959) used a simple linear two body dynamics to describe the relative motion of the Milky Way (MW) and M 31 galaxies. The motion of the galaxies was described (in the reference frame of the binary's center of mass) by the equation of motion,

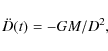
$\begin{displaymath}\ddot D(t) = - GM/D^2, \end{displaymath}$

(2)

where D is the distance between the galaxies and M is the total mass m₁+m₂ of the binary. In the well-known first integral,

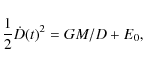
$\begin{displaymath}\frac{1}{2} \dot D(t)^2 = GM/D + E_0, \end{displaymath}$

(3)

E₀ is a constant total mechanical energy of the binary (per unit reduced mass). The energy is negative for a gravitationally bound system, E₀ < 0. This inequality and Eq. (2) with the observed values D = 0.7 Mpc and $\dot D = -120$ km s^-1 lead to an absolute lower limit for the estimated binary mass: $M > 1 \times 10^{12}~M_{\odot}$ . This is about an order of magnitude larger than the sum of the luminous masses of the two galaxies. With a ``timing argument'' additionally used (in integrating Eq. (2)), the mass is $M \simeq 3 \times 10^{12}~M_{\odot}$ if the maximal separation of the galaxies was 7 Gyr ago (see below). Both limits are estimated with an accuracy of 20-30%.

With a minimal modification of the original KW method, including the dark energy (DE) background $\rho _{\rm v}$ , the equation of motion and its first integral become:

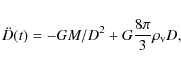
$\begin{displaymath}\ddot D(t) = - GM/D^2 + G \frac{8\pi}{3} \rho_{\rm v}D, \end{displaymath}$

(4)

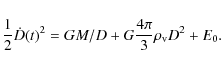
$\begin{displaymath}\frac{1}{2} \dot D(t)^2 = GM/D + G \frac{4\pi}{3} \rho_{\rm v}D^2 + E_0. \end{displaymath}$

(5)

Now the total energy for a bound system embedded in the DE background is

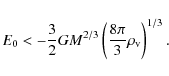
$\begin{displaymath}E_0 < - \frac{3}{2} G M^{2/3} \left(\frac{8\pi}{3} \rho_{\rm v}\right)^{1/3}. \end{displaymath}$

(6)

This may be easily seen from the gravitational potential $U = - GM/D - \frac{4\pi}{3} G \rho_{\rm v}D^2$ in the right side of Eq. (4). With the same values as above for the separation and relative velocity of the two galaxies (and with the same 20-30% accuracy), Eqs. (4), (5) lead to a new absolute lower mass limit: $M > M_1 = 3.2 \times 10^{12}~M_{\odot}$ , or 3 times the absolute lower limit of the original statement of the problem. The estimate assumes that the local density of the dark energy in the volume of the binary is identical to its global value (see Sect. 1).

The same data lead now to a larger value for the upper mass limit as well: $M < M_2 = 4.1 \times 10^{12}~M_{\odot}$ , assuming here the time-scale of the collapse t₀ > 7 Gyr (see also Fig. 1 where the dependence of the mass limit on the collapse time is showed for both original and modified models). It is motivated by the global $\Lambda$ CDM cosmology: gravitational instability is terminated in the linear regime about 7 Gyr ago with the start of the DE dominated epoch (e.g. Chernin et al. 2003).

Our estimated range of masses assuming the globally determined dark energy is $3.2 \times 10^{12}~M_{\odot}$ to $4.1 \times 10^{12}~M_{\odot}$ . This range of values is similar to but smaller than the interval, $(1.7{-}5.1) \times 10^{12}~M_{\odot}$ , found in the $\Lambda$ CDM Millennium Simulation (Li & White 2008) and a modern classical Kahn-Woltjer recalculation obtaining $5.3 \times 10^{12}~M_{\odot}$ (Binney & Tremaine 2008) both of which assume the global dark energy value.

$\begin{figure} \par\includegraphics[width=9cm,clip]{12762fig1.eps} \end{figure}$	Figure 1: The difference between the Local Group mass predictions from the classical Kahn-Woltjer estimator (KW) and its modified form here introduced (MKW). The x-axis gives the assumed look-back time of maximum separation and the y-axis gives the calculated total mass of the Milky Way & M 31 binary. The local DE density is assumed to be equal to the global value $\rho _{\rm v}$ .
Open with DEXTER

These results demonstrate the effect of the lost gravity in gravitationally bound systems embedded in the dark energy background. The relative motion of the bodies is controlled by the gravity (of dark matter and baryons) which is partly counterbalanced by the dark energy antigravity. Consequently, the mass estimate for dark matter and baryons must be corrected for dark energy. The true mass of the system given by the modified Kahn-Woltjer (MKW) estimator is larger than obtained without dark energy.

3 Zero-gravity radius

The local Hubble cell may be described by a simple model in which the Local Group is represented by the MW-M 31 binary. This is an interior component of the system. Its exterior component is the expansion flow of neighboring dwarf galaxies whose total mass is at least 100 times less than the mass of the central binary. In the model, the flow can be viewed as an ensemble of receding test particles moving in the gravitational potential of the binary and the antigravity potential of the dark energy background. The gravity-antigravity potential outside the binary becomes practically spherical and static at distances >1.5 Mpc from the group barycenter (Fig. 2). Therefore, at distances R > 1.5 Mpc, the gravity force is given by Newton's inverse square law relative to the group barycenter. The antigravity force produced by the dark energy density $\rho _{\rm v}$ is given by Einstein's linear law (e.g. Chernin 2001, 2008; Chernin et al. 2006) in the same reference frame:

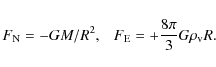
$\begin{displaymath}F_{\rm N} = - GM/R^2, ~~~ F_{\rm E} = + \frac{8 \pi}{3} G \rho_{\rm v} R. \end{displaymath}$

(7)

Gravity and antigravity are exactly balanced at the zero-gravity surface of the radius $R = R_{\rm v}$ (Chernin et al. 2000; Chernin 2001; Baryshev et al. 2001; Dolgachev et al. 2003):

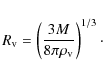
$\begin{displaymath}R_{\rm v} = \left(\frac{3 M}{8\pi \rho_{\rm v}}\right)^{1/3}\cdot \end{displaymath}$

(8)

Antigravity dominates at $R > R_{\rm v}$ , and gravity is stronger than antigravity at $R < R_{\rm v}$ . The lost-gravity effect (Sects. 1, 2) is one hundred percent at the zero-gravity surface. The total effective gravitating mass of the non-vacuum matter and vacuum energy contained within the surface is zero on the surface. No finite bound orbits are possible at $R \geq R_{\rm v}$ . Taking, for example, the value of the group mass to be $(3.3{-}4.1) \times 10^{12}~M_{\odot}$ from Sect. 2 and assuming again that the local density of the dark energy is identical to its global value $\rho _{\rm v}$ , we find: $R_{\rm v} = (1.4{-}1.6)$ Mpc. This shows that the group is located inside the sphere of radius $R_{\rm v}$ while the flow occurs outside the sphere. This two-component model of the local Hubble cell enables one to extract the group mass and the local density of the dark energy from the HST data on the local universe.

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{12762fig2.eps} \end{figure}$	Figure 2: Equipotential curves for the Milky Way-M 31 binary system, showing their near-sphericity at distances >1.5 Mpc. The LG mass $4 \times 10^{12}~M_{\odot}$ and the local DE density equal to the global value $\rho _{\rm v}$ are assumed.
Open with DEXTER

Conversely, if the zero-gravity radius is known from observations, the mass of the group may be found as a function of the dark energy density:

$\begin{displaymath}M = {\frac{8\pi}{3}} \rho_{\rm v} R_{\rm v}^{3} \simeq 0.9 \times 10^{12} [R_{\rm v}/({\rm Mpc})]^{3}~M_{\odot}. \end{displaymath}$

(9)

The position of the zero-gravity surface can be estimated from the observations of the local Hubble cell performed with the HST (Karachentsev 2005; Karachentsev et al. 2003-2009). There are sixty galaxies with good distances (8-10% accuracy) and velocities (5-10 km s^-1 accuracy) in the cell volume. Nearly half of them plus the Milky Way and M 31 galaxies form the Local Group. In the Hubble diagram, they occupy distances to somewhat more than 1 Mpc. Their radial velocities (relative to the group barycenter) range from -150 to +150 km s^-1. The other half of the observed galaxies (all dwarfs) recede from the group and have only positive velocities (Fig. 4). The minimal distance of outflowing galaxies is 1.2-1.6 Mpc from the group barycenter (Karachentsev 2005; Karachentsev et al. 2009). The flow of receding galaxies is rather regular, close to a linear velocity-distance relation. The flows velocity dispersion is about 25-30 km s^-1 which is 2-3 times less than within the group, a radical difference.

The radical difference in the phase-space structure of the group and the outflow around it is the most prominent feature of the local Hubble cell. We have argued earlier (Chernin et al. 2000, 2006; Chernin 2001; Teerikorpi et al. 2008) that the physics behind this feature might be due to the interplay between the gravity of the group and antigravity of the dark energy background, so that the group size is less than $R_{\rm v}$ and the flow starts at the distances $R > R_{\rm v}$ (as in the example above). Therefore the zero-gravity surface is located somewhere in the gap between the group and the outflow in the distance interval of 1.2-1.6 Mpc.

The double inequality $1.2 < R_{\rm v} < 1.6$ Mpc and Eq. (8) lead to lower and upper limits for the non-vacuum mass of the group, M₄ < M < M₃, where

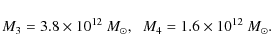
$\begin{displaymath}M_3 = 3.8 \times 10^{12}~M_{\odot}, \;\; M_4 = 1.6 \times 10^{12}~M_{\odot}. \end{displaymath}$

(10)

This result is quite compatible with the estimates obtained in Sect. 2 from the internal dynamics of the group binary.

Combining the four mass limits M₁, M₂, M₃, M₄, we may give a rather narrow interval for possible values of the Local Group mass: $3.3 < M < 3.8 \times 10^{12}~M_{\odot}$ . The interval is narrower than previously in the literature (see Sect. 1); it may be somewhat broadened, if one takes into account the accuracy of the estimation, about 20-30%.

4 Local density of dark energy

The results of Sects. 2, 3 for the group mass were obtained by taking the local density of dark energy equal to its global value $\rho _{\rm v}$ measured on scales of $\sim$ 1000 Mpc. This assumption is motivated by the standard $\Lambda$ CDM cosmology which views dark energy as a perfect fluid of constant density everywhere. It is obviously important to prove or disprove the assumption using only a local model and local data.

To do that, we develop further the approach of Sects. 2, 3 and consider the four characteristic masses introduced there as functions of the local density of dark energy $\rho_{\rm x}$ . It is assumed to be uniform in space and constant in time, but may not be equal to the global density $\rho _{\rm v}$ . The functions M₁(x), M₂(x), M₃(x), M₄(x), where $x = \rho _{\rm x} / \rho _{\rm v}$ , are shown in Fig. 3. We see that the two masses M₁(x) (which comes from the binding condition for the MW-M 31 binary) and M₂(x) (from the timing argument) form a strip on the M vs. x plot, which confines possible values of the group mass as a function of the local density. Note that the mass values grow with x - another sign of the lost-mass effect (Sects. 2-4).

The strip is crossed by two beams M₃ = 3.8 x (the upper limit to the zero-gravity radius) and M₄ = 1.6 x (the lower limit to the radius); the unit of mass here is $10^{12}~M_{\odot}$ . As a result, a closed elongated area appears in the plot which contains all possible values of the group mass. The mass proves to lie in the interval

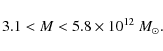
$\begin{displaymath}3.1 < M < 5.8 \times 10^{12}~M_{\odot}. \end{displaymath}$

(11)

This interval is considerably wider than that at x = 1 (see Sect. 3). The result agrees well (within the 20-30% accuracy) with the even wider interval $1.7 < M < 5.1 \times 10^{12}~M_{\odot}$ found for the groups like the Local Group in the $\Lambda$ CDM Millennium Simulation (Li & White 2008).

$\begin{figure} \par\includegraphics[width=9cm,clip]{12762fig3.eps} \end{figure}$

Figure 3:

The mass-DE density diagram for the local Hubble cell. Here M (in units of $10^{12} M_\odot$ ) is the total gravitating mass in the LG and $x = \rho _{\rm x} / \rho _{\rm v}$ is the local DE density in units of the global DE density. The limit M > M₁ (x) comes from the binding condition for the LG in the modified KW model; M < M₂ (x) is given by the timing argument within the model; the restrictions M < M₃ (x) and M > M₄ (x) reflect the upper and lower limits, respectively, to the zero-gravity radius. The shaded area contains all possible values of the Local Group mass and gives the empirical range of the local dark energy density estimate.

Open with DEXTER

Beyond this straightforward mass range, with the same Fig. 3 plot one can find the permitted interval for the local dark energy density,

$\begin{displaymath}0.8 < \rho_{\rm x} < 3.7 \rho_{\rm v}. \end{displaymath}$

(12)

The interval includes the global value $\rho_{\rm x} = \rho_{\rm v}$ . This is a new estimate of the local density which is quite independent of the data on dark energy on global scales. As we see, both key parameters of the nearby universe - the Local Group mass and the dark energy density - follow in a self-consistent way from local observational data and a general framework based on the model of the local Hubble cell.

The lower limit to the local density $\rho_{\rm x}$ is of special interest indicating that dark energy antigravity does indeed exist on a local scale. The value of the lower limit is near the value of the global density $\rho _{\rm v}$ . Note that the lower density limit follows from the equation M₁(x) = M₃(x), so that it is determined by the natural binding condition for the group binary and the clear upper limit to the zero-gravity radius. It does not depend on the timing argument for the group binary or the lower limit to the zero-gravity radius.

5 Consistency with the outflow beyond R $_{\textit {v}}$

Here we check whether the outflow of dwarf galaxies just beyond R_vis consistent with the relatively high mass of the Local Group suggested by the above discussion assuming the standard dark energy density in the concordance cosmological model.

Previously, we introduced the concept of a normalized Hubble diagram, in order to study the kinematic structure of a group and its surroundings (Teerikorpi et al. 2008) in the presence of dark energy. If one fixes the mass of the group and the local dark energy density, one can calculate the zero-gravity radius $R_{\rm v}$ (Eq. (7)) and the vacuum Hubble constant $H_{\rm v} = (8\pi G\rho_{\rm v}/3)^{1/2}$ . Then in the representation with $R/R_{\rm v}$ and $V/H_{\rm v}R_{\rm v}$ as x- and y-axes, respectively, one may conveniently describe different dynamical regions of the system (see Fig. 1 in Teerikorpi et al. 2008). Beyond $R_{\rm v}$ there is a minimum energy curve corresponding to the total mechanical energy $E = -\frac{3}{2} ~GM/R_{\rm v}$ . Test particles ejected from the region of bound orbits ( $R < R_{\rm v}$ ) cannot appear below this curve.

Here we note that the finite look-back time provides a stricter lower-limit curve which can be parametrized in terms of the vacuum Hubble time $T_{\rm v} = 1/H_{\rm v}$ . The flight time from the center of the group to the normalized distance $x = R/R_{\rm v}$ , for a particle with energy $E = -\alpha ~ GM/R_{\rm v}$ is

$\begin{displaymath}t = T_{\rm v} \int_{x_0}^x \! (x^2 + 2/x -2\alpha)^{-1/2} ~ {\rm d}x, \end{displaymath}$

(13)

while the normalized velocity y is related to x as

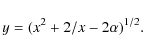
$\begin{displaymath}y = (x^2 + 2/x - 2\alpha)^{1/2}. \end{displaymath}$

(14)

Evidently, only such x-values and corresponding energies $\alpha$ are allowed for flight times, t, equal to or less than the age of the model universe. Conversely, by fixing the time of ejection, one can calculate the present position in the Hubble diagram (basically what is done in Lemaître-Tolman like solutions; e.g. Gromov et al. 2001; Peirani & de Freitas Pacheco 2006, 2008; Karachentsev et al. 2009).

$\begin{figure} \par\includegraphics[width=9cm,clip]{12762fig4.eps} \end{figure}$	Figure 4: The distance-velocity diagram for the Local Group and its near environment. The curves give outflow, for Local Group masses 2, 4 (the thick line), and $6 \times 10^{12}~M_{\odot}$ with the local DE density equal to the global value. The range of the zero-gravity radius and mass-values corresponding to the standard globally determined vacuum density are indicated.
Open with DEXTER

Using x₀ = 0.001 in the above integral we have calculated the predicted velocities for different present positions for the standard $\Lambda$ model, with t = 13.7 Gyr and $T_{\rm v} = 16.3$ Gyr, for different values of the LG mass. We show these curves in Fig. 4. One sees that $M = 2 \times 10^{12}~M_{\odot}$ puts the Hubble curve too high, and $M = 6 \times 10^{12}~M_{\odot}$ too low, while $M = 4 \times 10^{12}~M_{\odot}$ provides an admissible fit. If the flight time is made shorter (it cannot be longer than the universe model), the curves move up, meaning a still larger mass. Examining the curves versus the data points, the masses estimated from the outflowing dwarfs are also consistent with those in Sects. 2-4, which used the inner parts of the Local Group system.

We shall discuss the predicted outflow beyond $R_{\rm v}$ in more detail and for different models in a separate study.

6 Discussion and conclusions

The local volume proves to be a productive area for the studies of dark matter and dark energy (e.g. Chernin 2001, 2008; Ekholm et al. 2001; Baryshev et al. 2001; Byrd et al. 2007; Niemi et al. 2007; Teerikorpi et al. 2008). Study of the Local Group enables one to learn not only the mass in the system, but simultaneusly, the local density of the dark energy itself. Generally, the mass of a galaxy group determined using dynamical methods (like the zero-gravity radius, the zero-velocity radius & the nearby Hubble flow, the Kahn-Woltjer method and also the virial mass - see the Appendix) becomes higher when the ``lost-gravity'' effect of the dark energy is taken into account. We derived the total mass of the Local Group to lie within $3.1{-}5.8 \times 10^{12}~M_{\odot}$ , while the local dark energy density lies within $0.8{-}3.7\rho_{\rm v}$ ( $\rho _{\rm v}$ is the global density value). Indeed, the main result of this paper is our new estimate of the local density of the dark energy on a scale of $\sim$ 1 Mpc. The estimated range of values encompasses the global value which supports the validity of the cosmological constant formulation. The lower limit is only about 20% less than the global density dark energy value - impressive considering that the two values are measured with quite different methods on scales differing by a factor of 1000.

In our approach, we use the concept of the local Hubble cell as an isolated physical system with a two-component structure. The components are drastically different: the gravitationally bound Local Group dominated by the MW-M 31 binary and the surrounding cool local Hubble flow. The difference is due to the interplay between the gravity produced by the dark (and baryonic) matter of the Local Group and the antigravity from the DE background in a local volume only about 6 Mpc across. The bound group with a high velocity dispersion is located within the zero-gravity surface, while the low-dispersion expansion flow is found outside the surface, where antigravity dominates and dwarf galaxies move away from the group with acceleration. In this sense, the local dynamics reproduces (in one billionth of observed space) the global dynamics of the cosmological expansion. Our analysis indicates that the local and global antigravity effects are due to, most probably, the same agent - dark energy of the same density. The fact that the range of local density values encompasses the global density is strong new evidence for the cosmological constant formulation.

Acknowledgements

We thank A. Cherepashchuk, Yu. Efremov, I. Karachentsev, A. Silbergleit and A. Zasov for discussions. We also thank the anonymous referee for useful suggestions which improved the presentation.

Appendix A: The ``lost-gravity'' effect in the virial theorem

The conventional virial theorem needs an extra term due to the contribution of the particle-dark energy interaction to the total potential energy, for systems embedded in the dark energy background. This extra term has been pointed out and used in some applications (Lahav et al. 1991; Horellou & Berge 2005; see also Bertolami et al. 2007). Here we discuss in some detail the derivation of the modified virial theorem and show how it leads to a correction upwards for the mass estimates. How significant can this correction be?

Virial theorem estimators use the relation between the mean total kinetic $\langle K \rangle$ and potential $\langle U \rangle$ energies of a quasi-stationary gravitationally bound many-body system: $\langle K \rangle = 1/2 \vert \langle U \rangle \vert$ . In the presence of dark energy, the total potential energy includes not only the sum U₁ of the mutual potential energies of its member particles, but also the sum U₂ of the potential energies of the same particles in the force field of dark energy:

$\begin{displaymath}U_1 = - \frac{1}{2}\sum \frac{G m_i m_j}{\vert\vec{r}_i - \ve... ...j\vert}, \; U_2 = - \frac{4\pi \rho_v}{3}\sum m_i \vec{r}_i^2. \end{displaymath}$

(A.1)

Here $\vec{r}_i$ is the radius-vector of a particle in the frame of the system's barycenter; the summation in U₁ is over all particle pairs ( $i \neq j$ ). The major contribution to the sum is from dark matter particles whatever their individual masses may be. A hint to the structure of U₂ may be seen, e.g., from the second item in the right side of Eq. (4); the summation in U₂ is over all the particles. Dark energy comes to the virial theorem with an extra contribution to the potential energy of the system.

A link to the kinetic energy is provided by the equation of motion of an individual particle:

$\begin{displaymath}m_i \ddot{\vec{r}}_i = - \frac{\partial U}{\partial \vec{r}_i... ...frac{8\pi}{3}\rho_v m_i \vec{r}_i^2 \frac{\vec{r}_i}{r_i}\cdot \end{displaymath}$

(A.2)

Averaging over time and using the Euler theorem on homogeneous functions (applied separately to the two functions that come from the two terms in the right side of Eq. (A.2)), we find

$\begin{displaymath}\langle K \rangle = - \frac{1}{2} \langle U_1 \rangle + \langle U_2 \rangle. \end{displaymath}$

(A.3)

This is the modified virial relation adapted to the universe with the dark energy background include in the second term above. Now we ask how much the inclusion of the dark energy influences the usual virial mass estimates.

Equation (A.3) may be rewritten in terms of the total mass M, a characteristic velocity $\bar V$ and characteristic sizes $\bar R_1, \bar R_2$ :

$\begin{displaymath}M = \frac{\bar V^2 \bar R_1}{G} + \frac{8\pi}{3}\rho_v \bar R_2^3, \end{displaymath}$

(A.4)

or in convenient units:

$\begin{displaymath}\frac{M}{M_{\odot}} = 2.3 \times 10^8 \left(\frac{\bar V}{\rm... ...0.9 \times 10^{12}\left(\frac{\bar R_2}{\rm Mpc}\right)^3\cdot \end{displaymath}$

(A.5)

This new mass estimator - from the modified virial theorem - includes an additional positive term. It is equal to the absolute value of the effective (anti)gravitating mass of dark energy contained in the spherical volume of radius R₂: $M_{\rm eff} = - \frac{8\pi}{3}\rho_v \bar R_2^3$ . The term gives a quantitative measure of the lost-gravity effect.

Equations (A.4) and (A.5) can be calculated with representative values of the characteristic sizes $\bar R_1, \bar R_2$ and velocity $\bar V$ . In the simple example of only one body orbiting a gravitating mass M, the size $\bar R_1 = \bar R_2$ is the radius of curvature of the orbit and the velocity $\bar V$ is the orbital velocity. A similar identification of the quantities is obvious when the mass of a galaxy is derived from its rotation curve. In both cases, the estimated mass is larger than that in conventional estimations. The additional mass is $\vert M_{\rm eff}\vert$ .

Generally, the characteristic sizes and velocities for groups and clusters need more sophisticated analysis than the above - even in the absence of dark energy (e.g. Peebles 1971). The first (conventional) term in Eq. (A.5) is estimated for the Local Group as $2.3 \times 10^{12}~M_{\odot}$ (van den Bergh 1999) or $1.9 \times 10^{12}~M_{\odot}$ (Karachentsev 2005, Karachentsev et al. 2009). Then the second term in Eq. (A.5) contributes from 30 to 50% of the total mass, if the total size $\bar R_2$ is about 1 Mpc. Assuming $\bar R_1 = \bar R_2$ , one may see that the relative contribution of the dark energy scales as thecrossing time squared $(\bar R/\bar V)^2$ . In that case the lost-gravity effect is 10-30 times larger in a group like the Local Group than in a rich cluster like the Coma cluster.

A study of the lost-gravity effect in groups in general is complicated by the fact that in existing group catalogues, the virial masses tend to be overestimated for other reasons (Niemi et al. 2007). We will discuss this in detail elsewhere.

References

Baryshev, Yu. V., Chernin, A. D., & Teerikorpi, P. 2001, A&A, 378, 729 [NASA ADS] [CrossRef] [EDP Sciences]
Bertolami, O., Pedro, G., & Le Delliou, M. 2007, Phys. Lett. B, 654, 165 [NASA ADS] [CrossRef]
Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edition (Princeton and Oxford: Princeton University Press)
Byrd, G. G., Chernin A. D., & Valtonen M. J. 2007, Cosmology: Foundations and Frontiers (Moscow: Editorial URSS)
Chernin, A. D. 2001, Physics-Uspekhi, 44, 1099 [NASA ADS] [CrossRef]
Chernin, A. D. 2008, Physics-Uspekhi, 51, 253 [NASA ADS] [CrossRef]
Chernin, A. D., Teerikorpi, P., & Baryshev, Yu. V. 2000, Adv. Space Res., 31, 459 [NASA ADS] [CrossRef], 2003
Chernin, A. D., Nagirner, D. I., & Starikova, S. V. 2003, A&A, 399, 19 [NASA ADS] [CrossRef] [EDP Sciences]
Chernin, A. D., Karachentsev I. D., Valtonen M. J. et al. 2004, A&A, 415, 19 [NASA ADS] [CrossRef] [EDP Sciences]
Chernin, A., Teerikorpi, P., & Baryshev, Yu. 2006, A&A, 456, 13 [NASA ADS] [CrossRef] [EDP Sciences]
Dolgachev, V. P., Domozhilova, L. M., & Chernin, A. D. 2003, Astr. Rep., 47, 728 [NASA ADS] [CrossRef]
Einasto, J., & Lynden-Bell, D. 1982, MNRAS, 199, 67 [NASA ADS]
Ekholm, T., Baryshev, Yu., Teerikorpi, P., Hanski, M., & Paturel, G. 2001, A&A, 368, L17 [NASA ADS] [CrossRef] [EDP Sciences]
Gromov, A., Baryshev, Yu., Suson, D., & Teerikorpi, P. 2001, Gravitation & Cosmology, 7, 140 [NASA ADS]
Horellou, C., & Berge, J. 2005, MNRAS, 360, 1393 [NASA ADS] [CrossRef]
Kahn, F. D., & Woltjer, L. 1959, ApJ, 130, 705 [NASA ADS] [CrossRef]
Karachentsev, I. D. 2005, AJ, 129, 178 [NASA ADS] [CrossRef]
Karachentsev, I. D., Makarov, D. I., Sharina, M. E., et al. 2003, A&A, 398, 479 [NASA ADS] [CrossRef] [EDP Sciences]
Karachentsev, I. D., Karachentseva, V. E., Huchtmeier, W. K., & Makarov, D. I. 2004, AJ, 127, 2031 [NASA ADS] [CrossRef]
Karachentsev, I. D., Kashibadze, O. G., Makarov, D. I., & Tully, R. B. 2009, MNRAS, 393, 1265 [NASA ADS] [CrossRef]
Lahav, O., Lilje, P. B., Primack, J. R., & Rees M. J. 1991, MNRAS, 251, 128 [NASA ADS]
Li, Y.-S., & White, S. M. D. 2008, MNRAS, 384, 1459 [NASA ADS] [CrossRef]
Macciò, A. V., Governato, F., & Horellou, C. 2005, MNRAS, 359, 941 [NASA ADS] [CrossRef]
Niemi, S.-M., Nurmi, P., Heinämäki, P., & Valtonen M. J. 2007, MNRAS, 382, 1864 [NASA ADS]
Peebles, P. J. E. 1971, Physical Cosmology (New-Jersey: Princeton Univ. Press)
Peirani, S., & de Freitas Pacheco, J. A. 2006, New Ast., 11, 325 [NASA ADS] [CrossRef]
Peirani, S., & de Freitas Pacheco, J. A. 2008, A&A, 488, 845 [NASA ADS] [CrossRef] [EDP Sciences]
Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef]
Riess, A. G., Filippenko, A. V., Challis P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef]
Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef]
Teerikorpi, P., Chernin, A. D., Karachentsev, I. D., & Valtonen, M. J. 2008, A&A, 483, 383 [NASA ADS] [CrossRef] [EDP Sciences]
Valtonen, M. J., Byrd, G. G., McCall, M. L., & Innanen, K. A. 1993, AJ, 105, 886 [NASA ADS] [CrossRef]
van den Bergh, S. 1999, A&ARv, 9, 273 [NASA ADS]

Footnotes

... energy: The linear binary model for the relative motion of the Milky Way and M 31 galaxies is an idealization. The real dynamics of the Local Group must be more complex (see Einasto & Lynden-Bell 1982; and especially Valtonen et al. 1993). In particular, a transverse velocity might increase the mass value, but not more than by 10-15%. The earlier dynamical history of the binary (not saying about its formation) can hardly be described by this model. This process needs more studies, and the cosmological computer N-body simulations are a real tool to clarify the matter - see Li & White (2008) and Macció et al. (2005).

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{12762fig1.eps} \end{figure}$	Figure 1: The difference between the Local Group mass predictions from the classical Kahn-Woltjer estimator (KW) and its modified form here introduced (MKW). The x-axis gives the assumed look-back time of maximum separation and the y-axis gives the calculated total mass of the Milky Way & M 31 binary. The local DE density is assumed to be equal to the global value $\rho _{\rm v}$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{12762fig2.eps} \end{figure}$	Figure 2: Equipotential curves for the Milky Way-M 31 binary system, showing their near-sphericity at distances >1.5 Mpc. The LG mass $4 \times 10^{12}~M_{\odot}$ and the local DE density equal to the global value $\rho _{\rm v}$ are assumed.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{12762fig3.eps} \end{figure}$	Figure 3: The mass-DE density diagram for the local Hubble cell. Here M (in units of $10^{12} M_\odot$ ) is the total gravitating mass in the LG and $x = \rho _{\rm x} / \rho _{\rm v}$ is the local DE density in units of the global DE density. The limit M > M₁ (x) comes from the binding condition for the LG in the modified KW model; M < M₂ (x) is given by the timing argument within the model; the restrictions M < M₃ (x) and M > M₄ (x) reflect the upper and lower limits, respectively, to the zero-gravity radius. The shaded area contains all possible values of the Local Group mass and gives the empirical range of the local dark energy density estimate.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{12762fig4.eps} \end{figure}$	Figure 4: The distance-velocity diagram for the Local Group and its near environment. The curves give outflow, for Local Group masses 2, 4 (the thick line), and $6 \times 10^{12}~M_{\odot}$ with the local DE density equal to the global value. The range of the zero-gravity radius and mass-values corresponding to the standard globally determined vacuum density are indicated.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.