| Issue |
A&A
Volume 507, Number 3, December I 2009
|
|
|---|---|---|
| Page(s) | 1203 - 1210 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200912266 | |
| Published online | 16 July 2009 | |
A&A 507, 1203-1210 (2009)
Decay of the toroidal field in magnetically driven jets
R. Moll
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
Received 3 April 2009 / Accepted 4 July 2009
Abstract
A 3D simulation of a non-relativistic, magnetically driven jet
propagating in a stratified atmosphere is presented, covering about three
decades in distance and two decades in sideways expansion. The simulation
captures the jet acceleration through the critical surfaces and the development
of (kink-)instabilities driven by the free energy in the toroidal magnetic
field component. The instabilities destroy the ordered helical structure of
the magnetic field, dissipating the toroidal field energy on a length scale of
about 2-15 times the Alfvén distance. We compare the results with a 2.5D
(axisymmetric) simulation, which does not become unstable. The acceleration of
the flow is found to be quite similar in both cases, but the mechanisms of
acceleration differ. In the 2.5D case approximately 20% of the Poynting flux
remains in the flow, in the 3D case this fraction is largely dissipated
internally. Half of the dissipated energy is available for light emission; the
resulting radiation would produce structures resembling those seen in
protostellar jets.
Key words: magnetohydrodynamics (MHD) - ISM: jets and outflows - ISM: Herbig-Haro objects - galaxies: jets - gamma rays: bursts
1 Introduction and rationale of the calculations
A magnetized outflow produced by a rotating magnetic object has become the default interpretation for objects ranging from protostellar jets to gamma-ray bursts. The outflow in this model contains a tightly wound helical magnetic field. Such a nearly toroidal field represents a source of free energy that makes the flow inherently prone to non-axisymmetric magnetic instabilities. In this study we investigate the longer-term development of such instabilities and their consequences for jet phenomenology.
Instabilities are not necessarily fatal for the jet. Kink instabilities of helical magnetic field configurations typically saturate at a finite amplitude. Such instabilities at moderate amplitudes have been invoked to explain phenomena like the wiggly appearance of Herbig-Haro objects (Todo et al. 1993) or the orientation of VLBI jets in AGN (Königl & Choudhuri 1985).
The development of kink instability in a jet is not the same as in a laboratory configuration. Due to the sideways expansion of the flow, the ratio of poloidal (stabilizing) to toroidal (destabilizing) field components decreases with distance along the flow. Conditions favorable for instability are thus continually recreated in such a flow. In Moll et al. (2008, hereafter Paper I), we presented 3D MHD simulations showing the onset of instabilities in an expanding jet created by twisting a purely radial magnetic field. The degree of instability was found to depend on the kind of rotation that generates the twist. The highest degree of instability was attained with a constant angular velocity (rigid rotation); the jet produced in this case was subject to helical deformations with large amplitudes, causing sideways displacements of several degrees. However, the magnetic structure of the jet was not disrupted within the computational volume, and the instability did not lead to a significant decrease of the Poynting flux. These results indicate the need to follow the instabilities to larger distances from the source. We present here the results of simulations extending to a distance of 1000 times the diameter of the jet source.
In Paper I we showed how the degree of instability depends on the way in which the jet is collimated by its environment. If collimation conditions are such that the opening angle of the jet increases with distance, the Alfvén travel time across the jet increases more rapidly than the expansion time scale. As a result, instabilities soon ``freeze out'', and decay of the toroidal field becomes ineffective. In better collimating jets, such that the opening angle narrows with distance, instability is always effective. The calculations presented here are for such a case. It is probably the most relevant for both AGN and protostellar jets. Observations of the jets in M 87 (Junor et al. 1999) and HH30 (Mundt et al. 1990), for example, show a rapidly decreasing opening angle in the inner regions of the jet.
The dissipation of the magnetic energy in the toroidal field heats the plasma.
Radiation produced by this plasma would be an alternative or complement to the
standard mechanism invoked, which relies on dissipation in internal shocks.
Observations such as those of M 87 and HH30 indicate that dissipation starts
fairly close to the central object, compared with most observable length
scales, but also that the innermost regions, perhaps comparable to the Alfvén
distance ![]() ,
are quiet. Inferences from VLBI observations indicate
that AGN jets are not magnetically dominated on most observable scales
(cf. Sikora et al. 2005, and references therein); decay of the magnetic field
relatively close to the source of the jet would fit this observation (see
also discussion in Giannios & Spruit 2006).
,
are quiet. Inferences from VLBI observations indicate
that AGN jets are not magnetically dominated on most observable scales
(cf. Sikora et al. 2005, and references therein); decay of the magnetic field
relatively close to the source of the jet would fit this observation (see
also discussion in Giannios & Spruit 2006).
If dissipation takes place close enough to the source, it is possible that it
can be studied realistically by 3D simulations with current computational
resources. In Paper I, we already found indications that decay of the toroidal
field may become important at distances as close as 10-30 times
![]() .
.
The release of magnetic energy by the instability may also be important for accelerating the flow (Drenkhahn 2002). Dissipation of toroidal field causes the magnetic pressure gradient along the jet to steepen; this adds an accelerating force that is absent when the toroidal field is conserved (Giannios & Spruit 2006; Spruit 2008).
To facilitate extraction of physics from the numerical results, the 3D results in the following are compared systematically with a 2.5D (axisymmetric) simulation corresponding to the same initial and boundary conditions.
2 Methods
2.1 Numerical MHD solver, grid and coordinates
The following is a brief summary; for details see Paper I where the same numerical approach but different initial conditions were used. Details on the MHD code can also be found in Obergaulinger (2008).
We numerically solve the ideal adiabatic MHD equations in a static external
gravitational potential
![]() on a spherical grid
on a spherical grid
![]() .
In the 2.5D, axisymmetric simulation, the jet propagates
along the coordinate axis
.
In the 2.5D, axisymmetric simulation, the jet propagates
along the coordinate axis ![]() .
In the 3D simulation, the jet's axis is
taken in the direction
.
In the 3D simulation, the jet's axis is
taken in the direction
![]() .
The jet thus propagates in
equatorial direction of the coordinate system. This avoids the coordinate
singularity along the polar axis (
.
The jet thus propagates in
equatorial direction of the coordinate system. This avoids the coordinate
singularity along the polar axis (![]() ), which is numerically
problematic for trans-axial flows such as are caused by instabilities. The
computational volume covers a range
), which is numerically
problematic for trans-axial flows such as are caused by instabilities. The
computational volume covers a range
![]() that comprises
about twice the expected opening angle of the jet. The spacing of the
computational grid is uniform in the angular directions and logarithmic in the
radial direction. In this way, the varying numerical resolution approximately
matches the increase of the natural length scales in the expanding jet.
that comprises
about twice the expected opening angle of the jet. The spacing of the
computational grid is uniform in the angular directions and logarithmic in the
radial direction. In this way, the varying numerical resolution approximately
matches the increase of the natural length scales in the expanding jet.
For presentation and discussion, we transform the results to a different
coordinate system. This is again a spherical coordinate system, but with the
polar axis aligned with the jet. The polar and azimuthal angles in this
system are denoted by ![]() and
and ![]() ,
respectively:
,
respectively:
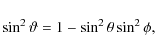
|
(1) |
| (2) |
in the 3D simulation and
Dissipation of magnetic energy in the flow causes heating. In nature this would lead to losses by radiation; in the computations it can cause numerical problems in regions where the magnetic energy dominates. Instead of a more realistic model for such losses, a temperature-control term is added in the energy equation, such that the temperature relaxes to that of the initial state on an appropriate time scale. In the simulations presented here this time scale is chosen such that the temperature stays within about a factor 100 around the initial value.
2.2 Initial and boundary conditions
The initial state consists of a current-free magnetic field embedded in a stratified atmosphere in the gravitational field of a point mass. The field configuration of this initial state is of a ``collimating'' type, the distance between neighboring field lines increases less rapidly than the distance from the source r. In Paper I, we showed that instabilities develop more strongly in such collimating configurations than in a purely radial initial field.
2.2.1 Initial field configuration
The initial field is axisymmetric around the jet axis and hence can be written
as
where
and a field with the stream function
(z>0) of which the field lines have a parabolic shape (Cao & Spruit 1994). Here,
the relative strength of the constituent fields at the lower boundary
The lower the value of
2.2.2 Stratification
We impose the static gravitational field of a point mass, located at the origin
of the coordinate system. The stratification is initially in hydrostatic
equilibrium in this potential. The gas pressure is chosen such that the
plasma-
![]() in the initial state is approximately
constant at small radii (
in the initial state is approximately
constant at small radii (
![]() ), where the monopole field
dominates:
), where the monopole field
dominates:
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() in the initial state. At large
radii, the value of the initial
in the initial state. At large
radii, the value of the initial ![]() is reduced as the magnetic field
strength decreases less rapidly than r-2.
is reduced as the magnetic field
strength decreases less rapidly than r-2.
2.2.3 Boundaries
Boundary conditions are maintained through the use of ``ghost cells'' outside
the computational domain. At the sides (![]() in the 2.5D simulation,
in the 2.5D simulation,
![]() and
and ![]() in the 3D simulation) and top (upper r), we use open
boundary conditions that allow for an almost force-free outflow or inflow of
material, including magnetic fields.
in the 3D simulation) and top (upper r), we use open
boundary conditions that allow for an almost force-free outflow or inflow of
material, including magnetic fields.
The bottom boundary is located at a finite height
![]() above the origin of
the gravitational potential. This distance is 1/200 of the size of the
computational volume. The jet is generated there by a ``rotating
disk''
above the origin of
the gravitational potential. This distance is 1/200 of the size of the
computational volume. The jet is generated there by a ``rotating
disk''![]() of radius
of radius
![]() around the axis. It is implemented by maintaining a velocity field
around the axis. It is implemented by maintaining a velocity field
![]() in the ghost zones:
in the ghost zones:
![]() for
for
![]() and 0elsewhere. The disk thus rotates rigidly like in the cases R2 and R3 in
Paper I.
and 0elsewhere. The disk thus rotates rigidly like in the cases R2 and R3 in
Paper I.
All quantities at the bottom boundary except for ![]() are fixed at their
initial values in the ghost cells.
are fixed at their
initial values in the ghost cells. ![]() is extrapolated from the interior
of the domain.
is extrapolated from the interior
of the domain.
2.3 Parameters and units
Table 1: Normalization units.
The above suggests a specification of the problem in terms of 7 parameters: the
field configuration parameter ![]() ,
a scale for the field strength, scales
for the pressure and density, the bottom boundary location
,
a scale for the field strength, scales
for the pressure and density, the bottom boundary location
![]() ,
the
radius
,
the
radius
![]() of the rotating disk, and its rotation rate. Because of the
symmetries of the problem, it is actually determined by only 4 parameters; the
remaining 3 dependences are equivalent to scaling factors. As the 4
independent parameters we choose the following dimensionless quantities: the
plasma-
of the rotating disk, and its rotation rate. Because of the
symmetries of the problem, it is actually determined by only 4 parameters; the
remaining 3 dependences are equivalent to scaling factors. As the 4
independent parameters we choose the following dimensionless quantities: the
plasma-![]() of the initial state, the angle
of the initial state, the angle
![]() which controls the opening
angle of the flow, the field configuration parameter
which controls the opening
angle of the flow, the field configuration parameter ![]() ,
and finally the
Alfvénic Mach number
,
and finally the
Alfvénic Mach number
![]() of the rotating velocity field at the edge
(
of the rotating velocity field at the edge
(
![]() )
of the launching disk, which controls the power of the jet.
They have the values
)
of the launching disk, which controls the power of the jet.
They have the values ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
(The simulations reported in Paper I corresponded to
.
(The simulations reported in Paper I corresponded to ![]() ,
,
![]() ,
,
![]() ,
,
![]() .)
.)
The units used for reporting the results below are the length scale
![]() ,
and the pressure and density on the axis at the bottom boundary,
,
and the pressure and density on the axis at the bottom boundary,
![]() ,
,
![]() .
Together with the 4 model
parameters
.
Together with the 4 model
parameters ![]() ,
,
![]() ,
,
![]() and
and
![]() ,
the units for
other quantities follow from these as shown in Table 1.
,
the units for
other quantities follow from these as shown in Table 1.
The simulations cover a distance of 2000 times the initial jet radius
![]() in the spherical range 5<r<1005. The resolution used in the 3D
simulation is
in the spherical range 5<r<1005. The resolution used in the 3D
simulation is
![]() ;
the corresponding domain size is
;
the corresponding domain size is
![]() .
The resolution used in the 2.5D
simulation is
.
The resolution used in the 2.5D
simulation is
![]() ;
the corresponding domain size
;
the corresponding domain size
![]() .
In both simulations, the radial width
.
In both simulations, the radial width ![]() of the grid
cells increases from 0.03 at the lower boundary to 6.92 at the upper
boundary in logarithmic steps.
of the grid
cells increases from 0.03 at the lower boundary to 6.92 at the upper
boundary in logarithmic steps.
3 Results
![\begin{figure}
\par\mbox{\includegraphics[width=10.5cm]{12266f1aRGB.eps}\includegraphics[width=6cm]{12266f1bRGB.eps} }\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg74.png)
|
Figure 1:
a) Selected magnetic field lines in the 3D simulation on
successively increasing length scales. The color coding gives the magnetic
field strength relative to its initial value. The field lines shown are the
ones that are anchored in the rotating disk at the lower boundary. The jet
starts out with a helical magnetic field ( left image) whose toroidal
component becomes increasingly stronger ( middle image) until
instabilities disrupt the ordered structure, the toroidal field decays and the
field becomes predominantly poloidal ( right image). b) Radial
component of the current density (
|
| Open with DEXTER | |
The 3D simulation was done using MPI parallelization on 128 CPUs, the 2.5D simulation was done with OpenMP parallelization on 32 CPUs.
The jet crossed the upper boundary of the computational volume at the physical
time
![]() on the 13th wall clock day of the 3D simulation. We
stopped it after 26 days, at which time t = 1055 had been reached. The 2.5D
simulation ran for 24 h, reaching t=1732.
on the 13th wall clock day of the 3D simulation. We
stopped it after 26 days, at which time t = 1055 had been reached. The 2.5D
simulation ran for 24 h, reaching t=1732.
The 3D jet is subject to non-axisymmetric instabilities, evidently of the kink (m=1) kind. They have a disruptive effect on the magnetic field structure and cause the toroidal field to decay, see Fig. 1. If such a jet was observed, it would probably look similar to Fig. 2, with bright knots and wiggles being prominent features. The knots move at a substantial fraction of the flow speed, sometimes merging or fading before leaving the computational domain. The 2.5D jet does not exhibit any form of instability.
3.1 Acceleration, collimation and mass flow
Most of the acceleration takes place below r=100, where the jet reaches
![]() of its terminal speed, see Fig. 3. The
location of the sonic (
of its terminal speed, see Fig. 3. The
location of the sonic (
![]() ,
the slow
magnetosonic cusp speed), Alfvén (
,
the slow
magnetosonic cusp speed), Alfvén (
![]() )
and fast magnetosonic
(
)
and fast magnetosonic
(
![]() )
radii depends on the direction
)
radii depends on the direction ![]() ,
see inset in
Fig. 3. This is because the acceleration is more effective
near the boundary of the jet, which is a consequence of the rigid rotation
profile used in its generation, and because the poloidal magnetic field is
being redistributed such that the local Alfvén velocity becomes relatively
high near the axis. As the toroidal field energy, which determines the jet
acceleration and the development of instabilities, is concentrated towards the
jet boundary (as opposed to the axis), the Alfvén radius there is probably the
most important for the subsequent considerations.
,
see inset in
Fig. 3. This is because the acceleration is more effective
near the boundary of the jet, which is a consequence of the rigid rotation
profile used in its generation, and because the poloidal magnetic field is
being redistributed such that the local Alfvén velocity becomes relatively
high near the axis. As the toroidal field energy, which determines the jet
acceleration and the development of instabilities, is concentrated towards the
jet boundary (as opposed to the axis), the Alfvén radius there is probably the
most important for the subsequent considerations.
The central velocity tends to be higher in the 3D simulation, presumably due to a more effective transfer of momentum from the boundary to the center. This may, together with the entrainment of ambient material discussed below, also explain why the peak velocities are somewhat lower in the 3D simulation.
The instabilities have a noticeable effect on the collimation behavior, see
Fig. 4. In the 2.5D simulation, the opening angle of the jet
decreases by about
![]() in the first half of the computational volume,
which is about
in the first half of the computational volume,
which is about
![]() less than what is marked by the shape of the initial
magnetic field. In the second half, well beyond the Alfvén surface, the
opening angle settles to a constant value. The jet in the 3D simulation is
less collimated
less than what is marked by the shape of the initial
magnetic field. In the second half, well beyond the Alfvén surface, the
opening angle settles to a constant value. The jet in the 3D simulation is
less collimated![]() , the location of the boundary fluctuates with time in the unstable
region. Averaged over time, we find it to be nearly conical.
, the location of the boundary fluctuates with time in the unstable
region. Averaged over time, we find it to be nearly conical.
The mass flow rate
![]() is somewhat higher in the 3D simulation and subject to strong fluctuations
above
is somewhat higher in the 3D simulation and subject to strong fluctuations
above
![]() :
the mean value over all radii at
:
the mean value over all radii at
![]() ,
measured
in the unit for
,
measured
in the unit for
![]() listed in Table 1, is
listed in Table 1, is
![]() in
the 2.5D and
in
the 2.5D and
![]() in the 3D simulation. The average over several
time steps shows a slight increase of
in the 3D simulation. The average over several
time steps shows a slight increase of
![]() with r in the 3D case,
whereas no trend can be deduced in the 2.5D case. This may be an indicator for
an enhanced entrainment of ambient material caused by the instabilities. It
may also in part explain the lower peak velocities in the 3D simulation.
with r in the 3D case,
whereas no trend can be deduced in the 2.5D case. This may be an indicator for
an enhanced entrainment of ambient material caused by the instabilities. It
may also in part explain the lower peak velocities in the 3D simulation.
3.2 Energy
A comparison of the different kinds of energy flow rates gives information
about energy transformations taking place in the jet. Integrating the radial
energy flux
over the
The final contribution of
![]() to
to
![]() is
is
![]() in the 2.5D simulation and
in the 2.5D simulation and ![]() in the 3D simulation.
in the 3D simulation.
![]() is up to about
is up to about ![]() smaller in the 3D simulation and
does not show a dissipation-induced increase.
smaller in the 3D simulation and
does not show a dissipation-induced increase.
![]() arises from
azimuthal and radial motion, with the relative share being highly similar in
the 2.5D and 3D case: the azimuthal contribution drops continuously to values
arises from
azimuthal and radial motion, with the relative share being highly similar in
the 2.5D and 3D case: the azimuthal contribution drops continuously to values
![]() at r>200 and the contribution from
at r>200 and the contribution from
![]() is
insignificant throughout.
is
insignificant throughout.
![]() can be decomposed further. The radial
component of the Poynting vector has 4 terms,
can be decomposed further. The radial
component of the Poynting vector has 4 terms,
Integrating these terms over the
We find a net outflow of magnetic enthalpy through the lateral boundaries of
the computational volume at the height of the jet front, with peak rates of
about 0.15 in the 2.5D case and 0.05 in the 3D case. The outflow is
transient in the 2.5D case, vanishing quickly after the jet front leaves the
computational volume. In the 3D case, however, it turns into an inflow of the
order -0.05 which persists until the end of the simulation. The energy in
the radial magnetic field increases correspondingly, mainly outside the jet at
![]() .
.
3.3 Magnetic field: poloidal vs. toroidal
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f2RGB.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg111.png)
|
Figure 2: Volume rendered image of the 3D jet that shows what it might look like in observations. For the volume rendering, a simple model was used in which emissivity and opacity depend on temperature and magnetic field strength. The jet exhibits a wiggly structure with bright knots, produced by the instabilities and the dissipation of magnetic energy. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f3}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg112.png)
|
Figure 3: Maximum velocity in jet direction as a function of distance. The inset shows the location of the critical surfaces. The flow passes first the sonic, then the Alfvén and finally the fast magnetosonic surface. |
| Open with DEXTER | |
| Figure 4: Jet boundary, defined by the angle that encloses 95% of the total energy flow (see Eq. (8)), as a function of distance. The unstable 3D jet is less collimated than the 2.5D jet. |
|
| Open with DEXTER | |
The red line in Fig. 6 shows the magnetic flux ![]() contained
within an angle
contained
within an angle
![]() from the axis,
from the axis,
divided by its initial value. For comparison, the green curve shows
Figure 7 compares the mean energy in the poloidal and toroidal
magnetic fields over the width of the jet as a function of distance, the width
of the jet being defined by a suitable velocity threshold. The 3D and 2.5D
jets start out similar, with the mean poloidal and toroidal fields becoming
comparable near the Alfvén surface. Beyond that distance, the mean toroidal
field energy increases more strongly in the 2.5D case, roughly proportional to
r-2. In the 3D case, the instability-induced destruction of the toroidal
field causes the slope to steepen substantially at
![]() ,
approximately as
,
approximately as
![]() .
The mean poloidal field
energy, on the other hand, stays near the initial value in the 3D case while
decreasing somewhat in the 2.5D case. Taking the ratio between the energies,
we find the magnetic field to be predominantly toroidal in the 2.5D case and
predominantly poloidal in the 3D case at large distances.
.
The mean poloidal field
energy, on the other hand, stays near the initial value in the 3D case while
decreasing somewhat in the 2.5D case. Taking the ratio between the energies,
we find the magnetic field to be predominantly toroidal in the 2.5D case and
predominantly poloidal in the 3D case at large distances.
We also experimented with means of the form
![]() ,
where the integral is performed over the whole
,
where the integral is performed over the whole
![]() surface,
and obtained similar results. Taking the mean within the static
surface,
and obtained similar results. Taking the mean within the static
![]() cone instead of using a velocity threshold yields a smaller value
for
cone instead of using a velocity threshold yields a smaller value
for
![]() in the 2.5D case, viz.
in the 2.5D case, viz. ![]() for r > 200. This is because an angle of
for r > 200. This is because an angle of
![]() includes more of the
environment of the jet (cf. Fig. 4).
includes more of the
environment of the jet (cf. Fig. 4).
In a ballistically expanding jet (constant velocity and opening angle) the
magnetic field components vary with distance r as
![]() ,
,
![]() .
Integrals over the width of the jet of Br,
.
Integrals over the width of the jet of Br,
![]() and
and
![]() are then constants. These integrals are shown in
Fig. 8. The ballistic approximation works well in the 2.5D
case, for Br as well as for
are then constants. These integrals are shown in
Fig. 8. The ballistic approximation works well in the 2.5D
case, for Br as well as for ![]() ,
if the acceleration region is
excluded. In the 3D case however, the integral of Br increases by about an
order of magnitude along the jet, while the integral of
,
if the acceleration region is
excluded. In the 3D case however, the integral of Br increases by about an
order of magnitude along the jet, while the integral of
![]() decreases
over the entire range.
decreases
over the entire range.
Figure 9 shows some poloidal magnetic field lines and the radial
velocity in the 2.5D and 3D jet. The latter was ``axisymmetrized'' by averaging
over the azimuthal coordinate ![]() .
In the outer, high-
.
In the outer, high-![]() ,
part
of the 2.5D jet, where the toroidal field is especially strong and jet
acceleration most efficient, there is an increase of the angular separation
between the field lines which is absent in the 3D jet. In other words, the
poloidal magnetic flux decreases locally faster with distance in the 2.5D case.
,
part
of the 2.5D jet, where the toroidal field is especially strong and jet
acceleration most efficient, there is an increase of the angular separation
between the field lines which is absent in the 3D jet. In other words, the
poloidal magnetic flux decreases locally faster with distance in the 2.5D case.
3.4 Forces and powers
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f5}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg128.png)
|
Figure 5:
Energy flow rates through the
|
| Open with DEXTER | |
| Figure 6:
Red: magnetic flux |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f7}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg130.png)
|
Figure 7: Mean magnetic energies in the poloidal and toroidal fields within the jet, normalized by the initial on-axis magnetic energy, and their ratio. Without instability (2.5D), the field becomes predominantly toroidal at large distances. With instability (3D), it becomes predominantly poloidal. |
| Open with DEXTER | |
| Figure 8: Magnetic field components, integrated over the jet cross section, as a function of distance, on a logarithmic scale. In a sphericallyexpanding ballistic flow these quantities would be constant, see text. |
|
| Open with DEXTER | |
To identify the accelerating forces that generate the kinetic energy flow
discussed in Sect. 3.2, we compute
![]() ,
the instantaneous power (rate of work) delivered by a specific force
,
the instantaneous power (rate of work) delivered by a specific force
![]() in the direction of the flow in the integrated volume. The
combination of gas pressure and gravitational forces,
in the direction of the flow in the integrated volume. The
combination of gas pressure and gravitational forces,
![]() ,
accounts for about one third of the power delivered by the
sum of all forces in the whole volume, the corresponding acceleration takes
place mainly below
,
accounts for about one third of the power delivered by the
sum of all forces in the whole volume, the corresponding acceleration takes
place mainly below
![]() (sonic surface). The rest is accounted for
by the Lorentz force, which we decompose as follows:
(sonic surface). The rest is accounted for
by the Lorentz force, which we decompose as follows:
with
The last force in Eq. (11) has only an azimuthal component. It is
important mainly below the Alfvén radius (![]() ), exerting a torque in
the same direction in which rotation is applied at the lower boundary. The
next-to-last force vanishes in the axisymmetric case. In the general case, it
has only non-azimuthal components. Unlike the last force, it works against the
flow; the two forces largely cancel each other in the 3D simulation. The
Lorentz force associated with
), exerting a torque in
the same direction in which rotation is applied at the lower boundary. The
next-to-last force vanishes in the axisymmetric case. In the general case, it
has only non-azimuthal components. Unlike the last force, it works against the
flow; the two forces largely cancel each other in the 3D simulation. The
Lorentz force associated with ![]() [second term in
Eq. (11)] performs the same work in the 3D and 2.5D cases,
despite the steepening of the toroidal magnetic pressure profile caused by the
dissipation. The total power is also similar in the two cases, in agreement
with the similarity of the kinetic energy flows in Fig. 5.
[second term in
Eq. (11)] performs the same work in the 3D and 2.5D cases,
despite the steepening of the toroidal magnetic pressure profile caused by the
dissipation. The total power is also similar in the two cases, in agreement
with the similarity of the kinetic energy flows in Fig. 5.
The situation is a bit different if only the radial power
![]() is taken into account. The Lorentz force associated with
is taken into account. The Lorentz force associated with ![]() does
approximately
does
approximately ![]() more work in the whole volume in the 3D case, the
additional power is delivered above
more work in the whole volume in the 3D case, the
additional power is delivered above
![]() .
The power of the net
force, however, is approximately the same in both cases.
.
The power of the net
force, however, is approximately the same in both cases.
4 Summary and discussion
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip=true]{12266f9aRGB.eps}\includegraphics[width=6cm,clip=true]{12266f9bRGB.eps} }\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg142.png)
|
Figure 9:
Poloidal magnetic field lines and radial velocity field, plotted as a
function of direction |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f10}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg143.png)
|
Figure 10: Rate of work done in the volume delimited by the lower boundary and r by the components of the Lorentz force in the direction of the flow. The power delivered by the total Lorentz force is about the same in the 3D and 2.5D cases. |
| Open with DEXTER | |
We have simulated jets generated by twisting a parabolically shaped large-scale magnetic field in both 3D and axisymmetric 2.5D. The shape of the initial field reflects itself in a fair amount of jet collimation, with an opening angle that decreases with distance, thus facilitating the growth of instabilities. The simulations cover the acceleration phase, where the jet passes through the critical surfaces (sonic, Alfvén and fast magnetosonic) for stationary MHD flows, as well as a substantial distance beyond these. We thus observe the onset of kink instabilities above the Alfvén surface in the 3D simulation. The instabilities disrupt the magnetic field structure. They cause magnetic dissipation, significantly reducing the toroidal field strength and with it the flow rate of magnetic enthalpy (surface integral of the Poynting flux) on a length scale of about 2-15 times the minimal Alfvén distance in the jet.
A direct comparison of the 2.5D and 3D simulations reveals no significant difference in the way the kinetic energy of the jet (integrated over its cross section) increases with distance. However, the distribution of the kinetic energy across the jet indicates differences in the acceleration process (cf. Fig. 9). In the axisymmetric flow, the acceleration is restricted to magnetic surfaces that diverge from each other more rapidly than in a flow with fixed opening angles. This creates a ``magnetic nozzle'' effect (Begelman & Li 1994) restricted to a limited range of angles within the flow (cf. discussion in Spruit 2008). A similar case of non-uniform expansion has been found in relativistic flows by Tchekhovskoy et al. (2008). In the 3D case, the (time averaged) acceleration is more uniform across the jet. It thus seems that while the steepening of the magnetic pressure gradient caused by the dissipation of the toroidal field leads to additional acceleration in the 3D case, this is made up for by a more favorably distributed poloidal magnetic flux in the 2.5D case which also enhances acceleration. In other words, there are different mechanism at work which yield the same result. Whether it is coincidence that the two effects have nearly the same strength is not clear.
The energy released by the dissipation of the toroidal magnetic field may be
radiated as light. The yield depends on the details of the dissipation
(reconnection) and radiation mechanisms involved. Since the magnetic energy
density (
![]() )
accounts for half of the Poynting flux
(
)
accounts for half of the Poynting flux
(
![]() ), the present simulations suggest that the available
luminosity may be as much as
), the present simulations suggest that the available
luminosity may be as much as ![]() of the initial magnetic enthalpy flow rate
(Fig. 5), provided that half of it is converted into kinetic
energy and the rest into light. As dissipation is not a smooth process, the
emission will be stronger in some regions. These would likely turn up as
bright knots in observations. Together with the wiggles caused by the kink
instabilities, the knots produce a structured appearance that is similar to
what has been observed in protostellar jets
(e.g. Heathcote et al. 1996; Reipurth & Bally 2001). The knots in the mocked jet image
move with the flow, consistent with observational findings
(Hartigan et al. 2005; Eislöffel & Mundt 1992). This provides an alternative to the
``internal shock'' interpretation usually invoked to explain jet knots
(e.g. Hartigan & Raymond 1993).
of the initial magnetic enthalpy flow rate
(Fig. 5), provided that half of it is converted into kinetic
energy and the rest into light. As dissipation is not a smooth process, the
emission will be stronger in some regions. These would likely turn up as
bright knots in observations. Together with the wiggles caused by the kink
instabilities, the knots produce a structured appearance that is similar to
what has been observed in protostellar jets
(e.g. Heathcote et al. 1996; Reipurth & Bally 2001). The knots in the mocked jet image
move with the flow, consistent with observational findings
(Hartigan et al. 2005; Eislöffel & Mundt 1992). This provides an alternative to the
``internal shock'' interpretation usually invoked to explain jet knots
(e.g. Hartigan & Raymond 1993).
The magnetic structure of a jet undergoes a dramatic change if it becomes subject to violent kink instabilities. The formerly ordered helical structure is largely destroyed and the poloidal field becomes the dominating field component. However, magnetic flux conservation still implies that the poloidal field declines faster with distance than the toroidal one. The toroidal field may thus, beyond the region covered by the here-presented simulations, become again dominant. This could, in principle, lead to a resurgence of instabilities until the Alfvén speed has dropped below the sideways expansion speed of the jet (times a factor of order unity). From this point on the toroidal field is effectively frozen in the flow (cf. discussion in Paper I).
4.1 Collimation and jet environment
Collimation of jets is popularly attributed to the ``hoop stress'' in the
toroidal field component. This is misleading: though the stress contributed by
the toroidal field can compress the configuration near the axis (as observed in
simulations), it eventually has to be taken up by an external agent (for a more
extended discussion, see Spruit 2008). In the simulations presented
above, as well as in other work, this agent is an external medium surrounding
the jet. It is included mostly because of limitations of the codes used, since
the demands of conserving energy typically cause numerical instabilities at low
gas densities or low plasma-![]() .
.
The boundary between the jet and the external medium actually expands due to
pressure exerted by the toroidal field. The role of a (material) external
medium in confining the jet can be taken over by a magnetic field, if it is
able to transfer stress in the jet's toroidal field to the surface of the
accretion disk. One might imagine that a toroidal field extending around the
jet might serve this role. The high Alfvén speeds in this field, however,
would make it violently unstable to non-axisymmetric instabilities, as the
early history of magnetic configurations for controlled fusion (linear pinches)
testifies. This obstacle does not become evident in the axisymmetric models in
the literature. A more realistic possibility, proposed by Shu et al. (1995), is
that the disk's poloidal field, assumed for launching the jet in the inner
regions, actually extends to much larger distances in the disk. Deformation of
the field can take up the lateral stress exerted by the jet. The collimation of
the jet would then be directly related to the properties of this poloidal
field. High degrees of collimation would be most easily achieved in disks with
a large ratio of outer to inner disk radius (Spruit et al. 1997). Numerical
simulations at much lower plasma-![]() than currently feasible would be
needed to study this form of ``poloidal collimation''.
than currently feasible would be
needed to study this form of ``poloidal collimation''.
As pointed out in the introduction, instabilities may take some distance to travel to become effective. The results presented above show that a distance of the order of 1000 times the source size of the jet is needed to capture the dissipation of the toroidal field. I surmise this to be the reason why the effect of instabilities is not as noticeable in the works of Anderson et al. (2006) and Ouyed et al. (2003), rather than the lack of external confinement of these winds.
4.2 Disruption
The possible presence of instabilities in jets sometimes raises concern about disruption. A complete dissipation of the jet into its surroundings is possible in principle through instabilities driven by the interaction of the jet with its surroundings, for example by Kelvin-Helmholtz instabilities, or its termination in a ``hot spot''. These processes extract their energy directly from the bulk kinetic energy of the flow. The effect of internal instabilities deriving from the free energy in the toroidal field is much less destructive, since these mainly redistribute internal energy forms within the jet. The comparison between the 2.5D and the 3D cases shows that the 3D jet widens by less than a factor 2 as a result of internal instabilities (cf. Figs. 4 and 9). Thenon-axisymmetric nature of the instabilities thus does cause some interaction with the environment, but its consequences remain relatively benign.
4.3 Cold flows
Current 3D simulations are poorly equipped to handle flows in which the magnetic or kinetic energy density, or both, dominate over the thermal energy density. In magnetically dominated flows driven from actual accretion disks, the temperature of the plasma is often sufficiently low that magnetic energy density dominates over plasma pressure already at a short distance from the disk surface (Blandford & Payne 1982). As a consequence, the sonic point in the present results is further away from the source than would be the case in e.g. actual protostellar disks. It is possible that the onset of the instabilities in more strongly magnetically dominated flows would be faster, and their consequences even stronger than in the simulations presented here. Codes specially designed to handle such ``cold'' flows would be needed to verify this.
AcknowledgementsThe author thanks H. C. Spruit for fruitful discussions and a critical reading of the manuscript, and M. Obergaulinger for providing his MHD code.
References
- Anderson, J. M., Li, Z.-Y., Krasnopolsky, R., & Blandford, R. D. 2006, ApJ, 653, L33 [NASA ADS] [CrossRef]
- Begelman, M. C., & Li, Z.-Y. 1994, ApJ, 426, 269 [NASA ADS] [CrossRef]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS]
- Cao, X., & Spruit, H. C. 1994, A&A, 287, 80 [NASA ADS]
- Drenkhahn, G. 2002, A&A, 387, 714 [NASA ADS] [CrossRef] [EDP Sciences]
- Eislöffel, J., & Mundt, R. 1992, A&A, 263, 292 [NASA ADS]
- Giannios, D., & Spruit, H. C. 2006, A&A, 450, 887 [NASA ADS] [CrossRef] [EDP Sciences]
- Hartigan, P., & Raymond, J. 1993, ApJ, 409, 705 [NASA ADS] [CrossRef]
- Hartigan, P., Heathcote, S., Morse, J. A., Reipurth, B., & Bally, J. 2005, AJ, 130, 2197 [NASA ADS] [CrossRef]
- Heathcote, S., Morse, J., Hartigan, P., et al. 1996, AJ, 112, 1141 [NASA ADS] [CrossRef]
- Junor, W., Biretta, J. A., & Livio, M. 1999, Nature, 401, 891 [NASA ADS] [CrossRef]
- Königl, A., & Choudhuri, A. R. 1985, ApJ, 289, 173 [NASA ADS] [CrossRef]
- Moll, R., Spruit, H. C., & Obergaulinger, M. 2008, A&A, 492, 621 [NASA ADS] [CrossRef] [EDP Sciences]
- Mundt, R., Buehrke, T., Solf, J., Ray, T. P., & Raga, A. C. 1990, A&A, 232, 37 [NASA ADS]
- Obergaulinger, M. 2008, Ph.D. Thesis, Max-Planck-Institut für Astrophysik, Garching bei München
- Ouyed, R., Clarke, D. A., & Pudritz, R. E. 2003, ApJ, 582, 292 [NASA ADS] [CrossRef]
- Reipurth, B., & Bally, J. 2001, ARA&A, 39, 403 [NASA ADS] [CrossRef]
- Shu, F. H., Najita, J., Ostriker, E. C., & Shang, H. 1995, ApJ, 455, L155 [NASA ADS] [CrossRef]
- Sikora, M., Begelman, M. C., Madejski, G. M., & Lasota, J.-P. 2005, ApJ, 625, 72 [NASA ADS] [CrossRef]
- Spruit, H. C. 2008, [arXiv:0804.3096]
- Spruit, H. C., Foglizzo, T., & Stehle, R. 1997, MNRAS, 288, 333 [NASA ADS]
- Tchekhovskoy, A., McKinney, J. C., & Narayan, R. 2008, MNRAS, 388, 551 [NASA ADS] [CrossRef]
- Todo, Y., Uchida, Y., Sato, T., & Rosner, R. 1993, ApJ, 403, 164 [NASA ADS] [CrossRef]
Footnotes
- ...
disk''
![[*]](/icons/foot_motif.png)
- Strictly speaking, because of the spherical grid, what we call ``disk'' here is really a spherical cap with small curvature.
- ... collimated
![[*]](/icons/foot_motif.png)
- Note, however, that with our definition of the jet boundary, a rigid displacement away from the center also increases the opening angle.
All Tables
Table 1: Normalization units.
All Figures
![\begin{figure}
\par\mbox{\includegraphics[width=10.5cm]{12266f1aRGB.eps}\includegraphics[width=6cm]{12266f1bRGB.eps} }\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg74.png)
|
Figure 1:
a) Selected magnetic field lines in the 3D simulation on
successively increasing length scales. The color coding gives the magnetic
field strength relative to its initial value. The field lines shown are the
ones that are anchored in the rotating disk at the lower boundary. The jet
starts out with a helical magnetic field ( left image) whose toroidal
component becomes increasingly stronger ( middle image) until
instabilities disrupt the ordered structure, the toroidal field decays and the
field becomes predominantly poloidal ( right image). b) Radial
component of the current density (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f2RGB.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg111.png)
|
Figure 2: Volume rendered image of the 3D jet that shows what it might look like in observations. For the volume rendering, a simple model was used in which emissivity and opacity depend on temperature and magnetic field strength. The jet exhibits a wiggly structure with bright knots, produced by the instabilities and the dissipation of magnetic energy. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f3}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg112.png)
|
Figure 3: Maximum velocity in jet direction as a function of distance. The inset shows the location of the critical surfaces. The flow passes first the sonic, then the Alfvén and finally the fast magnetosonic surface. |
| Open with DEXTER | |
| In the text | |
| |
Figure 4: Jet boundary, defined by the angle that encloses 95% of the total energy flow (see Eq. (8)), as a function of distance. The unstable 3D jet is less collimated than the 2.5D jet. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f5}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg128.png)
|
Figure 5:
Energy flow rates through the
|
| Open with DEXTER | |
| In the text | |
| |
Figure 6:
Red: magnetic flux |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f7}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg130.png)
|
Figure 7: Mean magnetic energies in the poloidal and toroidal fields within the jet, normalized by the initial on-axis magnetic energy, and their ratio. Without instability (2.5D), the field becomes predominantly toroidal at large distances. With instability (3D), it becomes predominantly poloidal. |
| Open with DEXTER | |
| In the text | |
| |
Figure 8: Magnetic field components, integrated over the jet cross section, as a function of distance, on a logarithmic scale. In a sphericallyexpanding ballistic flow these quantities would be constant, see text. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip=true]{12266f9aRGB.eps}\includegraphics[width=6cm,clip=true]{12266f9bRGB.eps} }\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg142.png)
|
Figure 9:
Poloidal magnetic field lines and radial velocity field, plotted as a
function of direction |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12266f10}
\end{figure}](/articles/aa/full_html/2009/45/aa12266-09/Timg143.png)
|
Figure 10: Rate of work done in the volume delimited by the lower boundary and r by the components of the Lorentz force in the direction of the flow. The power delivered by the total Lorentz force is about the same in the 3D and 2.5D cases. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



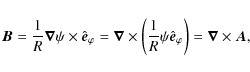
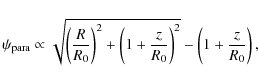

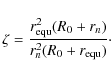
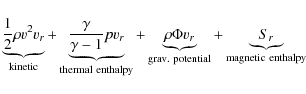
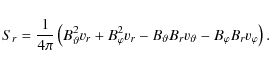
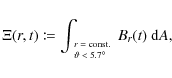
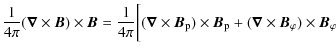
![$\displaystyle + (\vec{\nabla}\times \vec{B}_\ensuremath{{\rm p}} ) \times \vec{...
...(\vec{\nabla}\times \vec{B}_\varphi) \times \vec{B}_\ensuremath{{\rm p}}\bigg],$](/articles/aa/full_html/2009/45/aa12266-09/img136.png)