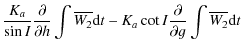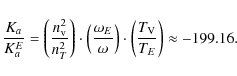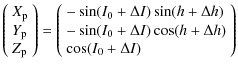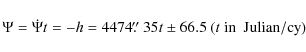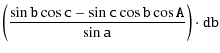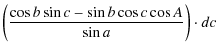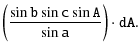| Issue |
A&A
Volume 507, Number 3, December I 2009
|
|
|---|---|---|
| Page(s) | 1635 - 1648 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912174 | |
| Published online | 01 October 2009 | |
A&A 507, 1635-1648 (2009)
Rotation of rigid Venus: a complete precession-nutation model
L. Cottereau - J. Souchay
Observatoire de Paris, Systèmes de Référence Temps Espace (SYRTE), CNRS/UMR8630, Paris, France
Received 24 March 2009 / Accepted 28 August 2009
Abstract
Context. With the increasing knowledge of the terrestrial
planets due to recent space probes it is possible to model their
rotation with increasing accuracy. Despite that fact, an accurate
determination of Venus precession and nutation is lacking
Aims. Although Venus rotation has been studied in several
aspects, a full and precise analytical model of its precession-nutation
motion remains to be constructed. We propose to determine this motion
with up-to-date physical parameters of the planet
Methods. We adopt a theoritical framework already used for a
precise precession-nutation model of the Earth, based on a Hamiltonian
formulation, canonical equations and an accurate development of the
perturbing function due to the Sun.
Results. After integrating the disturbing function and applying the canonical equations, we can evaluate the precession constant
![]() and the coefficients of nutation, both in longitude and in obliquity. We get
and the coefficients of nutation, both in longitude and in obliquity. We get
![]() ,
corresponding to a precession period of
,
corresponding to a precession period of
![]() years.
This result, based on recent estimations of the Venus moment of inertia
is significantly different from previous estimations. The largest
nutation coefficient in longitude with an argument 2 LS (where LS
is the longitude of the Sun) has a 2''19 amplitude and a 112.35 d
period. We show that the coefficients of nutation of Venus due to its
triaxiality are of the same order of amplitude as these values due to
its dynamical flattening, unlike of the Earth, for which they are
negligible.
years.
This result, based on recent estimations of the Venus moment of inertia
is significantly different from previous estimations. The largest
nutation coefficient in longitude with an argument 2 LS (where LS
is the longitude of the Sun) has a 2''19 amplitude and a 112.35 d
period. We show that the coefficients of nutation of Venus due to its
triaxiality are of the same order of amplitude as these values due to
its dynamical flattening, unlike of the Earth, for which they are
negligible.
Conclusions. We have constucted a complete theory of the
rotation of a rigid body applied to Venus, with up-to-date
determinations of its physical and rotational parameters. This allowed
us to set up a new and better constrained value of the Venus precession
constant and to calculate its nutation coefficients for the first time.
Key words: astrometry - celestial mechanics - planets and satellites: individual: Venus
1 Introduction
Among the planets of the Solar system, Venus shows peculiar
characteristics: its rotation is retrograde and very slow. Since its
243.02 d period was determined by radar measurements (Golstein 1964; Carpenter 1964), several authors have attempted to explain these two characteristics. Goldreich and Peale (1970)
showed that thermally driven atmospheric tidal torques and energy
dissipation at the boundary between a rigid mantle and a differentially
rotating liquid core are possible mechanisms to maintaine the retrograd
spin. Lago and Cazenave (1979)
studied the past evolution of the rotation of Venus using the
hypothesis that only solar tidal torques and core-mantle coupling have
been active since its formation. They found it conceivable that Venus
originally had a rotation similar to the other planets and evolved for
![]() years
from a rapid and direct rotation to the present slow retrograde one.
Others authors proposed different scenarios by supposing a high value
of the initial obliquity (Dobrovoskis 1980; Mc Cue & Dormand 1993). Yoder (1995)
gave a full account of the various internal mechanisms acting on
Venus'obliquity, such as core friction, CMB (core-mantle boundary)
ellipticity, and resonant excitations. Correia and Laskar (2001, 2003; Correia et al. 2003),
explored a large variety of initial conditions in order to cover
possible formation and evolutionary scenarios. They confirmed that
despite the variations in the models, only three of the four final spin
states of Venus are possible and that the present observed retrograd
spin state can be attained by two different processes: one prograde and
the other retrograde. Although these various studies concern the
evolution of Venus rotation on very long times scales, few attempts
have been made to accurately model the rotation for short times scales.
An analytical study of the rotation of a rigid Venus model carried out
by Habibullin (1995) with
rather uncommun parametrization, showing that Venus rotates almost
uniformly with negligible libration harmonics. In the following, we
propose an alternative construction of a rigid Venus rotation model,
contradicting to some extent these last results. First we show the
characteristics of Venus with respect to the corresponding ones for the
Earth (Sect. 2). We explain the parametrization of the rotation of a rigid Venus using the Andoyer variables (Sect. 3). We then determine the reference points and planes to study the rotational dynamics of Venus (Sect. 4).
We give the equations of motion and the analytical developments that
allow us to obtain the precession and the nutation of the planet
(Sects. 5-7). Finally we give the precession, the tables of nutation and the polar motion of Venus (Sects. 8 and 9). We will discuss our results in Sect. 10.
In this study we make some approximations: we suppose that the relative
angular distance between the three poles (the poles of angular
momentum, of figure and of rotation) is very small as is the case for
the Earth. Moreover we solve a simplified system where the second order
of the potential does not appear. Last, we suppose that the small
difference between the mean longitude and the mean anomaly of the Sun
which corresponds to the slow motion of the perihelion, can be
considered as constant. In Sects. 3 to 10,
the orbital elements of Venus and their time dependence are required to
carry out our numerical calculations. In these sections we used the
mean orbital elements given by Simon et al. (1994). These elements are valid over 3000 years with a relative accuracy of 10-5. This prevents our theory being used in long term calculations, our domain of validity being 3000 years.
years
from a rapid and direct rotation to the present slow retrograde one.
Others authors proposed different scenarios by supposing a high value
of the initial obliquity (Dobrovoskis 1980; Mc Cue & Dormand 1993). Yoder (1995)
gave a full account of the various internal mechanisms acting on
Venus'obliquity, such as core friction, CMB (core-mantle boundary)
ellipticity, and resonant excitations. Correia and Laskar (2001, 2003; Correia et al. 2003),
explored a large variety of initial conditions in order to cover
possible formation and evolutionary scenarios. They confirmed that
despite the variations in the models, only three of the four final spin
states of Venus are possible and that the present observed retrograd
spin state can be attained by two different processes: one prograde and
the other retrograde. Although these various studies concern the
evolution of Venus rotation on very long times scales, few attempts
have been made to accurately model the rotation for short times scales.
An analytical study of the rotation of a rigid Venus model carried out
by Habibullin (1995) with
rather uncommun parametrization, showing that Venus rotates almost
uniformly with negligible libration harmonics. In the following, we
propose an alternative construction of a rigid Venus rotation model,
contradicting to some extent these last results. First we show the
characteristics of Venus with respect to the corresponding ones for the
Earth (Sect. 2). We explain the parametrization of the rotation of a rigid Venus using the Andoyer variables (Sect. 3). We then determine the reference points and planes to study the rotational dynamics of Venus (Sect. 4).
We give the equations of motion and the analytical developments that
allow us to obtain the precession and the nutation of the planet
(Sects. 5-7). Finally we give the precession, the tables of nutation and the polar motion of Venus (Sects. 8 and 9). We will discuss our results in Sect. 10.
In this study we make some approximations: we suppose that the relative
angular distance between the three poles (the poles of angular
momentum, of figure and of rotation) is very small as is the case for
the Earth. Moreover we solve a simplified system where the second order
of the potential does not appear. Last, we suppose that the small
difference between the mean longitude and the mean anomaly of the Sun
which corresponds to the slow motion of the perihelion, can be
considered as constant. In Sects. 3 to 10,
the orbital elements of Venus and their time dependence are required to
carry out our numerical calculations. In these sections we used the
mean orbital elements given by Simon et al. (1994). These elements are valid over 3000 years with a relative accuracy of 10-5. This prevents our theory being used in long term calculations, our domain of validity being 3000 years.
2 Venus characteristics
From the point of view of its physical characteristics, Venus can be considered as similar to sister of the Earth: the two planets have roughly the same size, mass and mean density (see Table 1).
Table 1: Comparison between the orbital (at J2000.0) and physical parameters of Venus necessary for our study and the corresponding ones for the Earth.
Despite this fact, the rotation of the two planets has with h
distinctive characteristics. First, the rotation of Venus is retrograde
with a period of 243 days. Furthermore the obliquity of Venus is very
small (2.63) compared to that of the Earth (23.44). Last, as
we will see in the following, the perturbating function for the
rotational motion of the planets depends on the dynamical flattening
![]() and on the triaxiality
and on the triaxiality
![]() .
The Earth has a fast rotation, therefore it has a relatively large dynamical flattening. Moreover its main moments of inertia A and B according to the X and Y axes can be considered equal when comparing them to C.
Thus the coefficient of triaxiality is very small with respect to the
coefficient of dynamical flattening. On the other hand, Venus has slow
rotation. Therefore its coefficient of dynamical flattening is less
important than that of the Earth but its coefficient of triaxility is
of the same order as the coefficient of dynamical flattening (see
Table 1). For these reasons,
it is important to account for the effect of triaxiality on the
rotation of Venus and it is interesting to see what difference will
emerge with respect to the Earth's rotation. In Table 1,
for the sake of clarity we have written the orbital parameters
at J2000.0. However throughout this paper the orbital parameters
are considered as a function of time (containing terms of first and
third order in time).
.
The Earth has a fast rotation, therefore it has a relatively large dynamical flattening. Moreover its main moments of inertia A and B according to the X and Y axes can be considered equal when comparing them to C.
Thus the coefficient of triaxiality is very small with respect to the
coefficient of dynamical flattening. On the other hand, Venus has slow
rotation. Therefore its coefficient of dynamical flattening is less
important than that of the Earth but its coefficient of triaxility is
of the same order as the coefficient of dynamical flattening (see
Table 1). For these reasons,
it is important to account for the effect of triaxiality on the
rotation of Venus and it is interesting to see what difference will
emerge with respect to the Earth's rotation. In Table 1,
for the sake of clarity we have written the orbital parameters
at J2000.0. However throughout this paper the orbital parameters
are considered as a function of time (containing terms of first and
third order in time).
3 Description of the motion of rotation and torque-free motion of Venus
In order to describe in the most complete way the rotation for a rigid model of Venus around its center of mass we need four axes: an inertial axis (arbitrairly chosen), the figure axis, the angular momentum axis, and the axis of rotation (see Fig. 1).
- As an inertial plane (0, X, Y) we choose the Venus osculating orbital plane at the epoch J 2000.0. We note
 ,
the intersection between this orbital plane and the mean equator of Venus at J2000.0, which is the reference point on the (0, X, Y)
plane. The choice of this plane is natural because we want to compute
the variation of the obliquity of Venus which is the angle between the
orbit of Venus and the plane normal to L.
,
the intersection between this orbital plane and the mean equator of Venus at J2000.0, which is the reference point on the (0, X, Y)
plane. The choice of this plane is natural because we want to compute
the variation of the obliquity of Venus which is the angle between the
orbit of Venus and the plane normal to L.
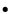
- The angular momentum axis of Venus is the axis directed along
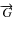 ,
with G the amplitude of the angular momentum. We denote
,
with G the amplitude of the angular momentum. We denote
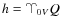 and I as respectively the longitude of the node with respect to
and I as respectively the longitude of the node with respect to
 and the inclination with respect to (0, X, Y). g and J are the longitude of the node and the obliquity of this same plane with respect to Q and to the equatorial plane.
and the inclination with respect to (0, X, Y). g and J are the longitude of the node and the obliquity of this same plane with respect to Q and to the equatorial plane.
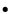
- The figure axis is the principal axis of Venus directed along Oz
and perpendicular to the equatorial plane. We choose it so that it
coincides with the axis of the largest moment of inertia C. We denote 0x
the axis that is pointed toward the origin meridian on Venus, which can
be defined in a conventional way. The axis of the figure is determined
with respect to the inertial plane (O,X,Y) through the Euler angles
hf, If. The parameter
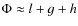 gives the position of the prime meridian (O,x) with respect to
gives the position of the prime meridian (O,x) with respect to
 .
.
- The axis of rotation is determined through the variables
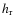 ,
,
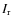 ,
i.e. the longitude of the node and the inclination with respect to
,
i.e. the longitude of the node and the inclination with respect to
 and the orbit of Venus at J2000.0. For the sake of clarity, these parameters are not represented in Fig. 1.
and the orbit of Venus at J2000.0. For the sake of clarity, these parameters are not represented in Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12174f1.ps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg38.png)
|
Figure 1: Relation between the Euler angles and the Andoyer variables. |
| Open with DEXTER | |
To describe the motion of the rotation of the rigid Earth, Kinoshita (1977) used Andoyer variables. Therefore we have introduced these variables to apply an analogous theory to Venus. The Andoyer variables (1923) are (see Fig. 1):
- L the component of the angular momentum along the 0z axis;
- H the component of the angular momentum along the 0Z axis;
- G the amplitude of the angular momentum of Venus;
- h the angle between
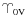 and the node Q between the orbital plane and the plane normal to the angular momentum;
and the node Q between the orbital plane and the plane normal to the angular momentum;
- g the angle between the node Q and the node P;
- l the angle between the origin meridian Ox and the node P;
where I, J are respectively the angle between the angular momentum axis and the inertial axis (O,Z), between the angular momentum axis and the figure axis.
By using the spherical trigonometry in the triangle (P, Q, R) (see Fig. 1), we determine the relations between the variables:
The angle J is supposed to be very small, so by neglecting the second order we obtain (Kinoshita 1977):
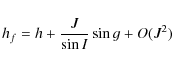
|
(4) |
hf and If correspond to the same definition as h and I, but for the axis of figure instead of the axis of angular momentum. The Hamiltonian for the torque-free motion of Venus corresponding to the kinetic energy is:
where A, B, C are the principal moments of inertia of Venus. Then the Hamiltonian equations are:
| = | 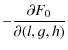
|
||
| = | 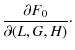
|
The Hamitonian is the full energy of the system. We see the Hamiltonian (7) corresponds to the kinetic energy.
4 Hamiltonian referred to a moving plane
This section is based on the pioneering work by Kinoshita (1977) for the rotation of the Earth. As a new reference plane, we choose the plane of the orbit of Venus at the date t
instead of the fixed orbital plane at J2000.0. The motion of this
new plane is due to the disturbances of the planets and it is defined
by two angles ![]() and
and ![]() which depend on time (cf Fig. 2). In Sect. 4.3 we will determine accuratly the numerical expressions of
which depend on time (cf Fig. 2). In Sect. 4.3 we will determine accuratly the numerical expressions of ![]() and
and ![]() .
.
| Figure 2: Motion of the orbit of Venus at the date t with respect to the same orbit at J2000.0. |
|
| Open with DEXTER | |
4.1 Canonical transformations
We denote
(G', H', L', g', h', l') as the new set of Andoyer canonical variables, wich play the same role as
(G, H, L, g, h, l) but with respect to the new moving reference plane instead of the inertial one. We denote I' as the angle between the plane normal to angular momentum and the orbit of Venus at t. To prove that the transformation is canonical, we have to determine a complementary function E depending on the new variables:
Because the tranformation does not depend on L,l these two variables do not appear in (8). In a given spherical triangle (A, B, C) one can show that the following differential relation stands (see appendix):
![\begin{figure}
\center
\includegraphics[width=8.5cm,clip]{12174f3.ps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg56.png)
|
Figure 3: Details of the spherical triangle M, N, O of Fig. 2 which represents the motion of the orbit of Venus at the date t with respect to the same orbit at J2000.0. |
| Open with DEXTER | |
| |
= | ||
| (10) |
Using the classical equation on the same triangle:
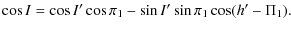
|
(11) |
Then, multiplying both sides by G and adding -
where
| E | = | ||
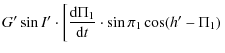
|
(13) | ||
![$\displaystyle \left. \frac{{\rm d}\pi_{1}}{{\rm d}t} \cdot \sin(h'-\Pi_{1})\right].$](/articles/aa/full_html/2009/45/aa12174-09/img68.png)
|
(14) |
We see that the time does not appear explicitly in
| Figure 4: Motion of the orbit of Venus at the date t with regard to the orbit at J2000.0. |
|
| Open with DEXTER | |
We have
![]() where
where
![]() is the so-called ``departure point'' for Venus, which constitutes our
new reference point. The choice of this point is justified by the
condition of non-rotation wich characterizes it, described in detail by
Guinot (1979) and Capitaine et al. (1986).
is the so-called ``departure point'' for Venus, which constitutes our
new reference point. The choice of this point is justified by the
condition of non-rotation wich characterizes it, described in detail by
Guinot (1979) and Capitaine et al. (1986).
![]() is the natural point to measure any motion along the moving plane.
is the natural point to measure any motion along the moving plane. ![]() is given by the equation:
is given by the equation:
with
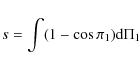
|
(16) |
To prove that this transformation is canonical, we can determine a function E' depending on the new variables such that:
Because the tranformation does not depend on G and g, these two variables do not appear in (17). Using Eq. (15) we have:
| (18) |
Thus:
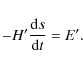
|
(19) |
Notice that s is a very small quantity, so that to a first approximation E' is negligible. Finally, we have a canonical transformation with K' as a new Hamiltonian of the system:
| K' | = | F0+E+E' | |
| = | 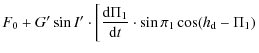
|
||
![$\displaystyle \left.\frac{{\rm d}\pi_{1}}{{\rm d}t} \cdot \sin(h_{\rm d}-\Pi_{1})\right].$](/articles/aa/full_html/2009/45/aa12174-09/img81.png)
|
(20) |
4.2 Ecliptic coordinates of the orbital pole and reference point

To calculate the angles that characterize the moving plane of the orbit of Venus at the date t, a reference point on the orbit of Venus at J2000.0 is needed. For the Earth the reference point is the vernal equinox
![]() which coincides with the ascending node of the ecliptic of J2000.0 with
the celestial equator of the same date. In a similar way we determine
the coordinates of the ascending node
which coincides with the ascending node of the ecliptic of J2000.0 with
the celestial equator of the same date. In a similar way we determine
the coordinates of the ascending node
![]() of the orbit of Venus at J2000.0 with respect to the equator of Venus at this same date. To calculate the coordinates of
of the orbit of Venus at J2000.0 with respect to the equator of Venus at this same date. To calculate the coordinates of
![]() we need
we need
![]() ,
the unit vector directed towards the orbital pole at t=0 defined by:
,
the unit vector directed towards the orbital pole at t=0 defined by:
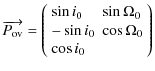
|
(21) |
where i0 is the angle between the orbit of Venus and the ecliptic at J2000.0.
| (22) |
The relative angular distance between the three poles (the poles of angular momentum, of figure and of rotation) is supposed to be very small, as is the case for the Earth. Throughout this study we will consider that the three poles coincide. So we denote
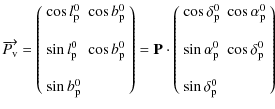
|
(23) |
where
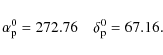
|
(24) |
To determine
where
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f5.ps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg102.png)
|
Figure 5: Relation between the venusian orbital pole and the venusian pole of angular momentum at the date t = 0. |
| Open with DEXTER | |
We finally obtain:
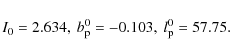
|
(27) |
4.3 Determination of  and
and 
Using the previous section we can now determine the angles ![]() and
and ![]() ,
which are respectively the longitude of the ascending node and the angle between the two orbital planes. The angle
,
which are respectively the longitude of the ascending node and the angle between the two orbital planes. The angle ![]() (see Fig. 4) is equal to the sum of the angle v and the angle v1 (see Fig. 6):
(see Fig. 4) is equal to the sum of the angle v and the angle v1 (see Fig. 6):
| Figure 6: Motion of the orbit of Venus at the date t with respect to the same orbit at J2000.0. |
|
| Open with DEXTER | |
| Figure 7: Motion of the orbit of Venus at the date t with regard to the same orbit at J2000.0. |
|
| Open with DEXTER | |
The relationship between ![]() ,
v, i0, it,
,
v, i0, it,
![]() and
and
![]() are derived from the spherical triangle (P,L,M):
are derived from the spherical triangle (P,L,M):
where i0, it are respectively the inclinations of the orbit of Venus at J2000.0 and at the date t with respect to the ecliptic at J2000.0.

where t is counted in thousands of Julian years starting from J2000.0. In this section we choose to carry our calculations to third order in time. The relationships between v1,
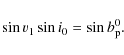
|
(32) |
Using the Eqs. (29)-(31) we obtain:
| |
= | 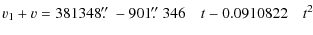
|
|
| (33) | |||
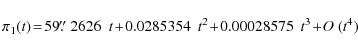
|
(34) |
where t is counted in thousands of Julian years starting from J2000.0. For the Earth we have:
| |
= | (35) | |
| |
||
| (36) |
The relative motion of the orbital plane at t with respect to the orbital plane at t = 0 is significantly greater for Venus than for the Earth. We used here the mean orbital elements given by Simon et al. (1994). These elements are valid over 3000 years with a relative accuracy of 10-5 and thus so too are our results
5 The Hamiltonian of the system and the equation of the motion of rotation
5.1 The equation of the motion of rotation
As explained in Sect. 4, the Hamiltonian related to the rotational motion of Venus is:
| (37) |
where
| U2 | = | 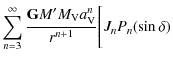
|
|
![$\displaystyle \left. \sum_{m=1}^n{P_{n}^m (\sin\delta)\cdot (C_{nm}\cos m\alpha +S_{nm} \sin m\alpha) }\right]$](/articles/aa/full_html/2009/45/aa12174-09/img127.png)
|
(39) |
where
The Hamiltonian equations are:
In the following the prime notations used above are omitted for the sake of clarity. Using the following equations seen in Sect. 3:
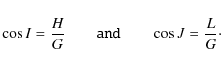
|
(43) |
The canonical Eqs. (41) and (42) become (Kinoshita 1977):
and
Replacing I by J in the precedent equation yields the variation of J. I is the obliquity and J is the small angle between the angular momentum axis and the figure axis. To solve the six differential Eqs. (41) and (42), Kinoshita (1977) used the Hori's method (1966). Here we solve a simplified system, i.e. the potential U2 does not appear in our study. To know the motion of precession and nutation of Venus, we have to solve only the following equations:
| |
= | ![$\displaystyle \frac{1}{G}\left[ \cot I \frac{{\rm d}G}{{\rm d}t}-\frac{1}{\sin I} \frac{{\rm d}H}{{\rm d}t}\right]$](/articles/aa/full_html/2009/45/aa12174-09/img139.png)
|
|
| = | ![$\displaystyle \frac{1}{G}\left[\frac{1}{\sin I} \frac{\partial K}{\partial h}-\cot I\frac{\partial K}{\partial g}\right]$](/articles/aa/full_html/2009/45/aa12174-09/img141.png)
|
(48) | |
| = | 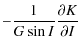
|
(49) |
where I characterizes the obliquity and h the motion of precession-nutation in longitude. These equations can also be written as:
Integrating these equations, we obtain the variations of the angles h and I:
5.2 Development of the disturbing function
The disturbing potential (38) is a functions of the modified Legendre polynomials
![]() and
and
![]() and of the planetocentric longitude
and of the planetocentric longitude ![]() and latitude
and latitude ![]() of
the Sun, with respect to the mean equator of Venus and with respect to
a meridian origin. From the ephemerides we only know the longitude
of
the Sun, with respect to the mean equator of Venus and with respect to
a meridian origin. From the ephemerides we only know the longitude ![]() and the latitude
and the latitude ![]() of the Sun with respect to the orbit of Venus. So we use the transformation described by Kinoshita (1977) and based on the Jacobi polynomials, which expresses
of the Sun with respect to the orbit of Venus. So we use the transformation described by Kinoshita (1977) and based on the Jacobi polynomials, which expresses ![]() and
and ![]() as a function of
as a function of ![]() and
and ![]() .
Applying this transformation we obtain:
.
Applying this transformation we obtain:
and
| |
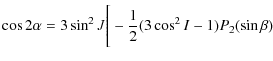
|
||
![$\displaystyle +\frac{1}{8}\sin^2 IP_{2}^2(\sin \beta)\cos 2(\lambda-h-\epsilon l)\Bigg]$](/articles/aa/full_html/2009/45/aa12174-09/img167.png)
|
|||
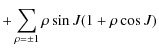
|
|||
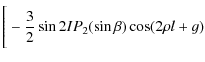
|
|||
![$\displaystyle P_{2}^2(\sin \beta)\cos(2\lambda-2h-2\rho\epsilon l-\epsilon g)\Bigg]$](/articles/aa/full_html/2009/45/aa12174-09/img173.png)
|
Using (40) we obtain:



where



Assuming that the angle J is small (
and
Thus the disturbing potential is simplified in the following form:
6 Determination of the precession and the nutation of Venus
Replacing U1 in (52) and (53) we obtain:
Table 2:
Development of
![]() of Venus (the corresponding values for the Earth are in square brackets). t is counted in Julian centuries.
of Venus (the corresponding values for the Earth are in square brackets). t is counted in Julian centuries.
| (61) |
Finally we have the following equations:
and:
where
| W1 | = | 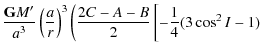
|
|
![$\displaystyle \left. \left. \frac{3}{4}\sin^2 I \cos 2 (\lambda-h)\right]\right)$](/articles/aa/full_html/2009/45/aa12174-09/img224.png)
|
(66) |
| W2 | = | 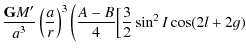
|
|
![$\displaystyle \cos 2(\lambda-h-\epsilon l-\epsilon g)\Big]\bigg).$](/articles/aa/full_html/2009/45/aa12174-09/img226.png)
|
(67) |
We adopt the following notations:
As the rotation of Venus is retrograd the convention used is not the same as IAU to the Earth.
7 Development of the disturbing function
Considering the level of accuracy and the time interval involved (3000 y), truncating the function e to first order in time is a sufficient approximation. Therefore we take the eccentricity of Venus from Simon et al. (1994) as:
| e=0.0067719164-0.0004776521t. | (70) |
7.1 Terms depending on the dynamical flattening
To solve the Eqs. (62) and (63) which give the nutation coming from the dynamical flattening, it is necessary to develop
![]() and
and
![]() with respect to time (i.e. with respect to the mean anomaly and the mean longitude of Sun). Using Kepler's equation:
with respect to time (i.e. with respect to the mean anomaly and the mean longitude of Sun). Using Kepler's equation:
where u is the eccentric anomaly, e the eccentricity, n the mean motion and M the mean anomaly of Venus, we have the following classical development:
For comparison we also give the corresponding coefficients of the development of the Earth (see Table 2).
We have the following definition:
| (73) |
where
From the trigonometric equation:
| (75) |
we obtain:
Using the developments (74) and (76) and the classical trigonometric relationships we obtain a development of
The coefficients of this development are given in Table 3.
Table 3:
Development of
![]() of Venus (the corresponding values for the Earth are in square brackets). t is counted in Julian centuries.
of Venus (the corresponding values for the Earth are in square brackets). t is counted in Julian centuries.
The periods in Tables 2 and 3 have been computed through the mean elements of the planets given by the ephemerides VSOP87 of Simon et al (1994). Because the eccentricity of Venus is smaller than the eccentricity of the Earth, the coefficients of the development for Venus are smaller than the corresponding ones for the Earth, except for the leading one in Table 3.
7.2 Terms depending on the triaxiality
To solve the Eqs. (64) and (65) it is necessary to develop
![]() ,
(
,
(
![]() and
and
![]() with respect to the mean anomaly M, the mean longitude LS of Sun and to the angle
with respect to the mean anomaly M, the mean longitude LS of Sun and to the angle
![]() according to (6). Using classical trigonometric equations and developments similar to those used in Sect. 7.1, we obtain the following:
according to (6). Using classical trigonometric equations and developments similar to those used in Sect. 7.1, we obtain the following:
These are given in Tables 4-6.
Table 4:
Development of
![]() of Venus. t is counted in Julian centuries.
of Venus. t is counted in Julian centuries.
Table 5:
Development of
![]() of Venus. t is counted in Julian centuries.
of Venus. t is counted in Julian centuries.
Table 6:
Development of
![]() of Venus. t is counted in Julian centuries.
of Venus. t is counted in Julian centuries.
We note that the coefficients in Tables 5 and 6 are the same as the coefficients of Table 3,
because the calculations are similar and they do not depend on the
frequency associated with each argument, but only on the eccentricity
of Venus. Nevertheless the corresponding periods are different because
their calculation includes the argument ![]() ,
the sideral rotation of Venus given by:
,
the sideral rotation of Venus given by:
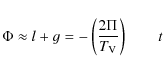
|
(81) |
where
8 Precession and nutation which depend on the longitude and obliquity
In the following, we calculate the precession and the nutation of Venus depending on both the dynamical flattening and the dynamical triaxiality.
8.1 Precession and the nutation of Venus depending on the dynamical flattening
According to (62) and (63) we compute the precession-nutation in longitude (
![]() )
and obliquity (
)
and obliquity (
![]() )
due to the dynamical flattening:
)
due to the dynamical flattening:
where
![$\displaystyle \overline{W_{1}}=\left(\frac{a}{r}\right)^3\left[-\frac{1}{12}(3\cos ^2 I-1)-\frac{1}{4} \sin^2 I \cos 2 (\lambda-h)\right].$](/articles/aa/full_html/2009/45/aa12174-09/img319.png)
|
(84) |
![\begin{displaymath}K_{s}=3\frac{{\tt\textbf{G}}M'}{G a^3}\Bigl[\frac{2C-A-B}{2}\Bigr]\cdot
\end{displaymath}](/articles/aa/full_html/2009/45/aa12174-09/img320.png)
|
(85) |
Using the third Kepler's law we obtain:
![\begin{displaymath}K_{s}=3\frac{n^2}{\omega}\left[\frac{2C-A-B}{2C}\right]=\frac{3n^2}{\omega} H_{\rm V}
\end{displaymath}](/articles/aa/full_html/2009/45/aa12174-09/img321.png)
|
(86) |
where n is the mean motion of Venus. The dynamical flattening, defined as
| (87) |
with the values of A, B, C adopted in Sect. 10 and that of the dynamical flattening given which is deduced directly from them (given in Table 1), we find:
| (88) |
In the case of the Earth, the scaling factor due to the gravitational influence of the Sun is (Souchay et al. 1999):
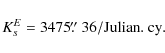
|
(89) |
Then we have the following result:
Thus for Venus, the value of the constant of the precession-nutation due to the Sun is roughly 2.6 times bigger that the corresponding one for the Earth. Through the development done previously (cf Sect. 7) and according to the conventional notations (68) and (69), we get the precession and the nutation of Venus depending on its dynamical flattening. We will see in the following sub-section that the triaxiality does not contribute to the precession. So we obtain the following result for the precession:
where t is counted in Julian centuries. The nutation coefficients in longitude and in obliquity are given respectively in Tables 7 and 8. All our results are given with respect to the moving orbit at the date t.
Table 7:
![]() :
nutation coefficients in longitude of Venus depending on its dynamical flattening.
:
nutation coefficients in longitude of Venus depending on its dynamical flattening.
Table 8:
![]() :
nutation coefficients in obliquity of Venus depending on its dynamical flattening.
:
nutation coefficients in obliquity of Venus depending on its dynamical flattening.
8.2 Precession and nutation of Venus depending on dynamical triaxiality
Starting from (64) and (65), we can compute the nutations
![]() and
and
![]() respectively in longitude and in obliquity, due to the triaxiality of Venus:
respectively in longitude and in obliquity, due to the triaxiality of Venus:
where
| |
= | 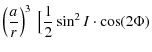
|
|
| (95) |
![\begin{displaymath}K_{a}=3\frac{{\tt\textbf{G}}M'}{G a^3}\Bigl[\frac{A-B}{4}\Bigr]
\end{displaymath}](/articles/aa/full_html/2009/45/aa12174-09/img348.png)
|
(96) |
where M',
![\begin{displaymath}K_{a}=3\frac{n^2}{\omega}\left[\frac{A-B}{4C}\right]\cdot
\end{displaymath}](/articles/aa/full_html/2009/45/aa12174-09/img349.png)
|
(97) |
The triaxiality, defined as
| (98) |
Then, with the value of the triaxiality (given in Table 1), we get:
| (99) |
In the case of the Earth, the scaling factor due to the gravitational influence of the Sun is (Souchay et al. 1999):
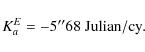
|
(100) |
Thus we have the following ratios:
This result shows that the coefficients of nutation due to the triaxility are considerably larger for Venus than for the Earth. Thanks to the development done previously (cf. Sect. 4.1) and according to the Eqs. (92) and (93), we get the nutation of Venus depending on its triaxiality. The nutation coefficients in longitude and in obliquity are given respectively in Tables 9 and 10. All our results are given with respect to the moving orbit at the date t.
Table 9:
![]() :
nutation coefficient in longitude of Venus depending on its triaxiality.
:
nutation coefficient in longitude of Venus depending on its triaxiality.
Table 10:
![]() :
nutation coefficients in obliquity of Venus depending on its triaxiality.
:
nutation coefficients in obliquity of Venus depending on its triaxiality.
For Venus, the largest nutation coefficient in longitude for the terms depending on its triaxiality has a 0
![]() 6 amplitude and the largest nutation coefficient in obliquity has a 0
6 amplitude and the largest nutation coefficient in obliquity has a 0
![]() 03 amplitude. Their period corresponds to half the period of rotation of the planets, 121.5 d.
03 amplitude. Their period corresponds to half the period of rotation of the planets, 121.5 d.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f8.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg369.png)
|
Figure 8: The precession and the nutation of Venus in longitude for a 4000 day time span. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f9.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg370.png)
|
Figure 9: The nutation in longitude of Venus depending on its dynamical flattening (cyan) and depending on its triaxiality (blue) for a 4000 day time span, from J2000.0. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f10.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg371.png)
|
Figure 10: The nutation in obliquity of Venus depending on its dynamical flattening (cyan) and depending on its triaxiality (blue) for a 4000 day time span, from J2000.0. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f11.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg372.png)
|
Figure 11: The nutation of Venus in longitude for a 4000 day time span, from J2000.0 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f12.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg373.png)
|
Figure 12: The nutation of Venus in obliquity for a 4000 day time span, from J2000.0. |
| Open with DEXTER | |
From the Tables 7 to 10, we choose to calculate numerically from their analytical expression the precession-nutation with respect to t, over a period of 4000 d. Figure 8 represents the combined precession and nutation of Venus in longitude. The periodic part stands for the nutation and the linear part for the precession (see (91)). In Fig. 9 and Fig. 10, we represent the nutation of Venus respectively in longitude and in obliquity depending on its dynamical flattening (black curve) and its triaxiality (red curve). In Figs. 11 and 12, we represent the nutation respectively in longitude and in obliquity when combining the two components above. In Figs. 8 to 12 we choose the 4000 d time span to clearly see the leading oscillations. Recall that our study is valid over 3000 years. The nutation of Venus depending on its triaxiality is dominated by a sinusoid with a period of 121.51 d and another one with a period of 58.37 d. On the other hand the nutation depending on its dynamical flattening is largely dominated by a single sinusoid with a period of 112.35 d. We can also remark (Figs. 9 and 10) that the nutation coefficients of Venus depending on its triaxiality are of the same order of magnitude as the nutation coefficients depending on its dynamical flattening, whereas for the Earth they are small and negligible in comparison (Kinoshita 1997; Souchay et al. 1999). Two reasons explain this:
- the ratio of scaling factors is
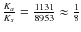 for Venus, whereas for the Earth it is two orders of magnitude smaller:
for Venus, whereas for the Earth it is two orders of magnitude smaller:
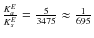
- the frequency of the sidereal angle
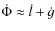 which enters in the denominator during the integrations in (92) and (93) is roughly 243 times larger for the Earth than for Venus.
which enters in the denominator during the integrations in (92) and (93) is roughly 243 times larger for the Earth than for Venus.
9 Motion of the pole of Venus in space
From the previous section, it is possible to describe the motion of the
pole of Venus with respect to its orbital plane at the date t. The rectangular coordinates
![]() of the pole are given by:
of the pole are given by:
The precession in longitude
I0 is the nominal value of the obliquity:
| (104) |
Replacing
From (103) we directly determine the period of precession of Venus, i.e.
![]() years. It is slightly longer than the period of precession of the Earth, i.e. 25712.4 y (Bretagnon et al. 1997).
Notice that in the case of the Earth, the Moon contributes
roughly 2/3 and the Sun 1/3 to the precession rate. In the
case of Venus, only the Sun contributes significantly to the precession
rate. However, as we have shown in Sect. 8,
this solar contribution is roughly 2.5 times greater than the
corresponding one for the Earth. This explains why the periods of
precession are rather equivalent.
years. It is slightly longer than the period of precession of the Earth, i.e. 25712.4 y (Bretagnon et al. 1997).
Notice that in the case of the Earth, the Moon contributes
roughly 2/3 and the Sun 1/3 to the precession rate. In the
case of Venus, only the Sun contributes significantly to the precession
rate. However, as we have shown in Sect. 8,
this solar contribution is roughly 2.5 times greater than the
corresponding one for the Earth. This explains why the periods of
precession are rather equivalent.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f13.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg384.png)
|
Figure 13: (X,Y) motion of Venus polar axis in space for a one century time span. |
| Open with DEXTER | |
10 Numerical values of
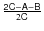 and
and
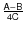 and comparison of results
and comparison of results
From the various calculations done in the previous sections, we know
that the accuracy in the determination of the precession rate
![]() and of the coefficients of nutation depends directly on the quality of determination of the dynamical ellipticity
and of the coefficients of nutation depends directly on the quality of determination of the dynamical ellipticity
![]() and of the triaxiality
and of the triaxiality
![]() .
Therefore for this purpose it is crucial to obtain accurate values of the moments of inertia. The value of ratio
.
Therefore for this purpose it is crucial to obtain accurate values of the moments of inertia. The value of ratio
![]() is inperfectly known. Kozlovskaya (1966) obtained a value in the [0.321;0.360] interval, Shen and Zhang (1988) in the [0.321;0.350] one and Yoder(1995)
in the [0.331; 0.341] one. Williams (private communication) gives the
following values relative to the differences of the moments of inertia:
is inperfectly known. Kozlovskaya (1966) obtained a value in the [0.321;0.360] interval, Shen and Zhang (1988) in the [0.321;0.350] one and Yoder(1995)
in the [0.331; 0.341] one. Williams (private communication) gives the
following values relative to the differences of the moments of inertia:
| |
= | ||
| = | (105) |
with these values and adopting
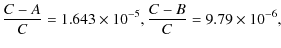
|
|||
| (106) |
All our calculations in this paper have been done with these values. When studying the rotation of Venus, Habbibulin (1995) has taken
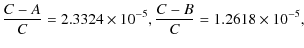
|
|||
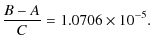
|
(107) |
In Table 11 we compare our results with those obtained by directly using the values of Habbibulin (1995) for the physical parameters of Venus, thus showing large differences.
Table 11: Comparison between our results computed with the recent values of the moment of inertia and those obtained with the values of Habbibulin et al. (1995).
Table 11 shows that the
values of the moments of inertia are crucial for our computations. The
comparison with the final results computed by Habbibulin (1995)
is not possible because in his paper different angles, parametrisation
and more complex developments were used. In another study, Zhang (1988) found a precession rate of
![]() /cy
corresponding to a period of 16 555 years. Altough no precise
information could be extracted from this paper, the difference is
probably due to different values of the moments of inertia. What we
highlight here is that different values of moment of inertia yield
fairly different results for the precession and the nutation as shown
in Table 11.
/cy
corresponding to a period of 16 555 years. Altough no precise
information could be extracted from this paper, the difference is
probably due to different values of the moments of inertia. What we
highlight here is that different values of moment of inertia yield
fairly different results for the precession and the nutation as shown
in Table 11.
11 Conclusion and prospects
In this paper we investigated by the rotation of Venus. We adopted a
well suited theory of the rotation of a rigid body set up by Kinoshita (1977) and developed in full detail by Souchay et al. (1999)
for the Earth. In a first step we defined the reference frames to the
various polar axes of the planet (axis of angular momentum, rotation
axis, figure axis) and on its moving orbital plane. We have also given
in full detail the parametrization of Venus rotation starting from the
set of Andoyer canonical variables with respect to the moving orbital
plane. In particular we have determined precisely the motion of the
orbit of Venus at t with respect to the orbit at J2000.0, through the parameters ![]() and
and ![]() ,
for which we have given polynomial expressions. Moreover we have checked the value of the Venus obliquity (263).
,
for which we have given polynomial expressions. Moreover we have checked the value of the Venus obliquity (263).
Then we calculated the disturbing function due to the gravitational
interaction with the Sun. Applying Kinoshita's Hamiltonian analytical
developments, we calculated the precession constant of Venus, with a
precision and an accuracy better than in previous works (Habillulin 1995; Zhang 1988). Our value for the precession in longitude is
![]() .
which is more than two times larger than the corresponding term for the Earth due to the Sun (
.
which is more than two times larger than the corresponding term for the Earth due to the Sun (
![]() /cy) and slightly smaller than the combined effect of the Moon and of the Sun for the Earth (
/cy) and slightly smaller than the combined effect of the Moon and of the Sun for the Earth (
![]() ). We have shown that the effect of the very small value of the dynamical ellipticity of Venus (
). We have shown that the effect of the very small value of the dynamical ellipticity of Venus (
![]() ),
which should directly lower the amplitude of its precession and
nutation, is more than fully compensated for by its very slow
retrograde rotation. Moreover, one of the specificities of Venus is
that its triaxiality (
),
which should directly lower the amplitude of its precession and
nutation, is more than fully compensated for by its very slow
retrograde rotation. Moreover, one of the specificities of Venus is
that its triaxiality (
![]() )
is of the same order as its dynamical ellipticity (see value above),
unlike what happens for the Earth for which it is considerably smaller.
Consequently, we have performed a full calculation of the coefficients
of nutation of Venus due to the Sun and presented the complete tables
of nutation in longitude (
)
is of the same order as its dynamical ellipticity (see value above),
unlike what happens for the Earth for which it is considerably smaller.
Consequently, we have performed a full calculation of the coefficients
of nutation of Venus due to the Sun and presented the complete tables
of nutation in longitude (
![]() )
and obliquity (
)
and obliquity (
![]() )
due both to the dynamical ellipticity and the triaxiality.These tables
have never been presented in previous works. We think that this work
can be a starting point for further studies dealing with Venus
rotation, for which it has set up the theoretical foundation
(parametrization, equations of motion etc...), such as a study of
precession-nutation over a long time scale, the calculation of Oppolzer
terms, the effects of the atmosphere.
)
due both to the dynamical ellipticity and the triaxiality.These tables
have never been presented in previous works. We think that this work
can be a starting point for further studies dealing with Venus
rotation, for which it has set up the theoretical foundation
(parametrization, equations of motion etc...), such as a study of
precession-nutation over a long time scale, the calculation of Oppolzer
terms, the effects of the atmosphere.
12 Appendix
Demonstration of Eq. (9):
Derivating the following classical relation:
we obtain:
| |
= | ||
| (108) |
Dividing by -
In the spherical triangle A, B, C the following equations holds:

Thus:
| |
= | ||
| |
= | ||
Replacing in (109), we obtain (9).
References
- Andoyer, H. 1923, Cours de mécanique céleste, vol. 1 (Paris: Gauthier-Villars)
- Bretagnon, P., Rocher, P., & Simon, J. L. 1997, A&A, 319, 305 [NASA ADS]
- Capitaine, N., Souchay, J., & Guinot, B. 1986, Celest. Mech., 39, 283 [NASA ADS] [CrossRef]
- Carpenter, R. L. 1964, AJ, 69, 2 [NASA ADS] [CrossRef]
- Correia, A. C. M., & Laskar J. 2001, Nature, 411, 767 [NASA ADS] [CrossRef]
- Correia, A. C. M., & Laskar, J. 2003, Icarus, 163, 24 [NASA ADS] [CrossRef]
- Correia, A. C. M., Laskar, J., & de Surgy O. N. 2003, Icarus, 163, 1 [NASA ADS] [CrossRef]
- Dobrovolskis, A. R. 1980, Icarus, 41, 18 [NASA ADS] [CrossRef]
- Goldreich, P., & Peale, S. J. 1970, AJ, 75, 273 [NASA ADS] [CrossRef]
- Goldstein, R. M. 1964, AJ, 69, 12 [NASA ADS] [CrossRef]
- Guinot, B. 1979, Time and the Earth's Rotation, 82, 7 [NASA ADS]
- Habibullin, S. T. 1995, Earth Moon and Planets, 71, 43 [NASA ADS] [CrossRef]
- Hori, G. 1966, PASJ, 18, 287 [NASA ADS]
- Kinoshita, H. 1977, Celest. Mech., 15, 277 [NASA ADS] [CrossRef]
- Kozlovskaya, S. V. 1966, AZh, 43, 1081 [NASA ADS]
- Lago, B., & Cazenave, A. 1979, Moon and Planets, 21, 127 [NASA ADS] [CrossRef]
- McCue, J., & Dormand, J. R. 1993, Earth Moon and Planets, 63, 209 [NASA ADS] [CrossRef]
- Simon, J. L., Bretagnon, P., Chapront, J., et al. 1994, A&A, 282, 663 [NASA ADS]
- Souchay, J., Loysel, B., Kinoshita, H., et al. 1999, A&AS, 135, 111 [NASA ADS] [CrossRef] [EDP Sciences]
- Yoder, C. F. 1995, Icarus, 117, 250 [NASA ADS] [CrossRef]
- Shen, M., & Zhang, C. Z. 1988, Earth Moon and Planets, 41, 289 [NASA ADS] [CrossRef]
- Williams, B. G., & Mottinger, N. A. 1983, Icarus, 56, 578 [NASA ADS] [CrossRef]
- Zhang, C.-Z. 1988, Chinese Astron. Astrophys., 12, 38 [NASA ADS] [CrossRef]
All Tables
Table 1: Comparison between the orbital (at J2000.0) and physical parameters of Venus necessary for our study and the corresponding ones for the Earth.
Table 2:
Development of
![]() of Venus (the corresponding values for the Earth are in square brackets). t is counted in Julian centuries.
of Venus (the corresponding values for the Earth are in square brackets). t is counted in Julian centuries.
Table 3:
Development of
![]() of Venus (the corresponding values for the Earth are in square brackets). t is counted in Julian centuries.
of Venus (the corresponding values for the Earth are in square brackets). t is counted in Julian centuries.
Table 4:
Development of
![]() of Venus. t is counted in Julian centuries.
of Venus. t is counted in Julian centuries.
Table 5:
Development of
![]() of Venus. t is counted in Julian centuries.
of Venus. t is counted in Julian centuries.
Table 6:
Development of
![]() of Venus. t is counted in Julian centuries.
of Venus. t is counted in Julian centuries.
Table 7:
![]() :
nutation coefficients in longitude of Venus depending on its dynamical flattening.
:
nutation coefficients in longitude of Venus depending on its dynamical flattening.
Table 8:
![]() :
nutation coefficients in obliquity of Venus depending on its dynamical flattening.
:
nutation coefficients in obliquity of Venus depending on its dynamical flattening.
Table 9:
![]() :
nutation coefficient in longitude of Venus depending on its triaxiality.
:
nutation coefficient in longitude of Venus depending on its triaxiality.
Table 10:
![]() :
nutation coefficients in obliquity of Venus depending on its triaxiality.
:
nutation coefficients in obliquity of Venus depending on its triaxiality.
Table 11: Comparison between our results computed with the recent values of the moment of inertia and those obtained with the values of Habbibulin et al. (1995).
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12174f1.ps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg38.png)
|
Figure 1: Relation between the Euler angles and the Andoyer variables. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2: Motion of the orbit of Venus at the date t with respect to the same orbit at J2000.0. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\center
\includegraphics[width=8.5cm,clip]{12174f3.ps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg56.png)
|
Figure 3: Details of the spherical triangle M, N, O of Fig. 2 which represents the motion of the orbit of Venus at the date t with respect to the same orbit at J2000.0. |
| Open with DEXTER | |
| In the text | |
| |
Figure 4: Motion of the orbit of Venus at the date t with regard to the orbit at J2000.0. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f5.ps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg102.png)
|
Figure 5: Relation between the venusian orbital pole and the venusian pole of angular momentum at the date t = 0. |
| Open with DEXTER | |
| In the text | |
| |
Figure 6: Motion of the orbit of Venus at the date t with respect to the same orbit at J2000.0. |
| Open with DEXTER | |
| In the text | |
| |
Figure 7: Motion of the orbit of Venus at the date t with regard to the same orbit at J2000.0. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f8.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg369.png)
|
Figure 8: The precession and the nutation of Venus in longitude for a 4000 day time span. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f9.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg370.png)
|
Figure 9: The nutation in longitude of Venus depending on its dynamical flattening (cyan) and depending on its triaxiality (blue) for a 4000 day time span, from J2000.0. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f10.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg371.png)
|
Figure 10: The nutation in obliquity of Venus depending on its dynamical flattening (cyan) and depending on its triaxiality (blue) for a 4000 day time span, from J2000.0. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f11.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg372.png)
|
Figure 11: The nutation of Venus in longitude for a 4000 day time span, from J2000.0 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f12.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg373.png)
|
Figure 12: The nutation of Venus in obliquity for a 4000 day time span, from J2000.0. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12174f13.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12174-09/Timg384.png)
|
Figure 13: (X,Y) motion of Venus polar axis in space for a one century time span. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



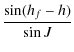
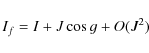
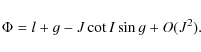
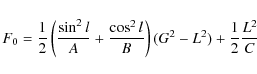
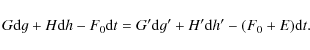
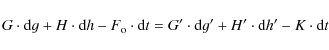
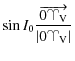
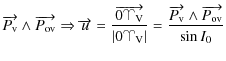
![\begin{displaymath}
U_{1} = \frac{{\tt\textbf{G}} M'}{r^3}\left[\frac{2C-A-B}{2}...
...elta) + \frac{A-B}{4}P_2^{2} (\sin \delta) \cos 2\alpha\right]
\end{displaymath}](/articles/aa/full_html/2009/45/aa12174-09/img125.png)
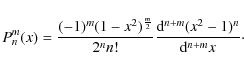
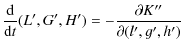
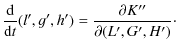
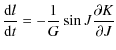
![$\displaystyle \frac{{\rm d}g}{{\rm d}t}= \frac{1}{G}\left[ \cot J \frac{\partial K}{\partial J}+ \cot I\frac{\partial K}{\partial I}\right]$](/articles/aa/full_html/2009/45/aa12174-09/img136.png)
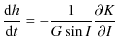
![$\displaystyle \frac{1}{G}\left[\frac{1}{\sin I} \frac{\partial K}{\partial h}-\cot I\frac{\partial K}{\partial g}\right]\cdot$](/articles/aa/full_html/2009/45/aa12174-09/img140.png)
![$\displaystyle = \frac{1}{G}\left[ \cot I\frac{{\rm d}G}{{\rm d}t}-\frac{1}{\sin I} \frac{{\rm d}H}{{\rm d}t}\right]$](/articles/aa/full_html/2009/45/aa12174-09/img144.png)
![$\displaystyle = \frac{1}{G}\left[\frac{1}{\sin I} \frac{\partial U_{1}}{\partial h}-\cot I\frac{\partial U_{1}}{\partial g}\right]$](/articles/aa/full_html/2009/45/aa12174-09/img145.png)
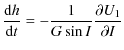
![$\displaystyle \Delta I =\frac{1}{G}\left[\frac{1}{\sin I} \frac{\partial}{\part...
... \int U_{1}{\rm d}t-\cot I\frac{\partial}{\partial g}\int U_{1} {\rm d}t\right]$](/articles/aa/full_html/2009/45/aa12174-09/img147.png)
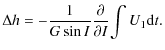
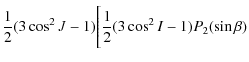
![$\displaystyle \frac{1}{2} \sin 2I P_{2}^1(\sin \beta)\cos 2(\lambda - h)\Bigg]$](/articles/aa/full_html/2009/45/aa12174-09/img155.png)
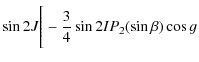
![$\displaystyle P_{2}^2(\sin \beta)\cos(2\lambda-2h-\epsilon g)\Bigg]+\sin^2 J$](/articles/aa/full_html/2009/45/aa12174-09/img160.png)
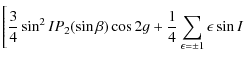
![$\displaystyle \sum_{\epsilon =\pm 1}(1+\epsilon \cos I)^2P_{2}^2(\sin \beta)\cos 2(\lambda-h-\epsilon g)\Bigg]$](/articles/aa/full_html/2009/45/aa12174-09/img163.png)
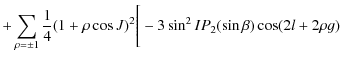
![$\displaystyle P_{2}^2(\sin\beta)\cos 2(\lambda-h-\rho\epsilon l- \epsilon g)\Bigg].$](/articles/aa/full_html/2009/45/aa12174-09/img178.png)
![$\displaystyle P_{2}(\sin \delta) = \left[-\frac{1}{4}(3\cos ^2 I-1)-\frac{3}{4}\sin^2 I \cos 2 (\lambda-h)\right]$](/articles/aa/full_html/2009/45/aa12174-09/img187.png)
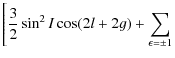
![$\displaystyle \times\!\left.\frac{3}{4}(1 \!+\! \epsilon \cos I)^2\cdot \cos 2(\lambda-h\!-\!\epsilon l\!-\!\epsilon g)\right].$](/articles/aa/full_html/2009/45/aa12174-09/img190.png)
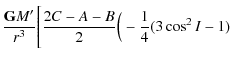
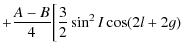
![$\displaystyle +\sum_{\epsilon=\pm 1}\frac{3}{4}(1+\epsilon \cos I)^2\cdot \cos 2(\lambda-h-\epsilon l-\epsilon g)\bigg]\Bigg].$](/articles/aa/full_html/2009/45/aa12174-09/img194.png)
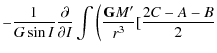
![$\displaystyle \cos 2(\lambda-h-\epsilon l-\epsilon g)\Big]\bigg]\Bigg){\rm d}t$](/articles/aa/full_html/2009/45/aa12174-09/img201.png)
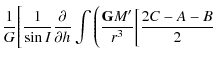
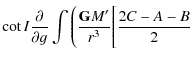
![$\displaystyle \cos 2(\lambda-h-\epsilon l-\epsilon g)\Big]\Bigg]\Bigg){\rm d}t\Bigg].$](/articles/aa/full_html/2009/45/aa12174-09/img205.png)
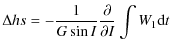
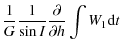
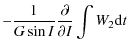
![$\displaystyle \frac{1}{G}\Bigg[\frac{1}{\sin I} \frac{\partial}{\partial h} \int W_{2} {\rm d}t -\cot I \frac{\partial}{\partial g} \int W_{2} {\rm d}t \Bigg]$](/articles/aa/full_html/2009/45/aa12174-09/img222.png)
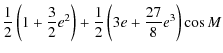
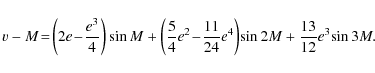
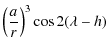
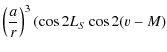
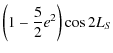
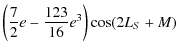
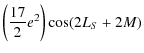
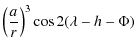
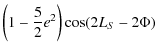
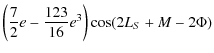
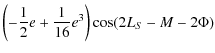
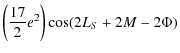
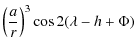
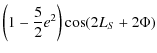
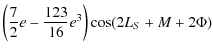
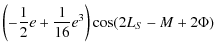
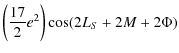
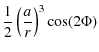
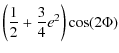
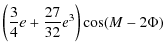
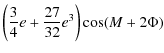
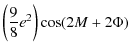
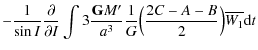
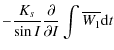
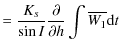
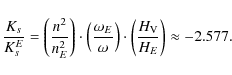
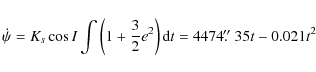
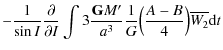
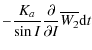
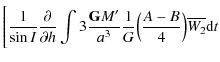
![$\displaystyle \cot I \frac{\partial}{\partial g} \int 3 \frac{{\tt\textbf{G}}M'}{a^3}\frac{1}{G}\frac{A-B}{4} \overline {W_{2}} {\rm d}t \Bigg]$](/articles/aa/full_html/2009/45/aa12174-09/img341.png)