| Issue |
A&A
Volume 507, Number 3, December I 2009
|
|
|---|---|---|
| Page(s) | 1313 - 1326 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912115 | |
| Published online | 01 October 2009 | |
A&A 507, 1313-1326 (2009)
The Hubble sequence: just a vestige of merger events?![[*]](/icons/foot_motif.png)
F. Hammer1 - H. Flores1 - M. Puech1 - Y. B. Yang1,2 - E. Athanassoula3 - M. Rodrigues1 - R. Delgado1
1 - Laboratoire Galaxies Étoiles Physique et
Instrumentation, Observatoire de Paris, CNRS-UMR 8111, 5 place Jules
Janssen, 92195 Meudon, France
2 -
National Astronomical Observatories, Chinese Academy of Sciences,
20A Datun Road, Chaoyang District, Beijing 100012, PR China
3 -
Laboratoire d'Astrophysique de Marseille, Observatoire Astronomique de
Marseille Provence, Technopole de l'Étoile - Site de Chateau-Gombert,
38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
Received 19 March 2009 / Accepted 2 September 2009
Abstract
We investigate whether the Hubble sequence can be reproduced by the relics of merger events. We verify that, at
![]() =
0.65, the abundant population of anomalous starbursts -
i.e. with peculiar morphologies and abnormal kinematics - is
mainly linked to the local spirals. Their morphologies are dominated by
young stars and are intimately related to their ionised-gas kinematics.
We show that both morphologies and kinematics can be reproduced by
using gas modelling from Barnes' (2002, MNRAS, 333, 481) study of major
mergers. Their gas content may be indirectly evaluated by assuming that
distant starbursts follow the Kennicutt-Schmidt relation: the median
gas fraction is found to be 31%. Using our modelling to estimate the
gas-to-star transformation during a merger, we identify the gas
fraction in the progenitors to be generally above 50%. All distant
and massive starbursts can be distributed along a temporal sequence
from the first passage to the nuclei fusion and then to the disk
rebuilding phase. This later phase has been recently illustrated for
J033245.11-274724.0, a distant compact galaxy dominated by a red,
dust-enshrouded disk. This active production of rebuilt disks is in
excellent agreement with model predictions for gaseous rich encounters.
It confirms that the rebuilding spiral disk scenario -
a strong and recent reprocessing of most disks by major
mergers - is possibly an important channel for the formation of
present-day disks in grand-design spirals. Because half of the
present-day spirals had peculiar morphologies and anomalous kinematics
at
=
0.65, the abundant population of anomalous starbursts -
i.e. with peculiar morphologies and abnormal kinematics - is
mainly linked to the local spirals. Their morphologies are dominated by
young stars and are intimately related to their ionised-gas kinematics.
We show that both morphologies and kinematics can be reproduced by
using gas modelling from Barnes' (2002, MNRAS, 333, 481) study of major
mergers. Their gas content may be indirectly evaluated by assuming that
distant starbursts follow the Kennicutt-Schmidt relation: the median
gas fraction is found to be 31%. Using our modelling to estimate the
gas-to-star transformation during a merger, we identify the gas
fraction in the progenitors to be generally above 50%. All distant
and massive starbursts can be distributed along a temporal sequence
from the first passage to the nuclei fusion and then to the disk
rebuilding phase. This later phase has been recently illustrated for
J033245.11-274724.0, a distant compact galaxy dominated by a red,
dust-enshrouded disk. This active production of rebuilt disks is in
excellent agreement with model predictions for gaseous rich encounters.
It confirms that the rebuilding spiral disk scenario -
a strong and recent reprocessing of most disks by major
mergers - is possibly an important channel for the formation of
present-day disks in grand-design spirals. Because half of the
present-day spirals had peculiar morphologies and anomalous kinematics
at
![]() = 0.65, they could indeed have been in major merger phases 6 Gyr ago, and almost all at
= 0.65, they could indeed have been in major merger phases 6 Gyr ago, and almost all at ![]() .
It is time now to study in detail the formation of spiral disks and of
their substructures, including bulge, disks, arms, bars and rings that
may mainly originate from instabilities created during the last major
merger. Many galaxies also show a helicoidal structure, which is
probably due to a central torque, and seems to play an important role
in regulating the angular momentum of the newly-formed disks.
.
It is time now to study in detail the formation of spiral disks and of
their substructures, including bulge, disks, arms, bars and rings that
may mainly originate from instabilities created during the last major
merger. Many galaxies also show a helicoidal structure, which is
probably due to a central torque, and seems to play an important role
in regulating the angular momentum of the newly-formed disks.
Key words: galaxies: formation - galaxies: spiral - galaxies: kinematics and dynamics
1 Introduction
The tidal torque theory (Peebles 1976; White 1984) assumes that the angular momentum of disk galaxies had been acquired by early interactions. This theory has been supported for a long time: in fact almost all massive galaxies are regular, including rotational disks and dispersion-supported bulges or their mixes, and they outline the local Hubble sequence. However, if spiral disks were formed at early epochs - z > 2 - they could have encountered severe damages from later major interactions. Galaxy collisions appear to be too frequent to allow many disks to survive (Toth & Ostriker 1992), and this might happen even at z < 1 (Hammer et al. 2009a).
What was the Hubble sequence 6 Gyr ago? Galaxy morphologies strongly evolve (Conselice et al. 2005; Zheng et al. 2004; van den Bergh 2002,2009)
towards much more peculiar structures. This combined with the coeval
evolution of star formation rate and stellar mass densities, of
O/H gas abundances and pair statistics, prompted us to propose the
disk rebuilding scenario (Hammer et al. 2005).
This scenario describes most of these evolutions as due to a recent
merger origin of most spirals. To reproduce the observed evolution
requires that 50 to 75% of the present-day spirals have been
formed - i.e. their disks reprocessed by mergers -
during the last 8 Gyr (z < 1). Within this
period, observations show that more than half of the stellar mass in
spirals has been formed and this can happen through gas compression
occurring during the different
phases of major gas-rich mergers (Hammer et al. 2005). In this theory, the disk angular momentum mostly results from the orbital angular momentum of the last major collision (Hammer et al. 2007; Hopkins et al. 2009a; Puech et al. 2007a).
A more recent epoch for disk formation is indeed supported by the
large decrease with redshift of the fraction of rotationally supported
disks. Neichel et al. (2008) (hereafter IMAGES-II) found that rotational disks were two times less abundant at
![]() = 0.65, a result that is based on a study combining detailed morphology and spatially resolved kinematics.
= 0.65, a result that is based on a study combining detailed morphology and spatially resolved kinematics.
How can mergers be related to the regular local galaxies, of which our Milky Way has been so often taken as typical? Deep observations attest to the rather tumultuous history of several nearby galaxies that is imprinted in their inner halo (e.g. M 31, see Brown et al. 2008; Ibata et al. 2005; see also Davidge 2008 for M 81). The Milky Way appears to be quite exceptional (Hammer et al. 2007), possibly related to its quiescent merger history. Particularly, its halo is the most primordial within galaxies with similar masses (Mouhcine 2006) and it shows an angular momentum two times lower than that of typical spirals.
Galaxy simulations can help to test various galaxy formation scenarios. Assuming large accretions of cold gas flows may reproduce several correlations, mostly those linking the gas consumption and the assembly of the stellar mass (Dekel et al. 2009). There is, however, no convincing observation of significant cold gas-flow in local or distant galaxies, while mergers are well identified in the local and distant Universe. Hopkins et al. (2009a) (see also Robertson et al. 2006) successfully tested disk survival during merging. The resulting mergers produce disks whose angular momentum differs in direction and amplitude from those of the progenitors. The predictions of Hopkins et al. (2009a) rely on processes dominated by pure gravitation, which are indirectly affected by feedback effects. This is certainly true for massive galaxies for which stellar feedback - including outflows - is unlikely to be an efficient way to redistribute the material during a collision. If the gas fraction is sufficient (about 50%), they predict that the re-formed disk can be the dominant component in the reshaped galaxy.
The rebuilding disk scenario proposes a merger origin for spirals and, by extension, of the whole Hubble sequence, from ellipticals (Barnes & Hernquist 1992; Toomre & Toomre 1972; Toomre 1981) to late type spirals. In fact, the orbital angular momentum provided by major mergers could solve the angular momentum problem (Maller et al. 2002). Considerable work is, however, needed to support the scenario. Could a cosmological distribution of orbital parameters rebuild small bulges within some rebuilt disks, and large bulges within others? Could it reproduce the Hubble sequence statistics of bulge to disk ratio? Hopkins et al. (2009b,a) partially brought a positive answer to this question. Their model indeed recovers the well-known correlation between bulge-to-disk ratio and mass.
Observations may prove or invalidate the rebuilding disk scenario. It is well known that the gaseous content of galaxies increases rapidly with redshift. But does it reach the values required to rebuild a disk in case of mergers? We must also observe the details of the physical processes in galaxies at different epochs and directly examine their evolution. At very high redshift (z > 2), cosmological dimming prohibits the examination of the optical radius of a disk even with the largest space telescopes, and it is difficult yet to gather a representative sample of such galaxies. At intermediate redshifts the situation is much better even if it requires pushing the present observational tools near their limits. Up to z=0.4 and z=1.3 the optical radius of a redshifted Milky Way can be retrieved from GOODS and UDF imageries, respectively.
The IMAGES study aims to identify the physical processes that link distant (z ![]() 0.65) to local galaxies. Its selection is limited by absolute J-band magnitude (MJ(AB)
0.65) to local galaxies. Its selection is limited by absolute J-band magnitude (MJ(AB) ![]() -20.3), a quantity relatively well linked to the mass (Yang et al. 2008, hereafter IMAGES-I). Using such a limit, Delgado-Serrano et al. (2009) have shown that z
-20.3), a quantity relatively well linked to the mass (Yang et al. 2008, hereafter IMAGES-I). Using such a limit, Delgado-Serrano et al. (2009) have shown that z ![]() 0.65 galaxies have to be the progenitors of local galaxies
selected in a similar way. They find that the fraction of E/S0 has not
evolve in the last 6 Gyr, while spiral galaxies were
2.3 times less abundant. They use a quite restrictive method to
classify morphologies, assuming that spiral galaxies in the past have
similar properties to what they possess today. Using such a
morphological classification, IMAGES-II (Neichel et al. 2008)
demonstrated an excellent agreement between morphological and
kinematical classifications. In other words, most rotating
galaxies (80%) show spiral morphologies while most
galaxies (90%) with anomalous kinematics present peculiar
morphologies. The above results have an important impact: anomalous
kinematics of the gaseous component (from the ionised gas,
0.65 galaxies have to be the progenitors of local galaxies
selected in a similar way. They find that the fraction of E/S0 has not
evolve in the last 6 Gyr, while spiral galaxies were
2.3 times less abundant. They use a quite restrictive method to
classify morphologies, assuming that spiral galaxies in the past have
similar properties to what they possess today. Using such a
morphological classification, IMAGES-II (Neichel et al. 2008)
demonstrated an excellent agreement between morphological and
kinematical classifications. In other words, most rotating
galaxies (80%) show spiral morphologies while most
galaxies (90%) with anomalous kinematics present peculiar
morphologies. The above results have an important impact: anomalous
kinematics of the gaseous component (from the ionised gas, ![]()
![]() 3726;
3729 lines) is almost always linked to an anomalous morphological
distribution of the stars. Altogether the above results imply that more than half of the present-day spirals had anomalous kinematics and morphologies, 6 Gyr ago.
3726;
3729 lines) is almost always linked to an anomalous morphological
distribution of the stars. Altogether the above results imply that more than half of the present-day spirals had anomalous kinematics and morphologies, 6 Gyr ago.
Anomalous galaxies are also responsible (Flores et al. 2006) for the most striking evolution of the Tully-Fisher relation, i.e. it is heavily scattered at z ![]() 0.6-1 (Conselice et al. 2005). Major mergers can reproduce this evolution (Covington et al. 2009) as well as a similar trend for the
0.6-1 (Conselice et al. 2005). Major mergers can reproduce this evolution (Covington et al. 2009) as well as a similar trend for the
![]() relationship (Puech et al. 2007a).
The goal of this paper is to verify whether the observed evolution is
mostly related to merger events, i.e. to test if the rebuilding
disk scenario is consistent with the observed evolution of morphology
and kinematics. We thus defined 3 different morpho-kinematical
classes following Table 4 of Neichel et al. (2008):
relationship (Puech et al. 2007a).
The goal of this paper is to verify whether the observed evolution is
mostly related to merger events, i.e. to test if the rebuilding
disk scenario is consistent with the observed evolution of morphology
and kinematics. We thus defined 3 different morpho-kinematical
classes following Table 4 of Neichel et al. (2008):
- rotating spiral disks are galaxies possessing a rotating velocity field, including a dispersion peak at the dynamical centre (see e.g. Flores et al. 2006), and showing the appearance of a spiral galaxy;
- non-relaxed systems are galaxies with velocity fields discrepant from a rotational velocity field and whose morphology is peculiar;
- semi-relaxed systems possess either a rotational velocity field and a peculiar morphology or a velocity field discrepant from rotation and a spiral morphology.
Table 1:
Morpho-kinematical classification of 52
![]() = 0.65 galaxies.
= 0.65 galaxies.
Morphological and kinematics properties come from the IMAGES survey
and the complete picture has been also provided by deep photometric and
spectroscopic measurements necessary to estimate their SFR (both in UV
and IR, see also Puech et al. 2009a),
their stellar masses and their
chemical and stellar population decomposition. Section 2 describes
our procedure to test whether or not morpho-kinematical properties of
distant starbursts can be reproduced by galaxy interaction processes,
including during the remnant phase. In Sect. 3 we show the overall
properties of distant starbursts, including their gas richness that is
of crucial relevance to infer whether mergers may lead to disk
rebuilding. In Sect. 4, we discuss the results and conclude
in Sect. 5 on the validity of the disk rebuilding scenario.
Throughout the paper, we adopt H0=70 km s-1 Mpc-1,
![]() ,
,
![]() and the AB magnitude system.
and the AB magnitude system.
2 Could distant starbursts properties be reproduced by merger or merger remnants?
2.1 Detailed analyses of individual distant galaxies
Detailed analyses of four distant galaxies of the IMAGES study have been performed by Puech et al. (2009a,2007a), Hammer et al. (2009b) and Peirani et al. (2008), and four other studies of individual galaxies are in progress (Yang et al. 2009; Fuentes et al.; and Peirani et al., in preparation). By modelling gas motions as well as morphologies, these studies have shown their ability to reproduce the properties of distant galaxies with a similar accuracy to what is done for nearby galaxies. Puech et al. (2007a) have demonstrated that spatially resolved kinematics is sufficiently sensitive to detect the infall of a 1:18 satellite in a z = 0.667 galaxy. Peirani et al. (2008) identified a giant and starbursting bar induced by a 3:1 merger, and simulated both morphologies and the off-centre dynamical axis. In this case, the gas pressured in the tidally formed bar has condensed into young and blue stars. Hammer et al. (2009b) identified a compact LIRG dominated by a dust-enshrouded compact disk that surrounds a blue, centred helix (so-called ``two arms-plus-bar'' structure). They interpret this structure (see their Fig. 7) as regulating the exchanges of the angular momentum and possibly stabilising the new disk (Hopkins et al. 2009a). Indeed, gas inflows along a helix are usual in simulations of mergers, especially in inclined and polar orbits. This gas-rich galaxy appears to be an archetype of disk rebuilding after a 1:1 or a 3:1 merger with an inclined orbit. Puech et al. (2009a) demonstrated that the presence of ionised gas without stars near a highly asymmetric disk can be only reproduced by a remnant of a merger.
These studies have been successful because they compared
simulations of the gas phases to observations of both the morphology
and the ionised gas motions. Morphologies of starbursts -
especially the numerous blue or dusty regions - are mostly relics
of gas phases recently transformed into young stars that ionise the
gas. Thus a common physical mechanism should reproduce them together
with the observed large-scale motions of the ionised gas. Within most
starbursts, the light is indeed dominated by ![]() 100 Myr-old
stars and at large distances, spatially-resolved kinematics only detect
large-scale motions, with typical scales of
100 Myr-old
stars and at large distances, spatially-resolved kinematics only detect
large-scale motions, with typical scales of ![]() 3 kpc. A typical motion of 100 km s-1 would cross such a length scale for
3 kpc. A typical motion of 100 km s-1 would cross such a length scale for ![]() 50 Myr
(32 Myr for motions parallel to the sky plane). Thus, many
morphological features with blue colors (bars, rings and
helixes, see Hammer et al. 2009b; Peirani et al. 2008) should be imprints of the gas hydrodynamics and they can be compared to the gas kinematics.
50 Myr
(32 Myr for motions parallel to the sky plane). Thus, many
morphological features with blue colors (bars, rings and
helixes, see Hammer et al. 2009b; Peirani et al. 2008) should be imprints of the gas hydrodynamics and they can be compared to the gas kinematics.
2.2 A general method to compare galaxy simulations to distant starbursts
For homogeneity, we study here the sub-sample of 33 IMAGES
starbursts (see IMAGES-I) in the CDFS-GOODS. This sub-sample is
representative of MJ(AB) ![]() -20.3 starbursts (see IMAGES-I).
Two galaxies have been rejected from the original sample of IMAGES-I,
one (J033210.76-274234.6) because it turns out not to be a starburst (Yang et al. 2009)
and another one (J033250.24-274538.9) because the HST/ACS images
are corrupted. We verified that this sub-sample is representative of
the stellar mass and star formation densities at
-20.3 starbursts (see IMAGES-I).
Two galaxies have been rejected from the original sample of IMAGES-I,
one (J033210.76-274234.6) because it turns out not to be a starburst (Yang et al. 2009)
and another one (J033250.24-274538.9) because the HST/ACS images
are corrupted. We verified that this sub-sample is representative of
the stellar mass and star formation densities at
![]() = 0.65 (see e.g. Ravikumar et al. 2007).
In this sample we find only 6 rotating spiral disks to which we
add one giant spiral (J033226.23-274222.8) that is also rotating, while
it likely experiences a satellite infall causing a small shift in the
observed dispersion map (Puech et al. 2007b). Note also that one of the rotating spiral galaxies (see Fig. 1,
right) is within a confirmed interaction with an elliptical galaxy. The
26 other galaxies all show peculiar morphologies and/or anomalous
kinematics and are classified as such as non or semi-relaxed systems.
= 0.65 (see e.g. Ravikumar et al. 2007).
In this sample we find only 6 rotating spiral disks to which we
add one giant spiral (J033226.23-274222.8) that is also rotating, while
it likely experiences a satellite infall causing a small shift in the
observed dispersion map (Puech et al. 2007b). Note also that one of the rotating spiral galaxies (see Fig. 1,
right) is within a confirmed interaction with an elliptical galaxy. The
26 other galaxies all show peculiar morphologies and/or anomalous
kinematics and are classified as such as non or semi-relaxed systems.
| Figure 1: b+v, i and z combined images of 2 rotating disks identified by IMAGES. The dotted line is the superposition of the dynamical axis, dotted squares indicate the dispersion peak element. On the left, the dynamical and optical axes are aligned, and the dispersion peak is at the mass center, as expected for rotation (see Flores et al. 2006). On the right (J033238.60-274631.4) there is a slight misalignment of the dispersion peak that is likely caused by the nearby passage - 15 kpc - of a bulge-dominated galaxy, causing the observed burst of star formation at the bottom edge of the spiral galaxy. The velocity difference between the two galaxies is 540 km s-1, a value based on spectroscopy. |
|
| Open with DEXTER | |
It is a Herculean task to analyse in detail the considerable amount of data for each of these galaxies, as described for few galaxies in Sect. 2.1. The accurate modelling of both morphology and kinematics takes from two to six months for a well-experimented user. This is due to the complexity of the morphologies and kinematics in these non-relaxed galaxies as well as the large parameter space offered by the simulations (mass ratio, orbit, temporal phase, peri-centre radius and parameters of the encounters, viewing angles). Our goal here is restricted to the following question: Can we assess both the morphological and kinematic main properties of the 26 non-(or semi-)relaxed galaxies by merger or merger remnants?
Recently, Barnes & Hibbard (2009)
defined a modelling tool to identify merger orbital parameters. It
allows users to change many parameters including the viewing angle.
However at high-z we cannot identify low surface brightness tidal features. We propose here to adapt a similar modelling tool for high-z observations, also allowing changes of the viewing angle. We then used the models from Barnes (2002) that include 12 configurations with a mass ratio
ranging from 1:1 to 3:1, orbits from INClined, DIRect, POLar and RETrograd and pericenter radii from ![]() = 0.2 to 0.4 (see Barnes 2002, for more details). We have recovered the ZENO code
source
= 0.2 to 0.4 (see Barnes 2002, for more details). We have recovered the ZENO code
source![]() and follow all the parameters in Barnes (2002),
except for a few differences in the values of the pericenter radius.
However, the adopted values in our simulations make them resemble the
Barnes simulations. In some cases we had to invert the spin of
interacting galaxies to match the observed velocity gradient. The
number of particles in each simulation is 95 040, slightly
more than in Barnes (2002).
and follow all the parameters in Barnes (2002),
except for a few differences in the values of the pericenter radius.
However, the adopted values in our simulations make them resemble the
Barnes simulations. In some cases we had to invert the spin of
interacting galaxies to match the observed velocity gradient. The
number of particles in each simulation is 95 040, slightly
more than in Barnes (2002).
We then developed an interactive system based on Barnes' command
``snapview'' which allows us to display/rotate the simulation in
3D space. We improved it by generating the projected image
(morphology) and velocities from which we can mimic the integral field
unit (IFU) observation. After
matching the morphology, the velocity of each particle is projected in
the line-of-sight direction. Then we mimicked the observation of an IFU
by calculating the mean velocity and velocity dispersion for those
particles that are projected to an IFU pixel. We first tried to
reproduce the gross morphological features and then we tried to
determine the kinematics by dithering the IFU grid within half IFU
pixel, and by rotating the system within ![]() 5-10 degrees. Figure 2
displays the final result after rotation for morphology, velocity field
and dispersion maps which compare the best simulation to the
observations within the adopted grid of models.
5-10 degrees. Figure 2
displays the final result after rotation for morphology, velocity field
and dispersion maps which compare the best simulation to the
observations within the adopted grid of models.
To measure the quality of the model, three sets of parameters are considered: the ones from morphology, from velocity field and from dispersion maps. Each set of parameters is graded from 0 (failure) to 2 (good fit). For each of them the following criteria were considered:
- morphological parameters: only large scale morphological structures were considered, including the presence of multiple nuclei, bars, ring, arms, helix etc.;
- velocity field parameters: orientation of the main velocity gradient(s), but not their amplitude(s);
- dispersion map parameters: position of the minima and maxima, but not their amplitudes.
Table 2: Classification of the quality of the model in reproducing morphology and kinematics.
![\begin{figure}
\begin{tabular}{ll}
IAU name and associated model \\
\includegr...
...& \includegraphics[height=2.85cm]{12115-fig2m.eps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg23.png)
|
Figure 2: Comparison between observations and models for the 26 distant starbursts that show non or semi-relaxed properties from their morphologies and kinematics. The top boxes indicates the significance of each panel. See Table 2 for the classification of the modelling and Table 3 for the general properties of these galaxies. |
| Open with DEXTER | |
![\begin{figure}
\begin{tabular}{ll}
J033230.57-274518.2 (POL 1:1 $r_{\rm peri}$\s...
... &\includegraphics[height=2.9cm]{12115-fig2za.eps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg24.png)
|
Figure 2: continued. |
| Open with DEXTER | |
Let us now examine whether or not these robust fits gives support to the merging hypothesis. The main limitation of this exercise is obviously the discrete number of orbits and of mass ratio between the modelled encounters. Since we allow the model to invert the spin of one or two of the interacting galaxies, the total number of models is 48. Notice that we had to invert the spin for 5 cases among the 17 robustly modeled starbursts. In fact our initial motivation to choose such a methodology, besides the obvious question of time requirements, came from our initial experience. For each individual detailed model (see Sect. 2.1), our initial guess for the orbit and mass ratio was close to the final result, or in other words, only a few changes of the latter quantities allowed us to recover the amplitudes of the kinematical parameters as well as most of the morphological details. It is indeed possible that the choice of the orbits by Barnes (2002) is quite representative of a cosmological distribution of merger orbits. Besides this, the use of 1:1 and 3:1 mass ratio also might be sufficient to reproduce the gross features of many major mergers.
Our models, including the robust ones, are not unique and this probably applies also to detailed models that have been discussed in Sect. 2.1. The important question to address is the possible degeneracy of the methodology applied, that would be the case if the number of model parameters is significantly higher than the number of constraints. To test this we consider two robust models, one of an on-going merger with two identified nuclei and one of a merger remnant. J033210.25-274819.5 is a galaxy showing two components with a strong colour difference (see Fig. 2) of 1.5 mag in observed (b-z)AB (see Neichel et al. 2008). To test the merger hypothesis we simply assumed that the two components are the relics of a 3:1 mass ratio merger with a DIRect orbit just before the first passage. This galaxy shows two peculiarities in its kinematics. First, the dynamical axis is significantly offset from the main optical axis and it points towards the secondary blue component, and second, the dispersion peak is offset in the direction of the secondary component. The constraints that need to be reproduced are:
- the location of the secondary component (2 constraints) and the presence of a small bar (1) in the center of the main component;
- the main dynamical axis (2) that is shifted towards the secondary component as well as the presence of a secondary dynamical axis (1) that follows the main optical axis of the main component;
- the location of the dispersion peak (2) as well as the minima (1 to 3) in the dispersion maps.
Another degeneracy that might affect the modeling process is the one associated with the uniqueness of the best model itself. Indeed, even if the number of constrains exceed the number of model parameters as discussed above, there remains the possibility that at a constant number of free parameters, several different models could match the observations with a similar quality. This model-degeneracy was extensively discussed by Barnes & Hibbard (2009). They pointed out that such a degeneracy can be broken by identifying specific features in the phase space (i.e., the 6D space of positions and velocities) after the encounter, because such features (e.g., tidal tails) allow us to trace back the initial configurations of the progenitors. They showed that such a methodology allowed them to robustly constrain the disk orientations, viewing angles, time since pericenter, pericentric separation, and scale factors, while they did not examine errors in center-of-mass position and velocity. In fact, our approach is very similar: we examined the 6D phase space using projections of different moments of the phase function (morphology, velocity field, and velocity dispersion maps) and tried to reproduce specific signatures, which are listed above. Hence, we are quite confident that the methodology used in this paper allows us to efficiently constrain the merging phases as well as the disk inclinations provided that the time since pericenter does not correspond to the latest merging phases where such specific features tend to vanish. However, strictly speaking, it is clear that it remains difficult, and probably even impossible, to claim that these models are truly unique, something which is anyway inherent to any modeling work, whatever the adopted methodology and/or data quality are.
In the sample of 33 emission line galaxies there are six rotating spiral galaxies, five of them isolated and one in interaction with an elliptical galaxy (see Fig. 1). Another galaxy is almost similar to a rotating disk although it experiences a satellite infall. Among the other 26 galaxies, 17 of them have their morphologies and kinematics robustly reproduced by a merger model with a number of parameters that is far below the number of constraints provided by the observations. There are nine other galaxies for which our modelling as mergers appears less secure. All these galaxies have anomalous velocity fields and peculiar morphologies and generally their dynamical axes show significant offset to the main optical axes. These galaxies have similar properties to those of the robustly modelled mergers or remnants discussed above. Some of them are obviously in strong interaction (e.g. J033220.48-275143.9) or are very likely merger remnants (e.g. J033214.97-275005.5 and J033230.57-274518.2) from their extremely distorted morphologies and kinematics. The larger uncertainty in modelling them could be due to the limitations of the templates used here. We classify them as possible mergers or merger remnants in the following.
2.3 Distribution of mass ratio, merger temporal phases and orbits
In summary, we find that among 33 distant galaxies, 17 are robustly and 9 are possibly reproduced by models of major mergers. In our simplified model, our goal is to identify which configuration (phase, orbit, mass ratio, and pericenter, see Table 3) is able to reproduce both morphology and kinematics. There are several possible biases in such an exercise and several of them have been discussed above. It is however interesting to examine the overall distribution of the configuration parameters that could reproduce the distant starbursts as mergers.
First, we consider the mass ratio between the two interlopers. For each
configuration in which the two interlopers can be identified, we have
used z-band photometry to calculate the mass ratio (see Table 2).
However, many starbursts have been identified with merger remnants for
which we derive the mass ratio from the modelling. Figure 3 (top) shows a distribution with two peaks at 1:1 and 3:1
![]() = 0
and -0.48, respectively), which are obviously related to the
adopted methodology. Photometric estimates of the mass ratio can be
done for mergers before the second passage (see Figs. 1 and 2)
when the two components can be separated. Nearly half of the sample
possesses photometric estimates of the mass ratio, and they have a
smoother distribution, ranging mostly from 0.25 to 0.65
for
M2/M1 (Fig. 3,
middle). One may wonder how the mass properties of a disturbed dark
matter component can be derived in such a way, especially for the minor
interloper that is likely harassed during the event. Stewart (2009a) studied such configurations (see their Fig. 2, right panel for gas-rich z=1 galaxies), and found that the
M2/M1 stellar value ranges
from 1/3 to 3/2 times the values for the dark matter,
assuming stellar masses in the range of 1010 to
= 0
and -0.48, respectively), which are obviously related to the
adopted methodology. Photometric estimates of the mass ratio can be
done for mergers before the second passage (see Figs. 1 and 2)
when the two components can be separated. Nearly half of the sample
possesses photometric estimates of the mass ratio, and they have a
smoother distribution, ranging mostly from 0.25 to 0.65
for
M2/M1 (Fig. 3,
middle). One may wonder how the mass properties of a disturbed dark
matter component can be derived in such a way, especially for the minor
interloper that is likely harassed during the event. Stewart (2009a) studied such configurations (see their Fig. 2, right panel for gas-rich z=1 galaxies), and found that the
M2/M1 stellar value ranges
from 1/3 to 3/2 times the values for the dark matter,
assuming stellar masses in the range of 1010 to
![]() ,
respectively. Figure 3 (bottom) shows the distribution of the dark matter ratio after applying the correction suggested by Stewart (2009a). The main difference between the top and middle/bottom panels of Fig. 3
is the vanishing of the 1:1 peak: it is not surprising that
equal mass mergers are rarer than 2:1 or 3:1 mergers, and
indeed one can notice that a large fraction of 1:1 mergers are not
robustly modelled. Both distributions are overwhelmingly dominated by
major mergers (all but the satellite infall Puech et al. 2007a).
The overall distribution shows the scarceness of events involving a
galaxy more massive than the observed one, since those are rarer due to
the exponential drop of the mass function towards the massive end. The
quasi absence of minor mergers may have a different meaning because
minor encounters should be numerous at
,
respectively. Figure 3 (bottom) shows the distribution of the dark matter ratio after applying the correction suggested by Stewart (2009a). The main difference between the top and middle/bottom panels of Fig. 3
is the vanishing of the 1:1 peak: it is not surprising that
equal mass mergers are rarer than 2:1 or 3:1 mergers, and
indeed one can notice that a large fraction of 1:1 mergers are not
robustly modelled. Both distributions are overwhelmingly dominated by
major mergers (all but the satellite infall Puech et al. 2007a).
The overall distribution shows the scarceness of events involving a
galaxy more massive than the observed one, since those are rarer due to
the exponential drop of the mass function towards the massive end. The
quasi absence of minor mergers may have a different meaning because
minor encounters should be numerous at
![]() = 0.65 (e.g. Davies et al. 2009). Minor mergers are expected to affect less and in a more sporadic way, kinematics, morphology and star formation (see also Hopkins et al. 2008,
and the discussion in Sect. 4.1). Overall, the distribution of
mass ratios seems consistent with a modelling of most distant
starbursts as major mergers as shown in Sect. 2.2.
= 0.65 (e.g. Davies et al. 2009). Minor mergers are expected to affect less and in a more sporadic way, kinematics, morphology and star formation (see also Hopkins et al. 2008,
and the discussion in Sect. 4.1). Overall, the distribution of
mass ratios seems consistent with a modelling of most distant
starbursts as major mergers as shown in Sect. 2.2.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig3.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg27.png)
|
Figure 3: Top: distribution of the logarithm of the mass ratio, with M1 representing the mass of the galaxy observed by IMAGES. The full black histogram corresponds to the 24 galaxies, the nature of which we have robustly identified, including the 17 robust mergers, the 5 isolated rotating disks (arbitrarily set at M2/M1 = 0.01), the spiral galaxy in interaction and the galaxy with a satellite infall. The vertical dotted lines represent the limit of major mergers (mass ratio between 5 and 1/5). Middle: same as above but for galaxies with separated components (see Fig. 2) for which we have been able to estimate the mass ratio using the z-band photometry from ACS, which corresponds to the rest-frame V-band. Bottom: same as above but after applying the correction by Stewart (2009a) to recover the dark matter M2/M1 ratio. We have generalised this correction factor to values of M2/M1 (stellar) different to 0.3. |
| Open with DEXTER | |
Figure 4 shows how the modelled galaxies are distributed during the various temporal phases of the merger. The combination of constraints from large-scale kinematics and from detailed morphology generally leaves few doubts about the merger phase. For example, for J033224.60-274428.1 (see Fig. 2), the collision could not be reproduced by a second passage because it would not fit both the morphology and the dispersion peak location in direct or inclined orbits. Furthermore, we believe that most galaxies have their phases quite robustly identified. This is even true for several of the nine ``possible'' mergers, including J033220.48-275143.9 for which the disturbed morphologies of both components shows a phase between the first and the second passage. Similarly, if J033214.97-275005.5, J033225.26-274524.0, J033228.48-274826.6, J033234.12-273953.5, and J033244.20-274733.5 are really mergers, their highly distorted morphologies or their compactness is difficult to understand if they were not near the fusion stage. For J033238.60-274631.4 (see Fig. 1, right) it is very plausible that the interaction is before a first passage, although it is unclear whether it could be a simple fly-by or a first stage of a merger.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig4.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg28.png)
|
Figure 4: Distribution of the merger phases for the modelled distant starbursts. The full black histogram corresponds to the same galaxies as in Fig. 3 (robust mergers/interactions and isolated rotating spirals). Phase 1 corresponds to the approaching phase until the first passage, phase 2 corresponds to the time elapsed between the first and the second passage, and phase 3 to the time after the second passage and before the elaboration of the rebuilt disk. During phase 3 the galaxy may show a chaotic morphology or a central starburst, always accompanied by a chaotic velocity field and dispersion peaks clearly offset from the mass center. Phase 4 correspond to the disk rebuilding phase, for which the disk is detected, the rotation is seen but could be offset from the main optical axis, and the dispersion peak(s) is (are) closer to the mass centre. The last phase corresponds to rotating spirals with regular velocity fields and a dispersion peak centred on the mass centre (e.g. Flores et al. 2006). |
| Open with DEXTER | |
The result shows a relatively equal distribution of the merger phases
in the IMAGES sample of distant-starburst galaxies. In Fig. 4, we have added the 5 rotating spirals with warm
gaseous disks from their low values of ![]() (see Puech et al. 2007a).
These galaxies could well correspond to the very last phase:
a relaxation after their disks have been rebuilt. This would also
explain why these galaxies form stars efficiently, mostly in their
outskirts (see Neichel et al. 2008): they are still fed by the late infall of the gas particles that have been expelled at larger radii by the collision.
(see Puech et al. 2007a).
These galaxies could well correspond to the very last phase:
a relaxation after their disks have been rebuilt. This would also
explain why these galaxies form stars efficiently, mostly in their
outskirts (see Neichel et al. 2008): they are still fed by the late infall of the gas particles that have been expelled at larger radii by the collision.
Figure 4 draws an evolutionary sequence in which all
distant starbursts can be identified as in a major merger phase and are
subsequently modelled. This sequence is complementary to that drawn
by Hammer et al. (2005) (see their Fig. 6).
Notice that distant starbursts represent a significant fraction of
distant galaxies as they correspond to 60% of the galaxy population at
![]() = 0.65 (Hammer et al. 1997).
= 0.65 (Hammer et al. 1997).
Conversely to the mass ratio and the merger phase, an accurate determination of the orbit is much more difficult, possibly due to the adopted methodology. Indeed we may have lost some configurations especially for phases during or after fusion. Another difficulty is a possible degeneracy between different orbits. For example, the galaxy morphology of J033234.12-273953.5 may be well reproduced by a retrograde merger (even better than with the adopted inclined orbit) although we have not been able to reproduce the location of the dispersion peak. Figure 5 shows the distribution of orbits within the sample of 26 mergers or possible mergers plus the rotating spiral in an interaction for which the orbit is not constrained at all (labelled N/A). Only 12 galaxies have their orbits robustly determined, i.e. galaxy morphologies and kinematics cannot be reproduced by other orbits. It also shows a lack of direct and retrograde orbits, which also could be related to the methodology. Indeed, we have tried to reproduce both kinematics and morphological details such as starbursting bars, rings and helicoidal structures that are generally associated with inclined and polar orbits.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig5.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg30.png)
|
Figure 5: Distribution of the interaction orbits adopted to model the 26 mergers plus one interaction in the sample of 33 distant starbursts observed with IMAGES. The full black histogram corresponds to the 12 objects for which we have robustly identified the orbit. The x-axis represents the different orbits displayed in the figure. |
| Open with DEXTER | |
Only detailed modelling may solve the degeneracy in the orbit determination and help to verify whether the orbital distribution is consistent with the hierarchical model of galaxy formation. In this section, we have simply demonstrated that for the many distant starbursts having complex morphologies and kinematics, most of them can be reproduced by a simple modelling of major mergers. The next step is to estimate whether this is just a coincidence, or if mergers may explain the elaboration of spirals, as suggested in Fig. 4. Robertson et al. (2006) and many subsequent studies (Governato et al. 2009; Hopkins et al. 2009a) have shown that within the conditions of sufficient gas richness - generally assumed to be over 40-50% - major mergers lead to the rebuilding of a significant disk.
3 Gaseous content of distant starbursts
3.1 Gas and stellar masses
The gas content of distant galaxies is still poorly known. The large
interferometric sub-mm baseline instrument ALMA will be essential in
providing estimates of the molecular gas that is related closely to
star formation (Gao & Solomon 2004).
We however may make use of galaxies in the local universe, for which
the surface densities of star formation and gas are observed to follow
a Schmidt-Kennicutt law,
![]()
![]()
![]() ,
over more than 6 orders of magnitude in SFR (Kennicutt 1998).
This empirical relation is usually explained by a model in which the
SFR scales with density-dependent gravitational instabilities in the
gas.
,
over more than 6 orders of magnitude in SFR (Kennicutt 1998).
This empirical relation is usually explained by a model in which the
SFR scales with density-dependent gravitational instabilities in the
gas.
It is plausible that
![]() =
0.65 starbursts, including those involved in mergers, follow the
same relation as local starbursts and mergers. Gaseous masses have been
estimated by Puech et al. (2009b) by
assuming that distant starbursts followed the Schmidt-Kennicutt
relation. This generates gas surface densities that range from 10
to 250
=
0.65 starbursts, including those involved in mergers, follow the
same relation as local starbursts and mergers. Gaseous masses have been
estimated by Puech et al. (2009b) by
assuming that distant starbursts followed the Schmidt-Kennicutt
relation. This generates gas surface densities that range from 10
to 250 ![]()
![]() ,
i.e. intermediate between normal spirals and ULIRGs. Such a method
has been used to derive the gas mass fraction of very distant galaxies (Erb et al. 2006). Because the local estimate of the gas surface density is independent of the IMF, Erb et al. (2006) noticed that by using the same Salpeter IMF adopted by Kennicutt (1998),
the derived gaseous mass is in principle an IMF independent quantity.
By accounting for the uncertainties in the SFR derived from
Spitzer/MIPS 24
,
i.e. intermediate between normal spirals and ULIRGs. Such a method
has been used to derive the gas mass fraction of very distant galaxies (Erb et al. 2006). Because the local estimate of the gas surface density is independent of the IMF, Erb et al. (2006) noticed that by using the same Salpeter IMF adopted by Kennicutt (1998),
the derived gaseous mass is in principle an IMF independent quantity.
By accounting for the uncertainties in the SFR derived from
Spitzer/MIPS 24 ![]() m measurements (Salpeter IMF Kennicutt 1998), Puech et al. (2009b) derived error bars ranging from 0.04 to 0.4 dex for gas mass estimates.
m measurements (Salpeter IMF Kennicutt 1998), Puech et al. (2009b) derived error bars ranging from 0.04 to 0.4 dex for gas mass estimates.
Ironically, the wealth of UV to mid-IR data in IMAGES does not provide
yet a better accuracy in estimating the stellar masses. Indeed at all
wavelengths, most of the emission are due to massive stars and not to
the main sequence stars that constitute the bulk of the stellar mass.
The results are heavily dependent on the IMF, the assumed history of
star formation and on various recipes for the extinction law. Puech et al. (2008)
(see their Appendix A) analysed the systematic effects of adopting
different schemes for the stellar mass estimates. They adopted stellar
masses (
![]() )
calculated from rest-frame K-band magnitudes, using the methodology of Bell et al. (2003) to correct for massive stars and assuming a diet-Salpeter IMF. By comparing the evolution of
)
calculated from rest-frame K-band magnitudes, using the methodology of Bell et al. (2003) to correct for massive stars and assuming a diet-Salpeter IMF. By comparing the evolution of
![]() /LK to that from comparable studies, they found that at
/LK to that from comparable studies, they found that at
![]() = 0.65 the Bell et al. (2003) method overestimates the stellar mass by
= 0.65 the Bell et al. (2003) method overestimates the stellar mass by ![]() 0.1 dex when compared to that derived from Bruzual & Charlot (2003)(BC03). Furthermore Maraston et al. (2006) showed that by including TP-AGB stars, the
0.1 dex when compared to that derived from Bruzual & Charlot (2003)(BC03). Furthermore Maraston et al. (2006) showed that by including TP-AGB stars, the
![]() /LK is overestimated by an additional
/LK is overestimated by an additional ![]() 0.14 dex. Thus stellar-mass estimates from Bell et al. (2003) (
0.14 dex. Thus stellar-mass estimates from Bell et al. (2003) (
![]() )
appear to be maximal estimates for the stellar masses of the IMAGES galaxies considered here. It also
gives an approximation of what could be estimated from a combination of the Salpeter IMF and Bruzual & Charlot (2003) models (see arrows in Fig. 6): the IMF effect (+0.15 dex) is compensated by the overestimate due to the Bell et al. (2003) methodology when compared to Bruzual & Charlot (2003). Note that the Salpeter IMF is the maximal IMF and also violates the maximum disk constraints for local spirals (see e.g. Bell et al. 2003). Adoption of other IMFs (for example Kroupa 2002) unavoidably
confirms that
)
appear to be maximal estimates for the stellar masses of the IMAGES galaxies considered here. It also
gives an approximation of what could be estimated from a combination of the Salpeter IMF and Bruzual & Charlot (2003) models (see arrows in Fig. 6): the IMF effect (+0.15 dex) is compensated by the overestimate due to the Bell et al. (2003) methodology when compared to Bruzual & Charlot (2003). Note that the Salpeter IMF is the maximal IMF and also violates the maximum disk constraints for local spirals (see e.g. Bell et al. 2003). Adoption of other IMFs (for example Kroupa 2002) unavoidably
confirms that
![]() overestimates the stellar mass (e.g. Bell et al. 2003).
Note that the above applies for the whole population of galaxies
considered here, and that the estimate of stellar masses for individual
galaxies is still challenging.
overestimates the stellar mass (e.g. Bell et al. 2003).
Note that the above applies for the whole population of galaxies
considered here, and that the estimate of stellar masses for individual
galaxies is still challenging.
Figure 6 shows how the gas masses are distributed against the maximal estimates of the stellar mass (see also Table 3).
All distant starbursts but one show gas fractions intermediate between
the local values and 50%, and there is a correlation between their
stellar and gas masses. Such a correlation may be expected as we
have selected starburst galaxies on the basis of their [OII] equivalent
widths and a proxy of their stellar masses (
![]()
![]() 15 Å and MJ(AB) < -20.3, see IMAGES-I).
15 Å and MJ(AB) < -20.3, see IMAGES-I).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig6.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg38.png)
|
Figure 6: Gas mass derived from Puech et al. (2009b) as a function of the stellar mass obtained from the Bell et al. (2003) prescriptions. The arrows in the upper left corner indicate how the stellar mass may be affected by different prescriptions of the galaxy synthesis population models (BC03 and M06 indicate the change by adopting Bruzual & Charlot 2003; and Maraston 2006 models, respectively), or of the IMF (S55 and K02 show the change due to the adoption of an IMF from Salpeter 1955 or from Kroupa 2002, respectively). The full and dashed lines indicate a gas fraction of 50% and a gas fraction from local galaxies (HI gas, Schiminovich 2008), respectively. The various symbols correspond to the morpho-kinematic classes defined in Sect. 1: rotating spirals (blue circles), heavily non-relaxed systems (red triangles) and semi-relaxed systems (green squares). Only error bars lower than 0.3 dex have been represented in this plot, and values with larger error bars are represented as open symbols. |
| Open with DEXTER | |
3.2 Gas fraction in distant starbursts and their progenitors
The median gas fraction of the sample is 31% ![]() 1%, which is much larger than the corresponding fraction for the
Milky Way (12%, Flynn et al. 2006) or for M 31 (5%, Carignan et al. 2006). It is
approximately twice the value found by ALFALFA (Schiminovich 2008).
Different prescriptions for synthesis models or IMFs would lead to
larger gas fractions in the distant sample: for example, combining a
Maraston model with a Kroupa IMF would divide the stellar mass by a
factor
1%, which is much larger than the corresponding fraction for the
Milky Way (12%, Flynn et al. 2006) or for M 31 (5%, Carignan et al. 2006). It is
approximately twice the value found by ALFALFA (Schiminovich 2008).
Different prescriptions for synthesis models or IMFs would lead to
larger gas fractions in the distant sample: for example, combining a
Maraston model with a Kroupa IMF would divide the stellar mass by a
factor ![]() 2, and thus the median gas fraction would become 47%. In fact, we generate minimal gas fractions
by applying maximal stellar masses. An independent confirmation of
higher gas fractions in distant galaxies is provided by Rodrigues et al. (2008)
who studied the O/H abundances in the gaseous phases of similar
distant starbursts. They found that the gas fraction should reach
2, and thus the median gas fraction would become 47%. In fact, we generate minimal gas fractions
by applying maximal stellar masses. An independent confirmation of
higher gas fractions in distant galaxies is provided by Rodrigues et al. (2008)
who studied the O/H abundances in the gaseous phases of similar
distant starbursts. They found that the gas fraction should reach ![]() 30% at z
30% at z ![]() 0.65 if one assumes that the gas fraction in present-day galaxies is
0.65 if one assumes that the gas fraction in present-day galaxies is ![]() 10%. Given the large uncertainties in our estimates of gas fraction, an independent confirmation is certainly reassuring.
10%. Given the large uncertainties in our estimates of gas fraction, an independent confirmation is certainly reassuring.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig7.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg40.png)
|
Figure 7: Gas fraction distribution as a function of the merger phases. The former corresponds to a minimal value of the gas fraction in the sample of IMAGES starbursts (see text). The various symbols correspond to the morpho-kinematic classes, as in Fig. 6. Note the presence of the massive dry merger at phase = 2 (see the inserted image in Fig. 6) with a very low gas fraction (Yang et al. 2009). The full blue line shows the median gas-fraction in the progenitors derived from the gas consumption during the merger (see text). The dot-long-dashed line shows the same, but for a combination of Maraston et al. (2006) models and Kroupa IMF. The black solid line gives the median of the gas fraction values. |
| Open with DEXTER | |
Figure 7 shows how the gas fractions are distributed in the different merger phases defined in Sect. 3. There is no specific trend between the two quantities. In the framework of a merger scenario, this is not unexpected because it results from the balance between two effects. Let us consider two sets of z=0.6 galaxies, one (hereafter called set A) including galaxies in a later merger stage (after the fusion) and the second (hereafter called set B) with galaxies before the first pass. By construction, progenitors of A galaxies lie at higher redshift and should have lower luminosities (and masses) than B galaxies, and then should have, on average, a significantly higher gas fraction. This is somewhat compensated for by the fact that A galaxies have had a supplementary star formation that is induced during the merger, which has transformed a part of the gas into stars, reducing the gas fraction. Given the small statistics (5 to 7 galaxies in each phase), we believe that Fig. 7 is consistent with the merger hypothesis. Indeed the main question is whether the progenitors of the observed galaxies are sufficiently gas-rich to lead to disk rebuilding.
There are two possible means to estimate the gas fraction in merger progenitors. Hammer et al. (2009b)
have modelled the stellar populations from deep spectroscopy of a
merger remnant assumed to be in a disk rebuilding phase. They found
that ![]() 50%
of the observed stellar mass had been formed during the merger by
comparing the stellar population ages to the merger dynamical time.
This implies that the progenitors of this system were on average more
than 50% gas-rich, supporting the evidence that this system is
rebuilding its disk after a major merger. Here we use the
characteristic doubling time,
50%
of the observed stellar mass had been formed during the merger by
comparing the stellar population ages to the merger dynamical time.
This implies that the progenitors of this system were on average more
than 50% gas-rich, supporting the evidence that this system is
rebuilding its disk after a major merger. Here we use the
characteristic doubling time,
![]() =
=
![]() /SFR,
to estimate the stellar mass formed during the event, and thus the gas
fraction in their assumed progenitors. Assuming that our maximal
stellar masses are a good representation of the stellar mass for a
Salpeter IMF and a Bruzual & Charlot (2003) synthesis model, this quantity is IMF independent, as our SFR estimates have been done using the Kennicutt (1998) calibration (Salpeter IMF) for the IR luminosities (Puech et al. 2009b, see details).
/SFR,
to estimate the stellar mass formed during the event, and thus the gas
fraction in their assumed progenitors. Assuming that our maximal
stellar masses are a good representation of the stellar mass for a
Salpeter IMF and a Bruzual & Charlot (2003) synthesis model, this quantity is IMF independent, as our SFR estimates have been done using the Kennicutt (1998) calibration (Salpeter IMF) for the IR luminosities (Puech et al. 2009b, see details).
Figure 8 gives the
distribution of the characteristic stellar mass doubling times for the
34 IMAGES starbursts. It is remarkable that their median
value takes its minimum near the fusion, which is expected in all model
of mergers. We have used the models shown in Sect. 3 to estimate
the time each galaxy spends in each of the phases (see time values in
Table 3). It assumes a rotating period time of
![]() = 1.2
= 1.2 ![]() 0.25 Gyr for a galaxy with the mass of the Milky Way (see Barnes 2002). We then scale the merger time with the observed baryonic mass (assuming
0.25 Gyr for a galaxy with the mass of the Milky Way (see Barnes 2002). We then scale the merger time with the observed baryonic mass (assuming
![]() = 5.5
= 5.5 ![]()
![]() )
and also apply a correction for the merger mass ratio as described in Jiang et al. (2008). Besides this, we calculate for each phase the median
)
and also apply a correction for the merger mass ratio as described in Jiang et al. (2008). Besides this, we calculate for each phase the median
![]() that is considered to be its effective star formation time. For a given
starburst assumed to be in a given phase, we may calculate the fraction
of gas that has been transformed into stars during each previous phases
of the merger. Table 3 (Col. 10) gives the time spent by each galaxy in the previous merger phases, that, after combination with the median
that is considered to be its effective star formation time. For a given
starburst assumed to be in a given phase, we may calculate the fraction
of gas that has been transformed into stars during each previous phases
of the merger. Table 3 (Col. 10) gives the time spent by each galaxy in the previous merger phases, that, after combination with the median
![]() ,
provides us with an estimate of the gas mass that has been transformed into stars during the merger.
,
provides us with an estimate of the gas mass that has been transformed into stars during the merger.
Figure 7 also shows the resulting (median) distribution of the progenitor gas fractions (see also Table 3). In 75% of the progenitors, the gas fraction is in excess of 40% or of 58% if we adopt a Maraston-Kroupa combination. The high gas fraction in progenitors is robust because:
- it only requires a modest star formation in the merger to reach large values since we already find a high fraction of gas (median 31%) in the observed starbursts;
- the gas-to-star transformed mass during the merger is independent of the observed mass and thus of the IMF choice, since both
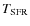 and the merger time scale with mass.
and the merger time scale with mass.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig8.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg45.png)
|
Figure 8:
Characteristic stellar mass doubling times as a function of the merger phases, as they are described in Fig. 4. The various symbols corresponds to morpho-kinematics classes as in Fig. 6.
The full blue line indicates their median value and the dashed red line
indicate the time during which the observed starbursts are involved in
the merger (median value for each phases 1 to 4),
as obtained from the simulations. It slightly decreases at
phase 4 because the masses of the 4 rebuilding disks (median
value, 2.1 |
| Open with DEXTER | |
4 Discussion
4.1 A self-consistent explanation of the galaxy transformation during the last 6 Gyr
In Sect. 2, we argued that distant starbursts have morphologies
and kinematics consistent with major mergers or their remnants. In
Sect. 3 we show that they have large gas fractions, and that their
progenitors would have to have gas fractions above 40-50% to account
for the stellar mass produced during the merger. Therefore most
starbursts at
![]() =
0.65 - those with anomalous morphologies and kinematics - are
consistent with gas-rich merger phases leading to rebuilt disks.
=
0.65 - those with anomalous morphologies and kinematics - are
consistent with gas-rich merger phases leading to rebuilt disks.
Our interpretation of the morpho-kinematic evolution (see Table 1) is then straightforward: ![]() 6 Gyr ago, 46% of the galaxy population was involved in major mergers and most of them
(75%
6 Gyr ago, 46% of the galaxy population was involved in major mergers and most of them
(75% ![]() 46% = 35%) were sufficiently gas rich to rebuild a disk. Those can
be considered as progenitors of the present-day numerous spirals -
although this deserves a careful analysis of the exchanges of angular
momenta - while the others could be progenitors of E/S0 and of the
scarce population of massive irregulars at the present-epoch (
46% = 35%) were sufficiently gas rich to rebuild a disk. Those can
be considered as progenitors of the present-day numerous spirals -
although this deserves a careful analysis of the exchanges of angular
momenta - while the others could be progenitors of E/S0 and of the
scarce population of massive irregulars at the present-epoch (![]() 10%, see Delgado-Serrano et al. 2009).
Thus as much as half of the present-day spirals come from disk
rebuilding from recent mergers, the other half being already assembled
into quiescent or warm disks at
10%, see Delgado-Serrano et al. 2009).
Thus as much as half of the present-day spirals come from disk
rebuilding from recent mergers, the other half being already assembled
into quiescent or warm disks at
![]() = 0.65 (Table 1).
= 0.65 (Table 1).
More statistics are needed to obtain a more precise estimate of the
amount of gas that has been consumed during the different merger
phases. The median time spent in each merger phase ranges from 0.5
to 1.4 Gyr (see Fig. 8 and also Table 3):
the scenario naturally explains why distant starbursts show such a
large contribution of intermediate-age stars revealed by their very
large Balmer absorption lines in their spectra (e.g. Hammer et al. 1997; Marcillac et al. 2006; see also Poggianti et al. 1999,
for another perspective in galaxy-cluster environments). The median
baryonic mass of the sample is 0.75 times that of the
Milky Way. Their progenitors should be galaxies at higher
redshifts, approximately 1 Gyr earlier, i.e. at z ![]() 0.83. At such redshifts, the large gas fractions in progenitors is
not exceptional. Accounting for the gas consumed during the merger, the
median stellar mass and gas fraction of their progenitors are 7.5
0.83. At such redshifts, the large gas fractions in progenitors is
not exceptional. Accounting for the gas consumed during the merger, the
median stellar mass and gas fraction of their progenitors are 7.5 ![]()
![]() and 50%, respectively. In present-day galaxies within this mass range, the gas fraction averages to
and 50%, respectively. In present-day galaxies within this mass range, the gas fraction averages to ![]() 26% for local galaxies (from Schiminovich 2008), and it could quite common that 7 Gyr ago such galaxies had twice their present gas content.
26% for local galaxies (from Schiminovich 2008), and it could quite common that 7 Gyr ago such galaxies had twice their present gas content.
Improvements are also required to estimate the stellar masses since a proxy (absolute J-band magnitude) of the stellar mass has been used in this study to select our sample. A combination of a realistic stellar population with different ages and metal content has to be performed on both the whole spectral energy distribution (from UV to near-IR) and the spectroscopic absorption lines (Lick indices). Nevertheless, we do find that all distant starbursts are consistent with major merger phases, and these sources are strong emitters in the near-IR. It is unclear whether we may have missed a significant population of massive starbursts without strong emission in near-IR. Besides this, technical limitations (see IMAGES-I) have prevented us from measuring the kinematics of 3 starbursts, because their emission line region are too compact (see Fig. 9). Their optical morphologies are also consistent with mergers (see Fig. 9 and its caption).
| Figure 9: b+v, i and z combined images of three additional starbursts whose kinematics has not been detected due to spatial resolution. The galaxy in the middle panel show a ring and possibly the nucleus of the secondary interloper. Kinematics are needed to confirm it as well as to verify the nature of the two other starbursts that could be in close interaction and just at the nuclei fusion, respectively. |
|
| Open with DEXTER | |
Figure 4 - see also Figs. 1 and 2 - suggests that all distant starbursts are part of the duty cycle of the disk rebuilding scenario (see Hammer et al. 2005, their Fig. 6). It also includes the distant rotating spirals with high star formation and warm disks, which are the natural last phase of such a gas-rich merger event. During the elapsed time to z=0, they may transform their gas into stars and simply relax to form the present-day thin disks. During such a phase, models predict that almost all the gas has reached the disk, which is confirmed by the fact that they lie on the same baryonic Tully Fisher relation as local disks (Puech et al. 2009b). This is a simple explanation of why some regular disks are LIRGs (Melbourne 2006).
The spiral disk rebuilding scenario explains the changes observed in
the galaxy population, the density evolution of star formation and
stellar mass, the dispersion of the evolved Tully Fisher relation (Puech et al. 2009b; Flores et al. 2006) as well as the strong evolution of the metal abundances of
their gas phases (Rodrigues et al. 2008). It is also consistent with the observations of galaxy pairs at z ![]() 0.6. The most robust estimate is that 5
0.6. The most robust estimate is that 5 ![]() 1% of galaxies are in pairs at that epoch (see e.g. Bell et al. 2006,
for a review): in our sample we identify only 4 galaxies which
could have been identified as well separated pairs. This corresponds to
a pair fraction of 4/33
1% of galaxies are in pairs at that epoch (see e.g. Bell et al. 2006,
for a review): in our sample we identify only 4 galaxies which
could have been identified as well separated pairs. This corresponds to
a pair fraction of 4/33 ![]() 0.6 = 7
0.6 = 7 ![]() 3% (see Table 1 in which 0.6 is the fraction of starburst galaxies) in the
3% (see Table 1 in which 0.6 is the fraction of starburst galaxies) in the
![]() =
0.65 population. Note that among these pairs, three are in
phase 2, i.e. between the first and the second passage. Last,
major mergers may explain why the ionised gas radius is larger than the
optical radii, especially for the starbursts with small optical radius (Puech et al. 2009b).
Indeed, during a close encounter and nuclei fusion phases, the gas is
heavily shocked by the collision and could be ionised this way (Puech et al. 2009a).
Another alternative is that dust-enshrouded clumps may ionise the gas
while they cannot be detected at visible wavelengths; this phenomenon
has been identified in a compact dust-enshrouded disk (see Hammer et al. 2009b).
=
0.65 population. Note that among these pairs, three are in
phase 2, i.e. between the first and the second passage. Last,
major mergers may explain why the ionised gas radius is larger than the
optical radii, especially for the starbursts with small optical radius (Puech et al. 2009b).
Indeed, during a close encounter and nuclei fusion phases, the gas is
heavily shocked by the collision and could be ionised this way (Puech et al. 2009a).
Another alternative is that dust-enshrouded clumps may ionise the gas
while they cannot be detected at visible wavelengths; this phenomenon
has been identified in a compact dust-enshrouded disk (see Hammer et al. 2009b).
Cosmological simulations confirm the importance of the gas in mergers. By accounting for the gas, Stewart et al. (2009b) found that almost all galaxies may have experienced a merger since z=2. A comparison to IMAGES observations would be highly desirable to clarify this prediction. It may be consistent with the whole formation of the Hubble sequence: a formation of spirals by the numerous gas-rich mergers and of massive ellipticals by gas-poor mergers. It is now time to study the formation (or re-formation) of the present-day spiral galaxies and of their substructures for understanding how the whole Hubble sequence may have been formed.
4.2 How other mechanisms contribute to the galaxy transformation
Numerous studies have attempted to describe the above evolution by assuming different mechanisms. It has been argued that only a small fraction of the star formation is triggered by major interactions (Jogee et al. 2009; Robaina et al. 2009). Although these studies are based on a large number of objects, they do not possess the kinematical information that is crucial to evaluate the presence or absence of merging. Indeed, Neichel et al. (2008) found that most massive galaxies showing irregularities or compactness have also anomalous velocity fields. Mechanisms other than merging then have to explain not only morphological irregularities but also their non-relaxed kinematics.
We have examined the spectra (see e.g. Rodrigues et al. 2008)
of 20 IMAGES starbursts to investigate
whether outflows can be detected. An outflow may lead to
significant differences between the velocity of the emission-line
system and that of the absorption-line system (Heckman & Lehnert 2000).
We find differences in only 3 (J033214.97-275005.5,
J033224.60-274428.1 and J033225.26-274524.0) of 19 objects, at the
level of ![]() 100 km s-1.
Thus, stellar feedback mechanisms are unlikely to considerably affect
distant starbursts, which is understandable as all of them are
relatively
massive with baryonic masses in excess of
100 km s-1.
Thus, stellar feedback mechanisms are unlikely to considerably affect
distant starbursts, which is understandable as all of them are
relatively
massive with baryonic masses in excess of
![]() .
The absence of minor mergers in our sample (only one case with an
18:1 mass ratio) could be simply explained by their considerably
lower
efficiency. Due to their lower impact and their longer duration (Jiang et al. 2008),
they are considerably less efficient to activate a starburst, and to
distort morphologies and kinematics or they do it in a somewhat
sporadic way (see Hopkins et al. 2008).
To explain both the stellar mass assembly and the peculiar
morpho-kinematics would probably need an extremely large (non-observed)
rate of minor mergers, that is certainly not consistent with the large
angular momenta of present-day disks (see e.g. Maller & Dekel 2002).
.
The absence of minor mergers in our sample (only one case with an
18:1 mass ratio) could be simply explained by their considerably
lower
efficiency. Due to their lower impact and their longer duration (Jiang et al. 2008),
they are considerably less efficient to activate a starburst, and to
distort morphologies and kinematics or they do it in a somewhat
sporadic way (see Hopkins et al. 2008).
To explain both the stellar mass assembly and the peculiar
morpho-kinematics would probably need an extremely large (non-observed)
rate of minor mergers, that is certainly not consistent with the large
angular momenta of present-day disks (see e.g. Maller & Dekel 2002).
5 Conclusion: a scenario to explain the formation of the Hubble sequence?
In this paper we considered the possibility that the formation of the Hubble sequence relies to a large extent on past merger events. We used a sample of objects around z=0.65 for which we have both morphology from the HST and high quality kinematics (both velocity field and 2D velocity dispersion maps) and compared them with simulation results varying the viewing angles to obtain the best fits. Although we cannot of course prove that the origin of these objects is a merger, we can safely say that their observed properties are well compatible with them being a merger or their remnants. This result was reached using all available data, i.e. our comparisons included morphology, mean velocities and dispersions. This strengthens our proposal very considerably.
A merger origin of the Hubble sequence is closely linked to the disk rebuilding scenario, which has been successfully argued both from the observational point of view and from simulations (Barnes 2002; Hopkins et al. 2009a; Springel & Hernquist 2005). Our quantitative estimates of gas fractions argue that more than a third of the galaxy population about 6 Gyr ago was sufficienty gas rich to rebuild a disk after the merger. Thus our work argues that a merger origin of the Hubble sequence, although it has not yet been proven, is a plausible alternative or channel for the formation of large disks in grand-design spirals.
Half of the present-day spirals being in merger phases at
![]() =
0.65 naturally implies that most and probably all were shaped during
gas-rich mergers at earlier epochs. These mergers at
=
0.65 naturally implies that most and probably all were shaped during
gas-rich mergers at earlier epochs. These mergers at
![]() = 0.65 generally begun 1 Gyr earlier, i.e. at z = 0.835. We may expect that a similar number of mergers had occurred a further 1 Gyr ago (from z = 0.835 to z =
1.07): then almost all spirals may have been rebuilt from their last
major merger, during the last 8 Gyr. This may apply to M 31 (Hammer et al. 2007),
but the Milky Way appears quite exceptional as its properties
imply a last merger only at much earlier epochs (10 to 11 Gyr
ago). The Milky Way quiescent history is well illustrated by its
exceptional pristine halo; combined with its lack of angular momentum
and stellar mass, this may simply indicate that our Galaxy has
exceptionally avoided any major merger during a large fraction of the
Hubble time (Hammer et al. 2007).
= 0.65 generally begun 1 Gyr earlier, i.e. at z = 0.835. We may expect that a similar number of mergers had occurred a further 1 Gyr ago (from z = 0.835 to z =
1.07): then almost all spirals may have been rebuilt from their last
major merger, during the last 8 Gyr. This may apply to M 31 (Hammer et al. 2007),
but the Milky Way appears quite exceptional as its properties
imply a last merger only at much earlier epochs (10 to 11 Gyr
ago). The Milky Way quiescent history is well illustrated by its
exceptional pristine halo; combined with its lack of angular momentum
and stellar mass, this may simply indicate that our Galaxy has
exceptionally avoided any major merger during a large fraction of the
Hubble time (Hammer et al. 2007).
A considerable task is thus awaiting us. We have to relate the distant starbursts to local galaxies by modelling in detail all the distant galaxies for which we possess detailed morphologies and kinematics, i.e. about 100 galaxies. Although large, such a number is barely sufficient to describe the wide variety of merger configurations. With such a modelling we will be able to derive the final properties of each starburst, by modelling their evolution 6 Gyr later, and verify whether they are consistent with the present-day distribution of galaxies within the Hubble sequence.
In order to make better comparisons between observations and simulations it would be useful to have a larger library of simulations covering longer evolution times and larger gas fractions. A better coverage of the parameter space would also be very useful, although from our experience, it will take some time before being able to recover a detailed modelling of each of the observed galaxies. Such a library (e.g. ``GALMER'', see Di Matteo et al. 2008) may be useful as it could be adapted to the IMAGES observational parameters.
Nevertheless, it was possible to reach a number of conclusions. It is instructive to note how frequent structures such as bars and rings are. We observe 9 bars and 6 rings in our sample of 34 galaxies, and they have colours consistent with young or intermediate-age stars, and as such they could have been formed during the merger. Figure 10 shows that such structures are still persistent at late merger phases. The fraction of barred galaxies that we find is compatible with that found by Sheth et al. (2008) for the same redshift range. Bars and rings are also observed in local galaxies and may well be triggered by the earlier interactions and merging. For example, it is known that interactions can trigger bar formation (Noguchi 1987; Gerin et al. 1990; Steinmetz & Navarro 1999). Polar encounters also can create rings, pseudo-rings, or spirals, which have characteristics similar to the observed ones (see also Berentzen et al. 2003). Spiral patterns can also be generated by encounters, as has been shown by both simulations and observations (e.g. Goldreich et al. 1979; Toomre 1981; Goldreich et al. 1978; Donner et al. 1991; Tutukov & Federova 2006, and references therein). Adjustment of the models is clearly a central issue. The helicoidal structure found in many distant starbursts (see examples in Fig. 2) is likely due to the central torque described by Hopkins et al. (2009a), and it may regulate the angular momentum transfer. This structure is predominant in the nuclei fusion phase and seems present in galaxies in later phases (Hammer et al. 2009b). Its efficiency in regulating the bulge-to-disk ratio is likely considerable (see Hopkins et al. 2009a) although larger statistics are mandatory to verify this prediction and its actual role.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12115-fig10.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg48.png)
|
Figure 10: Gas distribution in merger remnants from Barnes (2002) for 3:1 mergers, and for four different orbits, at the end of the simulations. |
| Open with DEXTER | |
We are especially indebted to Josh Barnes for making available his simulations of galaxy mergers on his web pages as well as letting us using the ZENO code We are very grateful to the referee whose suggestions considerably helped us improve the manuscript.
References
- Alonso-Herrero, A., Engelbracht, C. W., Rieke, M. J., & Quillen, A. C. 2001 ApJ, 546, 952
- Barnes, J. E. 2002, MNRAS, 333, 481 [NASA ADS] [CrossRef]
- Barnes, J. E., & Hernquist, L. 1992, ARA&A, 30, 705 [NASA ADS] [CrossRef]
- Barnes, J. E., & Hibbard, J. E. 2009, AJ, 137, 3071 [NASA ADS] [CrossRef]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef]
- Bell, E. F., Phleps, S., Somerville, R. S., et al. 2006, ApJ, 652, 270 [NASA ADS] [CrossRef]
- Berentzen, I., Athanassoula, E., Heller, C., & Fricke, K. 2003, MNRAS, 347, 220 [NASA ADS] [CrossRef]
- Brinchmann, J., Abraham, R., Schade, D., et al. 1998, ApJ, 499, 112 [NASA ADS] [CrossRef]
- Brown, T. M., Beaton, R., Chiba, M., et al. 2008, ApJ, 685, 121 [NASA ADS] [CrossRef]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef]
- Carignan, C., Chemin, L., Huchtmeier, W. K., & Lockman, F. J. 2006, ApJ, 641, L109 [NASA ADS] [CrossRef]
- Conselice, C. J., Bundy, K., Ellis, R. S. et al. 2005, ApJ, 628, 160 [NASA ADS] [CrossRef]
- Conselice, C. J., Yang, C., & Bluck, A. F. L. 2008, MNRAS, 394, 1956 [NASA ADS] [CrossRef]
- Covington, M. D., Kassin, S. A., Dutton, A. A., et al. 2009, ApJ, submitted [arXiv:0902.0566C]
- Davidge, T. J. 2008, PASP, 120, 1145 [NASA ADS] [CrossRef]
- Davies, G. T., Gilbank, D. G., Glazebrook, K., et al. 2009, MNRAS Lett., 395, 76 [NASA ADS] [CrossRef]
- Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [NASA ADS] [CrossRef]
- Delgado-Serrano, R., Hammer, F., Yang, Y. B., et al. 2009, A&A, in press [arXiv:0906.2805D]
- Di Matteo, P., Chilingarian, I., Melchior, A. M., Combes, F., & Semelin, B. 2008, Proc. of the Annual meeting of the French Soc. of Astron. and Astrophys., ed. C. Charbonnel, F. Combes, & R. Samadi, available online at http://proc.sf2a.asso.fr, 369
- Donner, K. J., Engström, S., & Sundelius, B. 1991, A&A, 252, 571 [NASA ADS]
- Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef]
- Fall, S. M., & Efstathiou, G. 1980, MNRAS, 193, 189 [NASA ADS]
- Flores, H., Hammer, F., Puech, M., Amram, P., & Balkowski, C. 2006, A&A, 455, 107 [NASA ADS] [CrossRef] [EDP Sciences]
- Gao, Y., & Solomon, P. M. 2004, ApJ, 606, 271 [NASA ADS] [CrossRef]
- Gerin, M., Combes, F., & Athanassoula, E. 1990, A&A, 230, 37 [NASA ADS]
- Goldreich, P., & Tremaine, S. 1978, Icarus, 34, 240 [NASA ADS] [CrossRef]
- Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [NASA ADS] [CrossRef]
- Governato, F., Brook, C. B., Brooks, A. M., et al. 2009, MNRAS, 398, 312 [NASA ADS] [CrossRef]
- Hammer, F., Flores, H., Lilly, S., et al. 1997, ApJ, 481, 49 [NASA ADS] [CrossRef]
- Hammer, F., Gruel, N., Thuan, T. X., et al. 2001, ApJ, 550, 570 [NASA ADS] [CrossRef]
- Hammer, F., Flores, H., Elbaz, D., et al. 2005, A&A, 430, 115 [NASA ADS] [CrossRef] [EDP Sciences]
- Hammer, F., Puech, M., Chemin, L., Flores, H., & Lehnert, M. 2007, ApJ, 662, 322 [NASA ADS] [CrossRef]
- Hammer, F., et al. 2009a, in Proc. Galaxy Evolution: Emerging Insights and Future Challenges [arXiv:0902.0361H]
- Hammer, F., Flores, H., Yang, Y. B., et al. 2009b, A&A, 496, 381 [NASA ADS] [CrossRef] [EDP Sciences]
- Heckman, T., & Lehnert, M. 2000, ApJS, 129, 493 [NASA ADS] [CrossRef]
- Hernquist, L. 1990, in Dynamics and Interactions of Galaxies, ed. R. Wielen (Berlin: Springer), 108
- Hopkins, P. F., Hernquist, L., Cox, T. J., Younger, J. D., & Besla, G. 2008, ApJ, 688, 757 [NASA ADS] [CrossRef]
- Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2009a, ApJ, 691, 1168 [NASA ADS] [CrossRef]
- Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2009b, MNRAS, 397, 802 [NASA ADS] [CrossRef]
- Ibata, R., Chapman, S., Ferguson, A. M. N., et al. 2005, ApJ, 634, 287 [NASA ADS] [CrossRef]
- Jiang, C. Y., Jing, Y. P., Faltenbacher, A., Lin, W. P., & Li, C. 2008, ApJ, 675, 1095 [NASA ADS] [CrossRef]
- Jogee, S., Miller, S. H., Penner, K., et al. 2009, ApJ, 697, 1971 [NASA ADS] [CrossRef]
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef]
- Liang, Y. C., Hammer, F., & Flores, H. 2006, A&A, 447, 113 [NASA ADS] [CrossRef] [EDP Sciences]
- Lilly, S., Schade, D., Ellis, R., et al. 1998, ApJ, 500, 75 [NASA ADS] [CrossRef]
- Lotz, J. M., Davis, M., Faber, S. M., et al. 2008, ApJ, 672, 177 [NASA ADS] [CrossRef]
- Lotz, J. M., Jonsson, P., Cox, T. J., & Primack, J. R. 2008, MNRAS, 391, 1137 [NASA ADS] [CrossRef]
- Maller, A. H., & Dekel, A. 2002, MNRAS, 335, 487 [NASA ADS] [CrossRef]
- Maller, A. H., Dekel, A., & Somerville, R. 2002, MNRAS, 329, 423 [NASA ADS] [CrossRef]
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 31 [CrossRef]
- Maraston, C., Daddi, E., Renzini, A., et al. 2006, ApJ, 652, 85 [NASA ADS] [CrossRef]
- Marcillac, D., Elbaz, D., Charlot, S., et al. 2006, A&A, 458, 369 [NASA ADS] [CrossRef] [EDP Sciences]
- Mouhcine, M. 2006, ApJ, 652, 277 [NASA ADS] [CrossRef]
- Melbourne, J. 2006, HST Proposal, 10965
- Nakamura, O., Fukugita, M., Brinkmann, J., & Schneider, D. P. 2004, AJ, 127, 2511 [NASA ADS] [CrossRef]
- Neff, S. G., Hutchings, J. B., Stanford, S. A., & Unger, S. W. 1990 ApJ, 99, 1088
- Neichel, B., Hammer, F., Puech, M., et al. 2008, A&A, 484, 159 [NASA ADS] [CrossRef] [EDP Sciences] (IMAGES-II)
- Noguchi, M. 1987, MNRAS, 228, 635 [NASA ADS]
- Peebles, P. J. 1976, ApJ, 205, 109 [NASA ADS] [CrossRef]
- Peirani, S., Hammer, F., Flores, H., Yang, Y., & Athanassoula, L. 2008, A&A, 496, 51 [NASA ADS] [CrossRef]
- Poggianti, B. M., Smail, I., Dressler, A., et al. 1999, ApJ, 518, 576 [NASA ADS] [CrossRef]
- Puech, M., Hammer, F., Flores, H., Östlin, G., & Marquart, T. 2006, A&A, 455, 119 [NASA ADS] [CrossRef] [EDP Sciences]
- Puech, M., Hammer, F., Lehnert, M., & Flores, H. 2007a, A&A, 484, 173 [NASA ADS] [CrossRef]
- Puech, M., Hammer, F., Flores, H., et al. 2007b, A&A, 476, 21 [NASA ADS] [CrossRef]
- Puech, M., Flores, H., Hammer, F., et al. 2008, A&A, 484, 173 [NASA ADS] [CrossRef] [EDP Sciences]
- Puech, M., Hammer, F., Flores, H., Neichel, B., & Yang, Y. 2009a, A&A, 493, 899 [NASA ADS] [CrossRef] [EDP Sciences]
- Puech, M., Hammer, F., Flores, H., et al. 2009b, A&A, submitted [arXiv:0903.3961]
- Ravikumar, C. D., Puech, M., Flores, H., et al. 2007, A&A, 465, 1099 [NASA ADS] [CrossRef] [EDP Sciences]
- Rawat, A., Kembhavi, A., Hammer, F., Flores, H., & Barway, S. 2007, A&A, 469, 483 [NASA ADS] [CrossRef] [EDP Sciences]
- Rawat, A., Hammer, F., Kembhavi, A., & Flores, H. 2008, ApJ, 681, 1089 [NASA ADS] [CrossRef]
- Robaina, A. R., Bell, E. F., Skelton, R. E., et al. 2009, ApJ, 704, 324 [CrossRef]
- Robertson, B., Bullock, J. S., Cox, T. J., et al. 2006, ApJ, 645, 986 [NASA ADS] [CrossRef]
- Rodrigues, M., Hammer, F., Flores, H., et al. 2008, A&A, 492, 371 [NASA ADS] [CrossRef] [EDP Sciences]
- Ryan, R. E., Jr., Cohen, S. H., Windhorst, R. A., & Silk, J. 2008, ApJ, 678, 751 [NASA ADS] [CrossRef]
- Sheth, K., Elmegreen, D. M., Elmegreen, B. G., et al. 2008, ApJ, 675, 1141 [NASA ADS] [CrossRef]
- Schiminovich, D. 2008, AIPC, 1035, 180 [NASA ADS]
- Silk, J. 1997, ApJ, 481, 703 [NASA ADS] [CrossRef]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef]
- Springel, V., & Hernquist, L. 2005, ApJ, 622, 9 [NASA ADS] [CrossRef]
- Steinmetz, M., & Navarro, J. 1999, ApJ, 513, 555 [NASA ADS] [CrossRef]
- Steinmetz, M., & Navarro, J. F. 2002, New Astron., 7, 155 [NASA ADS] [CrossRef]
- Stewart, K. 2009, in Proc. Galaxy Evolution: Emerging Insights and Future Challenges [arXiv:0902.2214]
- Stewart, K., Bullock, J. S., Wechsler, R., & Maller, A. 2009, ApJ, 702, 307 [NASA ADS] [CrossRef]
- Toomre, A. 1981, in The structure and evolution of normal galaxies, ed. S. M. Fall, & D. Lynden-Ball, Proc. of the Advanced Study Institute, Cambridge, 111
- Toomre, A., & Toomre, J. 1972, ApJ, 178, 623 [NASA ADS] [CrossRef]
- Toth, G., & Ostriker, J. P. 1992, ApJ, 389, 5 [NASA ADS] [CrossRef]
- Tutukov, A. V., & Federova, A. V. 2006, Astron. Rep., 50, 785 [NASA ADS] [CrossRef]
- van den Bergh, S. 2002, PASP, 114, 797 [NASA ADS] [CrossRef]
- Van den Bergh, S. 2009, ApJ, 694, 120 [NASA ADS] [CrossRef]
- White, S. D. M. 1984, ApJ, 286, 38 [NASA ADS] [CrossRef]
- Yang, Y., Flores, H., Hammer, F., et al. 2008, A&A, 477, 789 [NASA ADS] [CrossRef] [EDP Sciences] (IMAGES-I)
- Yang, Y., Hammer, F., Flores, H., Puech, M., & Rodrigues, M. 2009, A&A, 501, 437 [NASA ADS] [CrossRef] [EDP Sciences]
- Zheng, X. Z., Hammer, F., Flores, H., Assémat, F., & Pelat, D. 2004, A&A, 421, 847 [NASA ADS] [CrossRef] [EDP Sciences]
Online Material
Table 3: General properties of the 33 distant starbursts, of their progenitors whether they can be assumed to be reproduced by a major merger, as well as merger parameters adopted after the modelling.
Footnotes
- ... events?
![[*]](/icons/foot_motif.png)
- Table 3 is only available in electronic form at http://www.aanda.org
- ...
source
![[*]](/icons/foot_motif.png)
- The ZENO simulation code was retrieved from Josh Barnes' website (http://ifa.hawaii.edu/ barnes/software.html). The code was improved by GPU (execution 10 times faster than CPU).
All Tables
Table 1:
Morpho-kinematical classification of 52
![]() = 0.65 galaxies.
= 0.65 galaxies.
Table 2: Classification of the quality of the model in reproducing morphology and kinematics.
Table 3: General properties of the 33 distant starbursts, of their progenitors whether they can be assumed to be reproduced by a major merger, as well as merger parameters adopted after the modelling.
All Figures
| |
Figure 1: b+v, i and z combined images of 2 rotating disks identified by IMAGES. The dotted line is the superposition of the dynamical axis, dotted squares indicate the dispersion peak element. On the left, the dynamical and optical axes are aligned, and the dispersion peak is at the mass center, as expected for rotation (see Flores et al. 2006). On the right (J033238.60-274631.4) there is a slight misalignment of the dispersion peak that is likely caused by the nearby passage - 15 kpc - of a bulge-dominated galaxy, causing the observed burst of star formation at the bottom edge of the spiral galaxy. The velocity difference between the two galaxies is 540 km s-1, a value based on spectroscopy. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\begin{tabular}{ll}
IAU name and associated model \\
\includegr...
...& \includegraphics[height=2.85cm]{12115-fig2m.eps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg23.png)
|
Figure 2: Comparison between observations and models for the 26 distant starbursts that show non or semi-relaxed properties from their morphologies and kinematics. The top boxes indicates the significance of each panel. See Table 2 for the classification of the modelling and Table 3 for the general properties of these galaxies. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\begin{tabular}{ll}
J033230.57-274518.2 (POL 1:1 $r_{\rm peri}$\s...
... &\includegraphics[height=2.9cm]{12115-fig2za.eps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg24.png)
|
Figure 2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig3.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg27.png)
|
Figure 3: Top: distribution of the logarithm of the mass ratio, with M1 representing the mass of the galaxy observed by IMAGES. The full black histogram corresponds to the 24 galaxies, the nature of which we have robustly identified, including the 17 robust mergers, the 5 isolated rotating disks (arbitrarily set at M2/M1 = 0.01), the spiral galaxy in interaction and the galaxy with a satellite infall. The vertical dotted lines represent the limit of major mergers (mass ratio between 5 and 1/5). Middle: same as above but for galaxies with separated components (see Fig. 2) for which we have been able to estimate the mass ratio using the z-band photometry from ACS, which corresponds to the rest-frame V-band. Bottom: same as above but after applying the correction by Stewart (2009a) to recover the dark matter M2/M1 ratio. We have generalised this correction factor to values of M2/M1 (stellar) different to 0.3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig4.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg28.png)
|
Figure 4: Distribution of the merger phases for the modelled distant starbursts. The full black histogram corresponds to the same galaxies as in Fig. 3 (robust mergers/interactions and isolated rotating spirals). Phase 1 corresponds to the approaching phase until the first passage, phase 2 corresponds to the time elapsed between the first and the second passage, and phase 3 to the time after the second passage and before the elaboration of the rebuilt disk. During phase 3 the galaxy may show a chaotic morphology or a central starburst, always accompanied by a chaotic velocity field and dispersion peaks clearly offset from the mass center. Phase 4 correspond to the disk rebuilding phase, for which the disk is detected, the rotation is seen but could be offset from the main optical axis, and the dispersion peak(s) is (are) closer to the mass centre. The last phase corresponds to rotating spirals with regular velocity fields and a dispersion peak centred on the mass centre (e.g. Flores et al. 2006). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig5.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg30.png)
|
Figure 5: Distribution of the interaction orbits adopted to model the 26 mergers plus one interaction in the sample of 33 distant starbursts observed with IMAGES. The full black histogram corresponds to the 12 objects for which we have robustly identified the orbit. The x-axis represents the different orbits displayed in the figure. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig6.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg38.png)
|
Figure 6: Gas mass derived from Puech et al. (2009b) as a function of the stellar mass obtained from the Bell et al. (2003) prescriptions. The arrows in the upper left corner indicate how the stellar mass may be affected by different prescriptions of the galaxy synthesis population models (BC03 and M06 indicate the change by adopting Bruzual & Charlot 2003; and Maraston 2006 models, respectively), or of the IMF (S55 and K02 show the change due to the adoption of an IMF from Salpeter 1955 or from Kroupa 2002, respectively). The full and dashed lines indicate a gas fraction of 50% and a gas fraction from local galaxies (HI gas, Schiminovich 2008), respectively. The various symbols correspond to the morpho-kinematic classes defined in Sect. 1: rotating spirals (blue circles), heavily non-relaxed systems (red triangles) and semi-relaxed systems (green squares). Only error bars lower than 0.3 dex have been represented in this plot, and values with larger error bars are represented as open symbols. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig7.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg40.png)
|
Figure 7: Gas fraction distribution as a function of the merger phases. The former corresponds to a minimal value of the gas fraction in the sample of IMAGES starbursts (see text). The various symbols correspond to the morpho-kinematic classes, as in Fig. 6. Note the presence of the massive dry merger at phase = 2 (see the inserted image in Fig. 6) with a very low gas fraction (Yang et al. 2009). The full blue line shows the median gas-fraction in the progenitors derived from the gas consumption during the merger (see text). The dot-long-dashed line shows the same, but for a combination of Maraston et al. (2006) models and Kroupa IMF. The black solid line gives the median of the gas fraction values. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12115-fig8.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg45.png)
|
Figure 8:
Characteristic stellar mass doubling times as a function of the merger phases, as they are described in Fig. 4. The various symbols corresponds to morpho-kinematics classes as in Fig. 6.
The full blue line indicates their median value and the dashed red line
indicate the time during which the observed starbursts are involved in
the merger (median value for each phases 1 to 4),
as obtained from the simulations. It slightly decreases at
phase 4 because the masses of the 4 rebuilding disks (median
value, 2.1 |
| Open with DEXTER | |
| In the text | |
| |
Figure 9: b+v, i and z combined images of three additional starbursts whose kinematics has not been detected due to spatial resolution. The galaxy in the middle panel show a ring and possibly the nucleus of the secondary interloper. Kinematics are needed to confirm it as well as to verify the nature of the two other starbursts that could be in close interaction and just at the nuclei fusion, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12115-fig10.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2009/45/aa12115-09/Timg48.png)
|
Figure 10: Gas distribution in merger remnants from Barnes (2002) for 3:1 mergers, and for four different orbits, at the end of the simulations. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


