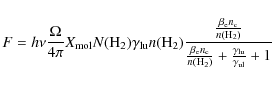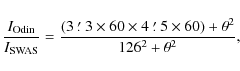EDP Sciences
Home All issues Volume 507 / No 3 (December I 2009) A&A, 507 3 (2009) 1455-1466 Full HTML
Free Access
Issue
A&A
Volume 507, Number 3, December I 2009
Page(s) 1455 - 1466
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200912064
Published online 08 October 2009

A&A 507, 1455-1466 (2009)

Odin observations of water in molecular outflows and shocks[*],[*],[*]

P. Bjerkeli1 - R. Liseau1 - M. Olberg1,2 - E. Falgarone3 - U. Frisk4 - Å. Hjalmarson1 - A. Klotz5 - B. Larsson6 - A. O. H. Olofsson7,1 - G. Olofsson6 - I. Ristorcelli8 - Aa. Sandqvist6

1 - Onsala Space Observatory, Chalmers University of Technology, 439 92 Onsala, Sweden
2 - SRON, Landleven 12, PO Box 800, 9700 AV Groningen, The Netherlands
3 - Laboratoire de Radioastronomie - LERMA, École Normale Supérieure, 24 rue Lhomond, 75231 Paris Cedex 05, France
4 - Swedish Space Corporation, PO Box 4207, 171 04 Solna, Sweden
5 - CESR, Observatoire Midi-Pyrénées (CNRS-UPS), Université de Toulouse, BP 4346, 31028 Toulouse Cedex 04, France
6 - Stockholm Observatory, Stockholm University, AlbaNova University Center, 106 91 Stockholm, Sweden
7 - GEPI, Observatoire de Paris, CNRS, 5 Place Jules Janssen, 92195 Meudon, France
8 - CESR, 9 Avenue du Colonel Roche, BP 4346, 31029 Toulouse, France

Received 13 March 2009 / Accepted 26 August 2009

Abstract
Aims. We investigate the ortho-water abundance in outflows and shocks in order to improve our knowledge of shock chemistry and of the physics behind molecular outflows.
Methods. We used the Odin space observatory to observe the H2O( 110-101) line. We obtain strip maps and single pointings of 13 outflows and two supernova remnants where we report detections for eight sources. We used RADEX to compute the beam averaged abundances of o-H2O relative to H2. In the case of non-detection, we derive upper limits on the abundance.
Results. Observations of CO emission from the literature show that the volume density of H2 can vary to a large extent, a parameter that puts severe uncertainties on the derived abundances. Our analysis shows a wide range of abundances reflecting the degree to which shock chemistry affects the formation and destruction of water. We also compare our results with recent results from the SWAS team.
Conclusions. Elevated abundances of ortho-water are found in several sources. The abundance reaches values as high as what would be expected from a theoretical C-type shock where all oxygen, not in the form of CO, is converted to water. However, the high abundances we derive could also be due to the low densities (derived from CO observations) that we assume. The water emission may in reality stem from high density regions much smaller than the Odin beam. We do not find any relationship between the abundance and the mass loss rate. On the other hand, there is a relation between the derived water abundance and the observed maximum outflow velocity.

Key words: ISM: jets and outflows - ISM: molecules - stars: pre-main sequence - ISM: supernova remnants

1 Introduction

Deeply embedded Class 0 stellar systems are observed to be associated with high velocity bipolar outflows (see e.g. Snell et al. 1980) which are believed to play an important role when stars are formed. During the phase when material is accreted onto the newborn star through the circumstellar disk, outflows are responsible for a necessary re-distribution of angular momentum. The specific angular momentum of the infalling material must at some point decrease to allow the final collapse. Although the basic theoretical concepts can be understood, there is still a great observational need to obtain further knowledge about the engine of these flows. Different models describing the driving mechanisms have been proposed and for that reason it is important to derive abundances of different species in order to distinguish between different physical scenarios. In this context, water is interesting in the sense that it is strongly affected by the presence of different types of shocks. At low temperatures, water is formed through a series of ion molecule reactions. This process is relatively slow and enhanced water abundances are thus not expected. At higher temperatures, the activation barrier for neutral-neutral reactions is reached, and for that reason water can be formed in a much more efficient way. Such elevated temperatures are reached in low velocity shocks, where the shock is smoothed by friction between ions and neutrals, called continuous shocks (see e.g. Bergin et al. 1998). Here, H2 is prevented from destruction and enhanced water abundances are expected. In this scenario, water is not only formed through reactions with oxygen but can also be released from its frozen state on dust grains (Kaufman & Neufeld 1996). In the discontinuous type of shock (jump shock), H2 is instead dissociated and water formation is prevented. The detection of water is aggravated by the difficulty of observing from ground based observatories. Prior to the launch of Odin (Hjalmarson et al. 2003; Nordh et al. 2003), two space born observatories capable of detecting water were in operation, the Infrared Space Observatory (ISO) (Kessler et al. 1996) and the Submillimeter Wave Astronomy Satellite (SWAS) (Melnick et al. 2000). The latter of these two also had the ability to observe the ground state transition of o-H2O  although the beam size was larger ( $3\hbox{$.\mkern-4mu^\prime$ }3 \times 4\hbox{$.\mkern-4mu^\prime$ }5$ elliptical compared to 2  $\stackrel {\prime}{_{\bf\cdot}}$1 circular for Odin). Water abundances derived from ISO data are in general higher than those derived from SWAS data. This discrepancy is addressed in the paper by Benedettini et al. (2002). In 2003, the Spitzer Space Telescope, capable of detecting hot water was launched (Werner et al. 2004).

Table 1:   Observation log for the sources analyzed in this paper.

Table 2:   Column densities of o-H2O and estimates of the ortho-water abundance, X(o-H2O) = N(o-H2O)/N(H2).

Table 3:   Column densities of o-H2O and estimates of the ortho-water abundance, X(o-H2O) = N(o-H2O)/N(H2).

In this paper, H2O( 110-101), observations of 13 outflows and two supernova remnants are discussed. Shocks from supernova explosions have a similar effect on the chemical conditions as molecular outflows. The different sources are discussed in Sect. 4.2 and summarized in Tables 1 and 2. Table 3 includes other outflows observed by Odin that have already been investigated by other authors or are in preparation for publication (W3, Orion KL, $\epsilon $ Cha-MMS1, IRAS 16293-2422, S140 and VLA1623). The analysis carried out in these papers is however different from the analysis made in the present paper. Similar observations as the ones discussed here have recently been presented by the SWAS team (Franklin et al. 2008). For that reason we make a brief comparison of the results for common sources.

2 Observations and reductions

2.1 H2O observations

All o-H2O observations were made with the Odin space observatory between 2002 and 2007 (see Table 1). Each revolution of 96 minutes allows for 61 minutes of observations, whereas the source is occulted by the Earth for the remaining 35 minutes. The occultations allow for frequency calibration using atmospheric spectral lines. At the wavelength of the ortho-water ground state transition, the 1.1 m Gregorian telescope has a circular beam with Full Width Half Maximum (FWHM) of 126 ${}^{\prime \prime}$(Frisk et al. 2003). The main beam efficiency is close to 90% as measured from Jupiter mappings (Hjalmarson et al. 2003). The main observing mode was sky switching, where simultaneous reference measurements from an unfocused 4 $.\!\!^\circ$4 FWHM sky beam were acquired. Position switching, where the entire spacecraft is re-orientated in order to obtain a reference spectrum, was the method of observation for a smaller number of targets. Three different spectrometers were used. Two of these are autocorrelators (AC1, AC2) and the third one is an acousto-optical spectrometer (AOS). The AOS has a channel spacing of 620 kHz (0.33  ${\rm km ~ s^{-1}}$ at 557 GHz), while the autocorrelators can be used in different modes. The majority of the data have a reconstructed pointing offset of less than 20 ${}^{\prime \prime}$. The data processing and calibration is described in detail by Olberg et al. (2003).

3 Results

The baseline-subtracted H2O spectra for the 15 previously not published sources are presented in the right column of Figs. B.1-B.4. All spectra are smoothed to a resolution of 0.5  ${\rm km ~ s^{-1}}$. The velocity interval has been chosen in order to emphasize the line profiles. In the left column, the calibrated raw data are plotted for comparison. These spectra have their baselines subtracted using a zeroth order polynomial.

4 Discussion

4.1 Densities, temperatures and radiative transfer analysis

In this paper we derive the beam averaged ortho-water abundance. The beam size is however likely to be larger than the emitting regions for several of the sources that are analyzed. We use RADEX[*] (van der Tak et al. 2007), a publicly available code that uses the method of mean escape probability for the radiative transfer. For interstellar gas at relatively low temperatures and densities ($\ll$108 cm-3), water excitation will be subthermal and the emission will be on the linear part of the curve of growth, i.e. even an optically thick line will behave as being effectively optically thin (Linke et al. 1977; Snell et al. 2000). For an effectively optically thin line, the result of a radiative transfer code like RADEX is essentially the same as that of the analytical expression for a collisionally excited transition

\begin{displaymath} F = h \nu \frac{\Omega}{4 \pi} X_{{\rm mol}} N({\rm H_2}) \... ...\rm H_2})} + \frac{\gamma_{{\rm lu}}}{\gamma_{{\rm ul}}} + 1} \end{displaymath} (1)

(Liseau & Olofsson 1999). F is the integrated line flux, $\gamma_{{\rm lu}}$ and $\gamma_{{\rm ul}}$ are the upward and downward collision coefficients, $n_{{\rm c}}$ is the critical density and $\beta_{{\rm e}}$ is the photon escape probability. The molecular datafiles that are used by RADEX are taken from the Leiden Atomic and Molecular Database (LAMDA)[*]. Here, the collision rates between o-H2O and H2 have been retrieved from Phillips et al. (1996), Dubernet & Grosjean (2002) and Faure et al. (2007). Recently, new rate coefficients of o-H2O with p-H2 have been published by Dubernet et al. (2009). According to the results presented in this paper (their Fig. 8), collision rates used in RADEX should not differ by more than a factor of three in the temperature regime below 40 K. The ortho to para ratio of H2 is in RADEX assumed to be thermal. As input parameters, the line intensity, line width, kinetic temperature and volume density of the observed gas must be supplied. The difficulty in obtaining good estimates for the two latter parameters has to be kept in mind. In Fig. 1, we plot the o-H2O column density as a function of volume density for a test case. The line intensity has been set to 0.1 K and the linewidth to 10  ${\rm km ~ s^{-1}}$. From this figure, it is clear that the derived abundances are very uncertain when the kinetic temperatures are low.
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12064f1.eps}} \end{figure} Figure 1:

The derived o-H2O column density as a function of volume density for different temperatures. The line intensity for this test case has been set to 0.1 K while the line width has been set to 10  ${\rm km ~ s^{-1}}$.

Open with DEXTER

In this study, the temperature is taken from the literature while the volume density is inferred from CO observations carried out by others. These two parameters however are not expected to have constant values across the large Odin beam due to the quite complex morphology of molecular outflows. For all the sources, we only include the cosmic microwave background as a radiation field. For simplicity we have chosen the line intensity to be equal to the peak value while the line width is taken as the width of the line at 50% of this value. The output column density of ortho-water is then used to derive the abundance relative to molecular hydrogen, X(o- $\rm {H_2O}$) = N(o- $\rm {H_2O}$)/N($\rm {H_2}$).

A widely used method to obtain the column density for H2 is to measure the CO abundance assuming a constant universal ratio, e.g. [ $\rm {CO/H_2}$] = 10-4 (see e.g. Dickman 1978). In this paper we use this method where feasible (different methods are used for TW Hya and 3C391 BML). Volume densities and beam averaged column densities are estimated from literature data assuming cylindrical geometry and a mean molecular weight $\mu = 2.4$. No correction for inclination is made. The inferred volume densities (Method 1) should be considered as lower limits for two reasons. First, the size of the water emitting regions is poorly known. These regions may very well be smaller than the CO emitting regions, potentially resulting in a higher average density. Secondly, shocks, if present, will compress the gas even further. For some of the sources, there are estimates of the volume density, given in the literature, that are significantly higher than the ones used in this paper. In these cases we also estimate an alternative ortho-water abundance (Method 2).

Table 2 includes the measured integrated intensity over the observed lines and the derived water abundance. The integrated intensity is measured over the entire line including the central region as well as the outflow wings. Exceptions are those outflow sources for which strong self absorption can be seen (e.g. L1157, Ser SMM1). For these objects, the integrated intensity has been measured for the red and the blue wings separately. For sources with no detection, we set a $3 \sigma$ upper limit on the integrated intensity in a velocity interval of 10  ${\rm km ~ s^{-1}}$ (except for TW Hya, where a linewidth of 1  ${\rm km ~ s^{-1}}$ has been used).

4.2 Notes on individual sources

4.2.1 L1448

L1448 is a dark cloud in the constellation of Perseus at the distance of 250 pc (Enoch et al. 2006). The large, highly collimated outflow originating from L1448-mm shows enhanced emission from SiO in both lobes (Nisini et al. 2007). Franklin et al. (2008) report o-H2O abundances of X(o-H2O) = 1.5 $\times$ 10-6 in the blue wing and X(o-H2O) = 3.7 $\times$ 10-6 in the red wing. We report observations in three positions across the structure, where the northern position also covers the outflow from L1448 IRS3. The possible detections in both lobes can, due to instabilities in the baselines, only be classified as likely. There is also a tentative detection of a bullet feature in the northern position at $v_{{\rm lsr}} \sim +35$  ${\rm km ~ s^{-1}}$and we note that this observation is consistent with the high speed CO bullet B3 reported by Bachiller et al. (1990). However, the preliminary analysis of HCO+ data, recently taken at the Onsala Space Observatory, does not reveal any emission at this velocity. Mass loss rates of M $_{\rm loss}$ = 4.6 $\times$ 10-6 $M_{\odot}$ yr-1 for L1448-mm and M $_{\rm loss}$ = 1.1 $\times$ 10-6 $M_{\odot}$ yr-1 for L1448 IRS3 were reported by Ceccarelli et al. (1997) based on CO observations carried out by Bachiller et al. (1990). N(H2) = 6 $\times$ 1019 cm-2 and n(H2) = 1 $\times$ 103 cm-3 are inferred from mass and size estimates reported by the same authors. We assume the width of the flow to be 40 ${}^{\prime \prime}$. Taking the gas temperature to be T = 37 K for all positions (Bachiller et al. 1995, dust temperature towards L1448-mm) we derive ortho-water abundances of between 6 $\times$ 10-4 and 2 $\times$ 10-3 in the outflow. Using the higher volume density ($\sim$104) estimated by Bachiller et al. (1990), we derive ortho-water abundances between 1 $\times$ 10-4 and 3 $\times$ 10-4.

4.2.2 HH211
The Herbig-Haro jet HH211 is also located in Perseus, 315 pc away (Herbig 1998). It was observed in three different positions enclosing the relatively small outflow. The central and northern beams contain the HH211-mm region. We use the mass estimates from Gueth & Guilloteau (1999) as the basis for our inferred volume densities, n(H2) = 1 $\times$ 104 cm-3 and column densities, N(H2) = 4 $\times$ 1019 cm-2 in all three positions. The size of the outflow is taken to be 90 ${}^{\prime \prime}$ $\times$ 10 ${}^{\prime \prime}$. The temperature in the clumps of the IC348 region varies between 12 K close to the centers and 20-30 K at the edges (Bachiller et al. 1987). Assuming a temperature T = 12 K we derive upper limits of X(o-H2O) < 8 $\times$ 10-4 at the central position and X(o-H2O) < (1-2) $\times$ 10-3 in the outflow. A temperature, of T = 30 K would lower these upper limits by almost a factor of ten. The two-sided mass loss rate was estimated by Lee et al. (2007) to be M $_{\rm loss}$ $\sim$ (0.7-2.8) $\times$ 10-6 $M_{\odot}$ yr-1.

4.2.3 L1551
L1551 is probably one of the most rigorously studied molecular outflows. The main source L1551 IRS5 is located at a distance of 140 pc in the Taurus-Auriga cloud complex (Kenyon et al. 1994). The mass loss rate is in the range 8 $\times$ 10-7 < M $_{\rm loss}$ < 2 $\times$ 10-6 $M_{\odot}$ yr-1 (Liseau et al. 2005, and references therein). In this paper, we use the mass estimate from CO observations provided by Stojimirovic et al. (2006) to calculate the volume density and column density as n(H2) = 3 $\times$ 103 cm-3 and N(H2) = 1 $\times$ 1021 cm-2, respectively. These authors estimate the mass of the outflow to be 7.2 $M_{\odot}$ and we estimate the size of the outflow to $1.3 \times 0.2$ pc. Assuming a kinetic temperature of 20 K we give upper limits on the ortho-water abundance in three positions across the outflow. We obtain upper limits, ranging from X(o-H2O) < 8 $\times$ 10-5 to X(o-H2O) < 2 $\times$ 10-4.
\begin{figure} \par\includegraphics[width=7.5cm,clip]{12064f2.eps} % \end{figure} Figure 2:

The three positions observed by Odin are shown overlaid on a CO (2-1) map of L1448 (Bachiller et al. 1995). The circles correspond to the Odin beam at 557 GHz. Coordinate offsets are given with respect to L1448-mm: $\alpha _{2000}$ = 03:25:38.8, $\delta _{2000}$ = 30:44:05.0. The positions of L1448-mm and L1448 IRS3 are indicated by star symbols.

Open with DEXTER

4.2.4 TW Hya
At the distance of 56 pc (Qi et al. 2008), TW Hya is the nearest known T Tauri star. Its accretion disk of size 7 ${}^{\prime \prime}$ is seen essentially face-on and is point-like to Odin, i.e. particularly for any H2O emission region, the beam filling factor would presumably be $\ll$3 $\times$ 10-3. In our sample, the object has the lowest mass loss rate, viz. $10^{-12~{\rm to}~-11}$ $ \le $M $_{\rm loss}$ < 7 $\times$ 10-10  $M_{\odot} ~ {\rm yr}^{-1}$(Dupree et al. 2005; Lamzin et al. 2004, respectively), and with an age of about 10 Myr (de la Reza et al. 2006), it is likely also the oldest. Herczeg et al. (2004) report the detection of $L\alpha$-excited H2, with an N(H2) =  $ 3 \times 10^{18}$ cm-2, which appears accurate to within an order of magnitude. This value refers to the innermost disk regions. In the outer disk, CO and other trace molecules, including their isotopic and/or deuterated forms, have also been detected (van Zadelhoff et al. 2001; Qi et al. 2008; Kastner et al. 1997). In the HCN forming regions, the densities are determined to be 106-108 cm-3 (van Zadelhoff et al. 2001). From intermediate J-transitions of CO, these authors estimated temperatures to be in the range $40 \le T < 150$ K.

Not entirely unexpected, Odin did not detect the H2O 557 GHz line[*]. For representative disk parameters and a line width of <1  ${\rm km ~ s^{-1}}$, the rms of 14 mK would imply an abundance, X(o-H2O) < 1 $\times$ 10-8. For the modeling we used a temperature of 40 K. However, increasing this parameter to 150 K will not decrease the derived upper limit by more than 20%.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{12064f3.ps} \end{figure} Figure 3:

L1448 spectra. The positions are listed in Table 2 and shown in Fig. 2. The letter in the upper right corner indicates in which part of the flow the spectra were collected (R = red, B = blue and C = center). The spectra were baseline subtracted and smoothed to a resolution of 0.5  ${\rm km ~ s^{-1}}$.

Open with DEXTER
4.2.5 $\epsilon $Cha  I N

The star forming cloud Chamaeleon  I is located at a distance of 150 pc (Knude & Hog 1998). From the estimated age (3.8 $\times$ 104 yr), mass (0.21 $M_{\odot}$) and maximum velocity ($\sim$6  ${\rm km ~ s^{-1}}$) reported by Mattila et al. (1989), we obtain a mass loss rate, M $_{\rm loss}$ = 3.3 $\times$ 10-7 $M_{\odot}$ yr-1. The velocity of the wind is assumed to be 100 ${\rm km ~ s^{-1}}$. We estimate N(H2) = 4 $\times$ 1020 cm-2 and n(H2) = 2 $\times$ 103 cm-3 from CO observations carried out by the same authors. The width of the flow is approximately 0.1 pc. Adopting the temperature 50 K, given by Henning et al. (1993), we obtain an upper limit, X(o-H2O) < 3 $\times$ 10-5.

\begin{figure} \par\includegraphics[width=6.5cm,clip]{12064f4.eps} \end{figure} Figure 4:

The three positions observed by Odin are shown overlaid on a CO (3-2) map of Sa136 (Parise et al. 2006). The circles correspond to the Odin beam at 557 GHz. Coordinate offsets are given with respect to: $\alpha _{2000}$ = 12:01:37.0, $\delta _{2000}$ = -65:08:53.5. The positions of the sources IRS1 and IRS2 are indicated with star symbols.

Open with DEXTER

4.2.6 Sa136 (BHR71)

The Sa136 Bok globule outflows (Sandqvist 1977), at about 200 pc distance, are driven by a binary protostellar system. The secondary CO outflow driven by IRS 2 is more compact (Bourke 2001) than the larger outflow driven by IRS 1.

Taking the column density measurements made by Parise et al. (2006), assuming a [CO/H2] ratio of $\rm {10^{-4}}$ we obtain N(H2) = 1 $\times$ 1021 cm-2, N(H2) = 4 $\times$ 1020 cm-2 and N(H2) = 3 $\times$ 1021 cm-2 in the red, central and blue part of the flows respectively. We assume that the flow has a depth of 0.07 pc, yielding volume densities $n({\rm H_2}) = 6$ $\times$ 103 cm-3, $n({\rm H_2})$ = 2 $\times$ 103 cm-3 and $n({\rm H_2})$ = 1 $\times$ 104 cm-3 in the same regions. Parise et al. (2008) estimate T = 30 - 50 K from CO and methanol observations. In our modeling we use T = 40 K. We estimate the ortho-water abundances as (0.1-1) $\times$ 10-5 in the outflow and 2 $\times$ 10-4 at the central position. However, Parise et al. (2008) give a density of $n({\rm H_2})$ = 1 $\times$ 105 cm-3 in the region. Using this higher value we obtain ortho-water abundances of (2-6) $\times$ 10-7 in the outflow and 3 $\times$ 10-6 towards the central source. The emission has broader wings in the central position, a feature present also in the SWAS data. The origin of this high velocity component and the elevated water abundance might be the smaller outflow originating from IRS 2, visible in Fig. 4. Based on the outflow mass (1.3 $M_{\odot}$), dynamical time scale (1 $\times$ 104 yr) and flow velocity (28  ${\rm km ~ s^{-1}}$) provided by Bourke et al. (1997)[*] for the larger flows, we estimate the mass loss rate to be M $_{\rm loss}$ = 3.6 $\times$ 10-5 $M_{\odot}$ yr-1. The wind velocity is assumed to be 100  ${\rm km ~ s^{-1}}$.

\begin{figure} \par\includegraphics[width=8cm,clip]{12064f5.ps} \end{figure} Figure 5:

The same as Fig. 3 but for Sa136.

Open with DEXTER

4.2.7 HH54 B

The Herbig-Haro object HH54 B is situated in the Cha  II cloud at roughly 200 pc (Hughes & Hartigan 1992). During the observations, the correlator suffered from ripple. This had the effect of increasing the line intensity and a substantial amount of data had to be abandoned. The signal detected can therefore only be classified as tentative although we are confident that the data do not show any systematic variations. Complementary data were obtained in CO(3-2), CO(2-1), SiO(5-4), SiO(3-2) and SiO(2-1) with the SEST telescope (see Appendix A) and in CO(5-4) with Odin. The CO(5-4) data suffer from frequency drift, something that adds an $\sim$10  ${\rm km ~ s^{-1}}$ uncertainty to our velocity scale. However, we do not believe that this gives large uncertainties on the line strength.

No shock-enhanced emission was detected in any of the observed SiO transitions. This result seems not easily reconcilable with the prediction from theoretical C-shock models (see Fig. 6 of Gusdorf et al. 2008), which appear closely adaptable to the conditions in HH 54 (Neufeld et al. 2006; Liseau et al. 1996).

Both the CO (2-1) and (3-2) lines show an absorption feature at +2.4  ${\rm km ~ s^{-1}}$, which corresponds to the LSR-velocity of the molecular cloud. In addition, a strong blue wing is observed in all positions, but essentially no redshifted gas, which is in agreement with the (1-0) observations by Knee (1992). Both (2-1) and (3-2) transitions peak at the central map position, i.e. on HH 54B itself and their integrated intensities, $\int\!\!T_{\rm A}^{\star}~\rm d\upsilon$, are given in Table A.1.

\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f6.ps}} \end{figure} Figure 6:

From top to bottom the CO(5-4), CO(3-2), CO(2-1) and ${\rm H_2O(1_{10}{-}1_{01})}$ spectra observed towards HH54 B are plotted. The dotted vertical line shows the cloud LSR-velocity at +2.4  ${\rm km ~ s^{-1}}$.

Open with DEXTER

For the comparison with the ISO-LWS model of Liseau et al. (1996), we use the average radiation temperature, approximated by $\langle T \rangle =\eta_{\rm mb}^{-1}~\int\!\!T_{\rm A}^{\star}~{\rm d}\upsilon/\int\!\rm d\upsilon$. This yields $\langle T_{21}\rangle = (1.2 \pm 0.02)$ K and $\langle T_{32}\rangle = (3.2 \pm 0.33)$ K for the CO (2-1) and (3-2) lines, respectively. Both values are smaller, by 25% and 40% respectively, than the model predictions of 1.6 K and 5.7 K, which were based on a single-temperature approximation. Even though the strength of the CO(5-4) line is uncertain, it shows a slightly higher temperature than the predicted 0.3 K. Putting it all together, the model predicts the radiation temperature in all three lines to within an order of 2. For the RADEX analysis we use the ISO-LWS model T = 330 K, n(H2) = 2 $\times$ 105 cm-3 and N(H2) = 3 $\times$ 1019 cm-2, where the column density has been diluted to the Odin beam. We obtain a beam averaged water abundance of X(o-H2O) = 3 $\times$ 10-6. However, recently Neufeld et al. (2006) estimate a higher H2 column density for the warm gas, a fact that could alter our derived abundance by an order of magnitude downwards. The mass loss rate of the unknown driving source has been estimated by Giannini et al. (2006) as M $_{\rm loss} = 3 \times 10^{-6}$ $M_{\odot}$ yr-1.

4.2.8 G327.3-0.6
The hot core G327.3-0.6 is located in the southern hemisphere at the distance of 2.9 kpc (Bergman 1992). CO line profiles obtained by Wyrowski et al. (2006) weakly indicate the presence of outflows, however, to date there has been no further study of this. From CO observations performed by these authors, we infer N(H2) = 2 $\times$ 1022 cm-2 and n(H2) = 4 $\times$ 105 cm-3, assuming [ $\rm {{}^{18}CO/H_2}$] = 10-7 and a source size 25 ${}^{\prime \prime}$. The volume density inferred is slightly lower than the range 106-108 cm-3 given by Bergman (1992), who also estimates the temperature to be within the range of 40-200 K. Using a value of 100 K gives an upper limit of X(o-H2O) < 8 $\times$ 10-10. A temperature of 40 K will increase the inferred upper limit by a factor of 8.

4.2.9 NGC 6334  I

At least two outflows are emerging from NGC 6334  I, located in the constellation Scorpius (McCutcheon et al. 2000) at the distance of 1.7 kpc (Neckel 1978). From CO observations provided by Leurini et al. (2006) we obtain a beam averaged column density 1 $\times$ 1020 cm-2 and a volume density 4 $\times$ 103 cm-3. We assume that the gas temperature is the same as the dust temperature, viz. T = 100 K (Sandell 2000). This is consistent with Leurini et al. (2006) who set a lower limit on the kinetic temperature at 50 K. With the above properties we derive an abundance of X(o-H2O) = 5 $\times$ 10-5.

The baseline subtracted spectrum does not show any evidence of high velocity gas. However, we do not find this easily reconcilable with the high velocity gas detected in several CO transitions by Leurini et al. (2006). One possibility could be the curved baseline hiding the outflow wings. Therefore, we investigate also an alternative case where we assume that the entire curvature stems from the outflowing gas. This secondary scenario is perhaps not very likely. However, at present it is not possible to draw any firm conclusions. The estimated depth of the absorption feature is greater than the continuum level of 360 Jy, interpolated from 800 $\mu$m observations provided by Sandell (2000). In this secondary case we derive the abundance X(o-H2O) = 2 $\times$ 10-3.

\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f7.ps}} \end{figure} Figure 7:

The same as Fig. 3 but for NGC 6334 I. The black spectrum represents the first case and the grey spectrum represents the second case as described in Sect. 4.2.9

Open with DEXTER

4.2.10 Ser SMM1

The Serpens star forming dark cloud is situated in the inner Galaxy at a distance of 310 pc (de Lara et al. 1991). Franklin et al. (2008) estimated ortho-water abundances of X(o-H2O) = 7.1 $\times$ 10-7 and X(o-H2O) = 3.8 $\times$ 10-7 in the blue and red wing respectively while Larsson et al. (2002) estimate the water abundance as X(H2O) = 1 $\times$ 10-5 in the region. Davis et al. (1999) provide the mass and size of the outflow based on CO observations. Assuming a width of 0.2 pc yields n(H2) = 1 $\times$ 103 cm-3 and N(H2) = 5 $\times$ 1020 cm-2. From O I(63 $\mu$m) measurements carried out by Larsson et al. (2002, and references therein) we obtain the mass loss rate, M $_{\rm loss}$ = 3 $\times$ 10-7 $M_{\odot}$ yr-1. The temperature of the dust was constrained by White et al. (1995) to be 30 K < T < 40 K. Using T = 35 K and the above properties we obtain X(o-H2O) = 9 $\times$ 10-5 and X(o-H2O) = 5 $\times$ 10-5 in the blue and red flow.

\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f8.ps}} \end{figure} Figure 8:

The same as Fig. 3 but for Ser SMM1.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7cm,clip]{12064f9.eps} \end{figure} Figure 9:

The four positions observed by Odin are shown overlaid on a CO (2-1) map of L1157 (Bachiller et al. 2001). The circles correspond to the Odin beam at 557 GHz. Coordinate offsets are given with respect to L1157-mm, indicated in the figure with a star symbol: $\alpha _{2000}$ = 20:39:06.4, $\delta _{2000}$ = +68:02:13.0. The black and white squares refer to the knots B0, B1, B2, R0, R1, R and R2 described in Bachiller et al. (2001).

Open with DEXTER

4.2.11 B335
The dense core in the B335 globule is believed to be one of the major candidates for protostellar collapse. This isolated source at the distance of 150 pc (Stutz et al. 2008) harbors several Herbig-Haro objects associated with a bipolar outflow (see e.g. Gålfalk & Olofsson 2007). Following the outflow mass estimate of 0.44 $M_{\odot}$ in Hirano et al. (1988) we derive n(H2) = 1 $\times$ 103 cm-3 and N(H2) = 3 $\times$ 1020 cm-2. The size of the outflow is taken to be 2$^{\prime}$ $\times$ 8$^{\prime}$. Based on the same mass, a dynamical time scale (2.3 $\times$ 104 yr) and a flow velocity (13  ${\rm km ~ s^{-1}}$), provided by these authors we derive M $_{\rm loss}$ = 2.5 $\times$ 10-6 $M_{\odot}$. The velocity of the wind is assumed to be 100 ${\rm km ~ s^{-1}}$. In our modeling we use a kinetic temperature of 20 K. This is an intermediate value in the modeling carried out by Evans et al. (2005, their Fig. 8) who give the temperature as a function of radius for the inner 0.1 pc region. The derived upper limit of the water abundance is X(o-H2O) < 1 $\times$ 10-3. The rms implies a water abundance, X(o-H2O) $ < \rm {\sim 10^{-7}}$ according to the infall model presented by Hartstein & Liseau (1998).

4.2.12 L1157

\begin{figure} \par\includegraphics[width=7.4cm,clip]{12064f10.ps} \end{figure} Figure 10:

The same as Fig. 3 but for L1157.

Open with DEXTER

L1157 is a Class 0 object in the constellation of Cepheus situated at a distance of 250 pc (Looney et al. 2007). It drives a prototype bipolar outflow which was observed by Odin in four different positions. The mass loss rate can be derived from mass (0.62 $M_{\odot}$) and time scale (15 000 yr) estimations given by Bachiller et al. (2001). Assuming a maximum CO velocity of 20  ${\rm km ~ s^{-1}}$ and a stellar wind velocity of 100 km s-1, we derive M $_{\rm loss}$ = 8.3 $\times$ 10-6 $M_{\odot}$ yr-1 . The Odin strip map covers the bulk of the outflow with two pointings in the red wing, one in the blue, and one on the driving source of the outflow itself (Fig. 9). The observations were carried out using the AOS and the AC2 simultaneously. The spectra shown in Fig. 10 are the averages of the merged data. The total mass in the different parts of the flow were obtained from CO observations carried out by Bachiller et al. (2001). From this we estimate n(H2) = 2 $\times$ 103 cm-3 and N(H2) = 2 $\times$ 1020 cm-2 in the northern lobe, while n(H2) = 3 $\times$ 103 cm-3 and N(H2) = 2 $\times$ 1020 cm-2 in the central and southern region. The size of the CO outflow is taken to be 50 ${}^{\prime \prime}$ $\times$ 375 ${}^{\prime \prime}$. For all four positions we set the kinetic temperature to T = 30 K, a rough global estimate based on Bachiller et al. (2001). We calculate the abundances in the outflow to be within the range of $\rm {2 \times 10^{-4}}$ and $\rm {1 \times 10^{-3}}$. The derived water abundance in the central region is slightly lower, X(o-H2O) = 2 $\times$ 10-4 in the blue lobe and X(o-H2O) = 3 $\times$ 10-5 in the red. The increased blue emission likely originates from the outflow. Within the Odin beam are the positions B0 and B1 that show peaked emission in H2CO, CS, CH3OH, SO (Bachiller et al. 2001, their Fig. 1) and SiO (Nisini et al. 2007). Franklin et al. (2008) estimated X(o-H2O) = 8.0 $\times$ 10-6 and X(o-H2O) = 9.7 $\times$ 10-6 in the blue and red wing respectively.

Bachiller et al. (2001) estimates the density around the protostar to be $\sim$106 cm-3. When moving from B0 to B2, the density changes from $\sim$3 to 6 $\times$ 105 cm-3. Using n(H2) = 1 $\times$ 106 cm-3 and n(H2) = 5 $\times$ 105 cm-3 for the central and southern part respectively we obtain the abundances X(o-H2O) = 5 $\times$ 10-7 and X(o-H2O) = 2 $\times$ 10-6.

4.2.13 NGC 7538 IRS1
NGC 7538 IRS1 is a region of ongoing high mass star formation. The main infrared source IRS1 is located at the boundary of an H II region in the Perseus arm, located at a distance of 2.7 kpc (Moscadelli et al. 2008). In addition to IRS1, and its high velocity outflow, also several other sub-mm sources fall into the large Odin beam. The mass loss rate from IRS1 was estimated by Kameya et al. (1989) to be M $_{\rm loss}$ = 1 $\times$ 10-4 $M_{\odot}$ yr-1. The total mass and size of this region is given by the same authors, yielding a volume density and column density of n(H2) = 3 $\times$ 103 cm-3 and N(H2) = 4 $\times$ 1020 cm-2respectively. The kinetic temperature is assumed to be the same as the dust temperature, i.e. T = 40 (Sandell & Sievers 2004). We infer a limit to the water abundance of X(o-H2O) < 1 $\times$ 10-4.

\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f11.ps}} \end{figure} Figure 11:

The same as Fig. 3 but for NGC 7538 IRS1.

Open with DEXTER

4.2.14 Supernova remnants
3C391 BML is a supernova remnant at a distance of 8 kpc (Chen & Slane 2001). The temperature, volume density and column density of the gas were constrained to 50 K $\leq T \leq 125$ K, 104 cm $^{-3} \leq n$(H2) $\leq$ 5 $\times$ 105 cm-3and N(H2) $\gtrsim$ 4 $\times$ 1020 cm-2 from OH 1720 MHz maser observations carried out by Lockett et al. (1999). Using the lowest values for the temperature and volume density we calculate an upper limit of X(o- ${\rm H_2O}) $ < 4 $\times$ 10-6.

IC443 is a shell type supernova remnant at the distance of about 1.5 kpc (Fesen 1984). The broad emission peaks are labeled A through H, where Odin has observed clump G. The volume density and temperature were modeled by van Dishoeck et al. (1993) as n(H2) = 5 $\times$ 105 cm-3 and T = 100 K. Using the CO column density inferred by the same authors, assuming a $\rm {[CO/H_2]}$ ratio of $\rm {10^{-4}}$ and a source size of 40 ${}^{\prime \prime}$ $\times$ 100 ${}^{\prime \prime}$, we obtain N(H2) = 3 $\times$ 1021 cm-2. The derived abundance is X(o- ${\rm H_2O}) = \rm {4\times 10^{-8}}$. This is in agreement with Snell et al. (2005) who derive an o-H2O abundance with respect to 12CO, X(o-H2O) = 3.7 $\times$ 10-4.

\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f12.ps}} \end{figure} Figure 12:

The same as Fig. 3 but for IC443-G.

Open with DEXTER

4.3 Water abundance

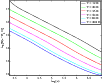
The water abundances inferred from our analysis are given with respect to the molecular column density within the Odin beam. The values span a wide range with most of the sources having an abundance of the order $\rm {10^{-5}}$- $\rm {10^{-4}}$. The highest abundances in our sample are found in the outflows of L1157 and L1448. Supposing that the assumed physical properties are correct, we see an increased abundance in both the blue and the red wing of L1157. The water abundance is low in G327.3-0.6. The reason for this is the combination of the high H2 column density and temperature used. The water emission is also very likely beam diluted due to the large distance, resulting in lower beam averaged o-H2O abundance.

Assuming an inclination angle of 60$^{\circ }$ with respect to the line of sight for all the targets, we plot the o-H2O abundances versus the maximum velocities (Fig. 13). The maximum velocities are taken from the spectra as the maximum offsets between the cloud velocity and the flow velocity. There is a correlation between the derived abundances and the maximum velocities of the outflowing gas. The solid line in Fig. 13 is the first order polynomial least square fit:

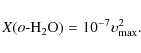
\begin{displaymath}X(o \mbox{-} {\rm H_2O}) = 10^{-7}\upsilon_{\rm max}^{2}. \end{displaymath} (2)

The correlation coefficient is 0.57 while the p-value, testing the hypothesis of no correlation is 0.04. Following the C-shock modelling carried out by Kaufman & Neufeld (1996), a relationship is expected when shocks are responsible for the emission. However, the abundances do not show any tendency to level off with velocities greater than $\sim$20  ${\rm km ~ s^{-1}}$as shown in their Fig. 3. This is an indication of a lack of J-type dissociative shocks in this sample of outflows. There are however uncertainties in our simplified analysis, for example the inclination of the outflow lobes and the RADEX analysis. The dependence between the water abundance and the maximum velocity is consistent with the analysis made by Franklin et al. (2008), although their method is based on binning the weak outflow lines into intervals of 5  ${\rm km ~ s^{-1}}$.
\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f13.eps}} \end{figure} Figure 13:

o-H2O abundance plotted against the maximum velocity for an overall inclination of 60$^{\circ }$ with respect to the line of sight. The solid line represents a linear fit of $\log$[X(o-H2O)] versus $\log (\upsilon_{\rm max})$ with the same inclination angle applied. The dotted dashed line represents the fit with a inclination correction of 35$^{\circ }$ while the dashed line represents the fit with an inclination angle correction of 85$^{\circ }$. The errorbars from the measurements are smaller than the circles.

Open with DEXTER
We also plot the ortho-water abundances versus mass loss rates in Fig. 14. G.327-0.6 is not included due to the lack of observations towards the assumed outflow, and NGC 6334 I is not included in Figs. 13, 14 due to the curvature in the baseline. No obvious relationship can be picked out. The absence of a correlation is surprising inasmuch as high mass loss rates affect the budget of material available for water formation.
\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f14.eps}} \end{figure} Figure 14:

o-H2O abundance plotted against the mass loss rate. The triangles represent the high upper limits for each source in the o-H2O abundance, while the circles symbolize values where a detection has been made. Dashed lines represent the cases where there is a range in the inferred abundances or mass loss rates.

Open with DEXTER

4.4 Comparison with SWAS data

For all the outflows except TW Hya the gas volume density, used as an input parameter to RADEX, has been derived from CO observations. This method generally underestimates the mass of the regions. The possibility that the water emission originates from gas with a higher volume density than this can therefore not be ruled out. Nevertheless, we are confident that the volume density does span a wide range of values. This is also one of the reasons why several of our derived abundances deviate from those inferred by Franklin et al. (2008). They use a single volume density of n(H2) = 105 cm-3 and our values differ from this by more than two orders of magnitude for some of the sources (see Table 2). Figure 15 shows a histogram of the numbers of sources within different volume density ranges. The difficulty to estimate the gas column density of the water emitting regions is a problem that has to be adressed in order to interpret future observations with Herschel.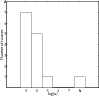
\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f15.eps}} \end{figure} Figure 15:

A histogram of the gas volume density estimated in the outflows studied in this paper showing a variation that spans over six orders of magnitude.

Open with DEXTER

The integrated intensities for the SWAS and Odin outflow spectra are compared in Fig. 16 to provide an estimate of the source size of the water emitting regions. The dashed 1:1 ratio line illustrates the case where the source fills both antenna beams while the dashed 3.37:1 line indicates a small source size compared to both beams. Assuming that both the emitting sources and the antenna responses are circularly symmetric and Gaussian, these ratios follow from the relation:

\begin{displaymath} \frac{I_{\tiny {{\rm Odin}}}}{I_{\tiny {{\rm SWAS}}}} = \fr... ...me}{_{\bf\cdot}}$ 5} \times 60) + \theta^2}{126^2 + \theta^2}, \end{displaymath} (3)

where $\theta$ is source size. The SWAS spectra have been retrieved from the SWAS spectrum server and baseline subtracted. The integrated intensities are measured in the same regions as for the Odin spectra and the spectra chosen for comparison are those where the pointing is equal or within a smaller fraction of the beam. We can conclude that the sources fills a large fraction of the beam for Ser SMM1, L1157 and NGC 7538 1. On the other hand, the source sizes are small for HH54 B and L1448.
\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f16.eps}} \end{figure} Figure 16:

Integrated intensities for common sources of Odin and SWAS. The dashed lines show the 3.37:1 and the 1:1 ratios between the Odin and SWAS integrated intensities. The error bars refer to the analysis and the solid lines represents ratios 1:1 and 3.37:1 with a 15% uncertainty applied. This is the estimated error limit from the data reduction.

Open with DEXTER

4.5 Outflows and observed water abundances

The main objective for these observations is to use the ground state o-H2O transition as a tracer for shocked gas. Available shock models by Bergin et al. (1998) show that a shock velocity in excess of 10  ${\rm km ~ s^{-1}}$ should convert essentially all oxygen not in the form of CO into water resulting in water abundances relative to H2 of the order of 10-4. This water is also believed to persist for $\sim$105 years. For several of our sources, the water abundance increases as high as what would be theoretically possible for these C-type shocks. The fact that we are observing abundances as high as this might be an indication that the shock velocities are in this regime. On the other hand, the large Odin beam does not show whether the water emission regions are small or not. The density in these regions may also very well be orders of magnitude higher than the values used in this paper, a fact that could alter our inferred values significantly. Future observations with the Herschel space observatory will give us the ability to spatially resolve outflows and it will also give us the possibility to observe several different transitions originating in gas of different temperatures. This will hopefully give a much deeper insight into the chemistry occurring in these structures.

5 Conclusions

We make the following primary conclusions:
1.
We have observed 13 outflows and two supernova remnants and detect the ortho-water ground state rotational transition in seven outflows and one supernova remnant.
2.
The column densities of o-H2O have been investigated with RADEX , having the volume density, temperature, line intensity and linewidth as input. Elevated abundances of water are found in several sources. The abundances are as high as one would expect if all gaseous oxygen had been converted to water in a C-type shock.
3.
There is no distinct relationship between the water abundance and the mass loss rate.
4.
There is a correlation between the o-H2O abundance and the maximum velocity of the gas.

Acknowledgements
The author enjoyed interesting discussions with John H. Black concerning radiative transfer in general and RADEX in particular. Carina M. Persson and Per Bergman are also acknowledged. We thank the Research Councils and Space Agencies in Sweden, Canada, Finland and France for their financial support. The valuable comments made by the anonymous referee are highly appreciated.

Appendix A: Ground based observations

The observations with the Swedish ESO Submillimetre Telescope (SEST) were made during 11-20 August 1997 and 2-6 August 1998. Some complementary SiO (2-1) map data were collected during 7-9 February 2003. The observed molecules and their transitions are listed in Table A.1 and for SiO (2-1) and (3-2), the observations were made simultaneously.

Table A.1:   Molecular line observations with the 15 m SEST.

SIS receivers were used as frontends and the backend was a $2\times 1$ GHz multi-channel acousto-optical spectrometer (AOS), split into two halves for the SiO (2-1) and (3-2) observations. For the SiO (5-4) and the CO observations, both the high resolution (HRS) and the low resolution (LRS) backends were used. The channel separation of the HRS was 43 kHz and the spectral resolution 80 kHz covering the bandwidth of 86 MHz, corresponding to $\delta \upsilon = 0.07$  ${\rm km ~ s^{-1}}$and $\Delta \upsilon = \pm 35$  ${\rm km ~ s^{-1}}$for the velocity resolution and range at 345 GHz, respectively. For the LRS, these parameters were channel separation 0.69 MHz and $\Delta \nu = 1.4$ MHz spectral resolution, providing $\delta \upsilon = 1.2$  ${\rm km ~ s^{-1}}$and $\Delta \upsilon = \pm 700$  ${\rm km ~ s^{-1}}$, respectively, for the CO (3-2) observations.

The data were chopper-wheel calibrated in the $T_{\rm A}^{\star}$-scale (Ulich & Haas 1976) and the main beam efficiencies at the different frequencies, $\eta_{\rm mb}$, are given in Table A.1. The pointing of the telescope was regularly checked towards point sources, masing in the SiO (v=1, J=2-1) line, and was determined to be better than 3 ${}^{\prime \prime}$ (rms). However, for HH 54, all SiO data refer to the vibrational ground state, v=0, and the (2-1) and (3-2) data were obtained in frequency switching mode, with a frequency chop of 4 MHz.

Knee (1992) assigned a kinetic gas temperature of $\sim$15 K to the bulk cloud material. In the CO (3-2) line, this should yield a high contrast between the cloud and the high velocity gas. To achieve flat, optimum baselines, the CO (3-2) observations therefore were made in wide dual beam switching with throws of $\pm$11$^{\prime}$ in azimuth. At this maximum amplitude available at the SEST, the reference beams were still inside the molecular cloud. For this reason, this mode could not be adopted for the CO (2-1) observations, which were performed in total power mode. The reference position was 1$^{\circ }$ north of HH 54. Centered on the object, nine point maps with 25 ${}^{\prime \prime}$ spacings were obtained in both CO lines. In addition, a tighter sampled nine point map with 15 ${}^{\prime \prime}$ spacings was also made in CO (3-2).

HH54 B was observed again on June 8th to June 11th, 2009. 8.2 h of integration time confirmed the presence of the H${\rm _2}$O 557 GHz line. Adding all observations results in an integrated intensity of $0.95 \pm 0.05$ K  ${\rm km ~ s^{-1}}$.

References

Online Material

Appendix B: Online Material

For comparision we show the calibrated rawdata together with the baseline subtracted and smoothed spectra already shown in the text.
\begin{figure}\par\mbox{\includegraphics[width=7.5cm]{12064f17.ps} \hspace{2cm} ... ...20.ps} \hspace{2cm} \includegraphics[width=7.5cm]{12064f12.ps} } \end{figure} Figure B.1:

This figure shows the L1448, HH211 and IC443-G spectra. The positions are listed in Table 1. All spectra on the right are smoothed to a resolution of 0.5  ${\rm km ~ s^{-1}}$ and clipped for clarity. These spectra are also calibrated in frequency. The spectra on the left are the calibrated rawdata with a zero order baseline subtraction. For strip maps, a letter in the upper right corner indicates in which part of the flow the spectra has been collected (R = red, B = blue and C = center).

Open with DEXTER

\begin{figure} \par\mbox{\includegraphics[width=7.5cm]{12064f21.ps} \hspace{2cm}... ...24.ps} \hspace{2cm} \includegraphics[width=7.5cm]{12064f25.ps} } \end{figure} Figure B.2:

The same as Fig. B.1 but for L1551, Sa136 and TW Hya.

Open with DEXTER

\begin{figure}\par\mbox{\includegraphics[width=7.5cm]{12064f26.ps} \hspace{2cm} ... ...f33.ps} \hspace{2cm} \includegraphics[width=7.5cm]{12064f8.ps} } \end{figure} Figure B.3:

The same as Fig. B.1 but for eps Cha  I N, HH54 B, G327.3-0.6, NGC 6334  I and Ser SMM1.

Open with DEXTER

\begin{figure}\par\mbox{\includegraphics[width=7cm]{12064f34.ps} \hspace{2cm} \... ...4f39.ps} \hspace{2cm} \includegraphics[width=7cm]{12064f10.ps} } \end{figure} Figure B.4:

The same as Fig. B.1 but for 3C391 BML, B335, NGC 7538 IRS1 and L1157. For L1157, the AC2 data are plotted in gray and the AOS data in black.

Open with DEXTER

Footnotes

... shocks[*]
Odin is a Swedish-led satellite project funded jointly by the Swedish National Space Board (SNSB), the Canadian Space Agency (CSA), the National Technology Agency of Finland (Tekes) and Centre National d'Étude Spatiale (CNES).
...[*]
The Swedish ESO Submillimetre Telescope (SEST) located at La Silla, Chile was funded by the Swedish Research Council (VR) and the European Southern Observatory. It was decommissioned in 2003.
...[*]
Appendix B is only available in electronic form at http://www.aanda.org
...RADEX[*]
http://www.strw.leidenuniv.nl/ moldata/radex.html
... (LAMDA)[*]
http://www.strw.leidenuniv.nl/ moldata/
... line[*]
Taking the difference in beam sizes into account, the Odin data are only a slight improvement over those obtained with SWAS. The SWAS upper limit was modeled to imply an H2O abundance >10-10 (Bergin and Plume, private communication).
...Bourke et al. (1997)[*]
These authors estimate $t\rm {_d}$ to 10 700 years and 10 200 years for the south east and the north west lobe respectively.

All Tables

Table 1:   Observation log for the sources analyzed in this paper.

Table 2:   Column densities of o-H2O and estimates of the ortho-water abundance, X(o-H2O) = N(o-H2O)/N(H2).

Table 3:   Column densities of o-H2O and estimates of the ortho-water abundance, X(o-H2O) = N(o-H2O)/N(H2).

Table A.1:   Molecular line observations with the 15 m SEST.

All Figures

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12064f1.eps}} \end{figure} Figure 1:

The derived o-H2O column density as a function of volume density for different temperatures. The line intensity for this test case has been set to 0.1 K while the line width has been set to 10  ${\rm km ~ s^{-1}}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{12064f2.eps} % \end{figure} Figure 2:

The three positions observed by Odin are shown overlaid on a CO (2-1) map of L1448 (Bachiller et al. 1995). The circles correspond to the Odin beam at 557 GHz. Coordinate offsets are given with respect to L1448-mm: $\alpha _{2000}$ = 03:25:38.8, $\delta _{2000}$ = 30:44:05.0. The positions of L1448-mm and L1448 IRS3 are indicated by star symbols.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{12064f3.ps} \end{figure} Figure 3:

L1448 spectra. The positions are listed in Table 2 and shown in Fig. 2. The letter in the upper right corner indicates in which part of the flow the spectra were collected (R = red, B = blue and C = center). The spectra were baseline subtracted and smoothed to a resolution of 0.5  ${\rm km ~ s^{-1}}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.5cm,clip]{12064f4.eps} \end{figure} Figure 4:

The three positions observed by Odin are shown overlaid on a CO (3-2) map of Sa136 (Parise et al. 2006). The circles correspond to the Odin beam at 557 GHz. Coordinate offsets are given with respect to: $\alpha _{2000}$ = 12:01:37.0, $\delta _{2000}$ = -65:08:53.5. The positions of the sources IRS1 and IRS2 are indicated with star symbols.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{12064f5.ps} \end{figure} Figure 5:

The same as Fig. 3 but for Sa136.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f6.ps}} \end{figure} Figure 6:

From top to bottom the CO(5-4), CO(3-2), CO(2-1) and ${\rm H_2O(1_{10}{-}1_{01})}$ spectra observed towards HH54 B are plotted. The dotted vertical line shows the cloud LSR-velocity at +2.4  ${\rm km ~ s^{-1}}$.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f7.ps}} \end{figure} Figure 7:

The same as Fig. 3 but for NGC 6334 I. The black spectrum represents the first case and the grey spectrum represents the second case as described in Sect. 4.2.9

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f8.ps}} \end{figure} Figure 8:

The same as Fig. 3 but for Ser SMM1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{12064f9.eps} \end{figure} Figure 9:

The four positions observed by Odin are shown overlaid on a CO (2-1) map of L1157 (Bachiller et al. 2001). The circles correspond to the Odin beam at 557 GHz. Coordinate offsets are given with respect to L1157-mm, indicated in the figure with a star symbol: $\alpha _{2000}$ = 20:39:06.4, $\delta _{2000}$ = +68:02:13.0. The black and white squares refer to the knots B0, B1, B2, R0, R1, R and R2 described in Bachiller et al. (2001).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.4cm,clip]{12064f10.ps} \end{figure} Figure 10:

The same as Fig. 3 but for L1157.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f11.ps}} \end{figure} Figure 11:

The same as Fig. 3 but for NGC 7538 IRS1.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f12.ps}} \end{figure} Figure 12:

The same as Fig. 3 but for IC443-G.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f13.eps}} \end{figure} Figure 13:

o-H2O abundance plotted against the maximum velocity for an overall inclination of 60$^{\circ }$ with respect to the line of sight. The solid line represents a linear fit of $\log$[X(o-H2O)] versus $\log (\upsilon_{\rm max})$ with the same inclination angle applied. The dotted dashed line represents the fit with a inclination correction of 35$^{\circ }$ while the dashed line represents the fit with an inclination angle correction of 85$^{\circ }$. The errorbars from the measurements are smaller than the circles.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f14.eps}} \end{figure} Figure 14:

o-H2O abundance plotted against the mass loss rate. The triangles represent the high upper limits for each source in the o-H2O abundance, while the circles symbolize values where a detection has been made. Dashed lines represent the cases where there is a range in the inferred abundances or mass loss rates.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f15.eps}} \end{figure} Figure 15:

A histogram of the gas volume density estimated in the outflows studied in this paper showing a variation that spans over six orders of magnitude.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{12064f16.eps}} \end{figure} Figure 16:

Integrated intensities for common sources of Odin and SWAS. The dashed lines show the 3.37:1 and the 1:1 ratios between the Odin and SWAS integrated intensities. The error bars refer to the analysis and the solid lines represents ratios 1:1 and 3.37:1 with a 15% uncertainty applied. This is the estimated error limit from the data reduction.

Open with DEXTER
In the text

  \begin{figure}\par\mbox{\includegraphics[width=7.5cm]{12064f17.ps} \hspace{2cm} ... ...20.ps} \hspace{2cm} \includegraphics[width=7.5cm]{12064f12.ps} } \end{figure} Figure B.1:

This figure shows the L1448, HH211 and IC443-G spectra. The positions are listed in Table 1. All spectra on the right are smoothed to a resolution of 0.5  ${\rm km ~ s^{-1}}$ and clipped for clarity. These spectra are also calibrated in frequency. The spectra on the left are the calibrated rawdata with a zero order baseline subtraction. For strip maps, a letter in the upper right corner indicates in which part of the flow the spectra has been collected (R = red, B = blue and C = center).

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=7.5cm]{12064f21.ps} \hspace{2cm}... ...24.ps} \hspace{2cm} \includegraphics[width=7.5cm]{12064f25.ps} } \end{figure} Figure B.2:

The same as Fig. B.1 but for L1551, Sa136 and TW Hya.

Open with DEXTER
In the text

  \begin{figure}\par\mbox{\includegraphics[width=7.5cm]{12064f26.ps} \hspace{2cm} ... ...f33.ps} \hspace{2cm} \includegraphics[width=7.5cm]{12064f8.ps} } \end{figure} Figure B.3:

The same as Fig. B.1 but for eps Cha  I N, HH54 B, G327.3-0.6, NGC 6334  I and Ser SMM1.

Open with DEXTER
In the text

  \begin{figure}\par\mbox{\includegraphics[width=7cm]{12064f34.ps} \hspace{2cm} \... ...4f39.ps} \hspace{2cm} \includegraphics[width=7cm]{12064f10.ps} } \end{figure} Figure B.4:

The same as Fig. B.1 but for 3C391 BML, B335, NGC 7538 IRS1 and L1157. For L1157, the AC2 data are plotted in gray and the AOS data in black.

Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.