| Issue |
A&A
Volume 507, Number 3, December I 2009
|
|
|---|---|---|
| Page(s) | 1541 - 1554 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200912004 | |
| Published online | 01 October 2009 | |
A&A 507, 1541-1554 (2009)
Uncertainties on the theoretical
predictions for classical Cepheid pulsational quantities![[*]](/icons/foot_motif.png)
G. Valle1 - M. Marconi3 - S. Degl'Innocenti1,2 - P. G. Prada Moroni1,2
1 - Dipartimento di Fisica ``Enrico Fermi'', Università di Pisa, largo
Pontecorvo 3, Pisa 56127, Italy
2 - INFN, Sezione di Pisa, Largo B. Pontecorvo 3, Pisa 56127, Italy
3 - INAF, Osservatorio Astronomico di Capodimonte, via Moiariello 16,
80131 Napoli, Italy
Received 7 March 2009 / Accepted 27 August 2009
Abstract
Context. With their period-luminosity relation,
``classical Cepheids'' (CC) are the most common primary distance
indicators within the Local Group, also providing an absolute
calibration of important secondary distance indicators. However, the
predicted position of these pulsators in the HR diagram, along the so
called blue loop, that is the expected distribution
of Cepheids within the instability strip is affected by several model
inputs, reflecting upon the predicted PL
relation.
Aims. The aim of this work is to quantitatively
evaluate the effects on the theoretical PL relation
of current uncertainties on the chemical abundances of Cepheids in the
Large Magellanic Cloud (LMC) and on several physical assumptions
adopted in the evolutionary models. We will separately analyse how the
different factors influence the evolutionary and pulsational
observables and the resulting PL relation.
Methods. To achieve this goal we computed new sets
of updated evolutionary and pulsational models.
Results. As a result, we find that present
uncertainties on the most relevant H and He burning
reaction rates do not influence in a relevant way the loop extension in
temperature. On the contrary, current uncertainties on the LMC chemical
composition significantly affect the loop extension and also reflect in
the morphology of the instability strip; however their influence on the
predicted pulsational parameters is negligible. We also discussed how
overshooting and mass loss, sometimes suggested as possible solutions
for the long-standing problem of the Cepheid mass discrepancy,
influence the ML relation and the
pulsational parameters.
Conclusions. In summary, the present uncertainties
on the physical inputs adopted in the evolutionary codes and in the LMC
chemical composition are negligible for the prediction of the main
pulsational properties. On the other hand, the inclusion of
overshooting in the previous hydrogen burning phase and/or of mass loss
is expected to significantly change the resulting theoretical
pulsational scenario for Cepheids, as well as the calibration of their
distance scale. These systematic effects are expected to influence the
theoretical Cepheid calibration of the secondary distance indicators
and in turn the resulting evaluation of the Hubble constant.
Key words: stars: variables: Cepheids - stars: evolution - stars: distances
1 Introduction
During the central helium burning phase, intermediate mass stars show an excursion toward higher effective temperature, in the Hertzprung-Russell (HR) diagram, subsequently coming back toward the asymptotic giant branch (blue loop). During this phase the stars cross the instability strip, becoming classical Cepheids. These variable stars, thanks to their characteristic period-luminosity (PL) relation, are the most common primary distance indicators within the Local Group. Moreover, from space, they are observable also in external galaxies, up to distances of 20-30 Mpc (see e.g. Freedman et al. 2001). On this basis they provide the absolute calibration of important secondary distance indicators, such as the maximum luminosity of supernovae Ia, the Tully-Fisher relation, surface brightness fluctuations, and the planetary nebulae luminosity function, that are the basis for measurement of the Hubble constant (Freedman et al. 2001; Saha et al. 2001). Any systematic error affecting the Cepheid PL relations affects the extragalactic distance scale and the estimate of the Hubble constant. Therefore, even though the Cepheid PL relation is assumed to be universal and calibrated through the sample in the Large Magellanic Cloud (LMC, see e.g. Udalski et al. 1999; Madore & Freedman 1991), the possibility that the Cepheid properties and PL relation depend on the chemical composition of the parent galaxies has been actively debated during the last decade (see e.g. Macri et al. 2006; Bono et al. 2008; Sakai et al. 2004; Romaniello et al. 2005; Marconi et al. 2005; Romaniello et al. 2008). On the other hand the theoretical prediction for the existence of a PL relation for classical Cepheids relies on the assumption that intermediate mass stars undergoing central helium burning are characterized by a mass-luminosity (ML) relation, as predicted by stellar evolution models. On very general grounds the pulsation period is expected to be tightly correlated with the luminosity, the mass and the effective temperature of the star, for each given chemical composition. It is only thanks to the ML relation that the period can be simply related to the luminosity and the effective temperature, allowing a theoretical prediction for the period-luminosity-color relation (PLC, see Feast 1995; Laney & Stobie 1986; Feast 1991; Sasselov et al. 1997; Feast 1984; Caldwell & Coulson 1986; Caldwell & Laney 1991; Stothers 1988). However the theoretical MLrelation depends on the several physical processes included in stellar evolutionary codes as well as on the adopted chemical composition.
By averaging the PLC relation on the color extension of the pulsation instability strip one obtains the PL relation. This implies that the PL relation has a statistical nature and observationally holds only when a statistically significant sample of Cepheids (at the same distance) is available. Thus the predicted temperature extension of the blue loop for a given mass also reflects upon the expected distribution of Cepheids within the instability strip and in turn upon the theoretical PL relation. This is a very critical point because the predicted extension of the blue loop in the HR diagram is affected by several model inputs (chemical composition, efficiency of external convection, nuclear burning cross sections, etc.) producing effects that are not yet completely understood (see e.g. Brunish et al. 1990; Stothers & Chin 1994; Xu & Li 2004a). In this context, a detailed comparison of evolutionary and pulsational models with the observations can provide insight into the physics of stellar evolution and pulsation.
The aim of this work is to quantitatively evaluate the effects on the predicted PL relation of current uncertainties on the chemical abundances of Cepheids in the LMC and of several physical assumptions adopted in the evolutionary models. In particular, we will separately analyse how the different factors influence the evolutionary and pulsational observables (extension in effective temperature of the blue loop, Mass-Luminosity relation, morphology of the instability strip, period distribution) and the resulting PL relation. For the chemical composition we choose that of the LMC with its associated uncertainty. All the relations based on the newly computed sets of evolutionary and pulsation models will be made available to the community. In a forthcoming paper (Valle et al. 2009, in preparation) we will focus on the comparison of these new predictions with the observations. The organization of the paper is the following: in Sect. 2 we present the theoretical scenario both from the evolutionary and the pulsational point of view; Sect. 3 contains a general discussion about the problems in calculating blue loop models; in Sect 4 the dependence of the predicted extension of the blue loop on the uncertainties affecting nuclear reaction rates is investigated; in Sect. 5 we focus on the effects of chemical abundance uncertainties on the most relevant evolutionary and pulsational features, whereas in Sect. 6.1 we take into account possible noncanonical effects in the evolutionary scenario. The conclusions, reported in Sect. 7, close the paper.
2 Theoretical scenario
In this section we present the new sets of evolutionary and pulsation models that have been used for the calculations.
2.1 Evolutionary stellar models
Evolutionary tracks were computed with an updated version of the FRANEC
evolutionary code (see e.g. Chieffi & Straniero 1989; Degl'Innocenti
et al. 2008) including
the OPAL 2006 equation of state (EOS)![]() (see also Rogers et al. 1996)
and radiative opacity
tables
(see also Rogers et al. 1996)
and radiative opacity
tables![]() (see also Iglesias & Rogers 1996)
for temperatures higher than
12 000 K. Moreover our models include the conductive
opacities by Shternin &
Yakovlev (2006) (see also Potekhin
1999) and the
atmospheric opacities by Ferguson
et al. (2005)
(see also Iglesias & Rogers 1996)
for temperatures higher than
12 000 K. Moreover our models include the conductive
opacities by Shternin &
Yakovlev (2006) (see also Potekhin
1999) and the
atmospheric opacities by Ferguson
et al. (2005)![]() .
All the adopted opacity tables have been calculated by assuming the
solar relative
metal abundances by Asplund
et al. (2005).
.
All the adopted opacity tables have been calculated by assuming the
solar relative
metal abundances by Asplund
et al. (2005).
Since the 12C(![]() ,
,
![]() )16O
and 14N(p,
)16O
and 14N(p, ![]() )15O
reaction rates affect the evolutionary properties of intermediate-mass
stars
and in particular the temperature blue loop extension (see
e.g. Brunish et al. 1990),
we adopted the updated rates by Hammer
et al. (2005) for the
12C
)15O
reaction rates affect the evolutionary properties of intermediate-mass
stars
and in particular the temperature blue loop extension (see
e.g. Brunish et al. 1990),
we adopted the updated rates by Hammer
et al. (2005) for the
12C![]() and by the LUNA collaboration (see Imbriani
et al. 2005, and references
therein) for the 14N + p
cross sections. For the other nuclear reactions we
adopted the same rates as in Ciacio
et al. (1997). The code implements weak screening
(Salpeter 1954),
weak-intermediate, intermediate-strong screening
(Graboske et al. 1973),
and strong screening (Itoh
et al. 1979,1977).
and by the LUNA collaboration (see Imbriani
et al. 2005, and references
therein) for the 14N + p
cross sections. For the other nuclear reactions we
adopted the same rates as in Ciacio
et al. (1997). The code implements weak screening
(Salpeter 1954),
weak-intermediate, intermediate-strong screening
(Graboske et al. 1973),
and strong screening (Itoh
et al. 1979,1977).
For convective mixing, we adopt the Schwarzschild criterion to define regions in which convection elements are accelerated (see the description in Brocato et al. 2003) with an additional algorithm to take into account the induced semiconvection during the central He-burning phase (Castellani et al. 1971b,a). Rotationally induced effects (see e.g. Palacios et al. 2003; Maeder & Zahn 1998) are not included in our models.
To model envelope convection we adopted, as usual, the mixing
length formalism
(Bohm-Vitense 1958). The
mixing length parameter, ![]() ,
governing the efficiency
of convection, has been calibrated to reproduce the observed stellar
colors in
the Large Magellanic Cloud cluster NGC 1866, obtaining
,
governing the efficiency
of convection, has been calibrated to reproduce the observed stellar
colors in
the Large Magellanic Cloud cluster NGC 1866, obtaining
![]() (Brocato et al. 2004).
This result is also dependent on the atmospheric models adopted to
transform
evolutionary calculations from the theoretical (
(Brocato et al. 2004).
This result is also dependent on the atmospheric models adopted to
transform
evolutionary calculations from the theoretical (
![]() )
to the
observational plane. In this paper we adopted the color-temperature
transformations by Bessel et al.
(1998).
)
to the
observational plane. In this paper we adopted the color-temperature
transformations by Bessel et al.
(1998).
The original helium mass fraction (Y)
cannot be measured
spectroscopically and it is generally estimated by assuming a linear
relation between Y and Z:
where
The metallicity adopted for the models is consistent with the most recent estimates of [Fe/H] for LMC Cepheids (see Luck et al. 1998; Romaniello et al. 2008) and also with several independent determinations of the LMC metallicity (see e.g. Andrievsky et al. 2001; Korn et al. 2000).
The total metallicity can be expressed as follows:
where
In this work we adopt the updated Asplund
et al. (2005) mixture, based on the analysis of
spectroscopic data by
means of tridimensional hydrodynamical atmospheric models, instead of
that by
Grevesse & Noels (1993),
hereinafter GN93, widely used in the past. This
leads to a significant reduction of the the Z/X ratio
for the Sun, from
![]() to
to
![]() .
As a result the traditionally assumed metallicity
for LMC decreases from
.
As a result the traditionally assumed metallicity
for LMC decreases from ![]() to
to ![]() .
With this choice of
metallicity, from Eq. (1),
one obtains
.
With this choice of
metallicity, from Eq. (1),
one obtains ![]() ,
which we
assume as our standard value.
,
which we
assume as our standard value.
Several investigations have dealt with the analysis of the effects of this revision of the solar abundance, revealing discrepancies between predicted and helioseismologically inferred quantities (see e.g. Basu & Antia 2004; Bahcall et al. 2005). This situation is further complicated by the fact that current uncertainties on the physical inputs adopted in the solar models can affect the results of the quoted investigations. Moreover some authors questioned the accuracy of the oxygen abundance derived by Asplund et al. (2005) (see e.g. Caffau et al. 2008). For these reasons, even if we adopted the Asplund et al. (2005) solar mixture as our reference mixture, in the following we will take into account the uncertainty related to this assumption and its influence on the LMC metallicity.
2.2 Nonlinear pulsation models
Our pulsational models are based on a nonlinear nonlocal time-dependent convective hydrodynamical code (Bono & Stellingwerf 1994; Bono et al. 1999a, and references therein). This code has been successfully applied to several classes of pulsating stars (see e.g. Bono et al. 1999b; Di Criscienzo 2004; Marconi et al. 2003,2004,2005; Marconi & Di Criscienzo 2007, and references therein). In this paper the physical ingredients of Cepheid pulsation models, and in particular the stellar opacity tables, have been updated in order to insure consistency between the pulsation and the evolutionary models. The new pulsation models have been constructed with the same chemical abundances of evolutionary models, covering the same range in stellar mass and assuming the luminosity predicted by the canonical Mass-Luminosity (ML) relation by Bono et al. (2000). For Z=0.005, a second luminosity brighter by 0.25 dex has been included to account for the effect of mild overshooting and mass loss (see Sect. 6.1).
3 Modeling the blue loop morphology
The extension in temperature of the blue loop is an important evolutionary feature. Stellar models show that the excursion to the blue is produced by an envelope contraction (see e.g. Renzini et al. 1992): models with more extended loops undergo a more significant envelope contraction which heats the hydrogen shell, increasing its luminosity. The return of the track to the red is due to a variety of effects (see e.g. Sestito et al. 2002) : a) when the central helium abundance decreases belowThe dependence of the loop morphology on changes in the chemical composition will be analysed in Sect. 5. In general, an increase of the original He abundance increases the mean molecular weight while it leads to a decrease of the mean opacity (see e.g. Vemury & Stothers 1978), even if the dependence on He abundance is not linear with metallicity. On the other hand a metallicity variation changes the blue loop extension mainly due to the opacity variation (see e.g. Stothers & Chin 1993) even if the behaviour can be more complicated and a quantitative explanation of the loop dependence on chemical composition is still lacking in the literature.
The evolutionary properties of intermediate and high mass stars in the central He burning phase strongly depend on the efficiency of the He burning nuclear reactions (see e.g. Bono et al. 2000; Iben 1972; Brunish et al. 1990). This point is discussed in the following subsections in the light of updated nuclear cross sections measurements.
Regarding the opacity dependence, any increase of the opacities deep in the stellar interiors could lead to fainter luminosities, cooler effective temperatures and longer lifetimes. Regarding the loop extension, in principle, a higher opacity leads to a reduced blue loop but the effect is in general very small (see e.g. Stothers & Chin 1991b). In addition, updated opacity tables agree amongst each other within 5-10% (see e.g. discussion in Badnell et al. 2005; Neuforge-Verheecke et al. 2001) thus very small opacity uncertainties are expected. Moreover, molecular opacities have almost negligible effects on the blue loop extension (see e.g. Stothers & Chin 1993).
Several authors (see e.g. Brocato & Castellani 1993; Chiosi et al. 1992; Stothers & Chin 1992) noticed that the extension of the convective H burning core affects the following He burning phase. This involves the convective core overshooting efficiency, whose influence on the blue loop extension will be discussed in detail in Sec. 6.1 and the method adopted for treating the semiconvective layers that develop around the H burning core close to the central H exhaustion. If a significant amount of overshooting is included in the calculations, during the core He burning phase the luminosity is brighter, the lifetime is shorter and the blue loop is less extended and rises less steeply than in absence of overshooting (see e.g. Chin & Stothers 1991; Matraka et al. 1982).
The possible
occurrence of convective shells and the consequent modification
of the internal chemical profile are strictly related to the adopted
stability
criterion, either Schwarzschild or Ledoux (see e.g. Canuto 2000;
Salasnich
et al. 1999; Stothers & Chin 1994).
However the stability criterion has a marginal effect on
stellar models ranging from ![]() 3
3 ![]() to
to ![]() 12
12 ![]() ,
as the ones taken into account in our work Stothers
& Chin (1993).
,
as the ones taken into account in our work Stothers
& Chin (1993).
Moreover downward convecting overshooting from the outer convection zone which modifies the envelope chemical profile influences the formation of blue loops.
For the same reason the occurrence of blue loops is thus
influenced by the mixing length value ![]() ,
which governs the convection
efficiency in the external convective envelope.
However when a blue loop develops (it is not true in some cases of
small
and moderate
,
which governs the convection
efficiency in the external convective envelope.
However when a blue loop develops (it is not true in some cases of
small
and moderate ![]() values)
the maximum effective temperature during the
blue loop was found to be only a very weak function of
values)
the maximum effective temperature during the
blue loop was found to be only a very weak function of ![]() (see
e.g. Chin & Stothers 1991).
Moreover, since the atmospheric
model is fixed,
(see
e.g. Chin & Stothers 1991).
Moreover, since the atmospheric
model is fixed, ![]() is generally calibrated through the
comparison between theory and observation for the stellar color. For
this reason, in this paper we will not
include variations of this parameter, which is fixed to
is generally calibrated through the
comparison between theory and observation for the stellar color. For
this reason, in this paper we will not
include variations of this parameter, which is fixed to
![]() .
.
Another important phenomenon affecting the evolution of He
burning
intermediate mass stars is mass loss (see e.g. the review by Chiosi & Maeder 1986
or the more recent work by Salasnich
et al. 1999). As discussed by several authors
(see e.g. Salasnich et al.
1999) mass loss mainly influences the evolution of
masses higher than ![]() 15
15 ![]() but its influence on the loop
morphology, as discussed in Sect. 6.2, can be
significant also for lower
masses. However the physical mechanisms which affect mass loss and its
dependence on metallicity are not still completely understood and thus
the
range of possible efficiencies for the phenomenon is very wide (see
e.g. the discussion in Maeder
& Meynet 2000; Vázquez et al. 2005). In
this paper we work in the canonical regime, also because we concentrate
on intermediate mass stars but to take into account a possible mass
loss contribution,
in Sect. 6.2
we discuss some additional models computed with different mass loss
efficiencies.
but its influence on the loop
morphology, as discussed in Sect. 6.2, can be
significant also for lower
masses. However the physical mechanisms which affect mass loss and its
dependence on metallicity are not still completely understood and thus
the
range of possible efficiencies for the phenomenon is very wide (see
e.g. the discussion in Maeder
& Meynet 2000; Vázquez et al. 2005). In
this paper we work in the canonical regime, also because we concentrate
on intermediate mass stars but to take into account a possible mass
loss contribution,
in Sect. 6.2
we discuss some additional models computed with different mass loss
efficiencies.
Due to the dependence of the loop extension on several physical parameters, if one compares recent sets of intermediate mass stars models available in the literature (which in general differ by the assumed chemical composition, the adopted physical inputs, the external convection efficiency etc.) one finds significant variations in the loop morphology. In the following sections we will discuss the main parameters which have already been demonstrated to potentially affect in a relevant way the blue loop morphology: He burning cross sections, chemical composition, overshooting and mass loss efficiency.
4 Dependence of the loop extension on the uncertainties on the nuclear reaction cross sections
Several authors have investigated the dependence of the loop extension on the H burning (through the CNO cycle) and the He burning reaction rates (see e.g. Weiss et al. 2005; Renzini et al. 1992; Sestito et al. 2002; Brunish et al. 1990; Xu & Li 2004a), and have shown that the loop morphology is sensitive to variations of the adopted cross sections.
In this section we focus on the dependence of the loop
formation and its
temperature extension on variations of the relevant nuclear fusion
cross
sections within their estimated uncertainties. For stars in the central
He burning phase, the most relevant nuclear reactions are
the 3![]() ,
the
12C(
,
the
12C(![]() ,
,
![]() )16O,
that affects the He burning efficiency
and the 14N(p,
)16O,
that affects the He burning efficiency
and the 14N(p, ![]() )15O
that governs the shell
H burning through the CNO cycle.
)15O
that governs the shell
H burning through the CNO cycle.
4.1 14N(p,
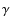 )15O
cross section
)15O
cross section
In stars with internal temperatures higher than ![]()
![]() K, the
hydrogen burning is dominated by the CNO cycle whose rate is
determined by the slowest process, the 14N(p,
K, the
hydrogen burning is dominated by the CNO cycle whose rate is
determined by the slowest process, the 14N(p,
![]() )15O reaction.
For this reaction the Gamow peak is at
)15O reaction.
For this reaction the Gamow peak is at ![]() 30 keV;
thus the capture cross section must be known down to this energy
at which it has a very low value, preventing a direct laboratory
measurement.
Instead, the cross sections are measured at higher energies and
then extrapolated, by means of the astrophysical S(E) factor, down
to the Gamow peak region. The occurrence of resonance and resonance
tails complicates the extrapolation and it results in very large
uncertainties on the evaluated cross sections. Recently, the
14N(p,
30 keV;
thus the capture cross section must be known down to this energy
at which it has a very low value, preventing a direct laboratory
measurement.
Instead, the cross sections are measured at higher energies and
then extrapolated, by means of the astrophysical S(E) factor, down
to the Gamow peak region. The occurrence of resonance and resonance
tails complicates the extrapolation and it results in very large
uncertainties on the evaluated cross sections. Recently, the
14N(p, ![]() )15O
cross section has been measured by the LUNA collaboration close to
70 keV (see e.g. Lemut
et al. 2006; Imbriani et al. 2005; Bemmerer
et al. 2006), leading to an improved estimate of the
S(E) factor at astrophysical
energies (
)15O
cross section has been measured by the LUNA collaboration close to
70 keV (see e.g. Lemut
et al. 2006; Imbriani et al. 2005; Bemmerer
et al. 2006), leading to an improved estimate of the
S(E) factor at astrophysical
energies (
![]() keV,
about half of the value of the NACRE
compilation by Angulo et al.
1999).
keV,
about half of the value of the NACRE
compilation by Angulo et al.
1999).
To quantify the effect of a variation of the 14N + p
cross section, we
computed stellar models for several stellar masses, varying the 14N + preaction
rate of the estimated uncertainty with respect to the LUNA value
(adopted in our standard models), models IX and X of
Table 1.
For all the investigated cases the effect on
the loop morphology of the present uncertainty on the
14N(p, ![]() )15O
rate is negligible, suggesting that this
uncertainty is not expected to contribute significantly to the final
error
budget for the predicted Cepheid pulsation properties.
)15O
rate is negligible, suggesting that this
uncertainty is not expected to contribute significantly to the final
error
budget for the predicted Cepheid pulsation properties.
4.2 3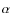 cross section
cross section
Recently Fynbo et al.
(2006) reported new measurements for the 3![]() rate,
finding, in particular, a resonance at energies of
rate,
finding, in particular, a resonance at energies of ![]() 11 MeV;
however, in the temperature range of interest, the differences with
respect to the most widely adopted 3
11 MeV;
however, in the temperature range of interest, the differences with
respect to the most widely adopted 3![]() rate are within the
uncertainty evaluated by the NACRE (Angulo
et al. 1999) compilation, reaching a
maximum of
rate are within the
uncertainty evaluated by the NACRE (Angulo
et al. 1999) compilation, reaching a
maximum of ![]() 20%
at temperatures of about 108 K (see
e.g. Weiss et al. 2005).
20%
at temperatures of about 108 K (see
e.g. Weiss et al. 2005).
For this reason we decided to take the error quoted by
NACRE (20%), in the
temperature range of interest, as a conservative estimate of the
uncertainty on
the 3![]() reaction rate. We computed specific models by varying the
3
reaction rate. We computed specific models by varying the
3![]() rate within the estimated uncertainty for different stellar masses
(in our ``standard'' case) finding no relevant variations in the loop
extension. These results suggest that the present uncertainties on the 3
rate within the estimated uncertainty for different stellar masses
(in our ``standard'' case) finding no relevant variations in the loop
extension. These results suggest that the present uncertainties on the 3![]() rate
do not substantially influence the evolutionary and pulsational
quantities for Cepheids stars.
rate
do not substantially influence the evolutionary and pulsational
quantities for Cepheids stars.
Table 1: Computed sets of evolutionary tracks and pulsation models.
4.3 12C(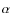 ,
,
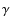 )16O
cross section
)16O
cross section
The measurement of the
![]() cross section at the energies
of interest in stars (
cross section at the energies
of interest in stars (![]() 300 keV)
is presently impossible due to the
smallness of the predicted value (
300 keV)
is presently impossible due to the
smallness of the predicted value (![]() 10-17 b).
The extrapolation
from higher energies is quite difficult, because the cross section in
this
energy region is a mixture of groundstate and cascade transitions, and
the
cross section for the ground state transitions is dominated by the
tails of
subthreshold resonances with the interference of other processes (see
e.g. Buchmann et al. 2006).
For these reasons the uncertainty quoted in the past for this rate was
very large, up to a factor of two, and the effect of this error on the
loop
extension was very strong (see e.g. Brunish
et al. 1990). Given the astrophysical
importance of this reaction, in the past decade a significant
experimental
effort has been devoted to the improvement of the determination of its
cross
section. Recent results by Hammer
et al. (2005) of direct
12C(
10-17 b).
The extrapolation
from higher energies is quite difficult, because the cross section in
this
energy region is a mixture of groundstate and cascade transitions, and
the
cross section for the ground state transitions is dominated by the
tails of
subthreshold resonances with the interference of other processes (see
e.g. Buchmann et al. 2006).
For these reasons the uncertainty quoted in the past for this rate was
very large, up to a factor of two, and the effect of this error on the
loop
extension was very strong (see e.g. Brunish
et al. 1990). Given the astrophysical
importance of this reaction, in the past decade a significant
experimental
effort has been devoted to the improvement of the determination of its
cross
section. Recent results by Hammer
et al. (2005) of direct
12C(![]() ,
,
![]() )16O
measurements in the temperature range
)16O
measurements in the temperature range
![]() ,
T9 being the temperature in 109 K,
lead to a new determination of the extrapolated astrophysical
reaction rate with a maximum total uncertainty of
,
T9 being the temperature in 109 K,
lead to a new determination of the extrapolated astrophysical
reaction rate with a maximum total uncertainty of ![]() 25%
(see Hammer et al. 2005).
25%
(see Hammer et al. 2005).
In the present work we adopt for the 12C(![]() ,
,
![]() )16O
reaction rate
the parametrization and the parameter values given by
Hammer et al. (2005); at
the typical He burning temperature (
)16O
reaction rate
the parametrization and the parameter values given by
Hammer et al. (2005); at
the typical He burning temperature (
![]() K)
this new rate is about 20% lower than the NACRE rate.
K)
this new rate is about 20% lower than the NACRE rate.
As discussed in Brunish
et al. (1990), the blue loop extension
depends on the ![]() cross section: the higher the
rate of this reaction, the higher the effective temperature excursion
of
the loop. Several authors (see e.g. Sestito et al. 2002; Xu & Li
2004a) showed that the
12C(
cross section: the higher the
rate of this reaction, the higher the effective temperature excursion
of
the loop. Several authors (see e.g. Sestito et al. 2002; Xu & Li
2004a) showed that the
12C(![]() ,
,
![]() )16O
cross section is related to the efficiency
of the envelope contraction and thus to the loop extension.
)16O
cross section is related to the efficiency
of the envelope contraction and thus to the loop extension.
We evaluated the influence on the loop extension of the
present uncertainty on the
12C(![]() ,
,
![]() )16O
reaction rate for
models of different masses. To this aim we calculated two additional
sets of tracks with ``standard'' chemical composition (Z=0.005
Y=0.26) and the 12C+
)16O
reaction rate for
models of different masses. To this aim we calculated two additional
sets of tracks with ``standard'' chemical composition (Z=0.005
Y=0.26) and the 12C+![]() rate by Hammer et al. (2005)
increased or decreased by the estimated uncertainty of 25%
(models VII and VIII of Table 1).
As shown in Fig. 1,
the effect
is negligible for all the masses.
rate by Hammer et al. (2005)
increased or decreased by the estimated uncertainty of 25%
(models VII and VIII of Table 1).
As shown in Fig. 1,
the effect
is negligible for all the masses.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12004fg1.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg47.png)
|
Figure 1:
Evolutionary tracks with standard chemical composition
with three different values of the 12C( |
| Open with DEXTER | |
Thus, at variance with results published in the past, now
the uncertainty in the 12C+ ![]() nuclear
rate is noticeably reduced
so that its effect on the loop morphology appears negligible.
Consequently, in this paper, we neglect the uncertainty associated with
this cross
section in the evaluation of the error budget.
nuclear
rate is noticeably reduced
so that its effect on the loop morphology appears negligible.
Consequently, in this paper, we neglect the uncertainty associated with
this cross
section in the evaluation of the error budget.
In conclusion, if one takes at their face value the present estimated uncertainties of the cross sections relevant for Cepheids star evolution, one finds that now the precision of the experimental measurements, at the energies of astrophysical interest, is high enough to rule out significant effects of these uncertainties on the loop extension and thus on the pulsational quantities.
5 Effects of the chemical composition uncertainties
In this section we present the effects of the LMC Cepheid chemical composition uncertainties on evolutionary properties such as the He burning loop extension and the ML relation, and on pulsation properties such as the instability strip morphology and the PL relations.
For the LMC iron content we adopt
[Fe/H] = -0.40 that, as quoted above, is
consistent with the estimates by Luck
et al. (1998) and Romaniello
et al. (2008). In particular
Luck et al. (1998)
suggest a range of -0.55 ![]() [Fe/H]
[Fe/H] ![]() -0.19. By adopting
the Asplund et al. (2005)
solar mixture, that is a
-0.19. By adopting
the Asplund et al. (2005)
solar mixture, that is a ![]() value of 0.0165,
from the assumed [Fe/H] one obtains (see Eq. (2)) Z=0.005
(our
``standard'' value). On the basis of the observed range suggested by
Luck et al. (1998) we
allowed Z to vary in the range
value of 0.0165,
from the assumed [Fe/H] one obtains (see Eq. (2)) Z=0.005
(our
``standard'' value). On the basis of the observed range suggested by
Luck et al. (1998) we
allowed Z to vary in the range
![]() .
Taking into account the current uncertainties on
.
Taking into account the current uncertainties on
![]() (see
e.g. Gennaro
et al. 2008; Pagel & Portinari 1998), we
allowed a variation of the original
helium content from Y=0.26 to Y=0.28.
With Z=0.005, Y=0.26
corresponds to
(see
e.g. Gennaro
et al. 2008; Pagel & Portinari 1998), we
allowed a variation of the original
helium content from Y=0.26 to Y=0.28.
With Z=0.005, Y=0.26
corresponds to
![]() ,
while Y=0.28 implies
,
while Y=0.28 implies
![]() .
.
One should also take into account the uncertainty on the solar mixture. As already discussed, tridimensional hydrodynamical atmospheric models by Asplund et al. (2005) reduced the derived abundances of CNO and other heavy elements with respect to previous estimates (Grevesse & Sauval 1998, hereafter GS98). GS98 already improved the mixture by Grevesse & Noels (1993), widely adopted in the literature, mainly revising the CNO and Ne abundance and confirming the very good agreement between the new photospheric and meteoric results for the solar iron abundance.
The change of the adopted heavy element ratios might affect
the evolutionary calculations
of LMC Cepheids in two different ways: 1) changing the evolutionary
characteristics at fixed metallicity; 2) changing the LMC inferred
metallicity from the observed [Fe/H]. Regarding the second point, the
adoption
of the GS98 solar mixture leads to a LMC metallicity of
![]() ,
which
is within the previous quoted metallicity uncertainty. The first point
is analysed by taking into account the effects on the evolutionary
features of a
solar mixture variation at fixed metallicity, as due
to its effect on opacity, nuclear burning and equation of state
calculations.
,
which
is within the previous quoted metallicity uncertainty. The first point
is analysed by taking into account the effects on the evolutionary
features of a
solar mixture variation at fixed metallicity, as due
to its effect on opacity, nuclear burning and equation of state
calculations.
Table 3: The same as Table 2 but for quadratic fits.
In the following we present different sets of models varying
the chemical composition within the quoted ranges of uncertainty. The
combinations of Y and Z values
adopted for the different sets of models are summarized in
Table 1.
The first column of
Table 1
gives the reference name of the treated
cases (std,
![]() ,
,
![]() etc.), the second and the
third columns
give the adopted Y and Z values,
whereas the fourth column reports the
adopted chemical mixture at fixed Z. The
cases XI, XII and XIII will be presented
in detail in Sect. 6.1
in which we will discuss the effect of a mild
core overshooting in the H-burning phase.
etc.), the second and the
third columns
give the adopted Y and Z values,
whereas the fourth column reports the
adopted chemical mixture at fixed Z. The
cases XI, XII and XIII will be presented
in detail in Sect. 6.1
in which we will discuss the effect of a mild
core overshooting in the H-burning phase.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f2a.eps}\vspace{4mm}
\includegraphics[width=6.5cm,clip]{12004f2b.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg53.png)
|
Figure 2:
Upper panel: effect of a metallicity
variation on the loop extension for a 7 |
| Open with DEXTER | |
For each case of Table 1 we
computed evolutionary and
nonlinear convective pulsation models spanning a stellar mass range
from
3-4 ![]() to 13-14
to 13-14 ![]() ,
which covers the range of masses
crossing the instability strip (see for details Sect. 5.3).
,
which covers the range of masses
crossing the instability strip (see for details Sect. 5.3).
All the computed sets for the cases I to VI of Table 1 are plotted in Fig. 4; the fits of the corresponding instability strips calculated as explained in Sect. 5.2 are superimposed on the evolutionary models.
Some models show a smaller secondary loop during the redward excursion in the central He burning phase (see e.g. Salasnich et al. 1999; Bono et al. 2000, too), which is not a numerical artifact. The physical reason for this secondary loop is a slight increase in the size of the convective core, due to the opacity increase in the C and O rich nucleus, leading to small variations of the H and He burning efficiency. The mechanism is the analog of the breathing pulses occurring in low mass stars (see e.g. Sweigart & Demarque 1972,1973; Castellani et al. 1985).
Table 4: The same as Table 2 but for the first overtone boundaries.
5.1 Loop extension
Figure 2
shows, for a 7 ![]() model, the
effects on the blue loop extension of variations in the helium and
metal contents within the uncertainties of these quantities (cases
from I to IV of
Table 1).
The upper panel shows that increasing the metal content, at fixed
helium abundance, the extension of the blue loop decreases, whereas the
lower panel shows that an increase of the helium content within its
uncertainty range, at fixed metallicity, leads to more extended loops,
even if the effect is reduced compared to that of lowering Z.
The behaviour is similar for the other analysed model masses.
model, the
effects on the blue loop extension of variations in the helium and
metal contents within the uncertainties of these quantities (cases
from I to IV of
Table 1).
The upper panel shows that increasing the metal content, at fixed
helium abundance, the extension of the blue loop decreases, whereas the
lower panel shows that an increase of the helium content within its
uncertainty range, at fixed metallicity, leads to more extended loops,
even if the effect is reduced compared to that of lowering Z.
The behaviour is similar for the other analysed model masses.
A simultaneous variation of Z and Y
within their uncertainty
ranges does not result in an additive effect on the temperature
extension of
the loop. An example of this behaviour is shown in Fig. 4f, for
which the set of evolutionary tracks was computed with the upper values
of Y and Z, namely Y=0.28
and Z=0.008 (case V of Table 1).
Beside the apparent non additivity in
![]() ,
there is rather complicated mass dependence with a more regular trend
for the intermediate mass values (
,
there is rather complicated mass dependence with a more regular trend
for the intermediate mass values (![]()
![]() )
and an inverted trend
for higher masses. Thus one should be very careful to predict the
extension of the loop when more
than one parameter is varied, as it cannot be simply evaluated by
combining the results obtained for the variation of each single
parameter separately.
)
and an inverted trend
for higher masses. Thus one should be very careful to predict the
extension of the loop when more
than one parameter is varied, as it cannot be simply evaluated by
combining the results obtained for the variation of each single
parameter separately.
The effect of changing the mixture at fixed Z
is shown by comparing
Fig. 4c
(case III of Table 1), in
which the set of tracks is computed with Z = 0.008
and the mixture of AGS05,
with Fig. 4e
(case VI of Table 1),
computed with the same total metallicity (Z = 0.008)
but with the GS98 mixture. To analyse this
case we changed the original element abundances of our models and we
calculated suitable opacity tables making advantage of the codes
available at
the OPAL web site![]() ;
the EOS is also varied following the mixture change (see Degl'Innocenti et al. 2006,
for a more detailed analysis of the effects of a mixture update on the
stellar models).
;
the EOS is also varied following the mixture change (see Degl'Innocenti et al. 2006,
for a more detailed analysis of the effects of a mixture update on the
stellar models).
The mixture change at fixed Z has a
negligible effect on the loop extension
for ![]() .
For higher masses we find that models with Asplund
et al. (2005)
composition do not show blue loops at all, whereas the ones with the Grevesse & Sauval (1998)
mixture display extended blue loops. As this effect is evident only for
about half of the analyzed mass range we decided to neglect it in the
following.
.
For higher masses we find that models with Asplund
et al. (2005)
composition do not show blue loops at all, whereas the ones with the Grevesse & Sauval (1998)
mixture display extended blue loops. As this effect is evident only for
about half of the analyzed mass range we decided to neglect it in the
following.
5.2 Instability strip
For each chemical composition, mass and luminosity, the modal stability
of pulsation models has been investigated for both the fundamental and
the first
overtone mode. The effective temperatures (hereafter in K) of
the hottest and coolest pulsating
fundamental models, increased and decreased, respectively, by the
extension of
the pass in temperature adopted in our analysis, 50 K,
correspond to the
fundamental blue and red edges (FBE and FRE). Similarly the first
overtone
blue (FOBE) and red (FORE) edges are evaluated. Table 3
reports the quadratic fit coefficients of the FBE and FRE, plotted in
Fig. 4
as solid lines. The linear fits of the FBE and FRE
are available on line in Table 2, whereas
the linear fits
for the FOBE and FORE, plotted in Fig. 4 as dashed
lines,
are reported in Table 4 in the
form
![]() ,
where
,
where ![]() is the least square estimate of the intrinsic dispersion.
Figures 4a-f
show the evolutionary tracks superimposed with the quadratic fits of
the edges of the fundamental mode instability strips and the linear
fits of
the first overtone ones for the cases I, II, III, IV, V, VI of
Table 1.
is the least square estimate of the intrinsic dispersion.
Figures 4a-f
show the evolutionary tracks superimposed with the quadratic fits of
the edges of the fundamental mode instability strips and the linear
fits of
the first overtone ones for the cases I, II, III, IV, V, VI of
Table 1.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f3a.eps}\vspace{4mm}
\includegraphics[width=6.5cm,clip]{12004f3b.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg58.png)
|
Figure 3: Upper panel: effect on the fundamental instability strip edges of a metallicity variation within its uncertainty (cases I, II, III of Table 1). Lower panel: as in the upper panel but for a variation of the original helium abundance (cases I, IV of Table 1). In both panels the quadratic fits corresponding to Table 3 are shown. |
| Open with DEXTER | |
To analyse the effect of the chemical composition uncertainty, the upper panel of Fig. 3 shows the instability strips computed for the different metallicities corresponding to the cases I, II, III of Table 1; whereas in the lower panel of the same figure the effect on the instability strip of the Y variation within its uncertainty is shown (cases I and IV of Table 1). As already found in our previous papers (Bono et al. 1999b; Caputo et al. 2000) the predicted instability strip becomes redder as the metallicity increases, while increasing the helium content from 0.26 to 0.28 at Z=0.005 only produces a slight narrowing of the instability strip at the highest luminosity levels, likely due to the slightly reduced efficiency of the H ionization region in driving pulsation.
5.3 The mass-luminosity relation
Inspection of Fig. 4
suggests that the loop extension generally increases with increasing
mass, but, in some cases, it decreases for the 5 ![]() model. As discussed by Castellani
et al. (1990) this is because for masses around this
value the first dredge-up (which is active for
lower masses) becomes inefficient and the star reaches the central He
burning
phase with a reduced external He abundance (and thus with a reduced
loop
extension) with respect to the lower masses.
model. As discussed by Castellani
et al. (1990) this is because for masses around this
value the first dredge-up (which is active for
lower masses) becomes inefficient and the star reaches the central He
burning
phase with a reduced external He abundance (and thus with a reduced
loop
extension) with respect to the lower masses.
For each model set we found the minimum (
![]() )
and maximum (
)
and maximum (
![]() )
mass which
cross the instability strip. The
)
mass which
cross the instability strip. The
![]() and
and ![]() values are listed in Table 5, except
for the cases including overshooting. The minimum mass in general
increases with the metallicity and the helium content while
the maximum mass increases for a decrease of the
metallicity and an increase of Y.
values are listed in Table 5, except
for the cases including overshooting. The minimum mass in general
increases with the metallicity and the helium content while
the maximum mass increases for a decrease of the
metallicity and an increase of Y.
![\begin{figure}
\par\mbox{\includegraphics[width=6.8cm,clip]{12004f4a.eps}\hspace...
...m}
\includegraphics[width=6.8cm,clip]{12004f4f.eps} }\vspace{2mm}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg59.png)
|
Figure 4: Panels a) to f): evolutionary tracks, quadratic fits of the fundamental mode instability strip boundaries and linear fits of the first overtone ones, for the cases I to VI of Table 1. |
| Open with DEXTER | |
Table 5:
Maximum (
![]() )
and minimum (
)
and minimum (
![]() )
mass entering
the instability strip, for the various model sets.
)
mass entering
the instability strip, for the various model sets.
To derive the ML relation (see e.g. Bono et al. 2000) we take into account the three crossings of the instability strip: the first crossing during the H burning and the second and third crossings during the He burning phases. The mean luminosity is obtained by averaging the luminosity behaviour during the three subsequent crossings with the corresponding evolutionary times. Following this procedure, for each case from I to IV of Table 1 we derived the corresponding ML relation (the results are available on line in Table 6).
Since one of the purposes of this work is to investigate the
spread of the
ML relation due to uncertainties on the
chemical composition, we calculated
the global ML relation by fitting together
all the ML data sets (cases I-IV
of Table 1).
As a result we find:
with a standard deviation of
To compare the present result with a previous published
relation based on evolutionary and pulsation models including older
physical inputs, we compared the present ML relation,
given by Eq. (3),
with the one by Bono et al. (2000),
which
explicitly takes into account the dependence on the chemical
composition, computed for the
values of Y and Z corresponding
to our standard case: Y=0.26, Z=0.005.
We found that the ML relation derived in
this paper is flatter than Bono
et al. (2000) with the disagreement reaching about
0.1 dex at masses around 10 ![]() .
However for
.
However for ![]() the two relations are consistent within the uncertainties.
the two relations are consistent within the uncertainties.
5.4 Period-luminosity relations
For the cases I to IV of Table 1 we
calculated the
![]() relations for the fundamental
and first overtone models; the tables
with the
coefficients for these relations are available on line in
Table 7.
relations for the fundamental
and first overtone models; the tables
with the
coefficients for these relations are available on line in
Table 7.
We derived the synthetic PL relations by
populating the predicted
instability strip according to an assumed mass distribution and
adopting, for each mass and chemical composition, the corresponding ML relation
derived on the basis of the corresponding set of evolutionary tracks
(see Sect. 5.3).
More in detail, for each treated case (I to IV of
Table 1),
we built a synthetic population by extracting masses according to a
Salpeter initial mass function (IMF) (![]() M-2.35).
The range of generated masses is given
by the values of
M-2.35).
The range of generated masses is given
by the values of ![]() and
and ![]() for the cases I to IV listed in
Table 5.
In agreement with the procedure adopted in previous papers (Caputo
et al. 2000; Kennicutt et al. 1998), we
fixed to N=1000 the total number of extractions
falling into the
instability strip. To each synthetic star we assigned the luminosity
derived from the
corresponding ML relation. Once the
luminosity is fixed, from the quadratic fits of the fundamental edges,
derived in Sect. 5.2,
we obtained the corresponding temperature of the FRE and the FBE. In
the temperature range from the
for the cases I to IV listed in
Table 5.
In agreement with the procedure adopted in previous papers (Caputo
et al. 2000; Kennicutt et al. 1998), we
fixed to N=1000 the total number of extractions
falling into the
instability strip. To each synthetic star we assigned the luminosity
derived from the
corresponding ML relation. Once the
luminosity is fixed, from the quadratic fits of the fundamental edges,
derived in Sect. 5.2,
we obtained the corresponding temperature of the FRE and the FBE. In
the temperature range from the ![]() of the FBE (decreased by 50 K)
to the
of the FBE (decreased by 50 K)
to the ![]() of the FRE (increased by 50 K), we then extracted randomly the
temperature
of the FRE (increased by 50 K), we then extracted randomly the
temperature ![]() of the synthetic star. For each extracted
of the synthetic star. For each extracted ![]() (in K) the period (in days) is obtained from the
(in K) the period (in days) is obtained from the
![]() relation,
resulting from a linear regression through the fundamental models of
each selected case. Then, by means of the static model atmospheres by Bessel et al. (1998), for
the explored chemical compositions, we converted the model intrinsic
luminosities into the various photometric bands, obtaining synthetic
distributions in period- magnitude planes. The PL relations
are derived by means of linear (or quadratic) regressions through these
model distributions.
relation,
resulting from a linear regression through the fundamental models of
each selected case. Then, by means of the static model atmospheres by Bessel et al. (1998), for
the explored chemical compositions, we converted the model intrinsic
luminosities into the various photometric bands, obtaining synthetic
distributions in period- magnitude planes. The PL relations
are derived by means of linear (or quadratic) regressions through these
model distributions.
Table 8:
Maximum (
![]() )
minimum (
)
minimum (
![]() )
periods in days derived from the synthetic Cepheid distributions.
)
periods in days derived from the synthetic Cepheid distributions.
The maximum and minimum periods corresponding to the obtained
synthetic distributions are reported in Table 8.
In Tables 9
and 11
we report the linear (
![]() )
and quadratic (
)
and quadratic (
![]() )
period-luminosity relations for fundamental
pulsators in the different photometric bands. In these Tables we listed
the fit coefficients for case I of Table 1
(std) and the global fit of cases I to IV taken
together ( all), as well as the results for the PL
relations obtained by
rejecting periods longer than
)
period-luminosity relations for fundamental
pulsators in the different photometric bands. In these Tables we listed
the fit coefficients for case I of Table 1
(std) and the global fit of cases I to IV taken
together ( all), as well as the results for the PL
relations obtained by
rejecting periods longer than
![]() (cut).
The case all provides an estimate of the effect of
the uncertainties on the chemical abundances on the predicted PL relations.
The linear and quadratic
(cut).
The case all provides an estimate of the effect of
the uncertainties on the chemical abundances on the predicted PL relations.
The linear and quadratic
![]() relations, computed for the
single cases II, III
and IV of Table 1, are
available on
line in Tables 10
and 12.
relations, computed for the
single cases II, III
and IV of Table 1, are
available on
line in Tables 10
and 12.
Passing from the individual cases to the global PL relations,
the coefficients and the intrinsic dispersion do not vary significantly
because the effects of these variations in the abundances are smaller
than the effect on the intrinsic scatter due to the finite width of the
instability strip, especially in the optical filters. Moreover,
inspection of Table 9
suggests that the PL relations become more
linear, less dependent on the chemical composition and with a smaller
intrinsic dispersion passing from the optical to the near-infrared
filters, confirming previous observational (Madore
& Freedman 1991) and theoretical (Bono et al.
1999b; Caputo
et al. 2000) results. The PL relations
obtained for ![]() are derived
because, as shown in Caputo
et al. (2000), removing the longest periods,
the period-magnitude distribution is better reproduced by a linear
relation
also in the optical bands. Moreover, many observed Cepheid samples
cover this
period range.
are derived
because, as shown in Caputo
et al. (2000), removing the longest periods,
the period-magnitude distribution is better reproduced by a linear
relation
also in the optical bands. Moreover, many observed Cepheid samples
cover this
period range.
Table 9: Theoretical linear period-luminosity relations in different photometric bands for fundamental pulsators in the standard and global cases.
The deviation from linearity of Cepheid PL relations
is a debated
issue (Sandage
et al. 2004; Kanbur et al. 2004,2006; Ngeow et al.
2005) and for this reason we
also computed quadratic PL relations. In
particular, Ngeow et al. (2005)
performed a statistical investigation of
the LMC classical Cepheid sample obtained from the MACHO database and
found that the
observed behaviour in period-magnitude diagrams is best reproduced by
two linear relations, with a break at 10 days. Nonlinear
pulsation models (see also Caputo et al. 2000; Fiorentino
et al. 2002; Marconi et al. 2005)
suggest a quadratic form of PL relations,
in particular in the optical
bands (see Table 11).
However the effect of this nonlinearity on the calibration of
the extragalactic distance scale is very small (see Koen
et al. 2007). In Fig. 5 we
plotted the predicted synthetic PL relations
in the V (upper panel) and I (lower panel) Johnson-Cousins
photometric bands with the quadratic fits superimposed (solid lines)
for cases I to IV taken together (case all
in Table 11).
As a comparison the two linear regressions (for
![]() and
and ![]() ,
dashed lines)
obtained observationally by Sandage
et al. (2004) are also
shown. In panel a of Fig. 6 we
show the residuals of the present linear PL relations
for
,
dashed lines)
obtained observationally by Sandage
et al. (2004) are also
shown. In panel a of Fig. 6 we
show the residuals of the present linear PL relations
for ![]() (case all cut of Table 9) in the
V, I bands and over the
whole period range for the K band with
respect to the empirical relations by Freedman
et al. (2001) (for V
and I) and Persson
et al. (2004) (for the K band).
According to this plot, we find differences smaller than
0.2 mag (in absolute value) in all the bands. Panel b of
Fig. 6
shows the differences
between the present linear solutions with
(case all cut of Table 9) in the
V, I bands and over the
whole period range for the K band with
respect to the empirical relations by Freedman
et al. (2001) (for V
and I) and Persson
et al. (2004) (for the K band).
According to this plot, we find differences smaller than
0.2 mag (in absolute value) in all the bands. Panel b of
Fig. 6
shows the differences
between the present linear solutions with
![]() and
the
theoretical PL linear relations with
and
the
theoretical PL linear relations with
![]() by Caputo et al. (2000).
Again we find differences within 0.2 mag with an opposite
trend as a function of the period with respect to the previous
comparison, thus suggesting that the the magnitudes predicted by the
new PL relations obtained in this paper
are somewhat intermediate between the ones based on empirical relations
and the theoretical relations by Caputo
et al. (2000).
by Caputo et al. (2000).
Again we find differences within 0.2 mag with an opposite
trend as a function of the period with respect to the previous
comparison, thus suggesting that the the magnitudes predicted by the
new PL relations obtained in this paper
are somewhat intermediate between the ones based on empirical relations
and the theoretical relations by Caputo
et al. (2000).
As far the physical assumptions of our pulsation models are concerned, we have already shown that changes in the adopted equation of state do not affect significantly the pulsation scenario (Petroni 2003). On the other hand, variations of the mixing length parameters used to close the nonlinear equation system (see Bono & Stellingwerf 1994) have been found to produce negligible effects on the predicted Cepheid relations (see Fiorentino et al. 2007, for details).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f5a.eps}\hspace{3.5mm}
\includegraphics[width=6.5cm,clip]{12004f5b.eps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg79.png)
|
Figure 5:
Synthetic period-luminosity relations in the V (
upper panel) and I (
lower panel) Johnson-Cousins photometric bands with the
quadratic fits (solid lines)
corresponding to the case all of Table 11.
Symbols: std case (case I, black dots);
|
| Open with DEXTER | |
6 Noncanonical models
6.1 Overshooting
The extension of the
mixing into a region that is stable following the Schwarzschild
criterion is generally called
``overshooting'' (see e.g. Cordier
et al. 2002, and references therein). An additional
extension of the canonical convective regions could also be due to
rotationally
induced mixing (see e.g. Meynet
& Maeder 2000); both phenomena
can be modeled, at least as far as the extension of the mixing zones is
concerned, with the same
``overshooting'' formalism. A complete understanding of these
extra-mixing mechanisms is still lacking in the literature due to the
complexity of the involved phenomena, that also prevents an analytical
approach (see e.g. Demarque
et al. 2007; Straka et al. 2005).
Three-dimensional hydrodynamical calculations are still under
development (Meakin
& Arnett 2007; Eggleton et al. 2007).
Thus a semi-empirical approach
is currently used by defining the extension of any additional mixing
region, starting from the border of the canonical
convective zones, in terms of the pressure scale height ![]() :
:
![]() .
The overshooting efficiency is generally
estimated through the comparison between theory and observations for
different
relevant quantities, and is still widely debated
point (see e.g. Brocato
et al. 2003; Chiosi et al. 1992; Claret 2007;
Barmina
et al. 2002, and references therein).
.
The overshooting efficiency is generally
estimated through the comparison between theory and observations for
different
relevant quantities, and is still widely debated
point (see e.g. Brocato
et al. 2003; Chiosi et al. 1992; Claret 2007;
Barmina
et al. 2002, and references therein).
We calculated additional sets of
evolutionary models including overshooting during the central
H burning phase
(Main Sequence, MS) with
![]() and
and ![]() ,
within the range suggested in the recent literature (see e.g. Girardi et al. 2000).
During the central He burning phase our code implements the
classical semi-convection criterion (see e.g. Castellani
et al. 1985) at the
border of the Schwarzschild convective core (which is driven by
mechanical
overshooting at the convective core boundary), while breathing pulses
(see e.g. Dorman
& Rood 1993; Castellani et al. 1985)
are suppressed following the
procedure described by Caputo
et al. (1989). In the present models the
overshooting region is fully homogenized but the
temperature gradient is kept at its radiative value.
,
within the range suggested in the recent literature (see e.g. Girardi et al. 2000).
During the central He burning phase our code implements the
classical semi-convection criterion (see e.g. Castellani
et al. 1985) at the
border of the Schwarzschild convective core (which is driven by
mechanical
overshooting at the convective core boundary), while breathing pulses
(see e.g. Dorman
& Rood 1993; Castellani et al. 1985)
are suppressed following the
procedure described by Caputo
et al. (1989). In the present models the
overshooting region is fully homogenized but the
temperature gradient is kept at its radiative value.
The inclusion of overshooting during central H burning in standard models leads to a higher luminosity and longer lifetime during the MS phase, larger He cores and luminosities and reduced lifetimes during the following central He burning phase. This reflects in the adoption of a different mass-luminosity relation for Cepheid pulsational models. The adopted luminosity levels for noncanonical models in this paper are taken as brighter than the canonical ones by 0.25 dex, following the prescriptions by Chiosi et al. (1993). We checked that it is true for current evolutionary models too.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f6a.eps}\hspace{3.5mm}
\includegraphics[width=6.5cm,clip]{12004f6b.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg82.png)
|
Figure 6:
a) Residuals of the present linear PL relations
for |
| Open with DEXTER | |
When the overshooting phenomenon is included, the blue loops in the color-magnitude diagram are less extended than in the absence of overshooting in such a way that for some chemical compositions intermediate-mass models do not cross the classical Cepheid instability strip. To avoid this problem, some authors include an ``ad hoc'' undershooting at the lower boundary of convective envelopes (see Girardi et al. 2000), even if there is no clear observational evidence for this mechanism (see e.g. Riello et al. 2003; Renzini & Ritossa 1994).
Relevant pulsation properties, such as the morphology and the
amplitude of
light and radial velocity curves, are affected by the assumed ML relation
(Bono
et al. 2002; Natale et al. 2008), and, in
turn, by the amount of overshooting accounted for
in the models (Keller
2008; Caputo
et al. 2005, and references therein). Independent
theoretical and observational evidence suggests that the Cepheid
pulsation
masses are lower than the canonical evolutionary values but the amount
of
this discrepancy is not firmly established even if several authors find
a
value of the order of 10-15![]() .
(e.g. Bono
et al. 2001; Natale et al. 2008; Beaulieu
et al. 2001; Caputo et al. 2005, and
references
therein).
.
(e.g. Bono
et al. 2001; Natale et al. 2008; Beaulieu
et al. 2001; Caputo et al. 2005, and
references
therein).
To quantify the effect of overshooting, we computed
models with standard chemical composition (Z=0.005,
Y=0.26) for two selected values of the overshooting
efficiency
(![]() and
and ![]() ,
models XI and XIII of Table 1).
However, due to the
reduced loop extension, some intermediate mass models
with
,
models XI and XIII of Table 1).
However, due to the
reduced loop extension, some intermediate mass models
with ![]() do not cross the instability strip, in
disagreement with observations of LMC Cepheids in this region. To avoid
this problem
without including overshooting for the convective envelopes, taking
into
account the present uncertainty in the original helium abundance, we
calculated overshooting models for Z=0.005, Y=0.28
(model XII of
Table 1)
which, as already
discussed, show a more extended loop than the standard models. In
this way, even models with
do not cross the instability strip, in
disagreement with observations of LMC Cepheids in this region. To avoid
this problem
without including overshooting for the convective envelopes, taking
into
account the present uncertainty in the original helium abundance, we
calculated overshooting models for Z=0.005, Y=0.28
(model XII of
Table 1)
which, as already
discussed, show a more extended loop than the standard models. In
this way, even models with ![]() 5 populate the instability
strip.
5 populate the instability
strip.
In Table 13 the
coefficients of the quadratic fits of
the FRE and FBE for models with
![]() and standard
chemical composition are reported.
and standard
chemical composition are reported.
Table 11: Theoretical quadratic period-luminosity relations for fundamental pulsators in the standard and global cases.
Table 13: Quadratic analytical relations for the fundamental edges, in the non canonical standard case.
The upper panel of Fig. 7 shows the
evolutionary tracks with
![]() ,
Z=0.005, Y=0.28 and the
quadratic fit of the
non canonical strip, while the lower panel of the same figure shows the
evolutionary tracks with
,
Z=0.005, Y=0.28 and the
quadratic fit of the
non canonical strip, while the lower panel of the same figure shows the
evolutionary tracks with
![]() ,
Z=0.005, Y=0.26 and
the quadratic fits of the canonical (dot-dashed lines) and non
canonical
(solid lines) instability strip boundaries calculated for standard
chemical
composition. We notice that the case with
,
Z=0.005, Y=0.26 and
the quadratic fits of the canonical (dot-dashed lines) and non
canonical
(solid lines) instability strip boundaries calculated for standard
chemical
composition. We notice that the case with ![]() is not significantly
different from the canonical one and for this reason in the following
we will
concentrate on the case with
is not significantly
different from the canonical one and for this reason in the following
we will
concentrate on the case with ![]() .
.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f7a.eps}\vspace{4mm}
\includegraphics[width=6.5cm,clip]{12004f7b.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg87.png)
|
Figure 7:
Evolutionary tracks with Y=0.28, Z=0.005,
|
| Open with DEXTER | |
The ML obtained with the set of tracks with
![]() ,
Z=0.005, Y=0.28 combined with
the noncanonical strip of
Fig. 7,
upper panel, is the following:
,
Z=0.005, Y=0.28 combined with
the noncanonical strip of
Fig. 7,
upper panel, is the following:
with
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12004fg8.eps}\hspace{3mm}\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg90.png)
|
Figure 8:
Comparison between the mass-luminosity relation from Eq. (4) (Y=0.28,
Z=0.005,
|
| Open with DEXTER | |
For the chemical composition of case I, in Table 1 we
calculated the
![]() relations for
noncanonical fundamental and first overtone models; the tables with the
coefficients for these relations are available on line in
Table 14.
relations for
noncanonical fundamental and first overtone models; the tables with the
coefficients for these relations are available on line in
Table 14.
Adopting the same procedure as for canonical models we derived
the multi-band period-luminosity relations for
![]() ,
Z=0.005, Y=0.28. The
coefficients of the linear PL in the V,
I, K bands are reported
in Table 17,
whereas the linear and quadratic PL relations in
the other photometric bands are available on line, in Tables 15
and 16.
,
Z=0.005, Y=0.28. The
coefficients of the linear PL in the V,
I, K bands are reported
in Table 17,
whereas the linear and quadratic PL relations in
the other photometric bands are available on line, in Tables 15
and 16.
A comparison between the canonical (case std of Table 9) and the noncanonical PL linear relation in the V, I, K bands (see Table 17) is shown in Fig. 9, where the errorbars refer to the intrinsic dispersions of the canonical relations. We notice that both the zero point and the slope of the PL relations are affected by the inclusion of mild overshooting. The noncanonical V band relation predicts brighter magnitudes than the canonical ones in the very short period range and fainter magnitudes than the canonical ones for periods longer than about 5 days, whereas the noncanonical I and K band PL predict almost identical magnitudes to the canonical ones at the shortest periods and fainter magnitudes than their canonical counterparts elsewhere, with the effect increasing toward longer periods. At a period of 10 days, the effect of applying the noncanonical relations instead of the canonical ones would be of about 0.15, 0.17 and 0.19 mag in the V, I and K band respectively, whereas at 30 days it would be as large as about 0.32, 0.29 and 0.24 in the V, I and K band respectively.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12004fg9.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg91.png)
|
Figure 9: Comparison, in the V, I and K photometric bands, between the present canonical and noncanonical linear PL relations (solid and dashed lines). |
| Open with DEXTER | |
Table 17: Theoretical PL relations for fundamental noncanonical pulsators (see text).
Referring to the upper panel of Fig. 7, we report in Table 18 the minimum and maximum masses with blue loops that cross the red edge of the instability strip, together with the corresponding values of the minimum and maximum period.
Table 18:
![]() ,
,
![]() ,
,
![]() ,
,
![]() (as in Table 5)
for
(as in Table 5)
for ![]() .
.
6.2 Mass loss
The possibility that mass loss might solve the long-standing problem of
the mass discrepancy of Cepheids between the value inferred from
pulsational and evolutionary models has been suggested by various
authors (see e.g. Bono
et al. 2002; Caputo et al. 2005). The
argument is that in order to solve the problem - that is, to provide
higher luminosity for He-burning stars of a given mass - a larger
He-core mass is needed. As previously discussed, this is precisely the
effect of the convective core-overshooting. On the other hand, a
similar result can be mimicked by a standard model affected by
significant mass loss.
In order to check this, we computed the evolution
of a 5 ![]() star taking into account the
effect of a mild core overshooting (
star taking into account the
effect of a mild core overshooting (
![]() )
during the
H-burning phase. We attempted to reproduce the minimum luminosity (
)
during the
H-burning phase. We attempted to reproduce the minimum luminosity (
![]() )
of this model during the central He-burning by standard models affected
by mass loss.
The mass loss process is not yet fully understood and it is still
lacking satisfactory knowledge of its efficiency along the various
evolutionary phases. As a consequence, we are forced to adopt different
mass loss prescriptions in the following numerical experiments in order
to study the problem. Thus we computed the evolution of stars with mass
in the range between 6.0 and 7
)
of this model during the central He-burning by standard models affected
by mass loss.
The mass loss process is not yet fully understood and it is still
lacking satisfactory knowledge of its efficiency along the various
evolutionary phases. As a consequence, we are forced to adopt different
mass loss prescriptions in the following numerical experiments in order
to study the problem. Thus we computed the evolution of stars with mass
in the range between 6.0 and 7 ![]() with different mass loss prescriptions adopting the classical
Schwarzschild criterion
to determine the convective core boundary; the results, discussed
below,
are shown in Fig. 10.
The models were evolved with constant mass during the main sequence and
subgiant phase, while
a substantial mass loss, with a constant rate, was imposed during the
red giant phase. Once the total mass of the models reached the
desired value, the subsequent evolution was performed at constant mass.
Following such a procedure, we computed for example the evolution of
the central He-burning phase of a 5.3
with different mass loss prescriptions adopting the classical
Schwarzschild criterion
to determine the convective core boundary; the results, discussed
below,
are shown in Fig. 10.
The models were evolved with constant mass during the main sequence and
subgiant phase, while
a substantial mass loss, with a constant rate, was imposed during the
red giant phase. Once the total mass of the models reached the
desired value, the subsequent evolution was performed at constant mass.
Following such a procedure, we computed for example the evolution of
the central He-burning phase of a 5.3 ![]() with a
progenitor star of 6.2
with a
progenitor star of 6.2 ![]() ,
whose behavior in the HR-diagram
is like that of our target, the 5
,
whose behavior in the HR-diagram
is like that of our target, the 5 ![]() with core overshooting.
However, further numerical experiments showed that the result
is not unique; models with different initial masses and
different prescriptions for the mass loss have a minimum luminosity
during the central He-burning very similar to
with core overshooting.
However, further numerical experiments showed that the result
is not unique; models with different initial masses and
different prescriptions for the mass loss have a minimum luminosity
during the central He-burning very similar to
![]() .
Such a result was expected since the Cepheid ML relation
depends appreciably on both the mass-loss rate and the evolutionary
phase at which it is turned on. An example is given by a star with
initial mass of 6.1
.
Such a result was expected since the Cepheid ML relation
depends appreciably on both the mass-loss rate and the evolutionary
phase at which it is turned on. An example is given by a star with
initial mass of 6.1 ![]() evolved
from the ZAMS, with the classical Reimers mass loss rate (with
evolved
from the ZAMS, with the classical Reimers mass loss rate (with ![]() );
even if this model describes a much more extended loop in color in the
HR-diagram, the minimum luminosity of the central He
burning phase is the same. The target luminosity can also be reproduced
by a more extreme model: a 3
);
even if this model describes a much more extended loop in color in the
HR-diagram, the minimum luminosity of the central He
burning phase is the same. The target luminosity can also be reproduced
by a more extreme model: a 3 ![]() with a progenitor of
6.4
with a progenitor of
6.4 ![]() .
In this case, the color of the He-burning model is
significantly redder than the model with core overshooting.
These few numerical examples prove that it does not make sense to try
to
compute a ML relationship for standard models with
mass loss, unless
a priori mass loss prescriptions have been fixed.
Moreover, the mass-loss solution of the Cepheid mass discrepancy sounds
rather ad hoc, at least until a physical process responsible
for the huge required mass loss is found and understood.
.
In this case, the color of the He-burning model is
significantly redder than the model with core overshooting.
These few numerical examples prove that it does not make sense to try
to
compute a ML relationship for standard models with
mass loss, unless
a priori mass loss prescriptions have been fixed.
Moreover, the mass-loss solution of the Cepheid mass discrepancy sounds
rather ad hoc, at least until a physical process responsible
for the huge required mass loss is found and understood.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f10.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg95.png)
|
Figure 10:
Comparison of the minimum luminosity during the central
He burning phase
for a 5 |
| Open with DEXTER | |
7 Conclusions
On the basis of an updated set of evolutionary and pulsation models for classical Cepheids in the LMC, we have investigated the effect of the uncertainties on the chemical composition and on the physical assumptions adopted in the codes on the most relevant pulsation observables and thus on the theoretical calibration of the Cepheid distance scale. We found that present uncertainties on relevant nuclear reaction rates have only a negligible effect on evolutionary and pulsational theoretical prediction. Moreover the uncertainties in the metal and helium abundances affect the results of the evolutionary computations but do not significantly change the pulsation scenario. On the other hand, the still present uncertainties on the efficiency of the overshooting phenomenon in the previous H burning phase and on the mass-loss rates are found to be the most important source of uncertainty in the theoretical Cepheid mass-luminosity and period-luminosity relations. In particular, using a theoretical PL relation that relies on the assumption of mildly overshooting evolutionary models, one infers distances that are significantly shorter than the values obtained when a canonical theoretical PL is used, especially in the optical bands. Therefore we conclude that the uncertainty on the Cepheid ML relation is expected to significantly affect the Cepheid calibration of the extragalactic distance scale and in turn the evaluation of the Hubble constant. The application of the theoretical analysis performed in this paper to LMC Cepheid data will be addressed in a forthcoming paper (Valle et al. 2009, in prep.).
AcknowledgementsWe thank our anonymous referee for his/her valuable comments that improved the quality of our paper. We also warmly thank S. Shore for a careful reading of the manuscript. Financial support for this study was provided by PRIN-INAF 2006 (PI G. Clementini).
References
- Alcock, C., & Paczynski, B. 1978, ApJ, 223, 244 [NASA ADS] [CrossRef]
- Andrievsky, S. M., Kovtyukh, V. V., Korotin, S. A., Spite, M., & Spite, F. 2001, A&A, 367, 605 [NASA ADS] [CrossRef] [EDP Sciences]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. F. N. Bash, & T. J. Barnes, ASP Conf. Ser., 336, 25
- Badnell, N. R., Bautista, M. A., Butler, K., et al. 2005, MNRAS, 360, 458 [NASA ADS] [CrossRef]
- Bahcall, J. N., Basu, S., Pinsonneault, M., & Serenelli, A. M. 2005, ApJ, 618, 1049 [NASA ADS] [CrossRef]
- Barmina, R., Girardi, L., & Chiosi, C. 2002, A&A, 385, 847 [NASA ADS] [CrossRef] [EDP Sciences]
- Basu, S., & Antia, H. M. 2004, ApJ, 606L, 85 [NASA ADS] [CrossRef]
- Beaulieu, J. P., Buchler, J. R., & Kollath, Z. 2001, A&A, 373, 164 [NASA ADS] [CrossRef] [EDP Sciences]
- Bemmerer, D., Confortola, F., Lemut, A., et al. 2006, Nucl. Phys. A, 779, 297 [NASA ADS] [CrossRef]
- Bessel, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS]
- Böhm-Vitense, E. 1958, Zs.f.Ap., 46, 108
- Bono, G., & Stellingwerf, R. F. 1994, ApJS, 93, 233 [NASA ADS] [CrossRef]
- Bono, G., Marconi, M., & Stellingwerf, R. F. 1997, ApJ, 477, 346 [NASA ADS] [CrossRef]
- Bono, G., Marconi, M., & Stellingwerf, R. F. 1999a, ApJS, 122, 167 [NASA ADS] [CrossRef]
- Bono, G., Caputo, F., Castellani, V., & Marconi, M. 1999b, ApJ, 512, 711 [NASA ADS] [CrossRef]
- Bono, G., Caputo, F., Cassisi, S., et al. 2000, ApJ, 543, 955 [NASA ADS] [CrossRef]
- Bono, G., Gieren, W. P., Marconi, M., Fouqué, P., & Caputo, F. 2001, ApJ, 563, 319 [NASA ADS] [CrossRef]
- Bono, G., Castellani, V., & Marconi, M. 2002, ApJ, 565, L83 [NASA ADS] [CrossRef]
- Bono, G., Caputo, F., Fiorentino, G., Marconi, M., & Musella, I. 2008, ApJ, 684, 102 [NASA ADS] [CrossRef]
- Brocato, E., & Castellani, V. 1993, ApJ, 410, 99 [NASA ADS] [CrossRef]
- Brocato, E., Castellani, V., Di Carlo, E., Raimondo, G., & Walker, A. R. 2003, AJ, 125, 3111 [NASA ADS] [CrossRef]
- Brocato, E., Caputo, F., Castellani, V., Marconi, M., & Musella, I. 2004, AJ, 128, 1597 [NASA ADS] [CrossRef]
- Brunish, W. M., & Becker, S. A. 1990, ApJ, 351, 258 [NASA ADS] [CrossRef]
- Buchmann, L. R., & Barnes, C. A. 2006, Nucl. Phys. A, 777, 254 [NASA ADS] [CrossRef]
- Caffau, E., Ludwig, H. G., Steffen, M., et al. 2008, A&A, 488, 1031 [NASA ADS] [CrossRef] [EDP Sciences]
- Caldwell, J. A. R., & Coulson, I. M. 1986, MNRAS, 218, 223 [NASA ADS]
- Caldwell, J. A. R., & Laney, C. D. 1991, in The Magellanic Clouds, IAU Symp., 148, 249
- Canuto, V. M. 2000, ApJ, 534, L113 [NASA ADS] [CrossRef]
- Caputo, F., Chieffi, A., Tornambé, A., Castellani, V., & Pulone, L. 1989, ApJ, 340, 241 [NASA ADS] [CrossRef]
- Caputo, F., Marconi, M., & Musella, I. 2000, A&A, 354, 610 [NASA ADS]
- Caputo, F., Bono, G., Fiorentino, G., Marconi, M., & Musella, I. 2005, ApJ, 629, 1021 [NASA ADS] [CrossRef]
- Castellani, V., Giannone, P., & Renzini, A. 1971a, Ap&SS, 10, 340 [NASA ADS] [CrossRef]
- Castellani, V., Giannone, P., & Renzini, A. 1971b, Ap&SS, 10, 355 [NASA ADS] [CrossRef]
- Castellani, V., Chieffi, A., Tornambé, A., & Pulone, L. 1985, ApJ, 296, 204 [NASA ADS] [CrossRef]
- Castellani, V., Chieffi, A., & Straniero, O. 1990, ApJS, 74, 463 [NASA ADS] [CrossRef]
- Castellani, V., Chieffi, A., & Straniero, O. 1992, ApJS, 78, 517 [NASA ADS] [CrossRef]
- Chieffi, A., & Straniero, O. 1989, ApJS, 71, 47 [NASA ADS] [CrossRef]
- Chin, C., & Stothers, R. B. 1991, ApJS, 77, 299 [NASA ADS] [CrossRef]
- Chiosi, C., & Maeder, A. 1986, ARA&A, 24, 329 [NASA ADS] [CrossRef]
- Chiosi, C., Bertelli, S., & Bressan, A. 1992, ARA&A, 30, 305 [NASA ADS] [CrossRef]
- Chiosi, C., Wood, P. R., & Capitanio, N. 1993, ApJS, 86, 541 [NASA ADS] [CrossRef]
- Ciacio, F., Degl'Innocenti, S., & Ricci, B. 1997, A&AS, 123, 449 [NASA ADS] [CrossRef] [EDP Sciences]
- Claret, A. 2007, A&A, 475, 1019 [NASA ADS] [CrossRef] [EDP Sciences]
- Cordier, D., Lebreton, Y., Goupil, M. J., et al. 2002, A&A, 392, 169 [NASA ADS] [CrossRef] [EDP Sciences]
- Cox, J. P., & Giuli, R. T. 1968, Principles of stellar Structure (New York, USA: Gordon and Breach Science publishers)
- Degl'Innocenti, S., Prada Moroni, P. G., & Ricci, B. 2006, Ap&SS, 305, 67 [NASA ADS] [CrossRef]
- Degl'Innocenti, S., Prada Moroni, P. G., Marconi, M., & Ruoppo, A. 2008, Ap&SS, 316, 25 [NASA ADS] [CrossRef]
- Demarque, P., Robinson, F. J., & Straka, C. W. 2007, in From Stars to Galaxies: Building the Pieces to Build Up the Universe, ed. A. Vallenari, R. Tantalo, L. Portinari, & A. Moretti, ASP Conf. Ser., 374, 27
- Di Criscienzo, M., Marconi, M., & Caputo, F. 2004, ApJ, 612, 1092 [NASA ADS] [CrossRef]
- Dorman, B., & Rood, R. T. 1993, ApJ, 409, 387 [NASA ADS] [CrossRef]
- Eggleton, P. P., Dearborn, D. S., & Lattanzio, J. C. 2007, ApJ, 677, 581 [NASA ADS] [CrossRef]
- Feast, M. W. 1984, in Structure and evolution of the Magellanic Clouds, IAU Symp., 108, 157
- Feast, M. W. 1991, in The Magellanic Clouds, IAU Symp., 148, 1
- Feast, M. W. 1995, PASP, 111, 775 [NASA ADS] [CrossRef]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef]
- Fiorentino, G., Caputo, F., Marconi, M., & Musella, I. 2002, ApJ, 576, 402 [NASA ADS] [CrossRef]
- Fiorentino, G., Marconi, M., Musella, I., & Caputo, F. 2007, A&A, 476, 863 [NASA ADS] [CrossRef] [EDP Sciences]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef]
- Fynbo, H. O. U., Diget, C. A., Bergmann, U. C., et al. 2005, Nature, 433, 136 [NASA ADS] [CrossRef]
- Gennaro, M., Prada Moroni, P. G., & Degl'Innocenti, S. 2008, proceedings of 52 congresso SAIt, Mem. Soc. Astron. Ital., in publication
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences]
- Graboske, H. C., Dewitt, H. E., Grossman, A. S., & Cooper, M. 1973, ApJ, 181, 457 [NASA ADS] [CrossRef]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the elements, ed. N. Prantzos, E. Vangioni-Flam, M. Cassé (Cambridge: Cambridge Univ. Press), 15
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef]
- Hammer, J. W., Fey, M., Kunz, R., et al. 2005, Nucl. Phys. A, 758, 363 [NASA ADS] [CrossRef]
- Huang, R. Q., & Weigert, A. 1983, ApJ, 127, 309 [NASA ADS]
- Iben, I. 1972, ApJ, 178, 433 [NASA ADS] [CrossRef]
- Iglesias, C., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences]
- Itoh, N., Totsuji, H., & Ichimaru, S. 1977, ApJ, 218, 477 [NASA ADS] [CrossRef]
- Itoh, N., Totsuji, H., Ichimaru, S., & Dewitt, H. E. 1979, ApJ, 234, 1079 [NASA ADS] [CrossRef]
- Izotov, Y. I., Thuan, T. X., & Stasinska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef]
- Jimenez, R., Flynn, C., MacDonald, J., & Gibson, B. K. 2003, Science, 299, 1552 [NASA ADS] [CrossRef]
- Kanbur, S. M., & Ngeow, C.-C. 2006, MNRAS, 369, 705 [NASA ADS] [CrossRef]
- Kanbur, S. M., Ngeow, C.-C., & Buchler, J. R. 2004, MNRAS, 354, 212 [NASA ADS] [CrossRef]
- Keller, S. 2008, ApJ, 677, 483 [NASA ADS] [CrossRef]
- Kennicutt, R. C., Jr., Stetson, P. B., Saha, A., et al. 1998, ApJ, 498, 181 [NASA ADS] [CrossRef]
- Koen, C., Kanbur, S., & Ngeow, C. 2007, MNRAS, 380, 1440 [NASA ADS] [CrossRef]
- Korn, A. J., Becker, S. R., Gummersbach, C. A., & Wolf, B. 2000, A&A, 353, 655 [NASA ADS]
- Lauterborn, D., Refsdal, S., & Weigert, A. 1971, A&A, 10, 97 [NASA ADS]
- Laney, C. D., & Stobie, R. S. 1986, MNRAS, 222, 449 [NASA ADS]
- Lemut, A., Bemmerer, D., Confortola, F., et al. 2006, Phys. Lett. B, 634, 483 [NASA ADS] [CrossRef]
- Luck, R. E., Moffett, T. J., Barnes, T. G. III, & Gieren, W. P. 1998, AJ, 115, 605 [NASA ADS] [CrossRef]
- Macri, L. M., Stanek, K. Z., Bersier, D., Greenhill, L. J., & Reid, M. J. 2006, ApJ, 652, 1133 [NASA ADS] [CrossRef]
- Madore, B., & Freedman, W. L. 1991, PASP, 103, 933 [NASA ADS] [CrossRef]
- Maeder, A., & Zahn, J. P. 1998, A&A, 334, 1000 [NASA ADS]
- Marconi, M., & Di Criscienzo, M. 2007, MNRAS, 467, 223
- Marconi, M., Caputo, F., Di Criscienzo, M., & Castellani, M. 2003, ApJ, 596, 299 [NASA ADS] [CrossRef]
- Marconi, M., Fiorentino, G., & Caputo, F. 2004, A&A, 417, 1101 [NASA ADS] [CrossRef] [EDP Sciences]
- Marconi, M., Musella, I., & Fiorentino, G. 2005, ApJ, 632, 590 [NASA ADS] [CrossRef]
- Matraka, B., Wassermann, C., & Weigert, A. 1982, A&A, 107, 283 [NASA ADS]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [NASA ADS] [CrossRef]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS]
- Natale, G., Marconi, M., & Bono, G. 2008, ApJL, 674, 93 [NASA ADS] [CrossRef]
- Ngeow, C.-C., Kanbur, S. M., Nikolaev, S., et al. 2005, MNRAS, 363, 831 [NASA ADS] [CrossRef]
- Neuforge-Verheecke, C., Guzik, J. A., Keady, J. J., et al. 2001, ApJ, 561, 450 [NASA ADS] [CrossRef]
- Noels, A., & Gabriel, M. 1973, A&A, 24, 201 [NASA ADS]
- Pagel, B. E. J., & Portinari, L. 1998, MNRAS, 298, 747 [NASA ADS] [CrossRef]
- Palacios, A., Talon, S., Charbonnel, C., & Forestini, M. 2003, A&A, 399, 603 [NASA ADS] [CrossRef] [EDP Sciences]
- Peimbert, M., Luridiana, V., Peimbert, A., & Carigi, L. 2007, ASP Conf. Ser., 374, 81 [NASA ADS]
- Persson, S. E., Madore, B. F., Krzemi
 ski, W., et al. 2004, AJ, 128, 2239 [NASA ADS] [CrossRef]
ski, W., et al. 2004, AJ, 128, 2239 [NASA ADS] [CrossRef]
- Potekhin, A. Y. 1999, A&A, 351, 787 [NASA ADS]
- Petroni, S., Bono, G., Marconi, M., & Stellingwerf, R. F. 2003, ApJ, 599, 522 [NASA ADS] [CrossRef]
- Renzini, A., & Ritossa, C. 1994, ApJ, 433, 293 [NASA ADS] [CrossRef]
- Renzini, A., Greggio, L., & Ritossa, C. 1992, ApJ, 400, 280 [NASA ADS] [CrossRef]
- Riello, M., Cassisi, S., Piotto, G., et al. 2003, A&A, 410, 553 [NASA ADS] [CrossRef] [EDP Sciences]
- Robertson, J. W. 1971, ApJ, 170, 353 [NASA ADS] [CrossRef]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef]
- Romaniello, M., Primas, F., Mottini, M., et al. 2005, A&A, 429, 37 [NASA ADS] [CrossRef]
- Romaniello, M., Primas, F., Mottini, M., et al. 2008, A&A, 488, 731 [NASA ADS] [CrossRef] [EDP Sciences]
- Saha, A., Sandage, A., Tammann, G. A., et al. 2001, ApJ, 562, 314 [NASA ADS] [CrossRef]
- Sakai, S., Ferrarese, L., Kennicutt, R. C. Jr., & Saha, A. 2004, ApJ, 608, 42 [NASA ADS] [CrossRef]
- Salasnich, B., Bressan, A., & Chiosi, C. 1999, A&A, 342, 131 [NASA ADS]
- Salpeter, E. E. 1954, Aust. J. Phys., 7, 373 [NASA ADS]
- Sandage, A., Tammann, G. A., & Reindl, B. 2004, A&A, 424, 43 [NASA ADS] [CrossRef] [EDP Sciences]
- Sasselov, D. D., Beaulieu, J. P., Renault, C., et al. 1997, A&A, 324, 471 [NASA ADS]
- Sestito, P., Castellani, V., Degl'Innocenti, S., & Prada Moroni, P. G. 2002, in Observed HR diagrams and stellar evolution: the interplay between observational constraints and theory, ed. T. Lejeune, & J. Fernandes, ASP Conf. Ser., 274, 73
- Shternin, P. S., & Yakovlev, D. G. 2006, PhRvD, 74(4), 3004
- Stothers, R. B. 1988, ApJ, 329, 712 [NASA ADS] [CrossRef]
- Stothers, R. B., & Chin, C. 1991a, ApJ, 374, 288 [NASA ADS] [CrossRef]
- Stothers, R. B., & Chin, C. 1991b, ApJ, 381, L67 [NASA ADS] [CrossRef]
- Stothers, R. B., & Chin, C. 1992, ApJ, 390, L33 [NASA ADS] [CrossRef]
- Stothers, R. B., & Chin, C. 1993, ApJ, 412, 294 [NASA ADS] [CrossRef]
- Stothers, R. B., & Chin, C. 1994, ApJ, 421, L91 [NASA ADS] [CrossRef]
- Straka, C. W., Demarque, P., & Guenther, D. B. 2005, ApJ, 629, 107 [NASA ADS] [CrossRef]
- Sweigart, A., & Demarque, P. 1972, A&A, 20, 445 [NASA ADS]
- Sweigart, A., & Demarque, P. 1973, in Variable Stars in Globular Clusters and in Related Systems, ed. J. D. Fernie, & D. Reidel, IAU Coll., 21, 221
- Udalski, A., Szymanski, M., Kubiak, M., et al. 1999, AcA, 49, 201 [NASA ADS]
- Xu, H. Y., & Li, Y. 2004a, A&A, 418, 213 [NASA ADS] [CrossRef] [EDP Sciences]
- Xu, H. Y., & Li, Y. 2004b, A&A, 418, 225 [NASA ADS] [CrossRef] [EDP Sciences]
- Vázquez, G. A., et al. 2005, ApJ, 663, 995 [NASA ADS] [CrossRef]
- Vemury, S. K., & Stothers, R. 1978, ApJ, 225, 939 [NASA ADS] [CrossRef]
- Weiss, A., Serenelli, A., Kitsikis, A., Schlattl, H., & Christensen-Dalsgaard, J. 2005, A&A, 441, 1129 [NASA ADS] [CrossRef] [EDP Sciences]
Online Material
Table 2: Coefficients of the linear analytical relations for the fundamental red and blue edges.
Table 6:
ML relations for the selected cases;
![]() .
.
Table 7:
Canonical ![]() relations for the selected cases;
relations for the selected cases;
![]() .
.
Table 10: Theoretical linear period-luminosity relations in different photometric bands for individual cases.
Table 12: Theoretical quadratic period-luminosity relations for fundamental pulsators in the various individual cases.
Table 14:
Non canonical ![]() relations:
relations:
![]() .
.
Table 15: Theoretical linear period-luminosity relations for the fundamental noncanonical pulsators.
Table 16: Theoretical quadratic period-luminosity relations for fundamental noncanonical pulsators.
Footnotes
- ... quantities
![[*]](/icons/foot_motif.png)
- Tables 2, 6, 7, 10, 12, 14, 15, 16 are only available at http://www.aanda.org
- ... (EOS)
![[*]](/icons/foot_motif.png)
- http://www-phys.llnl.gov/Research/OPAL/EOS_2005/
- ...
tables
![[*]](/icons/foot_motif.png)
- http://www-phys.llnl.gov/Research/OPAL/opal.html
- ...Ferguson et al. (2005)
![[*]](/icons/foot_motif.png)
- Available at http://webs.wichita.edu/physics/opacity
- ... site
![[*]](/icons/foot_motif.png)
- http://www-phys.llnl.gov/Research/OPAL/opal.html
All Tables
Table 1: Computed sets of evolutionary tracks and pulsation models.
Table 3: The same as Table 2 but for quadratic fits.
Table 4: The same as Table 2 but for the first overtone boundaries.
Table 5:
Maximum (
![]() )
and minimum (
)
and minimum (
![]() )
mass entering
the instability strip, for the various model sets.
)
mass entering
the instability strip, for the various model sets.
Table 8:
Maximum (
![]() )
minimum (
)
minimum (
![]() )
periods in days derived from the synthetic Cepheid distributions.
)
periods in days derived from the synthetic Cepheid distributions.
Table 9: Theoretical linear period-luminosity relations in different photometric bands for fundamental pulsators in the standard and global cases.
Table 11: Theoretical quadratic period-luminosity relations for fundamental pulsators in the standard and global cases.
Table 13: Quadratic analytical relations for the fundamental edges, in the non canonical standard case.
Table 17: Theoretical PL relations for fundamental noncanonical pulsators (see text).
Table 18:
![]() ,
,
![]() ,
,
![]() ,
,
![]() (as in Table 5)
for
(as in Table 5)
for ![]() .
.
Table 2: Coefficients of the linear analytical relations for the fundamental red and blue edges.
Table 6:
ML relations for the selected cases;
![]() .
.
Table 7:
Canonical ![]() relations for the selected cases;
relations for the selected cases;
![]() .
.
Table 10: Theoretical linear period-luminosity relations in different photometric bands for individual cases.
Table 12: Theoretical quadratic period-luminosity relations for fundamental pulsators in the various individual cases.
Table 14:
Non canonical ![]() relations:
relations:
![]() .
.
Table 15: Theoretical linear period-luminosity relations for the fundamental noncanonical pulsators.
Table 16: Theoretical quadratic period-luminosity relations for fundamental noncanonical pulsators.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12004fg1.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg47.png)
|
Figure 1:
Evolutionary tracks with standard chemical composition
with three different values of the 12C( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f2a.eps}\vspace{4mm}
\includegraphics[width=6.5cm,clip]{12004f2b.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg53.png)
|
Figure 2:
Upper panel: effect of a metallicity
variation on the loop extension for a 7 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f3a.eps}\vspace{4mm}
\includegraphics[width=6.5cm,clip]{12004f3b.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg58.png)
|
Figure 3: Upper panel: effect on the fundamental instability strip edges of a metallicity variation within its uncertainty (cases I, II, III of Table 1). Lower panel: as in the upper panel but for a variation of the original helium abundance (cases I, IV of Table 1). In both panels the quadratic fits corresponding to Table 3 are shown. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6.8cm,clip]{12004f4a.eps}\hspace...
...m}
\includegraphics[width=6.8cm,clip]{12004f4f.eps} }\vspace{2mm}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg59.png)
|
Figure 4: Panels a) to f): evolutionary tracks, quadratic fits of the fundamental mode instability strip boundaries and linear fits of the first overtone ones, for the cases I to VI of Table 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f5a.eps}\hspace{3.5mm}
\includegraphics[width=6.5cm,clip]{12004f5b.eps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg79.png)
|
Figure 5:
Synthetic period-luminosity relations in the V (
upper panel) and I (
lower panel) Johnson-Cousins photometric bands with the
quadratic fits (solid lines)
corresponding to the case all of Table 11.
Symbols: std case (case I, black dots);
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f6a.eps}\hspace{3.5mm}
\includegraphics[width=6.5cm,clip]{12004f6b.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg82.png)
|
Figure 6:
a) Residuals of the present linear PL relations
for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f7a.eps}\vspace{4mm}
\includegraphics[width=6.5cm,clip]{12004f7b.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg87.png)
|
Figure 7:
Evolutionary tracks with Y=0.28, Z=0.005,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12004fg8.eps}\hspace{3mm}\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg90.png)
|
Figure 8:
Comparison between the mass-luminosity relation from Eq. (4) (Y=0.28,
Z=0.005,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12004fg9.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg91.png)
|
Figure 9: Comparison, in the V, I and K photometric bands, between the present canonical and noncanonical linear PL relations (solid and dashed lines). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12004f10.eps}
\end{figure}](/articles/aa/full_html/2009/45/aa12004-09/Timg95.png)
|
Figure 10:
Comparison of the minimum luminosity during the central
He burning phase
for a 5 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



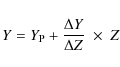
![\begin{displaymath}
Z = (1-Y_{\rm P})\left(1+\frac{\Delta Y}{\Delta Z}+ \frac{1}{(Z/X)_\odot} \times 10^{-[{\rm Fe/H}]}\right)^{-1} \quad \end{displaymath}](/articles/aa/full_html/2009/45/aa12004-09/img29.png)