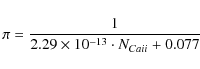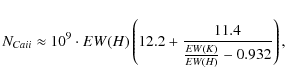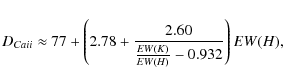| Issue |
A&A
Volume 507, Number 2, November IV 2009
|
|
|---|---|---|
| Page(s) | 833 - 840 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/20079144 | |
| Published online | 15 September 2009 | |
A&A 507, 833-840 (2009)
The interstellar Ca II distance
scale![[*]](/icons/foot_motif.png)
A. Megier1 - A. Strobel1 - G. A. Galazutdinov2 - J. Kre![]() owski1
owski1
1 - Nicolaus Copernicus University, Center for Astronomy, Gagarina 11, 87-100 Torun, Poland
2 -
Department of Physics and Astronomy, Seoul National University, Gwanak-gu, Seoul 151-747, Korea
Received 26 November 2007 / Accepted 7 July 2009
Abstract
Aims. We attempt to extend the relation between the strengths of the interstellar Ca II lines
and the distances to early-type stars to objects beyond
1 kiloparsec, with the line saturation taken into account.
Methods. We measure the Ca II K and Ca II H equivalent widths, and compute Ca II column densities for 262 lines of sight towards early-type stars with available Hipparcos parallaxes (![]() ).
The targets are located within a few hundred parsecs of the Galactic
plane, and span all the range of Galactic longitudes. We fit the
).
The targets are located within a few hundred parsecs of the Galactic
plane, and span all the range of Galactic longitudes. We fit the
![]() - parallax relation with a function of the form
- parallax relation with a function of the form
![]() ,
using a maximum-likelihood approach to take account of errors in both
variables. We use the resultant formula to estimate distances to stars
in OB associations and clusters, and compare them to those found
in the literature, usually estimated by spectrophotometric methods.
,
using a maximum-likelihood approach to take account of errors in both
variables. We use the resultant formula to estimate distances to stars
in OB associations and clusters, and compare them to those found
in the literature, usually estimated by spectrophotometric methods.
Results. For lines of sight with
EW(K)/EW(H) > 1.3, we obtain the following approximate formula for the distance:
![]() ,
where the equivalent widths EW(K) and EW(H) are in mÅ, and the distance
,
where the equivalent widths EW(K) and EW(H) are in mÅ, and the distance
![]() in parsecs. The errors in
in parsecs. The errors in
![]() ,
resulting from the uncertainty in the fit parameters and errors in the equivalent widths, are typically about 15
,
resulting from the uncertainty in the fit parameters and errors in the equivalent widths, are typically about 15![]() of the distance. We can also expect the equation not to hold for
objects situated farther than a few hundred parsecs from the Galactic
plane. We find several cases of significant column density differences
between association or cluster members, especially notable in the
Trumpler 16 cluster, indicating either a local
contribution to the Ca II column density, or background/foreground stars being confused with members. The ratio
of the distance. We can also expect the equation not to hold for
objects situated farther than a few hundred parsecs from the Galactic
plane. We find several cases of significant column density differences
between association or cluster members, especially notable in the
Trumpler 16 cluster, indicating either a local
contribution to the Ca II column density, or background/foreground stars being confused with members. The ratio
![]() appears to depend on the Galactic longitude, being highest in the range 70
appears to depend on the Galactic longitude, being highest in the range 70![]() < l < 120
< l < 120![]() and lowest for 200
and lowest for 200![]() < l < 300
< l < 300![]() .
This effect may be due to large-scale structure being present in the Ca II layer, or to the nonmember confusion being enhanced in these directions.
.
This effect may be due to large-scale structure being present in the Ca II layer, or to the nonmember confusion being enhanced in these directions.
Key words: ISM: lines and bands - stars: distances - stars: early-type - open clusters and associations: general
1 Introduction
Estimating distances to stars in our Galaxy, beyond the range of individual trigonometric parallaxes, is a challenging task. The most commonly used method of spectrophotometric parallaxes relies on accurate calibration of the absolute magnitude for the star's spectral type; it is also necessary to take into account interstellar extinction along the line of sight to the star.
The situation is most difficult for early-type stars - typically situated near the Galactic plane, where extinction is highest. Relatively low numbers of stars of any given early subtype make both the classification and calibration of absolute magnitudes for these objects difficult. The differences between MV values for spectral types O and B, given by different authors (e.g. Schmidt-Kaler 1982; Zorec & Briot 1991; Vacca et al. 1996; Wegner 2006), in some cases (B0III) exceed 1 mag; differences of 0.5 mag. are common. The problem is made more difficult by the fact that the spectral type and luminosity class of any given star is itself uncertain. As the difference of one spectral subclass in OB stars may change the effective temperature by 10 percent or more, any classification uncertainties heavily influence the derived distance. Unresolved binaries, common among early-type stars, may result in distance errors in excess of 40 percent.
It is thus tempting to try to estimate distances assuming as little as possible about the intrinsic parameters of the observed objects, and one of the ways of doing that relies on using the amount of interstellar matter in the line of sight towards the star, calculated on the basis of the star's observed spectrum. The relation of interstellar absorption lines to distance was first studied by Struve (1928). Further work on the subject was published by Sanford (1937), Wilson & Merrill (1937), Evans (1941), and Beals & Oke (1953). Later years saw a lot of research concerning the interstellar absorptions lines, e.g. Welty & Hobbs (2001), Crawford (2001), Price et al. (2001), Crawford et al. (2002), Smoker et al. (2003), Welty et al. (2003), Hunter et al. (2006), Smoker et al. (2006), to name just the more recent ones. However, the possible use of these spectral features for distance estimation was hampered by problems with the calibration of the distance - line strength relation, because of the necessity of finding a substantial sample of appropriately distant stars with well determined distances.
Another problem lies in selecting which of the possible measures of interstellar features should be used for distance estimation, as they correspond to different components of the interstellar medium. The necessary condition is that the given component must be relatively uniformly distributed, at least on the scale of typical distances to the observed stars. While the nonuniform, structure-rich distribution of the interstellar matter is well known, some components are markedly more clumpy than others, resulting in the lower correlation of the associated spectral features with distance. For example, Galazutdinov (2005) and Megier et al. (2005) show that the Ca II is a better distance indicator than K I, Na I or EB-V.
In Megier et al. (2005), the relation between the equivalent widths of the interstellar Ca II lines and the distances of Galactic OB stars was recalibrated with the use of the Hipparcos data. This resulted in formulae for estimating distances, applicable in the range from a few hundred parsecs to slightly over a kiloparsec. In this work, we attempt to extend the range of application of this method to larger distances. This necessitates taking into account the influence of line saturation; thus, we use column densities, instead of equivalent widths.
2 The Ca II observational data
2.1 Spectroscopic observations
Our observational material is listed in Table 1. Most of the spectra were collected during research projects concerning diffuse interstellar bands. The MV of the targets is between -2.5 and -11, usually between -6 and -10. The signal-to-noise ratio is typically between 50 and 200. The data were aquired during many observing runs between 1999 and 2007 using four Coudé échelle spectrometers:
- The first spectrometer is the MAESTRO
![[*]](/icons/foot_motif.png) fed by the 2-m telescope of
the Observatory at Peak Terskol (TE) in the Northern Caucasus (Musaev et al. 1999). The spectrometer is equipped with a Wright Instruments CCD 1242
fed by the 2-m telescope of
the Observatory at Peak Terskol (TE) in the Northern Caucasus (Musaev et al. 1999). The spectrometer is equipped with a Wright Instruments CCD 1242  1152 matrix (pixel size 22.5
1152 matrix (pixel size 22.5 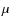 m
m 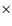 22.5
22.5 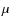 m)
camera. The instrument forms échelle spectra which cover the range from
3500 to 10 100 Å, divided into up to 96 orders. The
existing set of gratings and
cameras offers several spectral resolutions: from R = 45 000 to 180 000. In this project we used the R = 80 000 as a kind of compromise: it allows us to see discrepancies of the profiles from
single gaussians, and also - to observe relatively heavily reddened stars.
m)
camera. The instrument forms échelle spectra which cover the range from
3500 to 10 100 Å, divided into up to 96 orders. The
existing set of gratings and
cameras offers several spectral resolutions: from R = 45 000 to 180 000. In this project we used the R = 80 000 as a kind of compromise: it allows us to see discrepancies of the profiles from
single gaussians, and also - to observe relatively heavily reddened stars.
- The second spectrometer, covering the Southern hemisphere, is the FEROS
![[*]](/icons/foot_motif.png) spectrograph, fed by the 2.2 m ESO telescope. The resolution of these spectra is constant (R = 48 000). This instrument makes it possible to get the whole available spectral range (
spectrograph, fed by the 2.2 m ESO telescope. The resolution of these spectra is constant (R = 48 000). This instrument makes it possible to get the whole available spectral range (
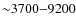 Å,
divided into 37 orders) recorded in a single exposure. The
flatfielding can be done very precisely in the case of FEROS as it is a
fiber-fed spectrograph. We used both the spectra acquired in our two
observing runs as well as data taken from the ESO archive.
Å,
divided into 37 orders) recorded in a single exposure. The
flatfielding can be done very precisely in the case of FEROS as it is a
fiber-fed spectrograph. We used both the spectra acquired in our two
observing runs as well as data taken from the ESO archive.
- Another set of spectra were obtained with the HARPS
![[*]](/icons/foot_motif.png) spectrometer, fed by the 3.6 m ESO telescope in Chile. This spectrograph covers the range
spectrometer, fed by the 3.6 m ESO telescope in Chile. This spectrograph covers the range 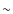 3800-
3800-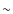 6900 Å with the resolution R = 115 000. As an instrument designed to search for exoplanets it guarantees a very precise wavelength calibration.
6900 Å with the resolution R = 115 000. As an instrument designed to search for exoplanets it guarantees a very precise wavelength calibration.
- The most recent observations were carried out using the
fiber-fed echelle spectrograph installed at 1.8-m telescope of the
Bohyunsan Optical Astronomy Observatory (BOAO) in South Korea. The
spectrograph has three observational modes providing resolving power
30 000, 45 000
and 90 000. In all the cases it allows to record the whole
spectral range from
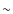 3500 to
3500 to 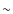 10 000 Å divided into 75-76 spectral orders. We used the highest resolution mode in our project.
10 000 Å divided into 75-76 spectral orders. We used the highest resolution mode in our project.
2.2 Ca II column densities
There are several methods of estimating column densities for partially
saturated multicomponent lines. Probably the most accurate
method - decomposing the lines into individual velocity components
and considering saturation of each of them separately - requires a
sample of spectra with very high (and preferably uniform) resolution.
The apparent optical depth method (e.g. Savage & Sembach 1991)
also requires good spectral resolution. As our aim was to obtain
formulae that can be used to estimate distances for relatively faint
and distant objects, where spectra of high resolution and quality may
be difficult to find, to compute the column densities for the whole
sample in a uniform way we used the classical doublet method
(e.g. Strömgren 1948). The wavelengths (
![]() and
and
![]() )
and the oscillator strengths (
)
and the oscillator strengths (
![]() and
and
![]() )
were taken from Morton (2003).
)
were taken from Morton (2003).
It is well known (see e.g. Nachman & Hobbs 1973) that the doublet method can in some cases produce a significant underestimation of the true column density, especially when the line contains a relatively narrow, heavily saturated component and a wider, partially saturated one. Jenkins (1986) has shown that, for lines containing many components, the straightforward curve-of-growth approach and the doublet method based on it give good results in the majority of cases, as long as the distribution function for various properties of the absorption lines is not too bizarre, enormously saturated lines are absent, and the individual components have curves of growth that saturate in a nearly Gaussian fashion.
To verify the accuracy of our
![]() estimation,
we compared the column densities calculated with the use of the doublet
method from our data with those determined by Hunter et al.
(2006) from UVES data, using
the apparent optical depth method, for the 41 lines of sight that
are common to both samples. As can be seen in Fig. 1, the agreement is satisfactory. We can conclude that the doublet method gives sufficiently accurate results
in the conditions typical in our sample. While we cannot exclude the possibility that large errors in our estimates of
estimation,
we compared the column densities calculated with the use of the doublet
method from our data with those determined by Hunter et al.
(2006) from UVES data, using
the apparent optical depth method, for the 41 lines of sight that
are common to both samples. As can be seen in Fig. 1, the agreement is satisfactory. We can conclude that the doublet method gives sufficiently accurate results
in the conditions typical in our sample. While we cannot exclude the possibility that large errors in our estimates of
![]() could be present, such cases should be rare enough not to bias our conclusions significantly.
could be present, such cases should be rare enough not to bias our conclusions significantly.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=7.2cm]{09144fg1.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg31.png)
|
Figure 1: Ca II column densities obtained in this paper with the doublet ratio method compared to the values computed with the apparent optical depth method by Hunter et al. (2006). The diagonal y = x line is shown for reference. |
| Open with DEXTER | |
The principal sources of measurement errors in the equivalent widths of Ca II
are noise in the wavelength interval occupied by the line, and the
errors in the placement of the continuum. The former was measured by
the spectral reduction packages; the latter is difficult to estimate
precisely. The sigmas given in Table 1 were computed under the assumption that the continuum placement results in errors of 5![]() ;
this is probably a conservative estimate for stronger lines. The Ca II H line is situated in the wing of the hydrogen
;
this is probably a conservative estimate for stronger lines. The Ca II H line is situated in the wing of the hydrogen ![]() line but in high resolution spectra the separation is not difficult.
line but in high resolution spectra the separation is not difficult.
3 Parallaxes
The accuracy of the Hipparcos parallaxes (ESA 1997)
is typically about 1 miliarcsecond. This makes individual distances
derived from these parallaxes very inaccurate beyond a few hundred
parsecs. When using the data for such distant objects in a statistical
manner, care must be taken to avoid problems that arise because the
errors and the measured values are comparable. As the distribution of
errors in Hipparcos parallaxes is approximately Gaussian (Arenou &
Luri 1999),
it is inevitable that for some objects the measured parallax will be
negative; it is thus impossible to derive a physically meaningful
distance from such values. However, rejection of such objects (or, in
general, objects for which
![]() is
above some threshold) from the sample leads to a statistical bias,
as it removes the stars from one wing of the error distribution
only. See Smith (2003)
for a thorough discussion of the bias and possible
corrective procedures. We decided to use parallax values directly,
without performing the inversion, and to keep stars with negative
parallaxes in the sample.
is
above some threshold) from the sample leads to a statistical bias,
as it removes the stars from one wing of the error distribution
only. See Smith (2003)
for a thorough discussion of the bias and possible
corrective procedures. We decided to use parallax values directly,
without performing the inversion, and to keep stars with negative
parallaxes in the sample.
The errors in the Hipparcos parallaxes may be correlated in objects located close (![]() )
on the sky; this is the probable cause of the surprisingly large
discrepancy between the distance of the Pleiades estimated
from the Hipparcos data and from other sources (Munari et al. 2004; Pan et al. 2004; Percival et al. 2005; Soderblom et al. 2005, and references therein). The same effect has been recently reported by Kaltcheva & Makarov (2007)
for Collinder 121. As long as there is no
systematic, global offset affecting Hipparcos parallaxes, the local
correlation of errors should have only limited influence on this work.
Our targets are spread in a fairly wide (
)
on the sky; this is the probable cause of the surprisingly large
discrepancy between the distance of the Pleiades estimated
from the Hipparcos data and from other sources (Munari et al. 2004; Pan et al. 2004; Percival et al. 2005; Soderblom et al. 2005, and references therein). The same effect has been recently reported by Kaltcheva & Makarov (2007)
for Collinder 121. As long as there is no
systematic, global offset affecting Hipparcos parallaxes, the local
correlation of errors should have only limited influence on this work.
Our targets are spread in a fairly wide (
![]() )
strip in Galactic latitude and cover all the range of longitudes (see Fig. 2).
While some grouping is inevitable as many of the stars are members of
OB associations, any significant interval of column densities in
Fig. 3 contains stars from different parts of the sky.
)
strip in Galactic latitude and cover all the range of longitudes (see Fig. 2).
While some grouping is inevitable as many of the stars are members of
OB associations, any significant interval of column densities in
Fig. 3 contains stars from different parts of the sky.
4 The Ca II - parallax relation
Of the 267 stars with Hipparcos parallaxes, contained in our sample,
262 were used to find the coefficients of the relation between the
![]() and parallax. The form of the function to fit was similar to that in Megier et al. (2005):
and parallax. The form of the function to fit was similar to that in Megier et al. (2005):
![]() ,
with the b parameter
corresponding to the average size of the Local Bubble. Two
stars, HD 66006 and HD 150135, were
excluded because of their parallax errors, 6.13 and 8.22
respectively; many times higher than that typical for the Hipparcos
data. We also used a
threshold of
EW(K)/EW(H) > 1.3 to exclude heavily
saturated cases, where the doublet method is less reliable; this
criterion resulted in the exclusion of three other stars:
HD 185859,
HD 220116, and HD 41997. We have verified
however that the elimination of the above five objects has a minimal
effect on the fit parameters.
,
with the b parameter
corresponding to the average size of the Local Bubble. Two
stars, HD 66006 and HD 150135, were
excluded because of their parallax errors, 6.13 and 8.22
respectively; many times higher than that typical for the Hipparcos
data. We also used a
threshold of
EW(K)/EW(H) > 1.3 to exclude heavily
saturated cases, where the doublet method is less reliable; this
criterion resulted in the exclusion of three other stars:
HD 185859,
HD 220116, and HD 41997. We have verified
however that the elimination of the above five objects has a minimal
effect on the fit parameters.
![\begin{figure}
\par\includegraphics[width=8.8cm, height=6cm]{09144fg2.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg36.png)
|
Figure 2: The distribution of our targets on the sky. |
| Open with DEXTER | |
Because of the nonlinear dependence of the column density on the
equivalent widths of the doublet lines, the resulting relative errors
in
![]() may
be significantly larger than those in the equivalent widths themselves.
While relative errors in parallax are still generally larger, they are
not so dominant as in the case of EW(Ca II H) vs parallax or EW(Ca II K) vs. parallax relations studied in Megier et al. (2005). We thus decided to fit the data using a maximum likelihood algorithm, taking into account errors in both coordinates.
may
be significantly larger than those in the equivalent widths themselves.
While relative errors in parallax are still generally larger, they are
not so dominant as in the case of EW(Ca II H) vs parallax or EW(Ca II K) vs. parallax relations studied in Megier et al. (2005). We thus decided to fit the data using a maximum likelihood algorithm, taking into account errors in both coordinates.
![\begin{figure}
\par\includegraphics[width=8.8cm, height=7.2cm]{09144fg3.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg37.png)
|
Figure 3: The column density - parallax relation. For clarity, only the largest errorbars are shown. The maximum likelihood fit is shown with a thick solid line. |
| Open with DEXTER | |
The equation of the best-fitting line in Fig. 3 is:
where parallax
![\begin{figure}
\par\includegraphics[width=8.8cm, height=7.8cm]{09144fg4.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg42.png)
|
Figure 4:
The distribution of the fit parameters obtained for 400 datasets
with added noise. The fit parameter values obtained for the original
data are indicated. a is expressed in |
| Open with DEXTER | |
To facilitate the computation of the distance directly from the Ca II equivalent widths, we can approximate the column density, as calculated with the doublet ratio method, by:
where the equivalent widths are in mÅ, and
Thus, after substituting into (1), the formula for estimating distance is:
where the equivalent widths EW(K) and EW(H) are in mÅ, and the distance
The errors of distances calculated with the above formula may be correlated for neighbouring stars, as lines of sight towards such objects may well pass through the same interstellar clouds.
Figure 5 presents the comparison of the distances estimated from the equivalent width of the Ca II H line using formula from Megier et al. (2005), and those obtained from formula (3). The differences reach 25 percent at 1000 pc, and 50 percent at 2000 pc. Also notable is the increase in scatter above 1000 pc, probably due to varying level of saturation for stars of the same equivalent width of the Ca II H line. In this paper we calculated column densities taking into account saturations of strong Ca II lines; since they get stronger with distance, the relations by Megier et al. (2005) and the one given in this paper lead to discrepancies at large distances. The formula (1) should give reasonable distance estimates up to 3 kpc in the Galactic plane. The current size of our sample of objects does not allow to involve into the formula terms describing any dependence on the Galactic latitude.
![\begin{figure}
\par\includegraphics[width=8.8cm, height=7.8cm]{09144fg5.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg45.png)
|
Figure 5: Distances computed from the equivalent width of the Ca II H line according to Megier et al. (2005), compared to distances obtained from formula (3) in this paper. The y = x diagonal is shown for reference. |
| Open with DEXTER | |
5 Comparison with association distances
As evident from Fig. 3, the majority of the stars on which the Ca II distance calibration is based, are located at distances of several hundred parsecs, corresponding to parallaxes ![]() 1 milliarcsecond. To check whether the formula (3)
can be successfully used for larger distances, we would need a
significant sample of early-type stars (so that the
interstellar Ca II can be accurately measured), with well determined distances from some
independent source. At distances
1 milliarcsecond. To check whether the formula (3)
can be successfully used for larger distances, we would need a
significant sample of early-type stars (so that the
interstellar Ca II can be accurately measured), with well determined distances from some
independent source. At distances ![]() 1 kpc, most of the stars bright enough to allow us to measure the Ca II lines
in reasonable observation time with telescopes of moderate size are
either very early-type (O7 and earlier) or supergiants; for such
objects the absolute magnitude calibration is particularly uncertain.
1 kpc, most of the stars bright enough to allow us to measure the Ca II lines
in reasonable observation time with telescopes of moderate size are
either very early-type (O7 and earlier) or supergiants; for such
objects the absolute magnitude calibration is particularly uncertain.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09144fg6.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg47.png)
|
Figure 6: Distances estimated from the Ca II lines (abscissa) versus distances from association membership from different sources (ordinate). Symbols: open circles - Humphreys (1978); open triangles - Garmany & Stencel (1992); full circles - de Zeeuw et al. (1999). Objects discussed in the text are indicated. |
| Open with DEXTER | |
We may however expect that the distances to OB associations and clusters, found in the literature, should be somewhat more accurate that those of individual early-type stars. Although they are usually, with the exception of the closest associations, dependent on luminosity calibration of early-type stars, they are based on a number of measurements for stars of different spectral types, and so should be less prone to errors resulting from the poorly known properties of stars of any specific spectral type or luminosity class.
The use of such distances poses another problem however: uncertain association membership of any given star. Many studies of Galactic OB associations have revealed that they can't be treated as spatially isolated, monolithic structures. The presence of substructures of different evolutionary ages is common. The definition of the borders and membership of the given association is often problematic. Irregular shape and nonuniform distribution of stars often make the delimitation of the association a matter of the researchers choice (Garmany 1994). The situation is made more complicated by selection effects resulting from the interstellar extinction, and the effects of projection on the sky: an elongated volume with enhanced, but not uniform, OB star density, seen along its length, is likely to be regarded as one association; the same structure seen from the perpendicular direction may be broken into several smaller associations.
We did not try to define our own criteria for the association
membership, relying predominantly on the members lists and distances
given by Humphreys (1978) and Garmany & Stencel (1992). We have also included the data for the nearby (![]() 1 kpc) association from de Zeeuw et al. (1999).
1 kpc) association from de Zeeuw et al. (1999).
As can be seen in Fig. 6, the relation between stellar distances estimated from the Ca II lines
and those ascribed on the basis of association/cluster membership is
far from perfect. There is no obvious systematic bias, however, the
scatter is large; the ratio
![]() may vary from below 0.5 to over 2.0. Below we discuss the most conspicuous cases of discrepancy.
may vary from below 0.5 to over 2.0. Below we discuss the most conspicuous cases of discrepancy.
The large difference between the Ca II distance and that given by de Zeeuw et al. (1999) for the Cep OB2 association (based on averaged Hipparcos parallaxes) may be partially due to a systematic bias resulting from selecting only stars with positive parallaxes; while a correction for this bias was applied by de Zeeuw et al. (1999), the value of the correction depends on the parallax errors and the shape and size of the association. Kaltcheva & Makarov (2007) show that, despite the correction, the combined effect of the correlated parallax errors and the bias resulting from the removal of the negative parallaxes can be significant (about 35 percent in the case of Collinder 121).
A very interesting case is that of the
Trumpler 16 stars in the Carina complex. The distance to
Trumpler 16 is usually estimated as about 2.5 kpc
(e.g. Walborn 1995);
however, Carraro et al. (2004) estimate it to be 4 kpc. The Ca II lines
in the five objects in our sample that are regarded as members of this
cluster (HD 93250, HD 303308,
CD-59 3300, CD-59 3303 and
HD 93403) vary from EW(K) =
414 mÅ (HD 93403) to 841 mÅ for
HD 93250 and 1074 mÅ in the case of
HD 303308. The corresponding range of distances
estimated from formula (3) is 2400-5800 pc. The
![]() of HD 93250 and HD 303308 are given by Sanchawala et al. (2007)
as -11.3 and -10.4 respectively, at the distance of 2500 pc.
Increasing the distances to 5200 and 5800 pc,
as suggested by the intensities of the Ca II lines, would make these stars as luminous as
of HD 93250 and HD 303308 are given by Sanchawala et al. (2007)
as -11.3 and -10.4 respectively, at the distance of 2500 pc.
Increasing the distances to 5200 and 5800 pc,
as suggested by the intensities of the Ca II lines, would make these stars as luminous as
![]() =
-12.9 and -12.2 respectively, making them the most luminous stars
known in our Galaxy. Such a concentration of superluminous stars at
different distances in a small region of the sky seems extremely
unlikely; the only apparent explanation of such a structure would be a
huge front of massive star formation, seen along its length. The more
probable hypothesis is that the local contributions to the column
density of the Ca II are responsible, possibly related to
the nearby
=
-12.9 and -12.2 respectively, making them the most luminous stars
known in our Galaxy. Such a concentration of superluminous stars at
different distances in a small region of the sky seems extremely
unlikely; the only apparent explanation of such a structure would be a
huge front of massive star formation, seen along its length. The more
probable hypothesis is that the local contributions to the column
density of the Ca II are responsible, possibly related to
the nearby ![]() Carinae
(about 1' away from HD 303308, and 8' away
from HD 93250). However, the very complex profiles of
the ionized Ca lines, seen in this object, are very likely due to
circumstellar envelopes since profiles of diffuse interstellar bands do
not show any sign of the Doppler splitting. They look like they
originated in a single cloud.
Carinae
(about 1' away from HD 303308, and 8' away
from HD 93250). However, the very complex profiles of
the ionized Ca lines, seen in this object, are very likely due to
circumstellar envelopes since profiles of diffuse interstellar bands do
not show any sign of the Doppler splitting. They look like they
originated in a single cloud.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09144fg7.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg51.png)
|
Figure 7: The Ca II lines in the Tr16 cluster. The order of the stars is the same in both panels. |
| Open with DEXTER | |
The Ca II lines of the five stars in the Trumpler 16 cluster are shown in Fig. 7. It is evident that the velocity structure of the material is complex. However, the main velocity component seen in HD 93403 is present in all other cases; if we interpret all the other components as originating in material local to the cluster, the distance to Trumpler 16 would be that of the HD 93403 (2360 pc), in good agreement with the majority of the spectrophotometric estimates.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09144fg8.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg52.png)
|
Figure 8: The Ca II lines in the Cru OB1 association. |
| Open with DEXTER | |
The distance to the Cru OB1 association in Humphreys (1978) is 2400 pc; Kaltcheva & Georgiev (1994) estimate it to be 2730 pc. The interstellar Ca II lines seen in the spectra of 10 stars in this association that are in our sample are shown in Fig. 8. All the spectra show two main radial velocity components, but their relative strength varies. The average distance to this association, estimated from formula (3), is 1510 pc, with the individual values ranging from 1180 pc for HD 101190 to 1730 pc for HD 100099.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09144fg9.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg53.png)
|
Figure 9: The Ca II lines in the Ser OB1 association. The spectra were adjusted in radial velocity so that the dominant components of the interstellar CH lines correspond. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm, height=6cm]{09144fg10.eps}\includegraphics[width=8cm, height=6cm]{09144fg11.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg54.png)
|
Figure 10:
The ratio
|
| Open with DEXTER | |
The distance to the Ser OB1 association in Humphreys (1978) is 2190 pc. As evident from Fig. 6, the distances to the individual stars estimated from Ca II vary in a fairly wide interval from 2480 to over 4850 pc. All the Ser OB1 stars in our sample are members of the cluster NGC 6611, rich in massive, early type stars. The minimum of the Ca II distances to objects in this association is in reasonably good agreement with the value given by Humphreys (1978). It would seem natural to attribute the spread in Ca II distances to additional radial velocity components due to matter related to the cluster, the situation being similar to that in Trumpler 16. However, Fig. 9 shows that, at least at the spectral resolution R = 48 000, we cannot separate any set of velocity components common to all the stars, which we could reliably attribute to ``truly interstellar'' matter in front of the cluster, and thus expect to be a reasonably good measure of the clusters distance. Note e.g. the striking differences between the Ca II profiles seen towards BD-13 4927 and BD-13 4929, situated about 3' apart on the sky.
HD 93249 (top of Fig. 6) is listed by Humphreys (1978) as a member of Trumpler 15, at the distance of 3720 pc. The more recent value given by Carraro (2002) is 2400 pc, in good agreement with our estimate.
Figure 10a presents the dependence of
![]() on galactic longitude. While scatter is conspicuous, there is apparently some systematic effect: the ratio
tends to be lower between 200 < l < 300 and higher in the region 50 < l < 120. The tendency is also visible in Fig. 10b showing the
on galactic longitude. While scatter is conspicuous, there is apparently some systematic effect: the ratio
tends to be lower between 200 < l < 300 and higher in the region 50 < l < 120. The tendency is also visible in Fig. 10b showing the
![]() as a function of galactic longitude. One of the possible reasons for
this effect is the presence of large scale structure in the Ca II layer. This would undermine the utility of the Ca II lines for distance determination, unless the effect is taken into account in the
formula (3).
Another possibility is the inclusion of background or foreground stars
in the associations. Such a situation is more likely in regions where
the density of early-type objects on the sky is higher - towards
the Galactic center, or along the direction of a spiral arm.
as a function of galactic longitude. One of the possible reasons for
this effect is the presence of large scale structure in the Ca II layer. This would undermine the utility of the Ca II lines for distance determination, unless the effect is taken into account in the
formula (3).
Another possibility is the inclusion of background or foreground stars
in the associations. Such a situation is more likely in regions where
the density of early-type objects on the sky is higher - towards
the Galactic center, or along the direction of a spiral arm.
![\begin{figure}
\par\includegraphics[width=8cm, height=6cm]{09144fg12.eps}\includegraphics[width=8cm, height=6cm]{09144fg13.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg55.png)
|
Figure 11:
The ratio
|
| Open with DEXTER | |
Figures 11a and b show the ratio
![]() and the difference
and the difference
![]() as a function of galactic latitude. While Fig. 11a might suggest some systematic effect, as the value of
as a function of galactic latitude. While Fig. 11a might suggest some systematic effect, as the value of
![]() is higher for positive b,
Fig. 11b shows that the actual differences in distance are small.
The few stars located at higher latitudes are relatively nearby, and
the differences are probably due to local inhomogeneities in the Ca II structure.
is higher for positive b,
Fig. 11b shows that the actual differences in distance are small.
The few stars located at higher latitudes are relatively nearby, and
the differences are probably due to local inhomogeneities in the Ca II structure.
The scale height of the Ca II layer in our Galaxy is estimated to be
![]() pc (Smoker et al. 2003). For objects located at |z| close to or greater than that value, we can expect the formula (3) to systematically underestimate the true distance.
However, it should be possible to detect such cases; the value of |z| computed from such an underestimated distance would be close to 800 pc. In our sample of stars the the values of |z| estimated from the Ca II distances do not exceed 450 pc, and in all except four stars fall below 300 pc.
pc (Smoker et al. 2003). For objects located at |z| close to or greater than that value, we can expect the formula (3) to systematically underestimate the true distance.
However, it should be possible to detect such cases; the value of |z| computed from such an underestimated distance would be close to 800 pc. In our sample of stars the the values of |z| estimated from the Ca II distances do not exceed 450 pc, and in all except four stars fall below 300 pc.
6 Conclusions
The Ca II lines apparently can provide information related to the distance of early-type stars beyond the current range of trigonometric parallaxes, but the accuracy and reliability of the method is limited. The possible local enhancements in the Ca II column density, related to the given star or its parent cluster/association, can lead to large errors in individual cases; while such local effects could probably be detected if very high resolution spectra of the star and its neighbours were available, their contribution might be difficult to estimate, especially in cases where saturation is significant. The possible large-scale structure in the Ca II layer, suggested by Figs. 10a and b, can also affect the accuracy of the distance determination. While such a structure, if confirmed, would merit a closer look itself, our present dataset is not sufficient to study it in any detail.
It is possible that combining (e.g. in a Bayesian framework) the distance information obtained from Ca II lines with other data, like Ti II lines, trigonometric, or spectroscopic parallaxes, could result in more accurate distance determinations. Future astrometric missions will provide a set of parallax measurements which, for their target stars, will supersede any distance estimates based on interstellar lines. They may also allow a refinement of the relation between interstellar line strength and distance, making it possible to estimate distances for the objects whose trigonometric parallaxes will not be measured.
AcknowledgementsThe authors acknowledge the financial support of the Polish State during the period 2007-2010 (grant N203 012 32/1550). We are deeply grateful to the ESO archive as well as to the ESO staff members who assisted us while conducting our own observing runs.
References
- Arenou, F., & Luri, X. 1999, ASP Conf. Ser., 167, 13 [NASA ADS]
- Beals, C. S., & Oke, J. B. 1953, MNRAS, 113, 530 [NASA ADS]
- Carraro, G. 2002, MNRAS, 331, 785 [CrossRef] [NASA ADS]
- Carraro, G., Romaniello, M., Ventura, P., & Patat, F. 2004, A&A, 418, 525 [EDP Sciences] [CrossRef] [NASA ADS]
- Crawford, I. A. 2001, MNRAS, 328, 1115 [CrossRef] [NASA ADS]
- Crawford, I. A., Lallement, R., Price, R. J., et al. 2002, MNRAS, 337, 720 [CrossRef] [NASA ADS]
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 (Noordwijk: ESA)
- Evans, J. W. 1941, ApJ, 93, 275 [CrossRef] [NASA ADS]
- Galazutdinov, G. A. 2005, JKAS, 38, 215 [NASA ADS]
- Garmany, C. D. 1994, PASP, 106, 25 [CrossRef] [NASA ADS]
- Garmany, C. D., & Stencel, R. E. 1992, A&AS, 94, 211 [NASA ADS]
- Humphreys, R. M. 1978, ApJSS, 38, 309 [CrossRef] [NASA ADS]
- Hunter, I., Smoker, J. V., Keenan, F. P., et al. 2006, MNRAS, 367, 1478 [CrossRef] [NASA ADS]
- Jenkins, E. B. 1986, ApJ, 304, 739 [CrossRef] [NASA ADS]
- Kaltcheva, N. T., & Georgiev, L. N. 1994, MNRAS, 269, 289 [NASA ADS]
- Kaltcheva, N., & Makarov, V. 2007, ApJ, 667, L155 [CrossRef] [NASA ADS]
- Megier, A., Strobel, A., Bondar, A., et al. 2005, ApJ, 634, 451 [CrossRef] [NASA ADS]
- Morton, D. C. 2003, ApJS, 149, 205 [CrossRef] [NASA ADS]
- Munari, U., Dallaporta, S., Siviero, A., et al. 2004, A&A, 418, L31 [EDP Sciences] [CrossRef] [NASA ADS]
- Musaev, F. A., Galazutdinov, G. A., Sergeev, A. V., et al. 1999, Kinematics Phys. Celest. Bodies, 15, 216 [NASA ADS]
- Nachman, P., & Hobbs, L. M. 1973, ApJ, 182, 481 [CrossRef] [NASA ADS]
- Pan, X., Shao, M., & Kulkarni, S. R. 2004, Nature, 427, 326 [CrossRef] [NASA ADS]
- Percival, S. M., Salaris, M., & Groenewegen, M. A. T. 2005, A&A, 429, 887 [EDP Sciences] [CrossRef] [NASA ADS]
- Price, R. J., Crawford, I. A., Barlow, M. J., & Howarth, I. D. 2001, MNRAS, 328, 555 [CrossRef] [NASA ADS]
- Sanchawala, K., Chen, W. P., Lee, H. T., et al. 2007, ApJ, 656, 462 [CrossRef] [NASA ADS]
- Sanford, R. F. 1937, ApJ, 86, 136 [CrossRef] [NASA ADS]
- Savage, B. D., & Sembach, K. R. 1991, ApJ, 379, 245 [CrossRef] [NASA ADS]
- Schmidt-Kaler, T. 1982, in Landolt-Börnstein New Series, Group VI, Volume 2b, ed. K. Schaifers, & H. H. Voigt (Berlin: Springer)
- Smith, H. 2003, MNRAS, 338, 891 [CrossRef] [NASA ADS]
- Smoker, J. V., Rolleston, W. R. J., Kay, H. R. M., et al. 2003, MNRAS, 346, 119 [CrossRef] [NASA ADS]
- Smoker, J. V., Lynn, B. B., Christian, D. J., & Keenan, F. P. 2006, MNRAS, 370, 151 [NASA ADS]
- Soderblom, D. R., Nelan, E., Benedict, G. F., et al. 2005, AJ, 129, 1616 [CrossRef] [NASA ADS]
- Strömgren, B. 1948, ApJ, 108, 242 [CrossRef] [NASA ADS]
- Struve, O. 1928, ApJ, 67, 353 [CrossRef] [NASA ADS]
- Vacca, W. D., Garmany, C. D., & Shull, J. M. 1996, ApJ, 460, 914 [CrossRef] [NASA ADS]
- Walborn, N. R. 1995, Rev. Mex. Astron. Astrofis., 2, 51
- Wegner, W. 2006, MNRAS, 371, 185 [CrossRef] [NASA ADS]
- Welty, D. E., & Hobbs, L. M. 2001, ApJS, 133, 345 [CrossRef] [NASA ADS]
- Welty, D. E., Hobbs, L. M., & Morton, D. C. 2003, ApJS, 147, 61 [CrossRef] [NASA ADS]
- Wilson, O. C., & Merrill, P. W. 1937, ApJ, 86, 44 [CrossRef] [NASA ADS]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J, Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [CrossRef] [NASA ADS]
- Zorec, J., & Briot, D. 1991, A&A, 245, 150 [NASA ADS]
Online Material
Table 1:
Target stars. Columns: name - star name; l, b - Galactic coordinates (from SIMBAD); ![]() ,
,
![]() - trigonometric parallax and its error (Hipparcos); K,
- trigonometric parallax and its error (Hipparcos); K,
![]() - the equivalent width of the Ca II K line and its error; H,
- the equivalent width of the Ca II K line and its error; H,
![]() - the equivalent width of the Ca II H line and its error;
- the equivalent width of the Ca II H line and its error;
![]() ,
,
![]() - Ca II column
density and its error; as, as ref: association membership and
reference: H stands for Humphreys (1978), GS for Garmany and
Stencel (1992), Z for de Zeeuw et al. (1999).
- Ca II column
density and its error; as, as ref: association membership and
reference: H stands for Humphreys (1978), GS for Garmany and
Stencel (1992), Z for de Zeeuw et al. (1999). ![]() - association distance (in parsecs) from Humphreys (1978);
- association distance (in parsecs) from Humphreys (1978);
![]() - association distance from Garmany & Stencel (1992);
- association distance from Garmany & Stencel (1992); ![]() - association membership and distance from de Zeeuw et al. (1999);
- association membership and distance from de Zeeuw et al. (1999);
![]() ,
,
![]() - distance estimated from formula (3), and its formal error.
- distance estimated from formula (3), and its formal error.
Footnotes
- ... scale
![[*]](/icons/foot_motif.png)
- Table 1 is only available in electronic form at http://www.aanda.org
- ... MAESTRO
![[*]](/icons/foot_motif.png)
- http://www.terskol.com/telescopes/maestro.htm
- ... FEROS
![[*]](/icons/foot_motif.png)
- http://www.ls.eso.org/lasilla/sciops/2p2/E2p2M/FEROS
- ... HARPS
![[*]](/icons/foot_motif.png)
- http://www.ls.eso.org/lasilla/sciops/3p6/harps
- ... MIDAS
![[*]](/icons/foot_motif.png)
- MIDAS is distributed by the European Southern Observatory.
- ... IRAF
![[*]](/icons/foot_motif.png)
- IRAF is distributed by the National Optical Astronomy Observatories, USA.
- ... DECH
![[*]](/icons/foot_motif.png)
- http://gazinur.com/DECH-software.html
All Tables
Table 1:
Target stars. Columns: name - star name; l, b - Galactic coordinates (from SIMBAD); ![]() ,
,
![]() - trigonometric parallax and its error (Hipparcos); K,
- trigonometric parallax and its error (Hipparcos); K,
![]() - the equivalent width of the Ca II K line and its error; H,
- the equivalent width of the Ca II K line and its error; H,
![]() - the equivalent width of the Ca II H line and its error;
- the equivalent width of the Ca II H line and its error;
![]() ,
,
![]() - Ca II column
density and its error; as, as ref: association membership and
reference: H stands for Humphreys (1978), GS for Garmany and
Stencel (1992), Z for de Zeeuw et al. (1999).
- Ca II column
density and its error; as, as ref: association membership and
reference: H stands for Humphreys (1978), GS for Garmany and
Stencel (1992), Z for de Zeeuw et al. (1999). ![]() - association distance (in parsecs) from Humphreys (1978);
- association distance (in parsecs) from Humphreys (1978);
![]() - association distance from Garmany & Stencel (1992);
- association distance from Garmany & Stencel (1992); ![]() - association membership and distance from de Zeeuw et al. (1999);
- association membership and distance from de Zeeuw et al. (1999);
![]() ,
,
![]() - distance estimated from formula (3), and its formal error.
- distance estimated from formula (3), and its formal error.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,height=7.2cm]{09144fg1.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg31.png)
|
Figure 1: Ca II column densities obtained in this paper with the doublet ratio method compared to the values computed with the apparent optical depth method by Hunter et al. (2006). The diagonal y = x line is shown for reference. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm, height=6cm]{09144fg2.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg36.png)
|
Figure 2: The distribution of our targets on the sky. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm, height=7.2cm]{09144fg3.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg37.png)
|
Figure 3: The column density - parallax relation. For clarity, only the largest errorbars are shown. The maximum likelihood fit is shown with a thick solid line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm, height=7.8cm]{09144fg4.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg42.png)
|
Figure 4:
The distribution of the fit parameters obtained for 400 datasets
with added noise. The fit parameter values obtained for the original
data are indicated. a is expressed in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm, height=7.8cm]{09144fg5.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg45.png)
|
Figure 5: Distances computed from the equivalent width of the Ca II H line according to Megier et al. (2005), compared to distances obtained from formula (3) in this paper. The y = x diagonal is shown for reference. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09144fg6.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg47.png)
|
Figure 6: Distances estimated from the Ca II lines (abscissa) versus distances from association membership from different sources (ordinate). Symbols: open circles - Humphreys (1978); open triangles - Garmany & Stencel (1992); full circles - de Zeeuw et al. (1999). Objects discussed in the text are indicated. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09144fg7.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg51.png)
|
Figure 7: The Ca II lines in the Tr16 cluster. The order of the stars is the same in both panels. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09144fg8.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg52.png)
|
Figure 8: The Ca II lines in the Cru OB1 association. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09144fg9.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg53.png)
|
Figure 9: The Ca II lines in the Ser OB1 association. The spectra were adjusted in radial velocity so that the dominant components of the interstellar CH lines correspond. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=6cm]{09144fg10.eps}\includegraphics[width=8cm, height=6cm]{09144fg11.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg54.png)
|
Figure 10:
The ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=6cm]{09144fg12.eps}\includegraphics[width=8cm, height=6cm]{09144fg13.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa9144-07/Timg55.png)
|
Figure 11:
The ratio
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.