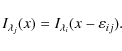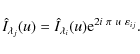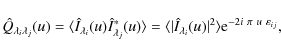Direct measurement of the formation height difference of the 630 nm Fe I solar lines

M. Faurobert; C. Aime; C. Périni; H. Uitenbroek; C. Grec; J. Arnaud; G. Ricort

doi:10.1051/0004-6361/200913330

Free Access

Issue		A&A Volume 507, Number 2, November IV 2009


Page(s)		L29 - L32
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200913330
Published online		04 November 2009

A&A 507, L29-L32 (2009)

LETTER TO THE EDITOR

Direct measurement of the formation height difference of the 630 nm Fe I solar lines

M. Faurobert¹ - C. Aime¹ - C. Périni¹ - H. Uitenbroek² - C. Grec³ - J. Arnaud¹ - G. Ricort¹

1 - UMR 6525 H. Fizeau, Université de Nice Sophia Antipolis, CNRS, Observatoire de la Côte d'Azur, Campus Valrose, 06108 Nice, France
2 - National Solar Observatory/Sacramento Peak, PO Box 62, Sunspot, NM88349, USA
3 - Institut d'Astrophysique Spatiale, Bâtiment 121, Université Paris XI, 91405 Orsay Cedex, France

Received 21 September 2009 / Accepted 21 October 2009

Abstract
Context. Spectral lines formed over a limited height range in either a stellar or planetary atmosphere provide us with information about the physical conditions within this height range. In this context, an important quantity is the so-called line formation depth. It is usually determined from numerical calculation of the atmospheric opacity in the line of interest and then converted into geometrical depth by using atmospheric models.
Aims. We develop a radically different approach, which allows us to measure directly line formation depths from spectroscopic observations without relying on assumptions about an atmospheric model. This method requires spatially resolved observations, which up to now have been available only for solar or planetary studies. We apply this method to images of the solar granulation.
Methods. The method was presented and tested numerically in previous papers. It is based on the measurement of the perspective shift between images at different wavelengths, formed at different heights, when they are observed away from disk center. Because of the Fourier transform properties, this shift gives rise to a deterministic linear phase term in the cross spectrum of the images.
Results. The method is applied to observations of solar quiet regions performed with the SOT spectropolarimeter on HINODE in the Fe I line pair at 630.15 and 630.25 nm. We derive the difference in formation heights between the two lines and its center-to-limb variations. We show that the high sensitivity of the measurements allows us to detect variations in the line formation heights between magnetized and non-magnetized regions of the solar atmosphere.
Conclusions. Our results are the first direct measurements of line formation depths in the solar photosphere. Cross spectral analysis provides us with a new observable quantity, which may be measured with an accuracy well bellow the spatial resolution of the observations. We recall that the Fe I line pair at 630.15 and 630.25 nm is often used to determine solar magnetic fields by spectropolarimetric observations and inversion methods. The difference in the line formation heights that we measure should be taken into account in the inversion procedures.

Key words: line: formation - techniques: high angular resolution - techniques: spectroscopic - Sun: photosphere

1 Introduction

Accurate determinations of line formation heights are beneficial, for instance, in the derivation of propagation speeds from wave phase information, magnetic field vector determination, and spectral line inversion. Here we use spectroscopic observations performed with the spectropolarimeter on the SOT telescope of the Hinode satellite to determine the formation height difference of the two FeI lines at 630 nm by employing the cross spectral method described in Grec et al. (2007, 2009). The observations were obtained on October 3, 2007, when the solar angular radius was 958.9 arcsec and the disk center latitude $B0= 6.6^\circ$ . A telescope pointing along solar north-south and from both hemispheres was chosen. The center of the slit corresponded to $\sin\theta$ values of 0.25, 0.5, and 0.75, where $\theta$ is the heliocentric angle. For each pointing, we recorded 240 short exposure spectrograms of the granulation. The pixel size is 0.16 arcsec, and the diffraction-limited spatial resolution is 0.32 arcsec at 630 nm.

We now briefly recall the cross spectral method. For more details, we refer to Grec et al. (2007, 2009). The basic idea is that when one observes solar structures at two different wavelengths away from disk center, their difference in formation depth is projected onto a spatial shift between the images. This spatial shift may be very small but it may be measured by a method inspired by differential interferometry, which we briefly recall here. We consider two brightness distributions $I_{\lambda_i}(x)$ and $I_{\lambda_j}(x)$ recorded along the spectrograph slit at two different wavelengths i and j, which reflect the spatial variations of the source function at their respective formation depths. Assuming that the vertical variation scale of the source function is large compared to the formation depth difference, we can write that $I_{\lambda_i}(x)$ and $I_{\lambda_j}(x)$ are similar but simply shifted by the perspective effect, i.e.,

$\begin{displaymath} I_{\lambda_j}(x) = I_{\lambda_i}(x- \varepsilon_{ij}). \end{displaymath}$

(1)

In Fourier space, this spatial shift gives rise to a phase term with a linear variation with respect to the spatial frequency variable u,

$\begin{displaymath} \hat{I}_{\lambda_j}(u) = \hat{I}_{\lambda_i}(u){\rm e}^ {2i~\pi~ u~\varepsilon_{ij}} . \end{displaymath}$

(2)

The cross spectrum ${\hat Q}_{\lambda_i \lambda_j}(u)$ between $I_{\lambda_i}(x)$ and $I_{\lambda_j}(x)$ is given by the ensemble average

$\begin{displaymath} \hat{Q}_{\lambda_i \lambda_j}(u) = \langle \hat{I}_{\lambda_... ..._i}(u)\vert^2 \rangle {\rm e}^ {- 2i~\pi~ u~\varepsilon_{ij}}, \end{displaymath}$

(3)

where the symbol * indicates the complex conjugate. An ensemble average is performed over a large number of short-exposure spectrograms to increase the signal-to-noise ratio. The spatial shift due to the perspective effect, and therefore the difference of the two image formation heights, can then be directly derived from a linear fit to the phase.

In general $I_{\lambda_i}(x)$ and $I_{\lambda_j}(x)$ are not only shifted but they also show some differences because of the height variations in the solar structures. To evaluate the degree of similarity between two spectrograms, we consider their coherence function defined by

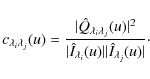
$\begin{displaymath}c_{\lambda_i\lambda_j}(u) ={ \vert{\hat{Q}_{\lambda_i\lambda_... ...I}_{\lambda_i}(u)\vert \vert\hat{I}_{\lambda_j}(u)\vert}}\cdot \end{displaymath}$

(4)

The coherence takes values between 0 and 1. It is equal to 1 if the two spectrograms are linearly related.

2 Difference between the two line-core formation heights

We consider the spectrograms obtained at the two line centers and compare their formation heights. As explained in Grec et al. (2007, Paper I), we must first correct the spectrograms for the Doppler shifts of the lines that vary along the slit due to granular motions. This correction proceeds as described in Paper I and is performed independently for the two line profiles.

We first show the modulus and phase of the cross-spectrum obtained with the full 1024 pixel image (see Figs. 1 and 2) with the spectrograph slit centered at 0.75 solar radius in the northern hemisphere. The 1024 pixel slit was covering a significant fraction of the solar angular radius between 0.66 and 0.83 solar radius. The coverage in cosine of the heliocentric angle is [0.55, 0.75] (the limb-darkening in the continuum is clearly seen in the images).

We consider the ensemble average of the cross spectra on a large number (240 at each slit position) of short exposure images. The modulus is shown on a log-lin scale, we notice that the noise level is low up to the spatial frequency u = 2.5 arcsec^-1, then the noise slightly increases up to the cut-off frequency $u_{\rm c} = 3.1$ arcsec^-1, which corresponds to the diffraction limit of the SOT telescope. The phase is linear on a broad spatial-scale interval where the noise level is low (up to u= 1.5 arcsec^-1), then the noise increases and the phase is no longer a linear function of u. We also show the coherence coefficient between the images as a function of u (Fig. 3), and we check that the linearity domain of the phase corresponds to the domain where the coherence coefficient of the spectrograms is close to one, namely greater than 0.8 (see Fig. 4). In this domain, the images of the granulation obtained in the two line cores are similar enough for the perspective measurement to be possible. From the slope of the phase, we measure the displacement between the two line center images, and the standard deviation of the slope allows us to estimate the accuracy of the measurement. After correction for the projection effect on the plane of the sky (i.e., division of the displacement observed along the slit by $\sin\theta$ ), we derive the difference between the formation depth of the line center spectrograms, namely $\Delta H = 63.2 \pm 0.9$ km. The high accuracy of the measurement is due to the quality of the linear fit to the cross-spectrum phase.

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg1.eps} \end{figure}$	Figure 1: Modulus of the cross spectrum at the two Fe I line centers on a log-lin scale.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg2.eps} \end{figure}$	Figure 2: Phase of the cross spectrum.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg3.eps} \end{figure}$	Figure 3: Coherence coefficient between the images in the two line cores as a function of the spatial scale u in arcsec^-1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg4.eps} \end{figure}$	Figure 4: Linear part of the phase of the cross spectrum as a function of the spatial scale u, in the interval where the coherence coefficient is larger than 0.8. (see Fig. 3).
Open with DEXTER

2.1 Small-scale variations along the slit

We take advantage of the quality of the data to explore the variation in the phase slope along the spectrograph slit, in the following way. The spectrograms are divided into 16 parts of 64 pixels each and the cross spectra are derived within the 16 shorter slits, while retaining a significant signal and a clear determination of the phase slope (see Fig. 5). To refine the measurement of the slope variations along the slit, we first derive it on the first 64-pixel part, then we move 4 pixels further down and compute the cross spectrum again for these 64 pixels, as if we have moved an imaginary 64 pixel-slit along the 1024-pixel observation slit. We keep going in this way until the imaginary slit is located at the edge of the observation slit. We thus obtain 241 measurements of the phase slope along the 1024-pixel slit. By convention, we ascribe the phase slope value of a given measurement to the location of the centerward edge of the 64-pixel sliding slit. The results are shown in Fig. 6 for the observation slit position at $\sin\theta =0.75$ . The error bar on one measurement is about 5 km, larger than when the phase is measured within the 1024-pixel slit, because the standard deviation in the slope of the linear part is larger.

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg5.eps} \end{figure}$	Figure 5: Phase of the cross-spectrum of the two line center spectrograms within a 64-pixel slit (thick line) and a 128-pixel one (thin line). The linear part of the phase is clearly defined in both cases.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg6.eps} \end{figure}$	Figure 6: Upper curve: formation height difference of the two line cores. Lower curve: stokes V absolute value distribution (in arbitrary units) as functions of the position in terms of the sine of the heliocentric angle.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg7.eps} \end{figure}$	Figure 7: Center-to-limb variations in the formation height difference of the two line cores obtained from the perspective effect measurement at all slit positions, in sine of the latitude.
Open with DEXTER

2.2 Comments on the results

The height difference between the two lines shows an approximately linear overall decrease as $\theta$ increases. Apart from this linear trend, some dips are observed for $\sin\theta$ values around 0.67, 0.70, 0.74, and 0.79.

We suspect that these dips are an effect of the magnetic network on the line formation heights. The FeI lines at 630.15 and 630.25 nm are sensitive to magnetic fields but with a different sensitivity (which is used to determine magnetic fields in the photosphere). The absorption profiles in both lines are broadened by the Zeeman splitting, the line opacity thus increases and the line formation depth is modified. Since the Zeeman sensitivity of the two lines differ, their formation height difference is sensitive to the presence of magnetic fields. Furthermore, the temperature stratification in magnetized regions is likely to differ from the non-magnetized one. As a tracer of the presence of magnetic fields, we considered the absolute value of Stokes V integrated on wavelength. The distribution of this tracer along the slit is shown in Fig. 6 superimposed on the line formation height difference. The magnetic effect is confirmed by comparing the locations at which a magnetic signal is detected in Stokes V and the locations of the dips in the formation height difference. We note that the effect on the line formation depth depends mainly on the magnetic field modulus, whereas the Stokes V signal depends on the longitudinal magnetic field. Our magnetic tracer is insensitive to fields in the direction perpendicular to the line of sight that do affect the line formation depth.

3 Center-to-limb variations

3.1 Measurements

Figure 7 shows the difference of the two line formation heights obtained for all the positions of the slit along the south-north axis. We note that here we show the results as a function of the sinus of the latitude $\sin\theta_a$ instead of $\sin\theta$ . Because of the offset due to the inclination of the solar polar axis with respect to the plane of the sky, the slit positions are not symmetrical with respect to the solar equator. The line formation depth difference is affected by the presence of magnetic fields, as discussed above, and we observe that its fluctuations are larger close to the solar equator than at high latitudes. We note that the error bar for one measurement is of the order of 5 km for all the slit positions, so the fluctuations are not produced by noise in the data. We expected to obtain identical averaged values of the line-formation-depth difference at symmetrical positions in the north and south hemispheres, but it seems that slightly smaller values are measured in the southern hemisphere than in the northern one and the asymmetry seems larger at high latitudes. This unexpected result should be confirmed by further observations. It could be due to differences in the quiet sun magnetic field at high latitudes in the two solar hemispheres.

3.2 Comparison with model calculations

We have computed the two line-center formation heights, defined as the heights where the line-center optical-depths are equal to one, assuming that both lines are formed under LTE conditions and according to the standard one-dimensional FALC quiet sun model (Fontenla et al. 1993). The difference between the two line formation depths that we derive is mainly constant and equal to 64 km over the $\sin\theta$ interval between 0.0 and 0.84 in absolute value. To compare with the measurements shown in Fig. 7, we must consider for every slit position only the highest values which should correspond to non-magnetic regions of the quiet sun. We see that the 1D-LTE model underestimates the difference between the formation heights in non-magnetic regions at low latitudes, but is in closer agreement with our measurements for the slit positions at higher latitudes. If we consider the average value of the line-formation-depth difference over magnetic and non-magnetic regions, we note that it is quite close to the 1D-LTE value for the slit positions at low latitudes.

Several authors have computed the line formation depths of the two Fe I lines at 630 nm using 3D simulations of the solar granulation and 3D radiative transfer codes (see Asplund et al. 2000; Shchukina & Trujillo Bueno 2001; Grec et al. 2009). Grec et al. (2009) find that the average height difference at a line optical depth of unity for 3D simulations at $\sin\theta =0.5$ is 75 km. This is in quite good agreement with our measured values in non-magnetic regions at this heliocentric angle.

The cross-spectral method that we propose allows us to measure differences in line formation heights. The accuracy of the measurement is not limited by the spatial resolution of the observations because it is obtained from the determination of a phase term that is not affected by the transfer function of the instrument. On the other hand, a high spectral resolution is required to correct the spectrograms for Doppler effects due to granular velocity fields (see Grec et al. 2009). Further investigations are needed to quantify the effect of the limited spectral resolution on the accuracy of the method.

Acknowledgements

We thank Bruce Lites for his help in the calibration of the Hinode data. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway).

References

Asplund, M., Nordlund, Å, Trampedach, R., & Stein, R. F. 2000, ApJ, 359, 743 [NASA ADS]
Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [CrossRef] [NASA ADS]
Grec, C., Aime, C., Faurobert, M., Ricort, G., & Paletou, F. 2007, A&A, 463, 1125 [EDP Sciences] [CrossRef] [NASA ADS] (Paper I)
Grec, C., Uitenbroek, H., Faurobert, M., & Aime, C. 2009, A&A, submitted
Shchukina, N., & Trujillo Bueno, J. 2001, ApJ, 550, 970 [CrossRef] [NASA ADS]

All Figures

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg1.eps} \end{figure}$	Figure 1: Modulus of the cross spectrum at the two Fe I line centers on a log-lin scale.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg2.eps} \end{figure}$	Figure 2: Phase of the cross spectrum.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg3.eps} \end{figure}$	Figure 3: Coherence coefficient between the images in the two line cores as a function of the spatial scale u in arcsec^-1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg4.eps} \end{figure}$	Figure 4: Linear part of the phase of the cross spectrum as a function of the spatial scale u, in the interval where the coherence coefficient is larger than 0.8. (see Fig. 3).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg5.eps} \end{figure}$	Figure 5: Phase of the cross-spectrum of the two line center spectrograms within a 64-pixel slit (thick line) and a 128-pixel one (thin line). The linear part of the phase is clearly defined in both cases.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg6.eps} \end{figure}$	Figure 6: Upper curve: formation height difference of the two line cores. Lower curve: stokes V absolute value distribution (in arbitrary units) as functions of the position in terms of the sine of the heliocentric angle.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{13330fg7.eps} \end{figure}$	Figure 7: Center-to-limb variations in the formation height difference of the two line cores obtained from the perspective effect measurement at all slit positions, in sine of the latitude.
Open with DEXTER

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.