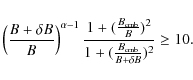On the evolution of giant radio halos and their connection with cluster mergers

G. Brunetti; R. Cassano; K. Dolag; G. Setti

doi:10.1051/0004-6361/200912751

Home

All issues

Volume 507 / No 2 (November IV 2009)

A&A, 507 2 (2009) 661-669

Full HTML

Free Access

Issue		A&A Volume 507, Number 2, November IV 2009


Page(s)		661 - 669
Section		Cosmology (including clusters of galaxies)
DOI		https://doi.org/10.1051/0004-6361/200912751
Published online		15 September 2009

A&A 507, 661-669 (2009)

On the evolution of giant radio halos and their connection with cluster mergers

G. Brunetti¹ - R. Cassano¹ - K. Dolag² - G. Setti³

1 - INAF- Istituto di Radioastronomia, via P. Gobetti 101, 40129 Bologna, Italy
2 - Max-Planck-Institut für strophysik, Karl-Schwarzschild Strasse 1, 85741 Garching bei München, Germany
3 - Dip. Astronomia, Universita' di Bologna, via Ranzani 1, 40127 Bologna, Italy

Received 23 June 2009 / Accepted 4 September 2009

Abstract
Aims. Giant radio halos are diffuse, Mpc-scale, synchrotron sources located in the central regions of galaxy clusters and provide the most relevant example of cluster non-thermal activity. Radio and X-ray surveys allow to investigate the statistics of radio halos and may contribute to constrain the origin of these sources and their evolution.
Methods. We investigate the distribution of clusters in the plane X-ray (thermal, $L_{\rm X}$ ) vs. synchrotron (non-thermal, P_1.4) luminosity, where clusters hosting giant radio halos trace the P_1.4- $L_{\rm X}$ correlation and clusters without radio halos populate a region that is well separated from that spanned by the above correlation. The connection between radio halos and cluster mergers suggests that the cluster Mpc-scale synchrotron emission is amplified during these mergers and then suppressed when clusters become more dynamically relaxed.
Results. In this context, by analysing the distribution in the P_1.4- $L_{\rm X}$ plane of galaxy clusters from X-ray selected samples with adequate radio follow up, we constrain the typical time-scale of evolution of diffuse radio emission in clusters and discuss the implications for the origin of radio halos.
Conclusions. We conclude that cluster synchrotron emission is suppressed (and amplified) in a time-scale significantly smaller than 1 Gyr. We show that this constraint appears difficult to reconcile with the hypothesis that the halo's radio power is suppressed due to dissipation of magnetic field in galaxy clusters. On the other hand, in agreement with models where turbulent acceleration plays a role, present constraints suggest that relativistic electrons are accelerated in Mpc-scale regions, in connection with cluster mergers and for a time-interval of about 1 Gyr, and then they cool in a relatively small time-scale, when the hosting cluster becomes more dynamically relaxed.

Key words: radio continuum: general - X-rays: general - radiation mechanisms: non-thermal - acceleration of particles - galaxies: clusters: general

1 Introduction

Radio observations of galaxy clusters unveil the presence of relativistic particles and magnetic fields in the intracluster medium (ICM) through the detection of diffuse Mpc-scale synchrotron emission in the form of radio halos and radio relics (e.g., Ferrari et al. 2008, for recent review).

Giant radio halos provide the most spectacular evidence of non-thermal phenomena in the ICM. They are giant diffuse radio sources located at the centre of galaxy clusters and extending similarly to the hot ICM; remarkably they are always found in clusters with evidence for ongoing mergers (e.g. Buote 2001; Govoni et al. 2004; Venturi et al. 2008). These halos prove that mechanisms of in situ particle acceleration or injection are active in the ICM since the diffusion time necessary to the radio emitting electrons to cover Mpc scales is much longer than their radiative lifetime (e.g., Jaffe 1977).

Correlations between the radio power at 1.4 GHz of giant radio halos (P_1.4) and their physical size, and between P_1.4 and the X-ray luminosity ( $L_{\rm X}$ ) and temperature of the hosting clusters have been found and discussed in the literature (e.g. Liang et al. 2000; Bacchi et al. 2003; Cassano et al. 2006, 2007; Brunetti et al. 2007; Rudnick et al. 2009). These correlations suggest that gravity provides the reservoir of energy to generate the non-thermal components responsible for the emission from the ICM.

Mergers drive shocks and turbulence in the ICM that may lead to the amplification of the magnetic fields (e.g., Dolag et al. 2002; Subramanian et al. 2006; Ryu et al. 2008) and to the acceleration of high energy particles (e.g., Enßlin et al. 1998; Roettiger et al. 1999; Sarazin 1999; Blasi 2001; Brunetti et al. 2001, 2004; Petrosian 2001; Fujita et al. 2003; Ryu et al. 2003; Hoeft & Brüggen 2007; Brunetti & Lazarian 2007). More specifically, extended and fairly regular diffuse radio emission may be produced by secondary electrons injected during proton-proton collisions, since relativistic protons can diffuse on large scales (hadronic or seconday models; e.g., Dennison 1980; Blasi & Colafrancesco 1999), or by relativistic electrons re-accelerated in situ by MHD turbulence generated in the ICM during cluster-cluster mergers (re-acceleration models; e.g., Brunetti et al. 2001; Petrosian 2001). Observations provide support to the idea that turbulence may play a role in the particle acceleration process (e.g., Brunetti 2008; Ferrari et al. 2008; Cassano 2009, for recent reviews). Low frequency radio observations (e.g., with LOFAR, LWA) and high energy observations (with FERMI) are expected to set crucial constraints.

$\begin{figure} \par\includegraphics[width=7cm]{12751f1a.ps}\includegraphics[width=7cm]{12751f1b.ps} \end{figure}$

Figure 1:

Left panel: distribution of GMRT galaxy clusters (blue) and of other radio-halo clusters from the literature (filled black symbols) in the P_1.4-0.1-2.4 keV luminosity plane (Table 1). Empty circles mark giant radio halos from the GMRT sample, empty triangles mark the two mini-halos in cool-core clusters from the GMRT sample, the cross marks the position of RXJ1314, and arrows mark upper limits for GMRT clusters with no evidence of Mpc-scale radio emission. The solid line gives the best fit to the distribution of giant radio halos (BCES Bisector, Table 2). Right panel: distribution of giant radio halos (GMRT + literature, Table 1) in the P_1.4-bolometric X-ray luminosity plane. The solid line gives the best fit to the distribution of giant radio halos (BCES Bisector, Table 2).

Open with DEXTER

In this paper we study the distribution of X-ray selected galaxy clusters in the P_1.4- $L_{\rm X}$ plane providing an extension of a previous work (Brunetti et al. 2007). More specifically, we discuss constraints on the relevant time-scales of the evolution of magnetic fields and emitting particles in the ICM and their consequence on the origin of radio halos.

In Sect. 2 we discuss the distribution of X-ray luminous galaxy clusters in the P_1.4- $L_{\rm X}$ plane and the P_1.4- $L_{\rm X}$ correlation traced by radio halos. In Sect. 3 we discuss the connection between mergers and radio halos and their evolution driven by these mergers. In Sects. 4 and 5 we constrain the evolution time-scale of radio halos and compare our results with model expectations, respectively. In Sect. 6 we give our conclusions.

H₀=70 km s^-1 Mpc^-1, $\Omega_{\rm m}=0.3$ , $\Omega_{\Lambda}=0.7$ are adopted throughout the paper.

2 The Radio - Lx correlation & cluster bi-modality

The ``GMRT Radio Halo Survey'' (Venturi et al. 2007, 2008) has provided a significant step to a statistically solid exploration of the properties of radio halos through a large observational project carried out with the Giant Metrewave Radio Telescope (GMRT, Pune-India) at 610 MHz. This pointed-radio survey completed the radio follow up of a complete sample of 50 X-ray luminous ( $L_{\rm X}\geq5\times 10^{44}$ erg/s) galaxy clusters in the redshift range 0.2-0.4 (taken from the REFLEX, Boehringer et al. 2004, and the extended BCS, Ebeling et al. 1998, 2000 catalogues) through high sensitivity observations of 34 clusters with no radio information. Large scale synchrotron emission at level of presently known radio halos was found only in $\sim$ $30\%$ of the selected (X-ray luminous and massive) clusters (Brunetti et al. 2007; Venturi et al. 2008), with evidence that this fraction depends on cluster X-ray luminosity (Cassano et al. 2008a).

Figure 1 shows the distribution of GMRT galaxy clusters (blue) in the P_1.4 - $L_{\rm X}$ plane (Left: 0.1-2.4 keV luminosity; Right: bolometric luminosity), together with that of clusters hosting giant radio halos (from the literature, Table 1): giant radio halos trace the P_1.4 - $L_{\rm X}$ correlation, clusters with no large scale radio emission populate the region of the radio upper limits that is well separated from that spanned by radio halos.

Table 1: Radio and X-ray properties of clusters used in this paper.

Table 2: Fitting parameters for the correlations between P_1.4- L_0.1-2.4 and P_1.4- $L_{\rm bol}$ of giant radio halos (see text).

The distribution of giant halos across the correlation is significantly broader than the typical error bars in their measured radio and X-ray luminosities thus implying a possible intrinsic scatter in the correlation. For this reason, as in Cassano et al. (2006), in our analysis we use the linear regression algorithm by Akritas & Bershady (1996) that indeed accounts for both intrinsic scatter and measured errors in both variables. The fits have been performed in the form:

$\begin{displaymath}{\rm Log} ( P_{1.4} ) - Y = A + b \left[ {\rm Log} ( L_{X} ) - X \right] \end{displaymath}$

(1)

where P_1.4 is in W/Hz, $L_{\rm X}$ is in erg/s, Y=24.5, and X=45 and 45.4 in the case of the 0.1-2.4 keV luminosity (Fig. 1 Left) and bolometric X-ray luminosity (Fig. 1 Right), respectively. The best-fit normalizations and slopes of the correlations for giant radio halos, and the measured scatters across the correlation are given in Table 2. We report best fits obtained from BCES-bisector and orthogonal approaches and from their bootstraps (10 000 bootstrap resamplings). The BCES bisector approach treats the variables symmetrically and is recommended for scientific problems where the goal is to estimate relationships between the variables and for a comparison with theory (e.g., Isobe et al. 1990).

Regardless of the nature of the scatter of the datapoint across the correlation, we point out that, even by restricting to the BCES-bisector approach that gives the flatter slope of the correlations, present data allow us to fairly constrain the slope of the correlations: at 99% slopes are $1.55 \leq b \leq 2.58$ in the case of the correlation between P_1.4 and the 0.1-2.4 keV luminosity, and $1.35 \leq b \leq 2.17$ in the case of the correlation between P_1.4 and the bolometric X-ray luminosity.

3 Evolution of radio halos and connection with cluster mergers

Correlations between radio and thermal properties in galaxy clusters may be explained by both hadronic and turbulent-acceleration models with the observed slopes that can be reproduced provided that also the magnetic field scales with cluster mass, temperature or luminosity (e.g. Dolag & Ensslin 2000; Miniati et al. 2001; Cassano et al. 2006; Dolag 2006).

The new result from the high sensitivity data of the ``GMRT Radio Halo Survey'' is the bi-modal behaviour in Fig. 1, with radio-halo clusters and clusters without radio halos clearly separated (Brunetti et al. 2007). It is not obvious to understand how two well separated classes of galaxy clusters can be generated in the context of the hierarchical process of large scale structure formation. Indeed clusters with similar thermal properties (mass, X-ray luminosity, ...) are expected to have a similar probability to host radio halos. In this case the observed differences in terms of cluster non-thermal properties should be understood by assuming different evolutionary stages of these clusters.

Clusters in the GMRT sample are selected with similar X-ray luminosity ( $\approx$ mass) and redshift. The radio halo - merger connection (e.g. Venturi et al. 2008) may suggest that the difference between giant radio halo and ``radio quiet'' clusters is due to their dynamics. Thus regardless of the details of the mechanisms that generate radio halos, we shall assume the following evolutionary cycle:

i) galaxy clusters host giant radio halos for a period of time, in connection with cluster mergers, and populate the P_1.4- 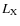$L_{\rm X}$ correlation;
ii) at later times, when clusters become dynamically relaxed, the Mpc-scale synchrotron emission is gradually suppressed and clusters populate the region of the upper limits.

In this case, when restricting to clusters of the GMRT complete sample, Fig. 1 provides a fair statistical sampling of the evolutionary flow of X-ray luminous clusters in the P_1.4- $L_{\rm X}$ plane at z=0.2-0.4.

Radio-halo clusters, always dynamically disturbed systems, must be the ``youngest'' systems, where an ongoing merger, leading to their formation (or accretion of a sizable fraction of their mass), is still supplying energy to maintain the synchrotron emission.

$\begin{figure} \par\includegraphics[width=7cm]{12751f2a.ps}\includegraphics[width=7cm]{12751f2b.ps} \end{figure}$

Figure 2:

Left panel: fraction of trials from Montecarlo simulations that match observations (i.e. 1 cluster in the ``empty'' region) as a function of f (see text), assuming ${\cal N}= 17$ (solid line), 19 (dotted line) and 20 (dashed line) (Table 3). Right panel: distributions of trials from Montecarlo simulations as a function of the number of clusters in the empty region, ${N}_{\rm emp}$ , assuming f=0.125 (solid line and filled circles), 0.17 (dotted line and empty circles), 0.3 (dashed line and empty squares), 0.4 (long-dashed line and empty triangles). $\tau = 3.5 f$ and =3.5 f/2 Gyr if one assumes that clusters cross the ``empty'' region one or two times, respectively. The vertical dashed line marks 1 cluster in the ``empty'' region.

Open with DEXTER

On the other hand, clusters with radio upper limits, typically more relaxed than radio halo clusters (Venturi et al. 2008), must have experienced the last merger at earlier epochs: after the last merger they already had sufficient time for suppression of the synchrotron emission and consequently they should be the ``oldest'' systems in the GMRT sample.

Clusters in the ``empty'' region may be (a) ``intermediate'' systems at late merging phases, where synchrotron emission is being suppressed, or (b) the ``very young'' systems in the very early phases of a merging activity, where synchrotron emission is increasing. One cluster in the GMRT sample is found in the ``empty'' region, this is the merging cluster RXJ1314 that hosts a small-scale radio halo and 2 radio relics (Feretti et al. 2005; Venturi et al. 2007) and consequently it likely belongs to the latter class (b) of galaxy clusters (although we cannot exclude that it is an ``intermediate'' system).

4 Constraining the evolution of radio halos

In the case that we admit that radio halos are transient phenomena connected with cluster-merging phases, the ``emptiness'' of the region between radio halos and ``radio quiet'' clusters in the P_1.4- $L_{\rm X}$ diagram can be used to constrain the time-scale of the evolution (suppression and amplification) of the synchrotron emission in these clusters (Brunetti et al. 2007). Indeed the significant lack of clusters in this region suggests that this time-scale is much shorter than both the ``life-time'' of clusters in the sample and the period of time clusters spent in the radio halo stage.

By restricting our analysis to the 19 clusters in the GMRT sample with $L_{\rm X} \geq 8.5 \times 10^{44}$ erg s^-1, in which case the radio power of giant radio halos is 1 order of magnitude larger than radio upper limits, we find 5 giant radio halos (and 2 mini-halos in cool-core clusters) on the correlation, 11 clusters in the region of the upper limits and only RXJ1314 in the ``empty'' region. Thus, the time interval that clusters may spend crossing this ``empty'' region is $\approx$ $f \tau_{\rm gc}$ , where f is the fraction of clusters in this region, 1/19, and $\tau_{\rm gc}$ is the period of time elapsed since the last merger in the case of the ``oldest'' clusters in our population. Since the GMRT sample is constituted by massive, M > 10¹⁵ $M_{\odot}$ , galaxy clusters at z=0.2-0.4, $\tau_{\rm gc}$ is essentially the time-scale between the epoch of formation of these clusters ( $z\approx 0.6$ -0.7, e.g. Giocoli et al. 2007) and the most recent epoch of observation (z=0.2, $\approx$ 11.2 Gyr), $\tau_{\rm gc} \approx 3.5$ Gyr. Consequently, the ``life-time'' of radio halos is $\tau_{\rm rh}=7/19 \tau_{\rm gc} \approx 1.3$ Gyr, the time interval that clusters may spend in the ``empty'' region is = $1/19 \tau_{\rm gc} \approx 180$ Myr, and the corresponding time-scale for suppression of the cluster-scale synchrotron emission from the level of radio halos to that of ``radio quiet'' clusters, $\tau$ , is roughly half of this period, $\tau \approx 90$ Myr, considering that clusters may cross the ``empty'' region two times (during the amplification and suppression of synchrotron emission, Sect. 3). We stress that this conclusion holds even if the two mini-halos, Abell 2390 and Z7160, are excluded from our analysis, in this case $\tau_{rh}\approx 1$ Gyr, f = 1/17, and $\tau \approx 200$ Myr.

Obviously the poor statistics allows fairly large uncertainties on the above numbers. Consequently, because in Sect. 5 we will discuss the implications of these constraints for the origin of radio halos, it is important to understand whether, due to the poor statistics, a significantly larger value of $\tau$ is still consistent with the distribution of galaxy clusters in Fig. 1. We use Montecarlo procedures: we assume that clusters spend a fraction of time $f_{\rm low}$ , $f_{\rm up}$ and f in the region of the upper-limits, on the correlation and in the ``empty'' region, respectively. Then we perform 10⁵ random extractions of $\cal{N}$ synthetic clusters with probability $f_{\rm low}$ , $f_{\rm up}$ and f (with $f_{\rm low} + f_{\rm up} + f =1$ ), and derive the fraction of trials where 1 cluster falls in the ``empty'' region. This is shown in Fig. 2 (Left) as a function of f: as expected the distribution peaks at $f \simeq 0.06$ , corresponding to $\tau \sim 1/2 f \tau_{\rm gc} \approx 100$ Myr, in which case about 38% of trials match observations. In the less constrained case, ${\cal N}= 17$ , where the 2 mini-halos in the GMRT sample are not considered, the fraction of trials that match observations falls to only 1% and 0.3% for f=0.33 ( $\tau = 0.57$ ) and f=0.39 (0.68 Gyr), respectively (see Table 3, where we also report the results obtained by considering different sub-samples).

This analysis allows us to conclude that values of $\tau$ significantly larger than a few tenths of Gyr are very unlikely. This is also highlithed by Fig. 2 (Right) that shows the distribution of trials (in the less constrained case, ${\cal N}= 17$ ) as a function of the number of galaxy clusters found in the ``empty'' region for different values of $\tau$ . Larger values of $\tau$ imply an increasing number of clusters expected in the ``empty'' region, and $\tau \geq 0.6$ Gyr can be excluded at > $99\%$ confidence level. We note that our conclusion is inconsistent with much larger values of the transition time-scale, $\tau \sim$ few Gyr, as recently claimed by Kushnir et al. (2009) that however estimate the transition time-scale as $\tau \sim 1/3 \tau_{\rm gc}$ , 1/3 being the fraction of clusters with radio halos and $\tau_{\rm gc}$ taken = 5 Gyr. On the other hand, our statistical analysis provides more quantitative support to previous conclusions (Brunetti et al. 2007; Brunetti 2008).

For completeness, we also consider the complementary scenario where clusters cross the ``empty'' region only one time, due to the suppression of their synchrotron emission. In this case we interpret RXJ1314 as an ``intermediate'' system in early-post merging phase (Sect. 3) that provides the most conservative approach to constrain $\tau$ (Table 3). Still also in this conservative approach we conclude that present data strongly favour values of $\tau$ substantially smaller than 1 Gyr ( $\tau \geq 1$ Gyr is excluded at >99% in our reference case, ${\cal N}=19$ , Table 3).

Table 3: Synchrotron dissipation time (in unit of Gyr) in galaxy clusters that allows to match observations (1 cluster in the ``empty'' region) in a fraction of Montecarlo trials = 10% (Col. 5), 5% (Col. 6), 1% (Col. 7) and 0.3% (Col. 8).

5 Implications for the origin of giant radio halos

5.1 Hadronic models

Theoretically relativistic protons are expected to be the dominant non-thermal particle component in galaxy clusters since they have very long life-times and remain confined within clusters for an Hubble time (e.g. Blasi et al. 2007, and ref. therein). Proton-proton (p-p) collisions provide a continuous source of secondary products in the ICM, and secondary electrons in turns generate diffuse synchrotron emission.

Radio halos are found in merging clusters and the passage of merger shocks through the ICM may increase the energy density of protons (e.g. due to acceleration of these protons at merger shocks) enhancing the rate of production of secondary electrons and the resulting cluster-scale synchrotron emission. However, since protons have very long life-times the production rate of secondary electrons in the ICM would remain unchanged with cosmic time and the mechanism itself does not allow a suppression of the synchrotron emission when clusters become more dynamically relaxed.

$\begin{figure} \par\vspace*{-1.5mm} \includegraphics[width=8.2cm]{12751f3.ps} \end{figure}$	Figure 3: Lower limit to the ratio between the energy density of the magnetic field in radio halos and in ``radio quiet'' clusters as a function of the magnetic field strength in radio halos. The vertical dashed line marks the value of the equivalent field of the Cosmic Microwave Background photons assuming z=0.25.
Open with DEXTER

Clusters of equal masses may experience different formation histories, yet the global budget of gravitational energy dissipated at merging and accretion shocks is expected to be similar yielding to fairly small differences in terms of energy content of relativistic protons (Jubelgas et al. 2008). Consequently, assuming that the ICM is magnetised at $\mu$ G level, radio halos generated by secondary emission are expected long-living and common; also, some trend between their radio power and the X-ray luminosity or temperature of the hosting clusters is expected (Dolag & Ensslin 2000; Miniati et al. 2001; Dolag 2006; Pfrommer et al. 2008). Due to the huge uncertainties in the physics of shock acceleration one may easily believe that large variations of the content of relativistic protons are possible among clusters with similar mass (temperature...), however there is no reason to expect a bi-modality in the cluster synchrotron emission.

Consequently, to explain the separation between radio-halo and ``radio quiet'' clusters and the merger-halo connection the magnetic field should play a major role and it must be admitted that merging clusters, hosting radio halos, have larger magnetic fields and that this excess in magnetic field is dissipated when clusters become ``radio quiet'' and dynamically relaxed (Brunetti et al. 2007, 2008; Kushnir et al. 2009).

Synchrotron emission in hadronic models scales as (e.g. Dolag & Ensslin 2000):

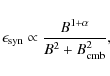
$\begin{displaymath}\epsilon_{\rm syn} \propto {{ B^{1+\alpha} }\over{B^2 + B_{\rm cmb}^2}}, \end{displaymath}$

(2)

where $B_{\rm cmb} =3.2 (1+z)^2 ~ \mu$ G is the equivalent field due to inverse Compton scattering of Cosmic Microwave Background photons and $\alpha \sim 1.3$ is the synchrotron spectral index of radio halos (e.g. Ferrari et al. 2008). Thus to explain a suppression $\geq$ 10 in terms of synchrotron emission (Fig. 1) the ratio between the magnetic fields in radio halos, $B + \delta B$ , and that in ``radio quiet'' clusters, B, must be:

$\begin{displaymath}\left( {{ B + \delta B }\over{ B }} \right)^{\alpha-1} {{ 1 +... ...ver {1 + ( {{B_{\rm cmb} }\over{B + \delta B}} )^2 }} \geq 10. \end{displaymath}$

(3)

The ratio between the magnetic field energy densities in the two cluster populations, $\omega_{\rm rh}/\omega_{\rm rq} \propto (1 + \delta B /B)^2$ , from Eq. (3) is shown in Fig. 3 for $z\approx 0.25$ , typical of GMRT clusters. In the case $B + \delta B \ll B_{\rm cmb}$ , hadronic models must admit that the energy density of the magnetic field in ``radio quiet'' clusters is $\geq$ 10 times smaller than that in radio halos, and even larger ratios must be admitted in the case $B + \delta B \gg B_{\rm cmb}$ .

Theoretically we might admit that the magnetic field is amplified in the ICM by turbulence generated in cluster mergers (Dolag et al. 1999, 2005; Ryu et al. 2008), and later dissipated since turbulent magnetic fields can decay.

On the other hand, to our knowledge, studies of Faraday Rotation in galaxy clusters do not find any statistical difference, in terms of energy density of the large scale (10-100 kpc coherent scales) magnetic field, between clusters hosting radio halos and clusters without Mpc-scale radio emission (e.g. Carilli & Taylor 2002 ).

Most important, dissipation of this magnetic field is expected to take long time. Even if we simply consider the case where the field is dissipated through the decay of cluster-MHD turbulence, the energy density of the rms field decreases only (about) linearly with the eddy turnover time-scale. This requires several eddy turnover times, $\approx$ a few Gyr, to gradually dissipate the bulk (i.e. 80-90%) of the energy density of the field in the ICM (Subramanian et al. 2006), that indeed also explains why few $\mu$ G-fields are common in galaxy clusters. Consequently the dissipation time-scale of the magnetic field is inconsistent with (larger than) that of the suppression of the cluster-scale synchrotron emission inferred from the statistical analysis in previous section.

This conclusion is based on the scenario, following Subramanian et al. (2006), that the magnetic field in the ICM is amplified by cluster turbulence generated on large scale, $\sim$ 150-300 kpc, in which case the thickness of magnetic filaments is expected to be $\sim$ 20-40 kpc. This is supported by Faraday Rotation measurements of extended sources in clusters that allow to observe ordering scales of the magnetic field $\sim$ 10-40 kpc (Clarke et al. 2001; Guidetti et al. 2008) and that indicate, at least in some cases, that the power spectrum of the magnetic field extends to very large scales, 100-500 kpc (e.g. Murgia et al. 2004). On the other hand our understanding of the origin and of the properties of magnetic field in galaxy clusters is still poor and leaves space to large uncertainties. Indeed, faster dissipation of the magnetic field in galaxy clusters, $\tau \approx$ several 100 Myr, may happen in the case that the magnetic field in excess, $\delta B$ , in clusters hosting radio halos is associated with a field component on smaller scales. The value of the small scale field, $\delta B$ , necessary to account for the difference between the synchrotron emission in radio halo and ``radio quiet'' clusters can be obtained from Eq. (3) and is reported in Fig. 4 as a function of the large scale magnetic field, B. Figure 4 clearly highlights the drawbacks of this hypothesis: first of all the small scale field must be energetically dominant with respect to that on larger scales (see also Fig. 3), in addition if the large scale field is $\geq$ $1.5{-}2 ~\mu$ G level (consistent with present RM studies) then $\delta B$ would be extremely large, $\geq$ 10 $\mu$ G. Since $\delta B$ must be dissipated in a few tenths of Gyr, we note that this would imply a magnetic-energy dissipation rate in a Mpc³ region $\geq$ $10^{46} (\tau~ /0.5~ {\rm Gyr})^{-1}$ erg/s, e.g. larger than the bolometric X-ray emission of clusters themselves.

$\begin{figure} \vspace*{-1.5mm} \includegraphics[width=8.2cm]{12751f4.ps} \end{figure}$	Figure 4: The intensity of the small-scale magnetic field in radio halos that must be dissipated to match observations is reported as a function of the strength of the large-scale magnetic field in ``radio quiet'' (and radio halo) clusters.
Open with DEXTER

5.2 Turbulent acceleration of particles

MHD turbulence generated during cluster mergers may accelerate relativistic particles (e.g. Brunetti et al. 2008). Even without considering the dissipation (or amplification) of the magnetic field in the ICM, the finite dissipation time-scale of turbulence implies that giant radio halos should be found in merging-clusters where turbulence is still generated and must be extremely rare in more relaxed clusters (e.g., Cassano & Brunetti 2005).

As soon as large scale turbulence in the ICM reaches smaller, resonant, scales (via cascading or induced plasma instabilities, e.g. Brunetti et al. 2004; Lazarian & Beresnyak 2006; Brunetti & Lazarian 2007), particles are accelerated and generate synchrotron emission. In the case of radio halos emitting at GHz frequencies the acceleration process should be relatively efficient and particles get accelerated to the energies necessary to produce synchrotron GHz-emission within a time-scale smaller than a couple of cooling times of these electrons, that is $\approx$ 100 Myr. Although the large uncertainties in the way large scale turbulence is generated in the ICM during cluster mergers, it is likely that the process persists for a few crossing times of the cluster-core regions, that is fairly consistent with a radio halo life-time $\tau_{\rm rh} \sim 1$ Gyr as derived in Sect. 4.

Most important, the cooling time of the emitting electrons is smaller than (or comparable to) the cascading time-scale of the large-scale turbulence implying that the evolution of the synchrotron power depends very much on the level of MHD turbulence in the ICM (e.g., Cassano & Brunetti 2005; Brunetti & Lazarian 2007). Consequently, if we simply assume that the injection of MHD turbulence is suppressed ``instantaneously'' at a given time (e.g. at late merging-phase), then also the synchrotron emission at higher radio frequencies is suppressed, falling below the detection limit of radio observations, as soon as the energy density of turbulence starts decreasing. This is shown in Fig. 5 where the synchrotron spectrum from turbulent accelerated electrons is reported for different energy density of the MHD turbulence. A reduction of the turbulent energy density of a factor 2 happens within about 1 eddy turnover time of the large scale turbulence, that is a few times 100 Myr, and this is sufficient to suppress the synchrotron emission at higher, GHz, frequencies by about 1 order of magntitude.

$\begin{figure} \vspace*{-1.5mm} \includegraphics[width=8.2cm]{12751f5.ps} \end{figure}$

Figure 5:

Example of the synchrotron emitted power (arbitrary units) as a function of frequency for different energy densities of turbulence (magnetosonic waves): 30% (solid line), 25% (dotted line), 20% (dashed line), 15% (long-dashed line) of the thermal energy density. In the calculations we adopt a homogeneus model with magnetic field strength = 3 $\mu$ G, number density of the thermal plasma = 10^-3 cm^-3 and temperature $T=7 \times 10^7$ K. Frequency ranges of interest for GMRT, VLA and LOFAR are also marked.

Open with DEXTER

Consequently cluster bi-modality in this scanario may be expected because the transition between radio halos and ``radio quiet'' clusters in the P_1.4- $L_{\rm X}$ diagram is expected to be fairly fast (Brunetti et al. 2007, 2008) provided that the acceleration process we are looking in these sources is not very efficient, being just enough to generate radio halos emitting at a few GHz frequencies. On the other way round, we might say that the observed cluster bi-modality constrains the efficiency of the particle acceleration process in radio halos. Interestingly, a relatively inefficient electron acceleration process in radio halos is in line with the steep spectrum observed in these sources and, most important, with the presence of a spectral steepening at higher frequencies in a few halos (e.g., Thierbach et al. 2003; Brunetti et al. 2008; Dallacasa et al. 2009).

Also, Fig. 5 suggests that under these conditions the suppression of synchrotron emission that follows the dissipation of MHD turbulence is more efficient at higher frequencies and thus cluster bi-modality is expected to be less pronounced in considering the synchrotron emission of galaxy clusters at lower frequencies. This is a clear expectation of the scenario that can be tested with future observations of samples of galaxy clusters at 100-200 MHz that may be carried out with LOFAR in a couple of years.

6 Conclusion

The ``GMRT Radio Halo Survey'' allows to study the statistics of radio halos in a complete sample of X-ray luminous galaxy clusters (Venturi et al. 2008). The high sensitivity of the radio observations at the GMRT allows to unveil a cluster radio bi-modality with ``radio quiet'' clusters well separated from the region of the P_1.4- $L_{\rm X}$ correlation defined by giant radio halos (Brunetti et al. 2007 and Fig. 1).

In the framework of the hierarchical model galaxy clusters are expected to evolve in the P_1.4- $L_{\rm X}$ plane, in which case the distribution of GMRT clusters in Fig. 1 results from a statistical sampling of this evolution. The connection between radio halos and cluster mergers suggests that the Mpc-scale synchrotron emission in galaxy clusters is amplified during these mergers and then suppressed when clusters become more dynamically relaxed. The separation between radio halo and ``radio quiet'' clusters in Fig. 1, and the rarity of galaxy clusters with intermediate radio power suggests that the processes of amplification and suppression of the synchrotron emission takes place in a relatively short time-scale.

The time-scale of the evolution from radio halos to ``radio quiet'' clusters (and vice versa) provides a novel tool to constrain models proposed for the origin of radio halos, namely the re-acceleration and hadronic model. In the former case the acceleration and cooling of relativistic electrons drive the level of the Mpc-scale synchrotron emission from clusters, while in the latter case the transition between radio halo and ``radio quiet'' clusters must be due to the amplification and dissipation of the magnetic field in the ICM.

We carried out statistical analysis of the cluster radio bi-modality in Fig. 1 and, although the still poor statistics, show that the suppression of the cluster-scale synchrotron emission must happen in a fairly short time-scale, a few 100 Myr, whereas longer time-scales, Gyr, are not consistent with present data. This short transition time-scale can be potentially reconciled with the hypothesis that the emitting electrons are accelerated by cluster-scale turbulence, in which case the synchrotron radiation emitted at GHz frequencies may rapidly decrease as a consequence of the dissipation of a sizeable fraction of that turbulence. In this case, however, we also claim that a less pronounced bi-modality is expected in the case of cluster samples observed at lower radio frequencies, that may be tested by future LOFAR and LWA observations.

On the other hand, it is more difficult to reconcile a short transition time-scale if the unique source of emitting electrons is provided by p-p collisions (hadronic models). In this case the dissipation of the cluster magnetic field that suppresses the synchrotron emission would take longer periods of time. In principle this difficulty could be considerably alleviated in the case that the energy density of the magnetic field in radio halos is dominated by that of small scale field. However, we would come into the untenable scenario in which a very strong, transient magnetic field (small scale) component, is present in the ICM. Future studies of source-depolarization in cluster radio sources will also help in constraining the level of the small-scale field component in the ICM.

We stress that our constraints come from the conservative (and simplified) assumption that the injection of turbulence (as well as the amplification of the magnetic field) switches off at the same time across the radio halo, Mpc³, region. In reality, depending on the way turbulence and large scale magnetic fields are generated in the ICM, the suppression and amplification of the synchrotron emission could start at different times in different parts of this volume. The most important consequence of that is an expected scatter in the correlation rather than in the way clusters become ``radio quiet'', since clusters are expected to start moving across the transition region only when synchrotron is suppressed across a substantial fraction of the radio halo's volume. Yet, overall this goes into the direction to strengthen our conclusion that an efficient process to suppress the cluster-scale synchrotron emission in galaxy clusters is necessary to explain observations.

Giant radio halos prove complex physical processes where a fraction of the gravitational energy dissipated during cluster-mergers is channelled into the acceleration of relativistic particles. The correlation traced by halos in Fig. 1 and its intrinsic scatter, together with the distribution of clusters in the P_1.4- $L_{\rm X}$ plane, provide novel tools to hopefully constrain the complex physics of turbulence and magnetic fields in the ICM and their interplay with the process of cluster formation. The deep surveys at low frequencies with LOFAR and LWA will be crucial to overcome present uncertainties due to the still poor statistics allowing a major step forward in understanding the origin and evolution of the cluster-scale synchrotron emission. Remarkably, as discussed in this paper, the scatter of the correlation and the distribution of clusters in the P_1.4- $L_{\rm X}$ plane are expected to depend on the observing radio frequency (Sect. 5.2, Fig. 5), and consequently deep complementary follow ups at intermediate and higher frequencies (GMRT, eVLA, SKA) will also be crucial.

Acknowledgements

This research is partially funded by INAF and ASI through grants PRIN-INAF2007 and ASI-INAF I/088/06/0. G.B. would like to acknowledge P. Blasi, T. Ensslin and D. Kushnir for stimulating discussions.

References

Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [CrossRef] [NASA ADS]
Bacchi, M., Feretti, L., Giovannini, G., & Govoni, F. 2003, A&A, 400, 465 [EDP Sciences] [CrossRef] [NASA ADS]
Blasi, P., & Colafrancesco, S. 1999, APh, 12, 169 [NASA ADS]
Blasi, P., Gabici, S., & Brunetti, G. 2007, IJMPA, 22, 681 [CrossRef] [NASA ADS]
Böhringer, H., Schuecker, P., Guzzo, L., et al. 2001, A&A, 369, 826 [EDP Sciences] [CrossRef] [NASA ADS]
Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [EDP Sciences] [CrossRef] [NASA ADS]
Brentjens, M. A. 2008, A&A, 489, 69 [EDP Sciences] [CrossRef] [NASA ADS]
Bonafede, A., Feretti, L., Giovannini, G., et al. 2009, A&A, 503, 707 [EDP Sciences] [CrossRef] [NASA ADS]
Brunetti, G. 2008 [arXiv:0810.0692]
Brunetti, G., & Lazarian, A. 2007, MNRAS, 378, 245 [CrossRef] [NASA ADS]
Brunetti, G., Setti, G., Feretti, L., & Giovannini, G. 2001, MNRAS, 320, 365 [CrossRef] [NASA ADS]
Brunetti, G., Blasi, P., Cassano, R., & Gabici, S. 2004, MNRAS, 350, 1174 [CrossRef] [NASA ADS]
Brunetti, G., Venturi, T., Dallacasa, D., et al. 2007, ApJ, 670, L5 [CrossRef] [NASA ADS]
Brunetti, G., Giacintucci, S., Cassano, R., et al. 2008, Nature, 455, 944 [CrossRef] [NASA ADS]
Buote, D. A. 2001, ApJ, 553, 15 [CrossRef] [NASA ADS]
Carilli, C. L., & Taylor, G. B. 2002, ARA&A, 40, 319 [CrossRef] [NASA ADS]
Cassano, R. 2009, ASPC, 407, 223 [NASA ADS]
Cassano, R., & Brunetti, G. 2005, MNRAS, 357, 1313 [CrossRef] [NASA ADS]
Cassano, R., Brunetti, G., & Setti, G. 2006, MNRAS, 369, 1577 [CrossRef] [NASA ADS]
Cassano, R., Brunetti, G., Setti, G., Govoni, F., & Dolag, K. 2007, MNRAS, 378, 1565 [CrossRef] [NASA ADS]
Cassano, R., Brunetti, G., Venturi, T., et al. 2008a, A&A, 480, 687 [EDP Sciences] [CrossRef] [NASA ADS]
Cassano, R., Gitti, M., & Brunetti, G. 2008b, A&A, 486, L31 [EDP Sciences] [CrossRef] [NASA ADS]
Clarke, T. E., & Ensslin, T. A. 2006, AJ, 131, 2900 [CrossRef] [NASA ADS]
Clarke, T. E., Kronberg, P. P., & Böhringer, H. 2001, ApJ, 547, L111 [CrossRef] [NASA ADS]
Dallacasa, D., Brunetti, G., Giacintucci, S., et al. 2009, ApJ, 699, 1288 [CrossRef] [NASA ADS]
Deiss, B. M., Reich, W., Lesch, H., & Wielebinski, R. 1997, A&A, 321, 55 [NASA ADS]
Dennison, B. 1980, ApJ, 239, L93 [CrossRef] [NASA ADS]
Dolag, K. 2006, AN, 327, 575 [NASA ADS]
Dolag, K., & Ensslin, T. A. 2000, A&A, 362, 151 [NASA ADS]
Dolag, K., Bartelmann, M., & Lesch, H. 1999, A&A, 348, 351 [NASA ADS]
Dolag, K., Bartelmann, M., & Lesch, H. 2002, A&A, 387, 383 [EDP Sciences] [CrossRef] [NASA ADS]
Dolag, K., Grasso, D., Springel, V., & Tkachev, I. 2005, JCAP, 1, 9 [NASA ADS]
Ebeling, H., Voges, W., Böhringer, H., et al. 1996, MNRAS, 281, 799 [NASA ADS]
Ebeling, H., Edge, A. C., Böhringer, H., et al. 1998, MNRAS, 301, 881 [CrossRef] [NASA ADS]
Ebeling, H., Edge, A. C., Allen, S. W., et al. 2000, MNRAS, 318, 333 [CrossRef] [NASA ADS]
Ebeling, H., Barrett, E., Donovan, D., et al. 2007, ApJ, 661, L33 [CrossRef] [NASA ADS]
Ensslin, T. A., Biermann, P. L., Klein, U., & Kohle, S. 1998, A&A, 332, 395 [NASA ADS]
Feretti, L. 2002, in The Universe at Low Radio Frequencies, ed. A. Pramesh Rao, G. Swarup, & Gopal-Krishna, (Cambridge: Cambridge Univ. Press), Proc. IAU Symp., 199, 133
Feretti, L., Fusco-Femiano, R., Giovannini, G., & Govoni, F. 2001, A&A, 373, 106 [EDP Sciences] [CrossRef] [NASA ADS]
Feretti, L., Schuecker, P., Böhringer, H., Govoni, F., & Giovannini, G. 2005, A&A, 444, 157 [EDP Sciences] [CrossRef] [NASA ADS]
Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., & Rephaeli, Y. 2008, SSRv, 134, 93 [NASA ADS]
Fujita, Y., Takizawa, M., & Sarazin, C. L. 2003, ApJ, 584, 190 [CrossRef] [NASA ADS]
Guidetti, D., Murgia, M., Govoni, F., et al. 2008, A&A, 483, 699 [EDP Sciences] [CrossRef] [NASA ADS]
Hoeft, M., & Brueggen, M. 2007, MNRAS, 375, 77 [CrossRef] [NASA ADS]
Jaffe, W. J. 1977, ApJ, 212, 1 [CrossRef] [NASA ADS]
Jubelbas, M., Springel, V., Ensslin, T. A., & Pfrommer, C. 2008, A&A, 481, 33 [EDP Sciences] [CrossRef] [NASA ADS]
Giacintucci, S. 2007, Ph.D. Thesis Multiwavelength study of cluster mergers and consequences for the radio emission properties of galaxy clusters, University of Bologna; http://amsdottorato.cib.unibo.it/353/
Giacintucci, S., Venturi, T., Brunetti, G., et al. 2009, A&A, 505, 45 [EDP Sciences] [CrossRef]
Giocoli, C., Moreno, J., Sheth, R. K., & Tormen, G. 2007, MNRAS, 376, 977 [CrossRef] [NASA ADS]
Giovannini, G., & Feretti, L. 2000, New Astron., 5, 335 [CrossRef] [NASA ADS]
Gitti, M., Brunetti, G., & Setti, G. 2002, A&A, 386, 456 [EDP Sciences] [CrossRef] [NASA ADS]
Govoni, F. 2006, AN, 327, 539 [NASA ADS]
Govoni, F., Feretti, L., Giovannini, G., et al. 2001, A&A, 376, 803 [EDP Sciences] [CrossRef] [NASA ADS]
Govoni, F., Markevitch, M., Vikhlinin, A., et al. 2004, ApJ, 605, 695 [CrossRef] [NASA ADS]
Govoni, F., Murgia, M., Feretti, L., et al. 2005, A&A, 430, 5 [CrossRef] [NASA ADS]
Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 1041 [CrossRef]
Kim, K.-T., Kronberg, P. P., Dewdnewy, P. E., & Landecker, T. L. 1990, ApJ, 355, 29 [CrossRef] [NASA ADS]
Kushnir, D., Katz, B., & Waxman, E. 2009, JCAP, 9, 24
Lazarian, A., & Beresnyak, A. 2006, MNRAS, 373, 1195 [CrossRef] [NASA ADS]
Liang, H., Hunstead, R. W., Birkinshow, M., & Andreani, P. 2000, ApJ, 544, 686 [CrossRef] [NASA ADS]
Mazzotta, P., & Giacintucci, S. 2008, ApJ, 675, L9 [CrossRef] [NASA ADS]
Miniati, F., Jones, T. W., Kang, H., & Ryu, D. 2001, ApJ, 562, 233 [CrossRef] [NASA ADS]
Murgia, M., Govoni, F., Feretti, L., et al. 2004, A&A, 424, 429 [EDP Sciences] [CrossRef] [NASA ADS]
Petrosian, V. 2001, ApJ, 557, 560 [CrossRef] [NASA ADS]
Pfrommer, C., Ensslin, T. A., & Springel, V. 2008, MNRAS, 385, 1211 [CrossRef] [NASA ADS]
Roettiger, K., Burns, J. O., & Stone, J. M. 1999, ApJ, 518, 603 [CrossRef] [NASA ADS]
Rudnick, L., & Lemmerman, J. A. 2009, ApJ, 697, 1341 [CrossRef] [NASA ADS]
Ryu, D., Kang, H., Hallman, E., & Jones, T. W. 2003, ApJ, 593, 599 [CrossRef] [NASA ADS]
Ryu, D., Kang, H., Cho, J., & Das, S. 2008, Science, 320, 909 [CrossRef] [NASA ADS]
Sarazin, C. L. 1999, ApJ, 520, 529 [CrossRef] [NASA ADS]
Subramanian, K., Shukurov, A., & Haugen, N. E. L. 2006, MNRAS, 366, 1437 [NASA ADS]
Thierbach, M., Klein, U., & Wielebinski, R. 2003, A&A, 397, 53 [EDP Sciences] [CrossRef] [NASA ADS]
Tsuru, T., Koyama, K., Huges, J. P., et al. 1996, in UV and X-ray Spectroscopy of Astronomical and Laboratory Plasmas, ed. K. Yamashita, & T. Watanabe (Tokyo: Universal Academy Press), Frontiers Science Series, 15, 375
van Weeren, R. J., Rottgering, H. J. A., Bruggen, M., & Cohen, A. 2009 [arXiv:astro-ph/0905.3650]
Venturi, T., Giacintucci, S., Brunetti, G., et al. 2007, A&A, 463, 937 [EDP Sciences] [CrossRef] [NASA ADS]
Venturi, T., Giacintucci, S., Dallacasa, D., et al. 2008, A&A, 484, 327 [EDP Sciences] [CrossRef] [NASA ADS]

Footnotes

... luminosity: These slopes are consistent with those found in previous papers (e.g., Bacchi et al. 2003; Cassano et al. 2006). Kushnir et al. (2009) recently found significantly flatter slopes, however they do not fit the data with their errors measured in both variables but assuming an error in P_1.4 equal to the scatter of data points across the correlation.
... analysis: Mini-halos in cooling-flow clusters may have a different origin with respect to giant radio halos, possibly connected with the presence of the cooling flow (Gitti et al. 2002; Mazzotta & Giacintucci 2008; Cassano et al. 2008b).
... taken = 5 Gyr: This approach indeed would give the life-time of radio halos, not the transition time-scale, and it is indeed consistent with our estimate of $\tau_{\rm rh}$ .
... emission: This might happen if the increase of the cluster X-ray luminosity during mergers takes longer times than that of the synchrotron luminosity, and consequently merging clusters may approach the range of X-ray luminosities of the GMRT sample ``along'' the correlation.
...2002: We would also point out that in some cases the magnetic field in ``radio quiet'' clusters, e.g. A119, is larger than that of radio halo clusters, A2255, with similar X-ray luminosity (Murgia et al. 2004; Govoni et al. 2005).

All Tables

Table 1: Radio and X-ray properties of clusters used in this paper.

Table 2: Fitting parameters for the correlations between P_1.4- L_0.1-2.4 and P_1.4- $L_{\rm bol}$ of giant radio halos (see text).

Table 3: Synchrotron dissipation time (in unit of Gyr) in galaxy clusters that allows to match observations (1 cluster in the ``empty'' region) in a fraction of Montecarlo trials = 10% (Col. 5), 5% (Col. 6), 1% (Col. 7) and 0.3% (Col. 8).

All Figures

$\begin{figure} \par\includegraphics[width=7cm]{12751f1a.ps}\includegraphics[width=7cm]{12751f1b.ps} \end{figure}$	Figure 1: Left panel: distribution of GMRT galaxy clusters (blue) and of other radio-halo clusters from the literature (filled black symbols) in the P_1.4-0.1-2.4 keV luminosity plane (Table 1). Empty circles mark giant radio halos from the GMRT sample, empty triangles mark the two mini-halos in cool-core clusters from the GMRT sample, the cross marks the position of RXJ1314, and arrows mark upper limits for GMRT clusters with no evidence of Mpc-scale radio emission. The solid line gives the best fit to the distribution of giant radio halos (BCES Bisector, Table 2). Right panel: distribution of giant radio halos (GMRT + literature, Table 1) in the P_1.4-bolometric X-ray luminosity plane. The solid line gives the best fit to the distribution of giant radio halos (BCES Bisector, Table 2).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7cm]{12751f2a.ps}\includegraphics[width=7cm]{12751f2b.ps} \end{figure}$	Figure 2: Left panel: fraction of trials from Montecarlo simulations that match observations (i.e. 1 cluster in the ``empty'' region) as a function of f (see text), assuming ${\cal N}= 17$ (solid line), 19 (dotted line) and 20 (dashed line) (Table 3). Right panel: distributions of trials from Montecarlo simulations as a function of the number of clusters in the empty region, ${N}_{\rm emp}$ , assuming f=0.125 (solid line and filled circles), 0.17 (dotted line and empty circles), 0.3 (dashed line and empty squares), 0.4 (long-dashed line and empty triangles). $\tau = 3.5 f$ and =3.5 f/2 Gyr if one assumes that clusters cross the ``empty'' region one or two times, respectively. The vertical dashed line marks 1 cluster in the ``empty'' region.
Open with DEXTER
In the text

$\begin{figure} \par\vspace*{-1.5mm} \includegraphics[width=8.2cm]{12751f3.ps} \end{figure}$	Figure 3: Lower limit to the ratio between the energy density of the magnetic field in radio halos and in ``radio quiet'' clusters as a function of the magnetic field strength in radio halos. The vertical dashed line marks the value of the equivalent field of the Cosmic Microwave Background photons assuming z=0.25.
Open with DEXTER
In the text

$\begin{figure} \vspace*{-1.5mm} \includegraphics[width=8.2cm]{12751f4.ps} \end{figure}$	Figure 4: The intensity of the small-scale magnetic field in radio halos that must be dissipated to match observations is reported as a function of the strength of the large-scale magnetic field in ``radio quiet'' (and radio halo) clusters.
Open with DEXTER
In the text

$\begin{figure} \vspace*{-1.5mm} \includegraphics[width=8.2cm]{12751f5.ps} \end{figure}$	Figure 5: Example of the synchrotron emitted power (arbitrary units) as a function of frequency for different energy densities of turbulence (magnetosonic waves): 30% (solid line), 25% (dotted line), 20% (dashed line), 15% (long-dashed line) of the thermal energy density. In the calculations we adopt a homogeneus model with magnetic field strength = 3 $\mu$ G, number density of the thermal plasma = 10^-3 cm^-3 and temperature $T=7 \times 10^7$ K. Frequency ranges of interest for GMRT, VLA and LOFAR are also marked.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.