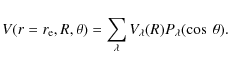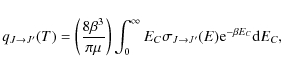| Issue |
A&A
Volume 507, Number 2, November IV 2009
|
|
|---|---|---|
| Page(s) | 1083 - 1086 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/200912663 | |
| Published online | 17 September 2009 | |
A&A 507, 1083-1086 (2009)
Rotational excitation of methylidynium (CH+) by a helium atom at high temperature
K. Hammami1 - L. C. Owono Owono2,3 - P. Stäuber4,5
1 - Laboratoire de Spectroscopie Atomique Moléculaire et Applications,
Département de Physique, Faculté des Sciences, France
2 - Université Tunis El Manar, Campus Universitaire, 1060 Tunis, Tunisia
3 - Department of Physics, Advanced Teachers Training College, University of Yaounde I, PO Box 47, Yaounde, Cameroon
4 - Centre for Atomic Molecular Physics and Quantum Optics,
Faculty of Science, University of Douala, PO Box 8580, Douala,
Cameroon
5 - Institute for Astronomy, ETH Zurich, 8093 Zurich, Switzerland
Received 9 June 2009 / Accepted 26 August 2009
Abstract
Context. The Herschel Space Observatory with its high-resolution instrument HIFI on board will observe the
![]()
![]() and
and
![]() rotational transitions in a wide range of gas temperatures up to
1000 K. Collisional parameters for such temperatures are thus
welcome.
rotational transitions in a wide range of gas temperatures up to
1000 K. Collisional parameters for such temperatures are thus
welcome.
Aims. We aim to obtain accurate rate coefficients for the collisional excitation of CH+ by He for high gas temperatures.
Methods. The ab initio coupled-cluster
Results. [CCSD(T)] approximation was used to compute the
interaction potential energy. Cross sections are then derived in the
close coupling (CC) approach and rate coefficients inferred by
averaging these cross sections over a Maxwell-Boltzmann distribution of
kinetic energies.
Conclusions. Cross sections are calculated up to
![]() for J ranging from 0 to 10. Rate coefficients are obtained at high temperatures up to
for J ranging from 0 to 10. Rate coefficients are obtained at high temperatures up to
![]() .
.
Key words: astrochemistry - molecular data - radiative transfer - ISM: molecules
1 Introduction
The molecular ion CH+ (
![]() )
is most commonly observed from the ground in the visible in absorption
lines against nearby bright stars. The lowest rotational transitions in
the submillimeter and far-infrared band are blocked from the earth's
atmosphere and therefore difficult to observe with ground-based
telescopes. A tentative detection of the
)
is most commonly observed from the ground in the visible in absorption
lines against nearby bright stars. The lowest rotational transitions in
the submillimeter and far-infrared band are blocked from the earth's
atmosphere and therefore difficult to observe with ground-based
telescopes. A tentative detection of the
![]() transition of the isotope 13CH+ has been reported recently by Falgarone et al. (2005). Cernicharo et al. (1997) reported the first emission lines of the
transition of the isotope 13CH+ has been reported recently by Falgarone et al. (2005). Cernicharo et al. (1997) reported the first emission lines of the
![]() ,
,
![]() and
and
![]() rotational transitions detected with the Infrared Space Observatory.
rotational transitions detected with the Infrared Space Observatory.
Table 1: MOLSCAT parameters used in the present calculations. Be and De are from Huber & Herzberg (1979).
Although CH+ has been observed frequently in the ISM
over the past few decades, its abundance is still an enigma. Chemical
models persistently fail to reproduce the large abundances, as it is
not yet clear, what the main source for CH+ is (Black et al. 1978; Nehmé et al. 2008; Black 1998). The highly endothermic reaction C+ + H2
![]() CH+ + H (-
CH+ + H (-
![]() K) is proposed as the most efficient route to CH+.
Besides high gas temperatures, an important part of the energy needed
to activate this reaction may come from vibrationally excited H2 (Sternberg & Dalgarno 1995). Since CH+
is also abundantly found in the cold neutral medium (CNM), this
reaction may not be fast enough though to compete with the destruction
reactions. Attempts to resolve this puzzle continue (Godard et al. 2009; Joulain et al. 1998). A thorough understanding of the CH+
abundance is important since it provides information about physical gas
properties such as temperature and fraction of ionization. Furthermore,
CH+ is a fundamental building block for more complex molecules and a relevant coolant in hot and dense interstellar gas.
K) is proposed as the most efficient route to CH+.
Besides high gas temperatures, an important part of the energy needed
to activate this reaction may come from vibrationally excited H2 (Sternberg & Dalgarno 1995). Since CH+
is also abundantly found in the cold neutral medium (CNM), this
reaction may not be fast enough though to compete with the destruction
reactions. Attempts to resolve this puzzle continue (Godard et al. 2009; Joulain et al. 1998). A thorough understanding of the CH+
abundance is important since it provides information about physical gas
properties such as temperature and fraction of ionization. Furthermore,
CH+ is a fundamental building block for more complex molecules and a relevant coolant in hot and dense interstellar gas.
Related to the problem to model observed CH+ abundances is the uncertainty in the excitation mechanism. The CH+ is likely to be destroyed rather than excited in collisions with hydrogen and electrons - the most abundant species. In addition, the excitation of CH+ is found to be sensitive to the dust continuum background of the CH+ emitting source (Black 1998). To model the CH+ abundance, the chemical reactions and radiative transfer equations may therefore need to be solved simultaneously. However, excitation calculations require accurate collisional rate coefficients.
Observations with the Herschel Space Observatory may shed some light on these problems. The high spectral resolution instrument HIFI onboard the satellite will observe the
![]() and
and
![]() rotational transitions in a wide range of interstellar gas from the
diffuse ISM to dense and hot star-forming regions. PACS, another
instrument for Herschel, will cover the CH+ transitions with
rotational transitions in a wide range of interstellar gas from the
diffuse ISM to dense and hot star-forming regions. PACS, another
instrument for Herschel, will cover the CH+ transitions with
![]() -6. Since the CH+ abundance is sensitive to far-ultraviolet (FUV) photons and X-rays (Stäuber et al. 2005; Sternberg & Dalgarno 1995; Stäuber et al. 2004),
it will be searched for in typical photo-dissociation regions (PDRs)
and X-ray dominated regions (XDRs). The gas temperature in such
areas can easily reach a few 1000 K (Tielens & Hollenbach 1985; Maloney et al. 1996).
Collisional rate coefficients are therefore needed for a large range of
gas temperatures and upper energy levels in order to interpret the
observations properly.
-6. Since the CH+ abundance is sensitive to far-ultraviolet (FUV) photons and X-rays (Stäuber et al. 2005; Sternberg & Dalgarno 1995; Stäuber et al. 2004),
it will be searched for in typical photo-dissociation regions (PDRs)
and X-ray dominated regions (XDRs). The gas temperature in such
areas can easily reach a few 1000 K (Tielens & Hollenbach 1985; Maloney et al. 1996).
Collisional rate coefficients are therefore needed for a large range of
gas temperatures and upper energy levels in order to interpret the
observations properly.
The aim of this paper is to obtain accurate rate coefficients for the collisional excitation of CH+ at high temperatures. As it is far more difficult to determine rate coefficients for excitation with H2, we focus on the rotational excitation by He, another major gas component. This study is thus an extension of an earlier published paper, where coefficients for temperatures up to 200 K were presented (Hammami et al. 2008).
2 Potential energy surface
Recently, we have computed the interaction PES for the
![]() van der Waals system using the rigid rotor approximation and the Jacobi coordinate system in which r is the
van der Waals system using the rigid rotor approximation and the Jacobi coordinate system in which r is the
![]() internuclear distance, R the distance from the center of mass (c.m.) of
internuclear distance, R the distance from the center of mass (c.m.) of
![]() to the
to the ![]() atom, and
atom, and ![]() the angle between the two distance vectors (Hammami et al. 2008). The collinear
the angle between the two distance vectors (Hammami et al. 2008). The collinear
![]() geometry corresponds to
geometry corresponds to
![]() while the CH+ bond distance was frozen at its value at the experimental equilibrium geometry of the ground
while the CH+ bond distance was frozen at its value at the experimental equilibrium geometry of the ground
![]() state, i.e.,
state, i.e.,
![]() Bohr (Huber & Herzberg 1979). Computations were carried out at the CCSD(T) level as it is implemented by Knowles et al. (1993,2000) in the MOLPRO molecular package (Werner et al. 2002). All our calculations were performed with the augmented correlation consistent valence quadruple zeta (aVQZ) basis set of Woon & Dunning (1994) for all atoms. The (
Bohr (Huber & Herzberg 1979). Computations were carried out at the CCSD(T) level as it is implemented by Knowles et al. (1993,2000) in the MOLPRO molecular package (Werner et al. 2002). All our calculations were performed with the augmented correlation consistent valence quadruple zeta (aVQZ) basis set of Woon & Dunning (1994) for all atoms. The (
![]() )
set of bond functions defined by Tao & Pan (1992) are added and placed at mid-distance between the c.m. of
)
set of bond functions defined by Tao & Pan (1992) are added and placed at mid-distance between the c.m. of
![]() and
and ![]() .
.
The basis set superposition errors (BSSE) was corrected at all geometries following the Boys & Bernardi (1970) counterpoise procedure. Our PES has a global minimum of 537 cm-1 at R=4.05 Bohr and
![]() .
This value is consistent with that obtained by Stoecklin & Voronin (2008) with the BCCD(T) method and a aug-cc-pVQZ basis set, i.e., 513 cm-1 at R=4.1 Bohr and
.
This value is consistent with that obtained by Stoecklin & Voronin (2008) with the BCCD(T) method and a aug-cc-pVQZ basis set, i.e., 513 cm-1 at R=4.1 Bohr and
![]() .
Indeed, our well depth is lower than their value.
.
Indeed, our well depth is lower than their value.
To perform the dynamical calculations, the basic inputs required by the MOLSCAT package (Hutson & Green 1994) were obtained by expanding the interaction potential in terms of Legendre polynomials as
The calculated surface is well reproduced by the analytical potential over the entire grid of used coordinate points. The standard deviation between the analytical and the calculated surface remains below 1.0%. Further details concerning calculations related to the interaction potential can be found in the paper by Hammami et al. (2008).
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{12663f01.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12663-09/Timg24.png)
|
Figure 1:
Deexcitation cross sections of
|
| Open with DEXTER | |
Table 2: Downward rate coefficients of rotational levels of CH+ in collision with He as a function of kinetic temperature (in units of cm3 s-1).
3 Cross sections
The quantum mechanical close coupling approach (Arthurs & Dalgarno 1960) implemented in the MOLSCAT code was used to calculate state to state rotational integral cross sections for values of J ranging from 0 to 10, and a total energy up to
![]() .
The energy range was carefully spanned in order to account for
resonances. The incremental steps were chosen as follows: From 0 to
.
The energy range was carefully spanned in order to account for
resonances. The incremental steps were chosen as follows: From 0 to
![]() ,
they were set to
,
they were set to
![]() ,
from
,
from
![]() to
to
![]() to
to
![]() ,
from
,
from
![]() to
to
![]() to
to
![]() ,
from
,
from
![]() to
to
![]() to
to
![]() ,
from
,
from
![]() to
to
![]() to
to
![]() ,
from
,
from
![]() to
to
![]() to
to
![]() ,
from
,
from
![]() to
to
![]() to
to
![]() ,
from
,
from
![]() to
to
![]() to
to
![]() ,
from
,
from
![]() to
to
![]() to
to
![]() ,
from
,
from
![]() to
to
![]() to
to
![]() ,
and finally
from
,
and finally
from
![]() to
to
![]() to
to
![]() .
To include all open channels and some closed channels, we have set
.
To include all open channels and some closed channels, we have set
![]() for
for
![]() ,
and
,
and
![]() for
for
![]() .
This corresponds to a rotational basis set of adequate size for a good
accuracy in the calculated cross sections. The input parameters
required by MOLSCAT are displayed in Table 1. These parameters were fixed after we have performed some tests to ensure the convergence of cross sections for energies up to
.
This corresponds to a rotational basis set of adequate size for a good
accuracy in the calculated cross sections. The input parameters
required by MOLSCAT are displayed in Table 1. These parameters were fixed after we have performed some tests to ensure the convergence of cross sections for energies up to
![]() .
The coupled equations were conveniently solved using the propagator of Manolopoulos (1986).
.
The coupled equations were conveniently solved using the propagator of Manolopoulos (1986).
Figure 1 presents the energy variation of the
![]() collisional deexcitation cross sections for the transitions
collisional deexcitation cross sections for the transitions
![]() ,
for J=1-5 and the transition
,
for J=1-5 and the transition
![]() .
Up to almost
.
Up to almost
![]() ,
resonances can be seen in the cross sections. These are due to the global minimum located at
,
resonances can be seen in the cross sections. These are due to the global minimum located at
![]() and whose well depth is
and whose well depth is ![]()
![]() .
As one can also see from the figure, the cross sections for the transition
.
As one can also see from the figure, the cross sections for the transition
![]() are larger than those with
are larger than those with
![]() almost over the entire range of energies. Some exceptions occur with the transition
almost over the entire range of energies. Some exceptions occur with the transition
![]() for which cross sections are slightly larger around 5 cm-1 and for
for which cross sections are slightly larger around 5 cm-1 and for
![]() cm-1. It is also obvious from the figure that the cross sections for the transition
cm-1. It is also obvious from the figure that the cross sections for the transition
![]() are larger than those of the other transitions plotted but remain of similar magnitude as those of the transition
are larger than those of the other transitions plotted but remain of similar magnitude as those of the transition
![]() with increasing energy. Turning our attention to Fig. 2,
it can be seen that our total cross sections are consistent both in
shape and magnitude with the quenching cross sections calculated by Stoecklin & Voronin (2008) for energies lower than 1000 cm-1.
with increasing energy. Turning our attention to Fig. 2,
it can be seen that our total cross sections are consistent both in
shape and magnitude with the quenching cross sections calculated by Stoecklin & Voronin (2008) for energies lower than 1000 cm-1.
An analysis of the excitation cross sections has been carried out by Hammami et al. (2008). It was pointed out in that for energies lower than 600 cm-1, the cross sections for the transition
![]() are larger than those for
are larger than those for
![]() while for energies greater than that, the converse holds. Similar observations were also made for the transition
while for energies greater than that, the converse holds. Similar observations were also made for the transition
![]() and
and
![]() for an energy of
for an energy of ![]()
![]() .
Indeed, for energies greater than that value, the transition
.
Indeed, for energies greater than that value, the transition
![]() is less favored (see also Hammami et al. 2008). It should be noticed that there is a propensity towards
is less favored (see also Hammami et al. 2008). It should be noticed that there is a propensity towards ![]() even parity transitions for almost the entire range of energy.
even parity transitions for almost the entire range of energy.
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{12663f02.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12663-09/Timg61.png)
|
Figure 2:
Rotational quenching cross sections of
|
| Open with DEXTER | |
4 Collisional rates
Downward rate coefficients are obtained by averaging the cross sections
![]() over a Maxwell-Boltzmann distribution of kinetic energies,
over a Maxwell-Boltzmann distribution of kinetic energies,
where T is the kinetic temperature,
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12663f03.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12663-09/Timg69.png)
|
Figure 3: Calculated downward rate coefficients for selected transitions as a function of the kinetic temperature. |
| Open with DEXTER | |
5 Summary
Using a previously computed PES (Hammami et al. 2008),
we have obtained results of a quantum mechanical close coupling
calculation of integral cross sections for transitions between the
lower rotational levels of
![]() induced by collisions with
induced by collisions with ![]() .
The cross sections were averaged over a Maxwell-Boltzmann distribution
of kinetic energies to determine downward rate coefficients. The
kinetic temperature spans a wide range of values up to
.
The cross sections were averaged over a Maxwell-Boltzmann distribution
of kinetic energies to determine downward rate coefficients. The
kinetic temperature spans a wide range of values up to
![]() .
The spectroscopic parameters obtained at high temperature exhibit the
general trends for such quantities. The rate
coefficients will help to understand and interpret
astrophysicalobservations in connection with the Herschel Space
Observatory mission.
.
The spectroscopic parameters obtained at high temperature exhibit the
general trends for such quantities. The rate
coefficients will help to understand and interpret
astrophysicalobservations in connection with the Herschel Space
Observatory mission.
Author L.C.O.O. acknowledges with thanks the financial support of the Abdus Salam International Centre for Theoretical Physics, Office of External Activities (ICTP-OEA ) under NET45 Programme.
References
- Arthurs, A. M., & Dalgarno, A. 1960, Royal Soc. London Proc. Ser. A, 256, 540 [CrossRef] [NASA ADS]
- Black, J. H. 1998, in Chemistry and Physics of Molecules and Grains in Space. Faraday Discussions No. 109, 257
- Black, J. H., Hartquist, T. W., & Dalgarno, A. 1978, ApJ, 224, 448 [CrossRef] [NASA ADS]
- Boys, S. F., & Bernardi, F. 1970, Mol. Phys., 19, 553 [CrossRef] [NASA ADS]
- Cernicharo, J., Liu, X.-W., Gonzalez-Alfonso, E., et al. 1997, ApJ, 483, L65 [CrossRef] [NASA ADS]
- Falgarone, E., Phillips, T. G., & Pearson, J. C. 2005, ApJ, 634, L149 [CrossRef] [NASA ADS]
- Godard, B., Falgarone, E., & Pineau Des Forêts, G. 2009, A&A, 495, 847 [EDP Sciences] [CrossRef] [NASA ADS]
- Hammami, K., Owono Owono, L. C., Jaidane, N., et al. 2008, Journal of Molecular Structure: THEOCHEM, 853, 18 [CrossRef]
- Huber, K. P., & Herzberg, G. 1979, Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules (New York: Van Nostrand)
- Hutson, J. M., & Green, S. 1994, MOLSCAT computer code, version 14, Collaborative Computational Project No. 6 of the Science and Engineering Research Council, UK
- Joulain, K., Falgarone, E., Des Forets, G. P., et al. 1998, A&A, 340, 241 [NASA ADS]
- Knowles, P. J., Hampel, C., & Werner, H.-J. 1993, J. Chem. Phys., 99, 5219 [CrossRef] [NASA ADS]
- Knowles, P. J., Hampel, C., & Werner, H.-J. 2000, J. Chem. Phys., 112, 3106 [CrossRef] [NASA ADS]
- Maloney, P. R., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 466, 561 [CrossRef] [NASA ADS]
- Manolopoulos, D. E. 1986, J. Chem. Phys., 85, 6425 [CrossRef] [NASA ADS]
- Nehmé, C., Le Bourlot, J., Boulanger, F., Pineau Des Forêts, G., & Gry, C. 2008, A&A, 483, 485 [EDP Sciences] [CrossRef] [NASA ADS]
- Stäuber, P., Doty, S. D., van Dishoeck, E. F., Jørgensen, J. K., & Benz, A. O. 2004, A&A, 425, 577 [EDP Sciences] [CrossRef] [NASA ADS]
- Stäuber, P., Doty, S. D., van Dishoeck, E. F., et al. 2005, A&A, 440, 949 [EDP Sciences] [CrossRef] [NASA ADS]
- Sternberg, A., & Dalgarno, A. 1995, ApJS, 99, 565 [CrossRef] [NASA ADS]
- Stoecklin, T., & Voronin, A. 2008, Eur. Phys. J. D, 46, 259 [EDP Sciences] [CrossRef] [NASA ADS]
- Tao, F.-M., & Pan, Y.-K. 1992, J. Chem. Phys., 97, 4989 [CrossRef] [NASA ADS]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [CrossRef] [NASA ADS]
- Werner, H.-J., Knowles, P. J., & Almöf, J., et al. 2002, MOLPRO, a package of ab initio programs, University College Cardiff Consultants Limited, see http://www.molpro.net
- Woon, D. E., & Dunning, Jr., T. H. 1994, J. Chem. Phys., 100, 2975 [CrossRef] [NASA ADS]
All Tables
Table 1: MOLSCAT parameters used in the present calculations. Be and De are from Huber & Herzberg (1979).
Table 2: Downward rate coefficients of rotational levels of CH+ in collision with He as a function of kinetic temperature (in units of cm3 s-1).
All Figures
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{12663f01.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12663-09/Timg24.png)
|
Figure 1:
Deexcitation cross sections of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{12663f02.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12663-09/Timg61.png)
|
Figure 2:
Rotational quenching cross sections of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12663f03.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12663-09/Timg69.png)
|
Figure 3: Calculated downward rate coefficients for selected transitions as a function of the kinetic temperature. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.