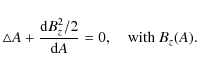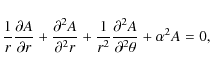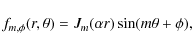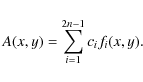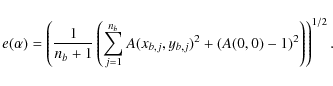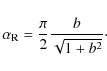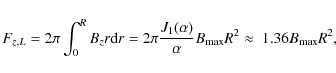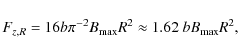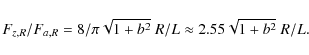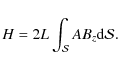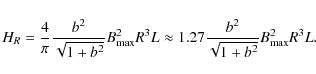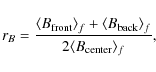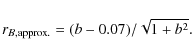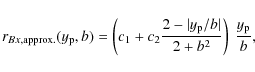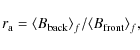Magnetic cloud models with bent and oblate cross-section boundaries

P. Démoulin; S. Dasso

doi:10.1051/0004-6361/200912645

Free Access

Issue		A&A Volume 507, Number 2, November IV 2009


Page(s)		969 - 980
Section		The Sun
DOI		https://doi.org/10.1051/0004-6361/200912645
Published online		15 September 2009

A&A 507, 969-980 (2009)

Magnetic cloud models with bent and oblate cross-section boundaries

P. Démoulin¹ - S. Dasso^2,3

1 - Observatoire de Paris, LESIA, UMR 8109 (CNRS), 92195 Meudon Principal Cedex, France
2 - Instituto de Astronomía y Física del Espacio, CONICET-UBA, CC. 67, Suc. 28, 1428 Buenos Aires, Argentina
3 - Departamento de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, 1428 Buenos Aires, Argentina

Received 5 June 2009 / Accepted 13 August 2009

Abstract
Context. Magnetic clouds (MCs) are formed by magnetic flux ropes that are ejected from the Sun as coronal mass ejections. These structures generally have low plasma beta and travel through the interplanetary medium interacting with the surrounding solar wind. Thus, the dynamical evolution of the internal magnetic structure of a MC is a consequence of both the conditions of its environment and of its own dynamical laws, which are mainly dominated by magnetic forces.
Aims. With in-situ observations the magnetic field is only measured along the trajectory of the spacecraft across the MC. Therefore, a magnetic model is needed to reconstruct the magnetic configuration of the encountered MC. The main aim of the present work is to extend the widely used cylindrical model to arbitrary cross-section shapes.
Methods. The flux rope boundary is parametrized to account for a broad range of shapes. Then, the internal structure of the flux rope is computed by expressing the magnetic field as a series of modes of a linear force-free field.
Results. We analyze the magnetic field profile along straight cuts through the flux rope, in order to simulate the spacecraft crossing through a MC. We find that the magnetic field orientation is only weakly affected by the shape of the MC boundary. Therefore, the MC axis can approximately be found by the typical methods previously used (e.g., minimum variance). The boundary shape affects the magnetic field strength most. The measurement of how much the field strength peaks along the crossing provides an estimation of the aspect ratio of the flux-rope cross-section. The asymmetry of the field strength between the front and the back of the MC, after correcting for the time evolution (i.e., its aging during the observation of the MC), provides an estimation of the cross-section global bending. A flat or/and bent cross-section requires a large anisotropy of the total pressure imposed at the MC boundary by the surrounding medium.
Conclusions. The new theoretical model developed here relaxes the cylindrical symmetry hypothesis. It is designed to estimate the cross-section shape of the flux rope using the in-situ data of one spacecraft. This allows a more accurate determination of the global quantities, such as magnetic fluxes and helicity. These quantities are especially important for both linking an observed MC to its solar source and for understanding the corresponding evolution.

Key words: Sun: coronal mass ejections (CMEs) - Sun: magnetic fields - interplanetary medium

1 Introduction

Magnetic clouds (MCs) are magnetized plasma structures ejected from the Sun as coronal mass ejections. They are characterized by a strongly enhanced magnetic field strength with respect to typical solar wind (SW) values, a smooth and large coherent rotation of the magnetic field vector, and a low proton temperature (e.g., Burlaga et al. 1981; Klein & Burlaga 1982). Moreover, after decades of researches, there is presently a consensus that MCs are formed by twisted magnetic flux tubes, called flux ropes (e.g., Burlaga 1995).

The in situ measurements are limited to the spacecraft trajectory crossing the arriving MC. Therefore, one needs to rely on modeling to derive the global magnetic structure from the local measurements. The determination of the proper magnetic configuration for MCs is important in order to provide good estimations of the global magneto-hydrodynamic (MHD) invariants contained in these structures, such as magnetic helicity or fluxes (see, e.g., Démoulin 2008, and references therein).

A key property of MCs is the small plasma $\beta$ , while the plasma velocity in the frame moving with the MC is typically well below the Alfvén velocity, therefore the magnetic configuration of MCs is force-free to a first approximation. The magnetic field in MCs can be relatively well modeled by a linear force-free field (Burlaga 1988). The simplest solution is obtained with a cylindrical boundary; this is the so-called Lundquist model (Lundquist 1950). It was, and is still, widely used to fit the magnetic field observed in MCs and to derive global quantities such as the magnetic flux and helicity (e.g., Burlaga 1988; Lepping et al. 1990; Dasso et al. 2003; Lynch et al. 2003; Dasso et al. 2005b; Mandrini et al. 2005; Dasso et al. 2006; Leitner et al. 2007). An extension of this model to an elliptical boundary was realized by Vandas & Romashets (2003). They derived analytical solutions for any value of the aspect ratio (ratio of the ellipse sizes).

Alternatively, non-linear force-free field models with a circular cross-section (Gold & Hoyle 1960) have been used to model the magnetic configuration of interplanetary flux ropes (e.g., Farrugia et al. 1999; Dasso et al. 2005b). The effect of plasma pressure has been considered for both circular and elliptical cross-sections (Hidalgo 2003; Mulligan et al. 1999; Cid et al. 2002). These models include a relatively large number of free coefficients which are determined by a least square fit to the in situ data.

The magnetic structure of MCs has also been analyzed by solving the equations as a Cauchy problem (e.g., Hu et al. 2005; Hu & Sonnerup 2002). It was found that the amount of distortion from a circular cross-section is variable in the MCs analyzed. The limitation of such an approach is that a Cauchy problem is ill-posed, so that the result of the integration is very sensitive to modifications of the boundary conditions. It implies that the results can be significantly affected by the temporal resolution, by the range of the data used, as well as by the method used to stabilize the integration (e.g. by a smoothing procedure). The method was recently tested successfully with MCs crossed by two spacecraft (Liu et al. 2008; Möstl et al. 2009).

Many of the above models/techniques have been compared by applying them to a flux rope obtained from an MHD simulation. Significant differences have been found for cases corresponding to large distances between the spacecraft path and the MC axis (Riley et al. 2004).

For many of the above methods which use analytical models, the free parameters of a given model are determined by minimizing a function which defines the difference of the model to the data. On one hand, the selected model should have enough freedom to provide a fit close enough to the data for a broad range of MCs. On the other hand, it should not have too many free parameters, since finding the absolute minimum of the difference function becomes rapidly a very time consuming task once the parameter space has a larger number of dimensions. Moreover, the probability of finding a local minimum associated with a wrong solution increases with the number of free parameters. Therefore, the wide use and the success of the Lundquist solution is a consequence of both its low number of free parameters and of the inclusion of the basic physics (flux rope).

Previous studies have shown that the core of MCs ( $\sim$ $30\%$ of their size) is generally more symmetric than the remaining part (Dasso et al. 2005a). Moreover, using combined observations of several spacecraft, some recent analyses have shown that the core of the MCs is significantly more circular than their oblate outer part (Liu et al. 2008; Möstl et al. 2009; Kilpua et al. 2009). Still, the Lundquist solution is known to have difficulties in fitting the magnetic field strength, in particular it was found that it frequently overestimates the axial component of the field near the flux-rope axis (e.g., Gulisano et al. 2005). The elliptical model of Vandas & Romashets (2003) provides a better fit to observed MCs having a field strength more uniform than in the Lundquist solution. This indicates the existence of some flat flux ropes (Vandas et al. 2005).

In some MHD simulations, the flux rope is strongly compressed in the propagation direction, such that it becomes relatively flat (e.g., Vandas et al. 2002), and it can even develop a bending of the lateral sides towards the front direction as it moves away from the Sun (e.g., Riley et al. 2003; Manchester et al. 2004). Owens et al. (2006) proposed a kinematic model of this evolution with an initial Lundquist solution passively deformed by a given velocity flow. However, inside MCs the magnetic pressure dominates both the plasma and the ram internal pressure (both a low plasma $\beta$ and, in the frame moving with the MC, a plasma velocity lower than the Alfvén velocity are typically found in MCs). With such dominance, the magnetic force is rather expected to react strongly to the SW deformation. Let us suppose that the SW is able to deform the exterior of the flux rope (e.g. with an asymmetric ram pressure), how then does the force free field inside the flux rope react? Is the magnetic field strength and orientation significantly affected? How strong should the variation of the total pressure around the flux rope be to flatten/bend the flux rope cross-section? Are the effects of a flat and/or bended flux rope easily detected from the magnetic field present along a linear cut of the flux rope (as observed by spacecraft)? In order to answer these questions, we develop a technique that can solve the internal equilibrium for various boundary shapes.

The paper is organized as follow. In Sect. 2 we define the internal and the boundary equations for a force-free flux rope. Next, we present the numerical method used to solve this problem. In Sect. 3 we analyze the magnetic field of flux ropes with various cross-section shapes. In particular, we derive the magnetic pressure along the flux rope boundary, as well as the total magnetic flux and helicity. In Sect. 4 we investigate the information contained in the magnetic field profile taken along a linear cut through the flux rope, as obtained from spacecraft observations. The aim is to identify the most appropriate functions of the observed field to estimate each parameter of the model. We summarize our results and conclude in Sect. 5.

2 Method

In this section we present the equations of the flux-rope model, as well as the numerical method used to solve them.

2.1 Force-free field evolution

In the frame moving with the mean MC speed, the plasma velocity is typically smaller than the Alfvén velocity (a few 100 km s^-1, Burlaga & Behannon 1982). Moreover, the plasma $\beta$ is low in MCs (typically $\beta \approx 0.1$ , with values ranging from less than $\approx$ 10^-2 to a few times 0.1, e.g., Wu & Lepping 2007; Feng et al. 2007; Lepping et al. 2003, and references therein). Other forces such as gravity are also negligible with respect to the magnetic pressure gradient, therefore the magnetic field evolution can be described, to first a approximation, by a sequence of force-free equilibria ( $\vec{j} \times \vec{B} \approx {0}$ ), e.g., as proposed by Démoulin & Dasso (2009).

An MC typically has an elongated flux rope structure with a cross-section size much smaller than the curvature radius of its axis, so locally the flux rope is approximately straight. We also assume that the magnetic field can be regarded as locally invariant along the flux rope axis. We use below an orthogonal frame, called the MC frame, with coordinates (x,y,z). z is along the local MC axis, x is in the direction of the mean MC velocity projected orthogonally to the MC axis, and the y direction completes the right-handed orthogonal frame. The equation ${\bf\nabla } \cdot \vec{B}=0$ and the invariance of $\vec{B}$ in z implies that one can write the field components as: $B_x = \partial A/ \partial y$ and $B_y = -\partial A/ \partial x$ , where A(x,y) is the magnetic-flux function. The projection of field lines in a plane orthogonal to the z axis is given by isocontours of A(x,y). The force-free condition implies

$\begin{displaymath} \triangle A + \frac{ {\rm d} B_z^{2}/2}{ {\rm d} A} = 0 {\rm , ~~~~with~} B_z(A) . \end{displaymath}$

(1)

For an elliptical partial differential equation, such as Eq. (1), a boundary condition is generally required all around the region where the solution is searched for (otherwise the problem is ill posed, and, in particular, the solution is typically very sensitive to small modifications of the selected boundary values). The boundary of the flux rope is defined by the set of field lines having a given value of A(x,y). Without loss of generality, the origin of A can be set at the boundary, therefore

A(x_b,y_b)=0 ,

(2)

where x_b,y_b are the coordinates of the boundary (they are more precisely defined in Sect. 2.2). The maximal value of A(x,y) within the flux rope defines both the maximum amount of azimuthal magnetic flux and the position (x,y) of the flux rope center. Below we simply set this maximum as

A(0,0)=1 ,

(3)

since the azimuthal flux is later re-normalized to any desired value. Equations ((1), (2), (3)) have a non-singular solution for A(x,y) only for some B_z(A) functions (for example for a discrete series of B_z(A=1) values). This series of solutions are called resonant solutions (e.g. Morse & Feshbach 1953). This point is further explained in Sect. 2.4.

2.2 Boundary

The flux-rope boundary can be generically defined by a closed parametric curve $\vec{r}_b= (x_b(s),y_b(s))$ , where s is the variable defining the position along the curve. The shape of the boundary influences the shape of the field lines within the flux rope. However, with an elliptic problem, such as given by Eq. (1), the small scale deformations of the boundary are rapidly damped inside the volume (see end of Sect. 3.2). Conversely, knowing A(x,y) in the deep interior of the flux rope, or on a cut through it (such as with spacecraft observations) does not provide reliable information on the spatial fluctuations of the boundary.

We define a boundary shape that includes the main distortions found in some MHD simulations (Sect. 1). In view of previous works, an elliptical shape is a natural starting point. A great variety of boundaries can be defined from the deformation of an ellipse, but small-scale variations have only a local influence on the force-free field, so we explore only large-scale deformations. To minimize the number of free parameters, we restrict our analysis to boundaries symmetric in the y direction (orthogonal to the mean MC velocity). With these constraints, we derive the following parametrization

x_b	=	$\displaystyle -\cos (\pi s) + a \sin^2(\pi s) ,$
y_b	=	$\displaystyle b \sin (\pi s) ,$	(4)

where s ranges from s=0 at the front to s=1 at the back, and to s=2 to close the boundary at the front. The central size of this boundary in the x direction (at y=0) is normalized to 2, so that $x_{\rm front}=-1$ and $x_{\rm back}=1$ . The maximal extension in the y direction is at $(x,y)=(a,\pm b)$ , with ${\rm d} y/ {\rm d} x =0$ at those points. The aspect ratio of the flux-rope sizes along the y and x (at y=0) directions is simply b. As |a| increases from zero, the boundary becomes bent in the x direction (see Figs. 3-5). The bending is increasing with |y|. Since the front and back boundaries are shifted by the same x amount for a given y value, the area of the cross-section is preserved.

A wider variety of boundaries can be analyzed with the method described below. However, Eq. (4) already provides a broad range of boundaries (see Figs. 3-5) with only two free parameters (a,b).

2.3 Linear force-free field

The Lundquist solution was, and still is, widely used for estimating the magnetic configuration of MCs crossed by a spacecraft (Sect. 1). We continue in the same line, by supposing a linear force-free magnetic field, i.e. with B_z(A) being a linear function of A. The axial component, B_z, is typically low at the boundary of MCs, so we restrict B_z(A) to an affine function of A. Therefore, Eq. (1) is simplified to

	$\displaystyle B_z(A) = \alpha A ,$	(5)
	$\displaystyle \triangle A + \alpha^2 A = 0 .$	(6)

Equation (6) is linear in A, therefore we can express A as a linear combination of solutions. Since the Lundquist solution is worked out in cylindrical coordinates, and since MCs are expected to be not too far from being cylindrical (as a consequence of magnetic tension), a set of functions can be searched for in cylindrical coordinates. Then Eq. (6) is rewritten as

$\begin{displaymath} \frac{1}{r} \frac{\partial A}{\partial r} + \frac{\partial^... ...2} \frac{\partial^2 A}{\partial^2 \theta } + \alpha^2 A = 0 , \end{displaymath}$

(7)

where $r,\theta$ are the classical cylindrical coordinates (radius and azimuth angle). We look for separable solutions in $r,\theta$ , i.e. of the form $A(r,\theta)=f(r) g(\theta)$ . A Fourier decomposition of A in the $\theta$ direction, together with the continuity of A, implies that $g(\theta)$ can be decomposed in a series of $\sin (m \theta + \phi)$ functions, where m is an integer and $\phi$ is real number. The remaining equation for f(r) can be reduced to the Bessel differential equation of order m (e.g., Botha & Evangelidis 2004). Therefore, any non-singular $A(r,\theta)$ can be expressed as a linear combination of an infinite number of functions (e.g. Vladimirov 1984)

$\begin{displaymath} f_{m,\phi}(r,\theta) = J_m(\alpha r) \sin (m \theta + \phi) , \end{displaymath}$

(8)

where J_m is the ordinary Bessel function of order m. Romashets & Vandas (2005) derived the magnetic components from a series of such functions, and determined the free coefficients by a fit to the magnetic data of some MCs (without imposing any boundary shape, different to the present study).

In practice, $A(r,\theta)$ is approximated by a finite series of $f_{m,\phi}$ . This series satisfies Eq. (6) exactly, but in most cases, it satisfies only approximately the selected boundary condition (Eq. (4)). The precision depends on both the number of functions kept in the series and on the shape of the boundary. Except for m=0 (which recovers the Lundquist solution), the $f_{m,\phi}(r,\theta)=0$ isocontour has a variety of non-circular shapes. So a combination of several m modes can approximate a wide variety of boundary shapes. Still, these modes have comparable sizes in the x,y directions, so this series of functions is not suited to approximate flat magnetic configurations. The numerical results obtained with the set of functions defined by Eq. (8) confirm this. Moreover, some MCs have a magnetic field norm which is nearly uniform in their cross-section (e.g., Vandas et al. 2005). This indicates an approximate magnetic-pressure balance, therefore a low magnetic tension, so a flat magnetic configuration.

Another set of functions satisfying Eq. (6) can be derived in Cartesian coordinates. We limit ourselves to functions even in y since we are analyzing symmetric configurations (Sect. 2.2). The basic functions are

$\displaystyle f_{c,\Phi}(x,y)$	=	$\displaystyle \cos(\alpha x \cos \Phi ) \cos(\alpha y \sin \Phi ) ,$
$\displaystyle f_{s,\Phi}(x,y)$	=	$\displaystyle \sin(\alpha x \cos \Phi ) \cos(\alpha y \sin \Phi ) ,$	(9)

where $\Phi$ is any real number in the interval $[0,\pi /2]$ (values beyond this interval only provide redundancy). Such a set of functions is, a priori, not well adapted to approximate the solution for a cylindrical boundary, since each of them has a rectangular shape for A(x,y)=0. However, we found that a set of such functions gives a good approximation to the Lundquist solution (see below). Moreover, they have the advantage of being able to approximate very flat configurations since the spatial wave vector in x and y directions can be very different (the ratio of the wave vectors is $\tan \Phi$ ).

2.4 Numerical solution with a linear force-free field

In practice, $\Phi$ in Eq. (9) is discretized, with an equi-partition of n values in $[0,\pi /2]$ since we do not privilege any direction. The case $\Phi=\pi /2$ gives $f_{s,\pi /2}(x,y)=0$ , so that the number of functions retained in the series is 2n-1. These functions are

f_i(x,y)	=	$\displaystyle \cos(\alpha x \cos \Phi_i ) \cos(\alpha y \sin \Phi_i ) ~~~ {\rm for~} i {\rm ~in~} [1,n]$
		$\displaystyle ~~{\rm with~} \Phi_i= \pi/2 ~(i-1)/(n-1) ,$
f_i(x,y)	=	$\displaystyle \sin(\alpha x \cos \Phi_i ) \cos(\alpha y \sin \Phi_i ) ~~~ {\rm for~} i {\rm ~in~} [n+1,2n-1]$
		$\displaystyle ~~{\rm with~} \Phi_i= \pi/2 ~(i-n-1)/(n-1) .$	(10)

Therefore, A(x,y) is written as the series

$\begin{displaymath} A(x,y) = \sum_{i=1}^{2n-1} c_i f_{i}(x,y) . \end{displaymath}$

(11)

The coefficients c_i are found so that A(x,y) best satisfy both the boundary condition of Eq. (2) and the normalization of Eq. (3).

Equations ((2), (3), (6)) define an eigenvalue problem that has a non singular solution inside the boundary only for a discrete series of $\alpha$ eigenvalues (e.g. Moon & Spencer 1988; Morse & Feshbach 1953). With A(x,y) described by 2n-1 functions (Eq. (11)), we should set A(x_b,j,y_b,j)=0 at 2n-1 boundary positions. Therefore, the $\alpha$ values can be obtained by finding the zeros of $\det (f_{i}(x_{b,j},y_{b,j}))$ with i, j within [1,2n-1] (e.g. Trott 2006; Morse & Feshbach 1953, Chap. 3.5). For the application to MCs, we are interested in the smallest $\alpha$ eigenvalues, since for larger eigenvalues A(x,y) and the magnetic field components also vanish inside the boundary, and this case is not observed in MCs. We find that this method works well for small values of n. However, as n increases, the determinant computation involves the sum/subtraction of a large number of terms, each being the product of 2n-1 functions ( f_i(x_b,j,y_b,j)). This implies that the determinant has huge variations with $\alpha$ . In particular, the determinant is very small when computed below the first eigenvalue, while it reaches large values just above. The range of variation can reach more than ten orders of magnitude. This huge range does not facilitate the precise localization of the first zero of the determinant, thus the determination of the first eigenvalue. We conclude that this approach is effective only for small values of n.

Another approach is to perform a least square fit of Eq. (11) to both n_b boundary points and to the normalization condition A(0,0)=1 (e.g. Trott 2006, Chap. 1.2). With this method $n_b\geq 2 n-2$ . The condition A(0,0)=1 is only approximately satisfied, but this can be corrected afterwards by multiplying A(x,y) by a constant factor. More importantly, the condition A(x_b,j,y_b,j)=0 is only approximately satisfied at the n_b boundary points. We defined the mean error as

$\begin{displaymath} e(\alpha) = \left( \frac{1}{n_b+1} \left( \sum_{j=1}^{n_b} A(x_{b,j},y_{b,j})^2 + (A(0,0)-1)^2 \right)\right)^{1/2} . \end{displaymath}$

(12)

The advantage of this approach is that $e(\alpha)$ has a restricted range of variations, with comparable values of the local maxima, while the minima are well marked. This implies that the eigenvalues are well defined (Fig. 1). This regular behavior is present for a wider range of n values than with the determinant method described above. This implies that we can investigate cases with a larger set of functions, and therefore with a broader range of boundary shapes. Still, the method is numerically limited to values of n typically below 15. For larger n, $e(\alpha)$ has rapid fluctuations due to the finite numerical precision in summing a large series (Eq. (11)). Here, the computations were done with decimal numbers having 16 digits of precision. The fluctuations of $e(\alpha)$ can be weakened by increasing the number of boundary points, n_b, but this is not efficient. Within these limitations, the least-square fitting method is precise enough to derive the solution of Eqs. ((2), (3), (6)) with an aspect ratio of the cross-section in the range 0.1 to 10 (Fig. 2).

A given non-zero value of a has a very different implication for small and large b: with a larger b, a larger a value is needed to distort the flux rope significantly (see Figs. 3-5). We choose to scale a with $\sqrt{b}$ in Figs. 2, 8-11, as the precision of the method decreases significantly for $\vert a\vert\geq 1.5 \sqrt{b}$ (Fig. 2).

$\begin{figure} \includegraphics[width=9cm, clip=]{12645f1.eps}\end{figure}$	Figure 1: Evolution of the mean error, Eq. (12), as a function of $\alpha$ for the least square fit of Eq. (11) to the boundary condition of Eq. (2) and the normalization of Eq. (3). The boundary is defined by Eq. (4) with a=0, and b=1 (continuous line) or b=2 (dashed line). The eigenvalues of $\alpha$ are found at the local minima of the mean error.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm]{12645f2.eps} \end{figure}$	Figure 2: Log-log plot of the smallest $\alpha$ -eigenvalue and the associated mean error, Eq. (12), as a function of the y-extension of the flux rope (parameter b). The three thicker curves are the numerical results for the boundary given by Eq. (4) and with a given in the inset. In a), the thin continuous line is the smallest eigenvalue of $\alpha$ for a rectangular boundary (Eq. (15)).
Open with DEXTER

$\begin{figure} \par\mbox{\includegraphics[width=4.4cm, clip=]{12645f3a.eps} , \includegraphics[width=4.4cm, clip=]{12645f3b.eps} } \par \end{figure}$

Figure 3:

Projected field lines orthogonal to the flux rope axis (isocontours of A, left panels) and isocontours of the magnetic field norm B ( right panels) for the first eigen solution (lowest $\alpha$ -eigenvalue, Fig. 2a) for an aspect ratio b=0.5. Both A and B are independently normalized to a maximal value of 1, and decrease monotonously from the flux rope center towards its boundary. The isocontours are equi-spaced between 0.1 to 0.9 in steps of 0.1. The isocontour 0.5 and the boundary are outlined with a thicker line. The top row is for a rectangular boundary and the second row for an elliptic boundary. The three bottom rows have boundaries defined by Eq. (4).

Open with DEXTER

$\begin{figure} \par {\includegraphics[width=4.4cm, clip=]{12645f4a.eps} , \includegraphics[width=4.4cm, clip=]{12645f4b.eps} } \par \end{figure}$	Figure 4: Projected field lines (isocontours of A, left panels) and isocontours of the magnetic field norm B ( right panels). The boundaries are defined by Eq. (4) with an aspect ratio b=1. The drawing convention is the same as in Fig. 3.
Open with DEXTER

$\begin{figure} \includegraphics[width=8.8cm, clip=]{12645f5.eps} \end{figure}$	Figure 5: Projected field lines (isocontours of A, top panels) and isocontours of the magnetic field norm B ( bottom panels). The boundaries are defined by Eq. (4) with an aspect ratio b=3. The drawing convention is the same as in Fig. 3.
Open with DEXTER

3 Flux rope solutions

In this section we analyze the force-free solutions found. We start with a summary of previously known force-free solutions in order to compare them later with our results.

3.1 Analytical solutions

The best-known solution is the Lundquist solution. It is simply the first eigen-solution of a linear force-free field

$\begin{displaymath} (B_r,B_{\theta},B_z)=(0,J_1(\alpha r),J_0(\alpha r)) , \end{displaymath}$

(13)

with $B_r,B_{\theta},B_z$ being the radial, azimuthal and axial component, respectively. With a flux rope radius normalized to unity and B_z=0 at the flux-rope boundary, $\alpha$ is the first zero of the Bessel function J₀, called $\alpha_L$ , therefore $\alpha_L \approx 2.4$ .

Another simple solution can be found in Cartesian coordinates. This geometry implies a rectangular boundary (of size $2 \times 2b$ with the same normalization as in Sect. 2.2). The magnetic field is

$\displaystyle % (B_x,B_y,B_z)=\left(-1/\sqrt{1+b^2}\right.$	$\displaystyle \cos (k_x x) \sin (k_y y),$
$\displaystyle b/\sqrt{1+b^2}$	$\displaystyle \sin (k_x x) \cos (k_y y),$
	$\displaystyle \left. \cos (k_x x) \cos (k_y y) \right) ,$	(14)

with $k_x=\pi/2$ and $k_y=\pi/(2b)$ . This rectangular solution can obviously not be applied to observed MCs. However, it is still useful to have an analytical expression for quantities such as the magnetic flux and helicity (Sects. 3.4 and 3.5), as well as for the $\alpha$ eigenvalue which is

$\begin{displaymath} \alpha_{\rm R}= \frac{\pi}{2} \frac{b}{\sqrt{1+b^2}} \cdot \end{displaymath}$

(15)

This provides an order of magnitude estimate for the flux-rope characteristics, as shown below.

A third analytical solution for a linear force-free field with an elliptical boundary (particular case of Eq. (4) with a=0) was found by Vandas & Romashets (2003). Equation (6) was solved with elliptic cylindrical coordinates, one of the few coordinates system where Eq. (6) has separable solutions. For all b values, they found an analytical solution expressed with the even Mathieu function of zero order. While analytical, the explicit solution needs numerical computations that they achieved through a series expansion of the Mathieu function. We confirm all their derivations, including their numerical results (we computed them differently by using the Mathieu function inside the Mathematica software). We found only minor differences in the numerical results. We also found small differences when using the numerical method described in Sect. 2 (within the mean error found at the boundary shown in Fig. 2b).

3.2 Flux rope structure

The projections of field lines orthogonal to the flux rope axis are given by isocontour values of A(x,y). For a force-free field, they are also iso-values of the axial field B_z (Eq. (1)). Typically, field line projections inside the flux rope are more circular than the imposed boundary. This effect is stronger closer to the flux-rope center (Figs. 3-5). This is due to the balance of force, as follows. The sharper parts of the boundary impose a strong curvature, therefore a strong magnetic tension which reduces the field line bending inside the flux rope (see the regions around the corner of the rectangular boundary in Fig. 3a or the region with the most negative x-values for $a\approx -1,-2$ for the other boundaries, Figs. 3-5).

The most important effect of the boundary on the core field is the aspect ratio (called b). The core field has approximately an elliptical shape with an aspect ratio closer to unity than the b value.

The next most important effect for the core field is a global deformation of the boundary such as the effect induced by increasing |a| in Eq. (4). This is already a relatively weak effect for the field line shape inside the flux-rope core, especially for large b values (Figs. 3-5). For a larger bending (i.e. a larger |a|), the magnetic tension increases, so the magnetic field lines slightly shrink towards the flux rope center (e.g. see the evolution of the $A/A_{\rm max}=0.5$ isocontour with increasing |a| in Fig. 5). We notice that the distance $x_{\rm back}-x_{\rm front}$ is preserved for each y value with increasing |a|, so there is no compression of the flux rope as |a| increases in all the examples shown, and the observed shrinkage is not due to a compression of the flux rope edges.

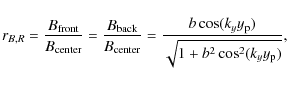
The bending of the flux rope introduces an asymmetry between the front and the back. Field lines in the front become flatter as |a| increases (Figs. 3-5). Even an inverse curvature (curved away from the flux-rope center) is present for the largest |a| values shown. This asymmetry is also present in the field strength, with the field being stronger in the front than in the back of the flux rope (Fig. 6). For a>0, symmetric results are obtained but such cases are usually not observed in MCs.

Next, let us consider a cut of the flux rope at y=0 in order to simulate observations made by a spacecraft. The deformation of the boundary much less affects the direction of the magnetic field than its norm. This is illustrated in Fig. 6 for one of the spherical angles ( $\theta$ ), defining the direction of $\vec{B}$ , and it is also true for the other angle $\varphi$ ( $\varphi=\sin^{-1}(B_y/\sqrt{B_x^2+B_y^2})$ ). This result holds approximately also for values of |y/b| not too large. Indeed, the isocontours of A in Figs. 3-5 show that the deformation of the projected field lines remains moderate if |a| is increased. Since these A isocontours are also isovalues of B_z, the magnetic field direction in most of the flux rope is only slightly affected if a is modified.

Inside the flux rope, small-scale distortions of the boundary have even a weaker effect than the effect of |a|. This can be shown by considering, for example, the field described by $A(r,\theta)= J_0(\alpha r)+ c J_m(\alpha r) \sin m \theta$ in cylindrical coordinates (Sect. 2.3). The coefficient c gives the spatial-fluctuation amplitude of the boundary (defined by $A(r,\theta)= 0$ ). Because the Bessel functions behave as r^m near the origin, the deformation of the field lines decreases rapidly with increasing m at a given distance r inside the flux rope. We conclude that the core of the flux rope is almost not affected by the small-scale fluctuations of the flux rope boundary.

$\begin{figure} \par\includegraphics[width=8.8cm, clip=]{12645f6.eps} \end{figure}$	Figure 6: Examples of magnetic field found across the flux rope along the x-axis (y=0). B is the magnetic field norm and $\theta = -\tan^{-1}(B_y/B_z)$ . b=0.5 and 2 for the top and bottom panels, respectively.
Open with DEXTER

3.3 Magnetic pressure at the boundary

The magnetic field strength (B) is always maximum at the flux rope center (where B_x=B_y=0, so where A, and therefore B_z(A), have an extremum). However, this center is not necessarily at the geometrical center of the shape defined by the boundary (see, e.g., Figs. 3-5). B decreases faster toward the boundary where the boundary is extended outward, or has a ``corner'', due to a stronger magnetic tension there (Figs. 3-5). For small b, high B values are concentrated in a range of x almost independently of y, while for large b values this range is located rather at low |y| values. Finally, the isocontours of B are remarkably different from the field lines (isocontours of A) with the exception of nearly circular contours for $a\approx 0$ , $b\approx 1$ .

The magnetic pressure at the boundary strongly depends on the flux rope deformation (Fig. 7). Starting from the cylindrically symmetrical case (a=0,b=1), where the pressure is by construction uniform along the boundary, a small |a| already is sufficient to create a significant decrease of pressure on the lateral sides of the flux rope (Figs. 4d-f, 7b). For b<1 and a=0, the magnetic pressure is significantly higher on the sides of the flux rope (Fig. 3f), this effect being more pronounced for smaller b values. This effect competes with the flux rope bending (increasing |a|) to shift the pressure maximum/minimum along the boundary (Fig. 7a). For b>1, both an increasing b and |a| produce a lower magnetic pressure on the flux-rope sides (Figs. 5d-f, 7c).

The equilibrium of the flux rope with its surroundings is achieved by the total pressure balance at the boundary. Therefore, the above magnetic pressure computation gives the total pressure needed in the surrounding SW to achieve such a boundary shape (assuming a dominant magnetic pressure inside the flux rope). The asymmetry of the SW pressure between the front and the back of the flux rope can be due to encountered different SW, but in most cases it is plausibly due to the ram pressure due to the relative motion of the flux rope with respect to the surrounding SW.

$\begin{figure} \par\includegraphics[width=8.5cm, clip=]{12645f7.eps} \end{figure}$	Figure 7: Magnetic pressure along the flux rope boundary (Eq. (4)) normalized to the maximum pressure (located at the flux rope center). The coordinate s ranges from s=0 at the front, to s=1 at the back.
Open with DEXTER

Moreover, if the SW conditions permit such low pressure on the flux rope sides, the force-free approximation is expected to be no longer valid in these regions (near the most bent parts of the boundary). More precisely, even with a plasma $\beta$ as low as 10^-2 in the flux rope center, the force-free approximation is no longer valid in the regions where the relative magnetic pressure reaches few 10^-2 in Fig. 7 (supposing a nearly uniform plasma pressure). Such regions are expected to be advected with the plasma flow (in the absence of reconnection), so that the extended parts of the flux rope are expected to be swept away by the SW. Reconnection with the encountered SW magnetic field is also expected; it will further contribute to remove these extended parts. It remains a strong core with an elliptical-like shape. This core field is expected to keep its identity while traveling in the SW (unless there is a large amount of magnetic flux reconnected with the overtaken SW).

$\begin{figure} \par\includegraphics[width=8.5cm, clip=]{12645f8ab.eps} \includegraphics[width=8.5cm, clip=]{12645f8c.eps} \end{figure}$	Figure 8: Modification with b of the magnetic flux and helicity contained in the flux rope(per unit length along the axial direction). a) The maximum magnetic field strength is set to unity, b) the axial flux is normalized to the azimuthal flux, and c) the helicity is normalized to the product of the fluxes.
Open with DEXTER

3.4 Magnetic flux

The axial flux of the Lundquist solution, Eq. (13), is

$\begin{displaymath} F_{z,L} = 2 \pi \int_{0}^{R} B_z r {\rm d} r = 2 \pi \frac... ... )} {\alpha} B_{\rm max} R^2 \approx ~1.36 B_{\rm max} R^2 , \end{displaymath}$

(16)

where the two first expressions are general (valid for any $\alpha$ ), while $\alpha=\alpha_L$ (defined by B_z(R)=0) for the numerical value. We have included the scaling with the radius (R) and the maximum field strength ( $B_{\rm max}$ ) for completeness. The azimuthal flux is

$\begin{displaymath} F_{a,L} = B_{\rm max} L R /\alpha \approx 0.42 B_{\rm max} L R , \end{displaymath}$

(17)

where L is the axial length of the flux tube. The ratio of fluxes is

$\begin{displaymath} F_{z,L}/F_{a,L} = 2 \pi J_1(\alpha ) R/L \approx 3.36~R/L . \end{displaymath}$

(18)

The axial flux within a rectangular cross-section is computed from Eq. (14)

$\begin{displaymath} F_{z,R} = 16 b \pi^{-2} B_{\rm max} R^2 \approx 1.62 ~b B_{\rm max} R^2 , \end{displaymath}$

(19)

where we keep the same field and size scaling (the cross-section size is $2R \times 2Rb$ ). The rectangular cross-section is larger than the circular one, so there is more axial flux, but only about 20% more (while the cross-section area is about 27% larger). The aspect ratio b could change the axial flux by a much larger amount. Therefore, the precise determination of b is more important in the estimation of the axial flux than the detailed shape of the boundary. The azimuthal flux is

$\begin{displaymath} F_{a,R} = A_{\rm max} L = B_{\rm max} R L /\alpha_R , \end{displaymath}$

(20)

where $\alpha_R$ is given by Eq. (15). For b=1, F_a,R is only $\approx$ 8% larger than F_a,L. The ratio of fluxes is

$\begin{displaymath} F_{z,R}/F_{a,R} = 8/\pi \sqrt{1+b^2} ~R/L \approx 2.55 \sqrt{1+b^2} ~R/L . \end{displaymath}$

(21)

At the limit of a small aspect-ratio b, this flux ratio is constant, while it increases linearly with b in the limit of large b (Fig. 8b).

With the same maximum field strength and maximum extension in both x and y directions, the axial flux obtained with the boundary defined by Eq. (4) is always lower than the axial flux obtained with the rectangular boundary (Fig. 8a). This is an expected result since the area defined by Eq. (4) is slightly smaller than the area of the rectangular boundary. The difference increases as the aspect ratio (b) departs from unity. This is a consequence of the shrinkage of the field lines as the core has a lower aspect ratio for an elliptical than for a rectangular boundary (Fig. 3-5). This difference reaches a factor about 2 (shift of $\approx$ 0.3 in $\log_{10}$ scale) both for $b\approx 0.1$ and $\approx$ 10. The bending of the flux-rope cross-section, so increasing |a|, has a much weaker effect (Fig. 8a).

The azimuthal flux, $F_{\rm a} = B_{\rm max} R L /\alpha$ , is also an increasing function of b because $\alpha$ is a decreasing function of b (Fig. 2). Therefore, the ratio $F_z/F_{\rm a}$ has a weaker dependence on b than F_z (Fig. 8b). $F_z/F_{\rm a}$ has a nearly linear dependence on b in a log-log plot, for the whole range of a explored. This contrasts with the result obtained with the rectangular cross-section. In the range 0.1<b<10, we deduced $3.36 \sqrt{b} \leq F_z/F_{\rm a} \leq 4 \sqrt{b}$ , the lower bound being given by the Lundquist solution and the upper bound being an approximation both for low and high b values.

3.5 Magnetic helicity

An efficient way to compute the magnetic helicity of the field $\vec{B}$ within a volume ${\mathcal V}$ is to split the field $\vec{B}$ into two parts, as $\vec{B}=\vec{B}_{\rm closed} + \vec{B}_{\rm open}$ , where $\vec{B}_{\rm closed}$ is fully contained inside ${\mathcal V}$ , and $\vec{B}_{\rm open}$ has the same distribution as $\vec{B}$ on the boundary of ${\mathcal V}$ (Berger 2003). For an element of length L of a flux rope, a simple choice for $\vec{B}_{\rm closed}$ and $\vec{B}_{\rm open}$ is the azimuthal ( $\vec{B}_{a}$ ) and axial ( $\vec{B}_{z}$ ) field components, respectively

H	=	$\displaystyle 2 \int_{ {\mathcal V}} \vec{A}_{\rm open} \cdot \vec{B}_{\rm closed} {\rm d} {\mathcal V}~,$	(22)
	=	$\displaystyle 2 L \int_{ {\mathcal S}} \vec{A}_{a} \cdot \vec{B}_{a} {\rm d} {\mathcal S},$	(23)

where $\vec{A}_{a}$ satisfies $B_z= ( {\bf\nabla} \times\vec{A}_{a}) \cdot \vec{\hat{z}}$ , and ${\mathcal S}$ is the area of the flux-rope cross-section. This is the classical way to compute H for a circular cross-section since Eq. (23) is reduced to $H=4 \pi L \int_{0}^{R} A_{\theta} B_{\theta} r {\rm d} r$ . For the Lundquist solution, it implies that

H_L	=	$\displaystyle 2 \pi (J_0^2(\alpha) +J_1^2(\alpha) -2 J_0(\alpha) J_1(\alpha)/\alpha) ~ B_{\rm max}^2 R^3 L$
	$\textstyle \approx$	$\displaystyle 0.70 ~B_{\rm max}^2 R^3 L,$	(24)

where the first expression is general, while $\alpha=\alpha_L$ (defined by B_z(R)=0) for the numerical value of the second expression. This expression was used to estimate H in MCs (e.g., Gulisano et al. 2005; Dasso et al. 2003).

However, Eq. (23) is not convenient to compute the helicity for a general cross-section shape, since one first needs to compute $\vec{A}_{\rm a}$ by integration of B_z. Equation (22) can be transformed with the vector identity ${\bf\nabla \cdot} (\vec{U}\times \vec{V}) = \vec{V}\cdot {\bf\nabla} \times\vec{U}- \vec{U}\cdot {\bf\nabla} \times\vec{V}$ where $\vec{U}=\vec{A}_{\rm open}=\vec{A}_{\rm a}$ and $\vec{V}=\vec{A}_{\rm closed}= A_z \vec{\hat{z}}$ . The surface integral on the flux rope boundary, $\int (\vec{A}_{\rm closed} \times A_z \vec{\hat{z}} ) \cdot {\rm d} \vec{S}_b$ , vanishes if A_z=A=0. This is a particular gauge for the vector potential, that we have already selected in Sect. 2.2. Therefore, with A=0 at the flux rope boundary, Eq. (22) can be rewritten as

$\begin{displaymath} H = 2 L \int_{ {\mathcal S}} A B_z {\rm d} {\mathcal S}. \end{displaymath}$

(25)

This integral is much easier to compute than the one in Eq. (23), since it involves only scalar quantities that are direct outputs of the model.

With Eq. (25), the helicity of a flux rope with a rectangular cross-section is easily computed as

$\begin{displaymath} H_R = \frac{4}{\pi} \frac{b^2}{\sqrt{1+b^2}} B_{\rm max}^2 ... ... \approx 1.27 \frac{b^2}{\sqrt{1+b^2}} B_{\rm max}^2 R^3 L . \end{displaymath}$

(26)

For b=1, a flux rope with a square cross-section contains only 28% more helicity than a flux rope with a circular cross-section. This is only slightly above the ratio obtained above for the axial flux (20%, Sect. 3.4).

As for F_z, magnetic helicity is greater for the rectangular cross-section, and this difference is larger for b values far from 1 (both smaller and larger values, Fig. 8a). Also, H(b) is a steeper function than F_z(b) for low b values, while H(b) and F_z(b) have a comparable slope for large b values.

Magnetic helicity quantifies how much the axial and azimuthal fluxes are interlinked. A useful quantity is the normalized helicity ( $H/(F_{\rm a} F_z)$ ); it is an average Gauss linking number (Berger & Field 1984). It is independent of b for a rectangular cross-section ( $=\pi^2/8\approx 1.23$ ), a value just below the result of the Lundquist solution ( $H/(F_{\rm a} F_z)\approx 1.25$ ). With the boundary defined by Eq. (4), $H/(F_{\rm a} F_z)$ depends only weakly on both a and b ( $1.2\pm0.05$ ) over the large range explored for b (Fig. 8c). Therefore, the magnetic helicity contained in these flux ropes is mainly defined by their magnetic flux (the mean flux linkage being almost constant). We anticipate that this result could be extended to a much broader ensemble of boundary shapes than those defined by Eq. (4).

4 Estimation of the boundary shape from B along a 1D cut of the flux rope

In this section, we analyze the magnetic field profile computed along a cut of the flux rope along the x direction (at a fixed y value). The aim is to provide a first step toward the analysis of in-situ data by identifying the characteristics of the field profile that permit us to determine approximately the parameters of the model that is most compatible with the observations. The final determination of the parameters will be realized by a least square fit to the data in a subsequent work. However, this procedure is not a trivial task due to the number of free parameters involved. The fitting method will largely benefit from the following approximate determination of the parameters since the iteration involved in the fitting can be initiated closer to the best solution (i.e., starting the iteration from a ``good'' seed). This will speed up the convergence towards the global minimum of the function defined as the distance of the model to the observations, and even more importantly, it will limit the possibility of converging to a local minimum, rather than the global minimum (i.e., the risk to end up at a false solution).

4.1 Aspect ratio

The aspect ratio, b, of the boundary has a strong effect on the field-line curvature, so on the contribution of the magnetic tension. Together with the force-free balance, it implies that b has a strong influence on the distribution of the field strength B inside the flux rope (Figs. 3-5). More precisely, cuts across the flux rope parallel to the x-axis, at a fixed $y=y_{\rm p}$ , have a clearly peaked B(x) profile for low b values, and this profile becomes flatter as b increases (Fig. 6).

We take advantage of the above property to present a method to estimate b from B(x). Several attempts have been investigated to characterize the B(x) profile as a function of b, for example by computing the mean curvature of the B(x) profile. However, this curvature depends on $y_{\rm p}$ and on the size of the x-interval crossed. From these explorations, we find that this approach is suited only to relatively low impact parameters. In our exploration of the different possibilities, we select the option which has the least dependence on other parameters (such as the y and a values). We also define global quantities, rather than local ones, to have less influence of local perturbations in future applications to observations.

The best estimator of the parameter b we found is the ratio

$\begin{displaymath} r_B = \frac{\langle B_{\rm front}\rangle_f+\langle B_{\rm back}\rangle_f}{2 \langle B_{\rm center}\rangle _f} , \end{displaymath}$

(27)

where the averaging is done over a fraction f of the x-extension of the analyzed B profile. $\langle B_{\rm center}\rangle$ extends symmetrically around the maximal value of B, and $\langle B_{\rm front}\rangle$ , $\langle B_{\rm back}\rangle$ are computed in the vicinity of the flux-rope boundaries. Increasing f provides a more global determination of the averages, but it decreases the range of variation of r_B with b, so its sensitivity. On the other hand, for a too small f value, r_B is too sensitive to local B perturbations (in the application to MC data). As a compromise, we select f=0.2.

Figure 9 demonstrates that r_B has a well defined variation with b. The saturation of r_B, close to 0 and 1 for small and large b values, respectively, is intrinsic to the force-free balance (Sect. 3.2). As a consequence, the estimation of b is less accurate for small and large b values. Next, r_B is weakly dependent on a, so on the bending of the flux rope. This is so because r_B is defined by an average of the front and back field. r_B is also weakly dependent on $y_{\rm p}$ , a result coming from the global force balance (Sect. 3.2). Finally, since r_B is defined as a function of B, this implies that r_B is explicitly independent of the estimation of the axis orientation. However, there is still an implicit dependence since the determination of the MC boundaries is more accurate in the MC frame (Dasso et al. 2006).

$\begin{figure} \par\includegraphics[width=8.8cm, clip=]{12645f9.eps} \end{figure}$

Figure 9:

Evolution of magnetic field ratio, r_B, defined by Eq. (27), as a function of $\log_{10} b$ , where b is the aspect ratio of the flux-rope cross-section. The averages are computed over 20% of the length along the cut across the flux rope. r_B is relatively independent of a as well as the y position of the cut in $y_{\rm p}$ , especially for low values of these parameters. The continuous lines are the numerical results, the dashed line represents the result for a rectangular boundary, Eq. (28) with $y_{\rm p}=0$ , and the dotted line is for the analytical approximation given by Eq. (29).

Open with DEXTER

The above numerical results could be directly used to estimate the aspect ratio b using the measured value of r_B (by interpolating a table of values). However, it is more practical to derive an analytical approximation. This task is largely facilitated by the dominant dependence of r_B on b. As a guide we compare with the result obtained with a rectangular cross-section. From Eq. (14), we find:

$\begin{displaymath} r_{B,R} = \frac{B_{\rm front}}{B_{\rm center}} = \frac{B_{... ... \cos (k_y y_{\rm p})}{\sqrt{1+b^2 \cos^2 (k_y y_{\rm p})}} , \end{displaymath}$

(28)

where $k_y=\pi/(2b)$ . In contrast to Eq. (27), we do not include an averaging in the definition of r_B,R, since we want only a qualitative comparison of the main trend, keeping the analytical formula simple. r_B,R is weakly dependent on $y_{\rm p}$ if it is small compared to b. In Fig. 9, we only show the case $y_{\rm p}=0$ (to provide a common guide for all panels). The rectangular boundary has $r_{B,R}(y_{\rm p}=0)$ slightly above r_B for small values of a and $y_{\rm p}$ , but still the global behavior is reproduced. After an exploration of possible functions, a better approximation is obtained by a simple modification of Eq. (28), using $y_{\rm p}=0$ :

$\begin{displaymath} r_{B,\rm approx.} = (b -0.07) /\sqrt{1+b^2 } . \end{displaymath}$

(29)

This provides a relatively good approximation for the numerical results for $\vert y_{\rm p}\vert\leq 0.5 b$ , and it results in an underestimation of r_B only for small b and for large |a| ( $\vert a\vert\geq \sqrt{b}$ , Fig. 9a-c). For large impact parameters, ( $\vert y_{\rm p}\vert > 0.5 b$ ), and significant a values, $r_{B,\rm approx.}$ significantly overestimates r_B for large b, while the reverse is true at low b. If such an extreme case is needed, the interpolation within a table of the numerical results can be used for a more accurate r_B estimation.

4.2 Orientation of the flux-rope axis

A classical method to determine the local axis orientation of an MC is the minimum variance method (MV, see e.g., Burlaga et al. 1982; Sonnerup & Cahill 1967). It is based on the different behavior of the axial and the two orthogonal components of the magnetic field which is expected, since an MC has a flux rope structure. The method finds the directions where the magnetic field has the lowest and the highest variance (the third direction, with an intermediate variance, being orthogonal). The MV requires that the three variance values are well separated, a condition generally met in MCs. Thus, the MV provides approximately the directions x,y,z used above (we recall that the flux rope is supposed to move away from the Sun along $-\vec{x}$ ).

The MV was extensively used to find the local axis of MCs (e.g., Gulisano et al. 2007; Bothmer & Schwenn 1998, and references therein). It provides more accurate results when it is applied to a normalized time series $\vec{B}(t)/B(t)$ . It was compared to other methods, in most cases successfully, with typical differences between the methods of the order of $10\hbox{$^\circ$ }$ . The most important deviation in the orientation is produced by changing the MC boundaries (Dasso et al. 2006). Also the systematic error in the orientation increases with the impact parameter, $y_{\rm p}$ . However, the tests of Gulisano et al. (2007) with Lundquist's test fields have shown a deviation of only $\approx$ $3\hbox{$^\circ$ }$ for $y_{\rm p} \approx 30$ % of the MC radius and of $\approx$ $20\hbox{$^\circ$ }$ for $y_{\rm p}$ as high as $\approx$ 90% of the MC radius.

The results of Sect. 3.2 show that the orientation of the magnetic field is weakly affected by the shape of the cross-section. This is true for low impact parameters (see the case $y_{\rm p}=0$ in Fig. 6b,d), as well as in about the half of the flux rope (as can be deduced qualitatively from Figs. 3-5, see Sect. 3.2). Therefore, we expect that the results previously obtained in tests of cylindrical models are approximately valid also for flux ropes with distorted cross-section.

The main advantage of the MV method is that it does not introduce an a priori on the detailed magnetic configuration of the flux rope (e.g., the distribution of the twist). The small dependence of the time series $\vec{B}(t)/B(t)$ on the cross-section shape further justifies the use of the MV. This provides an estimation of the MC frame, defined by the x,y,z directions, in which the data are transformed for the next steps.

$\begin{figure} \par\includegraphics[width=8.8cm, clip=]{12645f10.eps}\par \end{figure}$	Figure 10: Estimation of $\langle B_x\rangle/\langle B\rangle$ with averages computed along the entire cut of the flux rope (located at $y=y_{\rm p}$ ). The continuous lines are the numerical results and the dashed lines represent the analytical approximation given by Eq. (31). Two values of the distortion parameter are shown: a) a=0 and b) $a=-\sqrt {b}$ .
Open with DEXTER

4.3 Impact parameter

Global quantities, such as magnetic flux and helicity, are extensive quantities, i.e. they depend on the MC size. In order to estimate the true size of the flux rope, it is therefore important to relate the x extension measured along the flux-rope crossing to its value for a central crossing (where B is maximum). This is realized by estimating $y_{\rm p}$ .

The $y_{\rm p}$ position of the cut affects the three components of $\vec{B}$ , as can be deduced from Figs. 3-5. As for the determination of b above we search for the best way to estimate $y_{\rm p}$ . Gulisano et al. (2007) have used $\langle B_x\rangle$ normalized to the central field strength, $B_{\rm fit}$ , which was deduced by fitting the Lundquist solution to the data. They derived a quadratic relationship between $y_{\rm p}$ and $\langle B_x\rangle/B_{\rm fit}$ for a magnetic field defined by the Lundquist solution. Here, we extend this approach, by computing

$\begin{displaymath} r_{Bx} = \langle B_x\rangle/\langle B\rangle , \end{displaymath}$

(30)

where the averages are computed over the full crossing of the flux rope (at a given $y_{\rm p}$ ). This new definition removes the need to use a particular model to normalize $\langle B_x\rangle$ .

Figure 10 shows that r_Bx has a well defined variation with $y_{\rm p}$ , but that it also depends on b, and to a lesser extent on a. Moreover, since B_x is involved, r_Bx is also affected by the determination of the local MC frame (Sect. 4.2). With a rough estimation, we find $r_{Bx}\approx 1.2 y_{\rm p}/b$ . More precisely, the proportionality coefficient depends weakly on b, with a value $\approx$ 0.7 for $b\ll 1$ , and $\approx$ 1.7 for $b\gg 1$ , so the above affine relation can be systematically biased, up to 40%, for a very small or for a very large aspect ratio. A better approximation is:

$\begin{displaymath} r_{Bx, \rm approx.}(y_{\rm p},b) = \left(c_1 + c_2 \frac{2-\vert y_{\rm p}/b\vert}{2+b^2} \right) ~\frac{y_{\rm p}}{b} , \end{displaymath}$

(31)

where c₁ and c₂ are slightly function of $\vert a\vert \sqrt{b}$ : $c_1=0.7 + 0.2\vert a\vert \sqrt{b}$ and $c_2=0.9 - 0.2\vert a\vert \sqrt{b}$ . This formula approximates relatively well r_Bx (Fig. 10). Equation (31) can be used to estimate $y_{\rm p}/b$ , and therefore $y_{\rm p}$ when the two previous steps have been realized (Sects. 4.1, 4.2). The parameter a can first be set to zero, as r_Bx and $r_{Bx, \rm approx}$ depend only slightly on a (Fig. 10). Then, an iteration with the next step (estimating a) can be realized. Alternatively, this estimated $y_{\rm p}/b$ value can be used directly as a seed when fitting the model to the data.

Finally, the estimation of $y_{\rm p}/b$ permits us to estimate the x extension of a central crossing from the measure of $x_{\rm back}-x_{\rm front}$ , as deduced from the observed velocity, from the determination of the boundaries and from the axial orientation of the MC. With a boundary parametrized by Eq. (4), this step does not depend on a (as $x_{\rm back}-x_{\rm front}$ is independent of a for a given $y_{\rm p}/b$ value).

$\begin{figure} \par\includegraphics[width=8.8cm, clip=]{12645f11.eps} \end{figure}$	Figure 11: Evolution of the asymmetry ratio $r_{\rm a}$ , defined by Eq. (32), as a function of $\log_{10} b$ . The averages are computed over 20% of the length along the cut across the flux rope at $y=y_{\rm p}$ . The drawing convention is the same as in Fig. 9.
Open with DEXTER

4.4 Bending

A global bending of the flux rope has a relatively weak effect on the magnetic field (Figs. 3-5). The strongest effect is present on the B_y component as the front field is increasing with more negative a values, while the opposite occurs in the back of the flux rope (for not too large $\vert y_{\rm p}\vert$ values). Therefore, information on a is contained in the observed B_y profile. However, we prefer to use the B profile since it is independent of the flux-rope orientation, and because |B_y| is indeed close to B near the flux rope boundaries. We define

$\begin{displaymath} r_{\rm a} = \langle B_{\rm back}\rangle_f/\langle B_{\rm front}\rangle_f , \end{displaymath}$

(32)

where the averaging is done over a fraction f of the x-extension of the analyzed B profile. As for Eq. (27), we select f=0.2.

$r_{\rm a}$ strongly depends on a, but only for b lower than a few units (Fig. 11). Indeed, we show curves with fixed values of $a/\sqrt{b}$ , which implies an increasing value of a with b. Therefore, equivalent curves, with a fixed value for a, would show an even lower dependence on a for b>1. Indeed, when $b\gg 1$ , a comparable to b is required in order that magnetic tension modifies significantly the otherwise flat B(x) profile (Figs. 5-6). The choice of the scaling of a with $\sqrt{b}$ was guided by numerical errors (see the end of Sect. 2.4). However, values of a larger than ${\approx}\!\sqrt{b}$ are expected to be unphysical (in particular they were not found in MHD simulations, e.g., Riley et al. 2003; Manchester et al. 2004), so we claim that Fig. 11 represents a sufficiently broad range of the parameter space which covers most of the observed MC configurations.

$r_{\rm a}$ does not only depend on a, but also strongly on b, as well as on $y_{\rm p}/b$ as shown in Fig. 11. Moreover, these dependences are coupled (the curves evolved significantly with the three parameters), therefore we do not present an analytical approximation (which would be cumbersome). However, with b and $y_{\rm p}/b$ approximatively determined with the previous steps (Sects. 4.1, 4.3), a can be estimated from the interpolation of a table of $r_{\rm a}$ values.

These estimations can be refined by fitting the model developed in Sect. 2 to the data, with the initial parameters set to the above estimations. The purpose of the next paper will be to apply this new technique to a set of MCs. The difference between the initial parameters and the fitted ones will provide an estimation of the precision of the above estimations when applied to data.

5 Conclusions

The present work is motivated by the need for a magnetic model in order to derive the magnetic configuration of MCs from local measurements provided by spacecraft. The model should be able to compute a large variety of magnetic configurations, as broad as possible, but also the parameters of the model should be well defined from the observations.

To develop the above goal, we generalized the Lundquist solution, obtained in cylindrical symmetry, the MC boundary having a broad range of shapes. We express the solution with a series of functions satisfying the linear force-free equations. Such a development in series usually involve a large number of free parameters (the multiplicative coefficients of the functions in the series). Here we limit the freedom of the model by imposing the shape of the MC boundary (depending on few parameters). Moreover, it defines a well posed problem. For a given boundary shape, the internal magnetic-field solution is unique. This procedure provides a solution accurate enough over a broad range of aspect ratios of the flux rope cross-section (typically 0.1 to 10). While the boundary shape can be more general with this method, we limit our report to the boundary deformations which dominantly affect the observed magnetic field. Other deformations have a lower effect inside the flux rope, in particular on its core, and only future studies will be able to tell if some of these deformations could be estimated accurately enough from the data.

The physical origin of the cross-section deformation is the flux rope interaction with its surrounding SW. In particular, during the MC travel through the heliosphere, different parts of the MC boundary could be in contact with different parcels of SW having different pressure, therefore changing the original shape of the MC. These changes of the MC boundary drive a re-configuration of the internal magnetic field, in a similar way to the global expansion of MCs proposed by Démoulin & Dasso (2009). Thus, the shape of the MC boundary given by Eq. (4) can be interpreted as a consequence of the interaction of the flux rope with its environment. We found that a flat or/and bent flux-rope cross section requires a large gradient of the total pressure along the MC boundary (Fig. 7). Such a large gradient of pressure is unlikely to be present around MCs outside the interacting regions between two types of SW.

The most important deformation is a global elongation of the flux-rope cross-section. It is characterized by the aspect ratio (b), defined by the ratio of the dimension across to the one along the spacecraft trajectory projected orthogonally to the MC axis. Simulating the crossing of the flux rope by a spacecraft, we find that, for low b values, the magnetic field strength peaks inside the flux rope, while it becomes flatter as b increases. We quantify this property so that b can be estimated from the magnetic data collected across a MC. We also confirm the results of Vandas & Romashets (2003) who derived an analytical solution of a linear force-free field contained inside an elliptical boundary. We find that the configuration of the core inherits the oblate shape of the boundary but with a significantly lower aspect ratio, in agreement with previous observations (e.g., Dasso et al. 2005a; Liu et al. 2008; Möstl et al. 2009).

The next deformation in importance is the global bending of the flux rope coming from its interaction with surrounding SW streams (see refs. in Sect. 1). The symmetric bending mode (Figs. 3-5) can significantly affect the magnetic tension, therefore also the distribution of the field strength. With a bending in the direction of the MC propagation, a stronger field in the front than in the back is present, as frequently observed in MCs. Such asymmetry can also come from the temporal evolution of the magnetic field as the observations of the front and back are shifted in time (this effect is called the ``aging effect''). However, this effect can be corrected, and it is usually not the main cause of the observed asymmetry between the front and back of MCs (Démoulin et al. 2008). Moreover, even removing the aging effect, a front/back asymmetry can still be observed in some MCs (Mandrini et al. 2007; Dasso et al. 2007). Finally, we find that the deformation of the flux-rope core decreases with higher spatial frequency deformations of the boundary.

We next analyzed the results of the model with the perspective of applying it to MC data. In particular we search for the best way to have an efficient first estimation of the model parameters. This step is important as the parameter space to explore is large, and our previous experience of a direct fit of a simpler model to the data has shown us that a direct fit does not always converge to the correct solution. This consideration is even more important as the number of free parameters is larger in the present model. We also verify that the magnetic field taken only on a linear cut through the flux rope was sensitive enough to determine the parameters. We find that this is true for all parameter, when located in the expected physical range. The main limitation is the measurent of the bending (so a) for large aspect ratio (b).

In previous studies, the determination of the MC axis was realized mainly with the minimum variance or/and with a fit of the Lundquist model. We find that the distortions of the MC boundary shape mainly affect the magnetic field strength, but only weakly its direction. Therefore, the MC axis direction found in previous studies will remain weakly affected by applying the present new model. It implies that the local magnetic frame is relatively well defined. This is an important result to determine accurately the locations of the MC boundaries, as well as the impact parameter. We find a direct relationship between the impact parameter and the mean magnetic-field component present along the projection of the spacecraft trajectory orthogonally to the MC axis. We conclude that all the free parameters of the model can be constrained, and so determined, from a time series of a measured magnetic field within a MC.

Finally, we plan to study how much global quantities, such as magnetic flux and helicity, are modified in comparison with their previous estimations using the Lundquist field on MCs. Our model shows that the estimation of the aspect ratio (b) is the most important parameter of the MC cross-section for these global quantities. Other boundary deformation, such as the global bending (a), have a much smaller effect on the global quantities. We also found that the magnetic helicity, normalized by the product of the axial and azimuthal fluxes, is very weakly dependent on the boundary shape (at least with a linear force-free field).

Acknowledgements

We thank Tibor Török for reading carefully, and so, improving the manuscript. The authors acknowledge financial support from ECOS-Sud through their cooperative science program (No. A08U01). This work was partially supported by the Argentinean grants: UBACyT X425 and PICT 2007-00856 (ANPCyT). S.D. is member of the Carrera del Investigador Científico, CONICET.

References

Berger, M. A., & Field, G. B. 1984, J. Fluid. Mech., 147, 133 [CrossRef] [NASA ADS]
Berger, M. A. 2003, in Advances in Nonlinear Dynamics, 345
Botha, G. J. J., & Evangelidis, E. A. 2004, MNRAS, 350, 375 [CrossRef] [NASA ADS]
Bothmer, V., & Schwenn, R. 1998, Annales Geophys., 16, 1 [CrossRef] [NASA ADS]
Burlaga, L. F. 1988, J. Geophys. Res., 93, 7217 [CrossRef] [NASA ADS]
Burlaga, L. F. 1995, Interplanetary magnetohydrodynamics (New York: Oxford University Press)
Burlaga, L. F., & Behannon, K. W. 1982, Sol. Phys., 81, 181 [CrossRef] [NASA ADS]
Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [CrossRef] [NASA ADS]
Burlaga, L. F., Klein, L., Sheeley, Jr., N. R., et al. 1982, Geophys. Res. Lett., 9, 1317 [CrossRef] [NASA ADS]
Cid, C., Hidalgo, M. A., Nieves-Chinchilla, T., Sequeiros, J., & Viñas, A. F. 2002, Sol. Phys., 207, 187 [CrossRef] [NASA ADS]
Dasso, S., Mandrini, C. H., Démoulin, P., & Farrugia, C. J. 2003, J. Geophys. Res., 108, 1362 [CrossRef]
Dasso, S., Gulisano, A. M., Mandrini, C. H., & Démoulin, P. 2005a, Adv. Space Res., 35, 2172 [CrossRef] [NASA ADS]
Dasso, S., Mandrini, C. H., Démoulin, P., Luoni, M. L., & Gulisano, A. M. 2005b, Adv. Space Res., 35, 711 [CrossRef] [NASA ADS]
Dasso, S., Mandrini, C. H., Démoulin, P., & Luoni, M. L. 2006, A&A, 455, 349 [EDP Sciences] [CrossRef] [NASA ADS]
Dasso, S., Nakwacki, M. S., Démoulin, P., & Mandrini, C. H. 2007, Sol. Phys., 244, 115 [CrossRef] [NASA ADS]
Démoulin, P. 2008, Annales Geophys., 26, 3113 [NASA ADS]
Démoulin, P., & Dasso, S. 2009, A&A, 498, 551 [EDP Sciences] [CrossRef] [NASA ADS]
Démoulin, P., Nakwacki, M. S., Dasso, S., & Mandrini, C. H. 2008, Sol. Phys., 250, 347 [CrossRef] [NASA ADS]
Farrugia, C. J., Janoo, L. A., Torbert, R. B., et al. 1999, in Solar Wind Nine, ed. S. R. Habbal, R. Esser, J. V. Hollweg, & P. A. Isenberg, AIP Conf. Proc., 471, 745
Feng, H. Q., Wu, D. J., & Chao, J. K. 2007, J. Geophys. Res., 112, A02102 [CrossRef]
Gold, T., & Hoyle, F. 1960, MNRAS, 120, 89 [NASA ADS]
Gulisano, A. M., Dasso, S., Mandrini, C. H., & Démoulin, P. 2005, J. Atmosph. Sol.-Terrestr. Phys., 67, 1761 [CrossRef] [NASA ADS]
Gulisano, A. M., Dasso, S., Mandrini, C. H., & Démoulin, P. 2007, Adv. Space Res., 40, 1881 [CrossRef] [NASA ADS]
Hidalgo, M. A. 2003, J. Geophys. Res., 108, 1320 [CrossRef]
Hu, Q., & Sonnerup, B. U. Ö. 2002, J. Geophys. Res., 107, 1142 [CrossRef]
Hu, Q., Smith, C. W., Ness, N. F., & Skoug, R. M. 2005, J. Geophys. Res., 110, A09S [CrossRef]03
Kilpua, E. K. J., Liewer, P. C., Farrugia, C., et al. 2009, Sol. Phys., 254, 325 [CrossRef] [NASA ADS]
Klein, L. W., & Burlaga, L. F. 1982, J. Geophys. Res., 87, 613 [CrossRef] [NASA ADS]
Leitner, M., Farrugia, C. J., Möstl, C., et al. 2007, J. Geophys. Res., 112, A06113 [CrossRef]
Lepping, R. P., Burlaga, L. F., & Jones, J. A. 1990, J. Geophys. Res., 95, 11957 [CrossRef] [NASA ADS]
Lepping, R. P., Berdichevsky, D. B., Szabo, A., Arqueros, C., & Lazarus, A. J. 2003, Sol. Phys., 212, 425 [CrossRef] [NASA ADS]
Liu, Y., Luhmann, J. G., Huttunen, K. E. J., et al. 2008, ApJ, 677, L133 [CrossRef] [NASA ADS]
Lundquist, S. 1950, Ark. Fys., 2, 361
Lynch, B. J., Zurbuchen, T. H., Fisk, L. A., & Antiochos, S. K. 2003, J. Geophys. Res., 108, 1239 [CrossRef]
Manchester, W. B. I., Gombosi, T. I., Roussev, I., et al. 2004, J. Geophys. Res., 109, A02107 [CrossRef]
Mandrini, C. H., Pohjolainen, S., Dasso, S., et al. 2005, A&A, 434, 725 [EDP Sciences] [CrossRef] [NASA ADS]
Mandrini, C. H., Nakwacki, M., Attrill, G., et al. 2007, Sol. Phys., 244, 25 [CrossRef] [NASA ADS]
Moon, P., & Spencer, D. E. 1988, Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. (New York: Springer-Verlag)
Morse, P. M., & Feshbach, H. 1953, Methods of Theoretical Physics, Part I (New York: McGraw-Hill)
Möstl, C., Farrugia, C. J., Biernat, H. K., et al. 2009, Sol. Phys., 256, 427 [CrossRef] [NASA ADS]
Mulligan, T., Russell, C. T., Anderson, B. J., et al. 1999, in Solar Wind Nine, ed. S. R. Habbal, R. Esser, J. V. Hollweg, & P. A. Isenberg, AIP Conf. Proc., 471, 689
Owens, M. J., Merkin, V. G., & Riley, P. 2006, J. Geophys. Res., 111, A03104 [CrossRef]
Riley, P., Linker, J. A., Mikic, Z., et al. 2003, J. Geophys. Res., 108, 1272 [CrossRef]
Riley, P., Linker, J. A., Lionello, R., et al. 2004, J. Atmos. Sol. Terr. Phys., 66, 1321 [CrossRef] [NASA ADS]
Romashets, E. P., & Vandas, M. 2005, Adv. Spa. Res., 35, 2167 [CrossRef] [NASA ADS]
Sonnerup, B. U., & Cahill, L. J. 1967, J. Geophys. Res., 72, 171 [CrossRef] [NASA ADS]
Trott, M. 2006, The Mathematica Guidebook for Numerics (Springer)
Vandas, M., & Romashets, E. P. 2003, A&A, 398, 801 [EDP Sciences] [CrossRef] [NASA ADS]
Vandas, M., Odstrcil, D., & Watari, S. 2002, J. Geophys. Res., 107, 1236 [CrossRef]
Vandas, M., Romashets, E. P., & Watari, S. 2005, Planet. Space Sci., 53, 19 [CrossRef] [NASA ADS]
Vladimirov, V. S. 1984, Equations of Mathematical Physics (Mir, Moscow)
Wu, C.-C., & Lepping, R. P. 2007, Sol. Phys., 242, 159 [CrossRef] [NASA ADS]

All Figures

$\begin{figure} \includegraphics[width=9cm, clip=]{12645f1.eps}\end{figure}$	Figure 1: Evolution of the mean error, Eq. (12), as a function of $\alpha$ for the least square fit of Eq. (11) to the boundary condition of Eq. (2) and the normalization of Eq. (3). The boundary is defined by Eq. (4) with a=0, and b=1 (continuous line) or b=2 (dashed line). The eigenvalues of $\alpha$ are found at the local minima of the mean error.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm]{12645f2.eps} \end{figure}$	Figure 2: Log-log plot of the smallest $\alpha$ -eigenvalue and the associated mean error, Eq. (12), as a function of the y-extension of the flux rope (parameter b). The three thicker curves are the numerical results for the boundary given by Eq. (4) and with a given in the inset. In a), the thin continuous line is the smallest eigenvalue of $\alpha$ for a rectangular boundary (Eq. (15)).
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=4.4cm, clip=]{12645f3a.eps} , \includegraphics[width=4.4cm, clip=]{12645f3b.eps} } \par \end{figure}$	Figure 3: Projected field lines orthogonal to the flux rope axis (isocontours of A, left panels) and isocontours of the magnetic field norm B ( right panels) for the first eigen solution (lowest $\alpha$ -eigenvalue, Fig. 2a) for an aspect ratio b=0.5. Both A and B are independently normalized to a maximal value of 1, and decrease monotonously from the flux rope center towards its boundary. The isocontours are equi-spaced between 0.1 to 0.9 in steps of 0.1. The isocontour 0.5 and the boundary are outlined with a thicker line. The top row is for a rectangular boundary and the second row for an elliptic boundary. The three bottom rows have boundaries defined by Eq. (4).
Open with DEXTER
In the text

$\begin{figure} \par {\includegraphics[width=4.4cm, clip=]{12645f4a.eps} , \includegraphics[width=4.4cm, clip=]{12645f4b.eps} } \par \end{figure}$	Figure 4: Projected field lines (isocontours of A, left panels) and isocontours of the magnetic field norm B ( right panels). The boundaries are defined by Eq. (4) with an aspect ratio b=1. The drawing convention is the same as in Fig. 3.
Open with DEXTER
In the text

$\begin{figure} \includegraphics[width=8.8cm, clip=]{12645f5.eps} \end{figure}$	Figure 5: Projected field lines (isocontours of A, top panels) and isocontours of the magnetic field norm B ( bottom panels). The boundaries are defined by Eq. (4) with an aspect ratio b=3. The drawing convention is the same as in Fig. 3.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm, clip=]{12645f6.eps} \end{figure}$	Figure 6: Examples of magnetic field found across the flux rope along the x-axis (y=0). B is the magnetic field norm and $\theta = -\tan^{-1}(B_y/B_z)$ . b=0.5 and 2 for the top and bottom panels, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm, clip=]{12645f7.eps} \end{figure}$	Figure 7: Magnetic pressure along the flux rope boundary (Eq. (4)) normalized to the maximum pressure (located at the flux rope center). The coordinate s ranges from s=0 at the front, to s=1 at the back.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm, clip=]{12645f8ab.eps} \includegraphics[width=8.5cm, clip=]{12645f8c.eps} \end{figure}$	Figure 8: Modification with b of the magnetic flux and helicity contained in the flux rope(per unit length along the axial direction). a) The maximum magnetic field strength is set to unity, b) the axial flux is normalized to the azimuthal flux, and c) the helicity is normalized to the product of the fluxes.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm, clip=]{12645f9.eps} \end{figure}$	Figure 9: Evolution of magnetic field ratio, r_B, defined by Eq. (27), as a function of $\log_{10} b$ , where b is the aspect ratio of the flux-rope cross-section. The averages are computed over 20% of the length along the cut across the flux rope. r_B is relatively independent of a as well as the y position of the cut in $y_{\rm p}$ , especially for low values of these parameters. The continuous lines are the numerical results, the dashed line represents the result for a rectangular boundary, Eq. (28) with $y_{\rm p}=0$ , and the dotted line is for the analytical approximation given by Eq. (29).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm, clip=]{12645f10.eps}\par \end{figure}$	Figure 10: Estimation of $\langle B_x\rangle/\langle B\rangle$ with averages computed along the entire cut of the flux rope (located at $y=y_{\rm p}$ ). The continuous lines are the numerical results and the dashed lines represent the analytical approximation given by Eq. (31). Two values of the distortion parameter are shown: a) a=0 and b) $a=-\sqrt {b}$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm, clip=]{12645f11.eps} \end{figure}$	Figure 11: Evolution of the asymmetry ratio $r_{\rm a}$ , defined by Eq. (32), as a function of $\log_{10} b$ . The averages are computed over 20% of the length along the cut across the flux rope at $y=y_{\rm p}$ . The drawing convention is the same as in Fig. 9.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.