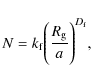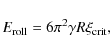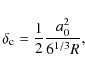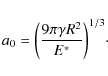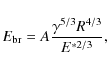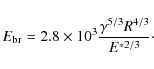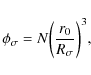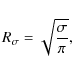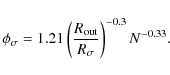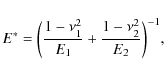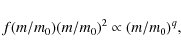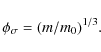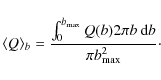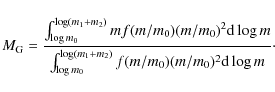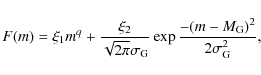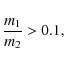Collisional evolution of dust aggregates. From compaction to catastrophic destruction

D. Paszun; C. Dominik

doi:10.1051/0004-6361/200810682

Free Access

Issue		A&A Volume 507, Number 2, November IV 2009


Page(s)		1023 - 1040
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/200810682
Published online		15 September 2009

A&A 507, 1023-1040 (2009)

Collisional evolution of dust aggregates. From compaction to catastrophic destruction

D. Paszun¹ - C. Dominik^1,2

1 - Sterrenkundig Instituut ``Anton Pannekoek'', Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
2 - Afdeling Sterrenkunde, Radboud Universiteit Nijmegen, Postbus 9010, 6500 GL Nijmegen, The Netherlands

Received 26 July 2008 / Accepted 15 August 2009

Abstract
The coagulation of dust aggregates occurs in various astrophysical environments. Each one is characterized by different conditions that influence the growth, e.g., relative velocities, composition, and size of the smallest constituents (monomers). Here we study the microphysics of collisions of dust aggregates in a four-dimensional parameter space. The parameters are the collision energy, the initial compactness of agglomerates, the mass ratio of collision partners, and the impact parameter. For this purpose we employ a state of the art molecular dynamics type of model that has been extensively and successfully tested against laboratory experiments. It simulates the motion of individual monomers interacting dynamically via van der Waals surface forces. The structure of aggregates is quantified by the filling factor that provides information about the internal structure, the packing density of monomers, and the projected surface area of aggregates. Our results show the importance of the impact parameter that causes formation of elongated particles, due to tensile forces acting in offset collisions. In head-on impacts, aggregates are compacted at lower energies. A sufficiently high energy causes restructuring to reach maximum compaction. If more energy is provided, pancake-like structures are formed. We find that the outcome of collisions can be represented in a simple way. A highly pronounced large fragment component coexists with a power-law distribution of small fragments. The structural parameter of these small fragments is described very well by a simple relation, largely independent of the initial compactness, impact energy or impact parameter. The simulations show that erosion by collisions with high mass-ratio can be significant. The ejected mass can be several orders of magnitude higher than the impactor mass. This contrasts with collisions of equal mass aggregates, where the same impact energy can lead to perfect sticking. These findings are summarized in the form of a simple collision recipe. The recipe specifies the outcome of a collision, averaged over the impact parameter. It is provided in tabular form for a range of physical parameters such as impact energy and pre-collision filling factor. The dependence on the mass ratio of impactor and target is taken into account by providing both a local and a global branch of the recipe.

Key words: planets and satellites: formation

1 Introduction

Dust plays an important role in many astrophysical environments, and it is also the building material of planets. Small grains can stick to each other thanks to van der Waals forces (Derjaguin et al. 1975; Johnson et al. 1971). Depending on the growth mechanism, the aggregates can acquire different structures. In low velocity collisions, which are dominant in the regime where particle velocities are dominated by Brownian motion, the narrow size distribution primarily leads to collisions between particles of a similar size, in turn leading to fractal aggregates. (Paszun & Dominik 2006; Kempf et al. 1999; Krause & Blum 2004; Blum et al. 2000). Fractals produced by Brownian growth have a typical fractal dimension of $D_{\rm f}=1.5$ (Paszun & Dominik 2006; Krause & Blum 2004), and higher gas densities shorten the mean free path of particles and result in even more fluffy structures. In the limiting case of very high densities, aggregates formed this way may be very elongated with the fractal dimension approaching unity (Paszun & Dominik 2006).

Velocities induced by turbulent gas motions and by radial drift in protoplanetary disks can be much higher. Furthermore, the dependence of velocities on particle size can become reversed, with larger particles moving faster than smaller particles. For a discussion of the relative velocities in protoplanetary disks, we refer the reader to a review article by Beckwith et al. (2000). Relative motion that emphasizes collisions between particles of different sizes leads to the production of aggregates with very different structures, because then the particles also grow by collecting smaller projectiles. In this case, the results are porous, non-fractal aggregates (Ball & Witten 1984; Paszun et al. 2009).

Low-impact velocities generally result in sticking. However, the growth of dust usually causes an increase in collision velocities when the particle start to decouple from the surrounding gas. When the collision energy becomes higher than the energy needed to roll monomers over each other (later referred to as rolling energy $E_{\rm roll}$ ), restructuring begins. Very fluffy and fractal aggregates are compacted upon collision (Blum & Wurm 2000; Dominik & Tielens 1997). A further increase in the impact velocity leads to compaction. However, eventually the kinetic energy is high enough to break contacts between individual monomers. Erosion then starts to remove parts of colliding aggregates. As the relative velocity increases further, erosion also becomes stronger, ultimately leading to the destruction of the aggregates.

Fragmentation of aggregates is a major obstacle in planet formation theory. Dust cannot grow all the way to form planetesimals because it gets destroyed once relative velocities become violent enough to disrupt aggregates. Similarly, radial drift may prevent growth by removing particles from the disk once they grow to a certain size and spiral towards the central star.

Johansen et al. (2006) show that, in the presence of turbulence, planetesimals might be produced by gravitational collapse of clumps of meter sized boulders. These clumps are generated by high-pressure turbulent eddies that trap and concentrate particles, which then become gravitationally bound. Before this process can take place, particles must already have grown by 18 orders of magnitude in mass. The only feasible way to do that is by collisional sticking. Because collisional fragmentation of aggregates may prevent growth of large, meter sized aggregates, it is crucial to fully understand mechanisms involved in collisions of porous aggregates.

Recently, Brauer et al. (2008) have studied the growth of dust particles in a local density maximum caused by the evaporation front at the snow line. This local pressure maximum in the disk can accumulate dust particles and reduce relative velocities considerably. In the midplane of the disk, weaker turbulence (Ciesla 2007) results in lower relative velocities. Brauer et al. (2008) have shown that for the fragmentation threshold velocity of at least 5 m/s, the growth can proceed to large boulders of up to several 100 m in size. However, a more realistic value of the threshold velocity, for aggregates made of micron-sized grains, is $\sim$ 1 m/s (Langkowski et al. 2008; Blum & Muench 1993; Poppe et al. 2000).

Blum & Wurm (2000) performed laboratory experiments of collisions of dust aggregates. They studied impacts at a wide range of energies, from low energy (perfect sticking), through restructuring to fragmentation of microscopic aggregates. Their results with respect to restructuring threshold are in agreement with theoretical findings of Dominik & Tielens (1997). The fragmentation energy, however, differs, which is a consequence of the discrepancy in sticking velocity. Poppe et al. (2000) measured the sticking velocity of micron-sized silica grains and found 1.2 m/s. Chokshi et al. (1993) and Dominik & Tielens (1997) on the other hand derived theoretically a much lower velocity, inconsistent with experiments. This problem was addressed by Paszun & Dominik (2008), who included an additional energy dissipation channel in order to match the experimental results. For details see Sect. 2.

Blum & Muench (1993) studied collisions of macroscopic, mm-sized, aggregates at velocities between 1 and a few m/s. In this case, however, a different behavior was observed. Although particles were very porous (up to $4\%$ filling factor) they did not observe restructuring. Instead, aggregates were bouncing off each other or, for faster impacts, fragmenting.

Very energetic collisions between large mm-sized and cm-sized aggregates were studied by Wurm et al. (2005). They showed that the fragmentation observed at high velocity impacts turns into a net growth of $50\%$ at velocities above 13 m/s. The distribution of fragments at velocities of about 20 m/s followed a power-law with a slope of $-5.6\pm0.2$ for larger fragments and was flat for the smallest ejecta.

Fujiwara et al. (1977) experimented with solid basalt rocks. High velocity impacts of a few km s^-1 result in a power-law distribution of small fragments $n(m) \sim m^k$ . The slope of the distribution was found to be k=-1.83. They distinguished several collisional outputs, depending on the target size:

1.: complete destruction;
2.: remaining core;
3.: transition from core to cratering;
4.: crater formation.

Sirono (2004) has developed a smoothed particles hydrodynamics (SPH) model to simulate meter sized and larger aggregates. A single particle in this model corresponds to a porous material described by compressive strength, tensile strength, density, and sound speed. This method was also used by Schäfer et al. (2007).

Although collisions of dust particles have been studied experimentally and theoretically, no one has formulated a quantitative recipe describing both mass distribution and structural properties of the collisional output, using a model based on empirical results. Both the distribution of masses and the compactness of fragments is required to fully understand the growth of dust. Here we present an extensive parameter study of many collisions of small dust aggregates. We provide a recipe for mass distribution and compactness of fragments.

In Sect. 2 we briefly present the model we adopt to simulate collisions of dust aggregates, it's strengths and limitations. In Sect. 3 we present findings of our study and discuss them qualitatively. Section 4 provides quantitative description of our results in a form of a collision recipe. We end this paper with interesting conclusions in Sect. 5.

2 The model

The simulations presented in this work are done using the N-body dynamics code SAND. Our model treats all monomers (also referred to as grains or particles) in the agglomerates (also referred to as aggregates, clusters, or particles) individually. Since we are currently not interested in long range interactions, electrostatic, magnetic and gravitational forces are not included even though the code can handle them (Dominik & Nübold 2002). We calculate motion of individual monomers that interact with each other via attractive van der Waals surface forces (Johnson et al. 1971).

The presence of the attractive surface on deformable particles inevitably leads to several energy dissipation mechanisms. The particles, when in contact, may roll over each other. This rolling motion is countered by a rolling friction force (Dominik & Tielens 1995), causing an energy loss. The same happens in the case of a sliding motion. The contacts may shift which again is work done against the sliding friction force (Dominik & Tielens 1996). Beside that, every time a contact between two monomers is broken, the elastic energy stored in it is partially lost (Johnson et al. 1971; Dominik & Tielens 1997; Chokshi et al. 1993). Some energy may also be lost due to a twisting motion of particles in contact (Dominik & Tielens 1997).

We also include an additional energy dissipation channel in order to fit the experimental results by Poppe et al. (2000). This process increases the sticking velocity from about $10~{\rm cm}~{\rm s}^{-1}$ (Dominik & Tielens 1997; Chokshi et al. 1993) to about $1~{\rm m}~{\rm s}^{-1}$ (Poppe et al. 2000). Since the measured attractive force agrees well with the theory provided by Johnson et al. (1971) and Derjaguin et al. (1975), the difference in sticking velocity points to additional energy losses in collisions. While our model does not specify what this mechanism is, a candidate would be plastic deformation of surface asperities on nm scales. In order to achieve agreement with the experimental results, a mechanism dissipating the energy upon the first contact of two particles was introduced (Paszun & Dominik 2008). For details regarding the implementation, we refer the reader to Dominik & Nübold (2002) and Paszun & Dominik (2008).

Although Paszun & Dominik (2008) tested the model extensively against the laboratory experiments and found a good agreement, this model has limitations as discussed below.

2.1 Limitations

Although our model presents a new approach to study collision dynamics of aggregates, the following limitations apply.

aggregate size Two monomers in contact oscillate in relative distance due to the competition between attractive forces that hold them together, and the elastic force that pushes them apart. For micron-sized grains (the monomers we consider here have radii of 0.5 $\ensuremath{\mu\mbox{m}}$ ) the vibration frequency is on the order of GHz. A correct simulation of this dynamical system requires that we must resolve the shortest timescales. These very short simulation time steps limit the number of monomers in the system we can model. The largest aggregates we can simulate are made of 10⁵ grains and take several hundreds of hours of a CPU time. In this study we model aggregates made of up to 1000 monomers.
The collisional outcome depends foremost on the strength of individual contacts in the impacting aggregates, thus the properties of monomers (size, composition). The aggregate size determines the amount of energy that can be dissipated ( $E_{\rm br}$ times the number of monomers). Note, however, that laboratory experiments of much larger aggregates (about 100 micron in size), made of billions of monomers, show phenomena not seen in the smallest aggregates. An example is bouncing (Langkowski et al. 2008). Although this is an important effect that significantly affects the growth of dust aggregates, it is still poorly understood;
irregular grains
Our model assumes spherical monomers, as the simulation of irregular grains is computationally very expensive and, therefore, is impractical. Moreover, we can directly compare our findings to the results of laboratory experiments (Blum & Wurm 2000). Here we briefly introduce the possible effect irregular grains may have on the collision outcome.
The strength of an aggregate strongly depends on the size of the contact between monomers. In the case of randomly shaped grains, contact is established between surface asperities and is very much limited. This reduces the strength of an aggregate and leads to disruption at lower impact energies. Moreover, irregular monomers can form more than one contact with each other, which means that individual contact points must break before restructuring can occur. In this way, chains of irregular particles can be more rigid than those made of spherical particles.
Poppe et al. (2000) performed laboratory experiments on both spherical and irregular grains. They showed that irregular particles can stick to a flat surface at much higher velocities than spherical grains (1.5 to 2.3 m s^-1 for spherical silica grains and 5 to 25 m s^-1 for irregular enstatite monomers). This suggests that additional energy dissipation may occur during a collision. The mechanism, however, is still unclear.
As the physical processes involved in collisions of irregular grains are unknown, we leave them for a future investigation. However, experiments have shown that the overall effects off collisions are well reproduced between experiments with spherical or round monomers (Langkowski et al. 2008). Therefore, we believe that the general conclusions of our study here will also hold for less perfect monomers.

2.2 Setup

A few examples of our aggregates, made of 1000 monomers each, are presented in Fig. 1. These particles consist of equal size monomers.

$\begin{figure} \par\includegraphics[width=14cm,clip]{10682fg01.eps} \end{figure}$	Figure 1: Sample aggregates used in our parameter study. Each of particles is made of 1000 monomers. Annotations show $\phi _\sigma$ for each particle. Black circles define the outer radius $R_{\rm out}$ , while gray circles indicate the projected surface equivalent radius $R_\sigma$ (see text).
Open with DEXTER

These aggregates are constructed using two different techniques. The first method, developed by Filippov et al. (2000), allows to create fractal aggregates of any specified fractal dimension $D_{\rm f}$ . This sequential tunable particle-cluster aggregation method forms agglomerates by successive addition of identical spherical particles. The fractal aggregates made according to this algorithm strictly obey the fractal scaling law (Filippov et al. 2000)

$\begin{displaymath}N=k_{\rm f}\Biggl(\frac{R_{\rm g}}{a}\Biggr)^{D_{\rm f}}, \end{displaymath}$

(1)

where $R_{\rm g}$ is the radius of gyration and $k_{\rm f}$ is the fractal pre-factor that is related to the central packing density. For the aggregates used in our study, we choose a pre-factor $k_{\rm f}=1.6$ and fractal dimensions of $D_{\rm f}=1.5$ , $D_{\rm f}=2.0$ , and $D_{\rm f}=2.5$ , respectively. We measure the filling factor of aggregates by considering a sphere with radius $R_\sigma$ , having a cross section $\pi R_{\sigma}^2$ which is equal to the projected surface of the aggregate, averaged over all angles (see Sect. 2.3.4). We then compute the filling factor $\phi _\sigma$ as the ratio of the solid volume in the aggregate and the volume of the equivalent sphere. With this definition, aggregates of the mentioned fractal dimensions, made of 1000 monomers, have filling factors $\phi_\sigma=0.07$ , $\phi_\sigma=0.09$ , and $\phi _\sigma =0.16$ , respectively.

The second method we use to produce aggregates is particle cluster aggregation (PCA). We successively add monomers from random directions. This method produces aggregates that, in the limit of very large sizes, have a filling factor of $\phi_\sigma=0.15$ . An aggregate made of 1000 monomers has, however, a lower filling factor of $\phi_\sigma=0.13$ . This is an effect of high porosity of the surface layer. In very large aggregates, this region will be negligibly thin compared to the size of an aggregate (Paszun et al. 2009).

2.3 Parameter space and expected scaling

To provide a qualitative and quantitative description of aggregate collisions, we explore an extensive parameter space. This provides an insight into the effects of different parameters on the outcome of a collision. As the final purpose is to provide a recipe for a collision between two aggregates, we limit the range of our parameters to realistic values.

The relevant parameters influencing the outcome of a collision are:

collision energy;
pre-collision compactness of the aggregate;
mass ratio of colliding particles;
impact parameter;
material properties of monomers.

The values used for the different parameters are shown in Table 1. The columns in the table refer to (1)- relative collision velocity v; (2)- pre-collision filling factor of an aggregate $\phi _\sigma$ ; (3)- impact parameter 5 $b/b_{\rm max}$ , and (4)-mass ratio of colliding aggregates m₁/m₂. Although not all combinations are simulated, each parameter set used it computed for six different orientations in order to obtain a fair average of possible collision outputs.

Table 1: Impact parameters and aggregate properties explored in this study.

2.3.1 Collision energy

The basic effect of impact energy is intuitive: The more energy is provided to the system, the more violent the outcome is. Dominik & Tielens (1997) and later Wada et al. (2007) provide a simple recipe of collisional output as a function of energy. Both these studies were limited to two dimensional aggregates. Their recipe predicts energy thresholds for processes such as erosion, compression, and fragmentation. To understand them, one needs to define the rolling energy and the breaking energy of a contact. The first one is the energy needed to roll two monomers over each other by 90 degrees, and it represents energy the related to restructuring of an aggregate. It is defined as (Dominik & Tielens 1997)

$\begin{displaymath}E_{\rm roll}=6\pi^2\gamma R \xi_{\rm crit}, \end{displaymath}$

(2)

where $\gamma$ is a surface energy, R is reduced radius of the two monomers in consideration, and $\xi_{\rm crit}$ is a critical displacement at which the rolling becomes irreversible and energy is dissipated. From measurements of the rolling friction between spheres it was shown that this quantity should be set to about 20 Å in order to reproduce the measured energy losses (Heim et al. 1999).

The second important quantity is the energy needed to separate two connected monomers and is defined as

$\begin{displaymath}E_{\rm br}=1.8 F_{\rm c} \delta_{\rm c}. \end{displaymath}$

(3)

Here $F_{\rm c}$ is the pull-off force, minimum force needed to disconnect two monomers and it is

$\begin{displaymath}F_{\rm c}=3 \pi \gamma R \end{displaymath}$

(4)

where $\delta_{\rm c}$ is the critical displacement from the equilibrium position (Dominik & Tielens 1997). Thus, two monomers in contact, when pulled apart, will separate at this position. $\delta_{\rm c}$ is defined as

$\begin{displaymath}\delta_{\rm c}=\frac{1}{2} \frac{a_0^2}{6^{1/3}R}, \end{displaymath}$

(5)

with the equilibrium contact radius

$\begin{displaymath}a_0= \biggl( \frac{9 \pi \gamma R^2}{E^*} \biggr)^{1/3}\cdot \end{displaymath}$

(6)

Putting these equations together we see that the critical energy is given by

$\begin{displaymath}E_{\rm br} = A \frac{\gamma^{5/3} R^{4/3}}{E^{\ast 2/3}}, \end{displaymath}$

(7)

with the dimensionless constant A=43.

The recipe of Dominik & Tielens (1997) is confirmed experimentally with one important modification (Blum & Wurm 2000). The energy scaling should be applied according to values determined empirically (i.e. $\xi_{\rm crit}\approx 20~{\rm\AA}$ and $E_{\rm br}$ corresponding to the experimental results). In order to satisfy this requirement, we introduce a scaled version of $E_{\rm br}$ . In this case the constant A is higher such that the sticking threshold in our model is in agreement with experiments (Poppe et al. 2000). This energy is given by

$\begin{displaymath}E_{\rm br} = 2.8\times 10^{3} \frac{\gamma^{5/3} R^{4/3}}{E^{\ast 2/3}}\cdot \end{displaymath}$

(8)

The recipe by Dominik & Tielens (1997) is summarized in Table 2.

Table 2: The collision recipe from Dominik & Tielens (1997) for a 2D case.

Low energies are insufficient to cause any visible restructuring. Before any restructuring occurs, contacts between monomers are displaced elastically. Only when the critical displacement is exceeded, an irreversible motion (i.e. rolling or sliding) follows. When the energy is sufficient to roll several contacts by a significant angle ( $\sim$ 90 degrees), monomers in the impact region begin to roll and visible restructuring occurs. The amount of restructuring increases with increasing energy. Maximum compression is typically reached, when all monomers have enough energy to roll by 90 degrees.

Monomers begin to be removed of an aggregate when the energy per contact reaches 3 times the breaking energy. A large fraction of the energy is then dissipated by rolling, but the excess is used to remove a few grains. As the impact energy increases, the amount of erosion increases and becomes catastrophic when each contact can access over 10 times the breaking energy.

Although this recipe is reasonable, it may differ when particles collide at an impact parameter other than b=0 or when the mass ratio of the two collision partners is not 1. The latter case was also considered by Dominik & Tielens (1997). They provided a recipe for collisions of a small grain with a cluster.

In this study we also explore the energy range from the hit-and-stick regime up to catastrophic destruction. This range of energies can be found by looking at a variety of astrophysical environments. For example, in protoplanetary disks, small particles are well coupled to the gas and have rather low relative velocities. In the cores of molecular clouds, however, low gas densities make it possible for particles to decouple from the gas even at small sizes. In this case, turbulent gas motions may lead to collisions velocities beyond the fragmentation limit (Ormel et al. 2009).

2.3.2 Mass ratio

The mass ratio is sampled within the available range of our model ( 10^-3 < m₁/m₂ < 1). As the largest aggregate simulated in this study is made of 1000 monomers, the lowest mass ratio we consider is m₁/m₂=10^-3 (a collision of a big aggregate with a monomer). Although we simulate collisions between particles with different mass ratios, we present only two limiting cases to illustrate the importance of the mass ratio.

This parameter influences the energy distribution during a collision. In the case of equal-mass impactors, the energy is spread over most of the monomers, causing a global effect. However, small projectiles act locally and concentrate the energy into a small volume close to the impact site. Thus, restructuring will be local and erosion can be expected at relatively low energies.

2.3.3 Impact parameter

Our sampling of the impact parameter $b\$ covers the range from a central impact up to a grazing collision, where the impact parameter b equals 95% of the sum of the outer radii of two colliding aggregates $R_{\rm out,1}+R_{\rm out,2}$ . We do not consider impact parameters above 95% as the irregular shape of aggregates generally causes such ``collisions'' to miss.

The impact parameter is important as it can significantly change the outcome of a collision. In the case of a central impact, aggregates are pushed towards each other and are compressed. Collisions with large impact parameters on the other hand cause aggregates to connect in the outer regions only and result in stretching of aggregates as they move apart again. In this way, large impact parameters tend to cause tensile forces acting on the aggregates, while central impacts are dominated by compressive stresses.

The importance of the off-center collisions should not be underestimated. Due to the geometrical arrangement, impacts with large impact parameter are considerably more frequent than head-on collisions. In impact parameter averaging, grazing impacts have a lot of weight.

2.3.4 Compactness parameter

To describe the structural changes of aggregates we define a compactness parameter $\phi _\sigma$ as

$\begin{displaymath}\phi_\sigma=N \biggl( \frac{r_0}{R_\sigma} \biggr)^3, \end{displaymath}$

(9)

where N is the number of monomers in the aggregate, r₀ is a monomer radius, and $R_\sigma$ is the projected surface equivalent radius (cf. Fig. 1), defined as

$\begin{displaymath}R_\sigma = \sqrt{\frac{\sigma}{\pi}}, \end{displaymath}$

(10)

with $\sigma$ being the projected surface averaged over many orientations. The inverse of this filling factor was introduced earlier by Ormel et al. (2007) as the enlargement factor $\psi$ . Note that this parameter alone is insufficient to fully describe the structure of an aggregate. An additional quantity is required to avoid ambiguity, e.g. the fractal dimension. However, for small aggregates such as the ones in this study, the possibilities to distribute mass within the particle are limited.

We sample the compactness parameter well within the applicable range. Random close packing (RCP) of spheres produces aggregates with the filling factor of about $\phi_\sigma\approx 0.635$ (Onoda & Liniger 1990) that is the densest form one can expect, given the assumption of spherical monomers. However, Blum et al. (2006) and later Paszun & Dominik (2008) have shown that aggregates being compressed can reach a maximum filling factor of about $\phi_\sigma= 0.33$ . Higher compaction cannot be achieved in a static experiment of uni-axial compression. As upper limit for the filling factor we use a slightly lower value of $\phi_\sigma=0.25$ . As lower limit, on the other hand, we use aggregates formed in the Brownian growth phase, where in the presence of rotation aggregates with the fractal dimension of about $D_{\rm f}=1.5$ are formed (Paszun & Dominik 2006; Krause & Blum 2004). Our largest aggregate of fractal dimension 1.5 has a filling factor $\phi_\sigma=0.07$ .

It is important to note the discrepancy between the radii used in the definition of the impact parameter space and the filling factor $\phi _\sigma$ . The impact parameter is defined in terms of the outer radius $R_{\rm out}$ , that is the radius of a sphere enclosing an entire aggregate and centered in its center of mass. The filling factor, however, uses the projected surface-equivalent radius $R_\sigma$ . For compact aggregates, these two radii are very similar, while the outer radius $R_{\rm out}$ becomes higher as the filling factor of an aggregate decreases. For completeness, we empirically determine the relation between the two radii. Figure 2 shows how the ratio $R_{\rm out}/R_\sigma$ influences the filling factor $\phi _\sigma$ .

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg02.eps} \end{figure}$

Figure 2:

he filling factor as a function of the ratio $R_{\rm out}/R_\sigma$ of the outer radius of an aggregate over its projected surface equivalent radius. Each point corresponds to an aggregate (see text) of different structure and mass and thus different ratio of the two radii. The dashed-dotted line shows the least square fit of the power-law to this data. A sharp transition between compact and fluffy particles occurs at about $R_{\rm out}/R_\sigma =1.2$ (dashed line). Compact aggregates have a smaller ratio of the two radii. Their filling factor is approximated by a separate power-law (dotted line).

Open with DEXTER

To obtain this relation we constructed (using Eq. (1)) many aggregates of different structures ( $D_{\rm f}$ , $k_{\rm f}$ ) and masses (N). Interestingly all data is very well confined along a simple curve. As the filling factor seems to depend on the mass of aggregate as $\phi_\sigma\propto N^{-0.33}$ , we plot $\phi_\sigma N^{0.33}$ in Fig. 2 to collapse all data on a single curve. This mass dependence is further discussed in Sect. 3.2. Compact particles in Fig. 2 ( $R_{\rm out}/R_\sigma<1.2$ ) have a similar outer radii $R_{\rm out}$ and projected surface equivalent radii $R_\sigma$ . They show little dependence of the $R_{\rm out}/R_\sigma$ ratio on the filling factor. Fluffy aggregates ( $R_{\rm out}/R_\sigma>1.2$ ) on the other hand show a power-law relation of the filling factor on the ratio of the two radii with a slope of -0.3. The fitted power-law is presented in Fig. 2 as dashed-dotted line. The complete relation that holds for ratio $R_{\rm out}/R_\sigma>1.2$ is given as

$\begin{displaymath}\phi_\sigma= 1.21 \left( \frac{R_{\rm out}}{R_\sigma} \right)^{-0.3} N^{-0.33}. \end{displaymath}$

(11)

2.3.5 Properties of monomers

The composition of monomers and their size strongly affect the strength of an aggregate. Both these parameters determine the breaking energy of two grains in contact and thus regulate the energy dissipation during a collision. Since normalization of the impact energy by the breaking energy puts monomer properties out of the equation, we study here only one monomer size and material. The physical parameters of Quartz used in our model are presented in Table 3. Other materials will be the subject of a future study.

Table 3: Properties of monomers used in this study.

Our monomers are silica spheres with a diameter of 1.2 $\ensuremath{\mu\mbox{m}}$ . The elasticity modulus $E^\ast$ is defined as

$\begin{displaymath}E^\ast = \biggl( \frac{1-\nu_1^2}{E_1} + \frac{1-\nu_2^2}{E_2} \biggr)^{-1}, \end{displaymath}$

(12)

where E_i and $\nu_i$ are the Young's modulus and the Poisson ratio of ith monomer, respectively.

3 Results and discussion

In this section we present results of our parameter study. We describe the collisional outcome in terms of the fragment mass distribution - growth versus fragmentation. Moreover, we keep track of the structure of the fragments formed in such a collision and present the collisional evolution of the structure of dust aggregates.

Our study spans a wide range of parameters. Here we select two specific cases for a detailed discussion of the effects seen in our study. Collisions of compact aggregates (filling factor of $\phi _\sigma =0.251$ for smaller aggregates and $\phi _\sigma =0.16$ for larger particles) are presented and compared with fluffy, fractal aggregates (filling factor of $\phi _\sigma =0.155$ for small aggregates and $\phi_\sigma=0.09$ for bigger ones). We use these two cases to illustrate the influence of compactness on the collisional outcome.

3.1 Fragment distribution

The products of a collision are generally quantified in terms of the fragment mass distribution. In the case of sticking, the resulting mass distribution contains one single element, with the mass given by the sum of impactor and projectile. With the onset of erosion, a second component appears - the distribution of small fragments, usually represented as a power-law of particle mass. While these are initially two clearly separated components, they can connect in increasingly destructive collisions.

3.1.1 The effect of impact energy

Basic mass distribution components

Although the impact energy seems to be the main quantity setting the mass spectrum after the collision, the collisional outcome depends very much on all parameters presented in Sect. 2.3. The largest collisional remnant is presented as a function of the impact energy in Fig. 3. At low collision energies, aggregates stick perfectly and the largest fragment contains the mass of both colliding particles. An increasing impact energy causes onset of erosion at the energy of about $E=0.1NE_{\rm br}$ . The fragmentation occurs at the energy of about $E\sim NE_{\rm br}$ , and depends also on the internal structure of the colliding aggregates and the impact parameter.

Compact aggregates with densely packed monomers ( $\phi _\sigma =0.251$ ) can sustain higher energies regardless of the impact parameter. Grains packed close to each other undergo more interaction, resulting in internal energy dissipation that is more efficient than in the case of loosely packed monomers ( $\phi _\sigma =0.155$ ).

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg03.eps} \end{figure}$	Figure 3: The mass of the largest collision remnant for central and offset collisions as a function of the impact energy. Diamonds correspond to compact aggregates, while triangles correspond to fluffy particles. Error bars indicate standard deviation and each point represents a mean value from 6 individual simulations (see Sect. 2.2).
Open with DEXTER

Interestingly, erosion occurs in off-center collisions already much earlier than in central collisions, while shattering has the opposite behavior: It occurs more readily in central collisions. Central impacts can cause catastrophic destruction at energies above $E=10NE_{\rm br}$ , while off-center collisions at this same energy usually cause two large fragments to remain and therefore must be classified as be classified as erosion. Both effects are caused by the distribution of the available impact energy within the colliding aggregates. In off-center collisions, the energy is concentrated into a small region of the aggregates and does break grain-grain connections locally near the point of impact. The remaining kinetic energy is then carried away by two massive fragments. In the limiting case of $(b=b_{\rm max})$ the interaction of the two aggregates occurs between only two monomers, if at all.

The degree of fragmentation during off-center impacts depends then on the packing density of grains in the two aggregates. Porous aggregates ( $\phi _\sigma =0.155$ ) show that even at very high energies, the energy is not efficiently absorbed by the aggregates, saving them from being shattered. However, in the case of compact aggregates, the mass of the largest collision remnant is significantly higher than in the case of central impact, but it decreases with an increasing impact energy.

The full mass distribution

A more complete picture is presented by studying the full distribution of fragment masses. This is illustrated for central impacts in Fig. 4. Collisions at

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg04.eps} \end{figure}$	Figure 4: Mass distribution resulting from head-on collisions of A&C - fluffy ( $\phi _\sigma =0.155$ ) and B&D - compact ( $\phi _\sigma =0.251$ ) aggregates at four different impact energies.
Open with DEXTER

intermediate speeds (top panels) erode aggregates and produce a number of small fragments. Both the power-law and the largest fragment components are present. Depending on the degree of erosion they can be separated or connected. However, the slope of the power-law remains more or less unchanged.

The distribution of small particles is defined as

$\begin{displaymath}f(m/m_0)(m/m_0)^2 \propto (m/m_0)^q, \end{displaymath}$

(13)

with the slope q depending on several parameters, including the internal structure of aggregates and the impact energy. Initially, too few small particles are produced and the power-law cannot be determined (e.g., for off-set impacts see Fig. 7a,b). In such a case we assume that the distribution is flat with the slope q=0, meaning equal mass per logarithmic mass interval. As the erosion progresses with increasing impact energy, the fitted slope remains at an approximately constant low value. Small particles slightly dominate the mass within this power-law distribution, since the slope is about $q \approx -0.3$ in the case of fluffy aggregates (Fig. 4a), and about $q \approx -1.2$ for compact aggregates (Fig. 4b). These slopes remain constant up to energies of about $E=NE_{\rm br}$ . Faster impacts provide sufficient energy to break all contacts in an aggregate. Therefore, full fragmentation sets in, which can significantly alter the fragment distribution. The head-on collision at energy of $E=3.66 N E_{\rm br}$ completely shatters fluffy aggregates with the largest fragment having only about 15% of the total mass. The large fragment component disappears altogether, shifting the entire mass into the power-law component with the now steeper slope $q\approx -1$ . Further increase in the energy results in heavier damage and a still steeper slope. At the energy of $E= 14.6 N E_{\rm br}$ the slope reaches $q\approx-2.5$ (see Fig. 4c). The steepening slope can be interpreted as monomers and very small fragments in the fragment distribution becoming dominant.

Although a similar trend is observed for compact particles ( $\phi _\sigma =0.251$ ), the fragmentation is not as effective as in the case of aggregates with $\phi _\sigma =0.155$ (see Fig. 4d). A head-on impact of compact particles at the energy of $E=3.66 N E_{\rm br}$ can still be classified as erosion. The large fragment component is still present and contains a significant fraction of the mass. This component is broader and is connected with the power-law distribution of small fragments, an effect which affects the determination of the slope. The slope appears to decrease to about $q \approx -0.3$ . However, an increase in the collision energy to $E= 14.6 N E_{\rm br}$ shatters the aggregates, leaving only the power-law component with a steeper slope of about $q\approx -1.7$ (see Fig. 4d).

The relation of the energy and the slope of the power-law distribution in central collisions is presented in Fig. 5. The left panel (a) shows the results for aggregates with compactness parameter $\phi _\sigma =0.155$ . The initially shallow and constant slope begins to steepen once the impact energy increases above $E=NE_{\rm br}$ . This behavior is similar for aggregates of different masses or for different mass ratio impacts. Note that for very weak erosion, the slope of the power-law cannot be determined and a value of q=0 is assumed. Shattering becomes catastrophic when the impact energy is increased by an order of magnitude. The slope steepens beyond q=-1, meaning that small particles dominate the mass spectrum. For small aggregates the distribution may be as steep as q=-2.5.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg05.eps} \end{figure}$	Figure 5: Slopes of the power-law size distribution of small fragments as a function of impact energy. Different symbols correspond to different masses of the colliding aggregates. The left panel (A) corresponds to fluffy aggregates ( $\phi_\sigma=0.09 \ldots 0.155$ ), while the right panel (B) shows the result of collisions between compact aggregates ( $\phi_\sigma=0.16 \ldots 0.251$ ).
Open with DEXTER

Compact particles behave in a similar manner (see Fig. 5b). In this case, however, the steepening occurs at slightly higher energies of about $E=5 N E_{\rm br}$ . Moreover, the steepening is limited in the explored energy range, and reaches values of q=-1.7. In this case, low energies also result in shallow slopes of the distribution and are again assumed to be q=0 when the data was too scarce to make a fit.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg06.eps} \vspace*{4mm} \end{figure}$	Figure 6: Mass distribution resulting from central collisions between a monomer and an aggregate made of 1000 grains. The presented distributions result from collisions with compact aggregate with the filling factor of $\phi _\sigma =0.16$ . Note that the energy is normalized to the reduced number of monomers $N_\mu =N_1N_2/(N_1+N_2)$ .
Open with DEXTER

3.1.2 The effect of impactor-to-target mass ratio

Below we discuss the effect of the mass ratio on the collision outcome. Although intermediate energies are required to erode particles in collisions of equal mass aggregates, this is not the case for impacts with high mass ratios, where the impact energy is localized to a small region, leading to erosion even in slow collisions. Figure 6 shows the fragment distribution produced in collision of a monomer with an aggregate made of 10³ grains. In these cases, the energy is sufficient to break only a low number of contacts and results in erosion. That same energy applied in a collision of equal mass aggregates results in a perfect sticking without any mass loss (cf. Fig. 3). This difference is a consequence of very localized energy input. The small particle (in this case a monomer) carries sufficient energy to break a number of contacts. This energy is transmitted locally to a limited number of grains rather than distributed over the entire target aggregate. The resulting ejecta can, due to the small physical size of the projectile, easily escape.

Similarly, off-center collisions (see Fig. 7) are characterized by distributions that resemble the erosion case. A highly pronounced large fragment component coexists with a power-law distribution of small fragments. The slope of the power-law is independent of the impact energy. It remains at about $q\approx -1$ for fluffy aggregates and $q\approx-0.6$ for compact particles even at very high energies above $E=10NE_{\rm br}$ . At low impact energies, the resulting distribution are

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg07.eps} \end{figure}$	Figure 7: Mass distribution as resulted from off-center ( $b=0.75\ b_{\rm max}$ ) collisions of A&C - fluffy ( $\phi _\sigma =0.155$ ) and B&D - compact ( $\phi _\sigma =0.251$ ) aggregates at four different impact energies.
Open with DEXTER

dominated by the largest fragment component and the slope of the power-law component is undetermined due to the low number of fragments.

Fluffy aggregates, when colliding at an energy of $E = 0.23 N E_{\rm br}$ and above, produce two large fragments that contribute to the big particles component and a few small particles. Compact aggregates can still grow at an energy of $E = 0.23 N E_{\rm br}$ , producing one large fragment containing most of the mass. At energies of about $E\approx N E_{\rm br}$ the erosion increases and the growth is stopped. The large fragment component contains now two large remnants of the initial aggregates. An increase of the collision energy causes mainly an increase in the mass in the power-law component, while the largest fragment remains weakly affected. In the case of compact aggregates ( $\phi _\sigma =0.251$ ), only very high energy impacts can significantly reduce the mass of the largest fragments (see Figs. 3 and 7d). For aggregates with lower packing density ( $\phi _\sigma =0.155$ ), the mass of the largest collision remnant seems to stabilize at a value of about $m_{\rm max}\approx 0.5 (m_1+m_2)$ once the impact energy exceeds $E=NE_{\rm br}$ . Very high energies influence the fragment distribution very weakly (see Figs. 3 and 7c).

The main effect of the impact parameter is that the energy is not transported very efficiently into aggregates. In the case of a central collision the kinetic energy is naturally transported efficiently into both aggregates, as the interaction spreads from the center (i.e., region right in between the aggregates) outwards. The monomers are pushed closer together, actively taking part in the energy dissipation. An increase in the impact parameter results in a decrease in the number of actively interacting grains. This means that fewer grains actually collide resulting in less fragmentation.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg08.eps} \end{figure}$	Figure 8: Schematic plot of the evolution of the fragment distribution as a function of different parameters.
Open with DEXTER

Our results show that the main factor determining the collisional outcome is the impact energy E. Other parameters influence the way this energy is transported to and distributed over the available monomers. Figure 8 shows a schematic picture of how the fragment distribution changes with variation of impact energy E, compactness parameter $\phi _\sigma$ , impact parameter b, and the mass ratio m₁/m₂. The arrows indicate schematically how the position and scaling of the different components of the fragment mass distributions shift as parameters vary.

3.2 Aggregate structure

3.2.1 Central collisions

The outcome of a collision can also be quantified in terms of the internal structure of the resulting aggregates. This quantity is very important as it determines the aerodynamic properties of aggregates and thus their relative velocities. Figure 9 shows examples of the effect of collisions involving aggregates with $\phi _\sigma =0.155$ . Central collisions evolve from the hit and stick regime through compaction and flattening to fragmentation. As the impact parameter increases, this path changes. Then the hit and stick regime is followed by the stretching regime, where aggregates are pulled into an elongated shape, exposing more surface in the process. Eventually, sufficient energy is reached to break fragile connection between the colliding aggregates, at the location of the highest stress. At this moment, two aggregates of similar mass are created. Depending on the impact parameter and energy, erosion may also occur in the vicinity of the interaction area.

This picture depends also on the initial compactness of the colliding aggregates. Particles with open structures (Fig. 9) are subject to drastic restructuring, while more compact ones are characterized by higher strength against compacting and tensile forces. For comparison we present the results

$\begin{figure} \par\includegraphics[width=14cm,clip]{10682fg09.eps} \end{figure}$	Figure 9: Images of aggregates formed in collisions at different impact energies E and at different impact parameters b. The aggregates have an initial filling factor of $\phi _\sigma =0.155$ . Top panels show the initial setup. Lower panels present result of a collision. Images are in different scales to show different processes, i.e. compaction or fragmentation.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=14cm,clip]{10682fg10.eps} \end{figure}$	Figure 10: Images of aggregates formed in collisions at different impact energies E and at different impact parameters b. Aggregates have the filling factor of $\phi _\sigma =0.251$ . Top panels show the initial setup. Lower panels present result of a collision. Images are in different scales to show different processes, i.e. compaction or fragmentation.
Open with DEXTER

for aggregates with geometrical filling factor of $\phi _\sigma =0.251$ in Fig. 10. In this case the produced aggregate is not stretched as much as in the case of more fluffy aggregate. Additionally, the erosion is much stronger at higher impact parameters. This is caused by the closer packing of monomers that enables more efficient energy transfer into the aggregates.

The quantitative picture is presented in Fig. 11. The geometrical filling factor is plotted as a function of the impact energy for central and off-center collisions. All post-impact aggregates are in the hit and stick energy regime, below a few times the rolling energy $E_{\rm roll}$ . This is consistent with the description provided by Dominik & Tielens (1997), where the visible restructuring occurs at impact energies above $5~E_{\rm roll}$ . However, the structure of the produced aggregate is different than that of the initial particles. Aggregates stick, forming dimer-like structure. Thus, they expose more surface area resulting in a decrease in the geometrical filling factor. This decrease depends on the initial structure of aggregates and appears to be more severe for compacter aggregates. In this case, particles cannot penetrate each other contrary to more open structure aggregates, where partial overlap hides some surface area. In fact, the difference is rather small, on the order of 20%, for both filling factors presented in Fig. 11.

Further increase in the impact energy, beyond $5~E_{\rm roll}$ , results in an increase of the filling factor. In the case of central collision aggregates undergo compression up to energy of about $0.5~ N~ E_{\rm roll}$ . At this energy, the maximum compaction is reached and this energy is close to threshold predicted by Dominik & Tielens (1997) and confirmed experimentally by Blum & Wurm (2000). The degree of compression depends on the initial compactness, as compact aggregates are more difficult to compress further. An aggregate with $\phi _\sigma =0.155$ reaches its maximum compression of about $\phi_\sigma=0.18 \pm 0.02$ , more compact than the pre-impact particles. A more compact aggregate with pre-impact filling factor $\phi _\sigma =0.251$ does not exceed it's initial compactness after impact. The maximum compression obtained in our study is somewhat lower than obtained in a quasi-static compression (Blum et al. 2006; Paszun & Dominik 2008). This, however, can be an effect of small aggregate sizes, where the filling factor is strongly affected by the porous outer layers (Paszun et al. 2009).

A further increase in the collision energy causes flattening and, formally, a decompaction of aggregates. Even thought the filled regions of the aggregates continue to show low porosity, the non-spherical global shape exposes more surface than a spherical structure would, leading to a decrease in the geometrical filling factor. In the case of fluffy aggregates with $\phi _\sigma =0.155$ , the flattening results in a small decrease in the compactness. At a collision energy of about $N~ E_{\rm roll}$ the maximum decompaction is reached and any further increase in the impact energy would lead to fragmentation. For more compact aggregates with initial $\phi _\sigma =0.251$ , however, the flattening is stronger, as the filling factor drops to about $\phi_\sigma\approx 0.18$ . This filling factor can is similar to what we have seen earlier in fluffy aggregates. Fragmentation is now only be reached at about $3~N~E_{\rm roll}$ .

3.2.2 The influence of the impact parameter

Off-center collisions, on the other hand, show different results. Energies that lead to compaction in central impacts also cause restructuring at large impact parameters. In this case, however, particles are pulled apart and stretched. Thus, more surface area is exposed resulting in a strong decrease in the geometrical filling factor $\phi _\sigma$ . The stretching energy regime extends, however, to lower energies than the compression regime. Aggregates connect with a lower number of contacts that are pulled off. Therefore, lower energy is sufficient to disconnect the two colliding aggregates. The critical energy is about $0.25~ E_{\rm roll}$ , and may be slightly higher for compact aggregates. Above that energy, two particles of similar mass are produced, accompanied by erosion. All small fragments produced both in central and off-center collisions closely follow a single power-law relation of

$\begin{displaymath}\phi_\sigma= (m/m_0)^{1/3}. \end{displaymath}$

(14)

The reason for this consistent behavior lies in the fact that the fragments are produced in highly dynamical events with energies close to breakup energies, allowing internal restructuring to lead to a scale-free structure.

3.2.3 Schematic representation

Figure 12 sketches a general picture of the structural evolution of aggregates. On the two axes, in arbitrary units, it shows filling factor and mass. We assume that initially, both impactor and target have equal properties, located at the center of the plot where the solid black curve starts. Along that curve, the impact energy increases in steps, and the position of points on that curve shows possible structures of the largest post-impact aggregate. The first segment shows the effect of a hit-and-stick collision, to double mass and lower filling factor, independently of impact parameter. At that point, the curve splits into two, for central (solid black) and grazing (gray) collisions. Higher impact energies can then, with equal mass, either increase or decrease the filling factor. Even higher energies move to the third point on each path. Grazing collisions return to the initial pre-impact properties, while central collisions go through a maximum compression point onto the fragmentation powerlaw $\phi_\sigma= (m/m_0)^{0.33}$ .

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg11.eps} \end{figure}$	Figure 11: The geometrical filling factor $\phi _\sigma$ as a function of impact energy for head-on (solid lines) and off-center (dashed lines) collisions. Black lines correspond to aggregates with lower initial filling factor of $\phi _\sigma =0.155$ , while gray lines correspond to higher filling factor of $\phi _\sigma =0.251$ .
Open with DEXTER

Small arrows in the sketch indicate how the different points shift around as model parameters are modified.

4 The recipe

In this section we put together the information regarding the collisional output in a form of a quantitative recipe. We provide the recipe in a form of tables that contain parameters needed to reconstruct appropriate distributions. Since the recipe is provided as discrete parameters, the intermediate cases should be interpolated. Our recipe describes two limiting cases separately. Equal mass collisions affect aggregates globally. Therefore we refer to this sub-recipe as the global recipe. On the other hand we have high mass ratio impacts that result in localized changes. This sub-recipe is referred to as the local recipe. In the case of large mass ratio collisions, we used impacts of monomers onto aggregates composed of 1000 grains. In this case, only central collisions were used to predict also the outcome of offset impacts, because the effects are extremely similar. This assumes that the geometry of the impact of small projectile onto a larger target depends on a local surface. Thus central and offset collisions should be indistinguishable. The only necessary correction is to exclude missed collisions that are more likely at larger impact parameters. The distinction between the two sub-recipes is described later in Sect. 4.5.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg12.eps} \end{figure}$	Figure 12: Sketch of the compactness evolution dependence on different parameters. See text.
Open with DEXTER

4.1 Average over the impact parameter

We present our recipe for aggregate collisions in an impact-parameter-averaged way. In this way, the recipe can be easily used in models that deal with size and structure distributions rather than individual particles. It is also possible to rewrite the recipe, keeping the impact parameter as one of the collisional parameters. This can be useful in a Monte-Carlo approach (Ormel et al. 2009) where individual collisions are treated.

Since we know the products of collisions at different offsets, we apply proper weights to the results. The weight for each impact parameter b is related to the fractional surface area of the ring with the radius b and width $\Delta b$ . Thus, grazing collisions get the highest weight, while the central impact has the lowest weight. The quantity Q averaged over the impact parameter is then given as

$\begin{displaymath}\langle Q\rangle_b = \frac{\int_0^{b_{\rm max}} Q(b) 2 \pi b\ {\rm d}b}{\pi b_{\rm max}^2}\cdot \end{displaymath}$

(15)

4.2 Hit and stick recipe

Although our simulations include the hit-and-stick energy regime, this growth mechanism strongly depends on the mass ratio and should be treated separately. The hit-and-stick growth is of little importance when only an insignificant mass is added before any restructuring occurs. Otherwise, an analytical prescription may be applied as in Ormel et al. (2009); Ossenkopf (1993); Ormel et al. (2007); Paszun et al. (2009).

4.3 Distribution of fragment masses

The simulation results have shown that collisions produce two components. The first component - the power-law of small fragments - is produced in high energy, head-on impacts resulting in erosion and fragmentation. The second component - the distribution of the largest fragments - is formed during low energy impacts, and also by grazing collisions at all energies. We model this component using (somewhat arbitrarily) a Gaussian distribution of particle masses. The overall effects seen in the previous chapter indicate that, as the energy increases, the Gaussian component will move its peak position to smaller masses, the powerlaw component will gain relative importance and will eventually steepen.

$\begin{figure} \par\includegraphics[width=14cm,clip]{10682fg13.eps} \end{figure}$	Figure 13: Distributions averaged over the impact parameter. Results for fluffy and compact aggregates at energies A: $E= 5.7\times 10^{-4} N E_{\rm br}$ , B: $E= 5.7\times 10^{-2} N E_{\rm br}$ , C: $E= 0.13 N E_{\rm br}$ , D: $E= 0.92 N E_{\rm br}$ , E: $E= 8.2 N E_{\rm br}$ , and F: $E= 14.6 N E_{\rm br}$ .
Open with DEXTER

The total set of parameters needed to reproduce such a distribution is presented in Table 4. The power-law component is determined by fitting a

Table 4: Quantities provided by the recipe to reproduce the mass distribution.

power-law to the first part of the distribution, which contains small fragments. That power-law is then subtracted from the distribution. The power-law slope and mass ratio of the two components is known at this point. The remaining part of the distribution is then used to determine the last two quantities, namely the mean and the width of the Gaussian component. The mean mass $M_{\rm G}$ is simply the mass-weighted mean mass of fragments in the Gaussian component

$\begin{displaymath}M_{\rm G} = \frac{\int_{\log m_0}^{\log (m_1+m_2)}m f(m/m_0) ... ...g m_0}^{\log (m_1+m_2)} f(m/m_0) (m/m_0)^2 {\rm d}\log m}\cdot \end{displaymath}$

(16)

The width of the Gaussian is chosen to obey two constraints:

1.: the Gaussian should have a sharp cut-off at masses larger than the total mass of colliding aggregates;
2.: the power-law component must dominate the low mass part of the distribution.

To obtain a representative fragment distribution, we average the mass spectrum over the impact parameters (see Sect. 4.1). Some impact-parameter-averaged distributions are shown in Fig. 13. The panels show the evolution of mass spectrum for both compact and fluffy aggregates. The effect of impact averaging is immediately visible through the presence of the large fragment component at all energies. At low energies, growth dominates, and from central collisions one would expect to only see the large mass component at the total mass. However, grazing collisions contribute in the original, pre-impact mass bin, and reduce the average mass of the large fragment component. An increase in the energy leads to the onset of erosion. Small fragments appear with a very flat slope of the power-law distribution. Further increase in the energy enhances the erosion. The component of small fragments grows and begins to steepen the powerlaw slope slightly. Eventually, growth changes into fragmentation. The large fragment component, however, remains in the distribution. Using impact-parameter-averages reduces both the effect of fragmentation and differences between fluffy and compact particles over what would be expected from head-on collisions.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg14.eps} \end{figure}$	Figure 14: The filling factor $\phi _\sigma$ averaged over the impact parameter vs. the collision energy scaled with the number of monomers N and in units of the rolling energy $E_{\rm roll}$ . The dashed areas correspond to the spread around the mean. The dotted lines indicate the initial value of the filling factor for the colliding particles.
Open with DEXTER

4.4 Compactness evolution

The filling factor $\phi _\sigma$ , similarly to mass spectrum, shows a different behavior in central and offset collisions, respectively. The effect of impact parameter averaging is presented in Fig. 14. Compact aggregates are decompressed. At higher energies of about $E=N E_{\rm roll}$ , aggregates undergo compression that mostly compensates the offset collisions and the dimer-like structure discussed in Sect. 3.2.

Fluffy aggregates also increase porosity in low energy collisions. The increasing energy, however, causes both a decrease in the mass of the largest fragment and compaction of the aggregates. Grazing collisions at a high energy produce aggregates with only weakly changed structure. Therefore, the structural change is dominated by compressing head-on impacts. A further increase in the collision energy results in stronger compression. The maximum filling factor of about $\phi_\sigma\approx 0.19$ is reached at $E=N E_{\rm roll}$ . Any further increase in the energy does not affect the porosity. Particles are completely disrupted and the filling factor is dominated by small, fluffy fragments.

Small fragments produced by erosion or fragmentation are easily described by a single power-law. Regardless of initial porosity of the impact energy, small particles have the filling factor given by Eq. (14).

4.5 Format

Our recipe provides parameters required to reconstruct mass distributions averaged over impact parameter. The distribution of fragment masses is given by $F(m)\ {\rm d}\!\log m= f(m)\ m^2\ {\rm d}\!\log m$ , where $f(m)\ {\rm d}m$ provides the number of particles of mass m in mass interval between m and $m+{\rm d}m$ . Thus, the functional form of our recipe consists of the two components and is given by

$\begin{displaymath}F(m)=\xi_1 m^{q} + \frac{\xi_2 }{\sqrt{2 \pi} \sigma_{\rm G}} \exp{\frac{-(m-M_{\rm G})^2} {2 \sigma_{\rm G}^2}}, \end{displaymath}$

(17)

where $\xi_1$ and $\xi_2$ are the normalization constants of the power-law component and the Gaussian, respectively. These constants are not provided since the distribution should be re-normalized in order to conserve the mass. Instead we give the mass ratio of the power-law and Gaussian components, which should be used to determine the mass and normalization constant in each component. The power-law component extends from a monomer mass to a quarter of the total mass.

Our recipe is provided in tabulated form. The parameters required to reproduce the collisional outcome may be interpolated linearly. Our parameter space is covered very well and spans from very fluffy aggregates of fractal dimension $D_{\rm f}=1.5$ through fluffy fractal ( $D_{\rm f}=2.0$ ) and non fractal PCA aggregates to very compact particles of $\phi _\sigma =0.251$ . The energy space is also well sampled. Our recipe is based on simulations from hit-and-stick regime up to a catastrophic destruction.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg15.eps} \end{figure}$	Figure 15: Algorithm to choose between local and global recipes.
Open with DEXTER

The main difference between the local and the global sub-recipes stems from the mass ratio between impactor and target. However, small projectiles, when carrying sufficient energy (i.e., impacting with very high speeds), may also shatter an entire large target aggregate, i.e. causing a global effect. Therefore, the global recipe must be used not only at mass ratio close to unity, but also at impact energies sufficient to globally affect the entire aggregate. Figure 15 presents an algorithm used to distinguish between the local and the global recipes. When a collision of aggregates characterized by their masses m_i, filling factors $\phi_i$ , and some material properties, occurs at a given impact energy, one must check whether the collision is in the recipe domain (restructuring or fragmentation) or in the hit-and-stick regime. The test checks whether the energy is sufficient to cause any restructuring. If the condition $E_{\rm coll} < 5 E_{\rm roll}$ is satisfied, the hit-and-stick mechanism is applied (for details see Ormel et al. 2007; Ormel et al. 2009). Otherwise, a second check is performed. The global recipe is applied if any of the two following conditions is true:

$\begin{displaymath}\frac{m_1}{m_2} > 0.1, \end{displaymath}$

(18)

$\begin{displaymath}E > 5 N E_{\rm br}. \end{displaymath}$

(19)

If none of the above is true, the local recipe must be used.

$\begin{figure} \par\includegraphics[width=14cm,clip]{10682fg16.eps} \end{figure}$	Figure 16: Parameters as a function of the filling factor and impact energy. Clockwise: mean mass of the Gaussian component, width of the Gaussian component, mass ratio of the power-law to Gaussian component, slope of the power-law.
Open with DEXTER

The recipe provides a description of the outcome of a collision between aggregates of the same filling factor. To describe collision of aggregates with different compactness, a mass weighted average filling factor must be determined

$\begin{displaymath}\langle \phi_\sigma\rangle_m = \frac{\sum_i \phi_{\sigma,i} m_i }{\sum_i m_i}\cdot \end{displaymath}$

(20)

Therefore, the filling factor that should be used is dominated by that of the more massive aggregate. In particular, the outcome of a collision between particles of different masses depends very much on the porosity of the target aggregates and how deep it can be penetrated. Collisions of equal mass particles, on the other hand, are not dominated by one species. Therefore, the contribution from both aggregates should be about equal. The compression or decompression is expected to be weaker than for fluffy particles, as compact aggregates are more resistant to restructuring (see Sect. 3).

4.6 A complete quantitative description

The mass distribution of the collisional outcome for equal mass colliding projectiles can be constructed using parameters read from Tables 6, 7. Figure 16 shows contour plots of the required 4 parameters. Intuitively, the mean mass of the large component (upper left panel) decreases with increasing energy. Similarly, the width of this component (upper right panel) decreases with increasing energy as a result of fragmentation and grazing collisions. Therefore, faster impacts cause formation of the largest fragments with the lower mass, and the tail of the Gaussian component decreases. This shattered mass shifts then to the small fragments power-law component. The power-law component does not exist at low energies and only large aggregates are produced in this stage due to growth and grazing collisions. Thus, the slope of this component (lower left panel) starts to decrease only at larger energies. Note that for a weak erosion, where the slope of the power-law cannot be determined we assume without loss of generality q=0.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10682fg17.eps} \end{figure}$	Figure 17: The change in the filling factor relative to the initial filling factor $\phi _\sigma ^{\rm ini}$ . $\phi _\sigma /\phi _\sigma ^{\rm ini}< 1$ indicates decompaction and $\phi _\sigma /\phi _\sigma ^{\rm ini} > 1$ means compaction.
Open with DEXTER

Figure 17 shows compression of aggregates in the global recipe. This contour plot illustrates Table 9. The low-energy collisions cause a decrease in the filling factor $\phi _\sigma$ for all aggregates. The effect of decompaction is similar for all particles, although the strongest decrease in $\phi _\sigma$ is observed for the most compact aggregates. Faster impacts result in compression and an increase in the filling factor. Aggregates with the lowest filling factor $\phi _\sigma$ show the lowest structural change. The density increases only by a factor of about $\phi_\sigma/\phi_\sigma^{\rm ini}=1.11$ at the highest energies. For very compact aggregates, at the same energy, this change is somewhat higher ( $\phi_\sigma/\phi_\sigma^{\rm ini}=1.22$ ). This value is strongly affected by fragmentation. The average largest collision remnant in this case consists of only 0.16 of the total mass. The maximum compression observed for head-on collisions at an energy of about $E=N E_{\rm roll}$ reaches only about 0.89 of the initial filling factor. This means that the average largest fragment is decompressed. Fluffy aggregates, both fractal and non fractal, show similar behavior. For these fluffy particles the boundary between decompaction and compression is at the energies of about $E=N E_{\rm roll}$ . The filling factor increases further at higher energies. The maximum compression is reached at highest energies. The largest fragment at this energy is about a quarter of the total mass, except of the most fluffy aggregates, that are very difficult to disrupt completely.

4.6.1 Global recipe

In this section we present tables containing the global recipe. They describe both the distribution of fragments (Tables 5-8) and the change in the filling factor of the largest fragment, relative to the initial $\phi _\sigma$ (Table 9).

The shape of the distribution of fragment masses depends on the number of contacts that can be broken. The higher the energy is, the stronger and steeper the power-law component is. Therefore, the collision energy is normalized to the breaking energy $E_{\rm br}$ . Moreover, the energy is distributed globally in the aggregates (hence the name global recipe). Therefore, the energy is also scaled with the total number of particles N (this is approximately equal to the number of contacts). The first column in each of Tables 5-8 shows the normalized energy $E/(N\ E_{\rm br})$ . The following four columns indicate the recipe output quantity (see Table 4) for aggregates with different initial filling factors $\phi _\sigma ^{\rm ini}$ . Table 5 presents the slope q of the power-law component of small fragments. The mass normalization can be done with the total mass of colliding aggregates m₁+m₂ and the ratio $M_{\rm r}$ of the mass in this power-law component over the Gaussian component given in Table 6.

Table 5: The slope of the power-law component.

Table 6: Mass ratio of the small fragments component (power-law) to the largest fragment component (the Gaussian).

The Gaussian component can be reconstructed using three quantities; the ratio of the mass in the two components $M_{\rm r}$ , the mean mass $M_{\rm G}$ , and the width $\sigma_{\rm G}$ . Table 7 provides the mean mass, and the width is given in Table 8.

Table 7: Mean mass of the Gaussian component normalized to the total mass.

Table 8: Width of the large fragments component (Gaussian) normalized to the total mass.

The change in porosity of aggregates depends on the number of contacts that can roll, as the rolling is the main mechanism responsible for the restructuring. Therefore, the energy in the first column of Table 9 is normalized to the rolling energy $E_{\rm roll}$ . The restructuring also affects the structure of aggregates globally. Thus, the collision energy is also normalized to the total number of monomers, which approximates the initial number of contacts. Table 9 shows the change in the geometrical filling factor $\phi _\sigma$ relative to the initial density $\phi _\sigma$ $^{\rm ini}$ . This new filling factor represents large fragments from the Gaussian component. The power-law component is simply described by Eq. (14).

The difference in energy scaling applied to the part of the recipe describing the fragment distribution and to the part of the recipe providing the compaction, respectively, accounts for cases of different material properties, where the ratio of the rolling energy $E_{\rm roll}$ to the breaking energy $E_{\rm br}$ may be different than for Quartz. Therefore, different physical processes (compaction/decompaction and erosion/fragmentation) are selected by different scalings, i.e., restructuring scales with the rolling energy, while the fragmentation scales with the breaking energy.

Table 9: A fractional change in the geometrical filling factor $\phi _\sigma /\phi _\sigma ^{\rm ini}$ , averaged over the impact parameter.

4.6.2 Local recipe

The local recipe describes the outcome of a collision between a small aggregate and a large target. For high energy impacts, erosion occurs, resulting in what is basically the large target aggregate accompanied by a distribution of small fragments. The energy is locally distributed over monomers of the small impactor and some surface grains of the target. Thus, in this case we scale the energy with the reduced number of monomers $N_\mu =N_1N_2/(N_1+N_2)$ , which basically is the number of grains in the small aggregate. As the erosion is determined by the number of contacts that can be broken, we scale the collision energy to the breaking energy $E_{\rm br}$ .

Table 10: Mean ejected mass relative to the projectile mass. The mass ratio of the colliding particles is 0.001.

Table 10 shows the mean mass that is ejected during a collision, relative to the mass of a smaller aggregate. The first column indicates the scaled energy, and the following four columns show the mean ejected mass for collisions of aggregates of different initial filling factors $\phi _\sigma$ $^{\rm ini}$ . The mass of the cratered target aggregate can then be immediately calculated.

The structure modification in the local recipe applies to the large target aggregate only, as the filling factor of small fragments follows a simple relation (see Eq. (14)). Bombarding large aggregates with small projectiles results in very small relative change in the filling factor (that of the target particle), as the filling factor quantifies the global structure of the large target aggregate. In this case, the energy scaling should thus be done in respect to the total number of monomers N, which is almost equal to the number of particles in the larger aggregate. Moreover, the restructuring mechanisms is determined by the number of monomers that can roll. Thus the energy is scaled by the rolling energy $E_{\rm roll}$ .

Table 11 presents the relative change in the geometrical filling factor for the target particle. The energy listed in the first column is normalized to the rolling energy $E_{\rm roll}$ and to the total number of monomers N.

Table 11: Relative change in the filling factor $\phi _\sigma /\phi _\sigma ^{\rm ini}$ . Mass ratio of the two colliding particle is 10^-3.

5 Conclusions and future work

In this work we present results of the extensive parameter study of collisions of three-dimensional aggregates. The outcome of a collision is provided in terms of the mass distribution of fragments as well as the structure of the produced particles. These simulations agree with the experimental results in this size regime and provide scaling that allows for extrapolation to slightly larger sizes as well as different material properties of monomers (i.e., composition and size of individual grains).

Our simulations indicate new important mechanisms that influence both the structure and the mass distribution of aggregates:

The restructuring of aggregates depends mainly on the collision energy. The compaction is reserved for head-on impacts, while offset collisions produce elongated and decompacted particles.
In the case of erosion and shattering, the structure of small fragments can be written in a very simple form (see Eq. (14)), regardless of the initial compactness of colliding aggregates or the impact energy.
The mass distribution of particles produced in a collision consists of two individual components. The power-law distribution of small fragments is accompanied by a strongly pronounced component of large fragments.
The shape of the mass distribution for the collision outcome averaged over the impact parameter is generally independent of the impact energy for slow collisions. At high energies, however, the shape of the distribution is almost independent of the structure of the colliding particles.

These points are combined together in a form of the recipe that provides the quantitative outcome of a collision. This recipe is formulated in a simple way that can be easily applied to models of dust coagulation in various environments (e.g., molecular clouds or protoplanetary disks). In fact, this recipe has already been applied to study growth of small dust aggregates in molecular clouds (Ormel et al. 2009).

Acknowledgements

We thank J. Blum for useful discussions and hospitality during several visits. We also thank M. Min for providing us with the program to produce the fractal aggregates and C. Ormel and A. Tielens for useful discussions that significantly improved the final shape of the recipe. The anonymous referee's careful review has lead to a useful resturcturing and compaction of the paper. We acknowledge SARA super computer center for access to the Lisa computer cluster, which made this parameter study possible. We also acknowledge financial support of Leids Kerkhoven-Bosscha Fonds. This work was supported by the Nederlandse Organisatie voor Wetenschapelijk Onderzoek, Grant 614.000.309.

References

Ball, R. C., & Witten, T. A. 1984, Phys. Rev. A, 29, 2966 [CrossRef] [NASA ADS]
Beckwith, S. V. W., Henning, T., & Nakagawa, Y. 2000, Protostars and Planets IV, 533
Blum, J., & Muench, M. 1993, Icarus, 106, 151 [CrossRef] [NASA ADS]
Blum, J., & Wurm, G. 2000, Icarus, 143, 138 [CrossRef] [NASA ADS]
Blum, J., Wurm, G., Kempf, S., et al. 2000, Phys. Rev. Lett., 85, 2426 [CrossRef] [NASA ADS]
Blum, J., Schräpler, R., Davidsson, B. J. R., & Trigo-Rodríguez, J. M. 2006, ApJ, 652, 1768 [CrossRef] [NASA ADS]
Brauer, F., Henning, T., & Dullemond, C. P. 2008, A&A, 487, L1 [EDP Sciences] [CrossRef] [NASA ADS]
Chokshi, A., Tielens, A. G. G. M., & Hollenbach, D. 1993, ApJ, 407, 806 [CrossRef] [NASA ADS]
Ciesla, F. J. 2007, ApJ, 654, L159 [CrossRef] [NASA ADS]
Derjaguin, B. V., Muller, V. M., & Toporov, Y. P. 1975, J. Colloid Interface Sci., 53, 314 [CrossRef]
Dominik, C., & Nübold, H. 2002, Icarus, 157, 173 [CrossRef] [NASA ADS]
Dominik, C. & Tielens, A. G. G. M. 1995, Philos. Mag. A, 72, 783 [CrossRef] [NASA ADS]
Dominik, C. & Tielens, A. G. G. M. 1996, Philos. Mag. A, 73, 1279 [CrossRef] [NASA ADS]
Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 [CrossRef] [NASA ADS]
Filippov, A., Zurita, M., & Rosner, D. 2000, J. Colloid Interface Sci., 229, 261 [CrossRef]
Fujiwara, A., Kamimoto, G., & Tsukamoto, A. 1977, Icarus, 31, 277 [CrossRef] [NASA ADS]
Heim, L., Blum, J., Preuss, M., & Butt, H. 1999, Phys. Rev. Lett., 83, 3328 [CrossRef] [NASA ADS]
Johansen, A., Klahr, H., & Henning, T. 2006, ApJ, 636, 1121 [CrossRef] [NASA ADS]
Johnson, K., Kendall, K., & Roberts, A. 1971, Proc. Roy. Soc. A, 324, 301 [CrossRef] [NASA ADS]
Kempf, S., Pfalzner, S., & Henning, T. K. 1999, Icarus, 141, 388 [CrossRef] [NASA ADS]
Krause, M., & Blum, J. 2004, Phys. Rev. Lett., 93, 021103 [CrossRef] [NASA ADS]
Langkowski, D., Teiser, J., & Blum, J. 2008, ApJ, 675, 764 [CrossRef] [NASA ADS]
Onoda, G. Y., & Liniger, E. G. 1990, Phys. Rev. Lett., 64, 2727 [CrossRef] [NASA ADS]
Ormel, C. W., Spaans, M., & Tielens, A. G. G. M. 2007, A&A, 461, 215 [EDP Sciences] [CrossRef] [NASA ADS]
Ormel, C. W., Paszun, D., Dominik, C., & Tielens, A. G. G. M. 2009, A&A, in press
Ossenkopf, V. 1993, A&A, 280, 617 [NASA ADS]
Paszun, D., & Dominik, C. 2006, Icarus, 182, 274 [CrossRef] [NASA ADS]
Paszun, D., & Dominik, C. 2008, A&A, 484, 859 [EDP Sciences] [CrossRef] [NASA ADS]
Paszun, D., Borel, H., & Dominik, C. 2009, A&A, submitted
Poppe, T., Blum, J., & Henning, T. 2000, ApJ, 533, 454 [CrossRef] [NASA ADS]
Schäfer, C., Speith, R., & Kley, W. 2007, A&A, 470, 733 [EDP Sciences] [CrossRef] [NASA ADS]
Sirono, S.-I. 2004, Icarus, 167, 431 [CrossRef] [NASA ADS]
Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2007, ApJ, 661, 320 [CrossRef] [NASA ADS]
Wurm, G., Paraskov, G., & Krauss, O. 2005, Icarus, 178, 253 [CrossRef] [NASA ADS]

Footnotes

... SAND: Soft Aggregate Numerical Dynamics.
... about: Although the value of 0.635 correspond to filling factor defined in respect to the outer radius $R_{\rm out}$ and not $R_\sigma$ , both radii are equal for these compact aggregates.
... study: The quantitative recipe presented in Sect. 4 does of course make use of the entire parameter study.
... contacts: Note that in Fig. 6 the energy is normalized to the reduced number of monomers 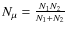$N_\mu=\frac{N_1N_2}{N_1+N_2}$ . Therefore, the energy per contact is a factor of 10³ lower than in the case of a collision of particles of equal mass.

All Tables