| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 549 - 571 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/200912844 | |
| Published online | 15 September 2009 | |
A&A 507, 549-571 (2009)
Soft gamma-ray sources detected by INTEGRAL
D. Petry1,2,4 - V. Beckmann2,3 - H. Halloin3 - A. Strong1
1 - Max Planck Institute for extraterrestrial Physics (MPE),
Giessenbachstr., 85748 Garching, Germany
2 - ISDC Data Centre for Astrophysics, Ch. d'Ecogia 16, 1290 Versoix,
Switzerland
3 - APC, UMR 7164, Université Paris 7 Denis Diderot, 10 rue Alice Domon
et Léonie Duquet, 75025 Paris Cedex 13, France
4 - now at European Southern Observatory, Karl-Schwarzschild-Str. 2,
85748 Garching, Germany
Received 18 July 2009 / Accepted 2 September 2009
Abstract
Aims. We aim to exploit the available INTEGRAL/SPI
data to provide time-averaged spectra of the brightest soft gamma-ray
sources.
Methods. Employing a maximum-likelihood fit
technique for our SPI data analysis, we take as input to our source
model the source catalog derived by Bouchet et al. (2008) from
a SPI all-sky study. We use the first four years of public SPI data and
extract spectra between 25 keV and 1 MeV for the
20 catalog sources detected by Bouchet et al. at
200-600 keV with ![]() 2.5
2.5![]() .
In order to verify our analysis, we also extract spectra for the same
sources from the corresponding INTEGRAL/ISGRI data.
We fit adequate spectral models to the energy range
25-1000 keV for SPI and 25-600 keV for ISGRI. We use
our spectra from the Crab (which is among the 20 sources
studied here) and an empty location in a crowded field to derive an
estimation of the systematic errors.
.
In order to verify our analysis, we also extract spectra for the same
sources from the corresponding INTEGRAL/ISGRI data.
We fit adequate spectral models to the energy range
25-1000 keV for SPI and 25-600 keV for ISGRI. We use
our spectra from the Crab (which is among the 20 sources
studied here) and an empty location in a crowded field to derive an
estimation of the systematic errors.
Results. The agreement between our SPI and ISGRI
measurements is good if we normalise them on the Crab spectrum. Our SPI
flux measurements also agree well with those by Bouchet et al.
(2008). All 20 sources in our sample are detected
independently in the bands 25-100 keV and
100-200 keV. At 200-600 keV we detect eight sources,
at 600-1000 keV we detect two sources. Our spectra agree well
with the results from previous publications where available. For six of
the 14 XRBs in our sample we find evidence for a hard
powerlaw-component which becomes dominant above the cutoff energy of
the thermal Comptonization component. In two of these cases, our study
provides the first indication of such emission. For the others, our
results confirm previous studies. Our spectrum of the Crab, integrated
over 1.3 Ms, shows a significant flux in all points and is
well described by a powerlaw with a break near 100 keV and
spectral indices 2.11 and 2.20.
Key words: gamma rays: observations - X-rays: binaries
1 Introduction
Soft gamma-rays have to be observed with satellite-based instruments, and so far there have been only three major missions taking data in the range from 100 keV to a few MeV with adequate sensitivity: GRANAT with the SIGMA instrument (Revnivtsev et al. 2004), CGRO with OSSE (Johnson et al. 1993) and COMPTEL (Schönfelder et al. 2000), and INTEGRAL with IBIS (Ubertini et al. 2003), and SPI (Vedrenne et al. 2003).
On INTEGRAL, the only soft gamma-ray observatory operational today, both the high-energy instruments, IBIS and SPI, are capable of measuring point source spectra. They complement each other in that IBIS provides angular resolution and good sensitivity at energies below a few 100 keV while SPI has superior energy resolution and high-energy sensitivity and permits the study of extended diffuse emission with its large field of view.
Sources of soft gamma radiation with photon energies between 100 keV and several MeV are astrophysically interesting because they permit us to study matter at supra-thermal energies. Essentially all known point-like emitters of such radiation consist of compact objects such as black holes or neutron stars which convert the gravitational energy of their surrounding matter or their own extreme rotational and magnetic energy into translational kinetic energy and then in turn partially into high-energy photons. The black holes come either as stellar black holes in X-ray binaries or as supermassive black holes in the centres of galaxies. All other sources of soft gamma-rays are spatially extended or unresolved and high in number-density. They form a continuum which seems, in the case of our Galaxy, to extend over the bulge and a significant part of the disk (Bouchet et al. 2005; Revnivtsev et al. 2006; Krivonos et al. 2007).
In the most recent all-sky study of INTEGRAL/SPI
soft gamma-ray data, Bouchet et al. (2008) have
presented a detailed analysis of both diffuse and point source emission
in the energy range from 25 keV to 600 keV based on
all SPI data from February 2003 up to
May 2006. They conclude that the diffuse component becomes
more prominent with increasing energy reaching 32% in the central
radian above 100 keV. The diffuse emission is bright over up
to ![]() 45
45![]() in galactic longitude and
in galactic longitude and ![]() 10
10![]() in galactic latitude depending on energy.
in galactic latitude depending on energy.
Bouchet et al. (2008),
B08 in the following, also present separate catalogs
of point sources for the four energy ranges 25-50 keV,
50-100 keV, 100-200 keV, and 200-600 keV
which they detect at least at a significance level ![]() 2.5
2.5![]() .
As the sensitivity of SPI relative to the steeply dropping
source spectra decreases with increasing energy and the diffuse
emission becomes more dominant, the number of detected point sources
decreases with increasing energy as well. In the energy range
200-600 keV a total of 20 sources are detected.
.
As the sensitivity of SPI relative to the steeply dropping
source spectra decreases with increasing energy and the diffuse
emission becomes more dominant, the number of detected point sources
decreases with increasing energy as well. In the energy range
200-600 keV a total of 20 sources are detected.
In this work, we take the B08 catalog for the energy range 200-600 keV and derive time-averaged INTEGRAL/SPI spectra for each of the 20 point sources contained in it. The resulting catalog of spectra of the 20 brightest soft gamma-ray sources will be useful to, among others, modellers of the hard X-ray and soft gamma-ray background caused by unresolved sources of the same source classes as in our catalog, high-energy observers of these sources who have to average over longer time-scales in order to achieve detections with acceptable significance, and generally researchers interested in the energy balance of the galaxy (most of the 20 sources are galactic).
We employ a newly developed maximum likelihood fit analysis technique based on the spimodfit software by Halloin & Strong (2007) to all public INTEGRAL data available for these sources (i.e. up to November 2006, the status when our dataset was frozen). In order to minimise inhomogeneities of our systematic uncertainties, the analysis method is not optimised for any individual source, in particular not for the Crab.
For comparison and verification of our method, we also derive the spectra for the same sources from the corresponding INTEGRAL/IBIS/ISGRI data.
This paper is meant to serve two purposes: (a) be a supplement to B08 and investigate the average spectra of the brightest known soft gamma-ray sources; and (b) demonstrate an analysis technique for INTEGRAL/SPI data based on spimodfit.
In Sect. 2, the SPI and ISGRI instruments are briefly introduced, and the observations and the data selection are described. Section 3 describes the analysis technique. Section 4 presents and discusses the spectra individually while Sect. 5 summarises the results, discusses them jointly and concludes.
2 Instruments and observations
This study uses data from the SPI and the ISGRI instruments on INTEGRAL. The properties of these instruments are discussed in detail elsewhere (see Vedrenne et al. (2003) and Roques et al. (2003) for SPI and Ubertini et al. (2003) for ISGRI). Here we just briefly summarise the main aspects.
The ISGRI instrument is part of the high-sensitivity
coded-mask imager IBIS. It has a fully coded field of view of 9![]()
![]() 9
9![]() ,
an angular resolution of 12' FWHM, and
a spectral resolution of 9% at 100 keV. Its well calibrated
energy range is 14 keV to ca. 700 keV. The
nominal continuum sensitivity (
,
an angular resolution of 12' FWHM, and
a spectral resolution of 9% at 100 keV. Its well calibrated
energy range is 14 keV to ca. 700 keV. The
nominal continuum sensitivity (
![]() ,
3
,
3![]() in 105 s) at 100 keV
is 3 mCrab.
in 105 s) at 100 keV
is 3 mCrab.
The SPI instrument is the coded-mask imaging high-resolution
spectrometer on INTEGRAL.
Its fully coded field of view has a radius of 8![]() .
With its 19 pixels (hexagonal, cooled Ge detectors)
it achieves an angular resolution of 2.5
.
With its 19 pixels (hexagonal, cooled Ge detectors)
it achieves an angular resolution of 2.5![]() FWHM.
The average
spectral resolution of the detectors deteriorates only marginally as a
function of energy from
FWHM.
The average
spectral resolution of the detectors deteriorates only marginally as a
function of energy from ![]()
![]() 1.8 keV below 200 keV to
1.8 keV below 200 keV to ![]()
![]() 4 keV at 3 MeV. This means, the relative
energy resolution improves from 0.9% at 200 keV to 0.13% above
3 MeV. The calibrated energy range is 25-8000 keV.
The nominal continuum sensitivity (as defined above for IBIS) at
100 keV is 16 mCrab. But above 1 MeV, the
continuum sensitivity for point sources becomes inadequate. Only the
Crab is detected at 1-8 MeV, and an electronic noise problem
between 1 and 2 MeV results in large systematic
errors in this interesting energy range. We therefore limit this study
to the range 25-1000 keV.
4 keV at 3 MeV. This means, the relative
energy resolution improves from 0.9% at 200 keV to 0.13% above
3 MeV. The calibrated energy range is 25-8000 keV.
The nominal continuum sensitivity (as defined above for IBIS) at
100 keV is 16 mCrab. But above 1 MeV, the
continuum sensitivity for point sources becomes inadequate. Only the
Crab is detected at 1-8 MeV, and an electronic noise problem
between 1 and 2 MeV results in large systematic
errors in this interesting energy range. We therefore limit this study
to the range 25-1000 keV.
Both energy resolution and sensitivity are time dependent: radiation damage degenerates the detectors leading to a deterioration of the energy resolution by a few tenths of a keV (negligible for continuum analysis) over timescales of months. This degradation is cured by regular annealings (controlled heatings) of the detectors. An annealing period lasts typically 12 days during which no science data can be taken.
While the spectral resolution is hence kept constant for our purposes, the sensitivity of SPI remains time dependent because the continued exposure to cosmic radiation leads to increasing background from the activation of all parts of the INTEGRAL satellite. In addition, the intensity of the cosmic radiation itself is strongly time dependent because of solar wind variablity (solar cycle) and solar flares. Over the course of the INTEGRAL mission so far, this has lead to a nearly steady increase in instrumental background. In November 2006, the instrumental background had increased by about 80% compared to the time shortly after launch (November 2002). It is expected that this trend will not continue (and possibly be reversed) beyond the end of the present solar minimum which has been a very prolonged one.
2.1 Data selection
The INTEGRAL data, as they are delivered to scientists, are subdivided into time periods of constant pointing, so-called science windows which typically have a duration of about 30 min. A second relevant time unit is the ``revolution'' or orbit which is important to the science analysis because the highly excentric orbit of the INTEGRAL spacecraft takes the instruments through the Earth's radiation belts every three days (``perigee passage'') making it necessary to temporarily switch off many of the INTEGRAL instruments including ISGRI. Observation scheduling and public data release is then organised per revolution.
This study is based on all available high-quality public data (at the time the dataset was frozen by us). These are the data from revolutions 21 to 500, i.e. from 15 December 2002 to 18 November 2006. From this time period, we select good data for each of the objects for which we want to derive spectra. The selection criteria are the following:
- 1.
- The angular distance between the pointing direction and the
position of the object of interest is required to be less
than 10
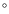 .
This is a compromise between maximum exposure time and maximum data
quality. For SPI the maximum off-axis angle could be further increased,
but for ISGRI, accepting data beyond 10
.
This is a compromise between maximum exposure time and maximum data
quality. For SPI the maximum off-axis angle could be further increased,
but for ISGRI, accepting data beyond 10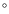 radius (which is well into ISGRI's partially coded field of view)
reduces the accuracy of the spectra significantly. Since INTEGRAL
does mainly pointed observations based on individual proposals (which
have emphasised galactic objects so far), the sky exposure
achieved by the INTEGRAL instruments up to now is
far from uniform. At low galactic latitudes our dataset
therefore contains up to a few thousand science windows while only a
few hundred are available for the typical object at higher latitudes.
radius (which is well into ISGRI's partially coded field of view)
reduces the accuracy of the spectra significantly. Since INTEGRAL
does mainly pointed observations based on individual proposals (which
have emphasised galactic objects so far), the sky exposure
achieved by the INTEGRAL instruments up to now is
far from uniform. At low galactic latitudes our dataset
therefore contains up to a few thousand science windows while only a
few hundred are available for the typical object at higher latitudes.
In those cases where a very large exposure is available, we can reduce the selection radius to 8
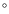 in order to improve data quality. Furthermore, if several objects of
interest form a
closely spaced group, we use a single dataset centred roughly on the
centre of the group.
in order to improve data quality. Furthermore, if several objects of
interest form a
closely spaced group, we use a single dataset centred roughly on the
centre of the group. - 2.
- Time periods where the data quality was known to be bad such as times near the radiation belt entry or exit of the spacecraft, times shortly after annealings, times during which solar flares strongly raised the background, or times during which hardware problems occurred, were excluded based on the publicly available database of such events included in the OSA software (version 7.0) provided by the INTEGRAL Science Data Centre (ISDC, Courvoisier et al. 2003). This results in the removal of about 31% of the archival data (based on elapsed time and averaged over the entire mission up to revolution 500).
- 3.
- In order to exclude time periods with problems which might
have been missed in the compilation of the database used in the
previous criterion, quality cuts were imposed on a number of
``housekeeping'' parameters using the SPI housekeeping database
compiled at MPE
![[*]](/icons/foot_motif.png) .
In particular, the cuts limited the values of the SPI detector
temperature, the veto rate of the SPI anti-coincidence shield (ACS),
the rate of SPI single interaction events, and the orbital phase. The
cuts were derived from inspecting the long term behaviour of these
parameters and assuming smoothness of their time dependence. The
orbital phase was conservatively limited to the range
between 0.1 and 0.87 in order to safely exclude any
radiation belt influence. These housekeeping parameter cuts removed
another 9.5% of the archival data (percentage defined as
above), mostly at the beginning of the mission.
.
In particular, the cuts limited the values of the SPI detector
temperature, the veto rate of the SPI anti-coincidence shield (ACS),
the rate of SPI single interaction events, and the orbital phase. The
cuts were derived from inspecting the long term behaviour of these
parameters and assuming smoothness of their time dependence. The
orbital phase was conservatively limited to the range
between 0.1 and 0.87 in order to safely exclude any
radiation belt influence. These housekeeping parameter cuts removed
another 9.5% of the archival data (percentage defined as
above), mostly at the beginning of the mission.
Table 1: The 20 objects investigated in this study and the properties of the corresponding datasets.
3 Data analysis
3.1 SPI data analysis using spimodfit
The spectral data analysis was carried out using the software packages spiselectscw v3.9 and spimodfit v3.0 (both written by Halloin & Strong 2007) with additional infrastructure software written by DP. The spimodfit package is part of the standard INTEGRAL data analysis software (OSA) since version 7.0.
Using spiselectscw, the data selection criteria described in Sect. 2.1 were applied to the calibrated and pre-binned data from the SPI database at the Max Planck Institute for extraterrestrial Physics. Using spimodfit, a source region model was then fitted to the selected data. The parameters of this model are in our case dynamically constructed by spimodfit from two main components:
- 1.
- an isotropic background component;
- 2.
- the contributions from those point sources which are
within 20
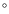 of the optical axis of the instrument for a given science window.
of the optical axis of the instrument for a given science window.
The common background scaling factor was permitted to vary on a short timescale of 2 h (corresponding to typically four science windows). This was the conservative choice determined by the actually observed changes in the overall event rate (which is strongly dominated by background) and the aim to minimise the number of model parameters in order to improve sensitivity.
The model components stemming from the point sources are
redetermined for every pointing: the algorithm first determines which
sources from the input catalog are within 20![]() of the pointing axis. Then the tabulated detector response (taking into
account the absolute time, spacecraft orientation, the coded mask
pattern, and the general spacecraft and instrument mass model) is used
to calculate the relative contribution of each source to the counts in
each detector. The model fit parameter is the common scaling factor of
the contributions in each detector, i.e. the source flux in
the time window corresponding to the pointing. Depending on the
variability timescale assumed for the individual source, this flux is
then assumed constant for a certain number of pointings.
of the pointing axis. Then the tabulated detector response (taking into
account the absolute time, spacecraft orientation, the coded mask
pattern, and the general spacecraft and instrument mass model) is used
to calculate the relative contribution of each source to the counts in
each detector. The model fit parameter is the common scaling factor of
the contributions in each detector, i.e. the source flux in
the time window corresponding to the pointing. Depending on the
variability timescale assumed for the individual source, this flux is
then assumed constant for a certain number of pointings.
When the model is constructed, all parameters are tested for
relevance, and parameters which
do not show an effect on the fit function are excluded. Using a maximum
likelihood fit which is initialised from a ![]() -fit, the
model is then fit to the data and the statistical errors are determined
from the covariance matrix. For more details see Halloin &
Strong (2007).
-fit, the
model is then fit to the data and the statistical errors are determined
from the covariance matrix. For more details see Halloin &
Strong (2007).
The entire analysis is carried out independently in each energy bin such that boundary conditions such as variability timescales and the input point source catalog can in principle be chosen differently for each energy bin.
In the largest of our datasets (the one containing
GRS 1758+258, see Table 1),
the
number of degrees of freedom is 74 292 per energy
bin, while the number of fit parameters is 2582. In the
smallest dataset (the one containing NGC 4151) there are only
665 degrees of freedom and 38 fit parameters per
energy bin. Thus, for an entire SPI spectrum with 17 energy
bins (see also the next section), the total number of degrees of
freedom in our datasets is between ![]() 11 000 and
11 000 and ![]() 1.3 million,
the number of fit parameters between 600
and 44 000.
1.3 million,
the number of fit parameters between 600
and 44 000.
The number of fit parameters is dominated by the background scaling factors and relative detector sensitivities. The source flux for an individual source from the input catalog constitutes only one fit parameter for each energy bin.
Unless otherwise noted, the reduced ![]() values of the model
fit in all energy bins for all results presented here were very close
to 1.0.
values of the model
fit in all energy bins for all results presented here were very close
to 1.0.
3.1.1 Energy binning
Our default energy binning was chosen a priori based on considerations of SPI energy resolution and flux sensitivity. It consists of 16 energy bins of logarithmically increasing width between 25 and 1000 keV. In addition, a narrow energy bin around 511 keV was inserted in order to check for possible annihilation radiation features.
As the analysis showed, many of our sources of interest are too weak to be detected significantly above 200 keV in individual bins of even this coarse (compared to the SPI energy resolution) energy binning. So a second wider binning consisting of 11 bins was introduced for weaker sources. The narrow and the wide binning have the first three bins (up to 48 keV) in common, then the wider binning roughly combines every two narrow bins up to 500 keV and after that every 3 narrow bins. The bin boundaries of the narrow binning are 25, 31, 39, 48, 60, 75, 93, 116, 144, 179, 223, 278, 346, 502, 520, 668, 832, and 1000 keV. The bin boundaries of the wider binning are 25, 31, 39, 48, 70, 103, 150, 219, 320, 502, 520, and 1000 keV.
3.1.2 Input catalog construction
![\begin{figure}
\par\includegraphics[width=18cm,clip]{1284401a.eps}\par\includegraphics[width=18cm,clip]{1284401b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg12.png)
|
Figure 1:
a) ( Top) the positions of
the sources from the input catalogs used in this study for the analysis
of the SPI data in three separate energy ranges:
catalog 1 (25-144 keV, crosses, 173 objects,
i.e. the entire B08 catalog), catalog 2
(144-346 keV, diamonds, 129 objects), and
catalog 3 (346-1000 keV, squares,
52 objects) on an all-sky map in galactic coordinates. The
20 objects investigated in this work are marked as thick
squares. The grid mesh size 15 |
| Open with DEXTER | |
As mentioned above, we base our input catalog on the one compiled by B08. This catalog comprises in total 173 sources and states fluxes for them in four energy bands (25-50 keV, 50-100 keV, 100-200 keV, and 200-600 keV). At low energies, all sources of the Bouchet catalog have to be included in the input catalog in order to have a complete model. But as the energy increases, many sources in the catalog drop below our flux sensitivity and need no longer be included. In order to optimise the sensitivity of our analysis, we therefore construct three separate catalogs for three energy ranges: (a) 25-144 keV; (b) 144-346 keV; and (c) 346-8000 keV. For range (a), we use the entire Bouchet catalog. For range (b) we use only those sources from the Bouchet catalog which are detected at 100-200 keV (i.e. a flux is stated in B08, not an upper limit) and which have at least 3 mCrab at 50-100 keV. Finally, for range (c) we include only those objects from the Bouchet catalog which have a flux >6 mCrab at 100-200 keV or which are marked as variable and detected at 50-100 keV. Figure 1 shows the positions of the sources in these three input catalogs in galactic coordinates.
The fraction of the sources from the input catalogs which are actually included in the model constructed by spimodfit for an individual dataset, depends on how crowded the field is and how widely spread the pointings are within the search radius. In our datasets (see Table 1) the number of sources included in the model ranges from 1 (in energy range (c) for the least crowded fields) to 83 (in energy range (a) of the most extended among our datasets, the one containing GRS 1758-258).
3.1.3 Time variability
The source variability is an important parameter in the flux extraction process. Bright and strongly variable sources can introduce some spurious features in the analysis if their model variability timescale is chosen too long and their true variability timescale and amplitude is large enough for SPI to detect a flux change.
We treat those sources as time-variable which are marked as such in the B08 catalog. These are the following 12 sources (in brackets we give the variability timescale chosen by us based on the ISGRI light curves (Courvoisier et al. 2008) and the sensitivity of SPI): 1A 0535+262 (180 ks), Vela X-1 (90 ks), GX 301-2 (90 ks), 4U 1700-377 (90 ks), IGR J17464-3213 (90 ks), Sco X-1 (90 ks), Swift J1753.5-0127 (2.6 Ms), Aql X-1 (180 ks), GRS 1915+105 (90 ks), Cyg X-1 (90 ks, 180 ks for E > 144 keV), EXO 0331 (2.6 Ms), Cyg X-3 (90 ks). Cyg X-1 is the only source which is significantly variable over the entire energy range. All other variable sources are only treated as signifcantly variable (given the SPI sensitivity) up to 144 keV.
The minimum timescales used here were determined from a study
of model fit convergence. We found that our model fits do not converge
well if we assume timescales much below 90 ks resulting
in increased statistical errors on all fit parameters. Particularly in
the case of the bright and strongly variable
source 4U 1700-377, B08 used a variability
timescale of ![]() 3 ks
(the minimum possible due to the way the data is stored). For
such sources, dedicated studies are necessary to further increase the
accuracy of spectra for short integration times. However, it is our aim
here to provide long-term average spectra with a coherent treatment of
all sources.
3 ks
(the minimum possible due to the way the data is stored). For
such sources, dedicated studies are necessary to further increase the
accuracy of spectra for short integration times. However, it is our aim
here to provide long-term average spectra with a coherent treatment of
all sources.
For the variable sources, the analysis yields a separate spectrum for each variability time bin, or in other words a separate light curve for each energy bin. We derive the average spectrum by applying a weighted least-squares procedure described in Alvarez-Gaumé et al. (2004), page 14, to the light curves from each energy bin.
3.1.4 Postprocessing and spectral model fitting
The analysis is sped up by processing each energy bin on a separate processor reducing the required computing time by about a factor equal to the number of energy bins, i.e. from several days to a few hours for each source data set.
In a final step, the data from each processor are collected, where necessary the time-averaging of the spectra is performed, and the spectra are converted to the PHA format suitable for the spectral analysis with XSpec 12.3.1 (Arnaud et al. 2007) which is then used for the fitting of spectral models taking into account the SPI response and energy-redistribution.
3.2 ISGRI data analysis
The analysis of the INTEGRAL IBIS/ISGRI data is based on a cross-correlation procedure between the recorded image on the detector plane and a decoding array derived from the mask pattern (see Goldwurm et al. 2003). Standard spectral extraction has been applied as provided by the OSA 7.0 software package, using the same energy binning and science windows as for the SPI data.
3.3 Statistical and systematic errors
The statistical errors of the photon count rates in each energy bin are determined both for the ISGRI and the SPI data by the fit software taking into account proper Poisson count statistics both for background and source signal.
In addition there is a systematic error on the flux
calculation stemming from the uncertainty of the calibration due to the
limited amount of calibration data and the propagation of other
uncertainties of the calibration process. We derive the relative error
of the calibration of the spectra by assuming a shape for the Crab
Nebula spectrum and independence of energy, i.e. that the
uncertainty caused by the error on the calibration is the same
percentage of the measured count rate for each energy bin.
This constant percentage is determined by varying it until the
reduced ![]() from the fit of the assumed spectral shape to the Crab spectrum is
close to 1.0 for the complete energy range.
from the fit of the assumed spectral shape to the Crab spectrum is
close to 1.0 for the complete energy range.
For both the ISGRI and the SPI data, we follow the INTEGRAL Cross-calibration status document by Jourdain et al. (2008) and assume the Crab Nebula spectrum between 25 keV and 1 MeV to be a broken powerlaw with break energy fixed at 100 keV (which is close to the break energy we actually measure, see Sect. 4.1). With this assumption we derive a calibration error of our ISGRI and SPI spectra of 0.5% in each energy bin. Unless otherwise noted, this error has been added in all spectral plots shown in this paper. For the fainter sources, it is, however, negligible.
The Crab is a bright source in a relatively quiet field
without many other neighbouring hard X-ray sources. In order
to assess the possible systematic errors arising in the analysis of
crowded fields in the galactic bulge where some of our
20 sources of interest are located, we have added a control
position to our input catalog at RA = 259.5![]() ,
Dec = -40.35
,
Dec = -40.35![]() (l = 347.7
(l = 347.7![]() ,
b = -2.1
,
b = -2.1![]() ). This position was randomly
chosen in an empty region (with respect to the B08 catalog) of
the crowded field near GX 354-0. The analysis for this
artificial reference source is discussed in Sect. 4.21.
). This position was randomly
chosen in an empty region (with respect to the B08 catalog) of
the crowded field near GX 354-0. The analysis for this
artificial reference source is discussed in Sect. 4.21.
4 Results
In this section we present our spectral analysis results and discuss the agreement of our SPI and ISGRI spectra with each other and with previously published measurements for each object in detail. The numerical results are later summarised in Tables 2, 3 and 5 in Sect. 5 where we also discuss the agreement with the fluxes given by B08.
Studying data below 25 keV would exceed the scope of this paper. Also, due to the small field-of-view of the INTEGRAL soft X-ray instrument Jem-X, a soft-X-ray dataset truly concurrent with our SPI and ISGRI dataset would have meant shrinking the SPI and ISGRI exposure by more than a factor two. When we compare to previously published measurements, this lack of soft X-ray data leads often to poorly constrained low energy features such as cutoffs near our lower energy limit (25 keV) or soft photon temperatures in thermal Comptonisation models. Where necessary, we try to overcome this by taking the appropriate values from the literature.
In the following, unless otherwise noted, the normalisation
parameters ``Norm'' or ``Norm1'' in the
spectral fit results are given in units of photons keV-1 cm-2 s-1.
They correspond to the flux at 1 keV. The letter ![]() designates a powerlaw spectral index. If we need to introduce a second
power-law component for high-energy emission, we use the XSpec model
PEGPWRLW with peg energy 200 keV. The normalization of it
(``Norm2'') is given as the differential flux
at 200 keV.
designates a powerlaw spectral index. If we need to introduce a second
power-law component for high-energy emission, we use the XSpec model
PEGPWRLW with peg energy 200 keV. The normalization of it
(``Norm2'') is given as the differential flux
at 200 keV.
In the figures in this section we show the spectra unfolded by XSpec with statistical errors (slightly increased by the calibration errors discussed in Sect. 3.3). The solid line always indicates the fitted model (as a step function according to the energy binning). If the model has several components, these are also separately shown with dashed lines.
4.1 Crab Nebula
The Crab Nebula is the standard candle of high-energy astronomy. Because of the steady, strong emission from this pulsar wind nebula, it has always been among the first objects to be observed by new instruments. For a recent compilation of X-ray data on the Crab see, e.g., Kirsch et al. (2005). Still, its high energy spectrum is not too well known. Many instruments use an assumption about the Crab's spectral shape as the basis of their calibration and can hence not say much about the fine details of the true spectrum. This is also the case for INTEGRAL/ISGRI. On the other hand, INTEGRAL/SPI with its high energy resolution could measure a Crab spectrum which is less dependent on such assumptions about the spectral shape.
Figure 2a shows the result of our analysis of the SPI Crab spectrum. A good fit is a broken powerlaw (XSpec model ``bknpow'') with the following parameters:
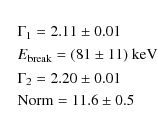
with a reduced
The corresponding ISGRI dataset gives the following Crab
spectrum (Fig. 2b):
![]() =
2.119
=
2.119 ![]() 0.006,
0.006, ![]() =
(96
=
(96 ![]() 4) keV,
4) keV, ![]() =
2.36
=
2.36 ![]() 0.02, Norm = 10.7
0.02, Norm = 10.7 ![]() 0.3, with a reduced
0.3, with a reduced ![]() of 1.3 for 11 d.o.f. (see Sect. 3.3).
of 1.3 for 11 d.o.f. (see Sect. 3.3).
This needs to be compared to our best fit for the SPI data.
The shape is in very good agreement below 100 keV.
Table 4
(see Sect. 5)
gives our measurements of the Crab flux in several energy bands. The
model fluxes between 25 and 100 keV (0.2287 ![]() 0.0004 cm-2 s-1
for SPI and 0.2046
0.0004 cm-2 s-1
for SPI and 0.2046 ![]() 0.0004 cm-2 s-1
for ISGRI) differ by a factor 1.11
0.0004 cm-2 s-1
for ISGRI) differ by a factor 1.11 ![]() 0.01 (SPI/ISGRI) which has to be regarded as a measurement of the
systematic difference in absolute flux normalisation.
0.01 (SPI/ISGRI) which has to be regarded as a measurement of the
systematic difference in absolute flux normalisation.
Above the fixed break, the ISGRI spectrum is significantly softer than the SPI spectrum. However, as the ISGRI response was made (by the authors of the OSA 7 ISGRI response) to give the Crab spectrum a powerlaw above 100 keV, this deviation tells us that there are probably significant systematic errors in the ISGRI calibration at the upper end of its energy range in addition to the calibration errors derived by us in Sect. 3.3.
Our SPI spectrum is in very good agreement with that derived from SPI data up to 1 MeV by Jourdain et al. (2008) whose analysis was not based on spimodfit. Furthermore, the smooth fit of the narrow energy bin around the 511 keV line, which is also a strong background line of the instrument, demonstrates that the background determination works well.
![\begin{figure}
\par\hspace*{1mm} \includegraphics[angle=-90,width=8.8cm,clip]{12...
...e*{3mm}
\includegraphics[angle=-90,width=8.7cm,clip]{1284402b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg18.png)
|
Figure 2: The unfolded spectra of the Crab Nebula as derived from dataset 1 (see Table 1) with statistical errors: a) ( top) SPI spectrum b) ( bottom) ISGRI spectrum; fit function is in both cases a broken powerlaw. Parameters of both fits are given in Sect. 4.1. |
| Open with DEXTER | |
4.2 Vela pulsar
![\begin{figure}
\par\hspace*{1.5mm}\includegraphics[angle=-90,width=8.8cm,clip]{1...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284403b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg19.png)
|
Figure 3: The unfolded spectra of the Vela Pulsar and Pulsar Wind Nebula derived from dataset 2 (see Table 1) with statistical errors: a) ( top) SPI spectrum; (b) ( bottom) ISGRI spectrum. Fit function is in both cases a simple powerlaw (parameters are given in Sect. 4.2). |
| Open with DEXTER | |
The other pulsar wind nebula/pulsar in our set of sources, the Vela PWN, is generally regarded as similar to the Crab. However, in hard X-rays the object is about two orders of magnitude fainter even though it is nearly an order of magnitude closer. It has been studied in detail by all high-resolution soft X-ray observatories (see e.g. Mangano et al. 2006, and references therein).
Figure 3a
shows the spectrum from our analysis of the SPI Vela Pulsar data.
Because of the weakness of the source, we choose the wider energy
binning in the SPI analysis. A simple powerlaw with ![]() =
2.13
=
2.13 ![]() 0.10, Norm = 0.12
0.10, Norm = 0.12 ![]() 0.05 describes the spectrum well. The reduced
0.05 describes the spectrum well. The reduced ![]() of the fit is 0.55 for 9 d.o.f.
of the fit is 0.55 for 9 d.o.f.
The SPI spectrum is in good agreement with our corresponding
ISGRI spectrum (Fig. 3b) which
has the
parameters ![]() =
2.04
=
2.04 ![]() 0.04, Norm = (0.057
0.04, Norm = (0.057 ![]() 0.008), with a reduced
0.008), with a reduced ![]() of 1.4 for 13 d.o.f.
of 1.4 for 13 d.o.f.
The hard X-ray spectrum of this source was studied up to
200 keV by Mangano et al. (2006) using
Beppo-SAX
data. They find a spectral index of 2.00 ![]() 0.05 at 15-200 keV which is in very good agreement with our
measurements.
0.05 at 15-200 keV which is in very good agreement with our
measurements.
At energies above 200 keV, our analysis does not show
significant evidence for emission. On the other hand, our
measurement is well consistent with a continuation of the spectrum in a
way similar to what we observe for the Crab. Given the nature of the
source and its morphological similarity to the Crab, this is to be
expected. OSSE detected the Vela PWN only marginally
between 200 and 760 keV with a spectral index of
1.8 ![]() 0.3 (Strickman et al. 1996b)
compatible with a continuation of our spectrum without
a break.
0.3 (Strickman et al. 1996b)
compatible with a continuation of our spectrum without
a break.
4.3 NGC 4151
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284404b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg20.png)
|
Figure 4: The unfolded spectra of NGC 4151 derived from dataset 3 (which has very low exposure, see Table 1) with statistical errors: a) ( top) SPI spectrum; b) ( bottom) ISGRI spectrum. The fit function is in both cases a powerlaw (parameters are given in Sect. 4.3). |
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284405b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg21.png)
|
Figure 5: The unfolded spectra of NGC 4945 derived from dataset 4 (which has low exposure, see Table 1) with statistical errors: a) ( top) SPI spectrum; (b) ( bottom) ISGRI spectrum. The fit function is in both cases a powerlaw with exponential cutoff and fixed photo-electric absorption (parameters are given in Sect. 4.4). |
| Open with DEXTER | |
The prototypical Seyfert galaxy NGC 4151 is one of the best studied active galaxies. For a comprehensive review on this object see Ulrich (2000). Unfortunately, this is our smallest dataset with less than 100 ks observation time. We show the resulting spectra here only for completeness. A detailed study of this source using INTEGRAL data up to 300 keV was published by Beckmann et al. (2005) (they use only ISGRI data and get a larger dataset by using data taken during SPI annealings).
Figure 4a
shows the SPI spectrum. The best fit is a simple powerlaw with
![]() =
2.10
=
2.10 ![]() 0.17, Norm = 0.38
0.17, Norm = 0.38 ![]() 0.25, and a reduced
0.25, and a reduced ![]() of 1.4 for 9 d.o.f. The excess in the annihilation
line bin is marginal (2.4
of 1.4 for 9 d.o.f. The excess in the annihilation
line bin is marginal (2.4![]() significance).
significance).
The ISGRI spectrum (Fig. 4b) gives
a
compatible fit result with ![]() = 2.03
= 2.03 ![]() 0.06, Norm = 0.24
0.06, Norm = 0.24 ![]() 0.05, reduced
0.05, reduced ![]() =
1.4 for 13 d.o.f.
=
1.4 for 13 d.o.f.
Fitting a powerlaw with exponential cutoff to the ISGRI data
as in Beckmann et al. (2005)
improves the fit slightly (![]() = 1.3)
and results in values well compatible with previously published
measurements:
= 1.3)
and results in values well compatible with previously published
measurements: ![]() =
1.57
=
1.57 ![]() 0.24,
0.24, ![]() =
121
=
121 ![]() 55 keV, Norm = 0.07
55 keV, Norm = 0.07 ![]() 0.04.
0.04.
4.4 NGC 4945
NGC 4945 is the brightest Seyfert 2 and the second brightest hard X-ray
source (after NGC 4151)
of all radio-quiet AGN (Done et al. 1996). Its
X-ray
spectrum has been extensively studied by various authors (see e.g. Itoh
et al. (2008)
and references therein). As a Seyfert 2, the source
is strongly absorbed at lower energies. Itoh et al. (2008) using Suzaku
measure a hydrogen column density ![]() of 5.4
of 5.4 ![]() 1024 cm-2 and a
hard X-ray spectrum with a powerlaw index of 1.5
1024 cm-2 and a
hard X-ray spectrum with a powerlaw index of 1.5
![]() and an exponential cutoff at
an energy of 150
and an exponential cutoff at
an energy of 150
![]() keV
(in agreement with previous measurements).
keV
(in agreement with previous measurements).
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284406b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg26.png)
|
Figure 6: The unfolded spectra of Cen A derived from dataset 5 (see Table 1) with statistical errors: a) ( top) SPI spectrum; b) ( bottom) ISGRI spectrum. The fit function is in both cases a powerlaw (parameters are given in Sect. 4.5). |
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...e*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284407b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg27.png)
|
Figure 7: The unfolded spectra of XTE J1550-564 derived from dataset 6 (see Table 1) with statistical errors: a) ( top) SPI spectrum; b) ( bottom) ISGRI spectrum (increased errors were required, see text). The fit function is in both cases a powerlaw with exponential cutoff (parameters are given in Sect. 4.6). |
| Open with DEXTER | |
Our dataset for NGC 4945, like the one for NGC 4151, has relatively low exposure. The hydrogen column density for this source is by far the highest of all the sources in our sample. We find that it is still low enough to be negligible for our SPI spectral modelling but the ISGRI sensitivity below 50 keV is high enough to make the spectral fits sensitive to the presence of the absorption. In order to compare better with previous measurements, we therefore include the photoelectric absorption in the spectral model (Xspec model WABS) and fit an absorbed powerlaw with exponential cutoff to the SPI and the ISGRI spectrum fixing the hydrogen column and the cutoff energy to the values found by Itoh et al. (2008).
Figure 5a
shows the resulting SPI spectrum. The best fit parameters are ![]() =
1.66
=
1.66 ![]() 0.17, Norm = 0.061
0.17, Norm = 0.061 ![]() 0.039 with a reduced
0.039 with a reduced ![]() of 0.4 for 9 d.o.f.
of 0.4 for 9 d.o.f.
The ISGRI spectrum is shown in Fig. 5b.
Keeping ![]() fixed as for SPI, the best fit parameters are
fixed as for SPI, the best fit parameters are ![]() = 1.56
= 1.56 ![]() 0.05, Norm = 0.033
0.05, Norm = 0.033 ![]() 0.006 with a reduced
0.006 with a reduced ![]() of 0.6 for 13 d.o.f.
of 0.6 for 13 d.o.f.
SPI and ISGRI spectrum are both consistent with each other and with the spectra measured by Itoh et al. (2008).
4.5 Cen A
The nearby radio galaxy Cen A has been observed by all X-ray
observatories (see Rothschild et al. 2006,
and
references therein). It has been classified as a Seyfert 2
(see Dermer & Gehrels 1995).
The consistently observed hard X-ray spectrum is, in spite of flux
variability, a simple powerlaw of index ![]() 1.8 (Rothschild
et al. 2006)
which extends to the MeV range where the spectrum steepens
(Steinle et al. 1998).
1.8 (Rothschild
et al. 2006)
which extends to the MeV range where the spectrum steepens
(Steinle et al. 1998).
Even though the available SPI exposure for Cen A is
modest, we obtain a clear detection also beyond 200 keV. The
SPI spectrum (Fig. 6a) gives
the best
fit parameters ![]() =
1.89
=
1.89 ![]() 0.05, Norm = 0.20
0.05, Norm = 0.20 ![]() 0.04, and a reduced
0.04, and a reduced ![]() of 1.2 for 9 d.o.f..
of 1.2 for 9 d.o.f..
Similarly, the ISGRI spectrum (Fig. 6b) gives a
best
fit with ![]() =
1.80
=
1.80 ![]() 0.02, Norm = 0.117
0.02, Norm = 0.117 ![]() 0.009 and a reduced
0.009 and a reduced ![]() of 0.9 for 13 d.o.f.
of 0.9 for 13 d.o.f.
SPI and ISGRI spectral shape are in excellent agreement with each other and previous measurements.
4.6 XTE J1550-564
The low-mass X-ray Binary XTE J1550-564 has been classified as a microquasar and a black hole candidate. Since its discovery in 1998 (Smith 1998) it has been subject of several detailed studies and was found to be similar to Cyg X-1, however, with lower luminosity (see e.g. Wu et al. 2007, and references therein). Sturner & Shrader (2005) studied the source using RXTE and INTEGRAL data and found that it stayed in its low-hard spectral state even when going through modest outbursts. According to the ISGRI lightcurve of the source (Courvoisier et al. 2008), XTE J1550-564 had only two short major outbursts with INTEGRAL coverage and was otherwise in a low state. The time-averaged spectrum we are determining here should therefore be close to the low-hard type, i.e. consistent with thermal Comptonisation which is essentially a powerlaw with exponential cutoff in our energy range.
We find that a powerlaw with exponential cutoff fits the
SPI data reasonably. From the SPI spectrum
(Fig. 7a)
we get the parameters ![]() =
1.36
=
1.36 ![]() 0.09,
0.09, ![]() =
(206
=
(206 ![]() 50) keV, Norm = 0.031
50) keV, Norm = 0.031 ![]() 0.010 with a reduced
0.010 with a reduced ![]() of 1.6 for 8 d.o.f.
of 1.6 for 8 d.o.f.
For the ISGRI spectrum we don't achieve a reduced ![]() below 2.0 with any common model (we tried cutoff powerlaw,
thermal Comptonisation, and black body + powerlaw) although
the residuals don't show any clear trend in the deviations. This can be
explained by additional systematic errors in the image reconstruction
caused by the complex source region. Allowing for this by doubling the
assumed calibration errors from 0.5% to 1.0% (see
also Sturner & Shrader 2005),
we get a reduced
below 2.0 with any common model (we tried cutoff powerlaw,
thermal Comptonisation, and black body + powerlaw) although
the residuals don't show any clear trend in the deviations. This can be
explained by additional systematic errors in the image reconstruction
caused by the complex source region. Allowing for this by doubling the
assumed calibration errors from 0.5% to 1.0% (see
also Sturner & Shrader 2005),
we get a reduced ![]() of 1.3 for 12 d.o.f. The best fit parameters are
marginally consistent with the ones obtained from the
SPI data:
of 1.3 for 12 d.o.f. The best fit parameters are
marginally consistent with the ones obtained from the
SPI data: ![]() =
1.00
=
1.00 ![]() 0.05,
0.05, ![]() = (108
= (108 ![]() 9) keV, Norm = 0.009
9) keV, Norm = 0.009 ![]() 0.002. This is due to higher photon fluxes measured by ISGRI below
200 keV. Above 200 keV, the fluxes are consistent
(cf. Table 5).
0.002. This is due to higher photon fluxes measured by ISGRI below
200 keV. Above 200 keV, the fluxes are consistent
(cf. Table 5).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{1284408.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg28.png)
|
Figure 8: The unfolded spectrum of 4U 1630-47 derived from the SPI dataset 7 (see Table 1) with statistical errors. The corresponding ISGRI data is flawed because of source contamination by IGR J16358-472 (see text). The fit function is a powerlaw (parameters are given in Sect. 4.7). |
| Open with DEXTER | |
For comparison with earlier publications, we also fit the thermal
Comptonisation model (COMPTT) by Titarchuk (1994)
which is
the best fit to the ISGRI and SPI data in Sturner & Shrader (2005).
Averaging
over their datasets, they obtain a plasma temperature kT =
(48.4 ![]() 2.7) keV, a plasma optical depth
2.7) keV, a plasma optical depth
![]() =
1.48
=
1.48 ![]() 0.07, and a soft photon temperature kT0 =
(0.5
0.07, and a soft photon temperature kT0 =
(0.5 ![]() 0.14) keV. Since we lack the data between 3 keV and
25 keV, kT0 is
not well constrained. We therefore fix it to the value 0.5 keV
by Sturner & Shrader. From the SPI data we then obtain
kT = (56.9
0.14) keV. Since we lack the data between 3 keV and
25 keV, kT0 is
not well constrained. We therefore fix it to the value 0.5 keV
by Sturner & Shrader. From the SPI data we then obtain
kT = (56.9 ![]() 7.7) keV and
7.7) keV and ![]() =
1.32
=
1.32 ![]() 0.18
(reduced
0.18
(reduced ![]() =
1.3 for 9 d.o.f.) in good agreement with Sturner &
Shrader.
=
1.3 for 9 d.o.f.) in good agreement with Sturner &
Shrader.
4.7 4U 1630-47
The X-ray transient 4U 1630-47 has been classified as a LMXB, a very
likely black hole candidate, and has also been found to show
indications of the presence of jets but is not yet regarded as a
microquasar (see Kubota et al. 2007, and
references therein). During the observation time covered by our
dataset, the source showed frequent but short outbursts. The
time-averaged spectrum should therefore be a superposition of the
various states the source can be in, with the low state dominating.
Tomsick et al. (2005)
analyse RXTE and INTEGRAL data
from 4U 1630-47. They distinguish five different spectral
states which they all fit with a two-component model made from a black
body with interstellar absorption and a powerlaw. They find that the
parameters of this model vary strongly between the states. The lowest
flux state is found to be the one where the emission is dominated by
black body emission (
![]() keV) below
15 keV, and above that by a steep powerlaw with index
keV) below
15 keV, and above that by a steep powerlaw with index
![]() .
A simple powerlaw is also the best fit to our spectra of this
on average relatively weak source.
.
A simple powerlaw is also the best fit to our spectra of this
on average relatively weak source.
The SPI spectrum for 4U 1630-47 (Fig. 8) is best
fit
by a powerlaw with ![]() =
3.3
=
3.3 ![]() 0.2 and Norm = 33
0.2 and Norm = 33 ![]() 21. The reduced
21. The reduced ![]() is 0.6 for 9 d.o.f.
is 0.6 for 9 d.o.f.
The ISGRI spectrum may suffer from source contamination from
the neighbouring source IGR J16358-4726, especially at higher
energies (see also Tomsick et al. 2005). We
try to
account for this approximately by increasing the systematic errors
to 5%. Fitting a powerlaw then results in ![]() =
2.33
=
2.33 ![]() 0.24, Norm = 0.04
0.24, Norm = 0.04 ![]() 0.04 with a reduced
0.04 with a reduced ![]() = 1.0 for
13 d.o.f. which is much harder than the SPI spectrum.
= 1.0 for
13 d.o.f. which is much harder than the SPI spectrum.
Furthermore, the observed fluxes (see Table 5) from SPI and ISGRI differ strongly at low energies while the SPI measurements agree with those from B08 who also note that the source may be confused with IGR J16358-472.
We conclude that the neighbouring source IGR J16358-472 may be hampering the measurement for ISGRI or SPI or both. Since this distortion is strongly dependent on the instrument characteristics, the effects are different for SPI and ISGRI and lead very probably to the observed difference in the spectra. The smaller differences between our spectra and those from Bouchet are to be expected since here the same instrument is used. The fact that the SPI spectrum agrees well with RXTE measurements of 4U 1630-47 in a low state by Tomsick et al. (2005) argues for the better quality of the SPI spectrum. Also, our source model for the SPI data explicitely includes IGR J16358-472. The SPI analysis should therefore in this case be more immune to contamination than the ISGRI analysis.
4.8 Swift J1656.3-3302
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{1284409.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg32.png)
|
Figure 9: The unfolded SPI spectrum of Swift J1656.3-3302 derived from dataset 10 (see Table 1) with statistical errors. The fit function is a powerlaw (parameters are given in Sect. 4.8). |
| Open with DEXTER | |
The recently discovered source Swift J1656.3-3302 (Okajima
et al. 2006)
has been identified with a high redshift (z = 2.4)
blazar (Masetti et al. 2008).
The late discovery of this source is due to its hard spectrum,
i.e. its weakness at soft X-rays, and to its location near the
galactic bulge which makes for a very complex field of view with many
variable and bright neighbouring sources. Probably because many bright
sources are very near the edge of the partially coded field of view
when Swift J1656.3-3302 is near its centre, our standard
modelling technique turned out to be inadequate for extracting a
SPI spectrum of Swift J1656.3-3302 from a dataset centred
at the source. The quality of the spimodfit fits was never acceptable
in more than a few energy bins. But when the source was observed by SPI
with high exposure and off-axis by at least 5![]() in the dataset selected for GRS 1758-258 (dataset 10,
see Table 1),
the extraction of a useful spectrum with our standard input catalog and
variability information was possible in all energy bins except for the
lowest two. The corresponding ISGRI spectrum of
Swift J1656.3-3302 from dataset 10, however, was not
useful since the object was too far outside the ISGRI fully coded field
of view. We therefore present in Fig. 9 only the
SPI spectrum for this source. It is well described by
a simple powerlaw with
in the dataset selected for GRS 1758-258 (dataset 10,
see Table 1),
the extraction of a useful spectrum with our standard input catalog and
variability information was possible in all energy bins except for the
lowest two. The corresponding ISGRI spectrum of
Swift J1656.3-3302 from dataset 10, however, was not
useful since the object was too far outside the ISGRI fully coded field
of view. We therefore present in Fig. 9 only the
SPI spectrum for this source. It is well described by
a simple powerlaw with ![]() =
1.49
=
1.49 ![]() 0.18 and Norm = 0.004
0.18 and Norm = 0.004 ![]() 0.005. The reduced
0.005. The reduced ![]() is 1.0 for 7 d.o.f.
is 1.0 for 7 d.o.f.
An ISGRI spectrum for Swift J1656.3-3302 was measured
by Masetti et al. (2008).
They find a spectral index of 1.64 ![]() 0.16 in agreement with our measurement.
0.16 in agreement with our measurement.
4.9 OAO 1657-415
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...e*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284410b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg33.png)
|
Figure 10: The unfolded spectra of OAO 1657-415 derived from dataset 7 (see Table 1) with statistical errors: a) ( top) SPI spectrum fit with powerlaw with exponential cutoff and additional powerlaw component b) ( bottom) ISGRI spectrum fit with powerlaw with exponential cutoff (with increased errors, see text). The fit parameters are given in Sect. 4.9. |
| Open with DEXTER | |
The high mass X-ray binary OAO 1657-415 is a system consisting
of an eclipsing 38 s pulsar and a highly reddened
B supergiant with orbital period 10.4 d (see e.g.
Audley et al. 2006,
and references therein). The object has been studied since its
discovery in the 1970s by a fair number of authors with several X-ray
observatories up to about 160 keV, recently also with INTEGRAL
(Filippova et al. 2005;
Barnstedt et al. 2008).
In the range from 3 to 160 keV they find consistently
an absorbed, exceptionally hard spectrum with index ![]()
![]() 1.0
which then softens with an exponential cutoff at energies
around 25 keV.
1.0
which then softens with an exponential cutoff at energies
around 25 keV.
We fit our time-averaged (and therefore also phase-averaged)
SPI spectrum initially with the simplest of these models, the
powerlaw with exponential cutoff. We obtain ![]() = 1.17
= 1.17 ![]() 0.23 and
0.23 and ![]() =
(23.9
=
(23.9 ![]() 3.2) keV with a reduced
3.2) keV with a reduced ![]() of 1.4 for 8 d.o.f., in good agreement with previous
measurements.
of 1.4 for 8 d.o.f., in good agreement with previous
measurements.
Inspecting the residuals, we find marginal evidence for a hard
tail diverging from the model above 150 keV. The feature is
not excluded by previous studies since they did not cover this energy
range. The significance of the hard tail is about 3![]() which does not warrant a much more detailed study. In order to quantify
the possible flux of this feature, we add a powerlaw to the model
keeping
which does not warrant a much more detailed study. In order to quantify
the possible flux of this feature, we add a powerlaw to the model
keeping
![]() fixed. This results in a lower
reduced
fixed. This results in a lower
reduced ![]() of 0.7 and best fit parameters
of 0.7 and best fit parameters ![]() = 1.23
= 1.23 ![]() 0.07, Norm1 = 0.16
0.07, Norm1 = 0.16 ![]() 0.04,
0.04, ![]() =
1.27
=
1.27 ![]() 0.58 and a flux of the second component at 200 keV of
0.58 and a flux of the second component at 200 keV of
![]()
![]() 10-6 cm-2 s-1 keV-1.
Figure 10a
shows the fit result with the added powerlaw.
10-6 cm-2 s-1 keV-1.
Figure 10a
shows the fit result with the added powerlaw.
For the ISGRI data, we increase the statistical errors by 5% of the flux in order to get take into account the larger systematic uncertainties of the analysis (this is the same dataset as the one for 4U 1630-47 where this increase was also necessary).
If we fit the same model with added powerlaw as for the
SPI data, we get reduced ![]() of 0.4 for 10 d.o.f. compatible with the
SPI fit. The parameters of the second powerlaw are essentially
unconstrained. The reality of the potential hard tail in the
SPI data is not ruled out.
of 0.4 for 10 d.o.f. compatible with the
SPI fit. The parameters of the second powerlaw are essentially
unconstrained. The reality of the potential hard tail in the
SPI data is not ruled out.
If we fit with the powerlaw with exponential cutoff without
the second powerlaw, we get a reduced ![]() of 0.4 for 12 d.o.f. and best fit parameters
of 0.4 for 12 d.o.f. and best fit parameters ![]() =
1.4
=
1.4 ![]() 0.3,
0.3,
![]() = 25
= 25 ![]() 4 keV, Norm = 0.23
4 keV, Norm = 0.23 ![]() 0.21 which is well compatible with the SPI data. This spectrum
in shown in Fig. 10b.
0.21 which is well compatible with the SPI data. This spectrum
in shown in Fig. 10b.
4.10 GX 339-4
The microquasar GX 339-4 in one of the classical black hole
X-ray binaries and has been studied by all X-ray and soft gamma-ray
observatories, also with Swift (Tomsick
et al. 2008)
and INTEGRAL (see Joinet et al. 2007, who
also
give a review of the literature). Like other black hole binaries, the
source has two main states, the low-hard state during which the
high-energy spectrum is essentially a powerlaw with index ![]() =
1.4-2.1 with an exponential cutoff at hundred to a few
hundred keV, and the high-soft state during which
=
1.4-2.1 with an exponential cutoff at hundred to a few
hundred keV, and the high-soft state during which ![]() goes to values
goes to values ![]() but without cutoff (see again Joinet et al. 2007).
Studies of
the soft-gamma ray emission with OSSE have also found emission up to
400 keV (Grabelsky et al. 1995).
Joinet
et al. (2007)
found evidence for emission above 200 keV in the low-hard
state at the 5
but without cutoff (see again Joinet et al. 2007).
Studies of
the soft-gamma ray emission with OSSE have also found emission up to
400 keV (Grabelsky et al. 1995).
Joinet
et al. (2007)
found evidence for emission above 200 keV in the low-hard
state at the 5![]() level.
level.
![\begin{figure}
\par\hspace*{1.5mm}\includegraphics[angle=-90,width=8.7cm,clip]{1...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284411b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg36.png)
|
Figure 11: The unfolded spectra of GX 339-4 derived from dataset 8 (see Table 1) with statistical errors: a) ( middle) SPI spectrum fit with two-component model: powerlaw with exponential cutoff and second powerlaw. b) ( Bottom) ISGRI spectrum fit with the same model as in a). The fit parameters are given in Sect. 4.10. |
| Open with DEXTER | |
Our time-averaged spectrum should be a superposition of all states of
the object. As a first step, we fit a simple powerlaw to the
data and obtain index ![]() =
2.08
=
2.08 ![]() 0.04, Norm = 0.35
0.04, Norm = 0.35 ![]() 0.05 with a reduced
0.05 with a reduced ![]() of 1.2 for 15 d.o.f. The residuals are systematically
negative from 100-300 keV but seem to be systematically
positive above 300 keV indicating a hard tail. The
significance of the emission above 200 keV is 6.4
of 1.2 for 15 d.o.f. The residuals are systematically
negative from 100-300 keV but seem to be systematically
positive above 300 keV indicating a hard tail. The
significance of the emission above 200 keV is 6.4![]() .
.
The same fit applied to the ISGRI data gives a good
reduced ![]() of 0.6 for 13 d.o.f. and best fit parameters
of 0.6 for 13 d.o.f. and best fit parameters ![]() =
2.07
=
2.07 ![]() 0.04 and Norm = 0.10
0.04 and Norm = 0.10 ![]() 0.01 confirming the shape of the SPI result up to
200 keV. Beyond 200 keV, the ISGRI result is
not sensitive enough. As in the SPI spectrum, there
is no evidence for a cutoff. A hard tail cannot be
ruled out by the ISGRI data.
0.01 confirming the shape of the SPI result up to
200 keV. Beyond 200 keV, the ISGRI result is
not sensitive enough. As in the SPI spectrum, there
is no evidence for a cutoff. A hard tail cannot be
ruled out by the ISGRI data.
In order to improve our fit to the SPI data and to better be able to compare with previous measurements, we fit a more complex model consisting of two components: (a) a powerlaw with exponential cutoff (in our energy range this is equivalent to a thermal Comptonisation model, one of the main candidate emission mechanisms for microquasars, see Sect. 4.6) and (b) an additional powerlaw in order to describe a potential hard tail which may obscure the observation of a cutoff in our spectrum.
Since we lack the soft X-ray data to better constrain the
cutoff energy, we fix it to 100 keV consistent with previous
measurements (if
![]() is permitted to vary freely,
we get a best fit value of 88
is permitted to vary freely,
we get a best fit value of 88 ![]() 56 keV). Figure 11a shows
the
result of this fit. The best fit parameters are
56 keV). Figure 11a shows
the
result of this fit. The best fit parameters are ![]() = 1.6
= 1.6 ![]() 0.1, Norm1 = 0.09
0.1, Norm1 = 0.09 ![]() 0.03,
0.03, ![]() =
1.0
=
1.0 ![]() 0.6, Norm2 (Flux at 200 keV) =
0.6, Norm2 (Flux at 200 keV) =
![]()
![]() 10-6 cm-2 s-1 keV-1with
an improved reduced
10-6 cm-2 s-1 keV-1with
an improved reduced ![]() of 0.8 for 13 d.o.f.
of 0.8 for 13 d.o.f.
The index ![]() of the dominant powerlaw at lower energies is well consistent with that
observed by Tomsick et al. (2008) up to
100 keV. The additional powerlaw becomes dominant at about
200 keV. This confirms the feature already noted by Joinet
et al. (2007)
who speculated that it could be produced in a jet.
of the dominant powerlaw at lower energies is well consistent with that
observed by Tomsick et al. (2008) up to
100 keV. The additional powerlaw becomes dominant at about
200 keV. This confirms the feature already noted by Joinet
et al. (2007)
who speculated that it could be produced in a jet.
The more complex model is also fully compatible with the
ISGRI data. Fitting the two-component model with fixed
![]() =
100 keV and
=
100 keV and ![]() =
1.0 to the ISGRI data, we obtain a reduced
=
1.0 to the ISGRI data, we obtain a reduced ![]() of 0.7 for 12 d.o.f. and best fit parameters
of 0.7 for 12 d.o.f. and best fit parameters ![]() =
1.7
=
1.7 ![]() 0.1 (Fig. 11b).
0.1 (Fig. 11b).
4.11 4U 1700-377
The eclipsing, 3.4 day X-ray binary 4U 1700-377
consists of a hot, bright supergiant and very probably a neutron star
because its overall X-ray spectrum is similar to that of an accreting
pulsar. The system has been studied in detail by many authors. For a
review see e.g. van der Meer et al. (2005).
In soft
X-rays, the source displays a multitude of line features. The high
energy spectrum has been modelled successfully by a powerlaw with high
energy cutoff with additional photoelectric absorption for the points
below ![]() 25 keV.
Authors have also employed more complex models like thermal
bremsstrahlung or thermal Comptonisation. In all cases, even though the
source is strongly variable, the spectral shape above about
25 keV was found to be independent of the flux state.
25 keV.
Authors have also employed more complex models like thermal
bremsstrahlung or thermal Comptonisation. In all cases, even though the
source is strongly variable, the spectral shape above about
25 keV was found to be independent of the flux state.
Our SPI spectrum is indeed well described by a powerlaw with
high energy cutoff (Xspec model HIGHECUT). Figure 12a shows
the
SPI spectrum. The best fit parameters are ![]() =
2.3
=
2.3 ![]() 0.1, Norm = 5.0
0.1, Norm = 5.0 ![]() 2.4,
2.4, ![]() =
(31
=
(31 ![]() 2) keV,
2) keV, ![]() =
(65
=
(65 ![]() 11) keV. The reduced
11) keV. The reduced ![]() is 0.9 for 7 d.o.f.
is 0.9 for 7 d.o.f.
This agrees well with the literature: e.g. Maisack
et al. (1994)
find ![]() =
2.55
+0.15-0.55,
=
2.55
+0.15-0.55,
![]() =
(20.1
+11.4-20.1) keV,
=
(20.1
+11.4-20.1) keV,
![]() =
(69.8
+9.7-38.3) keV.
But also a simpler power law with exponential cutoff at 48
=
(69.8
+9.7-38.3) keV.
But also a simpler power law with exponential cutoff at 48 ![]() 4 keV and
4 keV and ![]() =
2.0
=
2.0 ![]() 0.1 describes the data reasonably.
0.1 describes the data reasonably.
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...e*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284412b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg40.png)
|
Figure 12: The unfolded spectra of 4U 1700-377 derived from dataset 7 (see Table 1) with statistical errors: a) ( top) SPI spectrum; b) ( bottom) ISGRI spectrum. Spectral model is in both cases a powerlaw with high energy cutoff. The fit parameters are given in Sect. 4.11. |
| Open with DEXTER | |
As for the other two sources in dataset 7, the statistical
errors for the ISGRI spectrum of 4U 1700-377
(Fig. 12b)
had to be increased by 5% of the flux. This is certainly at
least partially caused by the strong variability of
4U 1700-377 (see also Sect. 3.1.3).
A fit with a power law and exponential cutoff gives
the best fit parameter values ![]() = 2.3
= 2.3 ![]() 0.2, Norm = 7
0.2, Norm = 7 ![]() 3,
3,
![]() =
(74
=
(74 ![]() 14) keV, in agreement with SPI. The reduced
14) keV, in agreement with SPI. The reduced ![]() is 0.9 for 12 d.o.f.
is 0.9 for 12 d.o.f.
4.12 IGR J17091-3624
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284413b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg41.png)
|
Figure 13: The unfolded spectra of IGR J17091-3624 derived from dataset 9 (see Table 1) with statistical errors: a) ( top) SPI spectrum with powerlaw fit; b) (middle) ISGRI spectrum with powerlaw fit. The fit parameters are given in Sect. 4.12. |
| Open with DEXTER | |
The object IGR J17091-3624 was discovered in 2003 by INTEGRAL
(Kuulkers et al. 2003) and subsequently studied by a small
number of authors based on archival data (Revnivtsev et al. 2003b)
and INTEGRAL
and RXTE data (Capitanio et al. 2006b).
Chaty
et al. (2008)
recently found that the most probable candidate for a companion star is
neither a giant nor a supergiant. They conclude that the system is most
probably a LMXB. The source is variable but weak (![]() 10 mCrab
above 25 keV). The spectrum above a few ten keV is in
good approximation a hard powerlaw with index varying
between 1.6 and 2.2, but has also been successfully
modelled with thermal Comptonisation (Capitanio et al. 2006b).
10 mCrab
above 25 keV). The spectrum above a few ten keV is in
good approximation a hard powerlaw with index varying
between 1.6 and 2.2, but has also been successfully
modelled with thermal Comptonisation (Capitanio et al. 2006b).
When fitting our time-averaged SPI spectrum of
IGR J17091-3624 (Fig. 13a),
we find
that a simple powerlaw describes it well. We find as best fit
parameters ![]() =
1.8
=
1.8 ![]() 0.2,
Norm = 0.02
0.2,
Norm = 0.02 ![]() 0.01 with a reduced
0.01 with a reduced ![]() of 0.4 for 9 d.o.f. This is consistent with the
previous measurements mentioned above and with the notion that the
source was mostly in the low-hard state during our observation time.
of 0.4 for 9 d.o.f. This is consistent with the
previous measurements mentioned above and with the notion that the
source was mostly in the low-hard state during our observation time.
Fitting a powerlaw to the corresponding ISGRI spectrum
(Fig. 13b)
gives a reduced ![]() of 1.2 for 16 d.o.f.,
of 1.2 for 16 d.o.f., ![]() = 1.93
= 1.93 ![]() 0.04, and Norm = 0.034
0.04, and Norm = 0.034 ![]() 0.005 consistent with the SPI spectrum.
0.005 consistent with the SPI spectrum.
In order to compare our spectra with the ISGRI spectra by
Captanio et al. (2006b),
we also fit a thermal Comptonisation model (Xspec model COMPTT). We
follow Captanio et al. and fix the soft photon temperature kT0 =
0.1 keV. From our ISGRI spectrum we then obtain a
plasma optical depth ![]() =
1.5
=
1.5 ![]() 0.3, and a plasma temperature kT =
(36
0.3, and a plasma temperature kT =
(36 ![]() 8) keV, Norm = 0.0016
8) keV, Norm = 0.0016 ![]() 0.0005, and a reduced
0.0005, and a reduced ![]() of 0.5 for 12 d.o.f. (Fig. 13c).
This is consistent with the values found by Captanio et al. (2006b).
of 0.5 for 12 d.o.f. (Fig. 13c).
This is consistent with the values found by Captanio et al. (2006b).
4.13 GX 354-0
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284414b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg43.png)
|
Figure 14:
The unfolded spectra of GX 354-0 derived from
dataset 9 (see Table 1)
with
statistical: a) ( top)
SPI spectrum with powerlaw fit; b) (
bottom) ISGRI spectrum fit with powerlaw. The fit
parameters are given in Sect. 4.13. The
combined significance of the emission above 200 keV from the
SPI and ISGRI data is 3 |
| Open with DEXTER | |
The LMXB GX 354-0, also known as 4U 1728-34, consists of an accreting neutron star and probably a main sequence star and has been classified as a bursting atoll source which implies significant spectral variability. It has been studied by most X-ray observatories including INTEGRAL (see Falanga et al. 2006, and references therein). Above 25 keV, the spectrum has been typically modelled with a thermal Comptonisation spectrum. However, the studies do not extend much beyond 100 keV.
In our spectral analysis of the time-averaged spectrum, we
initially fit a simple powerlaw. For the SPI data, this
already gives a satisfactory fit (Fig. 14a) with
a
reduced ![]() of 0.7 for 9 d.o.f. and best fit parameters
of 0.7 for 9 d.o.f. and best fit parameters ![]() =
3.26
=
3.26 ![]() 0.06 and Norm = 26.4
0.06 and Norm = 26.4 ![]() 5.9.
The same is true if we fit a powerlaw to the ISGRI data
(Fig. 14b):
we obtain a reduced
5.9.
The same is true if we fit a powerlaw to the ISGRI data
(Fig. 14b):
we obtain a reduced ![]() of 1.0 for 13 d.o.f., and parameters
of 1.0 for 13 d.o.f., and parameters ![]() =
3.53
=
3.53 ![]() 0.02, Norm = 43.3
0.02, Norm = 43.3 ![]() 3.0, steeper than the SPI spectrum.
3.0, steeper than the SPI spectrum.
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.7cm,clip]{128...
...e*{2mm}
\includegraphics[angle=-90,width=8.5cm,clip]{1284415b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg44.png)
|
Figure 15: The unfolded spectra of 1E 1740.7-2942 derived from dataset 9 (see Table 1) with statistical errors: a) ( top) SPI spectrum; b) ( bottom) ISGRI spectrum, in both cases fit by a powerlaw with exponential cutoff. The fit parameters are given in Sect. 4.14. |
| Open with DEXTER | |
Falanga et al. (2006)
find that a thermal Comptonisation model (Xspec model COMPTT) describes
the data well. Lacking soft X-ray information we take the values for
the soft photon temperature kT0
and the plasma temperature kT from the
recent measurement by Falanga et al. (for the low-hard state),
kT0 =
1.18 keV and kT =
35 keV, and fix them in our fit. Applied to the
SPI data this results in a reduced ![]() of 1.9 for 9 d.o.f. and unevenly scattered residuals
suggesting a hard tail. However, the sensitivity of our measurement
does not permit a more detailed study of this feature. Also the
ISGRI data are not compatible with the pure COMPTT spectrum
proposed by Falanga et al. Here we get
a reduced
of 1.9 for 9 d.o.f. and unevenly scattered residuals
suggesting a hard tail. However, the sensitivity of our measurement
does not permit a more detailed study of this feature. Also the
ISGRI data are not compatible with the pure COMPTT spectrum
proposed by Falanga et al. Here we get
a reduced ![]() of 7.6 for 11 d.o.f. even if we let all model
parameters vary freely.
of 7.6 for 11 d.o.f. even if we let all model
parameters vary freely.
We conclude that our data are not well compatible with a pure
thermal Comptonisation spectrum since it underpredicts the high-energy
emission. The combined significance of the emission above
200 keV from GX 354-0 is, however, only 3![]() .
Possibly, the averaging over several spectral states mimics
a power law.
.
Possibly, the averaging over several spectral states mimics
a power law.
4.14 1E 1740.7-2942
The black hole candidate 1E 1740.7-2942 is a bright persistent source
very near the Galactic Centre and the first source to be classified as
a microquasar (see Bosch-Ramon et al. 2006, for a
recent
review). Its classification as a LMXB is controversial. Like
other BHCs, 1E 1740.7-2942 exhibits low-hard and high-soft
states. Using ISGRI data, Del Santo et al. (2005) find
that
the average spectrum above 25 keV is approximately described
by a powerlaw of index ![]() =
2.3. In individual periods they find harder spectra (
=
2.3. In individual periods they find harder spectra (![]()
![]() 1.5)
with exponential cutoffs around 100 keV which can
alternatively be described with thermal Comptonisation models.
1.5)
with exponential cutoffs around 100 keV which can
alternatively be described with thermal Comptonisation models.
Bouchet et al. (1991), using GRANAT/SIGMA data, have reported a transient additional component (modelled by a Gaussian with FWHM of 240 keV) peaking at 480 keV which appeared for about a day in the spectrum and then disappeared. This observation has not yet been confirmed and our study would not pick up on such features since we are averaging over much longer timescales (unless such events would occur frequently).
We fit our SPI spectrum with a powerlaw and exponential cutoff
(Fig. 15a)
and obtain
a reduced ![]() of 1.4 for 10 d.o.f. with
of 1.4 for 10 d.o.f. with ![]() = 2.17
= 2.17 ![]() 0.14 in agreement
with the average spectrum by Del Santo et al. (2005). The
normalisation
is Norm = 0.9
0.14 in agreement
with the average spectrum by Del Santo et al. (2005). The
normalisation
is Norm = 0.9 ![]() 0.4. The cutoff energy is a badly constrained 434
0.4. The cutoff energy is a badly constrained 434 ![]() 400 keV.
400 keV.
The same model fit to the ISGRI data gives best fit parameters
of ![]() =
1.44
=
1.44 ![]() 0.04,
0.04, ![]() =
(113
=
(113 ![]() 8) keV, Norm = 0.040
8) keV, Norm = 0.040 ![]() 0.005, and a reduced
0.005, and a reduced ![]() of 0.7 for 12 d.o.f.
of 0.7 for 12 d.o.f.
The ISGRI spectrum is in agreement with spectra found by Del
Santo et al. (2005)
(see above) but the agreement with SPI is at best marginal. In
order to reconcile the two results, we fix the exponential cutoff in
the model for the SPI data at the value determined by ISGRI.
We obtain a reduced ![]() of 1.9 for 9 d.o.f. and best fit parameters
of 1.9 for 9 d.o.f. and best fit parameters ![]() =
1.80
=
1.80 ![]() 0.06, Norm = 0.28
0.06, Norm = 0.28 ![]() 0.06. The residuals suggest an additional hard component. But our
sensitivity
is not good enough to warrant a more detailed study. The agreement of
the SPI results with the fluxes reported by B08 is
very good (see Table 5).
0.06. The residuals suggest an additional hard component. But our
sensitivity
is not good enough to warrant a more detailed study. The agreement of
the SPI results with the fluxes reported by B08 is
very good (see Table 5).
4.15 IGR J17464-3213
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284416b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg45.png)
|
Figure 16:
The unfolded spectra of IGR J17464-3213
(a.k.a. H 1743-322) derived from dataset 9
(see Table 1)
with statistical errors: a) ( top)
SPI spectrum with powerlaw fit; b) (
bottom) ISGRI spectrum with same model as
a). The fit parameters are given in Sect. 4.15.
The
significance of the emission above 200 keV is 3 |
| Open with DEXTER | |
The transient IGR J17464-3213 was discovered by INTEGRAL
in 2003 (Revnivtsev et al. 2003a)
and
soon identified as the counterpart of the HEAO 1
X-ray source H 1743-322. The source was subsequently studied
by several authors at X-ray, optical and radio wavelengths, in
particular with INTEGRAL (see Joinet
et al. 2005,
for a recent review). Evidence for jets was found and the source is now
regarded to be a microquasar (Corbel et al. 2005).
Timing and
spectral properties of the object suggest that it is a LMXB
containing a black hole of about 10 ![]() .
.
The RXTE/ASM lightcurve of
IGR J17464-3213 (e.g. Capitanio et al. 2006a)
shows that the source can be in strong outburst for months at a time.
In between outbursts it
returns to a very low level of emission and remains there for months.
Using data from RXTE and INTEGRAL
up to 150 keV, Joinet et al. (2005) have
studied
the complex spectral variability of the object (typical of BHCs): the
source exhibits softening during flux increases followed by phases of
constant spectrum in spite of intensity changes by
factors 2-3. Above a few ten keV, the spectrum is described by
a powerlaw with index ![]() varying between 1.0 and 2.6, and a not very well
constrained exponential cutoff around 100 keV.
varying between 1.0 and 2.6, and a not very well
constrained exponential cutoff around 100 keV.
The ISGRI lightcurve (Courvoisier et al. 2008)
for
IGR J17464-3213 shows three strong outburst periods and
otherwise a low level of emission such that our time-averaged spectrum
should be a superposition of the low-hard and the high-soft state. When
examining our SPI spectrum, we find evidence for increased
uncertainties in the lowest two energy bins possibly due to to
insufficient source region modelling at the lowest energies.
To be on the safe side, we increase the statistical errors
by 5% of the flux for the entire spectrum. Fitting the
spectrum with a powerlaw (Fig. 16a),
then
leads to a reduced ![]() of 1.1 for 9 d.o.f. and best fit parameters
of 1.1 for 9 d.o.f. and best fit parameters ![]() =
2.82
=
2.82 ![]() 0.14, Norm = 2.1
0.14, Norm = 2.1 ![]() 1.1.
1.1.
Fitting a powerlaw to the ISGRI spectrum of (Fig. 16c)
gives a
perfect reduced ![]() of 0.9 and best fit parameters
of 0.9 and best fit parameters ![]() = 2.49
= 2.49 ![]() 0.02 and Norm = 0.63
0.02 and Norm = 0.63 ![]() 0.04. There is no evidence for
a cutoff. The powerlaw index is still in agreement with our
SPI measurement.
0.04. There is no evidence for
a cutoff. The powerlaw index is still in agreement with our
SPI measurement.
4.16 GRS 1758-258
![\begin{figure}
\par\hspace*{1.5mm}\includegraphics[angle=-90,width=8.7cm,clip]{1...
...ce*{2mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284417b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg47.png)
|
Figure 17: The unfolded spectra of GRS 1758-258 derived from dataset 10 (see Table 1) with statistical errors: a) ( top) SPI spectrum; and b) ( bottom) ISGRI spectrum, both fit by powerlaw with exponential cutoff. The fit parameters are given in Sect. 4.16. |
| Open with DEXTER | |
The LMXB GRS 1758+258 is one of the well known microquasars and regarded to be similar to 1E 1740.7-2942. It is also a black hole candidate. For a recent review see e.g. Pottschmidt et al. (2006). The source is bright and can show outburst which are however mostly too short for SPI's sensitivity. B08 and our analysis assume it to be a constant emitter. In the low-hard state, which the source mostly assumes, the high energy spectrum can roughly be described by a hard powerlaw with an exponential cutoff around 100 keV. In terms of physical models, thermal Comptonisation models and models involving black body emission from a disk have been applied. The spectrum above 200 keV was hardly studied.
We fit our SPI spectrum initially with a powerlaw with
exponential cutoff and obtain a reduced ![]() of 1.7 for 14 d.o.f. (Fig. 17a) and
well
constrained best fit parameters
of 1.7 for 14 d.o.f. (Fig. 17a) and
well
constrained best fit parameters ![]() = 1.54
= 1.54 ![]() 0.07,
0.07, ![]() =
(178
=
(178 ![]() 28) keV, Norm = 0.12
28) keV, Norm = 0.12 ![]() 0.03, in agreement with previous measurements.
0.03, in agreement with previous measurements.
The same spectral fit applied to the ISGRI data results in
best fit parameters ![]() =
1.36
=
1.36 ![]() 0.02,
0.02, ![]() =
(123
=
(123 ![]() 5) keV, Norm = 0.059
5) keV, Norm = 0.059 ![]() 0.004, and reduced
0.004, and reduced ![]() = 1.9 for
12 d.o.f., in marginal agreement with the SPI result.
= 1.9 for
12 d.o.f., in marginal agreement with the SPI result.
In both cases, the fit quality is not very good which may be
the result of assuming the source to be constant (but we chose to
follow B08 consistently). In the SPI spectrum, there is a hint
of a hard tail in the residuals. In fact, we achieve a fit improvement
(reduced ![]() =
1.6 for 13 d.o.f.) if we freeze the cutoff energy and add a
powerlaw as a second component. However, the chance probability of the
improvement is 0.2.
=
1.6 for 13 d.o.f.) if we freeze the cutoff energy and add a
powerlaw as a second component. However, the chance probability of the
improvement is 0.2.
4.17 Ginga 1826-24
![\begin{figure}
\par\hspace*{1.5mm}\includegraphics[angle=-90,width=8.7cm,clip]{1...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284418b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg48.png)
|
Figure 18: The unfolded spectra of Ginga 1826-24 derived from dataset 10 (see Table 1) with statistical errors: a) ( top) SPI spectrum fit with two-component model consisting of a powerlaw with exponential cutoff and a second powerlaw; b) ( bottom) ISGRI spectrum fit with powerlaw with exponential cutoff. The fit parameters are given in Sect. 4.17. |
| Open with DEXTER | |
The LMXB Ginga 1826-24 was discovered in 1988 and initially found
similar in spectrum and variability to the
BHC Cyg X-1. Not much later, the relatively low
cutoff energy (![]() 58 keV)
of its powerlaw spectrum above a few ten keV and the
observation of X-ray bursts led to the classification as a NS.
The exceptional precision of the reoccurrence of the bursts (period
58 keV)
of its powerlaw spectrum above a few ten keV and the
observation of X-ray bursts led to the classification as a NS.
The exceptional precision of the reoccurrence of the bursts (period ![]() 3.5 h)
also led to the nickname ``clocked burster''. For a recent review of
the source properties see Thompson et al. (2005). The
time-averaged high-energy spectrum up to about 300 keV was
measured by Strickman et al. (1996a)
and
modelled as a powerlaw with exponential cutoff. They found
3.5 h)
also led to the nickname ``clocked burster''. For a recent review of
the source properties see Thompson et al. (2005). The
time-averaged high-energy spectrum up to about 300 keV was
measured by Strickman et al. (1996a)
and
modelled as a powerlaw with exponential cutoff. They found ![]() =
1.59
=
1.59 ![]() 0.02 and
0.02 and ![]() = (57
= (57 ![]() 8) keV.
8) keV.
Fitting our SPI spectrum of Ginga 1826-24 with a
powerlaw with exponential cutoff, we obtain
a reduced ![]() of 1.2 for 14 d.o.f. and best fit parameters
of 1.2 for 14 d.o.f. and best fit parameters ![]() =
1.7
=
1.7 ![]() 0.1,
0.1, ![]() =
(60
=
(60 ![]() 7) keV, Norm = 0.36
7) keV, Norm = 0.36 ![]() 0.10 in good agreement with Strickman et al. (1996a).
0.10 in good agreement with Strickman et al. (1996a).
The residuals show evidence for a hard tail above
200 keV. Accommodating the possibility of such a tail by
adding a powerlaw component to the model, we obtain from the fit to the
SPI data (Fig. 18a) a
reduced ![]() of 0.5 for 12 d.o.f. and best fit parameters Norm1 =
0.24
of 0.5 for 12 d.o.f. and best fit parameters Norm1 =
0.24 ![]() 0.09,
0.09, ![]() =
0.8
=
0.8 ![]() 0.69, Norm2
(at 200 keV) =
0.69, Norm2
(at 200 keV) =
![]()
![]() 10-6 cm-2 s-1 keV-1.
The second powerlaw component becomes dominant
above ca. 300 keV.
10-6 cm-2 s-1 keV-1.
The second powerlaw component becomes dominant
above ca. 300 keV.
Applying the same modelling to the ISGRI data (Fig. 18b),
we
obtain for a simple powerlaw with exponential cutoff a reduced ![]() of 1.5 for 12 d.o.f. and best fit parameters
of 1.5 for 12 d.o.f. and best fit parameters
![]() =
1.78
=
1.78 ![]() 0.04,
0.04, ![]() =
(69
=
(69 ![]() 3) keV, Norm = 0.42
3) keV, Norm = 0.42 ![]() 0.05. The residuals don't show any posibility for improvement.
0.05. The residuals don't show any posibility for improvement.
We conclude that our time averaged spectra agree well with previously published results. SPI and ISGRI data are compatible with each other. The evidence for a hard tail above 200 keV is weak even though B08 still find 25 mCrab at 200-600 keV. We find less than half of that flux.
4.18 GRS 1915+105
![\begin{figure}
\par\hspace*{1.5mm}\includegraphics[angle=-90,width=8.7cm,clip]{1...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284419b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg50.png)
|
Figure 19: The unfolded spectra of GRS 1915+105 derived from dataset 11 (see Table 1) with statistical errors: a) ( top) SPI spectrum fit with two-component model consisting of powerlaw with exponential cutoff and second powerlaw; b) ( bottom) ISGRI spectrum fit by same model as used in a). The fit parameters are given in Sect. 4.18. |
| Open with DEXTER | |
The LMXB GRS 1915+105 is one of the most studied galactic
black holes. For a review see e.g. Fender & Belloni (2004) or
Rodriguez
et al. (2008a).
The object is a microquasar, the first to exhibit superluminal motion
in its jets, with a relatively large black hole mass of ![]() 14
14 ![]() ,
a large binary period of 33.5 d, and an extremely complex time
variability which is attributed to accretion disk instabilities
(Greiner et al. 1996;
Done et al. 2004).
,
a large binary period of 33.5 d, and an extremely complex time
variability which is attributed to accretion disk instabilities
(Greiner et al. 1996;
Done et al. 2004).
GRS 1915+105 was extensively monitored by INTEGRAL. A detailed study of two years of the INTEGRAL observations was published in Rodriguez et al. (2008a,2008b). They analyse ISGRI spectra up to 300 keV and distinguish several spectral states which they fit with a number of multi-component models involving for the high energy part thermal Comptonisation (Xspec model COMPTT) with seed photon temperatures between 0.7 and 2.1 keV and a powerlaw with index between 2.0 and 2.9.
Our time-averaged spectrum of the source is a superposition of
all spectral states. As for the previous sources we initially
try to fit a powerlaw with exponential cutoff. This results in a high
reduced ![]() of 2.4 for 14 d.o.f., a photon index of 3.30
of 2.4 for 14 d.o.f., a photon index of 3.30 ![]() 0.02, and a cutoff energy far beyond the upper end of our energy range.
The residuals indicate that a more sophisticated model is needed.
0.02, and a cutoff energy far beyond the upper end of our energy range.
The residuals indicate that a more sophisticated model is needed.
Next we try a powerlaw with exponential cutoff with an
additional powerlaw. This results in a reduced ![]() of 0.6 for 12 d.o.f. and badly constrained best fit
parameters
of 0.6 for 12 d.o.f. and badly constrained best fit
parameters ![]() =
1.7
=
1.7 ![]() 1.7,
1.7, ![]() =
(13
=
(13 ![]() 9) keV,
9) keV, ![]() =
2.8
=
2.8 ![]() 0.2, Norm1 = 3.7
0.2, Norm1 = 3.7 ![]() 16, and Norm2
(at 200 keV) =
16, and Norm2
(at 200 keV) =
![]()
![]() 10-5 cm-2 s-1 keV-1,
i.e. a dominant pure powerlaw with a weak additional
low-energy component becoming negligible at a few
ten keV.
10-5 cm-2 s-1 keV-1,
i.e. a dominant pure powerlaw with a weak additional
low-energy component becoming negligible at a few
ten keV.
Applying the same model to the ISGRI data results in ![]() =
2.87
=
2.87 ![]() 0.05 and Norm2
(at 200 keV) = 1.17
0.05 and Norm2
(at 200 keV) = 1.17 ![]() 0.04
0.04 ![]() 10-5 cm-2 s-s keV-1
for the dominant component and
10-5 cm-2 s-s keV-1
for the dominant component and ![]() = 0.8
= 0.8 ![]() 1.0,
1.0, ![]() =
8
=
8 ![]() 2 keV, Norm1 = 0.09
2 keV, Norm1 = 0.09 ![]() 0.25 for the weak low-energy component. The reduced
0.25 for the weak low-energy component. The reduced ![]() is 0.7 for 10 d.o.f.
The agreement with the SPI result is good.
is 0.7 for 10 d.o.f.
The agreement with the SPI result is good.
4.19 Cyg X-1
The HMXB Cyg X-1 consists of a black hole candidate of high but uncertain mass and an OB supergiant (see Gies et al. 2003; Ziolkowski 2005, and references therein). It is one of the brightest hard X-ray sources and has been studied extensively by many authors in all wavebands. For a brief review see e.g. Szostek & Zdziarski (2007) and Shaposhnikov & Titartchuk (2006) and references therein. The radio emission shows evidence of a moderately relativistic jet. The object has therefore recently been called a microquasar (e.g. Russell et al. 2007).
Long-term monitoring has revealed two main spectral states
like in other BH binaries, the low-hard state and the
high-soft state, between which the source transits. It spends the
dominant fraction of time in the low-hard state (Zhang et al. 1997;
Hjalmarsdotter et al. 2008).
Our
time-averaged spectrum of Cyg X-1 should therefore be more
similar to the low hard state which is roughly a hard
powerlaw (![]() between 1.4 and 2.1) with a break at E > 50 keV
(Cadolle Bel et al. 2006).
between 1.4 and 2.1) with a break at E > 50 keV
(Cadolle Bel et al. 2006).
The X-ray spectra of individual states have been modelled up to 300 keV by several authors with a variety of combinations of disk black body and thermal Comptonisation with additional Fe fluorescence line and reflection components (see again Cadolle Bel et al. 2006).
Lacking the soft X-ray information and averaging over all
source states, we fit our SPI spectrum of Cyg X-1
initially with a simple powerlaw with exponential cutoff and obtain a
very large reduced ![]() of 5.3 for 14 d.o.f. The best fit parameters (
of 5.3 for 14 d.o.f. The best fit parameters (![]() =
1.65
=
1.65 ![]() 0.01,
0.01, ![]() =
(180
=
(180 ![]() 5) keV, Norm = 2.3
5) keV, Norm = 2.3 ![]() 0.1) agree well with the expectations from previous measurements and,
up to about 300 keV, the model describes the data
reasonably well but there is a clear and very significant hard tail
above 300 keV.
0.1) agree well with the expectations from previous measurements and,
up to about 300 keV, the model describes the data
reasonably well but there is a clear and very significant hard tail
above 300 keV.
![\begin{figure}
\par\hspace*{1.5mm}\includegraphics[angle=-90,width=8.7cm,clip]{1...
...*{2.5mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284420b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg52.png)
|
Figure 20: The unfolded spectra of Cyg X-1 derived from dataset 12 (see Table 1) with statistical errors: a) ( top) SPI spectrum fit with two-component model consisting of a powerlaw with exponential cutoff and a second powerlaw; b) ( bottom) ISGRI spectrum fit by same model as in a). The fit parameters are given in Sect. 4.19. |
| Open with DEXTER | |
This hard tail in the low-hard state spectrum of Cyg X-1 was already observed up to about 5 MeV with COMPTEL by McConnell et al. (2000). They did not observe an indication of a cutoff. It was also already studied with INTEGRAL by Cadolle Bel et al.(2006) and Malzac et al. (2006).
Adding a powerlaw to our model to accommodate the hard tail,
but leaving all parameters free, we obtain a much better fit
(Fig. 20a)
with reduced ![]() 0.9
for 12 d.o.f. and residuals which don't show any sign of
systematic deviations. The best fit parameters are
0.9
for 12 d.o.f. and residuals which don't show any sign of
systematic deviations. The best fit parameters are ![]() =
1.3
=
1.3 ![]() 0.2,
0.2, ![]() =
(95
=
(95 ![]() 15) keV, Norm1 = 0.43
15) keV, Norm1 = 0.43 ![]() 0.35,
0.35, ![]() =
2.11
=
2.11 ![]() 0.1, Norm2
(at 200 keV) =
0.1, Norm2
(at 200 keV) =
![]()
![]() 10-5 cm-2 s-1 keV-1.
10-5 cm-2 s-1 keV-1.
Applying the same model to the ISGRI data (Fig. 20b), we
obtain
a reduced ![]() of 1.5 for 10 d.o.f. and best fit parameters
of 1.5 for 10 d.o.f. and best fit parameters ![]() =
1.44
=
1.44 ![]() 0.14,
0.14, ![]() =
(115
=
(115 ![]() 18) keV, Norm1 = 0.9
18) keV, Norm1 = 0.9 ![]() 0.5,
0.5, ![]() =
2.2
=
2.2 ![]() 0.14, Norm2
(at 200 keV) =
0.14, Norm2
(at 200 keV) =
![]()
![]() 10-5 cm-2 s-1 keV-1,
i.e. the best fit parameters are in agreement with those from
SPI but are not as well constrained because the ISGRI spectrum
is lacking high energy sensitivity.
10-5 cm-2 s-1 keV-1,
i.e. the best fit parameters are in agreement with those from
SPI but are not as well constrained because the ISGRI spectrum
is lacking high energy sensitivity.
![\begin{figure}
\par\hspace*{1.5mm}\includegraphics[angle=-90,width=8.7cm,clip]{1...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284421b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg55.png)
|
Figure 21: The unfolded spectra of Cyg X-3 derived from dataset 13 (see Table 1) with statistical errors: a) ( top) SPI spectrum fit with two-component model consisting of a powerlaw with exponential cutoff and a second powerlaw; b) ( bottom) ISGRI spectrum fit by same model as in a). The fit parameters are given in Sect. 4.20. |
| Open with DEXTER | |
To further compare with the COMPTEL data, we fit a powerlaw to our
SPI data above 500 keV. We find an index of
1.9 ![]() 0.5 which is much harder than the index 3.3
0.5 which is much harder than the index 3.3 ![]() 0.4 measured by McConnell et al. (2000) in
the
neighbouring energy range. One explanation of this difference could be
source variability, which has indeed been suggested to be present as a
variable broad line feature around 1 MeV (McConnell
et al. 1989,2000).
0.4 measured by McConnell et al. (2000) in
the
neighbouring energy range. One explanation of this difference could be
source variability, which has indeed been suggested to be present as a
variable broad line feature around 1 MeV (McConnell
et al. 1989,2000).
We conclude that even though our spectra have extremely high statistical significance, it is possible to model them with a phenomenological model with only five parameters consisting of a cutoff powerlaw and second powerlaw. The cutoff powerlaw can be interpreted as a contribution from thermal Comptonisation as already suggested by many previous authors (see above) while the hard tail is most likely a product of the jet.
4.20 Cyg X-3
Cyg X-3 is a HMXB with an unusually short binary period of 4.8 h and a Wolf-Rayet star as an unusual stellar companion. Despite its brightness and the intensive study at all wavebands over four decades, recently published articles still declare many of its properties as uncertain, in particular the nature of the compact object contained in it. Szostek & Zdziarski (2008) and Hjalmarsdotter et al. (2008), H08 in the following, give a brief review of the literature. They also argue that the compact object in Cyg X-3 could be a quite massive black hole. The object has also been called a microquasar because of its radio jets (Marti et al. 2007). At lower energies, the intense stellar wind from the companion star leads to strong absorption features. Above 25 keV, however, the effect on the spectral shape is small (H08).
Cyg X-3 has a binodal distribution of soft X-ray count rates. The distribution of its spectral hardness, however, only shows one peak at low hardness with a long asymmetric tail to higher hardness (H08). The authors note that the soft X-ray hardness in the case of Cyg X-3 may be a bad indicator of the state of the source because of its strong absorption. The source probably still has a separate hard state at higher energies which it occupies roughly two thirds of the time.
The time-averaged spectra we are studying here should therefore be a superposition of spectra from all states, but more similar to the harder spectra.
We initially fit our SPI spectrum of Cyg X-3 with a
powerlaw with exponential cutoff. This results in a relatively high
reduced ![]() of 1.8, an index
of 1.8, an index ![]() =
3.26
=
3.26 ![]() 0.04 and a cutoff beyond the upper end of our energy range. The
residuals suggest a hard tail beginning at about 100 keV.
Adding a powerlaw as second component, we obtain a reduced
0.04 and a cutoff beyond the upper end of our energy range. The
residuals suggest a hard tail beginning at about 100 keV.
Adding a powerlaw as second component, we obtain a reduced ![]() of 0.8 for 12 d.o.f. (Fig. 21a) but
the fit
parameters are poorly constrained (
of 0.8 for 12 d.o.f. (Fig. 21a) but
the fit
parameters are poorly constrained (![]() = 2.0
= 2.0 ![]() 0.7,
0.7, ![]() =
(20
=
(20 ![]() 10) keV, Norm1 = 3.5
10) keV, Norm1 = 3.5 ![]() 6.6,
6.6, ![]() =
2.4
=
2.4 ![]() 0.3, Norm2 (at 200 keV) =
0.3, Norm2 (at 200 keV) =
![]()
![]() 10-6 cm-2 s-1 keV-1)
because the best fit cutoff energy is outside our energy range. The
powerlaw component without cutoff constitutes the dominant part of the
emission above a few 10 keV. There is no evidence for
a cutoff at higher energies, but our data points become insignificant
above 350 keV.
10-6 cm-2 s-1 keV-1)
because the best fit cutoff energy is outside our energy range. The
powerlaw component without cutoff constitutes the dominant part of the
emission above a few 10 keV. There is no evidence for
a cutoff at higher energies, but our data points become insignificant
above 350 keV.
An unusually low cutoff energy implying a most likely plasma temperature of only 4 keV was also found in the INTEGRAL data analysis by H08 when assuming a thermal Comptonisation model.
When inspecting our ISGRI spectrum of Cyg X-3, we
find evidence for enlarged systematic errors
which are probably caused by the crowded field around the object
including the nearby and extremely bright Cyg X-1. We
increase the statistical errors by 0.5% of the flux. With this
change, the fit of the same two-component model as for the
SPI data with ![]() fixed to 20 keV results in a reduced
fixed to 20 keV results in a reduced ![]() of 1.7 for 11 d.o.f. and best fit parameters
of 1.7 for 11 d.o.f. and best fit parameters ![]() =
2.00
=
2.00 ![]() 0.08, Norm1 = 3.4
0.08, Norm1 = 3.4 ![]() 0.7,
0.7, ![]() =
2.7
=
2.7 ![]() 0.2, Norm2
(at 200 keV) =
0.2, Norm2
(at 200 keV) =
![]()
![]() 10-6 cm-2 s-1 keV-1
(Fig. 21b)
in agreement with the SPI results.
10-6 cm-2 s-1 keV-1
(Fig. 21b)
in agreement with the SPI results.
4.21 Systematic errors of flux measurements in crowded fields
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.8cm,clip]{128...
...ce*{3mm}
\includegraphics[angle=-90,width=8.6cm,clip]{1284422b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg58.png)
|
Figure 22:
The unfolded spectra for the control position ``Control1'' at
RA = 259.5 |
| Open with DEXTER | |
As described in Sect. 3.3
we derive our systematic error estimate from the study of our
Crab spectrum, i.e. from a source which is not in a
crowded field as opposed to many of the X-ray binaries studied in this
work. We need to verify to which extent our analysis is subject to
additional systematic errors when applied to sources in crowded fields.
In order to assess this possibility, we have randomly added a source
position ``Control1'' to the input catalog for one of our most complex
fields (dataset 9) near GX 354-0 and
4U 1700-377 (see Table 1).
This
position constitutes the worst case for our analysis as it is close to
variable bright sources in a location in the galactic plane less
than 15![]() from the galactic center where also significant diffuse emission is
present. Furthermore, it is about 10 arcmin away from
1RXS J171824.2-402934, an X-ray burster capable of very rare 4
minute bursts with peak intensities up to 1.3 Crab and a
thermal spectrum peaking at 5 keV detectable up to
28 keV (Kaptein et al. 2007).
As a control case, this position therefore also gives an
estimation of the influence of variable and on average faint sources
which are not included in our input catalog.
from the galactic center where also significant diffuse emission is
present. Furthermore, it is about 10 arcmin away from
1RXS J171824.2-402934, an X-ray burster capable of very rare 4
minute bursts with peak intensities up to 1.3 Crab and a
thermal spectrum peaking at 5 keV detectable up to
28 keV (Kaptein et al. 2007).
As a control case, this position therefore also gives an
estimation of the influence of variable and on average faint sources
which are not included in our input catalog.
The resulting SPI spectrum (Fig. 22a)
does not
contain any point with a flux significantly different from zero. All
points have less than 2![]() significance.
The only indication of any systematic signal which could fake the
presence of a source is in the first bin near 30 keV where a
level of 3 mCrab is reached. If we naively fit the points with
a powerlaw, we obtain a very steep spectrum with best fit parameters
significance.
The only indication of any systematic signal which could fake the
presence of a source is in the first bin near 30 keV where a
level of 3 mCrab is reached. If we naively fit the points with
a powerlaw, we obtain a very steep spectrum with best fit parameters ![]() =
5.5, Norm = 2075.
=
5.5, Norm = 2075.
Repeating the same procedure for the corresponding ISGRI
spectrum (Fig. 22b)
results
in best fit parameters ![]() =
1.0, Norm = 1.3
=
1.0, Norm = 1.3 ![]() 10-5. Also here all points are consistent with
zero. The most significant point is near 300 keV and has 2
10-5. Also here all points are consistent with
zero. The most significant point is near 300 keV and has 2![]() with a nominal flux of approx. 80 mCrab.
with a nominal flux of approx. 80 mCrab.
The fluxes derived from these powerlaws can serve as additional estimations of systematic errors on the flux values measured by us. They are given in Table 5 in the row labelled ``Estim. Syst. Error'' with negative sign in order to indicate that the values need to be subtracted from the other flux measurements in the table.
Table 2: Spectral fit parameters for sources other than X-ray binaries.
Table 3: Spectral fit parameters for X-ray binaries.
Table 4: Our measurements of the Crab flux with SPI and ISGRI assuming the spectral shape given in Table 2 for energy redistribution.
Table 5: Source fluxes [mCrab].
5 Summary and conclusions
Tables 2-5 summarise our spectral measurements. They provide a catalog of the time-averaged spectra of the brightest known soft gamma-ray sources. They also give an impression of the variety of possible spectral shapes for different source types, especially for X-ray binaries (XRBs) which represent more than half of the sources. Furthermore, the tables permit to compare the response of SPI and ISGRI. In particular Tables 2 and 3 permit to study the agreement of the corresponding measurements in terms of spectral shape while Table 5 can be used to compare the flux normalisation of the two instruments in several energy bands. In the latter table we also give the results from B08 for those energy ranges where they are available.
5.1 Agreement of SPI and ISGRI spectra
The study of 20 bright sources with SPI and ISGRI using nearly identical datasets permits us to carry out a quantitative comparison of the response of the two instruments and test the quality of the spectra obtained with our new spimodfit-based analysis method.
The comparison of the absolute flux normalisation should be carried out using a steady source such as the Crab. Our Crab flux measurements are given in Table 4. While the flux ratio SPI/ISGRI is consistent with a constant value of about 1.12 up to 200 keV, we observe a clear deviation at higher energies suggesting systematic differences in flux calibration of additional 18% at 200-600 keV (see Sect. 4.1).
If we correct for the differences in absolute flux calibration by normalising on the Crab flux, we obtain the flux values in Table 5. Plotting the SPI values versus the ISGRI values from this table, we obtain Figs. 23a-c. In all three energy ranges up to 600 keV, these plots show clearly a good agreement between the flux values from the two instruments for all sources with fluxes higher than a few ten mCrab. Only for the faintest sources and only below 100 keV do we see obvious systematic deviations from the linear relationship. Here the SPI fluxes tend to be lower than those from ISGRI. The origin of this is probably a combination of two causes: (1) systematic differences in the handling of source variability by the analysis software; and (2) systematic differences in the background determination.
5.2 Agreement of our SPI measurements with those by B08
To further verify our analysis method, we compare our SPI fluxes with those published by B08 who give their flux values as fraction of their Crab flux. All values are given in Table 5. Plotting our values versus those from B08 (Figs. 24a-c) we see that the flux values agree well in all energy bands for sources brighter than 20 mCrab. Below this flux level, our flux values seem to be systematically slightly lower. At least some of the differences can be attributed to source variability as our dataset is not exactly the same as that used by B08.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1284423.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg59.png)
|
Figure 23: Comparison of our flux values obtained from SPI with those from ISGRI for the energy bands a) ( top) 25-100 keV; b) ( middle) 100-200 keV; c) ( bottom) 200-600 keV. In each band, a linear function was fit to the points and fit parameters are shown in the figures. The flux values are also given in Table 5. Only the statistical errors are shown. They take into account the uncertainty of the Crab flux. See Sect. 5.1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1284424.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12844-09/Timg60.png)
|
Figure 24: Comparison of our flux values obtained from SPI with those by B08 (also obtained with SPI, largely using the same data but with a different analysis method) for the energy bands a) ( top) 25-100 keV; b) ( middle) 100-200 keV; c) ( bottom) 200-600 keV. In each band, a linear function was fit to the points and fit parameters are shown in the figures. The flux values are also given in Table 5. Only the statistical errors are shown. They take into account the uncertainty of the Crab flux. See Sect. 5.2. |
| Open with DEXTER | |
B08 defined the annihilation (positronium) emission between
300 keV and 511 keV as an individual component in
their source model and extracted its intensity as a result of their
fit. Since this emission is extended (to first order
a 8![]() FWHM Gaussian centered on the galactic centre) on a
scale similar to the SPI field-of-view, it is in our analysis
absorbed in the time-variable isotropic component of our background
model which does not have a separate annihilation component.
This is confirmed by the fact that our fluxes in the range
200-600 keV agree very well with those by B08 (see
Fig. 24),
also for sources near the galactic centre.
FWHM Gaussian centered on the galactic centre) on a
scale similar to the SPI field-of-view, it is in our analysis
absorbed in the time-variable isotropic component of our background
model which does not have a separate annihilation component.
This is confirmed by the fact that our fluxes in the range
200-600 keV agree very well with those by B08 (see
Fig. 24),
also for sources near the galactic centre.
5.3 Emission above 200 keV
We detect all of the 20 sources in our sample independently in the
25-100 keV and in the 100-200 keV band both with SPI
and with ISGRI. Above 200 keV we find evidence for emission of
more than 3![]() in 8 cases. In the 600-1000 keV band, we find such
evidence only for two sources.
in 8 cases. In the 600-1000 keV band, we find such
evidence only for two sources.
XRBs constitute 70% of our source sample. Table 3 summarises our measurements of the spectra of these 14 XRBs. They are not a random sample but the 14 brightest known X-ray binaries at 200 keV. Four of them are HMXBs, the remaining are LMXBs. Ten of them contain black hole candidates (eight of which are classified as microquasars), the remaining four contain neutron stars.
5.4 Conclusions
We present spectra for the 20 brightest soft gamma-ray sources averaged over timescales of years and give flux values in four energy bands between 25 keV and 1 MeV.
For SPI, these measurements were derived using a new tool (spimodift by Halloin & Strong 2007) which can coherently treat data from the whole SPI mission by performing a single, large maximum likelihood fit.
The agreement between our SPI and ISGRI measurements is good if we correct for systematic calibration differences by normalizing on the Crab spectrum. Our SPI flux measurements also agree well with those by Bouchet et al. (2008) (B08). Our Crab spectrum shows the also previously observed break near 100 keV where the spectral index softens from 2.1 to 2.2.
Up to 200 keV, all 20 sources in our sample are detected independently in two adjacent bands. At 200-600 keV we detect eight sources, and at 600-1000 keV we detect two sources. The spectra we find agree well with the results from previous publications. For six of the 14 XRBs in our sample (not counting the borderline case GRS 1758-258), we find evidence for a hard powerlaw-component which becomes dominant above the cutoff energy of the thermal Comptonization component, i.e. above about hundred to a few hundred keV. For GX 339-4, GRS 1915+105, Cyg X-1, and Cyg X-3 such hard tails have already been noted by previous studies. For OAO 1657-415 and Ginga 1826-24, our study provides the first weak indication of such emission.
AcknowledgementsWe would like to thank R. Diehl, J. Greiner, and G. Sala (MPE, Garching), and E. Jourdain and J. P. Roques (CESR/CNRS, Toulouse) for useful discussions. D.P. was supported in part by the German Bundesministerium für Bildung, Wissenschaft, Forschung und Technologie (BMBF/DLR) under contract No. FKZ 50 OG 0502.
References
- Alvarez-Gaumé, L., et al. 2004, Rev. Particle Phys., Phys. Lett. B, 592
- Arnaud, K., Dorman, B., & Gordon, C. 2007, Xspec - an X-ray fitting package, User's Guide for version 12.3.1, HEASARC, NASA/GSFC publications
- Audley, M. D., Nagase, F., Mitsuda, K., et al. 2006, MNRAS, 367, 1147 [CrossRef] [NASA ADS]
- Barnstedt, J., Staubert, R., Santangelo, A., et al. 2008, A&A, 486, 293 [EDP Sciences] [CrossRef] [NASA ADS]
- Beckmann, V., Shrader, C. R., Gehrels, N., et al. 2005, ApJ, 634, 939 [CrossRef] [NASA ADS]
- Bosch-Ramon, V., Romero, G. E., Paredes, J. M., et al. 2006, A&A, 457, 1011 [EDP Sciences] [CrossRef] [NASA ADS]
- Bouchet, L., Mandrou, P., Roques, J. P., et al. 1991, ApJ, 383, L45 [CrossRef] [NASA ADS]
- Bouchet, L., Roques, J. P., Mandrou, P., et al. 2005, ApJ, 635, 1115 [CrossRef]
- Bouchet, L., Jourdain, E., Roques, J. P., et al. 2008, ApJ, 679, 1315 [CrossRef] [NASA ADS]
- Cadolle Bel, M., Sizun, P., Goldwurm, A., et al. 2006, A&A, 446, 591 [EDP Sciences] [CrossRef] [NASA ADS]
- Capitanio, F., Bazzano, A., Ubertini, P., et al. 2006a, Adv. Space Res., 38, 2816 [CrossRef] [NASA ADS]
- Capitanio, F., Bazzano, A., Ubertini, P., et al. 2006b, ApJ, 643, 376 [CrossRef] [NASA ADS]
- Chaty, S., Rahoui, F., Foellmi, C., et al. 2008, A&A, 484, 783 [EDP Sciences] [CrossRef] [NASA ADS]
- Corbel, S., Kaaret, P., Fender, R. P., et al. 2005, ApJ, 632, 504 [CrossRef] [NASA ADS]
- Courvoisier, T. J.-L., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [EDP Sciences] [CrossRef] [NASA ADS]
- Courvoisier, T. J.-L., et al. 2008, INTEGRAL Source Results Version 2, available from the INTEGRAL Science Data Centre website http://isdc.unige.ch/
- Del Santo, M., Bazzano, A., Zdziarski, A. A., et al. 2005, A&A, 433, 613 [EDP Sciences] [CrossRef] [NASA ADS]
- Dermer, C. D., & Gehrels, N. 1995, ApJ, 447, 103 [CrossRef] [NASA ADS]
- Done, C., Madjeski, G. M., & Smith, D. A. 1996, ApJ, 463, L63 [CrossRef] [NASA ADS]
- Done, C., Wardzinski, G., & Gierlinski, M. 2004, MNRAS, 349, 393 [CrossRef] [NASA ADS]
- Falanga, M., Götz, D., Goldoni, P., et al. 2006, A&A, 458, 21 [EDP Sciences] [CrossRef] [NASA ADS]
- Fender, R., & Belloni, T. 2004, ARA&A, 42, 317 [CrossRef] [NASA ADS]
- Filippova, E. V., Tsygankov, S. S., Lutovinov, A. A., & Sunyaev, R. A. 2005, Astron. Lett., 30, 824 [CrossRef] [NASA ADS]
- Gies, D. R., Bolton, C. T., Thomson, J. R., et al. 2003, ApJ, 583, 424 [CrossRef] [NASA ADS]
- Goldwurm, A., David, P., Foschini, L., et al. 2003, A&A, 411, L223 [EDP Sciences] [CrossRef] [NASA ADS]
- Grabelsky, D. A., Maltz, S. M., Purcell, W. R., et al. 1995, ApJ, 441, 800 [CrossRef] [NASA ADS]
- Greiner, J., Morgan, E. H., & Remillard, R. A. 1996, ApJ, 473, L107 [CrossRef] [NASA ADS]
- Halloin, H., & Strong, A., 2007, spimodfit user manual, OSA documentation, available from the INTEGRAL Science Data Centre website http://isdc.unige.ch/
- Hjalmarsdotter, L., Zdziarski, A. A., Larsson, S., et al. 2008, MNRAS, 384, 278 [CrossRef] [NASA ADS]
- Itoh, T., Done, C., Makishima, K., et al. 2008, Publ. Astron. Soc. Japan, 60, S251
- Johnson, W. N., Kurfess, J. D., Purcell, W. R., et al. 1993, A&AS, 97, 21 [NASA ADS]
- Joinet, A., Jourdain, E., Malzac, J., et al. 2005, ApJ, 629, 1008 [CrossRef] [NASA ADS]
- Joinet, A., Jourdain, E., Malzac, J., et al. 2007, ApJ, 657, 400 [CrossRef] [NASA ADS]
- Jourdain, E., Gotz, D., Westergaard, N. J., et al. 2008 [arXiv:0810.0646], POS (integral08) 144
- Kaptein, R. G., in't Zand, J. J. M., Kuulkers, E., et al. 2000, A&A, 358, L71 [NASA ADS]
- Kirsch, M. G., Briel, U. G., Burrows, D., et al. 2005, in Proc. SPIE 5898, ed. O. H. W. Sigmund et al., 589803-1
- Krivonos, R., Revnivtsev, M., Churazov, E., et al. 2007, A&A, 463, 957 [EDP Sciences] [CrossRef] [NASA ADS]
- Kubota, A., Dotani, T., Cottam, J., et al. 2007, Publ. Astron. Soc. Japan, 59, S185
- Maisack, M., Kendziorra, E., Pan, H. C., et al. 1994, A&A, 283, 841 [NASA ADS]
- Malzac, J., Petrucci, P. O., Jourdain, E., et al. 2006, A&A, 448, 1125 [EDP Sciences] [CrossRef] [NASA ADS]
- Mangano, V., Bocchino, F., Cusumano, G., et al. 2006, Adv. Space Res., 37, 1984 [CrossRef] [NASA ADS]
- Marti, J., Perez-Ramirez, D., Luque-Escamilla, P., et al. 2007, Ap&SS, 309, 309 [CrossRef] [NASA ADS]
- Masetti, N., Mason, E., Landi, R., et al. 2008, A&A, 480, 712 [CrossRef] [NASA ADS]
- McConnell, M. L., Forrest, D. J., Owens, A., et al. 1989, ApJ, 343, 317 [CrossRef] [NASA ADS]
- McConnell, M. L., Ryan, J. M., Collmar, W., et al. 2000, ApJ, 543, 928 [CrossRef] [NASA ADS]
- Okajima, T., Tueller, J., Markwardt, C., et al. 2006, ATel, 799
- Pottschmidt, K., Chernyakova, M., Zdziarski, A. A., et al. 2006, A&A, 452, 285 [EDP Sciences] [CrossRef] [NASA ADS]
- Revnivtsev, M. G., Chernyakova, M., Capitanio, F., et al. 2003, ATel, 132, 1 [NASA ADS]
- Revnivtsev, M. G., Gilfanov, M., Churazov, E., & Sunyaev, R. 2003, ATel, 150, 1 [NASA ADS]
- Revnivtsev, M. G., Sunyaev, R. A., Gilfanov, M. R., et al. 2004, Astron. Lett., 30, 527 [CrossRef] [NASA ADS]
- Revnivtsev, M. G., Sazonov, S., Gilfanov, M., Churazov, E., & Sunyaev, R. 2006, A&A, 452, 169 [EDP Sciences] [CrossRef] [NASA ADS]
- Rodriguez, J., Hannikainen, D. C., Shaw, S. E., et al. 2008, ApJ, 675, 1436 [CrossRef] [NASA ADS]
- Rodriguez, J., Shaw, S. E., Hannikainen, D. C., et al. 2008, ApJ, 675, 1449 [CrossRef] [NASA ADS]
- Roques, J. P., Schanne, S., von Kienlin, A., et al. 2003, A&A, 411, L91 [EDP Sciences] [CrossRef] [NASA ADS]
- Rothschild, R. E., Wilms, J., Tomsick, J., et al. 2006, ApJ, 641, 801 [CrossRef] [NASA ADS]
- Russell, D. M., Fender, R. P., Gallo, E., & Kaiser, C. R. 2007, MNRAS, 376, 1341 [CrossRef] [NASA ADS]
- Schönfelder, V., Bennett, K., Blom, J. J., et al. 2000, A&AS, 143, 145 [EDP Sciences] [CrossRef] [NASA ADS]
- Shaposhnikov, N., & Titarchuk, L. 2006, ApJ, 643, 1098 [CrossRef] [NASA ADS]
- Smith, D. A. 1998, IAU Circ., 7008, 1 [NASA ADS]
- Steinle, H., Bennett, K., Bloemen, H., et al. 1998, A&A, 330, 97 [NASA ADS]
- Strickman, M., Skibo, J., Purcell, W., Barret, D., & Motch, C. 1996, A&AS, 120, 217 [NASA ADS]
- Strickman, M., de Jager, O., & Harding, A. 1996, A&AS, 120, 449 [NASA ADS]
- Sturner, S. J., & Shrader, C. R. 2005, ApJ, 625, 923 [CrossRef] [NASA ADS]
- Szostek, A., & Zdziarski, A. A. 2007, MNRAS, 375, 793 [CrossRef] [NASA ADS]
- Szostek, A., & Zdziarski, A. A. 2008, MNRAS, 386, 593 [CrossRef] [NASA ADS]
- Thompson, T. W. J., Rothschild, R. E., Tomsick, J. A., & Marshall, H. L. 2005, ApJ, 634, 1261 [CrossRef] [NASA ADS]
- Tomsick, J. A., Corbel, S., Goldwurm, A., & Kaaret, P. 2005, ApJ, 630, 413 [CrossRef] [NASA ADS]
- Tomsick, J. A., Kalemci, E., Kaaret, P., et al. 2008, ApJ, 680, 593 [CrossRef] [NASA ADS]
- Titarchuk, L. 1994, ApJ, 434, 570 [CrossRef] [NASA ADS]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [EDP Sciences] [CrossRef] [NASA ADS]
- Ulrich, M. H. 2000, A&ARv, 10, 135 [CrossRef] [NASA ADS]
- van der Meer, A., Kaper, L., di Salvo, T., et al. 2005, A&A, 432, 999 [EDP Sciences] [CrossRef] [NASA ADS]
- Vedrenne, G., Roques, J.-P., Schönfelder, V., et al. 2003, A&A, 411, L63 [EDP Sciences] [CrossRef] [NASA ADS]
- Wu, Y.-X., Liu, C.-Z., & Li, T.-P. 2007, ApJ, 660, 1386 [CrossRef] [NASA ADS]
- Zhang, S. N., Cui, W., Harmon, B. A., et al. 1997, ApJ, 477, L95 [CrossRef] [NASA ADS]
- Ziolkowski, J. 2005, MNRAS, 358, 851 [CrossRef] [NASA ADS]
Footnotes
All Tables
Table 1: The 20 objects investigated in this study and the properties of the corresponding datasets.
Table 2: Spectral fit parameters for sources other than X-ray binaries.
Table 3: Spectral fit parameters for X-ray binaries.
Table 4: Our measurements of the Crab flux with SPI and ISGRI assuming the spectral shape given in Table 2 for energy redistribution.
Table 5: Source fluxes [mCrab].
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


