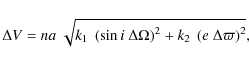| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 495 - 504 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912696 | |
| Published online | 03 September 2009 | |
A&A 507, 495-504 (2009)
Datura family: the 2009 update![[*]](/icons/foot_motif.png)
D. Vokrouhlický1
- J. Durech1 - T. Micha![]() owski2 -
Yu. N. Krugly3 -
N. M. Gaftonyuk4 -
A. Kryszczynska2 - F. Colas5
- J. Lecacheux6 - I. Molotov7
- I. Slyusarev3 - M. Polinska2
- D. Nesvorný8 - E. Beshore9
owski2 -
Yu. N. Krugly3 -
N. M. Gaftonyuk4 -
A. Kryszczynska2 - F. Colas5
- J. Lecacheux6 - I. Molotov7
- I. Slyusarev3 - M. Polinska2
- D. Nesvorný8 - E. Beshore9
1 - Institute of Astronomy, Faculty of Mathematics and Physics, Charles
University, V Holesovickách 2, 18000 Prague 8, Czech Republic
2 - Astronomical Observatory, Adam Mickiewicz University, S![]() oneczna 36, 60-286 Poznan,
Poland
oneczna 36, 60-286 Poznan,
Poland
3 - Institute of Astronomy, Karazin Kharkiv National University, Sumska
35, Kharkiv 61022, Ukraine
4 - Crimean Astrophysical Observatory, Simeiz Department, Simeiz 98680,
Ukraine
5 - IMCCE-CNRS-Observatoire de Paris, 77 avenue Denfert Rochereau,
75014 Paris, France
6 - LESIA-Observatoire de Paris, 77 avenue Denfert Rochereau, 75014
Paris, France
7 - Keldysh Institute of Applied Mathematics, RAS, Miusskaya 4, Moscow
125047, Russia
8 - Southwest Research Institute, 1050 Walnut St, Suite 300, Boulder,
CO 80302, USA
9 - Lunar and Planetary Laboratory, University of Arizona, Tucson, AZ
85719, USA
Received 15 June 2009 / Accepted 15 July 2009
Abstract
Context. Research of asteroid families has been
recently
refreshed by the discovery of very young ones. These families are of
great interest because they represent the product of their parent body
fragmentation before orbital and physical evolutionary processes can
change them. A cluster of seven objects around the largest body (1270)
Datura is of particular interest because it has enough known members
and resides in the inner part of the main asteroid belt, facilitating
observations.
Aims. We carried out photometric observations of the
two largest
members of the Datura family - asteroids (1270) Datura and (90265)
2003 CL5 - with the goal of inferring their physical
parameters.
We also used numerous astrometric observations of Datura-family members
in the past few years to revisit the age of this cluster.
Methods. We performed numerous photometric
observations of
(1270) Datura over several oppositions. We then used the
lightcurve inversion method to determine the spin state and shape of
this asteroid. In the case of (90265) 2003 CL5, for which only
limited lightcurve data have been acquired so far, we used Fourier
analysis to determine the synodic rotation period during the 2008
apparition. We also used backward numerical integration of the improved
orbits of Datura family members to reduce uncertainty in its age.
Results. We determined the rotation state of
(1270) Datura,
the largest member of its own family. Its major properties are a short
rotation period of ![]() 3.36 h
and small obliquity, which, however, exhibits
3.36 h
and small obliquity, which, however, exhibits ![]()
![]()
![]() excursions because of a forced Cassini state of the proper nodal
frequency. Any possible initial non-principal rotation state has
probably been damped and the asteroid rotates about the shortest axis
of the inertia tensor. Its global shape, although convex in our
representation, may reflect regions related to the excavation of the
family members from the parent body surface. Interestingly, the second
largest member of the Datura family - (90265) 2003 CL5 -
appears
to be very slow rotator with the rotation period
excursions because of a forced Cassini state of the proper nodal
frequency. Any possible initial non-principal rotation state has
probably been damped and the asteroid rotates about the shortest axis
of the inertia tensor. Its global shape, although convex in our
representation, may reflect regions related to the excavation of the
family members from the parent body surface. Interestingly, the second
largest member of the Datura family - (90265) 2003 CL5 -
appears
to be very slow rotator with the rotation period ![]() 24 h.
The large amplitude of its rotation curve suggests that its shape is
extremely elongated, possibly bi-lobed. Improved orbits of the family
members allow us to re-determine the possible age of this family. We
find an age that is slightly older than previously reported. Using a
conservative approach, we obtain an age in the 450 to 600 kyr
range. With strengthened, but plausible, conditions, we find that the
current data may support an age of
24 h.
The large amplitude of its rotation curve suggests that its shape is
extremely elongated, possibly bi-lobed. Improved orbits of the family
members allow us to re-determine the possible age of this family. We
find an age that is slightly older than previously reported. Using a
conservative approach, we obtain an age in the 450 to 600 kyr
range. With strengthened, but plausible, conditions, we find that the
current data may support an age of ![]() kyr.
Further astrometric and photometric observations of the Datura cluster
members are needed to determine its age more accurately.
kyr.
Further astrometric and photometric observations of the Datura cluster
members are needed to determine its age more accurately.
Key words: minor planets, asteroids - techniques: photometric
1 Introduction
The discovery of very young asteroid clusters (e.g., Nesvorný et al. 2006b; Nesvorný & Vokrouhlický 2006; Pravec & Vokrouhlický 2009) started a new phase in the analysis of the asteroid families. This is because we have become aware of many dynamical and physical processes that modify the configuration and the observable parameters of their individual members with time. These processes prevent information about the initial state of the asteroid families being derived from current observations. In very young families, of ages less than one million years, most of these processes had insufficient time to affect the physical properties of both their members and their overall orbital configuration. From their study, we might be able to directly infer properties of their parent object fragmentation. The very young asteroid families may also have some novel features in terms of the interplanetary dust distribution (e.g., Vokrouhlický et al. 2008; Espy et al. 2009).Table 1: Equinoctial orbital elements of the Datura family members as of MJD 55000.0.
Spectroscopic studies with the goal of calibrating space weathering
processes and spectral uniformity as a function of the rotational cycle
are ongoing
(Mothé-Diniz & Nesvorný 2008; Takato
2008;
Chapman et al. 2009;
Vernazza
et al. 2009).
Here we begin attempts to characterize the rotational state of the
young families' members. We focus on the Datura family for two reasons:
(i) this cluster has a wealth of currently known members
(Table 1);
and (ii) residing in the inner part of the
asteroid belt, its largest members are assessable for
physical studies to even limited-size instrumentation. Our ideal goal
would
be to determine the spin state and shape of as many members as
possible, and
relate them to their initial values immediately after the family
formation. We
shall see, however, that already in the (1270) Datura case
(Sect. 3)
the analysis may not be straightforward, and sometimes we may only be
able to infer lower and upper
bounds to the initial spin state. So far we have succeeded in acquiring
photometric observations of (1270) Datura and the second largest member
in its family (90265) 2003 CL5. While in the first case, we
have already sufficient data to reconstruct the current spin state and
shape (Sect. 3),
in the case of asteroid 2003 CL5, we present only
single-opposition data that poorly provides a constraint on its
rotation period. Nevertheless, we find that this incomplete information
is very
interesting because of the large disparity in the rotation rate of the
two largest
members in this family and the likely bi-lobed shape of
2003 CL5
(Sect. 4).
In the second part of the paper, we revise the age of
this family using new astrometric observations of the Datura family
members acquired since January 2006, and especially recovery
of the asteroid (215619) 2003 SQ168 in December 2007
(Sect. 5).
With six members on reasonably
well-constrained orbits (Table 1),
we are able to reconstruct the past configuration of this asteroid
cluster to higher accuracy
than before. Surprisingly, we find possible age solutions that are
older than the value of ![]() 450 kyr
previously reported by Nesvorný et al. (2006b).
450 kyr
previously reported by Nesvorný et al. (2006b).
2 Observations
With its near 10 km size, Datura is a relatively easy target
for photometric studies. It was observed by Wisniewski et al. (1997)
during the 1990/1991 opposition, and Székely et al. (2005)
during the 2000 opposition. Analyses of
both datasets indicated relatively short rotation period of ![]() 3.2-3.4 h,
but they were limited enough to allow linkage across the 10 yr
interval of time between them.
3.2-3.4 h,
but they were limited enough to allow linkage across the 10 yr
interval of time between them.
The discovery of the Datura family in late 2005 provided strong
motivation for
photometric and spectroscopic observations to infer the physical
properties
of (1270) Datura and other members of its family. We started our
photometric
campaign during the 2006 opposition and continued during subsequent
observing time
opportunities. Our main efforts were concentrated on the 2007/2008
opposition when
observations covering a period of nearly six months, and phase angle
values of up to ![]() ,
were obtained (we did not use the independent observations of
Takato (2008)
from mid February 2008 because they roughly coincided with our
data from the beginning of February 2008). These observations were very
important
because they allowed easy linkage of data from all oppositions and
helped us to resolve the asteroid shape.
The synodic period determined by combining lightcurves from this
opposition,
3.3583 h, also served as a good starting value of the sidereal
rotation period
in the global lightcurve inversion procedure. We note however, that the
data in 2006 and 2009 are also important, because they offer novel
viewing geometry to the asteroid, thus helping us to resolve its pole
and shape. The
calibrated observations of November 20/21, 2007 allowed us to determine
the
color indexes
,
were obtained (we did not use the independent observations of
Takato (2008)
from mid February 2008 because they roughly coincided with our
data from the beginning of February 2008). These observations were very
important
because they allowed easy linkage of data from all oppositions and
helped us to resolve the asteroid shape.
The synodic period determined by combining lightcurves from this
opposition,
3.3583 h, also served as a good starting value of the sidereal
rotation period
in the global lightcurve inversion procedure. We note however, that the
data in 2006 and 2009 are also important, because they offer novel
viewing geometry to the asteroid, thus helping us to resolve its pole
and shape. The
calibrated observations of November 20/21, 2007 allowed us to determine
the
color indexes ![]() ,
,
![]() ,
and
,
and ![]() ,
which are typical of S type asteroids (e.g., Shevchenko &
Lupishko 1998).
Additional calibrated observations at different phase angles in R
band allowed us to fit
,
which are typical of S type asteroids (e.g., Shevchenko &
Lupishko 1998).
Additional calibrated observations at different phase angles in R
band allowed us to fit ![]() ,
at maximum
lightcurve, and
,
at maximum
lightcurve, and ![]() using the H-G system (see
Fig. A.4 in the
Appendix). Using our derived V-R
value, we then obtained
using the H-G system (see
Fig. A.4 in the
Appendix). Using our derived V-R
value, we then obtained
![]() in visible band, which infers an equivalent diameter of
in visible band, which infers an equivalent diameter of ![]() 9.8 km
(for an albedo of 0.19). Details of observing geometries for
all 20 new lightcurves, including the 3 old ones, are given in
Table 2.
9.8 km
(for an albedo of 0.19). Details of observing geometries for
all 20 new lightcurves, including the 3 old ones, are given in
Table 2.
Table 2: Aspect data for observations of (1270) Datura.
The ![]() 3 km
size asteroid (90265) 2003 CL5, the second largest in the
Datura family, is a significantly more difficult target for small-scale
telescopes.
Fortunately, the asteroid was close to the pericenter of its
heliocentric orbit during
opposition in 2008 enabling our observations to take place. We
performed lightcurve
observations of (90265) 2003 CL5 in five nights during this
favorable apparition with the date and observing geometries indicated
in Table 3.
All observations were performed with the 1 m
telescope at the Crimean Astrophysical Observatory at Simeiz. Three
observations of (90265) 2003 CL5 were calibrated and performed
in the standard R band. We also obtained a
color index
3 km
size asteroid (90265) 2003 CL5, the second largest in the
Datura family, is a significantly more difficult target for small-scale
telescopes.
Fortunately, the asteroid was close to the pericenter of its
heliocentric orbit during
opposition in 2008 enabling our observations to take place. We
performed lightcurve
observations of (90265) 2003 CL5 in five nights during this
favorable apparition with the date and observing geometries indicated
in Table 3.
All observations were performed with the 1 m
telescope at the Crimean Astrophysical Observatory at Simeiz. Three
observations of (90265) 2003 CL5 were calibrated and performed
in the standard R band. We also obtained a
color index ![]() that fits well the Datura value given above and the spectral
classification S for this
object (e.g., Mothé-Diniz & Nesvorný 2008).
that fits well the Datura value given above and the spectral
classification S for this
object (e.g., Mothé-Diniz & Nesvorný 2008).
Table 3: Aspect data for new observations of (90265) 2003 CL5.
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{12696fig1.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg42.png)
|
Figure 1:
The shape model of (1270) Datura shown from equatorial level (
left and center, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{12696fig2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg43.png)
|
Figure 2:
Examples of Datura's lightcurves (symbols) fitted with our model (solid
curve). The viewing and illumination geometry is given by the aspect
angle |
| Open with DEXTER | |
Assuming a phase/slope parameter G=0.2, our
calibrated observations
allow us to determine absolute magnitude ![]() in visible band at the maximum of the lightcurve (in this case, the
phase-angle analysis was
partly affected by the slow rotation of the asteroid and thus different
observations were obtained at different phases of the rotation curve).
Assuming an albedo of 0.19, this translates into a 2.1 km size
equivalent to the maximal projection of the system. This is a slightly
smaller value than reported so far from photometry accompanying the
astrometric observations.
in visible band at the maximum of the lightcurve (in this case, the
phase-angle analysis was
partly affected by the slow rotation of the asteroid and thus different
observations were obtained at different phases of the rotation curve).
Assuming an albedo of 0.19, this translates into a 2.1 km size
equivalent to the maximal projection of the system. This is a slightly
smaller value than reported so far from photometry accompanying the
astrometric observations.
3 Spin state and shape of (1270) Datura
Our new observations were combined with the older data of Wisniewski
et al.
(1997)
and Székely et al. (2005), and
analysed using the lightcurve inversion method of Kaasalainen and
collaborators (e.g., Kaasalainen et al.
2001,
2003).
This procedure provides a simultaneous solution of the
fundamental rotation parameters, rotation period P,
and pole position
![]() ,
in addition to parameters describing the irregular shape of the
asteroid. Low-to-moderate phase angle lightcurves are insensitive to
concavities in the asteroid shape, so we are generally only able to
solve for a
convex realization of the body (e.g., Durech & Kaasalainen 2003).
Thus, we are unable to directly study the potential concavities of the
shape
that might indicate details of the fragmentation of the parent body of
the family. Nevertheless, the flat planar areas in the derived figure
are
indicative of the presence of these concavities.
The lightcurve inversion procedure also did not require a non-principal
axis (NPA) component indicating that Datura rotates close enough to the
shortest axis of its inertia tensor. Moderate initial NPA rotation
would
in all cases be damped with a characteristic timescale of
,
in addition to parameters describing the irregular shape of the
asteroid. Low-to-moderate phase angle lightcurves are insensitive to
concavities in the asteroid shape, so we are generally only able to
solve for a
convex realization of the body (e.g., Durech & Kaasalainen 2003).
Thus, we are unable to directly study the potential concavities of the
shape
that might indicate details of the fragmentation of the parent body of
the family. Nevertheless, the flat planar areas in the derived figure
are
indicative of the presence of these concavities.
The lightcurve inversion procedure also did not require a non-principal
axis (NPA) component indicating that Datura rotates close enough to the
shortest axis of its inertia tensor. Moderate initial NPA rotation
would
in all cases be damped with a characteristic timescale of ![]() 75 kyr
if
we adopted the parameters in Harris (1994),
short enough compared to the
estimated family age. So the present principal axis rotation does not
preclude initial NPA
75 kyr
if
we adopted the parameters in Harris (1994),
short enough compared to the
estimated family age. So the present principal axis rotation does not
preclude initial NPA![]() .
.
As usual for main-belt targets, the lightcurve inversion method is
affected by
a ![]()
![]() ambiguity in the pole longitude. We thus obtained two
possible pole positions: (i)
ambiguity in the pole longitude. We thus obtained two
possible pole positions: (i) ![]() ,
,
![]() (hereafter P1);
and (ii)
(hereafter P1);
and (ii)
![]() ,
,
![]() (hereafter P2) with sidereal
rotation period
(hereafter P2) with sidereal
rotation period ![]() h.
In each of the cases, the uncertainty in the pole direction is roughly
h.
In each of the cases, the uncertainty in the pole direction is roughly
![]() .
We note that P1 provides a slightly
better fit to the lightcurves, but P2 cannot be ruled out on the base
of the photometric data. Interestingly, well-planned
infrared observations could not only improve the size/albedo values for
Datura but also help to discriminate between P1 and P2 (see, e.g.,
Delbó
& Tanga 2009).
.
We note that P1 provides a slightly
better fit to the lightcurves, but P2 cannot be ruled out on the base
of the photometric data. Interestingly, well-planned
infrared observations could not only improve the size/albedo values for
Datura but also help to discriminate between P1 and P2 (see, e.g.,
Delbó
& Tanga 2009).
Our solution supersedes an attempt of Durech et al. (2009), who used the 1990/1991 lightcurves of Wisniewski et al. (1997) and complemented them with 79 sparse photometry data from the US Naval Observatory catalog. The latitude solution in this reference differs significantly from our result, probably because of the limited quality of the dense-photometry data and the small amount of sparse-photometry data. This example illustrates the continuing necessity to acquire dense photometry data, to supplement possibly for more numerous amount of sparse data from the sky-survey programs in the future.
The convex shape model of (1270) Datura associated with the P1 solution is shown in Fig. 1 and six representative lightcurves and the corresponding fits are shown in Fig. 2. The planar regions in the northern and southern hemispheres are probably not real, but caused by the apriori convex representation of the model. It is interesting to hypothesize that one, or both, may correspond to the impact feature related to the origin of the Datura family.
3.1 What was the initial obliquity of Datura?
Given the youth of the Datura family, one is tempted to interpret the current rotation state as the initial one, right after the family formation event. We assume that this is true for the short rotation period, because the only sizeable phenomenon, the Yarkovsky-O'Keefe-Radzievskii-Paddack (YORP) effect, could only have changed rotation period by a few per-mil fractionally (see, e.g., Capek & Vokrouhlický 2004). The situation is, however, different for the obliquity value.
The pole solutions P1 and P2 have current obliquities ![]()
![]() and
and ![]()
![]() ,
respectively, measured with respect to the orbital plane. While the
YORP effect may have changed the
obliquity by only a fraction of a degree (e.g., Capek &
Vokrouhlický 2004;
Bottke et al. 2006), its
initial value can
hardly be inferred because of the parameter-dependent interplay of the
gravitational torque due to the Sun and inertial torques due to moving
orbital plane (known as the Cassini dynamics; e.g. Henrard &
Murigande 1987;
Vokrouhlický et al. 2006).
To verify this conclusion, we used the symplectic
numerical scheme of Breiter et al. (2005) to
propagate the current rotation state
(pole P1 and P2) for 1 Myr into the future. The orbit of
Datura was
propagated using the SWIFT_MVS integrator with a
timestep of 5 d and
output sampling of 50 yr (the asteroid initial data from
Table 1
and planetary ephemeris from JPL DE405),
and then used by the Breiter et al. scheme to propagate the
spin state. The only unknown parameter is the asteroid's dynamical
flattening
,
respectively, measured with respect to the orbital plane. While the
YORP effect may have changed the
obliquity by only a fraction of a degree (e.g., Capek &
Vokrouhlický 2004;
Bottke et al. 2006), its
initial value can
hardly be inferred because of the parameter-dependent interplay of the
gravitational torque due to the Sun and inertial torques due to moving
orbital plane (known as the Cassini dynamics; e.g. Henrard &
Murigande 1987;
Vokrouhlický et al. 2006).
To verify this conclusion, we used the symplectic
numerical scheme of Breiter et al. (2005) to
propagate the current rotation state
(pole P1 and P2) for 1 Myr into the future. The orbit of
Datura was
propagated using the SWIFT_MVS integrator with a
timestep of 5 d and
output sampling of 50 yr (the asteroid initial data from
Table 1
and planetary ephemeris from JPL DE405),
and then used by the Breiter et al. scheme to propagate the
spin state. The only unknown parameter is the asteroid's dynamical
flattening ![]() ,
where (A,B,C)
are the principal moments of inertia of the body. We used our two shape
models for Datura associated with the P1 and
P2 solutions, assuming a homogeneous distribution of density, to infer
that
,
where (A,B,C)
are the principal moments of inertia of the body. We used our two shape
models for Datura associated with the P1 and
P2 solutions, assuming a homogeneous distribution of density, to infer
that ![]() ranges from
ranges from ![]() 0.15
to
0.15
to ![]() 0.3(note
that the lightcurve inversion method provides a reasonable shape
of the body but only poorly constrains its
0.3(note
that the lightcurve inversion method provides a reasonable shape
of the body but only poorly constrains its ![]() value).
value).
Figure 3
shows the future obliquity evolution of the current
pole positions P1 and P2 for the two assumptions of ![]() :
0.2 solid
curve and 0.3 dashed curve. In either of these two cases, the obliquity
undergoes large amplitude oscillations up to
:
0.2 solid
curve and 0.3 dashed curve. In either of these two cases, the obliquity
undergoes large amplitude oscillations up to ![]()
![]() with
with
![]() -dependent
periodicity. For instance, in the
-dependent
periodicity. For instance, in the ![]() case
the principal period of the obliquity change is
case
the principal period of the obliquity change is ![]() 54 kyr, significantly larger
than the principal nodal precession period of
54 kyr, significantly larger
than the principal nodal precession period of ![]() 35 kyr. This difference,
and the overall large amplitude of the obliquity oscillation, are
related to
significantly high obliquity value of the forced Cassini
state 2 (e.g., Henrard
& Murigande 1987;
Vokrouhlický et al. 2006).
For instance in the
35 kyr. This difference,
and the overall large amplitude of the obliquity oscillation, are
related to
significantly high obliquity value of the forced Cassini
state 2 (e.g., Henrard
& Murigande 1987;
Vokrouhlický et al. 2006).
For instance in the ![]() case, the forced Cassini state 2 is at
case, the forced Cassini state 2 is at ![]() and becomes larger than
and becomes larger than ![]()
![]() for
for ![]() .
.
Figure 3
shows that the period, and thus also a phase,
of obliquity oscillations critically depends on the unknown ![]() value.
Because the lightcurve inversion only poorly constrains
value.
Because the lightcurve inversion only poorly constrains ![]() ,
the
initial, post-breakup obliquity of Datura cannot be determined. It can
be any value between zero and
,
the
initial, post-breakup obliquity of Datura cannot be determined. It can
be any value between zero and ![]()
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696fig3.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg58.png)
|
Figure 3:
Obliquity of P1 ( top) and P2 ( bottom)
solutions during the next 1 Myr time interval. Numerical model
includes gravitational torque from the Sun and evolution of Datura's
orbit due to planetary perturbations. The solid lines are for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696fig4.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg59.png)
|
Figure 4:
Composite lightcurve of (90265) 2003 CL5 from the 2008
opposition. Different symbols for observations during 5 nights in
September and October as indicated in the labels. The ordinate is the
calibrated magnitude in standard R band;
the calibrated observations were related using the H-G fitted phase
curve assuming G=0.2 value. We used |
| Open with DEXTER | |
4 Rotation period for (90265) 2003 CL5
From the first night of observations, we were already able to infer
that
(90265) 2003 CL5
is a slow rotator. We then followed the object over five
nights in September and October 2008. The composite lightcurve
(Fig. 4)
has a very large amplitude of 1.5 mag
or more (because of the rotation period close to one day, our
observations unfortunately did not cover any of the lightcurve minima).
The insufficient coverage of the lightcurve prevents us from accurately
determining the apparent rotational
period during this opposition (we additionally note that the observing
geometry somewhat changed in-between our first and last observations).
One of the possible solutions, ![]() h,
has been used in
Fig. 4
to fold all observations into a single phase plot. There are, however,
other possible
solutions near this period.
h,
has been used in
Fig. 4
to fold all observations into a single phase plot. There are, however,
other possible
solutions near this period.
Given the slow rotation rate and small size of (90265)
2003 CL5, it is
interesting to explore the extent to which the YORP effect could have
changed the
rotation period within the estimated age of the Datura family. Using
the statistical data in Capek & Vokrouhlický (2004;
Figs. 6-8),
we estimate that the initial rotation period of this asteroid could not
have been shorter than ![]() 17.5 h,
while it could have been as
long as
17.5 h,
while it could have been as
long as ![]() 32 h.
The shorter limit is perhaps more interesting,
indicating that the initial rotation period of (90265)
2003 CL5 should
have been fairly long in any case. We should also mention that the
principal axis rotation of this asteroid, if confirmed by future
observations, may provide an important constraint on the formation
process after parent body fragmentation. We note that the canonical
estimate for the damping timescale of an excited rotation state (e.g.,
Harris 1994)
would give several hundreds of Myr, about a factor
100-1000 longer than the family age.
32 h.
The shorter limit is perhaps more interesting,
indicating that the initial rotation period of (90265)
2003 CL5 should
have been fairly long in any case. We should also mention that the
principal axis rotation of this asteroid, if confirmed by future
observations, may provide an important constraint on the formation
process after parent body fragmentation. We note that the canonical
estimate for the damping timescale of an excited rotation state (e.g.,
Harris 1994)
would give several hundreds of Myr, about a factor
100-1000 longer than the family age.
The very large amplitude of the lightcurve suggests an interesting
possibility that this object is an extremely elongated, possibly
bi-lobed
object or even a close synchronous binary system![]() .
We note that the hydrocode simulations of asteroid fragmentation do
predict large fraction of binary fragments, the so-called escaping
ejecta binaries (e.g., Durda et al. 2004;
Nesvorný et al. 2006b;
Richardson et al. 2009).
However, it seems that (90265) 2003 CL5 being a bi-lobed
object (perhaps a failed binary) would challenge several
current models. As a result, (90265) 2003 CL5 may provide
interesting information about the fragmentation process of large
asteroids in general, and our ability to model this particular asteroid
numerically. This strongly
motivates further photometric observations of this system in the
future. In particular, it is important to obtain calibrated
observations that would allow us to unambiguously link all available
data
and cover lightcurve minima that were not seen in our 2008-opposition
data.
.
We note that the hydrocode simulations of asteroid fragmentation do
predict large fraction of binary fragments, the so-called escaping
ejecta binaries (e.g., Durda et al. 2004;
Nesvorný et al. 2006b;
Richardson et al. 2009).
However, it seems that (90265) 2003 CL5 being a bi-lobed
object (perhaps a failed binary) would challenge several
current models. As a result, (90265) 2003 CL5 may provide
interesting information about the fragmentation process of large
asteroids in general, and our ability to model this particular asteroid
numerically. This strongly
motivates further photometric observations of this system in the
future. In particular, it is important to obtain calibrated
observations that would allow us to unambiguously link all available
data
and cover lightcurve minima that were not seen in our 2008-opposition
data.
Unfortunately, (90265) 2003 CL5 will be quite faint during the
2010 opposition such that small- and medium-scale telescopes will not
allow us to continue its photometry. The next truly favorable observing
conditions for this asteroid will occur in June and July 2011.
Interestingly, at this opposition the ecliptic longitude of the
asteroid will span values between ![]() and
and ![]() ,
suitably complementary to those in 2008 (Table 3).
As a result, observations from this opposition may themselves
help to exclude some pole positions, even though not yet able
to determine the pole accurately.
,
suitably complementary to those in 2008 (Table 3).
As a result, observations from this opposition may themselves
help to exclude some pole positions, even though not yet able
to determine the pole accurately.
5 Re-estimation of Datura family age
In a first attempt to reconstruct the Datura cluster past configuration, and thus infer its age, Nesvorný et al. (2006b) used orbits of four members of the family. Out of these, only (1270) Datura had very precisely determined orbital elements. Orbits of the other three asteroids - (60151) 1999 UZ6, (90265) 2003 CL5 and (203370) 2001 WY35 - were significantly less accurate, reflecting the small number of available astrometric observations over short time intervals of only 6 to 8 years. Since then, the situation has significantly improved.
First, Sergio Foglia and colleagues made a significant effort attempting to find young-families' members on archival plates and succeeded in several cases. For instance, discovery of (90265) 2003 CL5 on the NEAT program archival frames taken in January 1996 allowed us to extend the known orbital arc of this asteroid by several years into the past. Second, the discovery of the young families allowed us to prompt targeted astrometry observations to ensure that most of the objects are observed on every subsequent opposition. In this respect, we should point out in particular observations made with the 1.5 m telescope at Mt. Lemmon Observatory at the Catalina Sky Survey (CSS). Importantly, both lines of effort led to precovery and recovery of the Datura member (215619) 2003 SQ168 nearly simultaneously in December 2007. Since then, CSS also acquired astrometry of this object in April and May 2009 during its next opposition. As a result, we can now use this asteroid for the past reconstruction of the Datura cluster. The information about the currently available accuracy of the orbits of Datura members is given in Table 1 (compare with Table 1 in Nesvorný & Vokrouhlický 2006).
We used the same approach as Nesvorný et al. (2006b) and Nesvorný & Vokrouhlický (2006) to determine the past orbital configuration of the Datura members. We refer interested readers to these references for details, limiting ourselves here to a minimal description of the technique. We considered a large number of statistically identical orbital clones for the asteroids. This was necessary because the past orbital history of each of the members depends on: (i) the current orbital uncertainty (Table 2); and (ii) unknown physical parameters. The former simply means that we have to take a number of initial orbital data for the backward integration uniformly filling the uncertainty ellipsoid in the orbital element space (we call them geometric clones). The second refers to the thermal (Yarkovsky) forces that may significantly affect the orbital evolution over timescales of tens to hundreds of thousands of years and that depends on the spin state and surface properties of the body (e.g., Bottke et al. 2006). Therefore, we need to uniformly cover a range of possible past evolutions of the orbits with Yarkovsky forces applied. We call these variants the Yarkovsky clones.
Performing backward integrations![]() of the clone versions for each of the
asteroids, we can now at each time choose at random their
identification to construct one possible cluster configuration. Given
the large number
of integrated clones, many of these identifications are possible and
we can only characterize information about their proximity on a
statistical basis. To work quantitatively, we define a target
function
of the clone versions for each of the
asteroids, we can now at each time choose at random their
identification to construct one possible cluster configuration. Given
the large number
of integrated clones, many of these identifications are possible and
we can only characterize information about their proximity on a
statistical basis. To work quantitatively, we define a target
function![]() (e.g., Nesvorný & Vokrouhlický 2006)
(e.g., Nesvorný & Vokrouhlický 2006)
where (a,e,i) are the orbital elements of the largest asteroid in the family, n its heliocentric mean motion, k1=1 and k2=1/2 and the node and pericenter dispersions are defined by
The integration of thousands of clones with dense enough time output becomes computationally difficult, both as far as CPU time and disk space are concerned. For that reason, we adopted the following approximation:
- the past orbital evolution of (1270) Datura is represented
by 30 geometric clones, each of which has additionally
15 Yarkovsky clones with da/dt
value negative (this is because we integrate into the past and <
 obliquity for Datura guarantees the sense of its migration due to the
thermal forces), implying that altogether we have 450 geometric and
Yarkovsky clones;
obliquity for Datura guarantees the sense of its migration due to the
thermal forces), implying that altogether we have 450 geometric and
Yarkovsky clones; - the past orbital evolution of (60151) 1999 UZ6, (90265) 2003 CL5, and (203370) 2001 WY35 is represented by 30 geometric clones, each of which has additionally 30 Yarkovsky variants, so altogether there are 900 geometric and Yarkovsky clones;
- the past orbital evolution of (89309) 2001 VN36 and (215619) 2003 SQ168 is represented by 40 geometric clones, each of which has in addition 40 Yarkovsky variants, and altogether there are 1600 geometric and Yarkovsky clones.
When all six asteroids are included, the past Datura cluster
reconstruction
is in our integration represented by as many as ![]() clone identifications. This number
surpasses by far CPU possibilities to evaluate target functions
clone identifications. This number
surpasses by far CPU possibilities to evaluate target functions
![]() and
and ![]() for each one of these identifications
at each output from our integrations (20 yr in our case). We
thus
only compute the target functions for randomly chosen 50 million
different identifications at each output step. This is much less
than the maximum possible number of clone combinations and may imply
that
we significantly undersample the results. Fortunately, the situation is
improved by several factors: (i) clones of (1270) Datura and
(90265) 2003 CL5 have far more similar past evolutions than
other
bodies; (ii) the close nodal/pericenter configuration, for which
the target functions
for each one of these identifications
at each output from our integrations (20 yr in our case). We
thus
only compute the target functions for randomly chosen 50 million
different identifications at each output step. This is much less
than the maximum possible number of clone combinations and may imply
that
we significantly undersample the results. Fortunately, the situation is
improved by several factors: (i) clones of (1270) Datura and
(90265) 2003 CL5 have far more similar past evolutions than
other
bodies; (ii) the close nodal/pericenter configuration, for which
the target functions ![]() and
and ![]() remain smaller than some
threshold, may last up to 20 kyr, a factor 103
longer than our output
sampling of 20 yr; and (iii) not all clones have widely
different
past orbital evolutions. Taking these factors into consideration,
we estimate that the 50 million trial identifications at each time
output should be sufficiently representative.
remain smaller than some
threshold, may last up to 20 kyr, a factor 103
longer than our output
sampling of 20 yr; and (iii) not all clones have widely
different
past orbital evolutions. Taking these factors into consideration,
we estimate that the 50 million trial identifications at each time
output should be sufficiently representative.
Table 1
also indicates that orbits of (1270) Datura and (215619)
2003 SQ168 are very close to each other (including the mean
longitude
in orbit). For that reason, the two objects were assumed to be paired
objects. Vokrouhlický & Nesvorný (2008)
argued against this possibility, proposing instead that an anomalously
small initial separation of (215619) 2003 SQ168 from (1270)
Datura caused their current proximity![]() (see Fig. 6 in Vokrouhlický & Nesvorný 2008).
If well constrained, the convergence of the two orbits in the
mean anomaly value might then be used as an additional criterion
for the age determination of the Datura family. Unfortunately, the
present orbital uncertainty of (215619) 2003 SQ168, and lack
of knowledge
of its physical parameters, prevents this kind of approach. The
Yarkovsky clones of this small asteroid diverge in the mean
longitude in orbit by
(see Fig. 6 in Vokrouhlický & Nesvorný 2008).
If well constrained, the convergence of the two orbits in the
mean anomaly value might then be used as an additional criterion
for the age determination of the Datura family. Unfortunately, the
present orbital uncertainty of (215619) 2003 SQ168, and lack
of knowledge
of its physical parameters, prevents this kind of approach. The
Yarkovsky clones of this small asteroid diverge in the mean
longitude in orbit by ![]() after time T; here
after time T; here ![]() yr
is the heliocentric revolution period
and
yr
is the heliocentric revolution period
and ![]() is the accumulated change in semimajor axis a due
to the Yarkovsky effect in time T. For
is the accumulated change in semimajor axis a due
to the Yarkovsky effect in time T. For ![]() kyr,
and the
estimated size of (215619) 2003 SQ168, we have
kyr,
and the
estimated size of (215619) 2003 SQ168, we have ![]() AU.
We
thus note that after only
AU.
We
thus note that after only ![]() 100 kyr
the Yarkovsky clones extend
along the entire elliptic orbit and prevent any deterministic work
using the mean anomaly value.
100 kyr
the Yarkovsky clones extend
along the entire elliptic orbit and prevent any deterministic work
using the mean anomaly value.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696fig5.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg80.png)
|
Figure 5:
Number of clone combinations that provided target functions smaller
than 5 m/s: (i) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696fig6.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg81.png)
|
Figure 6:
An example of a good convergence of secular angles for the Datura
family members. Upper and lower panels show past
difference of longitude of node and longitude of pericenter with
respect to (1270) Datura, the largest asteroid in the family,
for: (90265) 2003 CL5 [red], (60151) 1999 UZ6 [green], (203370) 2001
WY35 [blue], (89309) 2001 VN36 [cyan] and (215619) 2003 SQ168
[magenta]. The vertical dashed line denotes the best convergence time
536 kyr for which |
| Open with DEXTER | |
5.1 Results
Figure 5
shows distribution of age values determined by a number of the clone
combinations corresponding to target functions
![]() from
Eq. (1)
(upper panel) and
from
Eq. (1)
(upper panel) and ![]() (lower panel)
smaller than 5 m/s, rather restrictive value. All Datura
asteroids,
except obviously the single-opposition case of 2003 UD112, and
50 million
trial identifications of different clones at each time have been used
in
this analysis. The age distribution is matched satisfactorily by a
Gaussian
(grey curves) with mean values of 530 kyr and
532 kyr, respectively, and standard
deviations both of
(lower panel)
smaller than 5 m/s, rather restrictive value. All Datura
asteroids,
except obviously the single-opposition case of 2003 UD112, and
50 million
trial identifications of different clones at each time have been used
in
this analysis. The age distribution is matched satisfactorily by a
Gaussian
(grey curves) with mean values of 530 kyr and
532 kyr, respectively, and standard
deviations both of ![]() 18 kyr.
Figure 6
illustrates
possible past convergence of the secular angles as referenced to the
(1270) Datura value for a good solution that has
18 kyr.
Figure 6
illustrates
possible past convergence of the secular angles as referenced to the
(1270) Datura value for a good solution that has ![]() m/s
some 536 kyr ago. This result comes as a surprise, because it
deviates significantly
from the solution of Nesvorný et al. (2006b)
and increments the previously determined age of the Datura family by
nearly 100 kyr. This disagreement in the two solutions
requires some explanation and/or
analysis and that prompted us to perform several further tests
m/s
some 536 kyr ago. This result comes as a surprise, because it
deviates significantly
from the solution of Nesvorný et al. (2006b)
and increments the previously determined age of the Datura family by
nearly 100 kyr. This disagreement in the two solutions
requires some explanation and/or
analysis and that prompted us to perform several further tests![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696fig7.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg82.png)
|
Figure 7:
Number of clone combinations that provided target functions smaller
than 13 m/s (light grey histogram) and 10 m/s (dark
grey histogram): (i) |
| Open with DEXTER | |
First, we tested how the solution depends on the chosen threshold
for the target function values, increasing it to 10 m/s and
13 m/s.
Resulting age distributions are shown in Fig. 7.
Because there are many more possible solutions now, we performed
only half a million trials of the clone identifications in
this case. Indeed, we observe that the possible age solutions now
extend to smaller values more compatible with the result of
Nesvorný et al. (2006b).
However, we would consider the 13 m/s
cutoff not to provide a strong constraint and this is also reflected in
the numerous solutions found: even if we restricted ourselves
to 50 thousand trials (out of the theoretical maximum value ![]() ), we would
obtain many solutions. The 13 m/s value translates
indeed into a mean quadratic nodal or pericenter distance of nearly
), we would
obtain many solutions. The 13 m/s value translates
indeed into a mean quadratic nodal or pericenter distance of nearly
![]() .
Past orbital evolutions in
Fig. 6
hint that this is rather easily matched over a long interval of time.
.
Past orbital evolutions in
Fig. 6
hint that this is rather easily matched over a long interval of time.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696fig8.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg85.png)
|
Figure 8:
Number of clone combinations that provided target functions smaller
than 13 m/s (light grey histogram) and 10 m/s (dark
grey histogram): (i) |
| Open with DEXTER | |
To determine more exactly the sources of difference between the two
solutions, we neglected the orbital history of (89309)
2001 VN36 from our
simulation. This approach was adopted by Nesvorný et al. (2006b)
because
the orbit of this asteroid was assumed to be too uncertain because of
resonance-related chaoticity. Performing again half a million random
identifications at each time instant in the past, as given by our
numerical propagation, we obtained results shown in Fig. 8.
While the bulk of the distribution
shifted toward the ![]() kyr
solution interval determined by Nesvorný et al. (2006b),
there is an extension beyond its 500 kyr age. Choosing a
limited amount of trials and effective high-cutoff values for the
target functions, one may preferentially find the optimal age solutions
in the
kyr
solution interval determined by Nesvorný et al. (2006b),
there is an extension beyond its 500 kyr age. Choosing a
limited amount of trials and effective high-cutoff values for the
target functions, one may preferentially find the optimal age solutions
in the ![]() kyr
interval and we believe that this is what happened.
Decreasing the cutoff limit again to 5 m/s for the target
functions,
the Datura age indeed moves beyond half a million value even in
this simulation where the highly-chaotic orbit of (89309)
2001 VN36
was excluded.
kyr
interval and we believe that this is what happened.
Decreasing the cutoff limit again to 5 m/s for the target
functions,
the Datura age indeed moves beyond half a million value even in
this simulation where the highly-chaotic orbit of (89309)
2001 VN36
was excluded.
To summarize, our main conclusions are that: (i) if we are not overly
optimistic, our analysis suggests an age in between 450 and
600 kyr
for the Datura cluster; and (ii) if we were to take our most
complete and restricted solution for granted, the cluster age would
decrease
within the ![]() kyr
interval. This
is where, effectively, the best-convergence solutions reside. More work
appears to be required to resolve the issue of the Datura cluster age.
This includes both new astrometric and physical observations (that
would
constrain the possible diverse Yarkovsky histories for small Datura
members),
but perhaps also more sophisticated theoretical methods than used so
far.
kyr
interval. This
is where, effectively, the best-convergence solutions reside. More work
appears to be required to resolve the issue of the Datura cluster age.
This includes both new astrometric and physical observations (that
would
constrain the possible diverse Yarkovsky histories for small Datura
members),
but perhaps also more sophisticated theoretical methods than used so
far.
6 Conclusions
This paper has presented our state-of-art knowledge of the Datura
asteroid
family at the dawn of the upcoming new-generation surveys such as
PanSTARRS or LSST (e.g., Jedicke et al. 2007;
Ivezic et al. 2007). It
will be interesting to see how many more Datura-family members will be
discovered in the next few years. Input from these new datasets seems
crucial, because with the current instrumentation
no additional Datura members have been found since the
discovery of the family in late 2005 (the last three members
were discovered in 2003). On the other hand, we argue that
it is equally important to continue with further astrometric and
photometric observations of the fainter, currently known members.
This is because the newly discovered asteroids will likely be
very small, ![]() 2 km,
and the lack of spin state information will make their past orbits
uncertain primarily due to unconstrained
Yarkovsky forces. As a result, continuing photometric observations of
the known
members may help us to constrain at least the sense of their rotation
and thus eliminate many of the clones used in the age determination
simulations in Sect. 5.
2 km,
and the lack of spin state information will make their past orbits
uncertain primarily due to unconstrained
Yarkovsky forces. As a result, continuing photometric observations of
the known
members may help us to constrain at least the sense of their rotation
and thus eliminate many of the clones used in the age determination
simulations in Sect. 5.
The work of D.V. and J.D. was supported by grants GACR 205/08/0064 and GACR 205/07/P070 of the Czech grant agency and by the Research Program MSM0021620860 of the Ministry of Education. The work of T.M. and A.K. was supported by grants N N203 302535 and N N203 382136 of the Polish Ministry of Science and Higher Education. This paper uses observations made in part at the South African Astronomical Observatory (SAAO). We thank Richard Kowalski from the Catalina Sky Survey for important help in obtaining astrometry of faint objects in young asteroid families including Datura, Alan Harris (SSI) for his comments and suggestions that improved the original version of this paper and Vasilij Shevchenko for help with phase curve analysis of (1270) Datura.
Appendix A: Composite lightcurves and phase function for (1270) Datura
In this Appendix, we present composite lightcurves of (1270) Datura containing all our new observations starting from the
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696figA1.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg88.png)
|
Figure A.1: Composite lightcurve of (1270) Datura during the 2006 apparition. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696figA2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg89.png)
|
Figure A.2: Composite lightcurve of (1270) Datura during the 2007/2008 apparition. Lightcurves obtained in January-February 2008 have smaller amplitudes since the phase angles were smaller (see Table 2). In the same way, the largest spread corresponds to the observations from beginning and end of the opposition because they were taken with slightly different viewing geometry. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696figA3.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg90.png)
|
Figure A.3: Composite lightcurve of (1270) Datura during the 2009 apparition. |
| Open with DEXTER | |
2006 apparition
(Figs. A.1-A.3). We also
show the phase curve for this asteroid using our calibrated R
and V band observations and the corresponding fit
in the H-G system (Fig. A.4). Our
best-fit model values are ![]() ,
at the maximum of the lightcurve, and
,
at the maximum of the lightcurve, and ![]() .
We
used data from 1991 (Wisniewski et al. 1997;
with the derived V-Rvalue),
2007/2008 (Simeiz, Kharkiv) and 2009 (Simeiz), see Table 2.
.
We
used data from 1991 (Wisniewski et al. 1997;
with the derived V-Rvalue),
2007/2008 (Simeiz, Kharkiv) and 2009 (Simeiz), see Table 2.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12696figA4.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12696-09/Timg91.png)
|
Figure A.4:
Solar phase angle behavior for (1270) Datura derived from our R band
calibrated observations (symbols). The dashed curve is the best-fit
model using |
| Open with DEXTER | |
References
- Bertotti, B., Farinella, P., & Vokrouhlický, D. 2003, Physics of the Solar System (Dordrecht: Kluwer Academic Publishers)
- Bottke, W. F., Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D. 2006, Ann. Rev. Earth Planet. Sci., 34, 157 [CrossRef] [NASA ADS]
- Breiter, S., Nesvorný, D., & Vokrouhlický, D. 2005, AJ, 130, 1267 [CrossRef] [NASA ADS]
- Broz, M. 2006, Yarkovsky effect and the dynamics of the Solar System, Ph.D. Thesis, Charles University, Prague, atsirrah.troja.mff.cuni.cz/ mira/mp/phdth/
- Capek, D., & Vokrouhlický, D. 2004, Icarus, 172, 526 [CrossRef] [NASA ADS]
- Chapman, C. R., Encke, B., Merline, W. J., et al. 2009, LPSC abstract 2258, at www.lpi.usra.edu/meetings/lpsc2009/pdf/2258.pdf
- Delbó, M., & Tanga, P. 2009, Planet. Space Sci., 57, 259 [CrossRef] [NASA ADS]
- Durda, D. D., Bottke, W. F., Encke, B. L., et al. 2004, Icarus, 170, 243 [CrossRef] [NASA ADS]
- Durech, J., & Kaasalainen, M. 2003, A&A, 404, 709 [EDP Sciences] [CrossRef] [NASA ADS]
- Durech, J., Kaasalainen, M., Warner, B. D., et al. 2009, A&A, 493, 291 [EDP Sciences] [CrossRef] [NASA ADS]
- Espy, A. J., Dermott, S. F., Kehoe, T. J. J., & Jayaraman, S. 2009, Planet. Space Sci., 57, 235 [CrossRef] [NASA ADS]
- Harris, A. W. 1994, Icarus, 107, 209 [CrossRef] [NASA ADS]
- Henrard, J., & Murigande, C. 1987, Celest. Mech., 40, 345 [CrossRef] [NASA ADS]
- Ivezic, Z., Tyson, J. A., Juric, M., et al. 2007, LSST: Comprehensive NEO Detection, Characterization, and Orbits, in Near Earth Objects, Our Celestial Neighbors: opportunity And Risk, ed. A. Milani, G. B. Valsecchi & D. Vokrouhlický (Cambridge: Cambridge University Press), 353
- Jedicke, R., Magnier, E. A., Kaiser, N., & Chambers, K. C. 2007, The Next Decade of Solar System Discovery with Pan-STARRS, in Near Earth Objects, Our Celestial Neighbors: opportunity And Risk, ed. A. Milani, G. B. Valsecchi, & D. Vokrouhlický (Cambridge: Cambridge University Press), 341
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [CrossRef] [NASA ADS]
- Kaasalainen, S., Piironen, J., Kaasalainen, M., et al. 2003, Icarus, 161, 34 [CrossRef] [NASA ADS]
- Knezevic, Z., Lemaitre, A., & Milani, A. 2002, The Determination of Asteroid Proper Elements, in Asteroids III, ed. W. F. Bottke et al. (Tuscon: Arizona University Press), 603
- Mothé-Diniz, T., & Nesvorný, D. 2008, A&A, 486, 9 [EDP Sciences] [CrossRef] [NASA ADS]
- Nesvorný, D., & Vokrouhlický, D. 2006, AJ, 132, 1950 [CrossRef] [NASA ADS]
- Nesvorný, D., Vokrouhlický, D., & Bottke, W. F. 2006a, Science, 312, 1490 [CrossRef] [NASA ADS]
- Nesvorný, D., Enke, B. L., Bottke, W. F., et al. 2006b, Icarus, 183, 296 [CrossRef] [NASA ADS]
- Pravec, P., & Vokrouhlický, D. 2009, Icarus, in press
- Richardson, D. C., Michel, P., Walsh, K. J., & Flynn, K. W. 2009, Planet. Space Sci., 57, 183 [CrossRef] [NASA ADS]
- Shevchenko, V. G., & Lupishko, D. F. 1998, Solar System Res., 32, 220 [NASA ADS]
- Székely, P., Kiss, L. L., Szabó, G. M., et al. 2005, Planet. Space Sci., 53, 925 [CrossRef] [NASA ADS]
- Takato, N. 2008, ApJ, 685, 161 [CrossRef] [NASA ADS]
- Vernazza, P., Binzel, R. P., Rossi, A., Fulchignoni, M., & Birlan, M. 2009, Nature, 458, 993 [CrossRef] [NASA ADS]
- Vokrouhlický, D., Nesvorný, D., & Bottke, W. F. 2006, Icarus, 184, 1 [CrossRef] [NASA ADS]
- Vokrouhlický, D., & Nesvorný, D. 2008, AJ, 136, 280 [CrossRef] [NASA ADS]
- Vokrouhlický, D., Nesvorný, D., & Bottke, W. F. 2008, ApJ, 672, 696 [CrossRef] [NASA ADS]
- Wisniewski, W. Z., Michaowski, T., Harris, A. W., & McMillan, R. S. 1997, Icarus, 126, 395 [CrossRef] [NASA ADS]
Footnotes
- ... update
![[*]](/icons/foot_motif.png)
- Photometric data is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/507/495
- ... NPA
![[*]](/icons/foot_motif.png)
- The derived shape model together with the complete lightcurve data set is available at astro.troja.mff.cuni.cz/projects/asteroids3D.
- ... system
![[*]](/icons/foot_motif.png)
- The long rotation period may support the model of a
bi-lobed shape rather than a synchronous detached system. For example,
if the binary system consisted of two spherical bodies with diameters
1 km and the bulk density 2 g/cm3,
the observed orbital period
 24 hr
would imply
24 hr
would imply  3 km
for the semimajor axis of the mutual orbit. Apparently, such a large
relative separation is not consistent with the shape of the observed
lightcurves. Assuming spherical components, the lightcurve amplitude
also cannot be larger than
3 km
for the semimajor axis of the mutual orbit. Apparently, such a large
relative separation is not consistent with the shape of the observed
lightcurves. Assuming spherical components, the lightcurve amplitude
also cannot be larger than 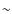 0.8 mag.
Triaxiality of the components may however slightly change these
conclusions.
0.8 mag.
Triaxiality of the components may however slightly change these
conclusions.
- ... integrations
![[*]](/icons/foot_motif.png)
- We use SWIFT_MVSY symplectic integrator (e.g., Broz 2006) with all planets included and timestep of 5 days. The initial state vectors for planets were obtained from JPL DE405 ephemerides at the same time as the elements of the Datura-cluster asteroids (Table 1). We use rather dense output sampling of 20 yr and integrate backward in time till 700 kyr.
- ...
function
![[*]](/icons/foot_motif.png)
- To see if our results are robust, we also evaluated another
target function
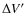 ,
defined as in Eq. (1),
where
,
defined as in Eq. (1),
where 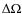 and
and 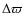 are performed with respect to the orbit of (1270) Datura only and the
summation is performed over the remaining members in the cluster. As
such, the
are performed with respect to the orbit of (1270) Datura only and the
summation is performed over the remaining members in the cluster. As
such, the 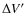 quantity measures dispersal velocity field of the Datura-family
fragments with respect to the largest fragment. Note the
quantity measures dispersal velocity field of the Datura-family
fragments with respect to the largest fragment. Note the 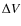 target function may become unrealistically small for a cluster of
fragments that reside on nearby orbits, yet distant from the largest
asteroid in the family.
target function may become unrealistically small for a cluster of
fragments that reside on nearby orbits, yet distant from the largest
asteroid in the family.
- ... proximity
![[*]](/icons/foot_motif.png)
- In this paper, we take this standpoint and do not investigate the less likely possibility that (215619) 2003 SQ168 separated from (1270) Datura in a more recent epoch.
- ... tests
![[*]](/icons/foot_motif.png)
- Obviously, the two age determinations used different orbit sets and this might have influenced the results. However, if the new observations caused simple shrinking of the uncertainty ellipsoid in the space of initial orbital elements, we would expect to obtain equally nested solutions: the one with more accurate orbits would be entirely within the one with less accurate orbits. This idea assumes uniform mixing of results from the uncertainty ellipsoid, which is likely, but not entirely guaranteed.
All Tables
Table 1: Equinoctial orbital elements of the Datura family members as of MJD 55000.0.
Table 2: Aspect data for observations of (1270) Datura.
Table 3: Aspect data for new observations of (90265) 2003 CL5.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.