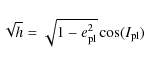| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 505 - 511 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912379 | |
| Published online | 03 September 2009 | |
A&A 507, 505-511 (2009)
Planet formation in highly inclined binaries
F. Marzari1 - P. Thébault2 - H. Scholl3
1 - Dipartimento di Fisica, University of Padova, via Marzolo 8, 35131
Padova, Italy
2 - LESIA, Observatoire de Paris, Section de Meudon, 92195 Meudon
Principal Cedex, France
3 - Laboratoire Cassiopée, Université de Nice Sophia Antipolis, CNRS,
Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex, France
Received 23 April 2009 / Accepted 20 July 2009
Abstract
Aims. We explore planet formation in binary systems
around the
central star where the protoplanetary disk plane is highly inclined
with respect to the companion star orbit. This might be the most
frequent scenario for binary separations larger than 40 AU. We
focus on planetesimal accretion and compute average impact velocities
in the habitable region and up to 6 AU from the primary.
Methods. Planetesimal trajectories are computed
within the frame
of the restricted 3-body problem determined by the central star, the
companion star and massless planetesimals. Relative velocities are
computed and interpreted in terms of accreting or eroding impacts.
Results. We first show that, for binary inclinations
higher than
10 degrees, planetesimals evolve, to a first approximation, in
a
gas-free environment. Planetesimal accretion is confined around the
central star in a region determined by two main parameters, firstly by
the mutual inclination between the binary plane and the disk, and,
secondly, by the binary eccentricity.
Conclusions. The onset of large mutual inclinations
between
planetesimals due to the nodal randomization causes an increase in the
relative velocity. The chances for a successful planet accumulation
process depend on the balance between the timescale for node
randomization and that of planetesimal accretion. When the binary
semimajor axis is larger than 70 AU, planet formation appears
possible even for eccentric binaries (up to 0.4). For
lower
binary separations the region where planetesimals accumulate into
protoplanets shrinks consistently. When the mutual inclination between
the binary plane and that of the planetesimal disk is larger
than
![]() ,
the Kozai mechanism strongly inhibits planetesimal accumulation.
,
the Kozai mechanism strongly inhibits planetesimal accumulation.
Key words: planetary systems: formation - methods: numerical
1 Introduction
Planetary formation in binary systems is a complex issue,
since each
step of the process can be affected in different ways by the companion
perturbations. Recent numerical studies (Xie
& Zhou 2008; Thébault
et al. 2009,2004,2006; Marzari &
Scholl 2000; Thébault
et al. 2008; Paardekooper
et al. 2008)
have shown that one stage is particularly sensitive to the presence of
the secondary star: the initial accretion of kilometer-sized
planetesimals (a review on this topic is given in Haghighipour 2009).
Indeed, the coupled effect of secular perturbations of the companion
star and friction due to gas in the nebulae induces a size-dependent
phasing of orbits which may lead to high impact velocities. This could
slow down or even halt the accretion process even in the terrestrial
planet region for a wide range of binary separations, i.e., up to
![]() AU
for high eccentricity systems
(see for example Figs. 8
and 9 in Thébault
et al. 2006).
AU
for high eccentricity systems
(see for example Figs. 8
and 9 in Thébault
et al. 2006).
However, these studies are based on the assumption that the
planetesimal disk is coplanar to the stellar orbit. Even if this
assumption might intuitively seems reasonable, a systematic study by Hale (1994)
of binary systems with solar-type components suggests that the spin of
the two stars is aligned only for binary systems of 30-40 AU
or
less. Beyond this distance, the primary's equator, and thus a putative
planetesimal disk, appears to be randomly inclined with respect to the
binary planet. As a consequence, the inclination between the binary's
orbital plane and the circumprimary disk is a parameter that has to be
taken into account when studying planetesimal accretion, at least for
systems with ![]() AU.
AU.
We will focus in this paper on binaries with intermediate separations, i.e. in the 40-100 AU range, exploring the inclination as a free parameter. Similarly to the studies for the coplanar case, the main outcome we are interested in is the impact velocity distribution within the planetesimal population, since this parameter controls the fate of planetesimal collisions, either accretion or erosion. For a significant mutual inclination between the binary orbital plane and the disk of planetesimals embedded in the gaseous disk, the forced inclination due to the companion star might be much more effective in increasing the relative velocities and halting planet formation. As the planetesimals decouple from the gaseous disk and evolve gravitationally, they would feel the binary perturbation and move into inclined orbits. The perturbations of the companion star leads to a progressive randomization of planetesimal node longitudes, starting from the outer region of the disk where the secular periods are shorter. The planetesimal disk gradually evolves into a cloud with an angular opening equal to twice the mutual initial inclination of the disk with respect to the binary plane. We explore in this paper the effects of the nodal randomization on the mutual relative velocities within the planetesimal swarm and on the accretion process. We also estimate the minimum inclination below which planet formation may occur in spite of the binary inclination.
The paper is organized as follows: in Sect. 2 we show that the planetesimal dynamics perturbed by the companion star keeps the swarm out of the gaseous disk for most of the orbital period. This makes gas drag a negligible perturbation. In Sect. 3 we describe the numerical model used to compute the planetesimal relative velocities. Section 4 is devoted to the analysis of the impact velocities for different binary parameters. In Sect. 5 we derive limiting inclinations for accretion at different binary separations. Finally, in Sect. 6 we summarize our results.
2 Decoupling between gaseous disk and planetesimals
Most recent studies of planetesimal accretion in a binary environment (Thébault et al. 2009; Marzari & Scholl 2000; Thébault et al. 2006; Paardekooper et al. 2008; Thébault et al. 2008) have focused on the influence of the gaseous component of the disk on particle dynamics. However, the implicit assumption that the planetesimal swarm is embedded in the gas disk is only valid if the disk is coplanar to the binary orbital plane. In this case, planetesimals feel a steady gas drag and have their orbital evolution significantly affected by frictional forces. However, if the companion star is on an inclined orbit with respect to the disk mid-plane, the situation is dynamically more complicated. Three possible scenarios can be envisaged for the interactions between gas and planetesimals:
- Planetesimals form within the gas disk which remains a
long-lived
coherent entity in spite of the binary perturbations. Numerical
simulations with constant viscosity and a polytropic equation of state
performed by Larwood et al.
(1996) with an
SPH code suggest that a disk perturbed by an inclined companion star
maintains a coherent structure if the Mach number is lower
than 30. It behaves like a rigid body preceding at a
rate
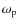 given by:
given by:
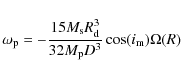
(1)
where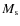 and
and 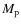 are the masses of the secondary and primary star, respectively, D is
the radius of the circular orbit of the binary,
are the masses of the secondary and primary star, respectively, D is
the radius of the circular orbit of the binary, 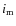 is the mutual
inclination between the disk and the binary orbit,
is the mutual
inclination between the disk and the binary orbit, 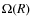 is
the Keplerian frequency and
is
the Keplerian frequency and 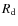 is
the disk radius. This equation is derived under the simplified
assumption that the disk has a constant density, but it is in general a
good approximation to more general cases. In this scenario, when the
planetesimals reach the size (1-10 km in diameter) for which
they
evolve under the dominating gravitational force of the two stars, they
leave the disk plane because of the forced component in the
inclination. Their orbits move in the binary orbital plane and their
nodes circulate at different rates, depending on their semimajor axis.
Gas drag is probably not a significant perturbation in this scenario,
since it affects planetesimal evolution only in the
fraction of time during which they cross the gaseous disk plane. This
is clearly illustrated in
Fig. 1,
where we show the
projection of the planetesimal positions with respect to the gaseous
disk when the inclination of the binary orbital plane is
is
the disk radius. This equation is derived under the simplified
assumption that the disk has a constant density, but it is in general a
good approximation to more general cases. In this scenario, when the
planetesimals reach the size (1-10 km in diameter) for which
they
evolve under the dominating gravitational force of the two stars, they
leave the disk plane because of the forced component in the
inclination. Their orbits move in the binary orbital plane and their
nodes circulate at different rates, depending on their semimajor axis.
Gas drag is probably not a significant perturbation in this scenario,
since it affects planetesimal evolution only in the
fraction of time during which they cross the gaseous disk plane. This
is clearly illustrated in
Fig. 1,
where we show the
projection of the planetesimal positions with respect to the gaseous
disk when the inclination of the binary orbital plane is
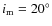 with respect to the initial disk plane. Planetesimals spend most of
their time out of disk where the gas density is negligible. According
to our simulations, for
with respect to the initial disk plane. Planetesimals spend most of
their time out of disk where the gas density is negligible. According
to our simulations, for
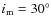 planetesimals
spend on average only 9% of their time within one scale height
of
the gaseous disk. This fraction increases to 13% when
planetesimals
spend on average only 9% of their time within one scale height
of
the gaseous disk. This fraction increases to 13% when
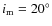 and to 27% when
and to 27% when 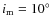 .
As a consequence, we estimate that for
.
As a consequence, we estimate that for 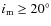 gas friction can be, to a first approximation, completely neglected
when computing planetesimal orbital evolution, while the
gas friction can be, to a first approximation, completely neglected
when computing planetesimal orbital evolution, while the 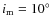 case appears as a limiting value below which gas friction has to be
taken into account.
case appears as a limiting value below which gas friction has to be
taken into account.
- The gaseous disk begins to warp and it is disrupted by
binary
perturbations. It loses coherence and the gas is dispersed in space.
According to Larwood
et al. (1996) such
disruption by differential precession might affect extremely thin
disks. Also in this case, the planetesimals would evolve in a gas-free
environment. If the disk is disrupted before the planetesimals detach
from the disk then this would be the most significant gas free case,
where planet formation would start from a disk of solid material made
of small planetesimal precursors which would evolve under gravity only.
- As in the first case, the disk remains coherent but it relaxes to the binary plane on a timescale comparable to the viscous timescale (Larwood et al. 1996). If the process is fast due to a high viscosity of the disk, kilometer-sized planetesimals not have the time to form before the disk relaxes to the binary plane. Planetesimals would then grow when their orbital plane, and that of the disk, are already aligned with that of the binary. In this case any information on the initial inclination would be lost and the system would evolve as a coplanar case (Thébault et al. 2009; Marzari & Scholl 2000; Thébault et al. 2006; Paardekooper et al. 2008; Thébault et al. 2008).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f1.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg30.png)
|
Figure 1:
Planetesimal positions (red squares) in the x-z Cartesian
plane after 1 |
| Open with DEXTER | |
Apart from the case of fast relaxation, which possibly occurs
in a
minority of cases with very high viscosity, in all other cases we
expect no or very weak coupling between the gas disk and the
planetesimal orbital evolution for binaries with inclination
![]() .
Note that this low-i case with gas drag has
been investigated by Xie & Zhou (2009),
who showed that small inclinations between the binary and a
circumprimary disc might favor planetesimal accretion as compared to
the fully coplanar case.
.
Note that this low-i case with gas drag has
been investigated by Xie & Zhou (2009),
who showed that small inclinations between the binary and a
circumprimary disc might favor planetesimal accretion as compared to
the fully coplanar case.
For our numerical exploration, we will thus make the simplifying assumption that planetesimals evolve in a gas-free environment: the gas-drag force, which introduces a de-phasing of the planetesimal perihelia, does not come into play as in the 2D case introducing a de-phasing of the planetesimal perihelia. The evolution of the swarm can be described as a pure gravitational N-body problem (Thébault et al. 2006) where the relative impact velocity steadily increases because of both the de-phasing of perihelia and nodes. In the next section we will numerically compute the evolution of planetesimal relative velocities.
3 Numerical procedure
Planetesimal trajectories are computed within the framework of
the
restricted 3-body problem made up of the central star, the companion
star and massless planetesimals. We use the same code as in previous
studies of the 2D case (e.g. Thébault et al.
2009,2006,2008),
since this code is 3D in essence and can handle out of plane
perturbers. As already mentioned, the main parameter we are
interested in is the evolution of the average impact velocities within
the population of test planetesimals. To that effect, our code
has
a build-in close encounter search algorithm, which tracks at each
timestep all 2-body encounters, allowing to precisely compute the
relative velocity for each collision (a ``collision'' being
defined as a close encounter within an ``inflated radius'' equal to
3 ![]() 10-4 AU assigned to each particle, see Thébault et al.
2009,
for more details). The precision we obtain in our relative velocity
estimate is of the order of 5 m/s
at 2 AU.
10-4 AU assigned to each particle, see Thébault et al.
2009,
for more details). The precision we obtain in our relative velocity
estimate is of the order of 5 m/s
at 2 AU.
These values of ![]() have
then to be interpreted in terms of accreting or eroding impacts. The
limit between erosion and accretion is defined by a threshold
velocity
v*s1,s2,
which depends on the respective sizes s1
and s2 of the
impactors, as well as on the value of
Q*s1,s2,
the threshold energy for catastrophic fragmentation. Unfortunately, the
parameter Q*
is very poorly constrained and estimates found in the literature can
differ by up to more than 2 orders of magnitude. We chose here
a
careful approach and consider
that Q* is comprised between 2 limiting values for
a ``hard'' and ``weak'' prescription. This will in turn result
in
2 bracketing values for
v*s1,s2
(see the discussion
in Thébault
et al. 2006, for more details).
have
then to be interpreted in terms of accreting or eroding impacts. The
limit between erosion and accretion is defined by a threshold
velocity
v*s1,s2,
which depends on the respective sizes s1
and s2 of the
impactors, as well as on the value of
Q*s1,s2,
the threshold energy for catastrophic fragmentation. Unfortunately, the
parameter Q*
is very poorly constrained and estimates found in the literature can
differ by up to more than 2 orders of magnitude. We chose here
a
careful approach and consider
that Q* is comprised between 2 limiting values for
a ``hard'' and ``weak'' prescription. This will in turn result
in
2 bracketing values for
v*s1,s2
(see the discussion
in Thébault
et al. 2006, for more details).
The initial planetesimal swarm is made of
15 000 bodies
initially set on a 2-dimensional disk inclined by an angle i0
with respect to the binary orbital plane. All the bodies in the disk
are started on circular orbits with a semimajor axis ranging
from 0.8 to 6.5 AU. All the nodal lines are parallel
since
all the bodies are clustered in a disk shape. The mass of the primary
and secondary stars are fixed to
![]() and
and ![]() respectively. The binary's
orbital parameters
respectively. The binary's
orbital parameters ![]() ,
,
![]() are chosen
as free parameters.
are chosen
as free parameters. ![]() ranges
from 40 to 100 AU; beyond those values the
perturbations of the companion in the initial phases of planetesimal
accretion are too weak. The binary eccentricity
ranges
from 40 to 100 AU; beyond those values the
perturbations of the companion in the initial phases of planetesimal
accretion are too weak. The binary eccentricity ![]() assumes different values from 0 to 0.4. The
inclination i0
varies from
assumes different values from 0 to 0.4. The
inclination i0
varies from ![]() to
to
![]() .
For larger inclinations the Kozai mechanism strongly inhibits
planetesimal accumulation, as we will see in the following.
.
For larger inclinations the Kozai mechanism strongly inhibits
planetesimal accumulation, as we will see in the following.
Our initial model setup is based on the assumption that
initially
the planetesimal swarm forms a flat disk, in other words that it is a
dynamically ``quiet'' system, with all planetesimals
![]() and
and ![]() .
For a gas rich environement this choice might be justified by the fact
that the progenitors of the km-sized planetesimals are coupled to the
gas and cannot have large
.
For a gas rich environement this choice might be justified by the fact
that the progenitors of the km-sized planetesimals are coupled to the
gas and cannot have large
![]()
![]() .
In the present case, this ``decoupling'' is harder to define, since it
could either be the consequence of the planetesimal vertical dispersion
around a coherent gas disc (case 1), or the consequence of
the gas disc dispersal (case 2). In each case, the relative
timing
between the arrival of the ``initial'' kilometre-sized planetesimals,
and the decoupling from the gas is difficult to pinpoint.
In a worst case scenario, we could have an initial orbital distribution
where some planetesimals have an inclination close to
.
In the present case, this ``decoupling'' is harder to define, since it
could either be the consequence of the planetesimal vertical dispersion
around a coherent gas disc (case 1), or the consequence of
the gas disc dispersal (case 2). In each case, the relative
timing
between the arrival of the ``initial'' kilometre-sized planetesimals,
and the decoupling from the gas is difficult to pinpoint.
In a worst case scenario, we could have an initial orbital distribution
where some planetesimals have an inclination close to
![]() while others are still around i=0. This would
introduce a high initial free relative velocity component that could
not be erased with time
(contrary to the gas-rich case, see Fig. 10 of Thébault et al.
2006).
This difficult issue clearly exceeds the scope of this paper, but our
results should probably be taken as a lower estimate in terms of
inhibition of planetesimal accretion.
while others are still around i=0. This would
introduce a high initial free relative velocity component that could
not be erased with time
(contrary to the gas-rich case, see Fig. 10 of Thébault et al.
2006).
This difficult issue clearly exceeds the scope of this paper, but our
results should probably be taken as a lower estimate in terms of
inhibition of planetesimal accretion.
4 Results
4.1 Dynamical behaviour, encounter velocities
When the planetesimals feel the binary gravitational pull, their node
longitude ![]() starts precessing at a rate which strongly depends on the individual
semimajor axis of the bodies as shown in Fig. 2. At the same
time, the binary perturbations cause a growth of the eccentricity and a
de-phasing of the perihelia. In Fig. 3 we
illustrate the orbital distribution of the planetesimal swarm at t
= 5
starts precessing at a rate which strongly depends on the individual
semimajor axis of the bodies as shown in Fig. 2. At the same
time, the binary perturbations cause a growth of the eccentricity and a
de-phasing of the perihelia. In Fig. 3 we
illustrate the orbital distribution of the planetesimal swarm at t
= 5 ![]() 104 and t = 105 yr
when the binary orbital plane is inclined by
104 and t = 105 yr
when the binary orbital plane is inclined by ![]() with
respect to the planetesimal disk and the eccentricity of the binary
orbit is 0.2 (the semimajor axis is 50 AU). The
different
timescales of perihelia and node circulation are manifest in the plot.
The different degree of randomization of
with
respect to the planetesimal disk and the eccentricity of the binary
orbit is 0.2 (the semimajor axis is 50 AU). The
different
timescales of perihelia and node circulation are manifest in the plot.
The different degree of randomization of ![]() and
and ![]() makes it a difficult task to predict the evolution of the relative
impact velocity between the planetesimals.
makes it a difficult task to predict the evolution of the relative
impact velocity between the planetesimals.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg43.png)
|
Figure 2:
Circulation period of the nodel longitude as a function of semimajor
axis for planetesimals started on a disk around the primary star. The
companion star has a semimajor axis
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f2_bis.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg44.png)
|
Figure 3:
Distribution of the planetesimal orbital elements at t=
5 |
| Open with DEXTER | |
The planetesimal disk moves to the binary orbital plane within
one
orbital period of the outer planetesimals and gradually loses coherence
as a disk. The nodes are randomized and the planetesimal Keplerian
orbits take them out of the disk plane. In Fig. 4 we illustrate
this behaviour by plotting the positions of the planetesimals at t=0,
when they are still grouped in a disk, and at t =
1 ![]() 105 yr
when the randomization has disrupted their initial spatial
configuration. We adopt this timescale since it is a higher limit for
the initial planetesimal accumulation process (e.g. Lissauer 1993)
105 yr
when the randomization has disrupted their initial spatial
configuration. We adopt this timescale since it is a higher limit for
the initial planetesimal accumulation process (e.g. Lissauer 1993)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{12379f3.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg45.png)
|
Figure 4:
3-D spatial distributions of planetesimals at t=0
(red dots) and t = 1 |
| Open with DEXTER | |
The randomization of the node longitudes affects the dynamics
of the
planetesimal population in two ways. The first is that the sparser
distribution of the bodies in space leads to a lower impact rate in
spite of the growth in the relative velocity. In Fig. 5
we plot the impact rate as a function of time and radial distance.
It shows a gradually declining trend as the nodes become more
randomly distributed. This trend is more marked at larger distances
from the primary star where the nodal randomization is faster. After 105 years
the impact rate is reduced by 55% at 1 AU and it drops by 94%
when ![]() ,
independent of the planetesimal size. This percentage can be
interpreted as the fractional reduction of the impact rate compared to
that of a planetesimal swarm around a single star. Around t=0
the
impact rate of our model is not yet affected by the binary
perturbations and it can be taken as representative of the impact rate
around a single star.
,
independent of the planetesimal size. This percentage can be
interpreted as the fractional reduction of the impact rate compared to
that of a planetesimal swarm around a single star. Around t=0
the
impact rate of our model is not yet affected by the binary
perturbations and it can be taken as representative of the impact rate
around a single star.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f4.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg47.png)
|
Figure 5:
Average impact rate in the planetesimal swarm as a function of time for
the binary configuration: |
| Open with DEXTER | |
The other, and more crucial effect is the progressive increase of
impact velocities, as can be clearly seen in Fig. 6. For values of ![]() ,
this increase is due to the combination of the particle small free
eccentricities
,
this increase is due to the combination of the particle small free
eccentricities
![]()
![]() and the large inclination oscillations induced by the inclined
companion star. Indeed, the small random horizontal excursion due to
and the large inclination oscillations induced by the inclined
companion star. Indeed, the small random horizontal excursion due to
![]() brings
in contact bodies having both i
and
brings
in contact bodies having both i
and ![]() values increasingly different over time as the node oscillations become
tighter. This effect is of course more pronounced in the outer regions
of the disk, where the pull of the companion star is felt more
strongly. Note however that the steady
values increasingly different over time as the node oscillations become
tighter. This effect is of course more pronounced in the outer regions
of the disk, where the pull of the companion star is felt more
strongly. Note however that the steady
![]() increase
is observed everywhere in the 0.8-6 AU region; it is just the
pace
of this progressive increase that depends on radial distance.
increase
is observed everywhere in the 0.8-6 AU region; it is just the
pace
of this progressive increase that depends on radial distance.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{f5.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg50.png)
|
Figure 6: Average
impact rate
in the planetesimal swarm as a function of time at different radial
distances from the primary star. The grey bands show the erosion limit
for planetesimals 1-10 km (lower band) and 10-50 km
(upper
band) in size. The initial inclination between the planetesimal disk
and the binary orbit is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f6.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg51.png)
|
Figure 7:
As in Fig. 6
for an initial inclination of the binary equal to |
| Open with DEXTER | |
For ![]() a
fully different behaviour is observed and the Kozai oscillations come
into play. The eccentricity of the planetesimal orbits begins to grow
while the inclination decreases in order to keep the action:
a
fully different behaviour is observed and the Kozai oscillations come
into play. The eccentricity of the planetesimal orbits begins to grow
while the inclination decreases in order to keep the action:
a constant of motion. The period of oscillation of
4.2 Effect on planetesimal accretion
As illustrated in Fig. 6
and
discussed above, the increase of impact velocities is an unavoidable
consequence of the node randomization due to the companion star's
perturbation
that affects all the simulated 0.8 to 6 AU region. However, in
spite of this undesired effect, planetesimals might still undergo
accretion and form planets. The critical condition is that the
timescale for both the mutual velocity growth and impact rate reduction
should be long compared to the accretion timescale. More precisely,
![]() have to stay at a low, accretion-friendly value long enough so that
large planetesimals have enough time to build up. When the high
velocity regime is reached, the growing objects have reached
a
v*s1,s2 value
high enough to have accreting impacts despite higher
have to stay at a low, accretion-friendly value long enough so that
large planetesimals have enough time to build up. When the high
velocity regime is reached, the growing objects have reached
a
v*s1,s2 value
high enough to have accreting impacts despite higher
![]() .
Of course, studying this effect in detail would require us to follow
the evolution of the planetesimal size distribution in addition to
their dynamical one. This is unfortunately beyond the reach of
deterministic N-body codes
.
Of course, studying this effect in detail would require us to follow
the evolution of the planetesimal size distribution in addition to
their dynamical one. This is unfortunately beyond the reach of
deterministic N-body codes![]() .
We shall thus adopt here a simplified criterion and consider the time
at which an averaged
.
We shall thus adopt here a simplified criterion and consider the time
at which an averaged
![]() is reached for two cases: a ``small planetesimals'' case with
is reached for two cases: a ``small planetesimals'' case with ![]() km
and
km
and ![]() km and a ``large
planetesimals'' case with
km and a ``large
planetesimals'' case with ![]() km
and
km
and ![]() km, assuming that
planetesimal sizes follow a centered Gaussian distribution
between
km, assuming that
planetesimal sizes follow a centered Gaussian distribution
between
![]() and
and
![]() .
These two limiting
.
These two limiting ![]() values
are indicated by light and dark grey areas in Fig. 6, the width of
these areas being due to our careful definition of
v*s1,s2
as being comprised between two extreme values for hard and weak
material (see Sect. 3).
values
are indicated by light and dark grey areas in Fig. 6, the width of
these areas being due to our careful definition of
v*s1,s2
as being comprised between two extreme values for hard and weak
material (see Sect. 3).
As can be seen in Fig. 6,
for our example case with ![]() AU,
AU,
![]() and
and ![]() ,
the whole system remains accretion-friendly for a population of large
,
the whole system remains accretion-friendly for a population of large ![]() km
bodies for the duration of the simulation, i.e. 105 years,
a conservative timescale for runaway growth. For kilometer-sized
planetesimals, the situation is less favorable and the
km
bodies for the duration of the simulation, i.e. 105 years,
a conservative timescale for runaway growth. For kilometer-sized
planetesimals, the situation is less favorable and the ![]() AU
region becomes hostile to kilometre-sized planetesimal accretion after
AU
region becomes hostile to kilometre-sized planetesimal accretion after ![]()
![]() 104 years. In these regions, planet
growth can proceed only if in a few 104 years
planetesimals can grow large enough to have accreting impacts in a
104 years. In these regions, planet
growth can proceed only if in a few 104 years
planetesimals can grow large enough to have accreting impacts in a ![]() m s-1
environment. Note however that even if planetesimal
accretion is possible, it can probably not lead to the same runaway
growth as around an unperturbed single star (Kortenkamp
et al. 2001).
Indeed, the increase of the impact velocity, even if it cannot stop
accretion, significantly slows it down by decreasing the value of the
gravitational focusing factor onto growing objects (see the detailed
discussion in Thébault
et al. 2006). Past
this initial planetesimal growth stage, it is difficult to predict the
evolution of the swarm at farther stages when large planetesimals and
planetary embryos will collide at these high relative velocities. Large
relative inclinations might be produced within the planetary system. Quintana et al.
(2002) have simulated the formation of terrestrial planets in
m s-1
environment. Note however that even if planetesimal
accretion is possible, it can probably not lead to the same runaway
growth as around an unperturbed single star (Kortenkamp
et al. 2001).
Indeed, the increase of the impact velocity, even if it cannot stop
accretion, significantly slows it down by decreasing the value of the
gravitational focusing factor onto growing objects (see the detailed
discussion in Thébault
et al. 2006). Past
this initial planetesimal growth stage, it is difficult to predict the
evolution of the swarm at farther stages when large planetesimals and
planetary embryos will collide at these high relative velocities. Large
relative inclinations might be produced within the planetary system. Quintana et al.
(2002) have simulated the formation of terrestrial planets in
![]() Centauri
and found that planets may indeed be formed with large mutual
inclinations if the orbital plane of the binary is inclined with
respect to that of the planetary embryos. However, their simulations
start from a coherent and flat disk of protoplanets, while the growing
protoplanets might have already developed significant inclinations by
the time they collide, according to our scenario. This suggests that
the final phase of planet formation in inclined binaries may need
additional investigation.
Centauri
and found that planets may indeed be formed with large mutual
inclinations if the orbital plane of the binary is inclined with
respect to that of the planetary embryos. However, their simulations
start from a coherent and flat disk of protoplanets, while the growing
protoplanets might have already developed significant inclinations by
the time they collide, according to our scenario. This suggests that
the final phase of planet formation in inclined binaries may need
additional investigation.
The situation is very different in the ![]() cases
where Kozai oscillations dominate the planetesimal dynamics. As
expected, these cases are much more hostile to planetesimal accretion.
As can be seen in Fig. 7
(for
cases
where Kozai oscillations dominate the planetesimal dynamics. As
expected, these cases are much more hostile to planetesimal accretion.
As can be seen in Fig. 7
(for ![]() AU,
AU, ![]() and
and ![]() ),
after 105 years
the impact velocities reach values beyond the erosion limit for both
``small'' and ``large'' planetesimals in the whole
),
after 105 years
the impact velocities reach values beyond the erosion limit for both
``small'' and ``large'' planetesimals in the whole ![]() AU
region. Like in the non Kozai case, the rate at which
AU
region. Like in the non Kozai case, the rate at which ![]() grows strongly depends on the radial distance. As an example, the
grows strongly depends on the radial distance. As an example, the ![]() AU
region becomes hostile to the accretion of 1-10 km bodies
after only
a few 103 years, whereas it takes
almost 105 years for this to be true
at
AU
region becomes hostile to the accretion of 1-10 km bodies
after only
a few 103 years, whereas it takes
almost 105 years for this to be true
at ![]() AU.
AU.
Thébault et al. (2006) derived analytically the timescale before the onset of large impact velocities between planetesimals in planar eccentric binary systems as a function of the binary parameters. In a gas free environment they computed the degree of perihelia randomization required to give high relative velocities and the time needed to reach it. Even if the inclined case may appear similar because accretion occurs in a gas free environment and the relative velocities grow because of the node randomization, it is not possible to derive a similar analytical expression. It is a complex task to estimate how the relative encounter velocity depends on the degree of node dispersion since this is a full 3D problem. In addition, in this scenario both nodes and perihelia, once dispersed, contribute to the grow of the planetesimal relative velocities.
5 Role of the binary configuration
In the previous section we have analyzed in detail the
dynamical and
accretional behaviour of a planetesimal population for two specific
test binary configurations. For pedagogical purposes, we chose cases
with ![]() to focus on the effect of the binary inclination and, in particular, on
the transition to a Kozai dominated regime when
to focus on the effect of the binary inclination and, in particular, on
the transition to a Kozai dominated regime when ![]() .
We now explore how these results depend on all the binary's orbital
parameters
.
We now explore how these results depend on all the binary's orbital
parameters ![]() ,
,
![]() and
and ![]() (the mass ratio between the 2 stars being kept constant and
equal
to 0.5). For clarity, the accretion/erosion scenario for each
binary configuration will be summarized by a single simplified
parameter, the semimajor axis al
within which accretion is possible for the 1-10 km
planetesimal population at a threshold timescale of
(the mass ratio between the 2 stars being kept constant and
equal
to 0.5). For clarity, the accretion/erosion scenario for each
binary configuration will be summarized by a single simplified
parameter, the semimajor axis al
within which accretion is possible for the 1-10 km
planetesimal population at a threshold timescale of ![]()
![]() 104 yr for the inner zone ranging from
1-3 AU and
104 yr for the inner zone ranging from
1-3 AU and ![]()
![]() 105 yr for the outer zone extending
from 4-6 AU. We assume that planet formation is possible if
105 yr for the outer zone extending
from 4-6 AU. We assume that planet formation is possible if ![]() is lower than
v*s1,s2
for any
is lower than
v*s1,s2
for any ![]() .
Under this condition, larger planetesimals can form and resist higher
velocity impacts. As an example, by inspecting Fig. 6 we can say that
planetesimals beyond 5 AU reach the erosion regime before
1
.
Under this condition, larger planetesimals can form and resist higher
velocity impacts. As an example, by inspecting Fig. 6 we can say that
planetesimals beyond 5 AU reach the erosion regime before
1 ![]() 105 yr while for 4 AU
105 yr while for 4 AU ![]() is still below the erosion limit. The inner region within 3 AU
always has impact velocities lower than
v*s1,s2
when t < 5
is still below the erosion limit. The inner region within 3 AU
always has impact velocities lower than
v*s1,s2
when t < 5 ![]() 104 yr.
104 yr.
The choice of ![]() is
somewhat difficult and arbitrary. Runaway growth in a planetesimal
swarm around a single star is supposed to start after about 104 yrs
while after 105 yrs
approximately 33% of the disk mass is supposed to be in
runaway bodies, according to Wetherill &
Stewart (1993).
These values cannot be directly applied to the binary case since
1) the binary perturbations increase the relative velocities
between the planetesimals, accelerating the erosion rate
2) the
collisional frequency decreases with time because of nodal dispersion.
In this scenario it is difficult to derive a reliable value for
the
is
somewhat difficult and arbitrary. Runaway growth in a planetesimal
swarm around a single star is supposed to start after about 104 yrs
while after 105 yrs
approximately 33% of the disk mass is supposed to be in
runaway bodies, according to Wetherill &
Stewart (1993).
These values cannot be directly applied to the binary case since
1) the binary perturbations increase the relative velocities
between the planetesimals, accelerating the erosion rate
2) the
collisional frequency decreases with time because of nodal dispersion.
In this scenario it is difficult to derive a reliable value for
the
![]() without
knowing the details of the planetesimal accretion process. This would
be possible only with a statistical code like the planet building code (Weidenschilling
et al. 1997) which, on the other hand, cannot model
the perturbations of a companion star. Here we cautiously consider a
value of
without
knowing the details of the planetesimal accretion process. This would
be possible only with a statistical code like the planet building code (Weidenschilling
et al. 1997) which, on the other hand, cannot model
the perturbations of a companion star. Here we cautiously consider a
value of
![]() for the inner and outer region of the planetesimal disk which is larger
than the runaway growth timescale and should be a good estimate for the
time required by planetesimals to grow large enough to sustain further
accretion into protoplanets.
for the inner and outer region of the planetesimal disk which is larger
than the runaway growth timescale and should be a good estimate for the
time required by planetesimals to grow large enough to sustain further
accretion into protoplanets.
The outcome of this analysis is shown in the form of 2-dimensional
maps. In Fig. 8
we plot al vs.
(![]() ,
,![]() )
for
)
for ![]() ,
,
![]() and
and ![]() .
The outcome for
.
The outcome for ![]() is
only a reference value since for low inclinations gas drag comes into
play and it must be included in the numerical model (for these low
inclination
cases, see the recent study by Xie
& Zhou 2009).
It is noteworthy that in the analysis of the data it never happens that
accretion is possible beyond 4 AU and is prevented
within 3 AU.
is
only a reference value since for low inclinations gas drag comes into
play and it must be included in the numerical model (for these low
inclination
cases, see the recent study by Xie
& Zhou 2009).
It is noteworthy that in the analysis of the data it never happens that
accretion is possible beyond 4 AU and is prevented
within 3 AU.
When the companion star is on a circular orbit (Fig. 8a), the effect of
inclination is noteworthy only for small values of ![]() .
The secular period of the nodes are short enough to perturb the disk on
a timescale comparable to the accretion timescale only for
.
The secular period of the nodes are short enough to perturb the disk on
a timescale comparable to the accretion timescale only for
![]() AU.
For these small separations and
AU.
For these small separations and ![]() ,
planet formation is always possible in the
,
planet formation is always possible in the ![]() AU region, except
for the Kozai regime at
AU region, except
for the Kozai regime at ![]() Beyond this point the swarm is quickly eroded because of the enhanced
relative velocities stirred up by the nodal randomization. At small
value of
Beyond this point the swarm is quickly eroded because of the enhanced
relative velocities stirred up by the nodal randomization. At small
value of ![]() there is a strong dependence of al
on
there is a strong dependence of al
on ![]() ,
showing that at the origin of the shrinking of the planet formation
zone there is the randomization of the nodes. For binary semimajor axes
larger than 50 AU, the situation is much more favorable to
accretion, which can only be stopped, before tf,
in the Kozai regime with
,
showing that at the origin of the shrinking of the planet formation
zone there is the randomization of the nodes. For binary semimajor axes
larger than 50 AU, the situation is much more favorable to
accretion, which can only be stopped, before tf,
in the Kozai regime with ![]() .
This means that
.
This means that ![]() AU
is approximately the border value within which secular perturbations alone
are efficient enough to affect planet accretion in the non Kozai
regime.
AU
is approximately the border value within which secular perturbations alone
are efficient enough to affect planet accretion in the non Kozai
regime.
For more eccentric binary orbits, the randomization of both
nodes
and perihelia combine destructively and push the limit for accretion to
larger values of ![]() .
As an illustration, Fig. 8c
shows the situation for
.
As an illustration, Fig. 8c
shows the situation for ![]() .
In the black zone, the relative velocity
is beyond the erosion value even at 0.8 AU from the primary
star
(the inner limit for our planetesimal population). In these cases, the
formation of planets, in particular in the outer regions of the disc,
is strongly inhibited. For inclinations lower than
.
In the black zone, the relative velocity
is beyond the erosion value even at 0.8 AU from the primary
star
(the inner limit for our planetesimal population). In these cases, the
formation of planets, in particular in the outer regions of the disc,
is strongly inhibited. For inclinations lower than
![]() ,
some
accretion is possible within 1-2 AU. However, as already
stated, our model for
,
some
accretion is possible within 1-2 AU. However, as already
stated, our model for ![]() is less accurate since gas drag may in this case affect the evolution
of planetesimals. For
is less accurate since gas drag may in this case affect the evolution
of planetesimals. For ![]() larger than 70 AU we retrieve the dependence of al
on
larger than 70 AU we retrieve the dependence of al
on ![]() and at
and at ![]() AU,
planetesimal accumulation can only be perturbed in the Kozai regime.
AU,
planetesimal accumulation can only be perturbed in the Kozai regime.
![\begin{figure}
\par\includegraphics[angle=-90,width=6.5cm,clip]{12379f7a.eps}\vs...
...vspace*{5mm}
\includegraphics[angle=-90,width=6.5cm,clip]{f7c.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg80.png)
|
Figure 8:
Maps showing the limiting values for accretion al
as a function of ( |
| Open with DEXTER | |
6 Conclusions
In this paper we explore the effect of high (
![]() )
binary inclination on the planetesimal accretion process. The main
outcomes of our work are:
)
binary inclination on the planetesimal accretion process. The main
outcomes of our work are:
- The gaseous disk and the planetesimals decouple because of
the
forced inclination of the companion star. As a consequence,
planetesimal accumulation should occur in an almost gas free
environment for inclinations larger than approximately
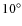 .
.
- The progressive randomization of the planetesimal node
longitudes
leads to the dispersion of the planetesimal disk that expands into a
cloud of bodies surrounding the star. The sparser configuration leads
to a significant reduction in the collisional rate.
- The onset of large mutual inclinations among planetesimals
causes
an increase of the relative impact velocity that may halt the planet
formation process. This effect is particularly strong for
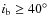 where the Kozai mechanism comes into play. Below this value,
planetesimal accretion might be possible, preferentially in the regions
closest to the primary star, depending on the value of
where the Kozai mechanism comes into play. Below this value,
planetesimal accretion might be possible, preferentially in the regions
closest to the primary star, depending on the value of 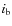
- The possibility of planetesimal accumulation depends on the
balance between the timescale of node randomization and that of
planetesimal accretion. For a binary on a circular orbit, the value of
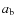 around which this balance occurs is around 50 AU. Within this
value the secular perturbations are fast enough to induce large
relative velocities on a timescale shorter than the typical timescale
for planetesimal accumulation. Outside this limit, planetesimals
probably have enough time to grow large enough to sustain high velocity
impacts.
around which this balance occurs is around 50 AU. Within this
value the secular perturbations are fast enough to induce large
relative velocities on a timescale shorter than the typical timescale
for planetesimal accumulation. Outside this limit, planetesimals
probably have enough time to grow large enough to sustain high velocity
impacts.
- When the binary is on an eccentric orbit, the randomization
of
nodes and periastra can lead to destructive collisions for binary
separations up to 70 AU.
- The dispersion of planetesimals in the nodal longitude, in those cases where the accretion is effective and lead to protoplanets, possibly leads to planetary systems a) that form on longer timescales because of the reduction of the accretion rate b) on highly mutually inclined orbits.
We thank the referee for useful comments and suggestions that helped to improve the paper.
References
- N. Haghighipour 2009, in Planets in Binary Systems, ed. N. Haghighipour (Springer), to be published
- Gillon, M. 2009, MNRAS, submitted [arXiv:0906.4904]
- Hale, A. 1994, AJ, 107, 306 [CrossRef] [NASA ADS]
- Kortenkamp, S. J., Wetherill, G. W., & Inaba, S. 2001, Science, 293, 1127 [CrossRef] [NASA ADS]
- Larwood, J. D., Nelson, R. P., Papaloizou, J. C. B., & Terquem, C. 1996, MNRAS, 282, 597 [NASA ADS]
- Lissauer, J. J. 1993, ARA&A, 31, 129 [CrossRef] [NASA ADS]
- Marzari, F., & Scholl, H. 2000, ApJ, 543, 328 [CrossRef] [NASA ADS]
- Paardekooper, S.-J., Thébault, P., & Mellema, G. 2008, MNRAS, 386, 973 [CrossRef] [NASA ADS]
- Pont, F., Hebrard, G., Irwin, J. M., et al. 2009, A&A, 502, 695 [EDP Sciences] [CrossRef] [NASA ADS]
- Quintana, E. V., Lissauer, J. J., Chambers, J. E., & Duncan, M. J. 2002, ApJ, 576, 982 [CrossRef] [NASA ADS]
- Thébault, P., Marzari, F., Scholl, H., Turrini, D., & Barbieri, M. 2004, A&A, 427, 1097 [EDP Sciences] [CrossRef] [NASA ADS]
- Thébault, P., Marzari, F., & Scholl, H. 2006, Icarus, 183, 193 [CrossRef] [NASA ADS]
- Thébault, P., Marzari, F., & Scholl, H. 2008, MNRAS, 388, 1528 [CrossRef] [NASA ADS]
- Thébault, P., Marzari, F., & Scholl, H. 2009, MNRAS, 393, L21 [CrossRef] [NASA ADS]
- Wetherill, G. W., & Stewart, G. R. 1993, Icarus, 106, 190 [CrossRef] [NASA ADS]
- Weidenschilling, S. J., Spaute, D., Davis, D. R., Marzari, F., & Ohtsuki, K. 1997, Icarus, 128, 429 [CrossRef] [NASA ADS]
- Wu, Y., & Murray, N. 2003, ApJ, 589, 605 [CrossRef] [NASA ADS]
- Xie, J.-W., & Zhou, J.-L. 2008, ApJ, 686, 570 [CrossRef] [NASA ADS]
- Xie, J.-W., & Zhou, J.-L. 2009, ApJ, 698, 2066 [CrossRef] [NASA ADS]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- Although this issue might be more complex than this simple picture, depending on how planetesimals are formed (see Discussion in Thébault et al. 2006).
- ...
![[*]](/icons/foot_motif.png)
- The existence of a non-zero
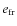 component is unavoidable.
Indeed, for an unperturbed disc of
kilometer-sized planetesimals, equilibrium encounter velocities are of
the order of the bodies escape velocities, i.e. a few
m s-1, corresponding to
component is unavoidable.
Indeed, for an unperturbed disc of
kilometer-sized planetesimals, equilibrium encounter velocities are of
the order of the bodies escape velocities, i.e. a few
m s-1, corresponding to
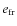 in the
10-5-10-4
range.
in the
10-5-10-4
range.
- ... codes
![[*]](/icons/foot_motif.png)
- The size evolution of a planetesimal population, under the effects of accreting, cratering and fragmenting impacts, can only be treated in statistical particle-in-a-box codes for which the dynamical modelling is necessarily very simplified.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f1.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg30.png)
|
Figure 1:
Planetesimal positions (red squares) in the x-z Cartesian
plane after 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg43.png)
|
Figure 2:
Circulation period of the nodel longitude as a function of semimajor
axis for planetesimals started on a disk around the primary star. The
companion star has a semimajor axis
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f2_bis.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg44.png)
|
Figure 3:
Distribution of the planetesimal orbital elements at t=
5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{12379f3.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg45.png)
|
Figure 4:
3-D spatial distributions of planetesimals at t=0
(red dots) and t = 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f4.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg47.png)
|
Figure 5:
Average impact rate in the planetesimal swarm as a function of time for
the binary configuration: |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{f5.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg50.png)
|
Figure 6: Average
impact rate
in the planetesimal swarm as a function of time at different radial
distances from the primary star. The grey bands show the erosion limit
for planetesimals 1-10 km (lower band) and 10-50 km
(upper
band) in size. The initial inclination between the planetesimal disk
and the binary orbit is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f6.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg51.png)
|
Figure 7:
As in Fig. 6
for an initial inclination of the binary equal to |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=6.5cm,clip]{12379f7a.eps}\vs...
...vspace*{5mm}
\includegraphics[angle=-90,width=6.5cm,clip]{f7c.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12379-09/Timg80.png)
|
Figure 8:
Maps showing the limiting values for accretion al
as a function of ( |
| Open with DEXTER | |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.