| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 277 - 281 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200911962 | |
| Published online | 03 September 2009 | |
A&A 507, 277-281 (2009)
Shape and lattice distortion effects on infrared absorption spectra of olivine particles
Y. Imai1 - C. Koike1 - H. Chihara1 - K. Murata1 - T. Aoki2 - A. Tsuchiyama1
1 - Department of Earth and Space Science, Osaka University, Toyonaka
560-0043, Japan
2 - Department of Earth and Planetary Sciences, Faculty of Sciences,
Kyushu University, Hakozaki, 812-8581, Japan
Received 27 February 2009 / Accepted 18 May 2009
Abstract
We prepared sub-micron olivine (
![]() )
particles of different shapes and different degrees of crystal lattice
distortion, and studied both effects on the infrared absorption spectra
experimentally. We found that the peak positions of the spectra shifted
to short wavelength when the number fraction of spherical grains became
large, consistent with spectral calculations using the continuous
distributions of ellipsoids (CDE) model. We also found for the first
time that the spectral features become broader by crystal lattice
distortion. The peak intensities are affected by both effects. The peak
intensity decreases with lattice distortion in general, but some peaks
are largely affected by particle shape. The spectral difference of
olivine measured in different laboratories can be explained by both the
shape and lattice distortion effects through sample preparation
methods. Broadening features in the infrared spectra of forsterite
ejecta from comet Tempel 1 obtained in the Deep Impact
mission,
and forsterite crystals in circumstellar regions, suggest that
forsterite crystals undergo lattice distortion.
)
particles of different shapes and different degrees of crystal lattice
distortion, and studied both effects on the infrared absorption spectra
experimentally. We found that the peak positions of the spectra shifted
to short wavelength when the number fraction of spherical grains became
large, consistent with spectral calculations using the continuous
distributions of ellipsoids (CDE) model. We also found for the first
time that the spectral features become broader by crystal lattice
distortion. The peak intensities are affected by both effects. The peak
intensity decreases with lattice distortion in general, but some peaks
are largely affected by particle shape. The spectral difference of
olivine measured in different laboratories can be explained by both the
shape and lattice distortion effects through sample preparation
methods. Broadening features in the infrared spectra of forsterite
ejecta from comet Tempel 1 obtained in the Deep Impact
mission,
and forsterite crystals in circumstellar regions, suggest that
forsterite crystals undergo lattice distortion.
Key words: stars: circumstellar matter - infrared: ISM - ISM: dust, extinction - methods: laboratory
1 Introduction
Circumstellar and interstellar dust has been investigated by
comparing infrared spectra of astronomical observations and laboratory
measurements. Crystalline silicates (e.g., olivine
![]() ,
and pyroxene
,
and pyroxene ![]() )
have been identified in circumstellar environments around oxygen rich
young and evolved stars (e.g., Waters et al. 1996;
Waelkens et al. 1996).
It is known that IR spectra of solid-state material depend not only on
intrinsic properties, such as temperature, structure and chemical
composition, but also on extrinsic properties related to
light-scattering of fine particles, such as particle size, shape, and
aggregation (Bohren & Huffman 1983).
In order to understand observational data correctly and infer the
physical conditions of circumstellar environments, laboratory
spectroscopic studies of these dependencies are required.
)
have been identified in circumstellar environments around oxygen rich
young and evolved stars (e.g., Waters et al. 1996;
Waelkens et al. 1996).
It is known that IR spectra of solid-state material depend not only on
intrinsic properties, such as temperature, structure and chemical
composition, but also on extrinsic properties related to
light-scattering of fine particles, such as particle size, shape, and
aggregation (Bohren & Huffman 1983).
In order to understand observational data correctly and infer the
physical conditions of circumstellar environments, laboratory
spectroscopic studies of these dependencies are required.
In recent years, a considerable number of studies have been conducted on the dependencies of the intrinsic properties. So far, effects of chemical composition and temperature on infrared absorption spectra of silicates have been investigated experimentally. For example, Jäger et al. (1998) reported the peak shift of the spectra of four olivine samples depending on the composition change from Mg to Fe end members. Chihara et al. (2002) and Koike et al. (2003) clarified the compositional dependency of pyroxene and olivine IR spectra. Bowey et al. (2001) measured the temperature effects on IR spectra of olivine and pyroxene. Koike et al. (2006) revealed the temperature dependence of IR spectra of olivine, and estimated temperatures in circumstellar environments. Fabian et al. (2000) and Murata et al. (2007) reported the evolution of IR spectra by crystallization of amorphous silicates.
In contrast, the extrinsic properties related to
light-scattering of
fine particles have not been determined experimentally yet, because, in
general, it is difficult to prepare fine particles of less than
1 ![]() m,
while still controlling the properties related to light-scattering,
such as shape and size. Since the size of dust is considered to be
sub-micron, which is smaller than the wavelength of infrared radiation,
scattering from the dust is through Rayleigh scattering. Thus,
measurements of infrared absorption spectra in the laboratory also have
been carried out in the regime of Rayleigh scattering. The work of
Tamanai et al. (2006) is an
experimental study of the dependency of the extrinsic properties of IR
spectra. Using aerosol techniques, particles were well dispersed in
air, and the structures of the particles can be analyzed by in situ
microscopic imaging. They investigated the influence of the medium and
of particle morphology on IR spectra.
They found that the difference between IR spectra of irregular and
ellipsoidal forsterite particles depends on the surrounding medium.
However, the irregular and ellipsoidal particles used are commercial
products made by different companies. So these particles may have
differences not only of shape but also other properties.
It is difficult to control the properties of fine particles, and it is
possible that the difficulty gives rise to differences of IR spectra,
when IR spectra are measured in the laboratory. In principle, there are
significant differences in infrared spectra measured in different
laboratories. This is a crucial problem for comparison between
observation and laboratory data. It is inferred that the difference is
caused not only by the dependencies of the intrinsic properties but
also by the dependency related to light-scattering of fine particles.
m,
while still controlling the properties related to light-scattering,
such as shape and size. Since the size of dust is considered to be
sub-micron, which is smaller than the wavelength of infrared radiation,
scattering from the dust is through Rayleigh scattering. Thus,
measurements of infrared absorption spectra in the laboratory also have
been carried out in the regime of Rayleigh scattering. The work of
Tamanai et al. (2006) is an
experimental study of the dependency of the extrinsic properties of IR
spectra. Using aerosol techniques, particles were well dispersed in
air, and the structures of the particles can be analyzed by in situ
microscopic imaging. They investigated the influence of the medium and
of particle morphology on IR spectra.
They found that the difference between IR spectra of irregular and
ellipsoidal forsterite particles depends on the surrounding medium.
However, the irregular and ellipsoidal particles used are commercial
products made by different companies. So these particles may have
differences not only of shape but also other properties.
It is difficult to control the properties of fine particles, and it is
possible that the difficulty gives rise to differences of IR spectra,
when IR spectra are measured in the laboratory. In principle, there are
significant differences in infrared spectra measured in different
laboratories. This is a crucial problem for comparison between
observation and laboratory data. It is inferred that the difference is
caused not only by the dependencies of the intrinsic properties but
also by the dependency related to light-scattering of fine particles.
An example of the difference is the infrared spectrum of forsterite ![]() particles measured by Koike et al. (1999)
(called the Kyoto sample hereafter), and by Jäger et al. (1998) (Jena
sample) on peak intensities, positions, and shapes (Molster
et al. 2002).
The mass absorption coefficients of the Kyoto samples are large as
twice as the Jena samples, while the peak widths of the Kyoto samples
are narrower than those of the Jena samples, especially
for the 33
particles measured by Koike et al. (1999)
(called the Kyoto sample hereafter), and by Jäger et al. (1998) (Jena
sample) on peak intensities, positions, and shapes (Molster
et al. 2002).
The mass absorption coefficients of the Kyoto samples are large as
twice as the Jena samples, while the peak widths of the Kyoto samples
are narrower than those of the Jena samples, especially
for the 33 ![]() m
feature. Molster et al. (2002)
proposed that the difference is due to the crystallinity of the
measured samples; that is, the Kyoto sample was a single crystal made
by the Czochralsky method (Koike et al. 2000),
while the Jena sample was crystallized from a melt by cooling and is
probably polycrystalline (Jäger et al. 1998). On
the other hand,
Koike et al. (2006)
proposed that the difference is not caused by crystallinity but
particle shape. They pointed out that the positions of many peaks of
the Jena sample are located at shorter wavelength than the Kyoto
sample. The difference is about 0.05-0.1
m
feature. Molster et al. (2002)
proposed that the difference is due to the crystallinity of the
measured samples; that is, the Kyoto sample was a single crystal made
by the Czochralsky method (Koike et al. 2000),
while the Jena sample was crystallized from a melt by cooling and is
probably polycrystalline (Jäger et al. 1998). On
the other hand,
Koike et al. (2006)
proposed that the difference is not caused by crystallinity but
particle shape. They pointed out that the positions of many peaks of
the Jena sample are located at shorter wavelength than the Kyoto
sample. The difference is about 0.05-0.1 ![]() m for 10, 11.2, and 19.5
m for 10, 11.2, and 19.5 ![]() m peaks,
and about 0.5
m peaks,
and about 0.5 ![]() m
for 23 and 33
m
for 23 and 33 ![]() m
peaks. They suggested that the particle shape of the Jena sample is
more spherical than the Kyoto sample, because the peak positions for
olivine particles with near-spherical shape are located at shorter
wavelengths than those with elongated or flat ellipsoidal shapes, as
pointed out
by Fabian et al. (2001).
m
peaks. They suggested that the particle shape of the Jena sample is
more spherical than the Kyoto sample, because the peak positions for
olivine particles with near-spherical shape are located at shorter
wavelengths than those with elongated or flat ellipsoidal shapes, as
pointed out
by Fabian et al. (2001).
In this paper, we propose a hypothesis that the spectrum difference is caused by differences in sample preparation; the Kyoto sample was prepared by grinding in a mortar by hand, and the particle shapes are irregular, while the Jena sample was prepared by grinding mechanically using a ball mill, and the particle shapes are spherical. Milling in a ball mill is indeed used as a technique for amorphization of organic matter (Font et al. 1997). It is possible that the crystal lattice of the Jena sample is distorted due to the strong impacts of the ball mill grinding. The purpose of this study is to test this hypothesis and to investigate the dependence of particle shape and lattice distortion on infrared absorption spectra of olivine particles. For this, we prepared fine particles from one natural olivine by different grinding methods to control their shape, and annealed them to relax lattice distortion. Then, we examined the variation in infrared absorption spectra to evaluate the effects of the particle shape and lattice distortion. Finally, we discuss differences in infrared spectra from different laboratories.
2 Experiment
We prepared sub-micron particles of olivine (
![]() :
from San Carlos, Arizona, USA) by grinding in a mortar by hand
and
a planetary ball mill. Since the Fe-bearing olivine sample is
softer than the Mg end-member (forsterite), it is more suitable to
examine the change of shape and lattice distortion by these sample
preparation methods. Olivine crystals were crushed in a tungsten
carbide mortar by hand for about 1 h. The samples were ground
in
an alumina mortar until the grains were less than 1
:
from San Carlos, Arizona, USA) by grinding in a mortar by hand
and
a planetary ball mill. Since the Fe-bearing olivine sample is
softer than the Mg end-member (forsterite), it is more suitable to
examine the change of shape and lattice distortion by these sample
preparation methods. Olivine crystals were crushed in a tungsten
carbide mortar by hand for about 1 h. The samples were ground
in
an alumina mortar until the grains were less than 1 ![]() m
in size (we named this sample ``hand-milled''). In addition, to obtain
smaller grains, these particles were ground in a planetary ball mill
using a zirconia pod and balls, with a rotation speed of 350 rpm for
10-20 h (we named this sample ``ball-milled''). In this way,
we
produced very fine grains (of less than 0.5
m
in size (we named this sample ``hand-milled''). In addition, to obtain
smaller grains, these particles were ground in a planetary ball mill
using a zirconia pod and balls, with a rotation speed of 350 rpm for
10-20 h (we named this sample ``ball-milled''). In this way,
we
produced very fine grains (of less than 0.5 ![]() m
in size). This sample may undergo crystal lattice distortion by the
collisions in the ball mill. In order to relax the distortion, the
sample was annealed at 650 and 1000
m
in size). This sample may undergo crystal lattice distortion by the
collisions in the ball mill. In order to relax the distortion, the
sample was annealed at 650 and 1000 ![]() C for 3 h. To prevent
oxidation of the
C for 3 h. To prevent
oxidation of the ![]() cation, oxidation-reduction conditions in the furnace were controlled
on the iron-wüstite buffer (partial pressure of oxygen is
10-22.8 atm) curve using
cation, oxidation-reduction conditions in the furnace were controlled
on the iron-wüstite buffer (partial pressure of oxygen is
10-22.8 atm) curve using ![]() and
and ![]() mixed gas (we named this sample ``annealed at 650 and 1000
mixed gas (we named this sample ``annealed at 650 and 1000 ![]() C'').
C'').
The size and shape of the samples were observed with a field
emission scanning electron microscope (FE-SEM, JEOL-7001F) at Osaka
University and the degree of lattice distortion was obtained by X-ray
powder diffraction (XRD) analysis using using a Gandolfi camera at
Kyushu University. Conventional powder XRD measurement was performed
with chromium
K![]() radiation (
radiation (
![]() Å).
The infrared absorption spectra of the samples were measured by FT-IR
spectrometry (Nicolet Nexus 670) at Osaka University. The samples were
dispersed and embedded in KBr and polyethylene for the mid-IR
(1.4-25
Å).
The infrared absorption spectra of the samples were measured by FT-IR
spectrometry (Nicolet Nexus 670) at Osaka University. The samples were
dispersed and embedded in KBr and polyethylene for the mid-IR
(1.4-25 ![]() m)
and the far-IR (15-200
m)
and the far-IR (15-200 ![]() m) measurements, respectively. The mass
absorption coefficient,
m) measurements, respectively. The mass
absorption coefficient, ![]() was obtained from the absorbance spectra by use of the following
equation;
was obtained from the absorbance spectra by use of the following
equation;
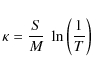
|
(1) |
where S is the surface area of the sample pellet, M is the sample mass in the pellet, and T is the transmittance.
3 Results
Figure 1
shows particle
shapes of ``hand-milled'', ``ball-milled'', and ``annealed'' samples.
Before grinding, particles have sharp edges and are irregular in shape
(Fig. 1a).
The particle size shows variation ranging
from 0.2 ![]() m
to 2
m
to 2 ![]() m.
After grinding (Fig. 1b),
the sharp edges have disappeared and the particle shape becomes more
spherical with smaller aspect ratios, and particles become roughly
uniform (about 0.1-0.5
m.
After grinding (Fig. 1b),
the sharp edges have disappeared and the particle shape becomes more
spherical with smaller aspect ratios, and particles become roughly
uniform (about 0.1-0.5 ![]() m).
After annealing, the particle sizes and shapes are similar to those of
the ball-milled sample, and the particles are not coarsened by the
annealing (Fig. 1c).
m).
After annealing, the particle sizes and shapes are similar to those of
the ball-milled sample, and the particles are not coarsened by the
annealing (Fig. 1c).
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{11962F1a.eps}\includegraph...
...]{11962F1b.eps}\par\includegraphics[width=4.2cm,clip]{11962F1c.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11962-09/Timg15.png)
|
Figure 1: SEI images of the samples. a) Hand-milled sample. b) Ball-milled sample. c) Annealed sample. |
| Open with DEXTER | |
The XRD patterns of ``hand-milled'', ``ball-milled'', and ``annealed''
samples are shown in Fig. 2.
All peaks in the XRD patterns were assigned to olivine. The samples may
be contaminated by material from the ball mill pod, balls and mortar
during ball milling. However the XRD profiles did not show any peaks of
zirconia. The XRD peaks of hand-milled sample were very sharp, showing
good crystalline quality. On the other hand, after grinding by the ball
mill, XRD peaks became broad and the intensity decreased.
This change was especially remarkable for peaks at large angles. The
XRD peaks became broader for longer durations. The change of the XRD
patterns corresponds to lattice distortion of olivine crystals by
impact during grinding in the ball mill. The XRD peaks of annealed
samples became narrower as the annealing temperature increased. This
result shows that the lattice distortions were relaxed by the
annealing.
We evaluated the degree of the lattice distortion e
from the XRD patterns, whose variation of lattice spacing corresponds
to (Wilson 1962)
| (2) |
where
| (3) |
Strictly, C has an angular dependency. However, it is not useful to estimate trends in the slopes of the fitting lines. For example, the size dependence is much weaker than that of lattice distortion in this experiment. The spread of the FWHM of the crystalline size dependency was evaluated by (Scherrer 1918)
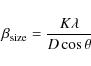
|
(4) |
where K is the Scherrer constant,
Figure 3
shows the relation between ![]() and
and ![]() .
By Eq. (3), the e value of each sample is
calculated from the relation between gradient of the
.
By Eq. (3), the e value of each sample is
calculated from the relation between gradient of the ![]() and
and ![]() .
The values of lattice distortion e, for
samples hand-milled, ball-milled for 20 h, and annealed at
1000
.
The values of lattice distortion e, for
samples hand-milled, ball-milled for 20 h, and annealed at
1000 ![]() C
were 0.043, 0.213, and 0.111%,
respectively. This result shows that lattice distortion occurred from
ball milling, and was partially relaxed by the annealing.
C
were 0.043, 0.213, and 0.111%,
respectively. This result shows that lattice distortion occurred from
ball milling, and was partially relaxed by the annealing.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{11962F2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11962-09/Timg26.png)
|
Figure 2: XRD patterns of each sample. The X-ray wavelength was 2.2896 Å. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{11962F3.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11962-09/Timg27.png)
|
Figure 3:
Relations between FWHM of XRD peaks of each sample
and lattice distortion. |
| Open with DEXTER | |
The infrared absorption spectra of ``hand-milled'', ``ball-milled for
20 hr'', and ``annealed at 1000 ![]() C'' samples are shown in
Fig. 4.
Table 1
shows peak positions and FWHMs for each spectrum.
The spectra are similar to a spectrum of San Carlos olivine measured by
Koike et al. (2006),
and did not show any peaks of contamination, such as material from the
ball mill pod, balls and mortar.
C'' samples are shown in
Fig. 4.
Table 1
shows peak positions and FWHMs for each spectrum.
The spectra are similar to a spectrum of San Carlos olivine measured by
Koike et al. (2006),
and did not show any peaks of contamination, such as material from the
ball mill pod, balls and mortar.
Many peaks of the spectrum of the ball-milled sample shifted
to
shorter wavelength compared to the hand-milled sample. For example, the
peak positions of the 24 and 34 ![]() m feature of the hand-milled sample shifted from
those of the ball-milled by 0.25 and 0.33
m feature of the hand-milled sample shifted from
those of the ball-milled by 0.25 and 0.33 ![]() m,
respectively. Peaks of the spectrum of the annealed sample also are at
shorter wavelength than the hand-milled sample and are similar to those
of the ball-milled sample.
In terms of shape of spectral features, the spectrum of the ball-milled
sample became broader than the hand milled sample, and the peak
intensities of the ball-milled sample were generally lower than the
hand-milled sample. This broadening was particularly remarkable in the
long wavelength region above 13
m,
respectively. Peaks of the spectrum of the annealed sample also are at
shorter wavelength than the hand-milled sample and are similar to those
of the ball-milled sample.
In terms of shape of spectral features, the spectrum of the ball-milled
sample became broader than the hand milled sample, and the peak
intensities of the ball-milled sample were generally lower than the
hand-milled sample. This broadening was particularly remarkable in the
long wavelength region above 13 ![]() m. For example, the FWHM of
the 16
m. For example, the FWHM of
the 16 ![]() m
feature changed
from 0.81 to 1.12
m
feature changed
from 0.81 to 1.12 ![]() m
and that of the 34
m
and that of the 34 ![]() m
feature from 2.66 to 2.92
m
feature from 2.66 to 2.92 ![]() m
for the hand-milled and ball-milled samples, respectively. However, the
spectral features of the annealed sample were as sharp as the
hand-milled sample, and the peak intensity of the annealed sample was
similar to that of the hand-milled sample. In addition, the shapes of
19
m
for the hand-milled and ball-milled samples, respectively. However, the
spectral features of the annealed sample were as sharp as the
hand-milled sample, and the peak intensity of the annealed sample was
similar to that of the hand-milled sample. In addition, the shapes of
19 ![]() m
feature are different among the three samples. This feature includes
two peaks at about 18.5 and 19.5
m
feature are different among the three samples. This feature includes
two peaks at about 18.5 and 19.5 ![]() m, and the 19
m, and the 19 ![]() m
feature is sensitive to the ball-milling and annealing.
The continuum absorptions of the samples also differ. It is surprising
that the continuum of the annealed sample is lower than that of the
hand-milled sample. It may be related to its crystallinity, however the
reason is not known.
m
feature is sensitive to the ball-milling and annealing.
The continuum absorptions of the samples also differ. It is surprising
that the continuum of the annealed sample is lower than that of the
hand-milled sample. It may be related to its crystallinity, however the
reason is not known.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11962F4a.eps}\par\includegra...
...p]{11962F4b.eps}\par\includegraphics[width=7cm,clip]{11962F4c.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11962-09/Timg28.png)
|
Figure 4:
The IR spectra of different shape and lattice distortion samples a)
from 8 to 15 |
| Open with DEXTER | |
Table
1:
Peak positions of each band for each samples (in ![]() m).
m).
4 Discussion
4.1 Lattice distortion effect on infrared spectra
Table 2
shows a summary of
the samples with particle shapes and lattice distortions determined by
the SEM observation and the XRD measurements. In order to discuss the
lattice distortion effect on infrared spectra, we compared the spectrum
of two different samples whose shapes are similar but whose lattice
distortions are different. Therefore, we used ``ball-milled'' and
``annealed'' samples (Table 2).
The peak positions are similar for both spectra, while the spectral
peaks of the ball-milled sample with large lattice distortions are
broader than the annealed sample, especially for the longer wavelength
region of greater
than about 13 ![]() m
(Fig. 4).
The peak intensity of the ball-milled sample is generally lower than
the annealed sample, although there are variations (the differences are
small for the 10, 11.5 and 16
m
(Fig. 4).
The peak intensity of the ball-milled sample is generally lower than
the annealed sample, although there are variations (the differences are
small for the 10, 11.5 and 16 ![]() m
features, while larger for other features). As a result, we found that
the crystal lattice distortion affects the peak broadening in infrared
spectra. Peak intensity is also affected for some peaks.
m
features, while larger for other features). As a result, we found that
the crystal lattice distortion affects the peak broadening in infrared
spectra. Peak intensity is also affected for some peaks.
4.2 Shape effect on spectra
In order to discuss shape effects on infrared spectra, we
compared
the spectrum of two different samples whose shapes are different but
whose lattice distortions are similar. We used the spectra of the
``hand-milled'' sample with irregular particle shapes and the
``annealed'' sample with rounded shapes (Table 2). Many peak
positions (e.g., 10.1, 11.3, 24 and 34 ![]() m) in the spectrum of the annealed sample are at
shorter wavelengths than the hand-milled sample (Fig. 4).
In general, the peak intensities of the annealed sample are slightly
higher than those of the hand-milled sample. It also should be noted
that
the shapes of the 19
m) in the spectrum of the annealed sample are at
shorter wavelengths than the hand-milled sample (Fig. 4).
In general, the peak intensities of the annealed sample are slightly
higher than those of the hand-milled sample. It also should be noted
that
the shapes of the 19 ![]() m
feature are different between the two samples. Therefore, we conclude
that particle shape mainly affects the peak position. The peak
intensities also are slightly affected by the shape.
m
feature are different between the two samples. Therefore, we conclude
that particle shape mainly affects the peak position. The peak
intensities also are slightly affected by the shape.
The shape effect can be discussed by comparing the experimental results
with those calculated. Fabian et al. (2001)
showed calculated IR spectra of spheres, and two continuous
distributions of ellipsoids (CDEs) of forsterite and olivine (
![]() ).
They considered the CDEs with random orientations, and the
distributions are characterized either by equal probability of all
shapes (CDE1; Bohren & Human, 1983), or
by a weighting where near-spherical shapes are most probable (CDE2;
Ossenkopf et al. 1992).
In both calculated spectra of forsterite and olivine, the spectral peak
positions of the near spherical particles (CDE2) shift to shorter
wavelength than the more elongated and flat ellipsoidal shapes (CDE1).
The trend in the shift of peak positions is not different between the
spectra of forsterite and olivine. This is consistent with our
experimental result, although the composition of the samples is
different.
).
They considered the CDEs with random orientations, and the
distributions are characterized either by equal probability of all
shapes (CDE1; Bohren & Human, 1983), or
by a weighting where near-spherical shapes are most probable (CDE2;
Ossenkopf et al. 1992).
In both calculated spectra of forsterite and olivine, the spectral peak
positions of the near spherical particles (CDE2) shift to shorter
wavelength than the more elongated and flat ellipsoidal shapes (CDE1).
The trend in the shift of peak positions is not different between the
spectra of forsterite and olivine. This is consistent with our
experimental result, although the composition of the samples is
different.
Table 2: Shape and lattice distortion of each sample.
4.3 Difference in spectra by different laboratories
As already mentioned, the IR spectra of a mineral measured in different laboratories are different from each other, and this poses serious problems in estimating the properties of circumstellar dust by comparing astronomical observations and laboratory data. Figure 5 shows IR spectra of San Carlos Olivine measured for the Kyoto and Jena samples. The spectral features of the hand-milled sample are similar to that of the Kyoto sample (Koike et al. 2006), in which the sample was prepared by hand-milling, while that of the ball-milled sample is similar to that of the Jena sample (Fabian et al. 2001), in which the sample was prepared by ball-milling. Consequently, it is highly probable that the difference in the spectra from different laboratories is due to differences in shape and lattice distortion of particles, caused by the different sample preparation methods: the Kyoto samples are irregular particles with less crystal lattice distortion, while the Jena samples are rounded particles with large lattice distortion. Therefore, we have to consider the difference in the sample properties when laboratory data are compared with observation data.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{11962F5.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11962-09/Timg30.png)
|
Figure 5: IR spectra of San Carlos olivine measured by Koike et al. (2006) (Kyoto sample) and Fabian et al. (2001) (Jena sample). |
| Open with DEXTER | |
4.4 Implications for astronomical observations
The effect of crystal lattice distortion, when spectral features become broader with increasing distortion, was reported for the first time in the present experiments. Here we will discuss some implications of this effect for astronomical observations.
In the Deep Impact mission, emission features of ejecta of
comet
Tempel 1 were observed with the Spitzer Space Telescope, and features
due to crystalline silicates were found (Lisse et al. 2006). The
33 ![]() m
emission feature of Tempel 1 ejecta almost fitted that of forsterite.
However, it is clear that
the 33
m
emission feature of Tempel 1 ejecta almost fitted that of forsterite.
However, it is clear that
the 33 ![]() m
feature of the observation is broader than the model fit. It is
suggested that this broadening is due to lattice distortion caused by
impacts with hypervelocity onto the nucleus of Tempel 1
m
feature of the observation is broader than the model fit. It is
suggested that this broadening is due to lattice distortion caused by
impacts with hypervelocity onto the nucleus of Tempel 1
It is known that peak positions and FWHMs of peaks
of IR spectra change depending on temperature and chemical composition
(e.g., Koike et al. 2003;
Chihara et al. 2001, 2002). In
terms of temperature dependency, peak positions shift to shorter
wavelength, and FWHMs decrease drastically as
temperature decreases (e.g., Chihara et al. 2001; Bowey
et al. 2001;
Koike et al. 2006).
Since we carried out all measurements of IR spectra at room temperature
in this work, the variations of the FWHMs
in our work are not caused by the temperature dependency. On the other
hand, in terms of compositional dependence, peak positions shift to
longer wavelength, and FWHMs increase with
increasing iron content of Mg-rich silicates (Chihara et al. 2002;
Koike et al. 2003).
With observational studies, Bowey et al. (2002) and Molster
et al. (2002)
discussed estimation of the Fe content of olivine and temperatures of
dust from the relation between the peak position and FWHM
of the 69 ![]() m
feature for observations of circumstellar dust.
m
feature for observations of circumstellar dust.
Koike et al. (2006)
superimposed temperature-dependent spectral data of forsterite on this
correlation between the peak positions and FWHM of
the 69 ![]() m
feature, and found that much observational data have lager FWHMs
than the laboratory trend of the Kyoto sample, and some FWHM
of observations are similar to the laboratory trend of the Jena sample.
Koike et al. (2006)
presented a correlation between the peak positions and FWHM
using spectra of forsterite (the Mg end-member); the trend of the
correlation shows a lower limit of peak position and an upper limit of FWHM
at each temperature. However, some observational data are located in
the left region of the correlation trend of forsterite. These
observational data means that the peak positions and the FWHMs
are lower and larger than those of forsterite (=Kyoto sample).
Therefore, the observational data cannot be explained only by
composition and temperature effects. In contrast, as our results show,
lattice distortion affects only broadening of the FWHM
and does not change peak positions. Therefore, the lattice distortion
effect can explain the difference between observational spectra and
laboratory measurements. Consequently, circumstellar forsterite might
have a lattice distortion, although the detailed conditions of
circumstellar environments are not yet well known. The crystal lattice
distortion might be caused by rapid growth of forsterite crystals in
largely saturated conditions from either amorphous silicates or gas
itself.
m
feature, and found that much observational data have lager FWHMs
than the laboratory trend of the Kyoto sample, and some FWHM
of observations are similar to the laboratory trend of the Jena sample.
Koike et al. (2006)
presented a correlation between the peak positions and FWHM
using spectra of forsterite (the Mg end-member); the trend of the
correlation shows a lower limit of peak position and an upper limit of FWHM
at each temperature. However, some observational data are located in
the left region of the correlation trend of forsterite. These
observational data means that the peak positions and the FWHMs
are lower and larger than those of forsterite (=Kyoto sample).
Therefore, the observational data cannot be explained only by
composition and temperature effects. In contrast, as our results show,
lattice distortion affects only broadening of the FWHM
and does not change peak positions. Therefore, the lattice distortion
effect can explain the difference between observational spectra and
laboratory measurements. Consequently, circumstellar forsterite might
have a lattice distortion, although the detailed conditions of
circumstellar environments are not yet well known. The crystal lattice
distortion might be caused by rapid growth of forsterite crystals in
largely saturated conditions from either amorphous silicates or gas
itself.
We would like to thank the referees for their constructive and helpful reports, which have improved this paper. This work was financially supported by JSPS Research Fellowships for Young Scientist, Grant-in-Aid from the Japanese Ministry of Education, Culture, Sports, Science, and Technology (18540243; 19104012) and Grant-in-Aid for Scientific Research on Priority Areas, ``Development of Extra-Solar Planetary Science'' (19015006).
References
- Bohren, C. F., & Human, D. R. 1983, Absorption and Scattering of Light by Small Particles (New York: Wiley and Sons Ins.)
- Bowey, J. E., Lee, C., Tucker, C., & Hofmeister, A. M. 2001, MNRAS, 325, 886 [CrossRef] [NASA ADS]
- Chihara, H., Koike, C., Tsuchiyama, A., Tachabana S., & Sakamoto D. 2002, A&A, 391, 267 [EDP Sciences] [CrossRef] [NASA ADS]
- Fabian, D., Jäger, C., Henning, T., Dorschner, J., & Mutschke, H. 2000, A&A, 364, 282 [NASA ADS]
- Fabian, D., Henning, T., Jäger, C., Mutschke, H., Dorschner, J., & Wehrhan O. 2001, A&A, 378, 228 [EDP Sciences] [CrossRef] [NASA ADS]
- Font, J., Muntasell, J., & Cesari, E. 1997, Mater. Res. Bull., 32, 12 [CrossRef], 1691
- Jäger, C., Molster, F. J., Dorschner, J., Mutschke, H., & Water, L. B. F. M. 1998, A&A, 339, 940 [NASA ADS]
- Koike, C., Tsuchiyama, A., Suto, H., et al. 1999, in Proc. of the 32nd ISAS Lunar and Planetary Symposium, 32, 175
- Koike, C., Chihara, H., Tsuchiyama, A., et al. 2000, in Proc. of the 33rd ISAS Lunar and Planetary Symposium, 33, 95
- Koike, C., Chihara, H., Tsuchiyama, A., Suto, H., Sogawa, H., & Okuda H. 2003, A&A, 399, 1101 [EDP Sciences] [CrossRef] [NASA ADS]
- Koike, C., Mutschke, H., Suto, H., Naoi T., H., Chihara, et al. 2006, A&A, 449, 583 [EDP Sciences] [CrossRef] [NASA ADS]
- Lisse, C. M., VanCleve, J., Adams, A. C., et al. 2006. Science, 313, 635
- Molster, F. J., Waters, L. B. F. M., Tielens, A. G. G. M., Koike, C., & Chihara, H. 2002. A&A, 382, 241
- Murata, K., Chihara, H., Tsuchiyama, A., Koike, C., & Takakura, T. 2007, ApJ, 668, 285 [CrossRef] [NASA ADS]
- Ossenkopf, V., Henning, Th., & Marthis, J. S. 1992, A&A, 261, 567 [NASA ADS]
- Scherrer, P. 1918, Nachr. Ges. Wiss. Gottingen, 26 September, 98
- Sogawa, H., Koike, C., Chihara, H., et al. 2006, A&A, 451, 357 [EDP Sciences] [CrossRef] [NASA ADS]
- Tamanai, A., Mutschke, H., Blum, J., & Meeus, G. 2006, ApJ, 648, L147 [CrossRef] [NASA ADS]
- Waelkens, C., Waters, L. B. F. M., de Grauw, M. S., et al. 1996, A&A, 315, L245 [NASA ADS]
- Waters L. B. F. M., Molster F.J., de Jong, T., et al. 1996. A&A, 315, L361
- Willson, A. J. C. 1962, X-Ray Optics (New York: Wiley and Sons Ins.)
All Tables
Table
1: Peak positions of each band for each samples (in ![]() m).
m).
Table 2: Shape and lattice distortion of each sample.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


