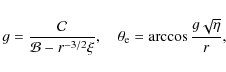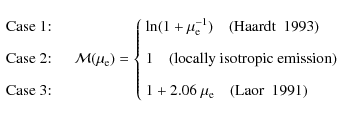| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 1 - 17 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200911941 | |
| Published online | 08 September 2009 | |
A&A 507, 1-17 (2009)
Role of emission angular directionality in spin determination of accreting black holes with a broad iron line
J. Svoboda -
M. Dovciak - R. Goosmann![]() - V. Karas
- V. Karas
Astronomical Institute, Academy of Sciences, Bocní II 1401, 14131 Prague, Czech Republic
Received 24 February 2009 / Accepted 4 August 2009
Abstract
Aims. The spin of an accreting black hole can be
determined by
spectroscopy of the emission and absorption features produced in the
inner regions of an accretion disc. In this work, we discuss the method
employing the relativistic line profiles of iron in the X-ray domain,
where the emergent spectrum is blurred by general relativistic effects.
Methods. Precision of the spectra fitting procedure
could be
compromised by inappropriate accounting for the angular distribution of
the disc emission. Often a unique profile is assumed, invariable over
the entire range of radii in the disc and energy in
the
spectral band. An isotropic distribution or a particular limb-darkening
law have been frequently set, although some radiation transfer
computations exhibit an emission excess towards the grazing angles
(i.e., the limb brightening). By assuming a rotating black
hole in
the centre of an accretion disc, we perform radiation transfer
computations of an X-ray irradiated disc atmosphere (NOAR code) to
determine the directionality of outgoing X-rays in the
2-10 keV energy band. Based on these computations, we produce
a
new extension to the ptmmscky software package for X-ray
spectra
fitting of relativistic accretion discs.
Results. We study how sensitive the spin
determination is to the
assumptions about the intrinsic angular distribution of
the emitted photons. The uncertainty of
the directional
emission distribution translates to ![]() 20%
uncertainty in the determination of the marginally stable
orbit.
We implemented the simulation results as a new extension to the
ptmmscky software package for X-ray spectra fitting of relativistic
accretion disc models. Although the parameter space is rather complex,
leading to a rich variety of possible outcomes, we find that on average
the isotropic directionality reproduces our model data to the best
precision. Our results also suggest that an improper use of limb
darkening can partly mimic a steeper profile of radial
emissivity.
We demonstrate these results in the case of XMM-Newton observation of
the Seyfert galaxy MCG-6-30-15, for which we construct confidence
levels of
20%
uncertainty in the determination of the marginally stable
orbit.
We implemented the simulation results as a new extension to the
ptmmscky software package for X-ray spectra fitting of relativistic
accretion disc models. Although the parameter space is rather complex,
leading to a rich variety of possible outcomes, we find that on average
the isotropic directionality reproduces our model data to the best
precision. Our results also suggest that an improper use of limb
darkening can partly mimic a steeper profile of radial
emissivity.
We demonstrate these results in the case of XMM-Newton observation of
the Seyfert galaxy MCG-6-30-15, for which we construct confidence
levels of ![]() statistics, and on the simulated data for the future
X-ray
IXO mission. Our simulations, with the tentative IXO response,
show a significant improvement that can qualitatively enhance
the accuracy of spin determination.
statistics, and on the simulated data for the future
X-ray
IXO mission. Our simulations, with the tentative IXO response,
show a significant improvement that can qualitatively enhance
the accuracy of spin determination.
Key words: accretion, accretion discs - black hole physics - galaxies: active - X-rays: binaries
1 Introduction
There is now strong evidence suggesting that the radiation of active galactic nuclei as well as some compact binary stars in the Galaxy originates in part from the gas of an accretion disc orbiting around a central black hole (Rees 1998; Kato et al. 1998). A great deal of information about these objects has been obtained via X-rays (Krolik 1999; Peterson 1997). Therefore, reliable models are needed to describe production of high-energy photons emerging from the accretion disc surface and subsequent propagation of these photons towards a distant observer.Directional distribution of the outgoing radiation is among the important aspects that must be addressed. Limb darkening traditionally refers to the gradual diminution of intensity in the image of the surface of a star as one moves from the centre of the image to the edge. It is a consequence of uneven angular distribution of the radiation flux emerging from the stellar surface (Mihalas 1978; Chandrasekhar 1960). Limb darkening results as a combination of two effects: (i) the density of the surface layers decreases in the outward direction; and (ii) temperature also drops as the distance from the centre of the star increases. The outgoing radiance is therefore distributed in a non-uniform manner. The actual form of the angular distribution depends on the physical mechanism responsible for the emission and the geometrical proportions of the source. The limb darkening law is widely applied also to describe radiation coming from an accretion disc around a black hole. In this case, relativistic effects can significantly enhance the observed anisotropy by bending the light rays and boosting the photon energy in the direction of motion of the emitter. As a result of this interplay between local physics of light emission and the global effects of the gravitational field, different processes contribute to the final (observed) directional anisotropy of the emission.
We consider the angular distribution of the emitted X-rays in the
context of accreting black holes. The source is an equatorial accretion
disc in which the energy is drawn by conversion of gravitational energy
of the orbiting matter gradually sinking into the black hole
(Pringle
1981; Shakura
& Syunyaev 1973; Frank
et al. 2002),
and electromagnetic process creating coronal flares and illuminating
the underlying accretion disc (Nayakshin
2000; Czerny
et al. 2004; Galeev
et al. 1979, and further references cited therein).
The relevant objects are accreting supermassive black holes in nuclei
of
galaxies and stellar-mass black holes in compact binary systems
(see, e.g., Nandra
et al. 2007; Miller 2007;
McClintock
& Remillard 2006, for broad reviews of the subject).
The form of the X-ray spectrum and, in particular, the discrete
features at
6-7 keV provide a powerful tool to explore the physical
properties of the
emitting region, close to the black hole horizon. The line profile
often appears to be smeared and asymmetric, with the red wing extending
down to ![]() 3 keV
or even less. Spectral modelling can help us to determine
the system parameters, namely, the black hole spin (Reynolds
et al. 2005; Miller
et al. 2009).
3 keV
or even less. Spectral modelling can help us to determine
the system parameters, namely, the black hole spin (Reynolds
et al. 2005; Miller
et al. 2009).
It is important to realise that the emission angular directionality probes the physical conditions of the emitting medium. Apart from the above-mentioned temperature stratification, it depends also on the opacity profile. The latter is typically a frequency-dependent quantity, hence the observed radiation also forms at a variable physical depth within the disc. Therefore, the limb darkening/brightening property depends on the wavelength. We take this into account by maintaining the energy resolution in our computations.
The resulting radiation is dominated by X-rays in a few kiloelectronvolt (keV) band, which come from the innermost regions of the accreting system and bear imprints of a strong gravitational field and rapid orbital motion at their origin (Fabian et al. 2000; Fabian 2008). The spectrum is a combination of a multi-colour thermal component from the accreting medium of the disc (Li et al. 2005; Page & Thorne 1974), the power-law component originating from the disc corona (Czerny et al. 2004; Galeev et al. 1979), and the reflection and absorption features arising on the disc surface and in the extended corona along the line of sight (Reynolds & Nowak 2003; Fabian et al. 1989). For active galaxies, the thermal multi-colour black body component dominates in the UV and rarely reaches the sub keV energies. This component, however, occurs at higher energy of the spectrum of black hole binaries.
This paper is organised as follows. Section 2
formulates the model and presents its basic assumptions.
Section 3
explores how the constraints on the black
hole spin depend on the directionality of the spectrum
emerging around the iron line energy. To this end we construct the
confidence level diagrams of the ![]() statistics which
demonstrate the level of expected sensitivity of the model. First
we explore simple analytical approximations of the limb-darkening
profile,
which do not depend on energy, and then we consider numerical results
of
our self-consistent radiative transfer computations of both the
continuum and the
spectral features between
statistics which
demonstrate the level of expected sensitivity of the model. First
we explore simple analytical approximations of the limb-darkening
profile,
which do not depend on energy, and then we consider numerical results
of
our self-consistent radiative transfer computations of both the
continuum and the
spectral features between ![]() 2-10 keV.
We demonstrate the results
by ``fitting'' the artificially simulated data, for which all
parameters
are perfectly under our control, and by reanalysing the XMM-Newton
observation of the Seyfert 1 galaxy MCG-6-30-15.
We discuss our results in Sect. 4 and
briefly
summarise them in Sect. 5.
2-10 keV.
We demonstrate the results
by ``fitting'' the artificially simulated data, for which all
parameters
are perfectly under our control, and by reanalysing the XMM-Newton
observation of the Seyfert 1 galaxy MCG-6-30-15.
We discuss our results in Sect. 4 and
briefly
summarise them in Sect. 5.
2 Model assumptions and requisites
2.1 Gravitational field near a rotating black hole
According to general relativity, the gravitational field of a rotating black hole influences the intrinsic spectrum of a nearby source by changing the energy of photons and bending the shape of light rays (Misner et al. 1973). The assumed geometry of the source, i.e. the accretion disc with high orbital velocity near its inner rim, is another factor contributing to significant anisotropy of the emission in the observer's frame. We remark that geometrical optics provides an appropriate framework describing these effects near astrophysical black holes, where the wavelength of X-rays is much shorter than the typical length-scale of the system represented by the black hole gravitational radiusThe gravitational field is described by the Kerr metric (Misner
et al. 1973, Chapt. 33):
where the Boyer-Lindquist spheroidal coordinates (
Unlike weakly gravitating, non-compact bodies (e.g. main-sequence
stars), black holes strongly affect light passing near their horizon.
This influence bears not only the signature of black hole mass but it
also depends on its rotation via frame-dragging. Although the latter
effect is rather weak, it does shape the details of the final spectrum
and
hence can be employed to measure the black hole angular momentum. The
conversion factor from the angular momentum ![]() (in
physical units) to the angular momentum J (in
geometrical units)
reads:
(in
physical units) to the angular momentum J (in
geometrical units)
reads: ![]() .
The geometrised dimension of J is the square of the
length [cm2].
.
The geometrised dimension of J is the square of the
length [cm2].
It is convenient to make all geometrised quantities dimensionless by
scaling them with the appropriate power of mass M.
The dimensionless specific angular momentum, ![]() ,
spans the
range
,
spans the
range ![]() ,
where the positive/negative value refers to the motion
co/counter-rotating with respect to the black hole. We will further
assume co-rotational motion only (
,
where the positive/negative value refers to the motion
co/counter-rotating with respect to the black hole. We will further
assume co-rotational motion only (![]() ).
We can scale all lengths by M to reach
dimensionless units.
).
We can scale all lengths by M to reach
dimensionless units.
For the Keplerian angular velocity of the orbital motion, we obtain (Bardeen
et al. 1972)
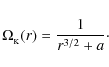
|
(2) |
For the linear velocity with respect to a locally non-rotating observer, we have (see Fig. 1)
The velocity at the marginally stable orbit reaches a considerable fraction of the light speed c and has a similar value
Notice that the above-mentioned interval of a-values follows from the assumption, traditionally accepted by astronomers, that we are dealing with a Kerr black hole, for which the outer horizon is located at r+=1+(1-a2)1/2. Hence, the magnitude of a is thought to be less than unity in order to have a regular horizon and avoid the case of naked singularity, although the latter possibility cannot be straightforwardly rejected just on the basis of spectra fitting.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11941f01.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg50.png)
|
Figure 1:
Orbital velocity |
| Open with DEXTER | |
2.2 Black-hole signatures in accretion disc radiation
The physical parameters of the black hole - namely, its angular momentum a - are imprinted in the spacetime geometry and they influence the velocity of the orbiting material as well as the radiation propagating through that spacetime. Thus, the observed spectrum is affected - the equivalent width and the centroid energy of spectral lines differ from the value expected on the basis of a purely Newtonian model (e.g. Vaughan & Fabian 2004; Martocchia et al. 2000; Dabrowski & Lasenby 2001; Miniutti et al. 2003, and further references cited therein). In other words, the relativistic effects offer the possibility to reveal the presence of a compact body in the centre of the accretion disc, and to determine its parameters. This assertion is based on an implicit assumption that we can constrain the local physics forming the intrinsic spectrum of the source with sufficient accuracy.The effects of strong gravity may be concealed from us if the
intrinsic spectrum of the accretion disc is not known well enough. This
is particularly an issue with respect to the angular
momentum determination because the geometrical effect of frame-dragging
due to a rotating black hole is a rather subtle one. In order to assess
potential inaccuracies, we investigate how sensitive the
determination of the a parameter is to the angular
distribution of the
disc emission, i.e., the limb-darkening (or the limb-brightening) law
in
the spectral range of ![]() keV.
keV.
Numerical as well as semi-analytical methods were developed and combined to study the spectral features from relativistic accretion discs, especially the profiles of the iron-line complex between 6-7 keV. An important practical attribute from the view point of applicability of any particular method is its implementation within the XSPEC data analysis package (Arnaud 1996). In this context, over almost two decades the most widely used model of the relativistic disc spectral line is the one by Laor (1991), which includes the effects of a rapidly rotating Kerr black hole. The ptmmsclaor model sets the dimensionless angular momentum a to the canonical value of a=0.998, so it cannot be the subject of a rigorous data fitting procedure (although see Svoboda et al. 2008).
Although the mathematical properties of the extreme Kerr spacetime (a2=1) are significantly different from the sub-extreme case (a2<1), the graphs of the redshift factor as well as the emission angle are practically identical. Therefore we do not expect any detectable differences of the observed spectra between these two cases. Secondly, the main effect on the standard accretion disc spectrum and the relativistic broad line formation arises from the assumed link between the inner edge of the disc and the black hole spin parameter (Reynolds & Fabian 2008). Svoboda et al. (2008) have examined the accuracy of the spin fitting using the ptmmsclaor model. They demonstrate that, although such an approach is not self-consistent, the accuracy of the resulting a-values is actually quite good.
Dovciak
et al. (2004b) have relaxed the limitation of the
ptmmsclaor
model regarding the fixed value of the spin. These authors
allowed for a to be fitted to the data by ![]() minimisation in a
suite of ptmmscky models. Furthermore, Beckwith
& Done (2004) have developed the ptmmsckdline, and Brenneman
& Reynolds (2006) have
developed the ptmmsckerrdisk models which are endowed with similar
functionality. The latter authors performed useful tests
demonstrating that ptmmscky and ptmmsckerrdisk give compatible results
when they are set to equivalent parameter values. Numerical codes have
been developed independently by several other groups
(Cadez
& Calvani 2005; Martocchia
et al. 2000; Zakharov
& Repin 2004; Fuerst
& Wu 2004; Viergutz
1993) using different techniques. The ptmmsclaor kernel has
been
recently applied by Miniutti
et al. (2007) who reanalysed the prototypical source
MCG-6-30-15 using Suzaku observations to determine the relativistic
blurring and to measure the black hole parameters. Their results
confirm the high value of the spin.
minimisation in a
suite of ptmmscky models. Furthermore, Beckwith
& Done (2004) have developed the ptmmsckdline, and Brenneman
& Reynolds (2006) have
developed the ptmmsckerrdisk models which are endowed with similar
functionality. The latter authors performed useful tests
demonstrating that ptmmscky and ptmmsckerrdisk give compatible results
when they are set to equivalent parameter values. Numerical codes have
been developed independently by several other groups
(Cadez
& Calvani 2005; Martocchia
et al. 2000; Zakharov
& Repin 2004; Fuerst
& Wu 2004; Viergutz
1993) using different techniques. The ptmmsclaor kernel has
been
recently applied by Miniutti
et al. (2007) who reanalysed the prototypical source
MCG-6-30-15 using Suzaku observations to determine the relativistic
blurring and to measure the black hole parameters. Their results
confirm the high value of the spin.
Miller et al. (2009) applied the modelling of relativistic spectral features to estimate the black hole spin from a sample of stellar-mass black holes. They used the joint constraints from both the disc reflection and continuum and found evidence for a broad range of black hole spin parameters.
The angular emissivity law, ![]() ,
defines the distribution of the intrinsic intensity outgoing from each
radius
,
defines the distribution of the intrinsic intensity outgoing from each
radius ![]() of the disc surface with respect to the perpendicular
direction. The emission angle
of the disc surface with respect to the perpendicular
direction. The emission angle ![]() is
measured from the disc normal direction to the equatorial plane, in
the disc co-moving frame, i.e. in the local Keplerian frame orbiting
with the angular velocity
is
measured from the disc normal direction to the equatorial plane, in
the disc co-moving frame, i.e. in the local Keplerian frame orbiting
with the angular velocity ![]() .
Likewise the
intrinsic energy
.
Likewise the
intrinsic energy ![]() is measured with respect to the local frame. The
total disc emission can be written in the form of product
is measured with respect to the local frame. The
total disc emission can be written in the form of product
where the radial part is well approximated by a power law,
and
The redshift factor g and the emission
angle ![]() are
are
where
The observed radiation flux is then obtained by integrating
the
intrinsic emission over the entire disc surface, from the inner edge (
![]() )
to the outer
edge (
)
to the outer
edge (
![]() ), weighted by the transfer
function
), weighted by the transfer
function
![]() determining the impact of relativistic
energy change (Doppler and gravitational) as well as the lensing effect
for a distant observer directed along the inclination angle
determining the impact of relativistic
energy change (Doppler and gravitational) as well as the lensing effect
for a distant observer directed along the inclination angle ![]() (see Asaoka 1989;
Cunningham
1975; Karas 2006;
Karas
et al. 1992).
(see Asaoka 1989;
Cunningham
1975; Karas 2006;
Karas
et al. 1992).
Given the high velocity of the orbital motion and the strong-gravity light bending near the black hole, the effect of directional anisotropy of the local emission is enhanced. For this reason it is important to describe the angular distribution in a correct manner; ad hoc choices of the limb-darkening law may lead to errors in the determination of the model best fit parameters, including the inaccuracy in a parameter which are difficult to control, or they may prevent us from estimating the statistical confidence of the model. In the case of black hole accretion discs, this complication becomes important because the aberration, beaming and light-bending effects grow rapidly towards the inner edge of the disc. Therefore, even a small discrepancy between the assumed and the correct angular emissivity profiles becomes greatly enhanced in the observer frame.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f02.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg78.png)
|
Figure 2:
Contours of redshift factor |
| Open with DEXTER | |
2.3 Effects of the emission angular directionality
In optics, Lambert's cosine law describes an emitter producing a radiation intensity that is directly proportional toIn the case of a fluorescence iron line produced by an illuminated plane-parallel slab, the angular distribution was investigated by various authors (Haardt 1993; Reynolds et al. 2000; Ghisellini et al. 1994; George & Fabian 1991; Basko 1978). In that case a complicated interplay arises among the angular distribution of the primary irradiation, reflection and scattering in the disc atmosphere. Several authors pointed out that it is essential for the reliable determination of the model parameters to determine the angular directionality of the broad line emission correctly. Martocchia et al. (2000) noted, by employing the lamp-post model, that ``...the broadening of the observed spectral features is particularly evident when strongly anisotropic emissivity laws, resulting from small h (i.e., the lamp-post elevation above the equatorial plane), are considered.``
The important role of the emission angular directionality was clearly spelled out by Beckwith & Done (2004): ``...the angular emissivity law (limb darkening or brightening) can make significant changes to the derived line profiles where light bending is important`` (see their Figs. 9-13). Similarly, Dovciak et al. (2004b,a) and Beckwith (2005) compared the relativistic broad lines produced under different assumptions about the emission angular directionality. However, to verify the real sensitivity of the models to the mentioned effect of directionality, it is necessary to connect the radiative transfer computations with the spectral fitting procedure, and to carry out a systematic analysis of the resulting spectra, taking into account both the line and the continuum in the full relativistic regime. Here we report on our results from such computations.
Reynolds et al. (2004, Sect. 4.3) argue that the combined effect of photoelectric absorption in the disc and Compton scattering in the corona more affect the iron line photons emerging along grazing light rays than continuum photons. They conclude that the line equivalent width should be diminished for observers viewing the accretion disc at high inclination angles. Such a trend can be seen also in the lamp-post model of Matt et al. (1992) and Martocchia et al. (2000, see their Fig. 11). However, in the latter work this diminution is less pronounced when we compare it with the case of intrinsically isotropic emissivity.
More recently, Niedzwiecki & Zycki (2008) studied the effect of different limb-darkening laws on the iron-line profiles. They point out that the role of emission directionality can be quite significant once the radial emissivity of the line is fixed with sufficient confidence. However, this is a serious assumption. In reality, the radial emissivity is not well constrained by current models.
The angular dependence of the outgoing radiation is determined by the
whole interconnection of various effects. We describe them in more
detail below (Sect. 3.4).
Briefly, the conclusion is such that realistic models require numerical
computations of the full radiative transfer.
We have developed a complete and consistent approach to such radiative
transfer computations in the context of the broad iron-line modelling together
with the underlying continuum computations. As described in
considerable detail below, we performed the extensive
computations which are necessary in order to reliably determine the
impact
of the emission angular anisotropy on spectral fitting results (namely,
on
the determination of the black hole angular momentum). In particular,
we
describe detailed results from the investigation of the model goodness
(by employing an adequate statistical analysis of the complicated ![]() parameter
space). Such the analysis has not been performed so far in previous
papers because detailed stepping through the parameter space and proper
re-fitting of the model parameters was not possible due to the enormous
complexity of the models and extensive computational costs.
parameter
space). Such the analysis has not been performed so far in previous
papers because detailed stepping through the parameter space and proper
re-fitting of the model parameters was not possible due to the enormous
complexity of the models and extensive computational costs.
In regular stars and their accretion discs, the relativistic effects
hardly affect the emerging radiation. The situation is very
different in the inner regions of a black hole accretion disc,
where the energy shift and gravitational lensing are significant.
The observed signal can be boosted or
diminished by the Doppler effect combined with gravitational redshift:
![]() ,
where the g values span more than a decade.
Figure 2
shows the
redshift factor g near the black hole, proving that
general relativistic
effects indeed change the photon energy significantly.
,
where the g values span more than a decade.
Figure 2
shows the
redshift factor g near the black hole, proving that
general relativistic
effects indeed change the photon energy significantly.
As mentioned above, many authors have adopted the defining choice
(Laor 1991;
Chandrasekhar
1960) of the cosine profile
for the line angular emissivity: ![]() .
This relation describes the
energy-independent limb-darkening type of profile. However, the choice
is somewhat arbitrary in the sense that the physical assumptions behind
this law are not satisfied at every radius over the entire surface of
the accretion disc. It has been argued that the limb-darkening
characteristics need to be modified, or even replaced
by some kind of limb brightening in the case of X-ray irradiated disc
atmospheres with Compton reflection
(Haardt 1993;
Zycki
& Czerny 1994; Ghisellini
et al. 1994). The latter should
include the energy dependence, as the Compton reprocessing of the
reflected component plays a significant role. The angle-dependent
computations of the Compton reflection demonstrate these effects
convincingly (Czerny
et al. 2004). Indeed, the same effect is
seen also in our computations, as shown in the right panel of
Fig. 4.
The increase of emissivity
with the emission angle strongly depends on the ionisation state of the
reflecting material, so the actual situation can be quite complex (Goosmann
et al. 2007).
.
This relation describes the
energy-independent limb-darkening type of profile. However, the choice
is somewhat arbitrary in the sense that the physical assumptions behind
this law are not satisfied at every radius over the entire surface of
the accretion disc. It has been argued that the limb-darkening
characteristics need to be modified, or even replaced
by some kind of limb brightening in the case of X-ray irradiated disc
atmospheres with Compton reflection
(Haardt 1993;
Zycki
& Czerny 1994; Ghisellini
et al. 1994). The latter should
include the energy dependence, as the Compton reprocessing of the
reflected component plays a significant role. The angle-dependent
computations of the Compton reflection demonstrate these effects
convincingly (Czerny
et al. 2004). Indeed, the same effect is
seen also in our computations, as shown in the right panel of
Fig. 4.
The increase of emissivity
with the emission angle strongly depends on the ionisation state of the
reflecting material, so the actual situation can be quite complex (Goosmann
et al. 2007).
A question arises of whether the current determinations of the black
hole
angular momentum might be affected by the uncertainty in the actual
emissivity angular distribution, and to what degree. In fact, this may
be of critical concern when future high-resolution data become
available
from the new generation of detectors. We have therefore carried out a
systematic investigation using the ptmmscky code to reveal how
sensitive
the constraints on the dimensionless a parameter
are with respect to
the possible variations in the angular part ![]() of
the emissivity.
of
the emissivity.
Figure 3
shows the contours of the local
emission angle ![]() from the accretion disc, taking into account their
distortion by the central black hole and assuming that the emitted
photons
reach a distant observer at a given view angle
from the accretion disc, taking into account their
distortion by the central black hole and assuming that the emitted
photons
reach a distant observer at a given view angle ![]() .
Although
the contours are most dramatically distorted near the horizon, where
both aberration and light bending effects grow significantly, the
emission
angle is visibly different from the observer inclination even quite far
from the horizon, at a distance of several tens
.
Although
the contours are most dramatically distorted near the horizon, where
both aberration and light bending effects grow significantly, the
emission
angle is visibly different from the observer inclination even quite far
from the horizon, at a distance of several tens ![]() .
This is
mainly due to special-relativistic aberration which decays slowly with
the distance as the disc obeys Keplerian rotation at all radii.
.
This is
mainly due to special-relativistic aberration which decays slowly with
the distance as the disc obeys Keplerian rotation at all radii.
In summary, Figs. 2, 3 demonstrate the main attributes of the photon propagation in black hole spacetime relevant to our problem: the energy shift and the direction of emission depend on the view angle of the observer as well as on the angular momentum of the black hole. Notice that, near the inner rim, the local emission angle is indeed highly inclined towards the equatorial plane where at the same time the outgoing radiation is boosted. These effects are further enhanced by gravitational focusing, which we also take into account in our calculations.
It should be noted that the energy shifts and emission angles near a black hole, such as those shown in Figs. 2, 3, have been studied by a number of authors in mutually complementary ways. The figures shown here have been produced by plotting directly the content of FITS format files that are encoded in the corresponding ptmmscky XSPEC routines (see Dovciak (2004), where an atlas of contour plots is presented for different inclinations and spins). Analogous figures were also shown in Beckwith & Done (2004), who depict the dependence of the cosine of the emission angle on the energy shift of the received photon and the emission radius.
The above quoted papers concentrated mainly on the discussion of the energy shifts and the emission directions of the individual photons, or they isolated the role of relativistic effects on the predicted shape of the spectral line profile. They clearly demonstrated that the impact of relativistic effects can be very significant. However, what is still lacking is a more systematic analysis which would reveal how these effects, when integrated over the entire source, influence the results of spectra fitting. To this end one needs to perform an extensive analysis of the model spectra including the continuum component, match the predicted spectra to the data by appropriate spectra fitting procedures, and to investigate the robustness of the fit by varying the model parameters and exploring the confidence contours.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f03.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg85.png)
|
Figure 3:
Contours of the local emission angle, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f04.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg86.png)
|
Figure 4:
Left: directional distribution of the
intrinsic emissivity
(see Sect. 3.1
for details). Right: an example of the directional
distribution from the numerical computations, showing
results from the reprocessing model with the continuum photon index |
| Open with DEXTER | |
One might anticipate the directional effects of the local emission to be quite unimportant. The argument for such an expectation suggests that the role of directionality should grow with the source inclination, whereas the unobscured Seyfert 1 type AGNs (where the relativistically broadened and skewed iron line is usually expected) are thought to have only small or moderate inclinations. However, this qualitative trend cannot be used to quantitatively constrain the model parameters and perform any kind of precise analysis, needed to determine the black hole spins from current and future high-quality data. Such an analysis has not been performed so far, and we embark on it here for the first time.
3 Iron K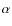 line band examined with different directionalities of the intrinsic
emissivity
line band examined with different directionalities of the intrinsic
emissivity
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f05.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg88.png)
|
Figure 5:
Left: theoretical
profiles of the relativistic line (the ptmmsckyrline model, without
continuum),
corresponding to the three cases in the left panel
of Fig. 4.
The lines are normalised with respect to the height of the blue peak.
Model parameters are a=0.9982, q=3,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f06.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg90.png)
|
Figure 6:
Left: the same as in Fig. 5, but for a
narrow ring with |
| Open with DEXTER | |
3.1 Approximations to the angular emission profile
We describe the methodology which we adopted in order to explore the effects of the spectral line emission directionality. To this end we first employ simple approximations, neglecting any dependence on the photon energy and the emission radius. We set the line intrinsic emissivity from the planar disc to be described by one of the following angular profiles,with the radial profiles being a power law
The limb-brightening law by Haardt
(1993) describes the
angular distribution of a fluorescent iron line emerging from an
accretion disc that is irradiated by an extended X-ray source. The
relation was obtained from geometrical considerations and agrees well
with more detailed Monte-Carlo computations (Matt
et al. 1992; George
& Fabian 1991). The physical circumstances relevant
for the limb-darkening law are
different, and we include this case mainly because it is implemented
in the LAOR model and frequently used in
the data analysis. The isotropic case, dividing all limb-brightening
and limb-darkening emissivity laws, is included in our analysis for
comparison.
Notice that an extra geometrical factor ![]() is involved due to simple geometrical projection of the disc surface in
Eq. (5).
is involved due to simple geometrical projection of the disc surface in
Eq. (5).
The radial profile of the emission is set to a unique power law,
Eq. (6),
over the entire range of radii across the disc.
The directionality formula (8) of the
intrinsic
emissivity and the resulting spectral profiles are illustrated in
Fig. 4
(left panel). Naturally, more elaborate and accurate approximations
have been discussed in the literature for some time. For example, Ghisellini
et al. (1994)
in their Eq. (2) include higher-order terms in ![]() to describe
the X-ray reprocessing in the single-scattering Rayleigh approximation.
However,
at this stage the first-order terms are sufficient for us to
demonstrate the differences between the three cases. Later on we will
proceed towards
numerical radiation transfer computations that are necessary to derive
realistic profiles of the emission angular distribution and to keep
their energy dependence.
to describe
the X-ray reprocessing in the single-scattering Rayleigh approximation.
However,
at this stage the first-order terms are sufficient for us to
demonstrate the differences between the three cases. Later on we will
proceed towards
numerical radiation transfer computations that are necessary to derive
realistic profiles of the emission angular distribution and to keep
their energy dependence.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f07.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg94.png)
|
Figure 7:
Left: unfolded spectrum generated by the
ptmmscpowerlaw + kyrline model with parameters of the line identical as
in Fig. 5. We assumed the limb-brightening profile, i.e.
Case 1
of Eq. (8).
Right: the ratio of the model on the left to
the same model with the Case 3 (limb-darkening) profile.
The normalisation of the line was allowed to vary during the fit. The
|
| Open with DEXTER | |
The dependence of the spectral profiles on the angular
distribution ![]() of the intrinsic emission is shown in Figs. 5, 6.
It is apparent from Fig. 5 that the limb
brightening case makes the line profile broader (in the left panel)
and the height of the blue peak lower (in the right panel) than the
limb darkening case for the same set of parameters, which can
consequently lead to discrepant evaluation of the spin.
While Fig. 5
shows the line profile for an extended
disc, Fig. 6
deals with a narrow ring. In this
case, a typical double-horn profile develops. Although the energy of
the
peaks is almost entirely insensitive to the emission angular
directionality,
the peak heights are influenced by the adopted limb darkening law. In
the right panel of Fig. 6, the ratio of
the two peaks
is shown for the three cases of the emission angular directionality
according to
Eq. (8).
The influence of the directionality is apparent and it is comparable to
the effect of the inclination angle. The spin value has only little
impact for large inclinations.
of the intrinsic emission is shown in Figs. 5, 6.
It is apparent from Fig. 5 that the limb
brightening case makes the line profile broader (in the left panel)
and the height of the blue peak lower (in the right panel) than the
limb darkening case for the same set of parameters, which can
consequently lead to discrepant evaluation of the spin.
While Fig. 5
shows the line profile for an extended
disc, Fig. 6
deals with a narrow ring. In this
case, a typical double-horn profile develops. Although the energy of
the
peaks is almost entirely insensitive to the emission angular
directionality,
the peak heights are influenced by the adopted limb darkening law. In
the right panel of Fig. 6, the ratio of
the two peaks
is shown for the three cases of the emission angular directionality
according to
Eq. (8).
The influence of the directionality is apparent and it is comparable to
the effect of the inclination angle. The spin value has only little
impact for large inclinations.
In general, we notice that the extension and prominence of the red wing of the line are indeed related to the intrinsic emission directionality. This was examined in detail by Beckwith & Done (2004), who plotted the expected broad-line profiles for different angular emissivity and explored how the red wing of the line changes as a result of this undetermined angular distribution. Similarly, the inferred spin of the black hole must depend on the assumed profile to a certain degree. This is especially so if the spin is determined by the extremal redshift of the line's red wing. It has been recently argued (Niedzwiecki & Zycki 2008) that the directionality effect could be a real issue for the accuracy of line fitting if other parameters (such as the radial emissivity profile) are well constrained.
However, simple arguments are insufficient to assess how inaccurate the spin determination might be in realistic situations, as the spectral fitting procedure involves several components extending over a range of energy above and below the iron-line band. We illustrate this in Fig. 7, noticing that the different prescriptions produce very similar results outside the line energy, but they do differ at the broad line energy range. The theoretical (background-subtracted) profiles of the relativistic line cannot alone be used to make any firm conclusion about the error of the best fit parameters that could result from the poorly known angular emissivity. To this end one has to study a consistent model of the full spectrum. With a real observation, the sensitivity to the problem of directionality (as well as any other uncertainty inherent in the theoretical model) will depend also on the achieved resolution, energy binning and the error bars of the data.
3.2 Example: MCG-6-30-15 reanalysis
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f08.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg95.png)
|
Figure 8:
The best-fit values of |
| Open with DEXTER | |
We reanalysed a long XMM-Newton observation of a nearby Seyfert 1
galaxy MCG-6-30-15 (Fabian
et al. 2002)
to test whether the different directionality approximations can be
distinguished in the current data.
The observation took place in summer 2001 and the acquired exposure
time was about 350 ks. The spectra reveal the presence of a
broad and skewed
iron line (Vaughan
& Fabian 2004; Fabian
et al. 2002; Ballantyne
et al. 2003).
We reduced the EPN data from three sequential revolutions (301, 302,
303)
using the SAS software version 7.1.2![]() .
We used standard tools for preparing and fitting the data contained in
the HEASOFT software package version 6.4
.
We used standard tools for preparing and fitting the data contained in
the HEASOFT software package version 6.4![]() .
Using the FTOOL MATHPHA (part of the HEASOFT) we joined the three
spectra to improve the statistical significance. Further, we used the
XSPEC version 12.2 for the spectral analysis.
We rebinned all the data channels to oversample the instrumental energy
resolution maximally by a factor of 3 and to have at least 20
counts per bin. The first condition is much stronger with respect to
the total flux of the source -
.
Using the FTOOL MATHPHA (part of the HEASOFT) we joined the three
spectra to improve the statistical significance. Further, we used the
XSPEC version 12.2 for the spectral analysis.
We rebinned all the data channels to oversample the instrumental energy
resolution maximally by a factor of 3 and to have at least 20
counts per bin. The first condition is much stronger with respect to
the total flux of the source - ![]() erg cm-2 s-1
(
erg cm-2 s-1
(
![]() cts) in the
2-10 keV energy interval.
cts) in the
2-10 keV energy interval.
We applied the same continuum model
as presented in Fabian
et al. (2002): the power law component
(photon index ![]() )
absorbed by neutral hydrogen (column density
)
absorbed by neutral hydrogen (column density ![]() cm-2).
This simple model is sufficient to fit the data above
cm-2).
This simple model is sufficient to fit the data above ![]() 2.5 keV,
which is also satisfactory for our goal of reproducing the overall
shape of
the broad iron line.
Other components need to be added to the model in order to fully
understand the spectrum formation and to decide between viable
alternatives, including
the presence of outflows and a combination of absorption and reflection
effects
(Miller
et al. 2008; Turner
& Miller 2009).
However, our goal here is not to give precedence to any of the
particular schemes.
Instead, we rely on the model of a broad line and we test
and compare different angular laws for the emission.
2.5 keV,
which is also satisfactory for our goal of reproducing the overall
shape of
the broad iron line.
Other components need to be added to the model in order to fully
understand the spectrum formation and to decide between viable
alternatives, including
the presence of outflows and a combination of absorption and reflection
effects
(Miller
et al. 2008; Turner
& Miller 2009).
However, our goal here is not to give precedence to any of the
particular schemes.
Instead, we rely on the model of a broad line and we test
and compare different angular laws for the emission.
The residuals from the simple power law model can be explained by a
complex of a broad line and two narrow lines.
Due to the complexity of the model, it is hard to
distinguish between the narrow absorption line at ![]() keV
and an emission line at
keV
and an emission line at ![]() keV
(Fabian
et al. 2002).
Although the level of
keV
(Fabian
et al. 2002).
Although the level of ![]() values stays almost the same,
the parameters of the broad iron line do depend on the
continuum model and the presence of narrow lines.
By adding an absorption line at
values stays almost the same,
the parameters of the broad iron line do depend on the
continuum model and the presence of narrow lines.
By adding an absorption line at ![]() keV,
the best fit rest energy of the broad component comes out to be E=6.7 keV,
and so the broad
line originates in a moderately ionised disc.
This result is consistent with Ballantyne
et al. (2003).
keV,
the best fit rest energy of the broad component comes out to be E=6.7 keV,
and so the broad
line originates in a moderately ionised disc.
This result is consistent with Ballantyne
et al. (2003).
More details of our reanalysis of the broad
iron line shape are described in Svoboda
et al. (2008).
Here, we present the results of the one-dimensional steppar
command in Fig. 8,
which demonstrates the expected confidence of a-parameter
best-fit values
for the two extreme cases of directionality, Case 1 and
Case 3.
The model used in the XSPEC syntax is:
ptmmscphabs*(ptmmscpowerlaw+ptmmsczgauss+ptmmsczgauss+ptmmsckyrline).
The fixed parameters of the model are the column density ![]() cm-2,
the photon index of power law
cm-2,
the photon index of power law ![]() ,
the redshift factor z = 0.008, the energy of the
narrow emission line
,
the redshift factor z = 0.008, the energy of the
narrow emission line ![]() keV,
and the energy of the narrow absorption line
keV,
and the energy of the narrow absorption line
![]() keV.
The parameters of the broad iron line were allowed to vary during the
fitting procedure. Their default values were
keV.
The parameters of the broad iron line were allowed to vary during the
fitting procedure. Their default values were ![]() keV
for the energy of the broad iron line,
keV
for the energy of the broad iron line,
![]() deg for the emission
angle, q1
= 4.5, q2 = 2 and
deg for the emission
angle, q1
= 4.5, q2 = 2 and ![]()
![]() for the radial dependence of the emissivity
(the radial part of the intensity needs to be rather complicated
to fit the data and can be expressed as a broken power law:
for the radial dependence of the emissivity
(the radial part of the intensity needs to be rather complicated
to fit the data and can be expressed as a broken power law:
![]() for
for ![]() ,
and
,
and ![]() for
for ![]() ).
).
The determined best-fit values for the spin are virtually the same for
both cases, independent of the details of the
limb-brightening/darkening profile. However, this result arises on
account of the growing complexity of the model.
The differences between the two cases become hidden in different values
of the other parameters - especially in q1,
q2 and ![]() ,
i.e. the parameters characterising the radial dependence of the line
emissivity in ptmmsckyrline as a broken power law with a break radius
,
i.e. the parameters characterising the radial dependence of the line
emissivity in ptmmsckyrline as a broken power law with a break radius ![]() .
We find: (i)
.
We find: (i) ![]() ,
,
![]() deg,
q1 = 3.7(1), q2
= 2.1(1),
deg,
q1 = 3.7(1), q2
= 2.1(1), ![]()
![]() for Case 1;
and (ii)
for Case 1;
and (ii) ![]() keV,
keV,
![]() deg,
q1 = 5.3(1), q2
= 2.8(1),
deg,
q1 = 5.3(1), q2
= 2.8(1), ![]()
![]() for Case 3.
The errors in brackets are evaluated as the 90% confidence region for a
single interesting parameter when the values of the other parameters
are fixed.
The combination of three parameters q1,
q2,
for Case 3.
The errors in brackets are evaluated as the 90% confidence region for a
single interesting parameter when the values of the other parameters
are fixed.
The combination of three parameters q1,
q2, ![]() thus adjusts the best fit in XSPEC. Nonetheless, the clear differences
between the models occur consistently with theoretical expectations:
for Case 3 the lower values of the spin,
a<0.87, produce larger
thus adjusts the best fit in XSPEC. Nonetheless, the clear differences
between the models occur consistently with theoretical expectations:
for Case 3 the lower values of the spin,
a<0.87, produce larger ![]() and the best-fit spin can
reach the extreme value within the 90% confidence threshold.
and the best-fit spin can
reach the extreme value within the 90% confidence threshold.
3.3 Analysis of simulated data for next generation X-ray missions
In order to evaluate the feasibility of determining the spin of a
rotating black hole
and to assess the expected constraints from future X-ray data, we
produced a set of
artificial spectra. We used a simple model prescription and preliminary
response matrices for the International X-ray Observatory (IXO) mission![]() . Here we limit the energy
band in the range 2.5-10 keV. The adopted model
consists of ptmmscpowerlaw for continuum (photon index
. Here we limit the energy
band in the range 2.5-10 keV. The adopted model
consists of ptmmscpowerlaw for continuum (photon index ![]() and the
corresponding normalisation
and the
corresponding normalisation ![]() ), plus ptmmsckyrline model
(Dovciak
et al. 2004b) for the broad line. The normalisation
factors of the model were chosen in such a way that
the model flux matches the flux of MCG-6-30-15.
In this section, the simulated flux is around
), plus ptmmsckyrline model
(Dovciak
et al. 2004b) for the broad line. The normalisation
factors of the model were chosen in such a way that
the model flux matches the flux of MCG-6-30-15.
In this section, the simulated flux is around ![]() erg cm-2 s-1with
about 3% of the flux linked to the broad iron line component.
The simulated exposure time was 100 ks.
erg cm-2 s-1with
about 3% of the flux linked to the broad iron line component.
The simulated exposure time was 100 ks.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f09.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg121.png)
|
Figure 9:
Test results of the theoretical fits with |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f10.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg123.png)
|
Figure 10:
The same as in Fig. 9,
but for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f11.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg124.png)
|
Figure 11:
The same as in Fig. 9,
but for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f12.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg125.png)
|
Figure 12:
The same as in Fig. 9,
but for |
| Open with DEXTER | |
We generated a set of ``fake'' spectra (i.e., artificial spectra in the
XSPEC terminology). These spectra were produced in a grid of angular
momentum values while assuming isotropic directionality,
Case 2 in Eq. (8).
We call the assumed angular moment of the black hole the fiducial spin
and we denote it as ![]() .
We performed the fitting loop to these data points using each of the
three angular emissivity profiles. Once the fit reached convergence, we
recorded the inferred spin a.
Figures 9-12 show the
results in terms of best-fit
.
We performed the fitting loop to these data points using each of the
three angular emissivity profiles. Once the fit reached convergence, we
recorded the inferred spin a.
Figures 9-12 show the
results in terms of best-fit ![]() profiles and the confidence contours
for two different fiducial values of the spin
(we assumed
profiles and the confidence contours
for two different fiducial values of the spin
(we assumed ![]() ,
and 0.998).
We summarise the values for the inferred spin
for two inclination angles i=30 deg and
i=60 deg in Table 1.
,
and 0.998).
We summarise the values for the inferred spin
for two inclination angles i=30 deg and
i=60 deg in Table 1.
The fitting procedure was performed in two different ways - having the
rest
of the parameters free or keeping them frozen. Obviously the former
approach
results in an extremely complicated ![]() space. Therefore, for simplicity of
the graphical representation, we plot only the results of the second
approach which, however, gives broadly consistent results (though it
misses some local minima of
space. Therefore, for simplicity of
the graphical representation, we plot only the results of the second
approach which, however, gives broadly consistent results (though it
misses some local minima of ![]() ). In other words, the plots
have the parameters of the power law continuum, the energy of the line
and the radial dependence parameter fixed at
). In other words, the plots
have the parameters of the power law continuum, the energy of the line
and the radial dependence parameter fixed at ![]() ,
E0=6.4 keV, and q=3.
,
E0=6.4 keV, and q=3.
The conclusion from this analysis is that the determination of a
indeed seems to be sensitive within certain limits to the assumed
directionality of the intrinsic emission. The suppression of the flux
of
the reflection component at high values of ![]() may
lead to overestimating the spin, and vice versa.
The middle panels of Figs. 9-12 show the fit
results
for isotropic directionality, which was also the seed model
used to generate the test data, and so these contours illustrate
the magnitude of combined dispersion due to the simulated noise and the
degeneracy between the spin and the inclination.. The fiducial values
are well inside the
may
lead to overestimating the spin, and vice versa.
The middle panels of Figs. 9-12 show the fit
results
for isotropic directionality, which was also the seed model
used to generate the test data, and so these contours illustrate
the magnitude of combined dispersion due to the simulated noise and the
degeneracy between the spin and the inclination.. The fiducial values
are well inside the ![]() confidence contour in all the graphs
in the middle panels.
confidence contour in all the graphs
in the middle panels.
However, systematically lower values of the angular momentum are obtained for the limb brightening profile and, vice versa, higher values are found for the limb darkening profile. The magnitude of the difference is larger for higher values of angular momentum.
Table 1: The best-fit spin values inferred for the three cases of the limb darkening/brightening law, Eq. (8), for the ptmmsckyrline model.
3.4 The angular emission profile of the detailed reprocessing model
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f13.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg138.png)
|
Figure 13:
Plots of data/model ratio, where the data are simulated as
ptmmscpowerlaw + ptmmsckyl2cr and the model applied to the data
is ptmmscpowerlaw + ptmmsckyl3cr with a particular analytical approach
of the directionality. The default angular momentum value is |
| Open with DEXTER | |
The results presented in the previous sections show that using
different emission directionality approaches
leads to a different location of the ![]() minimum
in the parameter space. Doubt about the correct prescription for the
emission directionality
thus brings some non-negligible inaccuracy into the evaluation of the
model parameters. The magnitude of this error cannot be easily assessed
as a unique number because other parameters are also involved.
minimum
in the parameter space. Doubt about the correct prescription for the
emission directionality
thus brings some non-negligible inaccuracy into the evaluation of the
model parameters. The magnitude of this error cannot be easily assessed
as a unique number because other parameters are also involved.
A possible way to tackle the problem is to derive the intrinsic spectrum from self-consistent numerical computations. This has the potential of removing the uncertainty about the emission directionality (although, to a certain degree this uncertainty is only moved to a different level of the underlying model assumptions). In this section, we present such results from modelling the artificial data generated by numerical simulations, i.e. independently of an analytical approximation of the emission directionality presented in the previous sections.
Let us first remind the reader that the orbital speed within the inner
![]()
![]() reaches
a considerable fraction of the speed of
light (Fig. 1).
Beaming, aberration, and the light-bending all affect the emitted
photons very significantly in
this region. Less energetic photons come
from the outer parts where the motion slows down and the relativistic
effects are of diminished importance. This reasoning suggests that the
analysis of the previous section may be inaccurate because the adopted
analytical approximations (8)
neglect any dependence on
energy and distance.
reaches
a considerable fraction of the speed of
light (Fig. 1).
Beaming, aberration, and the light-bending all affect the emitted
photons very significantly in
this region. Less energetic photons come
from the outer parts where the motion slows down and the relativistic
effects are of diminished importance. This reasoning suggests that the
analysis of the previous section may be inaccurate because the adopted
analytical approximations (8)
neglect any dependence on
energy and distance.
We applied the Monte-Carlo radiative transfer code NOAR (see Sect. 5 in Dumont et al. 2000) for the case of ``cold'' reflection, i.e. for neutral or weakly-ionised matter. The NOAR code computes absorption cross sections in each layer. Free-free absorption and the recombination continua of hydrogen- and helium- like ions are taken into account, as well as the direct and inverse Compton scattering. The NOAR code enables us to obtain the angle-dependent intensity for the reprocessed emission. The cold reflection case serves as a reference point that we will later, in a follow-up paper, compare against the models involving stronger irradiation and higher ionisation of the disc medium.
The directional distribution of the intrinsic emissivity of the
reprocessing model is shown in Fig. 4 (right panel).
The continuum photon index ![]() is considered
and the energies are integrated over the 2-100 keV range.
Although the results of the radiation transfer computations do show the
limb-brightening effect, it is a rather mild one,
and not as strong as the Case 1.
In the same plot we also show the angular profile of the emissivity
distribution in different energy ranges: (i) 2-6 keV
(i.e. below the iron K
is considered
and the energies are integrated over the 2-100 keV range.
Although the results of the radiation transfer computations do show the
limb-brightening effect, it is a rather mild one,
and not as strong as the Case 1.
In the same plot we also show the angular profile of the emissivity
distribution in different energy ranges: (i) 2-6 keV
(i.e. below the iron K![]() line
rest energy); (ii) 6-15 keV (including the iron K
line
rest energy); (ii) 6-15 keV (including the iron K![]() line);
(iii) 15-100 keV (including the ``Compton hump''). We
notice that
the energy integrated profile is dominated by the contribution from
the Compton hump, where much of the emerging flux originates.
However, all of the energy sub-ranges indicate the limb-brightening
effect, albeit with slightly different prominence.
line);
(iii) 15-100 keV (including the ``Compton hump''). We
notice that
the energy integrated profile is dominated by the contribution from
the Compton hump, where much of the emerging flux originates.
However, all of the energy sub-ranges indicate the limb-brightening
effect, albeit with slightly different prominence.
We implemented the numerical results of NOAR modelling of a reflected radiation from a cold disc as ptmmsckyl2cr in the ptmmscky collection of models. Furthermore, we produced an averaged model, ptmmsckyl3cr, by integrating ptmmsckyl2cr tables over all angles. Therefore, ptmmsckyl3cr lacks information about the detailed angular distribution of the intrinsic local emission from the disc surface. On the other hand, it has the advantage of increased computational speed and the results are adequate if the emission is locally isotropic. Furthermore, ptmmsckyl3cr can be a posteriori equipped with an analytical prescription for the angular dependence (Cases 1-3 in Eq. (8)), which brings the angular resolution back into consideration. This approach allows us to switch between the three prescriptions for comparison and rapid evaluation.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f14.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg141.png)
|
Figure 14:
The same plots of data/model ratio, but for a=0.998(
left: |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f15.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg142.png)
|
Figure 15:
Results from the test fits with |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f16.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg143.png)
|
Figure 16:
The same as in Fig. 15, but
for |
| Open with DEXTER | |
Table 2: The best-fit spin and inclination angle values inferred for the three cases of the limb darkening/brightening law in the ptmmsckyl3cr model.
In order to constrain the feasibility of the aforementioned approaches,
we
generated the artificial data using the ptmmscpowerlaw +
kyl2cr model.
The parameters of the model are:
photon index of the power law ![]() and its normalisation
and its normalisation
![]() ,
spin of the black hole a, inclination angle
,
spin of the black hole a, inclination angle
![]() ,
the inner and outer radii of the disc
,
the inner and outer radii of the disc ![]() and
and ![]() ,
the index of the radial dependence of the
emissivity q=3, and the normalisation of the
reflection component
,
the index of the radial dependence of the
emissivity q=3, and the normalisation of the
reflection component
![]() .
We simulated the data for two different values of
the spin, a=0.7 and a=0.998,
and for inclination angles
.
We simulated the data for two different values of
the spin, a=0.7 and a=0.998,
and for inclination angles
![]() and
and ![]() .
The simulated flux of the primary power law component is the same
as in the previous section. However, now an important fraction
of the primary radiation is reflected from the disc. The total
flux depends on the extension of the disc and its inclination. Its
value is
.
The simulated flux of the primary power law component is the same
as in the previous section. However, now an important fraction
of the primary radiation is reflected from the disc. The total
flux depends on the extension of the disc and its inclination. Its
value is ![]() erg cm-2 s-1
for our
choice of the parameters.
erg cm-2 s-1
for our
choice of the parameters.
As a next step, we replaced ptmmsckyl2cr by ptmmsckyl3cr and searched back for the best-fit results using the latter model. In this way, using ptmmsckyl3cr we obtained the values of the spin and the inclination angle for different directionalities. The fitting results are summarised in Table 2. Besides the spin and the inclination angle, only normalisation of the reflection component was allowed to vary during the fitting procedure. The remaining parameters of the model were kept frozen at their default values.
The resulting data/model ratios are shown in
Figs. 13
and 14.
For a=0.7and ![]() the graphs look very similar in all
three cases. However, the inferred spin value differs from the fiducial
value with which the test data were originally created.
The dependence of the best-fit
the graphs look very similar in all
three cases. However, the inferred spin value differs from the fiducial
value with which the test data were originally created.
The dependence of the best-fit ![]() statistic on the spin
and the corresponding graphs of the confidence contours for spin versus
inclination angle are shown
in Figs. 15-18,
again for the three cases of
angular directionality. These figures confirm that for the
limb-brightening
profile the inferred spin value comes out somewhat lower than the
correct value, whereas it is higher if the limb-darkening profile is
assumed.
statistic on the spin
and the corresponding graphs of the confidence contours for spin versus
inclination angle are shown
in Figs. 15-18,
again for the three cases of
angular directionality. These figures confirm that for the
limb-brightening
profile the inferred spin value comes out somewhat lower than the
correct value, whereas it is higher if the limb-darkening profile is
assumed.
In each of the three cases the error of the resulting a
determination
depends on the inclination angle and the spin itself. However,
we find that the isotropic directionality reproduces our data to the
best precision. The limb darkening profile is not accurate at higher
values
of the spin, such as a=0.998, when the resulting ![]() value
even exceeds 2. The limb darkening profile is characterised by an
enhanced blue peak of the line while the height of the red peak is
reduced (see Figs. 5, 6).
Consequently, the model
profile is too steep to fit the data. This is clearly visible in the
data/model ratio plots for a=0.998 shown in
Fig. 14.
The flux is underestimated by the model below a mean energy value
value
even exceeds 2. The limb darkening profile is characterised by an
enhanced blue peak of the line while the height of the red peak is
reduced (see Figs. 5, 6).
Consequently, the model
profile is too steep to fit the data. This is clearly visible in the
data/model ratio plots for a=0.998 shown in
Fig. 14.
The flux is underestimated by the model below a mean energy value ![]() of the
line (for a=0.998 and i=30 deg
of the
line (for a=0.998 and i=30 deg
![]() keV)
and overestimated above
keV)
and overestimated above ![]() .
This fact leads to
a noticeable jump in the data/model ratio plot. Only the qparameter
can mimic this limitation and suit the data by increasing its value. It
could be the case of the analysis of the MCG-6-30-15 data in the
previous
section.
.
This fact leads to
a noticeable jump in the data/model ratio plot. Only the qparameter
can mimic this limitation and suit the data by increasing its value. It
could be the case of the analysis of the MCG-6-30-15 data in the
previous
section.
A noteworthy result appears in comparing of the contours produced by
the model with limb brightening and limb darkening for a=0.7
and i=60 deg (Fig. 16).
Although the former model (limb brightening) gives a statistically
worse fit with ![]() than the limb darkening case (
than the limb darkening case (
![]() ),
the inferred values of the spin and the inclination angle are
consistent with the fiducial values within
the
),
the inferred values of the spin and the inclination angle are
consistent with the fiducial values within
the ![]() level. On the other hand, the spin value inferred from the limb
darkening model
is far from the fiducial (i.e., the correct) value.
level. On the other hand, the spin value inferred from the limb
darkening model
is far from the fiducial (i.e., the correct) value.
4 Discussion
We investigated whether the spin measurements of accreting black holes
are affected by the uncertainty of the angular emissivity law, ![]() ,
in the relativistically broadened iron K
,
in the relativistically broadened iron K![]() line models.
We employed three different approximations of the angular
profiles, representing limb brightening, isotropic and limb darkening
emission profiles.
For the radius-integrated line profile of the disc emission,
and especially for higher values of the spin, the
broadened line has a triangle-like profile. The
differences among the considered profiles concern
mainly the width of the line's red wing.
However, the height of the individual peaks,
also affected by the emission directionality,
is important for the case of an orbiting spot (or a narrow ring), which
produce a characteristic double-horn profile.
line models.
We employed three different approximations of the angular
profiles, representing limb brightening, isotropic and limb darkening
emission profiles.
For the radius-integrated line profile of the disc emission,
and especially for higher values of the spin, the
broadened line has a triangle-like profile. The
differences among the considered profiles concern
mainly the width of the line's red wing.
However, the height of the individual peaks,
also affected by the emission directionality,
is important for the case of an orbiting spot (or a narrow ring), which
produce a characteristic double-horn profile.
We reanalysed an XMM-Newton observation of MCG-6-30-15 to study the
emission directionality effect on
the broad iron line, as measured by current X-ray instruments.
We showed the graphs of ![]() values as a function
of spin for different cases of directionality. We can conclude that the
limb darkening law favors higher values of
spin and/or steeper radial dependence of the line emissivity;
vice versa for the limb brightening profile.
Both effects are comprehensible after examining the left panel of
Fig. 5.
The limb darkening
profile exhibits a deficit of flux in the red wing compared
with the limb brightening profile. Both higher spin value
and steeper radial profile of the intensity can compensate for this
deficit.
values as a function
of spin for different cases of directionality. We can conclude that the
limb darkening law favors higher values of
spin and/or steeper radial dependence of the line emissivity;
vice versa for the limb brightening profile.
Both effects are comprehensible after examining the left panel of
Fig. 5.
The limb darkening
profile exhibits a deficit of flux in the red wing compared
with the limb brightening profile. Both higher spin value
and steeper radial profile of the intensity can compensate for this
deficit.
The higher spin value has the effect of shifting the inferred position of the marginally stable orbit (ISCO) closer to the black hole, in accordance with Eq. (4). Consequently, the accretion disc is extended closer to the black hole. The radiation comes from shorter radii and it is affected by the extreme gravitational redshift. Hence, the contribution to the red wing of the total disc line profile is enhanced. Naturally, these considerations are based on the assumption that the inner edge of the line emitting region coincides with the ISCO. Likewise, the steeper radial dependence of the emissivity means that more radiation comes from the inner parts of the accretion disc than from the outer parts, and this produces a similar effect to decreasing the inner edge radius. With the limb brightening law the above-given considerations work the other way around.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f17.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg180.png)
|
Figure 17:
The same as in Fig. 15, but
for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{11941f18.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11941-09/Timg181.png)
|
Figure 18:
The same as in Fig. 15, but
for |
| Open with DEXTER | |
Although the interdependence of the model parameters is
essential
and it is not possible to give the result of our analysis in terms of a
single number, one can very roughly estimate that the uncertainties
in the angular distribution of the disc emission will produce an
uncertainty
of the inferred inner disc radius of about 20% for the high quality
data by IXO![]() . We consider this value as
realistic.
. We consider this value as
realistic.
In the next step, we applied the NOAR radiation transfer code to achieve a self-consistent simulation of the outgoing spectrum without imposing an ad hoc formula for the emission angular distribution. In this paper we assumed a cold isotropically illuminated disc with a constant density atmosphere. We created new models for the KY suite, ptmmsckyl2cr and ptmmsckyl3cr. The results of NOAR computations of the cold disc are implemented in the ptmmsckyl2cr model, while the ptmmsckyl3cr model uses the angle-integrated tables over the entire range of emission directions. This enables us to include, a posteriori, the analytical formulae for directionality and check how precisely they reproduce the original angle-resolved calculations. We simulated the data using the preliminary IXO response matrix and we analysed them using the ptmmscpowerlaw + ptmmsckyl2cr model. Then we used the ptmmsckyl3cr model to test the analytical directionality approaches on these artificial data.
We found that, for a=0.998, none of the three
assumed cases of the directionality profile covered
the fiducial values for the spin and the inclination angle
within the ![]() contour line (see Figs. 17, 18).
The suitability of the particular directionality prescription
depends on the fiducial values of the spin and the inclination
angle. The limb brightening profile successfully minimises the
contour line (see Figs. 17, 18).
The suitability of the particular directionality prescription
depends on the fiducial values of the spin and the inclination
angle. The limb brightening profile successfully minimises the ![]() values for a=0.998 and i=30 deg,
but for a=0.7 and i=60 deg
it gives the worst fit
of all studied cases of the directionality laws.
values for a=0.998 and i=30 deg,
but for a=0.7 and i=60 deg
it gives the worst fit
of all studied cases of the directionality laws.
On the whole, we found that the isotropic angular dependence of the
emission intensity fits best.
Especially for higher values
of the black hole spin, the model with the limb darkening profile was
not able to reproduce the data:
the best fit ![]() value exceeds 5 for a=0.998 and i=30 deg,
which means a more than three times worse fit than using isotropic or
limb brightening directionality. The inclination angle was
underestimated by more than 1 deg.
value exceeds 5 for a=0.998 and i=30 deg,
which means a more than three times worse fit than using isotropic or
limb brightening directionality. The inclination angle was
underestimated by more than 1 deg.
This is an important result because much of the recent work on the iron lines, both in AGN and black hole binaries, has revealed a significant relativistic broadening near rapidly rotating central black holes (Miller 2007). In some of these works, the limb darkening law was employed and different options were not tested. The modelled broad lines are typically characterised by a steep power law in the radial part of the intensity across the inner region of the accretion disc, as in the mentioned MCG-6-30-15 observation. This behaviour has been interpreted as a case of a highly spinning compact source where the black hole rotational energy is electromagnetically extracted (Wilms et al. 2001). We conclude that the significant steepness of the radial part of the intensity also persists in our analysis, however, the exact values depend partly on the assumed angular distribution of the emissivity of the reflected radiation.
It should be noted that, in reality, the angular distribution of the disc emission is significantly influenced by the vertical structure of the accretion disc. However, our comprehension of accretion disc physics is still evolving. In recent years, several detailed models have been developed for irradiated black hole accretion discs in hydrostatic equilibrium (see e.g. Nayakshin 2000; Ballantyne et al. 2001; Rózanska et al. 2002). These models combine radiative transfer simulations with calculations of the hydrostatic balance in the stratified disc medium. Aside from reprocessing spectra, the models provide solutions for the vertical disc profile of the density, temperature, and ionisation fractions. In Goosmann et al. (2007) the effects of general relativity and advection on the disc medium were added.
In Nayakshin (2000), Goosmann et al. (2007), and Rózanska & Madej (2008) the reprocessed spectra are evaluated at different local emission angles. The shape and normalisation of these spectra depend on various model assumptions. Until we know in more detail how accretion discs work, it is hard to choose which is the ``correct'' reprocessing model. One could always argue that more physical processes and properties should be included in the radiative transfer simulations, such as the impact of magnetic fields, macroscopic turbulence, or different chemical compositions of the medium. Using the above-mentioned models for an accretion disc in hydrostatic equilibrium may then easily become computationally intense.
For the practical purpose of data analysis, however, the computation of large model grids is necessary, which requires sufficiently fast methods. This is why simple constant density models are most often used to analyse the observational data. In fact, Ballantyne et al. (2001) have shown that their reprocessing spectra for a stratified disc medium in hydrostatic equilibrium can be satisfactorily represented by spectra that are computed for irradiated constant density slabs. Therefore, we include in our present analysis the angular emissivity obtained from the modelling of neutral reprocessing in a constant density slab. For the purpose of this paper we have not discussed in any further detail the dependence on the ionisation parameter, which we expect to be rather important. It will be addressed in a future article.
We emphasise that the main strategy of the present paper is not intended to find the ``correct'' angular emissivity, as this is still beyond our computational abilities and understanding of all the physical processes shaping the accretion flow. Instead, we examined the three different prototypical dependencies which are mutually disparate (i.e., the limb-darkening, isotropic, and limb-brightening cases), applied in current data analysis, and which presumably reflect the range of possibilities. By including these different cases we mimic various uncertainties, such as those in the vertical stratification, and we estimate the expected error that these uncertainties can produce in the spin determinations. Further detailed computations of reprocessing models and the angular emissivity are needed in the future in order to understand its role in different spectral states of accreting black holes.
5 Conclusions
Black hole spin measurements using X-ray spectroscopy of relativistically broadened lines depend on the definition employed of the angular distribution of the disc emission. We studied three cases of the directionality profile - limb brightening, isotropic and limb darkening.
We found that isotropic directionality is consistent with our radiation transfer computations of the reflection spectra of an irradiated cold disc. This eliminates any need for ad hoc approximations to the limb-darkening profile. Using an improper directionality profile could impact on the other parameters inferred for the relativistic broad line model. Especially for the often used case of limb darkening, the radial steepness can interfere with the line parameters of the best-fit model by enhancing the red wing of the line.
Uncertainties in the precise position of the inner edge can further increase the error of the spin determination; however, it appears that the expected magnitude of these errors does not prevent us from setting interesting and realistic constraints on the spin parameter. Our present treatment of the problem is incomplete by neglecting the magnetohydrodynamical effects and their influence on the ISCO location. Future improvements in our theoretical understanding of the inner edge location are highly desirable and will help to improve the confidence in the determination of the model parameters.
We verified our conclusions by comparing them with the results based on an XMM-Newton long observation of MCG-6-30-15, and we found them to be broadly consistent. The expected improvement of sensitivity of the future IXO mission will significantly advance the reliability of the spin determinations.
AcknowledgementsThe authors are grateful for useful comments and suggestions from the participants of two ``FERO'' (Finding Extreme Relativistic Objects) workshops, held at the European Space Astronomy Centre (ESAC, Spain) and Laboratoire d'Astrophysique de Grenoble (France). J.S. acknowledges the doctoral student program of the Czech Science Foundation, ref. 205/09/H033, and the student research grant of the Charles University, ref. 33308. V.K. and M.D. appreciate the continued support from research grants of the Academy of Sciences (300030510), the Czech Science Foundation (205/07/0052), and the Ministry of Education international collaboration programme (ME09036). R.G. acknowledges the support from the ESA Plan for European Cooperating States (project No. 98040). The Center for Theoretical Astrophysics is operated under the Czech Ministry of Education, Youth and Sports programme LC06014.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17
- Asaoka, I. 1989, PASJ, 41, 763 [NASA ADS]
- Ballantyne, D. R., Ross, R. R., & Fabian, A. C. 2001, MNRAS, 327, 10 [CrossRef] [NASA ADS]
- Ballantyne, D. R., Vaughan, S., & Fabian, A. C. 2003, MNRAS, 342, 239 [CrossRef] [NASA ADS]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [CrossRef] [NASA ADS]
- Basko, M. M. 1978, ApJ, 223, 268 [CrossRef] [NASA ADS]
- Beckwith, K. 2005, in RAGtime 6/7: Workshops on black holes and neutron stars, ed. S. Hledík, & Z. Stuchlík (Opava: Silesian University), 29
- Beckwith, K., & Done, C. 2004, MNRAS, 352, 353 [CrossRef] [NASA ADS]
- Beckwith, K., Hawley, J. F., & Krolik, J. H. 2008, MNRAS, 390, 21 [CrossRef] [NASA ADS]
- Brenneman, L. W., & Reynolds, C. S. 2006, ApJ, 652, 1028 [CrossRef] [NASA ADS]
- Cadez, A., & Calvani, M. 2005, MNRAS, 363, 177 [CrossRef] [NASA ADS]
- Chandrasekhar, S. 1960, Radiative Transfer (New York: Dover)
- Cunningham, C. T. 1975, ApJ, 202, 788 [CrossRef] [NASA ADS]
- Czerny, B., Rózanska, A., Dovciak, M., Karas, V., & Dumont, A.-M. 2004, A&A, 420, 1 [EDP Sciences] [CrossRef] [NASA ADS]
- Dabrowski, Y., & Lasenby, A. N. 2001, MNRAS, 321, 605 [CrossRef] [NASA ADS]
- Dovciak, M., Karas, V., Martocchia, A., Matt, G., & Yaqoob, T. 2004a, in RAGtime 4/5: Workshops on black holes and neutron stars, ed. S. Hledík, & Z. Stuchlík (Opava: Silesian University), 33
- Dovciak, M., Karas, V., & Yaqoob, T. 2004b, ApJS, 153, 205 [CrossRef] [NASA ADS]
- Dovciak, M. 2004, Ph.D. Thesis (Prague: Charles University) [arXiv:astro-ph/0411605]
- Dumont, A.-M., Abrassart, A., & Collin, S. 2000, A&A, 357, 823 [NASA ADS]
- Fabian, A. C. 2008, Astron. Nachr., 329, 155 [CrossRef] [NASA ADS]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS]
- Fabian, A. C., Iwasawa, K., Reynolds, C. S., & Young, A. J. 2000, PASP, 112, 1145 [CrossRef] [NASA ADS]
- Fabian, A. C., Vaughan, S., Nandra, K., et al. 2002, MNRAS, 335, L1 [CrossRef] [NASA ADS]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics (Cambridge: Cambridge University Press)
- Fuerst, S. V., & Wu, K. 2004, A&A, 424, 733 [EDP Sciences] [CrossRef] [NASA ADS]
- Galeev, A. A., Rosner, R., & Vaiana, G. S. 1979, ApJ, 229, 318 [CrossRef] [NASA ADS]
- George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [NASA ADS]
- Ghisellini, G., Haardt, F., & Matt, G. 1994, MNRAS, 267, 743 [NASA ADS]
- Goodman, J. 2003, MNRAS, 339, 937 [CrossRef] [NASA ADS]
- Goosmann, R. W., Mouchet, M., Czerny, B., et al. 2007, A&A, 475, 155 [EDP Sciences] [CrossRef] [NASA ADS]
- Haardt, F. 1993, ApJ, 413, 680 [CrossRef] [NASA ADS]
- Karas, V. 2006, Astron. Nachr., 327, 961 [CrossRef] [NASA ADS]
- Karas, V., Huré, J.-M., & Semerák, O. 2004, Classical and Quantum Gravity, 21, 1 [CrossRef] [NASA ADS]
- Karas, V., Vokrouhlický, D., & Polnarev, A. G. 1992, MNRAS, 259, 569 [NASA ADS]
- Kato, S., Fukue, J., & Mineshige, S., eds. 1998, Black-Hole Accretion Disks (Kyoto: Kyoto University Press)
- Krolik, J. H. 1999, Active Galactic Nuclei: from the Central Black Hole to the Galactic Environment (Princeton: Princeton University Press)
- Laor, A. 1991, ApJ, 376, 90 [CrossRef] [NASA ADS]
- Li, L.-X., Zimmerman, E. R., Narayan, R., & McClintock, J. E. 2005, ApJS, 157, 335 [CrossRef] [NASA ADS]
- Martocchia, A., Karas, V., & Matt, G. 2000, MNRAS, 312, 817 [CrossRef] [NASA ADS]
- Matt, G., Perola, G. C., Piro, L., & Stella, L. 1992, A&A, 257, 63 [NASA ADS]
- McClintock, J. E., & Remillard, R. A. 2006, Black hole binaries, in: Compact Stellar X-ray Sources, ed. W. H. G. Lewin, & M. van der Klis (Cambridge: Cambridge University Press), 157
- Mihalas, D. 1978, Stellar Atmospheres (San Francisco: W. H. Freeman and Co.)
- Miller, J. M. 2007, ARA&A, 45, 441 [CrossRef] [NASA ADS]
- Miller, J. M., Reynolds, C. S., Fabian, A. C., Miniutti, G., & Gallo, L. C. 2009, ApJ, 697, 900 [CrossRef] [NASA ADS]
- Miller, L., Turner, T. J., & Reeves, J. N. 2008, A&A, 483, 437 [EDP Sciences] [CrossRef] [NASA ADS]
- Miniutti, G., Fabian, A. C., Goyder, R., & Lasenby, A. N. 2003, MNRAS, 344, L22 [CrossRef] [NASA ADS]
- Miniutti, G., Fabian, A. C., Anabuki, N., et al. 2007, PASJ, 59, 315
- Misner, C. W., Thorne, K. S., & Wheeler, J. A. 1973, Gravitation (San Francisco: W. H. Freeman and Co.)
- Nandra, K., O'Neill, P. M., George, I. M., & Reeves, J. N. 2007, MNRAS, 382, 194 [CrossRef] [NASA ADS]
- Nayakshin, S. 2000, ApJ, 540, L37 [CrossRef] [NASA ADS]
- Niedzwiecki, A., & Zycki, P. T. 2008, MNRAS, 386, 759 [CrossRef] [NASA ADS]
- Page, D. N., & Thorne, K. S. 1974, ApJ, 191, 499 [CrossRef] [NASA ADS]
- Peterson, B. M. 1997, An Introduction to Active Galactic Nuclei (Cambridge: Cambridge University Press)
- Pringle, J. E. 1981, ARA&A, 19, 137 [CrossRef] [NASA ADS]
- Rees, M. J. 1998, in Black Holes and Relativistic Stars, ed. R. M. Wald (Chicago: University of Chicago Press), 79
- Reynolds, C. S., & Fabian, A. C. 2008, ApJ, 675, 1048 [CrossRef] [NASA ADS]
- Reynolds, C. S., & Nowak, M. A. 2003, Phys. Rep., 377, 389 [CrossRef] [NASA ADS]
- Reynolds, C. S., Nowak, M. A., & Maloney, P. R. 2000, ApJ, 540, 143 [CrossRef] [NASA ADS]
- Reynolds, C. S., Brenneman, L. W., Wilms, J., & Kaiser, M. E. 2004, MNRAS, 352, 205 [CrossRef] [NASA ADS]
- Reynolds, C. S., Brenneman, L. W., & Garofalo, D. 2005, Ap&SS, 300, 71 [CrossRef] [NASA ADS]
- Rózanska, A., Dumont, A.-M., Czerny, B., & Collin, S. 2002, MNRAS, 332, 799 [CrossRef] [NASA ADS]
- Rózanska, A., & Madej, J. 2008, MNRAS, 386, 1872 [CrossRef] [NASA ADS]
- Shakura, N. I., & Syunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS]
- Stuchlík, Z., Slaný, P., Török, G., & Abramowicz, M. A. 2005, Phys. Rev. D, 71, 024037 [CrossRef] [NASA ADS]
- Svoboda, J., Dovciak, M., Goosmann, R. W., & Karas, V. 2008, in WDS'08 Proceedings of Contributed Papers, ed. J. Safránková, & J. Pavlu, 204 [arXiv:0901.0670]
- Thorne, K. S. 1974, ApJ, 191, 507 [CrossRef] [NASA ADS]
- Turner, T. J., & Miller, L. 2009, A&A Rev., 17, 47 [NASA ADS]
- Vaughan, S., & Fabian, A. C. 2004, MNRAS, 348, 1415 [CrossRef] [NASA ADS]
- Viergutz, S. U. 1993, A&A, 272, 355 [NASA ADS]
- Wilms, J., Reynolds, C. S., Begelman, M. C., et al. 2001, MNRAS, 328, L27 [CrossRef] [NASA ADS]
- Zakharov, A. F., & Repin, S. V. 2004, Adv. Space Res., 34, 2544 [CrossRef] [NASA ADS]
- Zycki, P. T., & Czerny, B. 1994, MNRAS, 266, 653 [NASA ADS]
Footnotes
- ... R. Goosmann
![[*]](/icons/foot_motif.png)
- Present address: Observatoire Astronomique de Strasbourg, 11 rue de l'Université, 67000 Strasbourg, France.
- ...
radius
![[*]](/icons/foot_motif.png)
- The gravitational radius is
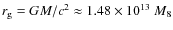 cm,
where the central
black hole mass is expressed in terms of
cm,
where the central
black hole mass is expressed in terms of
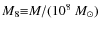 .
The velocity of the Keplerian orbital motion near a black hole is
.
The velocity of the Keplerian orbital motion near a black hole is
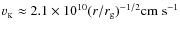 ,
and the corresponding orbital
period is
,
and the corresponding orbital
period is
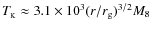 s
(here we neglect an order-of-unity correction factor due to the
relativistic frame-dragging effect which, however, will be included
later
in the paper).
s
(here we neglect an order-of-unity correction factor due to the
relativistic frame-dragging effect which, however, will be included
later
in the paper).
- ... 7.1.2
![[*]](/icons/foot_motif.png)
- http://xmm.esac.esa.int/sas
- ... version 6.4
![[*]](/icons/foot_motif.png)
- http://heasarc.gsfc.nasa.gov
- ... mission
![[*]](/icons/foot_motif.png)
- We used the current version of provisional response matrices available at http://ixo.gsfc.nasa.gov/science/responseMatrices.html for the glass core calorimeter, dated October 30, 2008. We used the energy resolution of 5 eV per bin.
- ... IXO
![[*]](/icons/foot_motif.png)
- Here, we refer to the inner disc radius instead of the spin because the latter is not as uniform a quantity as the corresponding ISCO radius to express the uncertainty simply as a percentage value. However, we still suppose that the inner edge of the line emitting region of the disc coincides with the marginally stable orbit. In realistic circumstances this assumption cannot be satisfied precisely, so it introduces an additional source of error. This has been extensively discussed (Beckwith et al. 2008). The magnitude of the resulting error was constrained most recently in work by Reynolds & Fabian (2008) who applied physical arguments about the emission properties of the inner flow. It is very likely that this discussion will have to continue for some time until the emission properties of the general relativistic MHD flows are fully understood.
All Tables
Table 1: The best-fit spin values inferred for the three cases of the limb darkening/brightening law, Eq. (8), for the ptmmsckyrline model.
Table 2: The best-fit spin and inclination angle values inferred for the three cases of the limb darkening/brightening law in the ptmmsckyl3cr model.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



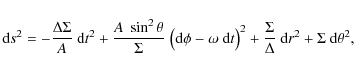
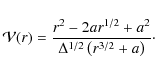
![\begin{displaymath}r_{\rm ms} = 3+Z_2-\big[\left(3-Z_1)(3+Z_1+2Z_2\right)\big]^{1 \over 2},
\end{displaymath}](/articles/aa/full_html/2009/43/aa11941-09/img52.png)