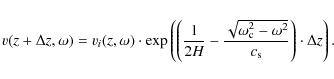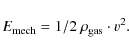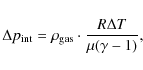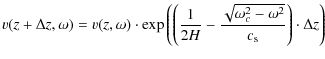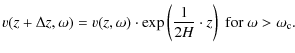| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 453 - 467 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200911851 | |
| Published online | 27 August 2009 | |
A&A 507, 453-467 (2009)
The energy of waves in the photosphere and lower chromosphere
I. Velocity statistics
C. Beck1,2 - E. Khomenko1,2 - R. Rezaei3 - M. Collados1,2
1 - Instituto de Astrofísica de Canarias (CSIC), Vía Lactéa, 38200 La
Laguna (Tenerife), Spain
2 - Departamento de Astrofísica, Universidad de La Laguna, 38205 La
Laguna (Tenerife), Spain
3 - Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104
Freiburg, Germany
Received 16 February 2009 / Accepted 13 August 2009
Abstract
Context. Acoustic waves are one of the primary
suspects besides magnetic fields for the chromospheric heating process
to temperatures above radiative equilibrium (RE).
Aims. We derived the mechanical wave energy as seen
in line-core velocities on disc centre to obtain a measure of
mechanical energy flux with height for a comparison with the energy
requirements in a semi-empirical atmosphere model, the
Harvard-Smithsonian reference atmosphere (HSRA).
Methods. We analyzed a 1-hour time series and a
large-area map of Ca II H spectra on the traces of propagating
waves. We analyzed the velocity statistics of several spectral lines in
the wing of Ca II H, and the line-core velocity of
Ca II H. We converted the velocity amplitudes into volume (![]()
![]() )
and mass energy densities (
)
and mass energy densities (![]() v2).
For comparison, we used the increase of internal energy (
v2).
For comparison, we used the increase of internal energy (![]()
![]() )
necessary to lift a RE atmosphere to the HSRA temperature
stratification.
)
necessary to lift a RE atmosphere to the HSRA temperature
stratification.
Results. We find that the velocity amplitude grows
in agreement with linear wave theory and thus slower with height than
predicted from energy conservation. The mechanical energy of the waves
above around ![]() km
is insufficient to maintain on a long-term average the chromospheric
temperature rise in the semi-empirical HSRA model. The intensity
variations of the Ca line core (
km
is insufficient to maintain on a long-term average the chromospheric
temperature rise in the semi-empirical HSRA model. The intensity
variations of the Ca line core (
![]() km) can, however, be
traced back to the velocity variations of the lowermost forming
spectral line considered (
km) can, however, be
traced back to the velocity variations of the lowermost forming
spectral line considered (
![]() km).
km).
Conclusions. The chromospheric intensity, and hence,
(radiation) temperature variations are seen to be induced by passing
waves originating in the photosphere. The wave energy is found to be
insufficient to maintain the temperature stratification of the
semi-empirical HSRA model above 500 km. We will in a following
paper of this series investigate the energy contained in the intensity
variations to see if the semi-empirical model is appropriate for the
spectra.
Key words: Sun: chromosphere - Sun: oscillations
1 Introduction
The chromospheric and coronal temperature rise above the photospheric temperature requires a heating mechanism in addition to radiative energy transport in the outer atmospheres of stars. The existence of chromospheres and coronae on the Sun and other stars is a well established fact, but still no generally accepted picture of the energy transport process responsible for their formation could be derived, especially for the corona (see e.g. Narain & Ulmschneider 1996).The scenarios suggested for the chromospheric heating process can be divided in three main categories: 1. field-free heating by the propagation of (acoustic) waves in a gas plasma; 2. indirect magnetic heating in which magnetic field lines act as ``catalyst'' without being destroyed in the process, and finally; 3. direct magnetic heating in which the reconnection of magnetic field lines leads to a conversion of magnetic to thermal energy, thereby removing the field lines.
In the first case, acoustic waves are generated by material (convective) motions as purely mechanical phenomenon (Musielak et al. 1994). The change of the atmospheric properties in the vertical direction in a gravitationally stratified medium leads to a ``steepening'' of vertically propagating waves producing a shock front. The energy of the propagating wave is dissipated in the ambient medium in and near the shock front, and hence, mechanical energy can be transported over some distance before conversion to thermal energy. Because of the stochastic nature of the excited acoustic waves, the energy transport process would not be continuous (e.g. Ulmschneider et al. 1978; Carlsson & Stein 1997; Ulmschneider 1971).
For the second case of indirect magnetic heating requiring the
presence of magnetic fields as a catalyst, two different scenarios are
possible in quiet Sun regions due to the specific topology of the
magnetic fields: the
(more) vertical strong network fields (Solanki
1993) and the (more)
inclined weaker internetwork (IN) fields
(Khomenko
et al. 2003; Lites
et al. 1996;
Khomenko
et al. 2005; Orozco
Suárez et al. 2007).
The network contains small-scale flux concentrations (some hundred kms)
in the form of isolated flux tubes or flux sheets. These concentrated
magnetic fields reside in the intergranular
lanes, because the interior of granules is swept free of magnetic
fields by
the directed convective flows as long as the ratio of mechanical to
magnetic
energy, ![]() ,
is above 1. The spatial extension of the flux
concentrations thus is strongly restricted in the photosphere by the
converging granular flows, but in the chromosphere the fields can
expand
because of the reduced outside gas pressure and the lack of directed
mass
flows (Steiner
et al. 1998; Keller
et al. 1990;
Hammer 1987;
Solanki
1993). This leads to a specific
topology with small-scale, mostly vertical fields in the photosphere
that get more inclined
in the chromosphere and fill the whole atmospheric volume at some
height. In
the layer of field expansion, a nearly horizontal canopy exists (Lites
et al. 2008; Jones
1985; Schaffenberger
et al. 2006). In this
topology, two possibilities exist to transfer energy from the
photosphere
upwards in or near the network. The first option is that acoustic waves
are generated outside
of the magnetic fields where some of them will propagate upwards as
before. The deposit of their mechanical energy is then not triggered by
the
steepening in the gravitationally stratified medium, but the contact of
the
propagating wave with (or transition into) the inclined magnetic field
lines
(Davila
& Chitre 1991; Chitre
& Davila 1991).
The second option is the
propagation of waves inside the magnetic fields
themselves. These waves
can come in different modes (fast and slow
magneto-acoustic waves, Alfven waves; see, e.g., Narain &
Ulmschneider
1996). They propagate along the field lines which with the topology of
solar
quiet Sun fields would yield automatically a predominantly vertically
propagation. The deposit of energy then would be governed by the
vertical
variation of atmospheric properties inside the field concentrations or
mode
conversion processes. The source of the magnetic-field-related
waves would again be the convective motions of the surrounding
granulation or p-mode oscillations that constantly buffet the magnetic
field concentrations in the photosphere (Hindman
& Jain 2008). The
indirect magnetic heating by waves inside the fields would tend to
affect a
larger volume in the chromosphere than in the photosphere, as the
magnetic field lines directly connect a large chromospheric volume with
its small photospheric counterpart.
,
is above 1. The spatial extension of the flux
concentrations thus is strongly restricted in the photosphere by the
converging granular flows, but in the chromosphere the fields can
expand
because of the reduced outside gas pressure and the lack of directed
mass
flows (Steiner
et al. 1998; Keller
et al. 1990;
Hammer 1987;
Solanki
1993). This leads to a specific
topology with small-scale, mostly vertical fields in the photosphere
that get more inclined
in the chromosphere and fill the whole atmospheric volume at some
height. In
the layer of field expansion, a nearly horizontal canopy exists (Lites
et al. 2008; Jones
1985; Schaffenberger
et al. 2006). In this
topology, two possibilities exist to transfer energy from the
photosphere
upwards in or near the network. The first option is that acoustic waves
are generated outside
of the magnetic fields where some of them will propagate upwards as
before. The deposit of their mechanical energy is then not triggered by
the
steepening in the gravitationally stratified medium, but the contact of
the
propagating wave with (or transition into) the inclined magnetic field
lines
(Davila
& Chitre 1991; Chitre
& Davila 1991).
The second option is the
propagation of waves inside the magnetic fields
themselves. These waves
can come in different modes (fast and slow
magneto-acoustic waves, Alfven waves; see, e.g., Narain &
Ulmschneider
1996). They propagate along the field lines which with the topology of
solar
quiet Sun fields would yield automatically a predominantly vertically
propagation. The deposit of energy then would be governed by the
vertical
variation of atmospheric properties inside the field concentrations or
mode
conversion processes. The source of the magnetic-field-related
waves would again be the convective motions of the surrounding
granulation or p-mode oscillations that constantly buffet the magnetic
field concentrations in the photosphere (Hindman
& Jain 2008). The
indirect magnetic heating by waves inside the fields would tend to
affect a
larger volume in the chromosphere than in the photosphere, as the
magnetic field lines directly connect a large chromospheric volume with
its small photospheric counterpart.
For the third case of direct magnetic heating by reconnection, again two options are possible. Recent observations (Lites et al. 2008; Steiner et al. 2008; Orozco Suárez et al. 2007) have shown that a large amount of weak (B<0.5 kG) horizontal magnetic flux is present inside of granules that seems to be swept upwards with the granular upflows. The existence of this magnetic flux was already suggested to explain the large differences of average magnetic flux between measurements using the Zeeman effect (sensitive to cancellation of sub-resolution opposite-polarity fields, around 20 G; Khomenko et al. 2005) and the Hanle effect (60-100 G, insensitive to cancellation; Trujillo Bueno et al. 2004). Martínez González et al. (2008) invoked turbulent stochastically oriented fields to explain the small amount of center-to-limb variation of linear and circular polarization signal amplitudes in IN areas. Lites et al. (2008) recently increased the Zeeman-based estimate of the flux amount to around 60 G, using seeing-free data from the Hinode satellite. The interaction of the weak horizontal flux with the magnetic canopy of the network or an increasing amount of reconnection between the horizontal fields with time could lead to an energy deposit in chromospheric layers, where the magnetic field energy would have been produced previously in the photosphere or below (cf. Ishikawa & Tsuneta 2009). The second option of magnetic heating would be the reconnection of network fields triggered by the constant buffeting and braiding of field lines due to the stochastic motion of the photospheric foot points (Peter et al. 2004; Narain & Ulmschneider 1996).
Recently, Fontenla et al. (2008) have suggested the Farley-Buneman instability as another possible source of chromospheric heating where cross-field motions of ionized material lead to an energy deposit in a small height layer. The horizontal magnetic fields again only act as a catalyst in the process, but the motion of the ionized plasma is thought to come mainly from convective motion rather than waves.
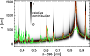
From the observational point of view, any heating process related to traveling waves is better accessible for detection than for example the direct magnetic heating processes (granted that they exist). The best studied chromospheric spectral lines, for which the importance of heating by waves, or at least, the influence of waves has been definitely established, are Ca II H and K at around 397 nm and 393 nm, respectively (Linsky & Avrett 1970). The Ca II H line allows for example to trace the signature of waves at different atmospheric heights due to its broad line wings where only a region of around 100-200 km vertical extent contributes to the intensity at each wavelength (see Fig. 1 or Fig. 5 of Rezaei et al. 2008). Carlsson & Stein (1997) have demonstrated that the (transient) bright grains seen in the core of H and K are due to acoustic waves forming shocks. It is at present strongly debated if (high-frequency) acoustic waves can supply enough energy to maintain a chromosphere (cf. Fossum & Carlsson 2005, and the vivid discussion spawned by it). The energy of the acoustic waves is, however, usually derived indirectly from measurements of intensity variations observed in (broad-band) imaging.
Beck
et al.
(2008) showed that the intensity of the emission peaks of
Ca II H has a clear phase relation to the intensity in the
line wing for a large range of oscillation frequencies,
i.e. brightenings in the core are preceded by the same in the
line wing (cf. also Liu 1974).
They also showed that the Ca spectra of network locations show
indications of transient events like the field-free![]() IN regions, in addition to
another contribution of steady emission. Thus, both magnetic network
and field-free IN are significantly influenced by the presence of
propagating waves.
IN regions, in addition to
another contribution of steady emission. Thus, both magnetic network
and field-free IN are significantly influenced by the presence of
propagating waves.
In this contribution, we want to investigate the energy of these propagating waves by a detailed analysis of spectra of Ca II H. The effect of the weak IN magnetic fields on the emission of Ca II H was estimated to be negligible by Rezaei et al. (2007). As the weak (or no) fields cover the largest part of the solar surface in the quiet Sun, a limitation to wave heating with neglect of direct magnetic heating processes seems reasonable. Note that the indirect magnetic heating processes are still included if they rely on propagating waves that have a LOS component at disc centre.
|
Figure 1: Normalized intensity contribution function of Ca II H in a LTE calculation. Red: center of contribution function. The green line was derived from phase differences (Beck et al. 2008). |
| Open with DEXTER | |

|
Figure 2: Average Ca II H spectrum with spectral lines 1 to 9 marked by vertical lines and intensity ranges OW, MW, H-index, and IW marked by pluses (+). |
| Open with DEXTER | |
After the description of the data sets used (Sect. 2), we determine the area fraction with signatures of magnetic fields in the chromosphere in Sect. 3, to check whether we can ignore field-related effects on the velocity statistics. We then investigate the relation between the line-core intensity and velocity of a set of spectral lines in Sect. 4, to exclude a convective origin for the patterns. We study the statistical properties of the LOS velocities and the relations between the spectral lines of different formation height and compare the mechanical energy contained in the waves with requirements of a semi-empirical atmosphere model in Sect. 5. The findings are summarized and discussed in Sect. 6. In a following paper of this series, we will investigate the energy in the intensity variations of the Ca II H line for comparison with the (mechanical) energy contained in the LOS velocities.
2 Observations, line selection, and overview maps
We used two observations taken in the morning of 24/07/2006. The first
is a
time series of around 1 h duration (see Beck
et al. 2008, for details, around
30 000 spectra); the second is a large-area map of
![]()
![]() extent (also around
30 000 spectra). The data sets were obtained with the
POlarimetric LIttrow Spectrograph (POLIS, Beck
et al. 2005b). In both cases, the Stokes vector
around 630 nm was obtained together with intensity profiles of
Ca II H. The slit width was 0
extent (also around
30 000 spectra). The data sets were obtained with the
POlarimetric LIttrow Spectrograph (POLIS, Beck
et al. 2005b). In both cases, the Stokes vector
around 630 nm was obtained together with intensity profiles of
Ca II H. The slit width was 0
![]() 5,
as was the step width of scanning. Spatial sampling along the slit was
0
5,
as was the step width of scanning. Spatial sampling along the slit was
0
![]() 29.
The integration time was 3.3 s per scan step for the
time-series, giving a cadence of around 21 s (repeated small
maps of 4 steps). As in Beck
et al. (2008), we only used the last step with
co-spatial spectra in 630 nm and Ca II H. For the large-area
map, the integration time per step was twice as large (6.6 s).
The data were reduced by the
respective set of routines for flat field and polarimetric correction
(Beck
et al. 2005a,b).
The noise level in the
polarization signal in continuum windows was around
29.
The integration time was 3.3 s per scan step for the
time-series, giving a cadence of around 21 s (repeated small
maps of 4 steps). As in Beck
et al. (2008), we only used the last step with
co-spatial spectra in 630 nm and Ca II H. For the large-area
map, the integration time per step was twice as large (6.6 s).
The data were reduced by the
respective set of routines for flat field and polarimetric correction
(Beck
et al. 2005a,b).
The noise level in the
polarization signal in continuum windows was around
![]() of the continuum intensity for the time-series and
of the continuum intensity for the time-series and
![]() for the large-area map. Using (pseudo
for the large-area map. Using (pseudo![]() -)continuum
intensity maps, the two wavelength ranges were aligned to be
co-spatial.
-)continuum
intensity maps, the two wavelength ranges were aligned to be
co-spatial.
Table 1: Line parameters.
Table 2: Line-core formation height ( 2nd column) and velocity amplitude ratios of left to right observed rms velocities, velocity of v1 propagated in linear wave theory, same for v5, and from the fit to the scatterplots.
![\begin{figure}
\par\includegraphics[width=7.2cm]{11851fg3.ps} %\end{figure}](/articles/aa/full_html/2009/43/aa11851-09/Timg34.png)
|
Figure 3:
Overview over the 1-hour time series. Left column, top to
bottom: continuum intensity at 630 nm ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm]{11851fg4.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa11851-09/Timg35.png)
|
Figure 4:
Same as Fig. 3
for the large-area scan. The grid lines have a spacing of 10
|
| Open with DEXTER | |
In the Ca II H data, we identified several of the photospheric spectral line blends in the line wing. We used a subset of 9 spectral lines with a sufficient line depth in our study (see Fig. 2), together with the two Fe I lines at 630.15 nm and 630.25 nm in the second channel. Table 2 lists all lines with line transition and adopted solar rest wavelengths. After deriving the velocity statistics of all of them, it became clear, however, that the lines 1 to 4 (and 630.15 nm and 630.25 nm) had nearly identical properties, as had the lines 5 to 7. This can be related directly to their line depth, and hence, their similar formation height (see Figs. 1 and 2 for lines 1 to 4 and 5 to 7). We then decided to used only lines 1, 5, 8, and 9 in the later evaluation. We attributed a ``line-core'' velocity to the displacement of the absorption core of Ca II H, but caution that its interpretation as a velocity is less secure than for the other spectral lines. It also turned out that the statistics of both time-series and large-area map were as good as identical, so we usually used quantities averaged over both data sets if not noted otherwise.
Figures 3
and 4 show
overview maps of the observations. The
right column shows the integrated unsigned Stokes
V signal (at top) to mark locations with
photospheric magnetic fields, and LOS velocities for the four chosen
spectral lines. No reasonable velocities (![]() km s-1) could be defined for the
Ca II H line core (line 8) on some locations because of the
absence of a well-defined absorption core. These locations tend to be
co-spatial to or close-by to strong photospheric magnetic fields and
often show a very strong H2v
emission peak with a plateau of constant intensity to the red of it,
making a definition of velocity arbitrary. The maximum polarization
degree
km s-1) could be defined for the
Ca II H line core (line 8) on some locations because of the
absence of a well-defined absorption core. These locations tend to be
co-spatial to or close-by to strong photospheric magnetic fields and
often show a very strong H2v
emission peak with a plateau of constant intensity to the red of it,
making a definition of velocity arbitrary. The maximum polarization
degree
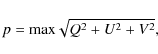
|
(1) |
can be used to estimate the presence and amount of photospheric magnetic flux. The fraction of pixels with a polarization degree p above 1% of
3 Influence of chromospheric magnetic field topology on Ca II H spectra
3.1 Indirect magnetic field signature in intensity
The direct measurement of the chromospheric magnetic fields in the lower chromosphere has not been possible up to now for a number of reasons. The spectral lines like Ca II H that form in a suited height range of the solar atmosphere are very deep and broad, leading to a low light level in observations of high spatial resolution. The magnetic fields are much weaker than in the photosphere; they induce only a weak polarization signal via the Zeeman effect. A detection of these weak polarization signals requires a high signal-to-noise ratio that is only possible with long integration times that, however, strongly reduce the spatial resolution again. Even if POLIS was designed for polarimetry in 630 nm and Ca II H, the latter could only be done for solar features with strong magnetic fields like pores or sunspots (see Beck et al. 2005b). Lacking the direct detection of chromospheric magnetic fields, often the bright structures seen in imaging observations of chromospheric lines are taken as tracers of the magnetic field lines.

|
Figure 5:
( 1st column, top to bottom): line-core velocity
of Ca II H, line-core intensity at 396.849 nm, intensity of H |
| Open with DEXTER | |
The map of the wavelength-integrated H-index in Fig. 4 shows the
strongest
brightenings at locations with photospheric polarization signal. If
one, however, reduces the averaged wavelength range significantly down
to a few wavelength points, the intensity patterns change drastically.
Figure 5
shows the FOV of the large-area map as seen in the very line core of
Ca II H (middle left). We averaged the
spectra over a fixed wavelength range of ![]() pm around the line core at 396.849 nm. This intensity map shows several
thin and elongated bright fibrils that originate from the patches with
strong photospheric polarization signal. An identification of such
fibrils with magnetic field lines is, however, not straightforward, if
one compares with the line-core velocity map (top left).
The intensity fibrils usually have a counterpart in the LOS velocity
map, implying that the apparent increase of intensity in the map taken
at a fixed wavelength is only due to a Doppler
shift of the absorption core. We marked two prominent example of
intensity fibrils with green parallelograms. The
intensity fibrils have a counterpart in the velocity map with exactly
the same morphology. This relation is not valid only for a few selected
case, but throughout the full FOV, as visualized by the yellow
contours that mark strong blueshifts of the Ca line core.
The shape of these velocity contours inside the green
rectangle is complementary to the bright fibrils in the
line-core intensity. To improve the visibility of the features, we
displayed the same line-core velocity and line-core intensity maps
twice in 1st and 2nd column, as the overlaid contour lines unavoidably
tend to hide the fine-structure. Leenaarts
et al. (2009) found a similar relation between
velocity and intensity for the Ca II IR line at
854 nm in observations and simulations.
pm around the line core at 396.849 nm. This intensity map shows several
thin and elongated bright fibrils that originate from the patches with
strong photospheric polarization signal. An identification of such
fibrils with magnetic field lines is, however, not straightforward, if
one compares with the line-core velocity map (top left).
The intensity fibrils usually have a counterpart in the LOS velocity
map, implying that the apparent increase of intensity in the map taken
at a fixed wavelength is only due to a Doppler
shift of the absorption core. We marked two prominent example of
intensity fibrils with green parallelograms. The
intensity fibrils have a counterpart in the velocity map with exactly
the same morphology. This relation is not valid only for a few selected
case, but throughout the full FOV, as visualized by the yellow
contours that mark strong blueshifts of the Ca line core.
The shape of these velocity contours inside the green
rectangle is complementary to the bright fibrils in the
line-core intensity. To improve the visibility of the features, we
displayed the same line-core velocity and line-core intensity maps
twice in 1st and 2nd column, as the overlaid contour lines unavoidably
tend to hide the fine-structure. Leenaarts
et al. (2009) found a similar relation between
velocity and intensity for the Ca II IR line at
854 nm in observations and simulations.
The apparent intensity increase in the line-core intensity map does not extend far beyond the locations of large photospheric polarization signal (blue and red contour lines, respectively), whereas for the H-index the brightest parts are to first order co-spatial with the polarization signal (middle right panel). The H-index is not sensitive to the Doppler shifts producing the bright fibrils due to its extended wavelength range, contrary to the line-core intensity map.
3.2 Direct signature of magnetic fields in spectral shape
Magnetic fields leave, however, also a more direct signature in the shape of the core of the Ca II H line profiles. A spectral pattern with double-peaked emission on the locations of the HTo determine the locations inside the FOV with a direct
magnetic field signature, we have analyzed the shape of the
Ca II H profiles with a routine similar to the one used by Rezaei
et al. (2008);
the routine searches for local intensity maxima in the spectrum.
Appendix A
explains the procedure in more detail and shows several examples of its
results on different profiles. With this routine the intensity of H![]() or H
or H![]() can only be determined when the peaks are present in the spectrum.
Following Rezaei
et al. (2007) we thus also determined the integrated
intensity in two 27 pm wide wavelength bands located
symmetrical around the line core that yield an estimate of H
can only be determined when the peaks are present in the spectrum.
Following Rezaei
et al. (2007) we thus also determined the integrated
intensity in two 27 pm wide wavelength bands located
symmetrical around the line core that yield an estimate of H![]() and H
and H![]() intensity for each profile.
intensity for each profile.
The bottom row of Fig. 5 shows the
results of both approaches that use the shape of the spectrum near the
line core. The appearance of spectra with both H![]() and H
and H![]() emission (green contour lines in the polarization
degree map at upper right) is basically
restricted to the locations with photospheric polarization signal, with
an additional extent of about 5
emission (green contour lines in the polarization
degree map at upper right) is basically
restricted to the locations with photospheric polarization signal, with
an additional extent of about 5
![]() distance around the
photospheric fields. In the rest of the FOV, either
single peaked profiles or those without intensity reversal are
prevailing. The area fraction of double-peaked profiles in the FOV is
13%, slightly larger than the estimate of photospheric magnetic field
coverage. The maps of H
distance around the
photospheric fields. In the rest of the FOV, either
single peaked profiles or those without intensity reversal are
prevailing. The area fraction of double-peaked profiles in the FOV is
13%, slightly larger than the estimate of photospheric magnetic field
coverage. The maps of H![]() and H
and H![]() using the 27 pm wavelength bands are displayed in the bottom
row, with an identical display range; they show that the H
using the 27 pm wavelength bands are displayed in the bottom
row, with an identical display range; they show that the H![]() emission is usually stronger than H
emission is usually stronger than H![]() ,
even on the locations with photospheric magnetic fields. For half of
the profiles with two emission peaks the asymmetry between H
,
even on the locations with photospheric magnetic fields. For half of
the profiles with two emission peaks the asymmetry between H![]() and H
and H![]() is above 10%. As discussed by Rezaei
et al. (2007) and Beck
et al. (2008), this is related to the fact that the
Ca profiles even above photospheric magnetic fields contain a
(dominant) contribution with the signature of acoustic shocks,
indicated by a pronounced H
is above 10%. As discussed by Rezaei
et al. (2007) and Beck
et al. (2008), this is related to the fact that the
Ca profiles even above photospheric magnetic fields contain a
(dominant) contribution with the signature of acoustic shocks,
indicated by a pronounced H![]() /H
/H![]() asymmetry (Beck
et al.
2008, their Fig. 17).
asymmetry (Beck
et al.
2008, their Fig. 17).
|
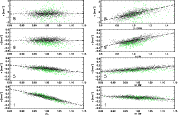
Figure 6: Left column: scatterplot of continuum intensity vs. LOS velocities. Dash-dotted lines show a linear regression fit. The data has been binned. Right column: scatterplot of the LOS velocities vs. their respective line-core intensities. The green pluses show the same for locations with two emission peaks in Ca II H. |
| Open with DEXTER | |
In total, the area fraction with chromospheric magnetic field signature
is small (![]() 15%),
half of the affected profiles show indications for the presence of
flows as well, and we are interested in the velocity statistics of all
type of waves regardless whether they are related to magnetic fields or
not. We thus assume that the magnetic field topology can be neglected
in the analysis of the velocity statistics of the full FOV. To
investigate whether the chromospheric magnetic fields have any effect
on the LOS velocities, we will use the statistics of all locations with
a double-peaked emission in the large-area map (light grey
area in bottom right of Fig. 5) later on
for a
comparison with the full FOV. These locations cover most of the
photospheric polarization signal as well, and thus indicate magnetic
fields at all heights.
15%),
half of the affected profiles show indications for the presence of
flows as well, and we are interested in the velocity statistics of all
type of waves regardless whether they are related to magnetic fields or
not. We thus assume that the magnetic field topology can be neglected
in the analysis of the velocity statistics of the full FOV. To
investigate whether the chromospheric magnetic fields have any effect
on the LOS velocities, we will use the statistics of all locations with
a double-peaked emission in the large-area map (light grey
area in bottom right of Fig. 5) later on
for a
comparison with the full FOV. These locations cover most of the
photospheric polarization signal as well, and thus indicate magnetic
fields at all heights.
We would like to also point out that the bright fibrils may nonetheless actually still outline chromospheric magnetic field lines. The reason for their appearance may be, however, not the presence of the field lines alone, but rather the passage of a wave or mass flows along them. This corresponds to one of the indirect magnetic heating scenarios discussed in the introduction.
4 Intensity-velocity relation
To obtain the intensity maps (outer wing (OW), middle wing (MW) and inner wing (IW), H-index) in the left columns of Figs. 3 and 4 that should correspond to approximately the same formation height as the LOS velocities, we averaged the intensity in the Ca II H spectrum over the line cores of the respective lines (pluses in Fig. 2). Even if the averaging extends over some spectral pixels, we will address the resulting intensity maps as the ``line-core intensity'' of the respective line in the following. The approach, however, only partly succeeded in the desired effect of producing intensity maps looking similar to the velocity maps. For the lowest forming spectral line (line 1, display rangeIn Fig. 6
we tried to quantify the relation between intensity and velocities for
two cases: velocity vs. the continuum intensity ![]() (left column) and velocity vs. the respective
line-core intensity of the spectral line (pluses in Fig. 2; right
column). The line-core intensities were normalized with
their mean values. To improve the visibility of the dependence, the
data were binned in the same way as in Beck
et al. (2007). We took the pairs of corresponding (I,
v) points, sorted the intensity values into fifty
equidistant bins
(left column) and velocity vs. the respective
line-core intensity of the spectral line (pluses in Fig. 2; right
column). The line-core intensities were normalized with
their mean values. To improve the visibility of the dependence, the
data were binned in the same way as in Beck
et al. (2007). We took the pairs of corresponding (I,
v) points, sorted the intensity values into fifty
equidistant bins ![]() ,
and then used the average values
,
and then used the average values
![]() and
and
![]() in each bin.
in each bin.
For lines 8 and 9, no correlation with the continuum intensity
remains, whereas line 5 and line 1 show a weak and strong
anti-correlation, respectively, with the granulation pattern of ![]() .
Comparing the velocities to the respective line-core intensities,
already line 5 shows a reversal of the relation, with red-shifts
corresponding to increased intensities. Restricting the FOV to only the
locations with double-peaked emission gives essentially the same
relationship between velocities and intensities (green pluses).
.
Comparing the velocities to the respective line-core intensities,
already line 5 shows a reversal of the relation, with red-shifts
corresponding to increased intensities. Restricting the FOV to only the
locations with double-peaked emission gives essentially the same
relationship between velocities and intensities (green pluses).
A second peculiarity of the velocity and intensity maps relates to the spatial scales. Whereas for the velocities the spatial scales of structures in the large-area map (Fig. 4) increase to a more diffuse pattern, this trend is less prominent in the line-core intensity maps. Along the temporal axis of the time series (Fig. 3), the velocity patterns do not turn diffuse with height. This should be related to the frequency shift of the oscillations with height (see Appendix B) that lead to a compression of the wave pattern in the temporal domain.
In brief, both the intensity and the velocity maps other than for line 1 do not show any clear relation to the granulation pattern, implying that they are dominated by processes other than the convective motions. The spatial structures in the velocity maps show a typical spatial scale that is larger than individual granules and that could be part of the inverse granulation pattern (e.g. Rutten et al. 2004). These authors concluded that the inverse granulation pattern should be a mixture of convection reversal and a contribution from gravity waves whose relative importance increases with height. The little visual correspondence between velocity and intensity maps then again supports the claim that line 5 and those higher up are dominated processes unrelated to convection.
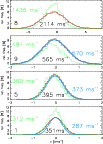
|
Figure 7: Histograms of LOS velocities. Spectral line and width of the Gaussian fit ( red line) are indicated in each plot. The blue curves and values at right refer to the Fourier-filtered velocity maps of the time-series; the green curves and the values at left are for locations with two emission peaks in Ca II H. |
| Open with DEXTER | |
| Figure 8:
Fourier-filtered velocities of line 1 and 5 of the
time-series. The grid lines have a spacing of 10
|
|
| Open with DEXTER | |
5 Statistics of LOS velocities with height
The histograms of the line-core velocities in Fig. 7 clearly show that the width of the velocity distribution increases with height, as the lines have been sorted according to their formation heights given in Table 2. We made a Gaussian fit to the distributions to define the root-mean-square (rms) value![\begin{figure}
\par\includegraphics[width=9cm,clip]{11851fg9.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa11851-09/Timg49.png)
|
Figure 9: Relation between co-spatial velocities of lines 1, 5, 9 and 8 in the time-series. Top to bottom: scatterplots of v1 vs. v5, v1 vs. v9, and v1 vs. v8. Black dots: all data points; red: after binning. Blue line: linear regression to the binned data. The slope is given in the upper left corner in each scatterplot. |
| Open with DEXTER | |
Up to this point, three arguments show that the patterns in the velocity maps cannot be of convective origin:
- the low-forming lines have been Fourier-filtered for the low-frequency part which removes the granular contribution; only the filtered time-series is used for lines 1 and 5;
- the velocity maps for lines 9 and 8 have no correlation to the granulation pattern;
- all lines are dominated by oscillatory behavior with recurrent positive and negative velocities with periods shorter than granular time scales (compare Figs. 3 and 8).
The question of the wave energy during the propagation through
the atmosphere is related to the growth of the velocity amplitude of
the vertical LOS velocities with height that has to compensate the
reduction of gas density. Figure 9
compares co-spatial and co-temporal velocities in the time-series. To
obtain the velocities co-temporal to line 1, the velocity maps
of line 5, 9, and 8 were shifted in time by 5 s, 10 s
and 59 s, respectively. Figure 10 shows
that
with these temporal shifts, the velocities of the lines at one location
along the slit are well in phase for lines 1, 5, and 9. For
the Ca line core, the agreement of phase is worse, but for most of the
large-amplitude velocity excursions the 1-min shift gives a good
agreement (e.g., at t = 5, 32, or 40 min). For the
co-spatial and co-temporal velocity maps, we did scatterplots vs. the
velocity of line 1 (Fig. 9). The
different
lines show a strong correlation with the lowermost forming
line 1 with an ever increasing velocity amplitude ratio. The
ratio was determined by a linear regression fit to binned values of the
scatterplot (red dots). The obtained ratio was
then used to scale up the velocity of line 1 to the velocities
to be expected for the other lines (colored crosses
in Fig. 10).
For line 5 and line 9, the usage of a constant
scaling factor reproduces the actual observed velocity amplitudes well,
regardless of the period of the velocity oscillations. For the Ca line
core, the scaling coefficient from the scatterplot (![]() 1) leads to
much too small predicted velocities; we thus scaled line 1 up
with the ratio of the rms velocities instead (
1) leads to
much too small predicted velocities; we thus scaled line 1 up
with the ratio of the rms velocities instead (![]() 7). This reproduces only the range of observed Ca
line core velocities; no close match in phase or amplitude at a given
time is achieved. The reduction of correlation between v1 and v8 in
comparison to the other lines could be due to two main sources: the
assumption of a constant time lag between the two quantities, and the
fact that the position of the Ca absorption core is not the optimal
tracer of the dynamical evolution because of the NLTE conditions in the
formation of both the emission peaks and the very line core. The
relation is clearer between v1 and chromospheric intensities averaged
over a wide wavelength range, as will be discussed later in
Sect. 6.
All velocity oscillations of line 1, however, generally appear
in the other lines with a time-lag and an amplitude increase.
7). This reproduces only the range of observed Ca
line core velocities; no close match in phase or amplitude at a given
time is achieved. The reduction of correlation between v1 and v8 in
comparison to the other lines could be due to two main sources: the
assumption of a constant time lag between the two quantities, and the
fact that the position of the Ca absorption core is not the optimal
tracer of the dynamical evolution because of the NLTE conditions in the
formation of both the emission peaks and the very line core. The
relation is clearer between v1 and chromospheric intensities averaged
over a wide wavelength range, as will be discussed later in
Sect. 6.
All velocity oscillations of line 1, however, generally appear
in the other lines with a time-lag and an amplitude increase.
The statistical properties of the lines are summarized in the upper
part of Fig. 11:
the extreme velocities increase from ![]() 1.5 km s-1
in line 1 to above
1.5 km s-1
in line 1 to above ![]() 8 km s-1
for the line core of Ca II H, the rms value increases from
0.3 km s-1 to
2 km s-1.
8 km s-1
for the line core of Ca II H, the rms value increases from
0.3 km s-1 to
2 km s-1.
![\begin{figure}
\includegraphics[width=9cm,clip]{11851f10.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa11851-09/Timg51.png)
|
Figure 10: Example of LOS velocities at a fixed position along the slit in the time-series. Black, blue, green and red lines show the velocity of lines 8, 9, 5, and 1, displaced by +4, 0, -2, -3 km s-1. The dashed lines mark the respective zero velocity. The colored crosses result from multiplying v1 with the coefficients of Fig. 9 for v5 and v9, and the ratio of the rms velocities for v8, respectively. |
| Open with DEXTER | |
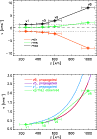
|
Figure 11:
Top: statistical properties of LOS
velocities: minimum, maximum and rms value ( red, black, green).
The horizontal dotted lines are at |
| Open with DEXTER | |
To investigate the consistency of the observed velocities, we
propagated the velocities in height using the linear perturbation
approximation for wave propagation. We used the Fourier transform of
the velocity maps of lines 1, 5 and 9, and propagated the
velocities upwards using (Mihalas
& Weibel Mihalas 1984)
A constant scale height of H = 100 km was used, the sound speed
Comparison to a semi-empirical atmosphere model.
All velocities can be converted to a mechanical energy equivalent byMore precisely,
For the comparison with a semi-empirical solar atmosphere
model, we chose the temperature enhancement over radiative equilibrium
(RE) temperature as the quantity that should correspond to the volume
energy density. RE conditions can be thought of as providing a lower
limit to the temperature for the upper photosphere and low chromosphere
on a long-term average because of the pervasive radiation field from
continuum layers that constantly tries to re-heat plasma above to RE
temperature (e.g. Cheung
et al. 2007;
Ulmschneider
et al. 1978). We selected the HSRA atmosphere model (Gingerich
et al. 1971),
because the differences between the various semi-empirical models
(e.g., in Fontenla
et al. 2006; Gingerich
et al. 1971;
Vernazza
et al. 1981; Avrett
2007; Fontenla
et al. 1999) on the location and strength of the
chromospheric temperature rise are minor in the present context. To
obtain a RE atmosphere model, we exchanged the temperature
stratification of the HSRA atmosphere model with that of the
Holweger-Mueller model (HOLMUL, Holweger
& Mueller 1974) for all optical depths smaller than
log ![]() km).
The HOLMUL model roughly corresponds to an atmosphere in RE condition
(see Fig. 13
for a plot of all stratifications). As the semi-empirical atmosphere
models like HSRA are assumed to correspond to a temporal and spatial
average of atmospheric conditions, we will do the comparison to the
velocity distributions, because their range
should cover the average status predicted by the semi-empirical model.
km).
The HOLMUL model roughly corresponds to an atmosphere in RE condition
(see Fig. 13
for a plot of all stratifications). As the semi-empirical atmosphere
models like HSRA are assumed to correspond to a temporal and spatial
average of atmospheric conditions, we will do the comparison to the
velocity distributions, because their range
should cover the average status predicted by the semi-empirical model.

|
Figure 12:
Top panel: mass energy density,
|
| Open with DEXTER | |
We convert the temperature enhancement over RE conditions, ![]() ,
to an enhancement of the internal energy density,
,
to an enhancement of the internal energy density,
![]() by
by
where
For the comparison of
![]() with the mechanical energy of the waves, it actually is not necessary
to take the gas density
with the mechanical energy of the waves, it actually is not necessary
to take the gas density ![]() into account.
into account. ![]() in chromospheric layers usually comes with a large uncertainty: if the
density is derived from the condition of hydrostatic equilibrium, it
strongly depends on the assumed temperature stratification. One can,
however, simply compare 1/2 v2
with
in chromospheric layers usually comes with a large uncertainty: if the
density is derived from the condition of hydrostatic equilibrium, it
strongly depends on the assumed temperature stratification. One can,
however, simply compare 1/2 v2
with ![]() .
Both equations yield a (mass) energy density in J kg-1.
Consider for example the Ca line-core velocity and the corresponding
enhancement of HSRA over RE at 1000 km.
.
Both equations yield a (mass) energy density in J kg-1.
Consider for example the Ca line-core velocity and the corresponding
enhancement of HSRA over RE at 1000 km.
![]() is around 9600 and
is around 9600 and ![]() K;
thus, the internal energy enhancement is
K;
thus, the internal energy enhancement is
![]() J kg-1.
This is to be compared with
J kg-1.
This is to be compared with
![]() J kg-1
from the LOS velocity, which is an order of magnitude smaller.
J kg-1
from the LOS velocity, which is an order of magnitude smaller.
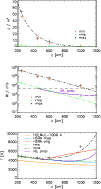
|
Figure 13:
Volume energy density, |
| Open with DEXTER | |
When the gas density is multiplied to obtain a volume energy
density, the trend with height is reversed. We used a gas density with
height that corresponds to our RE temperature stratification put to
hydrostatic equilibrium; the density is close to that of the HSRA model
up to z = 1000 km. As the histograms and
the value required to obtain the HSRA would simply be scaled by the
same coefficient, the same result as in Fig. 12
would result for the lower panels. We thus have used the plot of volume
energy density vs. height (upper panel of
Fig. 13)
differently. We made a (manual) fit to the exponentially decreasing
volume energy density with height to reproduce the observed values (dash-dotted
lines). For both extreme and rms velocities, a reasonable
agreement can be achieved with an exponential decay
![]() with a
with a ![]() 185 km
(middle panel). For easier comparison with other
work, we converted the volume energy density here to an acoustic flux
density by multiplying with a constant sound speed of
185 km
(middle panel). For easier comparison with other
work, we converted the volume energy density here to an acoustic flux
density by multiplying with a constant sound speed of
![]() 7 km s-1. We overplotted the
curve that comes from propagating the velocity of line
5 upwards (purple line). The horizontal
dashed line denotes 4.3 kW m2 s-1
as a reference of chromospheric radiative losses (Vernazza
et al. 1976);
for z > 500 km, the energy
contained in
the LOS velocities falls short of it. If the exponential decay curves
of the upper panel are converted to the corresponding temperature
enhancement over RE temperatures by equating Eqs. (3) and (4), the extreme
velocities would again be more than sufficient for the HSRA
requirements, whereas the rms velocities would at least suffice for an
increase of 500-1500 K above RE temperatures for heights above
1200 km.
7 km s-1. We overplotted the
curve that comes from propagating the velocity of line
5 upwards (purple line). The horizontal
dashed line denotes 4.3 kW m2 s-1
as a reference of chromospheric radiative losses (Vernazza
et al. 1976);
for z > 500 km, the energy
contained in
the LOS velocities falls short of it. If the exponential decay curves
of the upper panel are converted to the corresponding temperature
enhancement over RE temperatures by equating Eqs. (3) and (4), the extreme
velocities would again be more than sufficient for the HSRA
requirements, whereas the rms velocities would at least suffice for an
increase of 500-1500 K above RE temperatures for heights above
1200 km.
Thus, in this comparison of mechanical energy contained in mass motions and the enhancement of internal energy required to lift an RE model to the original HSRA model, the mass motions are insufficient to supply the necessary energy. Our interpretation of all line-core shifts as being due to mass motions corresponds to an upper limit, as some of the shifts of the blends inside the Ca II H line may also actually have been due to temperature effects.
6 Summary and discussion
We derived the mechanical energy contained in the LOS velocities of various spectral lines that form in different geometrical heights in the solar atmosphere. The lines could be grouped into four height ranges of which only the lowest two show a clear relation (anti-correlation) to the granulation pattern in the continuum intensity. When comparing the line-core velocities to the corresponding line-core intensities, a positive correlation is found for all lines but the lowest forming one: red-shifts are related to intensity increases. The amplitude of the velocity oscillations increases with height, both for the whole velocity distributions and co-spatial (but not co-temporal) velocities in a time-series, in good agreement with theoretical predictions from linear wave theory. When the wave energy is converted to a corresponding temperature enhancement of the internal energy, it falls short of the requirements of lifting a RE atmosphere model to the original HSRA model with a chromospheric temperature rise. The distributions of the LOS velocities barely reach these requirements for the most extreme, and thus rare, velocities. A fit of an exponential decay to the mechanical energy density with height yields a possible heating and a temperature increase in the chromospheric layers of around 500 to 1500 K, which is significantly less than in the HSRA atmosphere model.Magnetic field influence on the Ca II H line core.
The area fraction of Ca II H profiles that show signatures of
magnetic fields is around 15% (Sect. 3). The
rms
velocities of all spectral lines considered are reduced on these
locations, most prominent for the Ca II H line core
(Sect. 5).
The line-core velocity of Ca also shows a considerable contribution at
low temporal frequencies (![]() mHz)
that is not present in this way for the other lines (Appendix B). The velocity
amplitudes are constant to first order with oscillation frequency (see
Fig. B.4).
mHz)
that is not present in this way for the other lines (Appendix B). The velocity
amplitudes are constant to first order with oscillation frequency (see
Fig. B.4).

|
Figure 14:
Left to right: Ca II H line-core
velocity, low-frequency contributions, integrated absolute circular
polarization signal. Velocities are displayed in a |
| Open with DEXTER | |
The importance of this field-related velocity component should increase with height in the atmosphere when the magnetic field lines spread out to fill the whole chromospheric volume. In the formation height of Ca II H, only the locations with also photospheric polarization signal are affected which suggests that the Ca line in quiet Sun forms below the canopy layer that marks the transition from a basically field-free to fully magnetized atmosphere.
Range of temperature variations.
If the velocity distributions are converted to their (relative) temperature equivalent, the extreme velocities of the Ca line core lead to a sufficient enhancement of around 2000 K above RE temperature to reach the HSRA temperature values. The distributions span the full range from 0 to the 2000 K, implying a variation of the temperature by several hundred K. For line 9 at around 600 km height, the temperature variation range already covers around 1000 K. This is at odds with the claim of Avrett et al. (2006) that temperature variations in the low chromosphere should not exceedRelation between chromospheric intensity and LOS velocities.
The line-core position of Ca II H may be an unsuited tracer of the chromospheric dynamics due to the complex line formation. We thus use the intensity close to and in the line core of Ca II H to discuss the causal relationship between chromospheric intensity and photospheric velocities. Most of the LOS velocity oscillations have temporal frequencies below the commonly assumed cut-off frequency ofThat the frequency of the oscillations is of minor importance
for the wave propagation, is also demonstrated in Fig. 15,
where the
same spectra and LOS velocities as used for Fig. 9 are
displayed,
but without applying any temporal shifts to obtain co-spatial
velocities that are in phase. The position along the slit was at y
= 9
![]() 3;
Fig. 3
shows that there was a distance of at least 2-3
3;
Fig. 3
shows that there was a distance of at least 2-3
![]() to the nearest location with
detected photospheric flux. In addition to
the line-core velocities of lines 1 (orange line),
5 (green), 9 (blue), and 8 (black),
we plotted also the intensity at 396.7 nm, around 0.15 nm distance from
the Ca line core, and at the H2V
emission peak (upper two lines). The intensity
values were referenced vs. the Ca II H profile that resulted
from the RE temperature stratification in a LTE calculation with the
SIR code (Ruiz Cobo
& del Toro Iniesta 1992). The line-core velocity of
Ca II H, v8, was treated with a running mean over three time
steps to reduce the scatter and improve the visibility of the velocity
extrema.
to the nearest location with
detected photospheric flux. In addition to
the line-core velocities of lines 1 (orange line),
5 (green), 9 (blue), and 8 (black),
we plotted also the intensity at 396.7 nm, around 0.15 nm distance from
the Ca line core, and at the H2V
emission peak (upper two lines). The intensity
values were referenced vs. the Ca II H profile that resulted
from the RE temperature stratification in a LTE calculation with the
SIR code (Ruiz Cobo
& del Toro Iniesta 1992). The line-core velocity of
Ca II H, v8, was treated with a running mean over three time
steps to reduce the scatter and improve the visibility of the velocity
extrema.
It can be clearly seen in Fig. 15 that
in 90%
of the cases an intensity increase of H2V
is preceded by the same at 396.7 nm. The increase at 396.7 nm
can again be traced back in time to a velocity oscillation of initially
line 1. In some cases, the velocity oscillations of
lines 1, 5, and 9 appear almost in phase (e.g., at t
= 31 min), but still trigger an increase of intensity at
396.7 nm and H2V
with a time-lag, indicating a wave propagation with a photospheric
origin (see also Fig. B.2).
The inclined dashed lines indicate the
propagation from a velocity oscillation of line 1 to an
intensity increase of H2V in
around 1 min. Even if most of the power is found below 5 mHz, still
exactly these waves have a signature in the chromosphere in H2V
emission. If one would attribute a dominant period to the wave pattern
of line 1 in Fig. 15, it
would
be closer to 5 min than 3 min (see also Fig. B.1). This is
in
some conflict with Carlsson
& Stein (1997) who found in their simulations of wave
propagation driven by a photospheric piston that ``runs with
only low frequencies (![]() mHz) do
not produce grains''. This could be reconciled with the
present observations by the fact that the definition of a ``grain''
comes from the common usage of broad-band filter imaging and refers to
stronger cases of shocks. The long-period oscillations of the velocity
of line 1 lead to a transient intensity reversal in the Ca
line core that would most probably not qualify as bright ``grain'' in
most cases.
mHz) do
not produce grains''. This could be reconciled with the
present observations by the fact that the definition of a ``grain''
comes from the common usage of broad-band filter imaging and refers to
stronger cases of shocks. The long-period oscillations of the velocity
of line 1 lead to a transient intensity reversal in the Ca
line core that would most probably not qualify as bright ``grain'' in
most cases.

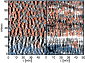
|
Figure 15:
Top: spectra at one fixed location along
the slit with time. The short vertical bars at bottom
denote lines 1, 5, 8 and 9, those at top
396.7 nm and the H |
| Open with DEXTER | |
|
Figure 16: Left: v1 of the time-series, right: H-index. Red contours: red-shifts, blue contours: low H-index. |
| Open with DEXTER | |
Energy flux at different heights.
The energy flux with height of Fig. 13 shows a clear decrease throughout the whole height range. The absolute amount is very similar to the numbers given by Straus et al. (2008, their Fig. 3) who, however, applied a severe filtering in the Fourier space and used only the velocities corresponding to gravity waves. Similarly to the latter authors, we also find that the mechanical energy at around z = 500 km is of the same order as the chromospheric radiative losses. If the formation height of line 9 is correctly assumed to be above 500 km, the mechanical energy seen in the velocity of this line, however, already falls below the common chromospheric energy requirements.What amount of mechanical energy may be hidden from the
observations ? In the time-series, one could invoke the temporal
sampling that excludes all oscillations with periods below ![]() 40 s.
The large-area map for comparison is a stochastic sample of waves at an
arbitrary phase. The velocity histograms of both types of observations
were found to be equivalent, thus, the temporal sampling of
21 s does not seem to have an influence on the observed
velocities. This leaves on the one hand the spatial resolution, and on
the other the extension of the height layers that contribute to the
respective line-core velocity. From the overview maps of the large-area
scan it can be seen that the velocity patterns in the higher layers are
spatially resolved, because they are more extended than the structures
in the intensity maps; the typical size of structures also exceeds that
of the clearly resolved granulation pattern. The typical width of
intensity contribution functions in the Ca line wing is around
100-200 km (see Fig. 1).
Assuming
that a similar height range contributes to each line-core velocity and
a sound speed of
40 s.
The large-area map for comparison is a stochastic sample of waves at an
arbitrary phase. The velocity histograms of both types of observations
were found to be equivalent, thus, the temporal sampling of
21 s does not seem to have an influence on the observed
velocities. This leaves on the one hand the spatial resolution, and on
the other the extension of the height layers that contribute to the
respective line-core velocity. From the overview maps of the large-area
scan it can be seen that the velocity patterns in the higher layers are
spatially resolved, because they are more extended than the structures
in the intensity maps; the typical size of structures also exceeds that
of the clearly resolved granulation pattern. The typical width of
intensity contribution functions in the Ca line wing is around
100-200 km (see Fig. 1).
Assuming
that a similar height range contributes to each line-core velocity and
a sound speed of ![]() km s-1
leads to the fact that waves with wavelengths below <200 km,
periods below 28 s, and frequencies larger than 35 mHz cannot
be observed. The power at frequencies above 20 mHz can be assumed to be
negligible for chromospheric heating (Fig. B.1; Fossum
& Carlsson 2005; Carlsson
et al. 2007),
but Wedemeyer-Böhm
et al. (2007) and Kalkofen
(2007) have cautioned that this question crucially depends on
the spatial resolution of the data used. On the lower end of the
frequency spectrum, many authors in the past did not consider
oscillations below a generic cutoff frequency of around 5 mHz, whereas
there are some indications that even these waves propagate vertically (Beck
et al. 2008; Straus
et al. 2008;
Centeno
et al. 2006; Khomenko
et al. 2008,
or the present Fig. 15)
and thus could contribute significantly to the chromospheric energy
balance.
km s-1
leads to the fact that waves with wavelengths below <200 km,
periods below 28 s, and frequencies larger than 35 mHz cannot
be observed. The power at frequencies above 20 mHz can be assumed to be
negligible for chromospheric heating (Fig. B.1; Fossum
& Carlsson 2005; Carlsson
et al. 2007),
but Wedemeyer-Böhm
et al. (2007) and Kalkofen
(2007) have cautioned that this question crucially depends on
the spatial resolution of the data used. On the lower end of the
frequency spectrum, many authors in the past did not consider
oscillations below a generic cutoff frequency of around 5 mHz, whereas
there are some indications that even these waves propagate vertically (Beck
et al. 2008; Straus
et al. 2008;
Centeno
et al. 2006; Khomenko
et al. 2008,
or the present Fig. 15)
and thus could contribute significantly to the chromospheric energy
balance.
Another source of energy that could be missing in the observations are wave-related processes that have no line-of-sight component at disc centre. This will apply mainly to wave modes of the magnetic field lines. The field lines of strong photospheric flux concentrations are close to vertical, and several wave modes like sausage or kink modes have their main component perpendicular to the field lines. These waves then will only contribute to the statistical analysis of the LOS velocities with their small vertical component and remain otherwise undetected.
7 Conclusions
We have analyzed the mechanical energy contained in line-of-sight velocity oscillations of spectral lines forming at different heights. The mechanical energy transported by the waves falls short of the requirements to lift a radiative equilibrium model atmosphere to one of the commonly used semi-empirical temperature stratifications with a strong chromospheric temperature rise. We find, however, that the chromospheric intensity variations are coupled to the LOS velocity of the lowermost forming spectral line, with a time-lag of around 1 min, and thus are triggered by photospheric motions. In the second paper of this series we will thus investigate, if the energy in the intensity variations, and in the intensity profiles as a whole, agree at all with the semi-empirical model. AcknowledgementsR.R. acknowledges support by the Deutsche Forschungsgemeinschaft under grant SCHM 1168/8-2. This research has been funded by the Spanish Ministerio de Educación y Ciencia through project AYA2007-63881 and AYA2007-66502. The VTT is operated by the Kiepenheuer-Institut für Sonnenphysik (KIS) at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias (IAC). The POLIS instrument has been a joint development of the High Altitude Observatory (Boulder, USA) and the KIS.
Appendix A: Analysis of Ca II H profile shape
The Ca II H line profile can show any number between zero or up to three intensity reversals near the line core. The number of reversals can be used for a qualitative estimate of which processes have led to the emission pattern. A symmetric double-peaked shape with equal intensity in blue (We used a similar routine as Rezaei
et al. (2008) to determine the number of emission
peaks in the line core. The routine passes in wavelength through every
profile, and searches for local maxima whose intensity exceeds that of
the neighboring wavelength points. Due to the presence of noise, the
spectra are treated with a running mean over five wavelengths points
prior to the search for local maxima. Figure A.1 shows
nine
randomly picked profile examples. The solid vertical lines
mark the locations of the intensity reversals found in each profile.
The uppermost right profile is a typical example
for the presence of a shock front in the lower atmosphere (lifted wings
at H![]() and H
and H![]() );
the lowermost left one for a shock in the upper
atmosphere (H
);
the lowermost left one for a shock in the upper
atmosphere (H![]() emission). The lowermost middle panel shows a
case of a reversal-free profile with a low H-index (see Rezaei
et al. 2008).
emission). The lowermost middle panel shows a
case of a reversal-free profile with a low H-index (see Rezaei
et al. 2008).

|
Figure A.1:
Examples of the analysis of the number of reversals in Ca II H
core. Dashed lines mark the analyzed wavelength
range. Dotted vertical line: Ca II H
core position. Solid vertical: locations of
intensity reversals. Wavelengths are |
| Open with DEXTER | |
Appendix B: Fourier analysis and vertical propagation of velocity distributions
Fourier power.
The time-series of Ca II H spectra allows for a Fourier analysis to determine the dominant frequency contributions to the variations of the LOS velocities. Figure B.1 shows a k-Phase differences.
In Fig. B.2, we show the phase difference between the lowermost forming line 1 and all others. The velocity variations show usually only a small or zero phase difference between the different lines, which would be expected if their frequencies are below the cut-off frequency. No clear relation with the line-core velocity of Ca II H can be seen at all. The phase-relation between the Ca II H line-core velocity and the low photospheric velocities shows a much larger scatter than the phase relation between the intensity of the H2V emission peak and photospheric velocities (see Beck et al. 2008, Fig. 10b). This may be caused by the complex formation of the Ca line that renders the interpretation of the location of minimum line core intensity as a velocity doubtful (see for example the lower left panel of Fig. A.1), and the fact that the main signature of the waves in the chromospheric layers is not a Doppler shift, but an intensity enhancement.| Figure B.1: Power spectra of the LOS velocity of ( left to right) line 1, 5, 9 and 8. The power is scaled between minimum and maximum in arbitrary units. The dash-dotted line denotes 5 mHz. |
|
| Open with DEXTER | |
Propagation of velocity with height.
| Figure B.2: Phase differences of LOS velocities as function of oscillation frequency. Left to right: v1 to v5, v1 to v9 and v1 to v8. The relative occurrence of a phase difference value is given by the color code in the range of 5% to 20% (7.5% to 15% for v1-v8). The red curve gives the center of gravity of the phase distribution at each frequency; red vertical dashed lines denote frequencies of 2 and 5 mHz, respectively. |
|
| Open with DEXTER | |
| Figure B.3: Propagation of the velocity of line 5 to the height of line 9. Left to right: LOS velocity map of line 5, its Fourier transform, Fourier transform at the new height, velocity map at the new height, observed LOS velocity map of line 9. Velocities/amplitudes are in km s-1 with the color coding at their top. |
|
| Open with DEXTER | |
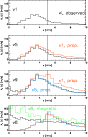
|
Figure B.4: Velocity amplitudes of the Fourier transform, averaged along the slit. Top to bottom: line 1, 5, 9, and 8. Black lines shows the distribution in the observations, blue and red lines the one resulting from propagating line 1 and line 5, respectively. The green line in the bottom panel shows the v8 amplitudes on magnetic locations. |
| Open with DEXTER | |
The velocities of the different lines can be propagated with height
using the linear wave theory. The corresponding equation for the
propagation contains a frequency-dependent amplitude scaling and is
given by (Mihalas
&
Weibel Mihalas 1984)
We used a constant scale height of H = 100 km, a constant sound speed
This close agreement also holds for the distribution of the
velocity power with frequency (see Fig. B.4).
The
propagated velocity of line 5 is again nearly
indistinguishable from the observed one of line 9. For
line 9 and for line 8 (Ca II H
line core), we used here the velocity maps without filtering
for granular low frequency power. line 8 shows a strong
contribution from low frequencies that is not reproduced by the
propagated velocities, even if the rms velocity values of both observed
and propagated velocities turn out to be similar. The velocity
amplitudes of v8, calculated separately for locations with high
photospheric polarization signal (green line in
bottom panel, y = 12-22
![]() and 46-50
and 46-50
![]() ), are slightly above those of
the full FOV by a factor of around 1.5.
), are slightly above those of
the full FOV by a factor of around 1.5.
References
- Avrett, E. H. 2007, in The Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovic, & R. J. Rutten, ASP Conf. Ser., 368, 81
- Avrett, E. H., & Loeser, R. 2008, ApJS, 175, 229 [CrossRef] [NASA ADS]
- Avrett, E. H., Kurucz, R. L., & Loeser, R. 2006, A&A, 452, 651 [EDP Sciences] [CrossRef] [NASA ADS]
- Beck, C., & Rezaei, R. 2009, A&A, 502, 969 [EDP Sciences] [CrossRef] [NASA ADS]
- Beck, C., Schlichenmaier, R., Collados, M., Bellot Rubio, L., & Kentischer, T. 2005a, A&A, 443, 1047 [EDP Sciences] [CrossRef] [NASA ADS]
- Beck, C., Schmidt, W., Kentischer, T., & Elmore, D. 2005b, A&A, 437, 1159 [EDP Sciences] [CrossRef] [NASA ADS]
- Beck, C., Bellot Rubio, L. R., Schlichenmaier, R., & Sütterlin, P. 2007, A&A, 472, 607 [EDP Sciences] [CrossRef] [NASA ADS]
- Beck, C., Schmidt, W., Rezaei, R., & Rammacher, W. 2008, A&A, 479, 213 [EDP Sciences] [CrossRef] [NASA ADS]
- Carlsson, M., & Stein, R. F. 1997, ApJ, 481, 500 [CrossRef] [NASA ADS]
- Carlsson, M., Hansteen, V. H., de Pontieu, B., et al. 2007, PASJ, 59, 663 [NASA ADS]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [CrossRef] [NASA ADS]
- Cheung, M. C. M., Schüssler, M., & Moreno-Insertis, F. 2007, A&A, 461, 1163 [EDP Sciences] [CrossRef] [NASA ADS]
- Chitre, S. M., & Davila, J. M. 1991, in Mechanisms of Chromospheric and Coronal Heating, ed. P. Ulmschneider, E. R. Priest, & R. Rosner, 402
- Davila, J. M., & Chitre, S. M. 1991, ApJ, 381, L31 [CrossRef] [NASA ADS]
- Fontenla, J., White, O. R., Fox, P. A., Avrett, E. H., & Kurucz, R. L. 1999, ApJ, 518, 480 [CrossRef] [NASA ADS]
- Fontenla, J. M., Avrett, E., Thuillier, G., & Harder, J. 2006, ApJ, 639, 441 [CrossRef] [NASA ADS]
- Fontenla, J. M., Peterson, W. K., & Harder, J. 2008, A&A, 480, 839 [EDP Sciences] [CrossRef] [NASA ADS]
- Fossum, A., & Carlsson, M. 2005, Nature, 435, 919 [CrossRef] [NASA ADS]
- Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18, 347 [CrossRef] [NASA ADS]
- Hammer, R. 1987, in Solar and Stellar Physics, ed. E.-H. Schröter, & M. Schüssler, Lecture Notes Physics (Berlin: Springer Verlag), 292, 77
- Heasley, J. N. 1975, Sol. Phys., 44, 275 [CrossRef] [NASA ADS]
- Hindman, B. W., & Jain, R. 2008, ApJ, 677, 769 [CrossRef] [NASA ADS]
- Holweger, H., & Mueller, E. A. 1974, Sol. Phys., 39, 19 [CrossRef] [NASA ADS]
- Ishikawa, R., & Tsuneta, S. 2009, A&A, 495, 607 [EDP Sciences] [CrossRef] [NASA ADS]
- Jones, H. P. 1985, Australian Journal of Physics, 38, 919 [NASA ADS]
- Kalkofen, W. 2007, ApJ, 671, 2154 [CrossRef] [NASA ADS]
- Keller, C. U., Steiner, O., Stenflo, J. O., & Solanki, S. K. 1990, A&A, 233, 583 [NASA ADS]
- Khomenko, E. V., Collados, M., Solanki, S. K., Lagg, A., & Trujillo Bueno, J. 2003, A&A, 408, 1115 [EDP Sciences] [CrossRef] [NASA ADS]
- Khomenko, E. V., Martínez González, M. J., Collados, M., et al. 2005, A&A, 436, L27 [EDP Sciences] [CrossRef] [NASA ADS]
- Khomenko, E., Centeno, R., Collados, M., & Trujillo Bueno, J. 2008, ApJ, 676, L85 [CrossRef] [NASA ADS]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Rouppe van der Voort, L. 2009, ApJ, 694, L128 [CrossRef] [NASA ADS]
- Linsky, J. L., & Avrett, E. H. 1970, PASP, 82, 169 [CrossRef] [NASA ADS]
- Lites, B. W., Rutten, R. J., & Kalkofen, W. 1993, ApJ, 414, 345 [CrossRef] [NASA ADS]
- Lites, B. W., Leka, K. D., Skumanich, A., Martinez Pillet, V., & Shimizu, T. 1996, ApJ, 460, 1019 [CrossRef] [NASA ADS]
- Lites, B. W., Kubo, M., Socas-Navarro, H., et al. 2008, ApJ, 672, 1237 [CrossRef] [NASA ADS]
- Liu, S.-Y. 1974, ApJ, 189, 359 [CrossRef] [NASA ADS]
- Liu, S.-Y., & Skumanich, A. 1974, Sol. Phys., 38, 109 [CrossRef] [NASA ADS]
- Liu, S.-Y., & Smith, E. V. P. 1972, Sol. Phys., 24, 301 [CrossRef] [NASA ADS]
- Martin, W. C., Wiese, W. L., Musgrove, A., et al. 1998, in Laboratory Space Science Workshop, held at Harvard-Smithosonian Center for Astrophysics, 1-3 April, Local Organizing Committee: W. H. Parkinson, K. Kirby, & P. L. Smith, 182
- Martínez González, M. J., Asensio Ramos, A., López Ariste, A., & Manso Sainz, R. 2008, A&A, 479, 229 [EDP Sciences] [CrossRef] [NASA ADS]
- Mihalas, D., & Weibel Mihalas, B. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press)
- Musielak, Z. E., Rosner, R., Stein, R. F., & Ulmschneider, P. 1994, ApJ, 423, 474 [CrossRef] [NASA ADS]
- Narain, U., & Ulmschneider, P. 1996, Space Sci. Rev., 75, 453 [CrossRef] [NASA ADS]
- Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P., & Brault, J. W. 1994, ApJS, 94, 221 [CrossRef] [NASA ADS]
- Orozco Suárez, D., Bellot Rubio, L., del Toro Iniesta, J., et al. 2007, ApJ, 670, L61 [CrossRef] [NASA ADS]
- Peter, H., Gudiksen, B. V., & Nordlund, Å. 2004, ApJ, 617, L85 [CrossRef] [NASA ADS]
- Reader, J., Wiese, W. L., Martin, W. C., Musgrove, A., & Fuhr, J. R. 2002, in NASA Laboratory Astrophysics Workshop, ed. F. Salama, et al., 80
- Rezaei, R., Schlichenmaier, R., Beck, C. A. R., Bruls, J. H. M. J., & Schmidt, W. 2007, A&A, 466, 1131 [EDP Sciences] [CrossRef] [NASA ADS]
- Rezaei, R., Bruls, J. H. M. J., Schmidt, W., et al. 2008, A&A, 484, 503 [EDP Sciences] [CrossRef] [NASA ADS]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [CrossRef] [NASA ADS]
- Rutten, R. J., de Wijn, A. G., & Sütterlin, P. 2004, A&A, 416, 333 [EDP Sciences] [CrossRef] [NASA ADS]
- Schaffenberger, W., Wedemeyer-Böhm, S., Steiner, O., & Freytag, B. 2006, in Solar MHD Theory and Observations: A High Spatial Resolution Perspective, ed. J. Leibacher, R. F. Stein, & H. Uitenbroek, ASP Conf. Ser., 354, 345
- Solanki, S. K. 1993, Space Sci. Rev., 63, 1 [CrossRef] [NASA ADS]
- Steiner, O., Grossmann-Doerth, U., Knoelker, M., & Schuessler, M. 1998, ApJ, 495, 468 [CrossRef] [NASA ADS]
- Steiner, O., Rezaei, R., Schaffenberger, W., & Wedemeyer-Böhm, S. 2008, ApJ, 680, L85 [CrossRef] [NASA ADS]
- Straus, T., Fleck, B., Jefferies, S. M., et al. 2008, ApJ, 681, L125 [CrossRef] [NASA ADS]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [CrossRef] [NASA ADS]
- Ulmschneider, P. 1971, A&A, 14, 275 [NASA ADS]
- Ulmschneider, R., Schmitz, F., Kalkofen, W., & Bohn, H. U. 1978, A&A, 70, 487 [NASA ADS]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1976, ApJS, 30, 1 [CrossRef] [NASA ADS]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [CrossRef] [NASA ADS]
- Wedemeyer-Böhm, S., Steiner, O., Bruls, J., & Rammacher, W. 2007, in The Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovic, & R. J. Rutten, ASP Conf. Series, 368, 93
Footnotes
- ... field-free
![[*]](/icons/foot_motif.png)
- ``Field-free'' is used here in the sense of ``no detectable circular polarization signal above noise level''.
- ... (pseudo
![[*]](/icons/foot_motif.png)
- For Ca II H a spectral region in the line wing without a photospheric blend was used.
All Tables
Table 1: Line parameters.
Table 2: Line-core formation height ( 2nd column) and velocity amplitude ratios of left to right observed rms velocities, velocity of v1 propagated in linear wave theory, same for v5, and from the fit to the scatterplots.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.