| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 355 - 368 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200810963 | |
| Published online | 08 October 2009 | |
A&A 507, 355-368 (2009)
Intermittency of interstellar turbulence:
extreme velocity-shears and CO emission on milliparsec scale![[*]](/icons/foot_motif.png)
E. Falgarone1 - J. Pety1,2 - P. Hily-Blant3
1 - LERMA/LRA, CNRS, UMR 8112, École Normale Supérieure &
Observatoire de Paris, 24 rue Lhomond, 75005 Paris, France
2 - Institut de Radio Astronomie Millimétrique, 300 rue de la Piscine,
38406 Saint-Martin-d'Hères, France
3 - LAOG, CNRS UMR 5571, Université Joseph Fourier, BP53, 38041
Grenoble, France
Received 13 September 2008 / Accepted 29 September 2009
Abstract
Aims. The condensation of diffuse gas into molecular
clouds and dense cores occurs at a rate driven largely by turbulent
dissipation. This process still has to be caught in action and
characterized.
Methods. We observed a mosaic of 13 fields with the
IRAM-PdB interferometer (PdBI) to search for small-scale structure in
the ![]() (1-0) line emission of the
turbulent and translucent environment of a low-mass dense core in the
Polaris Flare. The large size of the mosaic (1'
(1-0) line emission of the
turbulent and translucent environment of a low-mass dense core in the
Polaris Flare. The large size of the mosaic (1' ![]() 2')
compared to the resolution (4'') is unprecedented in the study
of the small-scale structure of diffuse molecular gas.
2')
compared to the resolution (4'') is unprecedented in the study
of the small-scale structure of diffuse molecular gas.
Results. The interferometer data uncover eight weak
and elongated structures with thicknesses as small as ![]() 3 mpc
(600 AU) and lengths up to 70 mpc, close to the size
of the mosaic. These are not filaments because once merged with
short-spacings data, the PdBI-structures appear to be the sharp edges,
in space and velocity-space, of larger-scale structures. Six out of
eight form quasi-parallel pairs at different velocities and different
position angles. This cannot be the result of chance alignment. The
velocity-shears estimated for the three pairs include the highest
values ever measured in regions that do not form stars (up to
780 km s-1 pc-1).
The CO column density of the PdBI-structures is in the range
3 mpc
(600 AU) and lengths up to 70 mpc, close to the size
of the mosaic. These are not filaments because once merged with
short-spacings data, the PdBI-structures appear to be the sharp edges,
in space and velocity-space, of larger-scale structures. Six out of
eight form quasi-parallel pairs at different velocities and different
position angles. This cannot be the result of chance alignment. The
velocity-shears estimated for the three pairs include the highest
values ever measured in regions that do not form stars (up to
780 km s-1 pc-1).
The CO column density of the PdBI-structures is in the range
![]() to 1015
to 1015
![]() and their
and their ![]() density,
estimated in several ways, does not exceed a few 103
density,
estimated in several ways, does not exceed a few 103
![]() .
Because the larger scale structures have sharp edges (with little or no
overlap for those that are pairs), they have to be thin layers of
CO emission. We call them SEE(D)S for sharp-edged extended
(double) structures. These edges mark a transition, on the milliparsec
scale, between a CO-rich component and a gas undetected in the
.
Because the larger scale structures have sharp edges (with little or no
overlap for those that are pairs), they have to be thin layers of
CO emission. We call them SEE(D)S for sharp-edged extended
(double) structures. These edges mark a transition, on the milliparsec
scale, between a CO-rich component and a gas undetected in the
![]() (1-0) line
because of its low CO abundance, presumably the cold neutral
medium.
(1-0) line
because of its low CO abundance, presumably the cold neutral
medium.
Conclusions. We propose that these SEE(D)S are the
first directly-detected manifestations of the intermittency of
interstellar turbulence. The large velocity-shears reveal an intense
straining field, responsible for a local dissipation rate several
orders of magnitude above average, possibly at the origin of the thin
CO layers.
Key words: ISM: evolution - ISM: kinematics and dynamics - ISM: molecules - ISM: structure - ISM: general - turbulence
1 Introduction
Turbulence in the interstellar medium (ISM) remains a puzzle in spite of dedicated efforts on observational and numerical grounds. This is because it is compressible, magnetized, and multi-phase, but also because of the huge range of scales separating those of injection and dissipation of energy. Moreover, because turbulence and magnetic fields are the main support of molecular clouds against their self-gravity, turbulent dissipation is a key process among all those eventually leading to star formation (see the reviews of Scalo & Elmegreen 2004; Elmegreen & Scalo 2004).
In molecular clouds, turbulence is observed to be highly
supersonic with respect to the cold gas. It is thus
anticipated to dissipate in shocks in a cloud-crossing time
(i.e. ![]() a few 10 Myr for giant molecular clouds of
100 pc with internal velocity dispersion of
a few km s-1).
Magnetic fields do not significantly slow the dissipation down (Mac Low et al.
1998).
Actually, this is the basis of the turbulent models of star formation (Mac Low &
Klessen 2004) -
one of the two current scenarii of low-mass star formation -
in which self-gravitating entities form in the shock-compressed layers
of supersonic turbulence.
a few 10 Myr for giant molecular clouds of
100 pc with internal velocity dispersion of
a few km s-1).
Magnetic fields do not significantly slow the dissipation down (Mac Low et al.
1998).
Actually, this is the basis of the turbulent models of star formation (Mac Low &
Klessen 2004) -
one of the two current scenarii of low-mass star formation -
in which self-gravitating entities form in the shock-compressed layers
of supersonic turbulence.
However, while it is unquestionable that the ISM is regularly swept by large-scale shock-waves triggered by supernovae explosions that partly feed the interstellar turbulent cascade (de Avillez & Breitschwerdt 2007; Joung & Mac Low 2006), the smallest scales, barely subparsec in these simulations, are still orders of magnitude above the smallest observed structures and are unlikely to provide a proper description of the actual dissipation processes. Whether turbulent dissipation occurs primarily in compressive (curl-free) or in solenoidal (divergence-free) modes in the interstellar medium has therefore to be considered as an open issue.
An ideal target to study turbulent dissipation is the diffuse
molecular gas because it is the component in which dense cores form,
with less turbulent energy density than their environment. The word
``diffuse'' here comprises all material in the neutral ISM at large
that is not in dense cores i.e. whose total hydrogen column density is
less than a few 1021
![]() .
This includes the mixture of cold and warm neutral medium (CNM and
WNM), the edges of molecular cloud complexes (also called translucent
gas), and the high latitude clouds. Diffuse gas builds up a major mass
fraction of the ISM. Actually, on the 30 pc scale, Goldsmith
et al. (2008)
find that half the mass of the Taurus-Auriga-Perseus complex lies in
regions having
.
This includes the mixture of cold and warm neutral medium (CNM and
WNM), the edges of molecular cloud complexes (also called translucent
gas), and the high latitude clouds. Diffuse gas builds up a major mass
fraction of the ISM. Actually, on the 30 pc scale, Goldsmith
et al. (2008)
find that half the mass of the Taurus-Auriga-Perseus complex lies in
regions having ![]() column
density below 2.1
column
density below 2.1 ![]() 1021
1021
![]() .
.
Turbulent dissipation may also provide clues to the
``outstanding mysteries'' raised by observations of diffuse molecular
gas (see the review of Snow &
McCall 2006): the ubiquitous small scale structure, down to
AU-scales (Heiles 2007),
the
remarkable molecular richness found in this hostile medium, weakly
shielded from UV radiation (e.g. Gredel
et al. 2002; Liszt
&
Lucas 1998), the bright emission in the ![]() pure
rotational lines exceeding the predictions of photon-dominated region
(PDR) models (Lacour
et al. 2005; Falgarone
et al. 2005),
the
pure
rotational lines exceeding the predictions of photon-dominated region
(PDR) models (Lacour
et al. 2005; Falgarone
et al. 2005),
the ![]() small-scale structures with a broad range of temperatures,
small-scale structures with a broad range of temperatures, ![]() densities
and linewidths that preclude a single interpretation in terms of cold
dense clumps (Sakamoto
& Sunada 2003; Ingalls
et al. 2000,2007;
Heithausen
2006,2004).
densities
and linewidths that preclude a single interpretation in terms of cold
dense clumps (Sakamoto
& Sunada 2003; Ingalls
et al. 2000,2007;
Heithausen
2006,2004).
The present paper extends the investigation of turbulence down to the mpc-scale in the translucent environment of a low-mass dense core of the Polaris Flare. Over the years, this investigation has progressed along three complementary directions:
- (i)
- A two-point statistical analysis of the velocity field
traced by the
 line emission, and conducted on maps of increasing size. Using
numerical simulations of mildly compressible turbulence, Lis et al. (1996)
and Pety & Falgarone
(2003) first proposed that the non-Gaussian
probability distribution functions (pdfs) of line
centroid velocity increments (CVI) be the signatures of the space-time
intermittency of turbulence
line emission, and conducted on maps of increasing size. Using
numerical simulations of mildly compressible turbulence, Lis et al. (1996)
and Pety & Falgarone
(2003) first proposed that the non-Gaussian
probability distribution functions (pdfs) of line
centroid velocity increments (CVI) be the signatures of the space-time
intermittency of turbulence![[*]](/icons/foot_motif.png) because the extrema of CVI (E-CVI) trace extrema of the
line-of-sight average of the modulus of the plane-of-the-sky (pos) vorticity.
Statistical analysis conducted on parsec-scale maps in two nearby
molecular clouds have revealed that these extrema form parsec-scale
coherent structures (Hily-Blant
& Falgarone 2009; Hily-Blant
et al. 2008,
resp. Paper III, HF09).
because the extrema of CVI (E-CVI) trace extrema of the
line-of-sight average of the modulus of the plane-of-the-sky (pos) vorticity.
Statistical analysis conducted on parsec-scale maps in two nearby
molecular clouds have revealed that these extrema form parsec-scale
coherent structures (Hily-Blant
& Falgarone 2009; Hily-Blant
et al. 2008,
resp. Paper III, HF09).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10963f1.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg12.png)
Figure 1: The location of the 13-field mosaic observed at the Plateau de Bure interferometer (centered at RA = 01:55:12.26 and Dec = 87:41:56.30) is shown as the box on top of the integrated emission of the
 and
and 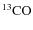 (J=1-0) maps obtained at the
IRAM-30m. This is a place of low, almost featureless, CO line
brightness. The arc-like structure visible in
(J=1-0) maps obtained at the
IRAM-30m. This is a place of low, almost featureless, CO line
brightness. The arc-like structure visible in
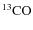 traces the outer layers of the low-mass dense core. Contour levels are
shown in the wedges.
traces the outer layers of the low-mass dense core. Contour levels are
shown in the wedges.
Open with DEXTER - (ii)
- A detailed analysis (density, temperature, molecular
abundances) of these coherent structures, based on their molecular line
emission. The gas there is more optically thin in the
 lines,
warmer and more dilute than the bulk of the gas (Hily-Blant
& Falgarone 2007, hereafter Paper II), and
large
lines,
warmer and more dilute than the bulk of the gas (Hily-Blant
& Falgarone 2007, hereafter Paper II), and
large 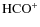 abundances, unexpected in an environment weakly shielded from
UV radiation, have been detected there (Falgarone
et al. 2006,
Paper I).
abundances, unexpected in an environment weakly shielded from
UV radiation, have been detected there (Falgarone
et al. 2006,
Paper I).
- (iii)
- Chemical models of non-equilibrium warm chemistry triggered
by bursts of turbulent dissipation (Joulain
et al. 1998). The most recent progresses along those
lines include the chemical models of turbulent dissipation regions
(TDRs) by Godard et al.
(2009) and their successful
comparison to several data sets, among which new submillimeter
detections of
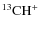 (1-0)
(Falgarone et al., in preparation).
(1-0)
(Falgarone et al., in preparation).
The ![]() (1-0)
observations reported in this paper have been performed in a field
located on one branch of the Polaris Flare E-CVI structure, in
the translucent and featureless environment of a dense core
(Fig. 1).
The outline of the paper is the following: the observations and data
reduction are described in Sect. 2. The observational results
are given in Sect. 3. The
characterization of the emitting gas is made in Sect. 4 and we
discuss, in Sect. 5, the possible origin and nature of the
CO structures that we have discovered. Section 6 puts
our results in the
broad perspective provided by other data sets and Sect. 7
compares them to chemical model predictions and numerical simulations
of turbulence. The conclusions are given in Sect. 8.
(1-0)
observations reported in this paper have been performed in a field
located on one branch of the Polaris Flare E-CVI structure, in
the translucent and featureless environment of a dense core
(Fig. 1).
The outline of the paper is the following: the observations and data
reduction are described in Sect. 2. The observational results
are given in Sect. 3. The
characterization of the emitting gas is made in Sect. 4 and we
discuss, in Sect. 5, the possible origin and nature of the
CO structures that we have discovered. Section 6 puts
our results in the
broad perspective provided by other data sets and Sect. 7
compares them to chemical model predictions and numerical simulations
of turbulence. The conclusions are given in Sect. 8.
2 IRAM Plateau de Bure Interferometer observations
We used the IRAM Plateau de Bure Interferometer (PdBI) to image, at
high angular resolution and in the
![]() (J=1-0) line, a region of
(J=1-0) line, a region of ![]()
![]() 2' in the translucent environment of a dense core in the Polaris Flare (Heithausen 1999;
Heithausen
et al. 2002). The location of the target field is
shown in Fig. 1
as a rectangle on larger scale, single-dish maps of integrated
2' in the translucent environment of a dense core in the Polaris Flare (Heithausen 1999;
Heithausen
et al. 2002). The location of the target field is
shown in Fig. 1
as a rectangle on larger scale, single-dish maps of integrated
![]() (J=1-0)
and
(J=1-0)
and ![]() (J=1-0)
emission from (Falgarone
et al. 1998, hereafter F98). The average column
density in this region (
(J=1-0)
emission from (Falgarone
et al. 1998, hereafter F98). The average column
density in this region (
![]()
![]() )
is about 100 times smaller than in the central parts of the
dense core (
)
is about 100 times smaller than in the central parts of the
dense core (
![]()
![]() ), 3 arcmin
westwards. The average integrated
), 3 arcmin
westwards. The average integrated
![]() intensity over the mosaic area is weak
intensity over the mosaic area is weak
![]()
![]() .
.
Table
1:
Observation parameters. The projection center of all the data displayed
in this paper is:
![]() ,
,
![]() .
.
2.1 Observations
The observations dedicated to this project were carried out in 1998 and
1999 with the IRAM interferometer at Plateau de Bure in the C and
D configurations (baseline lengths from 24 m to
161 m). One correlator band of 10 MHz was centered on
the ![]() (J=1-0)
frequency to cover
a
(J=1-0)
frequency to cover
a
![]() bandwidth
with a channel spacing of 39 kHz, i.e.
bandwidth
with a channel spacing of 39 kHz, i.e.
![]() .
Four additional correlator bands of 160 MHz were used to
measure the 2.6 mm continuum over the 500 MHz
instantaneous IF-bandwidth then available.
.
Four additional correlator bands of 160 MHz were used to
measure the 2.6 mm continuum over the 500 MHz
instantaneous IF-bandwidth then available.
We observed a 13-field mosaic centered on
![]() ,
,
![]() .
The field positions followed a compact hexagonal pattern to ensure
Nyquist
sampling in all directions and an almost uniform noise over a large
fraction of the mosaic area (see Fig. A.1 of
Appendix A). The imaged field-of-view is about a rectangle of
dimension of
85''
.
The field positions followed a compact hexagonal pattern to ensure
Nyquist
sampling in all directions and an almost uniform noise over a large
fraction of the mosaic area (see Fig. A.1 of
Appendix A). The imaged field-of-view is about a rectangle of
dimension of
85'' ![]() 130'' oriented at a position-angle of
130'' oriented at a position-angle of
![]() (because
the (RA, Dec) PdBI field was selected in
maps made in (l,b) coordinates).
(because
the (RA, Dec) PdBI field was selected in
maps made in (l,b) coordinates).
Polaris being a circumpolar source, this project was a good time-filler. It was thus observed at 22 different occasions, giving a total of about 180 hours of telescope time with most often 3 or 4 antennas and rarely 5 antennas. Taking into account the time for calibration and data filtering this translates into on-source integration time of useful data of 65.2 h for a full 5-antenna array. The typical 2.6 mm resolution of these data is 4.3''. The data used to produce the missing short-spacings are those of the IRAM key-program, fully described in F98 (see also Table 1).
2.2 Data reduction
The data processing was done with the GILDASf![]() software suite (Pety 2005).
Standard calibration methods implemented in the GILDAS/CLIC program
were applied using close bright quasars as calibrators. The
calibrated uv tables were processed through
an Hanning filter which spectrally smoothed the data
(to increase the intensity signal-to-noise ratio) while
keeping the same
velocity/frequency channel spacing.
software suite (Pety 2005).
Standard calibration methods implemented in the GILDAS/CLIC program
were applied using close bright quasars as calibrators. The
calibrated uv tables were processed through
an Hanning filter which spectrally smoothed the data
(to increase the intensity signal-to-noise ratio) while
keeping the same
velocity/frequency channel spacing.
All other processing took place into the GILDAS/MAPPING
software. Following Gueth
et al. (1996), the single-dish map from the IRAM-30m
key program were used to create the short-spacing visibilities not
sampled at the Plateau de Bure. These were then merged with the
interferometric observations. Two different sets of uv tables
(i.e. with and without short-spacings) were then imaged using the same
method. Each mosaic field was imaged and a dirty mosaic was built
combining those fields in the following optimal way in terms of
signal-to-noise ratio (Gueth 2001)

In this equation,
Deconvolution methods were different for both data sets (i.e. with and without short-spacings). The dirty image of the PdBI-only data was deconvolved using the standard Clark CLEAN algorithm. One spatial support per channel map was defined by selecting positive regions on the first clean image which was obtained without any constraint. This geometrical constraint was then used in a second deconvolution. While it can bias the result, this two-step process is needed when deconvolving interferometric observations of extended sources without short-spacings. Indeed, the lack of short-spacings implies (among other things) a zero valued integral of the dirty beam and dirty image, which in turn perturbs the CLEAN convergence when the source is extended because the algorithm searches as many positive as negative CLEAN components. The only way around is to guide the deconvolution by the definition of a support where the signal is detected. On the other hand, the deconvolution of the combined short-spacings and interferometric uv visibilities can process blindly (i.e. without the possible bias of defining a support where to search for CLEAN components). This is what has been done and the good correlation of the structures seen in the deconvolved images of the data with and without short-spacings (see Figs. 4 and 5) gives us confidence in our deconvolution of the PdBI-only data.
The two resulting data cubes (with and without short-spacings)
were then scaled from Jy/beam to
![]() temperature
scale using the synthesized beam size (see Table 1). Final
noise rms
measured at the centered of the mosaic is about 0.23 K in both
data cubes.
temperature
scale using the synthesized beam size (see Table 1). Final
noise rms
measured at the centered of the mosaic is about 0.23 K in both
data cubes.
3 Observational results
![\begin{figure}
\par\includegraphics[angle=270,width=9cm,clip]{10963f2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg30.png)
|
Figure 2:
Map of integrated emission of the PdBI data ( top left),
and signal-to-noise ratio ( top right) for the
|
| Open with DEXTER | |
3.1 PdBI structures: sharp edges of extended structures
At the adopted cloud distance of d=150 pc, 1'' corresponds to 0.75 mpc or 150 AU, so that the spatial resolution of the PdBI data is 3.2 mpc or 660 AU.
The integrated emission detected with the PdBI is displayed in
Fig. 2
(left panel), with the corresponding signal-to-noise ratio (right
panel). The integrated emission covers
most of the mosaic area. This is no longer true when this emission is
displayed in velocity slices (Fig. 3,
top
panels). Several distinct structures are detected in addition to the
bright CO peak, at velocities
[-3.1, -2.3] km s-1.
Most are weak (the first level in the PdBI channel maps of
Fig. 3
is 3![]() )
but they extend over many contiguous synthesized
beams (10 to 30).
)
but they extend over many contiguous synthesized
beams (10 to 30).
The PdBI data merged with the short-spacings provided by the
30m telescope and the ![]() (1-0)
emission detected by the IRAM-30m telescope are displayed in the same
velocity-slices, for comparison, in Fig. 3,
central
and bottom panels respectively. Most of the structures seen by the PdBI
lie at the edge in space and in velocity space of extended emission
present in the single-dish channel maps. This property is most visible
for the two structures in the north-west of the mosaic over
[-4.8, -4.4] km s-1
and [-2, -1.2] km s-1,
and in the central region at v=-2.8 km s-1.
It is even better seen by comparing the single-dish maps
before and
after combination with the PdBI data. The single-dish maps are
changed in two-ways: the structures exhibit sharper, more coherent
boundaries and these boundaries extend further in velocity-space (e.g.
channels -4.7 and -2.3 km s-1).
In a given channel of width
(1-0)
emission detected by the IRAM-30m telescope are displayed in the same
velocity-slices, for comparison, in Fig. 3,
central
and bottom panels respectively. Most of the structures seen by the PdBI
lie at the edge in space and in velocity space of extended emission
present in the single-dish channel maps. This property is most visible
for the two structures in the north-west of the mosaic over
[-4.8, -4.4] km s-1
and [-2, -1.2] km s-1,
and in the central region at v=-2.8 km s-1.
It is even better seen by comparing the single-dish maps
before and
after combination with the PdBI data. The single-dish maps are
changed in two-ways: the structures exhibit sharper, more coherent
boundaries and these boundaries extend further in velocity-space (e.g.
channels -4.7 and -2.3 km s-1).
In a given channel of width
![]() ,
the size of the detected structures in the CO emission
,
the size of the detected structures in the CO emission
![]() is inversely proportional to the velocity-shear,
is inversely proportional to the velocity-shear,
![]() .
Hence, the detection of small-scale structures at the edge of the
velocity coverage of larger-scale
structures may be favored by an increase of the velocity shear at these
edges.
.
Hence, the detection of small-scale structures at the edge of the
velocity coverage of larger-scale
structures may be favored by an increase of the velocity shear at these
edges.
The fact that these structures appear both in PdBI-only data and in combined (PdBI+30m) data gives confidence in their reality, independently of the deconvolution techniques.
In summary, the interferometer is sensitive by construction to small-scale (i.e. sharp) variations of the space-velocity CO distribution. It happens that the sharp structures detected by the interferometer lie at the edge in space and velocity of regions of shallow CO emission that extend over at least arcminutes, as displayed in the 30m channel maps. The PdBI-structures are therefore the sharp edges of extended structures.
![\begin{figure}
\par\includegraphics[angle=270,width=17.5cm,clip]{10963f3.eps}\pa...
....eps}\par\includegraphics[angle=270,width=17.5cm,clip]{10963f5.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg35.png)
|
Figure 3:
From top to bottom, maps of the PdBI,
PdBI+30m and 30m of |
| Open with DEXTER | |
Table
2:
Spatial and kinematic characteristics of the
![]() PdBI-only structures.
PdBI-only structures.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10963f6.eps}\hspace*{5mm}
\includegraphics[width=8.5cm,clip]{10963f7.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg49.png)
|
Figure 4:
The 8 structures described in Table 1.
Left
panels: PdBI-only |
| Open with DEXTER | |
3.2 Observed characteristics of the PdBI structures
We have identified eight structures in the space-velocity
![]() (J=1-0)
PdBI data cube that are well separated from one another in
direction and in velocity. They are shown in Fig. 4,
each drawn over its proper velocity range. The right panels show the
PdBI data combined with 30m data over the same velocity ranges
to further illustrate that the PdBI filtering emphasizes the sharpness
of the edge of the space-velocity structures. Figure 4 also
shows
that the single-dish structures cover a large fraction of the mosaic
area. For instance, in the case of structure #1, the
single-dish structure extends over the whole southern half of the
mosaic, while for structure #5 it almost covers the northern
half.
(J=1-0)
PdBI data cube that are well separated from one another in
direction and in velocity. They are shown in Fig. 4,
each drawn over its proper velocity range. The right panels show the
PdBI data combined with 30m data over the same velocity ranges
to further illustrate that the PdBI filtering emphasizes the sharpness
of the edge of the space-velocity structures. Figure 4 also
shows
that the single-dish structures cover a large fraction of the mosaic
area. For instance, in the case of structure #1, the
single-dish structure extends over the whole southern half of the
mosaic, while for structure #5 it almost covers the northern
half.
The observed properties of the 8 PdBI structures are given in
Table 2.
The peak ![]() (J=1-0)
temperature is that detected by the PdBI, therefore the excess above
the extended background, resolved out by the PdBI. The size
(J=1-0)
temperature is that detected by the PdBI, therefore the excess above
the extended background, resolved out by the PdBI. The size
![]() is the half-power thickness of
the elongated structures, deconvolved
from the beam size. The projected thickness, in mpc, is
called
is the half-power thickness of
the elongated structures, deconvolved
from the beam size. The projected thickness, in mpc, is
called ![]() by opposition to the unknown depth along the line-of-sight (los),
called
by opposition to the unknown depth along the line-of-sight (los),
called
![]() .
The position-angle PA is that of the direction defined,
within
.
The position-angle PA is that of the direction defined,
within
![]() ,
by the three brightest pixels of each structure. When they are not
aligned, as in the case of #8, we determine a direction with
the meaning of a least-square fit. It corresponds to an
average
,
by the three brightest pixels of each structure. When they are not
aligned, as in the case of #8, we determine a direction with
the meaning of a least-square fit. It corresponds to an
average ![]() over the detected structure that does not take into account the
substructure visible in Fig. 6 for
instance. Because of their different velocity width and
CO line temperature, the CO integrated brightness of
the eight structures varies by a factor 25.
over the detected structure that does not take into account the
substructure visible in Fig. 6 for
instance. Because of their different velocity width and
CO line temperature, the CO integrated brightness of
the eight structures varies by a factor 25.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10963f8.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg51.png)
|
Figure 5:
Comparison of spectra integrated over either the polygons defined in
Fig. 4
and the whole mosaic. The |
| Open with DEXTER | |
Most of the PdBI-structures are elongated and straight with different
position-angles in the sky. Interestingly, they do not shadow each
other in space and in velocity space (i.e. each fills only a
small area of the mosaic in a small velocity interval, and the
positions and areas of the detected structures are different). Their
cumulative surface filling factor in the mosaic field is large,
![]() (Fig. 2),
i.e.
(Fig. 2),
i.e.
![]() for the structures detected at
more than 1-sigma and
for the structures detected at
more than 1-sigma and ![]() for 3-sigma detections. However, the
fraction of the single-dish power (integrated over the mosaic) seen by
the PdBI in the
for 3-sigma detections. However, the
fraction of the single-dish power (integrated over the mosaic) seen by
the PdBI in the ![]() (1-0) line
is low. It depends on the velocity interval: it varies
between 2% in the
(1-0) line
is low. It depends on the velocity interval: it varies
between 2% in the ![]() line-core (defined as the velocity range,
[-5.0, -3.5] km s-1,
over which the single-dish
line-core (defined as the velocity range,
[-5.0, -3.5] km s-1,
over which the single-dish ![]() /
/
![]() is the largest, see F98),
and 6% in the line-wings.
Figure 5
displays the emission profile of the 8 PdBI-structures with
the single-dish
is the largest, see F98),
and 6% in the line-wings.
Figure 5
displays the emission profile of the 8 PdBI-structures with
the single-dish ![]() and
and ![]() (J=1-0)
emissions
over the same area (defined by the polygons of Fig. 4).
(J=1-0)
emissions
over the same area (defined by the polygons of Fig. 4).
Last, the PdBI-structures cover the full velocity range of the
single-dish CO line (see bottom panel of Fig. 5)
including
the far line-wings (e.g. structure #2 at
-5.5 km s-1). Note
however that the spectrum integrated over the whole mosaic peaks at
-3 km s-1, in the wing of the
single-dish ![]() line while its minimum, around -4.5 km s-1,
coincides with the peak of the single-dish
line while its minimum, around -4.5 km s-1,
coincides with the peak of the single-dish
![]() line (i.e. line core). The broad velocity distribution of the
PdBI-structures within the single-dish line coverage ensures that they
are not artefacts of radiative transfer. If they were, they
would appear preferentially at extreme velocities because
CO photons escape probability is larger there. There may be a
small effect since the power fraction in the line-wings is slightly
larger than in the line-core, but these fractions are a few percent in
each case. The structures found are therefore real edges in space and
velocity-space of larger structures.
line (i.e. line core). The broad velocity distribution of the
PdBI-structures within the single-dish line coverage ensures that they
are not artefacts of radiative transfer. If they were, they
would appear preferentially at extreme velocities because
CO photons escape probability is larger there. There may be a
small effect since the power fraction in the line-wings is slightly
larger than in the line-core, but these fractions are a few percent in
each case. The structures found are therefore real edges in space and
velocity-space of larger structures.
In this respect, it is interesting to place each
PdBI-structure in its ![]() (1-0)
larger-scale environment at the appropriate velocity (Fig. 8).
The PdBI-structures, marked as polygons, lie at the edge of structures
that extend beyond the field of the mosaic, up to
(1-0)
larger-scale environment at the appropriate velocity (Fig. 8).
The PdBI-structures, marked as polygons, lie at the edge of structures
that extend beyond the field of the mosaic, up to
![]() or 0.2 pc. In the case of structures #3, #4
and #5, the orientation of the edges of the large-scale
patterns is more visible in the
or 0.2 pc. In the case of structures #3, #4
and #5, the orientation of the edges of the large-scale
patterns is more visible in the
![]() (1-0) maps
(Fig. 9),
likely because of the
(1-0) maps
(Fig. 9),
likely because of the ![]() (1-0)
optical depth. This coincidence strongly suggests that the orientation
of the PdBI-structures is not only real but also rooted in the
larger-scale environment.
(1-0)
optical depth. This coincidence strongly suggests that the orientation
of the PdBI-structures is not only real but also rooted in the
larger-scale environment.
3.3 Pairs of parallel structures
![\begin{figure}
\par\includegraphics[angle=270,width=9cm,clip]{10963f9.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg56.png)
|
Figure 6: Structures #3 at -5 km s-1 and #8 at -1.5 km s-1 overplotted (resp. black and red contours) to display their close spatial correlation. |
| Open with DEXTER | |
One of the most challenging finding of this study is the fact that
among the eight elongated PdBI-structures, six form 3 close pairs
(separated by less than 20'' in projection) of structures
parallel within ![]() (Table 2
and Fig. 4).
These are the pairs of structures [#3, #8],
[#1, #5] and [#6, #7]. The average position-angles of
each pair
(Table 2
and Fig. 4).
These are the pairs of structures [#3, #8],
[#1, #5] and [#6, #7]. The average position-angles of
each pair ![]() 60, 100 and 168
60, 100 and 168
![]() are all different. Since the
structures (at least in the two first
pairs) are at different velocities, they are not due to artefacts of
the deconvolution process.
are all different. Since the
structures (at least in the two first
pairs) are at different velocities, they are not due to artefacts of
the deconvolution process.
The probability of a chance association of these three pairs
in the field of the mosaic is estimated to be at most 4 ![]() 10-9. It is the cube of the probability
of having one close pair of parallel structures. The latter is the
product of the probability, equal to 5.4
10-9. It is the cube of the probability
of having one close pair of parallel structures. The latter is the
product of the probability, equal to 5.4 ![]() 10-3, that two, out of eight, randomly oriented
straight structures be aligned within
10-3, that two, out of eight, randomly oriented
straight structures be aligned within
![]() 10
10![]() of each other (i.e. be together in a solid angle
of each other (i.e. be together in a solid angle
![]() sr),
by that (ranging between 0.2 and 0.3 depending on the
orientation of the pair) to be separated in projection by less
than 20'' in a mosaic of 1'
sr),
by that (ranging between 0.2 and 0.3 depending on the
orientation of the pair) to be separated in projection by less
than 20'' in a mosaic of 1' ![]() 2'. The probability
of a chance association
is only slightly underestimated if one considers the
structure #8 that is not straight, strictly speaking.
2'. The probability
of a chance association
is only slightly underestimated if one considers the
structure #8 that is not straight, strictly speaking.
Since the probability of a chance association of the observed
pairs is so low, we infer that the pairs are real
associations. This physical connexion is supported by the detail of the
spatial distribution of the ![]() emission integrated over the two velocity ranges of
structures #3 and #8 in Fig. 6: the
hole,
in the low-velocity emission is filled in by high-velocity emission,
while a common average orientation exists over
emission integrated over the two velocity ranges of
structures #3 and #8 in Fig. 6: the
hole,
in the low-velocity emission is filled in by high-velocity emission,
while a common average orientation exists over ![]() for the pair.
for the pair.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{10963f10.eps}\includegraphics[angle=-90,width=4.6cm,clip]{10963f11.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg60.png)
|
Figure 7: Position-velocity diagrams across the pair of structures [#3, #8]. Left: cut across the PdBI-only map. Center: rotated PdBI channel-map [-1.7, -1.3] km s-1, showing the direction and distance (horizontal size of the box) over which the CO emission is averaged for the cut. The cut runs from the southern to northern edge of the box. Right: same across the PdBI+30m data cube. |
| Open with DEXTER | |
Two position-velocity cuts (Fig. 7) across
the
pair [#3, #8] further illustrate what is meant by
sharp edges and real association. The cut across the PdBI-only data
cube (left panel) shows two CO peaks centered at offset
positions 40'' (resp. 46'') and velocities
-4.9 km s-1
(resp. -1.6 km s-1)
for the low- and high-velocity component respectively. These resolved
peaks are located exactly at the terminal pixels of the larger-scale
structures visible at the same velocities in the cut across the
PdBI+30m data cube (right panel). On this cut, the low-velocity
component may be followed over all offsets below
![]() ,
while the high-velocity component is visible at all offsets above
,
while the high-velocity component is visible at all offsets above
![]() .
This cut also illustrates a clear difference between the two velocity
components: the velocity of structure #3 (peak at
-5 km s-1 in the
PdBI spectrum of Fig. 5) falls
within
the velocity coverage of the bright extended gas (
.
This cut also illustrates a clear difference between the two velocity
components: the velocity of structure #3 (peak at
-5 km s-1 in the
PdBI spectrum of Fig. 5) falls
within
the velocity coverage of the bright extended gas (
![]() and
and
![]() line core in the single-dish spectra) while that of
structure #8 (peak at -1.5 km s-1
in the PdBI spectrum of Fig. 5) is not
blended with any other emission in that extreme velocity range and
appears as a weak emission in the single-dish spectrum
(i.e. a line-wing). Such blendings in space and
velocity projections with extended components resolved out by the
PdBI observations (Fig. 7, right
panel)
explain why such pairs of structures are so difficult to recognize in
single-dish observations or low sensitivity interferometric
observations.
line core in the single-dish spectra) while that of
structure #8 (peak at -1.5 km s-1
in the PdBI spectrum of Fig. 5) is not
blended with any other emission in that extreme velocity range and
appears as a weak emission in the single-dish spectrum
(i.e. a line-wing). Such blendings in space and
velocity projections with extended components resolved out by the
PdBI observations (Fig. 7, right
panel)
explain why such pairs of structures are so difficult to recognize in
single-dish observations or low sensitivity interferometric
observations.
The PdBI-structures cannot therefore be understood as isolated entities. Not only are they the sharp edges of larger CO-structures seen in the single-dish maps but also 6 out of 8 of these edges are paired. In the following, we will call the CO extended structures bounded by sharp edges either sharp-edged extended structures (SEES) or sharp-edged extended double structures (SEEDS) when they belong to a pair, to emphasize this essential property.
3.4 Velocity shears
The pairs being real associations, we ascribe a velocity-shear to each
of them. The projected separation
![]() and velocity
difference
and velocity
difference
![]() between the low- and
high-velocity components of each pair provide a
measure of the velocity-shear
between the low- and
high-velocity components of each pair provide a
measure of the velocity-shear
![]() .
We cannot determine whether this measure is a lower or upper limit of
the true velocity-shears because of the projection effects: both the
separation measured in the pos and the velocity
difference are lower limits.
.
We cannot determine whether this measure is a lower or upper limit of
the true velocity-shears because of the projection effects: both the
separation measured in the pos and the velocity
difference are lower limits.
The results are given in Table 4. The method
used is
illustrated in Fig. 7
(left panel) for the pair [#3, #8]: the projected
separation between the low- and high-velocity components
is 6'' or 4.5 mpc while the velocity separation is
3.5 km s-1, hence a
velocity-shear of 777 km s-1 pc-1,
the largest ever measured in CO emission in a molecular cloud
devoid of star formation activity. These values correspond to an
average over several positions along the shear direction, including
those where the two velocity components partially overlap. The
separation is therefore slightly underestimated by the averaging. Note
that one pair only, [#6, #7], has a very small velocity-shear,
probably because, in that case, the two velocity components involved in
the shear are mostly in the pos.
A rate-of-strain, defined as
![]() ,
and timescale
,
and timescale ![]() ,
are also given to help comparison with chemical models
(Sect. 7). The large observed velocity-shears translate into
timescales as short
as a few 103 yr, if
the Lagrangian and Eulerian views of the fluid can be exchanged (see Mordant
et al. 2002).
,
are also given to help comparison with chemical models
(Sect. 7). The large observed velocity-shears translate into
timescales as short
as a few 103 yr, if
the Lagrangian and Eulerian views of the fluid can be exchanged (see Mordant
et al. 2002).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10963f12.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg68.png)
|
Figure 8:
Integrated maps of the same velocity range as that defined
in Fig. 4
of the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10963f13.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg69.png)
|
Figure 9:
Same as Fig. 8
except that the single dish map is that of
|
| Open with DEXTER | |
3.5 The SEE(D)S are layers of CO emission
The small-scale structures detected by the PdBI have properties never seen before because the present observations are most sensitive and the field of view is large in comparison to the resolution: (1) they are not clumps, but elongated structures, only bounded by the limited size of the mosaic; (2) they all mark a sharp fall-off of the CO emission in selected velocity ranges: they are not isolated filaments, but the sharp edges (3 to 11 mpc in projection), simultaneously in space and velocity-space, of larger structures, the SEE(D)S, extending beyond the mosaic (l>0.2 pc); (3) six of these form three pairs of parallel structures at different velocities, with a small projected separation and the velocity-shears estimated for two of these pairs, several 100 km s-1 pc-1, are the largest ever measured in non-star forming clouds.
If the SEE(D)S were CO-emitting volumes (i.e. 3-dimensional
structures in space) of characteristic dimension l,
their edges would be surfaces commensurate with l2.
In projection, these edges
would appear as surfaces, also commensurate with l2
for a random viewing angle. Only if these surfaces were plane and
viewed edge-on (within ![]() deg for a projected
size less than one tenth of their real size) would these edges appear
as thin elongated structures. We rule this out on statistical grounds:
the mere fact that we detect 8 sharp CO-edges in the small
field-of-view of
the PdBI observations suggests that it is not a rare configuration and
that the eight sharp CO-edges are seen from random viewing angles. We
thus infer that the SEE(D)S are CO-layers, rather than volumes and that
their thickness is
deg for a projected
size less than one tenth of their real size) would these edges appear
as thin elongated structures. We rule this out on statistical grounds:
the mere fact that we detect 8 sharp CO-edges in the small
field-of-view of
the PdBI observations suggests that it is not a rare configuration and
that the eight sharp CO-edges are seen from random viewing angles. We
thus infer that the SEE(D)S are CO-layers, rather than volumes and that
their thickness is ![]() mpc
or less, on the order of the width of the PdBI-structures.
mpc
or less, on the order of the width of the PdBI-structures.
This statistical argument is reinforced by the presence of pairs. The SEEDS are structures that have sharp edges with only small or null overlaps. If their interface were 2-dimensional (i.e. if the SEEDS were volumes), the small overlap would occur only for an edge-on viewing, an unlikely case. Their interface is therefore 1-dimensional rather than 2-dimensional and the SEEDS are layers of CO emission. This ensures that under any viewing angle the two extended velocity components are detected with only a narrow or null spatial overlap in projection. The SEEDS could still be be 3-dimensional pure velocity-structures, where large velocity-shears produce sharp edges in channel maps of finite spectral resolution (see Sect. 3.1). However, with the same statistical argument as above, concerning density structures, we rule out the possibility that the SEEDS be 3-dimensional velocity structures. These must be CO layers.
In summary, the sharpness of the edges of the SEE(D)S, associated with the fact that we detect 8 cases in the mosaic and three close-pairs that do not overlap in space, implies that the SEE(D)S are thin layers of CO emission rather than volumes.
4 Gas density of the PdBI-structures
4.1 Estimates from CO line emission
Because of the elongated shape of most of the structures and the fact that they are edges of more extended emission, we have not tried to decompose the observed emission using clump finding algorithms such as GAUSSCLUMP (Stutzki & Guesten 1990). We estimate below the gas density in these structures in two independent ways and compare the results to those inferred from the dust continuum emission.
First, we compute upper limits of the ![]() densities
(Table 2)
by adopting the CO-to-
densities
(Table 2)
by adopting the CO-to-![]() conversion factor X= 1.56
conversion factor X= 1.56 ![]() 0.05
0.05 ![]() 1020
1020
![]() (
(
![]() )-1 (Hunter et al.
1997)
so that
)-1 (Hunter et al.
1997)
so that ![]()
![]()
![]() ,
for a los depth equal to the projected
thickness
,
for a los depth equal to the projected
thickness ![]() .
Since we are observing edges of layers (see Sect. 3.2), the
inferred densities are overestimated by the unknown factor
.
Since we are observing edges of layers (see Sect. 3.2), the
inferred densities are overestimated by the unknown factor
![]() .
The upper limits of the
.
The upper limits of the ![]() densities
derived from the galactic CO to
densities
derived from the galactic CO to ![]() conversion factor
(Table 2)
vary by a factor 10 only.
conversion factor
(Table 2)
vary by a factor 10 only.
Alternatively, one may use a LVG analysis to estimate the gas
properties in these structures. Two assumptions are made:
(1) the CO emission is not beam-diluted and
(2) the excitation is assumed to be the same as measured in
the same field with the IRAM-30m so that we adopt the line ratio
R(2-1/1-0)
=0.7 ![]() 0.1 (Falgarone
et al. 1998; Hily-Blant
et al. 2008).
This value may be representative of
the excitation of translucent molecular gas because the same line ratio
is found in different observations sampling a similar kind of molecular
gas (Pety et al. 2008).
Under these conditions, the CO column densities per unit
velocity are very well determined for all line temperatures. They are
given in Table 4
for the brightest, weakest, and most common CO peak
temperature observed. The inferred CO column densities differ
by only a factor 10 to 16 between the
brightest and weakest structure.
0.1 (Falgarone
et al. 1998; Hily-Blant
et al. 2008).
This value may be representative of
the excitation of translucent molecular gas because the same line ratio
is found in different observations sampling a similar kind of molecular
gas (Pety et al. 2008).
Under these conditions, the CO column densities per unit
velocity are very well determined for all line temperatures. They are
given in Table 4
for the brightest, weakest, and most common CO peak
temperature observed. The inferred CO column densities differ
by only a factor 10 to 16 between the
brightest and weakest structure.
Table 4
also gives the range of gas kinetic temperatures and associated range
of densities, thermal pressures
![]() and CO abundances of
possible solutions. The range of
temperatures is bounded towards high values by the thermal width of the
CO lines (Tk<250 K
for the broadest line, <35 K for the narrowest).
Solutions colder than 10 K are unlikely because the gas is
poorly shielded from the ambient ISRF. The CO optical depth is
therefore smaller than a few, in agreement with the results of
Paper II. A similar conclusion has been derived by Heithausen (2006)
after he
failed to detect the
and CO abundances of
possible solutions. The range of
temperatures is bounded towards high values by the thermal width of the
CO lines (Tk<250 K
for the broadest line, <35 K for the narrowest).
Solutions colder than 10 K are unlikely because the gas is
poorly shielded from the ambient ISRF. The CO optical depth is
therefore smaller than a few, in agreement with the results of
Paper II. A similar conclusion has been derived by Heithausen (2006)
after he
failed to detect the ![]() and
and ![]() (J=1-0)
line with the PdBI in a nearby small-area molecular structure (SAMS)
field.
(J=1-0)
line with the PdBI in a nearby small-area molecular structure (SAMS)
field.
Each set of ![]() density and kinetic temperature in the LVG solutions,
corresponds to a product
density and kinetic temperature in the LVG solutions,
corresponds to a product
![]() where
where ![]() is the CO abundance relative to
is the CO abundance relative to ![]() .
The range of CO abundances inferred from the
LVG computations are given in Table 2 for
.
The range of CO abundances inferred from the
LVG computations are given in Table 2 for
![]() .
They may be overestimated by the unknown ratio
.
They may be overestimated by the unknown ratio
![]() .
.
Table 3: Spatial and kinematic characteristics of the three pairs of parallel PdBI-only structures.
Table 4: Results of LVG radiative transfer calculations for representative observed values (see Table 2).
Table 4
shows the range of possible ![]() densities derived
from the LVG analysis for gas temperatures between
10 K and 200 K at most. The comparison of these
values with the upper limits inferred from the CO-to-
densities derived
from the LVG analysis for gas temperatures between
10 K and 200 K at most. The comparison of these
values with the upper limits inferred from the CO-to-![]() conversion factor (Table 2)
provides narrower
conversion factor (Table 2)
provides narrower ![]() density
ranges,
density
ranges, ![]() to 103
to 103
![]() ,
and 300 to 2
,
and 300 to 2 ![]() 103
103
![]() ,
for the weakest and most common structures respectively. In spite of
all the uncertainties, the two methods infer consistent
,
for the weakest and most common structures respectively. In spite of
all the uncertainties, the two methods infer consistent ![]() densities
that do not exceed 3
densities
that do not exceed 3 ![]() 103
103
![]() .
Moreover, whether the gas is cold or warm, its thermal pressure is
about the same, within a factor of a few, and is in harmony with that
inferred from carbon line observations in the local ISM that has an
average of
.
Moreover, whether the gas is cold or warm, its thermal pressure is
about the same, within a factor of a few, and is in harmony with that
inferred from carbon line observations in the local ISM that has an
average of ![]()
![]() 103 K
103 K
![]() with fluctuations up to
with fluctuations up to
![]() K
K
![]() (Jenkins &
Tripp 2007).
(Jenkins &
Tripp 2007).
4.2 Estimates from the dust continuum emission
In addition to ![]() lines, we have detected continuum emission. This emission is close to
the noise level, except for the large bright spot associated to the
lines, we have detected continuum emission. This emission is close to
the noise level, except for the large bright spot associated to the
![]() peak of emission. A comparison of the continuum emission with
the CO contour levels (Fig. 2)
suggests
that the elongated feature of continuum emission in the north-western
corner of the mosaic is also real.
peak of emission. A comparison of the continuum emission with
the CO contour levels (Fig. 2)
suggests
that the elongated feature of continuum emission in the north-western
corner of the mosaic is also real.
On the basis of the coincidence of the peaks of the
![]() and continuum emission in the mosaic, we ascribe the continuum emission
to thermal dust emission. The average continuum brightness over the
and continuum emission in the mosaic, we ascribe the continuum emission
to thermal dust emission. The average continuum brightness over the
![]() peak (Fig. 2)
is 2
peak (Fig. 2)
is 2 ![]() 1 mJy/beam, hence
1 mJy/beam, hence
![]()
![]() 0.5
0.5 ![]() 10-20
10-20
![]() Hz-1.
The dust opacity,
Hz-1.
The dust opacity,
![]() ,
depends on the dust temperature. We adopt a dust emissivity
,
depends on the dust temperature. We adopt a dust emissivity
![]()
![]()
![]() ,
deduced from COBE data for
dust heated by the ambient interstellar radiation field (ISRF) (Lagache
et al. 1999).
For
,
deduced from COBE data for
dust heated by the ambient interstellar radiation field (ISRF) (Lagache
et al. 1999).
For ![]() K and
K and ![]() GHz,
we find
GHz,
we find ![]()
![]() 10-7 and
10-7 and
![]()
![]() 1020
1020
![]() across the peak. For
across the peak. For
![]() K,
the most plausible value in translucent gas of the Solar Neighborhood,
this value would be lower by a factor 2 and for
K,
the most plausible value in translucent gas of the Solar Neighborhood,
this value would be lower by a factor 2 and for
![]() K
it would be larger by 40%, providing the range
K
it would be larger by 40%, providing the range
![]()
![]() 1020 to 5.6
1020 to 5.6 ![]() 1020
1020
![]() for high and low dust
temperatures, respectively. This estimate
of
for high and low dust
temperatures, respectively. This estimate
of ![]() may be compared to that inferred from
may be compared to that inferred from
![]() in the previous section. If we allow for a column density of
atomic hydrogen comparable to that of
in the previous section. If we allow for a column density of
atomic hydrogen comparable to that of ![]() ,
as found in the Polaris Flare by Heithausen
& Thaddeus (1990), the total H column
density inferred from CO for the peak of structure #5 ranges
between
,
as found in the Polaris Flare by Heithausen
& Thaddeus (1990), the total H column
density inferred from CO for the peak of structure #5 ranges
between
![]()
![]() 1019 to 2.4
1019 to 2.4 ![]() 1020
1020
![]() for the warm and cold
solutions respectively (assuming a size
of 9 mpc). The two ranges of values would overlap for
a depth a few times larger than the observed projected size, allowing
for warm and moderate density solutions where the dust temperature is
lower than that of the gas. Given the many uncertainties in the
different steps (the questionable validity of the CO line
analysis, the knowledge of dust emissivity and temperature), the
consistency between these two independent estimates is encouraging and
we are confident that we have detected the dust thermal emission of the
brightest small-scale
structure and that its
for the warm and cold
solutions respectively (assuming a size
of 9 mpc). The two ranges of values would overlap for
a depth a few times larger than the observed projected size, allowing
for warm and moderate density solutions where the dust temperature is
lower than that of the gas. Given the many uncertainties in the
different steps (the questionable validity of the CO line
analysis, the knowledge of dust emissivity and temperature), the
consistency between these two independent estimates is encouraging and
we are confident that we have detected the dust thermal emission of the
brightest small-scale
structure and that its ![]() density
is not higher than a few 103
density
is not higher than a few 103
![]() .
.
Aside from the peak, the rest of the structures have column
densities a few times smaller and their dust continuum emission is
expected to lie closer to the noise level. In addition, the surface
filling factor of the ![]() structures being large in the central area of the mosaic, the
PdBI visibility of the continuum emission of individual
structures is expected to be highly reduced compared to that of the
line which takes advantage of velocity-space. This may be the reason
that the continuum emission and the
structures being large in the central area of the mosaic, the
PdBI visibility of the continuum emission of individual
structures is expected to be highly reduced compared to that of the
line which takes advantage of velocity-space. This may be the reason
that the continuum emission and the
![]() emission do not coincide elsewhere: the continuum emission is more
heavily filtered out by the interferometer than the
emission do not coincide elsewhere: the continuum emission is more
heavily filtered out by the interferometer than the
![]() emission.
emission.
5 What are the SEE(D)S?
5.1 Manifestations of the small-scale intermittency of turbulence
The two largest velocity-shears given in Table 3 are more than
two
orders of magnitude larger (within the uncertainties due to
projections) than the average value of 1 km s-1 pc-1
estimated on the parsec scale in molecular clouds (Goldsmith
& Arquilla 1985).
The velocity field in these two SEEDS therefore significantly departs
from predictions based on scaling laws obtained from
![]() (1-0) in
molecular clouds, such as that shown in Fig. 10.
In spite of a significant scatter of the data points,
a power law
(1-0) in
molecular clouds, such as that shown in Fig. 10.
In spite of a significant scatter of the data points,
a power law
![]() characterizes the increase of the velocity
fluctuations with the size-scale l, at
least above
characterizes the increase of the velocity
fluctuations with the size-scale l, at
least above ![]() pc.
Below that scale-length, the scatter increases and
a slope 1/3 would not be inconsistent with the data.
According to the former scaling, the velocity-shear should increase
as l-1/2, therefore
by no more than
1401/2=
12 between 1 pc and 7 mpc. If the other scaling is
adopted, this factor becomes
1402/3= 26. Now, the observed shears increase by
more than two orders of magnitude between these two scales. This is
conspicuous in Fig. 10
where the 8 PdBI-structures of Table 2 are plotted
either
individually or as pairs (i.e. as they would be characterized
if the spatial resolution were poorer and individual structures were
not isolated in space, providing for instance a linewidth
pc.
Below that scale-length, the scatter increases and
a slope 1/3 would not be inconsistent with the data.
According to the former scaling, the velocity-shear should increase
as l-1/2, therefore
by no more than
1401/2=
12 between 1 pc and 7 mpc. If the other scaling is
adopted, this factor becomes
1402/3= 26. Now, the observed shears increase by
more than two orders of magnitude between these two scales. This is
conspicuous in Fig. 10
where the 8 PdBI-structures of Table 2 are plotted
either
individually or as pairs (i.e. as they would be characterized
if the spatial resolution were poorer and individual structures were
not isolated in space, providing for instance a linewidth
![]() km s-1
and a size
km s-1
and a size ![]() mpc
for the pair [#3, #8]).
mpc
for the pair [#3, #8]).
This result has to be put in the broader perspective described
in Sect. 1. The statistical analysis of the velocity field of
this high latitude cloud (Paper III, HF09) shows that the pdf
of the ![]() line-centroid velocity increments increasingly departs from Gaussian as
the lags over which the increments are measured decrease. The locus of
the positions that populate the pdf non-Gaussian
wings forms elongated and thin (
line-centroid velocity increments increasingly departs from Gaussian as
the lags over which the increments are measured decrease. The locus of
the positions that populate the pdf non-Gaussian
wings forms elongated and thin (
![]() ) structures that
have a remarkable coherence, up to more than a parsec. HF09 propose, on
this statistical basis, but also because of their thermal and chemical
properties given in Sect. 1, that these structures trace the
intermittency of turbulent dissipation in the field. The pair of
structures [#3, #8] belongs to that locus of
positions (see their Fig. 3).
The
extremely large velocity-shears measured in that small field are not
just exceptional values: they have to be understood as a manifestation
of the small-scale intermittency of interstellar turbulence, as studied
on statistical grounds in a much larger field.
) structures that
have a remarkable coherence, up to more than a parsec. HF09 propose, on
this statistical basis, but also because of their thermal and chemical
properties given in Sect. 1, that these structures trace the
intermittency of turbulent dissipation in the field. The pair of
structures [#3, #8] belongs to that locus of
positions (see their Fig. 3).
The
extremely large velocity-shears measured in that small field are not
just exceptional values: they have to be understood as a manifestation
of the small-scale intermittency of interstellar turbulence, as studied
on statistical grounds in a much larger field.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{10963f14.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg128.png)
|
Figure 10:
Size-linewidth relation for a large sample of
|
| Open with DEXTER | |
5.2 The emergence of CO-rich gas
The PdBI-structures mark sharp edges in the
![]() emission. As discussed in Sect. 3.3 and illustrated
in Fig. 7,
the CO emission of space-velocity structures extending over
arcminutes (the SEE(D)S) drops below the detection level
over 4.3'' (the resolution). Therefore, several questions
arise: what is the nature of the undetected gas that provides the
continuity of the flow? Is it undetected because its density is too low
to excite the J=1-0 transition of
emission. As discussed in Sect. 3.3 and illustrated
in Fig. 7,
the CO emission of space-velocity structures extending over
arcminutes (the SEE(D)S) drops below the detection level
over 4.3'' (the resolution). Therefore, several questions
arise: what is the nature of the undetected gas that provides the
continuity of the flow? Is it undetected because its density is too low
to excite the J=1-0 transition of
![]() ? Or is it
dense enough but with too low a CO abundance? For
simplicity, in the following discussion, ``CO-rich'' qualifies the gas
with
? Or is it
dense enough but with too low a CO abundance? For
simplicity, in the following discussion, ``CO-rich'' qualifies the gas
with ![]() ,
the CO abundance of the weakest detected structure
(Table 4),
and ``CO-poor'' the gas with a lower CO abundance.
,
the CO abundance of the weakest detected structure
(Table 4),
and ``CO-poor'' the gas with a lower CO abundance.
Acording to LVG calculations, the 3![]() detection limit of
our observations allows us to detect CO column densities as
low as
detection limit of
our observations allows us to detect CO column densities as
low as ![]()
![]() a few 1014
a few 1014
![]() in gas as diluted as
in gas as diluted as
![]()
![]() ,
at any temperature, and for a velocity dispersion of
0.2 km s-1, characteristic of
the structures found. This detection limit is very low. Therefore, if
the undetected gas on the other side of the edge is CO-rich (with a
total hydrogen column density comparable to that of the detected part),
it has to be at a density lower than
,
at any temperature, and for a velocity dispersion of
0.2 km s-1, characteristic of
the structures found. This detection limit is very low. Therefore, if
the undetected gas on the other side of the edge is CO-rich (with a
total hydrogen column density comparable to that of the detected part),
it has to be at a density lower than
![]()
![]() ,
not to excite the
,
not to excite the ![]() (J=1-0)
transition at a detectable level. We rule out this possibility because
this density is that of the CNM and it is unlikely that gas at that
density be CO-rich (see also the models of Pety
et al. 2008).
(J=1-0)
transition at a detectable level. We rule out this possibility because
this density is that of the CNM and it is unlikely that gas at that
density be CO-rich (see also the models of Pety
et al. 2008).
The alternative is that the undetected gas is CO-poor and that
it is not its low density but its low CO abundance that makes
it escape detection in ![]() (J=1-0).
Given the sharpness of the edges of the SEE(D)S, between 3 and
11 mpc (Table 2),
the process responsible for this transition has to be able to generate
a significant CO enrichment over that small scale.
(J=1-0).
Given the sharpness of the edges of the SEE(D)S, between 3 and
11 mpc (Table 2),
the process responsible for this transition has to be able to generate
a significant CO enrichment over that small scale.
In the above, we rule out the possibility that the sharp edges (i.e. the PdBI-structures) mark photodissociation fronts, because the orientations of such fronts would not be randomly distributed, as is observed. Moreover, there is no source of UV photons in that high-latitude cloud and the radiation field there is the ambient galactic ISRF. Photodissociation fronts would not have different orientations depending on gas velocities varying by only a few km s-1. The sharp edges are not either folds in layers of CO emission because those who belong to SEES (single structures) lack the second part of the layer, and those who belong to SEEDS have the two parts at different velocities.
We thus infer that the SEE(D)S are the outcome of a dynamical
process, that involves large velocity-shears, and takes place in a gas
undetected in ![]() (1-0) emission,
because it is CO-poor, not because it is too diluted. This gas may be
the CNM and the dynamical process has to be able to enrich the CNM in
CO molecules within a few 103 yr
and over a few milliparsec.
(1-0) emission,
because it is CO-poor, not because it is too diluted. This gas may be
the CNM and the dynamical process has to be able to enrich the CNM in
CO molecules within a few 103 yr
and over a few milliparsec.
6 Comparison with other data sets
Our results broaden the perspective regarding the existence of
small-scale CO structures in molecular clouds. Heithausen
(2002, 2004,
2006)
has found small-area
molecular structures (SAMS) that are truly isolated
CO features in the high latitude sky.
PdBI observations of the SAMS (Heithausen
2004) reveal bright sub-structures that are all brighter and
broader than our PdBI-structures. Unfortunately, the emission has been
decomposed into clumps, a questionable procedure because short-spacings
have not been combined to the PdBI data and the CLEAN
procedure tends to create structures on the
beam scale. The large ![]() densities
inferred are therefore likely overestimated. An interesting
feature can be seen in the channel maps, though. Two elongated thin
patterns cross the field, reminiscent for their thickness and length of
what is found in the present study. A velocity shear
of 180 km s-1 pc-1
is estimated between these two elongated structures for
a velocity separation of 0.9 km s-1
and a pos spatial separation
of 10'' on average (or 5 mpc at the assumed
distance of 100 pc). This velocity-shear is thus commensurable
with the two largest values found in the Polaris field.
densities
inferred are therefore likely overestimated. An interesting
feature can be seen in the channel maps, though. Two elongated thin
patterns cross the field, reminiscent for their thickness and length of
what is found in the present study. A velocity shear
of 180 km s-1 pc-1
is estimated between these two elongated structures for
a velocity separation of 0.9 km s-1
and a pos spatial separation
of 10'' on average (or 5 mpc at the assumed
distance of 100 pc). This velocity-shear is thus commensurable
with the two largest values found in the Polaris field.
Ingalls
et al.
(2007) have detected milliparsec clumps in a high latitude
cloud. They are located in the line-wings of the
CO single-dish spectrum and they model them as tiny
(1-5 mpc) clumps of density of a few 103
![]() .
A more detailed comparison with the present results is not
possible because they do not analyze individual structures.
.
A more detailed comparison with the present results is not
possible because they do not analyze individual structures.
Sakamoto
& Sunada
(2003) have discovered a number of CO small-scale
structures in the low-obscuration regions of long strip maps beyond the
edge of the Taurus molecular cloud. Their main characteristics are
their large line-width and their sudden appearance, and disappearance,
within 0.03 to 0.1 pc. The authors interpret these
features as the signature of structure formation induced by the thermal
instability of the warm neutral medium (WNM) in the turbulent cloud
envelope. These CO small-scale
structures thus carry the kinematic signatures of the embedding WNM,
hence their large velocity dispersion, both interclump and intraclump.
The inferred line ratio,
R(2-1)/(1-0)=0.4,
is low, consistent with a low excitation temperature and ![]() densities
lower than
densities
lower than ![]()
![]() .
The authors propose that their small-scale CO structures
pinpoint molecule-forming regions, driven by
the thermal instability in the turbulent diffuse ISM.
.
The authors propose that their small-scale CO structures
pinpoint molecule-forming regions, driven by
the thermal instability in the turbulent diffuse ISM.
Our data therefore share many properties with these different
samples. Figure 10
allows a comparison of the projected size and linewidth of the above
milliparsec-scale structures with those of
![]() (1-0)
structures identified in data cubes from non-star-forming regions of
all sizes, up to several 100 pc (see the relevant references
in Appendix B). Although some of them (a few
individual PdBI-structures of our sample) further extend the general
scaling law
down to 2 mpc, most of them significantly depart from this law
by a large factor. As already mentioned in Sect. 5.1,
the departure is the largest for the pairs of PdBI-structures, as they
would appear if they were not resolved spatially i.e. as anomalously
broad structures with respect to their size. The increased scatter of
velocity-widths of the structures below 0.1 pc down to
1 mpc may be seen as another manifestation of the
intermittency of turbulence in translucent
molecular gas.
(1-0)
structures identified in data cubes from non-star-forming regions of
all sizes, up to several 100 pc (see the relevant references
in Appendix B). Although some of them (a few
individual PdBI-structures of our sample) further extend the general
scaling law
down to 2 mpc, most of them significantly depart from this law
by a large factor. As already mentioned in Sect. 5.1,
the departure is the largest for the pairs of PdBI-structures, as they
would appear if they were not resolved spatially i.e. as anomalously
broad structures with respect to their size. The increased scatter of
velocity-widths of the structures below 0.1 pc down to
1 mpc may be seen as another manifestation of the
intermittency of turbulence in translucent
molecular gas.
7 Comparison with experiments, numerical simulations and chemical models
The present data set discloses small-scale structures of intense
velocity-shears that carry the statistical properties of intermittency
and, in conjunction with that of HF09, reveals a connexion between
parsec-scale and milliparsec scale velocity-shears. The dynamic range
of coupled scales in the Polaris Flare is therefore on the order
of
![]() .
Moreover, velocity differences, up to 3.5 km s-1,
close to the rms velocity dispersion of the
CNM turbulence measured on 10-pc scales (or more) (Miville-Deschênes
et al. 2003; Haud
& Kalberla 2007), are
found in the PdBI field over
.
Moreover, velocity differences, up to 3.5 km s-1,
close to the rms velocity dispersion of the
CNM turbulence measured on 10-pc scales (or more) (Miville-Deschênes
et al. 2003; Haud
& Kalberla 2007), are
found in the PdBI field over ![]() 10 mpc, without any detected density
enhancement nor shock signature. We argue that the SEE(D)S are the
CO-rich parts of straining sheets in a gas undetected in
10 mpc, without any detected density
enhancement nor shock signature. We argue that the SEE(D)S are the
CO-rich parts of straining sheets in a gas undetected in
![]() (1-0),
likely the CNM, and that the fast CO enrichment is driven by
enhanced turbulent dissipation in the intense velocity-shears. We show
below that these findings may be understood in the light of recent
numerical simulations of incompressible and compressible turbulence,
and the TDR chemical model of Godard
et al. (2009).
(1-0),
likely the CNM, and that the fast CO enrichment is driven by
enhanced turbulent dissipation in the intense velocity-shears. We show
below that these findings may be understood in the light of recent
numerical simulations of incompressible and compressible turbulence,
and the TDR chemical model of Godard
et al. (2009).
The fact that the most dissipative structures appear to be layers of intense strain-rate is consistent with recent results of numerical simulations of incompressible turbulence at high Reynolds number (Moisy & Jiménez 2004) and laboratory experiments (Ganapathisubramani et al. 2008). These regions are not randomly distributed and form inertial-range clusters (Moisy & Jiménez 2004) or develop at the boundaries regions of high level of vorticity (i.e. vortex tubes) (Ganapathisubramani et al. 2008). Coupling between small-scale statistics of the velocity field and the properties of the large-scale flows is also clearly probed in the high-Re numerical simulations of Mininni et al. (2006): correlations are observed between large-scale shear and small-scale intermittency.
In compressible turbulence, the fact that the most dissipative
structures are shear-layers is not expected. Yet, in their
hydrodynamical simulations of mildly compressible turbulence, Porter et al.
(2002)
show that the compressible component of the velocity field is weaker
than its solenoidal counterpart by a factor ![]() ,
independent of the nature of the driving process (compressible or
solenoidal) and Vestuto
et al. (2003) find that the energy fraction in the
solenoidal modes is dominant and increases with the magnetic field
intensity in compressible magneto-hydrodynamical (MHD) turbulence.
These numerical experiments are still far from approaching the ISM
conditions but they suggest that turbulent dissipation may occur
primarily in solenoidal modes, i.e. without direct gas
compression, and that the properties of the small scales are coupled to
the large-scales.
,
independent of the nature of the driving process (compressible or
solenoidal) and Vestuto
et al. (2003) find that the energy fraction in the
solenoidal modes is dominant and increases with the magnetic field
intensity in compressible magneto-hydrodynamical (MHD) turbulence.
These numerical experiments are still far from approaching the ISM
conditions but they suggest that turbulent dissipation may occur
primarily in solenoidal modes, i.e. without direct gas
compression, and that the properties of the small scales are coupled to
the large-scales.
In the TDR models of Godard
et al. (2009), the chemical enrichment of the CNM is
driven by high gas temperatures and enhanced ion-neutral drift, without
density enhancement. The temperature increase is due to viscous
dissipation in the layers of largest velocity-shears at the boundaries
of coherent vortices![]() .
The large ion-neutral drift occurs in the layers of largest rotational
velocity in which ions and magnetic fields decouple from neutrals.
These two dissipative processes trigger endothermic chemical reactions,
blocked at the low temperature of the CNM. Enrichments
consistent with observations are obtained for turbulent rates-of-strain
a= 10-11 s-1
induced by large scale turbulence and for moderately dense gas (
.
The large ion-neutral drift occurs in the layers of largest rotational
velocity in which ions and magnetic fields decouple from neutrals.
These two dissipative processes trigger endothermic chemical reactions,
blocked at the low temperature of the CNM. Enrichments
consistent with observations are obtained for turbulent rates-of-strain
a= 10-11 s-1
induced by large scale turbulence and for moderately dense gas (
![]()
![]() )
characteristic of the CNM. There is no direct determination of the
rates-of-strain generated by turbulence in the CNM. We note however
that the largest observed velocity-shear (Table 3) corresponds,
if the
projected quantities provide reasonable estimates, to a comparable
rate-of-strain. The range of observed CO column densities from
)
characteristic of the CNM. There is no direct determination of the
rates-of-strain generated by turbulence in the CNM. We note however
that the largest observed velocity-shear (Table 3) corresponds,
if the
projected quantities provide reasonable estimates, to a comparable
rate-of-strain. The range of observed CO column densities from
![]() to
1.6
to
1.6 ![]() 1015
1015
![]() can be reproduced by intense
velocity-shears occurring in gas of
density 100 to 200
can be reproduced by intense
velocity-shears occurring in gas of
density 100 to 200
![]() .
In this framework, the energy source tapped to enrich the medium in
molecules is the supersonic turbulence of the CNM.
.
In this framework, the energy source tapped to enrich the medium in
molecules is the supersonic turbulence of the CNM.
The association between the large observed velocity-shears and local enhanced dissipation rate is therefore supported not only by the earlier works presented in the Introduction but also by a quantitative agreement between the TDR chemical models and the present observational results. We cannot rule out however a contribution of low-velocity C-shocks to the turbulent dissipation. If they propagate in the CNM, they are not visible in the CO lines. Such shocks are not yet reliably modelled (Hily-Blant et al., in preparation).
8 Conclusions and perspectives
IRAM-PdBI observations of a mosaic of 13 fields in the
turbulent environment of a low-mass dense core have disclosed small and
weak ![]() (1-0) structures in
translucent molecular gas. They are straight and elongated structures
but they are not filaments because, once merged with short-spacings
data, the PdBI-structures appear as the sharp edges of larger-scale
structures. Their thickness is as small as
(1-0) structures in
translucent molecular gas. They are straight and elongated structures
but they are not filaments because, once merged with short-spacings
data, the PdBI-structures appear as the sharp edges of larger-scale
structures. Their thickness is as small as ![]() 3 mpc
(600 AU), and their length, up to 70 mpc, is only
limited by the size of the mosaic. Their CO column density is
a well determined quantity for the excitation conditions found at
larger scale and is in the range
3 mpc
(600 AU), and their length, up to 70 mpc, is only
limited by the size of the mosaic. Their CO column density is
a well determined quantity for the excitation conditions found at
larger scale and is in the range
![]() to 1015
to 1015
![]() .
Their
.
Their ![]() density,
estimated in several ways, including the continuum emission of the
brightest structure, does not exceed a few 103
density,
estimated in several ways, including the continuum emission of the
brightest structure, does not exceed a few 103
![]() .
Their well-distributed orientations can be followed in the larger-scale
environment of the field. Six of them form three pairs of
quasi-parallel structures, physically related. The velocity-shears
estimated for the three pairs include the largest ever measured in
non-star-forming clouds
(up to 780 km s-1 pc-1).
.
Their well-distributed orientations can be followed in the larger-scale
environment of the field. Six of them form three pairs of
quasi-parallel structures, physically related. The velocity-shears
estimated for the three pairs include the largest ever measured in
non-star-forming clouds
(up to 780 km s-1 pc-1).
The PdBI-structures are therefore not isolated and are the edges of so-called SEE(D)S for sharp-edged extended (double) structures. We show that the SEE(D)S are thin layers of CO-rich gas and that their sharp edges pinpoint a small-scale dynamical process, at the origin of the CO contrast detected by the PdBI. We propose that the SEE(D)S are the outcomes of the chemical enrichment driven by intense dissipation occurring in large velocity-shears and that they are CO-rich layers swept along by the straining field of CNM turbulence.
The present work is the first detection of mpc-scale intense velocity-shears belonging to a parsec-scale shear. The large departure from average of the kinematic properties of these structures, confirms that they are a manifestation of the small-scale intermittency of turbulence in this high latitude field, a property already established on statistical grounds (HF09). The values of the velocity-shears (or rate-of-strain) provide a quantitative constraint on the dissipation rate that can be compared to chemical models. The link between the turbulent dissipation in the diffuse gas and the dense core observed in the vicinity of the PdBI mosaic (Fig. 1) still remains to be established.
Last, we would like to stress that sub-structure still exists in these mpc-scale structures of the diffuse ISM and that the next generation of interferometers (e.g. ALMA) should be able to observe gas at the dissipation scale of turbulence (that is still unknown) or at least observe the effects on the ISM (temperature, excitation, molecular abundances) of the huge release of energy expected to occur there.
AcknowledgementsWe thank the IRAM staff at Plateau de Bure and Grenoble for their support during the observations. E.F. is most grateful to Michael Dumke, Emmanuel Dartois, Anne Dutrey and Stéphane Guilloteau for their help during the early stages of the data reduction. E.F. also acknowledges the stimulant discussions over the years with E. Ostriker, P. Hennebelle, A. Lazarian, B. G. Elmegreen, M. M. Mac-Low, E. Vasquez-Semadeni and many others that cannot be listed here. We thank J. Scalo, our (formerly anonymous) referee, for his dedicated efforts at making us write our observational paper accessible to numericists.
Appendix A: Noise level in the mosaic
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{10963f15.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa10963-08/Timg136.png)
|
Figure A.1:
Map of the noise level in
|
| Open with DEXTER | |
Mosaic noise is inhomogeneous due to primary beam correction. This is shown in Fig. A.1. The 13-field mosaic produces a large area with uniform noise level. Only at the edge of the mosaic does it increase sharply due to the primary beam correction (the contour shown are at a 2-4 sigma level, 1 sigma being measured at the map center on a channel devoided of signal).
Appendix B: The size-linewidth scaling law
Molecular cloud parameters have long been determined as those of
three-dimensional structures isolated in the four-dimensional space of
the molecular line data sets
TL(x,y,vz),
the line brightness temperature being a function of position in the pos
(two coordinates x,y),
and one spectral dimension, the projected velocity on the los
direction vz.
In this 4D space, 3D structures are isolated
following different methods (Falgarone
et al. 1992;
Loren 1989;
Williams
et al. 1994; Falgarone
& Perault 1987;
Stutzki
& Guesten 1990). The size and linewidth of the large
number of clouds displayed in Fig. 10 have been
obtained by using published values, corrected in several cases to allow
the size and linewidth obey the same definitions in all the samples
(see Falgarone 1998).
The structures are identified in
![]() (1-0) molecular
line surveys of the central parts of the Galaxy (stars, Dame et al. 1986;
open
triangles Solomon
et al.
1987) and of the third quadrant (open hexagons, May et al. 1997),
in the
Rosette (crosses) and Maddalena (open squares) molecular clouds (Williams
et al. 1994),
in non-star-forming clouds (solid triangles, Falgarone
& Perault 1987; solid squares, Falgarone
et al. 1992;
tripods, Lemme et al.
1995),
in
(1-0) molecular
line surveys of the central parts of the Galaxy (stars, Dame et al. 1986;
open
triangles Solomon
et al.
1987) and of the third quadrant (open hexagons, May et al. 1997),
in the
Rosette (crosses) and Maddalena (open squares) molecular clouds (Williams
et al. 1994),
in non-star-forming clouds (solid triangles, Falgarone
& Perault 1987; solid squares, Falgarone
et al. 1992;
tripods, Lemme et al.
1995),
in ![]() Ophiuchus
(solid hexagons, Loren
1989)
and in a
high latitude cloud (starred triangles, Heithausen
et al. 1998).
Ophiuchus
(solid hexagons, Loren
1989)
and in a
high latitude cloud (starred triangles, Heithausen
et al. 1998).
References
- Anselmet, F., Antonia, R. A., & Danaila, L. 2001, Planet. Space Sci., 49, 1177 [CrossRef] [NASA ADS]
- Arnéodo, A., Benzi, R., Berg, J., et al. 2008, Phys. Rev. Lett., 100, 254504 [CrossRef] [NASA ADS]
- Chevillard, L., Roux, S. G., Lévêque, E., et al. 2005, Phys. Rev. Lett., 95, 064501 [CrossRef] [NASA ADS]
- Dame, T. M., Elmegreen, B. G., Cohen, R. S., & Thaddeus, P. 1986, ApJ, 305, 892 [CrossRef] [NASA ADS]
- de Avillez, M. A., & Breitschwerdt, D. 2007, ApJ, 665, L35 [CrossRef] [NASA ADS]
- Elmegreen, B. G., & Scalo, J. 2004, ARA&A, 42, 211 [CrossRef] [NASA ADS]
- Falgarone, E. 1998, in Starbursts: Triggers, Nature, and Evolution, Les Houches School, ed. B. Guiderdoni, & A. Kembhavi, 41
- Falgarone, E., & Perault, M. 1987, in Physical Processes in Interstellar Clouds, ed. G. E. Morfill, & M. Scholer, NATO ASIC Proc., 210, 59
- Falgarone, E., Puget, J.-L., & Perault, M. 1992, A&A, 257, 715 [NASA ADS]
- Falgarone, E., Panis, J.-F., Heithausen, A., et al. 1998, A&A, 331, 669 [NASA ADS]
- Falgarone, E., Verstraete, L., Pineau Des Forêts, G., & Hily-Blant, P. 2005, A&A, 433, 997 [EDP Sciences] [CrossRef] [NASA ADS]
- Falgarone, E., Pineau Des Forêts, G., Hily-Blant, P., & Schilke, P. 2006, A&A, 452, 511 [EDP Sciences] [CrossRef] [NASA ADS]
- Frisch, U. 1995, Turbulence. The legacy of A.N. Kolmogorov, ed. U. Frisch
- Ganapathisubramani, B., Lakshminarasimhan, K., & Clemens, N. T. 2008, Journal of Fluid Mechanics, 598, 141 [CrossRef] [NASA ADS]
- Godard, B., Falgarone, E., & Pineau Des Forêts, G. 2009, A&A, 495, 847 [EDP Sciences] [CrossRef] [NASA ADS]
- Goldsmith, P. F., & Arquilla, R. 1985, in Protostars and Planets II, ed. D. C. Black, & M. S. Matthews, 137
- Goldsmith, P. F., Heyer, M., Narayanan, G., et al. 2008, ApJ, 680, 428 [CrossRef] [NASA ADS]
- Gredel, R., Pineau des Forêts, G., & Federman, S. R. 2002, A&A, 389, 993 [EDP Sciences] [CrossRef] [NASA ADS]
- Gueth, F. 2001, in Proceedings from IRAM Millimeter Interferometry Summer School 2, 207
- Gueth, F., Guilloteau, S., & Bachiller, R. 1996, A&A, 307, 891 [NASA ADS]
- Haud, U., & Kalberla, P. M. W. 2007, A&A, 466, 555 [EDP Sciences] [CrossRef] [NASA ADS]
- Heiles, C. 2007, in SINS - Small Ionized and Neutral Structures in the Diffuse Interstellar Medium, ed. M. Haverkorn, & W. M. Goss, ASP Conf. Ser., 365, 3
- Heithausen, A. 1999, A&A, 349, L53 [NASA ADS]
- Heithausen, A. 2004, ApJ, 606, L13 [CrossRef] [NASA ADS]
- Heithausen, A. 2006, A&A, 450, 193 [EDP Sciences] [CrossRef] [NASA ADS]
- Heithausen, A., & Thaddeus, P. 1990, ApJ, 353, L49 [CrossRef] [NASA ADS]
- Heithausen, A., Bensch, F., Stutzki, J., Falgarone, E., & Panis, J. F. 1998, A&A, 331, L65 [NASA ADS]
- Heithausen, A., Bertoldi, F., & Bensch, F. 2002, A&A, 383, 591 [EDP Sciences] [CrossRef] [NASA ADS]
- Hily-Blant, P., & Falgarone, E. 2007, A&A, 469, 173 [EDP Sciences] [CrossRef] [NASA ADS]
- Hily-Blant, P., & Falgarone, E. 2009, A&A, 500, L29 [EDP Sciences] [CrossRef] [NASA ADS]
- Hily-Blant, P., Falgarone, E., & Pety, J. 2008, A&A, 481, 367 [EDP Sciences] [CrossRef] [NASA ADS]
- Hunter, S. D., Bertsch, D. L., Catelli, J. R., et al. 1997, ApJ, 481, 205 [CrossRef] [NASA ADS]
- Ingalls, J. G., Bania, T. M., Lane, A. P., Rumitz, M., & Stark, A. A. 2000, ApJ, 535, 211 [CrossRef] [NASA ADS]
- Ingalls, J. G., Reach, W. T., Bania, T. M., & Carpenter, J. M. 2007, in SINS - Small Ionized and Neutral Structures in the Diffuse Interstellar Medium, ed. M. Haverkorn, & W. M. Goss, ASP Conf. Ser., 365, 201
- Jenkins, E. B., & Tripp, T. M. 2007, in SINS - Small Ionized and Neutral Structures in the Diffuse Interstellar Medium, ed. M. Haverkorn, & W. M. Goss, ASP Conf. Ser., 365, 51
- Joulain, K., Falgarone, E., Des Forets, G. P., & Flower, D. 1998, A&A, 340, 241 [NASA ADS]
- Joung, M. K. R., & Mac Low, M.-M. 2006, ApJ, 653, 1266 [CrossRef] [NASA ADS]
- Lacour, S., Ziskin, V., Hébrard, G., et al. 2005, ApJ, 627, 251 [CrossRef] [NASA ADS]
- Lagache, G., Abergel, A., Boulanger, F., Désert, F. X., & Puget, J.-L. 1999, A&A, 344, 322 [NASA ADS]
- Lemme, C., Walmsley, C. M., Wilson, T. L., & Muders, D. 1995, A&A, 302, 509 [NASA ADS]
- Lis, D. C., Pety, J., Phillips, T. G., & Falgarone, E. 1996, ApJ, 463, 623 [CrossRef] [NASA ADS]
- Liszt, H. S., & Lucas, R. 1998, A&A, 339, 561 [NASA ADS]
- Loren, R. B. 1989, ApJ, 338, 902 [CrossRef] [NASA ADS]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [CrossRef] [NASA ADS]
- Mac Low, M.-M., Klessen, R. S., Burkert, A., & Smith, M. D. 1998, Phys. Rev. Lett., 80, 2754 [CrossRef] [NASA ADS]
- May, J., Alvarez, H., & Bronfman, L. 1997, A&A, 327, 325 [NASA ADS]
- Mininni, P. D., Alexakis, A., & Pouquet, A. 2006, Phys. Rev. E, 74, 016303 [CrossRef] [NASA ADS]
- Miville-Deschênes, M.-A., Joncas, G., Falgarone, E., & Boulanger, F. 2003, A&A, 411, 109 [EDP Sciences] [CrossRef] [NASA ADS]
- Moffatt, H. K., Kida, S., & Ohkitani, K. 1994, Journal of Fluid Mechanics, 259, 241 [CrossRef] [NASA ADS]
- Moisy, F., & Jiménez, J. 2004, Journal of Fluid Mechanics, 513, 111 [CrossRef] [NASA ADS]
- Mordant, N., Delour, J., Léveque, E., Arnéodo, A., & Pinton, J.-F. 2002, Phys. Rev. Lett., 89, 254502 [CrossRef] [NASA ADS]
- Pety, J. 2005, in SF2A-2005: Semaine de l'Astrophysique Française, ed. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 721
- Pety, J., & Falgarone, E. 2003, A&A, 412, 417 [EDP Sciences] [CrossRef] [NASA ADS]
- Pety, J., Lucas, R., & Liszt, H. S. 2008, A&A, 489, 217 [EDP Sciences] [CrossRef] [NASA ADS]
- Porter, D., Pouquet, A., & Woodward, P. 2002, Phys. Rev. E, 66, 026301 [CrossRef] [NASA ADS]
- Sakamoto, S., & Sunada, K. 2003, ApJ, 594, 340 [CrossRef] [NASA ADS]
- Scalo, J., & Elmegreen, B. G. 2004, ARA&A, 42, 275 [CrossRef] [NASA ADS]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [CrossRef] [NASA ADS]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [CrossRef] [NASA ADS]
- Stutzki, J., & Guesten, R. 1990, ApJ, 356, 513 [CrossRef] [NASA ADS]
- Vestuto, J. G., Ostriker, E. C., & Stone, J. M. 2003, ApJ, 590, 858 [CrossRef] [NASA ADS]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [CrossRef] [NASA ADS]
Footnotes
- ... scale
![[*]](/icons/foot_motif.png)
- Based on observations obtained with the IRAM Plateau de Bure interferometer and 30m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
- ... turbulence
![[*]](/icons/foot_motif.png)
- Intermittency here refers to the empirical property of high Reynolds number turbulence to present an excess of rare events compared to Gaussian statistics, this excess being increasingly large as velocity fluctuations at smaller and smaller scales are considered (see the review of Anselmet et al. 2001). Although the origin of intermittency is still an open issue (but see Arnéodo et al. 2008; Mordant et al. 2002; Chevillard et al. 2005), it is quantitatively characterized by the anomalous scaling of the high-order structure functions of the velocity and the shape of non-Gaussian pdfs of quantities involving velocity derivatives (e.g. Frisch 1995).
- ... velocity-shears
![[*]](/icons/foot_motif.png)
- We use velocity-shear rather than velocity-gradient because the observations provide cross-derivatives of the velocity field, i.e. the displacement measured in the plane-of-the-sky (pos) is perpendicular to the line-of-sight velocity.
- ... GILDASf
![[*]](/icons/foot_motif.png)
- See http://www.iram.fr/IRAMFR/GILDAS for more information about the GILDAS softwares.
- ... vortices
![[*]](/icons/foot_motif.png)
- The ``sinews of turbulence'' put forward by Moffatt et al. (1994) that link large-scale strain and small-scale vorticity.
All Tables
Table
1: Observation parameters. The projection center of all the
data displayed
in this paper is:
![]() ,
,
![]() .
.
Table
2: Spatial and kinematic characteristics of the
![]() PdBI-only structures.
PdBI-only structures.
Table 3: Spatial and kinematic characteristics of the three pairs of parallel PdBI-only structures.
Table 4: Results of LVG radiative transfer calculations for representative observed values (see Table 2).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


