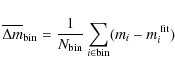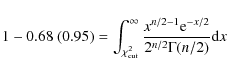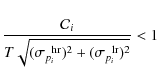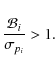| Issue |
A&A
Volume 506, Number 3, November II 2009
|
|
|---|---|---|
| Page(s) | 1095 - 1105 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200912811 | |
| Published online | 03 September 2009 | |
A&A 506, 1095-1105 (2009)
Cosmological parameter extraction and biases from type Ia supernova magnitude evolution
S. Linden1 - J.-M. Virey1 - A. Tilquin2
1 - Centre de Physique Théorique![]() , Université de Provence, CNRS de Luminy case 907, 13288 Marseille Cedex 9, France
, Université de Provence, CNRS de Luminy case 907, 13288 Marseille Cedex 9, France
2 - Centre de Physique des Particules de Marseille, Université de la
Mediterranée, CNRS de Luminy case 907, 13288 Marseille Cedex 9, France
Received 2 July 2009 / Accepted 11 August 2009
Abstract
We study different one-parametric models of type Ia supernova
magnitude evolution on cosmic time scales. Constraints on cosmological
and supernova evolution parameters are obtained by combined fits on the
actual data coming from supernovae, the cosmic microwave background,
and baryonic acoustic oscillations. We find that the best-fit values
imply supernova magnitude evolution such that high-redshift supernovae
appear some percent brighter than would be expected in a standard
cosmos with a dark energy component. However, the errors on the
evolution parameters are of the same order, and data are consistent
with nonevolving magnitudes at the ![]() level,
except for special cases. We simulate a future data scenario where
SN magnitude evolution is allowed for, and neglect the possibility
of such an evolution in the fit. We find the fiducial models for which
the wrong model assumption of nonevolving SN magnitude is not
detectable, and for which biases on the fitted cosmological parameters
are introduced at the same time. Of the cosmological parameters, the
overall mass density
level,
except for special cases. We simulate a future data scenario where
SN magnitude evolution is allowed for, and neglect the possibility
of such an evolution in the fit. We find the fiducial models for which
the wrong model assumption of nonevolving SN magnitude is not
detectable, and for which biases on the fitted cosmological parameters
are introduced at the same time. Of the cosmological parameters, the
overall mass density
![]() has the strongest chances to be biased due to the wrong model assumption. Whereas early-epoch models with a magnitude offset
has the strongest chances to be biased due to the wrong model assumption. Whereas early-epoch models with a magnitude offset
![]() show up to be not too dangerous when neglected in the fitting procedure, late epoch models with
show up to be not too dangerous when neglected in the fitting procedure, late epoch models with
![]() have high chances of undetectably biasing the fit results.
have high chances of undetectably biasing the fit results.
Key words: cosmology: cosmological parameters - cosmology: observations - stars: supernovae: general - surveys
1 Introduction
An important cosmological probe and the historically first indicator
of a presently accelerating expansion of the universe are type Ia
supernovae (SNe Ia, see Perlmutter et al. 1999; Riess et al. 1998).
SNe Ia are rare, massively luminous cosmic events that are
believed to be violent thermonuclear explosions of degenerate white
dwarfs, resulting from the ignition of degenerate nuclear fuel in
stellar material (Hoyle & Fowler 1960).
Observations of nearby extragalactic SNe Ia indicate that they
could be standardized, and could therefore be used as a distance
measure. In a universe described by a Robertson-Walker metric,
![\begin{displaymath}%
{\rm d}s^2=-c^2{\rm d}\tau^2+a^2(\tau)\left[{\rm d}\chi^2+f^2(\chi)({\rm d}\theta^2+(\sin\theta)^2{\rm d}\phi^2)\right],
\end{displaymath}](/articles/aa/full_html/2009/42/aa12811-09/img18.png)
|
(1) |
cosmic events of intrinsic luminosity
on Earth, where
![\begin{displaymath}%
d_{{L}}(z)=\frac{c}{H_0}\frac{(1+z)}{\sqrt{\vert\Omega_{{k}...
...t\limits_0^z { \frac{{\rm d}\tilde{z}}{E(\tilde{z})} }\right],
\end{displaymath}](/articles/aa/full_html/2009/42/aa12811-09/img27.png)
|
(3) |
where
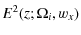
|
= | 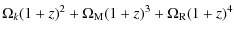
|
|
![$\displaystyle + ~ \Omega_{{x}} {\rm Exp} \left[ 3\int_{0}^{\ln(1+z)}\left(1+w_{{x}}(\tilde{z})\right) {\rm d}\ln(1+\tilde{z})\right].$](/articles/aa/full_html/2009/42/aa12811-09/img32.png)
|
(4) |
Therein
The normalization parameter
The use of the simple relation Eq. (5)
is complicated by several effects. The lightcurve data are not
available over the whole frequency range, but only in a small bandpass
that has to be related to the whole bolometric luminosity. The
adjustment to correct for this ``bandpass mapping'' is done by adding a
correction term, whose value depends not only on the source's redshift
but also on its spectrum (Drell et al. 2000).
The main complication, however, seems to be the deduction of the
object's intrinsic brightness, which cannot be measured directly, from
its spectroscopic and/or photometric properties. While SNe Ia
clearly do not always have the same brightness, but indeed have a
significant dispersion of
![]() in peak magnitude in most pessimistic estimations, one can establish a relation, however, between the decline rate
in peak magnitude in most pessimistic estimations, one can establish a relation, however, between the decline rate
![]() (the
total decline in brightness from peak to 15 days afterward) in the
SN lightcurve shape and its absolute peak-brightness
(the
total decline in brightness from peak to 15 days afterward) in the
SN lightcurve shape and its absolute peak-brightness
![]() :
:
within an error margin of around
The use of Eq. (5) would furthermore be complicated if the apparent luminosity m was systematically varying with redshift due to various astrophysical effects.
Intrinsic effects:
a first class of possible effects would affect the intrinsic properties of the SN, like the luminosityAnother problem with the progenitor age arises: the two principal models of supernova Ia progenitor systems, i.e. the single-degenerate and the double-degenerate progenitor system, differ in explosion delay time (and environmental conditions). The uncertainty in identifying the progenitor systems may mimick an evolutionary effect (Riess & Livio 2006).
Subpopulations:
Hamuy et al. (1996b,a) suggest that SN magnitude depends on the host galaxy (brighter SNe in early-type elliptic galaxies than in late-type spiral galaxies), and proposed a classification of SNe Ia into two subclasses. The study of Hatano et al. (2000) also indicates two subpopulations that may be identified as resulting from different explosion mechanisms, i.e. plain detonation, deflagration, or delayed detonation models. Progenitor population drift leads to different SN subpopulations dominating at different cosmological epochs and may translate into an overall evolutionary effect (Branch et al. 2001). The subpopulation bias has recently been studied by Sarkar et al. (2008a) and Linder (2009), showing that subpopulations with different mean peak magnitudes may bias the parameter of dark energy equation of state.Extrinsic effects:
another class of possible effects leading to an overall redshift evolution of apparent SN magnitude m and light-curve shape consists of extrinsic effects, which do not come from the intrinsic SN properties being altered, but from astrophysical effects between the SN and the observer. Gravitational lensing effects have been considered to possibly mimick an SN magnitude evolution on cosmic time scales, but have been shown to be negligible (Sarkar et al. 2008b). Also gray intergalactic dust has been proposed to mimick an evolutionary effect since Aguirre (1999), and has been shown to possibly bias the extraction of the cosmological parameters (Ménard et al. 2009; Corasaniti 2006). Also effects of the interstellar medium in the host galaxy may translate into evolutionary effects, the former systematically varying from early-epoch elliptic galaxies to late-epoch spiral galaxies.Given this rather rudimentary understanding of SN magnitude evolution in redshift range say 0<z<1.7, we find it reasonable to test the optimistic assumption that the calibration relations obtained for `local', low-redshift SNe be without modification valid for SNe at arbitrarily high redshift. We do not aim to extract evolutionary parameters or rule out models of SN magnitude evolution, but to study the systematics that are introduced when evolution is neglected in the analysis.
To this end we developed detection criteria and tested their
performance when confronted with the wrong model assumption on the
SN magnitude. In Sect. 2
we introduce some phenomenological models to describe systematical
shifts in SN magnitudes, discuss general aspects of
SN magnitude evolution, and give limits on the model parameters
obtained from current observational data in Sect. 3. In the main part, Sect. 4,
we study the implications, an unaccounted for evolutionary effect on
SN magnitudes would have on data analysis. Therein we make use of
a simulated SN sample consisting of
![]() SNe up to redshift z=1.7.
We present our approach to the detectability of such an effect, and
discuss the possible introduction of nondetectable biases on the
cosmological parameters. From merged detectability and bias results, we
introduce the concept of the danger of the phenomenological models.
This paper ends with Sect. 5, where the results are summed up and discussed.
SNe up to redshift z=1.7.
We present our approach to the detectability of such an effect, and
discuss the possible introduction of nondetectable biases on the
cosmological parameters. From merged detectability and bias results, we
introduce the concept of the danger of the phenomenological models.
This paper ends with Sect. 5, where the results are summed up and discussed.
2 Parameterizations
The possible evolution of SN magnitude with redshift is allowed for
by a simple modification of the magnitude-redshift relation, i.e. in
Eq. (5) we allow for a magnitude altering
![]() ,
,
supposed to originate in an overall time evolution of the SN peak luminosity. In the following we simply type
In the
where
which will be referred to as Model 1 throughout this study. We in some respects prefer this consideration of a varying
to study the contribution of powers in z to our results.
3 Real data
3.1 Constraints on evolution
We obtained current constraints on the ![]() parameters by a combined fit on the values of the cosmic microwave background (CMB) shift parameter R=1.71
parameters by a combined fit on the values of the cosmic microwave background (CMB) shift parameter R=1.71 ![]() 0.03 (see Efstathiou & Bond 1999; Wang & Mukherjee 2007), the baryonic acoustic oscillation (BAO) parameter A=0.469
0.03 (see Efstathiou & Bond 1999; Wang & Mukherjee 2007), the baryonic acoustic oscillation (BAO) parameter A=0.469 ![]() 0.017 (see Eisenstein et al. 2005), and the 307 SN magnitudes as compiled by Kowalski et al. (2008). Instead of a full CMB and BAO analysis, R and A are being used to save computing time, cf. Sect. 4. We impose flatness
0.017 (see Eisenstein et al. 2005), and the 307 SN magnitudes as compiled by Kowalski et al. (2008). Instead of a full CMB and BAO analysis, R and A are being used to save computing time, cf. Sect. 4. We impose flatness
![]() on
all fits. To take a possibly time-varying value of the equation of
state of the dark energy component into account, we used the
Chevallier-Polarski-Linder (CPL, Chevallier & Polarski 2001; Linder 2003) parameterization
on
all fits. To take a possibly time-varying value of the equation of
state of the dark energy component into account, we used the
Chevallier-Polarski-Linder (CPL, Chevallier & Polarski 2001; Linder 2003) parameterization
![]() ,
where
,
where
![]() depicts the overall time variation of wx. The fit parameters thus are
depicts the overall time variation of wx. The fit parameters thus are
![]() .
We neglected the radiation component
.
We neglected the radiation component
![]() in the fit.
in the fit.
The fit was performed with the cosmological analysis tool GFIT![]() . The best fit is found by a minimization of the
. The best fit is found by a minimization of the
where
Table 1: Best-fit values for models 1 and 2.
The results for all four models are assembled in Table 1, where we show the results for the case
![]() ,
and the dynamical case
,
and the dynamical case
![]() ,
case a) and b), respectively. The table also shows the results when
,
case a) and b), respectively. The table also shows the results when ![]() was imposed on the fit, cases i) and ii), respectively. These agree with the results of Kowalski et al. (2008), Komatsu et al. (2009), and Tilquin et al. (in preparation). In the following we call the model with
was imposed on the fit, cases i) and ii), respectively. These agree with the results of Kowalski et al. (2008), Komatsu et al. (2009), and Tilquin et al. (in preparation). In the following we call the model with
![]() the
the
![]() model.
model.
Concerning the ![]() per degrees of freedom n of the fit, all models of Table 1 perform equally well, i.e. there is no significant tendency toward considerably higher or smaller
per degrees of freedom n of the fit, all models of Table 1 perform equally well, i.e. there is no significant tendency toward considerably higher or smaller ![]() for any of the models.
for any of the models.
When we impose
![]() ,
we see a surprisingly high best-fit value of
,
we see a surprisingly high best-fit value of
![]() for Model 1, which corresponds to a magnitude drift
for Model 1, which corresponds to a magnitude drift
![]() at redshift z=1.7. The
at redshift z=1.7. The
![]() best-fit value is decreased by 0.03 compared to the standard
best-fit value is decreased by 0.03 compared to the standard ![]() fit, which gives
fit, which gives
![]() .
All
.
All ![]() ,
however, are consistent with
,
however, are consistent with
![]() at the
at the ![]() level.
Model 2.2's evolutionary parameter has a lower negative best-fit
value and is consistent with non-evolutionary SN magnitudes at the
level.
Model 2.2's evolutionary parameter has a lower negative best-fit
value and is consistent with non-evolutionary SN magnitudes at the
![]() -level, while wx in this model is closer to the
-level, while wx in this model is closer to the
![]() value -1, and errors on the parameters
value -1, and errors on the parameters ![]() and wx are smaller. Model 2.3 again shows smaller errors on the parameters
and wx are smaller. Model 2.3 again shows smaller errors on the parameters ![]() and wx, and the
and wx, and the
![]() and wx parameters approaching the
and wx parameters approaching the
![]() values 0.28 and -1, respectively. Its evolutionary parameter
values 0.28 and -1, respectively. Its evolutionary parameter ![]() ,
however, shows up to be inconsistent with non-evolving SN magnitudes at
,
however, shows up to be inconsistent with non-evolving SN magnitudes at ![]() .
Model 2.1 is a special case in this table, since it is the only one with a positive best-fit value for
.
Model 2.1 is a special case in this table, since it is the only one with a positive best-fit value for ![]() .
But it is consistent with no evolution at all at
.
But it is consistent with no evolution at all at ![]() .
We find that at
.
We find that at
![]() the sign of the best-fit
the sign of the best-fit ![]() turns around, and that we fit
turns around, and that we fit
![]() for all
for all
![]() .
Due to correlation between
.
Due to correlation between ![]() and wx, the best fit value of wx also changes qualitatively with decreasing
and wx, the best fit value of wx also changes qualitatively with decreasing ![]() ,
and we fit
,
and we fit
![]() for all
for all
![]() .
.
When we allow the dark energy equation of state to vary with time, i.e. if we include wa in the fit, the picture changes considerably. In Model 1 the w0 best-fit value drops significantly below -1. Equally the wa value is high, and the fit becomes inconsistent with a cosmological constant
![]() at the
at the ![]() -level. For Model 1 the wa value even is inconsistent with its cosmological constant value at
-level. For Model 1 the wa value even is inconsistent with its cosmological constant value at ![]() .
For models 2 we find the tendency that higher powers in redshift results in lower
.
For models 2 we find the tendency that higher powers in redshift results in lower ![]() best-fit values, and
best-fit values, and
![]() best fit-value increasing towards
best fit-value increasing towards
![]() .
w0 equally moves towards its
.
w0 equally moves towards its
![]() value -1, but remains inconsistent with it at the
value -1, but remains inconsistent with it at the ![]() level. The CPL parameter wa is inconsistent with wa=0 also in models 2.1 and 2.2, but becomes consistent with wa=0 in Model 2.3. We note for Model 2.1 that the introduction of the wa parameter pushed the
level. The CPL parameter wa is inconsistent with wa=0 also in models 2.1 and 2.2, but becomes consistent with wa=0 in Model 2.3. We note for Model 2.1 that the introduction of the wa parameter pushed the
![]() limit, where the best-fit value of
limit, where the best-fit value of ![]() became positive and w0>-1 in the
became positive and w0>-1 in the
![]() case, to lower redshift powers
case, to lower redshift powers
![]() due to the strong degeneracy between
due to the strong degeneracy between ![]() and wa. All models including Model 2.1 have
and wa. All models including Model 2.1 have ![]() best-fit values.
best-fit values.
Figure 1 illustrates the best-fit values of Table 1 in a magnitude redshift diagram; i.e., we plot the magnitude drifts
![]() obtained from the best-fit
obtained from the best-fit ![]() values via Eqs. (10) and (11) over redshift. The figure highlights that all
values via Eqs. (10) and (11) over redshift. The figure highlights that all
![]() are excluded at
are excluded at ![]() when
when
![]() in the fit. The data are consistent with
in the fit. The data are consistent with
![]() in all the fits, with two exceptions. Model 2.3 exludes the hypothesis of nonevolving magnitudes at
in all the fits, with two exceptions. Model 2.3 exludes the hypothesis of nonevolving magnitudes at ![]() in the case where a constant dark energy equation of state
in the case where a constant dark energy equation of state
![]() is assumed. And Model 1 does the same when wa is included in the fit.
is assumed. And Model 1 does the same when wa is included in the fit.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{P039fig1a.eps}\vspace*{5mm}
\includegraphics[width=7.5cm,clip]{P039fig1b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg154.png)
|
Figure 1:
Illustration of the |
| Open with DEXTER | |
Table 2 shows
all contours we obtain by a Model 1 fit, with the four different
fit-parameter sets i), ii), a) and b), respectively,
cf. Table 1. Contours in parameter spaces
![]() are obtained by a
are obtained by a ![]() -minimization over all other parameters
-minimization over all other parameters
![]() ,
and
,
and
![]() confidence level contours correspond to contours
confidence level contours correspond to contours
![]() ,
respectively. The parameter pairs pj
,
respectively. The parameter pairs pj ![]() pk in the headings of the columns depict the
pk in the headings of the columns depict the
![]()
![]()
![]() of the contour plots. We see that introducing the evolutionary parameter
of the contour plots. We see that introducing the evolutionary parameter ![]() in the fit results in a decrease of the best fit
in the fit results in a decrease of the best fit
![]() value, which as we saw above is valid for all models whenever
value, which as we saw above is valid for all models whenever
![]() .
Concerning the present value of dark energy's equation of state w0, including the
.
Concerning the present value of dark energy's equation of state w0, including the ![]() parameter in the fit has the same effect as including wa, i.e. it moves the w0 best-fit value beyond the phantom barrier
wx=-1. Whereas including either wa or
parameter in the fit has the same effect as including wa, i.e. it moves the w0 best-fit value beyond the phantom barrier
wx=-1. Whereas including either wa or ![]() keeps the fit result consistent with w0=-1, including both of them at the same time makes w0 inconsistent with w0=-1. This effect persists in all models, but is the strongest in the late-epoch model 2.1 and the logarithmic model 1.
keeps the fit result consistent with w0=-1, including both of them at the same time makes w0 inconsistent with w0=-1. This effect persists in all models, but is the strongest in the late-epoch model 2.1 and the logarithmic model 1.
Table 2:
All ![]() ,
and
,
and ![]() confidence level contours for Model 1. Full lines represent the
confidence level contours for Model 1. Full lines represent the
![]() values
values
![]() and the
(w0+wa)=0 constraint.
and the
(w0+wa)=0 constraint.
3.2 Hubble diagram
The general tendency to prefer a negative ![]() (negative magnitude drift
(negative magnitude drift
![]() )
and thus brighter SNe at higher redshift can also be seen from the
Hubble diagram of the SNe sample. We bin the sample in redshift
bins of width 0.1. Figure 2 shows the relative magnitude deviation
)
and thus brighter SNe at higher redshift can also be seen from the
Hubble diagram of the SNe sample. We bin the sample in redshift
bins of width 0.1. Figure 2 shows the relative magnitude deviation
of the SNe sample from the best-fit magnitudes of case ii). Here,
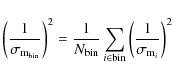
|
(14) |
come from the errors
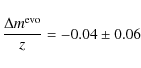
|
(15) |
magnitude per redshift, which corresponds to a magnitude drift
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{P039fig2.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg189.png)
|
Figure 2:
The relative magnitude deviation
|
| Open with DEXTER | |
From Sects. 3.1 and 3.2 we draw the conclusion that, while preferring negative magnitude drifts
![]() ,
data show no definite indication of SN magnitude evolution, in agreement with Kowalski et al. (2008), Ferramacho et al. (2009), Linder (2009), and the results reported by Bronder et al. (2007) and Sullivan et al. (2009).
,
data show no definite indication of SN magnitude evolution, in agreement with Kowalski et al. (2008), Ferramacho et al. (2009), Linder (2009), and the results reported by Bronder et al. (2007) and Sullivan et al. (2009).
4 Simulations
We now study the impact, an unaccounted for SN magnitude
evolution would have on the values of the extracted cosmological
parameters in the framework of a combined analysis. Our database is a
set of 2000 simulated SN magnitudes in redshift range 0<z<1.7, from which
![]() at
at ![]() .
The sample corresponds to what could be expected from a satellite mission with good control of systematics (Kim et al. 2004). We added 300 SNe in the nearby range z<0.1 as expected by nearby SN Ia surveys like the Nearby Supernova Factory (Wood-Vasey et al. 2004). The sample was binned into redshift bins of width 0.1. The intrinsic error on each SN magnitude is assumed to be
.
The sample corresponds to what could be expected from a satellite mission with good control of systematics (Kim et al. 2004). We added 300 SNe in the nearby range z<0.1 as expected by nearby SN Ia surveys like the Nearby Supernova Factory (Wood-Vasey et al. 2004). The sample was binned into redshift bins of width 0.1. The intrinsic error on each SN magnitude is assumed to be
![]() ,
and systematic errors
,
and systematic errors
![]() on magnitudes are included in the analysis. This systematic error enters the covariance matrix by
on magnitudes are included in the analysis. This systematic error enters the covariance matrix by
![]() and
and
![]() ,
where rij is the correlation coefficient between bins, which however is set to rij=0. In the simulation of the SN magnitudes we allowed for a redshift evolution according to Eqs. (10) and (11). Scan range in
,
where rij is the correlation coefficient between bins, which however is set to rij=0. In the simulation of the SN magnitudes we allowed for a redshift evolution according to Eqs. (10) and (11). Scan range in ![]() is
is
![]() for Model 1 and Model 2.1,
for Model 1 and Model 2.1,
![]() for Model 2.2,
for Model 2.2,
![]() for Model 2.3, and the other respective fiducial cosmological parameters are fixed to
for Model 2.3, and the other respective fiducial cosmological parameters are fixed to
![]()
![]() .
We checked the stability of our results to variations in these fiducial
parameters and found no significant variance from our general
conclusions. Fit parameters are the standard parameters
.
We checked the stability of our results to variations in these fiducial
parameters and found no significant variance from our general
conclusions. Fit parameters are the standard parameters
![]() .
The magnitude evolution inherent in the simulated data was thus neglected in the fitting procedure; i.e., we imposed
.
The magnitude evolution inherent in the simulated data was thus neglected in the fitting procedure; i.e., we imposed ![]() on the fit. To economize computing time we did not perform a
combination with full BAO and CMB data, but simulated the
CMB shift parameter R and the BAO reduced parameter A.
We find this simplification justified, because our task is not to
extract real cosmological parameter values but to study the systematics
introduced by a possibly wrong assumption on one of the probes. We
assumed an error of
on the fit. To economize computing time we did not perform a
combination with full BAO and CMB data, but simulated the
CMB shift parameter R and the BAO reduced parameter A.
We find this simplification justified, because our task is not to
extract real cosmological parameter values but to study the systematics
introduced by a possibly wrong assumption on one of the probes. We
assumed an error of ![]() on R (which is the estimate for future PLANCK data) and an error of
on R (which is the estimate for future PLANCK data) and an error of
![]() on A, to represent an experimental setup available in the near future.
on A, to represent an experimental setup available in the near future.
The numerical tool for our parameter study with simulated data is KOSMOSHOW![]() , which implements the
, which implements the ![]() -minimization procedure as described in Sect. 3. The errors on the cosmological parameters
-minimization procedure as described in Sect. 3. The errors on the cosmological parameters ![]() are estimated at the minimum by using the first-order error propagation technique:
are estimated at the minimum by using the first-order error propagation technique:
![]() ,
where
,
where ![]() is the error matrix on the cosmological parameters, and
is the error matrix on the cosmological parameters, and ![]() the Jacobian of the transformation. The fit of the simulated data gives the central values
the Jacobian of the transformation. The fit of the simulated data gives the central values ![]() and errors
and errors
![]() for the parameters, along with their correlations
for the parameters, along with their correlations ![]() ,
which in general are strong. We neglect the radiation component
,
which in general are strong. We neglect the radiation component
![]() and continue assuming spatial flatness in the following,
and continue assuming spatial flatness in the following,
![]() .
.
4.1 Illustration
We observe that, even with this high statistics at redshifts z>1 and forecasted small errors on R and A,
an unaccounted for evolution of SN magnitudes will possibly lead
to misinterpreting the fit results. Suppose a fiducial cosmological
model
![]() .
This is a cosmos with a dark energy component with a constant equation of state,
.
This is a cosmos with a dark energy component with a constant equation of state,
![]() ,
where SN magnitudes evolve with redshift according to Eq. (10). This fiducial model is represented by the small circle in the
,
where SN magnitudes evolve with redshift according to Eq. (10). This fiducial model is represented by the small circle in the
![]() parameter space of Fig. 3. A fit on this cosmology's SN magnitudes combined with R and A gives a best fit
parameter space of Fig. 3. A fit on this cosmology's SN magnitudes combined with R and A gives a best fit
![]() with a very low
with a very low
![]() when the possibility of an SN magnitude evolution is not taken into account in the fitting procedure. Here, n depicts the number of degrees of freedom of the fit. The best-fit value and the corresponding
when the possibility of an SN magnitude evolution is not taken into account in the fitting procedure. Here, n depicts the number of degrees of freedom of the fit. The best-fit value and the corresponding ![]() and
and ![]() confidence level contours are plotted in Fig. 3, which highlights that the fit result would lead us to reject the true cosmology at more than the
confidence level contours are plotted in Fig. 3, which highlights that the fit result would lead us to reject the true cosmology at more than the ![]() confidence
level. We point out that the best fit on this cosmology is consistent
with the actual real data best fit on SNe+BAO+CMB+WL (Tilquin et al. in preparation), which pins down the parameter values to
confidence
level. We point out that the best fit on this cosmology is consistent
with the actual real data best fit on SNe+BAO+CMB+WL (Tilquin et al. in preparation), which pins down the parameter values to
![]() .
Even with a mid-term prospective SN dataset and combination with R and A
with forecasted small errors, we would therefore risk misinterpreting
our best fit because of a wrong model assumption on one of the probes.
We have been unable to find an illustration of a confusion between a
fiducial
.
Even with a mid-term prospective SN dataset and combination with R and A
with forecasted small errors, we would therefore risk misinterpreting
our best fit because of a wrong model assumption on one of the probes.
We have been unable to find an illustration of a confusion between a
fiducial
![]() model with an SN magnitude evolution, and the ``full fit'' model given above. Indeed, we find that
model with an SN magnitude evolution, and the ``full fit'' model given above. Indeed, we find that
![]() whenever
whenever
![]() ,
whatever sign and model of
,
whatever sign and model of
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{P039fig3.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg216.png)
|
Figure 3: Illustration of the
possible risks introduced by the wrong assumption of nonevolving
SN magnitudes. The circle depicts the fiducial cosmology
|
| Open with DEXTER | |
Table 3:
The ![]() -intervall
in which an evolutionary effect on SN magnitudes would pass
undetected by statistical and physical detectability criteria.
-intervall
in which an evolutionary effect on SN magnitudes would pass
undetected by statistical and physical detectability criteria.
To avoid this misinterpretation, one of course would like to have
the means in hand to possibly detect a wrong model assumption on one of
the probes. We introduce three different generic criteria that allow
judging the performance of a fit. We then check, for which
fiducial cosmologies involving an SN magnitude evolution,
parameterized by ![]() ,
these criteria are strong enough to detect the wrong model assumption in the fit.
,
these criteria are strong enough to detect the wrong model assumption in the fit.
4.2 Statistical goodness criterion
As a first criterion for judging the goodness of the fit we use the ![]() -test. To evaluate the statistical goodness of the fit, we choose the
-test. To evaluate the statistical goodness of the fit, we choose the
![]() of the so-called ``p-value'' (Amsler et al. 2008):
of the so-called ``p-value'' (Amsler et al. 2008):
as statistically justified cut-off values, and consider all models with
4.3 Consistency criterion
In the literature it is a common approach to consider the terms
``low redshift'' and ``high redshift'' when discussing SN data,
where the definition of the limiting redshift between the two ranges,
however, is not uniform. Some authors refer to the scatter of the ![]() in the Hubble diagram Fig. 2,
and divide the sample into high and low redshift subsamples with equal
mean scatter, while others cut the sample by simply assuming that z>0.5 or z>1
be high redshift. We find it a good statistical means to cut an
SN sample into high and low redshift subsamples at a certain
in the Hubble diagram Fig. 2,
and divide the sample into high and low redshift subsamples with equal
mean scatter, while others cut the sample by simply assuming that z>0.5 or z>1
be high redshift. We find it a good statistical means to cut an
SN sample into high and low redshift subsamples at a certain
![]() such that the errors on the obtained fit parameters pk be equal for the two subsamples. That is to say, we impose
such that the errors on the obtained fit parameters pk be equal for the two subsamples. That is to say, we impose
![]() on
the high (hr) and low (lr) redshift subsamples. We therewith
ensure that the two subsamples have equal statistical weight with
respect to the parameter pk, but will find different cut redshifts for different pk. For our simulated SN sample as outlined above, we find
on
the high (hr) and low (lr) redshift subsamples. We therewith
ensure that the two subsamples have equal statistical weight with
respect to the parameter pk, but will find different cut redshifts for different pk. For our simulated SN sample as outlined above, we find
![]() with respect to equal errors on
with respect to equal errors on
![]() .
These
.
These
![]() are found by looking at the SNe only (and not at the combined set SNe+R+A), because we want it to be a criterion intrinsic to SNe.
are found by looking at the SNe only (and not at the combined set SNe+R+A), because we want it to be a criterion intrinsic to SNe.
Figure 4 illustrates the application of this criterion for a simulated Model 1 dataset with
![]() .
All other fiducial parameters are fixed to
.
All other fiducial parameters are fixed to
![]() in the simulation, and the SN sample has been split in two at redshift
in the simulation, and the SN sample has been split in two at redshift
![]() .
The figure shows the w0 obtained by separate fits on the
.
The figure shows the w0 obtained by separate fits on the
![]() +R+A and the
+R+A and the
![]() +R+A datasets, plotted over the varying
+R+A datasets, plotted over the varying
![]() .
We recall that the fitted parameters are
.
We recall that the fitted parameters are
![]() as throughout this section.
as throughout this section.
We find, as should be expected, consistent results around
![]() ,
i.e. 1. the
,
i.e. 1. the
![]() obtained by a fit on the high-redshift subsample lie well within the errors of the
obtained by a fit on the high-redshift subsample lie well within the errors of the
![]() obtained by a fit on the low-redshift subsample, and vice versa, and 2. both the
obtained by a fit on the low-redshift subsample, and vice versa, and 2. both the
![]() and the
and the
![]() are in agreement with the fiducial
are in agreement with the fiducial
![]() .
But the w0 clearly become inconsistent for larger
.
But the w0 clearly become inconsistent for larger
![]() .
To give the exact inconsistency bounds we look at the consistency bias
.
To give the exact inconsistency bounds we look at the consistency bias
![]() and consider
and consider
as the criterion of consistency between the low and high redshift subsamples. Here, T is a factor corresponding to the
4.4 Physical criteria
We impose
on the fit results. Equation (18) is implied by the condition that
![\begin{figure}
\par\includegraphics[width=8cm,clip]{P039fig4.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg250.png)
|
Figure 4:
Illustration of the consistency criterion. We plot the
|
| Open with DEXTER | |
We also impose
on the fit to allow for the presence of matter in the universe.
It however turns out that in the context of a combined analysis SNe+R+A neither Eqs. (18) nor (19) contribute any constraint on the
![]() in the range of study. We therefore do not discuss these criteria in the following, and omit them from Table 3.
in the range of study. We therefore do not discuss these criteria in the following, and omit them from Table 3.
4.5 Results
4.5.1 Detectability
Putting together the criteria developed above, we obtain ![]() -ranges
for all four fiducial evolutionary models where an SN magnitude
evolution would pass the fitting procedure undetected by these
statistical and physical detectability criteria. Table 3 shows the ensemble of the results. The consistency check is particularly powerful, and on the
-ranges
for all four fiducial evolutionary models where an SN magnitude
evolution would pass the fitting procedure undetected by these
statistical and physical detectability criteria. Table 3 shows the ensemble of the results. The consistency check is particularly powerful, and on the ![]() confidence level yet more decisive than the
confidence level yet more decisive than the ![]() -test in all cases. At the
-test in all cases. At the ![]() confidence level, the
confidence level, the ![]() -check performs better for
-check performs better for ![]() for all models. We note that the consistency check for
for all models. We note that the consistency check for
![]() is most powerful when the sample is split in two with respect to
is most powerful when the sample is split in two with respect to
![]() ,
i.e. when
,
i.e. when
![]() .
Inversely, when the cut is done with respect to
.
Inversely, when the cut is done with respect to
![]() ,
i.e. at
,
i.e. at
![]() ,
the most constraining test is the consistency check on w0. We underline the most constraining detectablitity limits in Table 3. We can translate the underlined
,
the most constraining test is the consistency check on w0. We underline the most constraining detectablitity limits in Table 3. We can translate the underlined ![]() confidence level
confidence level ![]() -limits from Table 3 into magnitude shifts
-limits from Table 3 into magnitude shifts
![]() at redshift z=1.7 via Eqs. (10) and (11), and obtain the Table 4.
at redshift z=1.7 via Eqs. (10) and (11), and obtain the Table 4.
Table 4:
The
![]() -intervall in which an SN magnitude evolution would not be detectable at the
-intervall in which an SN magnitude evolution would not be detectable at the ![]() confidence level.
confidence level.
We highlight that, at the ![]() confidence
level, the most performing detection criterion is the consistency
check. However, as noted, when going to higher confidence levels, one
may find the
confidence
level, the most performing detection criterion is the consistency
check. However, as noted, when going to higher confidence levels, one
may find the ![]() -check better suited to detecting the effect of SN magnitude evolution. From these
-check better suited to detecting the effect of SN magnitude evolution. From these
![]() limits one concludes that the power models Eq. (11) are the higher constraint, the larger the exponent
limits one concludes that the power models Eq. (11) are the higher constraint, the larger the exponent ![]() is. The early-epoch model 2.3 is detectable whenever the evolutionary magnitude shift
is. The early-epoch model 2.3 is detectable whenever the evolutionary magnitude shift
![]() at redshift 1.7. The late-epoch model 2.1 would pass undetected for all evolutionary effects
at redshift 1.7. The late-epoch model 2.1 would pass undetected for all evolutionary effects
![]() even in an SN survey with redshifts up to 1.7 and combination with R and A. The detectability limits derived in this section also underline the tendency that a negative magnitude drift
even in an SN survey with redshifts up to 1.7 and combination with R and A. The detectability limits derived in this section also underline the tendency that a negative magnitude drift
![]() is harder to detect than a positive one. We saw the preference for
is harder to detect than a positive one. We saw the preference for
![]() from real data in Sect. 3, cf. Figs. 1 and 2.
from real data in Sect. 3, cf. Figs. 1 and 2.
4.5.2 Biases
Whether this undetectability of the SN magnitude evolution is
dangerous or not depends on the quality of reconstruction of the fit
parameters ![]() .
For a fiducial cosmology involving, e.g., a
.
For a fiducial cosmology involving, e.g., a
![]() (corresponding to
(corresponding to
![]() )
evolutionary effect on SN magnitudes, the problem would not be
detected. But we would not need to worry because all the fiducial
parameters
)
evolutionary effect on SN magnitudes, the problem would not be
detected. But we would not need to worry because all the fiducial
parameters
![]() lie within the
lie within the ![]() error of the fitted value, and the fiducial cosmology would thus be ``correctly'' reconstructed at the
error of the fitted value, and the fiducial cosmology would thus be ``correctly'' reconstructed at the ![]() level despite the undetected SN magnitude evolution. We introduce the bias
level despite the undetected SN magnitude evolution. We introduce the bias
![]() on parameter pi as
on parameter pi as
![]() ,
and adopt the notion that the parameter pi is ``biased'' whenever:
,
and adopt the notion that the parameter pi is ``biased'' whenever:
By applying this notion, in this section we restrict ourselves to the
Whereas no bias is introduced in the fit in the preceding example, fiducial models exist where an evolutionary effect
![]() would pass our criteria undetected, and where, at the same time, one or several of the
would pass our criteria undetected, and where, at the same time, one or several of the ![]() are
biased. Our simulations, e.g., show that in a universe with an
unaccounted for Model 1 like SN magnitude evolution, the
are
biased. Our simulations, e.g., show that in a universe with an
unaccounted for Model 1 like SN magnitude evolution, the
![]() parameter is biased whenever
parameter is biased whenever
![]() .
We concluded in the previous section that only
.
We concluded in the previous section that only
![]() and
and
![]() can be detected, cf. Table 3.
Our ignorance of the evolution thus leaves us with a dangerous zone
where an SN magnitude evolution undetectably biases the results.
A full study of all the
can be detected, cf. Table 3.
Our ignorance of the evolution thus leaves us with a dangerous zone
where an SN magnitude evolution undetectably biases the results.
A full study of all the ![]() for models 1 and 2 yields the results of Table 5, which gives the validity zones for
for models 1 and 2 yields the results of Table 5, which gives the validity zones for
![]() ,
w0 and wa, for the four models.
,
w0 and wa, for the four models.
We see that the parameter
![]() has the highest chances of being biased for all models. Its validity zones are the smallest in comparison to the w0 and wa zones. All parameters
has the highest chances of being biased for all models. Its validity zones are the smallest in comparison to the w0 and wa zones. All parameters
![]() ,
however, share the general tendency: the higher the power
,
however, share the general tendency: the higher the power ![]() of models 2, the larger the validity zone. A particular feature of model 1 is that w0 is reconstructed without bias for all positive fiducial
of models 2, the larger the validity zone. A particular feature of model 1 is that w0 is reconstructed without bias for all positive fiducial
![]() .
.
Table 5:
The
![]() -intervall in which the fit parameters are reconstructed without biases.
-intervall in which the fit parameters are reconstructed without biases.
4.5.3 Danger
We can merge the obtained detectability and bias-risk limits, taken from Tables 3 and 5, respectively, to estimate the danger of a neglected magnitude evolution governed by the models of Eqs. (10) and (11). We limit our discussion to the parameter
![]() ,
because it is the parameter with the highest risk of undetected biased reconstruction for all models. Figure 5 shows the
,
because it is the parameter with the highest risk of undetected biased reconstruction for all models. Figure 5 shows the ![]() confidence level detectability and bias limits for the four models obtained from Tabels 3 and 5 in a magnitude-redshift-diagram. Dotted lines are the detectability limits obtained by the
confidence level detectability and bias limits for the four models obtained from Tabels 3 and 5 in a magnitude-redshift-diagram. Dotted lines are the detectability limits obtained by the ![]() -test,
dashed lines are the detectability limits obtained by the most
constraining consistency check (underlined values in Table 3), and full lines are the bias limits on
-test,
dashed lines are the detectability limits obtained by the most
constraining consistency check (underlined values in Table 3), and full lines are the bias limits on
![]() taken from Table 5.
taken from Table 5.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{P039fig5.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg285.png)
|
Figure 5:
|
| Open with DEXTER | |
The cross-shaded zones between the detectability and the bias limits
are the dangerous regions of the diagram, where the fiducial
evolutionary effect passes the analysis undetected, and where biases
are introduced at the same time on the parameter
![]() .
We may take the area S of the cross-shaded region, in the redshift range 0<z<1.7, as a measure of the danger of the model. The higher the value of S, the greater the risks of misinterpretation. We obtain the values of Table 6.
.
We may take the area S of the cross-shaded region, in the redshift range 0<z<1.7, as a measure of the danger of the model. The higher the value of S, the greater the risks of misinterpretation. We obtain the values of Table 6.
Table 6: Danger S of the four models as described in the text.
These values validate the tendency of higher power
![]() evolutionary effects being less dangerous than
evolutionary effects being less dangerous than
![]() models.
The late-epoch model 2.1 is more likely to undetectably bias the
fit results than the early-epoch model 2.3. The danger of the
linear model 2.2 and the logarithmic model 1 lie in between
the two extremes, having approximately the same values. Figure 5 also shows the values
models.
The late-epoch model 2.1 is more likely to undetectably bias the
fit results than the early-epoch model 2.3. The danger of the
linear model 2.2 and the logarithmic model 1 lie in between
the two extremes, having approximately the same values. Figure 5 also shows the values
![]() of the area of the upper (lower) dangerous region seperately. One finds S2>S1 for all models, which again means that a negative magnitude drift
of the area of the upper (lower) dangerous region seperately. One finds S2>S1 for all models, which again means that a negative magnitude drift
![]() carries the greater risk of undetectably biasing the fit results than a positive one.
carries the greater risk of undetectably biasing the fit results than a positive one.
We also extracted the danger of the models used by Linder (2006) and Ferramacho et al. (2009): S=0.36,
which turn out to be equivalent, and very close to our Model 2.1.
This agrees with these parameterizations being well described by a
model 2 with
![]() .
.
The analysis of the ![]() confidence level naturally yields higher absolute values for S, but the same conclusions hold. In particular, we obtain the same tendencies within the models, and S2>S1 for all models.
confidence level naturally yields higher absolute values for S, but the same conclusions hold. In particular, we obtain the same tendencies within the models, and S2>S1 for all models.
The absolute value of S also depends on the specifications of the data survey, i.e. in our case on errors on R and A, and on the statistics of the SNe in the redshift range. For example, when we neglect the assumed systematic error
![]() and
decrease the intrinsic magnitude error on each SN to 0.10, we
obtain bias limits that are tighter than those of Table 5 roughly by a factor 2. Also the dectectability limits from Table 3 decrease considerably from 30% to 50%, and the
and
decrease the intrinsic magnitude error on each SN to 0.10, we
obtain bias limits that are tighter than those of Table 5 roughly by a factor 2. Also the dectectability limits from Table 3 decrease considerably from 30% to 50%, and the ![]() test becomes more and more effective the smaller the intrinsic errors on magnitudes. The absolute values of S also depend on the priors of the fit. They may change when the flatness constraint is dropped or when
test becomes more and more effective the smaller the intrinsic errors on magnitudes. The absolute values of S also depend on the priors of the fit. They may change when the flatness constraint is dropped or when
![]() is imposed on the fit. In the latter case, we find a decrease in the
detectability ranges and also the bias limits. In particular, when
imposing
is imposed on the fit. In the latter case, we find a decrease in the
detectability ranges and also the bias limits. In particular, when
imposing
![]() one obtains results consistent with those of Sarkar et al. (2008a), i.e.
one obtains results consistent with those of Sarkar et al. (2008a), i.e.
![]() and wx are biased at
and wx are biased at ![]() for evolutionary effects
for evolutionary effects
![]() even in the Model 1 case.
even in the Model 1 case.
The measure of danger S we introduce in this section
therefore should not be taken as an absolute measure, because its
actual values depend on the specifications of the cosmological probes
applied in the fit, and on priors. However, we checked that variations
in the data model or of the priors do not change the conclusion that
the late-epoch model
![]() is the most dangerous one.
is the most dangerous one.
5 Discussion
We studied four different one-parametric models of SN magnitude
evolution on cosmic time scales and obtained constraints on its
parameters by combined fits on the actual real data coming from
Supernova surveys, observations of the cosmic microwave background, and
baryonic acoustic oscillation. We found by a minimization of the ![]() that data prefer a magnitude evolution of SNe type Ia such
that high-redshift supernovae are brighter than would be expected in a
standard
that data prefer a magnitude evolution of SNe type Ia such
that high-redshift supernovae are brighter than would be expected in a
standard
![]() cosmos:
cosmos:
![]() .
Data are, however, consistent with nonevolving magnitudes at the
.
Data are, however, consistent with nonevolving magnitudes at the ![]() level
except for special cases. The special cases we found are a fit with the
early-epoch model 2.3 when dark energy is allowed to be dynamical,
level
except for special cases. The special cases we found are a fit with the
early-epoch model 2.3 when dark energy is allowed to be dynamical,
![]() ,
and a fit with a logarithmic magnitude evolution Model 1 when a constant equation of state of dark energy
,
and a fit with a logarithmic magnitude evolution Model 1 when a constant equation of state of dark energy
![]() is assumed in the fit. A comparison of the SN magnitude
distribution with the CPL best-fit magnitudes in a Hubble-diagram also
indicate more luminous SN events at higher redshift. Our results
are, however, of limited strength because we do not use the full CMB
and BAO data but the reduced variables R and A. We also did not include constraints coming from other cosmological probes.
is assumed in the fit. A comparison of the SN magnitude
distribution with the CPL best-fit magnitudes in a Hubble-diagram also
indicate more luminous SN events at higher redshift. Our results
are, however, of limited strength because we do not use the full CMB
and BAO data but the reduced variables R and A. We also did not include constraints coming from other cosmological probes.
We simulated a future data scenario consisting of 2000 SN events out to redshift z=1.7 and forecasted small errors on the CMB shift parameter R and the BAO variable A.
In the simulation of the SN magnitudes, a redshift dependence of
the magnitudes according to the four models was allowed for. Then in
the fit we neglected the possibility of such an evolution and studied
the fit results with respect to detectability of this wrong model
assumption for a wide range of fiducial models. We quantified the range
of values of the fiducial evolution parameters ![]() where the wrong assumption is not detectable. We found that the linear
model 2.2 and the early-epoch model 2.3 are easier to detect
and reject from the fit than is the late-epoch model 2.1 and the
logarithmic model 1.
where the wrong assumption is not detectable. We found that the linear
model 2.2 and the early-epoch model 2.3 are easier to detect
and reject from the fit than is the late-epoch model 2.1 and the
logarithmic model 1.
Including the possible biasing of the fitted parameters when
neglecting magnitude evolution in the discussion, we were able to
determine the danger of the various fiducial evolutionary models; that
is to say, we determined the exact parameter zones where the wrong
model assumption of nonevolving intrinsic SN magnitude not only is
not detectable, but also introduces biases on the fitted cosmological
parameters ![]() .
The parameter of overall mass density
.
The parameter of overall mass density
![]() turned out to carry the highest risk of biased reconstruction. We found
that, whereas the dangerous zone is nearly negligible for the
early-epoch model 2.3 (
turned out to carry the highest risk of biased reconstruction. We found
that, whereas the dangerous zone is nearly negligible for the
early-epoch model 2.3 (
![]() ), it becomes significant in the logarithmic model 1 (
), it becomes significant in the logarithmic model 1 (
![]() )
and the linear model 2.2 (
)
and the linear model 2.2 (
![]() ), and dangerous for the late epoch model 2.1 (
), and dangerous for the late epoch model 2.1 (
![]() ). This becomes apparent in Fig. 5,
where we simultaneously plotted the detectability and bias limits of
the four fiducial models in a Hubble diagram. A comparison of
Figs. 5, 1, and 2
shows that the dangerous zone of Model 2.1 covers nearly the whole
area of magnitude dispersion of actual SN data in the
magnitude-redshift-diagram. Also negative magnitude drifts
). This becomes apparent in Fig. 5,
where we simultaneously plotted the detectability and bias limits of
the four fiducial models in a Hubble diagram. A comparison of
Figs. 5, 1, and 2
shows that the dangerous zone of Model 2.1 covers nearly the whole
area of magnitude dispersion of actual SN data in the
magnitude-redshift-diagram. Also negative magnitude drifts
![]() carry the greater risk of undetectably biasing the fit results than magnitude evolution effects with
carry the greater risk of undetectably biasing the fit results than magnitude evolution effects with
![]() ,
which are already excluded at
,
which are already excluded at ![]() by present data for dynamical dark energy.
by present data for dynamical dark energy.
In conclusion, special care should be accorded to effects yielding
late-time evolution of SN Ia magnitudes with a negative
magnitude drift. Early-time evolution is less severe. To avoid any
bias in determining the cosmological parameters, it is preferable to
include a new parameter to describe possible SN Ia magnitude
evolution in any combined analysis. From our results, it appears that
the models chosen to describe such an effect should favor late-epoch
evolution, as is done by our Model 2.1,
![]() .
.
We acknowledge useful discussions with A. Blanchard and P.-S. Corasaniti. We thank A. Ealet, C. Tao, C. Marinoni, P. Taxil and D. Fouchez for many interesting discussions. S.L. thanks the Gottlieb Daimler- and Karl Benz-Foundation and the DAAD for financial support.
References
- Aguirre, A. 1999, ApJ, 525, 583 [NASA ADS] [CrossRef]
- Amsler, C. et al. 2008, Phys. Lett. B, 667, 1 [NASA ADS] [CrossRef]
- Branch, D., Perlmutter, S., Baron, E., & Nugent, P. 2001, in The SNAP (Supernova Acceleration Probe) Yellow (Snowmass)
- Bronder, T. J. et al. 2007
- Chevallier, M. & Polarski, D. 2001, Int. J. Mod. Phys. C, 10, 213
- Corasaniti, P. S. 2006, MNRAS, 372, 191 [NASA ADS] [CrossRef]
- Drell, P. S., Loredo, T. J., & Wassermann, I. 2000, ApJ, 530, 593 [NASA ADS] [CrossRef]
- Efstathiou, G., & Bond, J. R. 1999, MNRAS, 304, 75 [NASA ADS] [CrossRef]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef]
- Ferramacho, L. D., Blanchard, A., & Zolnierowski, Y. 2009, A&A, 499, 21 [NASA ADS] [CrossRef] [EDP Sciences]
- Gallagher, J. S., Garnavich, P. M., Berlind, P., et al. 2005, ApJ, 634, 210 [NASA ADS] [CrossRef]
- Guy, J., Astier, P., Baumont, S., et al. 2007, A&A, 466, 11 [NASA ADS] [CrossRef] [EDP Sciences]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996a, AJ, 112, 2391 [NASA ADS] [CrossRef]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996b, AJ, 112, 2398 [NASA ADS] [CrossRef]
- Hatano, K., Branch, D., Lentz, E. J., et al. 2000, ApJ, 543, L49 [NASA ADS] [CrossRef]
- Hoeflich, P., Wheeler, J. C., & Thielemann, F. K. 1998, ApJ, 495, 617 [NASA ADS] [CrossRef]
- Howell, D. A., Sullivan, M., Conley, A., & Carlberg, R. 2007, ApJ, 667, L37 [NASA ADS] [CrossRef]
- Hoyle, F., & Fowler, W. A. 1960, ApJ, 132, 565 [NASA ADS] [CrossRef]
- Kim, A. G., Linder, E. V., Miquel, R., & Mostek, N. 2004, MNRAS, 347, 909 [NASA ADS] [CrossRef]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef]
- Kowalski, M., Rubin, D., Aldering, G., et al. 2008, ApJ, 686, 749 [NASA ADS] [CrossRef]
- Lentz, E. J., Baron, E., Branch, D., Hauschildt, P. H., & Nugent, P. E. 2000, ApJ, 530, 966 [NASA ADS] [CrossRef]
- Linder, E. V. 2003, , 90, 091301
- Linder, E. V. 2006, Astropart. Phys., 26, 102 [NASA ADS] [CrossRef]
- Linder, E. V. 2009, Phys. Rev. D, 79, 023509 [NASA ADS] [CrossRef]
- Ménard, B., Kilbinger, M., & Scranton, R. 2009, MNRAS, submitted
- Nordin, J., Goobar, A., & Jönsson, J. 2008, JCAP, 2, 8 [NASA ADS]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef]
- Riess, A. G. 2000, PASP, 112, 1284 [NASA ADS] [CrossRef]
- Riess, A. G., & Livio, M. 2006, ApJ, 648, 884 [NASA ADS] [CrossRef]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef]
- Riess, A. G., Filippenko, A. V., Li, W., & Schmidt, B. P. 1999, AJ, 118, 2668 [NASA ADS] [CrossRef]
- Röpke, F. K. 2005, A&A, 432, 969 [NASA ADS] [CrossRef] [EDP Sciences]
- Röpke, F. K., & Hillebrandt, W. 2004, A&A, 420, L1 [NASA ADS] [CrossRef] [EDP Sciences]
- Sarkar, D., Amblard, A., Cooray, A., & Holz, D. E. 2008a, ApJ, 684, L13 [NASA ADS] [CrossRef]
- Sarkar, D., Amblard, A., Holz, D. E., & Cooray, A. 2008b, ApJ, 678, 1 [NASA ADS] [CrossRef]
- Steinhardt, P. J., Wang, L., & Zlatev, I. 1999, Phys. Rev. D, 59, 123504 [NASA ADS] [CrossRef]
- Strolger, L.-G., Riess, A. G., Dahlen, T., et al. 2004, ApJ, 613, 200 [NASA ADS] [CrossRef]
- Sullivan, M., Ellis, R. S., Howell, D. A., et al. 2009, ApJ, 693, L76 [NASA ADS] [CrossRef]
- Tilquin, A., et al., in preparation
- Wang, Y., & Mukherjee, P. 2007, Phys. Rev. D, 76, 103533 [NASA ADS] [CrossRef]
- Wood-Vasey, W. M., Aldering, G., Lee, B. C., et al. 2004, New Astron. Rev., 48, 637 [NASA ADS] [CrossRef]
Footnotes
- ...éorique
![[*]](/icons/foot_motif.png)
- Centre de Physique Théorique is UMR 6207 - ``Unité Mixte de Recherche'' of CNRS and of the Universities ``de Provence'', ``de la Mediterranée'', and ``du Sud Toulon-Var'' - Laboratory affiliated with FRUMAM (FR2291).
- ... GFIT
![[*]](/icons/foot_motif.png)
- GFIT is a cosmological analysis tool developed by A.T. that allows studies of real or simulated data for various probes (SNe, CMB, BAO, weak lensing (WL), clusters, ...). Information on the code and its utilization can be obtained by contacting: tilquin@cppm.in2p3.fr
- ...
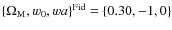
![[*]](/icons/foot_motif.png)
- In cases where a confusion is possible, we added a superscript ``Fid'' to fiducial parameters and a superscript ``fit'' to fitted parameters.
- ... KOSMOSHOW
![[*]](/icons/foot_motif.png)
- KOSMOSHOW is a cosmological analysis tool developed by A.T., and is available on http://marwww.in2p3.fr/renoir/Kosmo-Pheno.php3
All Tables
Table 1: Best-fit values for models 1 and 2.
Table 2:
All ![]() ,
and
,
and ![]() confidence level contours for Model 1. Full lines represent the
confidence level contours for Model 1. Full lines represent the
![]() values
values
![]() and the
(w0+wa)=0 constraint.
and the
(w0+wa)=0 constraint.
Table 3:
The ![]() -intervall
in which an evolutionary effect on SN magnitudes would pass
undetected by statistical and physical detectability criteria.
-intervall
in which an evolutionary effect on SN magnitudes would pass
undetected by statistical and physical detectability criteria.
Table 4:
The
![]() -intervall in which an SN magnitude evolution would not be detectable at the
-intervall in which an SN magnitude evolution would not be detectable at the ![]() confidence level.
confidence level.
Table 5:
The
![]() -intervall in which the fit parameters are reconstructed without biases.
-intervall in which the fit parameters are reconstructed without biases.
Table 6: Danger S of the four models as described in the text.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{P039fig1a.eps}\vspace*{5mm}
\includegraphics[width=7.5cm,clip]{P039fig1b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg154.png)
|
Figure 1:
Illustration of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{P039fig2.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg189.png)
|
Figure 2:
The relative magnitude deviation
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{P039fig3.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg216.png)
|
Figure 3: Illustration of the
possible risks introduced by the wrong assumption of nonevolving
SN magnitudes. The circle depicts the fiducial cosmology
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{P039fig4.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg250.png)
|
Figure 4:
Illustration of the consistency criterion. We plot the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{P039fig5.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12811-09/Timg285.png)
|
Figure 5:
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



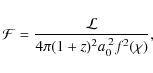
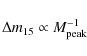
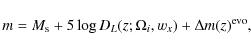
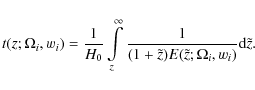
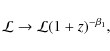
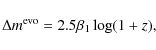
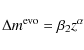
![\begin{displaymath}%
\chi^2=\left[\vec{m}-\vec{m}^{{\rm fit}}(z;p_i)\right]^{\rm T} \vec{V}^{-1}\left[\vec{m}-\vec{m}^{{\rm fit}}(z;p_i)\right],
\end{displaymath}](/articles/aa/full_html/2009/42/aa12811-09/img89.png)