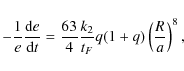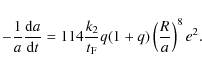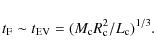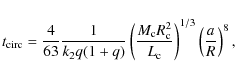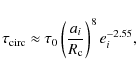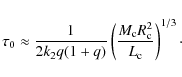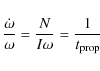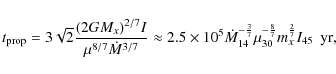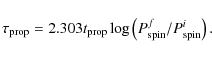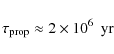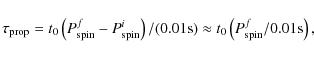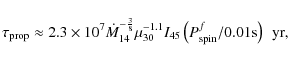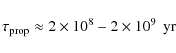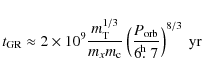| Issue |
A&A
Volume 506, Number 3, November II 2009
|
|
|---|---|---|
| Page(s) | 1297 - 1307 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200912552 | |
| Published online | 27 August 2009 | |
A&A 506, 1297-1307 (2009)
Young pre-low-mass X-ray binaries in the propeller phase
Nature of the 6.7-h periodic X-ray source 1E 161348-5055 in RCW 103
H. Bhadkamkar - P. Ghosh
Department of Astronomy & Astrophysics, Tata Institute of Fundamental Research, Mumbai 400 005, India
Received 21 May 2009 / Accepted 23 August 2009
Abstract
Context. Discovery of the 6.7-h periodicity in the X-ray source
1E 161348-5055 in RCW 103 has led to investigations of the nature of
this periodicity.
Aims. To explore a model for 1E 161348-5055 wherein a fast-spinning neutron star with a magnetic field ![]() 1012 G
in a young pre-low-mass X-ray Binary (pre-LMXB) with an eccentric orbit
of period 6.7 h operates in the ``propeller'' phase.
1012 G
in a young pre-low-mass X-ray Binary (pre-LMXB) with an eccentric orbit
of period 6.7 h operates in the ``propeller'' phase.
Methods. The 6.7-h light curve of 1E 161348-5055 is modeled in
terms of orbitally-modulated mass transfer through a viscous accretion
disk and subsequent propeller emission. Formation of eccentric binaries
in supernovae and their subsequent tidal evolution are studied.
Results. The light curve of 1E 161348-5055 can be quantitatively
accounted for by models of propeller torques of both Illarionov-Sunyaev
type and Romanova-Lovelace et al. type, and spectral and
other properties are also in agreement. Formation and evolution of
model systems are shown to be in accordance both with standard theories
and with X-ray observations of 1E 161348-5055.
Conclusions. The pre-LMXB model for 1E 161348-5055 and similar
sources agrees with observation. Distinguishing features between this
model and the recently-proposed magnetar model need to be explored.
Key words: X-rays: binaries - stars: neutron - stars: evolution - accretion, accretion disks - ISM: supernova remnants - X-rays: general
1 Introduction
The point soft X-ray source 1E 161348-5055 (henceforth 1E) near the
center of the young (![]() 2000 y old) supernova remnant (SNR)
RCW 103 has attracted much attention lately, following the discovery
of a strong 6.67 h periodic modulation in 1E by de Luca et al. (2006,
henceforth dL06) from a deep XMM-Newton
observation of the source in 2005. 1E was
discovered in 1980 (Touhy & Garmire 1980) as a soft Einstein X-ray source. The
original interpretation as an isolated neutron star was found to
be untenable in view of subsequent discovery by other X-ray satellites
(e.g., ROSAT, ASCA, Chandra)
of the large variability of 1E on the timesacle of a few years (dL06).
A periodicity at
2000 y old) supernova remnant (SNR)
RCW 103 has attracted much attention lately, following the discovery
of a strong 6.67 h periodic modulation in 1E by de Luca et al. (2006,
henceforth dL06) from a deep XMM-Newton
observation of the source in 2005. 1E was
discovered in 1980 (Touhy & Garmire 1980) as a soft Einstein X-ray source. The
original interpretation as an isolated neutron star was found to
be untenable in view of subsequent discovery by other X-ray satellites
(e.g., ROSAT, ASCA, Chandra)
of the large variability of 1E on the timesacle of a few years (dL06).
A periodicity at ![]() 6 h was first hinted at by Chandra
observations, but the first clear, strong detection came from the
above 2005 observations of
dL06, who also showed the existence of this periodicity in the data
from earlier 2001 observations of 1E with XMM-Newton, when
the source luminosity was higher by a factor
6 h was first hinted at by Chandra
observations, but the first clear, strong detection came from the
above 2005 observations of
dL06, who also showed the existence of this periodicity in the data
from earlier 2001 observations of 1E with XMM-Newton, when
the source luminosity was higher by a factor ![]() 6 during the
course of its sequence of several-year timescale outbursts nentioned
above, documented by these authors from archival data.
6 during the
course of its sequence of several-year timescale outbursts nentioned
above, documented by these authors from archival data.
The nature of the above 6.67 h periodicity is an interesting
question, on which preliminary discussions were reported in dL06.
Recently, Pizzolato et al. (2008, henceforth P08) have proposed a model
for the 1E system wherein it is a close binary consisting of a magnetar,
i.e., a neutron star with a superstrong magnetic field ![]() 1015 G, and a low-mass companion. The 6.67 h periodicity is identified in
this model with the spin period of the neutron star,
to which this young neutron star has been spun down in such a
short time by the torques associated with its enormous magnetic field.
This period has also been proposed by P08 to be in close synchronism
with the orbital period of the binary, in analogy with what is
believed to be happening in Polar Cataclysmic Variables or AM Her-type
systems. The observed X-ray emission from 1E is that from the magnetar
in this model.
1015 G, and a low-mass companion. The 6.67 h periodicity is identified in
this model with the spin period of the neutron star,
to which this young neutron star has been spun down in such a
short time by the torques associated with its enormous magnetic field.
This period has also been proposed by P08 to be in close synchronism
with the orbital period of the binary, in analogy with what is
believed to be happening in Polar Cataclysmic Variables or AM Her-type
systems. The observed X-ray emission from 1E is that from the magnetar
in this model.
In this paper, we explore an alternative model for the 1E system
wherein it is a close binary system consisting of a young neutron star with
a canonical magnetic field ![]() 1012 G, and a low-mass companion,
i.e., a pre-low-mass X-ray Binary (henceforth pre-LMXB), such as are
believed to be the standard progenitors of Low-mass X-ray Binaries
(henceforth LMXBs). Such pre-LMXBs are born after
the common-envelope (CE) evolution phase of the original progenitor
binary system consisting of a massive star and a low-mass companion,
which leads to the formation of a binary consisting of the He-core
of the original massive star and the low-mass companion
(Ghosh 2007, and references therein).
The He-star susequently explodes in a supernova, leading to a
neutron star in orbit with a low-mass companion, i.e., the pre-LMXB
referred to above. This is the standard He-star supernova scenario
for the formation of LMXBs (Ghosh 2007, and references therein).
The 6.67 h periodicity is identified in our model
with the orbital period of the binary. In our model the young neutron
star is still spinning very rapidly, with a canonical spin period
1012 G, and a low-mass companion,
i.e., a pre-low-mass X-ray Binary (henceforth pre-LMXB), such as are
believed to be the standard progenitors of Low-mass X-ray Binaries
(henceforth LMXBs). Such pre-LMXBs are born after
the common-envelope (CE) evolution phase of the original progenitor
binary system consisting of a massive star and a low-mass companion,
which leads to the formation of a binary consisting of the He-core
of the original massive star and the low-mass companion
(Ghosh 2007, and references therein).
The He-star susequently explodes in a supernova, leading to a
neutron star in orbit with a low-mass companion, i.e., the pre-LMXB
referred to above. This is the standard He-star supernova scenario
for the formation of LMXBs (Ghosh 2007, and references therein).
The 6.67 h periodicity is identified in our model
with the orbital period of the binary. In our model the young neutron
star is still spinning very rapidly, with a canonical spin period
![]() 10-100 ms, and is operating in the ``propeller'' regime,
wherein any matter approaching the fast-rotating magnetosphere of
the neutron star is expelled by the energy and angular momentum
deposited into it through its interaction with the magnetospheric
boundary (Illarionov & Sunyaev 1975, henceforth IS75; Davies & Pringle 1981; Illarionov & Kompaneets 1990; Illarionov et al. 1993; Ghosh 1995; Mineshige et al. 1991; Davies et al. 1979, and references therein,
henceforth G95; Lovelace et al. 1999, henceforth LRB99; Romanova et al. 2004,2005, henceforth RUKL05; Ustyugova et al. 2006, henceforth UKRL06).
10-100 ms, and is operating in the ``propeller'' regime,
wherein any matter approaching the fast-rotating magnetosphere of
the neutron star is expelled by the energy and angular momentum
deposited into it through its interaction with the magnetospheric
boundary (Illarionov & Sunyaev 1975, henceforth IS75; Davies & Pringle 1981; Illarionov & Kompaneets 1990; Illarionov et al. 1993; Ghosh 1995; Mineshige et al. 1991; Davies et al. 1979, and references therein,
henceforth G95; Lovelace et al. 1999, henceforth LRB99; Romanova et al. 2004,2005, henceforth RUKL05; Ustyugova et al. 2006, henceforth UKRL06).
The observed X-ray emission from 1E in our model is that from the propeller: indeed, it is well-known that soft X-ray transients (SXRTs) like Aquila X-1 and others (see Sect. 7.1) go through low/quiescent states during the decay of their outbursts, during which their luminosities and spectral properties are very similar to those of 1E, and the neutron stars in them are believed to be in the propeller regime (Campana et al. 1998; Stella et al. 2000). The observed 6.67 h periodicity in our model is due to the orbital modulation of the supersonic propeller, which is caused by the orbital modulation of the mass-transfer rate in the eccentric binary orbit of a young system like 1E. It is well-known that young post-SN binaries with low-mass companions like 1E are almost certain to have eccentric orbits, due to the large eccentricities produced in such systems in the SN explosion (see Sect. 6.1) and the duration of the subsequent tidal circularization compared to the ages of systems like 1E (see Sect. 6.2). By contrast, SXRTs are believed to be old LMXB systems with circular orbits, where such modulation will not occur.
We show in this work that the 6.67 h light curve of 1E can be accounted for quantitatively by our model for propeller torques of both Illarionov-Sunyaev type and Romanova-Lovelace et al. type (see Sect. 2), and that the observed spectral and other characteristics are also in general agreement with our overall picture. Thus, further diagnostic features need to be explored in order to distinguish between our model and the magnetar model as a viable description of this and similar sources.
2 Propeller phase in pre-LMXBs
In a pre-low-mass X-ray Binary (pre-LMXB: see above), the newborn, fast-rotating neutron star is unable at first to accrete the matter that is being transferred from the companion through the inner Lagrangian point L1, because of the fast rotation of the neutron star (IS75, Illarionov et al. 1993; Illarionov & Kompaneets 1990; Davies & Pringle 1981; Mineshige et al. 1991; Davies et al. 1979, G95, LRB99; Romanova et al. 2004, RUKL05, UKRL06). Because of its large angular momentum, this matter forms an accretion disk and reaches the magnetospheric boundary of the magnetized neutron star, whereupon this ionized matter interacts with the fast-rotating neutron star's magnetic field, and the energy and angular momentum deposited in it by magnetic stresses associated with this fast-rotating magnetic field expel it. This is the propeller phase of the system (IS75), during which the neutron star spins down as it loses angular momentum and rotational energy. During this propeller phase, the disk matter at the magnetospheric boundary is shock-heated as the ``vanes'' of the supersonic propeller (IS75) hit it, and the hot matter emits in the soft X-ray band. This emission appears unmodulated at the neutron-star spin frequency (as opposed to the X-ray emission from canonical accretion-powered pulsars, which comes from the neutron-star surface) to a distant observer, who sees only the total emission from the heated matter at the magnetospheric boundary. Observations of transient low-mass X-ray binaries (i.e., the soft X-ray transients or SXRTs) like Aquila X-1 (Campana et al. 1998) and SXJ1808.4-3658 (Stella et al. 2000) in quiescence, when the neutron stars in them are thought to be operating in the propeller phase, amply confirm this point.
The propeller luminosity L during the above phase is given by
![]() ,
where N is the propeller torque acting on the
neutron star and
,
where N is the propeller torque acting on the
neutron star and ![]() is its spin angular velocity.
The propeller torque N was first estimated by IS75 in their pioneering
suggestion of this mechanism, and subsequent work over approximately
the next two decades considered variations of this torque under different
circumstances, as summarized in G95. These works addressed themselves
largely to quasi-spherical accretion, and we shall call this kind of
propeller torque the Illarionov-Sunyaev type (or IS-type for short)
torque, which was widely used in that time-frame in propeller spindown
calculations. In the 2000s, Romanova, Lovelace and co-authors reported
a series of calculations of the propeller effect for disk-accreting
magnetic stars based on their numerical MHD simulations (Romanova et al. 2004,
RUKL05, UKRL06; also see the analytic estimates in LRB99). We shall
call the propeller torque obtained from this line of work the
Romanova-Lovelace et al. type (or RUKL-type for short) torque. In this
work, we shall consider both IS-type and RUKL-type propeller torques
for the problem at hand.
is its spin angular velocity.
The propeller torque N was first estimated by IS75 in their pioneering
suggestion of this mechanism, and subsequent work over approximately
the next two decades considered variations of this torque under different
circumstances, as summarized in G95. These works addressed themselves
largely to quasi-spherical accretion, and we shall call this kind of
propeller torque the Illarionov-Sunyaev type (or IS-type for short)
torque, which was widely used in that time-frame in propeller spindown
calculations. In the 2000s, Romanova, Lovelace and co-authors reported
a series of calculations of the propeller effect for disk-accreting
magnetic stars based on their numerical MHD simulations (Romanova et al. 2004,
RUKL05, UKRL06; also see the analytic estimates in LRB99). We shall
call the propeller torque obtained from this line of work the
Romanova-Lovelace et al. type (or RUKL-type for short) torque. In this
work, we shall consider both IS-type and RUKL-type propeller torques
for the problem at hand.
Consider IS-type torques first.
For such fast-rotating neutron stars as we are concerned with in this
work, the propeller operates in the supersonic regime, and its
torque is given by (G95 and the references therein),
In Eq. (1),
where
In Eq. (3),
Now consider RUKL-type torques. These authors summarized the
results of some of their extensive MHD simulations in RUKL05 and
UKRL06 in terms of power-law fits to these results, showing that the
scaling of the total propeller torque N with the magnetic
moment ![]() and the spin rate
and the spin rate ![]() of the neutron star was
of the neutron star was
However, the scaling of N with
First, we did an analytic estimate in the following manner. In
their analytic study, LRB99 argued that the radius ![]() of the
inner edge of the disk should depend on the stellar rotation rate
of the
inner edge of the disk should depend on the stellar rotation rate
![]() in addition to the parameters
in addition to the parameters ![]() and
and ![]() that
that
![]() (see above) depended upon. The scaling with
(see above) depended upon. The scaling with ![]() ,
,
![]() ,
and
,
and ![]() that these authors derived was revised in UKRL06,
the final result being given as
that these authors derived was revised in UKRL06,
the final result being given as
![]() .
(Note the closeness of the scalings with
.
(Note the closeness of the scalings with ![]() and
and
![]() with those which apply to
with those which apply to ![]() ,
as given above.)
,
as given above.)
In a simple first approach, if we argue that a reasonable estimate
of the torque scalings may be obtained by replacing ![]() with
with
![]() in Eq. (1) for disk accretion, we arrive at
the scaling
in Eq. (1) for disk accretion, we arrive at
the scaling
for RUKL-type torques. Noticing the qualitative similarity of the the scalings with
Before proceeding further, we recognized that RUKL-type torques may arise from more complicated interactions than are describable by the above arguments, and so attempted to verify the above
In order to obtain the dimensional values of the RUKL-type propeller
torques and related variables, we now insert the reference units
for the RUKL simulations given in RUKL05 and UKRL06, thus obtaining
for the torque:
Here, N33 is the propeller torque in units of 1033 g cm2 s-2, the units of other variables are as before, and we have kept the values of the turbulence and magnetic diffusivity parameters of the accretion disk in RUKL-type models at the canonical values given in RUKL05 and UKRL06. The RUKL propeller luminosity L is then obtained in a straightforward manner as
In Eq. (8), the units of all variables are as before.
Comparison of Eqs. (3) and (8)
immediately leads to the following conclusions about IS-type and
RUKL-type propeller luminosities. First, the scalings with ![]() and
and ![]() are almost identical for the two types. Secondly,
the scaling with the neutron-star spin period
are almost identical for the two types. Secondly,
the scaling with the neutron-star spin period
![]() is stronger
(-3 instead of -2) for the RUKL-type than for the IS-type. Finally,
for identical values of the variables
is stronger
(-3 instead of -2) for the RUKL-type than for the IS-type. Finally,
for identical values of the variables ![]() ,
,
![]() ,
and
,
and
![]() ,
the RUKL-type propeller luminosity is about three orders
of magnitude lower than the IS-type propeller luminosity.
Conversely, at fixed values of
,
the RUKL-type propeller luminosity is about three orders
of magnitude lower than the IS-type propeller luminosity.
Conversely, at fixed values of ![]() and
and ![]() ,
roughly equal
luminosities are given by the two types if the spin-rate for the
RUKL type is about an order of magnitude higher than that for the
IS type.
,
roughly equal
luminosities are given by the two types if the spin-rate for the
RUKL type is about an order of magnitude higher than that for the
IS type.
As indicated earlier, in this work we are exploring the properties of
such propellers as described above during the relatively early
stages of post-supernova binaries containing pre-LMXBs, when the
binary orbits are expected to be appreciably eccentric, as explained
in Sect. 6.1. In such a system, the mass-transfer rate
![]() through the inner Lagrangian point L1 is expected to
vary periodically with the orbital phase, as detailed below in
Sect. 3.
This flow of matter forms an accretion disk because of its large
specific angular momentum, as explained above, and slow viscous effects
in the disk modify the profile of the above periodic modulation
(making it less sharp), and the resultant periodic profile is that
which is shown by the mass-arrival rate
through the inner Lagrangian point L1 is expected to
vary periodically with the orbital phase, as detailed below in
Sect. 3.
This flow of matter forms an accretion disk because of its large
specific angular momentum, as explained above, and slow viscous effects
in the disk modify the profile of the above periodic modulation
(making it less sharp), and the resultant periodic profile is that
which is shown by the mass-arrival rate ![]() at the neutron
star. The propeller luminosity then follows suite, showing a periodic
modulation, as described by Eq. (3) for the
IS-type torque or Eq. (8)
for the RUKL-type torque.
In this scenario, therefore, we identify the 6.67 h period of 1E
with the binary period of a young, eccentric pre-LMXB, which is
expected to turn much later into a standard LMXB after passing through
further intermediate phases (see Sect. 6.4).
In the next section, we give details of the expected nature of the
mass-transfer modulation
at the neutron
star. The propeller luminosity then follows suite, showing a periodic
modulation, as described by Eq. (3) for the
IS-type torque or Eq. (8)
for the RUKL-type torque.
In this scenario, therefore, we identify the 6.67 h period of 1E
with the binary period of a young, eccentric pre-LMXB, which is
expected to turn much later into a standard LMXB after passing through
further intermediate phases (see Sect. 6.4).
In the next section, we give details of the expected nature of the
mass-transfer modulation
![]() at the orbital period.
at the orbital period.
3 Orbital modulation of mass transfer
The problem of orbital modulation of mass transfer in eccentric orbits
has been studied by a number of authors over almost three decades now,
adopting various approaches appropriate for various aspects of
the problem they have studied. These aspects have covered a
considerable range, from a scrutiny of the concept of the Roche lobe
in an eccentric orbit (Avni 1976), to a study of test-particle motion
through numerical integration of the restricted three-body problem
at or near periastron passage (Lubow & Shu 1975), to explicit calculations of
orbital phase-dependent flow through L1 from a suitably-modeled
stellar envelope (Joss & Rappaport 1984, and references therein).
For our purposes here, we have adopted the
results of the calculations described by Brown & Boyle (1984,
hereafter BB): these authors described the flow through L1 from
the atmosphere of the lobe-filling companion with a scale height H
as a sort of nozzle flow through the inner Lagrangian point,
integrating over a Maxwellian distribution of velocities
(characterized by thermal velocity scale ![]() )
for the stellar
matter. Their final result for the rate of mass transfer as a function
of the true anomaly
)
for the stellar
matter. Their final result for the rate of mass transfer as a function
of the true anomaly ![]() is given by:
is given by:
In Eq. (9), e is the orbital eccentricity, and the dimensionless function
where
It is convenient to work in
terms of the ratio ![]() as it varies relatively slowly with
orbital phase (and is, in fact, independent of this phase for a
non-rotating companion: see below). The other properties of the
binary system that
as it varies relatively slowly with
orbital phase (and is, in fact, independent of this phase for a
non-rotating companion: see below). The other properties of the
binary system that ![]() depends on are (a) the mass ratio
depends on are (a) the mass ratio
![]() ,
,
![]() being the mass of the low-mass
companion; and (b) the rate of rotation
being the mass of the low-mass
companion; and (b) the rate of rotation
![]() of the
companion, usually expressed in units of the orbital angular
velocity
of the
companion, usually expressed in units of the orbital angular
velocity
![]() at periastron as
at periastron as
![]() .
The scale
.
The scale
![]() of the mass-transfer rate in Eq. (9) is set by the
above velocity scale
of the mass-transfer rate in Eq. (9) is set by the
above velocity scale ![]() ,
the scale-size pH for the effective
cross-section of the above ``nozzle'', and the basic density scale
,
the scale-size pH for the effective
cross-section of the above ``nozzle'', and the basic density scale
![]() in the stellar atmosphere.
in the stellar atmosphere.
Prescriptions for ![]() have been given in the 1970s and '80s;
we use here the generalized Joss-Rappaport (Joss & Rappaport 1984) expressions
adopted by BB, namely,
have been given in the 1970s and '80s;
we use here the generalized Joss-Rappaport (Joss & Rappaport 1984) expressions
adopted by BB, namely,
where the coefficients in
and the variable K depends on the above rotation parameter
From Eqs. (11)-(13), it is clear that, for a non-rotating companion with K=0,
Detailed models with the mass transfer profile
![]() given by Eq. (9) are described below.
From general considerations, it is clear that this profile
peaks at the periastron and that the sharpness of the peak depends
on the quantity
given by Eq. (9) are described below.
From general considerations, it is clear that this profile
peaks at the periastron and that the sharpness of the peak depends
on the quantity
![]() .
Since
.
Since
![]() ,
and typical
values of
,
and typical
values of ![]() for the current problem are in the range
102-103 (BB), we see that the profile is expected to be
sharply peaked at the periastron even for realtively low values of
eccentricity, such as
for the current problem are in the range
102-103 (BB), we see that the profile is expected to be
sharply peaked at the periastron even for realtively low values of
eccentricity, such as ![]() .
.
4 Viscous flow in accretion disks
Matter transferred through L1 into the Roche lobe of the neutron
star first forms a ring around the neutron star, the radius
![]() of this ring being related to the specific angular momentum
of this ring being related to the specific angular momentum
![]() of the transferred matter as (Pringle 1981):
of the transferred matter as (Pringle 1981):
Through effective viscous stresses, this ring spreads into an accretion disk, wherein matter slowly spirals inward towards the neutron star as the viscous stresses remove angular momentum from it. The accretion disk extends from its outermost radius
The rate ![]() at which the matter drifting radially inward
through the accretion disk arrives at
at which the matter drifting radially inward
through the accretion disk arrives at ![]() depends, therefore,
both on the profile of mass supply
depends, therefore,
both on the profile of mass supply
![]() at L1, as
described above, and on the rate of viscous radial
drift through the accretion disk, which occurs on a timescale
at L1, as
described above, and on the rate of viscous radial
drift through the accretion disk, which occurs on a timescale
![]() .
.
In a quasi-steady state, the relation between the two profiles
![]() and
and
![]() is of the form
is of the form
The convolution integral in Eq. (15) describes the viscous drift with the timescale
Viscous-evolution profiles have been calculated analytically and
numerically at various levels of approximation by several authors
(Lynden-Bell & Pringle 1974; Lightman 1974). For our purposes here, we have
adopted an analytic approximation of the generic form
introduced and utilized by Pravdo & Ghosh (2001, hereafter PG). This reference has discussions of earlier analytical and numerical investigations. The generic PG profile in Eq. (16) reaches its maximum at
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12552f1a.ps}\hspace*{4mm}
\includegraphics[width=7cm,clip]{12552f1b.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12552-09/Timg74.png)
|
Figure 1:
X-ray light curve of 1E. Shown is the observed light
curve from dL06, superposed on the (common) best-fit model light
curve for IS-type and RUKL-type propellers.
Left panel: model curve for |
| Open with DEXTER | |
The following generic feature of viscous evolution of
accretion disks is a key aspect of the phenomenon we are
exploring here. Whereas the orbital modulation of the mass-supply
rate
![]() to the disk at its outer radius
to the disk at its outer radius
![]() is
expected to sharply peaked at periastron for typical values
of the scale height in the companion's atmosphere, as above,
the viscous drift of matter through the accretion disk would
decrease the sharpness of this modulation, since
variations on timescales much shorter than
is
expected to sharply peaked at periastron for typical values
of the scale height in the companion's atmosphere, as above,
the viscous drift of matter through the accretion disk would
decrease the sharpness of this modulation, since
variations on timescales much shorter than
![]() tend to be
``washed out'' by viscous diffusion. This is what makes the
orbital modulation of the mass-arrival rate
tend to be
``washed out'' by viscous diffusion. This is what makes the
orbital modulation of the mass-arrival rate
![]() at the
disk's inner radius
at the
disk's inner radius ![]() gentler, and therefore also the
modulation of the propeller luminosity L(t), leading naturally
to light curves of the form observed in 1E. Quantitative details
follow.
gentler, and therefore also the
modulation of the propeller luminosity L(t), leading naturally
to light curves of the form observed in 1E. Quantitative details
follow.
5 Model light curves
We constructed model light curves for 1E by combining the model
of mass transfer described in Sect. 3 with
that of viscous flow through the accretion disk described in
Sect. 4. We then fitted these models to the
observed light curve of 1E in 2005 (dL06).
The fitting parameters were (![]() ,
e), which come from the
above BB mass-transfer model in elliptic orbit, and also
(
,
e), which come from the
above BB mass-transfer model in elliptic orbit, and also
(
![]() ,
n), which come from the above PG parametrized
description of viscous evolution of accretion disks.
In this introductory work, we kept
,
n), which come from the above PG parametrized
description of viscous evolution of accretion disks.
In this introductory work, we kept ![]() constant at a canonical value of
constant at a canonical value of
![]() (BB), and varied
the parameters e,
(BB), and varied
the parameters e,
![]() ,
and n to obtain acceptable fits.
For the viscous timescale, we found it more convenient to work in
terms of the ratio
,
and n to obtain acceptable fits.
For the viscous timescale, we found it more convenient to work in
terms of the ratio
![]() of this timescale
to the known period
of this timescale
to the known period
![]() hr of the system, which
we of course identify with the orbital period in this model. The
ratio
hr of the system, which
we of course identify with the orbital period in this model. The
ratio ![]() is of immediate physical significance, since it
measures the relative importance of viscous diffusion to orbital
modulation in the system. For
is of immediate physical significance, since it
measures the relative importance of viscous diffusion to orbital
modulation in the system. For
![]() ,
viscous
diffusion would be so rapid as to enable the disk flow to adjust
to the orbital modulation of mass-supply rate, and flow-rate would
essentially follow the supply rate. For
,
viscous
diffusion would be so rapid as to enable the disk flow to adjust
to the orbital modulation of mass-supply rate, and flow-rate would
essentially follow the supply rate. For
![]() ,
on the other
hand, the viscous diffusion would be so slow as to wash out any
rapid variations in the mass-supply rate, and the
modulation would be essentially determined by the disk viscosity.
As we see below,
,
on the other
hand, the viscous diffusion would be so slow as to wash out any
rapid variations in the mass-supply rate, and the
modulation would be essentially determined by the disk viscosity.
As we see below, ![]() values of a few seem to describe the
1E system, indicating comparable importance of the two effects in
this system.
values of a few seem to describe the
1E system, indicating comparable importance of the two effects in
this system.
Table 1: Best fit model parameters: IS-type torque.
Table 2: Best fit model parameters: RUKL-type torque.
We fitted model light curves corresponding to both IS-type and
RUKL-type torques to the data on 1E, the best-fit values of the
parameters being given in Tables 1 and 2. In each case, we have considered both
a non-rotating secondary (![]() )
and a synchronously-rotating
secondary (
)
and a synchronously-rotating
secondary (![]() ), as indicated. Note that the best-fit values
for the two types of torques are very close to each other, as may
have been expected. This is so because the closeness of the scaling
of L with
), as indicated. Note that the best-fit values
for the two types of torques are very close to each other, as may
have been expected. This is so because the closeness of the scaling
of L with ![]() between the two types, as discussed in
Sect. 2, since only this aspect of the torque
is relevant for fitting the profile of the light curve.
Other aspects, e.g., the fact that the RUKL-type propeller luminosity
is about three orders magnitude below the IS-type propeller
lumnosity for identical vaues of
between the two types, as discussed in
Sect. 2, since only this aspect of the torque
is relevant for fitting the profile of the light curve.
Other aspects, e.g., the fact that the RUKL-type propeller luminosity
is about three orders magnitude below the IS-type propeller
lumnosity for identical vaues of ![]() ,
,
![]() and
and ![]() ,
have
important consequences elsewhere, as detailed in Sect. 6.3,
but not in this matter. Further, the absolute values of the observed
luminosities in the light curves are easily accounted for, e.g., by
having the stellar spin rate higher for RUKL-type torques by about
a factor of 10 than that for IS-type torques, and
,
have
important consequences elsewhere, as detailed in Sect. 6.3,
but not in this matter. Further, the absolute values of the observed
luminosities in the light curves are easily accounted for, e.g., by
having the stellar spin rate higher for RUKL-type torques by about
a factor of 10 than that for IS-type torques, and ![]() ,
,
![]() identical for the two types, as the scalings in
Eqs. (8) and (3) show. This implies
neutron-star spin periods in the range
identical for the two types, as the scalings in
Eqs. (8) and (3) show. This implies
neutron-star spin periods in the range
![]() s, i.e.,
the canonical range for propellers, for both type of torques,
as explained in Sect. 1.
s, i.e.,
the canonical range for propellers, for both type of torques,
as explained in Sect. 1.
This closeness of best-fit parameters is reflected in the best-fit light curves, which are visually essentially identical for the two types of torques. In Fig. 1, we display this common best-fit light curve, superposed on the data on 1E.
Our inferred best-fit value of ![]() in the above tables indicates
that the dominant contribution to the convolution integral described
in the last section comes from the second and third orbits preceding
the time of observation. The corresponding viscous timescale
in the above tables indicates
that the dominant contribution to the convolution integral described
in the last section comes from the second and third orbits preceding
the time of observation. The corresponding viscous timescale
![]() h is consistent with a rather thick disk with
h is consistent with a rather thick disk with
![]() and a canonical value
and a canonical value ![]() 0.1-1 for the disk
viscosity parameter (Shakura & Sunyaev 1973). This seems consistent with
the results of the RUKL numerical simulations. Note also that
the best-fit value of the viscous-profile index nis consistent with the range of values
0.1-1 for the disk
viscosity parameter (Shakura & Sunyaev 1973). This seems consistent with
the results of the RUKL numerical simulations. Note also that
the best-fit value of the viscous-profile index nis consistent with the range of values
![]() generally
expected for neutron-star systems, as per the discussion given
in PG. Indeed, we found that values of n in the above range
generally worked for the 1E system. Regarding the orbital
eccentricity e, the best-fit values are as given in the tables,
and we found that values of the eccentricity e in the range
generally
expected for neutron-star systems, as per the discussion given
in PG. Indeed, we found that values of n in the above range
generally worked for the 1E system. Regarding the orbital
eccentricity e, the best-fit values are as given in the tables,
and we found that values of the eccentricity e in the range
![]() 0.35-0.45 genearlly worked for the 1E system: we discuss
this in the next section. It is clear, therefore, that the model
explored in this paper can account quantitatively for the observed
1E light curve in 2005, for both IS-type and RUKL-type torques.
We discuss in Sect. 7.2 possible reasons for the
apparently different, ``jagged'' light curve hinted at by the 2001
observations of this system (dL06).
0.35-0.45 genearlly worked for the 1E system: we discuss
this in the next section. It is clear, therefore, that the model
explored in this paper can account quantitatively for the observed
1E light curve in 2005, for both IS-type and RUKL-type torques.
We discuss in Sect. 7.2 possible reasons for the
apparently different, ``jagged'' light curve hinted at by the 2001
observations of this system (dL06).
6 Formation and evolution of prototype systems
As indicated in Sect. 1, we are exploring in this work a model for systems like 1E wherein the binary system of a He-star and a low-mass star (left after completion of the CE evolution phase in which the extensive envelope of the evolved primary has been expelled and its He-core left behind) produces the pre-LMXB when the He-star explodes in a supernova (SN), leading to a newborn neutron star with a low-mass companion. Essential features of the formation and subsequent evolution of such systems are, therefore, essential components of this model. We now discuss these features in brief, considering in this section first the immediate post-SN status of the system, and then the evolution of this system with the low-mass companion in an eccentric orbit at or near the point of Roche-lobe contact at periastron, producing a system like 1E where orbitally-modulated mass transfer proceeds through the inner Lagrangian point, and the newborn, fast-spinning neutron star is operating in the propeller regime, expelling this matter instead of accreting. Subsequently, we summarize further evolution of such systems.
6.1 Immediate post-SN systems
A major question that concerns us here is the expected eccentricity
of systems formed by the SN in the above scenario, since this eccentricity
is crucial for the proposed mechanism. Qualitatively, it is obvious
that the immediate post-SN system is almost guaranteed to be highly
eccentric, as the mass loss from a typical pre-SN system of, say, a
![]() He-star and a
He-star and a
![]() low-mass companion (see
below) in forming the post-SN system of
low-mass companion (see
below) in forming the post-SN system of
![]() neutron star
with its
neutron star
with its
![]() low-mass companion is
low-mass companion is
![]() ,
which
is close enough to maximum allowed value of mass loss (=half of
the initial total mass of
,
which
is close enough to maximum allowed value of mass loss (=half of
the initial total mass of
![]() for zero kick velocity) to
ensure that the post-SN orbit would be very eccentric. We shall use
these values for the stellar masses throughout the rest of this paper.
for zero kick velocity) to
ensure that the post-SN orbit would be very eccentric. We shall use
these values for the stellar masses throughout the rest of this paper.
To see this quantitatively, we can adapt the extensive calculations of
Kalogera, who computed the probability of the formation of X-ray
binaries as a funtion of orbital parameters (Kalogera 1996). In the
following, we shall use the same masses for the pre- and post-SN
system as given above for illustrative purposes. The probability
density from Kalogera's work is:
Here,
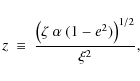
and
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12552fg2.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12552-09/Timg101.png)
|
Figure 2:
Formation probability-density
|
| Open with DEXTER | |
In the problem we are studying here, the semimajor axis of the
post-SN binary is determined by Kepler's third law from our
assumed stellar masses above, and the known orbital period of 1E.
However, when there is a kick associated with the SN, the inferred
semimajor axis of the pre-SN binary is not determined uniquely by
the semimajor axis and the eccentricity of the post-SN binary:
rather, there is a range of values corresponding to the range of
the kick-velocity. Thus, there is a range in the values of ![]() :
it is well-known that the allowed range for
:
it is well-known that the allowed range for ![]() is limited
from 1/(1+e) to 1/(1-e), these limits being first identified by
Flannery and van den Heuvel (1975). Thus, for our purposes, it is
aprropriate to integrate
is limited
from 1/(1+e) to 1/(1-e), these limits being first identified by
Flannery and van den Heuvel (1975). Thus, for our purposes, it is
aprropriate to integrate
![]() over the above allowed range
of
over the above allowed range
of ![]() ,
and display the resultant probability density
,
and display the resultant probability density
![]() as a function of the
eccentricity e. We show this in Fig. 2 for various
typical values of
as a function of the
eccentricity e. We show this in Fig. 2 for various
typical values of ![]() as indicated. In this figure, we have
used the symbol vk5 there to denote
as indicated. In this figure, we have
used the symbol vk5 there to denote ![]() in units of 105 m s
-1 = 100 km s-1, the typical scale for the SN kick
dispersion, and we have normalized the
probability density
in units of 105 m s
-1 = 100 km s-1, the typical scale for the SN kick
dispersion, and we have normalized the
probability density
![]() so that
so that
![]() in each case. As explained above, the closeness
of the value of
in each case. As explained above, the closeness
of the value of
![]() in this typical case to its lower
limit for no binary destruction in the SN (this limit is 0.5 for zero
kick velocity) ensures that the probability peaks at a high value of
e, as Fig. 2 shows. It is clear, therefore, that such a
pre-LMXB would generically have a considerable eccentricity at the
time of its formation in the SN.
in this typical case to its lower
limit for no binary destruction in the SN (this limit is 0.5 for zero
kick velocity) ensures that the probability peaks at a high value of
e, as Fig. 2 shows. It is clear, therefore, that such a
pre-LMXB would generically have a considerable eccentricity at the
time of its formation in the SN.
6.2 Tidal-evolution phase of pre-LMXBs
The above newly-formed pre-LMXB undergoes tidal evolution,
wherein three simultaneous processes occur, namely, (1) tidal
circularization, i.e., decrease in the orbital eccentricity e;
(2) tidal orbit-shrinkage or hardening, i.e., decrease in the
orbital semimajor axis a; and (3) tidal synchronization, whereby
the rotation frequency
![]() of the low-mass companion approaches
the orbital angular frequency
of the low-mass companion approaches
the orbital angular frequency
![]() .
These processes
happen through tidal torques, and their quantitative descriptions
pioneered by Zahn (1978,1977) are widely used for calculations: we
use them here, as have P08. Complete equations
are given in Zahn (1977), and an Erratum was published by Zahn (1978). We have found a further algebraic or transcription error in
the original paper, which we describe below, and which seems to have
gone unnoticed so far.
.
These processes
happen through tidal torques, and their quantitative descriptions
pioneered by Zahn (1978,1977) are widely used for calculations: we
use them here, as have P08. Complete equations
are given in Zahn (1977), and an Erratum was published by Zahn (1978). We have found a further algebraic or transcription error in
the original paper, which we describe below, and which seems to have
gone unnoticed so far.
Complete formulations for the rates of change of e, a, and
![]() are given in Zahn (1977), but for our work here we shall
utilize a widely-used simplification which comes naturally out of
these formulations, namely, that the timescale for tidal synchronization
comes out to be much shorter than that for tidal circularization and
tidal hardening (see, e.g., Meibom & Mathieu 2005; P08). This is appropriate,
since we shall be interested in this work only in phenomena which
occur on the timescales of tidal circularizatuion or longer. Under
such circumstances, we can look upon the system as being roughly
synchronous at all times, and describe tidal circularization and
tidal hardening respectively by Zahn's (1977) Eq. (4.7) and the
appropriately simplified (i.e., synchronized) version of Zahn's
Eq. (4.3), thereby obtaining:
are given in Zahn (1977), but for our work here we shall
utilize a widely-used simplification which comes naturally out of
these formulations, namely, that the timescale for tidal synchronization
comes out to be much shorter than that for tidal circularization and
tidal hardening (see, e.g., Meibom & Mathieu 2005; P08). This is appropriate,
since we shall be interested in this work only in phenomena which
occur on the timescales of tidal circularizatuion or longer. Under
such circumstances, we can look upon the system as being roughly
synchronous at all times, and describe tidal circularization and
tidal hardening respectively by Zahn's (1977) Eq. (4.7) and the
appropriately simplified (i.e., synchronized) version of Zahn's
Eq. (4.3), thereby obtaining:
and
In Eqs. (18) and (19),
Equations (18) and (19) describe simultaneous tidal circularization and hardening of close binaries, but before presenting our results, we need to correct two errors related to them. First, if we define a circularization timescale
which would be identical to Zahn's (1977) Eq. (4.13), except that the factor of 4 on the right-hand side is missing in Zahn (1977). Unfortunately, this error has propagated over the years into numerous papers, e.g., in P08, in their Eq. (2)
We have integrated Eqs. (18) and (19)
numerically for close binary systems like 1E, with values of
initial post-SN semimajor axes and eccentricities, ai and ei,
chosen over a range of plausible values for such systems. We find
that, in all cases, the systems circularize and harden in a way
that, in the (e vs. a) plane, the circularization point is
approached in a ``cut off'' like manner. This is shown in
Fig. 3 for a possible prototype 1E-like system, so
chosen that the parameters of it evolve to those roughly
corresponding to 1E in ![]() 2000 years. This cut-off approach
is similar to what Meibom & Mathieu (2005) found. Of course,
our detailed shape is slightly different from that of these authors,
since they fitted their results to an assumed parameterized
distribution shape applicable to observations on a collection of
``normal'' binaries.
These details will be given in a separate publication. For our
purposes here, we note that the total time
2000 years. This cut-off approach
is similar to what Meibom & Mathieu (2005) found. Of course,
our detailed shape is slightly different from that of these authors,
since they fitted their results to an assumed parameterized
distribution shape applicable to observations on a collection of
``normal'' binaries.
These details will be given in a separate publication. For our
purposes here, we note that the total time
![]() taken to
reach this circularization point (Meibom & Mathieu 2005) can be expressed
roughly as:
taken to
reach this circularization point (Meibom & Mathieu 2005) can be expressed
roughly as:
where ai and ei are the initial semimajor axis and eccentricity of the immediate post-SN orbit, and the scale parameter
Equation (22) is a rough analytic fit to the mumerical results, adequate for our purposes. Note that the scale parameter
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12552fg3.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12552-09/Timg120.png)
|
Figure 3: Tidal evolution of a prototype 1E-like system in the e vs. a plane. Semimajor axis a in units of solar radius. Note the ``cut off'' like approach to the circularization point (see text). |
| Open with DEXTER | |
It is clear from Eq. (22) that circularization is faster for orbits which are born more compact and more eccentric. The scaling with a is straightforward from the above equations of tidal evolution; the scaling with e is more complicated (although inspection of the same equations gives some clue), involving details of the numerical solution.
The lifetime
![]() of the eccentric phase of the pre-LMXB
is obviously also the lifetime of its orbital-modulation phase
which we are investigating in this work. The sensitive dependence
of this lifetime on the initial post-SN orbital parameters and
the companion mass (through the scale parameter
of the eccentric phase of the pre-LMXB
is obviously also the lifetime of its orbital-modulation phase
which we are investigating in this work. The sensitive dependence
of this lifetime on the initial post-SN orbital parameters and
the companion mass (through the scale parameter ![]() and due
to the mass-dependence of
and due
to the mass-dependence of ![]() in Eq. (22)) makes
for a wide range of possible values of this lifetime,
in Eq. (22)) makes
for a wide range of possible values of this lifetime, ![]() 103-108 years.
103-108 years.
A crucial point is, of course, that if the companion is at or close to filling its Roche lobe at periastron in the post-SN orbit, it must remain so throughout most of this eccentric phase in order for the scenario to be self-consistent. The size of the Roche lobe at periastron is simply p=a(1-e) multiplied by a well-known function of the mass ratio q. Since the latter does not change significantly during this phase, we need only study the evolution of the former. Our integration of the tidal-evolution equations show that, while a and e both decrease during this phase, p=a(1-e) decreases slowly through most of this phase, reaching a minimum and increasing thereafter at late stages. This is shown in Fig. 4 for the prototype 1E-like system displayed in Fig. 3 (see above). Thus, if the companion is initially at or close to filling its Roche lobe at periastron, it will remain so over most of this phase, and if it is inside its Roche lobe initially, it is likely to fill its Roche lobe later during this phase. It is also seen that Roche-lobe contact ends at the last parts of this phase (when the orbit is nearly circular), since p increases and becomes roughly constant there.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12552fg4.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12552-09/Timg122.png)
|
Figure 4: Evolution of periastron distance p=a(1-e) during tidal evolution of a prototype 1E-like system (see text). Shown is p in units of the solar radius vs. time in years. |
| Open with DEXTER | |
Thus, this tidal-evolution phase is a rough measure of the lifetime of Roche-lobe contact and orbital modulation of the propeller output. After this, the pre-LMXB becomes detached, and remains so until angular-momentum loss through gravitational radiation and/or magnetic braking brings it back to Roche-lobe contact on a long timescale of 108-109 yrs. We discuss this phase below in Sect. 6.4.
6.3 Duration of propeller phase
When the above tidal-evolution phase ends, is the neutron star
still operating in the propeller phase? To answer this question,
we consider the spindown of the neutron star from an initial
spin period
![]() to a final, longer spin period
to a final, longer spin period
![]() under the action of the propeller torque given by
either the IS-type torque (Eq. (1)) or the
RUKL-type torque (Eq. (7)). In each case,
this spindown is decsribed by
under the action of the propeller torque given by
either the IS-type torque (Eq. (1)) or the
RUKL-type torque (Eq. (7)). In each case,
this spindown is decsribed by
where I is the moment of inertia of the neutron star and
First consider IS-type torques, for which
![]() is
given by
is
given by
where I45 is I in units of 1045 gm cm2, and other units are as before. Equation (24) can be integrated readily in this case, the total spindown time
As discussed earlier, the ratio
for canonical values of
Now consider RUKL-type torques, for which
![]() is given by
is given by
Equation (24) can be integrated readily in this case also, the total spindown time
the second equality in the above equation coming from the fact that the ratio
which implies that, for canonical range
for canonical values of the variables
In comparing the total spindown times
![]() given by the
two types of torques, we notice that the time taken by the
RUKL-type torque is 2-3 orders of magnitude longer than that
taken by the IS-type torque for identical values of
given by the
two types of torques, we notice that the time taken by the
RUKL-type torque is 2-3 orders of magnitude longer than that
taken by the IS-type torque for identical values of ![]() ,
,
![]() and I. This reflects the relative weakness of the
RUKL-type torque discussed in Sect. 2.
Next, comparing the values of
and I. This reflects the relative weakness of the
RUKL-type torque discussed in Sect. 2.
Next, comparing the values of
![]() given by the above two
types of propeller torques with the lifetime
given by the above two
types of propeller torques with the lifetime
![]() of the
eccentric phase given in the previous section, we reach the
following conclusions. For the IS-type torque, we find that, over
most of the parameter space, the neutron star would still be in the
propeller phase at the end of the above tidal-evolution phase of
the binary. For the RUKL-type torque, we find that this conclusion
is valid over the entire parameter space. Thus, the RUKL-type
torque makes the conclusion stronger.
of the
eccentric phase given in the previous section, we reach the
following conclusions. For the IS-type torque, we find that, over
most of the parameter space, the neutron star would still be in the
propeller phase at the end of the above tidal-evolution phase of
the binary. For the RUKL-type torque, we find that this conclusion
is valid over the entire parameter space. Thus, the RUKL-type
torque makes the conclusion stronger.
As shown above, the companion has moved out of Roche-lobe contact by the time that the tidal-evolution phase of the binary reaches conclusion, so that mass transfer stops, and so does the propeller action and its consequent soft X-ray production. Accordingly, throughout this first Roche-lobe contact phase, we expect the system to be in the propeller phase.
6.4 Re-contact with Roche lobe and LMXB phase
After orbit circularization and the loss of its first Roche-lobe
contact, as described above, the pre-LMXB thus ceases to be an
X-ray source. But its orbit shrinks (i.e., the binary hardens)
on a long timescale (![]() 108-109 yr)
due to two mechanisms of angular momentum loss from the
system, viz., graviational radiation and magnetic braking
(Ghosh 2007, and references therein). These are the standard
mechanisms through which short-period pre-LMXBs are believed to
harden, until Roche-lobe contact is regained and mass transfer
restarts. But the transferred mass is now accreted by the neutron
star, because its spin has been slowed down sufficiently over
this long time that it acts as an accretor and not a propeller
at the (large) mass-transfer rates that occur at this second
Roche-lobe contact in the circularized binary. The system thus
turns on as a canonical LMXB now, emitting strongly (
108-109 yr)
due to two mechanisms of angular momentum loss from the
system, viz., graviational radiation and magnetic braking
(Ghosh 2007, and references therein). These are the standard
mechanisms through which short-period pre-LMXBs are believed to
harden, until Roche-lobe contact is regained and mass transfer
restarts. But the transferred mass is now accreted by the neutron
star, because its spin has been slowed down sufficiently over
this long time that it acts as an accretor and not a propeller
at the (large) mass-transfer rates that occur at this second
Roche-lobe contact in the circularized binary. The system thus
turns on as a canonical LMXB now, emitting strongly (
![]() erg s-1) in the canonical X-ray band characteristic
of emission from the neutron-star surface, rather than the soft
X-ray band characteristic of propeller emission from the vicinity
of the magnetospheric boundary.
erg s-1) in the canonical X-ray band characteristic
of emission from the neutron-star surface, rather than the soft
X-ray band characteristic of propeller emission from the vicinity
of the magnetospheric boundary.
The timescale
![]() of orbit shrinkage due to gravitational
radiation is given by (see, e.g., Faulkner 1971; Banerjee & Ghosh
2006):
of orbit shrinkage due to gravitational
radiation is given by (see, e.g., Faulkner 1971; Banerjee & Ghosh
2006):
where
Thus, the system becomes a canonical, bright LMXB with a circular
orbit and
![]() in the range of, say, 2-10 h. It is
well-known that systems with
in the range of, say, 2-10 h. It is
well-known that systems with
![]() exceeding about 12 h
cannot come into Roche lobe contact by the above orbit-shrinkage
mechanisms, since the time required would exceed the Hubble time,
as Eq. (32) readily shows. However, these long-period
systems also come into Roche-lobe contact eventually, as the
low-mass companion completes its main-sequence evolution and
expands. These systems thus also become canonical long-period
LMXBs with circular orbits. The lifetime of this standard, bright
LMXB phase is
exceeding about 12 h
cannot come into Roche lobe contact by the above orbit-shrinkage
mechanisms, since the time required would exceed the Hubble time,
as Eq. (32) readily shows. However, these long-period
systems also come into Roche-lobe contact eventually, as the
low-mass companion completes its main-sequence evolution and
expands. These systems thus also become canonical long-period
LMXBs with circular orbits. The lifetime of this standard, bright
LMXB phase is
![]() yr.
yr.
7 Discussion
In this work, we have explored a pre-LMXB model of 1E, wherein the eccentric orbit of the very young pre-LMXB causes an orbital modulation in the mass-transfer rate, and the newborn, fast-rotating neutron star operates in the propeller regime, the propeller emission in soft X-rays following the above modulation after viscous smoothening in the accretion disk. In this section, we first discuss first some essential spectral and luminosity-dependent features of 1E, and their connections with corresponding features in old, low-mass, soft X-ray transients (SXRTs) in their low/quiescent states, the prime example of this class being Aquila X-1 (Campana et al. 1998). Note that the well-known transient accretion-powered millisecond pulsar SAX J1808.4-3658 also shows a similar behavior (Stella et al. 2000). In these classes of low-mass X-ray binaries with old neutron stars, the neutron star is thought to operate in the propeller regime when the sources are in their low/quiescent states during decays of their outbursts. We then compare our model with the magnetar model which has been proposed recently for 1E (P08), and discuss how distinction between the two kinds of models might be attempted in future. Finally, we summarize our conclusions.
7.1 X-ray spectra
The XMM-Newton/EPIC (0.5-8 keV) X-ray spectra of 1E have been
described by dL06. The time-averaged spectra from
the 2005 low-state observations, when the source luminosity was
![]() erg s-1, can be fitted by a two-component model
consisting of a blackbody (BB) of temperature
erg s-1, can be fitted by a two-component model
consisting of a blackbody (BB) of temperature
![]() keV and an
equivalent blackbody radius
keV and an
equivalent blackbody radius
![]() km, plus a power-law (PL)
of index
km, plus a power-law (PL)
of index
![]() ,
with
,
with ![]() 70% of the total flux coming
from the blackbody component.
Alternatively, the second component can also be a
blackbody with a higher temperature. A re-analysis of the earlier 2001
XMM-Newton data, when 1E had a higher luminosity (by a factor
70% of the total flux coming
from the blackbody component.
Alternatively, the second component can also be a
blackbody with a higher temperature. A re-analysis of the earlier 2001
XMM-Newton data, when 1E had a higher luminosity (by a factor ![]() 6),
yielded a similar two-component (BB+PL) model with essentially the
same blackbody temperature
6),
yielded a similar two-component (BB+PL) model with essentially the
same blackbody temperature
![]() and power-law index
and power-law index ![]() ,
but
a larger equivalent blackbody radius
,
but
a larger equivalent blackbody radius
![]() km, and a higher
contribution from the PL component (the blackbody contribution was
km, and a higher
contribution from the PL component (the blackbody contribution was ![]() 50% of the total flux as opposed to the above
50% of the total flux as opposed to the above ![]() 70%),
which made the overall spectrum harder (dL06).
70%),
which made the overall spectrum harder (dL06).
We stress the remarkable similarity of the above observations with
those of the spectra of SXRTs in their low/quiescent states (when
the neutron stars in them are believed to be functioning in the
propeller regime), taking the well-known source Aquila X-1 as the
example. A detailed analysis of the BeppoSAX observations of Aquila X-1
in 1997 (Campana et al. 1998) has yielded the following results. At the
lowest state, with source luminosity
![]() erg s-1, the (BB+PL) fit had a BB of temperature
erg s-1, the (BB+PL) fit had a BB of temperature
![]() keV and an
equivalent blackbody radius
keV and an
equivalent blackbody radius
![]() km, plus a power-law (PL)
of index
km, plus a power-law (PL)
of index
![]() ,
with
,
with ![]() 60% of the total flux coming
from the blackbody component. As the luminosity increased by a
factor
60% of the total flux coming
from the blackbody component. As the luminosity increased by a
factor ![]() 150 to
150 to
![]() erg s-1, the
(BB+PL) fit yielded a BB of temperature
erg s-1, the
(BB+PL) fit yielded a BB of temperature
![]() keV and an
equivalent blackbody radius
keV and an
equivalent blackbody radius
![]() km, plus a power-law (PL)
of index
km, plus a power-law (PL)
of index
![]() ,
with
,
with ![]() 20% of the total flux coming
from the blackbody component. Remembering that the total range of
luminosities in these Aquila X-1 low-state observations during outburst
decay is roughly
1033-1035 erg s-1 (Campana et al. 1998),
essentially identical to that of the 1E observations reported by dL06,
the correspondence is very suggestive.
20% of the total flux coming
from the blackbody component. Remembering that the total range of
luminosities in these Aquila X-1 low-state observations during outburst
decay is roughly
1033-1035 erg s-1 (Campana et al. 1998),
essentially identical to that of the 1E observations reported by dL06,
the correspondence is very suggestive.
SXRTs are believed to be old systems with a neutron star and a
low-mass companion in a close circular orbit, undergoing outbursts due to
instabilties either in the accretion disk or in the mass supply from
the low-mass companion. In their low/quiescent states during decays
of outbursts, the fast-spining neutron star (spun up by accretion as
per standard LMXB scenario) is believed to operate in the propeller
regime. What we suggest in this work is that 1E-like systems are
very young systems in the same regime: the young systems can show
orbital modulation because of the orbital eccentricity, while the old
systems are in circular orbit and cannot show such orbital modulation.
However, the spectral signatures are very similar at similar
luminosities, which supports our basic suggestion. We note that
the timescales associated with 1E outburst appear to be ![]() 2-3 years while those associated with Aquila X-1 outbursts appear to be
2-3 years while those associated with Aquila X-1 outbursts appear to be
![]() 30-70 days. It is possible that the basic phenomenon is rather
similar in the two cases, and that the difference in detail is caused
by the fact that accretion onto the neutron-star surface (with
attendant high luminosities and hard X-ray spectra) does occur at
the high states during the outbursts for old systems like Aquila X-1,
but not for young systems like 1E.
30-70 days. It is possible that the basic phenomenon is rather
similar in the two cases, and that the difference in detail is caused
by the fact that accretion onto the neutron-star surface (with
attendant high luminosities and hard X-ray spectra) does occur at
the high states during the outbursts for old systems like Aquila X-1,
but not for young systems like 1E.
A comprehensive theory of the emission spectra of propeller sources appears to be lacking, though Illarionov and co-authors have studied some effects of Comptonization in propellers in wind-accreting massive X-ray binaries (Illarionov et al. 1993; Illarionov & Kompaneets 1990). Attempts at constructing such a theory for propellers in pre-LMXBs and in old LMXBs in low/quiescent states is clearly beyond the scope of this paper, and we shall confine ourselves here to the comment that the importance of Compton heating, considered in the above works on propellers in massive binaries, is also likely to be crucial for the systems we are focusing on in this work, as the observed power-law tails in the spectra at low luminosities suggest. These tails are particularly prominent in the low-state spectra of Aquila X-1 (Campana et al. 1998).
7.2 Luminosity dependence of light curve
dL06 have compared the 1E light curve in the
2005 low-state observations with that during the 2001 observations
when the source luminosity was a factor ![]() 6 higher. While
the former light curve is relatively smooth with some cycle-to-cycle
variations, the latter one shows more complex, somewhat ``jagged''
structure, with an occasional dip. Further, the pulsed fraction
decreses from
6 higher. While
the former light curve is relatively smooth with some cycle-to-cycle
variations, the latter one shows more complex, somewhat ``jagged''
structure, with an occasional dip. Further, the pulsed fraction
decreses from ![]() 43% to
43% to ![]() 12% as the luminosity
increases. We discuss qualitatively how such features may arise.
First, a propeller system is inherently more fluctuating than an
accreting system, because of a variety of fluctuations possible
at the site of shock-heating and outflow. As mass-supply rate
through the accretion disk increases, these fluctuations may
increase, causing more complex profiles. Secondly, accretion disks
in low-mass systems like LMXBs and CVs are thought to develop
structures at their outer edges, which obscure emission from the
compact object, and lead to dips. If these obscuring structures
increase in size as mass-supply rate through the accretion disk
increases, this would provide a natural explanation for the
above appearance of the dips. Thirdly, as the mass-arrival rate
12% as the luminosity
increases. We discuss qualitatively how such features may arise.
First, a propeller system is inherently more fluctuating than an
accreting system, because of a variety of fluctuations possible
at the site of shock-heating and outflow. As mass-supply rate
through the accretion disk increases, these fluctuations may
increase, causing more complex profiles. Secondly, accretion disks
in low-mass systems like LMXBs and CVs are thought to develop
structures at their outer edges, which obscure emission from the
compact object, and lead to dips. If these obscuring structures
increase in size as mass-supply rate through the accretion disk
increases, this would provide a natural explanation for the
above appearance of the dips. Thirdly, as the mass-arrival rate
![]() at
at ![]() increases,
increases, ![]() decreases (see Sect. 2),
matter at the magnetospheric boundary becomes hotter, and the propeller
becomes less supersonic, ultimately becoming subsonic. Now, it is
well-known that the subsonic propeller torque
decreases (see Sect. 2),
matter at the magnetospheric boundary becomes hotter, and the propeller
becomes less supersonic, ultimately becoming subsonic. Now, it is
well-known that the subsonic propeller torque
![]() is independent of
is independent of ![]() (see Ghosh 1995, and references therein), and so will not
follow the modulations of
(see Ghosh 1995, and references therein), and so will not
follow the modulations of ![]() .
Hence, as
.
Hence, as ![]() and L
increase, the following phenomenon is likely to happen. As the
upper limit of the excursions in
and L
increase, the following phenomenon is likely to happen. As the
upper limit of the excursions in ![]() goes beyond the critical
cross-over point from supersonic to subsonic propeller regime, the
pulsed fraction will decrease because that part of
goes beyond the critical
cross-over point from supersonic to subsonic propeller regime, the
pulsed fraction will decrease because that part of ![]() which
is above this critical point will not contribute to the pulsed
flux, and this decrease will increase with increasing
which
is above this critical point will not contribute to the pulsed
flux, and this decrease will increase with increasing ![]() .
This may be a natural explanation for the above observation of
reduced pulsed fraction at higher luminosity. More quantitative
considerations will be given elsewhere.
.
This may be a natural explanation for the above observation of
reduced pulsed fraction at higher luminosity. More quantitative
considerations will be given elsewhere.
7.3 Comparison with magnetar model
In a recent paper, P08 have described a model
in which 1E is a magnetar, i.e., a neutron star with a
superstrong magnetic field ![]() 1015 G with a low-mass
companion. The 6.7 h period is interpreted in this model as the
spin period of the neutron star, the idea being that a neutron
star with such strong magnetic field as above can be spun down to
such long spin period, or such low spin frequency, in
1015 G with a low-mass
companion. The 6.7 h period is interpreted in this model as the
spin period of the neutron star, the idea being that a neutron
star with such strong magnetic field as above can be spun down to
such long spin period, or such low spin frequency, in ![]() 2000 yrs. Magnetars are a fascinating possibility, and their relevance
to soft gamma repeaters (SGRs) and possibly to anomalous X-ray
pulsars (AXPs) has been the subject of much recent study.
P08 have invoked an analogy with polars or AM Her-type
cataclysmic variables containing white dwarfs with unusually
strong magnetic fields, wherein torques acting on the magnetar
spin it down in a short time to spin periods in close
synchronism with the binary orbital period. In this analogy,
they have been inspired by the similarity of the shape the 1E
light curve to those of AM Her systems.
2000 yrs. Magnetars are a fascinating possibility, and their relevance
to soft gamma repeaters (SGRs) and possibly to anomalous X-ray
pulsars (AXPs) has been the subject of much recent study.
P08 have invoked an analogy with polars or AM Her-type
cataclysmic variables containing white dwarfs with unusually
strong magnetic fields, wherein torques acting on the magnetar
spin it down in a short time to spin periods in close
synchronism with the binary orbital period. In this analogy,
they have been inspired by the similarity of the shape the 1E
light curve to those of AM Her systems.
We have desribed in this work a model which does not require a
neutron star with a superstrong magnetic field, but rather
interprets the 6.7 h period as the orbital period of the binary
system consisting of a neutron star with a canonical magnetic
field of ![]() 1012 G with a low-mass companion, the newborn,
fast-rotating neutron star being in the propeller phase, and the
propeller emission being modulated in the eccentric orbit of a
young post-SN binary. We find that the observed 1E light curve
can be quantitatively accounted for by our model. Our analogy
is with propeller regimes of SXRTs like Aquila X-1 in their
low/quiescent states, which we consider to be old, circularized
analogues of 1E which are no longer orbitally modulated, but
which have remarkably similar spectral properties. In this analogy,
we have been inspired by the similarity between 1E and the SXRTs in
both the spectral characteristics and their changes with source
luminosity, as well as the shapes of the outbursts and the way
in which propeller-like properties emerge at low luminosities
during outburst decays.
1012 G with a low-mass companion, the newborn,
fast-rotating neutron star being in the propeller phase, and the
propeller emission being modulated in the eccentric orbit of a
young post-SN binary. We find that the observed 1E light curve
can be quantitatively accounted for by our model. Our analogy
is with propeller regimes of SXRTs like Aquila X-1 in their
low/quiescent states, which we consider to be old, circularized
analogues of 1E which are no longer orbitally modulated, but
which have remarkably similar spectral properties. In this analogy,
we have been inspired by the similarity between 1E and the SXRTs in
both the spectral characteristics and their changes with source
luminosity, as well as the shapes of the outbursts and the way
in which propeller-like properties emerge at low luminosities
during outburst decays.
An interesting question is that of possible discriminators between the above two models. It appears to us that if all observed properties of 1E and similar systems can be accounted for by known characteristics of early stages of pre-LMXBs born according to the standard CE evolution and He-star supernova scenario, such as we have described in this paper (or by other possible models involving standard evolutionary scenarios), there would not be any compelling need for invoking exotic objects like magnetars for this class of objects. On the other hand, if one finds unique observed features in this class of objects that cannot be explained at all within the framework of standard evolutionary scenarios, presence of magnetars in such objects may well be hinted at. However, answering this question is beyond the scope of this paper: we are pursuing the matter, and the results will be reported elsewhere.
7.4 Conclusions
The work reported here suggests that 1E-type systems are early
stages of pre-LMXBs born in the SN of He-stars in binaries of
(He-star + low-mass star) produced by common-envelope
(CE) evolution. As long as the post-SN binary is eccentric, and
the neutron star is in the propeller regime, soft X-ray emission
modulated at the orbital period may be expected to occur. As
the orbit circularizes, modulation would stop, and as the low-mass
companion moves out of Roche-lobe contact, the source would not
be observed in X-rays. The companion would come into Roche-lobe
contact again on a long timescale due to orbit shrinkage by
emission of gravitational radiation and magnetic braking, and/or
by the evolutionary expansion of the companion. This would lead
to a standard LMXB: an old neutron star in circular orbit with
a low-mass companion. Thus, steady-state arguments, with lifetimes
of 1E-type systems estimated at ![]() 106-107 yrs and those
of LMXBs estimated at
106-107 yrs and those
of LMXBs estimated at ![]() 108-109 yrs, would lead us to expect
108-109 yrs, would lead us to expect ![]() 1 1E-type systems per
1 1E-type systems per ![]() 100 LMXBs, which is consistent
with current observations. However, we must be careful here, as
these are overall arguments for the whole population. If one
specifically investigates young supernova remnants (SNRs), the
chances of finding such systems may be considerably higher, since
eccentric binary systems are to be found preferentially in such
SNRs. More detailed considerations will be given elsewhere.
100 LMXBs, which is consistent
with current observations. However, we must be careful here, as
these are overall arguments for the whole population. If one
specifically investigates young supernova remnants (SNRs), the
chances of finding such systems may be considerably higher, since
eccentric binary systems are to be found preferentially in such
SNRs. More detailed considerations will be given elsewhere.
The lifetime of the eccentric-binary phase may be increased by an effect we have not included in this introductory work. The effect is that of an enhancement of eccentricity when mass and angular momentum are lost from a binary system which is already eccentric. This dynamical effect is well-known in the literature (see, e.g., Huang 1963) and its applications to compact X-ray binaries have been made earlier (Ghosh et al. 1981). For an eccentric compact binary with the neutron star in the propeller regime leading to the loss of both mass and angular momentum from the system, such considerations are applicable. However, it is possible that, at the rates of mass transfer and loss inferred for 1E-type systems, this effect is a minor one.
Several lines of further investigation are naturally suggested by the considerations we have given in this paper. Foremost among them is a theory of the spectral characteristics of propeller emission in disk-fed propeller systems. This would help clarify the remarkable spectral similarity (including changes in spectral parameters with luminosity) between 1E and SXRTs like Aquila X-1 in their low/quiescent state, as described in Sect. 7.1. A search for point soft X-ray sources in other young SNRs would clarify the observational situation greatly. We note that these sources may or may not be periodically modulated, as we have argued in Sect. 7.2 that such modulations may decrease and disappear in certain luminosity states. However, the spectral characteristics would still be a most valuable diagnostic. These and other investigations are under way, and results will be reported elsewhere.
AcknowledgementsIt is a pleasure to thank A. de Luca for sending data on the light curves, to thank E. P. J. van den Heuvel and L. Stella for stimulating discussions, and to thank the referee for comments which improved the paper considerably.
References
- Avni, Y. 1976, ApJ, 209, 574 [NASA ADS] [CrossRef]
- Bath, G., & Pringle, J. 1981, MNRAS, 194, 967 [NASA ADS]
- Brown, J., & Boyle, C. 1984, A&A, 141, 369 [NASA ADS]
- Campana, S., Stella, L., Mereghetti, S., et al.1998, ApJ, 499, L65
- Davies, R., & Pringle, J. E. 1981, MNRAS, 196, 209 [NASA ADS]
- Davies, R., Fabian, A. C., & Pringle, J. E. 1979, MNRAS, 186, 779 [NASA ADS]
- de Luca, A., Caraveo, P. A., Mereghetti, S., Tiengo, A., & Bignami, G. F. 2006, Science, 313, 814 [NASA ADS] [CrossRef] (dL06)
- de Luca, A., Mignani, R. P., Zaggia, S., et al. 2008, ApJ, 682, 1185 [NASA ADS] [CrossRef]
- Faulkner, J. 1971, ApJ, 170, L99 [NASA ADS] [CrossRef]
- Ghosh, P. 1995, ApJ, 453, 411 [NASA ADS] [CrossRef] (G95)
- Ghosh, P. 2007, Rotation and Accretion Powered Pulsars (Singapore: World Scientific Publications)
- Ghosh, P., Elsner, R. F., Weisskopf, M. C., & Sutherland, P. G. 1981, ApJ, 251, 230 [NASA ADS] [CrossRef]
- Heyl, J., & Hernquist, H. 2002, ApJ, 567, 510 [NASA ADS] [CrossRef]
- Huang, S.-S. 1963, ApJ, 138, 471 [NASA ADS] [CrossRef]
- Illarionov, A. F., & Kompaneets, D. A. 1990, MNRAS, 247, 219 [NASA ADS]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] (IS75)
- Illarionov, A. F., Igumenschev, I. V., & Kompaneets, D. A. 1993, The evolution of X-ray Binaries, ed. S. S. Holt, & C. S. Day (New York: AIP), 601
- Joss, P., & Rappaport, S. 1984, ARA&A, 22, 537 [NASA ADS] [CrossRef]
- Kalogera, V. 1996, ApJ, 471, 352 [NASA ADS] [CrossRef]
- Landin, N. R., Mendez, L. T. S., & Vaz, L. P. R. 2009, A&A, 494, 209 [NASA ADS] [CrossRef] [EDP Sciences]
- Lightman, A. 1974, ApJ, 194, 429 [NASA ADS] [CrossRef]
- Lovelace, R. V. E., Romanova, M. M., & Bisnovatyi-Kogan, G. S. 1999, ApJ, 514, 368 [NASA ADS] [CrossRef] (LRB99)
- Lubow, S., & Shu, F. 1975, ApJ, 198, 383 [NASA ADS] [CrossRef]
- Lynden-Bell, D., & Pringle, F. 1974, MNRAS, 168, 603 [NASA ADS]
- Meibom, S., & Mathieu, R. D. 2005, ApJ, 620, 970 [NASA ADS] [CrossRef]
- Mignani, R., et al. 2007 [arXiv:0711.0113]
- Mineshige, S., Rees, M. J., & Fabian, A. C. 1991, MNRAS, 251, 555 [NASA ADS]
- Pavlov, G., et al. 2002, Neutron Stars in Supernova Remnants, ASP Conf. Ser., 271, 2002
- Pizzolato, F., Colpi, M., De Luca, A., Mereghetti, S., & Tiengo, A. 2008, ApJ, 681, 530 [NASA ADS] [CrossRef] (P08)
- Pravdo, S., & Ghosh, P. 2001, ApJ, 554, 383 [NASA ADS] [CrossRef]
- Pringle, J. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2004, ApJ, 616, L151 [NASA ADS] [CrossRef]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2005, ApJ, 635, L165 [NASA ADS] [CrossRef] (RUKL05)
- Shakura, N., & Sunyaev, R. 1973, A&A, 24, 337 [NASA ADS]
- Stella, L., Campana, S., Mereghetti, S., Ricci, D., & Israel, G. L. 2000, ApJ, 537, L115 [NASA ADS] [CrossRef]
- Tuohy, I., & Garmire, G. 1980, ApJ, 239, L107 [NASA ADS] [CrossRef]
- Ustyugova, G. V., Koldoba, A. V., Romanova, M. M., & Lovelace, R. V. E. 2006, ApJ, 646, 304 [NASA ADS] [CrossRef] (UKRL06)
- Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7 [NASA ADS]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS]
- Zahn, J.-P. 1978, A&A, 67, 162 [NASA ADS]
Footnotes
- ...
Eq. (2)
![[*]](/icons/foot_motif.png)
- Because of this, the parameters adopted for
1E by P08 and by ourselves in this work actually
give
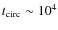 yr. In our work, we have used the values
of the apsidal-motion constant k2 given by Landin et al. (2009).
yr. In our work, we have used the values
of the apsidal-motion constant k2 given by Landin et al. (2009).
All Tables
Table 1: Best fit model parameters: IS-type torque.
Table 2: Best fit model parameters: RUKL-type torque.
All Figures
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12552f1a.ps}\hspace*{4mm}
\includegraphics[width=7cm,clip]{12552f1b.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12552-09/Timg74.png)
|
Figure 1:
X-ray light curve of 1E. Shown is the observed light
curve from dL06, superposed on the (common) best-fit model light
curve for IS-type and RUKL-type propellers.
Left panel: model curve for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12552fg2.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12552-09/Timg101.png)
|
Figure 2:
Formation probability-density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12552fg3.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12552-09/Timg120.png)
|
Figure 3: Tidal evolution of a prototype 1E-like system in the e vs. a plane. Semimajor axis a in units of solar radius. Note the ``cut off'' like approach to the circularization point (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12552fg4.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12552-09/Timg122.png)
|
Figure 4: Evolution of periastron distance p=a(1-e) during tidal evolution of a prototype 1E-like system (see text). Shown is p in units of the solar radius vs. time in years. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



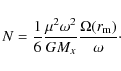
![\begin{displaymath}r_{\rm m} = \left[\frac{\mu^{2}}{\dot{M}\sqrt{2GM_x}}\right]^{\frac{2}{7}},
\end{displaymath}](/articles/aa/full_html/2009/42/aa12552-09/img14.png)
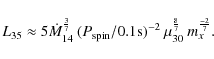
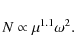
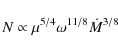
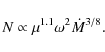
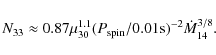
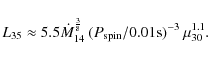
![\begin{displaymath}\dot{M}_{\rm tr}(\theta)=\dot{M_{0}}\frac{\gamma}{\gamma_{\rm...
...beta e\left(\frac{1-\cos\theta}
{1+e\cos\theta}\right)\right].
\end{displaymath}](/articles/aa/full_html/2009/42/aa12552-09/img34.png)
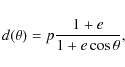
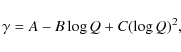
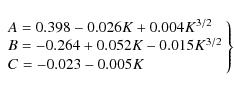
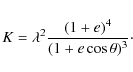
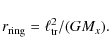
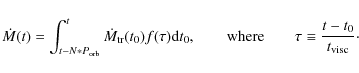
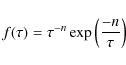
![$\displaystyle \left(\frac{\zeta}{2\pi\xi^2}\right)^{3/2}
\frac{2\pi e}{\left[\alpha (1-e^2)\right]^{1/2}}$](/articles/aa/full_html/2009/42/aa12552-09/img91.png)
![$\displaystyle \times\left[\left(\alpha-\frac{1}{1+e}\right)
\left(\frac{1}{1-e}-\alpha\right)\right]^{-1/2}$](/articles/aa/full_html/2009/42/aa12552-09/img92.png)
![$\displaystyle \times\exp\left[-\frac{1}{2\xi^2}\left(\zeta~\frac{2\alpha-1}
{\alpha}+1\right)\right]~I_{\rm o}(z).$](/articles/aa/full_html/2009/42/aa12552-09/img93.png)