Radiative rates and electron impact excitation rates for transitions in Cr VIII

K. M. Aggarwal; T. Kato; F. P. Keenan; I. Murakami

doi:10.1051/0004-6361/200912493

Home

All issues

Volume 506 / No 3 (November II 2009)

A&A, 506 3 (2009) 1501-1509

Full HTML

Free Access

Issue		A&A Volume 506, Number 3, November II 2009


Page(s)		1501 - 1509
Section		Atomic, molecular, and nuclear data
DOI		https://doi.org/10.1051/0004-6361/200912493
Published online		27 August 2009

A&A 506, 1501-1509 (2009)

Radiative rates and electron impact excitation rates for transitions in Cr VIII

K. M. Aggarwal¹ - T. Kato² - F. P. Keenan¹ - I. Murakami²

1 - Astrophysics Research Centre, School of Mathematics and Physics, Queen's University Belfast, Belfast BT7 1NN, Northern Ireland, UK
2 - National Institute for Fusion Science, Oroshi-cho, Toki, Gifu, 509-5292 Japan

Received 14 May 2009/ Accepted 24 August 2009

Abstract
Aims. In this paper we report on calculations of energy levels, radiative rates, oscillator strengths, line strengths, and effective collision strengths for transitions among the lowest 362 levels of the (1s²2s²2p⁶) 3s²3p⁵, 3s3p⁶, 3s²3p⁴3d, 3s3p⁵3d, 3s²3p³3d², 3s3p⁴3d², 3p⁶3d, and 3s²3p⁴4 $\ell$ configurations of Cr VIII.
Methods. The general-purpose relativistic atomic structure package ( GRASP) and flexible atomic code ( FAC) are adopted for the calculations.
Results. Radiative rates, oscillator strengths, and line strengths are reported for all electric dipole (E1), magnetic dipole (M1), electric quadrupole (E2), and magnetic quadrupole (M2) transitions among the 362 levels. Comparisons are made with earlier available results and the accuracy of the data is assessed. Additionally, lifetimes for all 362 levels are listed, although comparisons with other theoretical results are limited to only a few levels. Our energy levels are estimated to be accurate to better than 3% (within 0.4 Ryd), whereas results for other parameters are probably accurate to better than 20%. Finally, electron impact collision strengths and excitation rates are computed for all transitions over a wide energy (temperature) range. For these calculations, FAC is adopted and results in the form of effective collision strengths are reported over a wide temperature range of 10^5.0-10^6.6 K.

Key words: atomic data - atomic processes

1 Introduction

Iron group elements (Sc-Zn) are becoming increasingly important in the study of astrophysical plasmas, as many of their emission lines are frequently observed from different ionisation stages. These observations provide a wealth of data about the plasma characteristics, such as: temperature, density, and chemical composition. Additionally, iron group elements are often impurities in fusion reactors, and to estimate the power loss from the impurities, atomic data (namely energy levels, oscillator strengths or radiative decay rates, and excitation rates) are required for many ions. Since there is paucity of measured parameters, one must depend on theoretical results. Therefore, in the recent past we have reported atomic parameters for many ions of Fe (IX-XXVI; see Aggarwal et al. 2008a, and references therein) and Ni (XI-XIX; see Aggarwal & Keenan 2008, and references therein). In this paper we focus our attention on Cl-like Cr VIII.

Emission lines of Cr ions have been observed in astrophysical plasmas, as listed by Dere et al. (2001). Many emission lines of Cl-like Cr VIII have also been listed in the 100-430 ${\rm\AA}$ wavelength range in the Atomic Line List (v2.04) of Peter van Hoof at http://www.pa.uky.edu/ peter/atomic/, because these are useful in the generation of synthetic spectra. For an analysis of observations and/or estimating the power loss in fusion reactors, atomic data for energy levels, and radiative rates (A-values), and electron impact excitation rates are required. Since experimental data are not available, except for some energy levels, theoretical results are required.

Considering the importance of Cr VIII, a few calculations have been performed in the past, such as by Huang et al. (1983), Fawcett (1987), and more recently by Mohan et al. (2005) and Froese Fischer et al. (2006). Huang et al. adopted the relativistic Dirac-Fock computer code of Desclaux (1975) and calculated energies for the 31 levels of the 3s²3p⁵, 3s3p⁶, and 3s²3p⁴3d configurations. In their calculations they included configuration interaction (CI) with the additional 3s3p⁵3d, 3p⁵3d², 3s²3p³3d², 3p⁶3d, and 3s3p⁴3d² configurations. Additionally, they reported A-values for the electric dipole (E1) transitions from the levels of the (3s²3p⁵) ²P $^{\circ}_{3/2,1/2}$ ground configuration to higher excited levels, and for the magnetic dipole (M1) and electric quadrupole (E2) transitions between the two levels of the ground state. Similarly, Fawcett adopted the Hartree-Fock Relativistic (HFR) code of Cowan (1981), and reported energy levels among the same 31 levels, as considered by Huang et al. They included CI among the 3s²3p⁵, 3s3p⁶, 3s²3p⁴3d, 3s3p⁵3d, 3p⁶3d, 3s3p⁴3d², and 3s²3p⁴4s configurations, and reported A-values for E1 (and some E2, E3, M1, and M2) transitions from the levels of the (3s²3p⁵) ²P $^{\circ}_{3/2,1/2}$ ground configuration to higher excited levels. Froese Fischer et al. have adopted their Multi-Configuration Hartree-Fock (MCHF) method, and have reported energy levels of the 3s²3p⁵, 3s3p⁶, 3s²3p⁴3d, and 3s²3p⁴4s configurations, and A-values for most of the E1 transitions. Like other workers, they also included relativistic effects along with CI with many configurations up to n = 7 and $\ell$ = 4. However, their reported results are limited to only a few levels/transitions and hence are insufficient for the modelling of plasmas. Finally, Mohan et al. have performed a comparatively larger calculation, as they have also included levels of the 3p⁶3d, 3s²3p⁴4s, and 3s²3p⁴4d configurations, apart from the lowest 31 levels of the 3s²3p⁵, 3s3p⁶, and 3s²3p⁴3d configurations. Furthermore, they have included an extensive CI (see Table 3 of Mohan et al.) for the construction of wavefunctions apart from one-body relativistic operators in Breit-Pauli approximation. For the calculations, they adopted the CIV3 program of Hibbert (1975). However, as in earlier works, they too reported A-values for E1 transitions alone, whereas in plasma modelling A-values for all types of transitions, namely electric dipole (E1), electric quadrupole (E2), magnetic dipole (M1), and magnetic quadrupole (M2), are required as demonstrated by Del Zanna et al. (2004). Apart from this, Mohan et al. have not included the levels of the 3s²3p³3d², 3s3p⁴3d², and 3s3p⁵3d configurations, although these have been included in the generation of wavefunctions. The above listed three configurations give rise to 375 levels which closely interact and intermix with those of the 3s²3p⁵, 3s3p⁶, 3s²3p⁴3d, 3p⁶3d, 3s²3p⁴4s, and 3s²3p⁴4d configurations, included by Mohan et al. These missing levels from the calculations of Mohan et al. and other workers are required in the modelling of plasmas, as they affect the construction of the synthetic spectrum as well as the calculation of lifetimes. Therefore, the aim of the present paper is not only to improve upon the calculations of Mohan et al. but also to report a complete set of results, among the lowest 362 levels of Cr VIII, which can be confidently applied in plasma modelling.

For our calculations we have adopted the GRASP (General-purpose Relativistic Atomic Structure Package) code to generate the wavefunctions. This code was originally developed as GRASP0 by Grant et al. (1980) and has been updated by Dr. Norrington. It is a fully relativistic code, and is based on the jj coupling scheme. Further relativistic corrections arising from the Breit interaction and QED effects have also been included. Additionally, we have used the option of extended average level (EAL), in which a weighted (proportional to 2j+1) trace of the Hamiltonian matrix is minimized. This produces a compromise set of orbitals describing closely lying states with moderate accuracy, and generally yields results comparable to other options, such as average level (AL), as noted by Aggarwal et al. (2008b, 2010) for several ions of Kr and Xe. Furthermore, in order to assess the accuracy of our results we have performed parallel calculations using the Flexible Atomic Code ( FAC) of Gu (2003), which is available from the website http://kipac-tree.stanford.edu/fac. This is also a fully relativistic code which provides a variety of atomic parameters, and yields results comparable to GRASP, as already shown for three Mg-like ions by Aggarwal et al. (2007). Thus results from FAC will be helpful in assessing the accuracy of our energy levels and radiative rates.

In this paper we report our results for energy levels and radiative rates for E1, E2, M1, and M2 transitions among the lowest 362 levels of the (1s²2s²2p⁶) 3s²3p⁵, 3s3p⁶, 3s²3p⁴3d, 3s3p⁵3d, 3s²3p³3d², 3s3p⁴3d², 3p⁶3d, and 3s²3p⁴4 $\ell$ configurations of Cr VIII. We also report results of lifetimes for all levels. Comparisons are made with the earlier available theoretical results and the accuracy of the data is assessed. Finally, effective collision strengths are reported for all transitions over a wide temperature range of 10^5.0-10^6.6 K. For these calculations, we have adopted the FAC code, which is based on the well-known and widely-used distorted-wave (DW) method. As for other parameters, the calculations for collision strengths include relativistic effects, but the contribution of resonances has not been included in the determination of effective collision strengths.

2 Energy levels

Although Cr VIII is moderately heavy (Z = 24) and 7 times ionized, CI is still very important for an accurate determination of energy levels. For this reason all earlier workers have included CI with additional configurations, although their calculations have mostly been confined to the lowest 31 levels of the 3s²3p⁵, 3s3p⁶, and 3s²3p⁴3d configurations. After a few tests, with a number of n = 3-5 configurations, we too have arrived at the same conclusion that an elaborate CI needs to be included in order to achieve a better accuracy in the determination of energy levels. Therefore, we have included 36 configurations (namely 3s²3p⁵, 3s3p⁶, 3s²3p⁴3d, 3s3p⁵3d, 3s²3p³3d², 3s3p⁴3d², 3p⁶3d, 3s²3p²3d³, 3s3p³3d³, 3p⁵3d², 3s3p3d⁵, 3p²3d⁵, 3s²3d⁵, 3s3d⁶, 3p3d⁶, 3d⁷, 3s²3p3d⁴, 3s3p²3d⁴, 3s²3p⁴4 $\ell$ , 3s3p⁵4 $\ell$ , 3s²3p⁴5 $\ell$ , and 3s3p⁵5 $\ell$ ), which yield 4031 levels. However, we will focus our results on the lowest 362 levels. These levels include all 226 levels of the 3s²3p⁵, 3s3p⁶, 3s²3p⁴3d, 3s3p⁵3d, 3s²3p³3d², 3p⁶3d, 3s²3p⁴4s, and 3s²3p⁴4p configurations, but only some levels of the other configurations.

Table 1: Energy levels (in Ryd) of Cr VIII and their lifetimes (s). The complete table is available in electronic form at the CDS.

We list in Table 1 our calculated energies from GRASP (only limited levels are listed here but a complete table including all 362 levels is available electronically at the CDS), obtained with and without the inclusion of Breit and QED corrections. Also included in this table are the experimental energies compiled by NIST (http://physics.nist.gov/PhysRefData), and those obtained by Fawcett (1987) from the HFR code of Cowan (1981), Mohan et al. (2005) from the CIV3 program of Hibbert (1975), and Froese Fischer et al. (2006) who adopted their MCHF code. We note that neither the experimental nor the earlier theoretical energies are available for all the desired 362 levels of Cr VIII. The effect of the inclusion of Breit and QED corrections on the energy levels is limited to $\le$ 0.2%, except for the 3s²3p⁵ ²P $^{\circ}_{1/2 }$ level for which the energy has become lower by only 0.0025 Ryd, i.e. 3%. However, it has now become closer to the NIST energy. Among the lowest 31 levels for which a variety of calculations are available with which to compare, experimental values are limited to only seven levels, and our energies from GRASP are higher by up to 3% - see levels 27-31. It may be noted that our energies are particularly higher, by up to 0.4 Ryd, for the levels of the 3s²3p⁴4d configuration. Similarly, the CIV3 energies of Mohan et al. differ from the NIST compilation (and our calculations) by up to 3%, particularly for the 3s²3p⁵ ²P $^{\circ}_{1/2 }$ and 3s3p⁶ ²S_1/2 levels, in spite of the fact that they have also included a large CI apart from one-body relativistic operators. In addition, they have adjusted the diagonal elements of the Hamiltonian matrices in order to minimise the differences with the experimental energies. This exercise of adjusting the Hamiltonian is only useful if the experimental energies are available for a majority of levels, which is not the case for Cr VIII. Additionally, this exercise is not useful for adjusting the level orderings as discussed in detail by Aggarwal et al. (2007) for Mg-like ions. Finally, corrections to the energy levels alone are not sufficient to improve the accuracy of subsequent atomic parameters, i.e. the radiative rates, as discussed below in Sect. 3.

Table 2: Eigenvectors for some highly mixed levels of Cr VIII.

The energy levels of Froese Fischer et al. (2006) from the MCHF code are, in general, comparable in both magnitude (within 2%) and orderings with those of NIST and our calculations from GRASP. It may also be noted that like our calculations from GRASP, no adjustment of Hamiltonian matrices have been made by them. However, their energy for the 3s²3p⁵ ²P $^{\circ}_{1/2 }$ level is anomalous, as it is up to 11% lower than the experimental or other theoretical results, although the difference is only 0.01 Ryd. On the other hand, their calculated energies for the levels of the 3s²3p⁴4s configuration are probably the most accurate among those listed in Table 1. For the levels of this configuration, there is a possibility of interaction with 3p⁶4s, which we have not included in our calculations from GRASP. However, subsequent test calculations confirm that its inclusion makes no difference on the energies of the lowest 362 levels considered here. This is mainly because 3p⁶4s generates only one level, namely ⁴S_1/2 and its energy is $\sim$ 13 Ryd, i.e. well above those of the lowest 362 levels. Furthermore, our calculations from FAC, which are discussed below and include the 3p⁶4s configuration, do not show any appreciable difference for a majority of levels, including those of 3s²3p⁴4s.

The other theoretical results available in the literature for the lowest 31 levels of Cr VIII are from the calculations of Huang et al. (1983) and Fawcett (1987), who have adopted the multi-configuration Dirac-Fock (MCDF) and Hartree-Fock Relativistic (HFR) codes, respectively. Energy levels of Fawcett are comparable in both magnitude and orderings with those of NIST and our calculations, as may be noted from Table 1. In fact, their energies are almost identical with those of NIST, because they have also adjusted the ab initio Slater parameters with the Zeeman least-squares optimisation routines in order to minimise the discrepancies between the measured and computed energies. Finally, the energy levels of Huang et al. (not listed in Table 1) are not very accurate, because their energy for the 3s²3p⁵ ²P $^{\circ}_{1/2 }$ level is 6% lower than the experimental or other theoretical results. Additionally, their identification of the 3s²3p⁴(¹D)3d ²P $^{\circ}_{1/2,3/2}$ and 3s²3p⁴(³P)3d ²P $^{\circ}_{1/2,3/2}$ levels (i.e. 9/13 and 28/29) is in reverse order and hence agrees neither with the experiments nor other theories. This is mainly because they have included limited CI within the n = 3 configurations in the generation of wavefunctions, and have omitted the n = 4 configurations, as stated in Sect. 1.

Among the higher excited levels of the 3s²3p⁴4s and 3s²3p⁴4d configurations of Cr VIII, the CIV3 energies of Mohan et al. (2005) are closer to the NIST values, because they have adjusted their Hamiltonian as noted above. However, the differences with our calculations from GRASP are up to 2% ( $\le$ 0.15 Ryd) for some levels, such as 3p⁶3d ²D $^{\circ}_{3/2,5/2}$ (219 and 221). More importantly, their level orderings differ from our calculations in many instances, such as levels 275, 277, 295, 309, and 321. In the absence of experimental or other theoretical results, it is difficult to confirm the level orderings, particularly when some of the levels are highly mixed, such as 3s²3p³(²P)3d²(³P) ²S $^{\circ}_{1/2 }$ and 3s²3p³(²D)3d²(¹D) ²P $^{\circ}_{1/2 }$ (101 and 114), 3s²3p³(²P)3d²(¹D) ²D $^{\circ}_{5/2 }$ and 3s²3p³(²P)3d²(¹D) ²F $^{\circ}_{5/2 }$ (112 and 113), 3s²3p³(²D)3d²(³F) ⁴D $^{\circ}_{3/2 }$ and 3s²3p³(²P)3d²(³P) ⁴P $^{\circ}_{3/2 }$ (126 and 127), 3s²3p⁴(³P)4p ⁴P $^{\circ}_{1/2 }$ and 3s²3p³(²D)3d²(³P) ²P $^{\circ}_{1/2 }$ (165 and 170), and 3s²3p⁴(³P)4p ⁴D $^{\circ}_{5/2 }$ and 3s²3p³(²D)3d²(¹G) ²F $^{\circ}_{5/2 }$ (179 and 181) - see Table 2 for the mixing of eigenvectors for these levels. There are some more levels similar to those listed in Table 2 which are highly mixed and hence cannot be identified unambiguously. Among the lowest 31 levels, mixing is strong for two, namely 3s²3p⁴(³P)3d ⁴P_5/2 and 3s²3p⁴(¹D)3d ²D_5/2 (17 and 18). Therefore, in order to have confidence in our results, we have performed another calculation from the Flexible Atomic Code ( FAC) of Gu (2003), which we discuss below.

In our calculations from FAC we have included all possible combinations of the n = 3 configurations, in addition to 3s²3p⁴4 $\ell$ , 3s²3p⁴5 $\ell$ , 3s3p⁵4 $\ell$ , 3s3p⁵5 $\ell$ , 3p⁶4 $\ell$ , and 3p⁶5 $\ell$ . These configurations give rise to 4881 levels in total and hence the calculations are comparable with those from GRASP which included 4031 levels. The energy levels obtained from this calculation are also listed in Table 1. Differences between the two sets of calculations from GRASP and FAC are within 0.5% for a majority of levels, which is highly satisfactory. However, (particularly) for 10 levels (namely 219, 221, 234, 240, 296, 298, 326, 329, 334, and 362), the energies from FAC are lower by up to 1% (0.1 Ryd). This is mainly because it is not straightforward to compare the two independent sets of calculations due to mixing of some of the levels, as mentioned above. In general, there are no major differences between our calculations from GRASP and FAC, in both magnitude and ordering. Based on this and other comparisons, we may confidently state that the present calculations not only cover a larger range of levels but are probably the most accurate available to date. However, before concluding we discuss yet another calculation below.

Since CI is very important for the determination of the energy levels of Cr VIII, as already stated in Sect. 1, we have performed a calculation from FAC (FAC2), which includes a total of 16 102 levels. The 11 221 levels additional to the FAC1 calculations arise from the 3s²3p³4 $\ell^2$ , 3s²3p³5 $\ell^2$ , 3s²3p³4 $\ell$ 5 $\ell$ , 3p⁵4 $\ell^2$ , 3p⁵5 $\ell^2$ , and 3p⁵4 $\ell$ 5 $\ell$ configurations. However, all the lowest 362 levels under discussion from the FAC1 and FAC2 calculations agree within 0.6% and the orderings are also (nearly) the same. Therefore, the effect of additional CI on the energy levels of Cr VIII listed in Table 1 is negligible. To conclude, we may state with confidence that the energy levels listed in Table 1 from our calculations from both GRASP and FAC are accurate to better than $\sim$ 3%. Experimental energies are available for only a few levels for which differences with our calculations are up to 0.4 Ryd, particularly for the levels of the 3s²3p⁴4d configuration. Furthermore, the listed levels cover a wider range than available to date either experimentally or theoretically. However, we remind readers that the $\it LSJ$ designations listed in Table 1 have been chosen after a careful consideration, but the possibility of their redesignation cannot be ruled out in a few cases. This is because some of the levels are highly mixed, as noted above and demonstrated in Table 2.

Table 3: Radiative rates (A_ji in s^-1) and oscillator strengths (f_ij, dimensionless) for electric dipole (E1) transitions of Cr VIII with f $\ge$ 0.1. ( $a \pm b \equiv a \times 10^{{\pm }b}$ ). The complete table for transition wavelengths ( $\lambda _{ij}$ ), radiative rates, oscillator strengths, and line strengths (S) for all E1, and A_ji for E2, M1, and M2 transitions of Cr VIII is available in the electronic form at the CDS.

3 Radiative rates

The absorption oscillator strength (f_ij) and radiative rate A_ji (in s^-1) for a transition $i \to j$ are related by the following expression:

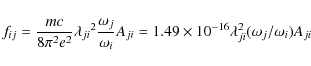
$\begin{displaymath}% f_{ij} = \frac{mc}{8{\pi}^2{e^2}}{\lambda_{ji}}^2 \frac{{\o... ...1.49 \times 10^{-16} \lambda^2_{ji} (\omega_j/\omega_i) A_{ji} \end{displaymath}$

(1)

where m and e are the electron mass and charge, respectively, c is the velocity of light, $\lambda_{ji}$ is the transition energy/wavelength in $\AA$ , and $\omega_i$ and $\omega_j$ are the statistical weights of the lower i and upper j levels, respectively. Similarly, the oscillator strength f_ij (dimensionless) and the line strength S (in atomic unit, 1 au = 6.460 $\times$ 10^-36 cm² esu²) are related by the following standard equations:

For the electric dipole (E1) transitions:

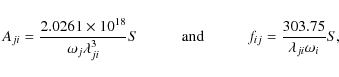
$\begin{displaymath}% A_{ji} = \frac{2.0261\times{10^{18}}}{{{\omega}_j}\lambda^3... ...ace*{1.0 cm} f_{ij} = \frac{303.75}{\lambda_{ji}\omega_i} S, \end{displaymath}$

(2)

for the magnetic dipole (M1) transitions:

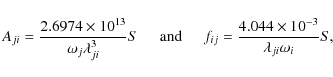
$\begin{displaymath}% A_{ji} = \frac{2.6974\times{10^{13}}}{{{\omega}_j}\lambda^3... ..._{ij} = \frac{4.044\times{10^{-3}}}{\lambda_{ji}\omega_i} S, ~ \end{displaymath}$

(3)

for the electric quadrupole (E2) transitions:

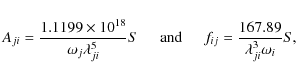
$\begin{displaymath}% A_{ji} = \frac{1.1199\times{10^{18}}}{{{\omega}_j}\lambda^5... ...ce*{0.5 cm} f_{ij} = \frac{167.89}{\lambda^3_{ji}\omega_i} S, \end{displaymath}$

(4)

and for the magnetic quadrupole (M2) transitions:

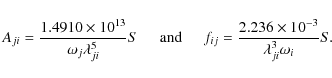
$\begin{displaymath}% A_{ji} = \frac{1.4910\times{10^{13}}}{{{\omega}_j}\lambda^5... ...} = \frac{2.236\times{10^{-3}}}{\lambda^3_{ji}\omega_i} S. ~~ \end{displaymath}$

(5)

In Table 3 we present transition energies ( $\Delta E_{ij}$ in $\AA$ ), radiative rates (A_ji in s^-1), oscillator strengths (f_ij, dimensionless), and line strengths (S in au), in length form only, for all 17 164 electric dipole (E1) transitions among the lowest 362 levels of Cr VIII. The indices used to represent the lower and upper levels of a transition have already been defined in Table 1. Also, in calculating the above parameters we have used the Breit and QED corrected theoretical energies/wavelengths as listed in Table 1. However, only A-values are included in Table 3 for the 9767 electric quadrupole (E2), 17 094 magnetic dipole (M1), and 24 182 magnetic quadrupole (M2) transitions. Corresponding results for f- or S-values can be easily obtained by using Eqs. (1)-(5). Furthermore, the complete table is available in the electronic form only at the CDS and here only the A- and f-values are listed for transitions with f $\ge$ 0.1.

In Table 4 we compare our f-values from both GRASP and FAC with the corresponding results of Huang et al. (1983), Fawcett (1987), Mohan et al. (2005), and Froese Fischer et al. (2006), among the lowest 31 levels of Cr VIII, common to all calculations. For all these (and many more) transitions there is a satisfactory agreement between our two sets of f-values from GRASP and FAC. The f-values of Fawcett are available for only a few transitions, and differ from other calculations by up to a factor of two for some of the transitions, such as 1-3, 2-3, and 2-28. Differences are even larger, by a factor of five, for the 2-25 transition, which is comparatively weaker (f $\sim$ 10^-3). This is in spite of the fact that the Fawcett energy levels agree closely with our calculations from GRASP and FAC as well as with the experimental compilations. The main reason for such large differences in the f-values is the inclusion of limited CI in their calculations, as stated in Sect. 1. For the same reason the f-values of Huang et al. also differ by up to a factor of six for some weak transitions, such as 1-5 (f $\sim$ 10^-5) and 1-12 (f $\sim$ 10^-6). It may also be noted that we have swapped the 9 and 13 levels of Huang et al. with 28 and 29 (see Sect. 2), in order to facilitate an easy comparison. However, there is comparatively a better agreement (within 50%) between our f-values and those of Froese Fischer et al. for most of the transitions, although the differences are larger for two weak transitions, namely 1-26 and 2-6. The other available calculations of Mohan et al. also differ with our as well as other calculations by up to an order of magnitude for many transitions, such as 1-6, 1-17, 1-26, 2-6, and 2-14. Although they have included extensive CI and one-body relativistic operators in their calculations from the CIV3 code, large differences between their f-values and all other calculations indicate an unreliability in their results. Finally, for the two most important transitions of Cr VIII, namely 1-3 and 2-3, two other sophisticated calculations by Biemont & Träbert (2000) and Berrington et al. (2001) are available for which there is no discrepancy with our results from GRASP and FAC, and those of Froese Fischer et al., but results from the MCDF, HFR, and CIV3 calculations differ by up to 50%.

One of the general criteria to assess the accuracy of radiative rates is to compare the length and velocity forms of the f- or A-values. However, such comparisons are only desirable, and are not a fully sufficient test to assess accuracy, as calculations based on different methods (or combinations of configurations) may give comparable f-values in the two forms, but entirely different results in magnitude. Generally, there is a good agreement between the length and velocity forms of the f-values for strong transitions (f $\ge$ 0.01), but differences between the two forms can sometimes be substantial even for some very strong transitions, as demonstrated through various examples by Aggarwal et al. (2007). Nevertheless, for almost all of the strong E1 transitions the two forms agree to within 20%, but differences for 196 ( $\sim$ 1%) of the transitions are higher by up to 50%, and for three transitions (49-198: f = 0.015, 90-316: f = 0.018, and 92-323: f = 0.015), the two forms differ by a factor of 5. Therefore, on the basis of these and earlier comparisons we may state that for a majority of the strong E1 transitions, our radiative rates are accurate to better than 20%. However, for the weaker transitions this assessment of accuracy does not apply, because weak transitions are very sensitive to mixing coefficients, and hence differing amount of CI (and methods) produce different f-values, as discussed in detail by Hibbert (2000). This is the main reason that the two forms of f-values for some weak transitions ( $\sim$ 3%) differ significantly (by over a factor of 1000), and examples include 1-256 (f = 1.1 $\times$ 10^-9), 13-196 (f = 2.1 $\times$ 10^-9), and 44-327 (f = 3.3 $\times$ 10^-11). The f-values for weak transitions are required in plasma modelling for completeness, but their contributions are less important in comparison to stronger transitions with f $\ge$ 0.01. For this reason many authors (and some codes) do not normally report the A-values for very weak transitions.

Table 4: Comparison of oscillator strengths (f-values) for transitions among the lowest 31 levels of Cr VIII. $a \pm b \equiv a \times 10^{{\pm }b}$ .

Finally, we compare the f-values for E1 transitions obtained from our GRASP and FAC calculations. In general, both sets of f-values from GRASP and FAC agree well (within $\sim$ 20%) for a majority of strong transitions. However, for some transitions the differences between the two calculations are higher, particularly for three, namely 37-359 (f = 0.195), 186-287 (f = 0.369), and 205-320 (f = 0.438), for which the discrepancy is up to an order of magnitude. Considering the large number of transitions being compared, such a good agreement between the two independent calculations is satisfactory and supports the accuracy of the listed results.

Table 5: Comparison of lifetimes ( $\tau$ in s) for levels of Cr VIII. $a \pm b \equiv a \times 10^{{\pm }b}$ .

4 Lifetimes

The lifetime $\tau$ of a level j is defined as follows:

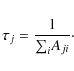
$\begin{displaymath}% {\tau}_j = \frac{1}{{\sum_{i}^{}} A_{ji}}\cdot \end{displaymath}$

(6)

In Table 1 we include lifetimes for all levels from our calculations from the GRASP code. These results include A-values from all types of transitions, i.e. E1, E2, M1, and M2. Unfortunately no experimental results for lifetimes are available with which to compare. However, theoretical results are available for some levels from the calculations of Mohan et al. (2005) and Froese Fischer et al. (2006). Therefore, in Table 5 we compare our values of $\tau$ from both the GRASP and FAC calculations with the corresponding available results for the lowest 31 levels of Cr VIII. It may be noted that for these levels, values of $\tau$ in our calculations from FAC and of Mohan et al. from CIV3 are based on the A-values from the E1 transitions alone. However, for these 31 levels the effect of E2, M1, and M2 transitions is negligible. Our values of $\tau$ from the GRASP and FAC codes compare well for (almost) all levels, because comparable CI has been included in both calculations. However, differences for some levels, such as 12 and 26, are up to 25%. This is because of the corresponding differences in A-values for some of the transitions as shown in Table 4. For a majority of the levels the $\tau$ values of Froese Fischer et al. differ from our calculations by up to two orders of magnitude, and examples include the levels 20, 21, 24, and 26. These differences are again a direct consequence of the corresponding differences in the A-values. Similarly, the $\tau$ values of Mohan et al. differ by up to an order of magnitude for many levels, such as 5, 12, 16, 18, and 26, and the differences are not only with our calculations but also with those of Froese Fischer et al. Clearly, the $\tau$ values of Mohan et al. are anomalous for many levels and are not assessed to be reliable as discussed earlier in Sect. 3. Since we have included a large CI apart from relativistic effects in the calculations of A- and subsequently the $\tau$ values, our results are expected to be more reliable, although their accuracy can only be fully assessed through the availability of measurements and/or equally large similar calculations.

5 Effective collision strengths

Using FAC we have performed calculations for collision strengths ( $\Omega$ ). However, for these calculations only 495 levels belonging to the 3s²3p⁵, 3s3p⁶, 3s²3p⁴3d, 3s3p⁵3d, 3s²3p³3d², 3p⁶3d, 3s3p⁴3d², and 3s²3p⁴4 $\ell$ configurations are considered. Furthermore, assuming a Maxwellian distribution of electron velocities, effective collision strengths ( $\Upsilon$ ) have also been calculated over a wide temperature range of 10^5.0-10^6.6 K. These results are listed in Table 6 for all transitions among the lowest 362 levels of Table 1. The indices adopted for defining the lower and upper levels of a transition are defined in Table 1. We would like to clarify here that the level orderings followed in Table 6 are corresponding to the orderings from the GRASP code, as listed in Table 1, although the (effective) collision strengths are from the FAC code. This is in order to facilitate a compatibility among orderings of different tables. However, we would like to emphasize here that resonances have not been included in these calculations. Generally, the contribution of resonances in the determination of effective collision strengths and subsequently the excitation rates is significant, especially for the forbidden transitions, even at temperatures as high as 10^6.6 K, as demonstrated in several of our earlier papers, such as by Aggarwal et al. (2009) for transitions in Kr XXXII. In order to account for the resonances, calculations based on the Dirac atomic R-matrix code ( DARC) need to be performed. Such calculations, although very useful, will be computationally expensive and time consuming, but should be considered in future. Therefore, our results for $\Upsilon$ have scope for improvement, both in the construction of the wavefunctions as well as in the accounting of resonances. Till such calculations become possible, we hope the presently listed data for $\Upsilon$ over a wide temperature range, along with the radiative rates, will be useful for the modelling of a variety of plasmas.

6 Conclusions

In this work, energy levels, radiative rates, oscillator strengths, and line strengths for transitions among 362 fine-structure levels of Cr VIII are computed using the fully relativistic GRASP code, and results are reported for electric and magnetic dipole and quadrupole transitions. For calculating these parameters an extensive CI has been included, apart from the relativistic effects, which has been observed to be significant, particularly for the accurate determination of energy levels. There is a paucity of measured energies for a majority of levels, but theoretical results are available, particularly for the lowest 31 levels. Based on a variety of comparisons among different calculations, the reported energy levels are assessed to be accurate to better than 3%. However, the accuracy of other parameters (A, f, and S) for a majority of strong transitions is $\sim$ 20%.

Lifetimes are also reported for all levels but no measurements are available with which to compare, and the limited calculations available earlier differ significantly for some levels.Further large calculations and particularly measurements for some of the levels will be highly useful for assessing the accuracy of our reported lifetimes.

Calculations for collision strengths and effective collision strengths have also been performed, but only among the 495 levels of Cr VIII. Since no other similar calculations are available in the literature for these parameters, the listed values of $\Upsilon$ over a wide temperature range should be highly useful for the modelling of a variety of plasmas. However, scope remains for improvement over the present results, mainly because the contribution of resonances in the thresholds region has not been accounted for. Their contribution generally enhances the values of $\Upsilon$ , for a majority of transitions and almost over the entire temperature range of consideration.

Finally, calculations for energy levels and radiative rates have been performed for 4031 levels of Cr VIII, but for brevity results have been reported for only the lowest 362 levels. However, a complete set of results for all calculated parameters can be obtained on request from KMA ( K.Aggarwal@qub.ac.uk) or IM ( murakami.izumi@nifs.ac.jp). Similarly, results for collision strengths and effective collision strengths for all transitions among the calculated 495 levels of Cr VIII can be obtained electronically on request from the authors.

Acknowledgements

This work has been jointly financed by the Engineering and Physical Sciences and Science and Technology Facilities Councils of the United Kingdom and the NIFS/NINS project of Formation of International Network for Scientific Collaborations. F.P.K. is grateful to A.W.E. Aldermaston for the award of a William Penney Fellowship, and KMA will like to acknowledge the hospitality of NIFS enjoyed during the visits in November 2007 and October 2008 when part of this work was performed. We thank the two Referees for the critical reading of the earlier version of the paper and for making useful suggestions for the overall improvement.

References

Aggarwal, K. M., & Keenan, F. P. 2008, A&A, 488, 365 [NASA ADS] [CrossRef] [EDP Sciences]
Aggarwal, K. M., Tayal, V., Gupta, G. P., & Keenan, F. P. 2007, At. Data Nucl. Data Tables, 93, 615 [NASA ADS] [CrossRef]
Aggarwal, K. M., Hamada, K., Igarashi, A., et al. 2008a, A&A, 484, 879 [NASA ADS] [CrossRef] [EDP Sciences]
Aggarwal, K. M., Keenan, F. P., & Lawson, K. D. 2008b, At. Data Nucl. Data Tables, 94, 323 [NASA ADS] [CrossRef]
Aggarwal, K. M., Keenan, F. P., & Lawson, K. D. 2009, At. Data Nucl. Data Tables, 95, 607 [NASA ADS] [CrossRef]
Aggarwal, K. M., Keenan, F. P., & Lawson, K. D. 2010, At. Data Nucl. Data Tables, in press
Berrington, K. A., Pelan, J. C., & Waldock, J. A. 2001, J. Phys. B, 34, L419 [NASA ADS] [CrossRef]
Biemont, E., & Träbert, E. 2000, J. Phys. B, 33, 2939 [NASA ADS] [CrossRef]
Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra, Univ. of California Press, Los Angeles
Del Zanna, G., Berrington, K. A., & Mason, H. E. 2004, A&A, 422, 731 [NASA ADS] [CrossRef] [EDP Sciences]
Dere, K. P., Landi, E., Young, P. R., & Del Zanna, G. 2001, ApJS, 134, 331 [NASA ADS] [CrossRef]
Desclaux, J. P. 1975, Comput. Phys. Commun., 9, 31 [NASA ADS] [CrossRef]
Fawcett, B. C. 1987, At. Data Nucl. Data Tables, 36, 151 [NASA ADS] [CrossRef]
Froese Fischer, C., Tachiev, G., & Irimia, A. 2006, At. Data Nucl. Data Tables, 92, 607 [NASA ADS] [CrossRef]
Grant, I. P., McKenzie, B. J., Norrington, P. H., Mayers, D. F., & Pyper, N. C. 1980, Comput. Phys. Commun., 21, 207 [NASA ADS] [CrossRef]
Gu, M. F. 2003, ApJ, 582, 1241 [NASA ADS] [CrossRef]
Hibbert, A. 1975a, Comput. Phys. Commun., 9, 141 [NASA ADS] [CrossRef]
Hibbert, A. 2000, AIP Conf. Proc., 543, 242 [NASA ADS]
Huang, K. N., Kim, Y. K., Cheng, K. T., & Desclaux, J. P. 1983, At. Data Nucl. Data Tables, 28, 355 [NASA ADS] [CrossRef]
Mohan, M., Singh, A. K., Jha, A. K. S., & Singh, N. 2005, Pramana J. Phys., 65, 75 [NASA ADS] [CrossRef]

Footnotes

... VIII: Full Tables 1, 3, and Table 6 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/506/1501

All Tables

Table 1: Energy levels (in Ryd) of Cr VIII and their lifetimes (s). The complete table is available in electronic form at the CDS.

Table 2: Eigenvectors for some highly mixed levels of Cr VIII.

Table 3: Radiative rates (A_ji in s^-1) and oscillator strengths (f_ij, dimensionless) for electric dipole (E1) transitions of Cr VIII with f $\ge$ 0.1. ( $a \pm b \equiv a \times 10^{{\pm }b}$ ). The complete table for transition wavelengths ( $\lambda _{ij}$ ), radiative rates, oscillator strengths, and line strengths (S) for all E1, and A_ji for E2, M1, and M2 transitions of Cr VIII is available in the electronic form at the CDS.

Table 4: Comparison of oscillator strengths (f-values) for transitions among the lowest 31 levels of Cr VIII. $a \pm b \equiv a \times 10^{{\pm }b}$ .

Table 5: Comparison of lifetimes ( $\tau$ in s) for levels of Cr VIII. $a \pm b \equiv a \times 10^{{\pm }b}$ .

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.