| Issue |
A&A
Volume 506, Number 3, November II 2009
|
|
|---|---|---|
| Page(s) | 1511 - 1539 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200912361 | |
| Published online | 27 August 2009 | |
A&A 506, 1511-1539 (2009)
Destriping CMB temperature and polarization maps
H. Kurki-Suonio1,2 - E. Keihänen1 - R. Keskitalo1,2 - T. Poutanen2,1,3 - A.-S. Sirviö1 - D. Maino4 - C. Burigana5,6
1 - University of Helsinki, Department of Physics, PO Box 64, 00014
Helsinki, Finland
2 - Helsinki Institute of Physics, PO Box 64, 00014 Helsinki, Finland
3 - Metsähovi Radio Observatory, Helsinki University of Technology,
Metsähovintie 114, 02540 Kylmälä, Finland
4 - Dipartimento di Fisica, Universitá di Milano, via Celoria 16,
20131, Milano, Italy
5 - INAF/IASF-BO, Istituto di Astrofisica Spaziale e Fisica Cosmica di
Bologna, via Gobetti 101, 40129, Bologna, Italy
6 - Dipartimento di Fisica, Università degli Studi di Ferrara, via
Saragat 1, 44100 Ferrara, Italy
Received 21 April 2009 / Accepted 14 August 2009
Abstract
We study destriping as a map-making method for
temperature-and-polarization data for cosmic microwave background
observations. We present a particular implementation of destriping
and study the residual error in output maps, using simulated data
corresponding to the 70 GHz channel of the P LANCK
satellite, but assuming idealized detector and beam properties. The
relevant residual map is the difference between the output map and a
binned map obtained from the signal + white noise part of the
data stream. For destriping it can be divided into six components:
unmodeled correlated noise, white noise reference baselines, reference
baselines of the pixelization noise from the signal, and baseline
errors from correlated noise, white noise, and signal. These six
components contribute differently to the different angular scales in
the maps. We derive analytical results for the first three components.
This study is related to P LANCK LFI
activities.
Key words: methods: data analysis - cosmology: cosmic microwave background
1 Introduction
Construction of sky maps from the time-ordered data (TOD) is an
important part of the data analysis of cosmic microwave background
(CMB) surveys. For large surveys like P LANCK![]() (Planck Collaboration 2005), this is a
computationally demanding task. Methods which aim at finding the
optimal minimum-variance map (Wright 1996;
Borrill 1999;
Doré et al. 2001;
Natoli et al. 2001;
Yvon & Mayet 2005;
de Gasperis et al. 2005)
are computationally heavy and require large computers. Also, a faster
method is needed for Monte Carlo studies to assess systematic
effects, noise biases, and error estimates.
(Planck Collaboration 2005), this is a
computationally demanding task. Methods which aim at finding the
optimal minimum-variance map (Wright 1996;
Borrill 1999;
Doré et al. 2001;
Natoli et al. 2001;
Yvon & Mayet 2005;
de Gasperis et al. 2005)
are computationally heavy and require large computers. Also, a faster
method is needed for Monte Carlo studies to assess systematic
effects, noise biases, and error estimates.
Destriping (Burigana et al. 1997b; Delabrouille 1998; Maino et al. 1999,2002; Revenu et al. 2000; Sbarra et al. 2003; Poutanen et al. 2004; Keihänen et al. 2004; Sutton et al. 2009) is a fast map-making method that removes correlated low-frequency noise from the TOD utilizing crossing points, i.e., the same locations on the sky observed at different times. Correlated noise is modeled as a sequence of (``uniform'') baselines, i.e., constant offsets in the TOD. High-frequency noise (frequency of the same order or higher than the inverse of the baseline length) cannot be modeled this way. Thus the method assumes that the high-frequency part of the noise is uncorrelated (white noise).
In some implementations, a set of base functions (e.g. low order Legendre polynomials) is used instead of just the uniform baseline (Delabrouille 1998; Maino et al. 2002; Keihänen et al. 2004,2005), or a spline is fitted to the TOD (Ganga 1994).
In this paper we describe one destriping implementation for making temperature and polarization maps of the sky and study the residual errors in the maps. This implementation was originally known as the ``Polar'' code, and used in the map-making comparison studies of the P LANCK CTP Working Group (Poutanen et al. 2006; Ashdown et al. 2007a,2007b,2009). Polar has now been merged into the ``Madam'' destriping code. The novel feature in Madam was the introduction of an optional noise prior (noise filter) that utilizes prior information on the noise power spectrum (Keihänen et al. 2005). Polar corresponds to Madam with the noise prior turned off. The results presented in this paper were obtained with the Madam code, with the noise prior turned off. We briefly comment on the effect of the noise prior in Sect. 8. The use and effect of the noise prior will be described in detail in Keihänen et al. (2009).
Destriping errors have been previously analyzed by Stompor & White (2004) and Efstathiou (2005,2007).
The TOD can be considered as a sum of signal + white noise + correlated (``1/f'') noise. If there were no correlated noise, the optimal way to produce a map would be a simple binning of the TOD samples onto map pixels. (We do not address here the question of correcting for the effect of the instrument beam. ``Deconvolution'' map-making methods that correct for the effect of the beam shape have been developed, Burigana & Saéz 2003; Armitage & Wandelt 2004; Harrison et al. 2008, but tend to be computationally very resource intensive. They also alter the noise properties of the maps in a way that is difficult to follow in CMB angular power spectrum estimation.) Thus the task of a map-making method is to remove the correlated noise as well as possible, with as little effect on the signal and white noise as possible. The difference of the output map from the binned signal + white noise map is thus the residual map to consider to judge the quality of the output map. We divide this residual into six components: unmodeled 1/f noise, 1/f baseline error, white noise reference baselines, white noise baseline error, pixelization noise reference baselines, and pixelization noise baseline error. We study the nature of each component, and its dependence on the baseline length.
We have used simulated data corresponding to 1 year of observations with 4 P LANCK LFI 70 GHz detectors (two horns, each with two orthogonally polarized detectors).
For simplicity, we did not include foregrounds in the signal (see Ashdown et al. 2007b,2009, for effect of foreground signal) or such systematic effects as beam asymmetries, sample integration, cooler noise, or pointing errors (see Ashdown et al. 2009). Even in Ashdown et al. (2009) the simulated data used was still fairly idealized. We are currently working on more realistic simulations.
In Sect. 2 we discuss some early-stage design choices made in the development of our map-making method. Section 3 contains the derivation and description of the method. Section 4 describes the simulated data used to test the method. In Sect. 5 we analyze residual errors in the time domain, and in Sect. 6 in the map domain. In Sect. 7 we discuss the effect of the noise knee frequency, and in Sect. 8 we give a preview of results obtained when a noise prior is added to the method. We mainly consider maps made from a full year of data, but in Sect. 9 we discuss maps made from shorter time segments. In Sect. 10 we summarize our conclusions.
2 Design choices
2.1 Ring set or not
For a P LANCK-like scanning strategy, where the detectors scan the same circle on the sky many times before the spin axis of the satellite is repointed, an intermediate data structure can be introduced between the TOD and the frequency map. The circles from one repointing period can be coadded to a ring, i.e., averaged to appear just as a single sweep of the circle. In this context it is natural to choose one baseline per ring. Destriping is then performed on this ring set, instead of the original uncoadded TOD. This reduces the memory and computing time requirements by a large factor.
If the scanning is ideal, i.e., the observations (samples) from the different circles of the same ring fall on exactly the same locations on the sky, destriping coadded rings is equivalent to destriping the uncoadded TOD with baseline length equal to the repointing period (i.e., one baseline per ring). In this case it is also almost equal (for map-making purposes) to destriping the uncoadded TOD with baseline length equal to the spin period (i.e. one baseline per circle), see Sect. 6.3.2.
In reality, the spin axis will nutate with some small amplitude, so that the different circles will not scan exactly the same path on the sky. The spin rate is also not exactly constant, and the detector sampling frequency is not synchronized with the spin. Binning the samples first into a ring (``phase binning'') (van Leeuwen et al. 2002) and then repixelizing the ring pixels into map pixels after destriping may then introduce some extra smoothing of the data.
We have chosen to sidestep this intermediate structure and to assign the samples directly to map pixels. The baseline length is then not necessarily tied to scan circles and rings, and also data taken during the repointing maneuvers can be used. For short baselines no data compression is possible and map-making is done from the full TOD, requiring large computer memory. For long baselines (many scan circles) the data can be compressed by binning observations directly to map pixels. For baselines one repointing period (one ring) long a similar data compression is achieved as by using the intermediate ring set structure. Whereas the phase-binned ring set is still closely connected to the time domain, our ``pixel binning'' destroys the time-ordered structure of the ring, and therefore works only with uniform baselines.
This way we have achieved a versatile destriping method, where the baseline length is an adjustable parameter. Shorter baselines can be used in large computers for higher accuracy, whereas longer baselines require less memory and computing time and can be used in medium-sized computers and for Monte Carlo studies. The baseline length is not tied to the scanning strategy, and our destriping method can be applied to any scanning strategy that has crossing points, not just to a P LANCK-like scanning strategy.
However, for a P LANCK-like scanning strategy there is a certain advantage in choosing the baseline length so that an integer number of baselines fits to one repointing period. Baseline segments that extend to two different repointing periods are avoided this way. This is mainly an issue for long baselines (not very much shorter than the repointing period). For baselines shorter than the spin period there seems to be some advantage in choosing the baseline length so that an integer number of baselines fits to one spin period. See Keihänen et al. (2009). In this paper we only consider such choices for baseline length.
2.2 Crossing points and signal error
The baselines are estimated from crossing points, i.e., observations falling on the same map pixels at different times. Samples are assigned to pixels based on the pointing of the detector beam center. The beam center may still point at a different location within the same map pixel for different samples. We do not attempt to correct for this effect and this results in a ``signal error'' in our output maps. The signal error due to in-pixel differences in beam pointing could be largely eliminated in another kind of destriping implementation, where the scanning circles are treated as exact geometrical curves (instead of just a sequence of map pixels), and the observations are interpolated to the exact crossing points of these lines (Revenu et al. 2000). In this case only actual crossings of the scan circles contribute to baseline determination, whereas in our implementation it is enough that two paths pass through the same pixel without actually crossing there. The latter situation is very common, since successive circles are almost parallel.
However, in a realistic situation there are other contributions to signal error that could not be eliminated this way. One such contribution is the different beam orientations of the different observations of the crossing point, as real beams are not circularly symmetric. In Ashdown et al. (2009) elliptic beams were considered for the P LANCK 30 GHz channel and it was found that this had a contribution to the signal error, which was of comparable size or larger.
3 Destriping technique
3.1 Derivation
The destriping method can be derived from a maximum-likelihood analysis
of an idealized model of observations. The signal observed by a
detector sensitive to one linear polarization direction is
proportional to
where
where
Since we are dealing with polarization data, the map ![]() is an object with 3np elements;
for each sky pixel the elements are the I, Q,
and U Stokes parameters. The pointing
matrix
P is of
size
(nt,3np).
Each row has 3 nonvanishing elements
is an object with 3np elements;
for each sky pixel the elements are the I, Q,
and U Stokes parameters. The pointing
matrix
P is of
size
(nt,3np).
Each row has 3 nonvanishing elements
![]() at the location corresponding to the sky pixel in which the detector
beam center falls for the sample in question (the sample ``hits'' the
pixel). We do not make any attempt at deconvolving the detector beam.
Thus the map
at the location corresponding to the sky pixel in which the detector
beam center falls for the sample in question (the sample ``hits'' the
pixel). We do not make any attempt at deconvolving the detector beam.
Thus the map ![]() represents the sky smoothed with the detector beam and the pixel window
function. The pointing matrix spreads the map into a signal
TOD
represents the sky smoothed with the detector beam and the pixel window
function. The pointing matrix spreads the map into a signal
TOD
![]() .
.
We divide the TOD into nb
segments of equal length ![]() ;
;
![]() .
For each segment we define an offset, called baseline.
The baselines model the low-frequency correlated noise component, ``1/f noise'',
which we want to remove from the data, and we approximate the rest of
the noise as white. Thus our idealized noise model is
.
For each segment we define an offset, called baseline.
The baselines model the low-frequency correlated noise component, ``1/f noise'',
which we want to remove from the data, and we approximate the rest of
the noise as white. Thus our idealized noise model is
where the vector
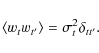
|
(4) |
Here
is thus diagonal (with elements
Given the TOD ![]() ,
and assuming we know the white noise variance
Cw,
we want to find the maximum likelihood map
,
and assuming we know the white noise variance
Cw,
we want to find the maximum likelihood map
![]() .
We assume no prior knowledge of the baseline amplitudes
.
We assume no prior knowledge of the baseline amplitudes ![]() ,
i.e., they are assigned uniform prior probability. (The variant of the
method, where such prior knowledge is used, is described in Keihänen
et al. 2009.)
,
i.e., they are assigned uniform prior probability. (The variant of the
method, where such prior knowledge is used, is described in Keihänen
et al. 2009.)
Given the input map ![]() and the baseline amplitudes
and the baseline amplitudes ![]() ,
the probability of the data
,
the probability of the data ![]() is
is
where
to be minimized. (We dropped the constant prefactor of Eq. (6).) We want to minimize this with respect to both
Minimization of Eq. (7)
with respect to ![]() gives the maximum-likelihood map
gives the maximum-likelihood map
for a given set of baseline amplitudes
The symmetric non-negative definite matrix
which operates in the map space, is 3
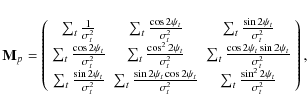
|
(10) |
where the sums run over all samples t that hit pixel p. Mp-1 is the white noise covariance matrix for the three Stokes parameters I, Q, U in pixel p. Mp can only be inverted if the pixel p is sampled with at least 3 sufficiently different polarization directions
If all ![]() are equal,
are equal, ![]() ,
gives the number of hits (observations) in pixel p.
Thus
M is
sometimes called the
,
gives the number of hits (observations) in pixel p.
Thus
M is
sometimes called the ![]() matrix.
The optimal distribution of
polarization directions
matrix.
The optimal distribution of
polarization directions ![]() measured from a pixel is one where they are uniformly distributed
over
measured from a pixel is one where they are uniformly distributed
over ![]() (Couchot et al. 1999).
In this case
(Couchot et al. 1999).
In this case
![]() and
and
![]() giving the maximum possible value rcond = 0.5.
giving the maximum possible value rcond = 0.5.
Substituting Eq. (8)
back into Eq. (7)
we get this into the form
where we have defined
Here I is the unit matrix. The matrix Z operates in TOD space and is a projection matrix, Z2 = Z. If all
We minimize Eq. (11) with respect to
where we have used Eq. (13).
The matrix
on the left-hand side of Eq. (14) operates in the baseline space. It is symmetric but singular. Equation (14) has a solution only if its right-hand side is orthogonal to the null space of D. The solution becomes unique when we require it to be orthogonal to the null space too.
The null space of D
contains the vector that gives all baselines the same amplitude. This
represents the inability to detect a constant offset of the entire
noise stream ![]() ,
because it has the same effect on
,
because it has the same effect on ![]() as a constant shift in the I of the
entire
as a constant shift in the I of the
entire
![]() (the monopole). This is of no
concern (but should be kept in mind)
since the goal is to measure the CMB anisotropy
and polarization, not its mean temperature. If the baselines are
sufficiently connected by crossing points (two different baseline
segments of the TOD hitting the same pixel), there are no other kind of
vectors in the null space, so that the dimension of the null space is
one. The right-hand side of Eq. (14) is
orthogonal to this one-dimensional null space, and thus
Eq. (14)
can now be solved. In practice it is solved by the conjugate gradient
method. If the initial guess is orthogonal to the null space, the
method converges to a solution that is also orthogonal to the null
space. Normally we start with the zero vector as the initial guess to
guarantee this. This means that the average of the solved baseline
amplitudes is zero. Strictly speaking this holds exactly only when no
pixels are excluded from the baseline determination due to their
poor rcond.
(the monopole). This is of no
concern (but should be kept in mind)
since the goal is to measure the CMB anisotropy
and polarization, not its mean temperature. If the baselines are
sufficiently connected by crossing points (two different baseline
segments of the TOD hitting the same pixel), there are no other kind of
vectors in the null space, so that the dimension of the null space is
one. The right-hand side of Eq. (14) is
orthogonal to this one-dimensional null space, and thus
Eq. (14)
can now be solved. In practice it is solved by the conjugate gradient
method. If the initial guess is orthogonal to the null space, the
method converges to a solution that is also orthogonal to the null
space. Normally we start with the zero vector as the initial guess to
guarantee this. This means that the average of the solved baseline
amplitudes is zero. Strictly speaking this holds exactly only when no
pixels are excluded from the baseline determination due to their
poor rcond.
We write the solution of Eq. (14) as
D-1 is interpreted as the inverse in this orthogonal subspace. D and D-1 will act in this subspace only.
Using the maximum likelihood baselines from Eqs. (16) in (8) we get the
output map of the destriping method:
Equations (16) and (17) summarize the destriping method.
Implementation details are discussed in Keihänen et al. (2009).
3.2 Description
Let us review the different operations involved:
![]() acts on a
TOD
acts on a
TOD ![]() to produce from it a sum map
to produce from it a sum map
![]() where each pixel has Stokes parameters representing a sum over
observations that hit the pixel,
where each pixel has Stokes parameters representing a sum over
observations that hit the pixel,
| (18) | |
| (19) | |
| (20) |
Instead of a sum, we should take the average of observations. This is accomplished by
B acts on a TOD to produce from it a binned map. Note that BP= I.
(It may be better to use the same
![]() for the two polarization directions of the same horn, to avoid
polarization artifacts from systematic effects (Leahy et al. 2009). In
case their true noise levels are different, destriping allows also the
option of using equal
for the two polarization directions of the same horn, to avoid
polarization artifacts from systematic effects (Leahy et al. 2009). In
case their true noise levels are different, destriping allows also the
option of using equal
![]() in solving baselines,
Eq. (16),
but the actual
in solving baselines,
Eq. (16),
but the actual
![]() in the final binning to the
map, Eq. (17).
We do not
study this issue in this paper, as we used simulated data with a
constant
in the final binning to the
map, Eq. (17).
We do not
study this issue in this paper, as we used simulated data with a
constant
![]() .)
.)
We can now see that the effect of
on a TOD is to bin it to a map, read a TOD out of this map, and subtract it from the original TOD. Thus
Likewise,
![]() acts on a TOD to sum up the samples of each baseline segment, weighting
each sample by
acts on a TOD to sum up the samples of each baseline segment, weighting
each sample by
![]() .
.
The effect of the matrix
on a baseline amplitude vector
These baselines are then subtracted from the TOD to produce
the cleaned TOD
![]() ,
which is then binned to produce the output map
,
which is then binned to produce the output map
| (24) |
in Eq. (17).
In a good scanning of the sky the number of hits in each pixel is large. From Eq. (22) we see that Z contains two parts. The first part I gives each row t a large diagonal element 1 corresponding to the TOD sample this row is acting on. The second part gives this row a large number of small nonzero elements corresponding to all samples t' that hit this same pixel. The sum of these elements is -1 so that the row sum is zero. Thus the first and second parts make an equally large contribution, but the second part comes in many small pieces.
The matrix D
has a similar structure. The first part (see Eq. (23)) is diagonal
containing the sum
![]() over
all samples in the baseline segment b.
The second part gives to each row b a
nonzero element for each baseline b' that
has a crossing point with b. For a good
scanning each baseline has a large number of crossing points, so
that this second part contributes a large number of small elements to
each row.
over
all samples in the baseline segment b.
The second part gives to each row b a
nonzero element for each baseline b' that
has a crossing point with b. For a good
scanning each baseline has a large number of crossing points, so
that this second part contributes a large number of small elements to
each row.
We define a shorthand notation for the matrix
which appears in Eq. (16) as
For easy reference, all the matrices introduced are collected
in Table 1.
The square matrices Cw,
M,
D,
and Cw-1Z
are symmetric, Cw
is diagonal, and M3 ![]() 3 block diagonal. Z is
a projection matrix. D is
singular, and D-1
is its inverse in the subspace orthogonal to its null space. The third
column in the table refers to the equation in which the matrix was
introduced. Note that all the matrices are constructed from
I,
P,
Cw,
and F. The
adjustable parameter in the destriping method is the baseline
length
3 block diagonal. Z is
a projection matrix. D is
singular, and D-1
is its inverse in the subspace orthogonal to its null space. The third
column in the table refers to the equation in which the matrix was
introduced. Note that all the matrices are constructed from
I,
P,
Cw,
and F. The
adjustable parameter in the destriping method is the baseline
length
![]() ,
which affects the matrix
F.
P is
determined by the scanning strategy and map pixelization, and
Cw
by detector noise properties.
,
which affects the matrix
F.
P is
determined by the scanning strategy and map pixelization, and
Cw
by detector noise properties.
Table 1: Table of matrices.
3.3 Destriping error
One can easily show that
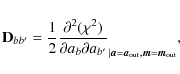
|
(26) |
i.e, the matrix D of Eq. (15) is the Fisher matrix of the baselines. Its inverse gives the covariance of the baseline error
Ignoring the nondiagonal terms we get an approximation
Assuming the white noise variance stays constant,
We can understand the approximate result (29) as follows. Destriping solves the baseline amplitude ab from the differences between samples from baseline segment b and from other baseline segments that hit the same pixel. Both the baselines
The approximation (29) corresponds to the white noise reference baseline contribution discussed in Sect. 5. We see in Sect. 6 that, while this approximation is good in the time domain, it is not that good in the map domain.
4 Simulation
In this study we tested the destriping method using simulated data that
is more realistic than the model used to derive the method in
Sect. 3.
The TOD was produced using P LANCK
Level-S simulation software (Reinecke et al. 2006) as a sum of
signal, white noise, and correlated noise (called also 1/f noise),
| (30) |
We produced the three time streams,
4.1 Signal
We considered the CMB signal only; no foregrounds were included in the
simulation. Detector pointings
![]() for
each sample t were produced to imitate
a realistic scanning strategy. We used a set of input spherical
harmonic coefficients
for
each sample t were produced to imitate
a realistic scanning strategy. We used a set of input spherical
harmonic coefficients
![]() ,
,
![]() to represent the sky. The
signal sample st
was then produced by the convolution of a circularly symmetric Gaussian
beam (fwhm = 12.68') centered at this
pointing
with the input
to represent the sky. The
signal sample st
was then produced by the convolution of a circularly symmetric Gaussian
beam (fwhm = 12.68') centered at this
pointing
with the input ![]() (Wandelt & Górski 2001;
Challinor 2000).
Thus the I, Q, and U
(Eq. (1))
of the signal parts of different samples hitting the same pixel are
different, as
(Wandelt & Górski 2001;
Challinor 2000).
Thus the I, Q, and U
(Eq. (1))
of the signal parts of different samples hitting the same pixel are
different, as
![]() can
vary within the pixel.
can
vary within the pixel.
To produce the input
![]() we used the CAMB
we used the CAMB![]() code to produce the theoretical angular power spectra
code to produce the theoretical angular power spectra
![]() ,
,
![]() ,
,
![]() for the
Friedmann-Robertson-Walker universe with cosmological parameter values
for the
Friedmann-Robertson-Walker universe with cosmological parameter values
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and with scale-invariant (n = 1) adiabatic
primordial scalar perturbations with amplitude 5
,
and with scale-invariant (n = 1) adiabatic
primordial scalar perturbations with amplitude 5 ![]() 10-5 for the curvature perturbations.
A realization
10-5 for the curvature perturbations.
A realization
![]() was then produced from these spectra. Effects of gravitational lensing
were ignored, and therefore there is no B mode
polarization in the input spectrum.
was then produced from these spectra. Effects of gravitational lensing
were ignored, and therefore there is no B mode
polarization in the input spectrum.
Figure 1
shows the input ![]() as well as the
as well as the ![]() of the binned (noiseless) signal map
of the binned (noiseless) signal map
![]() made from the simulated TOD.
made from the simulated TOD.
![\begin{figure}
\par\hspace*{-1mm} \includegraphics[width=8.5cm,clip]{12361f1a.ep...
...ps}\vspace*{3mm}
\includegraphics[width=8.5cm,clip]{12361f1c.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg155.png)
|
Figure 1:
Input angular power spectrum. Black lines show the
theoretical |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{12361f2a.ps}\vspace*{2mm}
\includegraphics[angle=90,width=8.8cm,clip]{12361f2b.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg156.png)
|
Figure 2: Binned CMB signal map, I and Q, full sky. All maps in this paper are shown using the ecliptic coordinate system. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{12361f3a.ps} \includegraphics[width=4.3cm,clip]{12361f3b.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg157.png)
|
Figure 3:
Binned CMB temperature (I) signal maps from
two |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{12361f4a.ps} \includ...
...ip]{12361f4c.ps} \includegraphics[width=4.3cm,clip]{12361f4d.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg158.png)
|
Figure 4: Same as Fig. 3, but for the Stokes parameters Q ( top) and U ( bottom). |
| Open with DEXTER | |
Figure 2
shows the binned signal maps
![]() ,
and Figs. 3
and 4
zoom into two
,
and Figs. 3
and 4
zoom into two ![]()
![]()
![]() regions
to reveal small-scale detail. Since the signal contains only E mode
polarization, Q shows structures elongated
along lines of latitude and longitude, whereas U
shows structures elongated
regions
to reveal small-scale detail. Since the signal contains only E mode
polarization, Q shows structures elongated
along lines of latitude and longitude, whereas U
shows structures elongated ![]() away from them (see Fig. 4).
away from them (see Fig. 4).
In this paper we keep using these same two ![]()
![]()
![]() regions,
one near the ecliptic north pole, one near the ecliptic, to show map
detail. We show all maps in the ecliptic coordinate system. This
coordinate system is good for showing map-making related systematics,
since the scanning direction is mostly close to the ecliptic meridians.
regions,
one near the ecliptic north pole, one near the ecliptic, to show map
detail. We show all maps in the ecliptic coordinate system. This
coordinate system is good for showing map-making related systematics,
since the scanning direction is mostly close to the ecliptic meridians.
4.2 Scanning
| Figure 5:
Hit map for the 1-year simulation. We show regions around the
ecliptic North Pole ( left) and South Pole (
right). The color scale is linear and goes from zero (blue)
to 50 000 (red). Lines of latitude are drawn at |
|
| Open with DEXTER | |
The sky scanning strategy was cycloidal (Dupac & Tauber 2005): the
satellite spin axis was repointed at 1 h intervals, causing it
to make a clockwise circle (radius ![]() )
around the anti-Sun direction in 6 months. When the spin axis
is north of the ecliptic, the motion along the circle subtracts from
the motion of the anti-Sun direction on the sky, making the repointing
step shorter; and when the spin axis is south of the ecliptic, the two
motions add up, making the repointing step longer.
)
around the anti-Sun direction in 6 months. When the spin axis
is north of the ecliptic, the motion along the circle subtracts from
the motion of the anti-Sun direction on the sky, making the repointing
step shorter; and when the spin axis is south of the ecliptic, the two
motions add up, making the repointing step longer.
Random errors (
![]() )
were added to the repointing. Between repointings the spin axis nutated
at an amplitude related to the repointing error. The mean nutation
amplitude was 1.6'. The nutation was dominated by a
combination of two periods,
)
were added to the repointing. Between repointings the spin axis nutated
at an amplitude related to the repointing error. The mean nutation
amplitude was 1.6'. The nutation was dominated by a
combination of two periods, ![]() s and
s and ![]() s.
In reality, the repointing errors and nutation amplitudes are expected
to be smaller. Thus effects of nutation and small-scale variations in
the map pixel hit count appear somewhat exaggerated in this study.
s.
In reality, the repointing errors and nutation amplitudes are expected
to be smaller. Thus effects of nutation and small-scale variations in
the map pixel hit count appear somewhat exaggerated in this study.
The satellite rotated clockwise (i.e., spin vector pointing
away from the Sun) at about 1 rpm (
![]() Hz);
spin rate variations (rms
Hz);
spin rate variations (rms
![]() )
around this nominal rate were chosen randomly at each repointing. (In
reality, the spin rate variations are expected to be smaller.) Coupled
with the 60 s spin period, the 45 s and 90 s
nutation periods produce a 3-min
periodicity in the detector scanning pattern.
)
around this nominal rate were chosen randomly at each repointing. (In
reality, the spin rate variations are expected to be smaller.) Coupled
with the 60 s spin period, the 45 s and 90 s
nutation periods produce a 3-min
periodicity in the detector scanning pattern.
We simulated 4 detectors corresponding to 2 horns
(19 and 22). The detectors were pointed
![]() away from the spin axis, causing them to draw almost great circles on
the sky, the ``22'' trailing the ``19'' detectors
by
away from the spin axis, causing them to draw almost great circles on
the sky, the ``22'' trailing the ``19'' detectors
by ![]() ,
but following the same path. The a and b detectors of
each horn shared the same pointing but had different polarization
directions by exactly
,
but following the same path. The a and b detectors of
each horn shared the same pointing but had different polarization
directions by exactly ![]() .
The polarization directions of the 19 and 22 detector
pairs differed from each other by
.
The polarization directions of the 19 and 22 detector
pairs differed from each other by
![]() .
.
The cycloidal scanning causes the detector scanning rings to form caustics around the ecliptic poles, where nearby scanning rings cross (see Fig. 5). A large number of ring crossings cluster at the four corners of these caustics. For destriping, such a clustering, where very many crossing points fall on the same pixel, is disadvantageous, since there is less independent information available for solving the baselines of these rings. The clustering occurs when the curvature of the path of satellite pointing on the sky equals the curvature of the scanning circle. The curvature changes sign when the spin axis is close to the ecliptic, but slightly north of it, and the clusterings near the north and south ecliptic poles occur a little bit before and after that. Conversely, the crossing points are spread more widely along the caustics when the spin axis is near its north or south extrema.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361fg6.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg171.png)
|
Figure 6:
Power spectrum of the noise stream |
| Open with DEXTER | |
The sampling frequency was
![]() Hz,
and each sample was simulated as an instantaneous measurement
(no integration along scan direction). The baseline
length
Hz,
and each sample was simulated as an instantaneous measurement
(no integration along scan direction). The baseline
length
![]() ,
is given in time units as
,
is given in time units as
![]() in the following. The beam center moves on the sky at an angular
velocity
in the following. The beam center moves on the sky at an angular
velocity
![]() ,
so that one baseline corresponds to a path of length
,
so that one baseline corresponds to a path of length
![]() on the sky. The samples are separated by
on the sky. The samples are separated by
![]() on the sky. The length of the simulated TOD was nt
= 4
on the sky. The length of the simulated TOD was nt
= 4 ![]() 366
366 ![]() 24
24 ![]()
![]()
![]()
![]() .
.
4.3 Noise
The noise part was produced as a sum of white and correlated noise,
| (31) |
where the correlated part (1/f noise) was produced by a stochastic-differential-equation (SDE) method, that produces noise whose power spectrum is approximately of the form
The white noise rms was set to
![]() K
(thermodynamic scale for CMB anisotropies), corresponding to
the P LANCK 70 GHz goal
sensitivity (Planck Collaboration 2005).
The 1/f noise was simulated with slope
K
(thermodynamic scale for CMB anisotropies), corresponding to
the P LANCK 70 GHz goal
sensitivity (Planck Collaboration 2005).
The 1/f noise was simulated with slope
![]() and
and ![]()
![]() 10-5 Hz (period of one day), so that
the power spectrum was flat for
10-5 Hz (period of one day), so that
the power spectrum was flat for
![]() .
See Fig. 6.
Since the white and 1/f streams were
produced separately, the knee frequency
.
See Fig. 6.
Since the white and 1/f streams were
produced separately, the knee frequency ![]() (where the white and 1/f noise powers are
equal) could be adjusted by multiplying the 1/f stream
with different factors. We used
(where the white and 1/f noise powers are
equal) could be adjusted by multiplying the 1/f stream
with different factors. We used
![]() mHz
as the reference case, representing a conservative upper limit for the
P LANCK 70 GHz detectors (Burigana
et al. 1997a;
Seiffert et al. 2002;
Tuovinen 2003),
but consider also
mHz
as the reference case, representing a conservative upper limit for the
P LANCK 70 GHz detectors (Burigana
et al. 1997a;
Seiffert et al. 2002;
Tuovinen 2003),
but consider also ![]() mHz
in Sects. 7
and 8.
mHz
in Sects. 7
and 8.
The power spectrum of the 1/f noise is thus
approximately
where
The 1/f noise was generated in
![]() d
pieces. The actual statistics calculated from the simulated 1/f stream
were: mean =
d
pieces. The actual statistics calculated from the simulated 1/f stream
were: mean = ![]() K,
stdev =
K,
stdev =
![]() K,
so that
K,
so that ![]() .
As can be seen from Fig. 6, the
simulated 1/f stream power falls below the
noise model for the lowest frequencies. This
rounding of the spectrum is a feature of the SDE method (see
Keihänen et al. 2009).
Although a sizable part of the variance in the 1/f stream
comes from the very lowest frequencies,
these low frequencies are removed well by destriping, and thus the
detailed shape of the spectrum at low frequencies is not that
important. For analytical estimates we use the noise model of
Eq. (32).
.
As can be seen from Fig. 6, the
simulated 1/f stream power falls below the
noise model for the lowest frequencies. This
rounding of the spectrum is a feature of the SDE method (see
Keihänen et al. 2009).
Although a sizable part of the variance in the 1/f stream
comes from the very lowest frequencies,
these low frequencies are removed well by destriping, and thus the
detailed shape of the spectrum at low frequencies is not that
important. For analytical estimates we use the noise model of
Eq. (32).
The nonzero mean of the 1/f stream has to be taken into account when comparing solved baselines to the input 1/f stream, since the destriping method sets the average of the solved baselines to zero.
4.4 Maps
The maps were produced in the HEALPix![]() pixelization
(Górski et al. 2005)
in ecliptic coordinates. We used the
pixelization
(Górski et al. 2005)
in ecliptic coordinates. We used the
![]() resolution
for all maps, corresponding to
np
= 3 145 728 for the full sky, with square root of
pixel solid angle
resolution
for all maps, corresponding to
np
= 3 145 728 for the full sky, with square root of
pixel solid angle
![]() .
For the full-year TOD the polarization of each pixel was well sampled;
the lowest rcond was 0.422. The mean rcond
was 0.492 and the maximum 0.49999. The hit
count
.
For the full-year TOD the polarization of each pixel was well sampled;
the lowest rcond was 0.422. The mean rcond
was 0.492 and the maximum 0.49999. The hit
count
![]() (number of hits per pixel)
varied from 818
to 273 480 for the full 1-year simulation. The mean
number of hits was
(number of hits per pixel)
varied from 818
to 273 480 for the full 1-year simulation. The mean
number of hits was
![]() .
The mean inverse hit count was
.
The mean inverse hit count was
![]() .
Figure 5
shows the hit count in the regions around the ecliptic poles, where it
varies a lot. Figure 7 shows
the hit count in the two
.
Figure 5
shows the hit count in the regions around the ecliptic poles, where it
varies a lot. Figure 7 shows
the hit count in the two ![]()
![]()
![]() regions.
regions.
| Figure 7:
Hit maps of the two |
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{12361f8a.ps}\includegraphics[width=4.3cm,clip]{12361f8b.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg198.png)
|
Figure 8:
Destriped (output) temperature map (one year survey, 15 s
baselines) for the two |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{12361f9a.ps}\includegraphics[width=4.3cm,clip]{12361f9b.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg199.png)
|
Figure 9: Even near the ecliptic poles, where the noise in the output map is the lowest, the pixel-scale noise from four 70 GHz detectors is higher than the CMB polarization signal in the map. Left: binned signal Q map. Right: output Q map (15 s baselines). (Both plots are from the same pole region.) |
| Open with DEXTER | |
Figure 8
shows the output temperature map
![]() for the case
for the case
![]() s.
The visual appearance is the same for other baseline lengths.
To see differences one has to look at residual maps, see
Sect. 6.
Polarization maps (Fig. 9)
are dominated by small-scale noise. The most obvious map-making related
feature in the output maps is the reduction of noise where the hit
count is larger. Other effects are more subtle and are analyzed in the
following sections.
s.
The visual appearance is the same for other baseline lengths.
To see differences one has to look at residual maps, see
Sect. 6.
Polarization maps (Fig. 9)
are dominated by small-scale noise. The most obvious map-making related
feature in the output maps is the reduction of noise where the hit
count is larger. Other effects are more subtle and are analyzed in the
following sections.
5 Time domain
We now analyze the application of the destriping method to this kind of
data. We consider the case of the full 1-year survey with
![]() mHz
noise, except for Sect. 7, where
we discuss the effect of changing the knee frequency, and for
Sect. 9,
where we consider maps made from shorter pieces of the TOD. Consider
this first in the time domain, i.e., look at the cleaned TOD
mHz
noise, except for Sect. 7, where
we discuss the effect of changing the knee frequency, and for
Sect. 9,
where we consider maps made from shorter pieces of the TOD. Consider
this first in the time domain, i.e., look at the cleaned TOD
| (33) |
We assume that the two noise streams,
Since the destriping method is linear, we can divide the
baseline amplitudes obtained by Eq. (16) into the parts
coming from the different TOD components,
| (34) |
Likewise, the cleaned TOD can be divided into five terms,
The first term is the signal and the second term is the white noise. We call the third term white noise baselines, the fourth term (in parenthesis) residual 1/f noise, and the fifth term signal baselines.
The TOD vector ![]() appearing in the signal baseline term
appearing in the signal baseline term
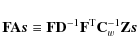
|
(36) |
is the pixelization noise (Doré et al. 2001). It is the noise estimate we get from the signal TOD (which contains no noise). Signal gradients (of the beam-smoothed input sky) within a map pixel are the origin of the pixelization noise.
5.1 Reference baselines
We define the reference baselines
![]() of a noise stream
of a noise stream ![]() as the weighted averages of each baseline segment, i.e.,
matrix
R is
defined as
as the weighted averages of each baseline segment, i.e.,
matrix
R is
defined as
Note that RF= I.
The reference baselines of the 1/f noise,
can be viewed as the ``goal'' of baseline estimation. Subtracting them from the full TOD gives us a TOD stream
| (39) |
which contains, beside the signal and the white noise, only the part
The actual cleaned TOD that results from destriping, can now
be written as
| (40) |
where the residual 1/f noise is split into the unmodeled 1/f noise and the 1/f baseline error,
white noise baselines, 1/f baseline error, and signal baselines.
Unlike the solved baseline contributions
![]() ,
the reference baselines
,
the reference baselines
![]() do not involve the pointing
matrix (except for the case of pixelization
noise), so the differences between them are related to how the scanning
strategy connects the baselines with crossing points. Thus, for
analyzing errors, it is useful to separate also the white noise
baselines into white noise reference baselines and white noise baseline
error,
do not involve the pointing
matrix (except for the case of pixelization
noise), so the differences between them are related to how the scanning
strategy connects the baselines with crossing points. Thus, for
analyzing errors, it is useful to separate also the white noise
baselines into white noise reference baselines and white noise baseline
error,
![]() ;
and likewise the signal baselines into reference baselines of
pixelization noise and signal baseline error
;
and likewise the signal baselines into reference baselines of
pixelization noise and signal baseline error
![]() .
.
The white noise baseline error stream
![]() is uncorrelated with the white noise reference baseline
stream
is uncorrelated with the white noise reference baseline
stream
![]() .
To show this, we note that
.
To show this, we note that
|
|
= | ||
| = | D-1 - RPBFD-1 | ||
| = | |||
| = | (42) |
so that
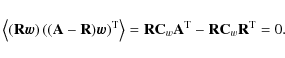
|
(43) |
5.2 Approximation to solved baselines
The solved baselines ![]() can now be written as
can now be written as
|
|
= | ||
| = | |||
| (44) |
(up to an overall constant), so that
| = | |||
| (45) |
For the TOD streams
Comparing to Eq. (41), we note that in Eq. (46) white noise baselines are approximated by white noise reference baselines, 1/f baseline error is ignored, and signal baselines are approximated by the reference baselines of pixelization noise. Thus, for a good scanning, the solved baselines
5.3 Division
The effect of destriping on the white noise is just harmful for the
maps (we elaborate on this in Sect. 6), so the
relevant time domain residual is
It consists of three components:
- 1.
- white noise baselines;
- 2.
- residual 1/f noise;
- 3.
- and signal baselines;
Each component can be further divided into two parts:
We call these six components:
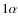 )
)
- white noise reference baselines;
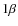 )
)
- white noise baseline error;
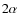 )
)
- unmodeled 1/f noise;
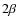 )
)
- 1/f baseline error;
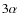 )
)
- reference baselines of pixelization noise;
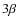 )
)
- signal baseline error.
We turn now to our results with simulated data to see how this comes out in practice, first for the noise part, and then for the signal part.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f10.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg249.png)
|
Figure 10:
First 15 minutes of the (1/f + white) noise
stream ( grey) and its reference ( black
solid) and solved ( black dashed)
|
| Open with DEXTER | |
In Fig. 10
we show a part of the simulated (1/f +
white) noise stream ![]() ,
both the reference and solved baselines,
,
both the reference and solved baselines,
![]() and
and ![]() ,
and their difference
,
and their difference
![]() ,
for
,
for ![]() s.
s.
We consider now separately the white noise and 1/f noise parts.
5.4 White noise baselines
Table 2: Statistics of the white noise baselines.
Table 3:
Stdev ![]() of white noise baseline error.
of white noise baseline error.
From Tables 2
and 3
we see that the white noise baselines track their reference baselines
well. The white noise reference baselines are just white noise
themselves, their variance
![]() down from the white noise
variance
down from the white noise
variance ![]() by
by
![]() .
The white noise baseline variance
.
The white noise baseline variance
is slightly larger. Table 2 shows the standard deviation (square root of the variance) of the baselines,
In Table 3
we give the standard deviation
![]() of the white noise baseline
error. We show it also for the average and
the difference between the two polarization
directions a and b,
which represent the contribution of this effect to the temperature and
polarization measurements.
of the white noise baseline
error. We show it also for the average and
the difference between the two polarization
directions a and b,
which represent the contribution of this effect to the temperature and
polarization measurements.
The white noise reference baselines are completely uncorrelated with each other. This is not true for the solved white noise baselines. The difference, the baseline errors, show significant autocorrelation, see Figs. 11 and 12, and correlation between detectors 19 and 22, see Table 4. Although the white noise baseline variance is not much larger than the white noise reference baseline variance, these correlations make the difference between them important.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f11.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg258.png)
|
Figure 11:
Autocorrelation function for the white noise baseline error
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f12.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg259.png)
|
Figure 12:
Autocorrelation function for the white noise baseline error
|
| Open with DEXTER | |
Table 4: Correlations between detectors 19 and 22.
These correlation properties are easy to understand. While the
amplitude of the reference baseline arises from the noise of the
baseline segment itself, the error
![]() is
caused by the
noise in the crossing baselines. Since the baseline segments that are
separated from each other by an integer number of spin periods, and not
too many pointing periods, cross almost the same set of
other baseline segments, often in the same pixels, their baseline
errors
is
caused by the
noise in the crossing baselines. Since the baseline segments that are
separated from each other by an integer number of spin periods, and not
too many pointing periods, cross almost the same set of
other baseline segments, often in the same pixels, their baseline
errors
![]() are
strongly correlated with each other.
are
strongly correlated with each other.
In Fig. 12 we
show the autocorrelation function of
![]() for the case
for the case ![]() s.
For short lags, only baselines whose lag is a multiple of
1 min (
s.
For short lags, only baselines whose lag is a multiple of
1 min (![]() the
spin period) show significant correlation with each other. For longer
lags this distinction disappears due to random spin rate variations.
Since these variations have a rms which is about 1/60 of the
spin rate, for lags around 30 min any one of the baseline
segments within a spin period is about equally likely to land on a
given location of the scan circle. The correlation between two
baselines that land on the same location of the circle is much larger
(presumably similar to the
the
spin period) show significant correlation with each other. For longer
lags this distinction disappears due to random spin rate variations.
Since these variations have a rms which is about 1/60 of the
spin rate, for lags around 30 min any one of the baseline
segments within a spin period is about equally likely to land on a
given location of the scan circle. The correlation between two
baselines that land on the same location of the circle is much larger
(presumably similar to the
![]() min
and 1 h cases), but the way we calculate the autocorrelation
function (in time domain, not in the spin phase domain) is not able to
pick this out.
min
and 1 h cases), but the way we calculate the autocorrelation
function (in time domain, not in the spin phase domain) is not able to
pick this out.
Also, since the corresponding baseline segments from the
horns 19 and 22 are only
![]() =
0.517 s shifted from each other, they crossed almost the same
set of other baseline segments, and are thus strongly correlated. The
overlap fraction
=
0.517 s shifted from each other, they crossed almost the same
set of other baseline segments, and are thus strongly correlated. The
overlap fraction
![]() is given in Table 4.
Note that this number does not take into account that the hits from the
two horns may still be distributed differently to the pixels in the
overlap region.
is given in Table 4.
Note that this number does not take into account that the hits from the
two horns may still be distributed differently to the pixels in the
overlap region.
More exactly, the ``temperature'' combinations (a+b)/2
of
![]() are
strongly correlated between 19 and 22, whereas
the ``polarization'' combinations (a-b)/2
are not. The polarization directions of the ab
pairs 19 and 22 differ from each other by
are
strongly correlated between 19 and 22, whereas
the ``polarization'' combinations (a-b)/2
are not. The polarization directions of the ab
pairs 19 and 22 differ from each other by
![]() making their polarization
measurements (a-b)/2
almost orthogonal. Thus they also pick almost orthogonal
error combinations from the crossing baseline segments, and remain
uncorrelated. This also explains why the stdev of the ``polarization
baseline error'' is larger than the ``temperature''
one in Table 3.
In effect, only half of the crossing baseline pairs ab
contribute to determining an (a-b)/2 baseline
combination, so the number of degrees of freedom is down
by 1/2 and the variance thus larger by 2.
making their polarization
measurements (a-b)/2
almost orthogonal. Thus they also pick almost orthogonal
error combinations from the crossing baseline segments, and remain
uncorrelated. This also explains why the stdev of the ``polarization
baseline error'' is larger than the ``temperature''
one in Table 3.
In effect, only half of the crossing baseline pairs ab
contribute to determining an (a-b)/2 baseline
combination, so the number of degrees of freedom is down
by 1/2 and the variance thus larger by 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f13.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg262.png)
|
Figure 13:
First 10 min of the 1/f noise
stream
|
| Open with DEXTER | |
5.5 Residual 1/f noise
Figure 13
shows the 1/f part of the noise
![]() ,
its reference baselines
,
its reference baselines
![]() and the solved 1/f baselines,
and the solved 1/f baselines,
![]() .
The difference between these two sets of baselines, 1/f baseline
error, is shown in Fig. 14.
.
The difference between these two sets of baselines, 1/f baseline
error, is shown in Fig. 14.
The 1/f noise can be separated into
reference baselines and unmodeled 1/f noise,
![]() .
When we separate the 1/f baseline error,
.
When we separate the 1/f baseline error,
![]() into the
corresponding components,
into the
corresponding components,
| (50) |
we note that the first term on the right hand side gives the same contribution to each baseline (=- the mean of the 1/f noise), and is thus irrelevant. Thus the 1/f baseline error arises from the unmodeled 1/f noise, in the same manner as white noise baseline error
5.5.1 Unmodeled 1/f noise
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1236114a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{1236114b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg270.png)
|
Figure 14:
The 1/f baseline error, i.e., the difference between
the solved and reference 1/f baselines
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f15.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg271.png)
|
Figure 15:
Power spectrum |
| Open with DEXTER | |
Since baselines can only model frequencies
![]() and do it better for lower frequencies, the power spectrum of the
unmodeled 1/f noise
and do it better for lower frequencies, the power spectrum of the
unmodeled 1/f noise
![]() is equal to
that of
is equal to
that of ![]() for
for ![]() and falls rapidly towards smaller f for f
< fx.
See Fig. 15.
and falls rapidly towards smaller f for f
< fx.
See Fig. 15.
Since the reference baselines
![]() are obtained from the stream
are obtained from the stream
![]() ,
the power spectrum
,
the power spectrum
![]() of the unmodeled 1/f noise
of the unmodeled 1/f noise
![]() can be obtained from the power spectrum
can be obtained from the power spectrum
![]() of
of
![]() through a transfer function,
through a transfer function,
This transfer function is
For
Table 5:
Stdev ![]() of the unmodeled 1/f Stream.
of the unmodeled 1/f Stream.
We get a rough estimate of the total power in
![]() by integrating the original
by integrating the original ![]() from fx
to
from fx
to ![]() and
and ![]() from
from ![]() to fx,
to fx,
For
For our case,
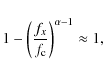
|
(55) |
so that Eq. (53) gives
In Table 5 we compare this approximation to a numerical integration of Eq. (51) and the actual standard deviation
Table 6:
Stdev ![]() of the 1/f Baseline Error.
of the 1/f Baseline Error.
5.5.2 1/f baseline error
Since the unmodeled 1/f noise is correlated, the
properties of 1/f baseline errors differ
from white noise baseline errors. Over timescales
![]() the unmodeled 1/f is positively
correlated, but since it averages to zero over each baseline segment,
there is a net anticorrelation.
the unmodeled 1/f is positively
correlated, but since it averages to zero over each baseline segment,
there is a net anticorrelation.
From Fig. 14
we see for short baselines a spin-synchronous pattern. For baselines of
![]() min,
the remaining pattern shows a 3-min period that comes from
spin-axis
nutation. For even longer baselines the long-time-scale correlation
shows up clearly. 1/f baseline error
decreases for longer baselines, but much less steeply than white noise
baseline error. See Table 6, where
we show the standard deviation
min,
the remaining pattern shows a 3-min period that comes from
spin-axis
nutation. For even longer baselines the long-time-scale correlation
shows up clearly. 1/f baseline error
decreases for longer baselines, but much less steeply than white noise
baseline error. See Table 6, where
we show the standard deviation
![]() of the 1/f baseline
error
of the 1/f baseline
error
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f16.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg294.png)
|
Figure 16: Same as Fig. 11, but now for the 1/f noise baseline error. |
| Open with DEXTER | |
Figure 16 shows the 1/f baseline error autocorrelation. For white noise baseline error we noted that we get a correlation for nearby baselines since they often cross the same other baseline in the same pixel. Since unmodeled 1/f noise is positively correlated over short timescales, it is not necessary for this crossing to occur in the same pixel to get the positive correlation. Therefore we now get positive correlations for even longer timescales. This makes 1/f baseline error more important than its small variance suggests, since it is not averaged away when binned onto the map.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f17.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg295.png)
|
Figure 17:
The 1/f baseline error,
|
| Open with DEXTER | |
In Fig. 17
we show the 1/f baseline error for
![]() h
over the full year of the simulation for the detector pair 19.
The effect of the 6-month period of the cycloidal scanning is clearly
visible.
h
over the full year of the simulation for the detector pair 19.
The effect of the 6-month period of the cycloidal scanning is clearly
visible.
5.6 Noise power spectra
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f18.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg298.png)
|
Figure 18:
Effect of baseline subtraction on the noise power spectrum. The
solid black line is the spectrum of the original noise
stream |
| Open with DEXTER | |
We show the power spectra of the cleaned (destriped) noise
streams
![]() for
different baseline lengths in Fig. 18. They
are compared to the spectrum of the original noise stream
for
different baseline lengths in Fig. 18. They
are compared to the spectrum of the original noise stream ![]() and the spectra where noise reference baselines are subtracted instead,
and the spectra where noise reference baselines are subtracted instead,
![]() .
.
Subtraction of baselines suppresses noise at
![]() .
For lower frequencies the noise is suppressed more, as baselines can
model the lower frequencies better. When reference baselines are
subtracted, the noise power keeps going down toward lower frequencies;
however the solved baselines seem to be able to suppress noise power
about 6 orders of magnitude only.
.
For lower frequencies the noise is suppressed more, as baselines can
model the lower frequencies better. When reference baselines are
subtracted, the noise power keeps going down toward lower frequencies;
however the solved baselines seem to be able to suppress noise power
about 6 orders of magnitude only.
For shorter baselines, spectral features appear at special frequencies. They do not appear when reference baselines are subtracted, so they are clearly related to the scanning strategy. 1) There are peaks at f = 1/min and f = 1/(3 min) corresponding to the spin and nutation frequencies, and their harmonics. 2) There is a notch in power at f = 1/h, corresponding to the repointing period, and its harmonics. These are easy to understand:
The solved baselines come from a noise estimate based on subtracting from each sample the average of all samples that hit the same pixel. Consider an ideal scanning where the same pixel sequence is hit during each spin period within a repointing period:
- 1)
- If the spin period is equal to or a multiple of the period of a noise frequency component, all samples hitting the same pixel during a given repointing period get the same value from this noise component. Thus this noise component can be detected as noise (and not signal) only by comparing hits from different repointing periods, resulting in a much poorer noise estimate.
- 2)
- On the other hand, if the repointing period is equal to or a multiple of the noise period, but the spin period is not, then the different samples hitting the same pixel average to zero. This noise component is then recognized as noise in its entirety, and the solved baseline becomes equal to the reference baseline.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f19.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg302.png)
|
Figure 19:
Effect of subtracting both the white noise and the 1/f baselines
on the power spectrum of the 1/f noise. The
solid black line is the original 1/f spectrum.
The solid colored lines show the power spectra of
|
| Open with DEXTER | |
As mentioned in Sects. 1
and 5.3
and elaborated in Sect. 6, the
relevant residual noise is the stream
![]() where
both white noise and 1/f baselines
are subtracted from the 1/f noise stream.
This is shown in Fig. 19.
The subtraction of the white noise baselines has added power to the
cleaned 1/f stream. At low frequencies the
spectrum appears now white, since the
white noise reference baseline stream is white at timescales longer
than
where
both white noise and 1/f baselines
are subtracted from the 1/f noise stream.
This is shown in Fig. 19.
The subtraction of the white noise baselines has added power to the
cleaned 1/f stream. At low frequencies the
spectrum appears now white, since the
white noise reference baseline stream is white at timescales longer
than
![]() .
The power of the baseline error rises towards the lowest frequencies
and shows up below 5
.
The power of the baseline error rises towards the lowest frequencies
and shows up below 5 ![]() 10-5 Hz. The subtraction of uniform
baselines from the noise stream has a chopping effect that transforms a
part of the low frequency,
10-5 Hz. The subtraction of uniform
baselines from the noise stream has a chopping effect that transforms a
part of the low frequency,
![]() ,
power into high frequency,
,
power into high frequency,
![]() .
.
5.7 Optimal baseline length
What is the optimal baseline length to use? A partial answer
can be found by minimizing the variance of the residual correlated
noise, i.e., the residual noise minus the original white noise,
| (57) |
The variances of the four components are
Using Eqs. (49)
and (53)
we find that ![]() is minimized for
is minimized for
for which
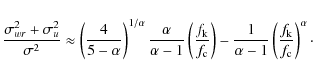
|
(59) |
For
and
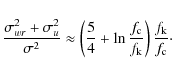
|
(61) |
For
However, because of the different correlation properties of the different residuals, they have a different impact in map-making, and it is not enough to consider the time-domain variance. So we need to return to this issue later, after we have studied the residuals in the map domain and their angular power spectra.
5.8 Pixelization noise and signal baselines
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f20.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg320.png)
|
Figure 20:
Pixelization noise. In the top panel we show a
piece of the original signal stream |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f21.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg321.png)
|
Figure 21: Autocorrelation function of the pixelization noise. Note the alternating correlation and anticorrelation for small lags, and the correlations at 1 min lag, when the scanning returns to the same location on the sky. Due to spin rate variations the correlations are spread around the 1 min value, and more around 2 min. |
| Open with DEXTER | |
Pixelization noise,
![]() ,
arises from signal gradients through a combination of pixelization,
scanning strategy, and sampling frequency. These lead to correlations
between close-by samples, and also correlations between samples from
the same locations on the sky which are not close to each other in time
domain.
,
arises from signal gradients through a combination of pixelization,
scanning strategy, and sampling frequency. These lead to correlations
between close-by samples, and also correlations between samples from
the same locations on the sky which are not close to each other in time
domain.
In Fig. 20 we show a short piece of the pixelization noise. Its autocorrelation function is shown in Fig. 21. We see that neighboring samples (lag = 1 = (1/76.8) s) are anticorrelated, whereas we have a positive correlation for lag = 2. The power spectrum is close to that of white noise, except that there are some features near the Nyquist frequency due to these correlations.
Comparing the pixel size
![]() to the sample separation
to the sample separation
![]() and remembering that the scanning direction is mostly close to the
direction of the pixel diagonal (both are often close to the ecliptic
meridians), so that the pixel geometry tends to repeat at
and remembering that the scanning direction is mostly close to the
direction of the pixel diagonal (both are often close to the ecliptic
meridians), so that the pixel geometry tends to repeat at
![]() intervals,
close to
intervals,
close to ![]() ,
we see that a pair of samples with lag 2 tends to land in
about the same relative location within their respective
pixels. With this small separation there is a positive correlation in
the CMB signal gradient (smoothed with the beam). These
combine to give a positive correlation between lag 2 samples.
On the other hand, neighboring samples often land at opposite sides of
the same pixel, or of neighboring pixels, leading to a negative
correlation in their pixelization noise. These correlations would be
different for different ratios of sample separation to pixel size.
,
we see that a pair of samples with lag 2 tends to land in
about the same relative location within their respective
pixels. With this small separation there is a positive correlation in
the CMB signal gradient (smoothed with the beam). These
combine to give a positive correlation between lag 2 samples.
On the other hand, neighboring samples often land at opposite sides of
the same pixel, or of neighboring pixels, leading to a negative
correlation in their pixelization noise. These correlations would be
different for different ratios of sample separation to pixel size.
Since the pixelization noise arises from the signal, we
analyze it in the combinations
![]() (``temperature'') and
(``temperature'') and
![]() (``polarization''), so that
(``polarization''), so that
| (62) |
Each of the
We find that the expectation value for the variance of the
pixelization noise is
where
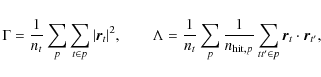
|
(64) |
and
This result, Eq. (63), can be compared to the variance of the signal itself
Assuming the pixels are perfect squares, in the limit of a large number of hits
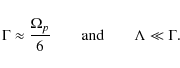
|
(66) |
Since HEALPix pixels are not square, but somewhat elongated, we expect the actual
For our input ![]() ,
setting
,
setting ![]() ,
Eqs. (63)
and (65)
give
,
Eqs. (63)
and (65)
give ![]() K,
K,
![]() K,
K,
![]() K,
and
K,
and ![]() K.
K.
The actual pixelization noise level in the simulation was
![]() K
and
K
and
![]() K.
K.
![\begin{figure}
\par\mbox{ \includegraphics[width=4.3cm,clip]{1236122a.ps} \includegraphics[width=4.3cm,clip]{1236122b.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg358.png)
|
Figure 22:
Pixelization noise rms in map pixels for the two |
| Open with DEXTER | |
By definition, a binned map of pixelization noise vanishes,
![]() .
Instead we can make a map of the rms of the pixelization noise at each
pixel, by squaring each
element of
.
Instead we can make a map of the rms of the pixelization noise at each
pixel, by squaring each
element of ![]() ,
binning the resulting time stream into a map, and taking the square
root of each I pixel. See Fig. 22. Comparing
to Fig. 3
we see that pixels of large pixelization noise tend to ``outline'' hot
and cold spots of the signal.
,
binning the resulting time stream into a map, and taking the square
root of each I pixel. See Fig. 22. Comparing
to Fig. 3
we see that pixels of large pixelization noise tend to ``outline'' hot
and cold spots of the signal.
Table 7: Stdev of contributions to signal baselines.
Signal baselines arise from the pixelization noise in the same
manner as white noise baselines arise from white noise, and we can
divide them into the reference baselines of pixelization noise, and
signal baseline errors,
![]() .
Approximating the pixelization noise as white, we get an estimate for
the standard deviation (stdev) of
.
Approximating the pixelization noise as white, we get an estimate for
the standard deviation (stdev) of
![]()
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1236123a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{1236123b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg366.png)
|
Figure 23:
Correlations in the signal baselines. The top panel
shows the
autocorrelation function of the reference baselines
|
| Open with DEXTER | |
In Table 7
we show the stdev of the signal baselines
![]() and their two
contributions
and their two
contributions
![]() (reference
baselines of pixelization noise) and
(reference
baselines of pixelization noise) and
![]() (signal baseline error), and compare them to the estimate (67) for
(signal baseline error), and compare them to the estimate (67) for
![]() .
We see the estimate is quite good for
.
We see the estimate is quite good for
![]() .
The estimate is slightly off mainly because the actual pixelization
noise was slightly larger for temperature and slightly smaller for
polarization than the analytical estimate (63). The column
marked ``(G)'' was obtained using galactic coordinates for the
HEALPix maps.
.
The estimate is slightly off mainly because the actual pixelization
noise was slightly larger for temperature and slightly smaller for
polarization than the analytical estimate (63). The column
marked ``(G)'' was obtained using galactic coordinates for the
HEALPix maps.
In Fig. 23 we show the autocorrelation functions of the reference baselines of pixelization noise and the signal baseline error. Unlike for white noise, now also the reference baselines are correlated. This correlation extends over several repointing periods. These correlations enhance the relevance of the signal baselines in the map domain.
6 Map domain
Destriping is a linear process. The output map can therefore be viewed
as a sum of component maps, each component map being a result of
destriping one individual TOD component: signal, 1/f noise
and white noise:
| (68) |
As the three TOD components are statistically independent, so are the corresponding component maps. The expectation value of the map rms is thus obtained as the root sum square (rss) of the expectation values of the rms of the component maps.
In this paper we have considered a single 1-year realization of each TOD component only. There are likely to be random correlations between the component maps. However, the output map and residual map rms we get when we produce maps from the full TOD, agree to better than 0.5% with the rss of the rms of the corresponding maps produced from component TODs.
6.1 Linearity
In practice the linearity of destriping is affected by the numerical accuracy of the baseline calculation, which depends on the convergence criterion for the conjugate gradient iteration. We checked the linearity by comparing the sum of the component maps to a map obtained directly from the sum of the component TODs. The difference is well below the nK level, except for baselines shorter than 10 s. See Fig. 24.
6.2 Splitting the residual map into components
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12361f24.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg368.png)
|
Figure 24: Linearity of destriping. The three thin black lines at the bottom shows the rms difference between the ``full'' map, obtained from the sum of the component TODs, and the sum of the component maps. This is compared to the signal and noise levels in the maps; different colors showing the different components and the thick black line the full map; different line styles correspond to the three Stokes parameters. |
| Open with DEXTER | |
The three component maps can each be further divided into a binned map and a baseline map.
The correlation properties of these components are different in the map domain from the TOD domain.
While the white noise baselines
![]() are correlated with the white noise
are correlated with the white noise ![]() in the TOD, the correlation vanishes in the map: writing
in the TOD, the correlation vanishes in the map: writing
| (69) | ||
| (70) |
we get that
|
|
= | ||
| (71) |
By substituting
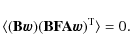
|
(72) |
Because the binned white noise map and the white noise baseline map are independent, the (expectation value of) the rms of the residual white noise map
This means, that while subtracting the white noise baselines removes power from the TOD, it adds power to the map. If the noise is pure white, naive binning produces a better map than destriping. On the other hand, baselines of the 1/f noise are correlated with the 1/f noise itself both in the TOD and in the map.
We can use the rms value taken over all the residual map pixels as a figure-of-merit for the map-making method. We calculate it separately for the three Stokes parameters, I (temperature), Q, and U. Note that we subtract the I monopole from the residual map before calculating the rms, since it is irrelevant for CMB anisotropy and polarization studies, and destriping leaves a spurious I monopole in the map. See Figs. 25-27.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12361f25.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg381.png)
|
Figure 25:
Residual temperature map rms as a function of baseline length.
The top panel is for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f26.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg382.png)
|
Figure 26: Same as the bottom panel of Fig. 25, but now we have further separated the residual 1/f noise into unmodeled 1/f noise ( dashed) and 1/f baseline error ( dot-dashed); the white noise baselines into reference baselines ( dashed) and baseline error ( dot-dashed); and signal baselines (shown here in green) into reference baselines of pixelization noise ( dashed) and baseline error ( dot-dashed). The dotted lines show the rss of the dashed and dot-dashed lines. For white noise it falls on the solid line, showing that the two white noise residual map components are uncorrelated. For 1/f noise and pixelization noise the two components are positively correlated. The black dotted line is the analytical approximation Eq. (86). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12361f27.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg383.png)
|
Figure 27: The rms of the residual I, Q, and U maps, and their different components. The overall residual power in a destriped polarization map is higher than in a temperature map. The CMB signal residual in turn is much weaker. Note how Q is larger than U in the signal baselines. Smoothing the residual maps with a Gaussian beam ( dashed lines) removes excess power at sub-beam scales. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{12361f28.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg385.png)
|
Figure 28:
Residual I map including binned white noise,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{1236129a.ps}\vspa...
...*{1.5mm}
\includegraphics[angle=90,width=8.5cm,clip]{1236129d.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg386.png)
|
Figure 29:
Residual I map (with binned white noise
subtracted),
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{1236130a.ps} \includ...
...ip]{1236130c.ps} \includegraphics[width=4.3cm,clip]{1236130d.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg387.png)
|
Figure 30:
Same as Fig. 29
but for the |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{ \includegraphics[width=4.3cm,clip]{1236131a.ps} \inclu...
...ip]{1236131e.ps} \includegraphics[width=4.3cm,clip]{1236131f.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg394.png)
|
Figure 31:
The six components of the residual I map
shown for the |
| Open with DEXTER | |
The difference between the output map and the binned signal map
| (73) |
is the residual map including binned white noise. We see that it can be divided into four uncorrelated contributions: the binned white noise map, the white noise baseline map, the residual 1/f noise map, and the signal baseline map.
The
![]() I map is shown in Fig. 28. This
map is dominated by the binned white noise map, which is independent of
the baseline length. Therefore the visual appearance of the residual
map is the same for all baseline lengths, as it looks the same as the
white noise map. Also the residual Q and U maps
look the same, just with
I map is shown in Fig. 28. This
map is dominated by the binned white noise map, which is independent of
the baseline length. Therefore the visual appearance of the residual
map is the same for all baseline lengths, as it looks the same as the
white noise map. Also the residual Q and U maps
look the same, just with ![]() larger amplitude.
larger amplitude.
The binned white noise map is independent of the baseline
length, and it is an unavoidable component of the residual map,
uncorrelated with the other components. Therefore we focus on the rest
of the residual map, without the binned white noise
component, i.e.,
For the rest of this paper, the residual map without further qualification, refers to this map. See Figs. 29 and 30.
We divide this further into
in analogy with Eq. (48). Of these six components, the unmodeled 1/f map
In Fig. 26, we show separately the rms of these components.
6.3 Analytical estimates
6.3.1 White noise baselines
We show in Table 8
the rms of the white noise reference baseline maps. Since the white
noise reference baselines are uncorrelated with each other, these map
rms can be estimated
analytically. If all hits to a pixel came from a different baseline, we
could treat them as white noise, with the white noise reference
baseline variance
![]() .
Thus the variances of Ip,
Qp, and Up
would be just
.
Thus the variances of Ip,
Qp, and Up
would be just
![]() ,
,
![]() ,
and
,
and
![]() .
.
For baseline lengths less than or equal to the spin period,
![]() min,
this holds if the sample separation is larger than the pixels,
min,
this holds if the sample separation is larger than the pixels,
![]() .
However, in our case
.
However, in our case
![]() ,
and two or three successive samples may hit the same pixel. These
successive hits are then almost always from the same baseline, and, for
the baseline components, fully correlated, i.e., equal.
,
and two or three successive samples may hit the same pixel. These
successive hits are then almost always from the same baseline, and, for
the baseline components, fully correlated, i.e., equal.
Denote by nfn
the fraction of hits to a pixel that belong to a sequence of exactly n
successive hits to the same pixel, i.e, there are
![]() such sequences, and
such sequences, and ![]() .
The variance of Ip
is then
.
The variance of Ip
is then
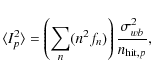
|
(76) |
where
With Eq. (49)
we have for the I map rms
To get an estimate for
For scanning in the direction of the pixel diagonal, for
![]() there are no successive hits to the same pixel and
there are no successive hits to the same pixel and
![]() .
For
.
For
![]() there can be a maximum of two hits, with
there can be a maximum of two hits, with
![]() and
and
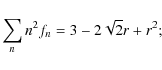
|
(78) |
and with
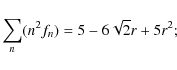
|
(79) |
where
For scanning in the direction of the pixel side, two hits, but no more,
are possible for
![]() with f2
= 1 - r.
with f2
= 1 - r.
For our case,
![]() ,
which gives
,
which gives
for scanning in the diagonal direction, and
However, HEALPix pixels are not square, but can be
significantly elongated. In principle, the mean value
![]() could be calculated from the pointing data
and the chosen pixelization. Here we just take it by comparing the
actual
could be calculated from the pointing data
and the chosen pixelization. Here we just take it by comparing the
actual
![]() from the maps to Eq. (77).
(See Table 8,
where the third column is an estimate of
from the maps to Eq. (77).
(See Table 8,
where the third column is an estimate of
![]() obtained this way.) This gives (from
obtained this way.) This gives (from
![]() s
and 1 min)
s
and 1 min)
![]() .
We denote
.
We denote
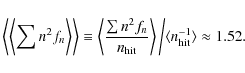
|
(81) |
Equation (80) is quite close to this.
For the other Stokes parameters, we expect
where the approximation corresponds to assuming an ideal distribution of polarization directions. We expect this approximation to be good for the full year data, since most pixels have rcond values close to 0.5.
For baselines longer than the spin period, contributions to a
pixel from successive scan circles tend to come from the same baseline,
so the reduction in the white noise baseline variance is canceled by
the reduction in the number of contributing baselines. Thus the map rms
from white noise baselines is almost flat between
![]() min
and
min
and ![]() h.
h.
Table 9
shows the rms of the white noise baseline error maps. Although in the
time domain the white noise baseline error is much smaller than white
noise reference baselines, their correlations make them important in
the map domain. Assuming the correlation between (a+b)/2 baselines
contributing to the same pixel were c, the
expected variance of the white noise baseline error map would be
where
Since the white noise reference baselines and the white noise baseline errors are uncorrelated, the full white noise baseline map rms is close to the rss of these two components. See Table 10.
Table 8: rms of the white noise reference baseline maps.
Table 9: rms of the white noise baseline error maps.
Table 10: rms of the white noise baseline maps.
6.3.2 Unmodeled 1/f noise
Most of the power in unmodeled 1/f noise is in
frequencies near
![]() .
Therefore, for
.
Therefore, for
![]() successive hits to the same pixel should be almost fully correlated.
When
successive hits to the same pixel should be almost fully correlated.
When ![]() is much below the spin period, hits from different spin periods should
be almost uncorrelated. Thus we can estimate the unmodeled 1/f noise
map rms in the same manner as the white noise baseline map, as
is much below the spin period, hits from different spin periods should
be almost uncorrelated. Thus we can estimate the unmodeled 1/f noise
map rms in the same manner as the white noise baseline map, as
When
Table 11: rms of the unmodeled 1/f noise maps.
6.3.3 Ideal scanning
We define ideal scanning so that the pointings from
the different scan circles of the same repointing period fall on top of
each other, i.e., there is no nutation and the sampling is
synchronized with the spin period. In this case, the part of the
unmodeled 1/f noise for long baselines (
![]() a multiple of the
spin period) that is modeled by 1 min baselines gets totally
averaged out, so that the contribution from unmodeled 1/f noise
to residual maps would stay constant from
a multiple of the
spin period) that is modeled by 1 min baselines gets totally
averaged out, so that the contribution from unmodeled 1/f noise
to residual maps would stay constant from
![]() min
to
min
to ![]() h. In our nonideal
case, some of this noise leaks out, so that the unmodeled
contribution rises slowly in this range also. See dashed red line in
Fig. 26.
h. In our nonideal
case, some of this noise leaks out, so that the unmodeled
contribution rises slowly in this range also. See dashed red line in
Fig. 26.
Likewise, for an ideal scanning, the white noise reference baselines make an equal contribution to the map for any baseline length that is an integer multiple of the spin period, and fits into the repointing period an integer number of times.
6.3.4 Total noise
From Fig. 26
we see that the two dominant contributions to the residual maps are the
white noise reference baselines and the unmodeled 1/f noise.
For both of them we have
analytical estimates, and both of them map from time domain to map
domain in roughly the same way. Thus we get an analytical estimate for
the residual I map rms by multiplying the
![]() estimate from Eqs. (49)
and (53)
with
estimate from Eqs. (49)
and (53)
with
![]() for
for ![]() min.
When
min.
When ![]() and
and ![]() ,
so that
,
so that ![]() ,
we have
,
we have
This gives for our case (
where
However, this estimate is not as good as in the time domain,
since the importance of the neglected components, the baseline errors,
has grown dramatically when going from the time domain to the map
domain. See Fig. 26.
Since these components rise towards shorter baselines, the residual map
rms is minimized at a somewhat larger
![]() than Eq. (58)
gives.
than Eq. (58)
gives.
6.4 Pixelization noise and signal baselines
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{1236132a.ps} \includ...
...ip]{1236132e.ps} \includegraphics[width=4.3cm,clip]{1236132f.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg457.png)
|
Figure 32:
Signal baseline I ( top), Q
( middle), and U (
bottom) maps
|
| Open with DEXTER | |
For pixelization noise, already the reference baselines are strongly correlated (see Fig. 23) and therefore their map rms cannot be estimated like for white noise reference baselines and unmodeled 1/f noise. Due to these correlations their impact in the map level is significantly larger than their small variance in the time level (see Table 7) would indicate. Instead, for both the pixelization noise reference baselines and the signal baseline error, the situation is similar to white noise and 1/f noise baseline error.
For the residual 1/f and white noise
baselines, the Q and U maps
look the same as the I maps, just with a
factor ![]() larger amplitude, since they originate from the
same time-domain noise, which is independent for each detector.
larger amplitude, since they originate from the
same time-domain noise, which is independent for each detector.
For the signal baselines (see Fig. 32)
the situation is, however, different, since they originate from the
signal, where Q and U are much
smaller than I. We also note that Q
is much larger than U, although they are of same
magnitude in the signal. This is related to the coordinate dependence
of the definition of the Stokes parameters Q
and Utogether with a combination of factors
in our study. First, the signal contains only E mode
polarization, which means that Q has structures
along the coordinate lines, whereas U has
structures oriented ![]() from them. Second, we are using ecliptic coordinates, and we have
employed a scanning strategy, where the scanning goes almost parallel
to the lines of longitude for a large part of the sky. The signal
baselines originate from the signal gradients within pixels. For a
signal structure oriented along the scanning direction, the signal
gradient structure remains similar for a sequence of pixels along the
scanning. Thus the measurement differences between different scans
through these pixels are similar for a sequence of pixels, favoring
their misinterpretation as noise baselines.
from them. Second, we are using ecliptic coordinates, and we have
employed a scanning strategy, where the scanning goes almost parallel
to the lines of longitude for a large part of the sky. The signal
baselines originate from the signal gradients within pixels. For a
signal structure oriented along the scanning direction, the signal
gradient structure remains similar for a sequence of pixels along the
scanning. Thus the measurement differences between different scans
through these pixels are similar for a sequence of pixels, favoring
their misinterpretation as noise baselines.
Table 12: Effect of the coordinate system on the signal baseline maps.
To verify the effect of the coordinate system, we redid the
![]() h
and 1 min cases using galactic coordinates. See Table 12
(E = ecliptic, G = galactic). Note that the map rms
is given in nK (not in
h
and 1 min cases using galactic coordinates. See Table 12
(E = ecliptic, G = galactic). Note that the map rms
is given in nK (not in ![]() K, like the other tables). P stands
for
K, like the other tables). P stands
for ![]() .
We see that the asymmetry between Q and U
largely disappears, but the total polarization signal residual is not
much affected. For the temperature residual we see a small improvement.
This is partly explained by the reduction of the signal baseline
variance, seen in
Table 7.
.
We see that the asymmetry between Q and U
largely disappears, but the total polarization signal residual is not
much affected. For the temperature residual we see a small improvement.
This is partly explained by the reduction of the signal baseline
variance, seen in
Table 7.
6.5 Residuals at different angular scales
The residual map rms alone is a poor measure of the quality of the output map. Since the nature of the residual (see Figs. 29 and 30) is different for different baseline lengths, we need to look at the structure of the different map residuals in more detail.
For long baselines, the residual mostly comes from the part of
the 1/f noise that cannot be modeled with
baselines, and appears mostly at very small angular scales on the map,
near the pixel
scale; whereas for shorter baselines it comes from unwanted baselines,
which appear as larger scale structures. This can be seen from
Fig. 27,
where we have smoothed the
residual map with the detector beam, before taking the rms. This
smoothing almost erases the difference between the 1/f residuals
for baseline lengths from ![]() min
to 1 h. This is
because the 1 min scanning circles fall almost on top of each
other during the 1 h repointing period, and the width (due to
nutation) of the ring on the sky traced by the beam center during a
repointing period is less than the beam width. Beam-smoothing has much
less effect on the white noise baseline map and the signal baseline
map. Baseline lengths
min
to 1 h. This is
because the 1 min scanning circles fall almost on top of each
other during the 1 h repointing period, and the width (due to
nutation) of the ring on the sky traced by the beam center during a
repointing period is less than the beam width. Beam-smoothing has much
less effect on the white noise baseline map and the signal baseline
map. Baseline lengths ![]() s
to 15 s still give the smallest total residuals, but the
difference from longer baselines is much reduced by beam-smoothing.
Since residuals at larger scales are for most purposes more harmful
than sub-beam residuals on the map, we conclude that it is better to
choose a somewhat longer baseline than
what would minimize the residual map rms.
s
to 15 s still give the smallest total residuals, but the
difference from longer baselines is much reduced by beam-smoothing.
Since residuals at larger scales are for most purposes more harmful
than sub-beam residuals on the map, we conclude that it is better to
choose a somewhat longer baseline than
what would minimize the residual map rms.
6.6 Angular power spectra of map residuals
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1236133a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{1236133b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg460.png)
|
Figure 33:
Angular power spectra of the residual temperature maps for different
baseline lengths: 1 h ( black),
4 min ( blue dashed), 1 min (
light blue), 30 s ( light green),
15 s ( green), 7.5 s (
pink), and 5 s ( red dashed). The
black horizontal line is the white noise
level and the black dot-dashed line is the
theoretical CMB input spectrum smoothed with the beam and pixel window
functions. Top: residual map including white
noise,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1236134a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{1236134b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg461.png)
|
Figure 34: Same as Fig. 33 bottom panel, but for the polarization E and B mode spectra. |
| Open with DEXTER | |
Since we are considering full-sky maps, their angular power
spectra
![]() can be calculated directly
from them (we used anafast
of the HEALPix package).
can be calculated directly
from them (we used anafast
of the HEALPix package).
We plot the angular power spectra of the residual maps in
Figs. 33
and 34
for different baseline lengths. It is clear that baselines
shorter than ![]() s,
lead to more large scale structure in the residuals. Long baselines
lead to a high-
s,
lead to more large scale structure in the residuals. Long baselines
lead to a high-![]() tail in the residual that appears much like white noise (flat
tail in the residual that appears much like white noise (flat ![]() ).
).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1236135a.eps}\vspace*{1mm}
...
...eps}\vspace*{1mm}
\includegraphics[width=7cm,clip]{1236135d.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg463.png)
|
Figure 35:
Angular temperature power spectra
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{1236136a.eps}\vspace*{1mm}...
...s}\vspace*{1mm}
\includegraphics[width=7.1cm,clip]{1236136d.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg464.png)
|
Figure 36:
Same as Fig. 35
but for the E mode polarization
spectrum
|
| Open with DEXTER | |
In Figs. 35
and 36
we show angular power spectra
![]() and
and
![]() of different map components
for the cases
of different map components
for the cases ![]() h,
1 min, 15 s, and 5 s.
h,
1 min, 15 s, and 5 s.
For baselines that are multiples of the spin period
(1 min and 1 h) we see the characteristic even-odd
variation in the ![]() of the baseline components. If the scanning circles had the full
of the baseline components. If the scanning circles had the full ![]() radius,
they would contribute only to the even multipoles. In our case the
circle radius is
radius,
they would contribute only to the even multipoles. In our case the
circle radius is
![]() ,
and therefore we see a beat pattern, where the maximum even-odd
multipole difference occurs at multipoles
,
and therefore we see a beat pattern, where the maximum even-odd
multipole difference occurs at multipoles ![]() that are near multiples of
that are near multiples of
![]() .
For the low
.
For the low ![]() of the unmodeled 1/f contribution we see
the
opposite pattern, since the unmodeled 1/f contains
mostly frequencies which vary just over those timescales over which the
baseline contributions are constant.
of the unmodeled 1/f contribution we see
the
opposite pattern, since the unmodeled 1/f contains
mostly frequencies which vary just over those timescales over which the
baseline contributions are constant.
The angular power spectrum of full-circle uncorrelated
baselines goes as
(Eftstathiou 2005). Therefore we have plotted
The other contributions have different angular scale
dependencies, related to the correlations between baselines. We see
that the baseline error components have steeper spectra than the
reference baseline and unmodeled 1/f contributions.
This makes them important at large scales (low multipoles), where they
are comparable or even stronger than the white noise reference baseline
and unmodeled 1/f components, which
dominate at high ![]() and contribute most to the residual map rms. If one considers just the
signal baselines, the baseline error completely dominates over the
reference baselines for short
and contribute most to the residual map rms. If one considers just the
signal baselines, the baseline error completely dominates over the
reference baselines for short
![]() and low
and low ![]() .
.
For long baselines (![]() min or longer), the
unmodeled 1/f noise dominates the residuals
for
min or longer), the
unmodeled 1/f noise dominates the residuals
for ![]() ,
but the 1/f baseline error contribution can
be comparable for
,
but the 1/f baseline error contribution can
be comparable for ![]() .
For
shorter baselines, the white noise baselines become more important.
.
For
shorter baselines, the white noise baselines become more important.
The ![]() spectra of different residual components look qualitatively
like
spectra of different residual components look qualitatively
like
![]() ,
except for the signal baseline components, which have less power,
reflecting the lack of B-mode signal in the input. Therefore we have
not plotted the
,
except for the signal baseline components, which have less power,
reflecting the lack of B-mode signal in the input. Therefore we have
not plotted the ![]() spectra,
except for these signal baseline components, which we have included in
Fig. 36
along with the
spectra,
except for these signal baseline components, which we have included in
Fig. 36
along with the ![]() spectra.
spectra.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1236137a.eps}\vspace*{3mm}...
...s}\vspace*{1mm}
\includegraphics[width=8.5cm,clip]{1236137c.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg474.png)
|
Figure 37:
Square roots of the cumulative angular power spectra (see
Eqs. (88)
and (89))
for the residual temperature ( top panel) and
polarization ( middle) maps and TE correlation
( bottom), up to a given multipole |
| Open with DEXTER | |
Because of large ![]() -to-
-to-![]() variations in the residual
variations in the residual ![]() ,
these plots are difficult to read. Therefore we also plot
(Fig. 37)
square roots of the cumulative angular power
spectra,
,
these plots are difficult to read. Therefore we also plot
(Fig. 37)
square roots of the cumulative angular power
spectra,
which give the total contribution to the residual I and P map rms from multipoles up to
The beam fwhm
Figure 37
provides probably the most concise meaningful comparison of the quality
of maps vs. baseline length. The
![]() s
case appears the best in terms of cumulative residual power in the map
for the relevant multipoles. Although
s
case appears the best in terms of cumulative residual power in the map
for the relevant multipoles. Although
![]() s
produces a smaller
residual map rms, it is only because of its small sub-beam-scale
residuals. Interestingly, the
s
produces a smaller
residual map rms, it is only because of its small sub-beam-scale
residuals. Interestingly, the
![]() h
baseline seems to be the best for minimizing residual
temperature-polarization
correlations at intermediate scales. It is also better overall
than the
h
baseline seems to be the best for minimizing residual
temperature-polarization
correlations at intermediate scales. It is also better overall
than the ![]() min
and 4 min cases for
min
and 4 min cases for ![]() .
.
If one is only interested in large-scale features
(low ![]() )
there are no big differences between any of the baseline lengths from
15 s to 1 h, but 10 s or less
should be avoided. For the lowest
multipoles there is some randomness in the results, since we studied
only one noise realization, so one should not try to draw
conclusions from the small differences seen there for
)
there are no big differences between any of the baseline lengths from
15 s to 1 h, but 10 s or less
should be avoided. For the lowest
multipoles there is some randomness in the results, since we studied
only one noise realization, so one should not try to draw
conclusions from the small differences seen there for
![]() s
to 1 h. (The noise residuals, for the cases
s
to 1 h. (The noise residuals, for the cases
![]() min
and
min
and ![]() s
with noise prior, have been studied via Monte Carlo in
Keskitalo et al. 2009.)
s
with noise prior, have been studied via Monte Carlo in
Keskitalo et al. 2009.)
The signal baseline contributions appear a minor effect at all scales. In this study the signal contained only the CMB. In reality, the gradients in the signal are often dominated by foregrounds, and therefore the signal baseline effect is larger. Foreground signals are considered in Keihänen et al. (2009). Foregrounds were also included in the map-making studies of Ashdown et al. (2007b,2009), and especially in the former there was a detailed study on the signal baseline contribution and how it could be minimized.
Map residuals influence the precision at which we are able to
determine the angular power spectrum of the CMB map. We can subtract
the expectation value of the ![]() of the residual from the map
spectrum, but individual realizations deviate from this expectation
value, leading to an error in the CMB
of the residual from the map
spectrum, but individual realizations deviate from this expectation
value, leading to an error in the CMB ![]() estimate. A multipole
estimate. A multipole
![]() of a map has
at best
of a map has
at best ![]() degrees of freedom.
Statistically isotropic signals (e.g. CMB or a white noise map of
uniform pixel variance) have these degrees of freedom. Deviations
from the statistical isotropy may lead to correlations in the
m-modes of a multipole which in turn decreases the
degrees of
freedom and therefore increase the error in
degrees of freedom.
Statistically isotropic signals (e.g. CMB or a white noise map of
uniform pixel variance) have these degrees of freedom. Deviations
from the statistical isotropy may lead to correlations in the
m-modes of a multipole which in turn decreases the
degrees of
freedom and therefore increase the error in ![]() .
Fortunately
the strongest correlations of the map residuals occur nearly along
the ecliptic meridians. Correlations along meridians do not lead to
correlations in the m-modes. Therefore we can
expect that the
m-mode couplings due to map residuals are weak and
the excess
spectrum error is small. For now, we did not investigate these
errors any further, but decided to leave this for future studies.
.
Fortunately
the strongest correlations of the map residuals occur nearly along
the ecliptic meridians. Correlations along meridians do not lead to
correlations in the m-modes. Therefore we can
expect that the
m-mode couplings due to map residuals are weak and
the excess
spectrum error is small. For now, we did not investigate these
errors any further, but decided to leave this for future studies.
6.7 Low multipoles of I, Q, and U maps
For cosmological purposes, one calculates the
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() angular power
spectra of the output maps, which represent the fundamental properties
of the temperature and polarization field, and are coordinate
independent. However, for analyzing residual map structure, it may be
more intuitive to consider the Q and U maps
as two separate maps of a scalar quantity, and calculate their ordinary
(spin-0) angular power spectra.
angular power
spectra of the output maps, which represent the fundamental properties
of the temperature and polarization field, and are coordinate
independent. However, for analyzing residual map structure, it may be
more intuitive to consider the Q and U maps
as two separate maps of a scalar quantity, and calculate their ordinary
(spin-0) angular power spectra.
The Q and U are given
in terms of the ![]() and
and ![]() as (Zaldarriaga & Seljak 1997)
as (Zaldarriaga & Seljak 1997)
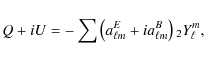
|
(90) |
where the
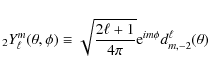
|
(91) |
are the spin-2 spherical harmonics (Newman & Penrose 1966; Goldberg et al. 1967) and the
Thus the monopoles ![]() and
and ![]() of the Q and U maps
are given by
of the Q and U maps
are given by
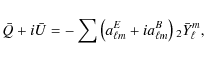
|
(92) |
where
|
|
|||
| = | 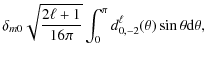
|
(93) |
which are real. Thus the Q and U monopoles are
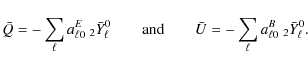
|
(94) |
Since in our case the input spectrum contained no B mode, the monopole vanishes in the input U map.
Figure 38 illustrates the effect of destriping on the I, Q, and U maps. Destriping is not able to remove the noise monopole of the I map (the monopole does change but does not become small), but the noise monopoles of Q and U maps are removed, about equally well as the other low multipoles.
The low multipoles of the residual maps are shown in Fig. 39, divided by the white noise level. We see that the residuals at lowest multipoles are larger than the white noise level. The baseline length does not make a large difference for these low multipoles, except that too short baselines (less than 15 s, not included in Fig. 39) should be avoided.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f38.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg496.png)
|
Figure 38:
Effect of destriping on the low multipoles of I (
blue), Q( red), and U
( green) maps. The solid lines
give the multipoles of the binned signal (CMB) map, where the monopoles
of I and U, and the dipole of I
should ideally
vanish in our case. The dashed lines are for the
naive binned map including the noise, and the dot-dashed
lines are for the destriped (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1236139a.eps}\vspace*{5mm}
\includegraphics[width=8.5cm,clip]{1236139b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg497.png)
|
Figure 39: The I, Q, and U low multipoles of the residual maps (with binned white noise subtracted) for different baseline lengths: 1 h ( black), 4 min ( blue), 1 min ( light blue), 30 s ( light green), and 15 s ( dark green). For this plot they are divided by the white noise level. The top panel shows I, the bottom panel Q ( solid) and U ( dashed). |
| Open with DEXTER | |
7 Effect of noise knee frequency
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12361f40.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg498.png)
|
Figure 40: Effect of knee frequency on the residual noise in the I map. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1236141a.eps}\vspace*{5mm}
\includegraphics[width=8.5cm,clip]{1236141b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg499.png)
|
Figure 41:
Same as Fig. 39,
but for a lower knee frequency
|
| Open with DEXTER | |
The importance of the correlated 1/f noise depends
on its amplitude and spectrum. In this paper we do not consider the
effect of possible spectral features in the noise, and we have
parameterized the noise just by the 1/f slope
![]() ,
knee frequency
,
knee frequency ![]() ,
and white noise level. Since we produced the simulated 1/f noise
separately from the white noise, we can change
,
and white noise level. Since we produced the simulated 1/f noise
separately from the white noise, we can change ![]() simply by multiplying the 1/f part by
simply by multiplying the 1/f part by
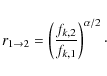
|
(95) |
This will change the residual 1/f contribution to the residual map by the same factor, while the white noise baseline and signal baseline contributions are unaffected (unless one changes to a different
In Fig. 40
we show also the rms of the binned 1/f noise
map. As we lower ![]() it moves down. For very small
it moves down. For very small ![]() it would fall below the white noise baseline rms. At this point simple
binning would produce a better result than destriping. For our
simulated 1/f noise, and for long
baselines, this would happen at the extremely low
it would fall below the white noise baseline rms. At this point simple
binning would produce a better result than destriping. For our
simulated 1/f noise, and for long
baselines, this would happen at the extremely low
![]() Hz.
It should be noted however, that in our case the binned 1/f rms
is heavily dominated by the lowest frequencies, and in other cases
(smaller slope
Hz.
It should be noted however, that in our case the binned 1/f rms
is heavily dominated by the lowest frequencies, and in other cases
(smaller slope ![]() ,
larger
,
larger
![]() )
the relevant 1/f rms could be smaller for a
given
)
the relevant 1/f rms could be smaller for a
given ![]() ,
so that simple binning could become superior already at
a higher
,
so that simple binning could become superior already at
a higher ![]() .
.
In Fig. 41
we show the low multipoles of the residual I, Q,
and U maps recalculated for
![]() mHz.
mHz.
8 Effect of noise prior
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f42.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg507.png)
|
Figure 42:
Same as the bottom panel of Fig. 25,
but the solid lines correspond to using a noise prior. The dashed lines
are from Fig. 25,
and correspond to the case without noise prior. Black
lines show the rms of the residual I map
without the binned white noise component. Red is
for the unmodeled 1/f map, blue
for the white noise baseline
map, and green for the signal baseline map. The
noise prior has practically no effect for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f43.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg508.png)
|
Figure 43:
Same as top panel of Fig. 37 but for the
case of using the noise prior. The colors and linestyles are the same
as in Fig. 37,
except we have added the
|
| Open with DEXTER | |
Although short baselines can potentially model correlated noise better,
they fail because of the large random amplitudes they pick from white
noise. This can be remedied by applying prior
information on the noise spectrum to prevent too large differences
between amplitudes of nearby baselines. This is discussed in detail in
Keihänen at al. (2009),
but we give a short preview of the results here. See Figs. 42-44.
The noise prior has little effect for
![]() ,
but for short baselines the effect is dramatic. We note that now the
results keep improving as the baseline is shortened, at least until
,
but for short baselines the effect is dramatic. We note that now the
results keep improving as the baseline is shortened, at least until
![]() s,
the shortest we tried. (Using very short baselines with the noise prior
makes the code more resource intensive.) For the very lowest
multipoles, the results with the short baselines do not, however,
become much better than the ones obtained with longer baselines (with
or without noise filter). Compare
Figs. 44
to 39
and 41.
s,
the shortest we tried. (Using very short baselines with the noise prior
makes the code more resource intensive.) For the very lowest
multipoles, the results with the short baselines do not, however,
become much better than the ones obtained with longer baselines (with
or without noise filter). Compare
Figs. 44
to 39
and 41.
9 Maps from shorter survey segments
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f44.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg510.png)
|
Figure 44:
Same as Fig. 39,
but with the noise prior, and using a short baseline
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f45.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg511.png)
|
Figure 45: Same as the bottom panel of Fig. 25, but now we have included results from 7-month ( dashed) and 1-month ( dot-dashed) survey segments also. The 1-month results show averages from all 12 months of the survey. |
| Open with DEXTER | |
We now consider making maps from a shorter time segment of the data. In a full year of observations, for a P LANCK-like scanning strategy, all parts of the sky are looked at two different seasons. About 7 months is needed to observe the full sky. Maps from a shorter segment cover just a part of the sky.
When maps are made from a shorter observation period, the number of crossing points is reduced and their pattern is different. Destriping 7 months of data differs qualitatively from the case of a full year, since for a large part of the sky the second-season observations are missing. We expect the loss of the corresponding crossing points to result in a loss of output map quality due to larger baseline errors. Destriping relies then more on the crossing points which are near the ecliptic poles. When the observation period is shortened further, only part of the sky is covered. Since the crossing point structure is not necessarily changed qualitatively, we expect the map quality to worsen more slowly as a function of survey duration. Because of the cycloidal scanning strategy, the crossing point structure, however, changes with a 6-month period, so it will be different for different weeks or months.
In Fig. 45 we
show the residual I map rms as a function
of ![]() for 1-month, 7-month, and 1-year surveys. The results for the Q
and U maps look qualitatively the same,
except that the signal baseline contribution is, of course, much lower.
We have excluded all pixels with rcond
for 1-month, 7-month, and 1-year surveys. The results for the Q
and U maps look qualitatively the same,
except that the signal baseline contribution is, of course, much lower.
We have excluded all pixels with rcond ![]() or
or ![]() from the residual maps.
from the residual maps.
There are basically two kinds of effects contributing to these
results. The more trivial effect is that of the lower hit count. The
average number of hits per pixel in the 7-month survey is 7/12
of that of the full-year survey, so we expect that alone to increase
the residual map rms by a factor of
![]() .
This, indeed, accounts for most of the change in the unmodeled 1/f contribution
to the residual map rms. When the survey segment is shortened below
7 months, the number of included pixels falls almost in line
with the number of samples, so the hit count per pixel stays now
roughly constant, and there is not much additional effect when going
from 7 months to 1 month.
.
This, indeed, accounts for most of the change in the unmodeled 1/f contribution
to the residual map rms. When the survey segment is shortened below
7 months, the number of included pixels falls almost in line
with the number of samples, so the hit count per pixel stays now
roughly constant, and there is not much additional effect when going
from 7 months to 1 month.
The other effect is that of the change in the pattern of crossing points on solving the baselines. This shows clearly in the white noise baseline and signal baseline contributions, where baseline errors were important already for the full 1-year survey. Here the change from 7 months to 1 month brings also a significant change. A closer inspection of the different months reveals, however, that it is only some of the months that are clearly worse than the 7-month case.
| Figure 46: Linear hit maps near the ecliptic North Pole for the one-month surveys corresponding to the first ( left) and second ( right) month of the full year survey. |
|
| Open with DEXTER | |
The first and the second month represent the two extreme cases. See Fig. 46. Note how different is the structure of crossing points between these two months. The same happens near the South Pole. For the first month we are close to the situation where all scanning circles cross each other at the same pixel. The effect of this is the most striking for the signal baseline component, for which it couples to the signal gradients in those few pixels where the circles cross and the pattern of hits within those pixels. In the second month the crossings are spread over a wide arc.
To study the effect of the length of the survey segment, and
also its timewise location with respect to the cycloid, we fixed the
baseline length to ![]() min,
and considered survey segments of 1, 2, 4, 6, 8, 10, 16, 24,
32, 40, 48, 64, 128, 256, and 366 days. We also considered the
effect of extending the mission to 488 days
(16 months). Moreover, for each survey segment length (except
the 16 month one) we considered three different starting
points for the segment. To separate the effect of the change
in hit count from the effect of crossing point structure on solving
baselines, we plot first the rms of the binned white noise map, which
has only the
first effect, in Fig. 47.
min,
and considered survey segments of 1, 2, 4, 6, 8, 10, 16, 24,
32, 40, 48, 64, 128, 256, and 366 days. We also considered the
effect of extending the mission to 488 days
(16 months). Moreover, for each survey segment length (except
the 16 month one) we considered three different starting
points for the segment. To separate the effect of the change
in hit count from the effect of crossing point structure on solving
baselines, we plot first the rms of the binned white noise map, which
has only the
first effect, in Fig. 47.
The binned white noise map rms is given by
![]() ,
calculated over the included pixels. Thus it falls and rises in inverse
relation to the mean hit count. In Fig. 47
we see it first falling, since additional rings partially overlap
preceding rings and thus do not bring in new pixels to the map as fast
as new samples accumulate. The rms begins to rise after the first three
months since the cycloidal scanning strategy brings then the satellite
spin axis south of the ecliptic, where the spin axis repointing step is
larger, causing new pixels to be added to the map at a faster rate than
when the spin axis was north of the ecliptic. After a little over half
a year, the whole sky is covered, and new
samples just increase the hit count causing the rms to fall.
,
calculated over the included pixels. Thus it falls and rises in inverse
relation to the mean hit count. In Fig. 47
we see it first falling, since additional rings partially overlap
preceding rings and thus do not bring in new pixels to the map as fast
as new samples accumulate. The rms begins to rise after the first three
months since the cycloidal scanning strategy brings then the satellite
spin axis south of the ecliptic, where the spin axis repointing step is
larger, causing new pixels to be added to the map at a faster rate than
when the spin axis was north of the ecliptic. After a little over half
a year, the whole sky is covered, and new
samples just increase the hit count causing the rms to fall.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f47.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg517.png)
|
Figure 47:
Binned white noise map rms as a function of survey length for
|
| Open with DEXTER | |
To see the second effect, we consider the ratio of the residual map rms to the rms of the binned white noise map from the same data. This tells us how well we are doing compared to the white noise level. See Fig. 48. We see that for all three starting points, the relative map quality consistently improves after 128 days with further increase in the survey length up to a full year. The relative quality (with respect to binned white noise) of the 16-month map is the same as the 12-month map.
For shorter survey pieces the behavior as a function of survey length depends on the starting point. For Q and U, short segments, 10 days or less, are clearly much worse than longer ones. For the I map, the relative quality in some cases worsens with time up to about 40 days. This is related to the changing pattern of crossing points in the cycloidal strategy. For some periods of time the pattern is more ill-conditioned and adding data from such a period to another short period makes things worse rather than better. From Fig. 49 we can conclude that one such period is somewhere between days 1 and 24 and another somewhere between days 70 and 101 of the simulated mission, since the residual I map rms is increasing during those periods. These coincide with the times when the cycloidal scanning strategy is producing a clustering of crossing points of nearby scanning rings at the corners of caustics around ecliptic poles. The baselines can be better solved from a more widely distributed set of crossing points (Wright 1996). We can see from Fig. 48, that the unmodeled 1/f and reference baseline contributions stay relatively constant, so the variation indeed comes from baseline error.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1236148a.eps}\vspace*{3mm}
\par\includegraphics[width=8.5cm,clip]{1236148b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg518.png)
|
Figure 48:
Ratio of the residual map rms to the binned white noise map rms (see
Fig. 47)
as a function of survey length for
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.5cm,clip]{12361f49.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg519.png)
|
Figure 49: The top panel of Fig. 48 replotted so that the horizontal axis corresponds to the distance of the end of the included data from the beginning of the simulated mission, so only for the case of the first starting point does it correspond to the length of the data used. |
| Open with DEXTER | |
10 Conclusions
We have described our destriping map-making method (Polar/Madam) for
CMB surveys. The method has a parameter, the baseline
length
![]() ,
that affects the performance of the method. With long
baselines, the Madam code is faster and requires less computer memory.
The computer time and memory requirements of the code are discussed in
Ashdown et al. (2009),
where it is compared
to other codes and methods.
,
that affects the performance of the method. With long
baselines, the Madam code is faster and requires less computer memory.
The computer time and memory requirements of the code are discussed in
Ashdown et al. (2009),
where it is compared
to other codes and methods.
Here we have done a detailed analysis of the residual errors in maps produced with the method. In this paper we concentrated on destriping without a noise prior. For short baselines the results can be improved by utilizing prior information on the noise spectrum. This will be described in (Keihänen et al. 2009).
We have divided the destriping residuals into six components.
Three of them, white noise reference baselines, unmodeled 1/f noise,
and pixelization noise reference baselines, are easy to estimate
analytically from the noise power spectrum and the signal angular power
spectrum. In the map domain the baseline components appear as a
superposition of thin constant stripes of length
![]() ,
whereas the unmodeled 1/f noise varies
along such stripes with a period comparable to
,
whereas the unmodeled 1/f noise varies
along such stripes with a period comparable to
![]() .
.
The three other components are related to how accurately baselines can be solved from crossing points, and depend on the scanning strategy. These baseline error components are minimized when there are very many crossing points widely distributed. Especially when making partial sky maps from short survey segments around a time when ring crossings cluster in the same small region of the sky these errors may blow up. Since the baseline errors are correlated over long time scales, they produce wide bands in the map domain and are important for low multipoles.
The relevance of this analysis is that it guides us in what kind of noise residuals to expect in the maps for given detector noise spectra, and what baseline length to use in destriping map-making.
For long surveys, with a good distribution of crossing points,
the dominant residual error components are the white noise baselines
and unmodeled 1/f noise. Their combined
effect can be minimized, when the baseline length is chosen according
to Eqs. (58)
or (60),
which put it close to
![]() ,
where
,
where ![]() is the knee frequency of the noise. Because of the other error
components, one should choose a somewhat longer
baseline than this. (When a noise prior is used, shorter baselines are
better.)
is the knee frequency of the noise. Because of the other error
components, one should choose a somewhat longer
baseline than this. (When a noise prior is used, shorter baselines are
better.)
For a P LANCK-like scanning strategy, where the same circle of the sky is observed many times, the difference between baseline lengths from the spin period to the repointing period is mainly due to nutation, and is small when the nutation is small compared to the map pixel size. If the knee frequency is comparable to, or smaller than, the spin frequency, then the baseline length should be chosen from this range, if no noise prior is used. For a higher knee frequency the residual errors are larger, and a shorter baseline is better.
AcknowledgementsThe work reported in this paper was done by the CTP Working Group of the P LANCK Consortia. P LANCK is a mission of the European Space Agency. We thank K. Górski, C. R. Lawrence, and J. P. Leahy for useful comments. This work was supported by the Academy of Finland grants 205800, 213984, 214598, 121703, and 121962. We acknowledge the support by the ASI contracts ``P LANCK LFI Activity of Phase E2'' and I/016/07/0 ``COFIS''. R.K. is supported by the Jenny and Antti Wihuri Foundation. H.K.S. thanks Waldemar von Frenckells stiftelse, H.K.S. and T.P. thank the Magnus Ehrnrooth Foundation, and E.K. and T.P. thank the Väisälä Foundation for financial support. This work was supported by the European Union through the Marie Curie Research and Training Network ``UniverseNet'' (MRTN-CT-2006-035863). We thank CSC (Finland) for computational resources. We acknowledge use of the CAMB code for the computation of the theoretical CMB angular power spectrum. This work has made use of the P LANCK satellite simulation package (level S), which is assembled by the Max Planck Institute for Astrophysics P LANCK Analysis Centre (MPAC). Some of the results in this paper have been derived using the HEALPix package (Górski et al. 2005).
References
- Armitage, C., & Wandelt, B. D. 2005, Phys. Rev. D, 70, 123007 [NASA ADS] [CrossRef]
- Ashdown, M. A. J., Baccigalupi, C., Balbi, A., et al. 2007a, A&A, 467, 761 [NASA ADS] [CrossRef] [EDP Sciences]
- Ashdown, M. A. J., Baccigalupi, C., Balbi, A., et al. 2007b, A&A, 471, 361 [NASA ADS] [CrossRef] [EDP Sciences]
- Ashdown, M. A. J., Baccigalupi, C., Bartlett, J. G., et al. 2009, A&A, 493, 753 [NASA ADS] [CrossRef] [EDP Sciences]
- Borrill, J. 1999, in Proceedings of the 5th European SGI/Gray MPP Workshop, Bologna, Italy [arXiv:astro-ph/9911389]
- Burigana, C., & Sáez, D. 2003, A&A, 409, 423 [NASA ADS] [CrossRef] [EDP Sciences]
- Burigana, C., Seiffert, M., Mandolesi, N., & Bersanelli, M. 1997a, Int. Rep. TeSRE/CNR, 186/1997, March
- Burigana, C., Malaspina, M., Mandolesi, N., et al. 1997b, Int. Rep. TeSRE/CNR, 198/1997, November [arXiv:astro-ph/9906360]
- Challinor, A., Fosalba, P., Mortlock, D., et al. 2000, Phys. Rev. D, 62, 123002 [NASA ADS] [CrossRef]
- Couchot, F., Delabrouille, J., Kaplan, J., & Revenu, B. 1999, A&AS, 135, 579 [NASA ADS] [CrossRef] [EDP Sciences]
- de Gasperis, G., Balbi, A., Cabella, P., Natoli, P., & Vittorio, N. 2005, A&A, 436, 1159 [NASA ADS] [CrossRef] [EDP Sciences]
- Delabrouille, J. 1998, A&ASS, 127, 555 [NASA ADS] [CrossRef]
- Doré, O., Teyssier, R., Bouchet, F. R., Vibert, D., & Prunet, S. 2001, A&A, 374, 358 [NASA ADS] [CrossRef] [EDP Sciences]
- Dupac, X., & Tauber, J. 2005, A&A, 430, 363 [NASA ADS] [CrossRef] [EDP Sciences]
- Eftstathiou, G. 2005, MNRAS, 356, 1549 [NASA ADS] [CrossRef]
- Eftstathiou, G. 2007, MNRAS, 380, 1621 [NASA ADS] [CrossRef]
- Ganga, K. 1994, Ph.D. Thesis, http://spider.ipac.caltech.edu/staff/kmg/
- Goldberg, J. N., Macfarlane, A. J., Newman, E. T., Rohrlich, F., & Sudarshan, E. C. G. 1967, J. Math. Phys. (N.Y.), 8, 2155 [NASA ADS] [CrossRef]
- Górski, K. M., Wandelt, B. D., Hivon, E., Hansen, F. K., & Banday, A. J. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef]
- Harrison, D. L., van Leeuwen, F., & Ashdown, M. A. J. 2008, in preparation
- Keihänen, E., Kurki-Suonio, H., Poutanen, T., Maino, D., & Burigana, C. 2004, A&A, 428, 287 [NASA ADS] [CrossRef] [EDP Sciences]
- Keihänen, E., Kurki-Suonio, H., & Poutanen, T. 2005, MNRAS, 360, 390 [NASA ADS] [CrossRef]
- Keihänen, E., Keskitalo, R., Kurki-Suonio, H., et al. 2009, A&A, accepted [arXiv:0907.0367]
- Keskitalo, R., Ashdown, M. A. J., Cabella, P., et al. 2009, A&A, submitted [arXiv:0906.0175]
- Leahy, J. P., Bersanelli, M., D'Arcangelo, O., et al. 2009, A&A, submitted
- Maino, D., Burigana, C., Maltoni, M., et al. 1999, A&ASS, 140, 383 [NASA ADS] [CrossRef]
- Maino, D., Burigana, C., Górski, K. M., Mandolesi, N., & Bersanelli, M. 2002, A&A, 387, 356 [NASA ADS] [CrossRef] [EDP Sciences]
- Natoli, P., de Gasperis, G., Gheller, C., & Vittorio, N. 2001, A&A, 372, 346 [NASA ADS] [CrossRef] [EDP Sciences]
- Newman, E. T., & Penrose, R. 1966, J. Math. Phys. (N.Y.), 7, 863 [NASA ADS] [CrossRef]
- Planck Collaboration 2005, The Scientific Programme of P LANCK (``P LANCK Bluebook''), ESA-SCI, 2005, 1 [arXiv:astro-ph/0604069]
- Poutanen, T., Maino, D., Kurki-Suonio, H., Keihänen, E., & Hivon, E. 2004, MNRAS, 353, 43 [NASA ADS] [CrossRef]
- Poutanen, T., de Gasperis, G., Hivon, E., et al. 2006, A&A, 449, 1311 [NASA ADS] [CrossRef] [EDP Sciences]
- Press, W. H., Teukolsky, S. A., Wetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes, 2nd edn. (Cambridge: Cambridge University Press)
- Reinecke, M., Dolag, K., Hell, R., Bartelmann, M., & Ensslin, T. 2006, A&A, 445, 373 [NASA ADS] [CrossRef] [EDP Sciences]
- Revenu, B., Kim, A., Ansari, R., et al. 2000, A&ASS, 142, 499 [NASA ADS] [CrossRef]
- Sbarra, C., Carretti, E., Cortiglioni, S., et al. 2003, A&A, 401, 1215 [NASA ADS] [CrossRef] [EDP Sciences]
- Seiffert, M., Mennella, A., Burigana, C., et al. 2002, A&A, 391, 1185 [NASA ADS] [CrossRef] [EDP Sciences]
- Stompor, R., & White, M. 2004, A&A, 419, 783 [NASA ADS] [CrossRef] [EDP Sciences]
- Sutton, D., Johnson, B. R., Brown, M. L., et al. 2009, MNRAS, 393, 894 [NASA ADS] [CrossRef]
- Tuovinen, J. 2003, P LANCK Newsletter Number 4, 7 (www.rssd.esa.int/SA/PLANCK/docs/Newsletters/PlanckNewsletter4.pdf)
- van Leeuwen, F., Challinor, A. D., Mortlock, D. J., et al. 2002, MNRAS, 331, 975 [NASA ADS] [CrossRef]
- Varshalovich, D. A., Moskalev, A. N., & Khersonskii, V. K. 1988, Quantum Theory of Angular Momentum (Singapore: World Scientific)
- Wandelt, B. D., & Górski, K. M. 2001, Phys. Rev. D, 63, 123002 [NASA ADS] [CrossRef]
- Wright, E. L. 1996, Report UCLA-ASTRO-ELW-96-03, November [arXiv:astro-ph/9612006]
- Yvon, D., & Mayet, F. 2005, A&A, 436, 729 [NASA ADS] [CrossRef] [EDP Sciences]
- Zaldarriaga, M., & Seljak, U. 1997, Phys. Rev. D, 55, 1830 [NASA ADS] [CrossRef]
Footnotes
- ... LANCK
![[*]](/icons/foot_motif.png)
- http://www.rssd.esa.int/index.php?project=PLANCK
- ... CAMB
![[*]](/icons/foot_motif.png)
- http://camb.info
- ... HEALPix
![[*]](/icons/foot_motif.png)
- http://healpix.jpl.nasa.gov
All Tables
Table 1: Table of matrices.
Table 2: Statistics of the white noise baselines.
Table 3:
Stdev ![]() of white noise baseline error.
of white noise baseline error.
Table 4: Correlations between detectors 19 and 22.
Table 5:
Stdev ![]() of the unmodeled 1/f Stream.
of the unmodeled 1/f Stream.
Table 6:
Stdev ![]() of the 1/f Baseline Error.
of the 1/f Baseline Error.
Table 7: Stdev of contributions to signal baselines.
Table 8: rms of the white noise reference baseline maps.
Table 9: rms of the white noise baseline error maps.
Table 10: rms of the white noise baseline maps.
Table 11: rms of the unmodeled 1/f noise maps.
Table 12: Effect of the coordinate system on the signal baseline maps.
All Figures
![\begin{figure}
\par\hspace*{-1mm} \includegraphics[width=8.5cm,clip]{12361f1a.ep...
...ps}\vspace*{3mm}
\includegraphics[width=8.5cm,clip]{12361f1c.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg155.png)
|
Figure 1:
Input angular power spectrum. Black lines show the
theoretical |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{12361f2a.ps}\vspace*{2mm}
\includegraphics[angle=90,width=8.8cm,clip]{12361f2b.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg156.png)
|
Figure 2: Binned CMB signal map, I and Q, full sky. All maps in this paper are shown using the ecliptic coordinate system. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{12361f3a.ps} \includegraphics[width=4.3cm,clip]{12361f3b.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg157.png)
|
Figure 3:
Binned CMB temperature (I) signal maps from
two |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{12361f4a.ps} \includ...
...ip]{12361f4c.ps} \includegraphics[width=4.3cm,clip]{12361f4d.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg158.png)
|
Figure 4: Same as Fig. 3, but for the Stokes parameters Q ( top) and U ( bottom). |
| Open with DEXTER | |
| In the text | |
| |
Figure 5:
Hit map for the 1-year simulation. We show regions around the
ecliptic North Pole ( left) and South Pole (
right). The color scale is linear and goes from zero (blue)
to 50 000 (red). Lines of latitude are drawn at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361fg6.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg171.png)
|
Figure 6:
Power spectrum of the noise stream |
| Open with DEXTER | |
| In the text | |
| |
Figure 7:
Hit maps of the two |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{12361f8a.ps}\includegraphics[width=4.3cm,clip]{12361f8b.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg198.png)
|
Figure 8:
Destriped (output) temperature map (one year survey, 15 s
baselines) for the two |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{12361f9a.ps}\includegraphics[width=4.3cm,clip]{12361f9b.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg199.png)
|
Figure 9: Even near the ecliptic poles, where the noise in the output map is the lowest, the pixel-scale noise from four 70 GHz detectors is higher than the CMB polarization signal in the map. Left: binned signal Q map. Right: output Q map (15 s baselines). (Both plots are from the same pole region.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f10.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg249.png)
|
Figure 10:
First 15 minutes of the (1/f + white) noise
stream ( grey) and its reference ( black
solid) and solved ( black dashed)
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f11.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg258.png)
|
Figure 11:
Autocorrelation function for the white noise baseline error
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f12.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg259.png)
|
Figure 12:
Autocorrelation function for the white noise baseline error
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f13.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg262.png)
|
Figure 13:
First 10 min of the 1/f noise
stream
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1236114a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{1236114b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg270.png)
|
Figure 14:
The 1/f baseline error, i.e., the difference between
the solved and reference 1/f baselines
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f15.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg271.png)
|
Figure 15:
Power spectrum |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f16.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg294.png)
|
Figure 16: Same as Fig. 11, but now for the 1/f noise baseline error. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f17.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg295.png)
|
Figure 17:
The 1/f baseline error,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f18.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg298.png)
|
Figure 18:
Effect of baseline subtraction on the noise power spectrum. The
solid black line is the spectrum of the original noise
stream |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f19.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg302.png)
|
Figure 19:
Effect of subtracting both the white noise and the 1/f baselines
on the power spectrum of the 1/f noise. The
solid black line is the original 1/f spectrum.
The solid colored lines show the power spectra of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f20.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg320.png)
|
Figure 20:
Pixelization noise. In the top panel we show a
piece of the original signal stream |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f21.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg321.png)
|
Figure 21: Autocorrelation function of the pixelization noise. Note the alternating correlation and anticorrelation for small lags, and the correlations at 1 min lag, when the scanning returns to the same location on the sky. Due to spin rate variations the correlations are spread around the 1 min value, and more around 2 min. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{ \includegraphics[width=4.3cm,clip]{1236122a.ps} \includegraphics[width=4.3cm,clip]{1236122b.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg358.png)
|
Figure 22:
Pixelization noise rms in map pixels for the two |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1236123a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{1236123b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg366.png)
|
Figure 23:
Correlations in the signal baselines. The top panel
shows the
autocorrelation function of the reference baselines
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12361f24.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg368.png)
|
Figure 24: Linearity of destriping. The three thin black lines at the bottom shows the rms difference between the ``full'' map, obtained from the sum of the component TODs, and the sum of the component maps. This is compared to the signal and noise levels in the maps; different colors showing the different components and the thick black line the full map; different line styles correspond to the three Stokes parameters. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12361f25.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg381.png)
|
Figure 25:
Residual temperature map rms as a function of baseline length.
The top panel is for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12361f26.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg382.png)
|
Figure 26: Same as the bottom panel of Fig. 25, but now we have further separated the residual 1/f noise into unmodeled 1/f noise ( dashed) and 1/f baseline error ( dot-dashed); the white noise baselines into reference baselines ( dashed) and baseline error ( dot-dashed); and signal baselines (shown here in green) into reference baselines of pixelization noise ( dashed) and baseline error ( dot-dashed). The dotted lines show the rss of the dashed and dot-dashed lines. For white noise it falls on the solid line, showing that the two white noise residual map components are uncorrelated. For 1/f noise and pixelization noise the two components are positively correlated. The black dotted line is the analytical approximation Eq. (86). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12361f27.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg383.png)
|
Figure 27: The rms of the residual I, Q, and U maps, and their different components. The overall residual power in a destriped polarization map is higher than in a temperature map. The CMB signal residual in turn is much weaker. Note how Q is larger than U in the signal baselines. Smoothing the residual maps with a Gaussian beam ( dashed lines) removes excess power at sub-beam scales. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{12361f28.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg385.png)
|
Figure 28:
Residual I map including binned white noise,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{1236129a.ps}\vspa...
...*{1.5mm}
\includegraphics[angle=90,width=8.5cm,clip]{1236129d.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg386.png)
|
Figure 29:
Residual I map (with binned white noise
subtracted),
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{1236130a.ps} \includ...
...ip]{1236130c.ps} \includegraphics[width=4.3cm,clip]{1236130d.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg387.png)
|
Figure 30:
Same as Fig. 29
but for the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{ \includegraphics[width=4.3cm,clip]{1236131a.ps} \inclu...
...ip]{1236131e.ps} \includegraphics[width=4.3cm,clip]{1236131f.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg394.png)
|
Figure 31:
The six components of the residual I map
shown for the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{1236132a.ps} \includ...
...ip]{1236132e.ps} \includegraphics[width=4.3cm,clip]{1236132f.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg457.png)
|
Figure 32:
Signal baseline I ( top), Q
( middle), and U (
bottom) maps
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1236133a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{1236133b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg460.png)
|
Figure 33:
Angular power spectra of the residual temperature maps for different
baseline lengths: 1 h ( black),
4 min ( blue dashed), 1 min (
light blue), 30 s ( light green),
15 s ( green), 7.5 s (
pink), and 5 s ( red dashed). The
black horizontal line is the white noise
level and the black dot-dashed line is the
theoretical CMB input spectrum smoothed with the beam and pixel window
functions. Top: residual map including white
noise,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1236134a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{1236134b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg461.png)
|
Figure 34: Same as Fig. 33 bottom panel, but for the polarization E and B mode spectra. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1236135a.eps}\vspace*{1mm}
...
...eps}\vspace*{1mm}
\includegraphics[width=7cm,clip]{1236135d.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg463.png)
|
Figure 35:
Angular temperature power spectra
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{1236136a.eps}\vspace*{1mm}...
...s}\vspace*{1mm}
\includegraphics[width=7.1cm,clip]{1236136d.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg464.png)
|
Figure 36:
Same as Fig. 35
but for the E mode polarization
spectrum
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1236137a.eps}\vspace*{3mm}...
...s}\vspace*{1mm}
\includegraphics[width=8.5cm,clip]{1236137c.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg474.png)
|
Figure 37:
Square roots of the cumulative angular power spectra (see
Eqs. (88)
and (89))
for the residual temperature ( top panel) and
polarization ( middle) maps and TE correlation
( bottom), up to a given multipole |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f38.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg496.png)
|
Figure 38:
Effect of destriping on the low multipoles of I (
blue), Q( red), and U
( green) maps. The solid lines
give the multipoles of the binned signal (CMB) map, where the monopoles
of I and U, and the dipole of I
should ideally
vanish in our case. The dashed lines are for the
naive binned map including the noise, and the dot-dashed
lines are for the destriped (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1236139a.eps}\vspace*{5mm}
\includegraphics[width=8.5cm,clip]{1236139b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg497.png)
|
Figure 39: The I, Q, and U low multipoles of the residual maps (with binned white noise subtracted) for different baseline lengths: 1 h ( black), 4 min ( blue), 1 min ( light blue), 30 s ( light green), and 15 s ( dark green). For this plot they are divided by the white noise level. The top panel shows I, the bottom panel Q ( solid) and U ( dashed). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12361f40.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg498.png)
|
Figure 40: Effect of knee frequency on the residual noise in the I map. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1236141a.eps}\vspace*{5mm}
\includegraphics[width=8.5cm,clip]{1236141b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg499.png)
|
Figure 41:
Same as Fig. 39,
but for a lower knee frequency
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f42.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg507.png)
|
Figure 42:
Same as the bottom panel of Fig. 25,
but the solid lines correspond to using a noise prior. The dashed lines
are from Fig. 25,
and correspond to the case without noise prior. Black
lines show the rms of the residual I map
without the binned white noise component. Red is
for the unmodeled 1/f map, blue
for the white noise baseline
map, and green for the signal baseline map. The
noise prior has practically no effect for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f43.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg508.png)
|
Figure 43:
Same as top panel of Fig. 37 but for the
case of using the noise prior. The colors and linestyles are the same
as in Fig. 37,
except we have added the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f44.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg510.png)
|
Figure 44:
Same as Fig. 39,
but with the noise prior, and using a short baseline
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f45.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg511.png)
|
Figure 45: Same as the bottom panel of Fig. 25, but now we have included results from 7-month ( dashed) and 1-month ( dot-dashed) survey segments also. The 1-month results show averages from all 12 months of the survey. |
| Open with DEXTER | |
| In the text | |
| |
Figure 46: Linear hit maps near the ecliptic North Pole for the one-month surveys corresponding to the first ( left) and second ( right) month of the full year survey. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12361f47.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg517.png)
|
Figure 47:
Binned white noise map rms as a function of survey length for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1236148a.eps}\vspace*{3mm}
\par\includegraphics[width=8.5cm,clip]{1236148b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg518.png)
|
Figure 48:
Ratio of the residual map rms to the binned white noise map rms (see
Fig. 47)
as a function of survey length for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.5cm,clip]{12361f49.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12361-09/Timg519.png)
|
Figure 49: The top panel of Fig. 48 replotted so that the horizontal axis corresponds to the distance of the end of the included data from the beginning of the simulated mission, so only for the case of the first starting point does it correspond to the length of the data used. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



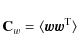
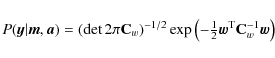
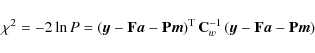
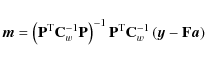
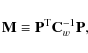
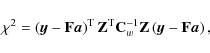
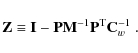
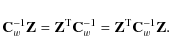
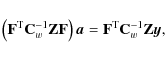
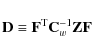
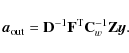
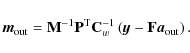
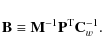
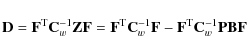
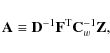
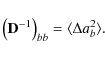
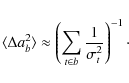
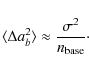
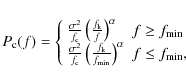
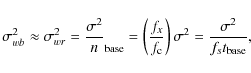
![\begin{displaymath}%
H(f) = \left[1- \frac {\sin^2 (\pi f t_{\rm base})} {(\pi f t_{\rm base})^2} \right]^2\cdot
\end{displaymath}](/articles/aa/full_html/2009/42/aa12361-09/img275.png)
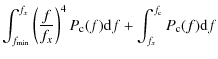
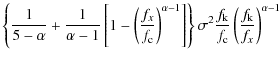
![$\displaystyle \sigma^2\left(\frac{f_{\rm k}}{f_{\rm c}}\right)^\alpha\left\{\fr...
...\alpha-1}\left[\left(\frac{f_{\rm c}}{f_x}\right)^{\alpha-1}
-1\right]\right\}.$](/articles/aa/full_html/2009/42/aa12361-09/img286.png)
![\begin{displaymath}%
\sigma_u^2 \approx \sigma^2\left(\frac{f_{\rm k}}{f_{\rm c}...
...ht)\left[\frac14
+\ln\frac{f_{\rm c}}{f_{\rm k}}\right]\cdot
\end{displaymath}](/articles/aa/full_html/2009/42/aa12361-09/img288.png)
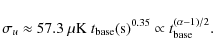
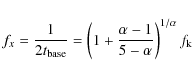
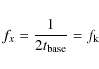
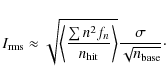
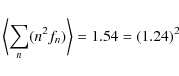
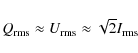
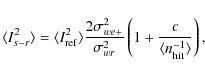
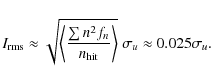
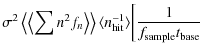
![$\displaystyle + ~\left(\frac{2f_{\rm k}}{f_{\rm sample}}\right)\left(2f_{\rm k}...
...base}\right)^{\alpha-1}
\left(\frac{4}{(5-\alpha)(\alpha-1)}\right)\biggr]\cdot$](/articles/aa/full_html/2009/42/aa12361-09/img452.png)