EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 506 / No 3 (November II 2009) A&A, 506 3 (2009) 1455-1467 Full HTML
Free Access
Issue
A&A
Volume 506, Number 3, November II 2009
Page(s) 1455 - 1467
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/200912306
Published online 03 September 2009

A&A 506, 1455-1467 (2009)

Search for cold debris disks around M-dwarfs. II

J.-F. Lestrade1 - M. C. Wyatt2 - F. Bertoldi3 - K. M. Menten4 - G. Labaigt5

1 - Observatoire de Paris - CNRS, 77 Av. Denfert Rochereau, 75014 Paris, France
2 - Institute of Astronomy, University of Cambridge, Cambridge, CB3 OHA, UK
3 - Argelander Institute for Astronomy, University of Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
4 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
5 - École Normale Supérieure de Cachan, 61 avenue du Président Wilson, 94235 Cachan, France

Received 8 April 2009 / Accepted 6 July 2009

Abstract
Although 70% of the stars in the Galaxy are M-dwarfs, thermal emission searches for cold debris disks have been conducted mostly for A-type and solar-type stars. We report on new $\lambda =1.2$ mm continuum observations of thirty M-dwarfs, using the MAMBO-2 bolometer array camera at the IRAM 30 m telescope. For a statistical analysis, we combine these data with our prior SCUBA and MAMBO-2 observations of 20 other M-dwarfs. Our sample consists of M-dwarfs in moving groups, with relatively young ages, and of nearby M-dwarfs with unknown ages. Only one cold debris disk (GJ842.2) was detected significantly. We compare the implied disk abundance constraints with those found in two comparable submillimeter surveys of 10 to 190 Myr old A- and FGK-type stars. For the 19 youngest (ages less than 200 Myr) M-dwarfs in our sample, we derive a cold disk fraction of 5.3+10.5-5.0%, compared to 15+11.5-11.5% for FGK-stars and 22+33-20% for A-stars. Hence, for this age group, there is an apparent trend of fewer cold disks for later stellar types. Although its statistical significance is marginal, this trend is strengthened by the deeper observations of our M-dwarf sample. We derive a cold disk fraction of <10% for the older (likely a few Gyr) M-dwarfs in our sample. Finally, although inconclusively related to a debris disk, we present the complex millimeter structure found around the position of the M 1.5 dwarf GJ526 in our sample.

Key words: stars: circumstellar matter - stars: low-mass, brown dwarfs - planetary systems: formation

1 Introduction

Cold debris disks around main sequence stars are left-over planetesimals (comets) that could not agglomerate into larger planets during the initial phase of planet formation. They are assembled as a belt within the periphery of the system in a manner analogous to the Kuiper Belt. The study of debris disks, including warm disks such as the asteroid belt in our Solar System, advances our knowledge of the origin and evolution of planetary systems around other stars, in a similar way to the study of the Kuiper Belt. It is well recognised that its present-day structure and dynamics retain important information about the formation and evolution of the Solar System. For example, the low mass and expanded size of the present-day Kuiper Belt can be traced back to the outward migrations of the giant planets, which exchanged orbital energy with an initially more compact and more massive disk (Hahn & Malhotra 1999; Tsiganis et al. 2005; Morbidelli et al. 2005; Gomes et al. 2005).

Our current understanding of debris disks was reviewed by Wyatt (2008). Mutual collisions between planetesimals in debris disks produce second-generation dust grains that are observable by means of their thermal emission or scattered light. Since the discovery of a first debris disk around the A0 main sequence star Vega by IRAS (Aumann et al. 1984), debris disks have been searched for photometrically with the infrared (IR) satellites IRAS, ISO, and Spitzer. In these observations, any flux excess above the photospheric level is interpreted as emission from warm (50-100 K) circumstellar dust.

By analyzing Spitzer observations, it was found that $ 32~\pm~5 \%$ of 160 A-dwarfs show a 70 $\mu $m excess (Su et al. 2006), while only $16^{+2.8}_{-2.9}\%$ of 225 observed FG-dwarfs show excess emission (Bryden et al. 2006; Trilling et al. 2008). Submillimeter photometry of A-to-G type stars with no detectable IRAS excess do however show cold (10-50 K) dust emission around some of them (Wyatt et al. 2003; Najita & Williams 2005). Imaging of scattered light with HST and of thermal continuum emission with SCUBA has measured disk radii between 50 and 150 AU (Smith & Terrile 1984; Kalas et al. 2005; Holland et al. 1998; Greaves et al. 2005); 22 debris disks have been imaged to date[*]. Azimuthal structures have been detected in a few of these disks and are thought to be caused by dust associated with planetesimals trapped in mean motion resonance with an orbiting planet (Wyatt 2003, 2006; Reche et al. 2008), or by dynamical perturbations from a distant stellar companion or passing stars (HD 141569A: Augereau & Paploizou 2004).

Although low-mass M-dwarfs are the most populous (70%) stars in the Galaxy, they have so far received little attention, mostly because their low luminosity makes the thermal emission and scattered light from their disks more difficult to detect. In a SCUBA survey of young stars of the $\beta$ Pic moving group and of the Local Association, Liu et al. (2004) detected the first two debris disks around M-dwarfs, AU Mic, and GJ182. Using SCUBA and MAMBO-2, Lestrade et al. (2006) surveyed 32 relatively young M-dwarfs of moving groups and newly detected one disk around the M 0.5 dwarf GJ842.2. Using Spitzer, Gautier et al. (2007) surveyed 62 nearby M-dwarfs at 24 $\mu $m, and subsamples of 41 at 70 $\mu $m and of 20 at 160 $\mu $m, and found no firm detection. AU Mic was also imaged in scattered light as an edge-on and structured disk (Liu 2004; Krist et al. 2005).

Here we present new MAMBO-2 observations of nearby M-dwarfs, and combined them with our previous survey to analyze a total sample of 50 M-dwarfs (Table 1) in terms of their cold debris disk abundance.

We present the new M-dwarfs surveyed in Sect. 2, we describe the observations in Sect. 3, and results for both debris disks and background sources in the fields of some of the M-dwarfs in Sect. 4. Finally, we compare the detected fraction of cold debris disks around the M-dwarfs of our sample with the fractions for other stellar types to discuss whether or not the characteristics of M-dwarfs - mass and luminosity lower than solar - impact the formation of debris disks around them or their detectability.

Table 1:   The 50 M-dwarfs of our (sub)mm surveys.

2 Sample of newly observed M-type dwarfs

To complement our first survey of M-dwarfs whithin moving groups of ages <600 Myr (Lestrade et al. 2006), we observed the most nearby M-dwarfs, irrespective of age. We selected single M-dwarfs at a distance of less than 6 pc and $\delta > -11^{\circ}$, and added five M-dwarfs binaries and six single M-dwarfs between 6 and 10 pc that are in common with the Spitzer survey by Gautier et al. (2007). The five binaries in our sample are: GJ725 (M 3 and M 3.5) separated by 15''  $(53~{\rm AU})$, GJ234 (M 4.5 and M 8) separated by 1''  $(5~{\rm AU})$, GJ412 (M 2 and M 6) separated by 32''  $(160~{\rm AU})$, GJ569 (M 2.5 and M 8.5) separated by 1''  $(10~{\rm AU})$, and GJ65 (M 5.5 and M 5.5) separated by 2''  $(5.2~{\rm AU})$. These angular separations are so small that a single MAMBO-2 map can cover both components. The ages of the targeted near-by M-dwarfs are presently unknown.

3 Observations

The diameter usually adopted for debris disks is 120 AU, which for near-by stars is larger than the IRAM 30-m telescope beam of 10.7'' FWHM at $\lambda =1.2$ mm. We therefore imaged each field with the 117-channel Max-Planck Bolometer array (MAMBO-2; Kreysa et al. 1998) of the 30 m telescope on Pico Veleta, Spain (2900 m). MAMBO-2 has a half-power spectral bandwidth from 210 to 290 GHz, with an effective frequency centered on 250 GHz (1.20 mm) for thermal emission spectra. The effective FWHM beam is 10.7'' and the undersampled field of view of the array is 4'. We used the standard on-the-fly mapping technique, where one map consists of 41 azimuthal subscans of 60 s each, with a scanning velocity of $\rm 4''/s$ and an elevation incremental step of 4'', while chopping the secondary mirror at 2 Hz by 60'' in azimuth. The bolometers are arranged in a hexagonal pattern with a beam separation of 22''. This scanning pattern produces time streams of data that are converted into a fully sampled spatial map with 3.5'' pixels. Our observations were completed within pooled observing runs spread over the winter and summer periods from 2005 to 2007. Atmospheric conditions were generally good during the observations, with typical zenith opacities between 0.1 and 0.3 at 250 GHz and low sky noise. The telescope pointing was checked before and after each map by using the same nearest bright point source, and was found to be stable to greater accuracy than 3'', except on a few occasions for which we discarded the data. The absolute flux calibration is based on observations of several standard calibration sources, including planets, and on a tipping curve (sky dip) measurement of the atmospheric opacity once every few hours. The resulting absolute flux calibration uncertainty is estimated to be about 10% (rms).

The data were analyzed using the mopsic software package written by R. Zylka at IRAM. The double-beam maps were combined to a single map using the shift-and-add procedure. Compared to a proper image restoration, this produces maps with about a factor 2 higher sensitivity, at the expense of no sensitivity to emission structures in scan direction that are larger that the wobbler throw of 60''. In our sample, the shortest integration time per field is 30 min, yielding an rms noise level of $\sim $ $\rm 2.5~mJy/11''$ beam in the central part of the map (r < 60''), steadily rising to $\sim $ $\rm 5~mJy/11''~beam$ at its edge ( $r \sim 140''$). This non-uniform noise across the maps exists because the scanned field is about twice as large as the bolometer array size, so that more data is taken in the central part of the map than near the edges. Because of this non-uniformity, it is more judicious to present Signal-to-Noise (S/N) maps rather than intensity maps. The longest observation, by far, had a 20 h duration and was targeted at GJ628, yielding an rms noise level of $\sim $ $\rm0.5~mJy/11''~beam$in the central part of the map and $\sim $ $\rm 1.2~mJy/11''~beam$ at $r \sim 140''$. The sky area covered by each map corresponds to $\sim $1700 independent antenna beams. The residual noise in the map was found to be nearly Gaussian. Hence, a 4$\sigma$ detection in our maps is statistically significant. Below, we describe the procedure we used to extract discrete sources and to search for extended emission.

\begin{figure} \par\includegraphics[width=8.5cm, angle=-90]{12306fg1.ps} \end{figure} Figure 1:

MAMBO-2 Signal-to-noise ratio map of the field around the M1.5 dwarf GJ526 at $\lambda =1.2$ mm. The pixel size is $3.5'' \times 3.5''$. The noise rms is $ \rm \sigma = 0.58~mJy/11''$ beam in the central region (r < 60'') and increases towards the edges of the map, $\sim $1.3 mJy/11'' beam at $r \sim 140''$. The contours are $-4 \sigma ,-3 \sigma , -2 \sigma , -1 \sigma $ (dotted lines), and $1 \sigma , 2 \sigma , 3 \sigma , 4 \sigma , 5 \sigma , 6 \sigma , 7 \sigma , 8 \sigma $. The ellipse (a=98'', b=15'', and PA =  $-30^{\circ }$) is almost centered on the star position and connects five sources that might be clumps of a debris disk inclined to the plane of the sky by $81^{\circ }$ (see Sect. 4.1.3). The field is centered on the position of GJ526 of early 2006: $\alpha ({\rm J2000}) =$ 13$^{\rm h}$ 45$^{\rm m}$ 44.52$^{\rm s}$ and $\delta ({\rm J2000})=$ $14^{\circ } 53' 20.6''$ (red star). See Table 2 for integrated flux densities and coordinates of sources.

Open with DEXTER

4 Results

Although initially intended, our complete survey of 50 M-dwarfs turns out not to be flux-limited, which makes its statistical interpretation not straightforward. First, we present the discrete millimeter sources detected in four MAMBO-2 maps (Figs. 1-3, and Table 2), and we discuss the nature of the intriguing cluster of sources around GJ526. Second, we present the deep search for faint debris disks made by averaging intensities over an effective area in the 42 MAMBO-2 maps of our complete survey (Tables 3 and 4). The 8 other M-dwarfs were observed in wide photometry mode with SCUBA (Table 5) and were already discussed by Lestrade et al. (2006). We use the complete sample of 50 M-dwarfs to estimate the fraction of cold debris disks around M-dwarfs and upper limits to their fractional dust luminosities. Three stars (GJ285, GJ393 and GJ4247) are in common between Tables 3-5.

4.1 Discrete sources and structure around GJ526

Table 2:   Millimeter sources found in our MAMBO-2 maps.

\begin{figure} \par\includegraphics[width=7.4cm, angle=-90]{12306fg2.ps} \end{figure} Figure 2:

MAMBO-2 Signal-to-noise ratio map of the field around the binary GJ725 (M3 + M3.5 dwarfs) at $\lambda =1.2$ mm. The pixel size is $3.5'' \times 3.5''$. The noise rms is $ \rm \sigma = 1.4~mJy/11''$ beam in the central region (r < 60'') and increases towards the edges of the map, $\sim $4.3 mJy/11'' beam at $r \sim 170''$. The contours are $-4 \sigma ,-3 \sigma , -2 \sigma , -1 \sigma $ (dotted lines), and $1 \sigma , 2 \sigma , 3 \sigma , 4 \sigma , 5 \sigma , 6 \sigma , 7 \sigma $. The source MM184222+593828 westward has an integrated flux density between 30 and 63 mJy ( $S/N \sim 7$). The other source, MM184253+593756, has an integrated flux density of 9.7 mJy and a S/N of 5.1. The field is centered on the position of GJ725A of early 2006: $\alpha ({\rm J2000}) =$ 18$^{\rm h}$42$^{\rm m}$45.48$^{\rm s}$ and $\delta ({\rm J2000})=$ $59^{\circ } 38' 01.7''$(red star). See Table 2 for integrated flux densities and coordinates of the sources.

Open with DEXTER

4.1.1 Source extraction

In Table 2, we summarize the characteristics of the discrete sources detected with Signal-to-Noise S/N > 4 in the 42 fields mapped with MAMBO-2, each being $\sim $ $400'' \times 400''$ in size and being centered on the position of an M-dwarf. The source extraction was done by searching each map for pixels with S/N > 4 to select a block of $7\times7$ pixels centered on each of them. We then minimized $\chi^2$ between the 2-D Gaussian $ F \times {\rm exp}\big(-0.5 \times \big[{(x-x_0)}^2 + {(y-y_0)}^2~\big] / {\sigma}^2\big)$ and the measured intensities over this block by varying the peak flux F, the parameter $\sigma$ ( ${\it FWHM} = 2.35~\sigma$), and the peak position (x0, y0) by less than a pixel from the S/N > 4 pixel. We used the mean brightness computed from the 32 pixels surrounding the $7\times7$ block to remove any constant level. With this scheme, this level is determined from pixels that are far enough from the 2-D Gaussian peak to be at the map floor, since the Gaussian FWHM is 3 to 5 pixels ( 11''-17'') for our sources. This correction amounted to between 5% and 20% of the integrated flux density. The integrated flux densities of sources in Table 2 are $S_{\rm int}=2 \pi \sigma F$. We extracted 13 discrete sources with S/N > 4 for F in 4 fields out of the 42 MAMBO-2 maps; 8 sources were newly found in the fields of GJ526, GJ725, and GJ569. They are all shown in Figs. 1-3. The 5 other sources are in the field of GJ628 as already reported in Lestrade et al. (2006); typographic errors in their coordinates in this first publication are corrected in Table 2. In this table, the lowest integrated flux density is $3.0 \pm 0.7 $ mJy and the highest is between 30 and 63 mJy. There is no optical counterpart within 7'' ($2\sigma$ MAMBO-2 position error) of any of these sources in the USNO-B1 catalogue (Monet et al. 2003), except for MM163007-123942 (GJ628W) at the $1 \sigma$ level in position (object I mag = 18.92) as already reported in Lestrade et al. (2006). Additionally, we searched the fields of GJ526 and GJ569 that were imaged in the Sloan Digital Sky Survey (SDSS). In the field of GJ526, there is only one SDSS object (z mag = 20.4) which is as close as 7'' from MM134540+145446. However, the confusion limit is reached over such a separation since the density of SDSS objets is $\sim $22 000 objects/deg2 as measured over the $4' \times 4'$ area centered on the star position. In the field of GJ569 ($\sim $33 000 SDSS objects/deg2), there are two SDSS objets (mag u = 19.9, g = 21.6) as close as 8'' from MM145428+160439, but again confusion prevents identification with the MAMBO-2 m source. We found no radio counterpart within the $3\sigma$ MAMBO-2 position uncertainty (10.5'') in the NVSS catalogue (Condon et al. 1998) to the flux density limit of 2.5 mJy at 1.4 GHz, except for MM163007-123942 (GJ628W) at the 1.7$\sigma$ level in position (object flux density = $ 5.6\pm 0.5$ mJy) as already reported in Lestrade et al. (2006). Finally, we found no IR counterpart within the 3$\sigma$ MAMBO-2 position uncertainty in the 2MASS All-Sky Catalog of Point Sources (Skrutskie et al. 2006).

4.1.2 A bright millimeter source
\begin{figure} \par\includegraphics[width=7.0cm, angle=-90]{12306fg3.ps} \end{figure} Figure 3:

MAMBO-2 Signal-to-noise ratio map of the field around the binary GJ569 (M 2.5 + M 8.5 dwarfs) at $\lambda =1.2$ mm. The pixel size is $3.5'' \times 3.5''$. The noise rms is $ \rm \sigma = 1.1~mJy/11''$ beam in the central region (r < 60'') and increases towards the edges of the map, $\sim $2.8 mJy/11'' beam at $r \sim 140''$. The contours are $-4 \sigma ,-3 \sigma , -2 \sigma , -1 \sigma $ (dotted lines), and $1 \sigma , 2 \sigma , 3 \sigma , 4 \sigma $. The source MM145428+160439 has an integrated flux density of 5.3 mJy and a S/N of 4.9. The field is centered on the position of GJ569A of early 2006: $\alpha ({\rm J2000}) =$ 14$^{\rm h}$54$^{\rm m}$29.35$^{\rm s}$ and $\delta ({\rm J2000})=$ $16^{\circ } 06' 03.2''$ (red star). See Table 2 for integrated flux density and coordinates of the source.

Open with DEXTER

The source MM184222+593828 in the field of GJ725 has a flux density of between 30 and 63 mJy (Table 2), which is bright compared to millimeter sources found previously in empty fields mapped with MAMBO-2 (Greve et al. 2004; Bertoldi et al. 2007; and Voss et al. 2006). These lower and upper limits were obtained by using different atmospheric correlation lengths in the skynoise reduction within the mopsic data reduction package, yielding similar detections of $S/N \sim 7$. Systematics affects the accuracy of the flux measurement for this source, which is near the edge of the map. This source is possibly resolved with a source FWHM between 12'' and 15'' depending on the reduction parameter used. Although this is rare, it has been shown that submm galaxies can have multiple components (Tacconi et al. 2008). We shall discuss this source together with complementary observations in a forthcoming paper.

Table 3:   Search for debris disks around nearby M-dwarfs with our new MAMBO-2 data.

4.1.3 Structure around GJ526

The map of GJ526 is shown in Fig. 1. There are five sources that can be connected by an ellipse almost centered on the star; precisely four robust ones with S/N >4 and an additional one, farthest to the SE, that is only detected with S/N >3.5. This source is possibly real since statistically less than 1 positive noise peak is expected at this level over the whole map if dominated by Gaussian noise. To estimate whether this is the case or not, we identified the negative noise spikes S/N < -3 and the positive spikes 3 < S/N < 4 in our $440''~\times~420''$ map ($\sim $2050 beams). The total of these 7 noise spikes found in the map is consistent with the 6 theoretically expected for |S/N| > 3 for Gaussian noise. Also, the detection of the SE source is robust since it appears at the same position in the two independent maps we made by dividing the data in half. There is also a $\sim $$3\sigma$ source to the West close to the ellipse but its detection is not robust to data selection. Finally, there is an S/N > 4 source farther away in the SW direction.

The ellipse is offset by two pixels in right ascension from the position of the star, its semi-major and semi-minor axes are a=98'' and b=15'', and its orientation is PA =  $-30^{\circ }$. This structure might be the projected ring of a clumpy debris disk, its inclination being $81^{\circ }$ from the plane of the sky. The offset between the star and the center of the ellipse is only 2 pixels and might be caused by position uncertainties or/and by true source structure. However, the 5 connected sources do not appear to be embedded in any extended emission as expected for a debris disk. The mean brightness over a rectangular box $220'' \times 40 ''$ (92 beams), oriented at PA =  $-30^{\circ }$, and centered on the star is $0.21 \pm 0.073$ mJy/11'' beam, i.e., $\sim $$3\sigma$. This mean brightness matches the mean of the 5 flux densities of the connected sources within the box, indicating that any extended emission must have a brightness < $3\rm\times 0.073~mJy/11''$ beam at 1.2 mm.

We now test whether or not such a source cluster can be produced by the distribution of background sources. We carry out a first test to estimate the probability that the connected sources around GJ526 can cluster as tightly as they do in Fig. 1 if they were background sources. For this test, we use the statistical analysis of spatial point patterns developed by Diggle (2003). This analysis is based on the nearest neighbour distance, defined as the distance between a point (a source for us) and its nearest neighbour. For GJ526, all the nearest neighbour distances for the 5 sources connected by the ellipse are <60''. The probability that k distances x be <60'' among N distances if the mean frequence of occurrence for x < 60'' over the whole sky is f, is given by the binomial distribution $ B_k = \big(^N_k \big)~f^k~(1-f)^{N-k}$. We can derive the mean frequence of occurrence f from the three empty fields (ELAIS N2, Lockman Hole, and COSMOS) maped by MAMBO-2 (Greves et al. 2004; and Bertoldi et al. 2007). We found that there are 9 distances <60'' between the 71 sources of these three fields, and so f=9/(71-3)=0.13. The factor (71-3) is the number of nearest neighbour distances for 71 sources distributed in the 3 separate fields. For the five sources around GJ526 in Fig. 1, all 5-1 nearest neighbour distances are <60'' as already mentioned, so k=N=4 and the probability Bk that background sources can produce such a number of small distances is as low as 0.1%.

As a second test, we use the elliptical pattern connecting 6 submm sources recognisable in the North-West part of the COSMOS field maped by MAMBO-2 and displayed in Fig. 2 of Bertoldi et al. (2007). This field is $20~\times~20$ arcmin2 in size and the mean occurrence of ellipse of major-axis 200'', as in the field of GJ526, is $1/20~\times~20$ arcmin-2. We compute the Poisson probability of finding a similar ellipse in a field that we take as small as $200~\times~200$ arcsec2 to account for the ellipse around GJ526 being in an area restricted to the central part of the map, i.e., centered on the position of GJ525. This probability is 2.7%. This test is only indicative because the COSMOS field has been mapped at the level of 1 mJy/beam rms, while our map is twice as deep for the field around GJ526.

In summary, the five sources in Fig. 1 that are symmetrically located around GJ526 are connected by an ellipse almost centered on the star. The two tests carried out above provide indications that this structure is statistically inconsistent with known spatial distributions of background submm galaxies. Hence, at this stage, we cannot rule out the hypothesis that the sources are associated with the star. In this case, the 5 connected sources could be indicative of azimuthal structures in an inclined debris disk around GJ526, whose extended emission is not seen because the map is not deep enough. Complementary observations at 850 $\mu $m, and at shorter wavelengths with Herschel, should attempt to detect the extended emission of the disk. Eventually, astrometry should detect the same proper motion for the 5 connected sources as for the star GJ526 (2.3''/yr in the SE direction) if indeed they are part of a debris disk. The mid-epoch of our MAMBO-2 data is early 2007, so that the 5 sources should have moved in concert with the star by a full IRAM-30 m beam by 2011, providing definitive proof of a disk.

Table 4:   Reanalysis of the MAMBO-2 data of the M-dwarfs associated with moving groups of survey I.

Such a debris disk would have a radius as large as $\sim $500 AU at the distance of GJ526. We examine whether or not this is conceivable. First, we note that exceptionally large debris disks, 520 AU and 600 AU in extent, have been found around the 184 Myr old A0-type dwarf $\gamma$ Oph at 70 $\mu $m (Su et al. 2008), and around the main sequence F8V q1 Eri at 870 $\mu $m (Liseau et al. 2008). Second, protoplanetary disks where planetesimals and planets form extend to almost 1000 AU as observed for example around the young close binary GG Tau (Dutrey et al. 1994). In the model proposed by Kenyon & Bromley (2004a), icy-planets successively form in waves outward in the disk producing larger and larger dusty rings from collisional cascades. In their model, the planet formation timescale is $15{-}20 \times (\Sigma_0 / \Sigma_{MMSN})^{-1} (a/{\rm 30~AU})^3$ Myr in a quiet disk (their Eq. (4)). Assuming for $\Sigma_0$ as much as 15 times the surface density of the minimum-mass solar nebula $\Sigma_{MMSN}$ as required for the formation of Jupiter in the solar system (Lissauer 1987), the timescale for planet formation to reach 500 AU in the GJ526 system is $\sim $5 Gyr. The stellar diameter of GJ526 measured by the optical interferometer CHARA (Berger et al. 2006) is about 2$\sigma$ larger than the ZAMS diameter predicted by Chabrier & Baraffe (1997) and Siess et al. (2000). If this deviation of only $2\sigma$ is real, it is an indication of youth instead for GJ526, and this would pose a problem for the Kenyon and Bromley model applied to the hypothetical debris disk around GJ526. We note that, with the dust surface density profile $15 \Sigma_{MMSN} \times (r/r_0)^{-3/2}$, the mass of solids in a ring at r=500 AU and 0.1 r in width is $1~M_{\oplus}$, which is enough to form planetesimals. Finally, the dust mass corresponding to the emission of the 5 sources is between $\sim $6 and $\sim $10 lunar masses as derived in the Appendix for dust grains with a Dohnanyi size distribution and heated both by the stellar luminosity and the interstellar radiation field. The dust mass is $\sim $22 lunar masses if derived conventionally for grey body dust with a mass opacity of $\rm 1.7~cm^2~g^{-1}$ at 850 $\mu $m and $\propto $ $\lambda ^{-1}$ for $\lambda > 210~\mu$m, and with the single dust temperature 4.9 K at large radius from the star (r = 500 AU) where the interstellar radiation field dominates the heating process of grains (see Appendix).

Table 5:   SCUBA observations of the M-dwarfs associated with moving groups in survey I (Lestrade et al. 2006).

4.2 Deep search for debris disks in the MAMBO-2 maps

We searched for faint debris disks in each MAMBO-2 map by averaging intensities over a disk of increasing radius out to 30'' to see whether or not the mean brightness peaks at some angular radius $\theta$. The radius limit of 30'' comes from the shift-and-add reduction method and the wobbler throw of 60'' used for the observations. The intention with this averaging was to identify a disk whose structure is not directly apparent in the map but whose mean brightness is statistically significant. Naturally, no information about its structure can be recovered with this procedure. The optimum sensitivity of this method is for face-on disks, while highly inclined disks might escape detection. This method is similar to the one used to determine extension limits of debris disks in the mid-IR surveys of Sun-like stars conducted by Smith et al. (2008), although, we do not have the complication of having to accurately substract the photosphere at $\lambda =1.2$ mm. Following this procedure, we plotted the mean brightness as a function of angular radius $\theta$ for each star presented in Tables 3 and 4. All the curves were inspected and found to wander around zero mean with excursions $\le$$3\sigma$ for $\theta$ comprised between 11''/2 and 30'', indicating that no disk was found by this method.

In Fig. 4, we provide the distribution of the mean brightness $\mu $/mean brightness uncertainty $\sigma _{\mu }$ listed in Tables 3 and4 and computed for $\theta$ corresponding specificly to the adopted disk radius 60 AU at the distances of the stars. The corresponding Gaussian probability density function is also plotted in Fig. 4. Comparison between the two distributions indicates there are more high positive and negative ratios $\mu / \sigma _{\mu }$ than expected, although they stay within $\pm 3\sigma $. It means that there are still some systematic errors in the maps but at a low level, likely caused by remaining atmospheric fluctuations.

4.3 Upper limits to both fractional dust luminosities and dust masses of the debris disks

\begin{figure} \par\includegraphics[width=6.5cm, angle=-90]{12306fg4.ps} \end{figure} Figure 4:

Distribution of the ratios mean brightness $\mu $/ uncertainty of mean  $\sigma _{\mu }$ for the 42 M-dwarfs observed with MAMBO-2, i.e., $\mu / \sigma _{\mu }$ listed in Tables 3 and 4. Here, the mean brightness $\mu $is computed over a disk of radius 60 AU adopted for each star. The Gaussian probability density function superimposed is scaled so that its integral is 42. Comparison between the two distributions indicates there are more high positive and negative ratios $\mu / \sigma _{\mu }$ than expected, although they stay within $\pm 3\sigma $. It means that there are still some systematic errors in the maps but at a low level, probably caused by remaining atmospheric fluctuations. No mean brightness is retained as statistically significant in the sample.

Open with DEXTER

\begin{figure} \par\includegraphics[width=6.3cm, angle=-90]{12306fg5.ps} \end{figure} Figure 5:

Constraints on the dust luminosity fraction versus disk radius. Note that the x-axis shows the single radius corresponding to the single temperature of a disk (ring) assumed infinitely narrow in our model. We consider the wide range of radii from 1 to 1000 AU as plausible for rings of debris. Upper limits are shown as dashed lines, detections as solid lines. Blue lines correspond to the (sub)millimeter observations: i.e., our sample of 50 M-dwarfs for which dark blue is used for ``young'' M-dwarfs (ages <200 Myr) and light blue for ``old'' M-dwarfs (likely a few Gyr); the submm disk detected around AU Mic and resolved (Liu et al. 2004; Liu 2004) is marked by a single dot; the two submm disks detected but not clearly resolved around GJ182 (Liu et al. 2004) and around GJ842.2 (Lestrade et al. 2006)  are marked as curves; and the submm transition disk detected around the pre-main sequence M 1 dwarf TWA7 (Matthews et al. 2007) is also included. Orange lines correspond to Spitzer 70 $\mu $m observations: i.e., the sample of 41 M-dwarfs of Gautier et al. (2007) and the detection of the M 0 dwarf HD95650 (Smith et al. 2006). There are 16 M-dwarfs in common between the two samples. These two sets of data are complementary to constrain the existence of warm dust around M-dwarfs at moderate radii (<20 AU) and cold dust at large radii (>20 AU). Disk diameters probed by the observations are limited by the angular size of 60'' for the MAMBO-2 maps, of 28'' for SCUBA wide photometry, and of 38.4'' for Spitzer aperture photometry (Gautier et al. 2007). Some curves are terminated at less than 1000 AU because of these angular limits. The calculation of the fractional dust luminosity is described in the text. (This figure is available in color in electronic form.)

Open with DEXTER

The fractional dust luminosity is the fraction of the stellar radiation absorbed and reprocessed to the infrared and (sub)mm by the dust grains; it is proportional to the fraction of the sky covered by dust as seen from the star (Dominik & Decin 2003). We used the Stefan-Boltzmann law - black body emission -to estimate dust luminosity, and modified it by emissivity $1/X_{\lambda}$, with $X_{\lambda} =1$ for $\lambda < 210~\mu$m, and $X_{\lambda} = \lambda/210$ for $\lambda > 210~\mu$m (Wyatt 2008). In these conditions, the fractional dust luminosity is

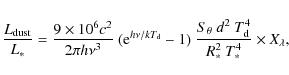
\begin{displaymath}{L_{\rm dust} \over L_*} = {{9 \times 10^{6} c^2} \over {2 \p... ...ta}~d^2~T_{\rm d}^4} \over {R_*^2~T_*^4}} \times X_{\lambda}, \end{displaymath} (1)

the normalization coefficient is such that the measured flux density $S_{\theta}$ is in Jy, the star distance d in pc, the stellar radius R* in m, the dust and stellar effective temperatures $T_{\rm d}$ and T* in K, the Planck and Boltzmann constants h and k in ${\rm J} \times {\rm s}$ and J/K, the speed of light c in m/s, and the frequency of observation $\nu$ in Hz.

The standard argument used to fix dust temperature $T_{\rm d}$ in mid-IR surveys of debris disks is that observations are most sensitive to the dust emission peak, and $T_{\rm d}$is derived from the Wien law. In the (sub)mm range, this law is inappropriate for $T_{\rm d}$ since we observe in the Rayleigh-Jeans limit. To keep full generality, we avoid choosing a dust temperature $T_{\rm d}$ at some arbitrary radius but plot in Figs. 5 and 6 fractional dust luminosities and dust masses as functions of disk radius r between 1 and 1000 AU following the approach by Bryden et al. (2006) and Wyatt (2008). At disk radius r, we use the dust temperature

$\displaystyle T_{\rm d}=278 \times (L_*^{0.25}) \times (r^{-0.5}),$     (2)

from Black Body equilibrium, where L* is the stellar luminosity in $L_{\odot}$ and r is in AU (Backman & Paresce 1993). We note that by combining Eqs. (1) and (2), one derives the expression for fractional dust luminosity given by Eq. (8) of Wyatt (2008), where the stellar luminosity L* cancels out.

We adopt the $3\sigma$ flux density limit for $S_{\theta}$ in Eq. (1) by integrating brightness over a face-on disk of radius r, or $\theta$ at the distance of the star. If $2 \theta > 11''$ (i.e., >IRAM 30 m beam):

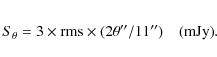
\begin{eqnarray*}S_{\theta} = 3 \times {\rm rms} \times (2 \theta''/11'') \quad {\rm (mJy)}. \end{eqnarray*}


This formula takes into account that the mean brightness uncertainty $\sigma _{\mu }$ improves as ${\rm rms}/\!\sqrt{\rm number~of~beams}$, while the integrated flux density increases as the number of beams of the disk area. Now if $2 \theta < 11''$

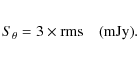
\begin{eqnarray*}S_{\theta} = 3 \times {\rm rms} \quad {\rm (mJy)}. \end{eqnarray*}


We used the rms of Tables 3 and 4 that correspond to the central part of the maps, thus underestimating slightly the upper limits computed.

In Fig. 5, we show the resulting fractional dust luminosity upper limits to r between 1 and 1000 AU. These functions first show a steep negative slope for $2 \theta < 11''$ making $S_{\theta}$ constant in Eq. (1), then these functions level off when $S_{\theta}$ linearly increases with $\theta$, and finally they increase when the dust temperature saturates at 4.9 K because the interstellar radiation field becomes dominant over the stellar field (see Appendix). In this figure, we have added the upper limits to the fractional dust luminosities for the 41 M-dwarfs observed at 70 $\mu $m by Spitzer (Gautier et al. 2007), computed in a similar fashion for their 3$\sigma$ flux densities. The figure shows that the two sets of data are complementary, and lead to a uniform fractional dust luminosity over a large extent of disk radii for the dozen of M-dwarfs common to the two data sets. In Fig. 6, we present the corresponding dust masses as a function of r for both samples computed with the optically thin emission model (e.g., Zuckerman 2001) and the mass opacity $\kappa_{\lambda} \propto \lambda^{-1}$ for $\lambda > 210~\mu$m and $\kappa_{850~\mu {\rm m}} = \rm 1.7~cm^2~g^{-1}$.

\begin{figure} \par\includegraphics[width=6.3cm, angle=-90]{12306fg6.ps} \end{figure} Figure 6:

Constraints on the dust mass versus disk radius. Note that the x-axis shows the single radius corresponding to the single temperature of a disk (ring) assumed infinitely narrow in our model. We consider the wide range of radii from 1 to 1000 AU as plausible for rings of debris. Upper limits are shown as dashed lines, detections as solid lines. Blue lines correspond to the (sub)millimeter observations and orange lines to the Spitzer 70 $\mu $m observations as described in the legend of Fig. 5. The mass opacity used to convert flux density to dust mass with the standard optically thin emission model is $\rm \kappa = 1.7~cm^2~g^{-1}$ at 850 $\mu $m and $\propto $ $\lambda ^{-1}$ for $\lambda > 210~\mu$m. Additional information are in the text. (This figure is available in color in electronic form.)

Open with DEXTER

5 Discussion

The single cold debris disk found in our surveys (GJ842.2, see details in Lestrade et al. (2006), and excluding GJ526 at this stage) makes the detection fraction to be 2+4.5-1.5% in our sample of 50 M-dwarfs. The limits are based on the Binomial distribution for a small number sample and are such that 68% of the probability is between the lower and upper uncertainties, and the peak probablity is the observed fraction 1/50, following Burgasser et al. (2003). We recall that Gautier et al. (2007) had no detection in a sample of 62 nearby M-dwarfs at 24 $\mu $m and no detection in a subsample of 41 of them at 70 $\mu $m, i.e., rate <7%. In a different way, Forbrich et al. (2008) detected photometric excesses at 24 $\mu $m tracing warm dust around 11 M-dwarfs in the young open cluster NGC2457 (20-40 Myr) representing 4.9 +1.8-1.8% of the 225 highly probable member M-stars identified within it.

To discuss how detectability of cold debris disks depends on the mass of the central star, we compared our result with the observed fractions of cold debris disks around stars more massive than M-dwarfs. In the literature, we find $\sim $30 cold debris disks around A-to-K type stars detected by submm observations (see Fig. 3 and caption of Wyatt 2008). However most of these detections are from JCMT/SCUBA surveys of IRAS biased samples, i.e., targets with prior IRAS excess detections, unlike our M-dwarfs, for which no such prior knowledge was used in the selection of the sample. There are only two submm surveys of A-to-K type stars that are unbiased in this respect and have depths of $\sim $1-3 mJy at 850 $\mu $m, comparable to our sensitivity at 1.2 mm: the JCMT survey by Najita & Williams (2005) of thirteen F5-to-K3 stars (10 Myr < ages <180 Myr, 10 < d < 78 pc, 3 detections) and the JCMT survey by Wyatt et al. (2003) of nine B7-to-A0 stars ( 86< d < 938 pc, 2 detections) and of thirteen F3-to-K5 stars ( 27< d < 250 pc, 1 detection) that are all part of Lindroos binaries (14 Myr < ages < 170 Myr). Combining these two submm surveys, we determine the cold disk fractions of 22+33-20% for young A stars (2 detections/9) and of 15 +11.5-11.5% for young FGK stars (4/26). For a meaningful comparison, instructed by Spitzer surveys where the age factor is crucial for detectability of warm debris disks, we selected the 19 youngest M dwarfs with ages between 20 and 200 Myr in our sample. The disk fraction for these ``young'' M-dwarfs is 5.3+10.5-5.0%. Therefore, for this age range, there is an apparent trend in these three fractions, indicative of fewer cold disks detected for later stellar types - lower star masses - although at a low statistical significance (Fig. 7). Nonetheless, this trend is notable because the surveys are deeper for later stellar types as shown in Fig. 8, for disk radii <100 AU. Interestingly, this trend has also been found at $70~\mu$m in a sample of A to M stars with ages between 8 Myr and 1 Gyr by Plavchan et al. (2009).

\begin{figure} \par\includegraphics[width=6.3cm, angle=-90]{12306fg7.ps} \end{figure} Figure 7:

Detection rates of cold debris disks versus stellar masses (stellar types) for stars younger than 200 Myr. These rates and uncertainties are for disks having dust fractional luminosities larger than the limits shown in Fig. 8 of the (sub)mm surveys used.

Open with DEXTER

\begin{figure} \par\includegraphics[width=6.3cm, angle=-90]{12306fg8.ps} \end{figure} Figure 8:

Dust luminosity versus disk radius limits of the three (sub)mm surveys used to determine the cold disk fractions of ``young'' M-, FGK- and A-type stars. Shown are the dust luminosity fractions of the 19 youngest M-dwarfs of our sample (blue), of the 9 young A-stars (green), and of the 26 young FGK-stars (red) in the two 850 $\mu $m surveys of Wyatt et al. (2003) and of Najita & Williams (2005). All these stars are less than 200 Myr old. Most of the curves are upper limits (dashed lines). The 7 detections are marked by full lines. This plot emphasizes that for stars of lower masses (later stellar types), even though the surveys are more sensitive, fewer disks are detected. Note that the x-axis shows the single radius corresponding to the single temperature of a disk (ring) assumed infinitely narrow in our model. We consider the wide range of radii from 1 to 1000 AU as plausible for rings of debris. (This figure is available in color in electronic form.)

Open with DEXTER

We also determine the cold disk fraction of <10% for the ``old'' M-dwarfs of our sample with undetermined ages but that are probably as old as average Galactic disk stars ( $8.8 \pm 1.7$ Gyr, del Peloso et al. 2005). This may indicate that the cold disk fraction decreases with stellar age, in a similar way to warm disks (Rieke et al. 2005). We note that the ``old'' M-dwarfs were observed with higher sensitivity as seen in Figs. 5 and 6, where ``young'' and ``old'' M-dwarfs have been color-coded in dark and light blue. The higher sensitivity to the ``old'' M-dwarfs is because they are nearer than the ``young'' M-dwarfs.

We now examine possible reasons why M-dwarfs have less detectable disks.

Theoretical models of star formation predict that protoplanetary disks are less massive around M-dwarfs than around higher mass stars. Vorobyov & Basu (2008) predict $\langle M_{\rm d}\rangle ~\propto~\langle M_* \rangle ^{1.3\pm0.1}$, where disk mass $\langle M_{\rm d} \rangle $ and star mass $\langle M_* \rangle $ are time-averaged over the star accretion period (0.5 to 2.5 Myr). Consequently, less primordial materials could limit planet formation around M-dwarfs. Collecting masses of protoplanetary disks determined by (sub)mm observations in the nearest star forming regions, Natta et al. (2000) found $M_{\rm d}~\propto~M_*^{0.64\pm0.14}$, but Andrews & Williams (2005, 2007) show that $M_{\rm d}$ versus M* in Taurus-Auriga is so widely scattered between 0.001 and 0.2 $M_{\odot}$ that it precludes any meaningful correlation fit. The comparison of the disk masses of 6 members of the nearby young TW Hydrae Association (TWA) also suggests no correlation between disk masses and stellar types for these reasonably coeval disks (Matthews et al. 2007).

Removal of circumstellar dust by the Poynting-Robertson effect and radiation pressure processes are diminished around M-dwarfs because they are less luminous than solar-type stars, and so dust generated by collisions in any remnant planetesimal belt should remain there longer, giving rise to detectable emission. However, the opposite conclusion has been reached by Plavchan et al. (2005), highlighting the fact that dust removal around M-dwarfs could be dominated by the drag caused by strong winds associated with their high coronal and chromospheric activities.

The formation of planetesimals and planets depends on the timescales between the competing processes of coagulation and evaporation in the early period of accumulation. Theory predicts that $t_{\rm coag}$ increases and $t_{\rm evap}$ decreases with both the central star mass and the strength of the FUV and EUV radiation field (Eq. (47) and (48) in Adams et al. 2004, respectively). From their Fig. 10, it can be seen that a time longer than 10 Myr is required to evaporate a protoplanetary disk around a solar-mass star, whereas only a few Myr are required to evaporate the same disk around a low-mass M-dwarf in a stellar cluster with a moderate UV flux of $\sim $3000 G0. This might quench planet formation around M-dwarfs.

Early stripping of planetesimals by passing stars is likely since most stars are born in clusters where stellar encounters as close as 160 AU are likely in the first 100 Myr (Kenyon & Bromley 2004b). The disruption of planetesimal disks by close stellar encounters was studied for the A6 star $\beta$ Pic by Larwood & Kalas (2001). Depending on both the passing star's trajectory and the relative star masses, they found that 1% to 48% of the planetesimals are lost after encounters. Related issues for planetary systems were also discussed by Malmberg et al. (2007).

A lack of gaseous giant planets around M-dwarfs is predicted by Laughlin et al. (2004), because of the longer duration required to build a core of 15  $M_{\oplus}$. This lack of giant planets might reduce the production of second generation dust in M-dwarf debris disks because of weaker gravitationnal stirring (Wilner et al. 2002), diminishing their detectability.

This series of arguments leads to the expectation that debris disks around M-dwarfs might be intrinsically less dusty and therefore more difficult to detect than those around more massive stars of the same age. However, most of these arguments assume that the initial protoplanetary disk mass scales with the central star mass, which may be plausible but is observationally not well established.

6 Conclusion

To search for emission from cold debris disks, we have used the MAMBO-2 bolometer camera at the IRAM 30 m telescope to map 42 nearby M-dwarfs at $\lambda =1.2$ mm to a noise level of between 0.6 and 2.8 mJy per 11'' beam. We also reanalyzed our earlier MAMBO-2 and SCUBA data to form a coherent sample of 50 M-dwarfs. Only one cold debris disk was detected, surrounding the M 0.5 dwarf GJ842.2. To discuss how the detectability of cold debris disks depends on the mass of the central star, we have compared this result to the observed fractions of cold disks for more massive stars in the two submm surveys of Wyatt et al. (2003) and Najita & Williams (2005), who report detection rates of 22+33-20% for A-stars and 15 +11.5-11.5% for FGK-stars with stellar ages between 10 and 180 Myr. For the 19 youngest M-dwarfs ($\le$200 Myr) of our sample, we found a detection rate of 5.3+10.5-5.0%. Hence, for this age range, there is a mild trend in these three detections rates, indicative of fewer cold debris disks detected for later stellar types - lower star masses - although at a low statistical significance. Nonethless this trend is notable because the sensitivities of these surveys are deeper for later stellar types. We also determine the cold disk fraction of <10% for the ``old'' M-dwarfs (likely to be a few Gyr) of our sample, indicative of the cold disk fraction decreasing with stellar age, as is also seen for warm disks. Future observations of a larger and more tightly controlled sample of stars of all stellar types with Herschel in the far-IR and deeper observations in the (sub)mm will help to clarify these issues.

Appendix A: Computation of the dust temperature and mass of the possible large debris disk around GJ526

The source that heats dust in debris disks is usually the stellar radiation field, but in a large debris disk, as possibly found around GJ526, the interstellar radiation field dominates at some radius from the star. We compute this transition radius for several stellar spectral types by numerically solving the integral equation of a grain at thermal equilibrium absorbing both the stellar and interstellar incident fields

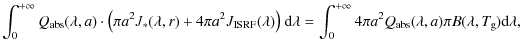
$\displaystyle \int_0^{+\infty} Q_{\rm abs}(\lambda,a)\cdot \big( \pi a^2 J_*(\l... ...nfty} 4 \pi a^2 Q_{\rm abs}(\lambda,a) \pi B(\lambda,T_{\rm g}) {\rm d}\lambda,$     (A.1)

\begin{figure} \par\includegraphics[width=6.5cm, angle=-90]{12306fA1.ps} \end{figure} Figure A.1:

Variation in the temperature of a grain 100 $\mu $m in diameter exposed to both the radiation of the stellar field and the isotropic interstellar radiation field. This latter field dominates at some disk radius R that depends on the stellar luminosity. The saturation temperation of 4.9 K due to the interstellar field is consistent with the computation of Krügel (2003, p. 249). For M 6 only, the dashed line indicates the grain temperature when the interstellar radiation field is not included. (This figure is available in color in electronic form.)

Open with DEXTER

where $Q_{\rm abs}(\lambda,a)= 1$ for $\lambda < \lambda_0$ and $Q_{\rm abs}(\lambda,a)= \lambda_0/\lambda$ with $\lambda_0 = 2 \pi a$ for $\lambda > \lambda_0$, which approximate the absorption efficiency computed for carbon by Laor & Draine (1993). The parameter a is the radius of a spherical grain. The expression $B(\lambda,T_{\rm g})$ is the Planck function at grain temperature $T_{\rm g}$ that depends on a. The intensity of the stellar radiation field $J_*(\lambda, r)$ is $ \pi B(T_*,\lambda) \times {(4 \pi R_* /4 \pi r)}^2 $ at disk radius r, where the star is characterized by its effective temperature T* and its radius R*. The intensity of the interstellar radiation field $J_{\rm ISRF}(\lambda)$ in the solar neighbourhood is

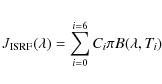
\begin{eqnarray*}J_{\rm ISRF}(\lambda)= \sum_{i=0}^{i=6} C_i \pi B(\lambda, T_i) \end{eqnarray*}


with components $C_0=1, T_0=2.7~{\rm K}, C_1=4\times10^{-17}, T_1=27~000~{\rm K}, C_2=10^{-14}, ... ...es 10^{-10}, T_5=400~{\rm K}, C_6= 0.5 \times 10^{-5}, {\rm and}~T_6=46~{\rm K}$, at galactocentric distance 10 kpc (Mathis et al. 1983). In Fig. A.1, we solved Eq. (A1) numerically to determine dust temperature $T_{\rm g}(r)$ as a function of disk radius in modelling grains with the single size $2 a = 100~\mu$m, typical of submm observations, and for several stellar spectral types. For GJ526 (M 1.5), this figure shows that the interstellar radiation field becomes dominant at r > 1000 AU, but this transition radius is only 200 AU for spectral type M 6.

\begin{figure} \includegraphics[width=6.5cm, angle=-90]{12306fA2.ps} \end{figure} Figure A.2:

Variation in temperature as a function of grain radius at 500 AU from the M 1.5 dwarf GJ526. Similar results are reported by Krügel (2003, p. 249). The discontinuity in the silicate curve arises from the piecewise-defined function $Q_{\rm abs}(\lambda ,a)$ adopted from Laor & Draine (1993). (This figure is available in color in electronic form.)

Open with DEXTER

In Fig. A.2, we use a more realistic model for the dust in adopting the standard grain size distribution ${\rm d}N=N_0 a^{-3.5} {\rm d}a$ (Dohnanyi 1969) to compute temperature $T_{\rm g}(a)$ as a function of grain size at r=500 AU with Eq. (A1) but modified to include the grain size distribution. Temperature increases significantly for $ a < 10~\mu$m, which is relevant for M-dwarfs because the grain blow-out size is small. For GJ526 (0.031 $L_{\odot}$), it is as small as 0.04 $\mu $m for carboneous grains, ignoring the effect of stellar wind drag for this star, which has a low coronal/chromospheric activity (Log $L_{\rm x} = 26.87$ [10-7 W], Schmitt & Liefke, 2004). Finally, we use this temperature function $T_{\rm g}(a)$ at r=500 AU to determine the dust mass around GJ526 by matching the total flux density of the 5 clumps ( $S_{\rm 1.2~mm}= 21.2 \pm 2$ mJy) to the flux density of our model. If d is the distance to the star, the predicted flux density is

$\displaystyle S_{\nu} = {N_0 \over 4 {\pi d^2}} \int_{a_{\rm min}}^{a_{\rm max}... ...\pi a^2~Q_{\rm abs}(\nu,a) \cdot \pi B(\nu,T_{\rm g}(a))~\cdot~a^{-3.5}{\rm d}a$     (A.2)

where the limit $a_{\rm min}$ is set by the blow-out size ( $a_{\rm min}=0.04~\mu$m for GJ526). The limit $a_{\rm max}$ is related to the total dust mass $M_{\rm d} = {8 \over 3} \pi \rho N_0 \sqrt{a_{\rm max}}$ for the size distribution above and spherical grains of density $\rho$. The dust mass $M_{\rm d}$ is probed by the measured flux density at the observing $\lambda$. Practically, the grain size limit $a_{\rm max}$ is the value corresponding to convergence of the computation of the power emitted by $M_{\rm d}$ over a band 2b centered on the observed wavelength (1.2 mm). We adopted the convergence criterium of 5% to match the relative accuracy of the measured flux density. In other words, $a_{\rm max}$ is increased until the integral below converges to within 5%:
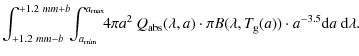
$\displaystyle \int_{+1.2~mm - b}^{+1.2~mm + b} \!\!\int_{a_{\rm min}}^{a_{\rm m... ...mbda,a)\cdot \pi B(\lambda,T_{\rm g}(a))\cdot a^{-3.5}{\rm d}a~ {\rm d}\lambda.$     (A.3)

This power would need to be computed more accurately by including the small contribution to the emission of larger pebbles only if the flux density were measured more accurately. We found that $a_{\rm max}$ is $\sim $24 mm and $\sim $36.4 mm for carboneous and silicate grains, respectively, and, independently of the choice $b=5\%, 10\%, 20\% \times 1.2$ mm. Similar calculation was made by Wyatt & Dent (2002) for the A3V dwarf Fomalhaut by integrating not only over grain size but also over a range of radius r to account for the spatial distribution of the dust in a ring. They found that 95% of the flux density is the emission from grains and pebbles smaller than 100mm in radius. This is comparable to our determination of $a_{\rm max}$ and the difference must be caused by the different function for $T_{\rm g}(a)$ and their hypothesis of spatially distributed dust.

\begin{figure} \includegraphics[width=6.2cm, angle=-90]{12306fA3.ps} \end{figure} Figure A.3:

SED of carboneous dust around GJ526 based on our model fitted to the 1.2 mm flux density. Our model includes the collisional dust size distribution ${\rm d}N=a^{-3.5}{\rm d}a$ and the resulting non-uniform temperature for grains of various sizes computed in Fig. A.2. Superimposed is the corresponding grey-body model computed with the single grain temperature 4.9 K and standard mass opacity $\rm 1.7~cm^2g^{-1}$ at $\lambda=850~\mu$m scaled with the efficiency $\rm 210~\mu m / \lambda$ (see text). (This figure is available in color in electronic form.)

Open with DEXTER
\begin{figure} \includegraphics[width=6.2cm, angle=-90]{12306fA4.ps} \end{figure} Figure A.4:

SED of silicate dust around GJ526 based on our model and fitted to the 1.2 mm flux density. Same comments as in Fig. A.3. (This figure is available in color in electronic form.)

Open with DEXTER

Figures A.3 and A.4 show the SED of the dust around GJ526 based on our model of both carboneous and silicate grains adjusted to the flux density measured at 1.2 mm. The dust mass determined by our model is between $\sim $6 and $\sim $10 lunar masses. We have added in these figures, the SED based on the standard grey-body model of optically thin dust emission (Hildebrand 1983; and Zuckerman 2001)

$\displaystyle S_{\nu}=~{M_{\rm d}~\times~B(\nu,T_{\rm g})~\times~\kappa_{\rm abs}}/{d^2}$     (A.4)

where the mass opacity $\kappa_{\rm abs}$ is conventionally taken to be $\rm ~1.7~cm^2~g^{-1}$ at $850~\mu$m and is scaled by $\rm 210~\mu m / \lambda$for $\lambda > 210~\mu$m. This grey dust mass is about 2 to 4 times higher than the one determined by our model. This level of accuracy is typical of current dust mass estimates for debris disks, presently.

The SED of our model is significantly more extended to the far-IR and to the radio than the grey-body model when both models match the flux density at $\lambda =1.2$ mm. We point out that this far-IR extension is much less pronounced if our model is applied to an A-star. Future observations with Herschel will test these SED differences and will thus probe, in essence, the collisional dust size distribution adopted and the non-uniform grain temperature.

Acknowledgements

We are grateful to the staff of the IRAM 30-m telescope, especially Dr S. Leon, for his dedication in managing the MAMBO-2 pool during the transistion period with the new contral system and for his unfailing determination to optimize the science return of the telescope despite harsh conditions. We would like to thank an anonymous referee for his careful reading of the manuscript and constructive remarks. This research has made use of the SIMBAD database and of the VizieR catalog access tool, opera ted at the Centre de Données Stellaires (CDS), Strasbourg, France. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This publication has made use of data products from the SDSS and SDSS-II funded by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA.

References

 

Footnotes

... date[*]
http://astro.berkeley.edu/ kalas/disksite/pages/gallery.html

All Tables

Table 1:   The 50 M-dwarfs of our (sub)mm surveys.

Table 2:   Millimeter sources found in our MAMBO-2 maps.

Table 3:   Search for debris disks around nearby M-dwarfs with our new MAMBO-2 data.

Table 4:   Reanalysis of the MAMBO-2 data of the M-dwarfs associated with moving groups of survey I.

Table 5:   SCUBA observations of the M-dwarfs associated with moving groups in survey I (Lestrade et al. 2006).

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm, angle=-90]{12306fg1.ps} \end{figure} Figure 1:

MAMBO-2 Signal-to-noise ratio map of the field around the M1.5 dwarf GJ526 at $\lambda =1.2$ mm. The pixel size is $3.5'' \times 3.5''$. The noise rms is $ \rm \sigma = 0.58~mJy/11''$ beam in the central region (r < 60'') and increases towards the edges of the map, $\sim $1.3 mJy/11'' beam at $r \sim 140''$. The contours are $-4 \sigma ,-3 \sigma , -2 \sigma , -1 \sigma $ (dotted lines), and $1 \sigma , 2 \sigma , 3 \sigma , 4 \sigma , 5 \sigma , 6 \sigma , 7 \sigma , 8 \sigma $. The ellipse (a=98'', b=15'', and PA =  $-30^{\circ }$) is almost centered on the star position and connects five sources that might be clumps of a debris disk inclined to the plane of the sky by $81^{\circ }$ (see Sect. 4.1.3). The field is centered on the position of GJ526 of early 2006: $\alpha ({\rm J2000}) =$ 13$^{\rm h}$ 45$^{\rm m}$ 44.52$^{\rm s}$ and $\delta ({\rm J2000})=$ $14^{\circ } 53' 20.6''$ (red star). See Table 2 for integrated flux densities and coordinates of sources.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.4cm, angle=-90]{12306fg2.ps} \end{figure} Figure 2:

MAMBO-2 Signal-to-noise ratio map of the field around the binary GJ725 (M3 + M3.5 dwarfs) at $\lambda =1.2$ mm. The pixel size is $3.5'' \times 3.5''$. The noise rms is $ \rm \sigma = 1.4~mJy/11''$ beam in the central region (r < 60'') and increases towards the edges of the map, $\sim $4.3 mJy/11'' beam at $r \sim 170''$. The contours are $-4 \sigma ,-3 \sigma , -2 \sigma , -1 \sigma $ (dotted lines), and $1 \sigma , 2 \sigma , 3 \sigma , 4 \sigma , 5 \sigma , 6 \sigma , 7 \sigma $. The source MM184222+593828 westward has an integrated flux density between 30 and 63 mJy ( $S/N \sim 7$). The other source, MM184253+593756, has an integrated flux density of 9.7 mJy and a S/N of 5.1. The field is centered on the position of GJ725A of early 2006: $\alpha ({\rm J2000}) =$ 18$^{\rm h}$42$^{\rm m}$45.48$^{\rm s}$ and $\delta ({\rm J2000})=$ $59^{\circ } 38' 01.7''$(red star). See Table 2 for integrated flux densities and coordinates of the sources.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.0cm, angle=-90]{12306fg3.ps} \end{figure} Figure 3:

MAMBO-2 Signal-to-noise ratio map of the field around the binary GJ569 (M 2.5 + M 8.5 dwarfs) at $\lambda =1.2$ mm. The pixel size is $3.5'' \times 3.5''$. The noise rms is $ \rm \sigma = 1.1~mJy/11''$ beam in the central region (r < 60'') and increases towards the edges of the map, $\sim $2.8 mJy/11'' beam at $r \sim 140''$. The contours are $-4 \sigma ,-3 \sigma , -2 \sigma , -1 \sigma $ (dotted lines), and $1 \sigma , 2 \sigma , 3 \sigma , 4 \sigma $. The source MM145428+160439 has an integrated flux density of 5.3 mJy and a S/N of 4.9. The field is centered on the position of GJ569A of early 2006: $\alpha ({\rm J2000}) =$ 14$^{\rm h}$54$^{\rm m}$29.35$^{\rm s}$ and $\delta ({\rm J2000})=$ $16^{\circ } 06' 03.2''$ (red star). See Table 2 for integrated flux density and coordinates of the source.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.5cm, angle=-90]{12306fg4.ps} \end{figure} Figure 4:

Distribution of the ratios mean brightness $\mu $/ uncertainty of mean  $\sigma _{\mu }$ for the 42 M-dwarfs observed with MAMBO-2, i.e., $\mu / \sigma _{\mu }$ listed in Tables 3 and 4. Here, the mean brightness $\mu $is computed over a disk of radius 60 AU adopted for each star. The Gaussian probability density function superimposed is scaled so that its integral is 42. Comparison between the two distributions indicates there are more high positive and negative ratios $\mu / \sigma _{\mu }$ than expected, although they stay within $\pm 3\sigma $. It means that there are still some systematic errors in the maps but at a low level, probably caused by remaining atmospheric fluctuations. No mean brightness is retained as statistically significant in the sample.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.3cm, angle=-90]{12306fg5.ps} \end{figure} Figure 5:

Constraints on the dust luminosity fraction versus disk radius. Note that the x-axis shows the single radius corresponding to the single temperature of a disk (ring) assumed infinitely narrow in our model. We consider the wide range of radii from 1 to 1000 AU as plausible for rings of debris. Upper limits are shown as dashed lines, detections as solid lines. Blue lines correspond to the (sub)millimeter observations: i.e., our sample of 50 M-dwarfs for which dark blue is used for ``young'' M-dwarfs (ages <200 Myr) and light blue for ``old'' M-dwarfs (likely a few Gyr); the submm disk detected around AU Mic and resolved (Liu et al. 2004; Liu 2004) is marked by a single dot; the two submm disks detected but not clearly resolved around GJ182 (Liu et al. 2004) and around GJ842.2 (Lestrade et al. 2006)  are marked as curves; and the submm transition disk detected around the pre-main sequence M 1 dwarf TWA7 (Matthews et al. 2007) is also included. Orange lines correspond to Spitzer 70 $\mu $m observations: i.e., the sample of 41 M-dwarfs of Gautier et al. (2007) and the detection of the M 0 dwarf HD95650 (Smith et al. 2006). There are 16 M-dwarfs in common between the two samples. These two sets of data are complementary to constrain the existence of warm dust around M-dwarfs at moderate radii (<20 AU) and cold dust at large radii (>20 AU). Disk diameters probed by the observations are limited by the angular size of 60'' for the MAMBO-2 maps, of 28'' for SCUBA wide photometry, and of 38.4'' for Spitzer aperture photometry (Gautier et al. 2007). Some curves are terminated at less than 1000 AU because of these angular limits. The calculation of the fractional dust luminosity is described in the text. (This figure is available in color in electronic form.)

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.3cm, angle=-90]{12306fg6.ps} \end{figure} Figure 6:

Constraints on the dust mass versus disk radius. Note that the x-axis shows the single radius corresponding to the single temperature of a disk (ring) assumed infinitely narrow in our model. We consider the wide range of radii from 1 to 1000 AU as plausible for rings of debris. Upper limits are shown as dashed lines, detections as solid lines. Blue lines correspond to the (sub)millimeter observations and orange lines to the Spitzer 70 $\mu $m observations as described in the legend of Fig. 5. The mass opacity used to convert flux density to dust mass with the standard optically thin emission model is $\rm \kappa = 1.7~cm^2~g^{-1}$ at 850 $\mu $m and $\propto $ $\lambda ^{-1}$ for $\lambda > 210~\mu$m. Additional information are in the text. (This figure is available in color in electronic form.)

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.3cm, angle=-90]{12306fg7.ps} \end{figure} Figure 7:

Detection rates of cold debris disks versus stellar masses (stellar types) for stars younger than 200 Myr. These rates and uncertainties are for disks having dust fractional luminosities larger than the limits shown in Fig. 8 of the (sub)mm surveys used.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.3cm, angle=-90]{12306fg8.ps} \end{figure} Figure 8:

Dust luminosity versus disk radius limits of the three (sub)mm surveys used to determine the cold disk fractions of ``young'' M-, FGK- and A-type stars. Shown are the dust luminosity fractions of the 19 youngest M-dwarfs of our sample (blue), of the 9 young A-stars (green), and of the 26 young FGK-stars (red) in the two 850 $\mu $m surveys of Wyatt et al. (2003) and of Najita & Williams (2005). All these stars are less than 200 Myr old. Most of the curves are upper limits (dashed lines). The 7 detections are marked by full lines. This plot emphasizes that for stars of lower masses (later stellar types), even though the surveys are more sensitive, fewer disks are detected. Note that the x-axis shows the single radius corresponding to the single temperature of a disk (ring) assumed infinitely narrow in our model. We consider the wide range of radii from 1 to 1000 AU as plausible for rings of debris. (This figure is available in color in electronic form.)

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.5cm, angle=-90]{12306fA1.ps} \end{figure} Figure A.1:

Variation in the temperature of a grain 100 $\mu $m in diameter exposed to both the radiation of the stellar field and the isotropic interstellar radiation field. This latter field dominates at some disk radius R that depends on the stellar luminosity. The saturation temperation of 4.9 K due to the interstellar field is consistent with the computation of Krügel (2003, p. 249). For M 6 only, the dashed line indicates the grain temperature when the interstellar radiation field is not included. (This figure is available in color in electronic form.)

Open with DEXTER
In the text

  \begin{figure} \includegraphics[width=6.5cm, angle=-90]{12306fA2.ps} \end{figure} Figure A.2:

Variation in temperature as a function of grain radius at 500 AU from the M 1.5 dwarf GJ526. Similar results are reported by Krügel (2003, p. 249). The discontinuity in the silicate curve arises from the piecewise-defined function $Q_{\rm abs}(\lambda ,a)$ adopted from Laor & Draine (1993). (This figure is available in color in electronic form.)

Open with DEXTER
In the text

  \begin{figure} \includegraphics[width=6.2cm, angle=-90]{12306fA3.ps} \end{figure} Figure A.3:

SED of carboneous dust around GJ526 based on our model fitted to the 1.2 mm flux density. Our model includes the collisional dust size distribution ${\rm d}N=a^{-3.5}{\rm d}a$ and the resulting non-uniform temperature for grains of various sizes computed in Fig. A.2. Superimposed is the corresponding grey-body model computed with the single grain temperature 4.9 K and standard mass opacity $\rm 1.7~cm^2g^{-1}$ at $\lambda=850~\mu$m scaled with the efficiency $\rm 210~\mu m / \lambda$ (see text). (This figure is available in color in electronic form.)

Open with DEXTER
In the text

  \begin{figure} \includegraphics[width=6.2cm, angle=-90]{12306fA4.ps} \end{figure} Figure A.4:

SED of silicate dust around GJ526 based on our model and fitted to the 1.2 mm flux density. Same comments as in Fig. A.3. (This figure is available in color in electronic form.)

Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.