Precise data on Leonid fireballs from all-sky photographic records

L. Shrbený; P. Spurný

doi:10.1051/0004-6361/200912305

Free Access

Issue		A&A Volume 506, Number 3, November II 2009


Page(s)		1445 - 1454
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/200912305
Published online		03 September 2009

A&A 506, 1445-1454 (2009)

Precise data on Leonid fireballs from all-sky photographic records

L. Shrbený^1,2 - P. Spurný¹

1 - Astronomical Institute of the Academy of Sciences v.v.i., Ondrejov Observatory, Czech Republic
2 - Department of Earth Science & Engineering, Imperial College London, SW7 2AZ, UK

Received 8 April 2009 / Accepted 29 June 2009

Abstract
In 1999, 2001, 2002, and 2006 favourable returns of Leonids occurred and were observable, at least partly, from Central Europe. We present results on 54 photographically recorded multi-station Leonid fireballs and their probable identification from five individual dust trails or the Leonid Filament. Atmospheric behaviour was studied on the basis of beginning and terminal heights, dynamic pressures, PE coefficients, and light curves. The apparent non-dependence of beginning heights on initial photometric mass suggests the existence of a height $h_{\lim} = 111 \pm 5$ km, which is the height where all Leonids reach an absolute magnitude of about -2 $^{\rm m}$ . Three different shapes of the light curves were recognized and a recently implemented photometric method was used for the determination of the brightness of the Leonids. The precise heliocentric orbits and geocentric radiants for 34 Leonids with known times of meteor passage are also presented.

Key words: techniques: photometric - meteors, meteoroids

1 Introduction

Leonids have one of the most variable activities among major meteor showers. The maximum of their activity occurs around November 18. Their activity increases approximately every 33 years with the return of their parent comet 55 P/Tempel-Tuttle to perihelion. The stream consist of a ribbon-like cloud of particles spread along the comet's orbit, which is called the Leonid Filament, and of smaller dust trails released from the comet in past returns. The Filament is the result of accumulation of debris in orbital resonances over the past 1000 years (Asher et al. 1999; Jenniskens & Betlem 2000); dust trails are responsible for occasional meteor storms. The last return of the comet to perihelion occurred in February 1998, and in the following several years, meteor outbursts with a Zenithal Hourly Rate (ZHR) of hundreds to thousands of meteors were observed (annual Leonids have ZHR about 13). Over the last decade or so, the Earth encountered the following dust trails: in 1998 the 1333 dust trail (the Fireball Night on November 16/17 was according to Asher et al. 1999 caused by the 1333 dust trail, according to Jenniskens 2006 rather by the Filament); in 1999 the 1899 and 1866 trails; in 2000 the 1932, 1733 and 1866 trails; in 2001 the 1767 and 1699 trails; in 2002 the 1767 and 1866 trails; and in 2006 the 1932 trail (McNaught & Asher 1999).

2 Instrumentation, observations and data processing

The multi-station photographic observation of fireballs in fireball networks represents a very efficient and precise method of recording the atmospheric interactions of larger meteoroids. During the short moment of meteoroid ablation, we can determine its atmospheric trajectory, orbit, light curve and basic physical properties. One of the most advanced operational fireball networks is the Czech part of the European Fireball Network (EN), where each station is equipped with the newest generation camera, the modern and sophisticated, completely Autonomous Fireball Observatory (AFO) (Spurný et al. 2007). The AFO imaging system consists of a Zeiss Distagon fish-eye objective (f/3.5, f = 30 mm) and a large-format sheet film ( $9 \times 12$ cm emulsion ILFORD FP4 125 with panchromatic spectral sensitivity approximately between 360 and 650 nm). All AFOs are equipped with a rotating shutter close to the focal plane to determine fireball velocity. At present we operate 11 stations almost uniformly deployed across the territory of the Czech Republic, but manually operated cameras with the same lenses and films were also in operation during all reported Leonid observations, except the last one in 2006.

The typical precision of measurement of any individual point on the luminous atmospheric trajectory for a fireball, up to approximately 200 km distance from a station, is 10-15 m. This precision proportionally decreases with the distance of the fireball from stations. In some ideal cases we can reliably detect fireballs at a distance of about 500 km from our territory. This enables us to observe fireballs over large parts of Central Europe. As well as direct fireball imaging, each AFO also includes an all-sky brightness sensor (radiometer) with a sampling rate of 500 measurements per second. Therefore, along with the accurate time of fireball passage and its duration, we also obtain a very detailed light curve. These sensors work reliably even under a cloudy sky, so we have basic information about fireball luminosity and its very approximate location even without photographic records. The time of meteor passage was also obtained using two additional methods. The first one, used in 1999 during the Dutch-Czech Leonid expedition, involves utilization of an all-sky intensified video camera; the second one involves utilization of a guided camera.

The frequency of the rotating shutter used significantly influences the precision of the determined velocity (especially for fast meteors like Leonids). The most common frequency used by AFOs gives 15 breaks on a meteor trail per second. During the Dutch-Czech Leonid expedition in 1999 a frequency of 45 breaks per second was used (cameras in the Czech Republic used 15 and 45); in 2001 cameras with frequencies of 15 and 21 breaks per second were used; in 2002 with 15 and 45.18; and in 2006 AFOs with frequencies of 15, 30, and 32.89 breaks per second were used.

In 1999, 2000, 2001, 2002, and 2006 the Earth's orbit intersected a few young dust trails, and the Leonid Filament. Multi-station fireballs were photographed in 1999 during two nights (15/16 and 18/19) in the Czech part of the EN, and two nights (17/18 and 18/19) in Spain (stations Punto Alto and Casa Nueva) by the same imaging system during the Dutch-Czech Leonid expedition. 13 double-station Leonids were photographed during the night of November 17/18, which covered the encounter with the 1899 dust trail. The year 2000 was adversely affected by weather, which resulted in no multi-station fireballs from the Czech part of the EN. In 2001, fireballs were photographed over two nights (14/15 and 17/18) in the Czech part of the EN. Two multi-station Leonids were recorded during the first night, and 20 fireballs during the second night. 2002 also was affected by bad weather conditions, and 10 multi-station fireballs were recorded above a small part of the Czech network during the night of November 18/19. Five multi-station Leonids were photographed in 2006 on November 15/16, 17/18 and 18/19.

Altogether, 54 fireballs were long and bright enough to be recorded photographically from more than one station, so that we can precisely determine all important parameters describing their atmospheric trajectories and basic physical properties. Unfortunately, only 34 fireballs have a precise time of passage, and thus only 34 heliocentric orbits could be reliably computed. All presented Leonid fireballs were measured and processed using our standard procedures (Ceplecha 1987; Borovicka et al. 1996). The Fishscan software, created by Dr. Jirí Borovicka, serves for positional and photometric measuring of fireballs on scanned copies of films. Therefore, all presented Leonid fireballs, besides precise atmospheric trajectories, also have precise Fishscan photometry.

$\begin{figure} \par\includegraphics[width=8.8cm]{12305fg1.eps} \end{figure}$

Figure 1:

Positions of individual dust trails (black ellipses - not real sizes) in years as presented by McNaught & Asher (1999). Vertical axes express distance $r_{\rm D}$ - $r_{\rm E}$ , where $r_{\rm D}$ is heliocentric distance of the dust trail's descending node and $r_{\rm E}$ heliocentric distance of the Earth at the same longitude, both in AU. Solar longitudes are expressed in J2000.0. Gray dots are positions of observed fireballs.

Open with DEXTER

Table 1: Atmospheric trajectories of the 1999, 2001, and 2006 Leonid fireballs with known time of meteor passage.

Fishscan photometry is a recently implemented method that uses the darkening of startrails on scanned negatives to determine the characteristic density curve and meteor brightness. Before the measurement, the image is corrected for decreasing sensitivity with distance from the center of projection (i.e. flat-fielded) using the factory curve for the Zeiss Distagon lens. The measured darkening of a star trail is corrected for star trailing velocity (daily motion). Stars are measured in wide interval of zenith distances and the actual extinction coefficient is determined together with the characteristic curve. When converting meteor darkening into magnitudes, the difference due to occultation by the rotating shutter (star images are occulted by the shutter, but the fireball image is not) and the fireball trailing velocity are taken into account. The Schwarzschild's coefficient of $0.80 \pm 0.05$ is assumed. Since the fireball is often the brightest object on image and the derived dependencies must be extrapolated, the standard deviations of fireball brightness may exceed one stellar magnitude in some cases.

3 Dust trails or filament

Positions of dust trails (black ellipses - not real sizes), as published by McNaught & Asher (1999), and positions of observed fireballs (gray dots, solar longitude corresponding to the time of the fireball passage) are plotted in Fig. 1. The vertical axes express the distance $r_{\rm D}$ - $r_{\rm E}$ , where $r_{\rm D}$ is the heliocentric distance of the dust trail's descending node, and $r_{\rm E}$ is the heliocentric distance of the Earth at the same longitude, both in AU. Solar longitudes are expressed in J2000.0.

According to positions of dust trails in 1999, observed meteor rates (Jenniskens 2006), and times of individual meteors (Tables 1 and 2), LEO02 to LEO14 most likely belong to the 1899 dust trail, and LEO15 to LEO17 probably belong to the 1866 trail, where activity lasted until a solar longitude of 236.4 $^\circ$ , when the Filament began to be more dominant (Jenniskens 2006). LEO01 belongs to the Filament. In 2001 it is hard to decide between trail or Filament. Meteors recorded on November 18 can belong to the 1767 dust trail, but its activity started approximately at $\lambda _{\odot} = 235.9^{\circ}$ (de La Peña et al. 2008; Gural et al. 2004; Jenniskens 2006) and observed fireballs LEO20 to LEO39 correspond to $\lambda _{\odot }$ between 235.71 $^\circ$ and 235.89 $^\circ$ . LEO18 and LEO19 most likely belong to the Filament. Leonids recorded in 2002 most likely belong (according to Fig. 1 and observed meteor rates Jenniskens 2006) to the 1800 or 1833 dust trails, however, this year was also affected by bad weather and only atmospheric trajectories are known. LEO54, photographed in 2006, probably belongs to the 1932 dust trail; the others most likely belong to the Filament.

4 Heights of atmospheric trajectories

All important parameters describing atmospheric trajectories are presented in Tables 1-3. A very interesting result is the non-dependence of beginning heights on the initial photometric mass (Fig. 2). The observed Leonid fireballs fulfill the same condition: beginning height, $h_{\rm B}$ , is equal to $111 \pm 5$ km for the range of photometric masses from $0.5 \times 10^{-1}$ to $2.1 \times 10^3$ g. The determination of the photometric masses depends very strongly on the luminous efficiency, $\tau$ , which is very difficult to derive for such fast meteors like the Leonids. For a mean initial velocity of 71.2 km s^-1 a value for $\log~\tau = -11.84$ (c.g.s. units with I = 1 for 0 stellar magnitude) was used (Ceplecha & McCrosky 1976), which corresponds to 2.2% of the total kinetic energy of mass loss. If we used an alternative value for $\tau$ from Revelle & Ceplecha (2001), which is dependent not only on velocity but also on mass, initial velocity, and bolide type (according to PE), we would derive an average value of 0.2%. This would lead to higher initial masses for the presented fireballs, but for consistency of the determination of the PE coefficient for all the fireballs in this paper we decided to keep the value of 2.2%. Other authors show an increasing dependency of beginning height on initial mass, but data are based on video observations (Jenniskens et al. 2008; Koten et al. 2004), or small cameras (Betlem et al. 2000), covering only a part of the sky and capable of detecting fainter meteors.

In our case the dependency is caused by the equipment used. The limiting apparent visual magnitude, which the meteor has to reach to be recorded on film by our all-sky camera, is about 0^m to -2^m (depends on angular velocity and observing conditions), and thus lower than the brightness of the actual beginning of the event. If we assume that all Leonids reach this limiting magnitude at some specific height, $h_{\lim}$ , then the fact that they are observed from different distances and with different slopes to the vertical would result in the spread of observed beginning heights around $h_{\lim}$ . This is exactly the observed dependency (Fig. 2). It means that there exists a height h $_{\lim}$ (equal to $111 \pm 5$ km), where all Leonids reach an absolute magnitude of approximately -2^m.

Table 2: Atmospheric trajectories of the 2001 and 2002 Leonid fireballs with unknown time of meteor passage.

Dependencies among initial photometric mass and the terminal height (black line), and the height of the maximum dynamic pressure (see explanation in Sect. 5) (dashed gray line), are plotted in Fig. 2. Both dependencies are decreasing functions of mass, which means that real terminal heights were not observed, but heights close to them. These fast cometary meteors often fragment at the end of the atmospheric trajectory into small particles that ablate very quickly, so the decrease of brightness is then faster than at the beginning of the meteor (this also holds for single-body solutions without fragmentation). The dependency of the maximum dynamic pressure shows that small meteoroids probably do not fragment and reach maximum dynamic pressure at their terminal height.

5 Dynamic pressures and PE coefficients

The dependency of dynamic pressure ( $p = \rho v^2$ ) on initial photometric mass is shown in Fig. 3. The dynamic pressures are determined at heights corresponding either to maximum pressure along the atmospheric trajectory (meteors with smooth light curves without flares) or at the first flare (often corresponds to the terminal flare). These flares likely correspond to a fragmentation and thus to the approximate strength of the material. The values of these dynamic pressures are listed in Table 3. Initial velocities were used to determine the dynamic pressures because the presented Leonids did not decelerate. There are only two exceptions - LEO02 and LEO04. These two Leonids, with a small inclination to the Earth's surface, likely experienced moderate deceleration, unfortunately not enough to determine a solution for the atmospheric motion (among others the ablation coefficient) using the gross-fragmentation model of Ceplecha et al. (1993). The model requires precisely measured values of heights and lengths for as many points as possible along the trajectory and a deceleration within the precision of these data. In the case of the fireballs described here, only a few final velocity points with deceleration were available. Spurný et al. (2000) published one Leonid fireball recorded in 1998, which fulfilled these conditions. The fireball was more than 150 km long and with a small inclination to the Earth's surface.

The approximate increase of dynamic pressure with mass is the result of the dependency of the dashed line in Fig. 2 (increasing mass means decreasing height and thus also increasing dynamic pressure). Most of the Leonids did not survive pressures higher than 0.02 MPa, which corresponds to their assumed cometary origin and fragility. The dependency of dynamic pressure on initial photometric mass, according to the type of the light curve (more details in the next section), is shown in Fig. 4. The fact that Leonids are fragile cometary meteors is confirmed also by their PE coefficients (Table 3). PE coefficients describe the empirical end height criterion that divides fireballs into four groups according to ablation abilities. The value of PE is a function of air density at the fireball terminal height, $\rho _{\rm E}$ , initial photometric mass, $m_{\infty }$ (with luminous efficiency according to Ceplecha & McCrosky 1976), initial velocity, v $_{\infty }$ , and zenith distance of the radiant at the fireball beginning, z (PE $= \log(\rho _{\rm E}) + A~\log(m_{\infty }) + B~\log(v_{\infty }) + C~\log(\cos~z)$ ). On the basis of values of the PE coefficients (Ceplecha & McCrosky 1976), more than one half of the Leonids discussed in the present work belong to the weakest type IIIB of the interplanetary matter; more than one third to type IIIA, and only less than 10% to type II (only LEO20 and LEO42 were long and bright enough to safely say that they are type II; no type II fireball had a terminal flare).

6 Light curves

Table 3: Physical data on the 1999, 2001, 2002, and 2006 Leonid fireballs.

In general, there are three types of light curves observed for the Leonids. The first type shows only one dominant flare near the end of a visual trajectory (from 3/4 to 9/10), after which the final fading portion of the light curve is very steep. This sudden end of the luminous trajectory is typical for bright fireballs of the PE type IIIB (the same type of light curve was observed for the 1998 Leonids (Spurný et al. 2000)). The second type shows quite symmetric shape, smooth course of brightness without flares, and looks like a light curve of a single-body model of a meteor. This light curve is typical for faint Leonid meteors and was observed for all the Leonids of November 17/18 in 1999, which belonged most likely to the 1899 dust trail. The third type, observed only for two Leonids, shows two humps of comparable brightness and duration. Members of this group are LEO15 (probably belongs to the 1866 dust trail) and LEO25 (maybe the 1767 dust trail), whose terminal flare corresponds to the highest observed dynamic pressure for the presented Leonids (0.194 MPa). An assignment of the presented Leonids to appropriate types of light curves is shown in the last column of Table 3.

Two Leonids of the first type of the light curve, LEO42 and LEO43, did not terminate their luminous trajectory right after the dominant flare, but continued down to lower heights and their end is similar to that of the second type. Also few Leonids of the second type exhibited additional events in their light curves. Five of them (LEO07, LEO12, LEO17, LEO21, LEO54) had a significant terminal flare (for example LEO21, Fig. 6); and four of them (LEO22, LEO26, LEO41, LEO49) had the flare at the maximum of the theoretical single-body light curve profile. LEO15, belonging to the third type, had a flare only at the second hump, while LEO25 had a flare at the first hump and showed a significant terminal flare. The first and the second type have the same relative frequency among observed light curves, approximately 48%, the rest of the Leonids, approximately 4%, belong to the third type.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12305fg2.eps} \end{figure}$	Figure 2: Dependencies of beginning and terminal height on initial photometric mass. The gray dashed line is the dependency for heights corresponding to the maximum dynamic pressure that was reached without fragmentation (more details in Sect. 5).
Open with DEXTER

Bright Leonid fireballs often leave persistent trains visible for several minutes after the passage of the fireball (Jenniskens 2006). For two of the presented fireballs, documented visual observations are available, both connected to observation of a persistent train. On November 18 2001, LEO27 was observed by Krocil (online database), who described it as a blue-white event that left a train visible by the naked eye for 5 to 10 min. This fireball was also recorded by Ondrejov's radiometer, with a time resolution of 1200 Hz (Spurný et al. 2001). According to photographic records, the fireball lasted for about 0.7 s but the radiometric data show an event lasting for 1.1 s, suggesting a decrease in brightness consistent with a persistent train. As we can see in Fig. 5, the decrease of intensity is an exponencial function of time $I \approx {\rm e} ^{At}$ , where A = -4.69. After the disappearance of the meteor, the absolute brightness of the train was about -8.5 mag, lasting for 0.5 s, and disappearing when it reached -6 mag (the limiting sensitivity of the detector). Most likely this was an afterglow phase of the persistent train, which was formed during expressive outburst at the end of the atmospheric trajectory, where the body fragmented into a large number of small particles that gradually ablated. Intensive increasing of the brightness started after 0.25 s of the trajectory, at a height of about 100 km (and a dynamic pressure of 0.003 MPa). The second visual fireball designated LEO54 on November 19 2006 was observed by Gembec (online database). He described a long-lasting train left by the fireball. The persistant train had a slightly ciliated appearance, and described a shape similar to a capital letter V. This fireball was not bright enough (-7.4 mag) to cause a wake, or a train observable either on images or by radiometers. However, having initial mass of 3.6 g and speed of 71.4 km s^-1 ( $E_{\rm k} = 9$ MJ), it caused a persistent train.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12305fg3.eps} \end{figure}$	Figure 3: Dependency of dynamic pressure (explanation in Sect. 5), p, on initial photometric mass, $m_{\rm inf}$ , for the 1999, 2001, 2002, and 2006 Leonids.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12305fg4.eps} \end{figure}$	Figure 4: Dependency of dynamic pressure (explanation in Sect. 5), p, on initial photometric mass, $m_{\rm inf}$ , for individual types of the light curve (explanation in Sect. 6).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=0.46\textwidth]{12305fg5.eps} \end{figure}$	Figure 5: Exponential courses of decrease of brightness of the Leonids LEO18, LEO27 and LEO51. LEO18 and LEO27 were recorded by Ondrejov's radiometer with a time resolution of 1200 Hz; and LEO51 by AFO's brightness sensor with a sampling rate of 500 measurements per second.
Open with DEXTER

For two fireballs we can see in the light curve a decrease in brightness of the persistant train - LEO18 and LEO51. According to photographic records, LEO18 lasted less than 0.8 s, but the light curve lasted for 2.6 s. In Fig. 5 there is a 1.8 s long exponential dependency of the train's brightness on time $I \approx {\rm e} ^{At}$ , where A = -1.22. After the disappearance of the meteor, the absolute brightness of the train was about -7.5 mag, and lasted 1.8 s. It disappeared when it reached about -5 mag. An intensive increase in brightness started after 0.5 s of the atmospheric trajectory, at a height of about 90 km (and a dynamic pressure of 0.015 MPa). In the light curve of LEO51 the train is visible for only about 0.1 s after the meteor disappeared, when its brightness was about -8 mag. It disappeared when it reached -5 mag (the sensitivity of the detector).

$\begin{figure} \par\mbox{\includegraphics[width=6cm]{12305f6a.eps} \includegraph... ...dth=6cm]{12305f6e.eps}\includegraphics[width=6cm]{12305f6f.eps} } \end{figure}$	Figure 6: Light curves from AFO's brightness sensors of the 2001 and 2006 Leonid fireballs. The 2001 Leonids were recorded by Ondrejov's radiometer with a time resolution of 1200 Hz; and the 2006 Leonids by AFO's brightness sensor with a sampling rate of 500 measurements per second.
Open with DEXTER

These three fireballs reached a maximum absolute brightness (corresponding to flares) at a height of 83 km, which corresponds to a dynamic pressure of 0.048 to 0.050 MPa (differing initial velocities). They all belong to the IIIB type and the heights of their persistent trains (assumed from merged breaks) correspond to values of the central altitude of trains published by Yamamoto et al. (2004). Nevertheless, no dependency on the rate of decrease of brightness (decay coefficient A), meteoroid initial mass, initial kinetic energy or duration of the train was observed. Perhaps a higher number of observations of this type of event are required, and/or more sensitive radiometers. According to Borovicka & Jenniskens (2000) the decay of line intensity depends on excitation potential, not on transition probability. This means that the decay is due to a decrease in temperature (not density), and thus we can say that there were different courses of temperature (across the cross-section) in the trains of these three fireballs.

Table 4: Radiants and orbital elements (J2000.0) of the 1999, 2001, and 2006 Leonid fireballs with known time of meteor passage.

7 Radiants and orbits

Radiant positions, geocentric velocity and orbital elements for all 34 Leonid fireballs with known time of passage are presented in Table 4. The positions of all the observed Leonid geocentric radiants, normalized to solar longitude 235.1 $^\circ$ (maximum of annual activity), are plotted in Fig. 7. The radiant motion used is according to IAU MDC web pages for a right ascension of 0.66 $^\circ$ per degree of solar longitude, and for a declination of -0.33 $^\circ$ per degree of solar longitude. The mean radiant is also plotted and is derived from all radiants except LEO25. Mean radiant values are $\alpha = 153.6 \pm 0.4$ deg, $\delta = 22.0 \pm$ 0.4 deg, which corresponds to the radiant position of the Leonid Fireball Night in 1998 ( $\alpha = 153.63^{\circ }$ , $\delta = 22.04^{\circ}$ for $\lambda _{\odot} = 235.1 ^{\circ}$ ) (Betlem et al. 1999). Mean radiants in individual years and for individual dust trails differ from each other but merge in the range of one standard deviation. Radiant of the 1899 dust trail in 1999 has values $\alpha = 153.5 \pm 0.5$ deg, $\delta = 21.8~\pm~~ 0.4$ deg and its position and halo-like structure corresponds to results published by Betlem et al. (2000) and Trigo-Rodriguez et al. (2002). The radiant of the 1866 dust trail in 1999 has a position $\alpha = 153.6 \pm 0.5$ deg, $\delta = 22.02 \pm 0.09$ deg. The radiant of Leonid fireballs on November 18, 2001 is $\alpha = 153.7 \pm 0.4$ deg, $\delta = 22.1 \pm 0.3$ deg (LEO25 not taken into account).

The dependency of orbital elements on the longitude of the ascending node and right ascension of the geocentric radiant on the node are presented in Figs. 8 and 9. Linear dependencies are fitted only for meteors belonging to the Filament (LEO01, LEO18, LEO19, LEO50 to LEO53). The gray dependency in Fig. 8 is a linear fit for theoretical radiant motion of 0.66 $^\circ$ in right ascension per degree of solar longitude. Trigo-Rodriguez et al. (2002) presented values for orbital elements of the 1899 dust trail meteoroids observed in 1999 which are very similar to each other, but as we can see in Figs. 8 and 9, a large spread of individual elements appears for fireballs recorded during a short period of activity (and so likely belonging to one dust trail). The same observation holds also for Leonids from the 1866 dust trail in the same year, and for Leonids in 2001 (which likely belong to the Filament, but according to this spread of elements rather to the 1767 dust trail). The observed spread in individual elements corresponding to individual years (dust trails) is much larger than the accuracy of the elements.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12305fg7.eps} \end{figure}$	Figure 7: Geocentric radiants of the 1999, 2001, and 2006 Leonids for solar longitude 235.1 $^\circ$ . Mean radiant position is determined from 33 Leonid fireballs (LEO25 was not taken into account).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=17cm,clip]{12305fg8.eps} \end{figure}$

Figure 8:

Dependencies of right ascension of observed geocentric radiants and inclination on the longitude of the ascending node for the 1999, 2001, and 2006 Leonids. Vertical lines denote ascending nodes 235.32 $^\circ$ , 235.80 $^\circ$ , and 236.28 $^\circ$ corresponding to storm fireballs. Black linear fit corresponds to likely Filament no-storm Leonids. The gray linear fit describes theoretical radiant motion +0.66 $^{\circ }/^{\circ }$ in RA. R² is the coefficient of determination describing the accuracy of the fit.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=17cm]{12305fg9.eps} \end{figure}$

Figure 9:

Dependencies of the argument of perihelion and perihelion distances on the longitude of the ascending node for the 1999, 2001, and 2006 Leonids. Vertical lines denote ascending nodes 235.32 $^\circ$ , 235.80 $^\circ$ , and 236.28 $^\circ$ corresponding to storm fireballs. Black linear fit corresponds to likely Filament no-storm Leonids. R² is the coefficient of determination describing the accuracy of the fit.

Open with DEXTER

Four Leonids (LEO10, LEO32, LEO34, LEO51) have initial velocities much lower than that of the mean (71.2 km s^-1), which results in orbits with semimajor axes significantly smaller than the mean of all orbits. This was observed previously by Betlem et al. (1999) and Trigo-Rodriguez et al. (2002). Betlem et al. (1999) concluded that this can only occur after a close encounter with Earth, and that in order to detect a significant number of such meteoroids, the Earth would have had to cross appropriate dust trails numerous times in the past. Since the Leonids are very fast and their atmospheric trajectories are short, one of the less accurate observed parameter is velocity. Due to this fact, only one meteor with a known time of passage, LEO10, is determined with sufficient accuracy that we can be confident that it could have experienced a previous close encounter with the Earth. LEO32 and LEO34, with unknown times of passage, may have experienced close encounters with the Earth (their semimajor axes determined from approximate radiant position have values of 2.6 and 2.2 AU, respectively).

8 Conclusions

Results of atmospheric trajectories and physical properties of 54 Leonid fireballs and the orbits of 34 of them are presented. These fireballs were recorded by all-sky photographic cameras during three nights in November 1999, two nights in 2001, one night in 2002 and three nights in 2006. Our main conclusions are as follows:

Five individual dust trails (released from the comet in 1800, 1833, 1866, 1899, 1932) were identified as probable sources of some of the observed Leonid fireballs, and the next trail (1767) as a less probable source. In each year fireballs from the Filament were also photographed (except for 2002).
An apparent non-dependence of beginning heights on initial photometric mass was observed and recognized as a result of the use of all-sky cameras. Nevertheless, this non-dependence suggests the existence of a height 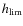$h_{\lim}$ (equal to 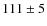$111 \pm 5$ km) which is the height where all Leonids reach an absolute magnitude of about -2 $^{\rm m}$ .
Most of the observed Leonids did not survive pressures higher than 0.02 MPa. The highest dynamic pressure of 0.19 MPa was observed in the terminal flare of LEO25, which was the deepest penetrating Leonid fireball among those studied.
According to atmospheric behavior and the PE criterion we can conclude that the parent comet 55P/Tempel-Tuttle is not homogeneous. Three different fireball types were observed among the presented Leonids: II, IIIA, and IIIB. The most numerous is type IIIB, which was derived for more than one half of the fireballs.
Two main types of light curves were recognized for the Leonids. The first type shows only one dominant flare near the end of a visual trajectory, after which the final fading portion of the light curve is very steep. This sudden end of the luminous trajectory is typical for bright fireballs of the PE type IIIB. The second type shows a symmetric shape, smooth course of brightness without flares, and looks like the light curve of a single-body model of a meteor. This light curve is typical for faint Leonid meteors.
The mean geocentric radiant (here normalized to solar longitude 235.1 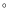$^\circ$ ) agrees with the position of the geocentric radiant for Leonids from the 1998 Fireball Night, and a halo-like structure of radiants was recognized for meteors from the 1899 dust trail in 1999.
A significant spread in orbital elements among meteoroids belonging to one dust trail was observed.

Acknowledgements

The authors are indebted to Dutch Meteor Society teams (especially to Hans Betlem) that participated in the 1999 Leonid campaign and to all observers who manually operated our all-sky cameras either in the Czech Republic or in Spain. This work was supported by grant No. 205/08/0411 of the GA CR, and EU grant MRTN-CT-2006-035519. The institutional research plan number is AV0Z10030501.

References

Asher, D. J., Bailey, M. E., & Emel'Yanenko, V. V. 1999, MNRAS, 304, L53 [NASA ADS] [CrossRef]
Betlem, H., Jenniskens, P., van't Leven, J., et al. 1999, Meteoritics and Planetary Science, 34, 979 [NASA ADS]
Betlem, H., Jenniskens, P., Spurný, P., et al. 2000, Earth Moon and Planets, 82, 277 [NASA ADS] [CrossRef]
Borovicka, J., & Jenniskens, P. 2000, Earth Moon and Planets, 82, 399 [NASA ADS] [CrossRef]
Borovicka, J., Spurny, P., & Keclikova, J. 1996, in Positional Astronomy and Celestial Mechanics, ed. A. Lopez Garcia, E. I. Yagudina, M. J. Martinez Uso, & A. Cordero Barbero, 39
Ceplecha, Z. 1987, Bull. Astron. Inst. Czechosl., 38, 222 [NASA ADS]
Ceplecha, Z., & McCrosky, R. E. 1976, J. Geophys. Res., 81, 6257 [NASA ADS] [CrossRef]
Ceplecha, Z., Spurny, P., Borovicka, J., et al. 1993, A&A, 279, 615 [NASA ADS]
de La Peña, S., Avery, S. K., & Avery, J. P. 2008, Icarus, 196, 164 [NASA ADS] [CrossRef]
Gural, P. S., Jenniskens, P., Koop, M., et al. 2004, Adv. Space Res., 33, 1501 [NASA ADS]
Jenniskens, P. 2006, Meteor Showers and their Parent Comets, ed. P. Jenniskens
Jenniskens, P., & Betlem, H. 2000, ApJ, 531, 1161 [NASA ADS] [CrossRef]
Jenniskens, P., de Kleer, K., Vaubaillon, J., et al. 2008, Icarus, 196, 171 [NASA ADS] [CrossRef]
Koten, P., Borovicka, J., Spurný, P., Betlem, H., & Evans, S. 2004, A&A, 428, 683 [NASA ADS] [CrossRef] [EDP Sciences]
McNaught, R. H., & Asher, D. J. 1999, WGN, Journal of the International Meteor Organization, 27, 85
online database: http://meteor.asu.cas.cz/db/report
Revelle, D. O., & Ceplecha, Z. 2001, in Proc. of the Meteoroids 2001 Conf., ESA SP-495, 507
Spurný, P., Betlem, H., van't Leven, J., et al. 2000, Meteoritics and Planetary Science, 35, 243 [NASA ADS]
Spurný, P., Spalding, R. E., & Jacobs, C. 2001, in Proc. of the Meteoroids 2001 Conf., ESA SP-495, 135
Spurný, P., Borovicka, J., & Shrbený, L. 2007, in IAU Symp. 236, ed. G. B. Valsecchi, D. Vokrouhlický, & A. Milani, 121
Trigo-Rodriguez, J. M., Llorca, J., & Fabregat, J. 2002, in Asteroids, Comets, and Meteors: ACM, ed. B. Warmbein, ESA SP, 500, 217
Yamamoto, M.-Y., Toda, M., Higa, Y., Maeda, K., & Watanabe, J.-I. 2004, Earth Moon and Planets, 95, 279 [NASA ADS] [CrossRef]

All Tables

Table 1: Atmospheric trajectories of the 1999, 2001, and 2006 Leonid fireballs with known time of meteor passage.

Table 2: Atmospheric trajectories of the 2001 and 2002 Leonid fireballs with unknown time of meteor passage.

Table 3: Physical data on the 1999, 2001, 2002, and 2006 Leonid fireballs.

Table 4: Radiants and orbital elements (J2000.0) of the 1999, 2001, and 2006 Leonid fireballs with known time of meteor passage.

All Figures

$\begin{figure} \par\includegraphics[width=8.8cm]{12305fg1.eps} \end{figure}$	Figure 1: Positions of individual dust trails (black ellipses - not real sizes) in years as presented by McNaught & Asher (1999). Vertical axes express distance $r_{\rm D}$ - $r_{\rm E}$ , where $r_{\rm D}$ is heliocentric distance of the dust trail's descending node and $r_{\rm E}$ heliocentric distance of the Earth at the same longitude, both in AU. Solar longitudes are expressed in J2000.0. Gray dots are positions of observed fireballs.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12305fg2.eps} \end{figure}$	Figure 2: Dependencies of beginning and terminal height on initial photometric mass. The gray dashed line is the dependency for heights corresponding to the maximum dynamic pressure that was reached without fragmentation (more details in Sect. 5).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12305fg3.eps} \end{figure}$	Figure 3: Dependency of dynamic pressure (explanation in Sect. 5), p, on initial photometric mass, $m_{\rm inf}$ , for the 1999, 2001, 2002, and 2006 Leonids.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12305fg4.eps} \end{figure}$	Figure 4: Dependency of dynamic pressure (explanation in Sect. 5), p, on initial photometric mass, $m_{\rm inf}$ , for individual types of the light curve (explanation in Sect. 6).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=0.46\textwidth]{12305fg5.eps} \end{figure}$	Figure 5: Exponential courses of decrease of brightness of the Leonids LEO18, LEO27 and LEO51. LEO18 and LEO27 were recorded by Ondrejov's radiometer with a time resolution of 1200 Hz; and LEO51 by AFO's brightness sensor with a sampling rate of 500 measurements per second.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=6cm]{12305f6a.eps} \includegraph... ...dth=6cm]{12305f6e.eps}\includegraphics[width=6cm]{12305f6f.eps} } \end{figure}$	Figure 6: Light curves from AFO's brightness sensors of the 2001 and 2006 Leonid fireballs. The 2001 Leonids were recorded by Ondrejov's radiometer with a time resolution of 1200 Hz; and the 2006 Leonids by AFO's brightness sensor with a sampling rate of 500 measurements per second.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12305fg7.eps} \end{figure}$	Figure 7: Geocentric radiants of the 1999, 2001, and 2006 Leonids for solar longitude 235.1 $^\circ$ . Mean radiant position is determined from 33 Leonid fireballs (LEO25 was not taken into account).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm,clip]{12305fg8.eps} \end{figure}$	Figure 8: Dependencies of right ascension of observed geocentric radiants and inclination on the longitude of the ascending node for the 1999, 2001, and 2006 Leonids. Vertical lines denote ascending nodes 235.32 $^\circ$ , 235.80 $^\circ$ , and 236.28 $^\circ$ corresponding to storm fireballs. Black linear fit corresponds to likely Filament no-storm Leonids. The gray linear fit describes theoretical radiant motion +0.66 $^{\circ }/^{\circ }$ in RA. R² is the coefficient of determination describing the accuracy of the fit.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm]{12305fg9.eps} \end{figure}$	Figure 9: Dependencies of the argument of perihelion and perihelion distances on the longitude of the ascending node for the 1999, 2001, and 2006 Leonids. Vertical lines denote ascending nodes 235.32 $^\circ$ , 235.80 $^\circ$ , and 236.28 $^\circ$ corresponding to storm fireballs. Black linear fit corresponds to likely Filament no-storm Leonids. R² is the coefficient of determination describing the accuracy of the fit.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.