| Issue |
A&A
Volume 506, Number 3, November II 2009
|
|
|---|---|---|
| Page(s) | 1249 - 1259 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200809913 | |
| Published online | 18 August 2009 | |
A&A 506, 1249-1259 (2009)
Supernova progenitor stars in the initial range of 23 to 33 solar masses and their relation with the SNR Cassiopeia A
B. Pérez-Rendón1,2 - G. García-Segura2 - N. Langer3
1 - Departamento de Investigación en Física, Universidad de Sonora, Apdo. Postal 5-088, Hermosillo, Sonora, México
2 -
Instituto de Astronomía, Universidad Nacional Autónoma de México, Apdo. Postal 877, Ensenada 22800, Baja Californa, México
3 -
Astronomical Institute, Utrecht University, PO Box 80000, 3508 TA Utrecht, The Netherlands
Received 5 April 2008 / Accepted 20 March 2009
Abstract
Context. Multi wavelength observations of Cassiopeia A (Cas A)
have provided us with strong evidence of circumstellar material
surrounding the progenitor star. It has been suggested that its
progenitor was a massive star with strong mass loss. But, despite the
large amount of observational data from optical, IR, radio, and x-ray
observations, the identity of Cas A progenitor is still elusive.
Aims. In this work, we computed stellar and circumstellar
numerical models to look for the progenitor of Cas A. The models
are compared with the observational constraints that come from chemical
observed abundances and dynamical information.
Methods. We first computed stellar evolution models to get
time-dependent wind parameters and surface abundances using the code
STERN. To explore the range of masses proposed by several previous
works, we chose a set of probable progenitor stars with initial masses
of 23, 28, 29, 30, and 33 ![]() ,
with initial solar composition (Y=0.28, Z=0.02)
and mass loss. The derived mass loss rates and wind terminal velocities
are used as inner boundary conditions in the explicit, hydrodynamical
code ZEUS-3D to simulate the evolution of the circumstellar medium. We
simplified the calculations by using one-dimensional grids in the main
sequence and red super-giant (RSG) stages, and two-dimensional grids
for the post-RSG evolution and supernova (SN) blast wave.
,
with initial solar composition (Y=0.28, Z=0.02)
and mass loss. The derived mass loss rates and wind terminal velocities
are used as inner boundary conditions in the explicit, hydrodynamical
code ZEUS-3D to simulate the evolution of the circumstellar medium. We
simplified the calculations by using one-dimensional grids in the main
sequence and red super-giant (RSG) stages, and two-dimensional grids
for the post-RSG evolution and supernova (SN) blast wave.
Results. Our stellar set gives distinct SN progenitors: RSG,
luminous blue super giants (LBSGs), and Wolf-Rayet (WR) stars. We named
these type of stars ``luminous blue super giant'' (LBSGs) to
distinguish them from normal blue super giants (BSGs) of much lower
initial masses. The 23 ![]() star explodes as an RSG in a
star explodes as an RSG in a
![]() dense, free-streaming wind surrounded by a thin, compressed, RSG shell. The 28
dense, free-streaming wind surrounded by a thin, compressed, RSG shell. The 28
![]() star explodes as an LBSG, and the SN blast wave interacts with a low
density, free streaming wind surrounded by an unstable and massive
``RSG+LBSG'' shell. Finally, the 30 and 33
star explodes as an LBSG, and the SN blast wave interacts with a low
density, free streaming wind surrounded by an unstable and massive
``RSG+LBSG'' shell. Finally, the 30 and 33 ![]() stars explode as WR stars surrounded by fast WR winds that
terminate in a highly fragmented ``WR+RSG shell''. We compared the
surface chemical abundances of our stellar models with the
observational abundances in Cas A. The abundance analysis shows
that the progenitor was a star with an initial mass of about 30
stars explode as WR stars surrounded by fast WR winds that
terminate in a highly fragmented ``WR+RSG shell''. We compared the
surface chemical abundances of our stellar models with the
observational abundances in Cas A. The abundance analysis shows
that the progenitor was a star with an initial mass of about 30 ![]() ,
while the hydrodynamical analysis favors progenitors with initial masses around 23.
,
while the hydrodynamical analysis favors progenitors with initial masses around 23.
Key words: stars: evolution - ISM: kinematics and dynamics - ISM: supernova remnants - ISM: bubbles - ISM: individual objects: Cassiopeia A
1 Introduction
Cas A is the youngest galactic SN remnant (![]() 327 years old
Thorstensen et al. 2001) and it has been extensively studied in all wavelengths from
radio to
327 years old
Thorstensen et al. 2001) and it has been extensively studied in all wavelengths from
radio to ![]() -rays. The observational data obtained in all
wavelengths has provided us with a wide set of observational constraints
that, taken together, put strong limits on the nature of its progenitor.
Optical emission in Cas A shows an expanding ring of
-rays. The observational data obtained in all
wavelengths has provided us with a wide set of observational constraints
that, taken together, put strong limits on the nature of its progenitor.
Optical emission in Cas A shows an expanding ring of
![]() 4
4![]() in diameter, which gives a radius of 2 pc, assuming a
distance of 3.4 kpc (Reed et al. 1995),
and it comes mainly from three distinctive types of objects:
(1) The fast moving knots (FMKs) with high velocities
(
in diameter, which gives a radius of 2 pc, assuming a
distance of 3.4 kpc (Reed et al. 1995),
and it comes mainly from three distinctive types of objects:
(1) The fast moving knots (FMKs) with high velocities
(![]() 4000-6000 km s-1)
that seem devoid of hydrogen and are enhanced in oxygen and other heavy
elements synthesized from stellar O burning (Si, S, Ca, Ar). Their
high velocities and chemical composition imply that they are material
ejected in the SN explosion as shrapnel from the stellar core or
mantle (Johnston & Yahil 1984). Most of the FMKs with
4000-6000 km s-1)
that seem devoid of hydrogen and are enhanced in oxygen and other heavy
elements synthesized from stellar O burning (Si, S, Ca, Ar). Their
high velocities and chemical composition imply that they are material
ejected in the SN explosion as shrapnel from the stellar core or
mantle (Johnston & Yahil 1984). Most of the FMKs with ![]()
![]() are located in the optical
main shell at
are located in the optical
main shell at ![]() 2 pc, although faster FMKs lies on the ``jet'';
(2) The quasi stationary floculii (QSFs) are optical knots with lower velocities
(
2 pc, although faster FMKs lies on the ``jet'';
(2) The quasi stationary floculii (QSFs) are optical knots with lower velocities
(![]()
![]() ), and strong spectral lines of helium and nitrogen, showing high N/H and He/H ratios (N/H
), and strong spectral lines of helium and nitrogen, showing high N/H and He/H ratios (N/H ![]() 10 and He/H
10 and He/H ![]() 5-10; Chevalier & Kirshner 1978) and they are located closer to the star, with average radii of
5-10; Chevalier & Kirshner 1978) and they are located closer to the star, with average radii of ![]() 1.5 pc;
(3) The nitrogen knots (NKs) have the highest velocities (
1.5 pc;
(3) The nitrogen knots (NKs) have the highest velocities (![]() 7000-9000 km s-1) and are distributed outside of the main, optical emission shell at an average radius of
7000-9000 km s-1) and are distributed outside of the main, optical emission shell at an average radius of ![]() 3 pc. Detected by Fesen (2001), the NKs spectra are dominated by two [N II] lines in the
4500-7500
3 pc. Detected by Fesen (2001), the NKs spectra are dominated by two [N II] lines in the
4500-7500 ![]() spectral range, and apparently, the NKs were ejected with a uniform, high velocity.
Their N to H
spectral range, and apparently, the NKs were ejected with a uniform, high velocity.
Their N to H![]() flux ratios imply N/H
flux ratios imply N/H ![]() 10-30 times solar abundances.
10-30 times solar abundances.
Cas A also shows strong emission in other wavelengths: radio
emission is generally associated with the contact discontinuity (Vink 2005). Bulk x-ray emission comes from hot material shocked by the SN shock fronts (Fabian et al. 1980). Soft x-rays have been detected associated to QSFs (De Laney et al. 2004)
and hard x-ray filaments are associated with the forward and reverse
shocks. The external x-ray filaments are associated with the forward
shock wave at an average distance of
![]() (
(
![]() pc) to the emission center, and evidence has been found about the reverse
shock position in an average radius of
pc) to the emission center, and evidence has been found about the reverse
shock position in an average radius of
![]() (
(
![]() pc)
to the x-ray emission centroid (Gotthelf et al. 2001). Proper
motion measurements made in optical, radio, and x-rays show variations
in the expansion rate from 0.1% to 0.3% yr-1 (Thorstensen et al. 2001).
pc)
to the x-ray emission centroid (Gotthelf et al. 2001). Proper
motion measurements made in optical, radio, and x-rays show variations
in the expansion rate from 0.1% to 0.3% yr-1 (Thorstensen et al. 2001).
Despite all the observational data from optical, infrared, radio,
and x-rays, the identity of Cas A progenitor has remained ambiguous. It
has been suggested that the progenitor was a massive star with a strong
mass-loss rate. Using optical abundances, Peimbert & van den Bergh (1971) and Chevalier (1976)
proposed that the Cas A progenitor star lost the H-He envelope
previous to the SN explosion and that the QSFs are remnants of that
material. Lamb (1978) explained
the nitrogen enrichment of QSFs as the result of CNO burning in
combination with mass loss. Based on the nitrogen abundances, many
authors have proposed that Cas A is the result of the explosion of a
WN star (Peimbert 1971; Fesen et al. 1987).
QSFs are thought to be RSG wind-shocked by the WR progenitor wind previous to the SN (García-Segura et al. 1996a,b).
The NKs are thought to be expelled from the photosphere of the
progenitor star at the SN explosion, and they are the evidence that the
progenitor star must have a nitrogen-rich photosphere, but is
H-deficient. Some authors suggested a RSG progenitor (Chevalier &
Oishi 2003) or a blue super giant (BSG) progenitor (Borkowski et al. 1996),
based on the CSM and shock front dynamics. Binary scenarios for the
Cas A progenitor have also been discussed by Young et al.
(2005). However, most authors agree that the progenitor stellar mass
(at ZAMS) lies between 20 and 35 ![]() with strong mass loss (Fabian et al. 1980; Fesen et al. 1987; Jansen et al. 1988; Vink et al. 1996; García-Segura et al. 1996a,b; Young et al. 2005).
with strong mass loss (Fabian et al. 1980; Fesen et al. 1987; Jansen et al. 1988; Vink et al. 1996; García-Segura et al. 1996a,b; Young et al. 2005).
Generally, hydrodynamical calculations of the CSM assumed idealized winds with constant properties, but the stellar winds depend on stellar luminosities, masses, radii, and metallicities so the wind parameters change as the stars evolve (Nieuwenhuijzen & de Jager 1990). More realistic models, however, require a prescription for the mass-loss rate and stellar wind velocity as the star evolves in the Hertzpung-Rusell (HR) diagram, coupling the evolution of the CSM to the star itself. The stellar wind interacts with the surrounding matter and the behavior of the CSM is tightly bound to the stellar evolution.
In this work we have combined the observed chemical abundances and dynamical information to make constraints for the Cas A progenitor, and compare the observations with our models to find the progenitor mass. We computed theoretical models of stellar and circumstellar evolution for stars in the mass range generally accepted by most authors.
We used the hydrodynamic, stellar evolution code STERN to build up a
set of evolutionary, non-rotating, stellar models with initial masses
in the range from 23 to 33 ![]() ,
with solar composition and mass loss. From our stellar models, we
obtained surface chemical abundances, mass-loss rates, and wind
velocities as a function of time during the whole stellar evolution,
from zero age main sequence (ZAMS) up to end-of-core O burning (i.e.,
almost pre-SN stage). Thereafter, we used the mass-loss rates and wind
velocities, and a prescription for the SN ejecta, to build up numerical
models of the CSM evolution, to compare them with the dynamical and
morphological features of Cas A. To simulate the CSM and the SN
blast wave, we used the ZEUS-3D code , using the stellar evolution
outputs as inner boundary conditions.
,
with solar composition and mass loss. From our stellar models, we
obtained surface chemical abundances, mass-loss rates, and wind
velocities as a function of time during the whole stellar evolution,
from zero age main sequence (ZAMS) up to end-of-core O burning (i.e.,
almost pre-SN stage). Thereafter, we used the mass-loss rates and wind
velocities, and a prescription for the SN ejecta, to build up numerical
models of the CSM evolution, to compare them with the dynamical and
morphological features of Cas A. To simulate the CSM and the SN
blast wave, we used the ZEUS-3D code , using the stellar evolution
outputs as inner boundary conditions.
The paper is organized as follows. Section 2 describes the computational methods and the input physics used in our numerical models. Section 3 describes the stellar evolution models from ZAMS to pre-SN. Section 4 shows the hydrodynamical simulations of the CSM covering the whole stellar evolution. The hydrodynamical simulations also includes the SN ejecta and the interaction with the CSM for 1000 yr after the explosion. Section 5 compare our numerical results with several observational constraints for Cas A. Finally, Sect. 6 gives a summary and our conclusions.
2 Computational methods
The numerical methods used in this work are similar to those in García-Segura et al. (1996a,b, hereafter GLM96AB). The stellar models were produced with the stellar code STERN (Langer et al. 1985; Heger 1998) for stars with 23, 28, 29, 30, and 33 ![]() (at ZAMS) with solar metallicity (Y = 0.28; Z = 0.02) and meteoritic proportion by Grevesse & Noels (1993). All models assume single stars without stellar rotation.
We adopted the OPAL opacities by Iglesias & Rogers (1996), equation of state from Langer
et al. (1988), and an external boundary condition to set a stellar atmosphere in expansion (Heger & Langer 1996). The network of nuclear reactions includes 35 isotopes,
(at ZAMS) with solar metallicity (Y = 0.28; Z = 0.02) and meteoritic proportion by Grevesse & Noels (1993). All models assume single stars without stellar rotation.
We adopted the OPAL opacities by Iglesias & Rogers (1996), equation of state from Langer
et al. (1988), and an external boundary condition to set a stellar atmosphere in expansion (Heger & Langer 1996). The network of nuclear reactions includes 35 isotopes,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and the reaction rates from Caughlan & Fowler (1988), except for the
,
and the reaction rates from Caughlan & Fowler (1988), except for the
![]() rate where we used the rate of Caughlan & Fowler (1988)
multiplied by 1.7. We used the Ledoux criterion for stellar
convection, and the processes of convective transport was considered as
diffusive processes according to Langer et al. (1985). Convective overshooting was taken into account during core H-burning with an effective convective,
overshooting distance of 0.2 times the local pressure scale height
(Stothers & Chin 1991). Also we adopt a mixing-length parameter of
rate where we used the rate of Caughlan & Fowler (1988)
multiplied by 1.7. We used the Ledoux criterion for stellar
convection, and the processes of convective transport was considered as
diffusive processes according to Langer et al. (1985). Convective overshooting was taken into account during core H-burning with an effective convective,
overshooting distance of 0.2 times the local pressure scale height
(Stothers & Chin 1991). Also we adopt a mixing-length parameter of
![]() in the main sequence. In the RSG the
in the main sequence. In the RSG the ![]() parameter was set to 2.0 to avoid dynamical instabilities in the
outer envelope of our models related to high radiation pressure and
partial ionization of the gases in the outer layers (Stothers &
Chin 2001). In the calculations, we adopted the empirical formulation of the mass-loss rate by Nieuwenhuijzen & de Jager (1990)
for all evolutionary stages, except in the RSG and WR phases.
Mass-loss rates in the upper end of the HR diagram are uncertain by a
large factor, particularly for RSG stars (Chiosi & Maeder 1986).
In the RSG phase we used the Nieuwenhuijzen & de Jager mass
loss rate multiplied by a factor of 2.0, to allow post-RSG evolution in
our models with masses higher than 30
parameter was set to 2.0 to avoid dynamical instabilities in the
outer envelope of our models related to high radiation pressure and
partial ionization of the gases in the outer layers (Stothers &
Chin 2001). In the calculations, we adopted the empirical formulation of the mass-loss rate by Nieuwenhuijzen & de Jager (1990)
for all evolutionary stages, except in the RSG and WR phases.
Mass-loss rates in the upper end of the HR diagram are uncertain by a
large factor, particularly for RSG stars (Chiosi & Maeder 1986).
In the RSG phase we used the Nieuwenhuijzen & de Jager mass
loss rate multiplied by a factor of 2.0, to allow post-RSG evolution in
our models with masses higher than 30 ![]() ,
according to empirical observations by Humphreys & Nichols (1985). If the surface hydrogen mass fraction fall below
,
according to empirical observations by Humphreys & Nichols (1985). If the surface hydrogen mass fraction fall below
![]() the star begins a WR phase, and the mass-loss rate was chosen according to Langer (1989).
More recent WR mass-loss rates, slightly lower than ours, have been
determined by Nugis & Lamers (2000), so that, our WR mass loss rates must be
considered as an upper limit.
The WN-H rich (or WNL) phase starts when a star becomes a WN star
(surface-H
the star begins a WR phase, and the mass-loss rate was chosen according to Langer (1989).
More recent WR mass-loss rates, slightly lower than ours, have been
determined by Nugis & Lamers (2000), so that, our WR mass loss rates must be
considered as an upper limit.
The WN-H rich (or WNL) phase starts when a star becomes a WN star
(surface-H ![]() 0.3) while WN-He (WNE) phase begins when the surface
hydrogen becomes zero; WC/WO indicate the stage when surface carbon abundance
increases
0.3) while WN-He (WNE) phase begins when the surface
hydrogen becomes zero; WC/WO indicate the stage when surface carbon abundance
increases
![]() .
.
The stellar evolution models was computed from ZAMS up to O core exhaustion previous to Si burning. At this stage, the star is in the pre-SN stage, a few days or hours from the SN explosion.
The derived mass-loss rates and terminal wind velocities are used as
time-dependent, inner boundary conditions in the magnetohydrodynamical
code ZEUS-3D, a three-dimensional, finite-difference, Eulerian explicit
code (Stone & Norman 1992;
Clarke 1996). This code integrates the hydrodynamical ideal gas
equations in the absence of viscosity. We used spherical coordinates,
with periodic boundary conditions in the alt-azimuthal direction. The
simulations we are done in one-dimensional (1D) or two-dimensional
(2D) grids as a function of the stellar evolutionary stage. We
calculated 1D simulations in the main sequence and red super giant
phases because of the dynamical behavior of their swept-up shells
(GLM96AB). Post-RSG evolution was computed on 2D grids because of the
strong unstable behavior of the formed structures, especially in
WR phases (GLM96AB). The size of the computational 1D domain is
![]() ,
with 1000 radial zones,
giving a spatial resolution of 0.05 pc/cell. Hereafter, the variables were interpolated on
smaller 2D grids to compare with the real dimensions of Cas A.
The 2D grids have a computational domain of r = 15 pc
,
with 1000 radial zones,
giving a spatial resolution of 0.05 pc/cell. Hereafter, the variables were interpolated on
smaller 2D grids to compare with the real dimensions of Cas A.
The 2D grids have a computational domain of r = 15 pc ![]()
![]() ,
with
,
with
![]() cells giving a resolution of 0.03 pc
cells giving a resolution of 0.03 pc ![]()
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f1}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg51.png)
|
Figure 1:
Evolutionary tracks for the models with 23 |
| Open with DEXTER | |
3 Stellar evolution models
3.1 23 M model
model
Figure 1 shows the path followed by the 23 ![]() model in the HR
diagram, and the evolutionary sequence is shown in Table 1.
The H-core burning phase lasts 6.374 Myr, and the star loses 0.81
model in the HR
diagram, and the evolutionary sequence is shown in Table 1.
The H-core burning phase lasts 6.374 Myr, and the star loses 0.81 ![]() as a
fast wind (
as a
fast wind (
![]() -3000 km s-1) with an average mass-loss rate of
-3000 km s-1) with an average mass-loss rate of
![]() .
After H-core burning exhaustion the star ignites
H shell burning, and late He core burning at 6.4 M yr, becoming an RSG.
The cusp in the HR diagram is related to the change in the mixing
length parameter.
.
After H-core burning exhaustion the star ignites
H shell burning, and late He core burning at 6.4 M yr, becoming an RSG.
The cusp in the HR diagram is related to the change in the mixing
length parameter.
In Fig. 2 the surface chemical evolution of the 23 ![]() star is shown.
The surface chemical composition does not change during MS, until a strong
dredge-up at the RSG phase transports H-burning CNO products to the surface:
H, O, and C diminish while He and N increase.
The RSG envelope abundances become homogeneous because of the
convective efficiency. In the RSG, the mass loss rate increases to
star is shown.
The surface chemical composition does not change during MS, until a strong
dredge-up at the RSG phase transports H-burning CNO products to the surface:
H, O, and C diminish while He and N increase.
The RSG envelope abundances become homogeneous because of the
convective efficiency. In the RSG, the mass loss rate increases to
![]() and the star loses 9
and the star loses 9 ![]() in a dense and slow wind
enriched with He and N from the CNO processing.
in a dense and slow wind
enriched with He and N from the CNO processing.
The RSG mass loss of the 23 ![]() star
is not large enough to produce a
blueward evolution in the HR diagram, and the star, after core
He-burning, ignites C, Ne, and O-core burning in the RSG phase
(Fig. 1).
The resulted pre-SN model is a 13
star
is not large enough to produce a
blueward evolution in the HR diagram, and the star, after core
He-burning, ignites C, Ne, and O-core burning in the RSG phase
(Fig. 1).
The resulted pre-SN model is a 13 ![]() RSG, with a H-rich envelope of 6.8
RSG, with a H-rich envelope of 6.8 ![]() and a stellar radius of
and a stellar radius of
![]()
![]() ,
,
![]() ,
and
log
,
and
log
![]() .
According to Heger et al. (2003), a pre-SN star with an envelope mass higher than 3
.
According to Heger et al. (2003), a pre-SN star with an envelope mass higher than 3 ![]() would produce an SN IIp.
would produce an SN IIp.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f2}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg59.png)
|
Figure 2:
Surface mass fractions of elements as function of time in the 23 |
| Open with DEXTER | |
3.2 28 M model
model
This model evolves according to the evolutionary channel shown in Table 1
and evolutionary path in Fig. 1. The star loses 1.39 ![]() in the MS
during 5.252 Myr with a mass-loss rate of
in the MS
during 5.252 Myr with a mass-loss rate of
![]() .
After core H-burning exhaustion the star becomes an RSG during
.
After core H-burning exhaustion the star becomes an RSG during
![]() yr. In the RSG stage, the stellar hydrogen envelope becomes enriched with He and
N from the CNO, H-shell burning.
During the RSG phase, the 28
yr. In the RSG stage, the stellar hydrogen envelope becomes enriched with He and
N from the CNO, H-shell burning.
During the RSG phase, the 28 ![]() star loses 16.9
star loses 16.9 ![]() and evolves to the blue
side of the HR diagram, performing a blue loop. During the blue loop,
we have a new increase in He and N surface abundances (Fig. 2),
whereas the central He mass fraction drops from
and evolves to the blue
side of the HR diagram, performing a blue loop. During the blue loop,
we have a new increase in He and N surface abundances (Fig. 2),
whereas the central He mass fraction drops from
![]() (blue loop onset) to
(blue loop onset) to
![]() at the blue tip (t = 5.73 Myr) and to total central He depletion
at the blue tip (t = 5.73 Myr) and to total central He depletion
![]() at t = 5.85 Myr. Semiconvection mixing
influences the formation and extension of the blue loops (El Eid 1995).
Such a feature is absent in the more recent set of models by
Limongi et al. (2000), Meynet & Maeder (2003),
Chieffi et al. (2003), but similar behaviour has been obtained by
Hirschi et al. (2004) for a 20
at t = 5.85 Myr. Semiconvection mixing
influences the formation and extension of the blue loops (El Eid 1995).
Such a feature is absent in the more recent set of models by
Limongi et al. (2000), Meynet & Maeder (2003),
Chieffi et al. (2003), but similar behaviour has been obtained by
Hirschi et al. (2004) for a 20 ![]() star as a consequence with a higher mass loss rates during He-burning.
Core C ignition occurs at 5.87 Myr followed by successive Ne and O burning.
The beginning of each burning phase is pointed in the HR diagram in
Fig. 1. From Ne-core burning onwards, the location of
the modeled star in the HR diagram does not vary because of the short
timescales of the late burning stages. The last stage corresponds to a star
with an envelope of 0.29
star as a consequence with a higher mass loss rates during He-burning.
Core C ignition occurs at 5.87 Myr followed by successive Ne and O burning.
The beginning of each burning phase is pointed in the HR diagram in
Fig. 1. From Ne-core burning onwards, the location of
the modeled star in the HR diagram does not vary because of the short
timescales of the late burning stages. The last stage corresponds to a star
with an envelope of 0.29 ![]() and surface abundances
and surface abundances
![]() ,
,
![]() ,
and
,
and
![]() .
The pre-SN star has a final total
mass of 9.4
.
The pre-SN star has a final total
mass of 9.4 ![]() ,
with a
,
with a
![]() and
and
![]() ,
resembling a BSG before SN explosion.
We called this type of stars ``luminous blue super giant''
(LBSG) to distinguish them from normal blue super giant (BSG) of much lower
masses. Using the envelope mass criterion from Heger et al. (2003), the
explosion would be an SNIIb type.
,
resembling a BSG before SN explosion.
We called this type of stars ``luminous blue super giant''
(LBSG) to distinguish them from normal blue super giant (BSG) of much lower
masses. Using the envelope mass criterion from Heger et al. (2003), the
explosion would be an SNIIb type.
Table 1: Evolutionary phases.
3.3 29 M model
model
The evolution is quite similar to the 28 ![]() stellar model,
because it loses 1.53
stellar model,
because it loses 1.53 ![]() in the MS during 5.1 Myr and 16.37
in the MS during 5.1 Myr and 16.37 ![]() in
the RSG during
in
the RSG during
![]() yr. After the RSG, the 29
yr. After the RSG, the 29 ![]() model also performs a blue loop becoming an LBSG star. Nevertheless, the blue loop is
shorter due to a higher mass loss rate in the RSG (Renzini et al. 1992).
During the He shell burning the star comes back to the red side of the
HR diagram igniting successively C, Ne and O in the core. The last
computed model is an O-core burning star with a final total mass of
model also performs a blue loop becoming an LBSG star. Nevertheless, the blue loop is
shorter due to a higher mass loss rate in the RSG (Renzini et al. 1992).
During the He shell burning the star comes back to the red side of the
HR diagram igniting successively C, Ne and O in the core. The last
computed model is an O-core burning star with a final total mass of ![]()
![]() .
The envelope
has 0.34
.
The envelope
has 0.34 ![]() composed mainly of H, He, and N (
composed mainly of H, He, and N (
![]() ,
,
![]() ,
,
![]() ). The pre-SN star has a
). The pre-SN star has a
![]() and a
and a
![]() ,
looking like a yellow super giant (YSG) before the SN explosion.
,
looking like a yellow super giant (YSG) before the SN explosion.
3.4 30 M model
model
The 30 ![]() loses 1.67
loses 1.67 ![]() in the MS during 4.959 Myr
and 18.3
in the MS during 4.959 Myr
and 18.3 ![]() in the RSG phase during
in the RSG phase during
![]() yr.
After RSG, the star evolves towards hotter temperatures because of the
high mass loss rate. At 5.28 Myr, the star becomes a 9.9
yr.
After RSG, the star evolves towards hotter temperatures because of the
high mass loss rate. At 5.28 Myr, the star becomes a 9.9 ![]() WR star while it is burning He in the core. The WR phase starts as WR-H
rich (WNL), and due to the strong mass loss rate, the star quickly
loses the stellar envelope, diminishing the stellar mass and
luminosity, as is notable in the HR diagram (Fig. 1). During WNL, the star loses 1.15
WR star while it is burning He in the core. The WR phase starts as WR-H
rich (WNL), and due to the strong mass loss rate, the star quickly
loses the stellar envelope, diminishing the stellar mass and
luminosity, as is notable in the HR diagram (Fig. 1). During WNL, the star loses 1.15 ![]() .
We note that recent WR mass-loss rate estimates are lowered by a factor
of 2-3 due to clumpiness (Hamman & Koesterke 1998), so our WR mass
loss rates are an upper limit. During WR, the star develops three
distinct phases: 1) the star spends
.
We note that recent WR mass-loss rate estimates are lowered by a factor
of 2-3 due to clumpiness (Hamman & Koesterke 1998), so our WR mass
loss rates are an upper limit. During WR, the star develops three
distinct phases: 1) the star spends
![]() yr
as WNL with a declining presence of surface-H. The He and N abundances
begin to increase steeply due to the high mass loss rate that peels off
the star and exposes layers enriched with elements from the CNO cycle.
At 5.33 Myr, the He and N reaches the maximum value on surface
(Fig. 3); 2) The surface-H vanishes
(
yr
as WNL with a declining presence of surface-H. The He and N abundances
begin to increase steeply due to the high mass loss rate that peels off
the star and exposes layers enriched with elements from the CNO cycle.
At 5.33 Myr, the He and N reaches the maximum value on surface
(Fig. 3); 2) The surface-H vanishes
(
![]() )
and the star begins the WN H-poor (WNE) stage during
)
and the star begins the WN H-poor (WNE) stage during
![]() yr
with a slightly lower mass loss rate. The WNL wind is highly enriched
with He and N. The high mass loss rate causes the He and N-surface
abundances to diminish when the star exposes its deeper layers
processed by 3
yr
with a slightly lower mass loss rate. The WNL wind is highly enriched
with He and N. The high mass loss rate causes the He and N-surface
abundances to diminish when the star exposes its deeper layers
processed by 3![]() reactions. 3) When the surface-C abundance is larger than 3% in
mass, a WC phase begins. During the WC phase, the stellar
surface temperature remains almost constant and the luminosity
decreases. Core He-exhaustion corresponds to the luminosity minimum. At
the ignition of an He-burning shell, the stellar luminosity increases
slightly and the star returns to the red
side of the HR diagram with lower luminosity. During the redward
evolution in the HR diagram, the star ignites C, Ne, and O-core
burning. The pre-SN model is a 5.9
reactions. 3) When the surface-C abundance is larger than 3% in
mass, a WC phase begins. During the WC phase, the stellar
surface temperature remains almost constant and the luminosity
decreases. Core He-exhaustion corresponds to the luminosity minimum. At
the ignition of an He-burning shell, the stellar luminosity increases
slightly and the star returns to the red
side of the HR diagram with lower luminosity. During the redward
evolution in the HR diagram, the star ignites C, Ne, and O-core
burning. The pre-SN model is a 5.9 ![]() star with a 1.6
star with a 1.6 ![]() Si/O core. The star loses the H envelope and it shows the He core partially processed by 3
Si/O core. The star loses the H envelope and it shows the He core partially processed by 3 ![]() reactions (
reactions (
![]() and
and
![]() ).
The stellar radius is
).
The stellar radius is
![]() and the stellar surface has a
and the stellar surface has a
![]() .
Here, the stellar radius or ``hydrostatic radius'' of a WR star is
defined as the radius of the sonic point in the outflow (Heger &
Langer 1996). The presence of surface-He indicates that the SN light curve would be an SNIb type.
.
Here, the stellar radius or ``hydrostatic radius'' of a WR star is
defined as the radius of the sonic point in the outflow (Heger &
Langer 1996). The presence of surface-He indicates that the SN light curve would be an SNIb type.
Table 2: Lifetimes of nuclear burning.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f3}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg89.png)
|
Figure 3:
Surface mass fractions of elements as function of time in the
30 |
| Open with DEXTER | |
3.5 33 M model
model
This stellar model loses 2.16 ![]() in the main sequence during 4.607 Myr. As an RSG, the star spends
in the main sequence during 4.607 Myr. As an RSG, the star spends
![]() yr losing 18.9
yr losing 18.9 ![]() .
In a similar way to the 30
.
In a similar way to the 30 ![]() star, this model also becomes a WR and the transition occurs at
star, this model also becomes a WR and the transition occurs at ![]() 4.8 Myr. Similar to the previous case, the whole WR phase is divided into three stages. The WNL (H-rich) stage lasts
4.8 Myr. Similar to the previous case, the whole WR phase is divided into three stages. The WNL (H-rich) stage lasts
![]() yr and the star loses almost 1
yr and the star loses almost 1 ![]() in
a WR wind. During WNL, the surface temperature of the star
increases steeply reaching values of 120 000 K when the star
peels off its hydrogen envelope (
in
a WR wind. During WNL, the surface temperature of the star
increases steeply reaching values of 120 000 K when the star
peels off its hydrogen envelope (
![]() )
starting the WNE (H-poor) stage. The mass-loss rate is reduced slightly and the star loses 0.8
)
starting the WNE (H-poor) stage. The mass-loss rate is reduced slightly and the star loses 0.8 ![]() in an He and N-rich wind, as is shown in Fig. 3. The He and N abundances reach their maximum values before the WNE (H-poor) stage. The strong mass loss exposes the 3
in an He and N-rich wind, as is shown in Fig. 3. The He and N abundances reach their maximum values before the WNE (H-poor) stage. The strong mass loss exposes the 3![]() processed
material and star becomes a WC/WO star when the star peels off deeper
layers. The strong mass-loss rate peels off the star so deep that we
observe a larger amount of material processed by 3
processed
material and star becomes a WC/WO star when the star peels off deeper
layers. The strong mass-loss rate peels off the star so deep that we
observe a larger amount of material processed by 3![]() reactions than the one observed
in the 30
reactions than the one observed
in the 30 ![]() model. In the WC/WO stage, the star evolves practically at a constant
surface temperature and the luminosity decreases. Shortly before C core
ignition, a He-burning shell expands the stellar envelope and the star
comes back to the red side of the HR diagram, igniting C, Ne, and O in
a successive way. Our last model has an Si/O core of 1.6
model. In the WC/WO stage, the star evolves practically at a constant
surface temperature and the luminosity decreases. Shortly before C core
ignition, a He-burning shell expands the stellar envelope and the star
comes back to the red side of the HR diagram, igniting C, Ne, and O in
a successive way. Our last model has an Si/O core of 1.6 ![]() ,
and it is close to SN explosion, only a few days or hours to ignite Si.
The intense WR mass loss has completely removed the stellar envelope
and the star is exposing the He burning shell where most of He has been
processed by 3
,
and it is close to SN explosion, only a few days or hours to ignite Si.
The intense WR mass loss has completely removed the stellar envelope
and the star is exposing the He burning shell where most of He has been
processed by 3![]() reaction. The C-surface abundance is higher than He or O.
There is no presence of either H or N in the stellar surface (the N has
been destroyed at the high temperatures of the 3
reaction. The C-surface abundance is higher than He or O.
There is no presence of either H or N in the stellar surface (the N has
been destroyed at the high temperatures of the 3![]() reaction). The pre-SN star is a WC with 4.57
reaction). The pre-SN star is a WC with 4.57 ![]() and
and
![]() .
The absence of H and the low He-surface abundance indicate that the most probable SN type would be an SNIc.
.
The absence of H and the low He-surface abundance indicate that the most probable SN type would be an SNIc.
Table 1 shows a summary of the evolutionary sequences of our stellar models, including the SN type associated to each star. The SN type was determined using the stellar envelope mass criterion according to Heger et al. (2003). There is no model ending as WNL/WNE due to the high mass-loss rates at WR stages. The WR mass loss rates used here are slightly higher than those in Nugis & Lamers (2000), and the effect of clumpiness have not been taken into account, thus, the WR mass loss rates can be considered as upper limits.
Table 2 shows the nuclear burning lifetimes for each star.
Core He-exhaustion corresponds to the
minimum in luminosity (similar to Fig. 2 by Woosley et al. 1995). The subsequent expansion is driven by shell
helium burning. Although burning lifetimes after C-ignition are short, the
final evolution in the HR diagram for 30 ![]() and 33
and 33 ![]() produce
redward excursions. The redward excursion of this type is an anomalous
feature, as our referee pointed out, and none of the models avaliable
in the literature show such behavior. We think that the reason for ``life after C-ignition'' in the
HR diagram of these models is the rather low final mass
(6
produce
redward excursions. The redward excursion of this type is an anomalous
feature, as our referee pointed out, and none of the models avaliable
in the literature show such behavior. We think that the reason for ``life after C-ignition'' in the
HR diagram of these models is the rather low final mass
(6 ![]() or less), giving long Kelvin-Helmholtz times (
or less), giving long Kelvin-Helmholtz times (
![]() yr in 30
yr in 30 ![]() and
and
![]() yr in 33
yr in 33 ![]() models at C-burning ignition, even larger than C-burning lifetimes).
This anomalous behavior will be the subject of a future study to
confirm our finding. Table 3 shows a summary of the main characteristics of our pre-SN models.
models at C-burning ignition, even larger than C-burning lifetimes).
This anomalous behavior will be the subject of a future study to
confirm our finding. Table 3 shows a summary of the main characteristics of our pre-SN models.
Table 3: Final stellar models.
4 Hydrodynamical simulations
4.1 Main sequence and red super giant phases
The CSM evolution strongly depends on stellar evolution throughout
the stellar wind properties (wind momentum and mechanical energy). In
this study, we do not consider the effects of photoionization from
stellar radiation, magnetic fields, or heat conduction. To simulate the
ionization post-RSG from the stellar radiation field, we change the
lower cutoff temperature to
![]() ,
saving a large amount of computational time (GLM96AB). By doing this,
we assume that the wind and RSG shell will be ionized (optically thin),
and its temperature corresponds to the ionization equilibrium
temperature.
,
saving a large amount of computational time (GLM96AB). By doing this,
we assume that the wind and RSG shell will be ionized (optically thin),
and its temperature corresponds to the ionization equilibrium
temperature.
For simplicity, the numerical calculation are divided into four stages: MS (1D), RSG (1D), blue loop or WR star (2D), and SN interaction (2D). Since our main focus is the final SN interaction with the nearby CSM, the HII region around the MS is not computed either.
Figures 4 and 5 show the stellar mass-loss rates and wind velocities as a function of time obtained from the stellar evolution calculations. The average wind velocities, total mass lost, and lifetimes at each stages are compiled in Tables 4-8. The quantities are obtained from STERN code and refer to average values.
Table 4:
Wind properties of the 23 ![]() model.
model.
Table 5:
Wind properties of the 28 ![]() model.
model.
Table 6:
Wind properties of the 29 ![]() model.
model.
Table 7:
Wind properties of the 30 ![]() model.
model.
Table 8:
Wind properties of the 33 ![]() model.
model.
Figures 4 and 5 reflect the different stellar evolutionary stages. During MS a slightly increase in the mass-loss rate is observed as a function of effective stellar radius and temperature. The opposite behavior for the velocity. During RSG, the mass-loss rate increases nearly by two orders of magnitude. The RSG wind is much slower and denser than the MS wind.
The hydrodynamical calculations start at ZAMS, in a homogeneous and
quiescent ambient medium with an uniform density appropriate for
Cas A of
![]() (Willingale et al. 2003),
and an initial thermal energy density of
(Willingale et al. 2003),
and an initial thermal energy density of
![]() .
.
During the MS, the wind kinetic energy is converted into thermal
energy by collision at the reverse shock, forming an adiabatic bubble
surrounded by a shocked, swept-up shell of interstellar material (MS
shell) (Weaver et al. 1977). Using an average value of
![]() for the mechanical luminosity and
for the mechanical luminosity and
![]() for the ISM density in
the Weaver et al. (1977) analytical solutions, we obtain MS shell radii in close
agreement with the calculations (Fig. 6).
for the ISM density in
the Weaver et al. (1977) analytical solutions, we obtain MS shell radii in close
agreement with the calculations (Fig. 6).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f4}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg108.png)
|
Figure 4:
Logarithm of the mass-loss rate as a function of time ( from top to bottom) for the 23, 28, 29, 30, and 33 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f5}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg109.png)
|
Figure 5:
Terminal wind velocities as a function of time
(from top to bottom) for the 23, 28, 29, 30, and 33 |
| Open with DEXTER | |
During the RSG phase, there is a large uncertainty in the wind velocity (Chiosi & Maeder 1986). In our case, the stellar wind-velocity outputs from the stellar evolution code decreases down to 250 km s-1, although we would expect
RSG wind velocities to be even lower.
Because of the uncertainty on RSG wind velocities, ranging between
10-160
![]() ,
and the lack of theoretical values (Dupree 1986),
we used a standard velocity of 10
,
and the lack of theoretical values (Dupree 1986),
we used a standard velocity of 10
![]() ,
in agreement with other authors (Chevalier & Oishi 2003).
,
in agreement with other authors (Chevalier & Oishi 2003).
We performed the CSM evolution for RSG phase in 1D, since the RSG shell is quite stable for low RSG wind velocities (García-Segura et al. 1996a,b; Freyer et al. 2006). Faster winds are subject to the Rayleigh-Taylor (R-T) instability (for LBVs see García-Segura et al. 1996a,b; for RSG see Dwarkadas 2007). The R-T instability produces fingers in the RSG shells, but the instability does not affect the position of their inner edge.
The duration of the RSG stage is different for each star, ranging from
![]() to
to
![]() yr,
but the impact in the CSM is quite similar. During RSG, the winds build
up shocked shells where the ram pressure of the RSG wind balances the
thermal pressure of the main sequence bubbles. The CSM density profiles
for each star at the end of the RSG phases is shown in Fig. 6.
We observe that larger RSG shells correspond to low masses since they
spend longer times as RSGs. Denser winds correspond to more massive
stars. On the other hand, MS shell radii are quite similar at the
end of RSG phases, since higher stellar masses with higher mechanical
luminosities live shorter.
yr,
but the impact in the CSM is quite similar. During RSG, the winds build
up shocked shells where the ram pressure of the RSG wind balances the
thermal pressure of the main sequence bubbles. The CSM density profiles
for each star at the end of the RSG phases is shown in Fig. 6.
We observe that larger RSG shells correspond to low masses since they
spend longer times as RSGs. Denser winds correspond to more massive
stars. On the other hand, MS shell radii are quite similar at the
end of RSG phases, since higher stellar masses with higher mechanical
luminosities live shorter.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f6}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg113.png)
|
Figure 6:
Logarithm of gas density at the end of each RSG phases.
The swept-up shells formed at the main sequence phases are located at
distances of |
| Open with DEXTER | |
4.2 Post-RSG evolution and SN blast wave
4.2.1 23 M model. RSG progenitor
model. RSG progenitor
The 23 ![]() model ends up as a
model ends up as a
![]() RSG SN progenitor.
At the time of SN explosion, the CSM is composed of a free-streaming and dense RSG wind with a density profile
RSG SN progenitor.
At the time of SN explosion, the CSM is composed of a free-streaming and dense RSG wind with a density profile
![]() surrounded by an RSG-shocked wind shell. A hot MS bubble remains outside the RSG shell, delimited by an ISM shocked shell at
surrounded by an RSG-shocked wind shell. A hot MS bubble remains outside the RSG shell, delimited by an ISM shocked shell at ![]() 33 pc (MS shell).
In this medium, we computed the ejection of mass from SN explosion in a two-dimensional numerical grid.
The simulation was done in a numerical grid of 500
33 pc (MS shell).
In this medium, we computed the ejection of mass from SN explosion in a two-dimensional numerical grid.
The simulation was done in a numerical grid of 500 ![]() 300, covering the surrounding space from the star up to 15 pc, in order to compare with the size
of Cas A. The numerical domain covers 15 pc
300, covering the surrounding space from the star up to 15 pc, in order to compare with the size
of Cas A. The numerical domain covers 15 pc ![]()
![]() with a resolution of
0.03 pc in radial direction and
with a resolution of
0.03 pc in radial direction and
![]() for the azimuthal direction.
for the azimuthal direction.
To study the blast wave interaction with the CSM, we assume an energy
of
![]() for the SN explosion appropriated for Cas A
(Hwang & Laming 2003; Willingale et al. 2003; Vink et al. 2004).
The outer stellar layers are ejected in the explosion (
for the SN explosion appropriated for Cas A
(Hwang & Laming 2003; Willingale et al. 2003; Vink et al. 2004).
The outer stellar layers are ejected in the explosion (
![]() )
leaving a stellar remnant of
)
leaving a stellar remnant of
![]() .
The remnant mass was chosen according to deleptonized cores in massive stars (Woosley et al. 2002).
For simplicity, we set up the explosion with an over-pressure region at
the center of the grid, with constant density (corresponding to the
ejecta mass over the volume region) and a high thermal energy (=1051 erg) and with an
initial velocity assuming that 1051 erg
were in the form of kinetic energy. The approximation is sufficient for
the scope of this study. The density profile, after several years, is
determined by the hydrodynamical expansion of the ejecta.
Using numerical inspection, we observed a density profile of
.
The remnant mass was chosen according to deleptonized cores in massive stars (Woosley et al. 2002).
For simplicity, we set up the explosion with an over-pressure region at
the center of the grid, with constant density (corresponding to the
ejecta mass over the volume region) and a high thermal energy (=1051 erg) and with an
initial velocity assuming that 1051 erg
were in the form of kinetic energy. The approximation is sufficient for
the scope of this study. The density profile, after several years, is
determined by the hydrodynamical expansion of the ejecta.
Using numerical inspection, we observed a density profile of
![]() at 167 yr after explosion, very similar to those proposed by Matzner & McKee (1999) for this SN type.
at 167 yr after explosion, very similar to those proposed by Matzner & McKee (1999) for this SN type.
Figure 7 shows the
logarithm of density snapshots for eight different times, from the
explosion up to 1167 yr after it. The first slice on the left
corresponds to the pre-SN CSM (
![]() yr), and the hydrodynamical evolution runs clockwise.
The SN ejecta interacts first with 5.8
yr), and the hydrodynamical evolution runs clockwise.
The SN ejecta interacts first with 5.8 ![]() of dense RSG wind
(
of dense RSG wind
(
![]() ). After that, the ejecta encounters a
3.14
). After that, the ejecta encounters a
3.14 ![]() RSG shell at a distance of 3.5 pc from the star, with a low expansion velocity
(5 km s-1) with respect to the star. The initial velocity of the forward shock is 4200 km s-1 and the ejected mass is 11.6
RSG shell at a distance of 3.5 pc from the star, with a low expansion velocity
(5 km s-1) with respect to the star. The initial velocity of the forward shock is 4200 km s-1 and the ejected mass is 11.6 ![]() .
The slice 2 shows the density at 334 yr after the explosion (the age of Cas A).
At this moment, the forward shock has a
.
The slice 2 shows the density at 334 yr after the explosion (the age of Cas A).
At this moment, the forward shock has a
![]() ,
and it has not interacted yet with the RSG shell. The forward shock front is at 2.2 pc and it has shocked 3.6
,
and it has not interacted yet with the RSG shell. The forward shock front is at 2.2 pc and it has shocked 3.6 ![]() of the RSG stellar wind. The blast wave hit the RSG shell 830 yr after the explosion.
of the RSG stellar wind. The blast wave hit the RSG shell 830 yr after the explosion.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f7}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg124.png)
|
Figure 7:
Blast wave evolution for the 23 |
| Open with DEXTER | |
4.2.2 28 and 29 M models. LBSG progenitors
models. LBSG progenitors
The hydrodynamical evolution of both modeled stars is quite similar, so we only discuss the
28 ![]() model.
After the RSG phase, the star evolves blueward performing a blue loop.
During the blue loop, the wind velocity increases to reach a maximum value of
550 km s-1 according to empirical LBSG wind velocities (Chevalier & Fransson 1987).
The interaction of the supersonic LBSG wind with the slow and dense RSG
wind material produces a double shock-front structure, and a new bubble
of hot shocked wind (LBSG bubble). The thermal pressure of the LBSG bubble pushes the medium in a
quasi-adiabatic shock and sets up a new shell of shocked, swept-up RSG wind
(LBSG shell).
Figure 8
shows the formation of the LBSG shell through the blue loop. The LBSG
shell is affected by Rayleigh-Taylor (RT) instabilities at the
interface, when it is accelerated by the LBSG bubble pressure. The LBSG
shell collides with the RSG shell at 3.4 pc. The expansion
velocity of the LBSG shell (35 km s-1) is higher than the one of
RSG shell (5 km s-1), and the LBSG and RSG shell remain separated for
model.
After the RSG phase, the star evolves blueward performing a blue loop.
During the blue loop, the wind velocity increases to reach a maximum value of
550 km s-1 according to empirical LBSG wind velocities (Chevalier & Fransson 1987).
The interaction of the supersonic LBSG wind with the slow and dense RSG
wind material produces a double shock-front structure, and a new bubble
of hot shocked wind (LBSG bubble). The thermal pressure of the LBSG bubble pushes the medium in a
quasi-adiabatic shock and sets up a new shell of shocked, swept-up RSG wind
(LBSG shell).
Figure 8
shows the formation of the LBSG shell through the blue loop. The LBSG
shell is affected by Rayleigh-Taylor (RT) instabilities at the
interface, when it is accelerated by the LBSG bubble pressure. The LBSG
shell collides with the RSG shell at 3.4 pc. The expansion
velocity of the LBSG shell (35 km s-1) is higher than the one of
RSG shell (5 km s-1), and the LBSG and RSG shell remain separated for ![]() 105 yr
previous to their collision. The peak density of the LBSG shell is
2.6 times more than the RSG shell. Both shells merge and form a
massive shell moving out with a common velocity of
105 yr
previous to their collision. The peak density of the LBSG shell is
2.6 times more than the RSG shell. Both shells merge and form a
massive shell moving out with a common velocity of ![]() 18 km s-1.
The new LBSG+RSG shell moves outwards into the MS bubble, and it
develops RT instabilities in the outer edge, since the shell is
decelerating. The outer edge is subsonic with
respect to the MS bubble, and there is not a forward shock. As the
shell propagates outwards eventually breaks-out (Fig. 8, slice 5).
18 km s-1.
The new LBSG+RSG shell moves outwards into the MS bubble, and it
develops RT instabilities in the outer edge, since the shell is
decelerating. The outer edge is subsonic with
respect to the MS bubble, and there is not a forward shock. As the
shell propagates outwards eventually breaks-out (Fig. 8, slice 5).
The final position of the merged shell is spread between 7.6-9 pc. It has a swept-up mass of 17.2 ![]() and some regions have a peak density higher than
and some regions have a peak density higher than
![]() ,
able to be detected in circumstellar nebula (GLM96A.) The mass of the wind inside the LBSG bubble is less than 0.05
,
able to be detected in circumstellar nebula (GLM96A.) The mass of the wind inside the LBSG bubble is less than 0.05 ![]() .
The density profile of the pre-SN medium around the star of 28
.
The density profile of the pre-SN medium around the star of 28 ![]() is shown in slice 8 of Fig. 8.
The LBSG shell is composed mainly of H, He, and N because it was
formed from swept-up RSG wind. The LBSG wind is enhanced with He and N,
and it is H deficient, although H still is an important wind component.
The stellar surface of the pre-SN LBSG is He, H and N abundant in that
order.
is shown in slice 8 of Fig. 8.
The LBSG shell is composed mainly of H, He, and N because it was
formed from swept-up RSG wind. The LBSG wind is enhanced with He and N,
and it is H deficient, although H still is an important wind component.
The stellar surface of the pre-SN LBSG is He, H and N abundant in that
order.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f8}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg126.png)
|
Figure 8:
Post-RSG CSM evolution of the 28 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f9}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg127.png)
|
Figure 9:
Blast wave evolution for the 28 |
| Open with DEXTER | |
The blast wave was simulated like in the 23 ![]() model, using the same SN energy. In this case, the SN ejects a mass of 7.86
model, using the same SN energy. In this case, the SN ejects a mass of 7.86 ![]() ,
leaving a stellar remnant of 1.5
,
leaving a stellar remnant of 1.5 ![]() .
The blast wave evolution is shown in Fig. 9.
The initial forward shock velocity is 8000 km s-1.
In slice 2 of Fig. 9 we observe the CSM at the age of Cas A (
.
The blast wave evolution is shown in Fig. 9.
The initial forward shock velocity is 8000 km s-1.
In slice 2 of Fig. 9 we observe the CSM at the age of Cas A (
![]() yr). Here, the blast wave has shocked all the free LBSG wind
and starts the interaction with the LBSG shocked wind (LBSG bubble). The
forward shock is at 3.3 pc and has shocked less than 0.1
yr). Here, the blast wave has shocked all the free LBSG wind
and starts the interaction with the LBSG shocked wind (LBSG bubble). The
forward shock is at 3.3 pc and has shocked less than 0.1 ![]() of
the LBSG stellar wind. The collision of the blast wave with the LBSG
bubble produces a direct shock front propagating into the bubble and a
reflected shock traveling back. The collision causes a sudden increase
in the temperature of the shocked gas and an increment in the x-ray
emission.
of
the LBSG stellar wind. The collision of the blast wave with the LBSG
bubble produces a direct shock front propagating into the bubble and a
reflected shock traveling back. The collision causes a sudden increase
in the temperature of the shocked gas and an increment in the x-ray
emission.
The direct (forward) shock collides with the merged (LBSG+RSG) shell at 1100 yr after the explosion, with a velocity of 6500 km s-1. The collision transmits a shock into the merged (LBSG+RSG) shell, with a strong acceleration of the shell. The shock loses a large amount of energy at the collision. At the collision knots traveling outwards are formed with a wide range of velocities and densities.
4.2.3 30 and 33 M models. WR progenitors
models. WR progenitors
After the RSG phases, the 30 and 33 ![]() models shed their H envelope and become WR stars with faster winds (
models shed their H envelope and become WR stars with faster winds (![]() 1000 km s-1)
and with lower densities than the RSG winds. The chemical composition
in the WR winds is mainly He, H and N, in the WNL phase with a
declining presence of H. WNE winds are composed mainly of He and
N. The WC/O winds are still He-rich but with a strong abundance
of C and O and declining presence of N (Fig. 3).
1000 km s-1)
and with lower densities than the RSG winds. The chemical composition
in the WR winds is mainly He, H and N, in the WNL phase with a
declining presence of H. WNE winds are composed mainly of He and
N. The WC/O winds are still He-rich but with a strong abundance
of C and O and declining presence of N (Fig. 3).
At the beginning of the WR phases, the RSG shells are located at 2.5 pc. They are
ionized by the intense stellar radiation coming from the WR stars and their
temperature increases to the photoionization equilibrium temperature (
![]() ). Fast WR winds sweep up the dense and slow RSG winds to build up
swept-up shells (WR shells). Figure 10
shows the logarithm of gas density at the end of the RSG phase
(slice 1) and the formation of the WR shell for the case of
the 30
). Fast WR winds sweep up the dense and slow RSG winds to build up
swept-up shells (WR shells). Figure 10
shows the logarithm of gas density at the end of the RSG phase
(slice 1) and the formation of the WR shell for the case of
the 30 ![]() model. The expansion velocity of the WR shell is
model. The expansion velocity of the WR shell is
![]() .
The WR shell hits the RSG shell at 5.3 Myr,
.
The WR shell hits the RSG shell at 5.3 Myr,
![]() yr
before SN explosion. As a result of the strong collision, both shells
are broken at radii smaller than 5 pc (slice 5 of Fig. 10),
forming clumps and tails of dragged shell material. At SN explosion,
the fragmented shell consists of dense knots lying at a distance
greater than 20 pc and irregular tails that are spread in an
annulus of 20 pc of inner boundary and 30-35 pc in the outer
edge (the MS shell at
yr
before SN explosion. As a result of the strong collision, both shells
are broken at radii smaller than 5 pc (slice 5 of Fig. 10),
forming clumps and tails of dragged shell material. At SN explosion,
the fragmented shell consists of dense knots lying at a distance
greater than 20 pc and irregular tails that are spread in an
annulus of 20 pc of inner boundary and 30-35 pc in the outer
edge (the MS shell at ![]() 35 pc).
35 pc).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f10}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg133.png)
|
Figure 10:
Post-RSG CSM evolution of the 30 |
| Open with DEXTER | |
The blast waves were simulated similar to the 23 and 28 ![]() models. The modeled
WR stars explode with an energy of
models. The modeled
WR stars explode with an energy of
![]() erg, ejecting into space less
than 5
erg, ejecting into space less
than 5 ![]() ,
leaving stellar remnants of
,
leaving stellar remnants of ![]() 1.5
1.5 ![]() (Table 9).
(Table 9).
Initial velocities of the SN forward shocks are ![]() 7000 km s-1,
and at the age of Cas A, they have slightly decayed to 6800 km s-1, at distances
of 3.1 pc from the explosion centers. At this age, the SN shock fronts are still interacting with the free WR winds.
7000 km s-1,
and at the age of Cas A, they have slightly decayed to 6800 km s-1, at distances
of 3.1 pc from the explosion centers. At this age, the SN shock fronts are still interacting with the free WR winds.
The wind termination shocks of the WR bubbles are at distances greater than 10 pc, and the SN shocks take more than 600 yr to reach them. The blast waves hit the knots from the broken WR shells at times longer than 1000 yr after the explosions.
Since the purpose of this work is to compare our simulations with the observational constraints of Cas A, we did not carry out the whole interaction of SN shock fronts with WR CSM. Interactions of SN shock fronts with WR bubbles has been simulated by Dwarkadas (2007).
5 Comparison with Cas A
There is a wide variety of observations to constraint the progenitor of Cas A. In this section we have used the strongest observational constraints to compare them with our stellar and hydrodynamical simulations in order to find the best progenitor model for Cas A.
5.1 Comparison with stellar models. Quasi stationary floculii
Chevalier & Kirschner (1978) report N and He excess in QSFs with ratios
of N/H ![]() 7-10 and He/H
7-10 and He/H ![]() 3-5 times the solar values. The overabundances
lead to proposing that QSFs were stellar material processed by the CNO cycle,
transported to the surface and lost by the stellar wind
(Kamper & van den Bergh 1978), or as clumpy ejecta (Chevalier & Oishi 2003).
Some authors have proposed that Cas A progenitor was a WN star (Peimbert 1971; Fesen et al. 1987; Willingale et al. 2003) from the QSFs chemical ratios.
3-5 times the solar values. The overabundances
lead to proposing that QSFs were stellar material processed by the CNO cycle,
transported to the surface and lost by the stellar wind
(Kamper & van den Bergh 1978), or as clumpy ejecta (Chevalier & Oishi 2003).
Some authors have proposed that Cas A progenitor was a WN star (Peimbert 1971; Fesen et al. 1987; Willingale et al. 2003) from the QSFs chemical ratios.
Figure 11 show the evolution of the
index 12 + log (N/H) and 12 + log (He/H) on the stellar surface of the 30 and 33 ![]() modeled stars to compare them with the observational ratios found in QSFs.
The stellar surfaces exhibit N/H and He/H ratios
similar to those in QSFs at t = 5.321 Myr for the 30
modeled stars to compare them with the observational ratios found in QSFs.
The stellar surfaces exhibit N/H and He/H ratios
similar to those in QSFs at t = 5.321 Myr for the 30 ![]() model, and at
t = 4.789 Myr for the 33
model, and at
t = 4.789 Myr for the 33 ![]() .
In both WR stars, we observe that the QSF ratios appear at the onset of
the WNE phase, so it is quite reasonable that QSFs come from WNE
stellar winds. After the WNE, the N/H and He/H ratios continue
increasing, and any mass ejections from the stellar surfaces after WNE
will contain at least QSF ratios, or even higher.
.
In both WR stars, we observe that the QSF ratios appear at the onset of
the WNE phase, so it is quite reasonable that QSFs come from WNE
stellar winds. After the WNE, the N/H and He/H ratios continue
increasing, and any mass ejections from the stellar surfaces after WNE
will contain at least QSF ratios, or even higher.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f11}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg135.png)
|
Figure 11:
Evolution of the 12 + log (N/H) ratio (solid line) and
12 + log (He/H) ratio (pointed line for 30 |
| Open with DEXTER | |
The 23, 28, and 29 ![]() models do not exhibit surface QSF ratios at
any time. The N/H and He/H ratios are always much lower than those values
observed in QSFs. If we accept the scenario in which QSFs were expelled
from the stellar surface as wind or blobs, then it is difficult to postulate a RSG
precursor for Cas A. However, this cannot be ruled out, since stronger N
enrichment is expected at the surface of rotating stars (Heger & Langer 2000).
models do not exhibit surface QSF ratios at
any time. The N/H and He/H ratios are always much lower than those values
observed in QSFs. If we accept the scenario in which QSFs were expelled
from the stellar surface as wind or blobs, then it is difficult to postulate a RSG
precursor for Cas A. However, this cannot be ruled out, since stronger N
enrichment is expected at the surface of rotating stars (Heger & Langer 2000).
5.2 Comparison with stellar models. Nitrogen knots
The NKs were identified for the first time in spectroscopic observations
of the outer optical knots by Fesen (2001). Fesen found four dozen fast knots
(![]() 8000-10 000 km s-1) with nitrogen-rich abundances with typical limit
of N/H
8000-10 000 km s-1) with nitrogen-rich abundances with typical limit
of N/H ![]() 30 times solar. Their estimated space velocities suggest a
nearly isotropic (
30 times solar. Their estimated space velocities suggest a
nearly isotropic (![]()
![]() )
ejection velocity.
Because of the isotropic ejection, the N-rich ejecta fragments were presumably
shrapnel from an N-rich envelope of the precursor.
The presence of an appreciable H emission in just 3 of the 50 NKs suggest an H-poor
photosphere when the SN occurs, since a significant mass accretion of
circumstellar material onto the NKs seems unlikely. The H + N rich photospheric
layers must have had very low mass (Fesen 2001), suggesting a pre-SN star
whose mass loss was not enough to expose the CO layers processed by 3
)
ejection velocity.
Because of the isotropic ejection, the N-rich ejecta fragments were presumably
shrapnel from an N-rich envelope of the precursor.
The presence of an appreciable H emission in just 3 of the 50 NKs suggest an H-poor
photosphere when the SN occurs, since a significant mass accretion of
circumstellar material onto the NKs seems unlikely. The H + N rich photospheric
layers must have had very low mass (Fesen 2001), suggesting a pre-SN star
whose mass loss was not enough to expose the CO layers processed by 3![]() reaction, where N is destroyed.
reaction, where N is destroyed.
The 23 ![]() model has a pre-SN star that is an RSG with a very massive H envelope
(
model has a pre-SN star that is an RSG with a very massive H envelope
(
![]() ,
,
![]() ). The surface N is the fourth element in abundance by mass.
This H envelope is unlikely to produce and eject H poor clumps like the NKs.
). The surface N is the fourth element in abundance by mass.
This H envelope is unlikely to produce and eject H poor clumps like the NKs.
The 28 and 29 ![]() models are LBSGs when they explode, and
have pre-SN envelopes of small masses (
models are LBSGs when they explode, and
have pre-SN envelopes of small masses (![]()
![]() )
composed mainly of He,
H, and N (in that order by mass abundances). The nitrogen on the surface is an
efficient coolant that quickly cools down the gas and forms knots resembling NKs during
SN ejection. The N/H ratio found in NKs comes from material that has
undergone CNO processing up to
)
composed mainly of He,
H, and N (in that order by mass abundances). The nitrogen on the surface is an
efficient coolant that quickly cools down the gas and forms knots resembling NKs during
SN ejection. The N/H ratio found in NKs comes from material that has
undergone CNO processing up to ![]() 90% of the H-depleted (Young et al.
2005), and the material in our LBSG pre-SN envelopes are
90% of the H-depleted (Young et al.
2005), and the material in our LBSG pre-SN envelopes are ![]() 60% H-depleted.
Then, our LBSG progenitors are the most likely stars to produce clumps resembling NKs.
60% H-depleted.
Then, our LBSG progenitors are the most likely stars to produce clumps resembling NKs.
The pre-SN of the 30 ![]() model has N on its surface, but does not have a signifiant stellar envelope.
During ejection, the N on the surface could cool down to form knots at high
velocities, but lacking hydrogen. In the 33
model has N on its surface, but does not have a signifiant stellar envelope.
During ejection, the N on the surface could cool down to form knots at high
velocities, but lacking hydrogen. In the 33 ![]() model, the WR mass loss
removes all of the N-rich material from the stellar surface. The peeling off
reaches deep layers where most of the material was processed
by the 3
model, the WR mass loss
removes all of the N-rich material from the stellar surface. The peeling off
reaches deep layers where most of the material was processed
by the 3![]() nuclear reaction, destroying the N, so the ejected mass
is unable to form NKs.
nuclear reaction, destroying the N, so the ejected mass
is unable to form NKs.
5.3 Comparison with stellar models. SN ejected mass
The mass ejected by the SN explosion of Cas A has been measured using several
methods. Willingale et al. (2002) combine x-ray spectral line fitting with
emission models to estimate the total amount of emitting material, estimating
an ejected mass of 2-4 ![]() with 1-3
with 1-3 ![]() of oxygen. Vink et al. (1996) has
determined an ejected mass of
of oxygen. Vink et al. (1996) has
determined an ejected mass of ![]()
![]() with an ejected oxygen mass
of
with an ejected oxygen mass
of ![]()
![]() .
.
The final masses of our stellar models are shown in Table 3, and the total ejected
masses and yields by elements are shown in Table 9, using mass cuts
according to Woosley et al. (2002). Ejected masses by the 23, 28, and 29 ![]() models
are higher than the observational values in Cas A. The RSG progenitor (23
models
are higher than the observational values in Cas A. The RSG progenitor (23 ![]() model) ejects the
highest amount of mass, 11.6
model) ejects the
highest amount of mass, 11.6 ![]() ,
and the LBSG progenitors (28 and 29
,
and the LBSG progenitors (28 and 29 ![]() models)
ejects
models)
ejects ![]() 8
8 ![]() .
Neither the RSG nor the LBSG models satisfy the low ejecta mass
constraint.
.
Neither the RSG nor the LBSG models satisfy the low ejecta mass
constraint.
To eject the
mass observed in Cas A (2-4 ![]() ), our RSG and LBSG stars must lose a large amount
of material previous to the SN explosion. Higher mass-loss rates in RSG have
been proposed recently (Schroder & Cuntz 2005) that
could reduce the final mass of our RSG and LBSG precursors. However, a stronger
mass loss in RSG phases will modify the stellar evolution, actually forming WR stars.
The ejected mass is also reduced if the stellar explosion leaves a black hole as a remnant,
with
), our RSG and LBSG stars must lose a large amount
of material previous to the SN explosion. Higher mass-loss rates in RSG have
been proposed recently (Schroder & Cuntz 2005) that
could reduce the final mass of our RSG and LBSG precursors. However, a stronger
mass loss in RSG phases will modify the stellar evolution, actually forming WR stars.
The ejected mass is also reduced if the stellar explosion leaves a black hole as a remnant,
with ![]() 6
6 ![]() .
The stellar remnant of Cas A was observed in x-rays (Tananbaum 1999),
whose nature is still being discussed (Mereghetti et al. 2002). However, stars with inital masses
lower than 25
.
The stellar remnant of Cas A was observed in x-rays (Tananbaum 1999),
whose nature is still being discussed (Mereghetti et al. 2002). However, stars with inital masses
lower than 25 ![]() seem unlikely to produce black holes (Heger et al. 2003).
seem unlikely to produce black holes (Heger et al. 2003).
Mass-loss rates in WR stars are high enough to uncover the CO-rich material, reducing
final masses to ![]() 6
6 ![]() .
An ejected mass of 2-4
.
An ejected mass of 2-4 ![]() leaves a stellar
remnant of 1-2
leaves a stellar
remnant of 1-2 ![]() and would produce a neutron-star remnant. Ejected masses by our
WR precursors lie in the range of 3-4.5
and would produce a neutron-star remnant. Ejected masses by our
WR precursors lie in the range of 3-4.5 ![]() ,
in excellent agreement with the values
measured in Cas A.
,
in excellent agreement with the values
measured in Cas A.
Table 9:
Ejected masses from the stellar models.
![]() is the mass cut
chosen from Woosley et al. (2002).
is the mass cut
chosen from Woosley et al. (2002).
![]() is
total ejected mass. Last five columns show the yields by element.
is
total ejected mass. Last five columns show the yields by element.
5.4 Comparison with hydrodynamical models. Forward and reverse shock fronts
The forward shock of Cas A has been detected in x-rays at a radius
of ![]()
![]() (
(
![]() pc), interacting with the CSM (Gotthelf et al. 2001).
This shock front has a velocity of
pc), interacting with the CSM (Gotthelf et al. 2001).
This shock front has a velocity of ![]() 6000-7000 km s-1 (DeLaney & Rudnick 2003).
The reverse shock position is less clear, at an average radius of
1.6 pc with a variation of 14% around the remnant (Gotthelf et al. 2001).
6000-7000 km s-1 (DeLaney & Rudnick 2003).
The reverse shock position is less clear, at an average radius of
1.6 pc with a variation of 14% around the remnant (Gotthelf et al. 2001).
The CSM around our RSG progenitor is a dense and uniform, free expanding
wind with a density profile of the type
![]() ,
extended up to 3.5 pc, surrounded by
a dense RSG, piled up shell. Beyond the RSG shell is the hot bubble and MS shell at 33 pc.
Initially, the computed blast wave expands at
,
extended up to 3.5 pc, surrounded by
a dense RSG, piled up shell. Beyond the RSG shell is the hot bubble and MS shell at 33 pc.
Initially, the computed blast wave expands at ![]() 4200 km s-1.
At 334 yr, the SN forward shock is located at 2.2 pc, still inside
of the RSG wind, with an expansion velocity of
4200 km s-1.
At 334 yr, the SN forward shock is located at 2.2 pc, still inside
of the RSG wind, with an expansion velocity of ![]() 4000 km s-1. The SN
reverse shock is at 1.7 pc , giving a ratio of 1.3 for their radii.
The observed ratio for the radii of Cas A is
4000 km s-1. The SN
reverse shock is at 1.7 pc , giving a ratio of 1.3 for their radii.
The observed ratio for the radii of Cas A is ![]() 1.5. The self-similar
solutions of Chevalier (1982) show that an ejecta of the type
1.5. The self-similar
solutions of Chevalier (1982) show that an ejecta of the type
![]() ,
interacting with a stellar wind,
produce a ratio of 1.26. Thus, the radii of both shocks and their ratio
are in close agreement with those observed in Cas A, in favor of the 23
,
interacting with a stellar wind,
produce a ratio of 1.26. Thus, the radii of both shocks and their ratio
are in close agreement with those observed in Cas A, in favor of the 23 ![]() model.
model.
The pre-SN CSM around the LBSG progenitor also has a
density profile
![]() ,
but less dense than the RSG medium because of the
higher wind velocity. The free LBSG wind has a mass below 0.1
,
but less dense than the RSG medium because of the
higher wind velocity. The free LBSG wind has a mass below 0.1 ![]() and
the termination shock is at
and
the termination shock is at ![]()
![]() .
The shocked
LBSG wind builds up a hot LBSG bubble, surrounded by a dense, piled-up ``LBSG+RSG'' shell at
.
The shocked
LBSG wind builds up a hot LBSG bubble, surrounded by a dense, piled-up ``LBSG+RSG'' shell at
![]() 7.6-9 pc from the star. The ``LBSG+RSG'' shell has a mass of 17.2
7.6-9 pc from the star. The ``LBSG+RSG'' shell has a mass of 17.2 ![]() .
Most of the mass in the shell has a peak density higher
than
.
Most of the mass in the shell has a peak density higher
than
![]() ,
which can be detected in the
CSM (GLM96A).
For this case, the blast wave has an initial
,
which can be detected in the
CSM (GLM96A).
For this case, the blast wave has an initial
![]() and the shock velocity does not change appreciably during the LBSG wind interaction,
due to the low density. At 334 yr, the SN forward shock is at 3.3 pc, with
and the shock velocity does not change appreciably during the LBSG wind interaction,
due to the low density. At 334 yr, the SN forward shock is at 3.3 pc, with
![]() ,
and the reverse shock is at 2.4 pc, giving a ratio of
,
and the reverse shock is at 2.4 pc, giving a ratio of
![]() ,
quite similar to the value observed in Cas A. However, the shock positions are larger than in Cas A
by a factor of 1.3-1.5.
,
quite similar to the value observed in Cas A. However, the shock positions are larger than in Cas A
by a factor of 1.3-1.5.
The CSM around the WR progenitors (30 and 33 ![]() models) is strongly affected by
the high mechanical luminosity of the WR winds, which completely clears out the surrounding
medium up to the termination shock at the inner edge of WR bubble. In the case of the
33
models) is strongly affected by
the high mechanical luminosity of the WR winds, which completely clears out the surrounding
medium up to the termination shock at the inner edge of WR bubble. In the case of the
33 ![]() ,
the stellar wind interacts directly with the clumps of the broken WR shell producing bow shocks. In
both cases, the strong WR winds clear out the CSM at least up to 10 pc,
so the pre-SN circumstellar medium inside of 10 pc only consists of a low-density, fast
wind, with
,
the stellar wind interacts directly with the clumps of the broken WR shell producing bow shocks. In
both cases, the strong WR winds clear out the CSM at least up to 10 pc,
so the pre-SN circumstellar medium inside of 10 pc only consists of a low-density, fast
wind, with
![]() profile. The SN ejecta interacts with this medium
at an initial velocity of 9500 km s-1. At 334 yr, the SN forward shock
is at 3.1 pc, with
profile. The SN ejecta interacts with this medium
at an initial velocity of 9500 km s-1. At 334 yr, the SN forward shock
is at 3.1 pc, with ![]()
![]() ,
and the reverse shock front is at
1.5 pc, with 5500 km s-1.
,
and the reverse shock front is at
1.5 pc, with 5500 km s-1.
5.5 Comparison with hydrodynamical models. QSF locations and shocked mass
QSFs in Cas A are distributed around the remnant center with typical radii of
![]() 1.9-2 pc. Their enhanced density was one of the reasons to argue
in favor of a dense circumstellar shell (Chevalier & Liang 1989). The
N enrichment in QSFs
seems to be the result of CNO-burning in combination with mass loss from the progenitor.
Based on the high N/H ratios, several authors have proposed WN and RSG stars as progenitors,
where the QSFs represent clumps ejected from the N-enriched
stellar surface with strong density contrasts (
1.9-2 pc. Their enhanced density was one of the reasons to argue
in favor of a dense circumstellar shell (Chevalier & Liang 1989). The
N enrichment in QSFs
seems to be the result of CNO-burning in combination with mass loss from the progenitor.
Based on the high N/H ratios, several authors have proposed WN and RSG stars as progenitors,
where the QSFs represent clumps ejected from the N-enriched
stellar surface with strong density contrasts (![]() 102 - 103) compared with a
smooth wind (Chevalier & Oishi 2003).
102 - 103) compared with a
smooth wind (Chevalier & Oishi 2003).
QSFs seem to lie in a circumstellar shell shocked by the SN forward shock; however, our SN precursors develop circumstellar piled-up shells much farther out than 2 pc. Even the nearest computed shell has a larger radius than the forward shock radius of Cas A. In our simulations, the blast wave hits the RSG shell at 830 yr after the explosion, the LBSG shell at 1100 yr, and the WR shell at 1670 yr, a much longer time than the age of Cas A.
To reproduce the QSF positions of Cas A, the inner shells in our models must be
closer to the star (Schure et al. 2008).
Smaller shells could be formed in different ways, for example, if the duration of the
latest evolutionary stage (LBSG or WR) is shorter.
Also, circumstellar shells could be smaller if their expansion were slower.
The velocity ![]() of an energy, wind-driven shell expanding in a previous wind is given
for example by (Chevalier & Imamura 1983):
of an energy, wind-driven shell expanding in a previous wind is given
for example by (Chevalier & Imamura 1983):
![\begin{displaymath}V_{\rm s} = \left[ \frac{\dot{M}_2 V^{2}_{2} V_1}{3 \dot{M}_1} \right]^{1/3}
\end{displaymath}](/articles/aa/full_html/2009/42/aa09913-08/img159.png)
|
(1) |
where subindex 1 refers to the slow wind and subindex 2 to the fast wind. If the RSG mass-loss rates were higher and/or LBSG/WR mass loss rates were lower, then the resulted swept-up shells would be slower and smaller. Increased RSG mass loss rates have recently been suggested by Schroder & Cuntz (2005), while lower mass loss rates in WR stars due to clumpiness have been taken into account recently by Hamann & Koesterke (1998), and by Eldridge & Tout (2004). Modifying the mass loss rates, however, would affect the entire stellar evolution so new computations would be required.
Most of the models for the emission of Cas A establish that a fraction of the pre-SN
mass loss becomes observable when hit by the blast wave.
For example, the x-ray emission in Cas A comes from high-temperature material heated by
both SN shocks. The total x-ray emitting mass in Cas A is ![]() 14
14 ![]() ,
being
approximately 2-4
,
being
approximately 2-4 ![]() from the SN shocked ejecta and
from the SN shocked ejecta and ![]() 8-9
8-9 ![]() from the
swept-up mass (Vink et al. 1996; Willingale et al. 2002).
Tsunemi et al. (1986), however, found a lower swept-up mass of
from the
swept-up mass (Vink et al. 1996; Willingale et al. 2002).
Tsunemi et al. (1986), however, found a lower swept-up mass of ![]() 2.4
2.4 ![]() ,
using a non-equilibrium, ionization plasma hypothesis.
When we compare our results with the shocked mass in Cas A, we find that only the
RSG progenitor is able to provide enough shocked mass due to the dense RSG wind.
The LBSG and WR SN progenitors have extended zones of free streaming wind with very low masses,
which are insufficient to explain the large amount of emitting mass in Cas A.
,
using a non-equilibrium, ionization plasma hypothesis.
When we compare our results with the shocked mass in Cas A, we find that only the
RSG progenitor is able to provide enough shocked mass due to the dense RSG wind.
The LBSG and WR SN progenitors have extended zones of free streaming wind with very low masses,
which are insufficient to explain the large amount of emitting mass in Cas A.
6 Summary and conclusions
We shown the results of evolutionary stellar models in the range of masses of 23, 28, 29, 30, and 33
![]() where
we used the derived mass loss rates and wind terminal velocities as
inner boundary conditions in an hydrodynamical code to simulate the gas
dynamics of their circumstellar medium, including the ejection of mass
from SN explosion, to compare our models to observational constraints
of Cas A. From our simulations we draw the following conclusions.
where
we used the derived mass loss rates and wind terminal velocities as
inner boundary conditions in an hydrodynamical code to simulate the gas
dynamics of their circumstellar medium, including the ejection of mass
from SN explosion, to compare our models to observational constraints
of Cas A. From our simulations we draw the following conclusions.
- The RSG progenitor (23
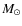 model) agrees quite well with the shock fronts
positions and shock fronts ratio observed in Cas A. Due to the dense RSG wind as pre-SN,
this kind of progenitor is the one able to explain the large amount of swept-up mass
observed in the remnant. The RSG progenitor, however, fails to produce the high N/H and He/H
ratios observed in QSFs, if we accept the scenario where QSFs were ejected from the
stellar surface as a smooth wind or blobs. The H-rich envelope of the RSG also fails to produce
the NKs. The large amount of ejecta mass (11.6
model) agrees quite well with the shock fronts
positions and shock fronts ratio observed in Cas A. Due to the dense RSG wind as pre-SN,
this kind of progenitor is the one able to explain the large amount of swept-up mass
observed in the remnant. The RSG progenitor, however, fails to produce the high N/H and He/H
ratios observed in QSFs, if we accept the scenario where QSFs were ejected from the
stellar surface as a smooth wind or blobs. The H-rich envelope of the RSG also fails to produce
the NKs. The large amount of ejecta mass (11.6 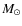 )
during the SN is not able
to explain the observed ejecta mass (2-4
)
during the SN is not able
to explain the observed ejecta mass (2-4 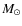 )
in Cas A, which is
)
in Cas A, which is  60% lower.
60% lower.
- The LBSG progenitors (28 and 29
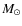 models) are the best candidates for producing
NKs as a result of N condensations from their low mass and H-poor envelopes. These
stars, however, do not develop QSF abundances in their surfaces,
although the He/H and N/H ratios are higher than those from the RSG progenitor.
The SN ejecta masses are higher than the observational values by a factor of 2.
models) are the best candidates for producing
NKs as a result of N condensations from their low mass and H-poor envelopes. These
stars, however, do not develop QSF abundances in their surfaces,
although the He/H and N/H ratios are higher than those from the RSG progenitor.
The SN ejecta masses are higher than the observational values by a factor of 2.
- The first WR progenitor (30
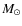 model) loses its H envelope but contains
enough N onto the surface to produce features similar to NKs. The final stellar
mass is low (5.85
model) loses its H envelope but contains
enough N onto the surface to produce features similar to NKs. The final stellar
mass is low (5.85 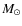 )
and the SN ejecta mass (4.40
)
and the SN ejecta mass (4.40 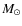 )
agrees with what is
observed in Cas A. Additionally, the 30
)
agrees with what is
observed in Cas A. Additionally, the 30 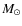 model shows QSFs ratios on it surface
at the beginning of WN-H poor stage.
model shows QSFs ratios on it surface
at the beginning of WN-H poor stage.
- The 33
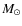 model has the advantages of a WR progenitor, i.e., surface QSF
abundances and low SN ejecta mass; however, the WR loses all the N on its surface to
produce NKs. The large WR mass-loss rate peels off the star and exposes the core
processed by 3
model has the advantages of a WR progenitor, i.e., surface QSF
abundances and low SN ejecta mass; however, the WR loses all the N on its surface to
produce NKs. The large WR mass-loss rate peels off the star and exposes the core
processed by 3 reactions.
reactions.
- The QSFs in Cas A are located at an average radius of
 1.5 pc.
None of our models give the correct position because the RSG, LBSG, or WR shells have larger radii.
To reproduce the QSF positions and to increase the amount of shocked, swept-up mass
as observed in Cas A, the inner shells of our LBSG/WR progenitors must be
closer to the star. This can be achieved by higher RSG mass loss rates (Schroeder & Cuntz 2005)
and/or by lower LBSG/WR mass loss rates (Hamann & Korestke 1998).
1.5 pc.
None of our models give the correct position because the RSG, LBSG, or WR shells have larger radii.
To reproduce the QSF positions and to increase the amount of shocked, swept-up mass
as observed in Cas A, the inner shells of our LBSG/WR progenitors must be
closer to the star. This can be achieved by higher RSG mass loss rates (Schroeder & Cuntz 2005)
and/or by lower LBSG/WR mass loss rates (Hamann & Korestke 1998).
We would like to thank our anonymous referee for the valuable comments, which have benefited the paper considerably. We would like also to thank Jacco Vink, Klara Schure, Allard Jan van Marle, and Robert Fesen for fruitful discussions. As usual, we also thank Michael L. Norman and the Laboratory for Computational Astrophysics for the use of ZEUS-3D. The computations were performed at the Instituto de Astronomía, Universidad Nacional Autónoma de México. This work has been partially supported by grants from DGAPA-UNAM (IN130698, IN117799 & IN114199) and CONACyT (32214-E).
References
- Borkowski, K., Szymkowiak, A. E., Blondin, J., & Sarazin, C. L. 1996, ApJ, 466, 866 [NASA ADS] [CrossRef]
- Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 283 [NASA ADS] [CrossRef]
- Chevalier, R. A. 1976, ApJ, 208, 826 [NASA ADS] [CrossRef]
- Chevalier, R. A., & Fransson, C. 1987, Nature, 328, 44 [NASA ADS] [CrossRef]
- Chevalier, R. A., & Imamura, J. N. 1983, ApJ, 270, 554 [NASA ADS] [CrossRef]
- Chevalier, R. A., & Kirshner, R. P. 1978, ApJ , 219, 931 [NASA ADS] [CrossRef]
- Chevalier, R. A., & Oishi, J. 2003, ApJ, 593, L23 [NASA ADS] [CrossRef]
- Chieffi, A., Domínguez, I., Hoflich, P., Limongi, M., & Straniero, O. 2003, MNRAS, 345, 111 [NASA ADS] [CrossRef]
- Chiosi, C., & Maeder, A. 1986, Ann. Rev. Astron. Astrophys., 24, 329 [NASA ADS] [CrossRef]
- DeLaney, T., Rudnick, L., Jones, T. W., et al. 2004, X-Ray and Radio Connections, ed. L. O. Sjouwerman, & K. K. Dyer, Published electronically by NRAO
- Dupree, A. K. 1986, ARA&A, 24, 377 [NASA ADS] [CrossRef]
- Dwarkadas, V. 2007, ApJ, 667, 226 [NASA ADS] [CrossRef]
- El Eid, M. 1995, MNRAS, 275, 983 [NASA ADS]
- Eldridge, J. J., & Tout, C. A. 2004, MNRAS, 353, 87 [NASA ADS] [CrossRef]
- Fabian, A. C., Willingale, R., Pye, J. P., Murray, S. S., & Fabbiano, G. 1980, MNRAS, 193, 175 [NASA ADS]
- Fesen, R. A. 2001, ApJSS, 133, 161 [NASA ADS] [CrossRef]
- Fesen, R. A., Becker, R. H., & Blair, W. P. 1987, ApJ, 313, 378 [NASA ADS] [CrossRef]
- Freyer, T., Hensler, G., & Yorke, H. 2006, ApJ, 638, 262 [NASA ADS] [CrossRef]
- García-Segura, G., Langer, N., & Mac Low, M. M. 1996a, A&A, 316, 133 [NASA ADS], Paper A
- García-Segura, G., Mac Low, M. M., & Langer, N. 1996b, A&A, 305, 229 [NASA ADS], Paper B
- Gotthelf, E. V., Koralesky, N., Rudnick, L., et al. 2001, ApJ, 552, L39 [NASA ADS] [CrossRef]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, ed. N. Prantzo, E. Vangioni-Flam, & M. Casse (Cambridge: Cambridge Univ. Press), 13
- Heger, A. 1998, Ph.D. Thesis, Technische Universität München
- Heger, A., & Langer, N. 1996, A&A, 315, 421 [NASA ADS]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef]
- Hirschi, R., Meynet, G., & Maeder, A. 2004, A&A, 425, 649 [NASA ADS] [CrossRef] [EDP Sciences]
- Hwang. U., & Laming, J. M. 2003, ApJ, 597, 362 [NASA ADS] [CrossRef]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef]
- Jansen, F. A., Smith, A., Bleeker, J. A. M., et al. 1988, ApJ, 331, 949 [NASA ADS] [CrossRef]
- Johnston, M. D., & Yahil, A. 1984, ApJ, 285, 587 [NASA ADS] [CrossRef]
- Lamb, S. A. 1978, ApJ, 220, 186 [NASA ADS] [CrossRef]
- Langer, N. 1989, A&A, 220, 135 [NASA ADS]
- Langer, N., & El Eid, M. F. 1986, A&A, 167, 265 [NASA ADS]
- Langer, N., El Eid, M. F., & Fricke, K. J. 1985, A&A, 145, 179 [NASA ADS]
- Langer, N., Kirkiadis, M., El Eid, M. F., Fricke, K. J., & Weiss, A. 1988, A&A, 192, 177 [NASA ADS]
- Limongi, M., Straniero, O., & Chieffi, A. 2000, ApJS, 129, 625 [NASA ADS] [CrossRef]
- MacDonald, J., & Bailey, M. E. 1981, MNRAS, 197, 995 [NASA ADS]
- Mereghetti, S., Tiengo, A., & Israel, G. L. 2002, ApJ, 569, 275 [NASA ADS] [CrossRef]
- Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences]
- Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS]
- Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS]
- Peimbert, M. 1971, ApJ, 170, 261 [NASA ADS] [CrossRef]
- Peimbert, M., & van den Bergh, S. 1971, ApJ, 157, 223 [NASA ADS] [CrossRef]
- Renzini, A., Greggio, L., Ritossa, C., & Ferrario, L. 1992, ApJ, 204, 461
- Reed, J. E., Hester, J. J., Fabian, A. C., & Winkler, P. F. 1995, ApJ, 440, 706 [NASA ADS] [CrossRef]
- Schroder, K. P., & Cuntz, M. 2005, ApJ, 630, L73 [NASA ADS] [CrossRef]
- Schure, K. M., Vink, J., García-Segura, G., & Achterberg, A. 2008, ApJ, 686, 399 [NASA ADS] [CrossRef]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [NASA ADS] [CrossRef]
- Stothers, R. B., & Chin, C.-W. 2001, ApJ, 560, 934 [NASA ADS] [CrossRef]
- Tananbaum, H. 1999, IAU Circ., 7246
- Thorstensen, J. R., Fesen, R. A., & van den Bergh, S. 2001, AJ, 122, 297 [NASA ADS] [CrossRef]
- Tsunemi, H., Yamashita, K., Masai, K., Hayakawa, S., & Koyama, K. 1986, ApJ, 306, 248 [NASA ADS] [CrossRef]
- Vink, J. 2005, in High Energy Gamma-Ray Astronomy, ed. F. A. Aharonian, H. J. Völk, & D. Horns, AIP Conf. Proc., 745, 160
- Vink, J., Kaastra, J. S., & Bleeker, J. A. M. 1996, A&A, 307, L41 [NASA ADS]
- Vishniac, E. T. 1983, ApJ, 274, 152 [NASA ADS] [CrossRef]
- Woosley, S. E., Langer, N., & Weaver, T. A. 1995, ApJ, 448, 315 [NASA ADS] [CrossRef]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef]
- Young, P. A., Fryer, C. L., Hungerford, A., et al. 2006, ApJ, 640, 891 [NASA ADS] [CrossRef]
All Tables
Table 1: Evolutionary phases.
Table 2: Lifetimes of nuclear burning.
Table 3: Final stellar models.
Table 4:
Wind properties of the 23 ![]() model.
model.
Table 5:
Wind properties of the 28 ![]() model.
model.
Table 6:
Wind properties of the 29 ![]() model.
model.
Table 7:
Wind properties of the 30 ![]() model.
model.
Table 8:
Wind properties of the 33 ![]() model.
model.
Table 9:
Ejected masses from the stellar models.
![]() is the mass cut
chosen from Woosley et al. (2002).
is the mass cut
chosen from Woosley et al. (2002).
![]() is
total ejected mass. Last five columns show the yields by element.
is
total ejected mass. Last five columns show the yields by element.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f1}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg51.png)
|
Figure 1:
Evolutionary tracks for the models with 23 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f2}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg59.png)
|
Figure 2:
Surface mass fractions of elements as function of time in the 23 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f3}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg89.png)
|
Figure 3:
Surface mass fractions of elements as function of time in the
30 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f4}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg108.png)
|
Figure 4:
Logarithm of the mass-loss rate as a function of time ( from top to bottom) for the 23, 28, 29, 30, and 33 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f5}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg109.png)
|
Figure 5:
Terminal wind velocities as a function of time
(from top to bottom) for the 23, 28, 29, 30, and 33 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f6}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg113.png)
|
Figure 6:
Logarithm of gas density at the end of each RSG phases.
The swept-up shells formed at the main sequence phases are located at
distances of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f7}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg124.png)
|
Figure 7:
Blast wave evolution for the 23 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f8}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg126.png)
|
Figure 8:
Post-RSG CSM evolution of the 28 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f9}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg127.png)
|
Figure 9:
Blast wave evolution for the 28 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f10}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg133.png)
|
Figure 10:
Post-RSG CSM evolution of the 30 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09913f11}
\end{figure}](/articles/aa/full_html/2009/42/aa09913-08/Timg135.png)
|
Figure 11:
Evolution of the 12 + log (N/H) ratio (solid line) and
12 + log (He/H) ratio (pointed line for 30 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


