| Issue |
A&A
Volume 506, Number 2, November I 2009
|
|
|---|---|---|
| Page(s) | 971 - 987 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912072 | |
| Published online | 27 August 2009 | |
A&A 506, 971-987 (2009)
Planet migration in three-dimensional radiative discs
W. Kley1 - B. Bitsch1 - H. Klahr2
1 - Institut für Astronomie & Astrophysik, Universität
Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany
2 - Max-Planck-Institut für Astronomie, Heidelberg, Germany
Received 15 March 2009 / Accepted 10 August 2009
Abstract
Context. The migration of growing protoplanets
depends on
the thermodynamics of the ambient disc. Standard modelling, using
locally isothermal discs, indicate an inward (type-I) migration in the
low planet mass regime. Taking non-isothermal effects into account,
recent studies have shown that the direction of the type-I migration
can change from inward to outward.
Aims. In this paper we extend previous
two-dimensional studies
and investigate the planet-disc interaction in viscous, radiative discs
using fully three-dimensional radiation hydrodynamical simulations of
protoplanetary accretion discs with embedded planets, for a range of
planetary masses.
Methods. We use an explicit three-dimensional (3D)
hydrodynamical code NIRVANA
that includes full tensor viscosity. We have added implicit radiation
transport in the flux-limited diffusion approximation, and to speed up
the simulations significantly we have newly adapted and implemented the
FARGO-algorithm in a 3D context.
Results. First, we present results of test
simulations that demonstrate the accuracy of the newly implemented FARGO-method
in 3D. For a planet mass of 20 ![]() ,
we then show that including radiative effects also yields a torque
reversal in full 3D. For the same opacity law, the effect is even
stronger in 3D than in the corresponding 2D simulations, due to a
slightly thinner disc. Finally, we demonstrate the extent of the torque
reversal by calculating a sequence of planet masses.
,
we then show that including radiative effects also yields a torque
reversal in full 3D. For the same opacity law, the effect is even
stronger in 3D than in the corresponding 2D simulations, due to a
slightly thinner disc. Finally, we demonstrate the extent of the torque
reversal by calculating a sequence of planet masses.
Conclusions. Through full 3D simulations of embedded
planets in
viscous, radiative discs, we confirm that the migration can be directed
outwards up to planet masses of about 33
![]() .
As a result, the effect may help to resolve the problem of inward
migration of planets that is too rapid during their type-I phase.
.
As a result, the effect may help to resolve the problem of inward
migration of planets that is too rapid during their type-I phase.
Key words: accretion, accretion disks - hydrodynamics - radiative transfer - planets and satellites: formation
1 Introduction
The process of migration in protoplanetary discs allows forming planets to move away from the location of creation and finally end up at a different position. The cause of this change in distance from the star are the tidal torques acting from the disturbed disc back on the protoplanet. These can be separated into two parts: i) the so-called Lindblad torques that are created by the two spiral arms in the disc and ii) the corotation torques that are caused by the co-orbital material as it periodically exchanges angular momentum with the planet on its horseshoe orbit. For comprehensive introductions to the field, see for example Papaloizou et al. (2007) or Masset (2008), and references therein. The Lindblad torques, caused by density waves launched at Lindblad resonances, quite generally lead to an inward motion of the planet explaining the observed hot planets very nicely (Ward 1997). The corotation torques are mainly caused by two effects, first by a gradient in the vortensity (Tanaka et al. 2002) and second by a gradient in the entropy (Baruteau & Masset 2008). For typical protoplanetary discs, both contributions can be positive, possibly counterbalancing the negative Lindblad torques (Paardekooper & Mellema 2006; Baruteau & Masset 2008). For the typically considered locally isothermal discs where the temperature only depends on the radial distance from the star, the net torque is negative, and migration is directed inwards for typical disc parameters (Tanaka et al. 2002). Through planetary synthesis models, the inferred rapid inward migration of planetary cores has been found to be inconsistent with the observed mass-distance distribution of exoplanets (Alibert et al. 2004; Ida & Lin 2008). Possible remedies are the retention of icy cores at the snow line or a strong reduction in the speed of type-I migration (of embedded low-mass planets). Here we focus on the latter process.
Different mechanisms for slowing down the too rapid inward migration have been discussed (Li et al. 2009; Masset et al. 2006), but including more realistic physics seems to be particularly appealing. As pointed out first by Paardekooper & Mellema (2006), the inclusion of radiative transfer can cause a strong reduction in the migration speed. The process has been subsequently investigated by several groups (Kley & Crida 2008; Paardekooper & Mellema 2008; Paardekooper & Papaloizou 2008; Baruteau & Masset 2008), who show that the migration process can indeed be slowed down or even reversed for sufficiently low-mass planets. This new effect occurs in non-isothermal discs and scales with the gradient of the entropy (Baruteau & Masset 2008), hence entropy-related torque. However, in a strictly adiabatic situation after a few libration time scales, the entropy gradient will flatten within the corotation region due to phase mixing. This will lead to saturation (and subsequent disappearance) of the part of the corotation torque that is caused by the entropy gradient in the horseshoe region (Paardekooper & Papaloizou 2009; Baruteau & Masset 2008). To prevent saturation of this entropy-related torque, some radiative diffusion (or local radiative cooling) is required (Kley & Crida 2008). Since for genuinely inviscid flows, the streamlines in the horseshoe region will be closed and symmetric with respect to the planet's location, some level of viscosity is always necessary to avoid torque saturation (Ogilvie & Lubow 2003; Paardekooper & Papaloizou 2008; Masset 2001; Paardekooper & Papaloizou 2009). This applies to both the vortensity- and entropy-related corotation torques. The maximum planet mass for which a change of migration may occur due to this effect lies for typical disc masses in the range of about 40 earth masses, beyond which the migration rate follows the standard (isothermal) case, as gap formation sets in which reduces the corotation effects (Kley & Crida 2008). Most of the above simulations have studied only the two-dimensional case, while three-dimensional models including radiative effects have been presented only for very low masses (Paardekooper & Mellema 2006), or for Jupiter type planets (Klahr & Kley 2006). A range of planet masses has not yet been studied systematically in full 3D.
In this paper we investigate the planet-disc interaction in
radiative discs
using fully three-dimensional radiation hydrodynamical simulations of
protoplanetary
accretion discs with embedded planets for a variety of planetary
masses.
For that purpose we modified and substantially extended an existing
multi-dimensional hydrodynamical code Nirvana
(Kley
et al. 2001; Ziegler & Yorke 1997a)
by incorporating the
FARGO-algorithm (Masset
2000a) and radiative transport in the flux-limited diffusion
approximation (Levermore & Pomraning
1981; Kley 1989).
The code Nirvana can in principle handle nested
grids which allows us to zoom-in on the detailed
structure in the vicinity of the planet (D'Angelo et al. 2002,2003),
however in the present context we limit ourselves to single grid
simulations.
We present several test cases to demonstrate first the accuracy of the FARGO-method
in 3D. We then proceed to analyse the effects of radiative transport
on the disc structure and torque balance. For our standard planet of ![]() ,
we find that the effect of torque reversal appears to be
even stronger in 3D than in 2D for an otherwise identical physical
setup.
We have a more detailed look at the implementation of the planet
potential
and show that it has definitely an influence on the strength of the
effect.
Finally, we perform simulations for a sequence of different planet
masses to evaluate
the mass range over which the migration may be reversed. The
consequence for the migration
process and the overall evolution of planets in discs is discussed.
,
we find that the effect of torque reversal appears to be
even stronger in 3D than in 2D for an otherwise identical physical
setup.
We have a more detailed look at the implementation of the planet
potential
and show that it has definitely an influence on the strength of the
effect.
Finally, we perform simulations for a sequence of different planet
masses to evaluate
the mass range over which the migration may be reversed. The
consequence for the migration
process and the overall evolution of planets in discs is discussed.
2 Physical modelling
The protoplanetary disc is treated as a three-dimensional (3D), non-self-gravitating gas whose motion is described by the Navier-Stokes equations. The turbulence in discs is thought to be driven by magneto-hydrodynamical instabilities (Balbus & Hawley 1998). Since we are interested in this study primarily on the average effect the disc has on the planet, we prefer in this work to simplify and treat the disc as a viscous medium. The dissipative effects can then be described via the standard viscous stress-tensor approach (e.g. Mihalas & Weibel Mihalas 1984). We assume that the heating of the disc occurs solely through internal viscous dissipation and ignore in the present study the influence of additional energy sources such as irradiation from the central star or other external sources. The internally produced energy is then radiatively diffused through the disc and eventually emitted from its surfaces. To describe this process we utilise the flux-limited diffusion approximation (FLD, Levermore & Pomraning 1981) which allows to treat approximately the transition from optically thick to thin regions near the disc's surface.
2.1 Basic equations
Discs with embedded planets have mostly been modelled through 2D simulations in which the disc is assumed to be infinitesimal thin, and vertical integrated quantities are used to describe the time evolution of the disc with the embedded planet. This procedure saves considerable computational effort but is naturally not as accurate as truly 3D simulations, in particular the radiation transport is difficult to model in a 2D context.
In this work we present an efficient method for 3D disc
simulations based on the
FARGO algorithm (Masset
2000a). For accretion discs where material is
orbiting a central object the best suited coordinates are
spherical polar coordinates ![]() where
r denotes the radial distance from the origin,
where
r denotes the radial distance from the origin, ![]() the
polar angle measured from the z-axis, and
the
polar angle measured from the z-axis, and ![]() denotes the
azimuthal coordinate starting from the x-axis.
denotes the
azimuthal coordinate starting from the x-axis.
In this coordinate system, the mid-plane of the disc coincides
with the
equator (
![]() ), and the origin of the
coordinate system is
centred on the star.
Sometimes we will need the radial distance from the polar axis which
we denote by a lower case s, which is the radial
coordinate in cylindrical
coordinates.
), and the origin of the
coordinate system is
centred on the star.
Sometimes we will need the radial distance from the polar axis which
we denote by a lower case s, which is the radial
coordinate in cylindrical
coordinates.
For a better resolution of the flow in the vicinity of the
planet, we
work in a rotating coordinate system which rotates with the orbital
angular velocity ![]() ,
which is identical to the orbital angular
velocity of the planet
,
which is identical to the orbital angular
velocity of the planet
![\begin{displaymath}\Omega_P = \left[\frac{G~(M_*+m_{\rm p})}{a^3}\right]^{1/2}
\end{displaymath}](/articles/aa/full_html/2009/41/aa12072-09/img28.png) |
(1) |
where M* is the mass of the star,
The Navier-Stokes equations in a rotating coordinate system in spherical coordinates read explicitly:
a) Continuity equation
Here
b) Radial momentum
Here
c) Meridional momentum
d) Angular momentum
where we defined the total specific angular momentum (in the inertial frame)
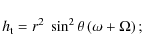 |
(6) |
i.e. the azimuthal velocity in the rotating frame is given by
The Coriolis force in Eq. (5) for ![]() (or
(or ![]() )
has been incorporated into the left hand side.
Thus, it is written in such a way as to conserve total angular momentum
best.
This conservative treatment is necessary to obtain an accurate
solution of the embedded planet problem (Kley 1998).
)
has been incorporated into the left hand side.
Thus, it is written in such a way as to conserve total angular momentum
best.
This conservative treatment is necessary to obtain an accurate
solution of the embedded planet problem (Kley 1998).
The function ![]() in the momentum equations
denotes the viscous
forces which are stated explicitly for the three-dimensional case in
spherical polar coordinates in Tassoul
(1978).
For the description of the viscosity we use a constant kinematic
viscosity coefficient
in the momentum equations
denotes the viscous
forces which are stated explicitly for the three-dimensional case in
spherical polar coordinates in Tassoul
(1978).
For the description of the viscosity we use a constant kinematic
viscosity coefficient ![]() .
.
e) Energy equation (internal energy)
Here T denotes the gas temperature in the disc and
where c is the speed of light,
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg01.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg67.png) |
Figure 1:
The gravitational potential of a |
| Open with DEXTER | |
2.2 Planetary potential
The total potential ![]() acting on the disc consists of two contributions,
one from the star
acting on the disc consists of two contributions,
one from the star ![]() ,
the other from the planet
,
the other from the planet ![]()

where
Typically in 2D simulations the planetary potential is
modelled by an
![]() -potential
-potential
where we denote the distance of the disc element to the planet with
However in a 3D configuration the same approach is not
necessary and would lead
to an unphysical ``spreading'' of the potential over a large region.
Hence, we apply a different type of smoothing, follow
Klahr & Kley (2006)
and use a cubic-potential of the form
This potential is constructed in such a way as to yield for distances dgreater than

and leads to a significant underestimate of the potential depth already at
We calculate the gravitational torques acting on the planet
by integrating over the whole disc, where we apply a tapering
function to exclude the inner parts of the Hill sphere of the planet.
Specifically, we use the smooth (Fermi-type) function
which increases from 0 at the planet location (d=0) to 1 outside
with the mass ratio
2.3 Setup
The three-dimensional (
![]() )
computational domain consists of a
complete annulus of the protoplanetary disc centred on the star,
extending from
)
computational domain consists of a
complete annulus of the protoplanetary disc centred on the star,
extending from ![]() to
to ![]() in units
of
in units
of ![]() AU.
In the vertical direction the annulus extends
from the disc's midplane
(at
AU.
In the vertical direction the annulus extends
from the disc's midplane
(at ![]() )
to about
)
to about ![]() (or
(or ![]() )
above
the midplane. In case of an inclined planet the domain has to be
extended
and cover the upper and lower half of the disc.
The mass of the central star is one solar
mass
)
above
the midplane. In case of an inclined planet the domain has to be
extended
and cover the upper and lower half of the disc.
The mass of the central star is one solar
mass ![]() ,
and the total disc mass inside
,
and the total disc mass inside ![]() is
is
![]() .
For the present study, we use a constant
kinematic viscosity coefficient with a value of
.
For the present study, we use a constant
kinematic viscosity coefficient with a value of ![]() cm2/s,
a value that relates to an equivalent
cm2/s,
a value that relates to an equivalent ![]() at r0 for a
disc aspect ratio of H/r
= 0.05, where
at r0 for a
disc aspect ratio of H/r
= 0.05, where ![]() .
In standard dimensionless units we have
.
In standard dimensionless units we have ![]() .
.
The models are initialised with a locally isothermal
configuration
where the temperature is constant on cylinders and has the
profile ![]() ,
where s is related to r through
,
where s is related to r through
![]() .
This yields a constant ratio of the disc's vertical height H
to the
radius s. The initial vertical density
stratification is approximately given by
a Gaussian:
.
This yields a constant ratio of the disc's vertical height H
to the
radius s. The initial vertical density
stratification is approximately given by
a Gaussian:
![\begin{displaymath}\rho(r,\theta)= \rho_0 (r) ~ \exp \left[ - \frac{(\pi/2 - \theta)^2 ~ r^2}{2 H^2} \right]\cdot
\end{displaymath}](/articles/aa/full_html/2009/41/aa12072-09/img100.png) |
(13) |
Here, the density in the midplane is
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg2a.eps}\par\includegr...
...{12072fg2b.eps}\par\includegraphics[width=9cm,clip]{12072fg2c.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg106.png) |
Figure 2:
Evolution of semi-major axis, eccentricity and inclination as a
function of time for a 20
|
| Open with DEXTER | |
2.4 Numerics
We adopt a coordinate system, which rotates at the orbital
frequency of the planet. For our standard cases, we use an
equidistant grid in ![]() with a resolution of
with a resolution of ![]() .
To minimise disturbances (wave reflections) from the radial boundaries,
we impose, at
.
To minimise disturbances (wave reflections) from the radial boundaries,
we impose, at ![]() and
and ![]() ,
damping boundary
conditions where all three velocity components are relaxed towards
their
initial state on a timescale of approximately the local orbital
period. The radial velocities at the inner and outer radius vanish.
The angular velocity is relaxed towards
the Keplerian values. For the density and temperature, we apply
reflective radial boundary conditions. In the azimuthal direction,
periodic boundary conditions are imposed for all variables.
In the vertical direction we apply outflow boundary conditions.
The boundary conditions do not allow for mass accretion through the
disc,
such that the total disc mass remains nearly constant during the time
evolution,
despite a possible small change due to little outflow through the
vertical boundaries and the used density floor (see below).
,
damping boundary
conditions where all three velocity components are relaxed towards
their
initial state on a timescale of approximately the local orbital
period. The radial velocities at the inner and outer radius vanish.
The angular velocity is relaxed towards
the Keplerian values. For the density and temperature, we apply
reflective radial boundary conditions. In the azimuthal direction,
periodic boundary conditions are imposed for all variables.
In the vertical direction we apply outflow boundary conditions.
The boundary conditions do not allow for mass accretion through the
disc,
such that the total disc mass remains nearly constant during the time
evolution,
despite a possible small change due to little outflow through the
vertical boundaries and the used density floor (see below).
The numerical details of the used finite volume code (NIRVANA) relevant for these planet disc simulations were described in Kley et al. (2001) and D'Angelo et al. (2003). In the latter paper the usage of the nested grid-technique is described in more detail as well. The original version of the NIRVANA code, on which our programme is based upon, has been developed by Ziegler & Yorke (1997b). The empowerment with FARGO is based on the original work by Masset (2000a). Our implementation appears to be the first inclusion of the FARGO-algorithm in a 3D spherical coordinate system. More details about the implementation are given in the appendix. The basic algorithm of the newly implemented radiation part in the energy Eq. (7) is presented in the appendix as well. To avoid possible time step limitations this part is always solved implicitly.
3 Test calculations
3.1 The FARGO-algorithm
To test the 3D implementation of the FARGO-algorithm
in our
NIRVANA-code we
have run several models with planets on circular, elliptic and inclined
orbits with and without the FARGO-method applied.
Here, we follow closely the models presented in Cresswell et al. (2007)
and consider moving planets in 3D discs. As the tests are dynamically
already
complicated we use here only the isothermal setup.
The different setups gave very similar results in all cases, and we
present results for one combined case of a 20
![]() planet
embedded in a locally isothermal disc with an initial non-zero
eccentricity
(e=0.2) and non-zero inclination (
planet
embedded in a locally isothermal disc with an initial non-zero
eccentricity
(e=0.2) and non-zero inclination (![]() ).
All physical parameters of this run are identical to those described
in Cresswell
et al. (2007), and we compare our results to the
last models
presented in that paper (their Fig. 16).
The outcome of this comparison is shown in Fig. 2, where we
display
the results of a standard non-Fargo run with the resolution
).
All physical parameters of this run are identical to those described
in Cresswell
et al. (2007), and we compare our results to the
last models
presented in that paper (their Fig. 16).
The outcome of this comparison is shown in Fig. 2, where we
display
the results of a standard non-Fargo run with the resolution
![]() with the data taken from Cresswell
et al. (2007) (where a different code has been used)
to two runs having a lower resolution of
with the data taken from Cresswell
et al. (2007) (where a different code has been used)
to two runs having a lower resolution of ![]() ,
one with FARGO and the other one without.
We can see that all 3 models (obtained with two different codes,
methods and resolutions)
yield very similar results. The scatter of the data points is slightly
reduced in the FARGO-run.
,
one with FARGO and the other one without.
We can see that all 3 models (obtained with two different codes,
methods and resolutions)
yield very similar results. The scatter of the data points is slightly
reduced in the FARGO-run.
| Figure 3: Radial stratification of surface density ( left) and the midplane temperature ( right) in the disc. This dashed lines represent simple approximations to the 3D stratified results. The solid (green) curves labelled ``flat'' refer to corresponding results for a vertically integrated flat 2D disc using the same input physics. |
|
| Open with DEXTER | |
| Figure 4: Vertical stratification of density ( left) and temperature ( right) at a radius of r=1.44. Thin dashed lines just represent simple functional relations. |
|
| Open with DEXTER | |
3.2 The radiation algorithm
To obtain an independent test of the newly implemented radiation
transport
module in our NIRVANA-code we performed a run
with the standard setup
as described above but with no embedded planet. Hence, this setup
refers to an axisymmetric disc with internal heating and radiative
cooling. For a fixed, closed computational domain it is only the
total mass enclosed that determines the final equilibrium state of the
system,
once the physics (viscosity, opacity, and equation of state) have been
prescribed.
The radial dependence of the vertically integrated surface density and
the midplane temperature are
displayed in Fig. 3,
and the corresponding vertical
profiles at a radius of r=1.44 in Fig. 4.
First of all, these new results obtained with NIRVANA
agree very well with those obtained with the completely
independent 2D-code RH2D used in the ![]() mode,
such as presented for example in Kley
et al. (1993),
which are not shown in the figures, however. As the final configuration
of the system is given by the equilibrium of
internal (viscous) dissipation and radiative transport, this test
demonstrates
the consistency of our implementations.
mode,
such as presented for example in Kley
et al. (1993),
which are not shown in the figures, however. As the final configuration
of the system is given by the equilibrium of
internal (viscous) dissipation and radiative transport, this test
demonstrates
the consistency of our implementations.
To relate our 3D results to previous radiative 2D runs which
use
vertically integrated quantities, and hence can only use an
approximative
energy transport and cooling (Kley
& Crida 2008), we
compare in Fig. 3
the results obtained with the two methods.
Both models are constructed for the same disc mass and identical
physics.
The label ``flat'' in the figure refers to the flat 2D case (obtained
with
RH2D, see Kley
& Crida 2008) and the ``stratified'' label to our new
3D implementation presented here. The left graph displays the
vertically integrated
surface density distribution, here ![]() ,
with
,
with ![]() for two-sided and 2 for one-sided discs.
Our result is well represented by a
for two-sided and 2 for one-sided discs.
Our result is well represented by a ![]() profile as expected
for a closed domain and constant viscosity. Interesting is the
irregular
structure at radii smaller than
profile as expected
for a closed domain and constant viscosity. Interesting is the
irregular
structure at radii smaller than ![]() in the full 3D stratified case,
and we point out that these refer to the onset of convection inside
that
radius. To model convection is of course not possible in a flat 2D
approach.
The temperature distribution for the full 3D case follows approximately
a
in the full 3D stratified case,
and we point out that these refer to the onset of convection inside
that
radius. To model convection is of course not possible in a flat 2D
approach.
The temperature distribution for the full 3D case follows approximately
a
![]() profile. Here, the approximate flat-disc model
leads to midplane temperatures that are about 40% higher for the bulk
part of the
domain than in the true 3D case. Possibly a refined modelling of the
vertical averaging procedure and the radiative losses
in the flat 2D case could improve the agreement here, but in the
presence of
convection we may expect differences in any case.
profile. Here, the approximate flat-disc model
leads to midplane temperatures that are about 40% higher for the bulk
part of the
domain than in the true 3D case. Possibly a refined modelling of the
vertical averaging procedure and the radiative losses
in the flat 2D case could improve the agreement here, but in the
presence of
convection we may expect differences in any case.
In Fig. 4
we display the vertical stratification of the disc at a specific
radius in the middle of the computational domain at r=1.44.
Two simple
approximations are over-plotted as dashed lines. Note, that in these
plots the stratification
is plotted along the ![]() lines which deviates for thin discs only slightly from
lines which deviates for thin discs only slightly from ![]() .
Taking z0=0.08, the Gaussian
curve for the density refers to
.
Taking z0=0.08, the Gaussian
curve for the density refers to ![]() and the temperature fit
to T(z)
= T0 [ 1 - 0.4 (z/z0)2].
These simple formulae are intended to guide the eye rather
than meant to model exactly the structure at this radius which depends
on the
used opacities. Given the simplicity of these, it is interesting that
they
approximate the true solution reasonably well within one scale height.
and the temperature fit
to T(z)
= T0 [ 1 - 0.4 (z/z0)2].
These simple formulae are intended to guide the eye rather
than meant to model exactly the structure at this radius which depends
on the
used opacities. Given the simplicity of these, it is interesting that
they
approximate the true solution reasonably well within one scale height.
3.3 Density floor
By expanding the computed area in the ![]() -direction beyond the
-direction beyond the ![]() to
to ![]() region
of our standard model,
the code would have to cover several orders of magnitude in the
density.
Thus, many more grid cells would be required to resolve the physical
quantities. In order to avoid this and save computation time, we apply
a minimum density
function (floor) for the low-density
regions high above the equatorial plane of the disc. It reads
region
of our standard model,
the code would have to cover several orders of magnitude in the
density.
Thus, many more grid cells would be required to resolve the physical
quantities. In order to avoid this and save computation time, we apply
a minimum density
function (floor) for the low-density
regions high above the equatorial plane of the disc. It reads
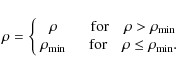 |
(14) |
Of course, applying a density floor like this will create mass inside the computed domain. The density floor
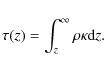 |
(15) |
Please note, that in the plot we do display the results along lines of constant (spherical) radius. Moving further away from the equatorial plane, one can see in the density profile the different minimum densities, but in the temperature profile there is hardly any difference at all. Above a certain distance from the equatorial plane the temperature remains constant. The little fluctuations visible in the profile are due to oscillations in the temperature for the low mass regions.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12072fg5a.eps} \includegraphics[width=8cm,clip]{12072fg5b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg128.png) |
Figure 5:
Vertical stratification of density in logarithmic scale ( top)
and temperature ( bottom) at a radius of r=1.00
for a simulation covering the |
| Open with DEXTER | |
By applying a minimum density the code is capable of resolving large
distances
above the equatorial plane with a reasonable number of grid cells.
Also note that it is not necessary to use a minimum density for
calculations
covering only the ![]() to
to ![]() regions, as the density is
always high enough.
regions, as the density is
always high enough.
4 Models with an embedded planet
For all the models with embedded planets we use our standard disc setup
as
described in Sect. 2.3
with the corresponding boundary conditions
in Sect. 2.4.
Here, we briefly summarise some important parameter of the setup.
The three-dimensional (
![]() )
structure of the disc extends form
)
structure of the disc extends form
![]() to
to ![]() in units of
in units of ![]() AU.
In the vertical direction the annulus
extends from the disc's midplane (at
AU.
In the vertical direction the annulus
extends from the disc's midplane (at ![]() )
to about
)
to about ![]() (or
(or
![]() )
above the midplane.
For our chosen grid size of
)
above the midplane.
For our chosen grid size of ![]() this
refers to linear grid resolution of
this
refers to linear grid resolution of ![]() at the location of
the planet, which corresponds to 3.3 gridcells per Hill radius, and to
about 5 gridcells per horseshoe half-width for a
at the location of
the planet, which corresponds to 3.3 gridcells per Hill radius, and to
about 5 gridcells per horseshoe half-width for a ![]() planet
in a disc with H/r =0.05. In
this configuration the planet is located exactly at the corner of a
gridcell.
In the fully radiative disc, the temperature at the disc surface is
kept at the
fixed ambient temperature of 10 K. This simple
``low-temperature'' boundary condition ensures that all the internally
generated
energy is liberated freely at the disc's surface. It is only suitable
for optically thin
boundaries and does not influence the inner parts of the optically
thick disc
(see Fig. 5).
The disc has a mass of
planet
in a disc with H/r =0.05. In
this configuration the planet is located exactly at the corner of a
gridcell.
In the fully radiative disc, the temperature at the disc surface is
kept at the
fixed ambient temperature of 10 K. This simple
``low-temperature'' boundary condition ensures that all the internally
generated
energy is liberated freely at the disc's surface. It is only suitable
for optically thin
boundaries and does not influence the inner parts of the optically
thick disc
(see Fig. 5).
The disc has a mass of ![]() ,
and an aspect ratio H/r
= 0.05 in the beginning.
,
and an aspect ratio H/r
= 0.05 in the beginning.
4.1 Initial setup
Before placing the planet into the 3D disc we have to bring it first
into a
radiative equilibrium state such that our results are not corrupted by
initial transients.
As described above this initial equilibration is performed in an
axisymmetric 2D setup that
is then expanded to full 3D.
Tests with our code have shown that we reach the 3D equilibrium state
(a constant torque) in a calculation with embedded planets
about ![]() faster when starting first with the 2D radiative equilibrium disc.
faster when starting first with the 2D radiative equilibrium disc.
| Figure 6: Density ( top) and Temperature ( bottom) for a fully radiative model in a 2D axisymmetric simulation. |
|
| Open with DEXTER | |
In Fig. 6 the 2D density and temperature distributions for such an equilibrated disc are displayed. In the equilibrium state of the fully radiative model the disc is much thinner than the isothermal starting case, see Fig. 7. Consequently, the density is increased in the equatorial plane, leaving the areas high above and below the disc with less material. Apparently, for this disc mass and the chosen values of viscosity and opacity, the balance of viscous heating and radiative cooling reduces the aspect ratio of the disc from initially 0.05 to about 0.037in the radiative case. Had we started with an initially thinner disc, the difference would of course not be that pronounced.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg7.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg134.png) |
Figure 7:
Vertical density distribution at r=1.4 for a fully
radiative model in a 2D axisymmetric simulation. ``+'': isothermal
starting configuration, `` |
| Open with DEXTER | |
After successfully completing the equilibration we now embed a
20
![]() planet
into the disc. The planet is held on a fixed orbit and we calculate the
torques acting on it
through integrating over the whole disc taking into account the above
tapering
function with a cutoff
planet
into the disc. The planet is held on a fixed orbit and we calculate the
torques acting on it
through integrating over the whole disc taking into account the above
tapering
function with a cutoff ![]() ,
which refers to b=0.8 in Eq. (11).
In addition to this value of the torque cutoff we have tested how the
obtained
total torque changes when using b=0.6. For our
standard
,
which refers to b=0.8 in Eq. (11).
In addition to this value of the torque cutoff we have tested how the
obtained
total torque changes when using b=0.6. For our
standard ![]() planet
presented in the following we found that for the isothermal cases
the results change by about 10% and in the radiative case by about 30%,
which can be considered as a rough estimate of the numerical
uncertainties of the
results. The deviation is greater in the radiative situation because
in this case important (corotation) contributions to the total torque
originate from a region very
close to the planet, which is influenced stronger by the applied torque
cutoff. Here, cancellation effects caused by adding the negative
Lindblad and the positive
corotation torque may explain part of the larger relative uncertainty
in the radiative case.
We note, that our applied torque cutoff is not hard but refers to the
smooth function (11).
Keeping in mind that there are only 3.3 gridcells per Hill radius,
lower
values for b are not useful.
planet
presented in the following we found that for the isothermal cases
the results change by about 10% and in the radiative case by about 30%,
which can be considered as a rough estimate of the numerical
uncertainties of the
results. The deviation is greater in the radiative situation because
in this case important (corotation) contributions to the total torque
originate from a region very
close to the planet, which is influenced stronger by the applied torque
cutoff. Here, cancellation effects caused by adding the negative
Lindblad and the positive
corotation torque may explain part of the larger relative uncertainty
in the radiative case.
We note, that our applied torque cutoff is not hard but refers to the
smooth function (11).
Keeping in mind that there are only 3.3 gridcells per Hill radius,
lower
values for b are not useful.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg8a.eps}\par\includegraphics[width=9cm,clip]{12072fg8b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg136.png) |
Figure 8:
Surface density distribution for isothermal simulations with H/r=0.05
at 100 planetary orbits. Displayed are results for the shallowest and
deepest potential. Top: |
| Open with DEXTER | |
4.2 Isothermal discs
Due to the applied smoothing, we expect the planetary potential to
modify the density structure of the disc near the
planet and subsequently change the torques acting on the planet.
First, we investigate the influence of the planetary potentials
(see Fig. 1)
on the disc and torques in the isothermal regime.
The 2D surface density distribution in the disc's midplane at 100
planetary orbits corresponding to
our two extreme planetary potentials (the shallowest and the deepest)
is displayed in Fig. 8, where
we used a cutoff for the maximum displayed
density to make both cases comparable.
As expected, a deeper planetary potential results in a higher density
concentration inside the planetary Roche lobe and to a slightly reduced
density
in the immediate surroundings.
This accumulation of mass near the planet for
deeper potentials is illustrated in more detail in Fig. 9. For our
deepest ![]() cubic potential the maximum density inside
the planet's Roche-lobe is over an order of magnitude greater than in
the shallowest
cubic potential the maximum density inside
the planet's Roche-lobe is over an order of magnitude greater than in
the shallowest ![]()
![]() -potential.
-potential.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg9.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg137.png) |
Figure 9:
Radial density distribution in the equator along (
|
| Open with DEXTER | |
In Fig. 10
we show the specific torques acting onto the planet using
different potentials for the case of H/r
= 0.05. The total torque is continuously
monitored and plotted versus time in the upper panel.
The radial torque density ![]() for the same models is displayed in the lower panel.
Here,
for the same models is displayed in the lower panel.
Here, ![]() is defined such that the total torque
is defined such that the total torque ![]() acting on the planet
is given by
acting on the planet
is given by
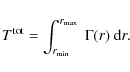 |
(16) |
The time evolution of the total torque displays a characteristic behaviour. Starting from the axisymmetric case, a first intermediate plateau is reached at early times between
where
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f10a.eps}\\ [1mm]
\includegraphics[width=9cm,clip]{12072f10b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg145.png) |
Figure 10:
Specific torque (in units of |
| Open with DEXTER | |
The two runs with the ![]() -potential
result in the most negative torque values, i.e.
the fastest inward migration (lower two curves in the upper panel).
While the total torques of the two
-potential
result in the most negative torque values, i.e.
the fastest inward migration (lower two curves in the upper panel).
While the total torques of the two ![]() -potentials are nearly
identical,
in the corresponding radial torque distribution
the cases are clearly separated, a fact which is due to cancellation
effects
when adding the inner (positive) and outer (negative) contribution.
The slightly deeper cubic
-potentials are nearly
identical,
in the corresponding radial torque distribution
the cases are clearly separated, a fact which is due to cancellation
effects
when adding the inner (positive) and outer (negative) contribution.
The slightly deeper cubic ![]() potential leads to a marginally decreased (in magnitude)
torque compared to the simulations with
potential leads to a marginally decreased (in magnitude)
torque compared to the simulations with ![]() -potential.
For the cubic
-potential.
For the cubic ![]() potential we obtain an even less negative
equilibrium torque compared to all the other isothermal simulations.
As most of the corotation torque is generated in the vicinity of the
planet, a change in the
density structure there (by deepening the potential) may have a
significant impact on the
torque values.
We can compare our values of the torque with the well known formulae
for the specific torque
in a 3D strictly isothermal disc as presented by Tanaka et al. (2002)
potential we obtain an even less negative
equilibrium torque compared to all the other isothermal simulations.
As most of the corotation torque is generated in the vicinity of the
planet, a change in the
density structure there (by deepening the potential) may have a
significant impact on the
torque values.
We can compare our values of the torque with the well known formulae
for the specific torque
in a 3D strictly isothermal disc as presented by Tanaka et al. (2002)
with
| (19) |
where
It seems at first surprising and unpleasing that the torques depend so
much on the
treatment of the planetary potential. However, an
![]() -potential
has an influence far beyond the Roche-radius of the
planet and certainly will change the torques acting on the planet. Here
the corotation torques are affected most prominently and become
more and more positive as the smoothing length is lowered
(see also Paardekooper
& Papaloizou 2009).
Nevertheless, in two-dimensional
simulations it has become customary to rely on
-potential
has an influence far beyond the Roche-radius of the
planet and certainly will change the torques acting on the planet. Here
the corotation torques are affected most prominently and become
more and more positive as the smoothing length is lowered
(see also Paardekooper
& Papaloizou 2009).
Nevertheless, in two-dimensional
simulations it has become customary to rely on ![]() -potentials for the purpose
to take into account the finite thickness of the disc.
In a three-dimensional context, the more localised cubic-potential
with its finite region of influence may be more realistic. But for the
isothermal case the increased potential depth leads to a very large
accumulation of mass, as seen in Fig. 9.
In such a case it will be very difficult to achieve convergence.
In the more realistic radiative case the situation is eased somewhat
through
a temperature increase near the planet, as outlined below.
-potentials for the purpose
to take into account the finite thickness of the disc.
In a three-dimensional context, the more localised cubic-potential
with its finite region of influence may be more realistic. But for the
isothermal case the increased potential depth leads to a very large
accumulation of mass, as seen in Fig. 9.
In such a case it will be very difficult to achieve convergence.
In the more realistic radiative case the situation is eased somewhat
through
a temperature increase near the planet, as outlined below.
To check numerical convergence we performed additional runs
using a larger number of
gridcells. In Fig. 11 we
display the total torque versus time
and the radial torque density ![]() for different grid resolutions, again
for the isothermal disc case.
In contrast to the previous plot we use here a slightly cooler disc
with H/r
=0.037,
as this matches more closely the results from the fully radiative
calculations presented below.
In this case the initial unsaturated torques reach even positive values
due to the smaller thickness of the disc.
The grid resolution seems to be sufficient for resolving the
structures near the Roche-lobe. For the displayed
for different grid resolutions, again
for the isothermal disc case.
In contrast to the previous plot we use here a slightly cooler disc
with H/r
=0.037,
as this matches more closely the results from the fully radiative
calculations presented below.
In this case the initial unsaturated torques reach even positive values
due to the smaller thickness of the disc.
The grid resolution seems to be sufficient for resolving the
structures near the Roche-lobe. For the displayed ![]() distribution in the lower panel
both cases are very similar and the higher resolution case is a bit
smoother.
distribution in the lower panel
both cases are very similar and the higher resolution case is a bit
smoother.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f11a.eps}\\ [1mm]
\includegraphics[width=9cm,clip]{12072f11b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg151.png) |
Figure 11:
Specific torque acting on the planet using different grid resolutions
for the isothermal case with H/r
= 0.037. In all cases the cubic potential with |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=0.81\linwx]{12072f12a.eps}\vspace*{0.5...
...vspace*{0.58mm}
\includegraphics[width=0.81\linwx]{12072f12d.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg152.png) |
Figure 12:
Surface density ( upper two panels) and temperature
in the equatorial plane ( lower two) for fully
radiative simulations at 100 planetary orbits. Displayed are results
for the shallowest and deepest potential. Upper panels refer to the |
| Open with DEXTER | |
4.3 Fully radiative discs
The simulations are started from the radiative disc in equilibrium as
described above,
and are continued with an embedded planet of ![]() .
The obtained equilibrium configuration for the surface density and
midplane-temperature is
displayed in Fig. 12
after an evolutionary time of 100 orbits.
As in the isothermal case the density within the Roche lobe of the
planet
is strongly enhanced for the deeper potentials, displayed are the two
extreme
cases of our different potentials.
Comparing with the corresponding density maps of the
isothermal case in Fig. 8,
one can also observe slightly smaller opening angles of the spiral arms
in the radiative case. For identical
H/r the sound speed would be
.
The obtained equilibrium configuration for the surface density and
midplane-temperature is
displayed in Fig. 12
after an evolutionary time of 100 orbits.
As in the isothermal case the density within the Roche lobe of the
planet
is strongly enhanced for the deeper potentials, displayed are the two
extreme
cases of our different potentials.
Comparing with the corresponding density maps of the
isothermal case in Fig. 8,
one can also observe slightly smaller opening angles of the spiral arms
in the radiative case. For identical
H/r the sound speed would be ![]() times larger in the radiative case
leading to a bigger opening angle.
Here, the effect is overcompensated by the reduced temperature (lower
thickness)
in the radiative case. A different opening angle of the spiral arms
will affect
the corresponding Lindblad torques acting on the planet.
times larger in the radiative case
leading to a bigger opening angle.
Here, the effect is overcompensated by the reduced temperature (lower
thickness)
in the radiative case. A different opening angle of the spiral arms
will affect
the corresponding Lindblad torques acting on the planet.
At the same time, a slight density enhancement is visible
``ahead'' of the planet (
![]() )
at a slightly smaller radius (
)
at a slightly smaller radius (![]() ).
This feature that is not visible in the isothermal case is caused
by including the thermodynamics of the disc.
Let us consider an adiabatic situation just after
the planet has
been inserted into the disc, and follow material on its horseshoe
orbit (in the co-rotating frame) as it makes a turn from the outer disc
(
).
This feature that is not visible in the isothermal case is caused
by including the thermodynamics of the disc.
Let us consider an adiabatic situation just after
the planet has
been inserted into the disc, and follow material on its horseshoe
orbit (in the co-rotating frame) as it makes a turn from the outer disc
(
![]() )
to the inner (r <1). The radial temperature
and density gradient imply for our ideal gas law a gradient in the
entropy function Sin the disc through
)
to the inner (r <1). The radial temperature
and density gradient imply for our ideal gas law a gradient in the
entropy function Sin the disc through

As shown above, in our simulations we find for the surface density
In this fully radiative case the temperature within the Roche radius of the planet has also increased substantially due to compressional heating of the gas (lower two panels in Fig. 12). In addition, the temperature in the spiral arms is increased as well due to shock heating.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f13a.eps}
\includegraphics[width=9cm,clip]{12072f13b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg160.png) |
Figure 13: Radial density ( top) and temperature ( bottom) distribution in the equator along a ray through the location of the planet for all 4 planetary potentials used, for the fully radiative case. |
| Open with DEXTER | |
The density and temperature runs in the disc midplane along a radial
line at ![]() cutting
through the planet are displayed in Fig. 13.
As in the isothermal case, deeper potentials lead to higher densities
within the Roche lobe. The increase is somewhat lower because now the
temperature
is higher as well due to the compression of the material.
The higher pressure lowers the density in comparison to the isothermal
case.
Interesting is that the maximum temperature is substantially higher
than in the ambient disc even
for this very low mass planet of
cutting
through the planet are displayed in Fig. 13.
As in the isothermal case, deeper potentials lead to higher densities
within the Roche lobe. The increase is somewhat lower because now the
temperature
is higher as well due to the compression of the material.
The higher pressure lowers the density in comparison to the isothermal
case.
Interesting is that the maximum temperature is substantially higher
than in the ambient disc even
for this very low mass planet of ![]() .
Considering accretion onto the planet the increase in temperature might
be even stronger due to the expected accretion luminosity.
.
Considering accretion onto the planet the increase in temperature might
be even stronger due to the expected accretion luminosity.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f14a.eps}
\includegraphics[width=9cm,clip]{12072f14b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg162.png) |
Figure 14:
Specific torques acting on a 20
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f15a.eps}\\
\includegraphics[width=9cm,clip]{12072f15b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg163.png) |
Figure 15:
Specific torque acting on the planet using different grid resolutions
for the fully radiative case. In all cases the cubic potential with |
| Open with DEXTER | |
4.4 Torque analysis for the radiative case
In the upper panel of Fig. 14 we
display the time
evolution of the total specific torque acting on a 20
![]() planet for the full radiative case.
In contrast to the isothermal situation, all four potentials result now
in a
positive total torque acting on the planet.
As in the previous isothermal runs, the torques reach their maximum
shortly after the onset of the simulations (between
planet for the full radiative case.
In contrast to the isothermal situation, all four potentials result now
in a
positive total torque acting on the planet.
As in the previous isothermal runs, the torques reach their maximum
shortly after the onset of the simulations (between ![]() )
and then settle toward their final value. In the corresponding
isothermal case with H/r
=0.037 the difference
between the initial positive unsaturated torque and the final saturated
value has
been very pronounced (see Fig. 11). In
contrast, in this fully radiative case the inclusion of energy
diffusion and the subsequent radiative cooling of the disc
will prevent saturation of the entropy-related corotation torque,
resulting in a positive
equilibrium torque. Very similar results have been found previously in
the fully radiative regime in
2D simulations (Kley
& Crida 2008).
It is important to notice, that the two cubic-potentials (which are
more
realistic in the 3D case) yield very similar
results. The more unrealistic
)
and then settle toward their final value. In the corresponding
isothermal case with H/r
=0.037 the difference
between the initial positive unsaturated torque and the final saturated
value has
been very pronounced (see Fig. 11). In
contrast, in this fully radiative case the inclusion of energy
diffusion and the subsequent radiative cooling of the disc
will prevent saturation of the entropy-related corotation torque,
resulting in a positive
equilibrium torque. Very similar results have been found previously in
the fully radiative regime in
2D simulations (Kley
& Crida 2008).
It is important to notice, that the two cubic-potentials (which are
more
realistic in the 3D case) yield very similar
results. The more unrealistic ![]() -potentials show rather strong
deviations because,
due to their extended smoothing of the potential, they tend to weaken
in particular the
corotation torques which originate in the close vicinity of the planet.
In the lower panel of Fig. 14 the
radial torque distribution
is displayed for the same 4 potentials. In comparison to the
corresponding plot for
the isothermal H/r
=0.037 case (see Fig. 11) we
notice
that the regular Lindblad part is slightly reduced in the
radiative case due to the higher sound speed.
-potentials show rather strong
deviations because,
due to their extended smoothing of the potential, they tend to weaken
in particular the
corotation torques which originate in the close vicinity of the planet.
In the lower panel of Fig. 14 the
radial torque distribution
is displayed for the same 4 potentials. In comparison to the
corresponding plot for
the isothermal H/r
=0.037 case (see Fig. 11) we
notice
that the regular Lindblad part is slightly reduced in the
radiative case due to the higher sound speed.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f16.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg165.png) |
Figure 16:
Radial variation of the specific torque acting on the planet using
different thermodynamical disc models. In all cases the cubic potential
with |
| Open with DEXTER | |
Additionally, clearly seen is the additional positive contribution just
inside r=1which appears to be responsible for the
torque reversal. This feature is caused by an asymmetric distribution
of the density in the very vicinity of the planet,
see also Fig. 17
below.
It pulls the planet gravitationally ahead, increasing its angular
momentum, leading to
a positive torque. Above we argued that this effect may be due to the
entropy-related corotation torque
of material moving on horseshoe orbits (see also Baruteau & Masset 2008).
Due to the symmetry of the problem one might expect
a similar feature caused by the material moving from inside out.
However, there is no sign of this present in the lower panel of
Fig. 14.
To analyse this asymmetry, we performed additional simulations varying
the grid
resolution and disc thermodynamics.
That the feature is not caused by lack of numerical resolution is
demonstrated in
Fig. 15,
where results obtained with two different grids are displayed.
Both models show the same characteristic torque enhancement just inside
the planet.
In Fig. 16
we compare the radial torque density of the isothermal and a new
adiabatic model for H/r=0.037
with the fully radiative model, all for the cubic potential with ![]() at intermediate resolution.
For the adiabatic case we show
at intermediate resolution.
For the adiabatic case we show ![]() at two different times. The first at t=10when the
torques are unsaturated, and the second at t=80
after saturation has occurred.
Please note, that the isothermal and adiabatic models start from the
same initial conditions
(locally isothermal), while the radiative model starts from the
radiative equilibrium
without the planet.
While the adiabatic model at t=10 shows signs of
the enhanced torque just inside
the planet, there is no sign of a similar feature at a radius just
outside of the planet.
Hence, this asymmetry of the entropy-related corotation torque is
visible in both the adiabatic and
radiative case. Outside of the planet the adiabatic model and the
radiative
agree very well as H/r is
similar, while the isothermal model deviates due to the
different sound speed. Whether the location of the maximum in the
torque density is identical in the radiative
and adiabatic case is hard to say from these simulations because in 3D
adiabatic runs
the peak appears to be substantially broader with respect to
corresponding 2D cases.
It has been argued by
Baruteau & Masset
(2008) that it should occur exactly at the corotation radius,
which is shifted (very slightly) from the planet's location due to the
pressure gradient in the disc. In our radiative simulations it seems
that the maximum is slightly shifted inwards,
an effect which may be caused by adding radiative diffusion to the
models and consider
discs in equilibrium. An issue that certainly needs further
investigation.
at two different times. The first at t=10when the
torques are unsaturated, and the second at t=80
after saturation has occurred.
Please note, that the isothermal and adiabatic models start from the
same initial conditions
(locally isothermal), while the radiative model starts from the
radiative equilibrium
without the planet.
While the adiabatic model at t=10 shows signs of
the enhanced torque just inside
the planet, there is no sign of a similar feature at a radius just
outside of the planet.
Hence, this asymmetry of the entropy-related corotation torque is
visible in both the adiabatic and
radiative case. Outside of the planet the adiabatic model and the
radiative
agree very well as H/r is
similar, while the isothermal model deviates due to the
different sound speed. Whether the location of the maximum in the
torque density is identical in the radiative
and adiabatic case is hard to say from these simulations because in 3D
adiabatic runs
the peak appears to be substantially broader with respect to
corresponding 2D cases.
It has been argued by
Baruteau & Masset
(2008) that it should occur exactly at the corotation radius,
which is shifted (very slightly) from the planet's location due to the
pressure gradient in the disc. In our radiative simulations it seems
that the maximum is slightly shifted inwards,
an effect which may be caused by adding radiative diffusion to the
models and consider
discs in equilibrium. An issue that certainly needs further
investigation.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f17a.eps}
\includegraphics[width=9cm,clip]{12072f17b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg167.png) |
Figure 17:
Results of a 2D fully radiative model using a resolution of |
| Open with DEXTER | |
In Fig. 17
we present additional results of supporting 2D simulations
for the fully radiative case, as shown for lower resolution in Kley & Crida (2008).
All physical parameter are identical to our 3D fully radiative case.
The top panel shows the surface density distribution next to the
planet. Seen is the
density enhancement just inside and ahead of the planet, and some
indication
for a lowering outside and behind.
Please note, that the planet moves counter-clockwise into the positive ![]() -direction.
i.e. upward in Fig. 17.
In the lower panel we display for each gridcell the net torque (
-direction.
i.e. upward in Fig. 17.
In the lower panel we display for each gridcell the net torque (
![]() )
acting on the planet.
It is constructed by adding each cell's individual contribution to the
torque
and that of the symmetric cell with respect to the planet location,
i.e.
)
acting on the planet.
It is constructed by adding each cell's individual contribution to the
torque
and that of the symmetric cell with respect to the planet location,
i.e.
![\begin{displaymath}\tilde{\Gamma}^\pm_{i,j} = \pm \left[ \Gamma(r_i, \phi_{\rm p...
... \phi_j)
+ \Gamma(r_i, \phi_{\rm planet} - \phi_j)
\right].
\end{displaymath}](/articles/aa/full_html/2009/41/aa12072-09/img169.png) |
(20) |
Hence, in absolute values the bottom half of the plot (with
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f18a.eps}
\includegraphics[width=9cm,clip]{12072f18b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg174.png) |
Figure 18:
Perturbed entropy ( top) and perturbed density (
bottom) for the 2D fully radiative equilibrium model using a
resolution of |
| Open with DEXTER | |
In Fig. 18
we show the perturbed entropy and density
in the 2D fully radiative model
in equilibrium, for a larger domain. Caused by the flow in the
horseshoe region, there is an entropy minimum for larger
![]() inside of
the planet, and a maximum for lower
inside of
the planet, and a maximum for lower ![]() outside, for
outside, for ![]() .
Both lie inside the horseshoe region and close to the separatrix.
The overall entropy distribution is very similar to that found by Baruteau & Masset (2008)
for adiabatic discs shortly after the insertion of the planet.
Due to the included radiative diffusion this effect does not saturate
in our case, and we
clearly support their findings even for the long term evolution. The
disturbed entropy shows in fact a slight asymmetry (in amplitude) with
respect to the planet, that reflects back on to to the density
distribution
(bottom panel).
.
Both lie inside the horseshoe region and close to the separatrix.
The overall entropy distribution is very similar to that found by Baruteau & Masset (2008)
for adiabatic discs shortly after the insertion of the planet.
Due to the included radiative diffusion this effect does not saturate
in our case, and we
clearly support their findings even for the long term evolution. The
disturbed entropy shows in fact a slight asymmetry (in amplitude) with
respect to the planet, that reflects back on to to the density
distribution
(bottom panel).
4.5 Planets with different planetary masses
Following the results obtained in the previous sections we adopt now
the cubic ![]() planetary potential assuming that it is closest
to reality, and study the effects of planets with various masses
in fully radiative discs. Starting from the 2D radiative equilibrium
state
(see Sect. 4.1)
we now place planets with masses ranging
from 5 up to 100
planetary potential assuming that it is closest
to reality, and study the effects of planets with various masses
in fully radiative discs. Starting from the 2D radiative equilibrium
state
(see Sect. 4.1)
we now place planets with masses ranging
from 5 up to 100
![]() in the initially axisymmetric 3D disc.
The numerical parameters for these simulations are identical to those
discussed
above.
in the initially axisymmetric 3D disc.
The numerical parameters for these simulations are identical to those
discussed
above.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f19.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg176.png) |
Figure 19: Specific torques acting on planets of different masses in the fully radiative (blue crosses) and isothermal (red plus signs) regime. Note, that the isothermal models are run for a fixed H/r =0.037. All torque values are displayed at a time when the equilibrium has been reached. |
| Open with DEXTER | |
In recent 2D simulations of radiative discs with embedded low mass
planets
the torque acting on the planet depends on the planetary mass in such a
way that for planets with a size lower than about 40 earth masses the
total torque is positive implying outward migration
(Kley & Crida 2008).
For large
masses the forming gap reduces the contribution of the corotation
torques,
and the results of the radiative simulations approach those of the
fixed temperature
(locally isothermal) runs.
Our 3D simulations show indeed very similar results for planets in this
mass regime, see Fig. 19. Planets
in the isothermal regime
migrate inward with a torque proportional to the planet mass squared,
as predicted for low mass planets undergoing Type-I-Migration.
Note, that we use in these models the temperature distribution for a
fixed H/r=0.037.
The values for the three lowest mass planets (with ![]() )
are not as accurate due to the insufficient grid resolution, remember
the ``kink''
in Fig. 11
which refers to
)
are not as accurate due to the insufficient grid resolution, remember
the ``kink''
in Fig. 11
which refers to ![]() at standard resolution.
For the fully radiative disc the planets up to about
at standard resolution.
For the fully radiative disc the planets up to about ![]() experience a
positive torque, while larger
mass planets migrate inward, due to the negative torque acting on them.
experience a
positive torque, while larger
mass planets migrate inward, due to the negative torque acting on them.
When comparing the 3D torques to the corresponding 2D values
as obtained by
Kley & Crida (2008)
for the same disc mass and opacity law, we note two
differences: i) the absolute magnitudes of the torques in the radiative
case are
enhanced in the 3D simulations with respect to the corresponding 2D
results,
resulting in even faster outward migration of the planets. This result
can be explained by the reduced temperature (i.e. vertical thickness)
of the 3D disc with respect to the 2D counterpart (cf. Fig. 3), as
a reduction in H typically increases the torques (Tanaka et al. 2002);
ii) the turnover mass from positive to negative torques is reduced in
the 3D
simulations. This effect is caused again by the reduced disc thickness,
as
now the onset of gap formation (
![]() )
occurs for lower planetary
masses.
The different form of the potential and the softening length may also
play a role in explaining some of the differences observed between the
3D and 2D results.
)
occurs for lower planetary
masses.
The different form of the potential and the softening length may also
play a role in explaining some of the differences observed between the
3D and 2D results.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f20.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg180.png) |
Figure 20: Radial torque distribution in equilibrium for various planet masses. The vertical dotted line indicates the location of the maximum. |
| Open with DEXTER | |
Finally, in Fig. 20 we show that the position of the maximum of the radial torque density is independent of the planet mass, and is therefore a result of the underlying disc physics.
5 Summary
We have investigated the migration of planets in discs using fully three-dimensional numerical simulations including radiative transport using the code NIRVANA. For this purpose we have presented and described our implementation of implicit radiative transport in the flux-limited diffusion approximation, and secondly our new FARGO-implementation in full 3D.
Before embedding the planets we studied the evolution of axisymmetric, radiative accretion discs in 2D. Starting with an isothermal disc model having a fixed H/r=0.05, we find that for our physical disc parameter the inclusion of radiative transport yields discs that are thinner ( H/r = 0.037 at r=1). We note that in the isothermal case the disc thickness is a chosen input parameter, while in the fully radiative situation it depends on the local surface density and the chosen viscosity and opacity. Interesting is here the direct comparison to the equivalent 2D models using the same viscosity, opacity and disc mass (Kley & Crida 2008), as displayed in Fig. 3. Here, our new 3D disc yields lower temperatures (by a factor of 0.6-0.7) than the 2D runs. Since the 2D simulations have to work with vertically averaged quantities, it will be interesting whether it might be possible to adjust those as to yield results in better agreement to our 3D results.
Concerning planetary migration we have confirmed the
occurrence
of outward migration for planetary cores in radiative discs.
As noticed in previous research, the effect is driven by a
radial entropy gradient across the horseshoe region in the disc,
that is maintained by radiative diffusion.
Our results show that planets below the turnover mass of about
![]() migrate outward while larger masses drift inward.
The reduced temperature in the 3D versus 2D runs has direct influence
on the magnitude
of the resulting torques acting on the planet.
As the disc is thinner in 3D the resulting torques, corotation as well
as Lindblad, are also stronger. The turnover mass from outward to
inward
migration is slightly reduced as well for the 3D disc since the smaller
vertical thickness allows for gap opening at lower planet masses.
Due to the reduced temperature in the 3D case,
the spiral waves have a slightly smaller opening
angle compared to the isothermal case.
migrate outward while larger masses drift inward.
The reduced temperature in the 3D versus 2D runs has direct influence
on the magnitude
of the resulting torques acting on the planet.
As the disc is thinner in 3D the resulting torques, corotation as well
as Lindblad, are also stronger. The turnover mass from outward to
inward
migration is slightly reduced as well for the 3D disc since the smaller
vertical thickness allows for gap opening at lower planet masses.
Due to the reduced temperature in the 3D case,
the spiral waves have a slightly smaller opening
angle compared to the isothermal case.
Another interesting, partly numerical, issue that we have
addressed
concerns the influence that the smoothing of the planetary potential
has
on the density structure in the vicinity of the planet and the speed
of migration.
We have compared the standard ![]() -potentials in contrast with
so-called
cubic-potentials. The results indicate, that a deeper (cubic) potential
results in a higher density inside the planet's Roche
lobe for isothermal, as well as radiative discs. Since the potential
depth influences the density in the immediate vicinity of the planet
the resulting torques show some dependence on the chosen smoothing
length.
We note that for the more realistic cubic-potential, changing the
smoothing
from 0.8 to 0.5 does not alter the results for the fully radiative
simulations considerably, and runs at different numerical resolutions
have
indicated numerical convergence. Hence, we believe that this value is
suitable
for performing planet disc simulations in 3D. The usage of an
-potentials in contrast with
so-called
cubic-potentials. The results indicate, that a deeper (cubic) potential
results in a higher density inside the planet's Roche
lobe for isothermal, as well as radiative discs. Since the potential
depth influences the density in the immediate vicinity of the planet
the resulting torques show some dependence on the chosen smoothing
length.
We note that for the more realistic cubic-potential, changing the
smoothing
from 0.8 to 0.5 does not alter the results for the fully radiative
simulations considerably, and runs at different numerical resolutions
have
indicated numerical convergence. Hence, we believe that this value is
suitable
for performing planet disc simulations in 3D. The usage of an ![]() -potential
cannot be recommended in 3D.
Outside of the planet's Roche lobe one can hardly notice a difference
in the
density structure.
Since the cubic-potential agrees with the true planetary potential
outside of the smoothing-length
-potential
cannot be recommended in 3D.
Outside of the planet's Roche lobe one can hardly notice a difference
in the
density structure.
Since the cubic-potential agrees with the true planetary potential
outside of the smoothing-length ![]() ,
it is of course desirable to choose
this transition radius as small as possible, but the achievable
numerical resolution always will set a lower limit. We found
,
it is of course desirable to choose
this transition radius as small as possible, but the achievable
numerical resolution always will set a lower limit. We found ![]() a suitable
value for our grid resolution and used that in our
parameter studies for different planet masses.
We note, that independent of the chosen form of the potential the
outward migration of planetary cores seems to be a robust result for
radiative discs. As the magnitude (and direction) of the effect depends
on the viscosity
and opacity, further studies, investigating different radial locations
in the
disc, will be very interesting.
a suitable
value for our grid resolution and used that in our
parameter studies for different planet masses.
We note, that independent of the chosen form of the potential the
outward migration of planetary cores seems to be a robust result for
radiative discs. As the magnitude (and direction) of the effect depends
on the viscosity
and opacity, further studies, investigating different radial locations
in the
disc, will be very interesting.
The outward migration of planet embryos with several earth
masses certainly
represents a solution to the too rapid inward migration found in this
mass
regime of classical type-I migration. Growing planets can spend more
time in the outer disc regions and move then later via type-II
migration
towards the star.
On the other hand it may be difficult to reconcile this finding with
the presence of the discovered Neptune-mass planets that reside closer
to the central star (
![]() AU), but still too
far away to be ablated by stellar
irradiation.
AU), but still too
far away to be ablated by stellar
irradiation.
As seen in our simulations, parts of the disc can display convection due to the form of the opacity law used. It will be certainly interesting in the future to analyse what influence the convective motions have on the migration properties of the embedded protoplanets. Additionally, fully radiative 3D-MHD simulations are definitely required to judge the efficiency of this process in turbulent discs.
AcknowledgementsVery fruitful discussions with Aurélien Crida and Fredéric Masset are gratefully acknowledged. H. Klahr and W. Kley acknowledge the support through the German Research Foundation (DFG) through grant KL 650/11 within the Collaborative Research Group FOR 759: The formation of Planets: The Critical First Growth Phase. B. Bitsch has been sponsored through the German D-grid initiative. The calculations were performed on systems of the Computer centre of the University of Tübingen (ZDV) and systems operated by the ZDV on behalf of bwGRiD, the grid of the Baden Württemberg state. Finally, we gratefully acknowledge the very helpful and constructive comments of an anonymous referee that inspired us to perform more detailed analysis.
Appendix A: Fargo algorithm
Multi-dimensional simulations of accretion discs that include the ![]() -direction
typically suffer from severe timestep limitations. This is due to the
fact that the azimuthal velocity
-direction
typically suffer from severe timestep limitations. This is due to the
fact that the azimuthal velocity ![]() is Keplerian and falls off with
radius. Hence, the innermost rings determine the maximum timestep
allowed even
though the region of interest lies much further out.
One suggestion to resolve this issue is given by the
FARGO algorithm which stands for ``Fast Advection
in Rotating Gaseous Objects''
(Masset 2000a).
It has originally been developed for 2D disc simulations
in a cylindrical coordinate system, for details of the implementation
see
Masset
(2000b,a).
Here, we briefly describe our extension to three spatial dimensions in
spherical
polar coordinates.
is Keplerian and falls off with
radius. Hence, the innermost rings determine the maximum timestep
allowed even
though the region of interest lies much further out.
One suggestion to resolve this issue is given by the
FARGO algorithm which stands for ``Fast Advection
in Rotating Gaseous Objects''
(Masset 2000a).
It has originally been developed for 2D disc simulations
in a cylindrical coordinate system, for details of the implementation
see
Masset
(2000b,a).
Here, we briefly describe our extension to three spatial dimensions in
spherical
polar coordinates.
The basic method relies on a directional splitting of the
advection part,
where first the radial and meridional (in ![]() direction) advection are performed in the standard way.
To calculate the azimuthal part we follow Masset (2000a) and
split
the angular velocity into three parts:
From the angular velocity of each grid cell
direction) advection are performed in the standard way.
To calculate the azimuthal part we follow Masset (2000a) and
split
the angular velocity into three parts:
From the angular velocity of each grid cell ![]() first an average angular velocity
first an average angular velocity ![]() is calculated for each radial ring i,
which is obtained here by averaging over the azimuthal (index k)
and vertical (index j) direction
is calculated for each radial ring i,
which is obtained here by averaging over the azimuthal (index k)
and vertical (index j) direction
where the summation runs of all azimuthal and meridional gridcells, and
| (A.2) |
where Nint denotes the nearest integer function. This corresponds to a transport by the angular ``shift velocity''
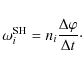 |
(A.3) |
Then we calculate the constant residual velocity of each ring
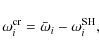 |
(A.4) |
and finally the residual velocity for each individual gridcell
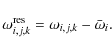 |
(A.5) |
Rewritten, we find for the angular velocity the following expression
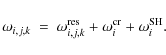 |
(A.6) |
The advection algorithm in the
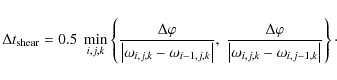 |
(A.7) |
The second restriction is only necessary in the case, where the above vertical averaging in Eq. (A.1) has not been performed. The sequencing of the advection sweeps in the FARGO algorithm has to be such that the azimuthal sweep comes at the end, hence in our simulations we use always: radial, meridional, and finally azimuthal.
In a staggered mesh code such as our NIRVANA
code, that is essentially
based on the ZEUS method, an additional
complication arises
in the straightforward application of the FARGO
method,
due to the fact that the velocity variables are located at the
cell interfaces and not at the centres.
Hence, the corresponding ``momentum cells'' for the radial and
meridional momenta
(![]() and
and ![]() )
are shifted with respect to the standard density
cells by half a gridcell in the radial or meridional direction,
respectively.
To apply the FARGO method one has first to split
all the momentum cells
in two halves, use the algorithm outlined above on each of the halves,
and then combine them again afterwards to calculate from the
updated momenta the new velocities on the interfaces.
This leads of course to an overhead in the simulation cost which is
counterbalanced
however by the much larger time step.
)
are shifted with respect to the standard density
cells by half a gridcell in the radial or meridional direction,
respectively.
To apply the FARGO method one has first to split
all the momentum cells
in two halves, use the algorithm outlined above on each of the halves,
and then combine them again afterwards to calculate from the
updated momenta the new velocities on the interfaces.
This leads of course to an overhead in the simulation cost which is
counterbalanced
however by the much larger time step.
Appendix B: Radiative transport
Here, we outline briefly the method to solve the flux-limited diffusion
equation in 3D. Radiative transport is treated as a sub-step of the
integration
procedure. In equilibrium viscous heating is balancing radiative
diffusion
and to ensure this also numerically we incorporate the dissipation into
this sub-step.
Using the appropriate parts of the energy Eq. (7) and
the flux (8)
we obtain a diffusion equation for the gas temperature.
where the diffusion coefficient is given by
and Q+ denotes the viscous dissipation that is added to the system. The flux-limiter
A straight forward finite difference form of Eq. (B.1)
in Cartesian Coordinates is given by
In orthogonal curvilinear coordinates additional geometry terms have to be added in the above equation. Here
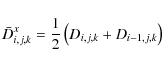 |
(B.4) |
and so forth.
The grid structure from which Eq. (B.3) follows is
outlined in the two-dimensional
case in Fig. B.1.
One has to
keep in mind that the temperature (being a scalar) is defined in the
cell centre, while
the values of ![]() are defined at the cell interfaces.
are defined at the cell interfaces.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12072fB1.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg211.png) |
Figure B.1:
The grid structure used in a staggered grid code for a two-dimensional
example.
Shown is the cell i,j where the
coordinates of the cell centre [
xci,
ycj]
is given by [
1/2(xi,j+xi+1,j),
1/2(yi,j+yi,j+1)].
The temperature Ti,j
is located at the cell centre where also the diffusion
coefficient D is defined.
The averaged diffusion coefficients |
| Open with DEXTER | |
In Eq. (B.3)
no time levels are specified on the right hand side.
For explicit differencing the time level should be tn
such that
the new temperature on the left Tn+1
is entirely given by the old values
Tn at time
tn.
This might lead to very small timesteps since the timestep limitation
is approximately given by
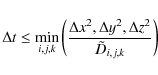 |
(B.5) |
where
Hence, often an implicit version of the equation has to be used, where all the temperature values Ti,j,k on the r.h.s. are evaluated at the new time tn+1 or an arithmetic mean between new and old times. Even though the diffusion coefficients may depend on temperature, we always evaluate those at the old time tn. Otherwise this would lead to a non-linear matrix equation.
Collection all the terms in Eq. (B.3) this leads
to a linear system of equations
with the form
| Axi,j,k Ti-1,j,k + Cxi,j,k Ti+1,j,k + Ayi,j,k Ti,j-1,k + Cyi,j,k Ti,j+1,k | |||
| Azi,j,k Ti,j,k-1 + Czi,j,k Ti,j,k+1 + Bi,j,k Ti,j,k = Ri,j,k | (B.6) |
where the superscript n+1 has been omitted on the left hand side. The coefficients Axi,j,k to Czi,j,k can be obtained straightforwardly from Eq. (B.3). The right hand side is given by

Written in matrix notation Eq. (B.6) reads
Obviously the matrix
Equation (B.7)
can in principle be solved by any linear equation package.
For simplicity and testing purposes we work presently with a standard
SOR
solver. Using an optimised relaxation parameter ![]() we need about 130 iterations
per timestep in the initial phase which is far from equilibrium and
only 80 iterations
at later times near equilibrium.
we need about 130 iterations
per timestep in the initial phase which is far from equilibrium and
only 80 iterations
at later times near equilibrium.
The radiation module of the code has been tested extensively in different coordinate systems in Bitsch (2008), and we have compared our new results on radiative viscous discs obtained with the 3D version of NIRVANA in detail with those of the existing 2D code RH2D.
References
- Alibert, Y., Mordasini, C., & Benz, W. 2004, A&A, 417, L25 [NASA ADS] [CrossRef] [EDP Sciences]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [NASA ADS] [CrossRef]
- Baruteau, C., & Masset, F. 2008, ApJ, 672, 1054 [NASA ADS] [CrossRef]
- Bitsch, B. 2008, Diploma Thesis, University of Tübingen
- Cresswell, P., Dirksen, G., Kley, W., & Nelson, R. P. 2007, A&A, 473, 329 [NASA ADS] [CrossRef] [EDP Sciences]
- Crida, A., Sándor, Z., & Kley, W. 2008, A&A, 483, 325 [NASA ADS] [CrossRef] [EDP Sciences]
- D'Angelo, G., Henning, T., & Kley, W. 2002, A&A, 385, 647 [NASA ADS] [CrossRef] [EDP Sciences]
- D'Angelo, G., Kley, W., & Henning, T. 2003, ApJ, 586, 540 [NASA ADS] [CrossRef]
- Ida, S., & Lin, D. N. C. 2008, ApJ, 673, 487 [NASA ADS] [CrossRef]
- Klahr, H., & Kley, W. 2006, A&A, 445, 747 [NASA ADS] [CrossRef] [EDP Sciences]
- Kley, W. 1989, A&A, 208, 98 [NASA ADS]
- Kley, W. 1998, A&A, 338, L37 [NASA ADS]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences]
- Kley, W., & Lin, D. N. C. 1996, ApJ, 461, 933 [NASA ADS] [CrossRef]
- Kley, W., & Lin, D. N. C. 1999, ApJ, 518, 833 [NASA ADS] [CrossRef]
- Kley, W., Papaloizou, J. C. B., & Lin, D. N. C. 1993, ApJ, 416, 679 [NASA ADS] [CrossRef]
- Kley, W., D'Angelo, G., & Henning, T. 2001, ApJ, 547, 457 [NASA ADS] [CrossRef]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef]
- Li, H., Lubow, S. H., Li, S., & Lin, D. N. C. 2009, ApJ, 690, L52 [NASA ADS] [CrossRef]
- Lin, D. N. C., & Papaloizou, J. C. B. 1985, in Protostars and Planets II, 981
- Masset, F. 2000a, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences]
- Masset, F. S. 2000b, in Disks, Planetesimals, and Planets, ed. G. Garzón, C. Eiroa, D. de Winter, & T. J. Mahoney, ASP Conf. Ser., 219, 75
- Masset, F. S. 2001, ApJ, 558, 453 [NASA ADS] [CrossRef]
- Masset, F. S. 2002, A&A, 387, 605 [NASA ADS] [CrossRef] [EDP Sciences]
- Masset, F. S. 2008, in EAS Publications Series, ed. M.-J. Goupil, & J.-P. Zahn, 29, 165
- Masset, F. S., D'Angelo, G., & Kley, W. 2006, ApJ, 652, 730 [NASA ADS] [CrossRef]
- Mihalas, D., & Weibel Mihalas, B. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press)
- Ogilvie, G. I., & Lubow, S. H. 2003, ApJ, 587, 398 [NASA ADS] [CrossRef]
- Paardekooper, S.-J., & Mellema, G. 2006, A&A, 459, L17 [NASA ADS] [CrossRef] [EDP Sciences]
- Paardekooper, S.-J., & Mellema, G. 2008, A&A, 478, 245 [CrossRef] [EDP Sciences]
- Paardekooper, S.-J., & Papaloizou, J. 2009, MNRAS, 394, 2283 [NASA ADS] [CrossRef]
- Paardekooper, S.-J., & Papaloizou, J. C. B. 2008, A&A, 485, 877 [NASA ADS] [CrossRef] [EDP Sciences]
- Papaloizou, J. C. B., Nelson, R. P., Kley, W., Masset, F. S., & Artymowicz, P. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 655
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [NASA ADS] [CrossRef]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef]
- Tassoul, J. 1978, Theory of rotating stars, Princeton Series in Astrophysics (Princeton: University Press)
- Ward, W. R. 1997, Icarus, 126, 261 [NASA ADS] [CrossRef]
- Ziegler, U., & Yorke, H. 1997a, Computer Physics Commun., 101, 54 [NASA ADS] [CrossRef]
- Ziegler, U., & Yorke, H. W. 1997b, Computer Physics Commun., 101, 54 [NASA ADS] [CrossRef]
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg01.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg67.png) |
Figure 1:
The gravitational potential of a |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg2a.eps}\par\includegr...
...{12072fg2b.eps}\par\includegraphics[width=9cm,clip]{12072fg2c.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg106.png) |
Figure 2:
Evolution of semi-major axis, eccentricity and inclination as a
function of time for a 20
|
| Open with DEXTER | |
| In the text | |
| |
Figure 3: Radial stratification of surface density ( left) and the midplane temperature ( right) in the disc. This dashed lines represent simple approximations to the 3D stratified results. The solid (green) curves labelled ``flat'' refer to corresponding results for a vertically integrated flat 2D disc using the same input physics. |
| Open with DEXTER | |
| In the text | |
| |
Figure 4: Vertical stratification of density ( left) and temperature ( right) at a radius of r=1.44. Thin dashed lines just represent simple functional relations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12072fg5a.eps} \includegraphics[width=8cm,clip]{12072fg5b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg128.png) |
Figure 5:
Vertical stratification of density in logarithmic scale ( top)
and temperature ( bottom) at a radius of r=1.00
for a simulation covering the |
| Open with DEXTER | |
| In the text | |
| |
Figure 6: Density ( top) and Temperature ( bottom) for a fully radiative model in a 2D axisymmetric simulation. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg7.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg134.png) |
Figure 7:
Vertical density distribution at r=1.4 for a fully
radiative model in a 2D axisymmetric simulation. ``+'': isothermal
starting configuration, `` |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg8a.eps}\par\includegraphics[width=9cm,clip]{12072fg8b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg136.png) |
Figure 8:
Surface density distribution for isothermal simulations with H/r=0.05
at 100 planetary orbits. Displayed are results for the shallowest and
deepest potential. Top: |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072fg9.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg137.png) |
Figure 9:
Radial density distribution in the equator along (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f10a.eps}\\ [1mm]
\includegraphics[width=9cm,clip]{12072f10b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg145.png) |
Figure 10:
Specific torque (in units of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f11a.eps}\\ [1mm]
\includegraphics[width=9cm,clip]{12072f11b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg151.png) |
Figure 11:
Specific torque acting on the planet using different grid resolutions
for the isothermal case with H/r
= 0.037. In all cases the cubic potential with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=0.81\linwx]{12072f12a.eps}\vspace*{0.5...
...vspace*{0.58mm}
\includegraphics[width=0.81\linwx]{12072f12d.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg152.png) |
Figure 12:
Surface density ( upper two panels) and temperature
in the equatorial plane ( lower two) for fully
radiative simulations at 100 planetary orbits. Displayed are results
for the shallowest and deepest potential. Upper panels refer to the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f13a.eps}
\includegraphics[width=9cm,clip]{12072f13b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg160.png) |
Figure 13: Radial density ( top) and temperature ( bottom) distribution in the equator along a ray through the location of the planet for all 4 planetary potentials used, for the fully radiative case. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f14a.eps}
\includegraphics[width=9cm,clip]{12072f14b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg162.png) |
Figure 14:
Specific torques acting on a 20
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f15a.eps}\\
\includegraphics[width=9cm,clip]{12072f15b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg163.png) |
Figure 15:
Specific torque acting on the planet using different grid resolutions
for the fully radiative case. In all cases the cubic potential with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f16.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg165.png) |
Figure 16:
Radial variation of the specific torque acting on the planet using
different thermodynamical disc models. In all cases the cubic potential
with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f17a.eps}
\includegraphics[width=9cm,clip]{12072f17b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg167.png) |
Figure 17:
Results of a 2D fully radiative model using a resolution of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f18a.eps}
\includegraphics[width=9cm,clip]{12072f18b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg174.png) |
Figure 18:
Perturbed entropy ( top) and perturbed density (
bottom) for the 2D fully radiative equilibrium model using a
resolution of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f19.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg176.png) |
Figure 19: Specific torques acting on planets of different masses in the fully radiative (blue crosses) and isothermal (red plus signs) regime. Note, that the isothermal models are run for a fixed H/r =0.037. All torque values are displayed at a time when the equilibrium has been reached. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12072f20.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg180.png) |
Figure 20: Radial torque distribution in equilibrium for various planet masses. The vertical dotted line indicates the location of the maximum. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12072fB1.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12072-09/Timg211.png) |
Figure B.1:
The grid structure used in a staggered grid code for a two-dimensional
example.
Shown is the cell i,j where the
coordinates of the cell centre [
xci,
ycj]
is given by [
1/2(xi,j+xi+1,j),
1/2(yi,j+yi,j+1)].
The temperature Ti,j
is located at the cell centre where also the diffusion
coefficient D is defined.
The averaged diffusion coefficients |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



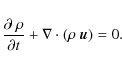
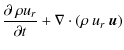
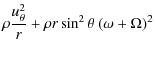
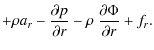
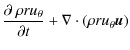
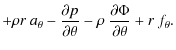
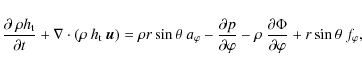
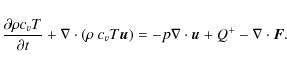
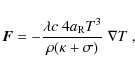
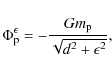
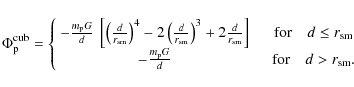
![\begin{displaymath}
f_b (d)=\left[\exp\left(-\frac{d/R_H-b}{b/10}\right)+1\right]^{-1}
\end{displaymath}](/articles/aa/full_html/2009/41/aa12072-09/img80.png)
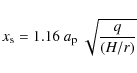
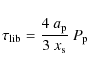
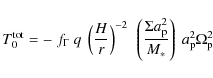
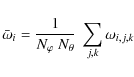
![\begin{displaymath}\frac{\partial T}{\partial t} =
\frac{1}{c_{\rm v} \rho} ~ \left[
\nabla \cdot ~ D \nabla T + Q^+ \right]
\end{displaymath}](/articles/aa/full_html/2009/41/aa12072-09/img199.png)
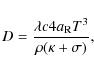
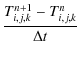 =
=
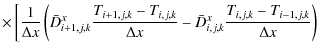
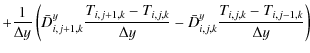
![$\displaystyle \left. +
\frac{1}{\Delta z} \left(
\bar{D}^z_{i,j,k+1} \frac{T_{i...
... \bar{D}^z_{i,j,k} \frac{T_{i,j,k} - T_{i,j,k-1}}{\Delta z}
\right)\right]\cdot$](/articles/aa/full_html/2009/41/aa12072-09/img207.png)