The influence of antikaon condensations on neutrino emissivity from neutron stars

W. B. Ding; G. Z. Liu; M. F. Zhu; Z. Yu; E. G. Zhao

doi:10.1051/0004-6361/200810814

Home

All issues

Volume 506 / No 2 (November I 2009)

A&A, 506 2 (2009) L13-L16

Full HTML

Free Access

Issue		A&A Volume 506, Number 2, November I 2009


Page(s)		L13 - L16
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200810814
Published online		17 September 2009

A&A 506, L13-L16 (2009)

LETTER TO THE EDITOR

The influence of antikaon condensations on neutrino emissivity from neutron stars

W. B. Ding¹ - G. Z. Liu¹ - M. F. Zhu¹ - Z. Yu¹ - E. G. Zhao²

1 - Center for Theoretical Physics Jilin University, Changchun 130023, PR China
2 - Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100080, PR China

Received 17 August 2008 / Accepted 9 September 2009

Abstract
Neutrino emissivity ( $I_{\rm URCA}$ ) from the direct URCA (dURCA) process and the URCA processes with K^- and $\overline{K}^{~0}$ condensations are considered simultaneously in neutron star matter. The neutrino emissivity due to the dURCA process plays a dominant role. However, antikaon condensations change the chemical potential of electrons, the effective masses of nucleons and the matrix elements of the reaction for the dURCA process. These changes make the neutrino emissivity for the dURCA process decrease. In this case, with antikaon condensations the total neutrino emissivity becomes lower. We believe that antikaon condensations are unfavorable for fast cooling of neutron stars.

Key words: stars: neutron - dense matter - neutrinos

1 Introduction

Neutron stars are born having an interior temperature greater than 10¹¹ K immediately after the supernova explosion, however, the temperature drops to 10⁹ K after several minutes. Neutrino emission dominates the cooling of stars over the first 10⁴-10⁵ years until the temperature falls to $\lesssim$ 10⁸ K and photon emission overtakes neutrino emission. With the accumulation and development of observations (e.g. Page et al. 2004; Heinke et al. 2007) and theoretical knowledge (e.g. Lattimer et al. 1991; Kubis & Kutschera 2003), much greater attention is being paid to the cooling of neutron stars (e.g. Prakash et al. 1992; Kubis 2006). Thus far, cooling models have been divided into two categories: slow (standard) cooling (e.g. Page et al. 2004; Yakovlev et al. 2001) with a magnitude of emissivity 10¹⁹-10²¹ erg s^-1 cm^-3, and enhanced cooling (e.g. Lattimer et al. 1991; Kubis & Kutschera 2003; Leinson 2002) with a magnitude of 10²⁵-10²⁷ erg s^-1 cm^-3. The former mainly includes the modified URCA process and nucleon bremsstrahlung, whereas the latter includes the direct URCA processes with nucleons (dURCA), hyperons, pion and kaon condensations and quark matter.

After Kaplan and Nelson first demonstrated that K^- mesons could undergo Bose-Einstein condensation in dense matter (Kaplan & Nelson 1986; Nelson & Kaplan 1987), numerous researchers have shown that antikaon condensations are very sensitive to the equation of state (EOS) and the optical potential depth of antikaons (e.g. Glendenning & Schaffner-Bielich 1999; Lee et al. 1995; Banik & Bandyopadhyay 2002; Kolomeistev & Voskresensky 2003; Gu et al. 2005; Ding et al. 2008). Antikaon condensations can change the distribution of particles, soften the EOS and reduce the maximum mass of neutron stars. Recently, it has been suggested that simultaneous K^- and $\overline{K}^0$ condensations enhance the cooling of neutron stars (Kubis 2006). The conditions required for the onset of the URCA process with K^- condensation (kURCA) are far more easily fulfilled than those necessary for the dURCA process. If we simply add the effect of the kURCA process to that of the dURCA process in a neutron star, the viewpoint that K^- condensation enhances the cooling is certainly justifiable; however, if the dURCA process, kURCA process and the URCA process with $\overline{K}^{~0}$ condensation (k0URCA) occur simultaneously and influence each other, the situation becomes very complicated. The magnitude of neutrino emissivity from the URCA processes due to antikaon condensations is 10²⁵ erg s^-1 cm^-3, which is lower than that from the dURCA process, 10²⁷ erg s^-1 cm^-3. Among the three URCA processes, dURCA plays the most important role. The impact of both the kURCA and k0URCA processes on the dURCA process is crucial to the total cooling effect of neutron stars. In fact, with antikaon condensations, the neutrino emissivity from the dURCA process decreases obviously, due to the changes of the chemical potential of electrons, the effective masses of nucleons and the matrix elements of the reaction for the dURCA process.

2 The models

We begin our calculation with the cooling mechanism investigated by Kubis (2006). This model describes the properties of the concurrence of the dURCA, kURCA and k0URCA processes. The three URCA channels are

$\displaystyle {\rm dURCA}$	:	$\displaystyle \tilde{n} \longleftrightarrow \tilde{p} + {e} + \overline{\nu}_{\rm e}$
$\displaystyle {\rm kURCA}$	:	$\displaystyle \tilde{n} \longleftrightarrow \tilde{n}+{e} + \overline{\nu}_{\rm e}$	(1)
		$\displaystyle \tilde{p} \longleftrightarrow \tilde{p}+{e} +\overline{\nu}_{\rm e}$
$\displaystyle {\rm k0URCA}$	:	$\displaystyle \tilde{p} \longleftrightarrow \tilde{n}+{e}+\overline{\nu}_{\rm e},$

$\tilde{p}$ and $\tilde{n}$ represent quasiparticles of the mixed states of normal nucleons. The emissivity due to neutrino emission can be derived from Fermi's rule. The energy per unit volume and time released in one cycle can be expressed as

$\displaystyle % I_{\rm URCA} = \frac{457\pi}{20~160}T^6{m_{\rm p}}^*{m_{\rm n}}^*\mu_{\rm e} \mid M_{\rm ij} \mid ^2 \Theta_{\rm ife}\cdot$

(2)

Here ${m_{\rm p}}^*$ and ${m_{\rm n}}^*$ are the effective masses of protons and neutrons, $\mu_{\rm e}$ is the chemical potential of electrons, and $\Theta_{\rm ife}$ is a step function corresponding to the triangle condition. $\mid M_{\rm ij}\mid^2$ corresponds to various URCA channels (refer to Kubis 2006 for details). The thresholds derived by ensuring the conservation of energy and momentum simultaneously for each URCA channel are

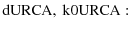	$\textstyle {\rm dURCA,~k0URCA} :$ $\displaystyle \mid p_{\rm n}-p_{\rm p} \mid ~ < p_{\rm e} < p_{\rm n} + p_{\rm p}~,$
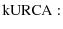
	$\textstyle {\rm kURCA} :$ $\displaystyle 2 p_{\rm n} > p_{\rm e}, 2 p_{\rm p} > p_{\rm e},$	(3)

where p_i is the Fermi momentum of nucleons or leptons. Here we assume that only negative leptons are present in the system. The situation for muons is similar to that for electrons.

The relativistic mean field theory (RMFT) is adopted here to describe the strong interactions, among which baryon-baryon and baryon-antikaon interactions are mediated by the exchange of $\sigma$ , $\omega$ and $\rho$ mesons (e.g. Glendenning & Schaffner-Bielich 1999; Pal et al. 2000). In neutron star matter including neutrons, protons, electrons, muons and antikaon condensations ( $np K^-\overline{K}^{~0}$ ) with the optical potential of $U_{\overline{K}}(n_0)=-120$ MeV, the effective masses of nucleons and the chemical potential of electrons at a fixed baryon density $n_{\rm B}$ can be derived by solving a set of nonlinear equations (Ding et al. 2008). Solving this set of nonlinear equations, we can obtain the EOS, which can then be used as an input to solve the Tolman-Oppenheimer-Volkoff (TOV) equations and obtain the mass-radius relations of neutron stars. When the properties of static neutron stars are obtained, we can calculate the radial distribution of neutrino emissivity for a neutron star with a given mass.

The relation between the interior temperature and the evolving time of a neutron star can be obtained by solving the cooling equation,

$\displaystyle C_v\frac{{\rm d}T}{{\rm d}t}=-(L_\nu+L_r),$

(4)

where C_v is the total heat capacity of the neutron star, $L_\nu$ is the total neutrino luminosity and L_r is the photon luminosity. Here we use the simple form of L_r, which is shown in Shapiro & Teukolsky (1983). With the neutrino luminosity $L_\nu$ , the photon luminosity L_r and the properties of the core of the neutron star, the cooling curves can be obtained (e.g. Page & Applegate 1992; Yakovlev & Pethick 2004; Gusakov et al. 2005).

3 Discussion

$\begin{figure} \par\includegraphics[width=15.5cm,height=8cm,clip]{10814fg1} \end{figure}$

Figure 1:

a) The neutrino emissivity $I_{\rm URCA}$ as a function of density. The dashed line represents the dURCA for eand $\mu$ in np matter, whereas in $np K^-\overline{K}^{~0}$ matter the curve for dURCA process is dash-dot-dotted. For $np K^-\overline{K}^{~0}$ matter, the line for the total neutrino emissivity (URCAt including the dURCA, kURCA and k0URCA processes for e and $\mu$ ) is solid, the lines for the kURCA is dash-dotted, and the line for the k0URCA is dotted. The interior temperature T is fixed at T = 10⁹ K. b) $I_{\rm URCA}$ versus the radial distance of neutron stars with different masses (in units of $M_{\odot }$ ) in $np K^-\overline{K}^{~0}$ matter. c) Same as b), but for several massive stars.

Open with DEXTER

In this letter, we exploit the GL91 set (Glendenning & Moszkowski 1991) for meson-nucleon couplings. The vector meson-kaon couplings $g_{\omega K} = 1/3 g_{\omega N}, g_{\rho K} = g_{\rho N}$ are derived from the quark and isospin counting rule. The scalar coupling is $g_{\sigma K}=1.50783$ , which is estimated from the optical potential of $U_{\overline{K}}(n_0)=-120$ MeV. Neutron star properties in both $np K^-\overline{K}^{~0}$ and nucleon-only (np) matter are listed in Table 1.

Table 1: The maximum mass $M_{\max}$ , radii R and central densities $u_{\rm cent}=n_{\rm cent}/n_0$ of neutron stars.

According to the restrictions of URCA processes, Eq. (3) and the thresholds of antikaon condensations, we obtain the baryon number density range of the URCA channels of electrons (URCAe) in $np K^-\overline{K}^{~0}$ matter

$\displaystyle {\rm dURCA}$	:	$\displaystyle 1.800\leq u\leq u_{\rm cent},~~M\geq1.08~M_{\odot};$
$\displaystyle {\rm kURCA}$	:	$\displaystyle 3.028\leq u\leq u_{\rm cent},~~M\geq1.95~M_{\odot};$	(5)
$\displaystyle {\rm k0URCA}$	:	$\displaystyle 4.869\leq u\leq u_{\rm cent},~~M\geq2.0625~M_{\odot}.$

However, the dURCA process with muons (dURCA $\mu$ ) occurs only when $M \geq 1.44~M_{\odot}$ . Adding the results for the URCA $\mu$ process to that for the URCAe we can calculate the neutrino emissivity $I_{\rm URCA}$ as a function of baryon density in np and $np K^-\overline{K}^{~0}$ matter. Here we choose $G_F = 1.16632\times10^{-11}$ MeV^-2, D = 0.756, F = 0.477 and $\cos\theta_C=0.973$ . The neutrino emissivity $I_{\rm URCA}$ is shown in Fig. 1a. The dashed line represents the dURCA for e and $\mu$ in np matter, in $np K^-\overline{K}^{~0}$ matter the curve for dURCA process is dash-dot-dotted. For $np K^-\overline{K}^{~0}$ matter, the line for the total neutrino emissivity (URCAt including the dURCA, kURCA and k0URCA processes for e and $\mu$ ) is solid. It is seen that the kURCA (dash-dotted lines) and the k0URCA processes (dotted line) occur at about 3n₀ and 4.9n₀, respectively. The magnitude of $I_{\rm URCA}$ is as high as 10²⁵ erg s^-1 cm^-3, indicating that if we only consider the kURCA and k0URCA processes, K^- and $\overline{K}^{~0}$ condensations will favor fast cooling of neutron stars. Moreover, the appearance of the k0URCA process actually enhances the neutrino emissivity of the kURCA process. Comparing the solid line and the dashed line, the total emissivity of the three URCA processes in $np K^-\overline{K}^{~0}$ matter is the same as that of the dURCA in np matter at lower densities. However, when the kURCA process occurs, the total emissivity of the three URCA processes in $npK^{-}\overline{K}^0$ matter turns out to be a few times lower than that of the dURCA in np matter.

The radial distribution of neutrino emissivity with various masses of neutron stars is shown in Fig. 1b. To interpret the properties of neutrino emission clearly, we present an amplification of the figure for massive stars, Fig. 1c. As shown in Fig. 1c, we divide the curve for the maximum mass star in npK^- $\overline{K}^{~0}$ matter into four parts. Part I corresponds to the dURCA process with electrons (dURCAe). The curves of $1.2~M_{\odot}{-}1.4~M_{\odot}$ in Fig. 1b reflect this case. When the mass of a neutron star becomes higher, the dURCA process with muons (dURCA $\mu$ ) occurs, which together with the dURCAe increases its emissivity, as shown in part II. The combination of part I and II corresponds to the curves with masses $1.5~M_{\odot}{-}1.9~M_{\odot}$ shown in Fig. 1b. From parts I and II in Fig. 1, one can notice that the neutrino emissivity increases with radius, which means $I_{\rm URCA}$ decreases with density. In the framework of the RMFT, the $\sigma$ field always increases with density, so the effective masses of nucleons ${m_{\rm p}}^*$ and ${m_{\rm n}}^*$ decrease. Though the chemical potential of electrons $\mu_{\rm e}$ increases with density in the region, the neutrino emissivity is still lower (see Eq. (2)). When the mass of a neutron star reaches $1.95~M_{\odot}$ , the kURCA process occurs, which corresponds to part III. It is interesting that the neutrino emissivity in part III is less than that indicated in parts I and II, even though part III includes the results of the dURCA and kURCA processes.

Table 2: The effective masses of nucleons and the chemical potential of electrons at the density u = 3.028 and u = 4.869.

This result is counterintuitive yet possible for three reasons. First, of the three URCA processes, the dURCA process in $np K^-\overline{K}^{~0}$ matter plays the most important role in emitting neutrinos. When K^- condensation occurs, |M_np|² of the dURCA process is reduced to the form $\vert M_{np}\vert^2=2{G_F}^2[1+3(D+F)^2]\cos^2 \frac{\theta}{2}\cos^2\theta_C$ , which means the quantity of $I_{\rm URCA}$ will reduce more than $0.2\times 10^{27}$ erg s^-1 cm^-3 in the case of $\theta = 1$ . However, the emissivity $I_{\rm URCA}$ due to the kURCA process only has the magnitude of 10²⁵ erg s^-1 cm^-3 and the total neutrino emissivity decreases. From Fig. 1a one can see that the curves of the neutrino emissivity for the dURCA process and the total neutrino emissivity almost overlap. Second, the chemical potential of electrons decreases violently after the onset of K^-condensation as K^- mesons replace the leptons in maintaining charge neutrality. Third, once K^- condensation sets in, the $\sigma$ field grows more quickly, and the effective masses of nucleons further decrease. The values of the effective masses of nucleons and the chemical potential of electrons at the beginning ( u=3.028,u=n_b/n₀, i.e. the threshold density for K^-condensation) and at the end (u=4.869, the threshold density for $\overline{K}^{~0}$ condensation) of part III are shown in Table 2. The ratio of |M_np|² at the density u=3.028 and |M_t|²( |M_t|² = |M_np|² + |M_nn|²+ |M_pp|²) at the density u = 4.869 is equal to 1.2898. From these data one can find that the total neutrino emissivity at the beginning of part III is 6.27 times larger than that at the end of part III. The end result is that the total neutrino emissivity decreases, even though we have added the contribution of the kURCA process. The curves in part IV drop further, because the k0URCA channel is opened. When the mass of a neutron star is higher than $2.0625~M_{\odot}$ , the k0URCA process occurs. Part IV in Fig. 1c includes the dURCA, kURCA and k0URCA processes with both electrons and muons. Once the k0URCA process occurs, the chemical potential of electrons and the effective masses of nucleons show a further decrease (Pal et al. 2000). At the threshold density for $\overline{K}^{~0}$ condensation, the matrix elements $\mid M_{np}\mid^2$ for the dURCA process undergoes a 0.21 decrease. Therefore, $I_{\rm URCA}$ in part IV becomes lower.

$\begin{figure} \par\includegraphics[width=6.7cm,height=7cm,clip]{10814fg2} \end{figure}$	Figure 2: Same as Fig. 1b, but for neutron stars with masses $2.0~M_{\odot}$ and $2.0625~M_{\odot}$ in both np (solid lines) and $np K^-\overline{K}^{~0}$ (dotted lines) matter, respectively.
Open with DEXTER

Figure 2 shows the neutrino emissivity of neutron stars in both np and npK^- $\overline{K}^{~0}$ matter with the same neutron star mass. It is seen that with the same mass, a neutron star in npK^- $\overline{K}^{~0}$ matter has lower neutrino emissivity and the disparity becomes larger with increasing mass. The reason is that with antikaon condensations, the neutrino emissivity becomes lower in npK^- $\overline{K}^{~0}$ matter.

Solving the cooling equation Eq. (4), one can obtain cooling curves of neutron stars. Figure 3 shows the cooling curves for neutron stars with the masses of $M=1.95~M_{\odot}$ , $2.04~M_{\odot}$ and $2.06~M_{\odot}$ in np and npK^- $\overline{K}^{~0}$ matter, respectively. From Fig. 3, one can find that the cooling curves with the masses of $M=1.95~M_{\odot}$ , $2.04~M_{\odot}$ and $2.06~M_{\odot}$ in np matter as well as the cooling curve with the mass of $M=1.95~M_{\odot}$ in npK^- $\overline{K}^{~0}$ matter almost overlap. The cooling curves of the stars in np K^- $\overline{K}^{~0}$ matter lie above the cooling curves of the stars in np matter. With the increase of the star masses in npK^- $\overline{K}^{~0}$ matter, the corresponding cooling curves become higher, meaning that the cooling of neutron stars in npK^- $\overline{K}^{~0}$ matter is slower than the cooling of neutron stars in np matter. Therefore, in the case we studied here, antikaon condensations cannot favor fast cooling, but produce a slower cooling history of neutron stars. The cooling curves presented here are estimates, in particular, effects of neutron star crusts are not considered (e.g. Shapiro & Teukolsky 1983; Lattimer et al. 1994; Gnedin et al. 2001).

$\begin{figure} \par\includegraphics[width=7.5cm,height=7cm]{10814fg3} \vspace*{14mm} \end{figure}$	Figure 3: Cooling curves of interior temperature versus time for stars with masses 1.95 $M_{\odot }$ , 2.04 $M_{\odot }$ and 2.06 $M_{\odot }$ within the first thousand years in np (dashed lines) and npK^- $\overline{K}^{~0}$ (solid lines) matter,respectively. The initial interior temperature $T_{\rm i} = 10^9$ K and the initial time $t_{\rm i} = 0.1$ yr.
Open with DEXTER

The typical value of $\theta$ and $\phi$ of between 1 and somewhat bigger than $\pi/2$ is generally accepted (Kubis 2006). In this work, our main purpose is to discuss the effects of K^- and $\overline{K}^0$ condensations on neutron star cooling. With different values of the condensation amplitudes $\theta$ and $\phi$ , the calculation results are similar. From Kubis (Kubis (2006)), we choose $\theta = \phi = 1$ .

In this paper, $U_{\overline{K}}(n_0)=-120$ MeV is chosen, and we also study the cases for other values of the optical potential of antikaons. The calculation results are similar to that of $U_{\overline{K}}(n_0)=-120$ MeV. With the increase of the $\vert U_{\overline{K}}(n_0)\vert$ , the threshold densities of antikaon condensations decrease and the total neutrino emissivity $I_{\rm URCA}$ is reduced.

4 Conclusions

We have studied the dURCA, kURCA and k0URCA processes of both electrons and muons in neutron stars with various masses in np and np $K^- \overline{K}^{~0}$ matter. The effect of antikaon condensations on the neutrino emission and cooling of neutron stars has been discussed. The neutrino emissivity due to the dURCA process plays a dominant role; however, antikaon condensations change the chemical potential of electrons, the effective masses of nucleons and the matrix elements of the reaction for the dURCA process. As a consequence, the magnitude of neutrino emissivity for dURCA process decreases noticeably. In this case, even if the contribution of both the kURCA and k0URCA processes to the total neutrino emissivity are considered, the total neutrino emissivity is reduced. From the cooling curves of neutron stars, it is also found that compared with np matter, antikaon condensations do not result in any significant increase in the cooling rate. From the discussion above, we believe that antikaon condensations are unfavorable for fast cooling of neutron stars.

Acknowledgements

This work was supported in part by National Natural Science Foundation of China Grant Nos. 10275029 and 10675054, and National Fundamental Fund Project Subsidy Funds of Personnel Training under Grant No. J0730311.

References

Banik, S., & Bandyopadhyay, D. 2002, Phys. Rev. C, 66, 065801 [NASA ADS] [CrossRef]
Ding, W. B., Liu, G. Z., Zhu, M., Yu, Z., & Zhao, E. 2008, Chin. Phys. Lett., 25, 458 [NASA ADS] [CrossRef]
Glendenning, N. K., & Moszkowski, S. A. 1991, Phys. Rev. Lett., 67, 2414 [NASA ADS] [CrossRef]
Glendenning, N. K., & Schaffner-Bielich, J. 1999, Phys. Rev. C, 60, 025803 [NASA ADS] [CrossRef]
Gnedin, O. Y., Yakovlev, D. G., & Potokhin, A. Y. 2001, MNRAS, 324, 725 [NASA ADS] [CrossRef]
Gu, J., Guo, H., Zhou, R., et al. 2005, ApJ, 622, 549 [NASA ADS] [CrossRef]
Gusakov, M. E., Kaminker, A. D., Yakovlev, D. G., et al. 2005, MNRAS, 363, 555 [NASA ADS] [CrossRef]
Heinke, C. O., Jonker, P. G., Wijnands, R., & Taam, R. E. 2007, ApJ, 660, 1424 [NASA ADS] [CrossRef]
Kaplan, D. B., & Nelson, A. E. 1986, Phys. Lett. B, 175, 57 [NASA ADS] [CrossRef]
Kolomeistev, E. E., & Voskresensky, D. N. 2003, Phys. Rev. C, 68, 015803 [NASA ADS] [CrossRef]
Kubis, S. 2006, Phys. Rev. C, 73, 015805 [NASA ADS] [CrossRef]
Kubis, S., & Kutschera, M. 2003, Nucl. Phys. A, 720, 189 [NASA ADS] [CrossRef]
Lattimer, J. M., Pethick, C. J., Prakash, M., et al. 1991, Phys. Rev. Lett., 66, 2701 [NASA ADS] [CrossRef]
Lattimer, J. M., Van Riper, K. A., Prakash, M., et al. 1994, ApJ, 425, 802 [NASA ADS] [CrossRef]
Lee, C. H., Brown, G. E., Min, D. P., et al. 1995, Nucl. Phys. A, 585, 401 [NASA ADS] [CrossRef]
Leinson, L. B. 2002, Nucl. Phys. A, 707, 543 [NASA ADS] [CrossRef]
Nelson, A. E., & Kaplan, D. B. 1987, Phys. Lett. B, 192, 193 [NASA ADS] [CrossRef]
Page, D., & Applegate, J. H. 1992, ApJ, 394, L17 [NASA ADS] [CrossRef]
Page, D., Lattimer, J. M., Prakash, M., et al. 2004, ApJS, 155, 623 [NASA ADS] [CrossRef]
Pal, S., Bandyopadhyay, D., & Greiner, W. 2000, Nucl. Phys. A, 674, 553 [NASA ADS] [CrossRef]
Prakash, M., Prakash, M., Lattimer, J. M., et al. 1992, ApJ, 390, L77 [NASA ADS] [CrossRef]
Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs, and Neutron Stars (Wiley-Interscience)
Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef]
Yakovlev, D. G., Kaminker, A. D., Gnedin, O. Y., et al. 2001, Phys. Rep., 354, 1 [NASA ADS] [CrossRef]

All Tables

Table 1: The maximum mass $M_{\max}$ , radii R and central densities $u_{\rm cent}=n_{\rm cent}/n_0$ of neutron stars.

Table 2: The effective masses of nucleons and the chemical potential of electrons at the density u = 3.028 and u = 4.869.

All Figures

$\begin{figure} \par\includegraphics[width=15.5cm,height=8cm,clip]{10814fg1} \end{figure}$	Figure 1: a) The neutrino emissivity $I_{\rm URCA}$ as a function of density. The dashed line represents the dURCA for eand $\mu$ in np matter, whereas in $np K^-\overline{K}^{~0}$ matter the curve for dURCA process is dash-dot-dotted. For $np K^-\overline{K}^{~0}$ matter, the line for the total neutrino emissivity (URCAt including the dURCA, kURCA and k0URCA processes for e and $\mu$ ) is solid, the lines for the kURCA is dash-dotted, and the line for the k0URCA is dotted. The interior temperature T is fixed at T = 10⁹ K. b) $I_{\rm URCA}$ versus the radial distance of neutron stars with different masses (in units of $M_{\odot }$ ) in $np K^-\overline{K}^{~0}$ matter. c) Same as b), but for several massive stars.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.7cm,height=7cm,clip]{10814fg2} \end{figure}$	Figure 2: Same as Fig. 1b, but for neutron stars with masses $2.0~M_{\odot}$ and $2.0625~M_{\odot}$ in both np (solid lines) and $np K^-\overline{K}^{~0}$ (dotted lines) matter, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,height=7cm]{10814fg3} \vspace*{14mm} \end{figure}$	Figure 3: Cooling curves of interior temperature versus time for stars with masses 1.95 $M_{\odot }$ , 2.04 $M_{\odot }$ and 2.06 $M_{\odot }$ within the first thousand years in np (dashed lines) and npK^- $\overline{K}^{~0}$ (solid lines) matter,respectively. The initial interior temperature $T_{\rm i} = 10^9$ K and the initial time $t_{\rm i} = 0.1$ yr.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.