| Issue |
A&A
Volume 506, Number 1, October IV 2009
The CoRoT space mission: early results
|
|
|---|---|---|
| Page(s) | 51 - 56 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200911937 | |
| Published online | 24 July 2009 | |
The CoRoT space mission: early results
Solar-like oscillations in HD 181420: data analysis of 156 days of CoRoT data![[*]](/icons/foot_motif.png)
C. Barban1 - S. Deheuvels1 - F. Baudin2 - T. Appourchaux2 - M. Auvergne1 - J. Ballot3 - P. Boumier2 - W. J. Chaplin4 - R. A. García5 - P. Gaulme2 - E. Michel1 - B. Mosser1 - C. Régulo6,7 - I. W. Roxburgh8,1 - G. Verner8 - A. Baglin1 - C. Catala1 - R. Samadi1 - H. Bruntt1 - Y. Elsworth4 - S. Mathur9
1 - LESIA, UMR8109, Université Pierre et Marie Curie, Université Denis Diderot, Observatoire de Paris, 92195 Meudon Cedex, France
2 - Institut d'Astrophysique Spatiale, UMR8617, Université Paris XI, Bâtiment 121, 91405 Orsay Cedex, France
3 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse,
CNRS, 14 avenue Edouard Belin, 31400 Toulouse, France
4 - School of physics and Astronomy, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
5 - Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot; CEA, IRFU, SAp, centre de Saclay, 91191 Gif-sur-Yvette, France
6 - Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
7 - Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
8 - Astronomy Unit, Queen Mary, University of London Mile End Road, London E1 4NS, UK
9 - Indian Institute of Astrophysics, Bangalore, India
Received 24 February 2009 / Accepted 24 June 2009
Abstract
Context. The estimate of solar-like oscillation properties, such as their frequencies, amplitudes and lifetimes, is challenging because of their low amplitudes and will benefit from long and uninterrupted observing runs. The space telescope CoRoT allows us to obtain high-performance photometric data over a long and quasi continuous period. Among its main targets are stars for which we expect solar-like oscillations.
Aims. HD 181420, an F2 main sequence star, has been observed by CoRoT during its first long run covering about 156 days. With this unprecedently high-quality set of data, our aim is to derive the p-mode parameters that can be used to probe the stellar interior.
Methods. The CoRoT data obtained on HD 181420 is analysed using a classical Fourier approach for the search for the p mode signature. The p-mode parameters are then derived using global fitting of the power spectrum by a Lorentzian model, as used widely in the solar case.
Results. From the p-mode frequencies, the mean value of the large spacing is estimated to be 75
![]() .
The p-mode amplitudes are slightly less than 4 ppm with a line width of about 8
.
The p-mode amplitudes are slightly less than 4 ppm with a line width of about 8
![]() at the maximum of the p modes. The inclination angle is estimated to be around
at the maximum of the p modes. The inclination angle is estimated to be around
![]() .
The large mode line-width combined with the observed mode spacing make it difficult to identify the
.
The large mode line-width combined with the observed mode spacing make it difficult to identify the ![]() modes and to estimate the rotational splitting. We explore two scenarios for the identification of the modes.
modes and to estimate the rotational splitting. We explore two scenarios for the identification of the modes.
Key words: stars: oscillations - stars: individual: HD 181420
1 Introduction
Solar-like oscillations are p modes excited by turbulent motion in the convective outer layers of stars, with periods ranging from a few min for main sequence stars to a few hours for red giants. The detection of such oscillations in distant stars is challenging because of their very low amplitude: the intensity variations range from a few ppm in the solar case up to a few tens of ppm for more evolved stars. However, the study of solar-like oscillations in other stars is a unique opportunity to directly probe the stellar interiors and to bring new constraints on stellar evolutionary models and to gain a better our understanding of stellar dynamics. Following on from the great advances in instrumentation during the last decades, these kinds of oscillations have been reported in some distant stars (e.g. Bedding & Kjeldsen 2007). In almost all the cases, a short duration of the run combined with interrupted observations due to limitations of the day-night cycle of ground-based facilities does not allow one to obtain precise estimates of the p-mode parameters (frequency, amplitude and life-time). Uninterrupted observations spanning a long period are useful for a detailed seismological study of stars on the main sequence or close to it.
This paper presents the data analyis of HD 181420 performed within the CoRoT Data Analysis Team (DAT) of the Seismology Working Group. This star is known to be an F2 star (mv = 6.57,
![]() = 4.28
= 4.28 ![]() 0.28,
0.28,
![]() = (6580
= (6580 ![]() 105) K, [Fe/H] = +0.00
105) K, [Fe/H] = +0.00 ![]() 0.06,
0.06,
![]() = 1.311
= 1.311 ![]() 0.063,
0.063, ![]() = (18
= (18 ![]() 1)
1)
![]() ,
see Bruntt 2009). Preliminary data analysis of the CoRoT target HD 181420 has been presented in Michel et al. (2008): a more detailed data analysis is performed in this paper, leading to an estimate of the p-mode parameters. Our methods and results are presented in Sect. 3; and our conclusions are given in Sect. 4.
,
see Bruntt 2009). Preliminary data analysis of the CoRoT target HD 181420 has been presented in Michel et al. (2008): a more detailed data analysis is performed in this paper, leading to an estimate of the p-mode parameters. Our methods and results are presented in Sect. 3; and our conclusions are given in Sect. 4.
2 CoRoT photometric data
HD 181420 was observed during the first long observing run from May to October 2007. The photometry was obtained in the seismology field totaling 156.6 days of photometric data. We use in this paper the so-called ``HELREG level 2'' data corresponding to light curves that have been corrected for known instrumental effects and sampled with a regular cadence in the heliocentric frame with one measurement every 32 s (Samadi et al. 2006). An additional long-term trend due to instrumental effects linked to the aging of the detectors has also been corrected. Indeed, Auvergne et al. (2009) pointed out that CoRoT light curves show a long-term decrease of the flux roughly linear in time with a slope that varies linearly with the absolute flux value. They attributed the flux decrease to a gain decrease, the relative flux variation being estimated to be about -5.32 ![]() 10-5 day-1. The duty cycle before interpolation for HD 181420 was 89.5%. The light curve is shown in Fig. 1. The ``V'' shape seen in the light curve does not correspond to any known instrumental effect and is most likely due to stellar activity corresponding to periods much longer than those of interest in the search for solar-like p mode oscillations.
10-5 day-1. The duty cycle before interpolation for HD 181420 was 89.5%. The light curve is shown in Fig. 1. The ``V'' shape seen in the light curve does not correspond to any known instrumental effect and is most likely due to stellar activity corresponding to periods much longer than those of interest in the search for solar-like p mode oscillations.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg1.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg16.png) |
Figure 1: Time series of the relative intensity variations of HD 181420 obtained by CoRoT corrected for known instrumental effects. |
| Open with DEXTER | |
3 Data analysis
3.1 Search for p mode signatures
The Fourier analysis of the CoRoT data is performed by computing the power density spectrum using a Fast Fourier Transform (FFT) algorithm. The Fourier transform is normalised so that the total power integrated from zero to twice the Nyquist frequency is equal to the variance of the residual light curve; in other words, the Fourier transform is normalised by
![]() where T is the total length of the observations.
where T is the total length of the observations.
Excess power is clearly seen around 1.5 mHz (see Fig. 2), with a so-called bell-shape and a comb-like structure, which are well-known properties of a solar-like oscillation spectrum. The frequency of maximum amplitude is known to scale with the frequency cut-off; by applying the scaling law given in Kjeldsen & Bedding (1995) with the stellar parameters given in the introduction,
we find a value of (1.5 ![]() 0.3) mHz which matches the peak of the oscillation spectrum seen in Fig. 2. Excess power has also been detected at very low frequencies, around 4.5
0.3) mHz which matches the peak of the oscillation spectrum seen in Fig. 2. Excess power has also been detected at very low frequencies, around 4.5
![]() ,
and can be attributed to the rotation period of the star through the variable distribution of stellar spots on its surface (see Fig. 3).
,
and can be attributed to the rotation period of the star through the variable distribution of stellar spots on its surface (see Fig. 3).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg2.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg18.png) |
Figure 2:
Power density spectrum of the light curve shown in Fig. 1. The spectrum has been smoothed using a 4.5-
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg3.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg19.png) |
Figure 3:
The power density spectrum of the light curve shown in Fig. 1 showing the signature of surface rotation around 4.5
|
| Open with DEXTER | |
To estimate the value for the frequency separations responsible for the comb-like pattern seen in the power spectrum, we have computed the autocorrelation of the power density spectrum between 1 and 2.4 mHz (Fig. 4). A clear signature of regularly spaced peaks with a mean spacing value of 75
![]() is seen in this autocorrelation. The spacing can be associated with a mean value,
is seen in this autocorrelation. The spacing can be associated with a mean value,
![]() ,
of the so-called large separation, i.e. the frequency spacing between adjacent modes with the same
,
of the so-called large separation, i.e. the frequency spacing between adjacent modes with the same ![]() value (
value (
![]() ). The other peak in the autocorrelation corresponds to half the value of large spacing, around 37.5
). The other peak in the autocorrelation corresponds to half the value of large spacing, around 37.5
![]() ,
as expected for a solar-like oscillation spectrum. It corresponds to the mean value of the spacing between
,
as expected for a solar-like oscillation spectrum. It corresponds to the mean value of the spacing between ![]() and
and ![]() modes. By applying the scaling law given in Kjeldsen & Bedding (1995) with the stellar parameters of Bruntt (2009), we found a value of (77
modes. By applying the scaling law given in Kjeldsen & Bedding (1995) with the stellar parameters of Bruntt (2009), we found a value of (77 ![]() 9)
9)
![]() ,
in agreement with the observed value of approximately 75
,
in agreement with the observed value of approximately 75
![]() .
.
We then used this value to build an echelle diagram to help identify the degrees of the modes. This is done by dividing the spectrum into regions of 75
![]() ;
these regions are then stacked on top of each other to build the echelle diagram seen in Fig. 5. In such a diagram, modes with same degree
;
these regions are then stacked on top of each other to build the echelle diagram seen in Fig. 5. In such a diagram, modes with same degree ![]() will be more or less in the same region. In Fig. 5 we can see two different ridges, either of which could be attributed to radial modes. It is not possible to say from this echelle diagram which ridge corresponds to the close-pair
will be more or less in the same region. In Fig. 5 we can see two different ridges, either of which could be attributed to radial modes. It is not possible to say from this echelle diagram which ridge corresponds to the close-pair ![]() -
-![]() and which to
and which to ![]() modes. This is due to a combination of low mode amplitude, large line-width and rotational splitting that make all the multiplet components overlap. In the following, we will therefore consider two possible mode identification scenarios: ``Scenario 1'' for
modes. This is due to a combination of low mode amplitude, large line-width and rotational splitting that make all the multiplet components overlap. In the following, we will therefore consider two possible mode identification scenarios: ``Scenario 1'' for ![]() modes corresponding to the ridge on the left and
modes corresponding to the ridge on the left and
![]() on the right in the echelle diagram shown in Fig. 5 and ``Scenario 2'' for the inverse.
on the right in the echelle diagram shown in Fig. 5 and ``Scenario 2'' for the inverse.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg4.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg26.png) |
Figure 4: Autocorrelation of the power density spectrum betwen 1 and 2.4 mHz (the power spectrum has not been smoothed). |
| Open with DEXTER | |
3.2 Determining the P-mode parameters
3.2.1 Method
To estimate the p-mode parameters, we have used a power spectrum fitting technique that has been successfully used in the solar case (Appourchaux et al. 1998; Toutain & Froehlich 1992). Since solar-like oscillations are stochastically excited by convection, they can be modelled as randomly forced, damped, simple-harmonic oscillators. The power spectrum of such oscillations is distributed around mean Lorentzian profiles with a ![]() probability distribution with two degrees of freedom. Following Toutain & Appourchaux (1994), we have used a maximum-likelihood technique to find the best fit between the model (Lorentzian) profiles and the observed power spectrum.
probability distribution with two degrees of freedom. Following Toutain & Appourchaux (1994), we have used a maximum-likelihood technique to find the best fit between the model (Lorentzian) profiles and the observed power spectrum.
To apply this method to HD 181420, we follow the same kind of approach that has been described in Appourchaux et al. (2008) for the data analysis of the CoRoT target HD 49933. We recall here the main steps.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg5.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg28.png) |
Figure 5:
Echelle diagram computed using a value for the large separation of 75
|
| Open with DEXTER | |
Table 1:
Mode parameters of radial modes for Scenario 1 as obtained from the reference fit. The error bars correspond to 1![]() .
.
Table 2:
Mode parameters of radial modes for Scenario 2 as obtained from the reference fit. The error bars correspond to 1![]() .
.
The power spectrum is fitted ``globally'' over a frequency range corresponding to the detected excess power, chosen to be a multiple of the large spacing
![]() ;
one large spacing frequency range defines an order (n).
;
one large spacing frequency range defines an order (n).
The modelled power spectrum, ![]() ,
is:
,
is:
![\begin{displaymath}%
P(\nu_k) = \sum_{n,\ell,m} \frac{H_{n,\ell}.r_{\ell,m}(i)}{...
...nu_k-(\nu_{n,\ell}+m.s)]\frac{2}{\Gamma_n}\right)^2} +B(\nu_k)
\end{displaymath}](/articles/aa/full_html/2009/40/aa11937-09/img39.png) |
(1) |
n varies from 1 to M, with M being the number of orders fitted; ![]() from 0 to 2; and m from
from 0 to 2; and m from ![]() to
to ![]() .
.
![]() are the Fourier frequencies and
are the Fourier frequencies and ![]() is the background model following Harvey (1985) with:
is the background model following Harvey (1985) with:
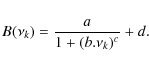 |
(2) |
The free parameters of the fitting process are:
-
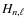 :
the height of the Lorentzian profile. A single height parameter is fitted per order. The ratio between the height of radial and non-radial modes is fixed:
:
the height of the Lorentzian profile. A single height parameter is fitted per order. The ratio between the height of radial and non-radial modes is fixed:
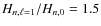 and
and
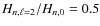 .
Relative heights inside a given multiplet,
.
Relative heights inside a given multiplet,
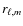 ,
are computed following Gizon & Solanki (2003) and depend on the inclination only.
,
are computed following Gizon & Solanki (2003) and depend on the inclination only.
We recall here that the relation between the height of the Lorentzian profile, Hn,0, in the power density spectrum and the mode amplitude in ppm, an, is given by:
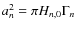 (see for example Baudin et al. 2005, for more details).
(see for example Baudin et al. 2005, for more details).
-
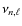 :
the mode frequency for each degree
:
the mode frequency for each degree 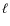 and for m=0.
and for m=0.
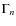 :
the mode line width (FWHM) with
:
the mode line width (FWHM) with
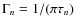 ,
,
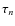 being the mode lifetime. A single line width parameter is fitted per order.
being the mode lifetime. A single line width parameter is fitted per order.
- s: the rotational splitting. A single value is fitted for all modes in the considered frequency range. Non-radial modes are assumed to show symmetric splitting in frequency.
- i: the inclination angle between the stellar axis of rotation and the line of sight.
- a,b,c,d: parameters describing the background model as mentioned above.
No oversampling has been used in the computation of the power spectrum for the fitting procedure in order to minimize the correlation of the points. The initial guess parameters were derived from a ``local'' fitting, i.e. the model is fitted to the observations over one order. The model was independently fit to the data by five authors (SD, PB, WJC, PG, GV). Since these 5 teams obtained results that agreed well with each other (for most cases within 1 sigma as noted in Tables 1-4) as presented in the next section, we picked one set of results, called the ``reference'' fit, to present in this paper.
3.2.2 Results
Table 3:
Mode parameters of non-radial modes for Scenario 1 as obtained from the reference fit. The error bars correspond to 1![]() .
.
Table 4:
Mode parameters of non-radial modes for Scenario 2 as obtained from the reference fit. The error bars correspond to 1![]() .
.
The best-fitting mode parameters of the reference fit are given in Tables 1 and 3 for mode identification Scenario 1 and in Tables 2 and 4 for mode identification Scenario 2. An estimate of the signal-to-noise ratio is given by
![]() in these tables. The most prominent modes have signal-to-noise values of about 5. The higher values of the signal to noise for the first three modes are due to an overestimate of the mode heights in this part of the spectrum. A combination of low S/N and a correlation between the fitted height and width make these modes difficult to fit. We noticed that the highest relative error bars for the height and the width are for these first three modes.
in these tables. The most prominent modes have signal-to-noise values of about 5. The higher values of the signal to noise for the first three modes are due to an overestimate of the mode heights in this part of the spectrum. A combination of low S/N and a correlation between the fitted height and width make these modes difficult to fit. We noticed that the highest relative error bars for the height and the width are for these first three modes.
We also provide in the tables an indication of the level of agreement between the results obtained by different teams (see table captions). For the ![]() and
and ![]() mode frequencies we found very good agreement, typically to better than
mode frequencies we found very good agreement, typically to better than ![]() ;
only in a few cases we do find worse agreement, and this was at the low- and high-frequency ends of the mode-fitting range where the modes are less prominent. The level of agreement between the different fitted solutions was not as good for the
;
only in a few cases we do find worse agreement, and this was at the low- and high-frequency ends of the mode-fitting range where the modes are less prominent. The level of agreement between the different fitted solutions was not as good for the ![]() modes. This was due to the lower amplitudes of these modes and significant mode blending problems in the power density spectrum, which made the
modes. This was due to the lower amplitudes of these modes and significant mode blending problems in the power density spectrum, which made the ![]() hard to distinguish from the
hard to distinguish from the ![]() modes. The blending resulted from the large rotational splitting and large mode linewidths compared to the spacing between
modes. The blending resulted from the large rotational splitting and large mode linewidths compared to the spacing between ![]() and
and ![]() modes.
modes.
For the Lorentzian heights, Hn, and mode line widths, ![]() ,
we found good overall agreement, with some increased scatter again seen at the low- and high-frequency ends of the fitting range.
,
we found good overall agreement, with some increased scatter again seen at the low- and high-frequency ends of the fitting range.
The frequencies derived from the global fits were used to build echelle diagrams for the two mode identification scenarios, which are shown in Figs. 6 and 7. These plots illustrate the difficulty in distinguishing ![]() modes from the
modes from the ![]() modes: sometimes the fitting returns frequencies that almost lie on top of one another.
modes: sometimes the fitting returns frequencies that almost lie on top of one another.
From the frequencies listed in Tables 1-4, we derived a mean value for the large frequency spacing,
![]() ,
of 75.3
,
of 75.3 ![]() 0.1
0.1
![]() for
for ![]() and
and ![]() modes for Scenario 1 and for Scenario 2: 75.4
modes for Scenario 1 and for Scenario 2: 75.4 ![]() 0.2
0.2
![]() for
for ![]() and 74.8
and 74.8 ![]() 0.2
0.2
![]() for
for ![]() (the error bar corresponds to
(the error bar corresponds to ![]() ). These mean values of spacings are derived by fitting a linear function to the measured frequencies assuming equidistant separation. These values are in agreement with the value derived from the autocorrelation of the power density spectrum (see Sect. 3.1).
). These mean values of spacings are derived by fitting a linear function to the measured frequencies assuming equidistant separation. These values are in agreement with the value derived from the autocorrelation of the power density spectrum (see Sect. 3.1).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg6.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg55.png) |
Figure 6:
Echelle diagram computed using a value for the large separation of 75
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg7.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg56.png) |
Figure 7:
Echelle diagram computed using a value for the large separation of 75
|
| Open with DEXTER | |
The mode amplitudes, an, computed from the heights and line widths (see Sect. 3.2.1), are plotted as a function of frequency in Fig. 8. Estimates are shown for both mode identification scenarios. As seen in the solar case, the mode amplitudes follow more or less a bell-shaped frequency distribution, though here with a shallower fall-off at high frequencies.
The maximum mode amplitude is (
![]() ) ppm at 1573
) ppm at 1573
![]() for Scenario 1; and (
for Scenario 1; and (
![]() ) ppm at 1535
) ppm at 1535
![]() for Scenario 2. These values - which are slightly higher than solar - are consistent with the value given in Michel et al. (2008), which was derived from a different method of analysis. It is important to recognise that, even when heights and widths have large errors or are biased, the power of modes - and hence their amplitudes - are generally correctly estimated and with a smaller fractional error than the two parameters separately; it has been shown, for instance, that poor estimation of the inclination could simultaneously bias the fitted heights and widths, but not the power (Ballot et al. 2008). In this sense, the derived values of the amplitudes are robust.
for Scenario 2. These values - which are slightly higher than solar - are consistent with the value given in Michel et al. (2008), which was derived from a different method of analysis. It is important to recognise that, even when heights and widths have large errors or are biased, the power of modes - and hence their amplitudes - are generally correctly estimated and with a smaller fractional error than the two parameters separately; it has been shown, for instance, that poor estimation of the inclination could simultaneously bias the fitted heights and widths, but not the power (Ballot et al. 2008). In this sense, the derived values of the amplitudes are robust.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg8.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg59.png) |
Figure 8:
Radial-mode amplitudes, (an), as a function of frequency for Scenario 1 (solid line; data from Table 1) and Scenario 2 (dashed line; data from Table 2). The error bars are |
| Open with DEXTER | |
The mode line widths, ![]() ,
are plotted as a function of frequency for both scenarios in Fig. 9. As in the solar case, this parameter increases with frequency and a ``plateau'' is seen where the modes are most prominent. Again, the error bars are largest at high frequencies because of the difficulty in fitting the Lorentzian model over wide, low amplitude profiles. The mode line widths estimated for HD 181420 are significantly wider than the solar linewidths: for the Sun, the line widths of low-degree modes in the ``plateau'' region are around 1
,
are plotted as a function of frequency for both scenarios in Fig. 9. As in the solar case, this parameter increases with frequency and a ``plateau'' is seen where the modes are most prominent. Again, the error bars are largest at high frequencies because of the difficulty in fitting the Lorentzian model over wide, low amplitude profiles. The mode line widths estimated for HD 181420 are significantly wider than the solar linewidths: for the Sun, the line widths of low-degree modes in the ``plateau'' region are around 1
![]() ;
for HD 181420, the line widths in this region are around 8
;
for HD 181420, the line widths in this region are around 8
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11937fg9.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg60.png) |
Figure 9:
Radial-mode line width ( FWHM), ( |
| Open with DEXTER | |
An estimate of the rotational splitting value was extracted by the global fitting procedure as explained in Sect. 3.2.1. The ``reference'' fit for Scenario 1 has a value of:

and for Scenario 2:

The error bar corresponds to
It was also possible to derive an estimate of the value of the inclination angle from the global fitting procedure. The ``reference'' fit for Scenario 1 has a value of:

and for Scenario 2:

The error bar corresponds to
The inclination angle can also be derived using the surface rotation frequency of (4.5 ![]() 1.5)
1.5)
![]() ,
directly deduced from the power spectrum (see Fig. 3), and the stellar radius and
,
directly deduced from the power spectrum (see Fig. 3), and the stellar radius and ![]() values in Sect. 1. A value of (35
values in Sect. 1. A value of (35 ![]() 21)
21)
![]() is then found, in agreement with the inclination derived from the global fitting of the p modes.
is then found, in agreement with the inclination derived from the global fitting of the p modes.
4 Conclusions
Using photometric observations from the CoRoT space telescope spanning 156 days and a duty-cycle of 90%, we havebeen able to detect and characterize solar-like oscillations in the F2 main sequence star HD 181420.
An excess of power due to the p modes is seen clearly in the power density spectrum. This bell-shaped power excess is centered at a frequency of
![]() ,
and carries the signature of nearly equidistant peaks, a characteristic of oscillation spectra of solar-like stars.
,
and carries the signature of nearly equidistant peaks, a characteristic of oscillation spectra of solar-like stars.
The p-mode parameters were estimated by fitting Lorentzians to the observed power density spectrum. Several groups used their fitting codes, and we found a good level of agreement, within 3![]() except for 4 of the 30 detected modes between the different sets of results. We did, however, find that it was difficult to identify the angular degrees of the mode peaks. This was because the large line widths of the modes, when combined with the values of the mode splittings and mode spacings, gave rise to significant peak-blending problems in the power density spectrum. We therefore presented results for both of the possible mode identification scenarios.
except for 4 of the 30 detected modes between the different sets of results. We did, however, find that it was difficult to identify the angular degrees of the mode peaks. This was because the large line widths of the modes, when combined with the values of the mode splittings and mode spacings, gave rise to significant peak-blending problems in the power density spectrum. We therefore presented results for both of the possible mode identification scenarios.
From the best-fitting p-mode frequencies given by both scenarios, we estimated the mean value of the large frequency spacing to be about 75
![]() .
We found that the p-mode amplitudes of the most prominent modes were slightly smaller than 4 ppm, while the line width of these modes was about 8
.
We found that the p-mode amplitudes of the most prominent modes were slightly smaller than 4 ppm, while the line width of these modes was about 8
![]() .
Both scenarios gave an estimated inclination angle of around 45
.
Both scenarios gave an estimated inclination angle of around 45
![]() .
The
.
The ![]() frequencies and the rotational splitting parameter were more difficult to estimate because of the blending problems.
frequencies and the rotational splitting parameter were more difficult to estimate because of the blending problems.
The next step is to use these p-mode parameters to improve our undestanding of the global parameters of this star and to test the physics used in the stellar codes. This is out of the scope of this paper and will be presented in forthcoming papers.
Other stars with solar-like oscillations are among the CoRoT targets. These very high-quality photometric data, which have high duty cycles, are opening a new era for the use of seismology as a tool to probe the interiors of stars in the same evolutionary stage as (or slightly more evolved than) the Sun.
Acknowledgements
I.W.R. and G.A.V. wish to thank the UK Science and Technology Facilities Council for support under grant PP/E001793/1. W.J.C. and Y.E. also wish to thank the UK Science and Technology Facilities Council for support under grant ST/F00204/1. J.B. acknowledges support through the ANR project Siroco.
References
- Appourchaux, T., Gizon, L., & Rabello-Soares, M.-C. 1998, A&AS, 132, 107 [NASA ADS] [CrossRef] [EDP Sciences]
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [CrossRef] [EDP Sciences] (In the text)
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [CrossRef] [EDP Sciences]
- Ballot, J., García, R. A., & Lambert, P. 2006, MNRAS, 369, 1281 [NASA ADS] [CrossRef]
- Ballot, J., Appourchaux, T., Toutain, T., & Guittet, M. 2008, A&A, 486, 867 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Baudin, F., Samadi, R., Goupil, M.-J., et al. 2005, A&A, 433, 349 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bedding, T. R., & Kjeldsen, H. 2007, in Unsolved Problems in Stellar Physics: A Conference in Honor of Douglas Gough, ed. R. J. Stancliffe, J. Dewi, R. G. Houdek, G. Martin, & C. Tout, AIP Conf. Ser., 948, 117 (In the text)
- Bruntt, H. 2009, A&A, 506, 235 [CrossRef] [EDP Sciences] (In the text)
- Gizon, L., & Solanki, S. K. 2003, ApJ, 589, 1009 [NASA ADS] [CrossRef] (In the text)
- Harvey, J. 1985, in Future Missions in Solar, Heliospheric & Space Plasma Physics, ed. E. Rolfe, & B. Battrick, ESA SP, 235, 199 (In the text)
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] (In the text)
- Michel, E., Baglin, A., Auvergne, M., et al. 2008, Science, 322, 558 [NASA ADS] [CrossRef] (In the text)
- Samadi, R., Fialho, F., Costa, J. E. S., et al. 2006, ESA SP 1306, 317, corrected in [arXiv:astro-ph/0703354] (In the text)
- Toutain, T., & Appourchaux, T. 1994, A&A, 289, 649 (In the text)
- Toutain, T., & Froehlich, C. 1992, A&A, 257, 287 [NASA ADS]
Footnotes
- ... data
![[*]](/icons/foot_motif.png)
- The CoRoT space mission, launched on 2006 December 27, was delopped and is operated by the CNES with participation of the Science Programs of ESA; ESA's RSSD, Austria, Belgium, Brazil, Germany and Spain.
All Tables
Table 1:
Mode parameters of radial modes for Scenario 1 as obtained from the reference fit. The error bars correspond to 1![]() .
.
Table 2:
Mode parameters of radial modes for Scenario 2 as obtained from the reference fit. The error bars correspond to 1![]() .
.
Table 3:
Mode parameters of non-radial modes for Scenario 1 as obtained from the reference fit. The error bars correspond to 1![]() .
.
Table 4:
Mode parameters of non-radial modes for Scenario 2 as obtained from the reference fit. The error bars correspond to 1![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg1.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg16.png) |
Figure 1: Time series of the relative intensity variations of HD 181420 obtained by CoRoT corrected for known instrumental effects. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg2.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg18.png) |
Figure 2:
Power density spectrum of the light curve shown in Fig. 1. The spectrum has been smoothed using a 4.5-
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg3.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg19.png) |
Figure 3:
The power density spectrum of the light curve shown in Fig. 1 showing the signature of surface rotation around 4.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg4.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg26.png) |
Figure 4: Autocorrelation of the power density spectrum betwen 1 and 2.4 mHz (the power spectrum has not been smoothed). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg5.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg28.png) |
Figure 5:
Echelle diagram computed using a value for the large separation of 75
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg6.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg55.png) |
Figure 6:
Echelle diagram computed using a value for the large separation of 75
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg7.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg56.png) |
Figure 7:
Echelle diagram computed using a value for the large separation of 75
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{11937fg8.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg59.png) |
Figure 8:
Radial-mode amplitudes, (an), as a function of frequency for Scenario 1 (solid line; data from Table 1) and Scenario 2 (dashed line; data from Table 2). The error bars are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11937fg9.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11937-09/Timg60.png) |
Figure 9:
Radial-mode line width ( FWHM), ( |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


