| Issue |
A&A
Volume 506, Number 1, October IV 2009
The CoRoT space mission: early results
|
|
|---|---|---|
| Page(s) | 79 - 83 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200911932 | |
| Published online | 27 July 2009 | |
The CoRoT space mission: early results
Asteroseismic analysis of the CoRoT 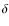 Scuti star HD 174936
Scuti star HD 174936![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
A. García Hernández1 - A. Moya1 - E. Michel2 - R. Garrido1 - J. C. Suárez1 - E. Rodríguez1 - P. J. Amado1 - S. Martín-Ruiz1 - A. Rolland1 - E. Poretti3 - R. Samadi2 - A. Baglin2 - M. Auvergne2 - C. Catala2 - L. Lefevre2 - F. Baudin4
1 - Instituto de Astrofísica de Andalucía (CSIC), CP3004, Granada, Spain
2 -
Observatoire de Paris, LESIA, CNRS, UMR 8109, 92195 Meudon, France
3 -
INAF - Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate (LC), Italy
4 -
Institut d'Astrophysique Spatiale, UMR8617, Université Paris XI, Bât. 121, 91405 Orsay, France
Received 23 February 2009 / Accepted 23 July 2009
Abstract
We present an analysis of the ![]() -Scuti star HD 174936 (ID 7613) observed by CoRoT during the first short run SRc01 (27 days). A total number of 422 frequencies were extracted from the light curve using standard prewhitening techniques. This number of frequencies was obtained by considering a spectral significance limit of sig = 10 using the software package SigSpec. Our analysis of the oscillation frequency spectrum reveals a spacing periodicity around 52
-Scuti star HD 174936 (ID 7613) observed by CoRoT during the first short run SRc01 (27 days). A total number of 422 frequencies were extracted from the light curve using standard prewhitening techniques. This number of frequencies was obtained by considering a spectral significance limit of sig = 10 using the software package SigSpec. Our analysis of the oscillation frequency spectrum reveals a spacing periodicity around 52 ![]() Hz. Although modes considered here are not in the asymptotic regime, a comparison with stellar models confirms that this signature may stem from a quasi-periodic pattern similar to the so-called large separation in solar-like stars.
Hz. Although modes considered here are not in the asymptotic regime, a comparison with stellar models confirms that this signature may stem from a quasi-periodic pattern similar to the so-called large separation in solar-like stars.
Key words: ![]() Sct - stars: rotation - stars: oscillations - stars: fundamental parameters - stars: interiors
Sct - stars: rotation - stars: oscillations - stars: fundamental parameters - stars: interiors
1 Introduction
The ![]() -Scuti stars are intermediate-mass pulsating variables with spectral types ranging from A2 to F0. They are located on and just off the main sequence in the lower part of the Cepheid instability strip (luminosity classes IV & V). The
-Scuti stars are intermediate-mass pulsating variables with spectral types ranging from A2 to F0. They are located on and just off the main sequence in the lower part of the Cepheid instability strip (luminosity classes IV & V). The ![]() -Scuti stars are considered as particularly suitable for asteroseismic studies of
poorly known hydrodynamical processes occurring in stellar interiors, such as convective overshoot, mixing of chemical elements, and redistribution of angular momentum (Zahn 1992), to mention only the most important ones. Because of the complexity of the oscillation spectra, their pulsating behaviour has not been understood very well. The reader is referred to the review by Cox (2002) for a more detailed description of unsolved problems in stellar pulsation physics.
-Scuti stars are considered as particularly suitable for asteroseismic studies of
poorly known hydrodynamical processes occurring in stellar interiors, such as convective overshoot, mixing of chemical elements, and redistribution of angular momentum (Zahn 1992), to mention only the most important ones. Because of the complexity of the oscillation spectra, their pulsating behaviour has not been understood very well. The reader is referred to the review by Cox (2002) for a more detailed description of unsolved problems in stellar pulsation physics.
The ![]() -Scuti star HD 174936 was uninterruptedly observed by CoRoT during 27 days of observation. The very precise space photometry supplied by the CoRoT mission gives us the possibility of working with a lower limit in amplitudes of
-Scuti star HD 174936 was uninterruptedly observed by CoRoT during 27 days of observation. The very precise space photometry supplied by the CoRoT mission gives us the possibility of working with a lower limit in amplitudes of ![]() 14
14 ![]() mag. As a consequence of such precision, never reached by any ground-based observation campaign, we obtained a wide range of oscillation frequencies ([0.05, 100] cd-1). This and the huge number of detected frequencies for such stars will help us in
understanding the internal structure of intermediate-mass,
main-sequence stars.
mag. As a consequence of such precision, never reached by any ground-based observation campaign, we obtained a wide range of oscillation frequencies ([0.05, 100] cd-1). This and the huge number of detected frequencies for such stars will help us in
understanding the internal structure of intermediate-mass,
main-sequence stars.
One of the aims of the mission is that such high resolution can enable us to detect some periodicities like rotational splitting (Baglin et al. 2006b). Using the CoRoT achievements, we can carry out statistical studies and look for other possible periodicities that could help us to better understand the oscillation spectra observed.
The paper is structured as follows: an explanation of the data analysis and the frequency content is described in Sect. 2; a description of the method used for identifying the periodic spacing distribution of the extracted frequencies is given in Sect. 3; equilibrium models and oscillation computations to check the origin of the signature noticed in the observations are described in Sect. 4; a brief discussion is carried out in Sect. 5; and some conclusions are reported in Sect. 6.
2 Data analysis
The fieldFirst, the data were detrended (Auvergne et al. 2009) performing a linear fit to the light curves. Second, Period04 was used for a preliminary inspection of the periodograms. Later, the timeseries was analysed using the computer program package SigSpec (Reegen 2007).
Nevertheless, the timeseries was previously investigated with Period04 for the first 20 peaks. They were identical to those achieved with SigSpec. This test has also been carried out successfully for the CoRoT target ID 123 (HD 50844, Poretti et al. 2009) with ![]() = 56.7 days and 140016 datapoints. In that case, Period04 was used to investigate the first 200 peaks, The agreement between the two methods was successful in 99% of the cases.
= 56.7 days and 140016 datapoints. In that case, Period04 was used to investigate the first 200 peaks, The agreement between the two methods was successful in 99% of the cases.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11932fig1.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg13.png) |
Figure 1: Spectral window of the short-run CoRoT dataset on HD 174936. |
| Open with DEXTER | |
Figure 1 shows the spectral window of HD 174936, which is typical of all the targets observed by the CoRoT satellite in the same run. As can be seen, the figure does not show the typical aliases at 1 cd-1 or the power levels that are common for ground-based data. On the contrary, all the aliases are related to effects produced by the satellite and its orbital frequency (
![]() cd-1), and their power levels are much lower than those usual for ground-based data. The alias peak at about 2 cd-1 comes from the South Atlantic Anomaly (SAA) crossing, which occurred twice each sidereal day. This means the alias peaks at 2.005 and 4.011 cd-1, respectively.
cd-1), and their power levels are much lower than those usual for ground-based data. The alias peak at about 2 cd-1 comes from the South Atlantic Anomaly (SAA) crossing, which occurred twice each sidereal day. This means the alias peaks at 2.005 and 4.011 cd-1, respectively.
To avoid problems with power close to zero frequency, the analysis with SigSpec was carried out in the range 0.05-100 cd-1. In the case of Period04, the limit commonly used to consider one datapoint as significant is the amplitude signal-to-noise ratio
![]() .
In the case of SigSpec, the parameter used for significance is ``sig'' (= spectral significance), and the limit used as default is sig = 5.0. This should be equivalent to about S/N = 3.8 (and sig = 5.46 should be approximately equivalent to S/N = 4.0) (Reegen 2007; Kallinger et al. 2008). However, we used a much more conservative limit, and our calculations with SigSpec stopped when sig = 10.0 because the corresponding S/N values, determined using Period04 on the residuals, were much lower than expected. This is probably caused by a high number of peaks still remaining among the residuals in the region of interest. This was explained in much more detail in similar recent works for other CoRoT targets (HD 50844, Poretti et al. 2009, HD 49434, Rodríguez et al., in preparation).
.
In the case of SigSpec, the parameter used for significance is ``sig'' (= spectral significance), and the limit used as default is sig = 5.0. This should be equivalent to about S/N = 3.8 (and sig = 5.46 should be approximately equivalent to S/N = 4.0) (Reegen 2007; Kallinger et al. 2008). However, we used a much more conservative limit, and our calculations with SigSpec stopped when sig = 10.0 because the corresponding S/N values, determined using Period04 on the residuals, were much lower than expected. This is probably caused by a high number of peaks still remaining among the residuals in the region of interest. This was explained in much more detail in similar recent works for other CoRoT targets (HD 50844, Poretti et al. 2009, HD 49434, Rodríguez et al., in preparation).
The limit of sig = 10 was achieved after removing 422 peaks. This means a level of about 14 ppm for the smallest amplitudes. The frequencies are listed in Table 1 along with the most relevant parameters. Column 6 lists the S/N values corresponding to each peak. These S/N values were calculated using Period04 on the residual file provided by SigSpec. Each S/N value was calculated on a box of width = 5 cd-1 centred on the corresponding peak, as is usual for this type of variable (Rodríguez et al. 2006b,a).
The range of statistically significant detected frequencies
goes from some value close to zero up to about 70 cd-1, i.e.
![]() (1 cd
(1 cd
![]() ).
But those with the highest amplitudes are grouped around 35 cd-1 (
).
But those with the highest amplitudes are grouped around 35 cd-1 (
![]() ,
see Fig. 2).
In the following theorical analysis, we work in
,
see Fig. 2).
In the following theorical analysis, we work in
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11932fig2.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg20.png) |
Figure 2: The 422 frequencies exctracted for HD 174936. |
| Open with DEXTER | |
3 Looking for periodic patterns in the extracted frequency set
Mode identification, mainly for ![]() -Scuti stars, is the present bottleneck for the
progress in asteroseismology.
Existing mode identification techniques are based on spectroscopy or
multi-colour photometry not available in CoRoT data. Considering that we have
unprecedented, rich spectra, we seek to reveal characteristic
structures in the frequencies
distribution and to start with quasi-regular spacings.
-Scuti stars, is the present bottleneck for the
progress in asteroseismology.
Existing mode identification techniques are based on spectroscopy or
multi-colour photometry not available in CoRoT data. Considering that we have
unprecedented, rich spectra, we seek to reveal characteristic
structures in the frequencies
distribution and to start with quasi-regular spacings.
We consider the frequency set as a series of
Dirac's ![]() 's of equal amplitude. Then, the technique is simply to use the
list of frequencies with unit amplitude and to normalise its Fourier transform
to unity at zero frequency spacing.
If we have a given
periodicity in the frequency set (
's of equal amplitude. Then, the technique is simply to use the
list of frequencies with unit amplitude and to normalise its Fourier transform
to unity at zero frequency spacing.
If we have a given
periodicity in the frequency set (![]() ), then its Fourier transform will show a
clear periodic structure on the corresponding inverse scale.
), then its Fourier transform will show a
clear periodic structure on the corresponding inverse scale.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{11932fig3.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg22.png) |
Figure 3:
Power spectrum for various subsets of frequencies, selected by amplitude. The solid line represents the power spectrum when the highest 50 frequencies are selected; the dashed line corresponds to the highest 100 frequencies; the dotted line, for 200; and dot-dashed line for all of them. The peak corresponding to the large separation (25.8
|
| Open with DEXTER | |
We started this analysis assuming the hypothesis that, selecting a subset with the highest
peaks of the entire frequency set, we are actually considering mainly the modes of the lowest
![]() values. The visibility of the modes
decreases approximately as
values. The visibility of the modes
decreases approximately as
![]() or
or
![]() ,
depending whether
the
,
depending whether
the ![]() degree is odd or even (Dziembowski 1977).
We analysed several subsets with an
arbitrary number of frequencies but always including the highest peaks. In Fig. 3
the results are given for different sets of peaks.
It can be seen that the
more frequencies in the subset, the flatter the peaks, although
the local maxima remain at the same position. This indicates that, when we only select the highest peaks, we are enhancing some periodicities corresponding to a few
degree is odd or even (Dziembowski 1977).
We analysed several subsets with an
arbitrary number of frequencies but always including the highest peaks. In Fig. 3
the results are given for different sets of peaks.
It can be seen that the
more frequencies in the subset, the flatter the peaks, although
the local maxima remain at the same position. This indicates that, when we only select the highest peaks, we are enhancing some periodicities corresponding to a few ![]() values. While, adding frequencies in the analysis, periodicities of all modes are powered and no pattern can be significantly distinguished from others.
values. While, adding frequencies in the analysis, periodicities of all modes are powered and no pattern can be significantly distinguished from others.
When we select 50 frequencies, a periodic pattern
can be recognised. Furthermore, the clear signature of a Dirac's comb is also present at 25.8, 13, 8, 6.5, and 4.9
![]() .
That
indicates that we probably have a Dirac's comb of 25.8
.
That
indicates that we probably have a Dirac's comb of 25.8
![]() ,
which is the lowest divisible number. The appearance of these peaks can be a clue to the confirmation that
they are being caused by a periodic structure in the frequency set. Other peaks around
25.8
,
which is the lowest divisible number. The appearance of these peaks can be a clue to the confirmation that
they are being caused by a periodic structure in the frequency set. Other peaks around
25.8
![]() can be explained by the separation not being strictly periodic but quasi-periodic, as can be expected for these modes (see Sect. 4). This can be the imprint of a large separation-like structure around 52
can be explained by the separation not being strictly periodic but quasi-periodic, as can be expected for these modes (see Sect. 4). This can be the imprint of a large separation-like structure around 52
![]()
![]() .
.
On the other hand, the rotational velocity measured for this star is high (
![]() km s-1,
see Sect. 4) giving a minimum rotational splitting of
km s-1,
see Sect. 4) giving a minimum rotational splitting of ![]() 20
20 ![]() Hz. It is then possible that the observed frequency pattern does not come from the large separation but from the rotational splitting. The pattern due to rotational effects should be observed only with
Hz. It is then possible that the observed frequency pattern does not come from the large separation but from the rotational splitting. The pattern due to rotational effects should be observed only with ![]() and a statistically significant number of
and a statistically significant number of ![]() values. However, because we mainly select the lowest
values. However, because we mainly select the lowest ![]() values, the large separation is more probable than the rotational splitting. In the next section, we discuss the validity of this hypothesis using a theoretical model representative of the star.
values, the large separation is more probable than the rotational splitting. In the next section, we discuss the validity of this hypothesis using a theoretical model representative of the star.
The other peaks in Fig. 3 probably come from periodic structures produced by the rotation and/or the small separation, mainly occupying the lowest part of the power spectrum. Works are in progress for understanding the meaning of these peaks.
4 Periodic structures in theoretical spectra
The periodic pattern structures are familiar in solar-like oscillators, which have reached the asymptotic regime, but not in ![]() -Scuti stars, which pulsate around the fundamental radial mode. To understand the physical origin of the present observed periodic pattern shown in the previous section, we computed a representative model of this star.
-Scuti stars, which pulsate around the fundamental radial mode. To understand the physical origin of the present observed periodic pattern shown in the previous section, we computed a representative model of this star.
4.1 Physical parameters
Table 2: Physical parameters of the star with its uncertainties to construct the theoretical model (Charpinet et al. 2006).
We consider the physical parameters of the star HD 174936, which are listed in Table 2. These values are taken from ``CorotSky Database'' (Charpinet et al. 2006).
![]() ,
,
![]() ,
and [Fe/H] were derived from
Strömgren photometry (Hauck & Mermilliod 1998), while the rotational velocity (
,
and [Fe/H] were derived from
Strömgren photometry (Hauck & Mermilliod 1998), while the rotational velocity (
![]() km s-1) was determined from high-resolution spectroscopy. The spectrum was taken in June 2, 2004 using the FEROS spectrograph attached to the ESO 2.2 m-telescope at La Silla (Chile). It was obtained in the framework of the mission preparation and is available at the GAUDI archive (Solano et al. 2005).
On the other hand, it has been shown that rapid rotation should be considered when calculating the stellar physical parameters from photometry. Michel et al. (1999)
propose a method for determining the effects of rotation and geometry (angle of
inclination) on photometric parameters for stars in clusters. For
km s-1) was determined from high-resolution spectroscopy. The spectrum was taken in June 2, 2004 using the FEROS spectrograph attached to the ESO 2.2 m-telescope at La Silla (Chile). It was obtained in the framework of the mission preparation and is available at the GAUDI archive (Solano et al. 2005).
On the other hand, it has been shown that rapid rotation should be considered when calculating the stellar physical parameters from photometry. Michel et al. (1999)
propose a method for determining the effects of rotation and geometry (angle of
inclination) on photometric parameters for stars in clusters. For ![]() -Scuti stars, that method
was further developed by Pérez Hernández et al. (1999), showing that uncertainties of around 100-150 K in effective temperature, and
-Scuti stars, that method
was further developed by Pérez Hernández et al. (1999), showing that uncertainties of around 100-150 K in effective temperature, and ![]() 0.10 dex in
0.10 dex in ![]() ,
can be found for moderately rotating stars. That result was later confirmed by Suárez et al. (2002). In the present case, considering the absence of additional information on the inclination angle of the star, uncertainty boxes of 200 K in the HR diagram in
,
can be found for moderately rotating stars. That result was later confirmed by Suárez et al. (2002). In the present case, considering the absence of additional information on the inclination angle of the star, uncertainty boxes of 200 K in the HR diagram in
![]() and
and ![]() 0.2 dex in
0.2 dex in ![]() were adopted. An uncertainty of
were adopted. An uncertainty of ![]() 0.2 in metallicity was taken.
0.2 in metallicity was taken.
This is a main-sequence intermediate-mass star (![]() 1.6
1.6 ![]() ). The hydrogen abundance in the core is
). The hydrogen abundance in the core is
![]() .
But it is younger than the star studied in Poretti et al. (2009).
.
But it is younger than the star studied in Poretti et al. (2009).
4.2 Theoretical models
Using the physical parameters measured for the star and given in the previous subsection as input, we computed a theoretical model representative of the star. The evolutionary code CESAM (Morel & Lebreton 2008; Morel 1997) and the pulsation code GRACO (Moya & Garrido 2008; Moya et al. 2004) were used as numerical codes to calculate frequencies, growth rates and other physical quantities.
For the model, we computed the oscillation spectrum (radial and non-radial), from ![]() to 3, in the
range of observed frequencies.
Then, we calculated the large separation defined as
to 3, in the
range of observed frequencies.
Then, we calculated the large separation defined as
![]() .
In Fig. 4 the large
separation calculated this way is depicted. It is quite evident that the large separation does not vary much but is bounded within a frequency range of 10
.
In Fig. 4 the large
separation calculated this way is depicted. It is quite evident that the large separation does not vary much but is bounded within a frequency range of 10
![]() .
In this particular case, the two discrepant points belonging to
.
In this particular case, the two discrepant points belonging to ![]() correspond to an avoided crossing. Similar results are expected for other higher
correspond to an avoided crossing. Similar results are expected for other higher ![]() values.
values.
However, this is not critical
for the detection of regularities using Fourier transform due to its
statistical character.
In Fig. 5 we show an identical analysis to the one for
the observed frequencies (see previous section). It can be seen
that we have similar results for the theoretical frequencies
for a given representative model (even in a nonrotating model). This indicates that such regularities,
even in the non-asymptotic regime, may be discerned by the Fourier transform technique explained in Sect. 3. This opens a new window in the analysis of ![]() -Scuti stars.
-Scuti stars.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11932fig4.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg37.png) |
Figure 4:
Frequency dependance of the large separation for the three lowest values of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11932fig5.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg38.png) |
Figure 5:
Power spectrum of the oscillation frequencies of a model obtained using the technique described in Sect. 3. We use only the range of observed data set, i.e., up to 700
|
| Open with DEXTER | |
5 Discussion
We have shown that a periodic pattern, possibly corresponding to large separation, is found in the frequency spectrum observed for the star (see Sect. 3). We have corroborated it through a theoretical model (see previous section). Clearly, the large separation found in the studied regime does not have the same physical meaning as found in the asymptotic regime (Christensen-Dalsgaard 2003). However, it is dependent on the internal structure of the star, and we can study how this signature is robust and sensitive to evolution or mass, in order to open up new perspectives about its diagnostic power.
To do so, we constructed seismic
models that lie within the uncertainties of the physical parameters measured for this star. That is, we computed models to reproduce the HR locations corresponding to the four corners (![]() )
and the centre of the uncertainty box. After that, for each equilibrium model, we computed its oscillations. This procedure is followed for models built with the observed metallicity and the two maximum errors (1
)
and the centre of the uncertainty box. After that, for each equilibrium model, we computed its oscillations. This procedure is followed for models built with the observed metallicity and the two maximum errors (1![]() )
considered. Then, we reduced the corners of the uncertainty box to half and computed the corresponding models. Finally, we calculated the large separation for all them. The uncertainty boxes (1
)
considered. Then, we reduced the corners of the uncertainty box to half and computed the corresponding models. Finally, we calculated the large separation for all them. The uncertainty boxes (1![]() )
for the 1
)
for the 1![]() extremes of the metallicity are depicted in Fig. 6. Two evolutionary tracks of the central model (
extremes of the metallicity are depicted in Fig. 6. Two evolutionary tracks of the central model (
![]() )
with and without rotation are plotted, too.
)
with and without rotation are plotted, too.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11932fig6.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg41.png) |
Figure 6:
HR diagram containing two uncertainty boxes corresponding to the |
| Open with DEXTER | |
Table 3: Models of the uncertainty boxes for each metallicity calculated with mass and large separation.
We can see in Table 3 the results of all these calculations. The large separation is close to the value found in the observed frequency set for the central models at each metallicity. Typically, it is higher for less massive models, and when reducing the half-bottom area of the uncertainty box it varies faster than the half-upper one.
On the other hand, we computed the instability range for these models (see Fig. 7). Some models covers the range (around 400
![]() )
of the highest amplitudes in the frequency set, others do not. But not one of them gives the necessary instability range to represent the full range in the observations. It is assumed that observed frequencies ([0.5, 900]
)
of the highest amplitudes in the frequency set, others do not. But not one of them gives the necessary instability range to represent the full range in the observations. It is assumed that observed frequencies ([0.5, 900]
![]() ), at least in ground-based data, must be within the instability range. However, as far as we know, no theory allows such a huge range of excited frequencies, even including the time-dependent convection theory. This is a new challenge for theory that should be improved in order to predict the instability range observed in the new era of space telescopes.
), at least in ground-based data, must be within the instability range. However, as far as we know, no theory allows such a huge range of excited frequencies, even including the time-dependent convection theory. This is a new challenge for theory that should be improved in order to predict the instability range observed in the new era of space telescopes.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11932fig7.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg43.png) |
Figure 7:
Frequency versus growth rate and amplitude for the 1.63 |
| Open with DEXTER | |
As seen, the observed frequency set contains a lot of information (small separation, rotational splitting, etc.), and work is progressing. We hope that such a large number of frequencies will allow us to obtain precise models representative of this star and to improve our understanding of the interiors of intermediate-mass stars.
6 Summary and conclusions
This work has presented an analysis of the ![]() -Scuti star object HD 174936 (ID 7613), observed by CoRoT during the first short run SRc01 (27 days). A total number of 422 frequencies (which reach up
-Scuti star object HD 174936 (ID 7613), observed by CoRoT during the first short run SRc01 (27 days). A total number of 422 frequencies (which reach up
![]() )
are extracted from the light curve using
standard prewhitening techniques. This represents one of the largest number of detected
frequencies for a
)
are extracted from the light curve using
standard prewhitening techniques. This represents one of the largest number of detected
frequencies for a ![]() -Scuti ever obtained so far.
-Scuti ever obtained so far.
We combined the classical seismic analysis with the use of statistical
properties of the modes distribution in the observed frequency range. In particular, we have
found periodic patterns in the observed frequency spectrum, which were not expected
for this kind of pulsating star.
We find a frequency distribution of the modes that seems to
correspond to the large separation, which is about 52
![]() .
This result is supported
by an equivalent analysis performed with a representative model of the star.
.
This result is supported
by an equivalent analysis performed with a representative model of the star.
All these results provide new prospects for the asteroseismology of ![]() -Scuti stars. In particular, the large separation found for this star opens the possibility of performing similar studies to those for solar-like stars. Although we have not explored the low-frequency region of Fig. 3, we cannot discard the possibility that relevant information concerning rotation and small differences are hidden in this peak forest.
-Scuti stars. In particular, the large separation found for this star opens the possibility of performing similar studies to those for solar-like stars. Although we have not explored the low-frequency region of Fig. 3, we cannot discard the possibility that relevant information concerning rotation and small differences are hidden in this peak forest.
Acknowledgements
A.G.H., A.M., J.C.S., R.G., E.R., P.J.A., S.M.R. and A.R. acknowledge support from the Spanish ``Plan Nacional del Espacio'' under project ESP2007-65480-C02-01. A.G.H. acknowledges support from a ``FPI'' contract of the Spanish Ministry of Science and Innovation. J.C.S. acknowledges support from the ``Consejo Superior de Investigaciones Científicas'' by an ``I3P'' contract financed by the European Social Fund. P.J.A. acknowledges financial support from a ``Ramón y Cajal'' contract of the Spanish Ministry of Science and Innovation. A.M. acknowledges financial support from a ``Juan de la Cierva'' contract of the Spanish Ministry of Science and Innovation. E.P. acknowledges support from the Italian ESS project, contract ASI/INAF I/015/07/0, WP 03170.
References
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [CrossRef] [EDP Sciences] (In the text)
- Baglin, A., Auvergne, M., Barge, P., et al. 2006a, in ESA SP-1306, ed. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 33 (In the text)
- Baglin, A., Michel, E., Auvergne, M., & The COROT Team 2006b, in Proceedings of SOHO 18/GONG 2006/HELAS I, Beyond the spherical Sun, ESA SP, 624 (In the text)
- Charpinet, S., Cuvilo, J., Platzer, J., et al. 2006, in ESA SP-1306, ed. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 353 (In the text)
- Christensen-Dalsgaard, J. 2003, Lecture notes on Stellar Oscillations, 5th edn (Institut for Fysik og Astronomi, Aarhus Universitet) (In the text)
- Cox, A. N. 2002, in Radial and Nonradial Pulsations As Probes of Stellar Physics, IAU Colloq. 185, ASP Conf. Ser., 259, 21 (In the text)
- Dziembowski, W. 1977, Acta Astron., 27, 203 [NASA ADS] (In the text)
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kallinger, T., Reegen, P., & Weiss, W. W. 2008, A&A, 481, 571 [NASA ADS] [CrossRef] [EDP Sciences]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] (In the text)
- Michel, E., Hernández, M. M., Houdek, G., et al. 1999, A&A, 342, 153 [NASA ADS] (In the text)
- Morel, P. 1997, A&AS, 124, 597 [NASA ADS] [CrossRef] [EDP Sciences]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef]
- Moya, A., & Garrido, R. 2008, Ap&SS, 316, 129 [NASA ADS] [CrossRef]
- Moya, A., Garrido, R., & Dupret, M. A. 2004, A&A, 414, 1081 [NASA ADS] [CrossRef] [EDP Sciences]
- Pérez Hernández, F., Claret, A., Hernández, M. M., et al. 1999, A&A, 346, 586 [NASA ADS] (In the text)
- Poretti, E., Michel, E., Garrido, R., et al. 2009, A&A, 506, 85 [CrossRef] [EDP Sciences] (In the text)
- Reegen, P. 2007, A&A, 467, 1353 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rodríguez, E., Amado, P. J., Suárez, J. C., et al. 2006a, A&A, 450, 715 [NASA ADS] [CrossRef] [EDP Sciences]
- Rodríguez, E., Costa, V., Zhou, A.-Y., et al. 2006b, A&A, 456, 261 [NASA ADS] [CrossRef] [EDP Sciences]
- Solano, E., Catala, C., Garrido, R., et al. 2005, AJ, 129, 547 [CrossRef] (In the text)
- Suárez, J.-C., Michel, E., Pérez Hernández, F., et al. 2002, A&A, 390, 523 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] (In the text)
Footnotes
- ... HD 174936
![[*]](/icons/foot_motif.png)
- The CoRoT space mission, launched on December 27, 2006, has been developed and is operated by the CNES, with the contribution of Austria, Belgium, Brasil, ESA, Germany, and Spain.
- ...
![[*]](/icons/foot_motif.png)
- Table 1 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/506/79
- ...

![[*]](/icons/foot_motif.png)
- Frequency values for
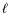 = 1 modes are placed around the centre of two consecutive
= 1 modes are placed around the centre of two consecutive 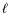 = 0 modes, so we expect to find a minimun periodicity of the half value of the large separation.
= 0 modes, so we expect to find a minimun periodicity of the half value of the large separation.
All Tables
Table 2: Physical parameters of the star with its uncertainties to construct the theoretical model (Charpinet et al. 2006).
Table 3: Models of the uncertainty boxes for each metallicity calculated with mass and large separation.
All Figures
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11932fig1.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg13.png) |
Figure 1: Spectral window of the short-run CoRoT dataset on HD 174936. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11932fig2.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg20.png) |
Figure 2: The 422 frequencies exctracted for HD 174936. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{11932fig3.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg22.png) |
Figure 3:
Power spectrum for various subsets of frequencies, selected by amplitude. The solid line represents the power spectrum when the highest 50 frequencies are selected; the dashed line corresponds to the highest 100 frequencies; the dotted line, for 200; and dot-dashed line for all of them. The peak corresponding to the large separation (25.8
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11932fig4.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg37.png) |
Figure 4:
Frequency dependance of the large separation for the three lowest values of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11932fig5.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg38.png) |
Figure 5:
Power spectrum of the oscillation frequencies of a model obtained using the technique described in Sect. 3. We use only the range of observed data set, i.e., up to 700
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11932fig6.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg41.png) |
Figure 6:
HR diagram containing two uncertainty boxes corresponding to the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11932fig7.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11932-09/Timg43.png) |
Figure 7:
Frequency versus growth rate and amplitude for the 1.63 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


