Accurate fundamental parameters of CoRoT asteroseismic targets - The solar-like stars HD 49933, HD 175726, HD 181420, and HD 181906

H. Bruntt

doi:10.1051/0004-6361/200911925

Free Access

Issue		A&A Volume 506, Number 1, October IV 2009 The CoRoT space mission: early results


Page(s)		235 - 244
Section		Stellar atmospheres
DOI		https://doi.org/10.1051/0004-6361/200911925
Published online		15 July 2009

The CoRoT space mission: early results

Accurate fundamental parameters of CoRoT asteroseismic targets

The solar-like stars HD 49933, HD 175726, HD 181420, and HD 181906

H. Bruntt^1,2

1 - Observatoire de Paris, LESIA, 5 place Jules Janssen, 92195 Meudon Cedex, France
2 - Sydney Institute for Astronomy, School of Physics, University of Sydney, NSW 2006, Australia

Received 23 February 2009 / Accepted 2 July 2009

Abstract
Context. The CoRoT satellite has provided high-quality light curves of several solar-like stars. Analysis of these light curves provides oscillation frequencies that make it possible to probe the interior of the stars. However, additional constraints on the fundamental parameters of the stars are important for the theoretical modelling to be successful.
Aims. We estimate the fundamental parameters (mass, radius, and luminosity) of the first four solar-like targets to be observed in the asteroseismic field. In addition, we determine their effective temperature, metallicity, and detailed abundance patterns.
Methods. To constrain the stellar mass, radius and age we used the SHOTGUN software, which compares the location of the stars in the Hertzsprung-Russell diagram with theoretical evolution models. This method takes the uncertainties of the observed parameters into account, including the large separation determined from the solar-like oscillations. We determined the effective temperatures and abundance patterns in the stars from the analysis of high-resolution spectra obtained with the HARPS, NARVAL, ELODIE and FEROS spectrographs.
Results. We determined the mass, radius, and luminosity of the four CoRoT targets to within 5-10%, 2-4% and 5-13%, respectively. The quality of the stellar spectra determines how well we can constrain the effective temperature. For the two best spectra we get 1- $\sigma$ uncertainties below 60 K and 100-150 K for the other two. The uncertainty on the surface gravity is less than 0.08 dex for three stars, while it is 0.15 dex for HD 181906. The reason for the larger uncertainty is that the spectrum has two components with a luminosity ratio of $L_{\rm p}/L_{\rm s} = 0.50\pm0.15$ . While Hipparcos astrometric data strongly suggest it is a binary star, we find evidence that the fainter star may be a background star, since it is less luminous but hotter.

Key words: stars: fundamental parameters - binaries: spectroscopic - stars: abundances

1 Introduction

One of the ultimate science goals of the asteroseismic investigation of the CoRoT mission is to compare the observed oscillation frequencies with theoretical pulsation models. This should allow us to probe the inside of stars and in particular determine how well we understand the physics of stars. We can examine to which degree the models describe the observations and hopefully be able to improve some of the approximations that are necessary when computing theoretical models.

To be able to confront the theoretical models with the observations, we need accurate and reliable estimates of the fundamental parameters of the stars, i.e. mass, radius, and luminosity. In this present work we will discuss how these parameters can be estimated by comparison with theoretical evolution models. In addition, we determine the atmospheric parameters from photometric indices and detailed spectroscopic analysis of absorption lines to get the chemical composition. In particular, we give results for four solar-like stars observed in the asteroseismic field of CoRoT: HD 49933, HD 175726, HD 181420, and HD 181906.

2 Observations

For the target HD 49933 we used spectra from a 10-day spectroscopic campaign with the HARPS spectrograph (Mosser et al. 2005). From their bisector analysis it was found that stellar activity was affecting the cores of the spectral lines and that this varied from night to night. We stacked 49 spectra from the quiet period (labelled ``H-C'' in the following) and collected 2001 January 19-20 from UT-22h to UT-06h. We stacked 35 from a more active period (labelled ``H-A'') collected the following night from UT-20h to UT-05h. The H-A and H-C spectra have signal-to-noise ratios (S/N) in the continuum of just over 400.

Spectra of HD 175726, HD 181420 and HD 181906 were obtained from the GAUDI database (Solano et al. 2005). These spectra were collected as preparation for the CoRoT mission with the ELODIE spectrograph mounted on the 1.93-m telescope at the Haute-Provence observatory. The typical S/N in these spectra is 120. Additional spectra of HD 175726 were obtained with the NARVAL spectrograph on the 2 m Bernard Lyot Telescope at the Pic du Midi observatory as part of the CoRoT follow-up program. We stacked 13 spectra to get a S/N of 900. A spectrum of HD 181420 was also obtained with the FEROS spectrograph at ESO.

A small section of the observed spectra is shown in Fig. 1 and the general properties of the spectra are listed in Table 1. The S/N was measured in the continuum as the average of several regions in the range 5500-6500 Å. We calculated the S/N for the original resolution and for a degraded resolution of R=42 000 (S/N₄₂ in Table 1), with two pixels per resolution element.

We determined the projected rotation velocity ( $v \sin i$ ) by fitting synthetic spectra to several isolated lines while assuming a macroturbulence of 2 km s^-1 for all stars. The uncertainty on $v \sin i$ is 5% except for HD 181906 which has two components in the spectrum, so the uncertainty is larger, $v \sin i=10\pm1$ km s^-1. Nordström et al. (2004) determined a much higher value of $v \sin i = 16$ km s^-1, which we also get if we assume it is a single star. We shall discuss the possible binary nature of HD 181906 in Sect. 5. For the other three stars our $v \sin i$ values agree with Nordström et al. (2004) within the uncertainty, although we note that their values are all exactly 1 km s^-1 higher.

$\begin{figure} \par\includegraphics[angle=90,width=7.8cm,clip]{11925f1.ps} \end{figure}$	Figure 1: A section of the observed spectra for the four stars (cf. Table 1). The absorption lines due to Fe, Si and Ba are marked.
Open with DEXTER

Table 1: Properties of the observed spectra of the four CoRoT targets.

3 Fundamental parameters of stars

The fundamental parameters of a star are its mass, M, radius, R, and luminosity, L. A direct measurement of mass can be done for the components in detached eclipsing binary systems with an accuracy of about 1-2 per cent (Andersen 1991) or for single stars in the rare case of a microlensing event (Alcock et al. 2001). The radius of single stars can be measured to about 1 per cent with interferometric methods or to about the same precision for eclipsing binary stars. The luminosity can be estimated from the V magnitude using the parallax and a bolometric correction, which is determined from model atmospheres.

For the relatively faint CoRoT asteroseismic targets we cannot apply these direct methods to get the mass and radius, so we must rely on indirect methods. An advantage for the solar-like CoRoT targets is that their density can be constrained from the large separation ( $\Delta \nu$ ) which is measured to 2 per cent or better (Michel et al. 2008) from the oscillation frequencies.

More detailed investigations involve comparison of the individual observed frequencies with theoretical models. The aim of this work is to estimate the parameters that are used by the theoreticians, namely L, effective temperature, $T_{\rm eff}$ , surface gravity, $\log g$ , and the chemical composition. In this section we shall discuss how the fundamental parameters of stars can be determined.

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{11925f2.ps} \end{figure}$

Figure 2:

Hertzsprung-Russell diagram showing the position of the four CoRoT stars. Full lines are evolution tracks from ASTEC for $[{\rm Fe/H}] = -0.176$ and the dashed line is for ${\rm [Fe/H]}=-0.480$ . The uncertainties and location of each target is marked by a box and identified by the last two digits in the HD number. The mass is indicated for each track and the location of the Sun is marked with ``S''.

Open with DEXTER

3.1 Surface gravity from M and R

The positions of the four CoRoT targets are shown in the Hertzsprung-Russell (H-R) diagram in Fig. 2, where ASTEC evolution tracks from Christensen-Dalsgaard (2008) are overlaid. The position of the Sun is shown for reference. The mass and radius of a single field star can be estimated by comparing its properties to such theoretical evolution tracks.

We adopted the so-called SHOTGUN method which is described in detail in Stello et al. (2009). In brief, we construct 200 values for the four parameters ( $T_{\rm eff}$ , $L/{L}_\odot$ , [Fe/H], $\Delta \nu$ ) with a mean value equal to our estimated values (see below) and a Gaussian random scatter equal to the uncertainty. For each of the 200 values we locate the closest matching grid point among the evolution tracks and the method saves the mass, radius and age. We finally calculate the mean value and the rms value as our estimate of the 1- $\sigma$ uncertainty. The method uses the large separation to constrain the fundamental properties of the targets, and we assume that it scales with the Sun as $\Delta \nu / \Delta \nu_\odot = \sqrt{\rho / \rho_\odot}$ , following the arguments by Kjeldsen & Bedding (1995). The inclusion of the large separation constrains the possible radii of the models as was discussed in detail by Stello et al. (2009).

Compared to the description of SHOTGUN in Stello et al. (2009) we have increased the number of random seed values from 100 to 200 and we have used both BASTI isochrones (Pietrinferni et al. 2004) and ASTEC evolution tracks Christensen-Dalsgaard (2008). We find that the results for the four targets agree within the 1- $\sigma$ uncertainty for both sets of models. In the following we quote the results using the ASTEC evolution tracks, for which we have a denser model grid.

The four input parameters to SHOTGUN are estimated from:

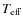$\mbox{$\bullet$}$: $T_{\rm eff}$ : The V-K index (calibration from Masana et al. 2006).
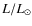$\mbox{$\bullet$}$: $L/{L}_\odot$ : V from SIMBAD, Hipparcos parallax (van Leeuwen 2007), and bolometric correction (Bessell et al. 1998).
Fe/H: : Initial value from the Strömgren m₁ index and the final value from the abundance analysis.
$\mbox{$\bullet$}$: $\Delta \nu$ : Results from CoRoT except for HD 175726.

For the $\Delta \nu$ values we used the most resent results from CoRoT. Appourchaux et al. (2008) analysed a 60-day light curve from CoRoT using different techniques and found $\Delta \nu = 85.9\pm0.15$ $\mu$ Hz. Michel et al. (2008) presented preliminary results of the analysis of HD 181420 and HD 181906 and found $\Delta \nu = 77\pm2$ and $88\pm2$ $\mu$ Hz, respectively. Finally, for HD 175726 we used $\Delta \nu = 97.2\pm0.5$ $\mu$ Hz from Mosser et al. (2009). This indicates a quite evolved star which is not in agreement with the location of the star in the H-R diagram. The detailed analysis of the oscillation frequencies show that the large separation is modulated with frequency (Mosser et al. 2009), so one should be cautious when using the scaling relation for $\Delta \nu$ . We therefore decided not to use the $\Delta \nu$ value as input to SHOTGUN for HD 175726.

In Table 3 we list the fundamental parameters from SHOTGUN. The 1- $\sigma$ uncertainty on the mass is 5-10%, radius 2-4% and luminosity to 5-13%. The surface gravity is computed as $\log g = \log (M/{M}_{\odot}) - 2 \log (R / {R}_{\odot}) + \log g_\odot$ , and the results are listed in Table 5. The formal 1- $\sigma$ uncertainty on $\log g$ is 0.06 dex or slightly less for the four targets. We note that our estimates of the uncertainties do not include the effects of changing the input physics of the models, e.g. mixing length, the equation of state or element diffusion. However, the more detailed investigation of Stello et al. (2009) shows that at least the radius is not significantly affected by changing these parameters.

3.2 The effective temperature

The effective temperature of a star, $T_{\rm eff}$ , is defined from the total flux per unit area from a black body: $\sigma~T_{\rm eff}^4 = F_{\rm tot} =\int_0^\infty F_\nu ~ {\rm d}\nu = L / 4 \pi R^2$ . To make a direct determination of $T_{\rm eff}$ one must measure $F_{\rm tot}$ from the angular diameter (from interferometry) and the flux integrated over all wavelengths (from spectrophotometry). This has been done recently for a few nearby solar-like asteroseismic targets (see North et al. 2009,2007) and yield $T_{\rm eff}$ to about 50 K. Interferometric measurements of the relatively faint CoRoT targets ( $V\simeq5{-}8$ ) may be possible in the near future with the recently installed PAVO instrument at the CHARA array (Ireland et al. 2008) or AMBER at VLTI (Petrov et al. 2007).

When such measurements are not available, $T_{\rm eff}$ can be estimated by indirect methods, e.g. using the Balmer lines, calibration of line depth ratios, photometric colour indices and detailed abundance analyses (see Sect. 4). We did not use the Balmer lines due to the difficulty of normalising these lines that cover several spectral orders. The calibration of line-depth rations of late F-K type stars was done by Kovtyukh et al. (2003), but the valid range is 4000-6150 K, and could thus only be used for the coolest star in our sample, HD 175726 (see Kovtyukh et al. 2004). Several calibrations of photometric indices exist in the literature, e.g. for F- and G-type main sequence stars the V-K index (Masana et al. 2006) and Strömgren indices (Ramírez & Meléndez 2005) have recently been calibrated. The V-K index has the advantage that it is less sensitive to interstellar reddening and in the following we have adopted the $T_{\rm eff}$ obtained from this index as our initial value for SHOTGUN and the abundance analyses.

Table 2: Fundamental parameters found from photometric indices.

Table 3: Fundamental parameters found using the SHOTGUN method.

We used the Strömgren indices from Hauck & Mermilliod (1998) as input to the TEMPLOGG (Kupka & Bruntt 2001; Rogers 1995) software to investigate if any of the stars have significant interstellar reddening. This requires the H $_\beta$ index, which has not been measured for HD 175726. For HD 49933, HD 181420 and HD 181906 we find slightly negative values for E(b-y), although they are consistent with zero within the uncertainties. The distance to the four CoRoT stars range from 26-68 parsec and in the following we assume that the targets have interstellar reddening close to zero, i.e. $E(b-y)=0.000\pm0.005$ . This corresponds to an uncertainty on $T_{\rm eff}$ of 50 K which we include in our estimates of $T_{\rm eff}$ from the photometric indices.

In Table 2 we give the results using the photometric indices. We used 2MASS V-K from Cutri et al. (2003) to get $T_{\rm eff}$ using the calibration of Masana et al. (2006). We also list $T_{\rm eff}$ using the Strömgren calibration of Ramírez & Meléndez (2005). There is a very good agreement on the $T_{\rm eff}$ determined from the photometric indices. The $T_{\rm eff}$ determined from line depth ratios for HD 175726 is $6036\pm15$ K (Kovtyukh et al. 2004; internal error is quoted) and this is fully consistent with the photometric calibrations. In Table 2 we also list $\log g$ from TEMPLOGG and [Fe/H] using the Strömgren calibration from Martell & Laughlin (2002) (see below).

3.3 Metallicity

The metallicity of F- and G-type stars has been calibrated through the Strömgren m₁ index, which measures the strength of metal lines in a narrow band around 400-420 nm. The calibration has recently been revised by Martell & Laughlin (2002) and the 1- $\sigma$ scatter of their calibration is 0.09 dex. To this we add the internal scatter assuming that each photometric index (b-y, c₁, m₁) has a 1- $\sigma$ uncertainty of 0.005. The results are given in the last column in Table 2.

A more detailed view of the composition of stars is found from abundance analysis of individual spectral absorption lines formed in the photosphere of the star. It is important to realise that we can only assume that this represents the global chemical composition of the star. Diffusion processes and element levitation are important in some stars and will change the radial distribution of elements. When modelling stars the chemical composition is often parametrised in terms of the mass fractions of hydrogen (X), helium (Y) and the rest is ``heavy elements'' (Z). From spectroscopy of solar-type stars we cannot constrain the helium content. Carbon, nitrogen and oxygen each give a significant contribution to Z. Therefore, it is important to obtain spectra that cover the near infrared where some carbon and oxygen lines are found (i.e. the spectra we have from FEROS and NARVAL).

The results of abundance analyses rely on the adopted model atmospheres that depend on $T_{\rm eff}$ , $\log g$ , [Fe/H], and microturbulence ( $\xi_t$ ). A detailed analysis requires a good spectrum, say S/N > 150 and covering 1000 Å or more in the optical range ( 4000-7000 Å). These data are easily obtained for the CoRoT targets - both in the asteroseismic field and the planet field - although for the faintest planet-hosting stars large telescopes are needed to get the required S/N. For slowly rotating stars ( $v \sin i < 25$ km s^-1) the metallicity can be determined to 0.05 dex, provided the atmospheric parameters are constrained to better than 100 K and 0.1 dex for $T_{\rm eff}$ and $\log g$ , respectively. We will discuss the uncertainties in more detail and describe our method and results in the next section.

4 Detailed spectral analysis with VWA

To analyse the spectra listed in Table 1 we used the software package VWA, which has been described in detail by Bruntt et al. (2004,2008). The software uses atomic data from the VALD database (Kupka et al. 1999) and interpolation of atmospheric models either from a modified ATLAS9 grid (Heiter et al. 2002) or the MARCS grid (Gustafsson et al. 2008). In the current study we have used the MARCS grid which implements the recently updated abundances in the Sun (Grevesse et al. 2007).

We first analysed the solar spectrum from Hinkle et al. (2000), originally published by Kurucz et al. (1984). We used a model atmosphere with $T_{\rm eff} = 5777$ K, $\log g = 4.44$ , ${\rm [Fe/H]} = 0.0$ and $\xi_t=1.0$ km s^-1, interpolated in the same grid as used for the four CoRoT stars. We determined abundances for 1413 lines in the solar spectrum in the range 3777 to 9290 Å using the VALD oscillator strengths ( $\log gf$ ). We next adjusted the $\log gf$ values so each line gives the same abundance as in Grevesse et al. (2007). Only lines with adjusted $\log gf$ values were used in the analysis of the CoRoT targets. In Tables A.1-A.3 we list the line parameters. This purely differential analysis was also used by Bruntt et al. (2008) who discussed the approach in more detail. As a test of the robustness of method we analysed three other solar spectra obtained with HARPS (Mayor et al. 2003) which have a resolution, wavelength coverage and S/N comparable to the best CoRoT spectra. We find that the determined $T_{\rm eff}$ , $\log g$ and individual abundances are consistent with the Sun within the uncertainties (for more details on this analysis see Bruntt et al. 2010, in preparation).

In the first step of the analysis, VWA automatically identifies isolated lines in the spectrum and fits them iteratively using the initial values of $T_{\rm eff}$ , $\log g$ , and metallicity from the photometric indices. By analysing the correlations of neutral Fe lines with equivalent width (EW) and excitation potential (EP) the $T_{\rm eff}$ and $\xi_t$ are automatically adjusted. Similarly, VWA requires that abundances of neutral and ionised Fe lines give the same abundance, which is adjusted by changing primarily $\log g$ . Changes in $T_{\rm eff}$ also modify the ionisation balance, i.e. the resulting $T_{\rm eff}$ and $\log g$ are correlated. For the stars we have analysed an adjustment of $T_{\rm eff}$ of +100 K can be compensated by a change in $\log g$ of +0.1 dex. However, this degeneration is partially lifted when the quality of the data is good.

To evaluate the uncertainties of the atmospheric parameters we repeat the analysis while perturbing $T_{\rm eff}$ , $\log g$ and $\xi_t$ . From this we can determine when the correlations with EW and EP become significant or the ionisation balance begins to deviate (for details see Bruntt et al. 2008). We emphasise that this way of evaluating the uncertainties gives only an internal estimate since the absolute temperature scale of the model atmospheres may be systematically wrong. In other words, our results may indicate a good precision of $T_{\rm eff}$ and $\log g$ , but the accuracy is most likely not as good. To evaluate the true accuracy we are currently undertaking the analysis of stars (Bruntt et al. 2010, in preparation) for which $T_{\rm eff}$ and $\log g$ are determined by methods that are only weakly model dependent (using interferometry and modelling of eclipsing binary stars). The preliminary results from this investigation indicate that the uncertainties given in the current work are realistic.

Rentzsch-Holm (1996) have investigated the effects of non-LTE on Fe abundances which is important for stars earlier than F type, especially for stars more metal poor than the Sun. Her calculations show that Fe I is affected while Fe II is nearly unaffected. As a consequence, the ionisation balance is shifted relative to results from our applied LTE atmosphere models and it is therefore necessary to make adjustments in $\log g$ (Bruntt et al. 2008). We refer to Collet et al. (2005) (and references therein) for a recent discussion of the effects of UV line blocking on non-LTE calculations for Fe. Extrapolating from Figs. 4 and 5 in Rentzsch-Holm (1996) we find a correction of +0.05 dex for Fe I in HD 49933, which is the hottest and most metal poor star in our sample. HD 181420 has a $T_{\rm eff}$ similar to HD 49933 but it is more metal rich, so we estimate the correction to be +0.03 dex. The adjustment of $\log g$ needed to get ionisation balance is about twice these corrections ( $\Delta \log g = +0.10$ and +0.06 dex, respectively). Since we have used extrapolations of the work by Rentzsch-Holm (1996) this leads to an additional uncertainty on $\log g$ . We have therefore added 0.05 to the uncertainty on $\log g$ from VWA for HD 49933 and HD 181420.

In Fig. 3 we show the abundances of Fe in the best spectrum for each of the four stars. The abundances are shown versus equivalent width and excitation potential. Open circles are Fe I and solid circles are Fe II lines. The horizontal dashed lines mark the solar abundance. The mean abundance and rms scatter of Fe I and Fe II lines are given in each panel. The results for the other spectra listed in Table 1 give similar results, but the overall scatter is larger.

We have checked whether the Fe abundances are correlated with other atomic line parameters. For HD 175726 and HD 181906 we find a significant correlation with wavelength. For HD 175726 this is especially true for the ELODIE spectrum, while it is less evident in the NARVAL spectrum. This could be an indication of problems with the subtraction of scattered light during the reduction of the ELODIE spectrum. For HD 181906 there is a strong correlation of Fe I and wavelength. From close inspection of the observed and synthetic spectra we see a clear asymmetry in the observed line profiles due to the contamination of light from another star. We shall discuss the detailed analysis of this star in Sect. 5.

The atmospheric parameters we determine for each spectrum are given in Table 4. For our final result we have computed the weighted mean values and they are listed in Table 5. For the reason stated above the result for the HD 175726/E spectrum was rejected. The $\log g$ determined from spectroscopy is systematically 0.1 dex higher than determined from the SHOTGUN method, and we will investigate this in future work. In Table 5 we also compare our results with values found in the literature. There is quite good agreement except for a few cases. For HD 49933 Kallinger et al. (2008) found $\log g = 3.9\pm0.1$ , which is significantly lower than the other determinations. For HD 175726 Gillon & Magain (2006) found a significantly higher $T_{\rm eff}$ and $\log g$ . They used the same ELODIE spectrum that we rejected. Also, as we have discussed, $T_{\rm eff}$ and $\log g$ are correlated and this could be an example of this problem (see also Sect. 6.2 in Bruntt et al. 2008).

The abundances in the four CoRoT targets are given in Table 6 and the abundance pattern is shown in Fig. 4. For each of the 17 elements the result is given from left to right for HD 49933, HD 175726, HD 181420 and HD 181906. The open and solid circles are the mean abundances determined from neutral and ionised lines, respectively. To be able to show the results on the same scale we plot all abundances relative to the Fe I abundance in each star. The uncertainty on the abundances includes contributions from the error on the mean value and the contribution from the uncertainty on the atmospheric parameters. When only one or two lines are available we assume an uncertainty of 0.1 dex. We have not included hyperfine structure levels for Mn and this probably explains the apparent underabundance of this element.

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{11925f3.ps} \end{figure}$	Figure 3: Abundance determined for Fe lines versus equivalent width and excitation potential. Results are shown for the best spectrum available for the four targets. Open and solid circles are for neutral and ionised lines, respectively. The dashed lines mark the abundance in the Sun.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=90,width=7.8cm,clip]{11925f4.ps} \end{figure}$	Figure 4: Abundance pattern in the four target stars for 17 elements. For each element the result is given from left to right for HD 49933, 175726, 181420 and 181906. Open circles are the mean abundances determined from neutral lines and solid circles are for singly ionised lines. To show the patterns on the same scale all elements are offset relative to the abundance of Fe I.
Open with DEXTER

Abundance analyses of two of the stars are found in the literature. Valenti & Fischer (2005) published a homogeneous set of fundamental parameters for 1,040 FGK-type stars with spectra from radial velocity surveys to find exoplanets. They used synthetic spectra to determine $T_{\rm eff}$ , $\log g$ , and abundances of Na, Si, Ti, Fe and Ni. Only HD 175726 is included in their study and they find the star to have an overall metallicity of ${\rm [M/H]}=-0.10$ . Our results agree remarkably well for the individual elements with the largest difference being 0.03 dex. Gillon & Magain (2006) analysed HD 49933 and HD 175726. Our results are in acceptable agreement for HD 49933 while for HD 175726 the results disagree. The differences can be explained by the higher $T_{\rm eff}$ and $\log g$ determined by Gillon & Magain (2006). Finally, Kallinger et al. (2008) also analysed HARPS spectra of HD 49933 but they found evidence that only Fe is underabundant while carbon and oxygen are close to the solar value. Our abundance for carbon is based only two lines, but does not confirm this result.

$\begin{figure} \par\includegraphics[width=13cm,clip]{11925f5.ps} \end{figure}$	Figure 5: Examples of four Fe I lines fitted by VWA for HD 181906. The observed lines (black) are asymmetric due to the contribution from a fainter star in the blue wing of the lines. The contribution to the spectrum from the contaminating star is taken into account in the analysis. The synthetic spectrum for the faint star is shown in grey and the combined spectrum is shown in green.
Open with DEXTER

Table 4: Atmospheric parameters determined with VWA.

5 The binary nature of HD 181906

Examples of lines fitted by VWA for HD 181906 are shown in Fig. 5. The observed profiles show an asymmetry due to the contamination of a fainter star in the blue wing of the absorption lines. We have recently expanded VWA to be able to analyse binary stars, where each component has a different atmospheric model, line list and chemical composition (Clausen et al. 2008). We initially assumed the composite spectrum was a binary since Makarov & Kaplan (2005) and Frankowski et al. (2007) have found strong evidence for this based on Hipparcos astrometric data.

Due to the relatively relatively weak lines in the fainter star, we assumed a low luminosity ratio ( $R_{\rm L}=L_{\rm p}/L_{\rm s}=0.3$ at 6000 Å). For the secondary we initially assumed $T_{\rm eff}=5~500$ K and $\log g=4.4$ and for the primary we used $T_{\rm eff}$ from the V-K index and $\log g$ from SHOTGUN. The values of $\log g$ were fixed throughout the analysis since not enough usable Fe II lines were available. VWA takes into account the change in $R_{\rm L}$ with wavelength while assuming Planck curves are valid representations of the variation of the flux with wavelength. We computed abundances for a grid for different assumptions of $R_{\rm L}$ and $T_{\rm eff}$ of the two components. Unfortunately, the S/N of the spectrum is quite poor and few lines are available. Therefore, the parameters of the secondary star cannot be determined very accurately. The best solution was found by minimising the correlations of Fe I with EW and EP (as for single stars) and the ionisation balance (only for the primary), and with the additional requirement that both stars have the same Fe abundance. We found $R_{\rm L}=0.50\pm0.15$ and for the secondary $T_{\rm eff}=6500\pm250$ K. Since the secondary is fainter but apparently a hotter star, we speculate that it is likely a background star rather than a part of a binary system. If this is true our assumption that the two stars have the same metallicity breaks down.

HD 181906 has the lowest power per oscillation mode of the four CoRoT stars analysed here (Michel et al. 2008). Our discovery that another relatively bright star is within the photometric aperture may partially explain this low amplitude. To investigate this possibility it is important to further constrain the parameters of the two stars, so we will acquire new spectra with high S/N.

Table 5: Fundamental parameters from this study and the literature.

Table 6: Abundances relative to the Sun for the four CoRoT targets.

6 Conclusion

We have determined the fundamental parameters of four solar-like stars observed with CoRoT. This work provides important input for the detailed theoretical modelling of the stars based on comparison with individual observed oscillation frequencies.

We described the SHOTGUN software from which the mass, radius and age are estimated by comparison with theoretical evolution tracks. The uncertainty on the mass is 5-10% and for the radius 2-4%. We can thus constrain $\log g$ better than 0.06 dex.

The luminosity was estimated using the updated parallaxes from van Leeuwen (2007) and the uncertainty lies in the range 5-13%. We determined $T_{\rm eff}$ from photometric indices and find excellent agreement with results from our detailed abundance analysis using high-S/N spectra. For the two stars with the highest S/N spectra (HD 49933 and HD 175726) we can constrain $T_{\rm eff}$ to within 60 K, which is better than through photometric indices. This is not the case for the two stars with relatively poor spectra (HD 181420 and HD 181906). We have determined the metallicity of the stars and the abundance pattern for up to 17 elements. Within the uncertainties the abundance pattern can be scaled from the Sun through the metallicity.

We found that the spectrum of HD 181906 consists of two components. From our analysis of the composite spectrum we obtain a luminosity ratio of $R_{\rm L}=0.50\pm0.15$ . However, the fainter star appears to be hotter than the bright component. We therefore think the faint star may be a background star rather than being physically bound in a binary system. Further observations are needed to confirm this result.

Acknowledgements

This project was supported by the Australian and Danish Research Councils. We made use of the SIMBAD database, operated at CDS, Strasbourg, France. We used data from GAUDI, the data archive and access system of the ground-based asteroseismology programme of the CoRoT mission. The GAUDI system is maintained at LAEFF. LAEFF is part of the Space Science Division of INTA. We used atomic data extracted from the VALD data base made available through the Institute of Astronomy in Vienna, Austria. We thank C. Catala for providing the NARVAL spectrum of HD 175726.

Appendix A: Lists of lines used in the abundance analysis

Table A.1: The atomic number, element name, wavelength, and $\log gf$ from the VALD database and the adjusted $\log gf$ value. The letters a-d indicate in which spectra the line was used in the analysis: a = HD 49933/H-C, b = HD 175726/N, c = 181420/F and d = HD181906/E.

Table B.2: The atomic number, element name, wavelength, and $\log gf$ from the VALD database and the adjusted $\log gf$ value. The letters a-d indicate in which spectra the line was used in the analysis: a = HD 49933/H-C, b = HD 175726/N, c = 181420/F and d = HD181906/E.

Table B.3: The atomic number, element name, wavelength, and $\log gf$ from the VALD database and the adjusted $\log gf$ value. The letters a-d indicate in which spectra the line was used in the analysis: a = HD 49933/H-C, b = HD 175726/N, c = 181420/F and d = HD181906/E.

References

Alcock, C., Allsman, R. A., Alves, D. R., et al. 2001, Nature, 414, 617 [NASA ADS] [CrossRef] (In the text)
Andersen, J. 1991, A&A Rev., 3, 91 [NASA ADS] (In the text)
Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] (In the text)
Bruntt, H., Bikmaev, I. F., Catala, C., et al. 2004, A&A, 425, 683 [NASA ADS] [CrossRef] [EDP Sciences]
Bruntt, H., De Cat, P., & Aerts, C. 2008, A&A, 478, 487 [NASA ADS] [CrossRef] [EDP Sciences]
Cenarro, A. J., Peletier, R. F., Sánchez-Blázquez, P., et al. 2007, MNRAS, 374, 664 [NASA ADS] [CrossRef]
Christensen-Dalsgaard, J. 2008, Ap&SS, 316, 13 [NASA ADS] [CrossRef] (In the text)
Clausen, J. V., Torres, G., Bruntt, H., et al. 2008, A&A, 487, 1095 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Collet, R., Asplund, M., & Thévenin, F. 2005, A&A, 442, 643 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources. (NASA/IPAC Infrared Science Archive http://irsa.ipac.caltech.edu/applications/Gator/) (In the text)
Frankowski, A., Jancart, S., & Jorissen, A. 2007, A&A, 464, 377 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gillon, M., & Magain, P. 2006, A&A, 448, 341 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [NASA ADS] [CrossRef] (In the text)
Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Heiter, U., Kupka, F., van't Veer-Menneret, C., et al. 2002, A&A, 392, 619 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727-9300 A (San Francisco USA: ASP) (In the text)
Ireland, M. J., Mérand, A., ten Brummelaar, T. A., et al. 2008, in SPIE Conf. Ser., 7013 (In the text)
Kallinger, T., Gruberbauer, M., Guenther, D. B., Fossati, L., & Weiss, W. W. 2008, A&A, submitted, [arXiv:0811.4686] (In the text)
Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] (In the text)
Kovtyukh, V. V., Soubiran, C., Belik, S. I., & Gorlova, N. I. 2003, A&A, 411, 559 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Kovtyukh, V. V., Soubiran, C., & Belik, S. I. 2004, A&A, 427, 933 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Kupka, F., & Bruntt, H. 2001, First COROT/MONS/MOST Ground Support Workshop, ed. C. Sterken (Belgium: Vrije Universiteit Brussel), 39
Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm (New Mexico, USA: National Solar Observatory Atlas, Sunspot) (In the text)
Makarov, V. V., & Kaplan, G. H. 2005, AJ, 129, 2420 [NASA ADS] [CrossRef] (In the text)
Martell, S., & Laughlin, G. 2002, ApJ, 577, L45 [NASA ADS] [CrossRef] (In the text)
Masana, E., Jordi, C., & Ribas, I. 2006, A&A, 450, 735 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] (In the text)
Michel, E., Baglin, A., Auvergne, M., et al. 2008, Science, 322, 558 [NASA ADS] [CrossRef] (In the text)
Mosser, B., Bouchy, F., Catala, C., et al. 2005, A&A, 431, L13 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Mosser, B., Michel, E., Appourchaux, T., et al. 2009, A&A, 506, 33 [CrossRef] [EDP Sciences] (In the text)
Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
North, J. R., Davis, J., Bedding, T. R., et al. 2007, MNRAS, 380, L80 [NASA ADS] [CrossRef]
North, J. R., Davis, J., Robertson, J. G., et al. 2009, MNRAS, 393, 245 [NASA ADS] [CrossRef]
Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] (In the text)
Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] (In the text)
Rentzsch-Holm, I. 1996, A&A, 312, 966 [NASA ADS] (In the text)
Rogers, N. Y. 1995, Commun. Asteroseismol., 78, 1
Solano, E., Catala, C., Garrido, R., et al. 2005, AJ, 129, 547 [NASA ADS] [CrossRef] (In the text)
Stello, D., Chaplin, W. J., Bruntt, H., et al. 2009, ApJ, 700, 1589 [NASA ADS] [CrossRef] (In the text)
Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] (In the text)
van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)

Footnotes

... software: On line version: http://www.univie.ac.at/asap/templogg/main.php.
... HARPS: http://www.eso.org/sci/facilities/lasilla/instruments/harps/inst/monitoring/sun.html
... abundance: In the following we call this the ``ionisation balance'', which is the difference in abundance: A(Fe II) -A(Fe I)

All Tables

Table 1: Properties of the observed spectra of the four CoRoT targets.

Table 2: Fundamental parameters found from photometric indices.

Table 3: Fundamental parameters found using the SHOTGUN method.

Table 4: Atmospheric parameters determined with VWA.

Table 5: Fundamental parameters from this study and the literature.

Table 6: Abundances relative to the Sun for the four CoRoT targets.

All Figures

$\begin{figure} \par\includegraphics[angle=90,width=7.8cm,clip]{11925f1.ps} \end{figure}$	Figure 1: A section of the observed spectra for the four stars (cf. Table 1). The absorption lines due to Fe, Si and Ba are marked.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{11925f2.ps} \end{figure}$	Figure 2: Hertzsprung-Russell diagram showing the position of the four CoRoT stars. Full lines are evolution tracks from ASTEC for $[{\rm Fe/H}] = -0.176$ and the dashed line is for ${\rm [Fe/H]}=-0.480$ . The uncertainties and location of each target is marked by a box and identified by the last two digits in the HD number. The mass is indicated for each track and the location of the Sun is marked with ``S''.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{11925f3.ps} \end{figure}$	Figure 3: Abundance determined for Fe lines versus equivalent width and excitation potential. Results are shown for the best spectrum available for the four targets. Open and solid circles are for neutral and ionised lines, respectively. The dashed lines mark the abundance in the Sun.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=7.8cm,clip]{11925f4.ps} \end{figure}$	Figure 4: Abundance pattern in the four target stars for 17 elements. For each element the result is given from left to right for HD 49933, 175726, 181420 and 181906. Open circles are the mean abundances determined from neutral lines and solid circles are for singly ionised lines. To show the patterns on the same scale all elements are offset relative to the abundance of Fe I.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=13cm,clip]{11925f5.ps} \end{figure}$	Figure 5: Examples of four Fe I lines fitted by VWA for HD 181906. The observed lines (black) are asymmetric due to the contribution from a fainter star in the blue wing of the lines. The contribution to the spectrum from the contaminating star is taken into account in the analysis. The synthetic spectrum for the faint star is shown in grey and the combined spectrum is shown in green.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.