| Issue |
A&A
Volume 506, Number 1, October IV 2009
The CoRoT space mission: early results
|
|
|---|---|---|
| Page(s) | 33 - 40 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200911917 | |
| Published online | 15 July 2009 | |
The CoRoT space mission: early results
The CoRoT target HD 175726:
an active star with weak solar-like oscillations![[*]](/icons/foot_motif.png)
B. Mosser1 - E. Michel1 - T. Appourchaux2 - C. Barban1 - F. Baudin2 - P. Boumier2 - H. Bruntt1,3 - C. Catala1 - S. Deheuvels1 - R. A. García4 - P. Gaulme2 - C. Regulo5,6 - I. Roxburgh7,1 - R. Samadi1 - G. Verner7 - M. Auvergne1 - A. Baglin1 - J. Ballot8 - O. Benomar2 - S. Mathur9
1 - LESIA, CNRS, Université Pierre et Marie Curie, Université Denis Diderot, Observatoire de Paris, 92195 Meudon Cedex, France
2 - Institut d'Astrophysique Spatiale, UMR8617, Université Paris XI, Bâtiment 121, 91405 Orsay Cedex, France
3 - Sydney Institute for Astronomy, School of Physics, The University of Sydney, NSW 2006, Australia
4 - Laboratoire AIM, CEA/DSM-CNRS - Univ. Paris 7 Diderot - IRFU/SAp, 91191 Gif-sur-Yvette Cedex, France
5 - Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
6 - Universidad de la Laguna, 38206 La Laguna, Tenerife, Spain
7 - Astronomy Unit, Queen Mary, University of London Mile End Road, London E1 4NS, UK
8 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 av. Edouard Belin, 31400 Toulouse, France
9 -
Indian Institute of Astrophysics, Bangalore, India
Received 20 February 2009 / Accepted 5 July 2009
Abstract
Context. The CoRoT short runs give us the opportunity to observe a large variety of late-type stars through their solar-like oscillations. We report observations of the star HD 175726 that lasted for 27 days during the first short run of the mission. The time series reveals a high-activity signal and the power spectrum presents an excess due to solar-like oscillations with a low signal-to-noise ratio.
Aims. Our aim is to identify the most efficient tools to extract as much information as possible from the power density spectrum.
Methods. The most productive method appears to be the autocorrelation of the time series, calculated as the spectrum of the filtered spectrum. This method is efficient, very rapid computationally, and will be useful for the analysis of other targets, observed with CoRoT or with forthcoming missions such as Kepler and Plato.
Results. The mean large separation has been measured to be
![]()
![]() Hz, slightly below the expected value determined from solar scaling laws. We also show strong evidence for variation of the large separation with frequency. The bolometric mode amplitude is only
Hz, slightly below the expected value determined from solar scaling laws. We also show strong evidence for variation of the large separation with frequency. The bolometric mode amplitude is only
![]() ppm for radial modes, which is 1.7 times less than expected. Due to the low signal-to-noise ratio, mode identification is not possible for the available data set of HD 175726.
ppm for radial modes, which is 1.7 times less than expected. Due to the low signal-to-noise ratio, mode identification is not possible for the available data set of HD 175726.
Key words: techniques: photometric - stars: interiors - stars: evolution - stars: oscillations - stars: individual: HD 175726
1 Introduction
HD 175726, a solar-like star suspected to show measurable solar-like oscillations, was the main target of the first CoRoT short run, and was observed for 27 days in October 2007. In Sect. 2, we discuss the physical parameters of HD 175726 and the prediction of the asteroseismic signal by scaling from the Sun. Observations are presented in Sect. 3, with the analysis of the time series and of the activity signal. The analysis of the power spectrum is analysed in Sect. 4, with the identification of the large separation and of its variation with frequency. Section 5 is devoted to discussions, Sect. 6 to conclusions.
2 Stellar parameters
HD 175726, or HIP 92984, is known as an F9/G0 dwarf. It is the third component of ![]() Serpentis, separated by 7' from the two major components. Its primary parameters were given by Nordström et al. (2004), using Strömgren photometry, with values revisited in Holmberg et al. (2007). HD 175726 belongs to their large kinematically unbiased sample of
Serpentis, separated by 7' from the two major components. Its primary parameters were given by Nordström et al. (2004), using Strömgren photometry, with values revisited in Holmberg et al. (2007). HD 175726 belongs to their large kinematically unbiased sample of ![]() 16 000 nearby F and G dwarf stars, for which metallicity, rotation, age, kinematics, and galactic orbits were determined. During the preparation of the mission, this star was also the scope of a refined analysis by Gillon & Magain (2006). The temperature and
16 000 nearby F and G dwarf stars, for which metallicity, rotation, age, kinematics, and galactic orbits were determined. During the preparation of the mission, this star was also the scope of a refined analysis by Gillon & Magain (2006). The temperature and ![]() value in Gillon & Magain (2006) are significantly different from other determinations. Their parameters have not been taken into account for our estimate of the stellar asteroseismic parameters, since they seem incompatible with other values and indicates a star that is too dense. Bruntt (2009) proposed new parameters that take into account very high signal-to-noise ratio high-resolution spectrometric measurements. Concerning rotation, Kovtyukh et al. (2004) give a measurement of the projected rotational velocity of about 13.5 km s-1, whereas Cutispoto et al. (2002) give 12 km s-1. The values and uncertainties of the primary parameters proposed by Bruntt (2009) are reported in Table 1.
value in Gillon & Magain (2006) are significantly different from other determinations. Their parameters have not been taken into account for our estimate of the stellar asteroseismic parameters, since they seem incompatible with other values and indicates a star that is too dense. Bruntt (2009) proposed new parameters that take into account very high signal-to-noise ratio high-resolution spectrometric measurements. Concerning rotation, Kovtyukh et al. (2004) give a measurement of the projected rotational velocity of about 13.5 km s-1, whereas Cutispoto et al. (2002) give 12 km s-1. The values and uncertainties of the primary parameters proposed by Bruntt (2009) are reported in Table 1.
Table 1: Primary parameters of HD 175726.
The estimated mass and radius derived from the physical parameters are very close to the solar values.
We therefore expect the value of the large separation to be close to the solar value too, namely around
![]()
![]() Hz, according to the 1-
Hz, according to the 1-![]() error bars (Kjeldsen & Bedding 1995). We nevertheless have to take into account that the estimated mass and radius depend on the physical modeling of the stellar photosphere. Furthermore, experience tells us that we have to consider 2-
error bars (Kjeldsen & Bedding 1995). We nevertheless have to take into account that the estimated mass and radius depend on the physical modeling of the stellar photosphere. Furthermore, experience tells us that we have to consider 2-![]() error bars for a reliable prediction. Therefore, we should search for a large separation in the range
error bars for a reliable prediction. Therefore, we should search for a large separation in the range
![]()
![]() Hz.
Hz.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11917f1.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg28.png) |
Figure 1: Level-2 light curve of HD 175726. The maximum variations are typically 1% peak-to-peak. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f2.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg29.png) |
Figure 2: Power spectrum of the window. Side lobes occur at the harmonics of the orbital frequency, modulated by the diurnal frequency. |
| Open with DEXTER | |
Similarly derived from scaling laws, the maximum amplitude should occur around
![]() mHz (Kjeldsen & Bedding 1995).
Also, from the
(L/M)0.7 amplitude law reported from Doppler measurements by Samadi et al. (2007) and adapted for photometric measurement by Michel et al. (2008), we should expect a maximum amplitude of about
mHz (Kjeldsen & Bedding 1995).
Also, from the
(L/M)0.7 amplitude law reported from Doppler measurements by Samadi et al. (2007) and adapted for photometric measurement by Michel et al. (2008), we should expect a maximum amplitude of about
![]() ppm for HD 175726. All these inferred values are used to delimit the search for the asteroseismic signal.
ppm for HD 175726. All these inferred values are used to delimit the search for the asteroseismic signal.
3 CoRoT observations
This first short run lasted 27.2 days in October 2007 with HD 175726 as principal solar-like target. The mean stellar flux, derived from aperture photometry, corresponds to
![]() electrons per unit integration. At the usual 32-s sampling of CoRoT seismic data, the mean total flux in the 73 432 data points is about
electrons per unit integration. At the usual 32-s sampling of CoRoT seismic data, the mean total flux in the 73 432 data points is about
![]() photoelectrons (Fig. 1).
photoelectrons (Fig. 1).
3.1 Gaps and interpolation
According to the status flag of the data delivered by the chain analysis, 10.3% of the data were lost or affected by some suspect event, mainly due to the South Atlantic Anomaly (SAA) crossing where high-energy particles preclude precise photometric observation. The gaps are responsible for the duty cycle of about 89.7%, with 65 887 original data points, and the remainders obtained from interpolation. The signature of the orbital period seen in the power spectrum of the window is not purely harmonic, since the repetition of the lost data is modulated by the changing location and size of the SAA area (Fig. 2). We retrieve the complex pattern reported by Auvergne et al. (2009), with sidelobes at the CoRoT orbital frequency and its harmonics and additional modulation due to the diurnal frequency. Power in the main sidelobes represents about 1% of the total power, as expected from the observed duty cycle.
![\begin{figure}
\par\includegraphics[width=8cm]{11917f3.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg34.png) |
Figure 3: Sample of the time series, with the original data (dotted line) and the corrected data based on an interpolated time series for filling the gaps (solid line). |
| Open with DEXTER | |
Due to the large low-frequency variations in the time series possibly combined with the incomplete window, we have to take care of the quality of the interpolation used for replacing the missing or possibly corrupted data, in order to avoid power leaking to high frequency. Therefore, we have replaced the contaminated data by values derived from the low-frequency interpolation of the time series based on the algorithm proposed by Holdschneider et al. (1989) (Fig. 3). This treatment proved to be efficient, as shown in Fig. 4, where we verify that the power at medium frequency, where granulation is suspected, cannot be due to the power leaking from the low frequency peaks.
![\begin{figure}
\par\includegraphics[width=8.2cm]{11917f4.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg35.png) |
Figure 4: Power density spectra of the corrected time series (light grey line), of the low-frequency interpolation (black line) and, with an adapted scale, of the window (dark grey line). Note the axes use logarithmic scale. |
| Open with DEXTER | |
The low-frequency interpolation does not correct the power residuals at the high harmonics of the orbital frequency. These harmonics, due to the window and the high-frequency signal where the seismic signature is searched for, still dominate the spectrum up to 2 mHz. Therefore, we had to correct the power observed around the harmonics of the satellite rotation, by replacing the spurious peaks by the local mean power observed in the spectrum.
3.2 Time series and low-frequency pattern
The time series shown in Fig. 1 exhibits a strong periodic modulation, with a period of about 4 days and a peak to peak amplitude of about 1%. A detailed analysis of this time series is given by Mosser et al. (2009). In the Fourier spectrum, this modulation results in a strong peak at about 2.8 ![]() Hz, and corresponds to a rotation period of about 4.0 days. (Fig. 5). According to this measurement and to the
Hz, and corresponds to a rotation period of about 4.0 days. (Fig. 5). According to this measurement and to the ![]() value, the star seems to be seen nearly edge-on.
value, the star seems to be seen nearly edge-on.
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f5.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg36.png) |
Figure 5:
Zoom on the spectrum at low frequency (dashed line: oversampled fast Fourier transform). The signature of the rotation peaks at 2.80 |
| Open with DEXTER | |
Table 2: Parameters of the low-frequency fit.
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f6.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg39.png) |
Figure 6:
Power density spectrum on log-scale axes.
The peaks around 2.8 |
| Open with DEXTER | |
Following Michel et al. (2009), we propose a fit for the stellar background component in the low-frequency pattern, with three Lorentzian-like components in the low-frequency range (below 1 mHz):
As in Michel et al. (2009), we note that an exponent of 4 provides a better fit. Values of the parameters are given in Table 2. An exponent of 2, as in the original model proposed by Harvey (1985), seems to be excluded by the mean slope observed in the frequency range [4, 40
Table 3: Mean power densities.
3.3 High-frequency pattern
The high-frequency variations of the time series, after high-pass filtering above 0.8 mHz, present a standard deviation of about 100 ppm, in agreement with the 95 ppm value expected from pure photon noise for such a star. Photon-noise limited performance should give a power density of about 0.29 ppm2 ![]() Hz-1. The observed value is 0.31 ppm2
Hz-1. The observed value is 0.31 ppm2 ![]() Hz-1.
Hz-1.
Contrary to other CoRoT targets showing solar-like oscillations (Appourchaux et al. 2008; Barban et al. 2009; García et al. 2009), no clear signature of pressure modes can be seen in the log-scale plot of the Fourier spectrum (Fig. 6), even after a slight smoothing process intended to enhance the signal. A strong smoothing of the spectrum is necessary to show evidence of excess power around 2 mHz (Fig. 7). This signature, even if tiny, corresponds undoubtedly to an excess of energy, and therefore cannot be confused with a low frequency contribution as described by Eq. (1). We notice that this excess of energy appears at a somewhat lower frequency than expected. A plot of the Fourier spectrum centered at 2 mHz does not exhibit the usual comb pattern expected for pressure modes (Fig. 8).
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f7.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg46.png) |
Figure 7:
Smoothed power spectrum (with an apodized 200- |
| Open with DEXTER | |
From Fig. 7, we can derive that the contribution of the seismic power density at 2 mHz represents only 13% of the total energy density. Table 3 gives the different contributions to the signal for HD 175726, compared to other targets. It also gives the mean seismic signal-to-noise ratio (SNR), defined as the square root of the ratio of the smoothed power density of the maximum seismic signal compared to that of the noise. HD 175726 shows the lowest signal-to-noise ratio among the observed asteroseismic targets. Also, the granulation power density is smaller than for other solar-like stars.
4 Data analysis
4.1 Determination of the large separation
A number of different methods were used to analyse the oscillation spectra in the region where power is observed in excess. For the determination of the large separation, we applied an échelle diagram analysis, collapsed échelle diagrams (Appourchaux et al. 2006), time frequency analysis, and a test of the H0 hypothesis (Appourchaux 2004). All methods converge on the same value for the large separation, at about 97 ![]() Hz. However, due to the low signal-to-noise ratio, none of thes method were able to give a clear and unambiguous result. For example, systematic trials of collapsed échelle diagrams show many possible solutions for a plausible large separation in the range [80-160
Hz. However, due to the low signal-to-noise ratio, none of thes method were able to give a clear and unambiguous result. For example, systematic trials of collapsed échelle diagrams show many possible solutions for a plausible large separation in the range [80-160 ![]() Hz]. Also, the échelle diagram representations folded on the suspected values are unable to unambiguously confirm any of those values.
Hz]. Also, the échelle diagram representations folded on the suspected values are unable to unambiguously confirm any of those values.
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f8.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg47.png) |
Figure 8:
Smoothed power density spectrum (with a 2- |
| Open with DEXTER | |
The most explicit signature of the large separation is derived from the autocorrelation analysis proposed by Roxburgh & Vorontsov (2006). The Wiener-Khinchin theorem relates the autocorrelation function to the power spectrals density. Here, we calculate the envelope of the autocorrelation, by determining the power spectrum of the power spectrum, with the Fourier spectrum first filtered by a cosine window covering a frequency range
![]() ,
as proposed by Roxburgh et al. (2009)
(
,
as proposed by Roxburgh et al. (2009)
(
![]() is the centre of the window and
is the centre of the window and
![]() its width). The first large peak in the autocorrelation appears at time
its width). The first large peak in the autocorrelation appears at time
![]() ,
related to the local large separation by:
,
related to the local large separation by:
This relates to twice the stellar acoustic diameter. When calculated over a large frequency range centered on 2 mHz, the autocorrelation time peaks at about 5.72 h, which gives
One of us (TA) determined that the statistics of the envelope of the autocorrelation signal is a ![]() with 2 degrees of freedom. Accordingly, we tested the reliability of the signature given by Fig. 9: the H0 test (assuming a pure noise contribution) has been rejected at a value of 1%.
with 2 degrees of freedom. Accordingly, we tested the reliability of the signature given by Fig. 9: the H0 test (assuming a pure noise contribution) has been rejected at a value of 1%.
4.2 Variations of the large separation
Roxburgh et al. (2009) describes a method for inferring the variation of the large separations
![]() with frequency from the autocorrelation power by taking narrow windows centered on different frequencies. We have applied this procedure, taking windows centered on different frequencies
with frequency from the autocorrelation power by taking narrow windows centered on different frequencies. We have applied this procedure, taking windows centered on different frequencies
![]() in the range [1.5-2.5 mHz], with narrow windows
in the range [1.5-2.5 mHz], with narrow windows
![]() varying from 0.2 up to 0.7 mHz. The maximum peak identified near 5.7 h gives then a local value of
varying from 0.2 up to 0.7 mHz. The maximum peak identified near 5.7 h gives then a local value of
![]() (Fig. 9). To test this technique and determine realistic error bars, we constructed artificial power spectra with varying large separations, and repeated the same analysis on both noise-free power spectra and ones with noise. To demonstrate its reliability, we also performed H0 tests.
(Fig. 9). To test this technique and determine realistic error bars, we constructed artificial power spectra with varying large separations, and repeated the same analysis on both noise-free power spectra and ones with noise. To demonstrate its reliability, we also performed H0 tests.
Thanks to the synthetic power spectra, we identified three main contributions to error bars: time resolution, internal error, and noise, which we will discuss here:
- the relative uncertainty on the large separation due to the time resolution is defined by
 ,
with
,
with  the sampling time (32 s). The absolute value,
the sampling time (32 s). The absolute value,
 ,
is of about 0.30
,
is of about 0.30  Hz. This incompressible term represents the smallest contribution to the error bars for this noisy target;
Hz. This incompressible term represents the smallest contribution to the error bars for this noisy target;
- the internal error of the method is due to the cosine window. This window allows us to select a given band-pass in the Fourier spectrum, but simultaneously, it correlates the resulting autocorrelation signal for all frequencies in this bandpass. Therefore, the internal error increases with increasing
 value, since a large value of
value, since a large value of
 smooths out any variation of the large separation
smooths out any variation of the large separation
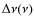 ;
simultaneously, the internal error decreases when
;
simultaneously, the internal error decreases when
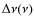 is nearly constant. For the same reason, this error is not symmetrical. Simulations help us to estimate the asymmetric error bars.The contribution of the internal error is shown in grey in Fig. 10;
is nearly constant. For the same reason, this error is not symmetrical. Simulations help us to estimate the asymmetric error bars.The contribution of the internal error is shown in grey in Fig. 10;![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11917f9.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg58.png)
Figure 9: Autocorrelation of the time series, calculated as the spectrum of the spectrum filtered with a cosine window centered on 2.0 mHz and with 0.8 mHz half-width, normalized to 1 at maximum. The dotted horizontal line indicates the mean noise level, derived from the autocorrelation of a pure noise spectrum. The grey region delimits the frequency range where the mean large separation is searched for.
Open with DEXTER - the third term contributing to the error bar is related to the interference between noise and signal. The noise complicates significantly the autocorrelation function as shown by Fig. 10, and compared to solar results obtained by Roxburgh & Vorontsov (2006). At low seismic amplitude, this term represents of course the main source of error. At maximum signal, around 2 mHz, the autocorrelation peaks have a signal-to-noise ratio of about 10.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11917f10.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg61.png) |
Figure 10: Variation of the large separation with frequency, derived from the autocorrelation. The power spectrum was first windowed with a 0.35 mHz-half width cosine filter, as indicated in the lower-right corner. The sampling of the curve corresponds crudely to the mean large separation. The size of the dots is representative of the amplitude of the correlated signal. Error bars derived from simulations are overplotted: total error is given in black, whereas the grey bar corresponds to the contribution of the internal error. |
| Open with DEXTER | |
We also tested the reliability of the pattern given by Fig. 10 with the H0 test. The level at which the test is rejected is indicated in Fig. 11. It shows that the bump in the frequency range [1.65-1.9 mHz] is less confident than the lower values in the surrounding frequency ranges. If real, the modulation of the large separation with a period W of the order of 0.8-1.0 mHz could be caused primarily by the He II ionisation zone or be due to the internal phase shifts. Following Monteiro & Thompson (2005), we infer the acoustic depth ![]() of this region which is
of this region which is
![]() resulting in the range
resulting in the range ![]() -670 s.
-670 s.
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f11.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg65.png) |
Figure 11: Autocorrelation signal as a function of frequency, normalized to the mean signal due to a pure noise spectrum. Dashed lines indicate the level at which the H0 test is rejected. |
| Open with DEXTER | |
4.3 Analysis of the frequency pattern
Given the estimates of the function
![]() and assuming it is real, we have tried to use this information to extract eigenfrequencies. First, we have searched for the peaks that show the highest height-to-background ratios (Fig. 12). Most of the major peaks are located in 2 ridges, presumably related to modes with even and odd degrees. We then constructed a rectified échelle diagram, where the spectrum is not folded on a fixed frequency, but on varying frequencies according to the function
and assuming it is real, we have tried to use this information to extract eigenfrequencies. First, we have searched for the peaks that show the highest height-to-background ratios (Fig. 12). Most of the major peaks are located in 2 ridges, presumably related to modes with even and odd degrees. We then constructed a rectified échelle diagram, where the spectrum is not folded on a fixed frequency, but on varying frequencies according to the function
![]() .
This representation then helps to identify vertically aligned ridges (Fig. 13). We applied the H0 test to the selected peaks: only 4 out of the peaks have less than 10% probability of being due to pure noise. The frequencies of these peaks are indicated in Table 4.
.
This representation then helps to identify vertically aligned ridges (Fig. 13). We applied the H0 test to the selected peaks: only 4 out of the peaks have less than 10% probability of being due to pure noise. The frequencies of these peaks are indicated in Table 4.
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f12.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg66.png) |
Figure 12: Échelle diagram of the smoothed spectrum, with indication of the possible ridges identified according to the varying large separations shown in Fig. 10. The grey squares indicate the location of the peaks with a height-to-background ratio greater than 3; the black squares indicate the location of the most confident peaks (above 95%) identified by the H0 test. |
| Open with DEXTER | |
The surface rotation period being determined from the light curve, we have searched for the signature of rotationals multiplets, without any success. A precise analysis of these ridges is out of the scope of this paper. Due to the low signal-to-noise ratio, no precise eigenmode identification is expected.
4.4 Mode amplitudes and lifetimes
Due to the impossibility of reliably extracting many individual peak, mode amplitudes were determined according to the global recipe exposed in Michel et al. (2009). According to this work, the maximum bolometric amplitude per radial mode is about
![]() ppm (Fig. 14).
ppm (Fig. 14).
With such a low signal-to-noise ratio, estimating lifetimes in the spectrum is at least as difficult as estimating eigenfrequencies. A clue indicating that the lifetimes are short is given by the use of the H0 hypothesis (Appourchaux 2004). Appourchaux addresses the case of the H0 test with binned data, in order to enhance the detection of modes with finite lifetime. Most of the peaks revealed by the analysis above remain undetectable with the test applied to unbinned data, but can be found when considering large bins. The maximum number of peaks exceeding the limit defined by the H0 test occurs as soon as 9 bins ares considered, which corresponds to 3.8 ![]() Hz. Accordingly, the mean mode lifetime is then estimated to be about 3 days.
Hz. Accordingly, the mean mode lifetime is then estimated to be about 3 days.
5 Discussion
5.1 The small observed value of the large separation
The observed value of the mean large separation at
![]()
![]() Hz is significantly lower than the expected value (
Hz is significantly lower than the expected value (
![]()
![]() Hz), but is fully compatible with the value already noticed for the frequency of maximum power. We consider that the unambiguous excess power at 2 mHz (Fig. 7) reinforces the identification of the large separation.
The observed large separation and in particular the frequency of maximum power indicate a less dense star than our target, which is a quasi-solar twin as deduced from the fundamental parameters.
In order to reconcile these seismic values with the fundamental parameters, we have to examine in which cases these parameters could be incorrect, or translate into incorrect mass and radius. We are aware that this requires a change of about 3.5
Hz), but is fully compatible with the value already noticed for the frequency of maximum power. We consider that the unambiguous excess power at 2 mHz (Fig. 7) reinforces the identification of the large separation.
The observed large separation and in particular the frequency of maximum power indicate a less dense star than our target, which is a quasi-solar twin as deduced from the fundamental parameters.
In order to reconcile these seismic values with the fundamental parameters, we have to examine in which cases these parameters could be incorrect, or translate into incorrect mass and radius. We are aware that this requires a change of about 3.5![]() compared to the nominal values of the mass and radius, respectively around
compared to the nominal values of the mass and radius, respectively around
![]() and
and
![]() .
For comparison, in Table 1, we present the parameters
.
For comparison, in Table 1, we present the parameters ![]() and
and ![]() from Bruntt (2009).
from Bruntt (2009).
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f13.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg71.png) |
Figure 13:
Rectified échelle diagram, folded according to the function
|
| Open with DEXTER | |
Table 4: Highest peaks.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11917f14.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg75.png) |
Figure 14: Bolometric amplitude per radial mode, calculated according to Michel et al. (2009). |
| Open with DEXTER | |
An error in the luminosity of HD 175726 could significantly modify the inferred seismic parameters. We first verified that the photon count registered for HD 175726 is in agreement with its V magnitude, by comparison with other targets. Contrary to the case of HD 181906, Bruntt (2009) does not suspect HD 175726 of being member of a double system according to the spectrum analysis. The SIMBAD database identifies it as the 3rd component of the system ![]() Serpentis, but 7 arcmin away from the two major components. We further checked in the CoRoT database that the point spread function of HD 175726 is nominal. This means that a second component, if present, should have a magnitude fainter than 13.5 or be very close to HD 175726. Since a 6-mag fainter star would not affect the determination of the fundamental parameters, we consider more probable the possible presence of a very close object with a negligible spectral signature (for instance due to very broad lines). However, this explanation fails to explain the discrepancy: a lower flux for HD 175726 yields a lower mass, hence a higher density and a higher large separation.
Serpentis, but 7 arcmin away from the two major components. We further checked in the CoRoT database that the point spread function of HD 175726 is nominal. This means that a second component, if present, should have a magnitude fainter than 13.5 or be very close to HD 175726. Since a 6-mag fainter star would not affect the determination of the fundamental parameters, we consider more probable the possible presence of a very close object with a negligible spectral signature (for instance due to very broad lines). However, this explanation fails to explain the discrepancy: a lower flux for HD 175726 yields a lower mass, hence a higher density and a higher large separation.
An error on the mean effective temperature is another possible explanation, for example due to a rapidly rotating star seen nearly pole-on. However, this seems to be excluded by the spot analysis achieved by Mosser et al. (2009), in favor of an inclination in the range [60-90![]() ]
when taking into account all available information on this star.
]
when taking into account all available information on this star.
The large discrepancies reported by the different works addressing the fundamental parameters of HD 175726, as reported in Sect. 2 and in Bruntt (2009), should favor the hypothesis that some unexplained feature affects the high-resolution spectrum and perturbs its analysis.
The pressure sensitive calcium lines at 6122 and 6162 Å show for instance that either
![]() or that the Ca abundance in these lines is slightly higher than the nearly solar abundance measured from several weak Ca lines. This discrepancy indicates that the spectrum of HD 175726 is not completely understood.
or that the Ca abundance in these lines is slightly higher than the nearly solar abundance measured from several weak Ca lines. This discrepancy indicates that the spectrum of HD 175726 is not completely understood.
At this stage, we fail to understand the observed discrepancies. Further modeling of the stellar spectrum is necessary. In forthcoming work we will present an interior structure model derived from the observed seismic parameters. Also, we wills acquire high angular resolution imaging with adaptive optics, to examine any possible faint stars in the vicinity of the star.
5.2 The low observed mode amplitudes
The amplitude reported in Sect. 4.4 is 1.7 times less than expected, significantly below the value derived from the scaling law. We already noticed that undermetallic stars show low amplitude (Mosser et al. 2008). Samadi et al. (2009) have recently quantified the effect of the surface metal abundance on the efficiency of the mode driving excitation by turbulent convection. However, HD 175726 is only slightly undermetallic, and other reasons are needed to explain the low observed amplitudes.
The low amplitudes are likely related to the large activity signal of HD 175726. This observation reinforces the idea that a large magnetic field inhibits the stellar convection, hence the p mode excitation, as was shown for the Sun by Jacoutot et al. (2008). Part of the discrepancy may also be due to an overestimated luminosity, but this seems to be excluded from the discussion above.
6 Conclusion
The analysis of the spectrum of HD 175726 is hampered by the very low seismic signal and a complicated spectrum showing large discrepancies compared to the 2nd order Tassoul-like oscillation pattern. At signal maximum, the mean signal-to-noise ratio (derived from the square root of the smoothed power density) is only 0.37. Despite the fact that the granulation signal is smaller compared to other CoRoT targets, as given in Michel et al. (2008), the power density of the seismic signal represents only 13% of the total power.
To best extract information from the power spectrum of HD 175726, we have determined the most efficient methods. The autocorrelation method proves to give the best result in extracting the large separation. Furthermore, even with a low signal-to-noise ratio, it allows us to extract further information on the variation of the large separation with frequency. This shows an increase of the large separation with frequency and a possible modulation. The H0 test confirms this modulation only at a level of about 85%. If real, this modulation is compatible with the seismic signature of the He II ionization zone. Information about small separations cannot be derived due to the weak signal.
As already discussed by Roxburgh & Vorontsov (2006), the method based on the autocorrelation power to extract information from a noisy spectrum is very cheap computationally, and can be particularly productive in some very common cases for the CoRoT, Kepler and Plato missions: efficient initial analysis of the data and in particular the analysis of noisy data.
The large separation and location of the maximum signal we can derive for this star disagree with the expected values and this will require further analysis. The maximum amplitude shows a strong deficiency compared to the value expected from the scaling law in (L/M)0.7. This reinforces the idea that a large magnetic field inhibits the stellar convection, hence the p mode excitation.
Comparison with other CoRoT targets proves that the short-run data set is prejudicial for retrieving precise eigenfrequencies in the oscillation spectrum. We have compared the spectrum of HD 175726 with the ones of CoRoT solar-like targets, calculated for a similar reduced 27.2-day time span. According to their greater mean power densities, the spectra of the short time series of HD 49933 (Appourchaux et al. 2008) and HD 181420 (Barban et al. 2009) still show a clear seismic signature. However, the spectrum of HD 181906 (García et al. 2009), when reduced to 27.2 days, shows no clear signal, contrary to the full time series spectrum. Since HD 175726 and HD 181906 have very similar signal-to-noise ratios, we can expect that mode identification of HD 175726 will be possible in a long-run spectrum. HD 175726 presents the lowest effective temperature among current solar-like CoRoT targets. A long run would permit us to extend the CoRoT seismic analysis to a much wider region of the HR diagram.
In most aspects (mass, radius, chemical composition), HD 175726 seems to be a solar twin, differing by a somewhat higher effective temperature (300 K) and luminosity (21%), and a slightly lower metallicity. On the other hand, the asteroseismic parameters indicate a significantly less dense star; this discrepancy reinforces the importance of continuing studies of the star.
Acknowledgements
J.B. acknowledges support through the ANR project Siroco.
References
- Appourchaux, T. 2004, A&A, 428, 1039 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Appourchaux, T., Andersen, B., & Sekii, T. 2002, In: Proc. SOHO 11 Symposium on From Solar Min to Max: Half a Solar Cycle with SOHO, ESA SP, 508, 47 (In the text)
- Appourchaux, T., Berthomieu, G., Michel, E., et al. 2006, ESA SP, 1306, 429 [NASA ADS] (In the text)
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [CrossRef] [EDP Sciences] (In the text)
- Barban, C., Deheuvels, S., Baudin, F., et al. 2009, A&A, 506, 51 [CrossRef] [EDP Sciences] (In the text)
- Baudin, F., et al. 2009, Science, Submitted (In the text)
- Bruntt, H. 2009, A&A, 506, 235 [CrossRef] [EDP Sciences] (In the text)
- Cutispoto, G., Pastori, L., Pasquini, L., et al. 2002, A&A, 384, 491 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- García, R. A. Régulo, C., Samadi, R., et al. 2009, A&A, 506, 41 [CrossRef] [EDP Sciences] (In the text)
- Gillon, M., & Magain, P. 2006, A&A, 448, 341 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Harvey, J. 1985, Future Missions in Solar, Heliospheric and Space Plasma Physics, 199 (In the text)
- Holdschneider, M., Kronland-Martinet, R., Morlet, J., et al. 1989, A real time algorithm for the Signal Analysis with the help of the wavelet transform, in Wavelets, ed. J. M. Combes, et al. (Berlin: Springer-Verlag), 286 (In the text)
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jacoutot, L., Kosovichev, A. G., Wray, A., et al. 2008, ApJ, 684, L51 [NASA ADS] [CrossRef] (In the text)
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] (In the text)
- Kovtyukh, V. V., Soubiran, C., & Belik, S. I. 2004, A&A, 427, 933 [CrossRef] [EDP Sciences] (In the text)
- Michel, E., Baglin, A., Auvergne, M., et al. 2008, Science, 322, 558 [NASA ADS] [CrossRef] (In the text)
- Michel, É., Samadi, R., Baudin, F., et al. 2009, A&A, 495, 979 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Monteiro, M. J. P. F. G., & Thompson, M. J. 2005, MNRAS, 361, 1187 [NASA ADS] [CrossRef] (In the text)
- Mosser, B., Bouchy, F., Martic, M., et al. 2008, A&A, 478, 197 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mosser, B., Baudin, F., Lanza, A. F., et al. 2009, A&A, 506, 245 [CrossRef] [EDP Sciences] (In the text)
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Provost, J., Mosser, B., & Berthomieu, G. 1993, A&A, 274, 595 [NASA ADS] (In the text)
- Roxburgh, I. W. 2009, A&A, 506, 435 [CrossRef] [EDP Sciences] (In the text)
- Roxburgh, I. W., & Vorontsov, S. V. 2006, MNRAS, 369, 1491 [NASA ADS] [CrossRef] (In the text)
- Samadi, R., Georgobiani, D., Trampedach, R., et al. 2007, A&A, 463, 297 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Samadi, R., Ludwig, H.-G., Belkacem, K., Goupil, M. J., & Dupret, M.-A. 2009, A&A, submitted (In the text)
Footnotes
- ... oscillations
![[*]](/icons/foot_motif.png)
- The CoRoT space mission, launched on 2006 December 27, was developed and is operated by the CNES, with participation of the Science Programs of ESA, ESAs RSSD, Austria, Belgium, Brazil, Germany and Spain.
All Tables
Table 1: Primary parameters of HD 175726.
Table 2: Parameters of the low-frequency fit.
Table 3: Mean power densities.
Table 4: Highest peaks.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11917f1.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg28.png) |
Figure 1: Level-2 light curve of HD 175726. The maximum variations are typically 1% peak-to-peak. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f2.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg29.png) |
Figure 2: Power spectrum of the window. Side lobes occur at the harmonics of the orbital frequency, modulated by the diurnal frequency. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11917f3.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg34.png) |
Figure 3: Sample of the time series, with the original data (dotted line) and the corrected data based on an interpolated time series for filling the gaps (solid line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm]{11917f4.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg35.png) |
Figure 4: Power density spectra of the corrected time series (light grey line), of the low-frequency interpolation (black line) and, with an adapted scale, of the window (dark grey line). Note the axes use logarithmic scale. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f5.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg36.png) |
Figure 5:
Zoom on the spectrum at low frequency (dashed line: oversampled fast Fourier transform). The signature of the rotation peaks at 2.80 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f6.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg39.png) |
Figure 6:
Power density spectrum on log-scale axes.
The peaks around 2.8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f7.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg46.png) |
Figure 7:
Smoothed power spectrum (with an apodized 200- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f8.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg47.png) |
Figure 8:
Smoothed power density spectrum (with a 2- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11917f9.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg58.png) |
Figure 9: Autocorrelation of the time series, calculated as the spectrum of the spectrum filtered with a cosine window centered on 2.0 mHz and with 0.8 mHz half-width, normalized to 1 at maximum. The dotted horizontal line indicates the mean noise level, derived from the autocorrelation of a pure noise spectrum. The grey region delimits the frequency range where the mean large separation is searched for. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11917f10.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg61.png) |
Figure 10: Variation of the large separation with frequency, derived from the autocorrelation. The power spectrum was first windowed with a 0.35 mHz-half width cosine filter, as indicated in the lower-right corner. The sampling of the curve corresponds crudely to the mean large separation. The size of the dots is representative of the amplitude of the correlated signal. Error bars derived from simulations are overplotted: total error is given in black, whereas the grey bar corresponds to the contribution of the internal error. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f11.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg65.png) |
Figure 11: Autocorrelation signal as a function of frequency, normalized to the mean signal due to a pure noise spectrum. Dashed lines indicate the level at which the H0 test is rejected. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f12.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg66.png) |
Figure 12: Échelle diagram of the smoothed spectrum, with indication of the possible ridges identified according to the varying large separations shown in Fig. 10. The grey squares indicate the location of the peaks with a height-to-background ratio greater than 3; the black squares indicate the location of the most confident peaks (above 95%) identified by the H0 test. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11917f13.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg71.png) |
Figure 13:
Rectified échelle diagram, folded according to the function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11917f14.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11917-09/Timg75.png) |
Figure 14: Bolometric amplitude per radial mode, calculated according to Michel et al. (2009). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




