| Issue |
A&A
Volume 506, Number 1, October IV 2009
The CoRoT space mission: early results
|
|
|---|---|---|
| Page(s) | 41 - 50 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200911910 | |
| Published online | 15 July 2009 | |
The CoRoT space mission: early results
Solar-like oscillations with low amplitude in the CoRoT target HD 181906![[*]](/icons/foot_motif.png)
R. A. García1 - C. Régulo2,3 - R. Samadi4 - J. Ballot5 - C. Barban4 - O. Benomar6 - W. J. Chaplin7 - P. Gaulme6 - T. Appourchaux6 - S. Mathur8 - B. Mosser4 - T. Toutain7 - G. A. Verner9 - M. Auvergne4 - A. Baglin4 - F. Baudin6 - P. Boumier6 - H. Bruntt4,10 - C. Catala4 - S. Deheuvels4 - Y. Elsworth7 - S. J. Jiménez-Reyes2 - E. Michel4 - F. Pérez Hernández2,3 - I. W. Roxburgh 9,4 - D. Salabert2
1 - Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot; CEA, IRFU, SAp, centre de Saclay, 91191 Gif-sur-Yvette, France
2 - Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
3 - Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
4 - LESIA, UMR8109, Université Pierre et Marie Curie, Université Denis Diderot, Obs. de Paris, 92195 Meudon Cedex, France
5 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 Av. Edouard Belin, 31400 Toulouse, France
6 - Institut d'Astrophysique Spatiale, UMR8617, Université Paris XI, Bâtiment 121, 91405 Orsay Cedex, France
7 - School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
8 - Indian Institute of Astrophysics, Koramangala, Bangalore 560034, India
9 - Astronomy Unit, Queen Mary, University of London Mile End Road, London E1 4NS, UK5
10 - Sydney Institute for Astronomy, School of Physics, The University of Sydney, NSW 2006, Australia
Received 20 February 2009 / Accepted 2 June 2009
Abstract
Context. The F8 star HD 181906 (effective temperature
![]() K) was observed for 156 days by the CoRoT satellite during the first long run in the direction of the galactic centre. Analysis of the data reveals a spectrum of solar-like acoustic oscillations. However, the faintness of the target (mv= 7.65) means the signal-to-noise (S/N) in the acoustic modes is quite low, and this low S/N leads to complications in the analysis.
K) was observed for 156 days by the CoRoT satellite during the first long run in the direction of the galactic centre. Analysis of the data reveals a spectrum of solar-like acoustic oscillations. However, the faintness of the target (mv= 7.65) means the signal-to-noise (S/N) in the acoustic modes is quite low, and this low S/N leads to complications in the analysis.
Aims. We extract global variables of the star, as well as key parameters of the p modes observed in the power spectrum of the lightcurve.
Methods. The power spectrum of the lightcurve, a wavelet transform and spot fitting were used to obtain the average rotation rate of the star and its inclination angle. Then, the autocorrelation of the power spectrum and the power spectrum of the power spectrum were used to properly determine the large separation. Finally, estimations of the mode parameters were done by maximizing the likelihood of a global fit, where several modes were fit simultaneously.
Results. We have been able to infer the mean surface rotation rate of the star (![]() 4
4 ![]() Hz) with indications of the presence of surface differential rotation, the large separation of the p modes (
Hz) with indications of the presence of surface differential rotation, the large separation of the p modes (![]() 87
87 ![]() Hz), hence also the ``ridges'' corresponding to overtones of the acoustic modes.
Hz), hence also the ``ridges'' corresponding to overtones of the acoustic modes.
Key words: stars: individual: HD 181906 - stars: oscillations - methods: observational - methods: statistical
1 Introduction
Several solar-like oscillation stars have already been observed with CoRoT (García et al. 2008). One of them is HD 181906 (or HIP 95221), a faint F8 dwarf, with a magnitude mv=7.65, observed during the first long run looking in the galactic centre direction at the same time as HD 181420 (Barban et al. 2009). We report the first detailed seismic analysis of HD 181906 using CoRoT data. This star is probably a binary system as suggested by astrometric measurements (Frankowski et al. 2007; Makarov & Kaplan 2005) or high-resolution spectroscopy (Bruntt 2009). The new reduction of Hipparcos data by van Leeuwen (2007) provides a parallax
![]()
![]()
![]() (i.e. a distance d=68
(i.e. a distance d=68 ![]()
![]() ), which leads to an absolute magnitude of MV=3.49
), which leads to an absolute magnitude of MV=3.49 ![]() 0.13. Using BCV = -0.044
0.13. Using BCV = -0.044 ![]() 0.058 for the bolometric correction in the V band (Masana et al. 2006), we deduce the stellar luminosity L= 3.32
0.058 for the bolometric correction in the V band (Masana et al. 2006), we deduce the stellar luminosity L= 3.32 ![]()
![]() .
Very recently, Bruntt (2009) has derived global parameters for this star from high-resolution spectroscopy. He found a value of
.
Very recently, Bruntt (2009) has derived global parameters for this star from high-resolution spectroscopy. He found a value of
![]()
![]() 150 K which is in perfect agreement with the value he derived from 2MASS photometry (
150 K which is in perfect agreement with the value he derived from 2MASS photometry (
![]()
![]() 100 K). He also deduced a surface gravity
100 K). He also deduced a surface gravity
![]()
![]() 0.056 and a metallicity
0.056 and a metallicity
![]() = -0.11
= -0.11 ![]() 0.14. Using his observations as inputs for stellar modelling, he estimated a mass M=1.144
0.14. Using his observations as inputs for stellar modelling, he estimated a mass M=1.144 ![]()
![]() ,
a radius R = 1.392
,
a radius R = 1.392 ![]()
![]() and an age of 4.2
and an age of 4.2 ![]() 1.6 Gyr for this star. These values are used to approximate seismic quantities and are summarized in Table 1.
1.6 Gyr for this star. These values are used to approximate seismic quantities and are summarized in Table 1.
Table 1: Global parameters of HD 181906 used for this work.
We compared these values to those derived in previous works using differents techniques. This star is included in the Geneva-Copenhagen survey of the Solar neighbourhood (Nordström et al. 2004; revisited by Holmberg et al. 2007). This survey based mainly on Strömgren photometry, provides an effective temperature
![]()
![]() 91 K and metallicity
91 K and metallicity
![]()
![]() 0.10 dex. The age is also estimated to
2.7+0.3-0.4 Gyr and the mass to
0.10 dex. The age is also estimated to
2.7+0.3-0.4 Gyr and the mass to
![]() .
All of these values are in very good agreement with those of Bruntt (2009). By using V and 2MASS IR photometry, Masana et al. (2006) recover a slightly higher effective temperature of 6532
.
All of these values are in very good agreement with those of Bruntt (2009). By using V and 2MASS IR photometry, Masana et al. (2006) recover a slightly higher effective temperature of 6532 ![]() 66 K and provide an angular semi-diameter SD = 0.102
66 K and provide an angular semi-diameter SD = 0.102 ![]() 0.001 mas. Thus, using the new Hipparcos parallax, we estimated the stellar radius to 1.50
0.001 mas. Thus, using the new Hipparcos parallax, we estimated the stellar radius to 1.50 ![]()
![]()
![]() , which is consistent with Bruntt (2009).
, which is consistent with Bruntt (2009).
For the rotation velocity, Nordström et al. (2004) report a measurement based on earlier CORAVEL observations and estimate the rotation velocity
![]()
![]()
![]() .
However, according to Bruntt (2009), this value is overestimated because of the blend with a second star. By taking the presence of this second star into account,
.
However, according to Bruntt (2009), this value is overestimated because of the blend with a second star. By taking the presence of this second star into account, ![]() decreases to 10
decreases to 10 ![]()
![]() .
For consistency, we consider the latter.
.
For consistency, we consider the latter.
We first infer some expected pulsation properties in Sect. 2. After a description of the CoRoT observations (Sect. 3), we derive the surface rotation of the star (Sect. 4), we then determine the region where the p modes are (Sect. 5), and finally explain how to take the convective background into account (Sect. 6). We finish by analysing the p-mode spectrum (Sect. 7) and extracting the p-mode parameters (Sect. 8).
2 Estimated oscillation properties
Using the parameters of HD 181906, summarized in the introduction, we were able to obtain approximate values of some global seismic parameters using scaling laws. The large separation,
![]() ,
can be estimated from the mass and the radius as follows (Kjeldsen & Bedding 1995):
,
can be estimated from the mass and the radius as follows (Kjeldsen & Bedding 1995):
 |
(1) |
A value of
The frequency of the maximum of the p modes scales as the cut-off frequency (Kjeldsen & Bedding 1995). This law has been verified lately using spectrometric data (Bedding & Kjeldsen 2003). Therefore we can express
![]() as:
as:
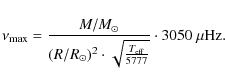 |
(2) |
We obtain
Finally, the maximum expected amplitude (an estimate of the intrinsic mode amplitude in terms of bolometric intensity fluctuations) can be deduced from Samadi et al. (2007):
 |
(3) |
where we changed the solar value of
3 CoRoT observations
We collected 156.6 days of continuous data - from 2007 May 11 until 2007 October 15 - with an overall duty cycle of 89.3%. Most of the gaps (each of a few minutes duration) are due from data loss during the crossings of the South Atlantic Anomaly (see for a detailed explanation: Auvergne et al. 2009). These gaps were linearly interpolated in the lightcurve to avoid putting zeros. We verified that this interpolation does not introduce any spurious frequencies into the Fourier domain. The original 1-s cadence raw data were corrected and calibrated into level-2 (or N2) data following the methods described in Samadi et al. (2006). The N2 lightcurve is sampled on a regular grid in the heliocentric frame with a cadence of 32 s. Then we removed a low-frequency trend due to the aging of the CCD (Auvergne et al. 2009), and finally we removed some outlier points (0.013%). The resulting lightcurve shows a small modulation during the first 60 days (see Fig. 1) and then a very flat behavior. At this point, it is impossible to disentangle a real modulation of the star from an instrumental effect. A second modulation - around 3 days - is also visible and could be related to the surface rotation due to the signature of magnetic activity on the surface of the star.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg1N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg47.png) |
Figure 1: N2-lightcurve (in ppm) corrected for the ageing of the CCD and interpolated onto a regular grid in the heliocentric frame. |
| Open with DEXTER | |
To compute the power spectrum density (PSD) we used a standard fast Fourier transform algorithm and normalized it as the so-called one-sided power spectral density (Press et al. 1992). The resulting PSD is shown in Fig. 2. In the PSD, several peaks rise above the general trend dominated by the photon noise from the Nyquist frequency down to approximately 100 ![]() Hz and by the convective noise from this frequency until
Hz and by the convective noise from this frequency until ![]() 10
10 ![]() Hz (Michel et al. 2008a). Below this, the spectrum is dominated by two peaks, at around 4 and 8
Hz (Michel et al. 2008a). Below this, the spectrum is dominated by two peaks, at around 4 and 8 ![]() Hz, which could be the signature of the surface rotation of the star - already seen in its lightcurve - as well as its first harmonic (Fig. 2). We will discuss this rotation rate in detail in the next section. The signature of the CoRoT orbital periodicity produces a peak at 161.7
Hz, which could be the signature of the surface rotation of the star - already seen in its lightcurve - as well as its first harmonic (Fig. 2). We will discuss this rotation rate in detail in the next section. The signature of the CoRoT orbital periodicity produces a peak at 161.7 ![]() Hz, together with several harmonics (Fig. 2).
Hz, together with several harmonics (Fig. 2).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11910fg2N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg48.png) |
Figure 2: Power spectrum density of the full 156-day N2-lightcurve shown in Fig. 1. The two red-dotted vertical lines show the lowest significant peak and the first harmonic that could be the signature of the surface rotation of the star. The five blue-dotted vertical lines indicate the first harmonics of the orbital period of the satellite. |
| Open with DEXTER | |
The combination of a lower-than-expected signal-to-noise ratio of the oscillation amplitudes (Michel et al. 2008a) with the faintness of the target (mv = 7.65) means that the p-mode hump is not clearly visible in Fig. 2, but there is a small excess in power around ![]() 2000
2000 ![]() Hz. A more sophisticated treatment is necessary to clearly unveil the acoustic spectrum of this star.
Hz. A more sophisticated treatment is necessary to clearly unveil the acoustic spectrum of this star.
4 Surface rotation
As already mentioned in previous sections, the lightcurve of HD 181906 shows a periodic modulation of about 3 days that produces two peaks in the PSD. It is interesting to analyse this periodicity in a more detailed way.
We started by calculating a time-period diagram using wavelets (Torrence & Compo 1998). The advantage of this technique relies on our using a wave, the Morlet wavelet - a sine wave modulated by a Gaussian (Goupillaud et al. 1984) - which has a finite duration and a specific frequency. By changing the frequency of this wavelet and sliding it along our time series, we calculated the correlation between the wavelet and the data. That enabled us to compute the wavelet power spectrum (see Fig. 3). Most of the power is concentrated along a horizontal line centred at ![]() 2.8 days. This signal appears to be stronger during the first half of the run than during the second period.
2.8 days. This signal appears to be stronger during the first half of the run than during the second period.
| |
Figure 3: Left: wavelet power spectrum for HD 181906 at low frequency. Right: global wavelet power spectrum where the dotted-line represents the 95% confidence level. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg4N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg50.png) |
Figure 4: Zoom on the spectrum at low frequency. The power spectrum density has been computed using the total length of data. |
| Open with DEXTER | |
With the global wavelet power spectrum defined as the horizontal average of the time-period diagram (see Fig. 3 (right)), we observe that most of the power - more than 99% - is concentrated in this main periodicity at 2.81 days. A smaller peak is also visible at 1.41 days but containing much less power. This method (successfully tested with numerical simulations and with solar data from the GOLF instrument, Mathur et al. 2008) allows us to disentangle between the peak corresponding to the main periodicity and that of the harmonic by the simple visual inspection of the PSD where 2 peaks of similar characteristics stand at 4.04 and 8.2 ![]() Hz.
Hz.
A closer inspection of the rotation period,
![]() ,
in the PSD reveals that it is composed of a double structure, with a strong peak centred at 4
,
in the PSD reveals that it is composed of a double structure, with a strong peak centred at 4 ![]() Hz - 2.9 days (Fig. 4) - and a smaller one at 4.45
Hz - 2.9 days (Fig. 4) - and a smaller one at 4.45 ![]() Hz (2.6 days). Having these two peaks instead of just one may suggest the presence of spots at different latitudes with a differential surface rotation. The spot modeling done by Mosser et al. (2009a) states this point explicitly, indicating two rotation periods associated with a clear gradient of the rotational velocity as a function of spot latitude. Another less probable explanation is the presence of a hot star in the background of HD 181906, as suggested by Bruntt (2009) who proposed a detailed analysis of the fundamental parameters of CoRoT asteroseismic targets based on high-resolution spectrometric measurements.
Hz (2.6 days). Having these two peaks instead of just one may suggest the presence of spots at different latitudes with a differential surface rotation. The spot modeling done by Mosser et al. (2009a) states this point explicitly, indicating two rotation periods associated with a clear gradient of the rotational velocity as a function of spot latitude. Another less probable explanation is the presence of a hot star in the background of HD 181906, as suggested by Bruntt (2009) who proposed a detailed analysis of the fundamental parameters of CoRoT asteroseismic targets based on high-resolution spectrometric measurements.
If the 156-day time series is divided into two segments of 78 days or into three independent 52-day subsets, a slightly different low-frequency structure is observed each time, as can be seen in Figs. 5 and 6.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg5N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg52.png) |
Figure 5: Zoom on the spectrum at low frequency. In black the Fourier spectrum of the first 78 days of data. In blue the spectrum of the last 78 days. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg6N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg53.png) |
Figure 6: Zoom on the spectrum at low frequency. In black the Fourier spectrum of the first 52 days of data. In red the spectrum of the 52 intermediate days of data, and in green the spectrum of the last 52 days. |
| Open with DEXTER | |
In Fig. 5, we calculated the PSD of the first 78 days and the PSD of the last 78 days. In Fig. 6, we computed the PSD of the first 52 days, the next 52 days, and the last 52-day segment. Details of the prominent peaks that appear in each of these spectra are summarized in Table 2. In this table, we listed the frequencies (in ![]() Hz) and the respective rotational periods (in days) of the peaks that appear at low frequency in the Fourier spectrum of the full-length series and the smaller subseries considered in the analysis. The peaks are located at rotational periods in the range from 2.3 to 3.1 days. The different behaviour of the peaks (in frequency and amplitude) - behaviour that depends on the observed period - suggests that they could be the signatures of differential rotation on the surface of the star, and not the rotation period of the secondary star in the binary system (which would be expected to produce a stable peak in all the considered periods). Therefore, HD 181906 shows a slightly larger differential rotation than the Sun, but with the same order of magnitude. A more detailed analysis of this behaviour will be the topic of a future work.
Hz) and the respective rotational periods (in days) of the peaks that appear at low frequency in the Fourier spectrum of the full-length series and the smaller subseries considered in the analysis. The peaks are located at rotational periods in the range from 2.3 to 3.1 days. The different behaviour of the peaks (in frequency and amplitude) - behaviour that depends on the observed period - suggests that they could be the signatures of differential rotation on the surface of the star, and not the rotation period of the secondary star in the binary system (which would be expected to produce a stable peak in all the considered periods). Therefore, HD 181906 shows a slightly larger differential rotation than the Sun, but with the same order of magnitude. A more detailed analysis of this behaviour will be the topic of a future work.
Table 2: Length of spectra and corresponding rotational periods.
4.1 Constraining the inclination angle
The angle of inclination of HD 181906 can be inferred from the measured value of
![]() and the surface rotation that we have just derived:
and the surface rotation that we have just derived:
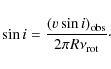 |
(4) |
Using a rotation frequency of
5 Finding the p-mode region
To find the region where the p modes are centred, we computed the power spectrum of the power spectrum (PSPS) (or the autocorrelation of the PSD) in the region determined by the scaling laws (see Fig. 7 and a more detailed explanation in Sect. 7.2).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg7N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg62.png) |
Figure 7:
Power spectrum of the power spectrum (PSPS) normalized by its standard deviation in the region between 1400 and 2100 |
| Open with DEXTER | |
This revealed a strong peak at half the large separation,
![]() ,
with the location of the peak implying
,
with the location of the peak implying
![]()
![]() Hz, which is close to the upper limit of the value estimated in Sect. 2, using existing, non-seismic data on the star. To narrow down the range more carefully, we then performed the following procedure.
Hz, which is close to the upper limit of the value estimated in Sect. 2, using existing, non-seismic data on the star. To narrow down the range more carefully, we then performed the following procedure.
We moved a 300-![]() Hz-wide window through the frequency range of interest and computed the PSPS at each location. The window was shifted in steps of
Hz-wide window through the frequency range of interest and computed the PSPS at each location. The window was shifted in steps of
![]() .
We measured the height of the peak in each PSPS at
.
We measured the height of the peak in each PSPS at
![]() relative to the local background level. The noise distribution in each PSPS follows
relative to the local background level. The noise distribution in each PSPS follows ![]() two-degrees-of-freedom statistics; given this known distribution, it is possible to calculate a false-alarm probability for the
two-degrees-of-freedom statistics; given this known distribution, it is possible to calculate a false-alarm probability for the
![]() peak to appear by chance (as part of the background) anywhere in the PSPS. We calculated the level corresponding to a 5%
of probability of appearing by chance (Chaplin et al. 2002).
peak to appear by chance (as part of the background) anywhere in the PSPS. We calculated the level corresponding to a 5%
of probability of appearing by chance (Chaplin et al. 2002).
The maximum relative height of the
![]() peak (i.e., the height divided by the measured background in the PSPS) is plotted in Fig. 8. We find here that the p-mode power is prominent between 1400 and 2100
peak (i.e., the height divided by the measured background in the PSPS) is plotted in Fig. 8. We find here that the p-mode power is prominent between 1400 and 2100 ![]() Hz.
Hz.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg8N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg67.png) |
Figure 8:
Maximum of the PSPS in a region around the expected half-large separation computed in 300 |
| Open with DEXTER | |
6 Background fitting
To estimate the non-p-mode background, we fit the following three-component model to those parts of the PSD where the observed p-mode power is insignificant (
![]() ):
):
There are two power-law components in the summation: a component to represent the significant power at very low frequencies from surface activity and a component to represent power from surface granulation. Both power-law components are modeled in terms of three parameters: a power spectral density A, a characteristic timescale B, and a power-law index C. The third component in Eq. (5), D, models the contribution from shot noise.
Rather than fit the raw power spectrum, we fitted a smoothed spectrum generated by applying an ![]() -bin-wide boxcar, taking only the independent averages. With
-bin-wide boxcar, taking only the independent averages. With
![]() ,
independent
,
independent ![]() -bin averages show normally-distributed scatter about the (underlying) limit spectrum we seek to estimate from the fit. A standard least-squares fitting was therefore applied, with weights fixed by the uncertainties on each independent
-bin averages show normally-distributed scatter about the (underlying) limit spectrum we seek to estimate from the fit. A standard least-squares fitting was therefore applied, with weights fixed by the uncertainties on each independent ![]() -bin average. These uncertainties were each given by
-bin average. These uncertainties were each given by
![]() ,
where s is the standard deviation of the
,
where s is the standard deviation of the ![]() contributing power values.
contributing power values.
The alternative approach is to fit the raw spectrum by maximizing a likelihood function commensurate with the ![]() two-degrees-of-freedom statistics. It turns out that the smoothed spectrum may also be fitted by applying the same maximum likelihood estimator (as shown by Appourchaux 2004). These approaches are, however, more sensitive to the choice of initial
first-guess parameters than is the least-squares fitting approach applied here, and can as such be prone to poor convergence.
two-degrees-of-freedom statistics. It turns out that the smoothed spectrum may also be fitted by applying the same maximum likelihood estimator (as shown by Appourchaux 2004). These approaches are, however, more sensitive to the choice of initial
first-guess parameters than is the least-squares fitting approach applied here, and can as such be prone to poor convergence.
There are a total of seven free parameters defining the background model in Eq. (5). We did not, however, fit them all simultaneously: some parameters were fixed, as we are now explaining. We assumed power in the very low-frequency activity component arises predominantly from the exponential decay of active regions and plage. This decay implies a limiting power density spectrum that is Lorentzian, so we fixed the activity-component index to a value C1=2 during fitting.
Exercises performed with the asteroFLAG artificial asteroseismology data (Chaplin et al. 2008) showed that attempts to fit A1 and B1 simultaneously with the other parameters could lead to instability in the procedure and to poor convergence. We found that we could stabilize the fitting by fixing A1 at the value of the power spectral density of the first element of the averaged spectrum, leaving B1 as the only parameter of the activity component to be fitted. This approach does mean that some care is needed in interpreting the best-fitting value of B1, since the value for A1 can be affected by the appearence in the power spectrum of narrow-band features arising from rotational modulation, which are not modeled in Eq. (5). The aforementioned approach to the fitting does, however, give a good representation of the power from the active-region decay that leaks into the frequency region where the granulation is important, which in turn means we can in principle have more confidence in the accuracy of the best-fitting granulation parameters.
7 The p-mode spectrum
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg9N.eps}\vspace*{3mm}
\includegraphics[width=8.4cm,clip]{11910f10N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg73.png) |
Figure 9:
Power spectrum density of the full length lightcurve smoothed by a boxcar of 70 points ( top). The continuous green curve is the background fitted using the method explained in Sect. 6. The bottom panel shows a closer region of the p-mode band between 1000 and 3000 |
| Open with DEXTER | |
Figure 9 plots the PSD of the full-length lightcurve smoothed with a boxcar of 70 points (![]()
![]() Hz). A clear excess of power is observed, relative to the best-fitting background model, in the region where the p-mode excess was detected (see Sect. 5). To visually enhance the excess we also show a heavily smoothed spectrum computed by applying a 5000-point boxcar
(
Hz). A clear excess of power is observed, relative to the best-fitting background model, in the region where the p-mode excess was detected (see Sect. 5). To visually enhance the excess we also show a heavily smoothed spectrum computed by applying a 5000-point boxcar
(![]()
![]() Hz) to the raw spectrum.
Hz) to the raw spectrum.
Figure 10 shows the Echelle diagram (Grec et al. 1983) of the 70-point-boxcar smoothed PSD. The diagram covers the frequency region from 792.5 to 3000 ![]() Hz, with each horizontal strip covering 87.5
Hz, with each horizontal strip covering 87.5 ![]() Hz of the spectrum (see Fig. 7). Two ridges appear in the diagram, corresponding to the odd and even modes. Inspection of the diagram shows that it is not possible to visually distinguish between the two ridges, making the angular-degree tagging uncertain.
Hz of the spectrum (see Fig. 7). Two ridges appear in the diagram, corresponding to the odd and even modes. Inspection of the diagram shows that it is not possible to visually distinguish between the two ridges, making the angular-degree tagging uncertain.
7.1 Global amplitude
The procedure for measuring the mode amplitudes begins by averaging the power spectral density in independent frequency slices of
![]() ,
where q=1 or 2, and
,
where q=1 or 2, and ![]() is the estimated large frequency spacing of the acoustic mode spectrum. The fitted background is then subtracted. The resulting residuals in power spectral density will be greater than zero over ranges occupied by significant mode power.
is the estimated large frequency spacing of the acoustic mode spectrum. The fitted background is then subtracted. The resulting residuals in power spectral density will be greater than zero over ranges occupied by significant mode power.
Re-calibration of the residual averages then allows for an estimate of the equivalent l=0 mode amplitudes (Kjeldsen et al. 2008). To re-calibrate, one must (i) multiply by
![]() ,
to give the average power across frequency intervals of this length; and (ii) normalize to power per l=0 mode, by dividing by
,
to give the average power across frequency intervals of this length; and (ii) normalize to power per l=0 mode, by dividing by
![]() ,
where
,
where
![]() is the combined visibility of the l=0, 1, 2 and 3 modes (again, see Kjeldsen et al. 2008). In practice, we ran a boxcar of width
is the combined visibility of the l=0, 1, 2 and 3 modes (again, see Kjeldsen et al. 2008). In practice, we ran a boxcar of width
![]() through the spectrum in order to better estimate the maximum power (one could miss the true maximum if the independent slices cut through pairs of modes). The measured maximum mode rms amplitude was
through the spectrum in order to better estimate the maximum power (one could miss the true maximum if the independent slices cut through pairs of modes). The measured maximum mode rms amplitude was
![]()
![]()
![]() .
.
We also applied a different approach to estimating the amplitudes. This approach assumed that the envelope of excess power due to the modes could be modeled by a Gaussian function. We fitted a Gaussian profile to the recalibrated residual averages (see above), and we estimated
![]()
![]()
![]() from the best-fitting maximum. The location in frequency of maximum also allowed us to estimate the frequency of maximum power, which was
from the best-fitting maximum. The location in frequency of maximum also allowed us to estimate the frequency of maximum power, which was
![]()
![]()
![]() .
.
To convert these instrumental values into maximum intrinsic bolometric amplitudes per radial mode,
![]() ,
we considered the instrumental response functions for CoRoT, as presented by
(Michel et al. 2009). We then found that
,
we considered the instrumental response functions for CoRoT, as presented by
(Michel et al. 2009). We then found that
![]() = 3.26
= 3.26 ![]() 0.42 ppm (Michel et al. 2008a). This amplitude is about one third less than the expected value deduced from the scaling laws. Such a deficit is also seen for the other hot, solar-like oscillators observed by CoRoT (Michel et al. 2008a). HD 181906 is not significantly undermetallic, so it is hard to appeal to a metallicity effect as a possible explanation (e.g., as in Mosser et al. 2008). However, we note that this star - like the other solar-like CoRoT targets HD 49933, HD 175726, and HD 181420 - rotates significantly faster than the Sun (10 times for this target) and exhibits clear magnetic activity (cf. Sect. 4). It could be an indication that the magnetic activity plays a role in suppressing the p-mode amplitudes by changing the surface convection and thus modifying the efficiency of p-mode excitation processes. Some 3D compressible radiative magnetohydrodynamics simulations (Jacoutot et al. 2008) have shown these effects.
0.42 ppm (Michel et al. 2008a). This amplitude is about one third less than the expected value deduced from the scaling laws. Such a deficit is also seen for the other hot, solar-like oscillators observed by CoRoT (Michel et al. 2008a). HD 181906 is not significantly undermetallic, so it is hard to appeal to a metallicity effect as a possible explanation (e.g., as in Mosser et al. 2008). However, we note that this star - like the other solar-like CoRoT targets HD 49933, HD 175726, and HD 181420 - rotates significantly faster than the Sun (10 times for this target) and exhibits clear magnetic activity (cf. Sect. 4). It could be an indication that the magnetic activity plays a role in suppressing the p-mode amplitudes by changing the surface convection and thus modifying the efficiency of p-mode excitation processes. Some 3D compressible radiative magnetohydrodynamics simulations (Jacoutot et al. 2008) have shown these effects.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910f11N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg86.png) |
Figure 10:
Echelle diagram of the full PSD smoothed by a 70 point boxcar starting at a frequency of 792.5 |
| Open with DEXTER | |
There is another possibility that the discrepancy could be explained by a blending effect. Bruntt (2009) shows evidence in the spectrum of HD 181906 for the superimposition of a second spectrum, which could be a companion or a star in the background field. If this is the case, the relative amplitudes of modes could easily be underestimated by a factor of 1.5, making them compatible with the observations.
Table 3: Comparison of published global parameters for different F stars.
7.2 The mean large separation
Different methods have been used for extracting the large separation of the p-mode spectrum. A good signature of this large separation can be derived from the PSPS, or from the autocorrelation of the power spectrum, computed in the region where the excess of power has been detected (see Fig. 9).
Taking the frequency interval where the p-mode excess has been found (see Sect. 5), i.e. from 1400 to 2100 ![]() Hz, we find that the PSPS is dominated by a peak at 6.35 h (see Fig. 7), which corresponds to half the large separation of 43.75
Hz, we find that the PSPS is dominated by a peak at 6.35 h (see Fig. 7), which corresponds to half the large separation of 43.75 ![]() Hz. Indeed, the main periodicity we found is not the large separation itself but the distance between peaks of even and odd degree. Therefore, the large separation is
Hz. Indeed, the main periodicity we found is not the large separation itself but the distance between peaks of even and odd degree. Therefore, the large separation is
![]() = 87.5
= 87.5 ![]() 2.6
2.6 ![]() Hz (see Fig. 7). Depending on the range in frequency used to look for the large separation, different groups have found slightly different values. For example, if we reduce the search range to 1400 to 2000
Hz (see Fig. 7). Depending on the range in frequency used to look for the large separation, different groups have found slightly different values. For example, if we reduce the search range to 1400 to 2000 ![]() Hz, the large separation is reduced to a value of 85.7
Hz, the large separation is reduced to a value of 85.7 ![]() 2.6
2.6 ![]() Hz.
Hz.
Another powerful way to estimate the value of the large separation is to build the so-called collapsogram (Korzennik 2008). The first step consists in calculating all the Echelle diagrams for a frequency range in which we expect the large separation (e.g. 60-100 ![]() Hz). The second step then consists in collapsing the vertical dimension of each Echelle diagram. In the last step the collapsed diagrams are stacked vertically, to yield the final collapsogram.
Hz). The second step then consists in collapsing the vertical dimension of each Echelle diagram. In the last step the collapsed diagrams are stacked vertically, to yield the final collapsogram.
The collapsogram presents two advantages. First, it allows us to explore on a single diagram a wide range of possible values of the large separation. Secondly, it increases the visibility of the separation compared to that seen in the Echelle diagram (although it does rely on the separation being almost uniform over the frequency range used to construct the collapsogram).
In Fig. 11, we present the collapsogram of the smoothed power spectrum obtained with a weighted moving average over 11 bins. The presence of the two mode ridges is seen, with the large
separation indicated as being between 85 to 90 ![]() Hz. Note that we have considered only the power spectrum in the frequency range between 1300 and 2300
Hz. Note that we have considered only the power spectrum in the frequency range between 1300 and 2300 ![]() Hz to build the collapsogram.
Hz to build the collapsogram.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910f12N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg93.png) |
Figure 11:
Collapsogram of the smoothed power spectrum (11 bins) obtained by collapsing the power spectrum in the frequency range between 1280 and 2300 |
| Open with DEXTER | |
7.3 Comparison with other observed F stars
A comparison of published global parameters (and their associated error bars when available) from different F stars is presented in Table 3 where ![]() is the large spacing,
is the large spacing,
![]() is the frequency in the spectrum with the maximum power and
is the frequency in the spectrum with the maximum power and
![]() is the bolometric maximum amplitude per radial mode. In the case of Procyon, the bolometric amplitude is obtained from the velocity measurements following Arentoft et al. (2008). The stars HD 181906, HD 49933, HD 181420 and HD 175726 are observed by CoRoT. However, the length of observations is not the same for all of them, being 156 days for HD 181906 (the star analysed in this paper) and HD 181420 (Barban et al. 2009), 60 days for HD 49933 (Appourchaux et al. 2008) and only 27 days for HD 175726 (Mosser et al. 2009b). The data from Procyon correspond to velocity measurements obtained during 26 days for a multisite campaign involving 11 telescopes (Arentoft et al. 2008).
is the bolometric maximum amplitude per radial mode. In the case of Procyon, the bolometric amplitude is obtained from the velocity measurements following Arentoft et al. (2008). The stars HD 181906, HD 49933, HD 181420 and HD 175726 are observed by CoRoT. However, the length of observations is not the same for all of them, being 156 days for HD 181906 (the star analysed in this paper) and HD 181420 (Barban et al. 2009), 60 days for HD 49933 (Appourchaux et al. 2008) and only 27 days for HD 175726 (Mosser et al. 2009b). The data from Procyon correspond to velocity measurements obtained during 26 days for a multisite campaign involving 11 telescopes (Arentoft et al. 2008).
The data in Table 3 were obtained mainly from the above-mentioned papers, except the bolometric maximum amplitude per radial mode (
![]() )
for the 3 CoRoT stars mentioned first that were obtained from Michel et al. (2008a). For Procyon, the
)
for the 3 CoRoT stars mentioned first that were obtained from Michel et al. (2008a). For Procyon, the
![]() ,
,
![]() ,
and [Fe/H] were obtained from Allende Prieto et al. (2002). The value of the maximum amplitude in the spectrum is a translation from cm/s to ppm done by Arentoft et al. (2008), a value that agrees well with the one obtained by Bruntt et al. (2005) using white-light photometric data from the WIRE satellite.
,
and [Fe/H] were obtained from Allende Prieto et al. (2002). The value of the maximum amplitude in the spectrum is a translation from cm/s to ppm done by Arentoft et al. (2008), a value that agrees well with the one obtained by Bruntt et al. (2005) using white-light photometric data from the WIRE satellite.
8 Extracting individual p-mode characteristics
Although fitting low-degree p-mode profiles in helioseismology and asteroseismology might appear very similar, the unknown stellar inclination angle makes the fitting of asteroseismic data much more difficult (see for example Appourchaux et al. 2008, for the case of the star HD 49933; or Gizon & Solanki 2003, for Monte-Carlo simulations with artificial p-mode profiles). It is not only the lower signal-to-noise ratio of the p-mode asteroseismic signal that makes the fitting difficult, but also the high correlation between the inclination and the rotational splitting (Ballot et al. 2006,2008). Because of that, the determination of these two parameters can be rather poor and will consequently affect the determination of the other parameters (frequencies, widths, heights, etc.). Therefore, instead of fitting each multiplet or pair of modes individually - as commonly done in helioseismology - we chose to perform a global fitting of all the multiplets above a given amplitude threshold around the maximum of the p-mode hump, assuming that the rotational splitting is independent of the frequency (see Appourchaux et al. 2008, for all the details). This type of global method was pioneered by Roca Cortés et al. (1999) using solar data. By doing so, the splitting and the inclination angle are better constrained, even though HD 181906 is then modeled as a rigidly rotating star. Each multiplet is described by five parameters: the central frequencies of the modes l=0,1,2, one line width (the same for all modes within a large separation), and one mode height. We assumed the same visibility ratio between angular degrees as the ones used in full-disk helioseismology and the visibilities between m-components given by Gizon & Solanki (2003).
Eight teams performed a global fitting of the HD 181906 data, seven of them using a maximum-likelihood minimization and one using a least square fitting over an averaged spectrum. All the teams did the fits for both scenarios (A and B) depending on the identification of the ridges as the odd or even modes.
Two teams decided to split the observations into four subseries and computed the joint power statistics (JPS, see Appendix A for a detailed explanation). The JPS is an alternative method that
contains the same underlying information as the average spectrum but with a different treatment of the noise. The rest of the teams worked on the full-resolution power spectrum. The number of overtones fitted was 5, 7, 9 and 16 overtones. Different strategies were also followed by each team to obtain the initial parameters for the fit. In particular, one team used the results from HD 49933 (Appourchaux et al. 2008) as a guideline since their PSDs look very similar and HD 49933 has a much better signal-to-noise ratio. Figure 12 shows the superposition of the PSD of HD 181906 and the one of HD 49933 - properly scaled in amplitude - and shifted by 17 ![]() Hz. Thus, the initial guesses were obtained directly from the fitted values of HD 49933. Another team repeated the fits 200 times for each scenario, adding scatter to the initial parameters in order to test the robustness of the fits and identify any correlation between the initial seed values and the fitted ones. As expected, the inclination angle was identified to be strongly correlated with the initial seed angle.
Hz. Thus, the initial guesses were obtained directly from the fitted values of HD 49933. Another team repeated the fits 200 times for each scenario, adding scatter to the initial parameters in order to test the robustness of the fits and identify any correlation between the initial seed values and the fitted ones. As expected, the inclination angle was identified to be strongly correlated with the initial seed angle.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910f13N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg94.png) |
Figure 12:
Smoothed power spectrum of HD 181906 (black curve) and smoothed and shifted by 17 |
| Open with DEXTER | |
The mode parameters were then extracted using different approaches based on the recipe developed by the data analysis team (DAT) and explained in Appourchaux et al. (2008). However, to have a more reliable characterization of the p-mode signal, given the low signal-to-noise ratio of the
observations, some more a-priori information needed to be introduced. To stabilize the fits and avoid systematic outliers, some of the fitting teams fixed some parameters to be equal over the range of considered overtones. For instance, without some a priori conditions, the minimization procedures failed to return reliable estimates at high frequency, fitting mostly spikes and overestimated heights. Tables 4 and 5 show the fitted mode frequencies obtained from the less constrained fit for both scenarios A and B, respectively, with the analysis performed on the power spectrum of the whole HD 181906 time series. The only condition applied to those fits is that the mode widths and mode heights were set to be uniform (the same for all the modes) over the fitted frequency range. In the central part of the p-mode hump, those frequency estimates are consistent within ![]() with the estimates returned using more constrained fits and different dataset lengths. In the low- and high-frequency ranges, the discrepancies are greater but still within
with the estimates returned using more constrained fits and different dataset lengths. In the low- and high-frequency ranges, the discrepancies are greater but still within ![]() .
Unfortunately, neither of the scenarios seems to be favored: for instance, the likelihood ratio test does not allow us to distinguish between the two possibilities, since the likelihood ratio is not greater than 5 (for the fits presented here).
.
Unfortunately, neither of the scenarios seems to be favored: for instance, the likelihood ratio test does not allow us to distinguish between the two possibilities, since the likelihood ratio is not greater than 5 (for the fits presented here).
Table 4:
HD 181906 frequencies (in ![]() Hz) for scenario A.
Hz) for scenario A.
Table 5:
HD 181906 frequencies (in ![]() Hz) for scenario B.
Hz) for scenario B.
Nevertheless, we can still obtain some global characteristics of HD 181906. On one hand, the fitted inclination angle, for both scenarios (around
![]()
![]()
![]() ), is very close to the one derived from the analysis of the low-frequency peak of the PSD (see Sect. 4) when a
), is very close to the one derived from the analysis of the low-frequency peak of the PSD (see Sect. 4) when a
![]()
![]()
![]() is considered, but quite far from the
is considered, but quite far from the
![]() obtained considering
obtained considering
![]() .
On the other hand, the extracted rotational splitting (5.8 and 6.1
.
On the other hand, the extracted rotational splitting (5.8 and 6.1 ![]() 0.14
0.14 ![]() Hz respectively for A and B scenarios) is overestimated compared to the surface rotation rate (see Sect. 4). This could come from an increase in the rotation rate of the stellar interior or a biased estimation from the a-priori conditions applied to the fit (a common height and width for all the fitted modes). These results show, once again, the strong correlation between these two parameters and the necessity of having an external good determination of the inclination angle or the rotation of the star to be able to tell the difference between the possible solutions.
Hz respectively for A and B scenarios) is overestimated compared to the surface rotation rate (see Sect. 4). This could come from an increase in the rotation rate of the stellar interior or a biased estimation from the a-priori conditions applied to the fit (a common height and width for all the fitted modes). These results show, once again, the strong correlation between these two parameters and the necessity of having an external good determination of the inclination angle or the rotation of the star to be able to tell the difference between the possible solutions.
Another parameter - the global line width - was found to be rather small (1.25 -0.3/+0.4 and 1.28 -04/+0.6 ![]() Hz for scenarios A and B, respectively), which is probably a consequence of the low SNR that could bias this estimate when we apply our peak-bagging codes: the low SNR means the
modes will appear ``spikier'' than they really are (we lose the Lorentzian tails in the background noise), meaning we will be biased to fitting small line widths. We expect that the autocorrelation of the power spectrum will have better SNR than seen in individual modes, hence we look there for the features associated with mode line width. The features in it are quite wide, implying that the line widths are large and probably in line with what we saw for HD 49933 (see Fig. 12). Indeed, the widths of the modes in both stars, around the maximum of the p-mode spectrum, seem to be similar, which favors shorter mode lifetimes than in the Sun.
Hz for scenarios A and B, respectively), which is probably a consequence of the low SNR that could bias this estimate when we apply our peak-bagging codes: the low SNR means the
modes will appear ``spikier'' than they really are (we lose the Lorentzian tails in the background noise), meaning we will be biased to fitting small line widths. We expect that the autocorrelation of the power spectrum will have better SNR than seen in individual modes, hence we look there for the features associated with mode line width. The features in it are quite wide, implying that the line widths are large and probably in line with what we saw for HD 49933 (see Fig. 12). Indeed, the widths of the modes in both stars, around the maximum of the p-mode spectrum, seem to be similar, which favors shorter mode lifetimes than in the Sun.
Finally, we would like to emphasize that the combination of a low SNR, a possible small inclination angle of the star (close to
![]() ), and large-mode line widths produce similar Lorentzian
profiles for the modes l=0, 2, and 1 (Ballot et al. 2004). This effect could contribute to explaining why we obtain very similar fitting results in both scenarios. More work will be necessary to obtain more reliable individual p-mode parameters.
), and large-mode line widths produce similar Lorentzian
profiles for the modes l=0, 2, and 1 (Ballot et al. 2004). This effect could contribute to explaining why we obtain very similar fitting results in both scenarios. More work will be necessary to obtain more reliable individual p-mode parameters.
9 Conclusion and perspectives
In this paper we have shown the first seismic analysis of HD 181906 (HIP 95221), a faint CoRoT target (mv = 7.65) that was observed continuously during 156.6 days in 2007. The surface rotation of the star has been inferred by analysing the very low-frequency part of the power spectrum. A rotation rate of 2.9 days (4 ![]() Hz) was established. The presence of a second peak close to the previous one in the power spectrum and produced during a different period of time, was interpreted as the signature of magnetic structures on the stellar surface at different latitudes, so it was deduced that this star could have a slightly higher differential rotation than the Sun. Coupling this rotation rate with the previous result of the
Hz) was established. The presence of a second peak close to the previous one in the power spectrum and produced during a different period of time, was interpreted as the signature of magnetic structures on the stellar surface at different latitudes, so it was deduced that this star could have a slightly higher differential rotation than the Sun. Coupling this rotation rate with the previous result of the
![]()
![]() 16
16 ![]()
![]() allowed us to infer an inclination angle of
allowed us to infer an inclination angle of
![]()
![]()
![]() ,
but this value could be reduced to
,
but this value could be reduced to ![]()
![]()
![]() if we consider that HD 181906 has a companion, which implies a reduction in the
if we consider that HD 181906 has a companion, which implies a reduction in the
![]() to 10
to 10 ![]()
![]() .
.
A comb-like structure was unveiled between 1400 and 2100 ![]() Hz, which corresponds to the acoustic-mode spectrum with a maximum power at 1912
Hz, which corresponds to the acoustic-mode spectrum with a maximum power at 1912 ![]() 47
47 ![]() Hz and a large separation of 87.5
Hz and a large separation of 87.5 ![]() 2.6
2.6 ![]() Hz measured inside this frequency interval. However, the low signal-to-noise ratio of the modes prevents us from unambiguously identifying them. To go any further, however, more a priori information is needed to constrain the fits.
Hz measured inside this frequency interval. However, the low signal-to-noise ratio of the modes prevents us from unambiguously identifying them. To go any further, however, more a priori information is needed to constrain the fits.
Acknowledgements
The CoRoT space mission, launched on December 27, 2006, was developed and is operated by the CNES, with the contribution of Austria, Belgium, Brazil, ESA (RSSD and Science Programme), Germany and Spain. J.B. acknowledges support through the ANR project Siroco. I.W.R. and G.A.V. wish to thank the UK Science and Technology Facilities Council for support under grant PP/E001793/1. W.J.C. and Y.E. also wish to thank the UK Science and Technology Facilities Council for support under grant ST/F00204/1. H.B. was supported by the Australian and Danish Research Councils. D.S. acknowledges the support of the Spanish National Research Plan under the grant PNAyA2007-62650. Wavelet software was provided by C. Torrence and G. Compo, and is available at URL: http://atoc.colorado.edu/research/wavelets/
Appendix A: Joint power statistic
In cases where the signal-to-noise ratio of a power spectrum is low, it can be useful to increase the signal and decrease the noise at a cost of decreasing the resolution in frequency. This has often been accomplished by calculating either the arithmetic or geometric mean of a set of power spectra obtained from independent contiguous subsets of the complete time series. The expected statistics of these averaged power spectra can be calculated, but they do not have the same negative exponential distribution as a single power spectrum. The standard maximum-likelihood estimation (MLE) fitting techniques are designed for power spectra with negative exponential statistics (i.e. ![]() with 2 d.o.f.), making it desirable to calculate an averaged power spectrum with the same statistics as the original spectrum.
with 2 d.o.f.), making it desirable to calculate an averaged power spectrum with the same statistics as the original spectrum.
The joint power statistic (JPS) (Sturrock et al. 2005) resembles a correlation function in the sense that it increases the contribution of signals present in a number of independent power spectra, while decreasing the uncorrelated noise. It also has the important property that the JPS is distributed with negative exponential statistics and can, therefore, be immediately fitted using established MLE techniques. The JPS can be calculated using the power spectra of any number of independent subseries, with the resolution in frequency decreasing by a proportional amount compared with the power spectrum of the complete time series. In the case of HD 181906, the best compromise between increasing the amplitude-to-background ratio and maintaining sufficient resolution in frequency was found when the complete detrended time series was divided into four contiguous subseries. The appropriate fourth order JPS can be approximated by
where X is the geometric mean of the power spectra (Si) calculated from four independent subseries
| X = (S1S2S3S4)1/4. | (A.2) |
In the JPS calculated from four subseries, after smoothing with a Gaussian filter of width 1
References
- Allende Prieto, C., Asplund, M., López, R. J. G., & Lambert, D. L. 2002, ApJ, 567, 544 [NASA ADS] [CrossRef] (In the text)
- Appourchaux, T. 2004, A&A, 428, 1039 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Arentoft, T., Kjeldsen, H., Bedding, T. R., et al. 2008, ApJ, 687, 1180 [NASA ADS] [CrossRef] (In the text)
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [CrossRef] [EDP Sciences] (In the text)
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in COSPAR, Plenary Meeting, 36, 36th COSPAR Scientific Assembly, 3749
- Ballot, J., García, R. A., Lambert, P., & Teste, A. 2004, in SOHO 14 Helio- and Asteroseismology: Towards a Golden Future, ed. D. Danesy, ESA SP, 559, 309 (In the text)
- Ballot, J., García, R. A., & Lambert, P. 2006, MNRAS, 369, 1281 [NASA ADS] [CrossRef]
- Ballot, J., Appourchaux, T., Toutain, T., & Guittet, M. 2008, A&A, 486, 867 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Barban, C., Deheuvels, S., Baudin, F., et al. 2009, A&A, 506, 51 [CrossRef] [EDP Sciences] (In the text)
- Bedding, T. R., & Kjeldsen, H. 2003, PASA, 20, 203 [NASA ADS] (In the text)
- Bruntt, H. 2009, A&A, 506, 235 [CrossRef] [EDP Sciences] (In the text)
- Bruntt, H., Kjeldsen, H., Buzasi, D. L., & Bedding, T. R. 2005, ApJ, 633, 440 [NASA ADS] [CrossRef] (In the text)
- Chaplin, W. J., Elsworth, Y., Isaak, G. R., et al. 2002, MNRAS, 336, 979 [NASA ADS] [CrossRef] (In the text)
- Chaplin, W. J., Appourchaux, T., Arentoft, T., et al. 2008, Astron. Nachr., 329, 549 [NASA ADS] [CrossRef] (In the text)
- Frankowski, A., Jancart, S., & Jorissen, A. 2007, A&A, 464, 377 [NASA ADS] [CrossRef] [EDP Sciences]
- García, R. A., Appourchaux, T., Baglin, A., et al. 2008, Commun.Asteroseismol., 157, 288 [NASA ADS] (In the text)
- Gizon, L., & Solanki, S. K. 2003, ApJ, 589, 1009 [NASA ADS] [CrossRef] (In the text)
- Goupillaud, P., Grossmann, A., & Morlet, J. 1984, Geoexploration, 23, 85 [CrossRef] (In the text)
- Grec, G., Fossat, E., & Pomerantz, M. A. 1983, Sol. Phys., 82, 55 [NASA ADS] [CrossRef] (In the text)
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jacoutot, L., Kosovichev, A. G., Wray, A., & Mansour, N. N. 2008, ApJ, 684, L51 [NASA ADS] [CrossRef] (In the text)
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 (In the text)
- Kjeldsen, H., Bedding, T. R., Arentoft, T., et al. 2008, ApJ, 682, 1370 [NASA ADS] [CrossRef] (In the text)
- Korzennik, S. G. 2008, Adv. Space Res., 41, 897 [NASA ADS] [CrossRef] (In the text)
- Makarov, V. V., & Kaplan, G. H. 2005, AJ, 129, 2420 [NASA ADS] [CrossRef]
- Masana, E., Jordi, C., & Ribas, I. 2006, A&A, 450, 735 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mathur, S., Jimenez-Reyes, S. J., & Garcia, R. A. 2008, in Proceedings of GONG 2008/SOHO XXI, Solar-stellar dynamos as revealed by helio- and asteroseismology (In the text)
- Michel, E., Baglin, A., Auvergne, M., et al. 2008a, Science, 322, 558 [NASA ADS] [CrossRef] (In the text)
- Michel, E., Baglin, A., Weiss, W. W., et al. 2008b, Commun. Asteroseismol., 156, 73 [NASA ADS] [CrossRef]
- Michel, E., Samadi, R., Baudin, F., et al. 2009, A&A, 495, 979 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mosser, B., Deheuvels, S., Michel, E., et al. 2008, A&A, 488, 635 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mosser, B., Baudin, F., & Lanza, A. F. 2009a, A&A, 506, 245 [CrossRef] [EDP Sciences] (In the text)
- Mosser, B., Michel, E., Appourchaux, T., et al. 2009b, A&A, 506, 33 [CrossRef] [EDP Sciences] (In the text)
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing (Cambridge: University Press), 2nd edn. (In the text)
- Roca Cortés, T., Jiménez, A., Pallé, P. L., GOLF team, & VIRGO Team 1999, in Magnetic Fields and Solar Processes, ed. A. Wilson et al., ESA SP, 448, 135 (In the text)
- Samadi, R., Fialho, F., Costa, J. E. S., et al. 2006, ESA SP 1306, 317, corrected in [arXiv:astro-ph/0703354] (In the text)
- Samadi, R., Georgobiani, D., Trampedach, R., et al. 2007, A&A, 463, 297 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sturrock, P. A., Scargle, J. D., Walther, G., & Wheatland, M. S. 2005, Sol. Phys., 227, 137 [NASA ADS] [CrossRef] (In the text)
- Torrence, C., & Compo, G. P. 1998, Bull. Am. Meteorol. Soc., 79, 61 [CrossRef] (In the text)
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Footnotes
- ... HD 181906
![[*]](/icons/foot_motif.png)
- CoRoT (Convection, Rotation and planetary Transits) is a minisatellite developed by the French Space agency CNES in collaboration with the Science Programmes of ESA, Austria, Belgium, Brazil, Germany and Spain.
- ...
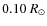
![[*]](/icons/foot_motif.png)
- This number is 5% lower than the one derived by Masana et al. (2006), since the parallax has been revised, but is fully compatible within the error bar.
All Tables
Table 1: Global parameters of HD 181906 used for this work.
Table 2: Length of spectra and corresponding rotational periods.
Table 3: Comparison of published global parameters for different F stars.
Table 4:
HD 181906 frequencies (in ![]() Hz) for scenario A.
Hz) for scenario A.
Table 5:
HD 181906 frequencies (in ![]() Hz) for scenario B.
Hz) for scenario B.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg1N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg47.png) |
Figure 1: N2-lightcurve (in ppm) corrected for the ageing of the CCD and interpolated onto a regular grid in the heliocentric frame. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11910fg2N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg48.png) |
Figure 2: Power spectrum density of the full 156-day N2-lightcurve shown in Fig. 1. The two red-dotted vertical lines show the lowest significant peak and the first harmonic that could be the signature of the surface rotation of the star. The five blue-dotted vertical lines indicate the first harmonics of the orbital period of the satellite. |
| Open with DEXTER | |
| In the text | |
| |
Figure 3: Left: wavelet power spectrum for HD 181906 at low frequency. Right: global wavelet power spectrum where the dotted-line represents the 95% confidence level. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg4N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg50.png) |
Figure 4: Zoom on the spectrum at low frequency. The power spectrum density has been computed using the total length of data. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg5N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg52.png) |
Figure 5: Zoom on the spectrum at low frequency. In black the Fourier spectrum of the first 78 days of data. In blue the spectrum of the last 78 days. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg6N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg53.png) |
Figure 6: Zoom on the spectrum at low frequency. In black the Fourier spectrum of the first 52 days of data. In red the spectrum of the 52 intermediate days of data, and in green the spectrum of the last 52 days. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg7N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg62.png) |
Figure 7:
Power spectrum of the power spectrum (PSPS) normalized by its standard deviation in the region between 1400 and 2100 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg8N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg67.png) |
Figure 8:
Maximum of the PSPS in a region around the expected half-large separation computed in 300 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910fg9N.eps}\vspace*{3mm}
\includegraphics[width=8.4cm,clip]{11910f10N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg73.png) |
Figure 9:
Power spectrum density of the full length lightcurve smoothed by a boxcar of 70 points ( top). The continuous green curve is the background fitted using the method explained in Sect. 6. The bottom panel shows a closer region of the p-mode band between 1000 and 3000 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910f11N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg86.png) |
Figure 10:
Echelle diagram of the full PSD smoothed by a 70 point boxcar starting at a frequency of 792.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910f12N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg93.png) |
Figure 11:
Collapsogram of the smoothed power spectrum (11 bins) obtained by collapsing the power spectrum in the frequency range between 1280 and 2300 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11910f13N.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11910-09/Timg94.png) |
Figure 12:
Smoothed power spectrum of HD 181906 (black curve) and smoothed and shifted by 17 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




