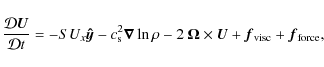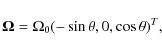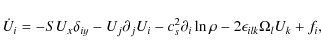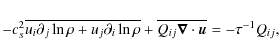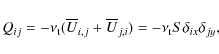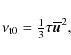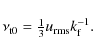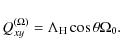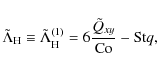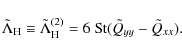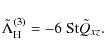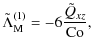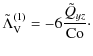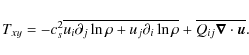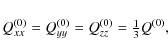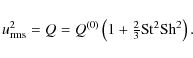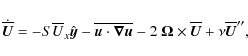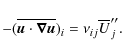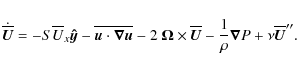EDP Sciences
Home All issues Volume 505 / No 3 (October III 2009) A&A, 505 3 (2009) 955-968 Full HTML
Free Access
Issue
A&A
Volume 505, Number 3, October III 2009
Page(s) 955 - 968
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/200912653
Published online 18 August 2009

Reynolds stresses from hydrodynamic turbulence with shear and rotation[*]

J. E. Snellman1 - P. J. Käpylä1,2 - M. J. Korpi1 - A. J. Liljeström1

1 - Observatory, PO Box 14, 00014 University of Helsinki, Finland
2 - NORDITA, Roslagstullsbacken 23, 10691 Stockholm, Sweden

Received 8 June 2009 / Accepted 3 August 2009

Abstract
Aims. We study the Reynolds stresses which describe turbulent momentum transport from turbulence affected by large-scale shear and rotation.
Methods. Three-dimensional numerical simulations are used to study turbulent transport under the influences of large-scale shear and rotation in homogeneous, isotropically forced turbulence. We study three cases: one with only shear, and two others where in addition to shear, rotation is present. These cases differ by the angle (0 or $90\hbox{$^\circ$ }$) the rotation vector makes with respect to the z-direction. Two subsets of runs are performed with both values of $\theta $ where either rotation or shear is kept constant. When only shear is present, the off-diagonal stress can be described by turbulent viscosity whereas if the system also rotates, nondiffusive contributions ($\Lambda $-effect) to the stress can arise. Comparison of the direct simulations are made with analytical results from a simple closure model.
Results. We find that the turbulent viscosity is of the order of the first order smoothing result in the parameter regime studied and that for sufficiently large Reynolds numbers the Strouhal number, describing the ratio of correlation to turnover times, is roughly 1.5. This is consistent with the closure model based on the minimal tau-approximation which produces a reasonable fit to the simulation data for similar Strouhal numbers. In the cases where rotation is present, separating the diffusive and nondiffusive components of the stress turns out to be challenging but taking the results at face value, we can obtain nondiffusive contributions of the order of 0.1 times the turbulent viscosity. We also find that the simple closure model is able to reproduce most of the qualitative features of the numerical results provided that the Strouhal number is of the order of unity.

Key words: hydrodynamics - turbulence - accretion, accretion disks - Sun: rotation - stars: rotation

1 Introduction

Turbulent angular momentum transport is considered to be of importance in various astrophysical objects, such as accretion disks (e.g. Balbus & Hawley 1998) and convectively unstable layers within stars (e.g. Rüdiger 1989) where they take part in shaping the internal rotation profile of the object. Due to the immense numerical requirements, direct global simulations of these systems are not yet feasible in large quantities, although some simulations are able to capture many features of, for example, the solar rotation profile (see e.g. Robinson & Chan 2001; Brun & Toomre 2002; Miesch et al. 2006,2008). However, in many cases it would be desirable to be able to use simplified, and computationally less demanding, mean-field models where the effects of small-scale turbulence are accurately parameterized in some collective way. Although a rich literature of mean-field models of solar internal rotation exist (e.g. Brandenburg et al. 1992; Küker et al. 1993; Kitchatinov & Rüdiger 2005; Rempel 2005), many of the models use simple and often untested parameterizations of the turbulent quantities.

Parameterizing turbulence entails a closure model for the turbulent correlations. One of the most often used closures in astrophysics is the $\alpha$-prescription (Shakura & Sunyaev 1973), widely used in accretion disk theory, which relates the turbulent viscosity to the local gas pressure. This very simple parameterization allows analytically tractable solutions of accretion disk structure but suffers from the drawback that important physics, such as magnetic fields, are not taken into account. More recently, dynamical turbulent closure models yielding all the relevant components of the Reynolds and Maxwell stresses in simplified setups with homogeneous magnetized shear flows have started to appear (e.g. Ogilvie 2003; Pessah et al. 2006).

For these more sophisticated models to be useful, they need to be validated somehow. The obvious validation method is to compare to numerical simulations that work in a parameter regime which is as similar as possible. Comparisons of closure models with numerical simulations of the magnetorotational instability in periodic local slab geometry have appeared recently (e.g. Pessah et al. 2008; Liljeström et al. 2009) and yield encouraging results in that the closure models are able to capture, at least qualitatively, many of the main features of the numerical simulations. However, these studies concentrate on a situation where the turbulence is generated via the magnetorotational instability (Velikhov 1959; Chandrasekhar 1961; Balbus & Hawley 1991), the nonlinear behaviour of which is still not very well understood (e.g. Fromang et al. 2007).

In the present paper we avoid these complications and consider only the simplest possible hydrodynamic case and assume that isotropic and homogeneous background turbulence already exists in the system upon which large-scale shear and rotation can be imposed. Such turbulence can be generated by using suitable forcing in the Navier-Stokes equation. Although flows of this kind are not likely to occur in nature, they are perfect testbeds for the developement and testing of turbulent closure models.

The present paper is a continuation to an earlier study (Käpylä & Brandenburg 2008, hereafter KB08; see also Käpylä & Brandenburg 2007) where simulations of anisotropic homogeneous turbulence under the influence of rotation were compared to a simple closure model applying the so-called tau-approximation (hereafter MTA, see e.g. Blackman & Field 2002,2003; Brandenburg et al. 2004). In the present study we adopt an isotropic forcing and add a large-scale shear flow using the shearing box approximation. Such a setup allows us to determine the turbulent viscosity (see preliminary results in Käpylä & Brandenburg 2007; and Käpylä et al. 2009). The imposed shear flow also introduces anisotropy into the turbulence which, under the influence of rotation, can produce additional non-diffusive Reynolds stresses (Leprovost & Kim 2007,2008a,b), which are more commonly known as the $\Lambda $-effect (Krause & Rüdiger 1974; Rüdiger 1980, 1989). We make an effort to separate the diffusive and nondiffusive contributions from the numerical data. As in KB08, one of the main goals of the study is to compare the simulation results to a simple closure model, similar to that introduced by Ogilvie (2003).

The remainder of the paper is organised as follows: the models used in the study are presented in Sect. 2, whereas Sects. 3 and 4 give the results and conclusions of the study, respectively.

2 The model and methods

2.1 Basic equations

We model compressible hydrodynamic turbulence in shearing periodic cube of size $(2\pi)^3$. The gas obeys an isothermal equation of state characterized by a constant speed of sound, $c_{\rm s}$. The continuity and Navier-Stokes equations read

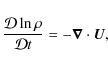\begin{displaymath}\frac{\mathcal{D} \ln \rho}{\mathcal{D} t} = - \vec{\nabla} \cdot \vec{U}, \end{displaymath} (1)


\begin{displaymath}\frac{\mathcal{D} \vec{U}}{\mathcal{D} t} = -SU_x\vec{\hat{y}... ...ga} \times \vec{U} + \vec{f}_{\rm visc} + \vec{f}_{\rm force}, \end{displaymath} (2)

where $\mathcal{D}/\mathcal{D} t=\partial/\partial t+(\vec{U}+\overline{\vec U}_0)\cdot\vec{\nabla}$ denotes the advective derivative and $\overline{\vec U}_0=(0,Sx,0)$ is the imposed shear flow. $\vec{U}$ is the velocity, $\rho$ is the density, $\vec{f}_{\rm visc}$ is the viscous force, and $\vec{f}_{\rm force}$ is the forcing function. Compressibility is retained but low Mach number flows, i.e. ${\rm Ma}= u_{\rm rms}/c_{\rm s} \approx 0.05{-}0.1$, where $u_{\rm rms}$ is the average root mean square velocity, are considered. The viscous force is given by

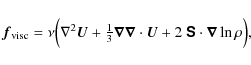\begin{displaymath}\vec{f}_{\rm visc} = \nu \Big(\nabla^2 \vec{U} +{\textstyle{1... ...ec{U} + 2~ \vec{\mathsf{S}} \cdot \vec{\nabla} \ln \rho \Big), \end{displaymath} (3)

where $\nu$ is the kinematic viscosity and

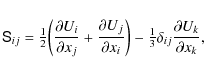\begin{displaymath}\mathsf{S}_{ij} = {\textstyle{1\over2}}\bigg(\frac{\partial U... ...tstyle{1\over3}}\delta_{ij} \frac{\partial U_k}{\partial x_k}, \end{displaymath} (4)

is the traceless rate of strain tensor. The forcing function $\vec{f}_{\rm force}$ is given by
$\displaystyle \vec{f}(\vec{x},t) = {\rm Re} \{N \vec{f}_{\vec{k}(t)} \exp [i \vec{k}(t) \cdot \vec{x} - i \phi(t) ] \} ,$     (5)

where $\vec{x}$ is the position vector, $N = f_0 c_{\rm s} (k c_{\rm s}/\delta t)^{1/2}$ is a normalization factor, f0 is the forcing amplitude, $k = \vert\vec{k}\vert$, $\delta t$ is the length of the time step, and $-\pi < \phi(t) < \pi$ a random delta-correlated phase. The vector $\vec{f}_{\vec{k}}$ is given by
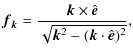$\displaystyle \vec{f}_{\vec{k}} = \frac{\vec{k} \times \hat{\vec{e}}}{\sqrt{\vec{k}^2 - (\vec{k} \cdot \hat{\vec{e}})^2}} ,$     (6)

where $\hat{\vec{e}}$ is an arbitrary unit vector. Thus, $\vec{f}_{\vec{k}}$describes nonhelical transversal waves with $\vert\vec{f}_{\vec{k}}\vert^2 = 1$, where $\vec{k}$ is chosen randomly from a predefined range in the vicinity of the average wavenumber $k_{\rm f}/k_1 = 5$ at each time step. Here k1 is the wavenumber corresponding to the domain size, and $k_{\rm f}$ is the wavenumber of the energy-carrying scale. The choice $k_{\rm f}/k_1 = 5$ is somewhat arbitrary but provides a clear scale separation between the turbulent eddies and the system size.

The numerical simulations were performed with the P ENCIL C ODE[*], which uses sixth-order accurate finite differences in space, and a third-order accurate time-stepping scheme (Brandenburg & Dobler 2002; Brandenburg 2003). Resolutions up to 10243 grid points were used.

2.2 Dimensionless units and parameters

We obtain nondimensional variables by setting

$\displaystyle c_{\rm s}=k_1=\rho_0=1.$     (7)

This means that the units of length, time, and density are
$\displaystyle [x]=k_1^{-1},\;\; [t]=(c_{\rm s}k_1)^{-1},\;\; [\rho]=\rho_0.$     (8)

However, in what follows we present the results in explicitly dimensionless form using the quantities above.

The strengths of shear, rotation, and viscous effects are measured by the shear, Coriolis and Reynolds numbers, respectively, based on the forcing scale as

 
$\displaystyle {\rm Sh}= \frac{S}{u_{\rm rms}k_{\rm f}}, \quad {\rm Co}= \frac{2... ..._{\rm rms} k_{\rm f}}\;, \quad{\rm Re} = \frac{u_{\rm rms}}{\nu k_{\rm f}}\cdot$     (9)

See Fig. 1 for a typical snapshot from a high resolution run with ${\rm Re}\approx387$.

2.3 Coordinate system, averaging, and error estimates

The simulated domain can be thought to represent a small rectangular portion of a spherical body of gas. We choose (x,y,z) to correspond to $(\theta,\phi,r)$ of spherical coordinates. With this choice the rotation vector can be written as

\begin{displaymath}\vec{\Omega} = \Omega_0(-\sin \theta,0,\cos \theta)^T, \end{displaymath} (10)

where $\theta $ is the angle between the rotation axis and the local vertical (z-) direction, i.e. the colatitude. We consider two cases: $\theta =0$ and $\theta=90\hbox{$^\circ$ }$. We can consider these cases to represent the north pole and the equator of a rotating star, respectively. However, if an additional a shear flow of the form $\overline{\vec U}_0=(0,Sx,0)$ is introduced into the system there are multiple ways to interpret the physical system that is described by the model.

Firstly, the case $\theta =0$ can be considered to describe a local portion of a disk rotating around a central object sufficiently far away that the effects of curvature can be neglected. Then the rotation profile of the disk is characterized by $\Omega\propto R^{-q}$ where R is the radius and $q=-S/\Omega_0$. Now, a Keplerian rotation profile is obtained for q=1.5, a flat profile, such as those observed in many galaxies, is given by q=1, and for perfectly rigid rotation we have q=0.

Alternatively, the shear flow can be understood to represent either radial or latitudinal shear in a convection zone of a star. This approach has been used by Leprovost & Kim (2007) who consider that in the case $\theta =0$, $\overline{\vec U}^{(0)}$ corresponds to latitudinal shear near the equator, and in the case $\theta=90\hbox{$^\circ$ }$to the radial shear in near the pole of the star.

Since the turbulence is homogeneous, volume averages are employed and denoted by overbars. An additional time average over the statistically saturated state of the simulation is also taken. Errors are estimated by dividing the time series into three equally long parts and computing mean values for each part individually. The largest departure from the mean value computed for the whole time series is taken to represent the error.

 \begin{figure} \par\includegraphics[width=9cm]{12653fg1.eps} \end{figure} Figure 1:

Velocity component Uy, in the units of the sound speed, from the Run B6 with ${\rm Re}=387$, ${\rm Sh}=-0.20$, and ${\rm Co}=0$, resolution 10243.
Open with DEXTER

2.4 Reynolds stresses from the minimal tau-approximation

We follow here the same procedure as in KB08 and derive a simple analytical model for the Reynolds stresses in the case of homogeneous turbulence under the influences of rotation and shear. Although we present the model in terms of the minimal tau-approximation (see, e.g. Blackman & Field 2002,2003; Brandenburg et al. 2004, KB08) the closure used here is quite similar to that originally presented by Ogilvie (2003; see also Garaud & Ogilvie 2005). A more detailed comparison is given below.

One of the main purposes of this study is to compare the results from the closure model with numerical simulations. Since the numerical setup is homogeneous, it is sufficient to compare the volume averaged data with a closure model with no spatial extent. In this case, the Navier-Stokes equations yield

\begin{displaymath}\dot{U}_i = -SU_x \delta_{iy} -U_j\partial_jU_i -c_s^2 \partial_i \ln \rho -2 \epsilon_{ilk} \Omega_l U_k + f_i, \end{displaymath} (11)

where the dot represents time derivative, and fi describes both the viscous force and external forcing. Now we decompose the velocity as $U_i=\overline{U}_i+u_i$, where $\overline{U}_i$is the average velocity and ui the fluctuation. It is straightforward to derive the equation for $\dot{u}_i$ from Eq. (11) which allows us to derive an evolution equation for the Reynolds stress $Q_{ij} = \overline{u_iu_j}$,
                               $\displaystyle \dot{Q}_{ij}$ = $\displaystyle -S\delta_{yi}Q_{xj} -S\delta_{yj}Q_{xi} -2 \epsilon_{ilk} \Omega_l Q_{ki} -2 \epsilon_{jlk} \Omega_l Q_{kj}$  
    $\displaystyle -c_s^2 \overline{ u_i \partial_j \ln \rho + u_j \partial_i \ln \r... ...ij}\vec{\nabla} \cdot {\vec{u}}}\!+\!\overline{f_i u_j}\!+\!\overline{f_j u_i},$ (12)

where the overbars denote averaging. In the minimal tau-approximation closure scheme the nonlinear terms in Eq. (12) are modeled collectively by a relaxation term

\begin{displaymath}-c_s^2 \overline{ u_i \partial_j \ln \rho + u_j \partial_i \l... ...erline{Q_{ij}\vec{\nabla} \cdot {\vec{u}}} = -\tau^{-1}Q_{ij}, \end{displaymath} (13)

where $\tau$ is a relaxation time. Terms involving the forcing and viscosity, fi, can be parameterized in the same spirit with

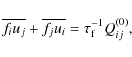\begin{displaymath}\overline{f_i u_j} + \overline{f_j u_i}=\tau_{\rm f}^{-1}Q_{ij}^{(0)}, \end{displaymath} (14)

where Qij(0) is the equilibrium solution in the absence of shear and rotation. Throughout this paper we assume that the time scale associated with the forcing is equal to the relaxation time, i.e. $\tau=\tau_{\rm f}$. We note that there is no compelling theoretical argument to enforce this equality but we rather use it for the sake of simplicity. Thus we arrive at the equation
$\displaystyle \dot{Q}_{ij} = -S\delta_{yi}Q_{xj} -S\delta_{yj}Q_{xi} -2 \epsilo... ...-2 \epsilon_{jlk} \Omega_l Q_{kj} -\tau^{-1}\left(Q_{ij} - Q_{ij}^{(0)}\right).$     (15)

We use the same values of $\Omega $ and S as in the simulations and take the quantity Qij(0) from a nonrotating run with ${\rm Co}={\rm Sh}=0$. The free parameter in the model is the relaxation time, $\tau$, which can be represented in terms of the Strouhal number

\begin{displaymath}{\rm St}=\tau u_{\rm rms}k_{\rm f}, \end{displaymath} (16)

which is the ratio of correlation and turnover times.

2.4.1 Comparison to the Ogilvie (2003) model

In the model of Ogilvie (2003) the Reynolds stresses in the hydrodynamical case are given by

$\displaystyle \dot{Q}_{ij} + \mbox{linear terms} = C_1 \sqrt{Q} L^{-1}Q_{ij}+ C_2 \sqrt{Q} L^{-1} \left(Q_{ij}- {\textstyle{1\over3}}Q \delta_{ij}\right),$     (17)

where Ci are dimensionless parameters of the order of unity, Q is the trace of the Reynolds tensor and L is a lenght scale, e.g. the system size. The first term on the rhs can be identified as a relaxation term similar to that used in the minimal tau-approximation

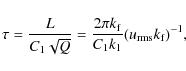\begin{displaymath}\tau=\frac{L}{C_1 \sqrt{Q}} = \frac{2\pi k_{\rm f}}{C_1 k_1} (u_{\rm rms}k_{\rm f})^{-1}, \end{displaymath} (18)

where we have used $\sqrt{Q}=u_{\rm rms}$, and $L=2\pi/k_1$. Comparing with Eq. (16), we see that ${\rm St}=2\pi k_{\rm f} (C_1k_1)^{-1}=10\pi~C_1^{-1}$ for our value of $k_{\rm f}/k_1 = 5$.

Our Eq. (15) also lacks the term $C_2 \sqrt{Q} L^{-1}(Q_{ij}-\frac{1}{3} Q \delta_{ij})$ which appears in the model of Ogilvie. This term describes isotropization of the turbulence, and a similar term can be added to the minimal tau-approximation in the form $\tau_{\rm I}^{-1}(Q_{ij}-\frac{1}{3} Q \delta_{ij})$, where $\tau_{\rm I}$ could have a value unequal to $\tau$. However, after experimenting with such a term, we did not find substantially better agreement with simulation results. Thus, in order to keep our model as simple as possible with the minimum amount of free parameters, also this term is neglected in our analysis.

We note that if the saturated solutions of Eqs. (15) and (17) are independent of time, the two models yield the same results provided that C2 is zero. However, if $\dot{Q}\neq0$ in the saturated state, e.g. if the solution is oscillatory, then differences will occur because the relaxation time in our model is based on a constant $u_{\rm rms}$ and not on the Q that emerges as a results of time integration of the model itself. We also stress that in the original work of Ogilvie (2003), the turbulence due to the shear flow, rotation, and magnetic fields was studied. In our case, however, the turbulence pre-exists due to the external forcing and we mainly study the effects of shear and rotation on this background turbulence.

3 Results

We study the Reynolds stresses from three different systems: one where only shear flow is present and two others where nonzero rotation is present with either $\theta =0$ or $\theta=90\hbox{$^\circ$ }$. For the first system we perform four different sets of simulations (see Table 1 for a summary of the different sets of runs) where we either fix ${\rm Sh}$ (Sets A and B) or ${\rm Re}$ (Sets C and D). In the setups with rotation we perform two sets of calculations for both values of $\theta $ where we fix either ${\rm Sh}$ (Sets E and G) or ${\rm Co}$ (Sets F and H). In Sets E to H we vary the parameter q in the range -5<q<1.9. More detailed descriptions of the runs can be found in Tables D.1 to C.3. Furthermore, we compute the stresses from corresponding closure models making use of the stationary solution of Eq. (15) given in Appendix A.

Table 1:   Summary of the different sets of simulations. The values of ${\rm Re}$, ${\rm Co}$, and ${\rm Sh}$ are given in terms of $u_{\rm rms}$ from a run with ${\rm Co}={\rm Sh}=0$.

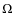3.1 Case $\Omega $ = 0: turbulent viscosity

Consider first the case where rotation is absent and the only large-scale flow is the imposed shear $\overline{\vec U} = (0,xS,0)$ with isotropic background turbulence. The Reynolds stress generated by the shear can be represented by the expression

\begin{displaymath}Q_{ij}= -\nu_{\rm t}(\overline{U}_{i,j} + \overline{U}_{j,i}) = -\nu_{\rm t}S \delta_{ix} \delta_{jy}, \end{displaymath} (19)

where $\nu_{\rm t}$ is the turbulent viscosity. The expression (19) can be considered to be valid for weak shear. On the other hand, we can estimate the turbulent viscosity from

\begin{displaymath}\nu_{\rm t0}= {\textstyle{1\over3}}\tau \overline{\vec{u}}^2, \end{displaymath} (20)

where $\tau$ is the correlation time and $\overline{\vec{u}^2}$ is the average turbulent velocity squared. Equation (20) is the same as the one that can be derived for the magnetic diffusivity using first order smoothing approximation (e.g. Krause & Rädler 1980). Here we have assumed a turbulent magnetic Prandtl number of unity to arrive at Eq. (20). This formulation is supported by numerical results although analytical studies often yield somewhat different results (e.g. Yousef et al. 2003, and references therein).

The correlation time can be related to the turnover time of the turbulence via the Strouhal number, Eq. (16). If we assume that ${\rm St}=1$, as is suggested by numerical turbulence models (e.g. Brandenburg & Subramanian 2005, 2007) similar to ours, the turbulent viscosity is given by

\begin{displaymath}\nu_{\rm t0}= {\textstyle{1\over3}}u_{\rm rms}k_{\rm f}^{-1}. \end{displaymath} (21)

In what follows we use $\nu_{\rm t0}$ as the normalization for the turbulent viscosity. However, later on we allow ${\rm St}\neq1$ and write $\nu_{\rm t}={\rm St}\nu_{\rm t0}$ in order to obtain an independent estimate of ${\rm St}$ from the numerical simulations.

3.1.1 Simulation results

We find that in the non-rotating case it is difficult to avoid large-scale vorticity generation (see also Käpylä et al. 2009). This phenomenon is likely to be related to a vorticity dynamo discussed in the analytical studies of Elperin et al. (2003,2007). Similar large-scale structures have been observed earlier in the numerical works of Yousef et al. (2008a,b) using an independent method. The problem becomes increasingly worse as the shear is increased. Thus we need to limit the range of ${\rm Sh}$ and carefully analyze the data so that the effect of the vorticity dynamo on the turbulence is minimized (see the related discussion in Mitra et al. 2009). What this means is that we limit the time averaging to a range where turbulence is established but where the large-scale flow is still weak in comparison to the turbulent rms-velocity. We stress that the vorticity dynamo occurs only if turbulence already exists in the system, i.e. it does not arise if the forcing is turned off in the simulations.

The only nonzero off-diagonal component in the simulations is now Qxy that can be interpreted in terms of turbulent viscosity. This is also consistent with symmetry arguments. Once a suitable averaging interval has been found, the turbulent viscosity is obtained from Eq. (19). If the first order smoothing result, Eq. (21) is valid, we should expect the ratio of turbulent to molecular viscosity to be proportional to the Reynolds number,

\begin{displaymath}\nu_{\rm t}/\nu \propto {\rm Re}. \end{displaymath} (22)

We find this scaling to be valid for large enough ${\rm Re}$ in the simulation results of Sets A and B, see the upper panel of Fig. 2. The vorticity generation is more vigorous for smaller Reynolds numbers which can explain the deviating values for small ${\rm Re}$. The vorticity dynamo exists at least up to ${\rm Re}\approx100$ (Käpylä et al. 2009), but the growth rate seems to decrease somewhat as ${\rm Re}$ is increased. We also find that the turbulence becomes more isotropic as ${\rm Re}$increases (cf. Table D.1) and conjecture that this behaviour is also linked to the less efficient large-scale vorticity generation.

Furthermore, we can estimate the Strouhal number by comparing the simulation results for  $\nu_{\rm t}$ and the FOSA estimate, Eq. (21), see the lower panel of Fig. 2. We find that for large Reynolds numbers, $\nu_{\rm t}/\nu_{\rm t0}\approx 1.5$, indicating that ${\rm St}\approx1.5$. This value is in accordance with earlier numerical studies of passive scalar transport (Brandenburg et al. 2004) and nondiffusive Reynolds stresses (Käpylä & Brandenburg 2008).

The shear dependence of the non-zero components of the normalized Reynolds stresses, $\tilde{Q}_{ij}\equiv Q_{ij}/u_{\rm rms}^2$, from Sets C and D is shown in Fig. 3 (see also Table D.1). We find that $\tilde{Q}_{xx}$ decreases and $\tilde{Q}_{yy}$ increases as a function of ${\rm Sh}$, although the latter trend is barely significant due to the large error bars. $\tilde{Q}_{zz}$, on the other hand, seems to increase slightly for strong shear but the error bars are again so large that this trend is not statistically significant. For $-{\rm Sh}\ga0.2$ the errors are generally quite large due to the short averaging interval that we are forced to use due to the vorticity generation.

We can rewrite Eq. (19) in terms of ${\rm Sh}$ and ${\rm St}$ by substituting $\nu_{\rm t0}={\textstyle{1\over3}}{\rm St}u_{\rm rms}k_{\rm f}^{-1}$ and using the definition of ${\rm Sh}$ to obtain

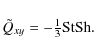\begin{displaymath}\tilde{Q}_{xy} = -{\textstyle{1\over3}}{\rm St}{\rm Sh}. \end{displaymath} (23)

This relation is valid for weak shear and is also borne out of the closure model (see Appendix A.1). We find that the stress component $\tilde{Q}_{xy}$ in the Sets C and D is approximately consistent with a relation $-\tilde{Q}_{xy}\propto (0.5 \ldots 0.67) {\rm Sh}$, suggesting that ${\rm St}\approx1.5\ldots2$ (see the bottom panel of Fig. 3 and the next section). The Reynolds number in the Sets C and D varies between 27 and 123 so the results for the Strouhal number are consistent with the corresponding data in Fig. 2.

 \begin{figure} \par\includegraphics[width=9cm]{12653fg2.eps} \end{figure} Figure 2:

Upper panel: turbulent viscosity divided by the molecular viscosity for the simulation Sets A (solid line) and B (dashed line) as a function of the Reynolds number. The dotted line, proportional to ${\rm Re}$, is shown for reference. Lower panel: the Strouhal number, ${\rm St}=\nu _{\rm t}/\nu _{\rm t0}$, for the same sets of simulations as in the upper panel.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=8.8cm]{12653fg3.eps} \end{figure} Figure 3:

From top to bottom: Reynolds stress components Qxx, Qyy, Qzz, and Qxy, normalised by $u_{\rm rms}^2$, as functions of the shear parameter for simulation Sets C and D with Reynolds numbers, based on $u_{\rm rms}$ from a run with ${\rm Co}={\rm Sh}=0$, of $\approx $27 (diamonds) and $\approx $75 (triangles), respectively. The curves in each panel show the results of the MTA-closure with three Strouhal numbers. The linestyles are as indicated in the legend in the top panel.
Open with DEXTER

3.1.2 Closure model results

We now turn to the simple closure model that was introduced in Sect. 2.4. We compare the stationary solutions of the MTA-model with the time and volume averaged simulation data. The closure model predicts that the absolute values of Qxx and Qzz remain constant as functions of ${\rm Sh}$ (see Appendix A for more details)

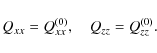\begin{displaymath}Q_{xx}=Q_{xx}^{(0)}, \quad Q_{zz}=Q_{zz}^{(0)}. \end{displaymath} (24)

However, since Qyy, and thus $Q=u_{\rm rms}^2$, can vary, the normalised data shows a decreasing trend for Qxx and Qzz as a function of shear. The MTA-model also shows that Qxy is linearly proportional to the shear parameter for weak shear whereas the other two off-diagonal components are zero as expected from symmetry cosiderations.

We find that the closure model is in qualititive agreement with the numerical results for $\tilde{Q}_{xx}$, $\tilde{Q}_{yy}$, and $\tilde{Q}_{xy}$ for all values of ${\rm Sh}$, see Fig. 3. For $\tilde{Q}_{zz}$ the numerical data shows large scatter for increasing values of $\vert{\rm Sh}\vert$, although the points around $-{\rm Sh}\approx0.12$ are consistent with a declining trend. Considering the other components, the best fit to the simulation data for $\tilde{Q}_{yy}$ and $\tilde{Q}_{xy}$ is obtained if ${\rm St}\approx1.5\ldots2$ is used in the MTA-model (see the dotted and dashed lines in Fig. 3), whereas a somewhat larger ${\rm St}$ fits the results of $\tilde{Q}_{xx}$ best. Especially the off-diagonal component $\tilde{Q}_{xy}$is quite well reproduced with our simple model.

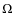
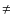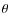3.2 Case $\Omega $ $\neq $ 0, $\theta $ = 0

When adding shear, we consider two distinct lines in the parameter space: in simulation Set E we keep ${\rm Sh}$ constant and vary ${\rm Co}$, whereas in Set F the rotation is kept constant and the shear is varied (see also Table E.2). The range in which these parameters is varied is given by $-5\le q\le1.9$ where the parameter $q=-S/\Omega_0$ can be considered to describe the shear in a differentially rotating disk (see Sect. 2.3). Whilst the cases q=1.5 and q=1 can be thought to represent Keplerian and galactic disks, respectively, the regime q<1 is not likely to occur in the bulk of the disk in any system, but such configurations can occur in convectively unstable parts of stellar interiors, such as the solar convection zone. Cases q>2 are Rayleigh unstable (see Appendix B.1) and lead to a large-scale instability of the shear flow so simulations in this parameter regime are not considered here.

3.2.1 Simulation results

In Set E we fix the shear flow, measured by ${\rm Sh}$, and vary the rotation rate. In this case the value of ${\rm Sh}\approx-0.16$ is very close to being constant in all runs. The simulation results for the nonzero components of the stress are shown in Fig. 4. We find that the components $\tilde{Q}_{xx}$ and $\tilde{Q}_{yy}$ behave very similarly to each other but with opposite trends as functions of q, i.e. the sum of the two is roughly constant. The quantity $\tilde{Q}_{zz}$ varies much less than the two other diagonal components, and is consistent with a constant value as a function of q within the error bars in all cases apart from three points in the range $\vert q\vert\le0.5$. The off-diagonal stress $\tilde{Q}_{xy}$ shows almost a symmetric profile with respect to q=0, with somewhat steeper rise on the positive side. We note that since ${\rm Sh}\approx\mbox{const.}<0$, the very small values of $\tilde{Q}_{xy}$ around q=0 indicate that the more rapid rotation there either quenches the turbulent viscosity or that additional nondiffusive contributions with the opposite sign are present.

In Set F, we keep $\Omega $ constant and vary the magnitude of the shear. In this case, however, the Coriolis number no longer stays exactly constant because the rms-velocity is affected by the rather strong shear for the extreme values of |q|. This also affects the anisotropy of the turbulence which is much greater than in Set E, see Fig. 5. The trends of $\tilde{Q}_{xx}$ and $\tilde{Q}_{yy}$ are again opposite to each other as in Set E, but here the variation as a function of q is significantly greater. Similarly as in Set E, the $\tilde{Q}_{zz}$-component is less affected, although a weakly incresing trend is seen for small q and a clearly decreasing trend is seen for positive values of q. The off-diagonal component $\tilde{Q}_{xy}$ changes sign at q=0 where also ${\rm Sh}$ changes sign. However, it is clear that Qxy is not linearly proportional to q as might naively be expected if the stress is fully due to turbulent viscosity. Thus it is important to try to sepatate the nondiffusive and diffusive contributions (see below).

 \begin{figure} \par\includegraphics[width=8.5cm]{12653fg4.eps} \end{figure} Figure 4:

Same as Fig. 3 but for Set E, and different Strouhal numbers as indicated by the legend in the uppermost panel.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=8.8cm]{12653fg5.eps} \end{figure} Figure 5:

Same as Fig. 4 but for the simulation Set F.
Open with DEXTER

3.2.2 Closure model results

The Reynolds stresses obtained from the closure model are compared with the results of the numerical simulations from Sets E and F in Figs. 4 and 5 with constant Sh and Co, respectively. In both cases we observe rather good qualitative agreement between the numerical simulations and the closure model with the exception of $\tilde{Q}_{zz}$ in Set F when q<-2 (see the third panel of Fig. 5). Another discrepancy for $\tilde{Q}_{zz}$ occurs in the Set E near q=0 where the simulation results indicate a higher value than what is obtained from the closure model. The discrepancies for $\tilde{Q}_{zz}$ occur for rapid rotation (Set E near q=0) and large shear (Set F for q<-2) which suggests that the simple closure model used here could be inadequate in such regimes. We also note that the fit generally tends to get worse as qapproaches 2. Partially due to this we cannot ascribe a single Strouhal number that would fit the simulation data in the full parameter range studied here. In Set E the data is within error bars consistent with ${\rm St}=0.75\ldots1.00$ in the range q<0.5 except for Qzz near q=0. Furthermore, ${\rm St}>1$ would be required to reproduce Qxx and Qyy for 0.5<q<2. In Set F the situation is similar with Qzz and Qxy deviating for large negative q and Qyydeviating for q>1. All in all, the correspondence between the simple closure and the simulation results is rather good.

3.2.3 Separating diffusive and nondiffusive contributions

When both, shear and rotation are present, the Reynolds stress can also contain nondiffusive contributions proportional to the rotation rate, i.e.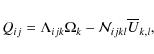

\begin{displaymath}Q_{ij} = \Lambda_{ijk}\Omega_k - \mathcal{N}_{ijkl} \overline{U}_{k,l}, \end{displaymath} (25)

where $\Lambda_{ijk}$ describes the $\Lambda $-effect (Krause & Rüdiger 1974; Rüdiger 1980,1989; Kitchatinov & Rüdiger 1993), which contributes to the generation of differential rotation. In the case that we have shear in addition to rotation, the problem is that for a given stress component we have two unknown coefficients which makes it difficult to distinguish the different contributions without a method similar to the test field procedure in magnetohydrodynamics (see, e.g. Schrinner et al. 2005,2007). However, if we consider that the diffusive contribution is given by Eq. (19) with $\nu_{\rm t}={\rm St}~\nu_{\rm t0}$, it is possible to separate the two provided that the shear and rotation are sufficiently weak.

Considering the case $\vec{\Omega}=\Omega_0(0,0,1)$, the nondiffusive part of the Reynolds stress can be described by a single coefficient that is commonly denoted (cf. Rüdiger 1989) by

\begin{displaymath}Q_{xy}^{(\Omega)}=\Lambda_{\rm H} \cos\theta \Omega_0. \end{displaymath} (26)

This is often referred to as the horizontal $\Lambda $-effect because it generates horizontal differential rotation in mean-field models of stellar interior rotation. Let us now write the total stress as a sum of the contributions from the $\Lambda $-effect and the turbulent viscosity

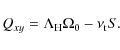\begin{displaymath}Q_{xy}= \Lambda_{\rm H}\Omega_0 - \nu_{\rm t}S. \end{displaymath} (27)

The turbulent viscosity is given by $\nu_{\rm t}={\textstyle{1\over3}}\tau u_{\rm rms}^2$ with $\tau={\rm St}/(u_{\rm rms}k_{\rm f})$, so $\nu_{\rm t}={\textstyle{1\over3}}{\rm St}u_{\rm rms}k_{\rm f}^{-1}={\rm St} \nu_{\rm t0}$. Substituting this above we obtain

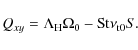\begin{displaymath}Q_{xy}= \Lambda_{\rm H}\Omega_0 - {\rm St}\nu_{\rm t0}S. \end{displaymath} (28)

Solving for $\Lambda_{\rm H}$ and dividing by $\nu_{\rm t0}\Omega_0$ yields

\begin{displaymath}\tilde{\Lambda}_{\rm H}\equiv \tilde{\Lambda}_{\rm H}^{(1)} = 6 \frac{\tilde{Q}_{xy}}{{\rm Co}} - {\rm St}q, \end{displaymath} (29)

where $\tilde{Q}_{xy}=Q_{xy}/u_{\rm rms}^2$, $\tilde{\Lambda}_{\rm H}= \Lambda_{\rm H}/\nu_{\rm t0}$, $q=-S/\Omega_0$ and where the definition of ${\rm Co}$, Eq. (9) has been used.

On the other hand, for slow rotation and in the absence of shear the nondiffusive stress due to the anisotropy of the turbulence can be written as (Rüdiger 1989, see also KB08)

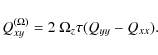\begin{displaymath}Q_{xy}^{(\Omega)}=2~\Omega_z \tau (Q_{yy}-Q_{xx}). \end{displaymath} (30)

Equating this with Eq. (26) gives

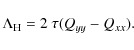\begin{displaymath}\Lambda_{\rm H}=2~\tau (Q_{yy}-Q_{xx}). \end{displaymath} (31)

Dividing by $\nu_{\rm t0}$ and eliminating $\tau$ using ${\rm St}$ yields

\begin{displaymath}\tilde{\Lambda}_{\rm H}\equiv \tilde{\Lambda}_{\rm H}^{(2)} = 6~{\rm St}(\tilde{Q}_{yy}-\tilde{Q}_{xx}). \end{displaymath} (32)

We can now compare the expressions (29) and (32) by using the stresses and ${\rm Co}$ from the simulations and keeping the Strouhal number as a free parameter.

The results for the two measures of the $\Lambda $-effect for the Sets E and F are shown in Fig. 6. In Set E the qualitative behaviour of the two expressions is the same for Strouhal numbers greater than $\approx $0.7, whereas the best correspondence between $\tilde{\Lambda}_{\rm H}^{(1)}$ and $\tilde{\Lambda}_{\rm H}^{(2)}$ is obtained for ${\rm St}\approx0.85$. For larger ${\rm St}$ the qualitative trend of $\tilde{\Lambda}_{\rm H}^{(1)}$ stays the same but the deviation between the two expressions becomes increasingly greater for large values of |q|. In summary, in Set E we seem to be able to extract a reasonable estimate of the nondiffusive contribution to the Reynolds stress with the method outined above. The magnitude of $\Lambda_{\rm H}$ is of the order of $(0.2\ldots0.4)\nu_{\rm t0}$ when a similar Strouhal number is used in the fitting as was required for the closure model to approximately reproduce the simulation results. The magnitude of $\Lambda_{\rm H}$ is also quite close to the values obtained by KB08 in a system without shear.

In Set F the qualitative behaviours of $\tilde{\Lambda}_{\rm H}^{(1)}$ and $\tilde{\Lambda}_{\rm H}^{(2)}$ are the same for Strouhal numbers greater than about $\approx $0.5. We find that in the Set F a q-independent Strouhal number does not give a very good fit to the numerical data. We have plotted the curves for ${\rm St}=0.75$ which yields a reasonable fit to the data in the vicinity of q=0 where $\vert{\rm Sh}\vert$ is small, and Eqs. (29) and (32) can be considered to be the least affected by the shear. Thus the results for the $\Lambda $-effect in Set F leave more room for speculation. One contributing factor is likely to be the significantly stronger shear for the extreme values of |q| which possibly renders the expressions (29) and (32) inaccurate in this regime.

 \begin{figure} \par\includegraphics[width=8.8cm]{12653fg6.eps} \end{figure} Figure 6:

Upper panel: the two measures of the horizontal $\Lambda $-effect from Set E according to Eq. (29) (solid line) and Eq. (32) (dashed). Lower panel: the same as above but from Set F.
Open with DEXTER

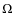
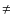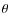3.3 Case $\Omega $ $\neq $ 0, $\theta $ = 90 $\hbox {$^\circ $ }$

Finally, we consider the case where, in addition to the shear flow, rotation with $\theta=90\hbox{$^\circ$ }$ is used, i.e. $\vec{\Omega}=\Omega_0(-1,0.0)$. As is noted by Leprovost & Kim (2008b) this system is unstable even in the absence of turbulence. The instability generates large-scale vorticity due to the fact that no stationary solution to the equations of the large-scale velocity exist (Leprovost & Kim 2008b, see also Appendix B.2) in the absence of forcing on the large scales. If the system is interpreted as the polar region in the solar tachocline, such large-scale forcing can be available, e.g.  by thermally driven flows but in the present simulation setup such effects are difficult to implement.

In spite of the unstable nature of the system, we find that when turbulence due to the forcing is present we can still extract information about the Reynolds stresses from the early stages of the simulations where the large-scale flows are still weak. The procedure is similar to the case where rotation was absent (see Sect. 3.1.1). However, this means that the error bars in Figs. 7 and 8 are greater than those in Figs. 4 and 5 because much shorter averaging intervals must be used. The situation is aggravated in Set H (see, Fig. 8) where the amplitude of the shear flow increases when |q| increases.

3.3.1 Simulation results

We perform again two sets of simulations (see Table C.3) where either the shear flow (Set G) or rotation (Set H) is kept fixed. In the previous cases the source of anisotropy was either only large-scale shear with mean vorticity $\overline{\vec W}=\vec{\nabla} \times {\overline{\vec U}}=S\hat{\vec{z}}$ (Sets A to D), or shear and rotation of the form $\vec{\Omega}=\Omega_0\hat{\vec{z}}$ (Sets E and F). In the present case the rotation vector points to the negative x-direction due to which further symmetries are broken and the other off-diagonal stresses Qxz and Qyz can have nonzero values (e.g. Rüdiger 1989).

The results from Set G are shown in Fig. 7. Due to the large error bars, the results for the diagonal components are consistent with a value independent of q. The component Qxx seems to increase and Qyyto decrease near q=0, but these results are not statistically significant. The off-diagonal stress Qxy shows a similar qualitative and quantitative trend as in Set E. The component Qxzis negative (positive) for q<0 (q>0) with absolute values peaking near q=0. The magnitude of Qxz is approximately one third of Qxy. The Qyz component is smaller by another factor of two to three in comparison to Qxz with a profile consistent with linear proportionality to q. However, the large errors for $q\le0.25$ imply that the results there are not statistically significant.

The results from Set H are shown in Fig. 8. The diagonal stresses show again little dependence on q except for q<-2.5, where Qxx decreases and Qyy increases, although the error bars are again so large that the results for Qyy are also consistent with a constant profile. Within error estimates, Qzz is consistent with a constant profile as a function of q. In general, the results for q<-2.5 are rather unreliable due to the rapid generation of large-scale flows. The off-diagonal stress Qxyhas a similar profile and somewhat larger magnitude than in Set F. Since the shear flow in both sets is the same the difference can be due to the different nondiffusive contributions. Component Qxz shows a similar profile, and a magnitude of about one third of the stress Qxy. Qyz, on the other hand, exhibits a profile symmetric around q=0, apart from a few unrealiable points in the regime q<-2.5.

 \begin{figure} \par\includegraphics[width=17cm]{12653fg7.eps} \end{figure} Figure 7:

Left column: $\tilde{Q}_{xx}$ ( top panel), $\tilde{Q}_{yy}$ ( middle), and $\tilde{Q}_{zz}$ ( bottom) from the simulation Set G. Right column: $\tilde{Q}_{xy}$ ( top panel), $\tilde{Q}_{xz}$ ( middle), and $\tilde{Q}_{yz}$ ( bottom) from Set G. The curves in each panel show the closure model results with three different Strouhal numbers as indicated in the legend ( righ column, middle panel).
Open with DEXTER

 \begin{figure} \par\includegraphics[width=17cm]{12653fg8.eps} \end{figure} Figure 8:

Same as Fig. 7 but for the simulation Set H.
Open with DEXTER

3.3.2 Closure model results

The Reynolds stresses obtained from the closure model are compared with the results from the numerical simulations of the Sets G and H in Figs. 7 and 8, respectively. In Set G the error bars for the diagonal components are so large that a wide range of Strouhal numbers are consistent with the results. Because the shear in this set is rather weak in all runs, the anisotropy of the turbulence remains weak in all simulations. It also appears that the simulation results for $\tilde{Q}_{xx}$ and $\tilde{Q}_{zz}$ are not captured by the closure model for some points near q=0. The off-diagonal components $\tilde{Q}_{xy}$ and $\tilde{Q}_{xz}$ show a clearer picture and the closure model is consistent with the numerical results if ${\rm St}=0.75\ldots1$. The simulation results for $\tilde{Q}_{yz}$ are for the most part not distinguishable from zero for q<0.5. For q greater than this, the closure model is consistent with the simulations for ${\rm St}=1$.

In Set H the diagonal components show weak signs of anisotropy if |q|<2. However, the errors increase substantially for greater qand the data is still almost consistent with isotropic turbulence even for q=-5. This is due to the short averaging interval that results in from the vigorous vorticity generation that is excited very early in these runs. This is because the extreme values of |q| correspond to large values of ${\rm Sh}$ in this set. All of the off-diagonal stresses show qualitatively correct behaviours and the simulation data is again consistent with ${\rm St}=0.75\ldots1$ for |q|<3.

 \begin{figure} \par\includegraphics[width=8.8cm]{12653fg9.eps} \end{figure} Figure 9:

Nondiffusive contributions to the Reynolds stresses parameterized by the coefficients $\tilde{\Lambda}_{\rm H}$ ( top panel), $\tilde{\Lambda}_{\rm M}$ ( middle), and $\tilde{\Lambda}_{\rm V}$ ( bottom) from the simulation Set G. In each panel two expressions are compared and the linestyles are explained in the legends.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=8.8cm]{12653f10.eps} \end{figure} Figure 10:

Same as Fig. 9 but for the simulation Set H.
Open with DEXTER

3.3.3 Separating diffusive and nondiffusive contributions

In the case with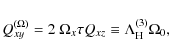 $\theta=90\hbox{$^\circ$ }$, Eq. (26) no longer applies, but we can still use Eq. (29) to estimate the nondiffusive contribution $\tilde{\Lambda}_{\rm H}^{(1)}$. On the other hand Eq. (32) is no longer valid because $\Omega_z=0$. To replace Eq. (32), we can use the tau-approximation to derive another expression for the nondiffusive stress. We arrive at a term proportional to $\Omega_x$ in the equation of Qxy

\begin{displaymath}Q_{xy}^{(\Omega)}=2~\Omega_x \tau Q_{xz}\equiv \Lambda_{\rm H}^{(3)} \Omega_0, \end{displaymath} (33)

where the superscript differentiates this contribution from those used in the case where $\theta =0$. Division by $\nu_{\rm t0}$ yields

\begin{displaymath}\tilde{\Lambda}_{\rm H}^{(3)} = - 6~ {\rm St}\tilde{Q}_{xz}. \end{displaymath} (34)

Furthermore, to lowest order, the other two off-diagonal stresses can contain nondiffusive contributions
 
         $\displaystyle Q_{xz}^{(\Omega)}$ = $\displaystyle \Lambda_{\rm M}\Omega_0,$ (35)
$\displaystyle Q_{yz}^{(\Omega)}$ = $\displaystyle \Lambda_{\rm V}\sin \theta \Omega_0.$ (36)

Solving for the $\Lambda $-coefficients and normalizing by $\nu_{\rm t0}$gives
             $\displaystyle \tilde{\Lambda}_{\rm M}$ $\textstyle \equiv$ $\displaystyle \tilde{\Lambda}_{\rm M}^{(1)} = -6 \frac{\tilde{Q}_{xz}}{{\rm Co}},$ (37)
$\displaystyle \tilde{\Lambda}_{\rm V}$ $\textstyle \equiv$ $\displaystyle \tilde{\Lambda}_{\rm V}^{(1)} = -6 \frac{\tilde{Q}_{yz}}{{\rm Co}}\cdot$ (38)

We note that whilst Eq. (36) coincides with that commonly assumed for the $\Lambda $-effect, Eq. (35) does not. Typically the ``meridional'' $\Lambda $-effect, $\Lambda_{\rm M}$, is proportional to $\sin\theta \cos\theta \Omega$ (e.g. Pulkkinen et al. 1993; Käpylä et al. 2004) which derives from symmetry considerations in a rotating spherical system. However, here these symmetry considerations are no longer obeyed due to the added shear flow. Furthermore, applying the minimal tau-approximation to the Reynolds stress equation yields
             $\displaystyle Q_{xz}^{(\Omega)}$ = $\displaystyle -2~\Omega_x \tau Q_{xy},$ (39)
$\displaystyle Q_{yz}^{(\Omega)}$ = $\displaystyle 2~\Omega_x \tau (Q_{zz}-Q_{yy}).$ (40)

Equating these with Eqs. (35), and (36), respectively, and bearing in mind that $\Omega_x=-\Omega_0$, we obtain, after normalization with the turbulent viscosity $\nu_{\rm t0}$,
             $\displaystyle \tilde{\Lambda}_{\rm M}^{(2)}$ = $\displaystyle 6~{\rm St}\tilde{Q}_{xy},$ (41)
$\displaystyle \tilde{\Lambda}_{\rm V}^{(2)}$ = $\displaystyle -6~{\rm St}(\tilde{Q}_{zz}-\tilde{Q}_{yy}).$ (42)

We now proceed with the comparison in the same manner as in Sect. 3.2.3.

We find that in Set G the correspondence between the two measures for each of the $\Lambda $-coefficients are in rough qualitative agreement for ${\rm St}\approx1$, but matching the quantitative values is not possible (see Fig. 9). Compared to Set E, the profile and amplitude of $\tilde{\Lambda}_{\rm H}\approx0.05\ldots0.3$ are similar, although a precise value is difficult to determine due to the disagreement between the two expressions. The other two nondiffusive components have magnitudes similar to $\tilde{\Lambda}_{\rm H}$ at least in the range |q|<2. For $\tilde{\Lambda}_{\rm M}$ the analytical expressions seem to agree rather well in the range |q|<2. For $\tilde{\Lambda}_{\rm V}$, on the other hand, the correspondence is not very good, although the sign of the coefficient is for the most part reproduced correctly. Here, however, the indeterminate nature of $\tilde{Q}_{yz}$ is likely to affect the results from Eq. (38).

In Set H the correspondence between the different expressions for the $\Lambda $-coefficients is somewhat better. For q<-2 the simulations begin to exhibit vigorous vorticity generation at a very early stage making the error estimates increase significantly and the results for the $\Lambda $-effect in this regime are not very reliable. Again the best fit is achieved with ${\rm St}\approx1$, although a unique value that would fit all components cannot be found. The maxima of all $\Lambda $-coefficients are of the order 0.5 in this set.

3.4 On the validity of the MTA

We note that the largest deviations between the simulations and the closure model are seen when rapid rotation or strong shear are used. This may suggest that the simple closure model used here can break down at such circumstances. In order to test the validity of the present formulation of the MTA, we perform a set of simulations where q=1 is constant and the values of ${\rm Co}$ and ${\rm Sh}$ are varied. These results are compared to those from the MTA-closure model where the relaxation time is independent of ${\rm Co}$ and ${\rm Sh}$. The results are shown in Fig. 11. It appears that the simulation results for all of the stress components are in accordance with the closure model only for ${\rm Co}\la0.1$. The components Qxx and Qyy are not well reproduced for greater ${\rm Co}$. Rather surprisingly the Qzz component is consistent with the closure model for all values of ${\rm Co}$ explored here. For Qxy the agreement is rather good for ${\rm Co}\la0.3$, but for greater ${\rm Co}$ the stress changes sign as a function of ${\rm Co}$ in the simulations which is not reproduced by the closure model. Due to the differing behaviour of the stresses we cannot estimate the validity range of the MTA-closure very precisely based on this data only. It is likely that with strong enough rotation or shear the relevant time scale to be used in the closure model is associated with rotation or shear instead of our naive estimate of the eddy turnover time Eq. (16). For comparison, the time scales related to rotation and shear are of the same order of magnitude as the turnover time of the turbulence when ${\rm Co}=0.5$. At face value, the present results suggest that the effects of rotation and shear begin to affect the results even at somewhat slower rotation.

 \begin{figure} \par\includegraphics[width=8.8cm]{12653f11.eps} \end{figure} Figure 11:

Same as Fig. 4 but for a set of runs with $q=1=\mbox{const}.$ and ${\rm Re}\approx 28$.
Open with DEXTER

Furthermore, it turns out that in the presence of a shear flow of the form $\overline{U}_y(x)$ it is possible to estimate the relaxation time using the basic assumption of the MTA, Eq. (13), from the equation of Qxy. This is analogous to the passive scalar case where the flux due to an imposed gradient was found to the proportional to the triple correlation (Brandenburg et al. 2004). Let us now write

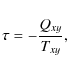\begin{displaymath}\tau=-\frac{Q_{xy}}{T_{xy}}, \end{displaymath} (43)

where

\begin{displaymath}T_{xy}=-c_s^2 \overline{ u_i \partial_j \ln \rho + u_j \partial_i \ln \rho} + \overline{Q_{ij}\vec{\nabla} \cdot {\vec{u}}}. \end{displaymath} (44)

We find that the last term of Eq. (44) is negligible in comparison to the other terms in all cases considered here. Representative results for the Strouhal number defined by Eq. (16) from two sets of runs are shown in Fig. 12. Firstly, as a function of rotation, the Strouhal number is between 1.5 and 3 for ${\rm Co}\la0.3$, whereas the value decreases for more rapid rotation and shear. The relaxation time can even be negative for ${\rm Co}\ga1$, indicating that the basic assumption of the MTA breaks down. Furthermore, for weak rotation and shear, the Strouhal number is constant as a function of the Reynolds number provided that ${\rm Re}>1$. This is consistent with the fact that in the regime ${\rm Re}\approx1$ the viscous time scale is of the same order of magnitude as the turnover time and neglecting the viscous terms in the equation of the stress is not justified. However, as we use Reynolds numbers of the order of 30 in most of our simulations, omitting the viscosity is permitted.

 \begin{figure} \par\includegraphics[width=8.8cm]{12653f12.eps} \end{figure} Figure 12:

Upper panel: strouhal number from the triple correlations as a function of ${\rm Co}$ for the same runs as in Fig. (11). Lower panel: ${\rm St}$ as a function of ${\rm Re}$ for runs with ${\rm Co}\approx 0.06$ and q=1.
Open with DEXTER

4 Conclusions

We have performed simulations of isotropically forced homogeneous turbulence under the influences of shear and rotation in order to study the turbulent transport properties. We find that in the absence of rotation the turbulent viscosity is of the order of the first order smoothing estimate $\nu_{\rm t0}={\textstyle{1\over3}}u_{\rm rms}k_{\rm f}^{-1}$, and that the Strouhal number saturates to a value of ${\rm St}\approx1.5$ for large Reynolds numbers.

When both rotation and shear are present, we seek to distinguish the diffusive (turbulent viscosity) and nondiffusive parts ($\Lambda $-effect) of the stress. In the case of Qxy this is achieved by assuming the turbulent viscosity to be proportional to ${\rm St}\nu_{\rm t0}$ and solving for the $\Lambda $-part from the equation of total stress, whereas for the other two off-diagonal components no diffusive contributions are assumed to appear in the equation of the total stress. As an independent check we derive analytical expressions for the $\Lambda $-effect using the minimal tau-approximation. The two expressions are then compared by using the Strouhal number as a free parameter. Although the results for the $\Lambda $-effect from the different approaches are not fully consistent in all cases, we find that they agree at least qualitatively, if not quantitatively, in most cases. The magnitude of the $\Lambda $-effect is a few times $0.1\nu_{\rm t0}$ in most cases in accordance with earlier studies (e.g. Käpylä & Brandenburg 2007,2008). However, a more precise determination and separation of the different coefficients requires a method akin to the test field method used succesfully in magnetohydrodynamics (Schrinner et al. 2005,2007).

We have also studied the Reynolds stresses using the minimal tau-approximation closure model where the Strouhal number ${\rm St}$ is the only free parameter. Comparing the results of this very simple closure model with our simulations shows that they generally agree surprisingly well with rather few exceptions. We find that in most cases the best fit between the closure model and full simulations is achieved when ${\rm St}\approx1$. We note, however, that the agreement between the closure model and the simulations becomes worse as the rotation rotation rate or shear are increased. The reason is likely to be that the relevant time scale in those regimes is no longer the turnover time but rather the time scale related to the rotation or shear. We feel that investigating the validity of the tau-approximation more precisely and futher improving its performance in reproducing the simulation results is a valid subject for further study.

Finding a closure model that reproduces the relevant properties of turbulence would be very useful in a variety of astrophysical applications. From the viewpoint of the present paper the most interesting application is the angular momentum balance of convectively unstable stellar interiors where rotation and shear flows are known to play important roles. Although the present model is highly idealised in comparison to stratified convection, the present results using the MTA-closure are promising. A logical step towards more general description of convective turbulent transport would be to study Boussinesq convection (e.g. Spiegel & Veronis 1960) and extend the closure model to work in the same regime (Miller & Garaud 2007). In addition to the Reynolds stresses, such models could be used to study anisotropic turbulent heat transport (e.g. Rüdiger 1982; Kitchatinov et al. 1994; Kleeorin & Rogachevskii 2006). Furthermore, these models could help in answering how some enigmatic results of local convection simulations, such as the narrow regions of very strong stresses near the equator (Chan 2001; Käpylä et al. 2004; Rüdiger et al. 2005) in the rapid rotation regime, can be explained. These subjects will be studied in subsequent publications.

Acknowledgements
We acknowledge the helpful comments from an anonymous referee. The computations were performed on the facilities hosted by the CSC - IT Center for Science in Espoo, Finland, who are financed by the Finnish ministry of education. The authors acknowledge financial support from the Academy of Finland grant Nos. 121431 (P.J.K.) and 112020 (J.E.S., M.J.K., A.J.L.). P.J.K. and M.J.K. acknowledge the hospitality of Nordita during the program `Turbulence and Dynamos.' J.E.S. acknowledges the financial support from the Finnish Cultural Foundation.

Appendix A: Stationary solutions to the MTA-closure model

Stationary solution to Eq. (15) can be obtained by setting $\dot{Q}_{ij}=0$ and solving the resulting equations

 
                                 Qxx = $\displaystyle 4~\Omega_z\tau Q_{xy}+ Q_{xx}^{(0)},$ (A.1)
Qxy = $\displaystyle -S \tau Q_{xx}+2~\Omega_x \tau Q_{xz}+2~\Omega_z \tau (Q_{yy}-Q_{xx}),$ (A.2)
Qxz = $\displaystyle 2~\Omega_z \tau Q_{yz}-2~\Omega_x \tau Q_{xy},$ (A.3)
Qyy = $\displaystyle -2~S\tau Q_{xy}+4~\Omega_x\tau Q_{yz}-4~\Omega_z\tau Q_{xy} + Q_{yy}^{(0)},$ (A.4)
Qyz = $\displaystyle -(S+2~\Omega_z)\tau Q_{xz} +2~\Omega_x \tau (Q_{zz}-Q_{yy}),$ (A.5)
Qzz = $\displaystyle -4~\Omega_x\tau Q_{yz}+ Q_{zz}^{(0)},$ (A.6)

where $\Omega_x$ and $\Omega_z$ are the components of the rotation vector as defined in Eq. (10), and we have used the fact that Qxy(0) = Qxz(0) = Qyz(0) =0.

A.1 Only shear, Sh 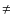$\neq $ 0, Co = 0

In the absence of rotation, the stationary solution to Eqs. (A.1) to (A.6) is


                                       Qxx= Qxx(0), (A.7)
    $\displaystyle Q_{xy}= -{\rm St}{\rm Sh}Q_{xx}^{(0)},$ (A.8)
    $\displaystyle Q_{yy}= 2~{\rm St}^2 {\rm Sh}^2 Q_{xx}^{(0)} + Q_{yy}^{(0)},$ (A.9)
    Qzz= Qzz(0), (A.10)
    Qxz= Qyz= 0, (A.11)
    $\displaystyle Q = Q_{xx}^{(0)} \left(1+2~{\rm St}^2 {\rm Sh}^2\right) + Q_{yy}^{(0)} + Q_{zz}^{(0)}.$ (A.12)

Since the forcing in the present case is isotropic, we can write

\begin{displaymath}Q_{xx}^{(0)} = Q_{yy}^{(0)} = Q_{zz}^{(0)} = {\textstyle{1\over3}}Q^{(0)}, \end{displaymath} (A.13)

where Q(0) is the trace of Qij(0) in the case without rotation or shear. Substituting (A.13) into the expression of Q, we obtain

\begin{displaymath}u_{\rm rms}^2 = Q = Q^{(0)} \left(1 + {\textstyle{2\over3}}{\rm St}^2 {\rm Sh}^2 \right). \end{displaymath} (A.14)

Using Eqs. (A.13) and (A.14) the normalised stresses, $\tilde{Q}_{ij}=Q_{ij}/u_{\rm rms}^2$ can be written in terms of the dimensionless parameters ${\rm St}$ and ${\rm Sh}$ as
                   $\displaystyle \tilde{Q}_{xx}$ = $\displaystyle \tilde{Q}_{zz}= \frac{1}{3+2~{\rm St}^2 {\rm Sh}^2},$ (A.15)
$\displaystyle \tilde{Q}_{xy}$ = $\displaystyle \frac{-{\rm St}{\rm Sh}}{3+2~{\rm St}^2 {\rm Sh}^2},$ (A.16)
$\displaystyle \tilde{Q}_{yy}$ = $\displaystyle 1 - \frac{2}{3+2~{\rm St}^2 {\rm Sh}^2}\cdot$ (A.17)

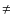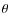A.2 Shear and rotation, Sh, Co $\neq $ 0, $\theta $ = 0

If rotation is present in the system and $\theta =0$, the solution of Eqs. (A.1) to (A.6) can be written as


                                        $\displaystyle Q_{xx} = \frac{[2~ {\rm Co}{\rm St}^2 ({\rm Co}+ {\rm Sh})+1] Q_{... ...rm Co}^2 {\rm St}^2 Q_{yy}^{(0)}}{1+4~ {\rm Co}{\rm St}^2 ({\rm Co}+{\rm Sh})},$ (A.18)
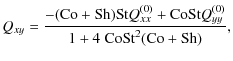    $\displaystyle Q_{xy} = \frac{-({\rm Co}+ {\rm Sh}) {\rm St}Q_{xx}^{(0)}+{\rm Co}{\rm St}Q_{yy}^{(0)}}{1+4~ {\rm Co}{\rm St}^2 ({\rm Co}+{\rm Sh})},$ (A.19)
    $\displaystyle Q_{yy} = \frac{[2~ {\rm Co}{\rm St}^2 ({\rm Co}+ {\rm Sh})+1] Q_{yy}^{(0)}}{1+4~ {\rm Co}{\rm St}^2 ({\rm Co}+{\rm Sh})}$  
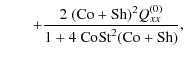    $\displaystyle \qquad+ \frac{2~ ({\rm Co}+{\rm Sh})^{2} Q_{xx}^{(0)}}{1+4~ {\rm Co}{\rm St}^2 ({\rm Co}+{\rm Sh})},$ (A.20)
    Qzz= Qzz(0), (A.21)
    Qxz = Qyz=0, (A.22)
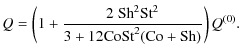    $\displaystyle Q = \left(1 + \frac{2~ {\rm Sh}^2 {\rm St}^2}{3 + 12{\rm Co}{\rm St}^2 ({\rm Co}+{\rm Sh})}\right)Q^{(0)}.$ (A.23)

If we allow $\tau \neq\tau_{\rm f}$ the solution can be obtained by simply multiplying the above solutions with a factor $\tau/\tau_{\rm f}$.

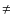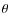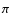A.3 Shear and rotation, Sh, Co $\neq $ 0, $\theta $ = $\pi $/2

Considering the case $\theta =\pi /2$, the solution is

                                Qxx = Qxx(0), (A.24)
Qxy = 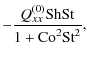$\displaystyle -\frac{Q_{xx}^{(0)} {\rm Sh}{\rm St}}{1+ {\rm Co}^2 {\rm St}^2},$ (A.25)
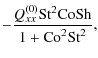Qxz = $\displaystyle -\frac{ Q_{xx}^{(0)} {\rm St}^2 {\rm Co}{\rm Sh}}{1+ {\rm Co}^2 {\rm St}^2},$ (A.26)
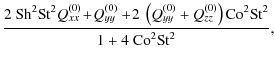Qyy = $\displaystyle \frac{ 2~ {\rm Sh}^2 {\rm St}^2 Q_{xx}^{(0)}\!+\!Q_{yy}^{(0)}+\!2... ...{(0)} + Q_{zz}^{(0)} \right){\rm Co}^2 {\rm St}^2}{1+4~ {\rm Co}^2 {\rm St}^2},$ (A.27)
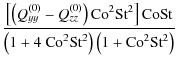Qyz = $\displaystyle \frac{ \left[\left(Q_{yy}^{(0)} - Q_{zz}^{(0)}\right) {\rm Co}^2 ... ...}{\left(1+4~ {\rm Co}^2 {\rm St}^2\right)\left(1+ {\rm Co}^2 {\rm St}^2\right)}$  
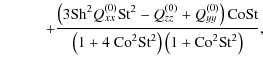    $\displaystyle \hspace{1cm} + \frac{\left(3 {\rm Sh}^2 Q_{xx}^{(0)} {\rm St}^2-Q... ...{\left(1+4~ {\rm Co}^2 {\rm St}^2\right)\left(1+ {\rm Co}^2 {\rm St}^2\right)},$ (A.28)
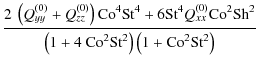Qzz = $\displaystyle \frac{ 2~ \left(Q_{yy}^{(0)} + Q_{zz}^{(0)}\right) {\rm Co}^4 {\r... ... }{\left(1+4~ {\rm Co}^2 {\rm St}^2\right)\left(1+{\rm Co}^2 {\rm St}^2\right)}$  
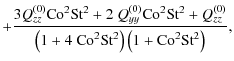    $\displaystyle + \frac{3 Q_{zz}^{(0)}{\rm Co}^2 {\rm St}^2+2~ Q_{yy}^{(0)} {\rm ... ...}{\left(1+4~ {\rm Co}^2 {\rm St}^2\right)\left(1+{\rm Co}^2 {\rm St}^2\right)},$ (A.29)
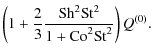Q = $\displaystyle \left(1+\frac{2}{3}\frac{ {\rm Sh}^2 {\rm St}^2}{1+{\rm Co}^2 {\rm St}^2}\right)Q^{(0)}.$ (A.30)

If $\tau \neq\tau_f$, the solution can be obtained in the same way as in the $\theta =0$ case.

Appendix B: Stability analysis

B.1 Vorticity dynamo in the presence of rotation

The existence of the vorticity dynamo in the present case can be studied using the same procedure used in Käpylä et al. (2009). When one assumes that the average velocity field depends only on z, the relevant mean field equation has the form

\begin{displaymath}\dot{\overline{\vec U}} = -S \overline{U}_x \hat{\vec{y}} - \... ...{\Omega} \times \overline{\vec U} + \nu {\overline{\vec U}}'', \end{displaymath} (B.1)

where the primes denote z-derivatives. Assuming the flow to be incompressible, $\vec{\nabla} \cdot \overline{\vec U}=\overline{\vec U}_{z,z}=0$, so $\overline{U}_z=\mbox{const.}=0$ by a suitable choice of the initial condition. The nonlinear term $-\overline{\vec{u} \cdot \vec{\nabla} \vec{u}}$can be represented in terms of the large-scale velocity by introducing a turbulent eddy viscosity tensor $\nu_{ij}$ (see, e.g. Elperin et al. 2003; Käpylä et al. 2009)

\begin{displaymath}-(\overline{\vec{u} \cdot \vec{\nabla} \vec{u}})_i = \nu_{ij} \overline{U}''_j. \end{displaymath} (B.2)

Substituting Eq. (B.2) to Eq. (B.1) gives
 
                                 $\displaystyle \dot{\overline{U}}_x$ = $\displaystyle (\nu+\nu_{xx}) {\overline{U}_x}''+\nu_{xy} {\overline{U}_y}''+ 2~\Omega_z \overline{U}_y,$ (B.3)
$\displaystyle \dot{\overline{U}}_y$ = $\displaystyle (\nu+\nu_{yy}) {\overline{U}_y}''+\nu_{yx} {\overline{U}_x}''-(S+2~\Omega_z) \overline{U}_x.$ (B.4)

We note that because $\overline{U}_z=0$, no terms proportional to $\Omega_x$appear. Similarly as in Käpylä et al. (2009), we assume a stationary state and seek solutions to Eqs. (B.3) and (B.4). Now we can apply a Fourier transform and arrive at


 
    $\displaystyle (\nu+\nu_{xx})k^2 {\hat{U}_x}+(\nu_{xy}k^2-2~\Omega_z) \hat{U}_y = 0,$ (B.5)
    $\displaystyle (\nu+\nu_{yy}) k^2 {\hat{U}_y}+(\nu_{yx}k^2+S+2~\Omega_z) \hat{U}_x = 0,$ (B.6)

where $\hat{U}_i$ are the Fourier amplitudes of $\overline{U}_i$, and k is the wavenumber. Equations (B.5) and (B.6) imply that the sufficient condition for the mean vorticity dynamo to appear is

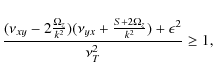\begin{displaymath}\frac{(\nu_{xy} - 2 \frac{\Omega_z}{k^2})(\nu_{yx}+\frac{S+2\Omega_z}{k^2})+\epsilon^2}{\nu_T^2} \ge 1, \end{displaymath} (B.7)

where $\nu_T=\nu+\frac{1}{2}(\nu_{xx}+\nu_{yy})$ and $\epsilon=\frac{1}{2}(\nu_{xx}-\nu_{yy})$. In the absence of shear we recover the expression derived in Käpylä et al. (2009), suggesting that $\nu_{xy}S>0$. On the other hand, if we set $\nu=0$ and $\nu_{ij}=0$, we have

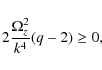\begin{displaymath}2 \frac{\Omega_z^2}{k^4} (q-2) \ge 0, \end{displaymath} (B.8)

where $q=-S/\Omega_z$. Since $\Omega_z^2/k^4$ is always positive, this inequality holds if $q \ge 2$. This is the standard Rayleigh stability condition (for instability). It is clear that rotation has a stabilizing effect in the system provided that q<2. It is, however, conceivable that for small enough q the component $\nu_{xy}$ overcomes the rotational stabilization. However, even for our most extreme runs with q=-5 this appears not to be the case.

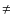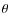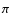B.2 Force balance for Sh, Co $\neq $ 0, $\theta $ = $\pi $/2

We find that large-scale flows tend to always appear in the simulations at $\theta =\pi /2$. A very similar setup was studied by Leprovost & Kim (2008b) who studied the force balance for the large-scale flow including also the pressure gradient

\begin{displaymath}\dot{\overline{\vec U}} = -S \overline{U}_x \vec{\hat{y}} - \... ...c U}-\frac{1}{\rho}\vec{\nabla} P + \nu {\overline{\vec U}}''. \end{displaymath} (B.9)

Assuming that there is no turbulence ( $-\overline{\vec{u} \cdot \vec{\nabla}\vec{u}}=0$) and no large-scale flows ( $\overline{\vec U}=0$), apart from the imposed shear $\overline{\vec U}^{(0)}=(0,Sx,0)$, one finds the following equations


 
    $\displaystyle \partial_x P = 0,$ (B.10)
    $\displaystyle \partial_z P -2\rho~\Omega_0 S x = 0.$ (B.11)

We see that Eq. (B.10) indicates that the pressure P is independent of x. The other Eq. (B.11), however, gives an explicit x-dependence for P. Therefore, we can conclude that unless there exists some sort of large-scale forcing to cancel the pressure gradient, there can be no equilibrium for this system. As noted by Leprovost & Kim (2008b), in the real physical situations phenomena like the thermal winds can balance the system.

References

Online Material

Table B.1:   Summary of the runs with shear flow only. Here $\tilde{Q}_{ij}=Q_{ij}/u_{\rm rms}^2$, and brackets around a quantity signify that the number is not statistically significant.

Table B.2:   Summary of the runs in the Sets E and F with $\theta =0$.


Footnotes

... rotation[*]
Tables B1-B3 are only available in electronic form at http://www.aanda.org
... ODE[*]
http://code.google.com/p/pencil-code/

All Tables

Table 1:   Summary of the different sets of simulations. The values of ${\rm Re}$, ${\rm Co}$, and ${\rm Sh}$ are given in terms of $u_{\rm rms}$ from a run with ${\rm Co}={\rm Sh}=0$.

Table B.1:   Summary of the runs with shear flow only. Here $\tilde{Q}_{ij}=Q_{ij}/u_{\rm rms}^2$, and brackets around a quantity signify that the number is not statistically significant.

Table B.2:   Summary of the runs in the Sets E and F with $\theta =0$.

All Figures

  \begin{figure} \par\includegraphics[width=9cm]{12653fg1.eps} \end{figure} Figure 1:

Velocity component Uy, in the units of the sound speed, from the Run B6 with ${\rm Re}=387$, ${\rm Sh}=-0.20$, and ${\rm Co}=0$, resolution 10243.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{12653fg2.eps} \end{figure} Figure 2:

Upper panel: turbulent viscosity divided by the molecular viscosity for the simulation Sets A (solid line) and B (dashed line) as a function of the Reynolds number. The dotted line, proportional to ${\rm Re}$, is shown for reference. Lower panel: the Strouhal number, ${\rm St}=\nu _{\rm t}/\nu _{\rm t0}$, for the same sets of simulations as in the upper panel.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm]{12653fg3.eps} \end{figure} Figure 3:

From top to bottom: Reynolds stress components Qxx, Qyy, Qzz, and Qxy, normalised by $u_{\rm rms}^2$, as functions of the shear parameter for simulation Sets C and D with Reynolds numbers, based on $u_{\rm rms}$ from a run with ${\rm Co}={\rm Sh}=0$, of $\approx $27 (diamonds) and $\approx $75 (triangles), respectively. The curves in each panel show the results of the MTA-closure with three Strouhal numbers. The linestyles are as indicated in the legend in the top panel.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{12653fg4.eps} \end{figure} Figure 4:

Same as Fig. 3 but for Set E, and different Strouhal numbers as indicated by the legend in the uppermost panel.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm]{12653fg5.eps} \end{figure} Figure 5:

Same as Fig. 4 but for the simulation Set F.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm]{12653fg6.eps} \end{figure} Figure 6:

Upper panel: the two measures of the horizontal $\Lambda $-effect from Set E according to Eq. (29) (solid line) and Eq. (32) (dashed). Lower panel: the same as above but from Set F.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm]{12653fg7.eps} \end{figure} Figure 7:

Left column: $\tilde{Q}_{xx}$ ( top panel), $\tilde{Q}_{yy}$ ( middle), and $\tilde{Q}_{zz}$ ( bottom) from the simulation Set G. Right column: $\tilde{Q}_{xy}$ ( top panel), $\tilde{Q}_{xz}$ ( middle), and $\tilde{Q}_{yz}$ ( bottom) from Set G. The curves in each panel show the closure model results with three different Strouhal numbers as indicated in the legend ( righ column, middle panel).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm]{12653fg8.eps} \end{figure} Figure 8:

Same as Fig. 7 but for the simulation Set H.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm]{12653fg9.eps} \end{figure} Figure 9:

Nondiffusive contributions to the Reynolds stresses parameterized by the coefficients $\tilde{\Lambda}_{\rm H}$ ( top panel), $\tilde{\Lambda}_{\rm M}$ ( middle), and $\tilde{\Lambda}_{\rm V}$ ( bottom) from the simulation Set G. In each panel two expressions are compared and the linestyles are explained in the legends.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm]{12653f10.eps} \end{figure} Figure 10:

Same as Fig. 9 but for the simulation Set H.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm]{12653f11.eps} \end{figure} Figure 11:

Same as Fig. 4 but for a set of runs with $q=1=\mbox{const}.$ and ${\rm Re}\approx 28$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm]{12653f12.eps} \end{figure} Figure 12:

Upper panel: strouhal number from the triple correlations as a function of ${\rm Co}$ for the same runs as in Fig. (11). Lower panel: ${\rm St}$ as a function of ${\rm Re}$ for runs with ${\rm Co}\approx 0.06$ and q=1.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.