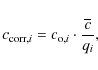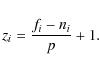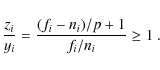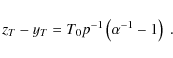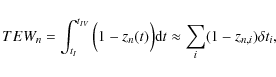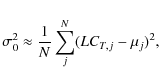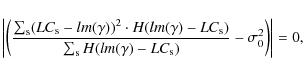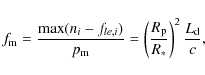| Issue |
A&A
Volume 505, Number 3, October III 2009
|
|
|---|---|---|
| Page(s) | 1277 - 1282 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912454 | |
| Published online | 18 August 2009 | |
How stellar activity affects the size estimates of extrasolar planets
S. Czesla - K. F. Huber - U. Wolter - S. Schröter - J. H. M. M. Schmitt
Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
Received 8 May 2009 / Accepted 1 July 2009
Abstract
Light curves have long been used to study stellar activity and have more recently become a major tool in the field of exoplanet research.
We discuss the various ways in which stellar activity can influence transit light curves, and study the effects using
the outstanding photometric data of the CoRoT-2 exoplanet system.
We report a relation between the ``global'' light curve and the transit profiles, which turn out to be
shallower during high spot coverage on the stellar surface.
Furthermore, our analysis reveals a color dependence of the transit light curve
compatible with a wavelength-dependent limb darkening law as observed on the Sun.
Taking into account activity-related effects, we redetermine the orbit inclination and planetary radius and find the
planet to be ![]() 3% larger than reported previously.
Our findings also show that exoplanet research cannot generally ignore the effects of stellar activity.
3% larger than reported previously.
Our findings also show that exoplanet research cannot generally ignore the effects of stellar activity.
Key words: techniques: photometric - stars: activity - starspots - stars: individual: CoRoT-2a - planetary systems
1 Introduction
The brightness distribution on the surface of active stars is both spatially inhomogeneous and temporally variable. The state and evolution of the stellar surface structures can be traced by the rotational and secular modulation of the observed photometric light curve. In the field of planet research, light curves including planetary transits are of particular interest, since they hold a wealth of information about both the planet and its host star.
The outstanding quality of the space-based photometry provided by the CoRoT mission (e.g., Auvergne et al. 2009) provides stellar
light curves of unprecedented precision, temporal cadence and coverage. While primarily designed
as a planet finder, the CoRoT data are also extremely interesting in the context of
stellar activity. Lanza et al. (2009) demonstrated the information content to be extracted from
these light curves in the specific case of CoRoT-2a. This star is solar-like in mass and radius, but
rotates faster at a speed of
![]() km s-1 (Bouchy et al. 2008). Its rotation period
of
km s-1 (Bouchy et al. 2008). Its rotation period
of ![]() 4.52 days was deduced from slowly evolving active regions, which dominate the photometric variations.
Thus, CoRoT-2a is a very active star by all standards. Even more remarkably, CoRoT-2a is orbited by a giant
planet (Alonso et al. 2008), which basically acts as a shutter scanning the surface of CoRoT-2a along a well defined
latitudinal band.
4.52 days was deduced from slowly evolving active regions, which dominate the photometric variations.
Thus, CoRoT-2a is a very active star by all standards. Even more remarkably, CoRoT-2a is orbited by a giant
planet (Alonso et al. 2008), which basically acts as a shutter scanning the surface of CoRoT-2a along a well defined
latitudinal band.
The transiting planetary companion provides a key to understanding the surface structure of its host star. While previous analyses have either ignored the transits (Lanza et al. 2009) or the ``global'' light curve (Wolter et al. 2009), we show that there is a relation between the transit shape and the global light curve, which cannot generally be neglected in extrasolar planet research.
2 Observations and data reduction
Alonso et al. (2008) discovered the planet CoRoT-2b using the photometric CoRoT data (see Table 1). Its host star
has a spectral type of G7V with an optical (stellar) companion too close to be resolved by CoRoT.
According to Alonso et al. (2008), this secondary contributes a constant
![]() % of the total CoRoT-measured flux.
CoRoT-2b's orbital period of
% of the total CoRoT-measured flux.
CoRoT-2b's orbital period of ![]() 1.74 days is about one third of CoRoT-2a's rotation period, and the almost continuous CoRoT data span 142 days, sampling about 30 stellar rotations and more than 80 transits.
The light curve shows clear evidence of strong activity: there is substantial modulation
of the shape on timescales of several days, and the transit profiles are considerably deformed as a consequence of surface inhomogeneities
(Wolter et al. 2009).
1.74 days is about one third of CoRoT-2a's rotation period, and the almost continuous CoRoT data span 142 days, sampling about 30 stellar rotations and more than 80 transits.
The light curve shows clear evidence of strong activity: there is substantial modulation
of the shape on timescales of several days, and the transit profiles are considerably deformed as a consequence of surface inhomogeneities
(Wolter et al. 2009).
Table 1: Stellar/planetary parameters of CoRoT-2a/b.
Our data reduction starts with the results provided by the CoRoT N2 pipeline (N2_VER 1.2). CoRoT provides three-band photometry (nominally red, green, and blue), which we extend by a virtual fourth band resulting from the combination (addition) of the other bands. This ``white'' band is, henceforth, treated as an independent channel, and our analysis will mainly refer to this band. It provides the highest count rates and, more importantly, is less susceptible to instrumental effects such as long-term trends and ``jumps'' present in the individual color channels.
In all bands, we reject those data points
flagged as ``bad'' by the standard CoRoT pipeline (mostly related to the South Atlantic anomaly).
The last step leaves obvious outliers in the light curves. To remove them, we estimate the standard deviation of the data point distribution in short (![]() 3000 s) slices and reject
the points more than 3
3000 s) slices and reject
the points more than 3![]() off a (local) linear model.
Inevitably, we also remove a fraction of physical data (statistical outliers) in this step, but we estimate
that loss to be less than a percent of the total number of data points, which we consider acceptable.
off a (local) linear model.
Inevitably, we also remove a fraction of physical data (statistical outliers) in this step, but we estimate
that loss to be less than a percent of the total number of data points, which we consider acceptable.
In all bands apart from the white, we find photometric discontinuities (jumps), which are caused by particle impact on the CoRoT detector. In the case of CoRoT-2a, the jumps are of minor amplitude compared to the overall count rate level, and we correct them by adjusting the part of the light curve following the jump to the preceding level.
Finally, we correct the CoRoT photometry for systematic, instrumental trends visible in all bands apart from white. To approximate the instrumental trend, we fit the (entire) light curve with a second order polynomial, q, and apply the equation
where
The resulting light curve still shows a periodic signal clearly related to the orbital motion of the CoRoT satellite. This is again a minor effect in the white band, and we neglect this in the context of the following analysis.
In a last step, we subtract 5.6% of the median light curve level to account for the companion contribution. We use the same rule for all bands, which is only an approximation because, as Alonso et al. (2008) point out, the companion has a later type (probably K or M) and, therefore, a different spectrum from CoRoT-2a.
3 Analysis
3.1 Transit profiles and stellar activity
A planet crossing the stellar disk imprints a characteristic transit feature on the light curve of the star (e.g., Pont et al. 2007; Wolter et al. 2009). The exact profile is determined by planetary parameters as well as the structure of the stellar surface. A model that describes the transit profile must account for both. One of the key parameters of the surface model is the limb darkening law. The presence of limb darkening seriously complicates transit modeling, because it can considerably affect the transit profile, while it is difficult to recover its characteristics from light curve analyses (e.g., Winn 2009).
Stellar activity adds yet another dimension of complexity to the problem, because a (potentially evolving) surface brightness distribution also affects the transit profiles. The local brightness on the surface can either be decreased by dark spots or increased by bright faculae compared to the undisturbed photosphere. Spots (or faculae) located within the eclipsed section of the stellar surface lead to a decrease (increase) in the transit depth, and the true profile depends on the distribution of those structures across the planetary path. Spots and faculae located on the non-eclipsed section of the surface do not directly affect the transit profile but change the overall level of the light curve. As transit light curves are, however, usually normalized with respect to the count rate level immediately before and after the transit, the non-eclipsed spot contribution enters (or can enter) the resulting curve as a time-dependent modulation of the normalized transit depth.
3.2 Transit light-curve normalization
As mentioned above, the normalization may affect the shape of the transit profiles. We now discuss two normalization approaches and compare their effect on the transit profiles. We define fi to be the measured flux in time bin i, ni an estimate of the count rate level without the transit (henceforth referred to as the ``local continuum''), and p a
measure of the unspotted photospheric level in the light curve, i.e., the count rate obtained in the respective band,
when the star shows a purely photospheric surface. Usually, the quantity
is referred to as the ``normalized flux''.
If we normalize the flux according to Eq. (2), we may produce variations in the transit light-curve depth in response to non-uniform surface flux distributions as encountered on active stars. To demonstrate this, we assume that a planet transits its host star twice. During the first transit, the stellar surface remains free of spots, but during the second transit there is a large active region on any part of the star not covered by the planetary disk (but visible). Consequently, the local continuum estimate, ni, for the second transit is lower, and the normalized transit appears deeper, although it is exactly the same transit in absolute (non-normalized) numbers.
To overcome this shortcoming, we define the alternative normalization to be
In both cases, the transit light curve is normalized with respect to the local continuum either by division or subtraction. The conceptual difference lies in the treatment of the local continuum level and how it enters the normalized transit light curve. Using Eq. (3), the observed transit is shifted, normalized by a constant, and shifted again. While the scaling in this case remains the same for all transits, the scaling applied in Eq. (2) is a function of the local continuum.
Following the above example, we assume that the same transit can be normalized by using Eqs. (2) and (3). To evaluate the differences between the approaches, we consider the expression
For ni=p, Eq. (4) holds as a strict equality, i.e., both normalizations yield identical results. The inequality equates to true, if p>ni and ni>fi. The first condition reflects that the local continuum estimate should not exceed the photospheric light-curve level, and the second one says that the light-curve level is below the local continuum. The second condition is naturally fulfilled during a transit, and the first is also met as long as faculae do not dominate over the dark spots during the transit. In the case of CoRoT-2a, Lanza et al. (2009) find no evidence of a significant flux contribution due to faculae, so that we conclude that the normalized transit obtained using Eq. (3) is always shallower than that resulting from Eq. (2), unless ni=p, in which case the outcomes are equal.
3.2.1 Quantifying the normalization induced difference in transit depth
We now study a single transit and consider data points covered by index set j, for which the term nj-fj reaches a
maximal value of T0 at some index value j=T. At this position, the normalization obtained from Eq. (3) is
given by
zT=(fT-nT)/p+1=-T0/p+1, whereas
Eq. (2) yields
yT=fT/nT=(nT-T0)/nT. These values are now used to compare the transit depths provided by the
two normalizations.
We note that we assume that the normalized depth is
maximal at index T; this is always true for Eq. (3), but not necessarily for Eq. (2), a point that we assume to be a minor issue.
We again find that zT=yT if nT=p. If, however,
the local continuum estimate is given by
![]() (
(
![]() ), the results differ by
), the results differ by
Using the extreme values observed for CoRoT-2a (
3.2.2 Which normalization should be used?
For planetary research it is important to ``clean'' the transit light curves of stellar activity before deriving the ``undisturbed'' profile associated with the planet only. Since transit light curves normalized using Eq. (3) are all scaled using the same factor, they preserve their shape and depth (at least relative to each other) and can, therefore, be combined consistently, which is not necessarily the case when Eq. (2) is used. This does not mean that the obtained transit depth is necessarily the ``true'' depth, because Eq. (3) includes the photospheric brightness level, p, as a time-independent scaling factor. At least in the context of the light-curve analysis, p cannot be determined with certainty since the star may not show an undisturbed surface during the observation, which may actually never be shown.
A problem evident in CoRoT light-curve analyses is the
existence of long-term instrumental gradients in the data (cf. Sect. 2). By modeling these trends with
a ``sliding'' response, ![]() ,
of the detector, so that the relation between ``true'' photometry, ci, and observation,
,
of the detector, so that the relation between ``true'' photometry, ci, and observation,
![]() ,
is given by
,
is given by
![]() ,
we find that Eq. (1) yields
,
we find that Eq. (1) yields
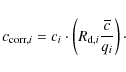 |
(6) |
Obviously, the true photometry is recovered when the embraced term equates to one. However, the scaling of
For our transit analysis, we argue in favor of the normalization along Eq. (3). We estimate the photospheric level from the highest count rate during the most prominent global maximum (at
![]() )
in each individual band. These estimates are based on the reduced light curves; in particular, we have accounted for both the instrumental trend and the stellar companion.
Throughout our analysis, we use the values
)
in each individual band. These estimates are based on the reduced light curves; in particular, we have accounted for both the instrumental trend and the stellar companion.
Throughout our analysis, we use the values
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() (in units of e-/32s).
Since even at that time, spots are likely to have been present on the stellar disk, these estimates might represent lower limits to the
true value of p.
(in units of e-/32s).
Since even at that time, spots are likely to have been present on the stellar disk, these estimates might represent lower limits to the
true value of p.
3.3 Transit profiles in CoRoT-2a
The global light curve of CoRoT-2a shows pronounced maxima and minima and a temporally variable amplitude of the global modulation (Alonso et al. 2008). It is natural to expect the spot coverage on the eclipsed section of the stellar surface to be smallest where the global light curve is found at a high level, and transit events occurring during those phases should, thus, be least contaminated with the effects of stellar activity. The opposite should be true for transits during low light-curve levels.
To quantify the impact of activity on the transit profile, we define the transit equivalent width (TEW) of transit n
where tI and tIV must be chosen so that they enclose the entire transit. Extending the integration boundaries beyond the true extent of the transit does not change the expectation value of Eq. (7), but only introduces an extra amount of error. The nominal unit of the TEW is time.
3.3.1 The relation between transit equivalent width and global light-curve modulation
As outlined above, we expect activity to have greater impact when the overall light-curve level is low. When this is true, it should be reflected by a relation between the transit equivalent width and the transit continuum level (the overall light-curve level at transit time).
| |
Figure 1: Transit equivalent width (TEW) versus transit continuum level as well as the best-fit linear model. |
| Open with DEXTER | |
In Fig. 1, we show the distribution of TEWs as a function of the local continuum level for all 79 transits observed with a 32 s sampling. There is a clear tendency for larger TEWs to be associated with higher continuum levels, thus, providing obvious evidence of activity-shaped transit light curves. In the same figure, we also show the best-fit linear model relation, which has a gradient of d(TEW)/d(CL)
![]() s/(e-32 s).
s/(e-32 s).
To corroborate the reality of the above stated correlation, we calculated the correlation coefficient, R.
Its value of R = 0.642 confirms the visual impression of
a large scatter in the distribution of data points (cf., Fig. 1). We estimate the statistical error for
a single data point to be ![]() 0.1%, so that the scatter cannot be explained by measurement errors. To check whether the continuum level and the TEW are
independent variables, we employ a t-test and find the null hypothesis (independent quantities) to be rejected with an error probability
of
0.1%, so that the scatter cannot be explained by measurement errors. To check whether the continuum level and the TEW are
independent variables, we employ a t-test and find the null hypothesis (independent quantities) to be rejected with an error probability
of
![]() ,
so that
the correlation between the TEWs and the continuum level must be regarded as highly significant.
,
so that
the correlation between the TEWs and the continuum level must be regarded as highly significant.
As a cross-check of the interpretation of this finding, we also investigated the distribution of TEWs against time, which shows no such linear relation (R=0.110). Therefore, we argue that the effect is not instrumental or caused by our data reduction, but physical.
3.4 Comparing high and low continuum level transits
Since activity is evident in the profiles of the transit light curves, we further investigate its effect by comparing the most and least affected transit light curves. Therefore, we average the ten transits with the highest continuum levels (No. 3, 16, 42, 47, 50, 55, 68, 73, 76, and 81) and compare the result to an average of the ten transits with the lowest continuum level (No. 15, 23, 35, 40, 43, 69, 72, 75, 77, and 80). In Fig. 2, we show the two averages as well as our computed lower envelope (see Sect. 3.5) superimposed on the entire set of folded photometry data points. The distribution of the entire set is denoted by a color gradient (red) with stronger color indicating a stronger concentration of data points. The curve obtained from the transits at a ``low continuum state'' is clearly shallower, as was already indicated by the TEW distribution presented in Fig. 1.
![\begin{figure}
\par\includegraphics[height=8.8cm, angle=-90]{12454fg2.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12454-09/Timg45.png) |
Figure 2: Average transit light curves obtained by combining the ten profiles exhibiting the highest (thick dashes) and lowest (thin dashes) continuum levels. The crosses indicate our lower envelope estimate and the color gradient (red) illustrates the distribution of data points for all available transits. |
| Open with DEXTER | |
The difference in TEW amounts to ![]() 15.5 s in this extreme case.
We checked the significance of this number with a Monte Carlo
approach. On the basis of 20 randomly chosen transits, we constructed two averaged light curves using 10 transits for each and calculated the difference in TEW. Among 1000 trials, we did not find a single pair with a difference beyond 12 s, so that the result is not likely to be caused by an accidental coincidence.
15.5 s in this extreme case.
We checked the significance of this number with a Monte Carlo
approach. On the basis of 20 randomly chosen transits, we constructed two averaged light curves using 10 transits for each and calculated the difference in TEW. Among 1000 trials, we did not find a single pair with a difference beyond 12 s, so that the result is not likely to be caused by an accidental coincidence.
3.5 Obtaining a lower envelope to the transit profiles
As was demonstrated in the preceding section, activity shapes the transit light curves, and we cannot exclude that every transit is affected so that a priori no individual profile can be used as a template representing the ``undisturbed'' light curve. The distortion of the individual profiles is, however, not completely random, but the sign of the induced deviation is known as long as we assume that the dark structures dominate over bright faculae, which seems justified for CoRoT-2a (Lanza et al. 2009). In this case, activity always tends to raise the light-curve level and, thus, decreases the transit depth. Therefore, the most suitable model of the undisturbed profile can be estimated to be a lower envelope to the observed transit profiles.
We take a set of NT transit observations and fold the
associated photometry at a single transit interval, providing us with the set
LCT,i of transit data points. If the lower envelope were already among the set of observed transits, it would in principle look like every other light curve. In particular, it shows
the same amount of intrinsic scattering (not including activity), characterized by the variance
![]() .
.
We estimate the variance to be
where
where H denotes the Heaviside function (H(x)=1 for x>0, and H(x)=0 otherwise). In this way, we search for the local model compatible with the known variance of the lower envelope. The ratio on the left-hand side of Eq. (9) represents a variance estimator exclusively based on data points below the local model. It increases (strictly) monotonically except for the values of
In Fig. 2, we show the lower envelope, which is in far closer agreement with the average of
the high continuum transit profiles than with its low continuum counterpart. The derivation of the lower envelope is based on
Eq. (9). To obtain an estimate of
![]() ,
we fitted a 500 s long span within the transit
flanks (
,
we fitted a 500 s long span within the transit
flanks (
![]() s from the transit center), where activity has little effect, with a straight line and calculated the variance with respect to this model. The resulting value (using normalized flux)
of
s from the transit center), where activity has little effect, with a straight line and calculated the variance with respect to this model. The resulting value (using normalized flux)
of
![]() was adopted in the calculation.
Furthermore, we chose a bin width of 150 s, and the ``local model'' was defined as a regression line within a
was adopted in the calculation.
Furthermore, we chose a bin width of 150 s, and the ``local model'' was defined as a regression line within a ![]() 100 s time span around the bin center. Additionally, we postulated that
at least 8 (out of
100 s time span around the bin center. Additionally, we postulated that
at least 8 (out of ![]() 350) data points per bin should be located below the envelope, which improved the stability of the method to the effect of outliers but has otherwise little impact.
350) data points per bin should be located below the envelope, which improved the stability of the method to the effect of outliers but has otherwise little impact.
3.6 Transit profiles in different color channels
CoRoT observes in three different bands termed ``red'', ``green'', and ``blue''. In the following, we present a qualitative analysis of the transit profiles in the separate bands. In the case of CoRoT-2a, approximately 70% of the flux is observed in the red band, and the remaining 30% is more or less equally distributed among the green and blue channels. To compare the profiles, we average all available transits in each band individually and normalize the results with respect to their TEW, i.e., after this step they all have the same TEW. The resulting profiles represent the curves that would be obtained if the stellar flux integrated along the planetary path was the same in all bands.
In Fig. 3, we show the transit light curves normalized in this way (TEW=1) obtained in the three bands.
![\begin{figure}
\par\includegraphics[height=8.8cm, angle=-90]{12454fg3.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12454-09/Timg54.png) |
Figure 3: Left panel: normalized transit in the three CoRoT bands red, green, and blue obtained by averaging all available data. Upper right: close-up of the transit center. Lower right: close-up of the ingress flank of the transit. |
| Open with DEXTER | |
The normalized transits show a difference in both their flank profile and their depth. The blue and green transit profiles are both narrower than the red one, and deeper at the center. This behavior is most pronounced in the blue band, so that the green transit light curve virtually always lies in-between the curves obtained in red and blue.
The behavior described above can be explained by a color-dependent limb darkening law, with stronger limb darkening at shorter wavelengths as predicted by atmospheric models (Claret 2004) and observed on the Sun (Pierce & Slaughter 1977). We checked that analytical transit models (Pál 2008) generated for a set of limb darkening coefficients, indeed, reproduce the observed behavior when normalized with respect to their TEW.
Normalizing the averaged transits not with respect to TEW but using Eq. (3) yields approximately the same depth in all bands, while the difference in the flanks becomes more pronounced. The reason for this could be an incorrect relative normalization, which can e.g., occur if the eclipsed section of the star is (on average) redder than the remainder of the surface because of pronounced activity or gravity darkening, or it may be a relic of an inappropriate treatment of the companion's flux contribution. Whatever the explanation, it is clear from Fig. 3 that the flanks and centers in the individual bands cannot be reconciled simultaneously by a renormalization. Therefore, our analysis shows that the transit light curves are color dependent.
4 Stellar activity and planetary parameters
The preceding discussion shows that stellar activity has a considerable influence on the profile of the transit light curves, and the derivation of the planetary parameters will therefore also be affected. We now determine the radius and the orbit inclination of CoRoT-2b taking activity into account, and discuss the remaining uncertainties in the modeling.
4.1 Deriving the planetary radius and inclination from the lower envelope profile
In the analysis presented by Alonso et al. (2008), the fit to the planetary parameters is based on the average of 78 transit light curves (see Table 1 for an excerpt of their results). While this yields a good approximation, the results still include a contribution of stellar activity, and an undisturbed transit is needed to calculate ``clean'' planetary parameters.
We follow a simplified approach to estimate the impact of activity on the planetary parameters. In particular, we use the lower envelope derived in Sect. 3.4 as the most suitable available model for the undisturbed transit. Starting from the results reported by Alonso et al. (2008), we reiterate the fit of the planetary parameters. In our approach, we fix the parameters of transit timing, i.e., the semi-major axis and stellar radius, and the limb darkening coefficients at the values given by Alonso et al. (2008) (cf. Table 1). The two free parameters are the planetary radius and its inclination.
We note that limb darkening coefficients recovered
by light curve analyses are not reliable, especially when more than one coefficient is fitted (e.g., Winn 2009).
However, since an accurate calibration
of the CoRoT color bands is not yet available and the coefficients determined by Alonso et al. (2008) roughly correspond to
numbers predicted by stellar atmosphere models![]() , we
decided to use the Alonso et al. values, which also simplifies the comparison of the results.
, we
decided to use the Alonso et al. values, which also simplifies the comparison of the results.
For the fit, we use the analytical models given by Pál (2008) in combination with a Nelder-Mead simplex algorithm (e.g., Press et al. 1992).
| |
Figure 4: Lower envelope of all normalized transit light curves (already shown in Fig. 2) and our model fit. |
| Open with DEXTER | |
The result of our modeling is illustrated in Fig. 4. The most probable radius ratio is
![]() at an inclination of
at an inclination of
![]() .
The quoted errors are statistical errors and
only valid in the context of the model. These numbers should be compared with the values
.
The quoted errors are statistical errors and
only valid in the context of the model. These numbers should be compared with the values
![]() and
and
![]() (cf., Table 1) derived without taking activity effects into account. The best-fit model inclination is compatible with the
value determined by Alonso et al. (2008), but ``our'' planet is larger by
(cf., Table 1) derived without taking activity effects into account. The best-fit model inclination is compatible with the
value determined by Alonso et al. (2008), but ``our'' planet is larger by ![]() 3%.
The planet's size depends mainly on the transit depth, which is, indeed, affected at about
this level by both normalization (Sect. 3.2.1) and stellar activity (Sect. 3.4).
3%.
The planet's size depends mainly on the transit depth, which is, indeed, affected at about
this level by both normalization (Sect. 3.2.1) and stellar activity (Sect. 3.4).
Clearly, the derived change in
![]() of 0.005 is much larger than the statistical error obtained from light-curve
fitting, and, therefore, the neglect of activity leads to systematic errors in excess of statistical errors. While the overall
effect in planet radius is
of 0.005 is much larger than the statistical error obtained from light-curve
fitting, and, therefore, the neglect of activity leads to systematic errors in excess of statistical errors. While the overall
effect in planet radius is ![]() 3%, the error in density becomes
3%, the error in density becomes ![]() 10%. These errors are certainly
tolerable for modeling planetary mass-radius relationships, but they are unacceptable for precision measurements of possible
orbit changes in these systems.
10%. These errors are certainly
tolerable for modeling planetary mass-radius relationships, but they are unacceptable for precision measurements of possible
orbit changes in these systems.
4.1.1 Planetary parameters and photospheric level
As already indicated the normalization according to Eq. (3) relies on a ``photospheric light-curve level'', p, which enters as a global scaling factor and, therefore, also impedes the constraint of the planet's properties.
In a simple case, the star appears as a sphere with a purely photospheric surface, and the observed transit
depth, f0, can be identified with the square of the ratio of the planetary to the stellar radius
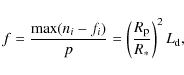 |
(10) |
where
Assume our estimate, ![]() ,
of the photospheric level underestimates the true value, p, by a factor of
,
of the photospheric level underestimates the true value, p, by a factor of
![]() so that
so that
![]() and fle,i denotes the lower envelope transit light curve. The measured transit depth,
and fle,i denotes the lower envelope transit light curve. The measured transit depth, ![]() ,
then becomes
,
then becomes
and another scaling factor must be applied to the radius ratio. While
The value of c cannot be quantified in the context of this work; only an estimate can be provided. Doppler imaging studies
have found that polar spots are common and persistent structures in young, active stars (e.g., Huber et al. 2009). Assuming
that polar spots also exist on Corot-2a and that they reach to a latitude of ![]() ,
they occupy roughly
2% of the visible stellar disk. Adopting a spot contrast of 50%,
c becomes 0.99 in this case, and the planet size
would be overestimated by 0.5%.
Since the poles of CoRoT-2a are seen under a large viewing angle, their impact would, thus, be appreciably smaller than the amplitude of
the global brightness modulation (ca. 4%).
Nonetheless, in terms of sign, this effect counteracts the transit depth decrease caused by activity, and
if the polar spots are larger or symmetric structures at lower latitudes contribute, it may even balance it.
,
they occupy roughly
2% of the visible stellar disk. Adopting a spot contrast of 50%,
c becomes 0.99 in this case, and the planet size
would be overestimated by 0.5%.
Since the poles of CoRoT-2a are seen under a large viewing angle, their impact would, thus, be appreciably smaller than the amplitude of
the global brightness modulation (ca. 4%).
Nonetheless, in terms of sign, this effect counteracts the transit depth decrease caused by activity, and
if the polar spots are larger or symmetric structures at lower latitudes contribute, it may even balance it.
5 Discussion and conclusion
Stellar activity is clearly seen in the CoRoT measured transit light curves of CoRoT-2a, and an appropriate normalization is necessary to derive the true transit light curve profile accurately.
The transit profiles observed in CoRoT-2a are affected by activity, as is obvious in many transits where active regions cause distinct ``bumps'' in the light curve (e.g., Wolter et al. 2009). Furthermore, our analysis indicates that not only profiles with bumps but presumably all transit profiles are influenced by stellar activity. This is evident in the relationship between the transit equivalent width and the level of the global light curve: transits observed during periods where the star appears relatively bright are deeper than those observed during faint phases. We demonstrated that this correlation is extremely significant, but also that the data points show a large scatter around an assumed linear model relation. If the star were to modulate its surface brightness globally and homogeneously, this relation would be perfectly linear except for measurement errors. Therefore, we interpret the observed scatter as a consequence of surface evolution. When the global light curve is minimal, we also find more spots on the eclipsed portion of the surface, but only on average, and for an individual transit, this may not be the case. Thus, the surface configuration is clearly not the same for every minimum observed.
In addition, we demonstrated that the transit profiles exhibit a color dependence compatible with a color-dependent limb darkening law as expected from stellar atmospheric models and the analogy with the solar case.
All these influences can potentially interfere with the determination of the planetary parameters. Using our lower (white light) transit envelope, we determined new values for the planet-to-star radius ratio and the orbital inclination. While the latter remains compatible with previously reported results, the planet radius turns out to be larger (compared to the star) by about 3%. Although our approach takes into account many activity-related effects, a number of uncertainties remain. For example, the photospheric light curve level needed for transit normalization cannot be determined with certainty from our analysis and the same applies to the limb darkening law. We are therefore more certain than for the planetary parameters themselves, in our conclusion that the errors in their determination are much larger than the statistical ones.
While CoRoT-2a is certainly an extreme example of an active star, stellar activity is a common phenomenon especially on young stars. Therefore, in general, stellar activity cannot be neglected in planetary research, if the accuracy of the results should exceed the percent level.
Acknowledgements
S.C. and U.W. acknowledge DLR support (50OR0105). K.H. is a member of the DFG Graduiertenkolleg 1351 Extrasolar Planets and their Host Stars. S.S. acknowledges DLR support (50OR0703).
References
- Alonso, R., Auvergne, M., Baglin, A., et al. 2008, A&A, 482, L21 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, ArXiv e-prints (In the text)
- Bouchy, F., Queloz, D., Deleuil, M., et al. 2008, A&A, 482, L25 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Huber, K. F., Wolter, U., Czesla, S., et al. 2009, A&A, accepted (In the text)
- Lanza, A. F., Pagano, I., Leto, G., et al. 2009, A&A, 493, 193 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pál, A. 2008, MNRAS, 390, 281 [NASA ADS] [CrossRef] (In the text)
- Pierce, A. K., & Slaughter, C. D. 1977, Sol. Phys., 51, 25 [NASA ADS] [CrossRef] (In the text)
- Pont, F., Gilliland, R. L., Moutou, C., et al. 2007, A&A, 476, 1347 [NASA ADS] [CrossRef] [EDP Sciences]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., et al. 1992, Numerical recipes in C. The art of scientific computing, ed. W. H. Press, S. A. Teukolsky, W. T. Vetterling, & B. P. Flannery (In the text)
- Winn, J. N. 2009, in IAU Symposium, 253, IAU Symp., 99 (In the text)
- Wolter, U., Schmitt, J. H. M. M., Huber, K. F., et al. 2009, A&A, accepted (In the text)
Footnotes
- ... models
![[*]](/icons/foot_motif.png)
- For
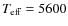 K and
K and
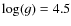 ,
the PHOENIX models given by Claret (2004) yield quadratic limb darkening coefficients of
,
the PHOENIX models given by Claret (2004) yield quadratic limb darkening coefficients of
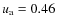 and
and
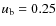 in the Sloan-r' band.
in the Sloan-r' band.
All Tables
Table 1: Stellar/planetary parameters of CoRoT-2a/b.
All Figures
| |
Figure 1: Transit equivalent width (TEW) versus transit continuum level as well as the best-fit linear model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm, angle=-90]{12454fg2.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12454-09/Timg45.png) |
Figure 2: Average transit light curves obtained by combining the ten profiles exhibiting the highest (thick dashes) and lowest (thin dashes) continuum levels. The crosses indicate our lower envelope estimate and the color gradient (red) illustrates the distribution of data points for all available transits. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.8cm, angle=-90]{12454fg3.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12454-09/Timg54.png) |
Figure 3: Left panel: normalized transit in the three CoRoT bands red, green, and blue obtained by averaging all available data. Upper right: close-up of the transit center. Lower right: close-up of the ingress flank of the transit. |
| Open with DEXTER | |
| In the text | |
| |
Figure 4: Lower envelope of all normalized transit light curves (already shown in Fig. 2) and our model fit. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.