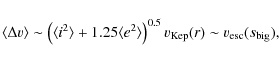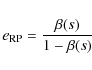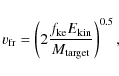| Issue |
A&A
Volume 505, Number 3, October III 2009
|
|
|---|---|---|
| Page(s) | 1269 - 1276 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912396 | |
| Published online | 18 August 2009 | |
Vertical structure of debris discs
P. Thébault1,2
1 - LESIA, Observatoire de Paris,
92195 Meudon Principal Cedex, France
2 -
Stockholm Observatory, Albanova Universitetcentrum, 10691 Stockholm, Sweden
Received 27 April 2009 / Accepted 30 June 2009
Abstract
Context. The vertical thickness of debris discs is often used as a measure of these systems' dynamical excitation, and as clues to the presence of hidden massive perturbers such as planetary embryos. However, this argument might be flawed because the observed dust should be naturally placed on inclined orbits by the combined effect of radiation pressure and mutual collisions.
Aims. We critically reinvestigate this issue and numerically estimate the ``natural'' vertical thickness of a collisionally evolving disc, in the absence of any additional perturbing body.
Methods. We use a deterministic collisional code, to follow the dynamical evolution of a population of indestructible test grains suffering mutual inelastic impacts. Grain differential sizes as well as the effect of radiation pressure are taken into account.
Results. We find that, under the coupled effect of radiation pressure and collisions, grains naturally acquire inclinations of a few degrees. The disc is stratified with respect to grain sizes, the smallest grains having the largest vertical dispersion and the largest being clustered closer to the midplane.
Conclusions. Debris discs should have a minimum ``natural'' observed aspect ratio
![]() from visible to mid-IR wavelengths, where the flux is dominated by the smallest bound grains. These values are comparable to the estimated thicknesses of several vertically resolved debris discs, as illustrated by the specific example of AU Mic. For all systems with
from visible to mid-IR wavelengths, where the flux is dominated by the smallest bound grains. These values are comparable to the estimated thicknesses of several vertically resolved debris discs, as illustrated by the specific example of AU Mic. For all systems with
![]() ,
the presence (or absence) of embedded perturbing bodies cannot be inferred from the vertical dispersion of the disc.
,
the presence (or absence) of embedded perturbing bodies cannot be inferred from the vertical dispersion of the disc.
Key words: stars: circumstellar matter - stars: individual: AU Mic - planetary systems: formation
1 Introduction
1.1 Vertical structure of debris discs
Dusty debris discs have been observed around main sequence stars for over two decades. It is believed that the detected dust is the lower end of a collisional cascade starting at larger, possibly planetesimal-sized bodies that are steadily eroding because of high velocity impacts (Wyatt 2008). As of April 2009, 18 of these debris discs have been spatially resolved (see http://www.circumstellardisks.org/), mostly in scattered light (visible and near IR) but also in some cases at mid-IR and up to millimetre wavelengths. These images contain a great variety of radial and azimutal features, such as rings, clumps, or two-side asymmetries, and almost no system displays a featureless structure. These features have been extensively studied, mostly by means of numerical modelling, considerably improving our understanding of the processes at play in debris discs. Depending on the characteristics of each system, they have been interpreted as the signatures of perturbing planets or stellar companions, of transitory catastrophic events, or of interactions between the dust and remnant gas.
In comparison, fewer discs have been resolved in the vertical direction. Systems seen edge-on are in this respect the most favourable cases. The best resolved disc to date is ![]() -Pictoris, for which the vertical structure is fairly well constrained, with a relatively constant thickness
-Pictoris, for which the vertical structure is fairly well constrained, with a relatively constant thickness
![]() AU
(defined by half the vertical FWHM) in the r<120 AU region and an aspect ratio
AU
(defined by half the vertical FWHM) in the r<120 AU region and an aspect ratio![]()
![]() in the outer regions (Golimowski et al. 2006; Heap et al. 2000). Observations in scattered light have also shown a striking warped profile and possibly the presence of two slightly tilted distinct discs (e.g., Golimowski et al. 2006; Heap et al. 2000; Mouillet et al. 1997). The other relatively well resolved disc is around the
in the outer regions (Golimowski et al. 2006; Heap et al. 2000). Observations in scattered light have also shown a striking warped profile and possibly the presence of two slightly tilted distinct discs (e.g., Golimowski et al. 2006; Heap et al. 2000; Mouillet et al. 1997). The other relatively well resolved disc is around the ![]() Pic coevol star Au Mic. To some extent, it resembles a scaled-down
Pic coevol star Au Mic. To some extent, it resembles a scaled-down ![]() Pic, with a roughly flat disc in the inner r<30 AU region and a
Pic, with a roughly flat disc in the inner r<30 AU region and a
![]() beyond that (Krist et al. 2005), but no obvious vertical asymmetries or warps.
For the two other resolved edge-on systems, HD 15115 and HD 139664, the vertical structure is more poorly constrained because of lower resolution and signal-to-noise ratios. HD 15115 has a measured aspect ratio of
beyond that (Krist et al. 2005), but no obvious vertical asymmetries or warps.
For the two other resolved edge-on systems, HD 15115 and HD 139664, the vertical structure is more poorly constrained because of lower resolution and signal-to-noise ratios. HD 15115 has a measured aspect ratio of ![]() 0.05 but seems to display pronounced asymmetries in its half-width at quarter maximum profile (Kalas et al. 2007), while HD 139664's vertical profile has not yet been constrained (Kalas et al. 2006). For discs seen head-on or at a large inclintation angle, the geometrical configuration is less favourable, and the vertical structure is difficult to retrieve, or only by means of model dependent inversion of brightness profiles. The HD 181327 rings, for example, might have a H/r ratio as high as about 0.1 at the positions of maximum surface density, but the true ratios could be two times lower (Schneider et al. 2006). However, there is one non-edge-on system for which a precise thickness estimate has been provided, Fomalhaut, which might have an aspect ratio as low as 0.0125 (Kalas et al. 2005). We discuss this specific case in more detail in Sect. 4.3.
0.05 but seems to display pronounced asymmetries in its half-width at quarter maximum profile (Kalas et al. 2007), while HD 139664's vertical profile has not yet been constrained (Kalas et al. 2006). For discs seen head-on or at a large inclintation angle, the geometrical configuration is less favourable, and the vertical structure is difficult to retrieve, or only by means of model dependent inversion of brightness profiles. The HD 181327 rings, for example, might have a H/r ratio as high as about 0.1 at the positions of maximum surface density, but the true ratios could be two times lower (Schneider et al. 2006). However, there is one non-edge-on system for which a precise thickness estimate has been provided, Fomalhaut, which might have an aspect ratio as low as 0.0125 (Kalas et al. 2005). We discuss this specific case in more detail in Sect. 4.3.
We note that there is often an ambiguity regarding the way that the thickness H is defined. For an edge-on seen system, this thickness, and all the directly related parameters, such as aspect ratio or opening angle, is measured on the disc's luminosity profile along its two radial extensions. In other words, it is not a measure of the disc's local thickness at a given radial location, but an observed thickness, integrating along the line of sight grains from different radial distances![]() . For systems seen at higher angle, however, the thickness inferred by model-dependent fitting is usually the true local thickness at a given radial distance from the star.
. For systems seen at higher angle, however, the thickness inferred by model-dependent fitting is usually the true local thickness at a given radial distance from the star.
1.2 Disc thickness as a measure of dynamical excitation
Despite the relative lack of observational data, disc vertical structures, or at least their global aspect ratios, have often been used as crucial parameters in debris disc studies, in particular those aimed at modelling their dynamical and collisional evolution. Disc thickness is commonly considered to be the only observable that can provide a direct information about the system's dynamical excitation, and hence about the processes and bodies shaping it. The argument is the following: a system of mutually colliding bodies orbiting around a central object tends toward an equilibrium where impact velocities ![]() are close to the surface escape velocity of the bodies
are close to the surface escape velocity of the bodies
![]() .
In addition, there is an equipartition between in-plane and vertical motions such as
.
In addition, there is an equipartition between in-plane and vertical motions such as
![]() ,
where i and e are the orbital inclinations and eccentricities respectively. This means that if the system only consists of small dust grains, then it should be almost razor thin, with
,
where i and e are the orbital inclinations and eccentricities respectively. This means that if the system only consists of small dust grains, then it should be almost razor thin, with
![]() .
If, in contrast, it has a finite observable thickness, then ``something'' is dynamically stirring the system to these large values. This argument is often used to infer the presence of unseen large bodies governing the disc's dynamics, and also to quantitatively estimate their size
.
If, in contrast, it has a finite observable thickness, then ``something'' is dynamically stirring the system to these large values. This argument is often used to infer the presence of unseen large bodies governing the disc's dynamics, and also to quantitatively estimate their size
![]() from the value of the disc's aspect ratio H/r (e.g., Thébault & Augereau 2007; Artymowicz 1997; Quillen et al. 2007). A detailed description of this procedure, taking into account several parameters such as the disc's age and surface density, can be found in Quillen et al. (2007). We only present here a simplified version, based on the first order assumption that the encounter velocity dispersion
from the value of the disc's aspect ratio H/r (e.g., Thébault & Augereau 2007; Artymowicz 1997; Quillen et al. 2007). A detailed description of this procedure, taking into account several parameters such as the disc's age and surface density, can be found in Quillen et al. (2007). We only present here a simplified version, based on the first order assumption that the encounter velocity dispersion
![]() is of the order of
is of the order of
![]() (Artymowicz 1997). The large bodies' size
(Artymowicz 1997). The large bodies' size
![]() can then be estimated using the equipartition condition
can then be estimated using the equipartition condition
![]() coupled to the relation (Wyatt & Dent 2002; Wetherill & Stewart 1993):
coupled to the relation (Wyatt & Dent 2002; Wetherill & Stewart 1993):
where
This argument seems to be supported by the fact that the inferred
![]() values make sense within the frame of our understanding of debris disc evolution. It is indeed believed that the debris disc phase starts when the bulk of the planet formation process is over, and large, Ceres-to-Moon-sized planetary embryos have formed (e.g., Kenyon & Bromley 2004). Observations thus seem to corroborate theory.
values make sense within the frame of our understanding of debris disc evolution. It is indeed believed that the debris disc phase starts when the bulk of the planet formation process is over, and large, Ceres-to-Moon-sized planetary embryos have formed (e.g., Kenyon & Bromley 2004). Observations thus seem to corroborate theory.
However, there could be a major problem with this observation-based derivation of
![]() .
Indeed, it overlooks one crucial fact, i.e. that the smallest observable dust grains, those dominating the flux in scattered light, are strongly affected by radiation pressure from the central star. These particle eccentricities are thus not solely imposed by the gravitational perturbations of hypothetical large embedded bodies but also by the eccentricity
.
Indeed, it overlooks one crucial fact, i.e. that the smallest observable dust grains, those dominating the flux in scattered light, are strongly affected by radiation pressure from the central star. These particle eccentricities are thus not solely imposed by the gravitational perturbations of hypothetical large embedded bodies but also by the eccentricity
![]() that they naturally gain when being produced. For the simplified case of a body of size s produced from a parent body on a circular orbit, this eccentricity reads
that they naturally gain when being produced. For the simplified case of a body of size s produced from a parent body on a circular orbit, this eccentricity reads
where
In this study, we propose to numerically investigate this issue by quantifying the ``natural'' vertical structure of a collisionally evolving debris disc, and in particular its equilibrium vertical thickness.
2 Model
Numerical studies of debris discs fall into two main categories: those investigating the collisional and size distribution evolution of the system are usually statistical particle-in-the-box models, of no or poor spatial resolution and very limited dynamical evolution (e.g., Löhne et al. 2008; Thébault & Augereau 2007; Krivov et al. 2006), while those studying the dynamics and the formation and evolution of spatial structures are mostly N-body type codes, where size distributions and mutual collisions are usually neglected (see for example Reche et al. 2008).
However, the present problem poses a specific challenge, inasmuch as it aims to quantify the effect of mutual collisions, within a population of bodies of different sizes, on the dynamical structure. Unfortunately, the study of both the dynamical and the collisional (and size) evolution of a dusty disc is far beyond the present day computing capacities, and only a simplified approach is possible. In this respect, one of the most suitable available codes is probably that developed 3 decades ago by Brahic (1977) and Brahic & Hénon (1977) to study the collisional evolution of planetary rings, later upgraded by Thébault & Brahic (1998) for the study of collisions among planetesimals. In this study, we chose to use a revised version of this code, that has been adapted to the present problem.
2.1 Code
We adopt an N-body type deterministic code, that follows the dynamical evolution of a population of massless test particles affected by a central body's potential as well as possible additional gravitational perturbers. It has a build-in collision search algorithm, which tracks, at each time step, all possible 2-body mutual encounters within the population. Because of the unavoidable limited number of test particles, typically a few 104, the statistics of impacts would be too low if we take the particles' true sizes. We thus take the usual ``inflated radius'' assumption, assigning a numerical size
![]() to each particle, that is large enough to provide enough impact statistics. This approximation is justified as long as
to each particle, that is large enough to provide enough impact statistics. This approximation is justified as long as
![]() is smaller than the minimal distance over which dynamical conditions change in the system (e.g., Charnoz et al. 2001).
is smaller than the minimal distance over which dynamical conditions change in the system (e.g., Charnoz et al. 2001).
Collisions are then treated as inelastic rebounds. Collision outcomes are estimated by computing the momentum before and after impact
![]() and
and
![]() in the two-body centre-of-mass frame. The link between
in the two-body centre-of-mass frame. The link between
![]() and
and
![]() is parameterized by normal and transversal rebound coefficients,
is parameterized by normal and transversal rebound coefficients,
![]() and
and
![]() ,
such as
,
such as
![]() and
and
![]() for a perfectly elastic collision.
for a perfectly elastic collision.
For the present problem, we modified the code to account for a size distribution within the test particle population, and more specifically for impacts between objects of different sizes. In this case, the momentum balance is weighted by the mass ratio of the 2 impacting bodies. Another crucial improvement is that we now take into account the effect of radiation pressure on the smallest particles. This force is computed by correcting the gravitational force from the central star by a factor
![]() ,
where
,
where
![]() .
In this respect, it might be more convenient to scale particle sizes by their
.
In this respect, it might be more convenient to scale particle sizes by their ![]() value, where
value, where
![]() for the smallest bound objects (if released from circular orbits).
for the smallest bound objects (if released from circular orbits).
Of course, this ``bouncing ball'' model is a crude approximation of the true behaviour of a collisionally evolving debris disc. In a real system, high-![]() collisions should result in fragmentation rather than inelastic rebounds, each time producing a cloud of small fragments. As mentioned before, such chain reactions of fragment-producing collisions are impossible to model numerically. However, if we make the reasonable assumption that a steady-state has been reached in the system, so that the size distribution no longer globally evolves because of collisions
collisions should result in fragmentation rather than inelastic rebounds, each time producing a cloud of small fragments. As mentioned before, such chain reactions of fragment-producing collisions are impossible to model numerically. However, if we make the reasonable assumption that a steady-state has been reached in the system, so that the size distribution no longer globally evolves because of collisions![]() , then the present code provides a first order estimate of how mutual collisions between bodies of different sizes redistribute in and out-of-plane velocities. Indeed, for each impact this effect is proportional to the relative velocity, the mass ratio of the impactors, the geometry of the impact and the energy dissipated at impact, all parameters that our code handles (the energy dissipation being tuned-in by the values for
, then the present code provides a first order estimate of how mutual collisions between bodies of different sizes redistribute in and out-of-plane velocities. Indeed, for each impact this effect is proportional to the relative velocity, the mass ratio of the impactors, the geometry of the impact and the energy dissipated at impact, all parameters that our code handles (the energy dissipation being tuned-in by the values for
![]() and
and
![]() ). We discuss these issues in more details in Sect. 4.1.
). We discuss these issues in more details in Sect. 4.1.
2.2 Setup
Table 1: Nominal case set up.
For the sake of clarity, we consider a nominal reference case, around which several free parameters are explored individually. This reference case corresponds roughly to a hypothetic typical debris disc, spatially extended from 10 to 100 AU. We consider
![]() test particles. The absolute values of their physical radius are not important here. Indeed, for the collision-outcome procedure, the decisive factor is the impactor mass (or s3) ratio. For the collision-search routine, the assumed inflated radius is proportional to the physical size s, but the proportionality factor, and thus the ``true'' value of s, is of no importance, the only constraint being on the absolute value of
test particles. The absolute values of their physical radius are not important here. Indeed, for the collision-outcome procedure, the decisive factor is the impactor mass (or s3) ratio. For the collision-search routine, the assumed inflated radius is proportional to the physical size s, but the proportionality factor, and thus the ``true'' value of s, is of no importance, the only constraint being on the absolute value of
![]() ,
which has to be large enough for a reliable impact statistics and small enough not to introduce any bias (see below). As for the orbital evolution computation, the important parameter is the value of
,
which has to be large enough for a reliable impact statistics and small enough not to introduce any bias (see below). As for the orbital evolution computation, the important parameter is the value of ![]() for estimating the radiation pressure force. We thus chose to scale all particle sizes by their
for estimating the radiation pressure force. We thus chose to scale all particle sizes by their
![]() value. We assume that the size distribution has reached a steady state profile following a power law
value. We assume that the size distribution has reached a steady state profile following a power law
![]() ,
or more exactly
,
or more exactly
![]() .
We assume here the classical value q=-3.5 for idealized infinite self-similar collisional cascades (Dohnanyi 1969), but other possible values are explored. With such steep size distributions, the size range that can be modelled with
.
We assume here the classical value q=-3.5 for idealized infinite self-similar collisional cascades (Dohnanyi 1969), but other possible values are explored. With such steep size distributions, the size range that can be modelled with
![]() particles is necessarily limited. We consider here
particles is necessarily limited. We consider here ![]() and
and ![]() ,
such that
,
such that
![]() (close to the blow-out cut-off size) and
(close to the blow-out cut-off size) and
![]() .
This size range covers however most of the crucial grain population that dominates the flux in scattered light. For the collision-search routine, the inflated radius
.
This size range covers however most of the crucial grain population that dominates the flux in scattered light. For the collision-search routine, the inflated radius
![]() is taken to be proportional to the real sizes of the particles and is set so as to provide enough collision statistics without introducing a bias in impact rate and velocity estimates. We consider
is taken to be proportional to the real sizes of the particles and is set so as to provide enough collision statistics without introducing a bias in impact rate and velocity estimates. We consider
![]() AU
AU ![]()
![]() ,
which is a typical value for similar impact search routines (e.g., Xie & Zhou 2008; Charnoz et al. 2001).
,
which is a typical value for similar impact search routines (e.g., Xie & Zhou 2008; Charnoz et al. 2001).
For collision outcomes, we follow Thébault & Brahic (1998), Charnoz et al. (2001), and Thébault & Beust (2001) and assume that
![]() and
and
![]() .
This corresponds to a
.
This corresponds to a ![]() energy dissipation for head-on impacts, which is the usual first-order estimate for high velocity impacts (e.g., Fujiwara et al. 1989; Petit & Farinella 1993), but other values are explored.
energy dissipation for head-on impacts, which is the usual first-order estimate for high velocity impacts (e.g., Fujiwara et al. 1989; Petit & Farinella 1993), but other values are explored.
To avoid confusion, we label
![]() the ``dynamical'' component of the particles initial eccentricities.
the ``dynamical'' component of the particles initial eccentricities.
![]() is a size-independent quantity, the other component being the (size-dependent) radiation-pressure-imposed eccentricity
is a size-independent quantity, the other component being the (size-dependent) radiation-pressure-imposed eccentricity
![]() (see Eq. (2)). For the starting dynamical conditions, we consider an extreme fiducial case with
(see Eq. (2)). For the starting dynamical conditions, we consider an extreme fiducial case with
![]() ,
i.e., the most dynamically quiet state possible for the system. This is to obtain a minimum value for the ``natural'' thickening effect studied here, i.e., the collisonal transfer of high
,
i.e., the most dynamically quiet state possible for the system. This is to obtain a minimum value for the ``natural'' thickening effect studied here, i.e., the collisonal transfer of high ![]() induced by radiation pressure. We note that even if
induced by radiation pressure. We note that even if
![]() ,
small grains will have a non-zero initial eccentricity because of radiation pressure.
All initial conditions are summarized in Table 1.
,
small grains will have a non-zero initial eccentricity because of radiation pressure.
All initial conditions are summarized in Table 1.
We allowed the simulations to run until we did not see any further evolution in the average dynamical characteristics for the different particle size groups. In practice, this is achieved as soon as the average number of impacts per particle is ![]() 3. Beyond this point, the system has reached a steady state and only the slow and progressive decrease of
3. Beyond this point, the system has reached a steady state and only the slow and progressive decrease of
![]() and
and
![]() ,
due to the energy dissipation at impact, is observed (see Fig. 2 and Sect. 4.1 for a more detailed discussion). In this respect, the absolute timescale is not relevant as long as the relaxation time of a few impacts per bodies is short compared to the age of the system, a condition that is most likely to be fulfilled for any observed debris disc (see for instance Wyatt 2005).
,
due to the energy dissipation at impact, is observed (see Fig. 2 and Sect. 4.1 for a more detailed discussion). In this respect, the absolute timescale is not relevant as long as the relaxation time of a few impacts per bodies is short compared to the age of the system, a condition that is most likely to be fulfilled for any observed debris disc (see for instance Wyatt 2005).
3 Results
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12396fg1.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg66.png) |
Figure 1:
Final positions in the vertical plane, once the system has reached a collisional steady state, for the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{12396fg2.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg67.png) |
Figure 2:
Evolution in
|
| Open with DEXTER | |
Figure 1 shows the final positions, once the system is collisionally relaxed, of all particles in the (x, z) plane. An obvious result is that, in sharp contrast to its initially perfectly thin structure, the disc is now significantly extended in the vertical direction, with a large fraction of the test particles being more than 10 AU above or below the midplane. Moreover, the disc's vertical structure is strongly stratified with respect to grain sizes. The larger objects are clustered close to the midplane, while the (most numerous) smaller grains of high ![]() have a much larger spread in z. This feature appears more clearly in Fig. 2 showing the evolution in
have a much larger spread in z. This feature appears more clearly in Fig. 2 showing the evolution in
![]() for different size ranges: particles close to the blow-out size reach inclinations of about 8
for different size ranges: particles close to the blow-out size reach inclinations of about 8![]() ,
but the largest simulated grains (about 15 times this minimum size) settle to less than 0.5
,
but the largest simulated grains (about 15 times this minimum size) settle to less than 0.5![]() .
These results are logical since the smallest grains are those that have the most eccentric orbits because of radiation pressure. As such, they have the highest impact velocities and thus more kinetic energy to transfer from the horizontal to the vertical direction. Likewise, since they are the smallest grains, they are those most likely to acquire large dynamical ``kicks'' from impacts with larger impactors (because of the momentum balance in the centre of frame).
.
These results are logical since the smallest grains are those that have the most eccentric orbits because of radiation pressure. As such, they have the highest impact velocities and thus more kinetic energy to transfer from the horizontal to the vertical direction. Likewise, since they are the smallest grains, they are those most likely to acquire large dynamical ``kicks'' from impacts with larger impactors (because of the momentum balance in the centre of frame).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12396fg3.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg69.png) |
Figure 3:
Synthetic image of a disc seen edge-on, once the steady collisonal state is reached, in scattered light assuming grey scattering. The dotted line corresponds to the vertical full width at half maximum ( FWHM), while the full line marks the location of the full width at one tenth maximum FW0.1M. The fluxes have been averaged over 2 AU |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12396fg4.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg70.png) |
Figure 4: Same run as in Fig. 3, but displaying the FWHM and FW0.1M for the azimuthally averaged local geometrical thickness as a function of radial distance. |
| Open with DEXTER | |
To visualize more clearly the effect of this inclination increase on the disc's aspect, we consider two cases: a disc seen edge-on, for which we show a synthetic profile of the disc's vertical FWHM and FW0.1M in scattered light assuming grey scattering (Fig. 3), and a disc seen at higher angle, for which we display the azimuthally averaged local thickness (FWHM and FW0.1M)
![]() of the disc, derived from the vertical profile of the integrated geometrical cross section of all particles present in a given radial annulus (Fig. 4). Because of the limited number of particles, the resolution is limited to 2 AU
of the disc, derived from the vertical profile of the integrated geometrical cross section of all particles present in a given radial annulus (Fig. 4). Because of the limited number of particles, the resolution is limited to 2 AU ![]() 1 AU and the profiles are relatively noisy, especially in the outermost regions because of the radial and vertical dilution of the particle number density. It is however enough to resolve both the FWHM and the FW0.1M in the entire 0-120 AU region. As can be seen, the two different thicknesses, i.e., the edge-on profile derived
1 AU and the profiles are relatively noisy, especially in the outermost regions because of the radial and vertical dilution of the particle number density. It is however enough to resolve both the FWHM and the FW0.1M in the entire 0-120 AU region. As can be seen, the two different thicknesses, i.e., the edge-on profile derived
![]() and the local geometrical
and the local geometrical
![]() have relatively comparable values, and can as a first approximation be considered to be identical within the error bars imposed by the noisiness of our profiles. The only differences occur close to the inner edge of the parent bodies disc around 10 AU, where
have relatively comparable values, and can as a first approximation be considered to be identical within the error bars imposed by the noisiness of our profiles. The only differences occur close to the inner edge of the parent bodies disc around 10 AU, where
![]() drops to 0, while the edge-on seen luminosity has a roughly constant thickness in the entire
drops to 0, while the edge-on seen luminosity has a roughly constant thickness in the entire
![]() to 20 AU region because it integrates, along the line-of-sight, contributions from particles at different radial locations. We neglect these limited differences here (we rediscuss them in Sect. 4.3) and consider hereafter that the parameter H represents both possible definitions of the disc's thickness.
to 20 AU region because it integrates, along the line-of-sight, contributions from particles at different radial locations. We neglect these limited differences here (we rediscuss them in Sect. 4.3) and consider hereafter that the parameter H represents both possible definitions of the disc's thickness.
In both cases, we see that the system's aspect ratio h=H/r is relatively constant and is roughly ![]() 0.04. The FW0.1M profile is much wider, at
0.04. The FW0.1M profile is much wider, at
![]() .
The seemingly ``flatter'' aspect of the disc, when compared to the (x, z) positions displayed in Fig. 1 is due to the fact that in deriving the scattered light flux, the geometrical cross sections of the particles are taken into account, which increases the contribution of larger grains that have smaller z dispersion. This is illustrated in Fig. 5 showing
.
The seemingly ``flatter'' aspect of the disc, when compared to the (x, z) positions displayed in Fig. 1 is due to the fact that in deriving the scattered light flux, the geometrical cross sections of the particles are taken into account, which increases the contribution of larger grains that have smaller z dispersion. This is illustrated in Fig. 5 showing
![]() ,
the average inclination for the entire grain population weighted by each particle's cross section. It can be seen that
,
the average inclination for the entire grain population weighted by each particle's cross section. It can be seen that
![]() ,
roughly half that of the smallest grains (Fig. 2). We note that this weighted
,
roughly half that of the smallest grains (Fig. 2). We note that this weighted
![]() is approximately equal to
is approximately equal to ![]() ,
which is consistent with the relation between inclination and aspect ratio, for small
,
which is consistent with the relation between inclination and aspect ratio, for small
![]() values, in single-sized particle discs (Quillen et al. 2007).
values, in single-sized particle discs (Quillen et al. 2007).
3.1 Exploration of parameter space
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{12396fg5.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg79.png) |
Figure 5:
Evolution of
|
| Open with DEXTER | |
Using
![]() as an approximate measure of the disc's vertical
thickness (because of the relation
as an approximate measure of the disc's vertical
thickness (because of the relation
![]() ), we display in Fig. 5 how our results vary when changing the values of the main parameters considered here.
), we display in Fig. 5 how our results vary when changing the values of the main parameters considered here.
We first consider two extreme values for the normal rebound coefficient
![]() ,
-0.2 and -0.5, corresponding to a 96% and 75% energy dissipation, respectively, both values being the upper and lower range of expected energy losses for high velocity fragmenting impacts (Fujiwara et al. 1989). As could be logically expected,
,
-0.2 and -0.5, corresponding to a 96% and 75% energy dissipation, respectively, both values being the upper and lower range of expected energy losses for high velocity fragmenting impacts (Fujiwara et al. 1989). As could be logically expected,
![]() decreases with increasing energy dissipation, but the dependence on
decreases with increasing energy dissipation, but the dependence on
![]() remains relatively weak,
remains relatively weak,
![]() varying only by
varying only by ![]() 50% between our two extreme cases.
50% between our two extreme cases.
Surprisingly, varying the dynamical excitation of the system doesn't cause any change in the final
![]() as long as
as long as
![]() .
For this range of
.
For this range of
![]() ,
the inclinations acquired by collisional redistribution of the eccentric velocities due to radiation pressure (which do not depend on
,
the inclinations acquired by collisional redistribution of the eccentric velocities due to radiation pressure (which do not depend on
![]() )
dominate over the value of
)
dominate over the value of
![]() .
The only case for which we obtain a significantly flatter disc is when considering a much shallower slope for the size distribution (q=-2.5). In this case,
.
The only case for which we obtain a significantly flatter disc is when considering a much shallower slope for the size distribution (q=-2.5). In this case,
![]() ,
almost half the inclination of the nominal case. This is because in this case the system's geometrical cross section, and thus the flux in scattered light, is now dominated by the larger bodies of the distribution, which remain on low inclination orbits close to the mid-plane.
,
almost half the inclination of the nominal case. This is because in this case the system's geometrical cross section, and thus the flux in scattered light, is now dominated by the larger bodies of the distribution, which remain on low inclination orbits close to the mid-plane.
4 Discussion
4.1 Limitations and strength of our approach
We emphasize that this work does not attempt to realistically model the coupled dynamical and collisional evolution of debris discs. As already mentioned, no deterministic code can presently achieve this task, mainly because a correct treatment of collisions would require us to take into account the numerous individual small fragments produced after each high-velocity impact, thus leading to an exponential increase in the number of simulated test particles, rapidly exceeding any reasonable value![]() . Our study should be regarded as a numerical experiment aimed at exploring one specific mechanism: the ability of mutual collisions to convert the high in-plane velocities of small, radiation-pressure affected particles into vertical ones.
. Our study should be regarded as a numerical experiment aimed at exploring one specific mechanism: the ability of mutual collisions to convert the high in-plane velocities of small, radiation-pressure affected particles into vertical ones.
The main and unavoidable problem with our approach is that it considers that particles acquire their dynamics through a succession of inelastic rebounds. This is obviously unrealistic, especially for the smallest grains close to the blow-out size
![]() .
In our runs, these grains evolve mostly through rebounds with grains their own size (which dominate the total population), whereas in reality they should be fragments produced by collisions with larger parent bodies (while collisions between
.
In our runs, these grains evolve mostly through rebounds with grains their own size (which dominate the total population), whereas in reality they should be fragments produced by collisions with larger parent bodies (while collisions between
![]() grains should produce small
grains should produce small
![]() debris quickly removed by radiation pressure). However, for the specific issue addressed here, it is only important whether this departure from reality introduces a systematic error when estimating the final
debris quickly removed by radiation pressure). However, for the specific issue addressed here, it is only important whether this departure from reality introduces a systematic error when estimating the final
![]() .
Quantifying exactly this potential bias is clearly beyond the scope of this study, but it is possible to obtain a first idea. Statistical collisional evolution models (e.g., Thébault & Augereau 2007) show that, for extended debris discs with low dynamical excitation (
.
Quantifying exactly this potential bias is clearly beyond the scope of this study, but it is possible to obtain a first idea. Statistical collisional evolution models (e.g., Thébault & Augereau 2007) show that, for extended debris discs with low dynamical excitation (
![]() ,
grains close to
,
grains close to
![]() are produced mostly by cratering and shattering collisions between
are produced mostly by cratering and shattering collisions between
![]() projectiles
projectiles![]() and targets in the
and targets in the
![]() to
to
![]() range. In other words, the most common way of producing an
range. In other words, the most common way of producing an
![]() fragment is by an impact involving a previous (and ultimately shattered)
fragment is by an impact involving a previous (and ultimately shattered)
![]() projectile. If we now use the simplified estimate of Stern & Colwell (1997) for the velocity of fragments produced after an impact at speed
projectile. If we now use the simplified estimate of Stern & Colwell (1997) for the velocity of fragments produced after an impact at speed ![]()
![]()
where
A second issue is that, because of the succession of dissipative collisions, the numerical system's total kinetic energy is steadily decreasing. In particular, the high initial
![]() of the smaller particles are progressively damped as they experience more and more impacts. This is an artificial behaviour, since in reality the smaller grains should not survive several high-
of the smaller particles are progressively damped as they experience more and more impacts. This is an artificial behaviour, since in reality the smaller grains should not survive several high-![]() impacts and should be destroyed before having had the time to be dynamically damped, while newly produced grains of the same size should progressively enter the system with high initial eccentricities (``automatically'' acquired when they are collisionally released from their parent body). To minimize this numerical bias, simulations are stopped before the average number of collisions per body exceeds 3. As can be seen from Fig. 2, this is enough for the system to reach a steady state in terms of
impacts and should be destroyed before having had the time to be dynamically damped, while newly produced grains of the same size should progressively enter the system with high initial eccentricities (``automatically'' acquired when they are collisionally released from their parent body). To minimize this numerical bias, simulations are stopped before the average number of collisions per body exceeds 3. As can be seen from Fig. 2, this is enough for the system to reach a steady state in terms of
![]() for each grain population. Nevertheless, an artificial decrease of the system's excitation is observed, which leads to an underestimate of the final
for each grain population. Nevertheless, an artificial decrease of the system's excitation is observed, which leads to an underestimate of the final
![]() .
.
We can thus observe that it is impossible to ensure that our N-body approach is fully bias free. Nevertheless, for the reasons just discussed, the two main sources of systematic errors should remain relatively limited. They should also compensate each other to some extent. We are thus relatively confident that, for systems sufficiently evolved to have reached a steady state where both the size distribution and dynamical structure no longer evolves because of collisions, the present code provides a satisfying first-order estimate. As mentioned in Sect. 2, its main strength is that it takes into account the main parameters that drive the in-to-out-of-plane kinetic energy transfer: collision velocity, impact geometry, and mass ratio between the impactors and energy loss at impact. We note that a similar ``bouncing balls'' approach was proposed by Chiang et al. (2009) as the best way of addressing a not-so-different issue, i.e., the collisional relaxation of grain orbits in the Fomalhaut ring.
4.2 The ``natural'' thickness of debris discs
Despite the limitations inherent to our numerical approach (see previous section), we believe that our main result is relatively robust, i.e., that there is a ``natural'' thickening of a debris disc because of the combined action of radiation pressure and mutual collisions. Expressing the disc's thickness in terms of its average aspect ratio h=H/R, we find (from Fig. 5 and using the relation
![]() )
that
)
that
where the error bar is probably overestimated, because if was derived assuming rather extreme values for our parameter exploration (see Sect. 3.1). A direct consequence is that there should in principle be no debris disc with an aspect ratio lower than
Another important result is that the disc's vertical thickness is almost independent of its intrinsic dynamical excitation as long as
![]() .
In this case, all intrinsic dynamical effects, in particular the out-of-plane excursion caused by the ``dynamical'' i, are masked by the ``natural'' thickening effect studied here. Likewise, it means that for a disc with an observed
.
In this case, all intrinsic dynamical effects, in particular the out-of-plane excursion caused by the ``dynamical'' i, are masked by the ``natural'' thickening effect studied here. Likewise, it means that for a disc with an observed
![]() (or 0.06 to be conservative), the correlation between vertical structure and intrinsic dynamical excitation is lost. In particular, no information about potential embedded perturbing objects can be retrieved, except that they cannot be larger than
(or 0.06 to be conservative), the correlation between vertical structure and intrinsic dynamical excitation is lost. In particular, no information about potential embedded perturbing objects can be retrieved, except that they cannot be larger than
![]() km (Eq. (1)).
km (Eq. (1)).
A third result is that discs should be stratified with respect to particle sizes, with the bigger grains being clustered much closer to the midplane. This might have interesting observational consequences. It should imply that discs should appear much thinner at longer wavelengths, where smaller grains are poor scatterers/emitters and where the flux is dominated by larger particles. For a typical value
![]() m, this should thus happen for
m, this should thus happen for
![]() m, i.e., in the mid to far IR thermal emission. Unfortunately, high-resolution images are difficult to obtain at these long wavelengths and to our knowledge, there is no debris disc that has been vertically resolved beyond the mid-IR.
m, i.e., in the mid to far IR thermal emission. Unfortunately, high-resolution images are difficult to obtain at these long wavelengths and to our knowledge, there is no debris disc that has been vertically resolved beyond the mid-IR.
However, there might be one marginal possibility for a disc to appear flatter than ![]() even in scattered light, i.e., if its total geometrical cross-section is dominated by grains significantly larger than the blow out size. This is clearly not the case for a Dohnanyi size distribution with
even in scattered light, i.e., if its total geometrical cross-section is dominated by grains significantly larger than the blow out size. This is clearly not the case for a Dohnanyi size distribution with
![]() ,
as well as for most of the more realistic ``wavy'' distributions derived from collisional evolution models (e.g., Thébault & Augereau 2007; Krivov et al. 2006). However, there is a range of systems for which these numerical studies have shown that they could be depleted of small grains, i.e., those with very low dynamical excitation
,
as well as for most of the more realistic ``wavy'' distributions derived from collisional evolution models (e.g., Thébault & Augereau 2007; Krivov et al. 2006). However, there is a range of systems for which these numerical studies have shown that they could be depleted of small grains, i.e., those with very low dynamical excitation
![]() .
As identified by Thébault & Wu (2008), for
.
As identified by Thébault & Wu (2008), for
![]() ,
there is an imbalance between the rates of small grain production, which strongly decreases with
,
there is an imbalance between the rates of small grain production, which strongly decreases with
![]() ,
and destruction, which only moderately changes for low
,
and destruction, which only moderately changes for low
![]() values (because it is mostly imposed by
values (because it is mostly imposed by
![]() ). For these systems, the scattered light flux should be dominated by grains typically 10-100
). For these systems, the scattered light flux should be dominated by grains typically 10-100
![]() in size, which should have very low i and thus lead to a very flat aspect. However, we note that the Thébault & Wu (2008) estimates did not take into account the mechanism identified here of collisional redistribution of in-plane to out-of-plane velocities, which should reduce the rate of small grain destructions by spatially diluting them in z. It remains to be seen the extent to which this effect might reduce the depletion of
in size, which should have very low i and thus lead to a very flat aspect. However, we note that the Thébault & Wu (2008) estimates did not take into account the mechanism identified here of collisional redistribution of in-plane to out-of-plane velocities, which should reduce the rate of small grain destructions by spatially diluting them in z. It remains to be seen the extent to which this effect might reduce the depletion of
![]() grains and if these dynamically cold, small-grain-depleted systems are a realistic alternative.
grains and if these dynamically cold, small-grain-depleted systems are a realistic alternative.
We emphasize that this discussion regards the global aspect ratio or thickness of the disc, not possible local clumps, blobs, or other asymmetries in its vertical structure, as for the famous beta Pic warp. These local features may well be the signature of hidden perturbers but are not the purpose of the present work.
4.3 Comparison to real systems
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12396fg6.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg111.png) |
Figure 6:
Vertical FWHM (=2H) for the AU Mic disc, as derived from observations (Krist et al. 2005) and obtained for a test numerical disc initially confined to a narrow annulus at |
| Open with DEXTER | |
As already mentioned, the two best resolved debris discs, ![]() Pictoris and AU Mic
Pictoris and AU Mic![]() , have aspect ratios of
, have aspect ratios of
![]() and 0.05 respectively. Thus, AU Mic's vertical thickness falls within the range for the ``natural''
and 0.05 respectively. Thus, AU Mic's vertical thickness falls within the range for the ``natural'' ![]() derived in Eq. (4), whereas
derived in Eq. (4), whereas ![]() Pictoris is around the upper end of this range. We note that the preliminary estimate for HD 15115 aspect's ratio, i.e.,
Pictoris is around the upper end of this range. We note that the preliminary estimate for HD 15115 aspect's ratio, i.e., ![]() 0.05, also falls within our estimated range for
0.05, also falls within our estimated range for ![]() .
To push our analysis a step further, we performed one additional run specifically designed to AU Mic (
.
To push our analysis a step further, we performed one additional run specifically designed to AU Mic (![]() Pictoris has a far more complex radial and vertical structure, especially its warp, and is thus not an ideal candidate for such a simple fit). For this task, we take input parameters adapted to this specific system, i.e., a ``birth ring'' (where all non-radiation-pressure-affected larger particles are located) centered on
Pictoris has a far more complex radial and vertical structure, especially its warp, and is thus not an ideal candidate for such a simple fit). For this task, we take input parameters adapted to this specific system, i.e., a ``birth ring'' (where all non-radiation-pressure-affected larger particles are located) centered on ![]() 40 AU and of width
40 AU and of width ![]() 5 AU (Augereau & Beust 2006; Strubbe & Chiang 2006). As in our previous runs, we consider a limiting dynamically cold case with
5 AU (Augereau & Beust 2006; Strubbe & Chiang 2006). As in our previous runs, we consider a limiting dynamically cold case with
![]() ,
the remaining parameters being those for our nominal set-up (Table 1). As can be seen in Fig. 6, a reasonably good fit to the system's FWHM radial profile is obtained. We note that this simple fit was obtained with our arbitrarily defined nominal set-up, and we expect far tighter fits to be possible when tuning all free parameters (e.g., rebound coefficients, size distribution). Of course, this result should not be regarded as proof that the AU Mic disc is completely dynamically cold. It is just a numerical test showing that this system's vertical structure is easily explained by the natural thickening mechanism identified in this study, without the need of additional exciting sources, such as hidden large planetesimals or planets. The presence of these hidden objects can of course not be excluded, and they might even make sense within the frame of our current understanding of debris discs, but we want to emphasize that nothing can be inferred about either their presence or absence from the disc's observed aspect ratio.
,
the remaining parameters being those for our nominal set-up (Table 1). As can be seen in Fig. 6, a reasonably good fit to the system's FWHM radial profile is obtained. We note that this simple fit was obtained with our arbitrarily defined nominal set-up, and we expect far tighter fits to be possible when tuning all free parameters (e.g., rebound coefficients, size distribution). Of course, this result should not be regarded as proof that the AU Mic disc is completely dynamically cold. It is just a numerical test showing that this system's vertical structure is easily explained by the natural thickening mechanism identified in this study, without the need of additional exciting sources, such as hidden large planetesimals or planets. The presence of these hidden objects can of course not be excluded, and they might even make sense within the frame of our current understanding of debris discs, but we want to emphasize that nothing can be inferred about either their presence or absence from the disc's observed aspect ratio.
However, there is one specific system that might appear as a counter example to our study: Fomalhaut and its striking debris ring surrounding a recently discovered giant planet (Kalas et al. 2008). This ring's aspect ratio has indeed been observationally estimated to be
![]() (Kalas et al. 2005), a value that was corroborated by the numerical estimate
(Kalas et al. 2005), a value that was corroborated by the numerical estimate
![]() by Chiang et al. (2009). These values are below the minimum value for
by Chiang et al. (2009). These values are below the minimum value for ![]() derived in Eq. (4) and seem to invalidate our conclusions. However, two important points should be stressed here. The first one is that the disc's thickness estimates were obtained for one specific region, i.e., the sharp inner edge of the bright ring located at 133 AU
derived in Eq. (4) and seem to invalidate our conclusions. However, two important points should be stressed here. The first one is that the disc's thickness estimates were obtained for one specific region, i.e., the sharp inner edge of the bright ring located at 133 AU![]() . The second one is that the thickness that was estimated for Fomalhaut is the local geometrical vertical thickness
. The second one is that the thickness that was estimated for Fomalhaut is the local geometrical vertical thickness
![]() ,
and not the line-of-sight integrated thickness of the luminosity profile as for an edge-on seen disc. In Sect. 3, we have seen that, although these two different thicknesses have similar values most of the time,
,
and not the line-of-sight integrated thickness of the luminosity profile as for an edge-on seen disc. In Sect. 3, we have seen that, although these two different thicknesses have similar values most of the time,
![]() distinguishes itself in one specific case, i.e., the inner edge of the parent bodies disc, where it can reach very small values (see Fig. 4). It is difficult to evaluate exactly how small because of the limited radial resolution of our synthetic profiles, but it is clearly below
distinguishes itself in one specific case, i.e., the inner edge of the parent bodies disc, where it can reach very small values (see Fig. 4). It is difficult to evaluate exactly how small because of the limited radial resolution of our synthetic profiles, but it is clearly below ![]() ,
and could thus be compatible with the Fomalhaut estimate. This specific case has clearly to be investigated in more detail. It would in particular be of great help to obtain a thickness estimate further out in the disc, where our model predicts a wider vertical dispersion.
,
and could thus be compatible with the Fomalhaut estimate. This specific case has clearly to be investigated in more detail. It would in particular be of great help to obtain a thickness estimate further out in the disc, where our model predicts a wider vertical dispersion.
5 Summary and conclusions
The main results of our numerical investigation can be summarized as follows:
- Even in the absence of perturbing bodies, debris disc should naturally thicken because of the coupled effect of radiation pressure and mutual grain collisions.
- The basic mechanism is the following: because of radiation pressure, the smallest grains have high in-plane velocities which are partially converted into vertical motions by collisions with other grains. The dynamical outcome depends on the grain differential sizes and the collision geometry.
- The disc is stratified in the vertical direction according to particle sizes, the smallest grains having the largest dispersion while the larger ones remain close to the midplane.
- At wavelengths where the flux is dominated by the smallest grains, i.e., in the visible to mid-IR, this natural thickening effect places a minimum value
 on a disc's aspect ratio. We find
on a disc's aspect ratio. We find
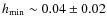 ,
although this estimate should be interpreted with some care given the unavoidable limitations of our model.
,
although this estimate should be interpreted with some care given the unavoidable limitations of our model.
- Most vertically resolved debris discs have aspect ratios compatible with
 ,
which can thus be explained without resorting to the perturbing presence of large ``hidden'' bodies. As an illustration, we obtain a relatively satisfying fit of AU Mic's vertical profile.
,
which can thus be explained without resorting to the perturbing presence of large ``hidden'' bodies. As an illustration, we obtain a relatively satisfying fit of AU Mic's vertical profile.
- For all systems with
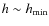 ,
a corollary is that no information about the presence of embedded planetary embryos can be directly inferred by measuring the disc's vertical dispersion.
,
a corollary is that no information about the presence of embedded planetary embryos can be directly inferred by measuring the disc's vertical dispersion.
References
- Artymowicz, P. 1997, Ann. Rev. Earth Planet. Sci., 25, 175 [NASA ADS] [CrossRef]
- Augereau, J.-C., & Beust, H. 2006, A&A, 455, 987 [NASA ADS] [CrossRef] [EDP Sciences]
- Beauge, A., & Aarseth, S. J. 1990, MNRAS, 245, 30 [NASA ADS]
- Brahic, A. 1977, A&A, 54, 895 [NASA ADS] (In the text)
- Brahic, A., & Hénon 1977, A&A, 59, 1 [NASA ADS] (In the text)
- Charnoz, S., Thébault, P., & Brahic, A. 2001, A&A, 373, 683 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chiang, E., Kite, E., Kalas, P., Graham, J. R., & Clampin, M. 2009, ApJ, 693, 734 [NASA ADS] [CrossRef] (In the text)
- Dohnanyi, J. S. 1969, JGR, 74, 2531 [NASA ADS] [CrossRef] (In the text)
- Fitzgerald, M. P., Kalas, P. G., Duchêne, G., Pinte, C., & Graham, J. R. 2007, ApJ, 670, 536 [NASA ADS] [CrossRef]
- Fujiwara, A., Cerroni, P., Davis, D., Ryan, E., & di Martino, M. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson: Univ. of Arizona Press), 240
- Golimowski, D. A., Ardila, D. R., Krist, J. E., et al. 2006, AJ, 131, 3109 [NASA ADS] [CrossRef]
- Grigorieva, A., Artymwicz, P., & Thébault, P. 2007, A&A, 461, 537 [NASA ADS] [CrossRef] [EDP Sciences]
- Heap, S. R., Lindler, D. J., Lanz, T. M., et al. 2000, ApJ, 539, 435 [NASA ADS] [CrossRef]
- Kalas, P., Graham, J., & Clampin, M. 2005, Nature, 435, 1067 [NASA ADS] [CrossRef] (In the text)
- Kalas, P., Graham, J., Clampin, M., & Fitzgerald, M. 2006, ApJ, 637, 57 [NASA ADS] [CrossRef] (In the text)
- Kalas, P., Fitzgerald, M., & Graham, J. 2007, ApJ, 661, 85 [NASA ADS] [CrossRef] (In the text)
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] (In the text)
- Kenyon, S. J., & Bromley, B. 2004, ApJ, 602, L133 [NASA ADS] [CrossRef] (In the text)
- Krist, J. E., Ardila, D. R., Golimowski, D. A., et al. 2005, AJ, 129, 1008 [NASA ADS] [CrossRef] (In the text)
- Krivov, A., Löhne, T., & Sremcevic, M. 2006, A&A, 455, 509 [NASA ADS] [CrossRef] [EDP Sciences]
- Leinhardt, Z., & Richardson, D. 2005, ApJ, 625, 427 [NASA ADS] [CrossRef]
- Lissauer J., & Stewart, G. 1993, in Protostars and Planets III (Tucson: the Univ. of Arizona Press), 1061
- Löhne, T., Krivov, A., & Rodmann, J. 2008, ApJ, 673, 1123 [NASA ADS] [CrossRef]
- Mouillet, D., Larwood, J. D., Papaloizou, J. C. B., & Lagrange, A. M. 1997, MNRAS, 292, 896 [NASA ADS]
- Petit, J.-M., & Farinella, P. 1993, CeMDA, 57, 1 [NASA ADS]
- Quillen, A. C., Morbidelli, A., & Moore, A. 2007, MNRAS, 380, 1642 [NASA ADS] [CrossRef]
- Reche, R., Beust, H., Augereau, J.-C., & Absil, O. 2008, A&A, 480, 551 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schneider, G., Silverstone, M. D., & Hines, D. C., et al. 2006, ApJ, 650, 414 [NASA ADS] [CrossRef] (In the text)
- Stern, A., & Colwell, J. 1997, ApJ, 480, 879 [NASA ADS] [CrossRef] (In the text)
- Strubbe, L. E., & Chiang, E. I. 2006, ApJ, 648, 652 [NASA ADS] [CrossRef]
- Thébault, P., & Augereau, J. C. 2007, A&A, 472, 169 [NASA ADS] [CrossRef] [EDP Sciences]
- Thébault, P., & Beust, H. 2001, A&A, 376, 621 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Thébault, P., & Brahic, A. 1998, Planet. Space Sci., 47, 233 [NASA ADS] [CrossRef] (In the text)
- Thébault, P., & Wu, Y. 2008, A&A, 481, 713 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wetherill, G. W., & Stewart, G. R. 1993, Icarus, 106, 190 [NASA ADS] [CrossRef]
- Wood, B. E., Muller, H.-R., Zank, G. P., & Linsky, J. L. 2002, ApJ, 574, 412 [NASA ADS] [CrossRef]
- Wyatt, M. C. 2005, A&A, 433, 1007 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wyatt, M. C. 2008, ARA&A, 46, 339 [NASA ADS] [CrossRef] (In the text)
- Wyatt, M. C., & Dent, W. R. F. 2002, MNRAS, 334, 589 [NASA ADS] [CrossRef]
- Xie, J.-W., & Zhou, J.-L. 2008, ApJ, 686, 570 [NASA ADS] [CrossRef]
Footnotes
- ... ratio
![[*]](/icons/foot_motif.png)
- The aspect ratio should not be confused with the opening angle 2H/r.
- ... distances
![[*]](/icons/foot_motif.png)
- All those with
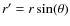 ,
where r is the distance measured along the ansae and r' is the true radial distance.
,
where r is the distance measured along the ansae and r' is the true radial distance.
- ... density
![[*]](/icons/foot_motif.png)
- This is a first order estimate. In reality, the constraint is not directly on
 but on the product
but on the product
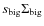 ,
where
,
where
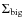 is the surface density of
is the surface density of
 bodies (see Quillen et al. 2007, for more details).
bodies (see Quillen et al. 2007, for more details).
- ... collisions
![[*]](/icons/foot_motif.png)
- For each given size there is an equilibrium between the particles lost by fragmenting collisions and the ones newly produced as fragments from collisions involving larger bodies.
- ... value
![[*]](/icons/foot_motif.png)
- Note however the pioneering work of Beauge & Aarseth (1990), whose code produced 4 fragments after each shattering collision, but had to be restricted to only 200 initial bodies, or that of Leinhardt & Richardson (2005), allowing the breakup of large rubble piles of gravitationally bound hard spheres, as well as the work by Grigorieva et al. (2007), who combined the statistical and N-body approaches by using numerical ``super-particles'', but were limited to short timescales.
- ... projectiles
![[*]](/icons/foot_motif.png)
- This is mainly because grains close to the blow-out size are the impactors carrying the highest kinetic energy and thus have an increased excavating/shattering capacity (see Thébault & Augereau 2007, for a detailed discussion on these issues.).
- ...

![[*]](/icons/foot_motif.png)
- This is of course a very simplified expression, which neglects that
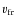 should in principle depend on both fragment size and the way in which fragments are produced: cratering or shattering of the target. Nevertheless, we can ignore these refinements for the order-of-magnitude purpose of our discussion.
should in principle depend on both fragment size and the way in which fragments are produced: cratering or shattering of the target. Nevertheless, we can ignore these refinements for the order-of-magnitude purpose of our discussion.
- ... Mic
![[*]](/icons/foot_motif.png)
- AU Mic is an M star where, in addition to radiation pressure, a stellar wind is also acting to place small grains on eccentric or unbound orbits (Augereau & Beust 2006; Wood et al. 2002; Fitzgerald et al. 2007; Strubbe & Chiang 2006). To first order, this additional force has the same dependency on particle size and radial distance as radiation pressure.
- ... 133 AU
![[*]](/icons/foot_motif.png)
- They are based on the measure of this edge's drop-off in surface brightness, which, because of the system's inclination to the line of sight, could either be due to an infinitely flat disc with a finite spread in the radial direction, or a perfectly sharp radial edge with a finite vertical thickness (see Sect.3.2.2 of Chiang et al. 2009).
All Tables
Table 1: Nominal case set up.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12396fg1.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg66.png) |
Figure 1:
Final positions in the vertical plane, once the system has reached a collisional steady state, for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{12396fg2.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg67.png) |
Figure 2:
Evolution in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12396fg3.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg69.png) |
Figure 3:
Synthetic image of a disc seen edge-on, once the steady collisonal state is reached, in scattered light assuming grey scattering. The dotted line corresponds to the vertical full width at half maximum ( FWHM), while the full line marks the location of the full width at one tenth maximum FW0.1M. The fluxes have been averaged over 2 AU |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12396fg4.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg70.png) |
Figure 4: Same run as in Fig. 3, but displaying the FWHM and FW0.1M for the azimuthally averaged local geometrical thickness as a function of radial distance. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{12396fg5.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg79.png) |
Figure 5:
Evolution of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12396fg6.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa12396-09/Timg111.png) |
Figure 6:
Vertical FWHM (=2H) for the AU Mic disc, as derived from observations (Krist et al. 2005) and obtained for a test numerical disc initially confined to a narrow annulus at |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.