| Issue |
A&A
Volume 505, Number 3, October III 2009
|
|
|---|---|---|
| Page(s) | 1041 - 1048 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912118 | |
| Published online | 11 August 2009 | |
Wide and deep near-UV (360 nm) galaxy counts and the extragalactic background light with the Large Binocular Camera
A. Grazian1 - N. Menci1 - E. Giallongo1 - S. Gallozzi1 - F. Fontanot2,3 - A. Fontana1 - V. Testa1 - R. Ragazzoni4 - A. Baruffolo4 - G. Beccari5 - E. Diolaiti6 - A. Di Paola1 - J. Farinato4 - F. Gasparo2 - G. Gentile4 - R. Green7 - J. Hill7 - O. Kuhn7 - F. Pasian2 - F. Pedichini1 - M. Radovich8 - R. Smareglia2 - R. Speziali1 - D. Thompson7 - R. M. Wagner7
1 - INAF - Osservatorio Astronomico di Roma, via Frascati 33,
00040 Monteporzio, Italy
2 - INAF - Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11,
34131 Trieste, Italy
3 - MPIA Max-Planck-Institute für Astronomie, Königstuhl 17, 69117
Heidelberg, Germany
4 - INAF - Osservatorio Astronomico di Padova, vicolo dell'Osservatorio 5,
35122 Padova, Italy
5 - ESA, Space Science Department, 2200 AG Noordwijk, The Netherlands
6 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1,
40127 Bologna, Italy
7 - Large Binocular Telescope Observatory, University of Arizona, 933 N.
Cherry Ave., Tucson, AZ 85721-0065, USA
8 - INAF - Osservatorio Astronomico di Capodimonte, via Moiariello 16,
80131 Napoli, Italy
Received 19 March 2009 / Accepted 15 June 2009
Abstract
Context. Deep multicolour surveys are the main tool for exploring the formation and evolution of the very faint galaxies that are beyond the spectroscopic limit of present technology. The photometric properties of these faint galaxies are usually compared with current renditions of semianalytical models to provide constraints on the detailed treatment of the fundamental physical processes involved in galaxy formation and evolution, namely the mass assembly and the star formation.
Aims. Galaxy counts over large sky areas in the 360 nm near-UV band are particularly difficult to obtain given the low efficiency of near-UV instrumentation, even at 8 m class telescopes. Observing in the near-UV bands can provide a first assessment of the distribution of star formation activity in distant (up to ![]() )
galaxies. A relatively large instrumental field of view helps to minimize the biases caused by cosmic variance.
)
galaxies. A relatively large instrumental field of view helps to minimize the biases caused by cosmic variance.
Methods. We obtained deep images in the 360 nm U band provided by the blue channel of the Large Binocular Camera at the prime focus of the Large Binocular Telescope. Over an area of ![]() 0.4 sq. deg., we derived the galaxy number counts down to U=27 in the Vega system (corresponding to U=27.86 in the AB system) at a completeness level of 30% reaching the faintest current limit for this wavelength and sky area.
0.4 sq. deg., we derived the galaxy number counts down to U=27 in the Vega system (corresponding to U=27.86 in the AB system) at a completeness level of 30% reaching the faintest current limit for this wavelength and sky area.
Results. The shape of the galaxy number counts in the U band can be described by a double power-law, the bright side being consistent with the shape of shallower surveys of comparable or greater areas. The slope bends over significantly at U>23.5 ensuring the convergence of the contribution by star-forming galaxies to the extragalactic background light in the near-UV band to a value that is more than 70% of the most recent upper limits derived for this band. We jointly compared our near-UV and K band counts collected from the literature with a few selected hierarchical CDM models, concentrating on specific critical issues in the physical description of the galaxy formation and evolution.
Key words: surveys - techniques: image processing - galaxies: photometry - galaxies: statistics
1 Introduction
Wide and deep multicolour surveys are useful tools for investigating in detail the processes of galaxy formation and evolution, especially beyond the spectroscopic capabilities of current instrumentation. One of the main aims of these deep multicolour surveys is to provide a clear picture of the processes involved in the mass assembly and star formation of galaxies across cosmic time. Galaxy observables, such as luminosity and mass functions, and two-point correlation function, are typically compared with current renditions of semi-analytical models in hierarchical CDM scenarios, to determine the key ingredients for an accurate description of the physics of galaxy formation (Croton et al. 2006; Menci et al. 2006; Bower et al. 2006; Nagamine et al. 2006; Fontanot et al. 2007; De Lucia & Blaizot 2007; Somerville et al. 2008; Keres et al. 2009; Dekel et al. 2009).
The observed properties of the galaxy population, however, are affected mainly by the limited statistics. Deep pencil beam surveys, such as GOODS (Giavalisco et al. 2004) or HUDF (Beckwith et al. 2003), have been carried out on relatively small sky areas and are affected significantly by cosmic variance. Larger surveys such as COSMOS, which extends over a 2 deg2 area, are indeed shallower and limit the knowledge of the faint galaxy population at intermediate and high redshifts.
To probe the statistical properties of the faint galaxy population and reduce the biases due to the cosmic variance, a major imaging campaign should be performed over large areas with efficient multicolour imagers at 8 m class telescopes. This is especially true in the near-UV band (hereafter UV), where instrumentation is in general less efficient but where it is possible to extract information about the star formation activity and dust absorption present in distant galaxies.
In this context, we are exploiting the unique power of the Large
Binocular Camera (LBC) installed at the prime focus of the Large
Binocular Telescope (LBT,
Pedichini et al. 2003; Speziali et al. 2004; Ragazzoni et al. 2006; Hill et al. 2008; Giallongo et al. 2008) to reach faint
magnitude limits in the U band (
![]() Å) over areas of
several hundreds of sq. arcmin.
Å) over areas of
several hundreds of sq. arcmin.
Long LBC observations in the UV band are of comparable depth to those
of the HDFs (although, obviously, the image quality is
poorer). Even a single pointing with LBC produces a field two
orders of magnitude larger than that of the combined HDF-N and
HDF-S. This is very important because the transverse extent of the
HDFs corresponds to about 1 Mpc at
![]() where dark matter
clustering is still important.
where dark matter
clustering is still important.
The goal of this paper is to provide UV (360 nm) galaxy number counts to the faintest magnitude limits available from ground-based observations. The comparison of both the normalization and shape of the observed counts with that predicted by theoretical hierarchical models can help to constrain the descriptions of galaxy formation and evolution, such as dust extinction and the formation of dwarf galaxies.
Throughout this paper, we adopt the Vega magnitude system
(
![]() )
and we refer to differential number counts
as simply ``number counts'', unless otherwise stated.
)
and we refer to differential number counts
as simply ``number counts'', unless otherwise stated.
2 The data
The deep UV observations described here were carried out with the
Large Binocular Camera (LBC, Giallongo et al. 2008), a double imager
installed at the prime foci stations of the 8.4 m telescopes LBT (Large
Binocular Telescope, Hill et al. 2008). Each LBT telescope unit is
equipped with similar prime focus cameras. The blue channel (LBC-Blue)
is optimized for imaging in the UV-B bands and the red channel
(LBC-Red) for imaging in the VRIZY bands. The unvignetted FoV of each
camera is 27 arcmin in diameter, and the detector area is
equivalent to a
![]() arcmin2 field, covered by four 4 K by
2 K chips of pixel scale 0.225 arcsec. Because the mirrors of both
channels are mounted on the same pointing system, a given target can
be observed simultaneously over a wide wavelength range, improving the
operation efficiency. Extensive descriptions of the twin LBC instrument
can be found in Giallongo et al. (2008); Pedichini et al. (2003); Ragazzoni et al. (2006), and Speziali et al. (2008).
arcmin2 field, covered by four 4 K by
2 K chips of pixel scale 0.225 arcsec. Because the mirrors of both
channels are mounted on the same pointing system, a given target can
be observed simultaneously over a wide wavelength range, improving the
operation efficiency. Extensive descriptions of the twin LBC instrument
can be found in Giallongo et al. (2008); Pedichini et al. (2003); Ragazzoni et al. (2006), and Speziali et al. (2008).
We used a deep U-BESSEL image of 3 hours, acquired in normal seeing conditions
(
![]() arcsec) during the commissioning of the LBC-Blue camera, to derive
faint UV galaxy-counts in a 478.2 arcmin2 sky area to a faintness limit of
arcsec) during the commissioning of the LBC-Blue camera, to derive
faint UV galaxy-counts in a 478.2 arcmin2 sky area to a faintness limit of
![]() ,
in the Q0933+28 field (Steidel et al. 2003).
The data were reduced using the LBC pipeline described in
detail in Giallongo et al. (2008), applying the standard debias, flat-fielding,
and stacking procedures to derive the coadded image. The flux calibration
of the U-BESSEL image was
derived by using observations of photometric standards from the fields
SA98 and SA113 (Landolt et al. 1992) and the photometric fields
of Galadi-Enriquez et al. (2000), as described in detail in Giallongo et al. (2008).
The precision of the zeropoint calibration in the U-BESSEL filter
is typically of the order of 0.03 mag at 68% confidence level.
A correction to the photometric zeropoint of 0.11 mag due to the
Galactic extinction was applied to the final coadd U-BESSEL image.
,
in the Q0933+28 field (Steidel et al. 2003).
The data were reduced using the LBC pipeline described in
detail in Giallongo et al. (2008), applying the standard debias, flat-fielding,
and stacking procedures to derive the coadded image. The flux calibration
of the U-BESSEL image was
derived by using observations of photometric standards from the fields
SA98 and SA113 (Landolt et al. 1992) and the photometric fields
of Galadi-Enriquez et al. (2000), as described in detail in Giallongo et al. (2008).
The precision of the zeropoint calibration in the U-BESSEL filter
is typically of the order of 0.03 mag at 68% confidence level.
A correction to the photometric zeropoint of 0.11 mag due to the
Galactic extinction was applied to the final coadd U-BESSEL image.
The Q0933+28 field was also imaged in the SDT-Uspec![]() filter of LBC for
an additional hour in the first quarter of 2007, in normal seeing
conditions (1.1 arcsec). These images are reduced and coadded in the same
way as the U-BESSEL ones, except for the photometric calibration procedure,
which is carried out using a spectrophotometric standard star of Oke (1990).
The precision of the zeropoint calibration in the SDT-Uspec filter
is typically of the order of 0.05 mag at 68% c.l.
A Galactic extinction correction of 0.13 was used for this image.
filter of LBC for
an additional hour in the first quarter of 2007, in normal seeing
conditions (1.1 arcsec). These images are reduced and coadded in the same
way as the U-BESSEL ones, except for the photometric calibration procedure,
which is carried out using a spectrophotometric standard star of Oke (1990).
The precision of the zeropoint calibration in the SDT-Uspec filter
is typically of the order of 0.05 mag at 68% c.l.
A Galactic extinction correction of 0.13 was used for this image.
To analyze the galaxy number counts deeper in
the UV band, we coadded the image obtained in the U-BESSEL filter (with
exposure time of 3 h) with this new one, after rescaling the two
images to the same zeropoint. We verified that the effective
wavelengths of these two filters are the same, the only difference
being the higher transmission efficiency (1.5 times, after integrating its
efficiency curve from
![]() to 4000 Å) of the SDT-Uspec
filter compared to the U-BESSEL one. The colour term between these two
filters is 0.01, which we thus neglect when summing up the two
images. The resulting image goes
to 4000 Å) of the SDT-Uspec
filter compared to the U-BESSEL one. The colour term between these two
filters is 0.01, which we thus neglect when summing up the two
images. The resulting image goes ![]() 0.5 mag deeper than the original 3 h with U-BESSEL filter, given the higher image quality of the new
SDT-Uspec image due to the general improvement of the telescope-instrument
system, in particular the reduction of scattered light from the telescope and
dome environment after the first run of the LBC-Blue commissioning.
We use this final coadded image to improve the
magnitude limit in the UV band and extend the number counts in this
band to faint fluxes.
0.5 mag deeper than the original 3 h with U-BESSEL filter, given the higher image quality of the new
SDT-Uspec image due to the general improvement of the telescope-instrument
system, in particular the reduction of scattered light from the telescope and
dome environment after the first run of the LBC-Blue commissioning.
We use this final coadded image to improve the
magnitude limit in the UV band and extend the number counts in this
band to faint fluxes.
To decrease the effects of cosmic variance in the number counts at
![]() ,
we used 3 additional LBC fields with shallower magnitude limits
,
we used 3 additional LBC fields with shallower magnitude limits
![]() but of much larger area (892 arcmin2) in the Subaru XMM Deep
Survey (SXDS, Sekiguchi et al. 2004) region. These images were reduced and
calibrated as described above for the Q0933+28 field.
The FWHM of these images (SXDS1, SXDS2, SXDS3) is higher (1.2, 1.25, 1.4
arcsec) than the one in the Q0933+28 field and the exposure
time per LBC pointing is 1.0, 1.5, and 1.5 h, respectively,
in the U-BESSEL filter.
These three LBC images, combined with the deep point in the Q0933+28, field
are then used to derive wide and deep galaxy number counts in the U band,
from U=19.5 to 25.0 over a FoV of 1370 arcmin2 (0.38 sq. deg.)
and to U=27.0 for a subsample of
but of much larger area (892 arcmin2) in the Subaru XMM Deep
Survey (SXDS, Sekiguchi et al. 2004) region. These images were reduced and
calibrated as described above for the Q0933+28 field.
The FWHM of these images (SXDS1, SXDS2, SXDS3) is higher (1.2, 1.25, 1.4
arcsec) than the one in the Q0933+28 field and the exposure
time per LBC pointing is 1.0, 1.5, and 1.5 h, respectively,
in the U-BESSEL filter.
These three LBC images, combined with the deep point in the Q0933+28, field
are then used to derive wide and deep galaxy number counts in the U band,
from U=19.5 to 25.0 over a FoV of 1370 arcmin2 (0.38 sq. deg.)
and to U=27.0 for a subsample of ![]() 480 arcmin2.
480 arcmin2.
3 The number counts in the U band
3.1 Deep U-band galaxy number counts
We computed galaxy number counts using the SExtractor package
(Bertin & Arnouts 1996). For objects of area greater than that
corresponding to a circular aperture of radius equal to the FWHM, we
used the ``best'' photometry (Kron magnitude or corrected
isophotal magnitude, if
the galaxy is severely blended with surrounding objects) provided by
SExtractor. For smaller sources, we computed magnitudes in circular
apertures of diameter equal to 2 times the FWHM, and corrected them
with an aperture correction that we derived using relatively bright stars
in the field. This allows us to avoid the well known underestimate of
the flux of faint galaxies provided by the isophotal method. To
isolate the few stars from the numerous faint galaxies in this field,
we relied on the class_star classifier provided by SExtractor. It is
known that the morphological star/galaxy classifier of SExtractor is
not reliable for faint objects, but according to the model of Bahcall & Soneira (1980)
the contamination from stars at
faint U band fluxes and at high galactic latitude is very limited
(1%). At brighter magnitudes,
![]() ,
the contamination from stars cannot be neglected, but at
high S/N ratio, the morphological classification of SExtractor is
robust. Moreover, the agreement between the LBC number counts at
,
the contamination from stars cannot be neglected, but at
high S/N ratio, the morphological classification of SExtractor is
robust. Moreover, the agreement between the LBC number counts at ![]() and those of both SDSS and other large area surveys (e.g., VVDS) indicates
that the contamination from Galactic stars is also lower for brighter U band
magnitudes.
and those of both SDSS and other large area surveys (e.g., VVDS) indicates
that the contamination from Galactic stars is also lower for brighter U band
magnitudes.
We search for an optimal configuration of SExtractor detection parameters to maximize the completeness at faint magnitude limits and reduce the number of unreliable detections. The two parameters regulating the depth, completeness, and reliability of the photometric catalog are the threshold (relative to the rms of the image) adopted for detection of objects and the minimum area of connected pixels above this threshold. We used the negative image technique, described in Yan & Windhorst (2004); Dickinson et al. (2004) and Bouwens et al. (2007), as an estimate of the reliability of the catalog. Using SExtractor, we produce the ``-OBJECTS'' image, i.e., the image with the detected objects subtracted, and then compute the negative of this image and run SExtractor with the same detection parameters used for the positive image. The sources detected on the negative image provide an estimate of the contamination from spurious sources, provided that the noise statistic is symmetric (towards positive and negative pixel values) in the image.
After several tests with different parameter sets, the most suitable
combination are thresh = 0.7, and area = 8 pixels for Q0933+28
field, and thresh = 0.8, and area = 9 for SXDS fields (where the seeing is a bit
worse), which minimize the
number of spurious sources (measured in the negative image), while
ensuring that the number counts and completeness of true sources remain
relatively high at faint magnitude limits (
![]() ). In the
Q0933+28 field, the contamination from spurious sources is
). In the
Q0933+28 field, the contamination from spurious sources is ![]() 2.2%
at U=26.5, and remains lower than
2.2%
at U=26.5, and remains lower than ![]() to U=27.0(corresponding to
to U=27.0(corresponding to
![]() ).
).
The results of the galaxy number count analysis can be affected by the
blending of galaxies when deep fields are investigated. In SExtractor,
the two parameters affecting the deblending of sources are the DEBLEND_NTHRESH and DEBLEND_MINCONT parameters. We produce
different catalogs using various combination of these two parameters
for each LBC image, and we find that the raw number counts are
insensitive to these parameters, since the number of galaxies per
magnitude bin and per square degree varies between
![]() at
U=24-25 and
at
U=24-25 and
![]() at U=27, our faintest bin in the
galaxy number counts. We adopt DEBLEND_NTHRESH = 32 and DEBLEND_MINCONT = 0.002 for all the fields described here, based on
visual inspection of the reliability of deblended sources on the
Q0933+28 field.
at U=27, our faintest bin in the
galaxy number counts. We adopt DEBLEND_NTHRESH = 32 and DEBLEND_MINCONT = 0.002 for all the fields described here, based on
visual inspection of the reliability of deblended sources on the
Q0933+28 field.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12118fg1.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12118-09/Timg22.png) |
Figure 1: Number counts of galaxies in the U-BESSEL band for the Q0933+28 and SXDS LBC fields. Black crosses represent the raw galaxy number counts, while filled big circles show the number counts corrected for incompleteness. Magnitudes are in the Vega system. We compare our counts with shallow surveys of similar or larger area (SDSS EDR, GOYA, VVDS F2), and with deeper pencil beam surveys (Hawaii HDFN, WHT, HDFN, HDFS). |
| Open with DEXTER | |
The resulting raw counts are shown in Fig. 1, where a clear
decrease is apparent for
![]() .
The typical photometric
error at
.
The typical photometric
error at ![]() is
is
![]() magnitudes, corresponding to a total
integrated number count of
magnitudes, corresponding to a total
integrated number count of ![]() 100 galaxies per arcmin2. An
estimate of the completeness level should be performed to
evaluate the amount of correction to the raw counts at the faint
limits. This was evaluated by including in the true image 1000
simulated galaxies per 0.25 mag bin in the magnitude
interval
100 galaxies per arcmin2. An
estimate of the completeness level should be performed to
evaluate the amount of correction to the raw counts at the faint
limits. This was evaluated by including in the true image 1000
simulated galaxies per 0.25 mag bin in the magnitude
interval
![]() using the standard ``artdata'' package in
IRAF. We included disk galaxies of half light radius 0.2-0.4 arcsec,
convolved with the PSF of stellar objects in the field. We then
run SExtractor on this new image using the same detection parameters
described above, and determined how effective SExtractor is in
recovering the simulated galaxies as a function of magnitude. The
resulting sizes of the simulated galaxies are typical of real galaxies
in the magnitude interval
using the standard ``artdata'' package in
IRAF. We included disk galaxies of half light radius 0.2-0.4 arcsec,
convolved with the PSF of stellar objects in the field. We then
run SExtractor on this new image using the same detection parameters
described above, and determined how effective SExtractor is in
recovering the simulated galaxies as a function of magnitude. The
resulting sizes of the simulated galaxies are typical of real galaxies
in the magnitude interval
![]() ,
so the completeness that we
computed at U=26-27 can be considered to be a robust estimate. Using
different datasets, i.e., Windhorst et al. (2002) and
GOODS-South Grazian et al. (2006), we verified
that, at
,
so the completeness that we
computed at U=26-27 can be considered to be a robust estimate. Using
different datasets, i.e., Windhorst et al. (2002) and
GOODS-South Grazian et al. (2006), we verified
that, at ![]() ,
the half light radius of these galaxies is always
between 0.2 and 0.4 arcsec. We choose not to use real sources to
simulate the completeness of the images mainly for two reasons: the
half light radii of galaxies decrease with magnitude, and it is
known that fainter galaxies are smaller. If we use bright (
,
the half light radius of these galaxies is always
between 0.2 and 0.4 arcsec. We choose not to use real sources to
simulate the completeness of the images mainly for two reasons: the
half light radii of galaxies decrease with magnitude, and it is
known that fainter galaxies are smaller. If we use bright (![]() )
high
signal-to-noise objects, their size, once dimmed to
)
high
signal-to-noise objects, their size, once dimmed to
![]() ,
can be overestimated with respect to
their true size, enhancing artificially the completeness correction
at fainter magnitudes. If we use real faint sources as input in our
simulations, the signal-to-noise ratio of these galaxies is
very low, enhancing even in this case the completeness correction. We
tried instead a robust and realistic assumption, which is to
simulate galaxies with half light radius between 0.2 and 0.4 arcsec,
the range observed at faint magnitude limits where
morphological analysis is still reliable (see e.g. Conselice et al. 2008).
The completeness at
,
can be overestimated with respect to
their true size, enhancing artificially the completeness correction
at fainter magnitudes. If we use real faint sources as input in our
simulations, the signal-to-noise ratio of these galaxies is
very low, enhancing even in this case the completeness correction. We
tried instead a robust and realistic assumption, which is to
simulate galaxies with half light radius between 0.2 and 0.4 arcsec,
the range observed at faint magnitude limits where
morphological analysis is still reliable (see e.g. Conselice et al. 2008).
The completeness at ![]() does not depend on the half light radius
of the simulated galaxies, while at fainter magnitudes it does depend on
the galaxy size: in particular, at U=26.0 the scatter in
the completeness for various half light radii between 0.2 and 0.4
arcsec is 3%, increasing to 6% at U=26.5, and reaching 16% at
U=27.0. The resulting 50% completeness level is measured
at
does not depend on the half light radius
of the simulated galaxies, while at fainter magnitudes it does depend on
the galaxy size: in particular, at U=26.0 the scatter in
the completeness for various half light radii between 0.2 and 0.4
arcsec is 3%, increasing to 6% at U=26.5, and reaching 16% at
U=27.0. The resulting 50% completeness level is measured
at
![]() ,
while at U=27.0 we have a formal completeness of
30%.
,
while at U=27.0 we have a formal completeness of
30%.
The number counts corrected for incompleteness are shown in
Fig. 1. Given the wide magnitude interval from
![]() to
to
![]() available in the present survey, the
shape of the count distribution can be derived from a single survey in a
self-consistent way, possibly minimizing offsets due to systematics in
the photometric analysis of data from multiple surveys (zeropoint
calibration, and field-to-field variation). A clear bending is
apparent at
available in the present survey, the
shape of the count distribution can be derived from a single survey in a
self-consistent way, possibly minimizing offsets due to systematics in
the photometric analysis of data from multiple surveys (zeropoint
calibration, and field-to-field variation). A clear bending is
apparent at
![]() .
To quantify the effect, we fitted the
shape of the counts in the above magnitude interval with a double
power-law. The slope changes from
.
To quantify the effect, we fitted the
shape of the counts in the above magnitude interval with a double
power-law. The slope changes from
![]() to
to
![]() for
magnitudes fainter than
for
magnitudes fainter than
![]() .
The uncertainty in the
break magnitude is however large,
.
The uncertainty in the
break magnitude is however large, ![]() 0.5, since the transition
between the two regimes of the number counts is gradual.
0.5, since the transition
between the two regimes of the number counts is gradual.
In Fig. 1, we compare our galaxy number counts with those
derived by shallow surveys of large area (SDSS EDR, Yasuda et al. 2001) or
of similar area (GOYA by Eliche-Moral et al. 2006;
VVDS-F2 by Radovich et al. 2004), and with deep pencil beam surveys
(Hawaii HDFN by Capak et al. 2004; WHT, HDFN, and HDFS by Metcalfe et al. 2001). In
particular, the WHT galaxy counts (Metcalfe et al. 2001) are based on a 34 h
exposure time image reaching
![]() but at the much lower
3
but at the much lower
3![]() level in the photometric noise and in an area of
level in the photometric noise and in an area of ![]() 50 arcmin2, while the GOYA survey at the INT telescope is complete at
the 50% level at
50 arcmin2, while the GOYA survey at the INT telescope is complete at
the 50% level at
![]() .
These counts are shown together with the
two pencil beam surveys in the Hubble Deep Fields (Metcalfe et al. 2001).
The agreement with the GOYA survey (900 sq. arcmin.) is remarkable,
and suggests that once big areas of the sky are investigated, the
effects of cosmic variance are slightly reduced.
The present UV counts obtained during the commissioning of
LBC-Blue are thus a unique combination of deep imaging in the U band
and of large sky area, resulting in considerable reduction in
the cosmic variance effects for
.
These counts are shown together with the
two pencil beam surveys in the Hubble Deep Fields (Metcalfe et al. 2001).
The agreement with the GOYA survey (900 sq. arcmin.) is remarkable,
and suggests that once big areas of the sky are investigated, the
effects of cosmic variance are slightly reduced.
The present UV counts obtained during the commissioning of
LBC-Blue are thus a unique combination of deep imaging in the U band
and of large sky area, resulting in considerable reduction in
the cosmic variance effects for ![]() .
For brighter magnitude limits,
we refer to larger area surveys, shallower than our survey, as shown in
Fig. 1.
.
For brighter magnitude limits,
we refer to larger area surveys, shallower than our survey, as shown in
Fig. 1.
Table 1 summarizes the galaxy number counts, corrected for
incompleteness, with their upper and lower 1![]() confidence level
uncertainties, assuming Poisson noise and the cosmic variance effect.
For the latter, we used the cosmic variance calculator (v1.02)
developed by Trenti & Stiavelli (2008) using as input values a linear size of 22 arcmin
(corresponding to our deeper area of 478.2 arcmin2) and redshift from
0.0 to 3.0, for a standard
confidence level
uncertainties, assuming Poisson noise and the cosmic variance effect.
For the latter, we used the cosmic variance calculator (v1.02)
developed by Trenti & Stiavelli (2008) using as input values a linear size of 22 arcmin
(corresponding to our deeper area of 478.2 arcmin2) and redshift from
0.0 to 3.0, for a standard ![]() -CDM cosmology. At U=27, for example,
the computed cosmic variance is 4.5%.
-CDM cosmology. At U=27, for example,
the computed cosmic variance is 4.5%.
Using the Q0933+28 and the three fields in the SXDS area, we study
the field to field variation in the number counts in the U band.
We find that the typical variation from one LBC field to another is 0.04
in Log N for ![]() ,
while it reduces gradually to 0.01 at U=24.5,
well below the Poissonian uncertainties described in Table 1.
This ensures that the zeropoint calibration of the images is robust
and the area of this survey is sufficient to decrease the cosmic variance
effects below the statistical uncertainties in the galaxy number counts.
We complement these internal checks on the galaxy number counts in U with
an external consistency test, comparing our final number counts with shallower
ones derived in different areas or deep pencil beam surveys in
Fig. 1. We find that the survey-to-survey maximal variations
are of the order of 0.1 in Log N at all magnitudes, with lower scatter
for the wider surveys considered here (GOYA, SDSS-EDR, VVDS-F2).
,
while it reduces gradually to 0.01 at U=24.5,
well below the Poissonian uncertainties described in Table 1.
This ensures that the zeropoint calibration of the images is robust
and the area of this survey is sufficient to decrease the cosmic variance
effects below the statistical uncertainties in the galaxy number counts.
We complement these internal checks on the galaxy number counts in U with
an external consistency test, comparing our final number counts with shallower
ones derived in different areas or deep pencil beam surveys in
Fig. 1. We find that the survey-to-survey maximal variations
are of the order of 0.1 in Log N at all magnitudes, with lower scatter
for the wider surveys considered here (GOYA, SDSS-EDR, VVDS-F2).
Table 1: LBC U galaxy number counts.
3.2 The UV extragalactic background light
The slope of the galaxy number counts in the U band at
![]() changes from 0.58 to 0.24, which implies that the
contribution of galaxies to the integrated EBL in the UV has a maximum
around this magnitude. The contribution of observed galaxies to the
optical extragalactic background light (EBL) in the UV band can be
computed directly by integrating the emitted flux multiplied by the
differential number counts down to the completeness limit of the
survey.
changes from 0.58 to 0.24, which implies that the
contribution of galaxies to the integrated EBL in the UV has a maximum
around this magnitude. The contribution of observed galaxies to the
optical extragalactic background light (EBL) in the UV band can be
computed directly by integrating the emitted flux multiplied by the
differential number counts down to the completeness limit of the
survey.
Following the work of Madau & Pozzetti (2000), we compute the EBL in the U band,
![]() measured in erg s-1 cm-2 Hz-1 Sr-1, using the
method
measured in erg s-1 cm-2 Hz-1 Sr-1, using the
method
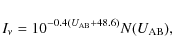 |
(1) |
where we use the following correction from Vega to AB:
Figure 2 shows the EBL obtained by the LBC deep number counts
and compares it with the results of Madau & Pozzetti (2000). Our data agrees well
with previous estimates of the EBL in the U band, and indeed it allows us
to derive precisely the peak of the differential EBL, at
![]() ,
and place strong constraints on the contributions of
faint galaxies to U=27.0 to the integrated EBL in this band.
At magnitudes
,
and place strong constraints on the contributions of
faint galaxies to U=27.0 to the integrated EBL in this band.
At magnitudes ![]() ,
our estimate of the EBL is significantly
higher than the one of Madau & Pozzetti (2000). Checking Fig. 1
in detail, it is clear that the HDFS is slightly underdense
with respect to the HDFN or other deep pencil beam surveys, probably
because of cosmic variance effects, and this is reflected in the lower
EBL of Madau & Pozzetti (2000) compared to the LBC estimate.
,
our estimate of the EBL is significantly
higher than the one of Madau & Pozzetti (2000). Checking Fig. 1
in detail, it is clear that the HDFS is slightly underdense
with respect to the HDFN or other deep pencil beam surveys, probably
because of cosmic variance effects, and this is reflected in the lower
EBL of Madau & Pozzetti (2000) compared to the LBC estimate.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12118fg2.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12118-09/Timg49.png) |
Figure 2:
The extragalactic background light per magnitude bin |
| Open with DEXTER | |
The integrated galaxy contribution to the EBL in the UV band implies that
![]() nW/m2/Sr at the effective wavelength of
the LBC U-BESSEL filter, 3590 Å, taking into account the magnitude
range U=17-27. This estimate is 20% higher than the one estimated by
Madau & Pozzetti (2000) (
2.87+0.58-0.42 nW/m2/Sr), although their value
is still consistent with our measurement due to their large
uncertainties. Moreover, our estimate reduces the uncertainties by an
order of magnitudes, which is of fundamental importance
to placing strong constraints on galaxy
evolution models. Extrapolating the observed number counts in the Uband down to flux = 0, we derive an integrated EBL of
nW/m2/Sr at the effective wavelength of
the LBC U-BESSEL filter, 3590 Å, taking into account the magnitude
range U=17-27. This estimate is 20% higher than the one estimated by
Madau & Pozzetti (2000) (
2.87+0.58-0.42 nW/m2/Sr), although their value
is still consistent with our measurement due to their large
uncertainties. Moreover, our estimate reduces the uncertainties by an
order of magnitudes, which is of fundamental importance
to placing strong constraints on galaxy
evolution models. Extrapolating the observed number counts in the Uband down to flux = 0, we derive an integrated EBL of
![]() nW/m2/Sr,
i.e., in our survey to U=27 we resolve 92% of the EBL produced by
galaxies.
nW/m2/Sr,
i.e., in our survey to U=27 we resolve 92% of the EBL produced by
galaxies.
The integrated flux from resolved galaxies, however, should be considered as a lower limit to the total EBL in the universe, since our estimate could be affected by different systematics:
- incompleteness in the number counts at faint magnitudes caused by the presence of very extended/diffuse sources that escape detection in our LBC deep images and in the HDFs surveys. The adopted detection algorithms usually select galaxies down to a threshold in their surface brightness limits, and so are prone to selection effects against low surface brightness galaxies. We computed the completeness of galaxies assuming a conservative half light radius of 0.3 arcsec, and we cannot exclude the presence of a population of diffuse and extended galaxies in the UV bands, even this hypothesis is quite unlikely, because of the well known relation between observed optical magnitudes and half light radius of galaxies (Totani et al. 2001);
-
the surface brightness dimming of sources at high redshifts. This is
not a serious problem in the U band, since all the light in this
wavelengths originates from
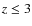 galaxies (non U-dropout galaxies) and,
as discussed in the next paragraph, the redshift distribution of galaxies
contributing to the peak of the EBL are at
galaxies (non U-dropout galaxies) and,
as discussed in the next paragraph, the redshift distribution of galaxies
contributing to the peak of the EBL are at 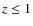 .
.
With the present observations, we reject the hypothesis of
Bernstein et al. (2002) that an enormous contribution to the sky background
in the U band is made by the overlapping wings of extended
galaxies. With the present observations, we reach a surface brightness limit
of U=28.2 mag/arcsec2 at 3![]() and thus exclude the presence of
faint and extended wings in the galaxy UV light distributions.
and thus exclude the presence of
faint and extended wings in the galaxy UV light distributions.
The discrepancy between the resolved and total EBL could be explained
by a population of ultra faint and numerous galaxies at ![]() ,
beyond the current limits of the present surveys and with a log N-log S
slope steeper than 0.5, or by an improper subtraction of the
foreground components, as stated in Mattila (2003) and Bernstein (2007).
,
beyond the current limits of the present surveys and with a log N-log S
slope steeper than 0.5, or by an improper subtraction of the
foreground components, as stated in Mattila (2003) and Bernstein (2007).
Recently, Georganopoulos et al. (2008) proposed a new method to derive stringent
limits to the diffuse light in the UV bands, by measuring the inverse Compton
emission in ![]() -rays of the EBL by the high energy electrons in
the radio lobes of Fornax A. This technique will allow to derive
constraints to the EBL at shorter wavelengths than the limits obtained
by the TeV blazar emission (Stanev & Franceschini 1998; Aharonian et al. 2006; Albert et al. 2008). At the
present stage, Albert et al. (2008) give an upper limit of
-rays of the EBL by the high energy electrons in
the radio lobes of Fornax A. This technique will allow to derive
constraints to the EBL at shorter wavelengths than the limits obtained
by the TeV blazar emission (Stanev & Franceschini 1998; Aharonian et al. 2006; Albert et al. 2008). At the
present stage, Albert et al. (2008) give an upper limit of
![]() nW/m2/Sr to the total EBL in the UV. This limit strengthens the
hypothesis that the discrepancy between our estimate of the EBL in Uband and that of Bernstein (2007) is due to a foreground local
component.
nW/m2/Sr to the total EBL in the UV. This limit strengthens the
hypothesis that the discrepancy between our estimate of the EBL in Uband and that of Bernstein (2007) is due to a foreground local
component.
Our derivation of the EBL by integrated galaxy counts is marginally consistent
with the lower limit derived by Kneiske & Dole (2008) of
![]() nW/m2/Sr at
nW/m2/Sr at
![]() Å.
Å.
4 Comparison with theoretical models
The availability of galaxy number counts to faint magnitude limits and over large sky areas can be used to test the predictions of different theoretical models without being strongly affected by cosmic variance. Among the various models (numerical and semi-analytical) developed in the framework of the standard hierarchical CDM scenario, we selected the models developed by Menci et al. (2006, hereafter M06), the Kitzbichler & White (2007) model based on the Millennium Simulation (hereafter K07), and the model developed by Monaco et al. (2007, hereafter MORGANA). All these models simulate the formation and evolution of galaxies, starting from a statistical description of the evolution of the DM halo population (merger trees), and using a set of approximated, though physically motivated, ``recipes'' to treat the physical processes (gas cooling, star formation, AGN and SF feedback, stellar population synthesis) acting on the baryonic component. An appropriate treatment of dust attenuation is also important when comparing model predictions to the UV observations, given the efficient scattering of radiation at these wavelengths by dust grains, as shown by the GALEX number counts of Xu et al. (2005).
The comparison of the observed counts with that predicted by the three selected models is used to enlighten different critical issues concerning the physical description of the galaxy formation and evolution.
In particular, the M06 model is characterized by a specific
implementation of the AGN feedback on the star formation activity in
high redshift galaxies. The description is based on the expanding
blast waves as a mechanism for propagating outwards the AGN energy
injected into the interstellar medium at the centre of galaxies (see
Menci et al. 2008); such a feedback is only active during the active
AGN phase (``QSO mode''), and it is effective in suppressing the star
formation in massive galaxies already by
![]() ,
thus yielding a
fraction of massive and extremely-red objects in approximate agreement
with observations (Menci et al. 2006).
The M06 model uses three different prescriptions
for the dust absorption, namely the Small Magellanic Cloud model (SMC),
the Milky Way (MW) law, and the Calzetti et al. (2000) extinction curve (C00).
In Fig. 3, the two short-dashed curves enclose the minimum
and maximum number counts predicted by the M06 model, taking into account the
three different extinction curves (SMC, MW, and C00).
,
thus yielding a
fraction of massive and extremely-red objects in approximate agreement
with observations (Menci et al. 2006).
The M06 model uses three different prescriptions
for the dust absorption, namely the Small Magellanic Cloud model (SMC),
the Milky Way (MW) law, and the Calzetti et al. (2000) extinction curve (C00).
In Fig. 3, the two short-dashed curves enclose the minimum
and maximum number counts predicted by the M06 model, taking into account the
three different extinction curves (SMC, MW, and C00).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12118fg3.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12118-09/Timg63.png) |
Figure 3:
Number counts of galaxies in the U-BESSEL band for the Q0933+28 LBC
field, complemented at brighter magnitudes ( |
| Open with DEXTER | |
The model of Kitzbichler & White (2007) is based on the Millennium Simulation
(Springel et al. 2005) and a concordance Lambda CDM cosmology. In the
model, the particle mass resolution of the code can affect
the physical and statistical
properties of faint low-luminosity galaxies. The adopted CDM mass
resolution is sufficient to resolve a halo hosting a galaxy as faint
as 0.1 L* with at least 100 particles of
![]() .
The model also adopts a different AGN feedback called
``radio mode'' in which cooling is suppressed by the continuous
accretion of hot gas onto supermassive black holes at the centre of
groups or cluster of galaxies.
The only difference between K07 and both Croton et al. (2006) and De Lucia & Blaizot (2007)
is in the
dust model used in their simulations. For the local galaxies, they adopt
a simple relationship between face-on optical depth and intrinsic luminosity
.
The model also adopts a different AGN feedback called
``radio mode'' in which cooling is suppressed by the continuous
accretion of hot gas onto supermassive black holes at the centre of
groups or cluster of galaxies.
The only difference between K07 and both Croton et al. (2006) and De Lucia & Blaizot (2007)
is in the
dust model used in their simulations. For the local galaxies, they adopt
a simple relationship between face-on optical depth and intrinsic luminosity
![]() with
with ![]() .
At high redshifts,
they take into account the different dust and gas contents, the varying
metallicities, and the shorter rest-frame emitted wavelengths. In particular,
their average extinction increases significantly towards high redshifts
because of
the smaller disc sizes of the galaxies. We refer to Kitzbichler & White (2007) for
details of their dust model.
.
At high redshifts,
they take into account the different dust and gas contents, the varying
metallicities, and the shorter rest-frame emitted wavelengths. In particular,
their average extinction increases significantly towards high redshifts
because of
the smaller disc sizes of the galaxies. We refer to Kitzbichler & White (2007) for
details of their dust model.
Finally, the MORGANA model is characterized by a different
treatment of the processes of gas cooling and infall (following Viola et al. 2008), star formation, and feedback (using the multi-phase
model of Monaco 2004). Black hole accretion is described in detail in
Fontanot et al. (2006): the accretion rate in Eddington units
determines the nature of feedback from the AGN. Synthetic SEDs for
model galaxies are obtained using the GRASIL code (Silva et al. 1998),
which explicitly solves the equation of radiative transfer in a dusty
medium. Fontanot et al. (2006) show that MORGANA is able to
reproduce both sub-mm (850 ![]() m) number counts and the redshift
distribution observed in K-limited samples with a conservative choice
of the stellar IMF. Galaxy SEDs, magnitudes, and colours for a
variety of passbands are obtained using the GRASIL
spectrophotometric code (Silva et al. 1998), which explicitely solves
the equations for the radiative transfer in a dusty medium taking into
account the composite geometry (bulge+disc) of each model galaxy. The
dust properties (dust-to-gas mass fractions, composition, and size
distribution) are kept fixed to values providing good agreement with
local observations (see Fontanot et al. 2007, for more details about the coupling
between MORGANA and GRASIL). In this work, we take
advantage of updates to the model, which was adapted for a WMAP3
cosmology and Chabrier IMF as presented in Lo Faro et al. (2009).
m) number counts and the redshift
distribution observed in K-limited samples with a conservative choice
of the stellar IMF. Galaxy SEDs, magnitudes, and colours for a
variety of passbands are obtained using the GRASIL
spectrophotometric code (Silva et al. 1998), which explicitely solves
the equations for the radiative transfer in a dusty medium taking into
account the composite geometry (bulge+disc) of each model galaxy. The
dust properties (dust-to-gas mass fractions, composition, and size
distribution) are kept fixed to values providing good agreement with
local observations (see Fontanot et al. 2007, for more details about the coupling
between MORGANA and GRASIL). In this work, we take
advantage of updates to the model, which was adapted for a WMAP3
cosmology and Chabrier IMF as presented in Lo Faro et al. (2009).
It is worth noticing that photoelectric absorption by the interstellar medium is redshifted, for high redshift galaxies, into the observed UV band. For this reason, only galaxies with z<3 contribute to the UV number counts. The common characteristics of the models is that only galaxies in the 1.5<z<2.5 redshift intervals provide the main contribution to the counts at U>26 (see Barro et al. 2009). This implies that the shape of the faint counts is provided by the average faint-end shape of the galaxy luminosity function in the same redshift interval.
The comparison of the observed galaxy number counts in the U(360 nm) band with the predictions of theoretical models shown in Fig. 3 indicates that:
- the M06 and K07 models reasonably reproduce the UV number counts from U=17 to U=27, while the MORGANA model exhibits the greatest disagreement with the observed data;
- the three models show different shapes for the UV galaxy number counts at faint fluxes, implying that discrepancies increase with increasing magnitudes. This can be evaluated in more detail by dividing the counts in redshift bins (see Barro et al. 2009);
- with the current observations of the UV number counts down to U=27, both M06 and K07 models show similar behaviour, although the K07 model appears to curve over for U>27 in contrast to the steeper slope of the M06 model.
Another physical quantity relevant to the correct reproduction of the
faint counts is the amount of star formation activity in faint low-mass
galaxies. This effect is particularly important in the MORGANA model,
where it is responsible for the flat shape of the predicted counts.
Fontanot et al. (2009) show that the underprediction of UV number counts of
faint galaxies can be explained by a rapid decline in their star
formation activity and consequently in their associated UV emission at
![]() .
These galaxies are predicted to be too passive and to host
too old stellar populations at later times with respect to observations.
The reduced SFRs can easily explain the flat shape of the predicted
counts in MORGANA.
.
These galaxies are predicted to be too passive and to host
too old stellar populations at later times with respect to observations.
The reduced SFRs can easily explain the flat shape of the predicted
counts in MORGANA.
As an attempt to disentangle dust/SFR effects from
number density evolution, we extended the model comparison to the
NIR K band number counts, which are much less sensitive to dust
absorption and short episodes of star formation.
The observed flux in the K band is more related
to the star formation history in the galaxy quantified by its
assembled stellar mass (see e.g., Fontana et al. 2006).
Figure 4 compares observed number
counts in the K band collected from the literature and provided by
different instruments/telescopes and surveys (SSDF: Minowa et al. 2005; HDFS:
Labbé et al. 2003; KDS: Moustakas et al. 1997; UDS: Cirasuolo et al. 2008; WHTDF: Cristobal-Hornillos et al. 2003;
HWDF: Huang et al. 1997; GOODS: Grazian et al. 2006) with the model predictions of M06,
K07, and MORGANA. The observed K band galaxy counts show a clear
bend at
![]() ,
where the average slope changes from 0.69 to a
flatter value of 0.33. Here the bending is clearer than
observed in the UV, since the break magnitude is brighter than
the faintest survey limits.
,
where the average slope changes from 0.69 to a
flatter value of 0.33. Here the bending is clearer than
observed in the UV, since the break magnitude is brighter than
the faintest survey limits.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12118fg4.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12118-09/Timg70.png) |
Figure 4: Number counts of galaxies in the K band for different deep surveys in the literature. The model predictions come from the same models described in the previous figure. |
| Open with DEXTER | |
In the K band, the models tend to overestimate the number counts both
at the bright end K<15 and at faint magnitudes K>20. The
excess in the predicted K band number counts resembles that at the
faint end of the theoretical luminosity functions in the NIR (see for
example Poli et al. 2003; and Fontanot et al. 2009). This can be indicative of
an excess in the production of galaxies with low luminosity and high
redshifts. If the NIR number counts are extrapolated to fainter
limits, the amount of excess differs among the models, being
smaller in the K07 model at ![]() .
The latter however is affected
by a threshold in the mass resolution used
by the numerical code of the Millennium simulation adopted in the K07
model. This could provide an artificial removal of faint galaxies.
.
The latter however is affected
by a threshold in the mass resolution used
by the numerical code of the Millennium simulation adopted in the K07
model. This could provide an artificial removal of faint galaxies.
The simultaneous comparison of the UV and NIR K band number counts at faint fluxes seems to indicate that the underprediction of the modelled UV number counts could be caused by dust extinction or reduced SF activity rather than intrinsic evolution in the galaxy number density.
Finally, we identify a third problem when comparing the bright end of the
galaxy counts, where the treatment of the feedback on SF processes due to
AGN activity can play an important role. The M06 model
for example shows the effect of a different treatment of AGN feedback
based on the so-called QSO mode compared to the radio mode
feedback used by the K07 model, while MORGANA is characterized
by both the radio and QSO modes. The different treatment of AGN feedback is
plausibly responsible for the differences in the predictions of
NIR galaxy number counts at ![]() .
The excess in the UV number
counts predicted by models is related to the quenching of the star formation
activity. MORGANA tends to overpredict star formation activity
in massive central galaxies at low-z. This is
related to the less efficient, or delayed, quenching of the cooling
flows in massive halos by radio-mode feedback. In this model,
gas accretion onto the central black hole is related to star formation
activity in the spheroidal component: this implies that AGN heating
switches on only after some cooled gas has already started forming stars
in the host galaxy (see Kimm et al. 2008, for a complete discussion and
a comparison of different radio-mode implementations in semi-analytical
models).
.
The excess in the UV number
counts predicted by models is related to the quenching of the star formation
activity. MORGANA tends to overpredict star formation activity
in massive central galaxies at low-z. This is
related to the less efficient, or delayed, quenching of the cooling
flows in massive halos by radio-mode feedback. In this model,
gas accretion onto the central black hole is related to star formation
activity in the spheroidal component: this implies that AGN heating
switches on only after some cooled gas has already started forming stars
in the host galaxy (see Kimm et al. 2008, for a complete discussion and
a comparison of different radio-mode implementations in semi-analytical
models).
As a last comment, all the three models include a contribution to the UV EBL that is broadly consistent with the upper limits described in Sect. 3.2. Using the same method described there for the observed data, we derived an EBL of 0.71-1.18 nW/m2/Sr for the M06 model in the UV band, while the MORGANA and K07 model have 2.66 and 3.26 nW/m2/Sr, respectively.
5 Summary
To summarize the main results of the paper:
- We have derived in a relatively wide field of 0.4 deg2 the deepest counts published to date in the 360 nm UV band. This has allowed us to evaluate the shape of the galaxy number counts in a wide magnitude interval U=19-27with the advantage of mitigating cosmic variance effects. The agreement with the number counts of shallower surveys confirms the low impact of systematic errors on LBC galaxy statistics.
-
The shape of the counts in UV can be described by a double power-law
with a steep slope 0.58 followed beyond
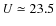 by a flatter
shape 0.24. Our counts are consistent at the bright end with surveys
of comparable or greater areas. At the faint end, our counts are more
consistent with that found in the HDF-N.
by a flatter
shape 0.24. Our counts are consistent at the bright end with surveys
of comparable or greater areas. At the faint end, our counts are more
consistent with that found in the HDF-N.
-
The faint-end slope of the counts is below 0.4 and this ensures
the convergence of the
contribution by star-forming galaxies to the EBL in the UV band. The
total value in the UV band obtained by extrapolating the slope of our
counts to flux = 0 is indeed
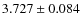 nW/m2/Sr.
It is consistent with upper limits derived from TeV
observations of Albert et al. (2008),
nW/m2/Sr.
It is consistent with upper limits derived from TeV
observations of Albert et al. (2008),
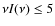 nW/m2/Sr,
showing that the UV EBL is resolved at
nW/m2/Sr,
showing that the UV EBL is resolved at 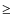 74% level.
74% level.
- We have compared our counts in the UV and K bands with the predictions of a few selected hierarchical CDM models considering different and important issues in the physical description of the galaxy formation and evolution.
- The mass resolution of numerical models is critical to reproducing the faint end of the UV galaxy number counts.
-
The discrepancies between predicted and observed UV galaxy number counts
at faint magnitudes could be mainly due to the treatment of dust extinction and
the star formation activity in low mass galaxies at
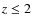 .
.
- The AGN feedback (radio versus QSO mode) may affect galaxy counts at the bright end of the log N-log S in the K band.
Adding colour information for galaxies with UV emission as faint as U=27-28 will require very deep observations in the red bands that are feasible with several hours of integration at 8 m class telescopes. Very deep multicolour information over areas of the order of a square degree can help in extracting physical information about the star formation history of the dwarf population at intermediate and high redshifts.
Acknowledgements
Observations have been carried out using the Large Binocular Telescope at Mt. Graham, Arizona, under the Commissioning phase of the Large Binocular Blue Camera. The LBT is an international collaboration among institutions in the United States, Italy and Germany. LBT Corporation partners are: the University of Arizona on behalf of the Arizona university system; Istituto Nazionale di Astrofisica, Italy; LBT Beteiligungsgesellschaft, Germany, representing the Max-Planck Society, the Astrophysical Institute Potsdam, and Heidelberg University; The Ohio State University, and The Research Corporation, on behalf of The University of Notre Dame, University of Minnesota and University of Virginia. The Millennium Simulation databases used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory. Some of the calculations were carried out on the PIA cluster of the Max-Planck-Institut für Astronomie at the Rechenzentrum Garching. We thank the anonymous referee for useful comments which helps in improving the quality of the present paper. A.G. warmly thanks Kalevi Mattila and Martin Raue for useful comments on the EBL limits.
References
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, Nature, 440, 1018 [NASA ADS] [CrossRef] (In the text)
- Albert, J., Aliu, E., Anderhub, H., et al. 2008, Science, 320, 1752 [NASA ADS] [CrossRef] (In the text)
- Bahcall, J. N., & Soneira, R. M. 1980, ApJS, 44, 73 [NASA ADS] [CrossRef] (In the text)
- Barro, G., Gallego, J., Pérez-González, P. G., et al. 2009, A&A, 494, 63 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Beckwith, S. V. W., Caldwell, J., Clampin, M., et al. 2003, A&AS, 202, 1705 (In the text)
- Bernstein, R. A. 2007, ApJ, 666, 663 [NASA ADS] [CrossRef] (In the text)
- Bernstein, R. A., Freedman, W. L., & Madore, B. F. 2002, ApJ, 571, 56 [NASA ADS] [CrossRef] (In the text)
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] (In the text)
- Bouwens, R. J., Illingworth, G. D., Franx, M., & Ford, H. 2007, ApJ, 670, 928 [NASA ADS] [CrossRef] (In the text)
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] (In the text)
- Capak, P., Cowie, L. L., Hu, E. M., et al. 2004, AJ, 127, 180 [NASA ADS] [CrossRef] (In the text)
- Cirasuolo, M., McLure, R. J., Dunlop, J. S., et al. 2008, MNRAS, submitted,submitted, [arXiv:0804.3471] (In the text)
- Conselice, C. J., Rajgor, S., & Myers, R. 2008, MNRAS, 386, 909 [NASA ADS] [CrossRef] (In the text)
- Cristobal-Hornillos, D., Balcells, M., Prieto, M., et al. 2003, ApJ, 595, 71 [NASA ADS] [CrossRef] (In the text)
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] (In the text)
- Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [NASA ADS] [CrossRef] (In the text)
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] (In the text)
- Dickinson, M., Stern, D., Giavalisco, M., et al. 2004, ApJ, 600, L99 [NASA ADS] [CrossRef]
- Eliche-Moral, M. C., Balcells, M., Prieto, M., et al. 2006, ApJ, 639, 644 [NASA ADS] [CrossRef] (In the text)
- Fontana, A., Salimbeni, S., Grazian, A., et al. 2006, A&A, 459, 745 [NASA ADS] [CrossRef] [EDP Sciences]
- Fontanot, F., Monaco, P., Cristiani, S., & Tozzi, P. 2006, MNRAS, 373, 1173 [NASA ADS] [CrossRef] (In the text)
- Fontanot, F., Monaco, P., Silva, L., & Grazian, A. 2007, MNRAS, 382, 903 [NASA ADS] [CrossRef] (In the text)
- Fontanot, F., De Lucia, G., Monaco, P., Somerville, R. S., & Santini, P. 2009, MNRAS, 397, 1776 [NASA ADS] [CrossRef] (In the text)
- Galadi-Enriquez, D., Trullols, E., & Jordi, C. 2000, A&AS, 146, 169 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Georganopoulos, M., Sambruna, R. M., Kazanas, D., et al. 2008, ApJ, 686, L5 [NASA ADS] [CrossRef] (In the text)
- Giallongo, E., Ragazzoni, R., Grazian, A., et al. 2008 A&A, 482, 349 (In the text)
- Giavalisco, M., & the GOODS Team 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] (In the text)
- Grazian, A., Fontana, A., De Santis, C., et al. 2006, A&A, 449, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hill, J. M., Green, R. F., Slagle, J. H., et al. 2008, Proc. SPIE, 7012, 701203 (In the text)
- Huang, J. S., Cowie,, L. L., Gardner, J. P., et al. 1997, ApJ, 476, 12 [NASA ADS] [CrossRef] (In the text)
- Keres, D., Katz, N., Dave, R., Fardal, M., & Weinberg, D. H. 2009, MNRAS, 396, 2332 [NASA ADS] [CrossRef] (In the text)
- Kimm, T., Somerville, R. S., Yi, S. K., et al. 2009, MNRAS, 394, 1131 [NASA ADS] [CrossRef]
- Kitzbichler, M. G., & White, S. D. M. 2007, MNRAS, 376, 2 [NASA ADS] [CrossRef] (In the text)
- Kneiske, T. M., & Dole, H. 2008, High Energy Gamma-Ray Astronomy: 4th International Symposium, Proceedings of the conference held July 7-11, in Heidelberg, Germany (In the text)
- Labbé, I., Franx, M., Rudnick, G., et al. 2003, ApJ, 125, 1107 [NASA ADS] (In the text)
- Landolt, A. U. 1992, AJ, 104, 372 [NASA ADS] [CrossRef] (In the text)
- Lo Faro, B., Monaco, P., Vanzella, E., et al. 2009, MNRAS, tmp 1225,[arXiv:0906.4998]
- Madau, P., & Pozzetti, L. 2000, MNRAS, 312, L9 [NASA ADS] [CrossRef] (In the text)
- Mattila, K. 2003, ApJ, 591, 119 [NASA ADS] [CrossRef] (In the text)
- Menci, N., Fontana, A., Giallongo, E., Grazian, A., & Salimbeni, S. 2006, ApJ, 647, 753 [NASA ADS] [CrossRef] (In the text)
- Metcalfe, N., Shanks, T., Campos, A., McCracken, H. J., & Fong, R. 2001, MNRAS, 323, 795 [NASA ADS] [CrossRef] (In the text)
- Minowa, Y., Kobayashi, N., Yoshi, Y., et al. 2005, ApJ, 629, 29 [NASA ADS] [CrossRef] (In the text)
- Monaco, P. 2004, MNRAS, 352, 181 [NASA ADS] [CrossRef] (In the text)
- Monaco, P., Fontanot, F., & Taffoni, G. 2007, MNRAS, 375, 1189 [NASA ADS] [CrossRef] (In the text)
- Moustakas, L. A., Davis, M., Graham, J. R., et al. 1997, ApJ, 475, 445 [NASA ADS] [CrossRef] (In the text)
- Nagamine, K., Ostriker, J. P., Fukugita, M., & Cen, R. 2006, ApJ, 653, 881 [NASA ADS] [CrossRef] (In the text)
- Oke, J. B. 1990, AJ, 99, 1621 [NASA ADS] [CrossRef] (In the text)
- Pedichini, F., Giallongo, E., Ragazzoni, R., et al. 2003, Proc. SPIE, 4841, 815 [NASA ADS] (In the text)
- Poli, F., Giallongo, E., Fontana, A., et al. 2003, ApJ, 593, L1 [NASA ADS] [CrossRef] (In the text)
- Radovich, M., Arnaboldi, M., Ripepi, V., et al., 2004, A&A, 417, 51 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ragazzoni, R., Giallongo, E., Pasian, F., et al. 2006, Proc. SPIE, 6267, 33 [NASA ADS] (In the text)
- Sekiguchi, K., et al. 2004, Multiwavelength Cosmology. Proceedings of the Multiwavelength Cosmology conference, held on Mykonos Island, Greece, 17-20 June, 2003, ed. M. Plionis (In the text)
- Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [NASA ADS] [CrossRef] (In the text)
- Somerville, R. S., Hopkins, P. F., Cox, T. J., et al. 2008, MNRAS, 391, 481 [NASA ADS] [CrossRef] (In the text)
- Speziali, R., Pedichini, F., Di Paola, A., et al. 2004, SPIE, 5492, 900 [NASA ADS] (In the text)
- Speziali, R., Di Paola, A., Giallongo, E., et al. 2008, SPIE, 7014, 158 [NASA ADS] (In the text)
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] (In the text)
- Stanev, T., & Franceschini, A. 1998, ApJ, 494, L159 [NASA ADS] [CrossRef] (In the text)
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2003, ApJ, 592, 728 [NASA ADS] [CrossRef] (In the text)
- Trenti, M., & Stiavelli, M. 2008, ApJ, 676, 767 [NASA ADS] [CrossRef] (In the text)
- Totani, T., Yoshii, Y., Iwamuro, F., et al. 2001, ApJ, 550, L137 [NASA ADS] [CrossRef] (In the text)
- Viola, M., Monaco, P., Borgani, S., Murante, G., & Tornatore, L. 2008, MNRAS, 383, 777 [NASA ADS] (In the text)
- Windhorst, R., Cohen, S., Jansen, R., et al. 2002, AAS, 201, 3207 [NASA ADS] (In the text)
- Xu, C. K., Donas, J., Arnouts, S., et al. 2005, ApJ, 619, L11 [NASA ADS] [CrossRef] (In the text)
- Yan, H., & Windhorst, R. A. 2004, ApJ, 612, L93 [NASA ADS] [CrossRef]
- Yasuda, N., Fukugita, M., Narayanan, V. K., et al. 2001, AJ, 122, 1104 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... SDT-Uspec
![[*]](/icons/foot_motif.png)
- This is an
interference filter with a wavelength range similar to a U-BESSEL filter, but
the peak transmission is
 30% more efficient than that filter, as
described in Fig. 2 of Giallongo et al. (2008).
30% more efficient than that filter, as
described in Fig. 2 of Giallongo et al. (2008).
All Tables
Table 1: LBC U galaxy number counts.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12118fg1.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12118-09/Timg22.png) |
Figure 1: Number counts of galaxies in the U-BESSEL band for the Q0933+28 and SXDS LBC fields. Black crosses represent the raw galaxy number counts, while filled big circles show the number counts corrected for incompleteness. Magnitudes are in the Vega system. We compare our counts with shallow surveys of similar or larger area (SDSS EDR, GOYA, VVDS F2), and with deeper pencil beam surveys (Hawaii HDFN, WHT, HDFN, HDFS). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12118fg2.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12118-09/Timg49.png) |
Figure 2:
The extragalactic background light per magnitude bin |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12118fg3.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12118-09/Timg63.png) |
Figure 3:
Number counts of galaxies in the U-BESSEL band for the Q0933+28 LBC
field, complemented at brighter magnitudes ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12118fg4.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12118-09/Timg70.png) |
Figure 4: Number counts of galaxies in the K band for different deep surveys in the literature. The model predictions come from the same models described in the previous figure. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


