On the afterglow from the receding jet of γ-ray bursts

X. Wang; Y. F. Huang; S. W. Kong

doi:10.1051/0004-6361/200811612

Home

All issues

Volume 505 / No 3 (October III 2009)

A&A, 505 3 (2009) 1213-1219

Full HTML

Free Access

Issue		A&A Volume 505, Number 3, October III 2009


Page(s)		1213 - 1219
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/200811612
Published online		11 August 2009

On the afterglow from the receding jet of 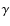$\gamma$ -ray bursts

X. Wang - Y. F. Huang - S. W. Kong

Department of Astronomy, Nanjing University, Nanjing 210093, PR China

Received 31 December 2008 / Accepted 29 June 2009

Abstract
According to popular progenitor models of gamma-ray bursts, twin jets should be launched by the central engine, with a forward jet moving toward the observer and a receding jet (or the counter jet) moving backwardly. However, in calculating the afterglows, usually only the emission from the forward jet is considered. Here we present a detailed numerical study on the afterglow from the receding jet. Our calculation is based on a generic dynamical description, and includes some delicate ingredients such as the effect of the equal arrival time surface. It is found that the emission from the receding jet is generally rather weak. In radio bands, it usually peaks at a time $t \geq 1000$ d, with the peak flux nearly 4 orders of magnitude lower than the peak flux of the forward jet. Also, it usually manifests as a short plateau in the total afterglow light curve, but not as an obvious rebrightening as once expected. In optical bands, the contribution from the receding jet is even weaker, with the peak flux being $\sim$ 23 mag lower than the peak flux of the forward jet. We thus argue that the emission from the receding jet is very difficult to detect. However, in some special cases, i.e., when the circum-burst medium density is very high, or if the parameters of the receding jet are quite different from those of the forward jet, the emission from the receding jet can be significantly enhanced and may still emerge as a marked rebrightening. We suggest that the search for receding jet emission should mostly concentrate on nearby gamma-ray bursts, and the observation campaign should last for at least several hundred days for each event.

Key words: gamma rays: bursts - ISM: jets and outflows - stars: neutron

1 Introduction

Thanks to the discovery of X-ray, optical and radio afterglows of gamma-ray bursts (GRBs), it is now clear that most GRBs are situated at cosmological distances (Costa et al. 1997; van Paradijs et al. 1997; Frail et al. 1997). Much progress has been achieved during the past decade (Piran 2004; Mészáros 2006). Especially, through the detection of GRB 030329, the association of long GRBs with supernovae is firmly established (Hjorth et al. 2003), which strongly supports the collapsar model as the energy mechanism for long GRBs (Woosley 1993; MacFadyen & Woosley 1999). Theoretically, the collapse of a massive star will most likely give birth to a black hole, surrounded by a temporal accretion disk. It is logical that the accretion system will produce double-sided jets (MacFadyen & Woosley 1999; Aloy et al. 2000; Rhoads 1999; Mészáros 2002). The GRB can be observed only when our line of sight lies on one of the two jets. The collimation of GRB ejecta can be tested observationally, through various beaming effects, such as the achromatic break in GRB afterglow light curves (Sari et al. 1999; Liang et al. 2008), the polarization in both the main burst phase and the afterglow phase (Lazzati 2006), the predicted existence of orphan afterglows (Rhoads 1997; Huang et al. 2002; Granot & Loeb 2003), and the ``energy crisis'' already noted in some GRBs (Frail et al. 2001). In fact, more and more observational evidence has been accumulated supporting the idea that many GRB ejecta might be highly collimated.

Current studies on beaming effects are mostly concentrated on the emission from the forward jet, i.e., the jet moving toward the observer. The emission from the receding jet (or the counter jet) is generally omitted. It is interesting to note that this ingredient recently has been studied by a few authors (Granot & Loeb 2003; Li & Song 2004). By some simple analytical derivations, Li & Song (2004) argued that the emission from the receding jet can be detected in a few cases in the non-relativistic phase of GRB afterglows. However, previous studies did not consider some important effects, such as the action of the equal arrival time surface (EATS). Recently, Zhang & MacFadyen (2009) presented a two-dimensional simulation of GRB outflow. The emission from the receding jet was included in their calculations, but they did not investigate the effects of various parameters on the receding jet component.

In this paper, we will present our detailed numerical investigation of the emission from the receding jet of GRBs in the deep Newtonian stage. Although the GRB jet may be complicatedly structured (Mészáros et al. 1998; Kumar & Granot 2003; Huang et al. 2004), and the circum-burst environment may be a wind medium and even associated with some complex density variations (Mészáros et al. 1998; Chevalier & Li 2000; Gou et al. 2001; Wu et al. 2004), here we will only consider the simplest situation, i.e, the homogeneous double-sided jets expanding into a homogeneous interstellar medium, which is favored by some recent fits (Huang et al. 2000a; Yost et al. 2003).

The structure of our paper is as follows. Section 2 is a review of the dynamics and radiation model we used in our calculations. In Sect. 3 we present the numerical results, together with our explanations. Section 4 is our conclusion and discussion.

2 Model description

In the afterglow phase, the GRB ejecta expand into the interstellar medium (ISM) and are decelerated continuously, giving rise to a strong external shock. The swept-up electrons are accelerated by the blastwave, producing the afterglow mainly through synchrotron radiation. In radio bands, the shell is no longer optically thin, so that the synchrotron self-absorption should be considered. In our study, we will use the simplified dynamical equations suggested by Huang et al. (1999, 2000b), which are consistent with the self-similar solution of Blandford & McKee (1976) in the ultra-relativistic phase, and consistent with the Sedov solution (Sedov 1969) in the non-relativistic phase. The beaming effects (Rhoads 1997, 1999) can also be conveniently simulated in this way. Here, for completeness, we first describe the dynamics and the radiation process.

2.1 Hydrodynamic evolution

In our description, t is the photon arrival time measured in the lab frame; R is the radial coordinate measured in the burst frame relative to the initiation point; m is the rest mass of the swept-up medium; $\theta$ is the half-opening angle of the ejecta; $\gamma$ is the bulk Lorentz factor of the moving material; p is the electron distribution index which is typically between 2 and 3; n is the number density of ISM; $\xi _{\rm e}$ and $\xi^2_{\rm B}$ are the energy equipartition factors for electrons and the comoving magnetic field. We further denote the initial values of the rest mass, the isotropic equivalent energy, the Lorentz factor and the half-opening angle of the ejecta as $M_{\rm ej}, E_{\rm0,iso}, \gamma_0, \theta_{\rm j}$ , respectively.

The overall dynamical evolution of the GRB ejecta can be depicted by

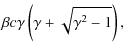$\displaystyle \frac{{\rm d}R}{{\rm d}t}$	=	$\displaystyle \beta c\gamma \left( {\gamma + \sqrt {\gamma ^2 - 1} } \right),$	(1)
$\displaystyle \frac{{\rm d}m}{{\rm d}R}$	=	$\displaystyle 2\pi \left( {1 - \cos \theta } \right)R^2nm_{\rm p} ,$	(2)
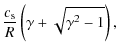$\displaystyle \frac{{\rm d}\theta}{{\rm d}t}$	=	$\displaystyle \frac{c_ {\rm s}}{R} \left( {\gamma + \sqrt {\gamma ^2 - 1} } \right),$	(3)
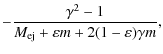$\displaystyle \frac{{\rm d}\gamma }{{\rm d}m}$	=	$\displaystyle - \frac{\gamma ^2 - 1}{M_{\rm ej} + \varepsilon m + 2(1 - \varepsilon )\gamma m},$	(4)

where $\beta = \sqrt {1- 1/\gamma ^2}$ , c is the speed of light, and $c_{\rm s}$ is the comoving sound speed, which can be calculated by $c_ {\rm s}^2 = \hat \gamma (\hat \gamma - 1)(\gamma - 1) c^2 / \left[ 1 + \hat \gamma (\gamma - 1) \right]$ with $\hat \gamma \approx (4\gamma + 1)/({3\gamma })$ being a reasonable approximation for the adiabatic index. In Eq. (4), $\varepsilon$ is the radiative efficiency. In the extreme case, $\varepsilon = 0$ means adiabatic condition and $\varepsilon = 1$ refers to highly radiative situation. Note that in a realistic case, $\varepsilon$ should evolve gradually from 1 to 0, in about several hours.

Equations (1)-(4) is a convenient description of GRB afterglow dynamics that is applicable in both the initial ultra-relativistic phase and the late Newtonian phase.

2.2 Radiation process

We assume that the shock-accelerated electrons follow a power-law distribution according to their energies, ${\rm d}N'_{\rm e} / {{\rm d} \gamma_{\rm e}} \propto \gamma_{\rm e}^{- p}$ , However, to ensure that the calculation in the deep Newtonian phase is correct, we need to modify the basic distribution function as ${\rm d}N'_{\rm e} / {{\rm d}\gamma_{\rm e}} \propto \left( \gamma_{\rm e} -1 \right)^{- p}$ (Huang & Cheng 2003). The minimum and maximum Lorentz factors of electrons can be calculated as $\gamma_{\rm e,\min} = \xi_{\rm e} (\gamma - 1) m_{\rm p} (p - 2)/[ m_{\rm e} (p - 1) ] + 1$ and $\gamma_{\rm e,\max} = \sqrt { 6\pi e / \left( \sigma_{\rm T} B' \right) } \approx 10^8 (B'/ 1 {\rm G})^{-1/2}$ , where B' is the comoving magnetic field strength, $m_{\rm p}$ and $m_{\rm e}$ are masses of the proton and electron, respectively. As usual, we assume that the energy ratio of the magnetic field with respect to internal energy is $\xi^2_{\rm B}$ , so that the energy density of the magnetic field is $B'^2/(8\pi) = \xi^2_{\rm B} \left( \hat \gamma - 1 \right)^{-1} ( \hat \gamma \gamma + 1)(\gamma - 1) n m_{\rm p} c^2$ .

The cooling of electrons due to synchrotron radiation will lead to a steep distribution function above a critical Lorentz factor, $\gamma_{\rm c}$ . The expression for $\gamma_{\rm c}$ can be derived as $\gamma_{\rm c} = 6\pi m_{\rm e} c / \left( \sigma_{\rm T} \gamma B'^2 t \right)$ , where $\sigma_{\rm T}$ is the Thompson scattering cross section (Sari et al. 1998). Considering all the above ingredients, we finally use the following electron distribution function in our calculations (Huang & Cheng 2003):

1. $\gamma_{\rm c} \le \gamma_{\rm e,\min}$ ,

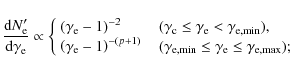$\begin{displaymath}\frac{{\rm d}N'_{\rm e}}{{\rm d}\gamma _{\rm e} } \propto \le... ..._{\rm e} \le \gamma _{\rm e,\max } ); \\ \end{array} \right. \end{displaymath}$

(5)

2. $\gamma_{\rm e,\min} < \gamma _{\rm c} \le \gamma _{\rm e,\max}$ ,

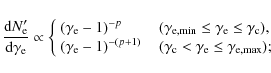$\begin{displaymath}\frac{{\rm d}N'_{\rm e}}{{\rm d}\gamma _{\rm e} } \propto \le... ..._{\rm e} \le \gamma _{\rm e,\max } ); \\ \end{array} \right. \end{displaymath}$

(6)

3. $\gamma _{\rm c} > \gamma _{\rm e,\max}$ ,

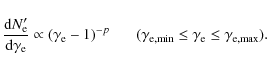$\begin{displaymath}\frac{{\rm d}N'_{\rm e}}{{\rm d}\gamma _{\rm e}} \propto \lef... ...{\rm e,\min } \le \gamma _{\rm e} \le \gamma _{\rm e,\max } ). \end{displaymath}$

(7)

In the comoving frame, the synchrotron radiation power at $\nu'$ is (Rybicki & Lightman 1979)

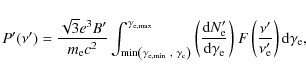$\begin{displaymath}P'(\nu') = \frac{\sqrt 3 e^3 B'}{m_{\rm e} c^2 } \int_{\min \... ...eft( \frac{\nu'}{\nu'_{\rm e }} \right) {\rm d}\gamma_{\rm e}, \end{displaymath}$

(8)

with $F(x) = x\int_x^{ + \infty } {K_{5/3}(k) ~ {\rm d}k}$ being the Bessel function and $\nu'_{\rm e} = 3\gamma^2_{\rm e} e B' / \left( 4\pi m_{\rm e} c \right)$ being the characteristic emission frequency (Shu 1991; Longair 1992). To calculate the radio afterglows, we must consider the synchrotron self-absorption. The optical depth of synchrotron self-absorption can be obtained as

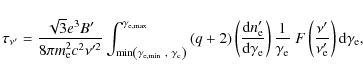$\begin{displaymath}\tau _{\nu '} = \frac{\sqrt 3 e^3 B'}{8 \pi m^2_{\rm e} c^2 \... ...eft( \frac {\nu'}{\nu'_{\rm e} } \right){\rm d}\gamma_{\rm e}, \end{displaymath}$

(9)

where ${\rm d}n'_{\rm e} /{\rm d}\gamma_{\rm e}$ denotes the column density distribution of electrons measured in the comoving frame on the line of sight; q is the electron power-law distribution index which varies from 2 to p+1 for fast-cooling and from p to p+1 for slow-cooling. The synchrotron self-absorption will affect the radiation by a reduction-factor (Waxman et al. 1998)

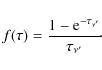$\begin{displaymath}f(\tau) = \frac {1- {\rm e}^{-\tau _{\nu '}}} {\tau _{\nu '}}\!\cdot \end{displaymath}$

(10)

Let us define the Doppler-factor as $D = \left[ \gamma \left( 1 - \beta \mu \right) \right]^{- 1}$ (Mészáros 2006), where $\mu =\cos \Theta$ and $\Theta$ is the angle between the velocity of the emitting material and the line of sight. Also we denote the viewing angle as $\theta _{\rm obs}$ . Then the observed frequency is $\nu = D \nu' /(1 + z)$ , and the observed flux density from a point-like source is

$\begin{displaymath}F_\nu = \frac{(1 + z) D^3 }{4\pi d_{\rm L}^2 } f(\tau) P'\left[ (1 + z)D^{-1} \nu \right], \end{displaymath}$

(11)

where $d_{\rm L}$ is the luminosity distance. Finally, we can integrate the flux density over the EATS (Waxman 1997; Sari 1998) determined by

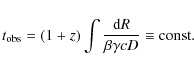$\begin{displaymath}t_ {\rm obs} = (1+z) \int \frac{{\rm d}R}{\beta \gamma c D} \equiv \rm {const}. \end{displaymath}$

(12)

3 Numerical results

In this section, we present our numerical results concerning the emission from the receding jet. For simplicity, we assume that the twin jets have the same characteristics, i.e., the same initial energy, opening angle, initial Lorentz factor, and the circum-burst ISM density. We also assume that the microphysics shock parameters (p, $\xi _{\rm e}$ , $\xi^2_{\rm B}$ ) are the same for the receding and forward blastwaves. For convenience, we define a set of parameter values as the ``standard'' condition: $n=1 / {\rm cm}^{3}$ , $E_{\rm0,iso} =10^{53}~ {\rm erg}$ , $\theta_{\rm j} =0.1$ , $\varepsilon = 0$ , $\xi_{\rm e} = 0.1$ , $\xi^2_{\rm B}=0.01$ , p=2.5, $\theta_{\rm obs}=0$ , and $\gamma_0 = 300$ . These values are typical in the study of GRB afterglows. For redshift, we adopt the value of z=0.1 (which corresponds to $d_{\rm L}= 454$ Mpc according to the popular cosmology model, Wright 2006).

$\begin{figure} \par\includegraphics[width=9cm,clip]{11612f1.eps} \end{figure}$	Figure 1: The evolution of the Lorentz factors of the twin jets. The solid line corresponds to the receding jet and the dashed line is plotted for the forward jet. The twin jets are in the ``standard'' condition as defined in Sect. 3. The observers' time has been corrected for the cosmological effect (z=0.1).
Open with DEXTER

We illustrate the evolution of the Lorentz factors of the twin jets in Fig. 1. Note that the X-axis is observers' time. For the observer, the dynamical evolution of the receding jet is quite different from that of the forward jet, especially in the relativistic phase. We see that for a rather long time ( $t \sim 50$ d), $\gamma$ of the receding jet remains almost constant. This is due to the time delay induced by the long distance between the twin jets. It also implies that the emission from the receding jet will be very weak in this period, since it is highly beamed backward. At the observers' time of $t \sim 340$ d, the Lorentz factor of the receding jet is still more than 10, while the forward jet's Lorentz factor has already decreased to less than 1.1.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11612f2.eps} \end{figure}$

Figure 2:

Schematic illustration of the EATSs at three moments, $t_1 \approx 114$ d, $t_2 \approx 286$ d and $t_3 \approx 572$ d. In this calculation, we have used the ``standard'' parameter set as defined in Sect. 3. ``O'' is the position of the central engine, and the observer is on the far right side with Y=0. The dotted lines indicate the jet boundary. For the receding jet, the EATSs are plotted in thick solid lines, while for the forward jet the surfaces are plotted in thin solid lines. Note that on the forward jet branches, the bulk Lorentz factors of the material at the peak of the EATSs are 1.17, 1.07, and 1.03 for t₁, t₂, and t₃, respectively. On the receding jet branches, the bulk Lorentz factors of the material at the peak of the EATSs are 56.07, 11.79, and 3.95 for t₁, t₂, and t₃, respectively.

Open with DEXTER

In Fig. 2, we show some examples of the equal arrival time surfaces (EATSs) at three moments. As expected, at any particular moment, the typical radius of the surface is much larger for the forward jet branch compared to that for the receding jet branch. Also, we notice that the curvature of the two branches is quite different. Generally, the EATS is much flatter on the receding jet. Another interesting feature is that the area of the EATS on the forward branch is much larger than that of the corresponding receding branch.

$\begin{figure} \par\includegraphics[width=7cm,clip]{11612f3a.eps}\hspace*{1cm} \includegraphics[width=7cm,clip]{11612f3b.eps} \end{figure}$

Figure 3:

8.46 GHz radio afterglow a) and R-band optical afterglow b) from the forward jet and the receding jet. The thick lines are plotted for a ``standard'' double-sided jet as defined in Sect. 3. The thin lines are plotted for the double-sided jet with only one parameter altered compared to the ``standard'' condition, i.e. $n=1000 / {\rm cm}^{3}$ . In each group, the dotted line reflects the emission from the forward jet, the dashed line reflects the contribution from the receding jet, and the solid line is the total light curve.

Open with DEXTER

Figure 3 shows the radio and optical afterglow light curves under the ``standard'' condition (thick lines). Here, the thick dotted line corresponds to emission from the forward jet, the thick dashed line corresponds to emission from the receding jet, and the thick sold line is the total light curve. Under the ``standard'' condition, for the forward jet, the afterglow light curve (the dotted line) becomes slightly flattened in the non-relativistic phase. It is consistent with previous results in the deep Newtonian phase (Huang & Cheng 2003). Also it can be seen that the receding jet really can contribute a significant portion in the total emission at very late stage. The role played by the receding jet is reasonably more important in the radio band than in the optical band. However, the dashed component is generally not very strong, so that it can only lead to a plateau in the total light curve, but not an obvious rebrightening or a marked peak as expected by Li & Song (2004). Interestingly, our result is consistent with the simulation of Zhang & Macfadyen (2009). We believe that the discrepancy between our numerical result and Li & Song's analytical result mainly comes from the effect of the EATS. Below, we will give some detailed analyses on this point. Additionally, it should be noted that in the radio band, the peak flux of the receding component is about 4 orders of magnitude weaker than that of the forward component. It essentially means that the receding component is very weak, and is very difficult to detect. In the optical band, the condition is even more awkward. The peak flux of the receding component is about 23 mag dimmer than that of the forward component in R band. Even comparing with the flux of the forward jet at the jet break time, it is still 16-17 mag weaker. So, in the optical band, it is even much more difficult to observe the receding jet component.

According to Li & Song (2004), the time when the receding jet becomes notably visible ( $t_{\rm NR}^{\rm RJ}$ ) is relevant to the time when the forward jet enters the non-relativistic phase ( $t_{\rm NR}$ ), i.e.,

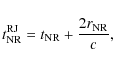$\begin{displaymath}t_{\rm NR}^{\rm RJ} = t_{\rm NR} + \frac {2r_{\rm NR}}{c}, \end{displaymath}$

(13)

where $r_{\rm NR}$ is the radius of the forward jet at $t_{\rm NR}$ . In the standard framework (Blandford & Mckee 1976; Rhoads 1999), the sphere-like phase of a highly collimated GRB ejecta ends at the so-called jet break time determined by $\gamma _ {\rm j} = 1/ \theta_{\rm j}$ , with the shock radius being $r_{\rm j}= ( 3 E_{\rm0,iso} \theta_{\rm j}^2 /[ {4\pi n m_{\rm p} c^2}])^ {1/3}$ . After the sphere-like phase, the jet spreads laterally at the co-moving sound speed $c_{\rm s}$ so that we have $\gamma \propto t^{-1/2}$ and $r_{\rm NR} \approx r_{\rm j}$ (Rhoads 1999). Then finally we obtain

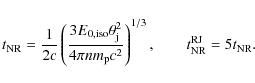$\begin{displaymath}t_{\rm NR} = \frac{1}{2c} \left( \frac{3 E_{\rm0,iso} \theta_... ... \right) ^{1/3}, \\ \qquad t_{\rm NR}^{\rm RJ} = 5t_{\rm NR}. \end{displaymath}$

(14)

Adopting the standard values of our parameters, Eq. (14) yields $t_{\rm NR} \approx 104$ d and $t_{\rm NR}^{\rm RJ} \approx 520$ d. After correcting for the cosmological time dilation (z=0.1), we get the corresponding observers' time of $t_1=(1+z)\ t_{\rm NR} \approx 114$ d and $t_3=(1+z)\ t_{\rm NR}^{\rm RJ} \approx 572$ d. In Fig. 2, the EATSs for these two moments have been displayed. So, according to Li & Song's suggestion, the contribution from the receding jet should peak at $t_3 \approx 572$ d. In our Fig. 3, for the ``standard'' condition, the peak is postponed to $t_{\rm peak} \sim 1140$ d for 8.46 GHz, and to $t_{\rm peak}\sim 1700$ d in the R band. So, the EATS effect and the deceleration of the external shock can lead to some subtle differences between the analytical results and the numerical results. Zhang & MacFadyen's numerical results have clearly shown that the observers' time does not equal the burst frame time at $t_{\rm NR}$ (Zhang & MacFadyen 2009). Unfortunately, in previous analyses it is usually assumed that these two times are equal.

Another reason that suppresses the rebrightening of the receding jet is as follows. According to Li & Song's analysis, at the observers' time t₃, the receding jet should be at the radius of $r_{\rm NR}$ . However, from our Fig. 2, we see that the typical radius of the EATS at t₃ on the receding jet is much smaller than the radius of the forward jet at t₁. The reason is again due to the EATS effect. This means that the receding jet still does not decelerate enough at t₃ (actually, the bulk Lorentz factor is still 3.95), and its emission is still mainly directed forward (not backward toward the observer). Additionally, Fig. 2 shows clearly that the area of the receding jet at t₃ (corresponding to $t_{\rm NR}^{\rm RJ}$ ) is much smaller than that of the forward jet at t₁ (corresponding to $t_{\rm NR}$ ). So, the number of electrons involved in the radiation process is typically much smaller in the receding jet at $t_{\rm NR}^{\rm RJ}$ , compared to that in the forward jet at $t_{\rm NR}$ . Due to the above reasons, the contribution from the receding jet is naturally much weaker than that deduced from $L_{\rm\nu}^{\rm RJ}(t) \approx L_{\rm \nu}(t-4t_{\rm NR}),\ (t\geq t_{\rm NR}^{\rm RJ})$ (Eq. (7) in Li & Song 2004).

However, although the receding jet emission is generally very weak in our ``standard'' condition, we hypothesize that in some special cases it still can be enhanced. Obviously, a denser environment will help to decelerate the jet more quickly, thus lead to a smaller $t_{\rm peak}$ and a higher intensity. In Fig. 3, we have also plotted in thin lines our numerical results for a double-sided jet located in a dense circum-burst medium ( $n=1000 / {\rm cm}^{3}$ ). Note that other parameters involved here are the same as the ``standard'' case. Encouragingly, in Fig. 3a we see that the peak time of the receding jet can be as early as $t_{\rm peak} \sim 150$ d, with the peak flux as large as a few mJy in radio band (i.e., only several times less than the peak level of the forward jet). In Fig. 3b, the optical contribution from the receding jet is still very weak, with the peak flux being about 28 $^{\rm m}$ .

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{11612f4a.eps}\hspace*{0.8cm} \includegraphics[width=7cm,clip]{11612f4b.eps} \end{figure}$	Figure 4: Multiwavelength afterglow light curves of a double-sided jet. Radio afterglows are illustrated in panel a), and optical/IR afterglows are plotted in panel b). In this calculation, we have used the ``standard'' parameter set as defined in Sect. 3.
Open with DEXTER

In Fig. 4, we plot the afterglow light curves in more radio and optical/infrared bands. Generally speaking, $t_{\rm peak}$ is about 1140 d in radio bands and is about 1700 d in optical bands. Such a difference in the peak time is insignificant, considering that the frequency difference between radio and optical wavelengths is very large. We notice that $t_{\rm peak}$ almost remains the same from radio to X-ray bands in Fig. 7 of Zhang & MacFadyen (2009). Thus our results are roughly consistent with Zhang & MacFadyen's. Another interesting conclusion that can be drawn from our Figs. 3 and 4 is that at lower frequency, the relative intensity of the receding jet component (its peak flux), as compared with the peak of the forward jet component, becomes stronger. Such a tendency can also be roughly seen in Fig. 7 of Zhang & MacFadyen (2009).

$\begin{figure} \par\includegraphics[width=6.7cm,clip]{11612f5a.eps}\hspace*{1cm}... ...s}\hspace*{1cm} \includegraphics[width=6.7cm,clip]{11612f5d.eps} \end{figure}$

Figure 5:

The effects of various parameters (n, $E_{\rm0,iso}$ , $\theta _{\rm j}$ , and $\varepsilon$ ) on the 8.46 GHz radio afterglow light curves of double-sided jets. In each panel, ``(s)'' corresponds to the ``standard'' condition as defined in Sect. 3, and other lines are drawn with only one certain parameter altered or one condition changed. In panel d), the dash-dotted line is plotted for a double-sided jet without lateral expansion; and the dotted line is plotted for a double-sided jet with a low initial Lorentz factor ( $\gamma _{\rm0} = 30$ ), which may correspond to the so-called failed GRBs.

Open with DEXTER

Figure 5 illustrates the effects of some parameters (n, $E_{\rm0,iso}$ , $\theta _{\rm j}$ , and $\varepsilon$ ) on the receding jet component in the afterglow light curve. Figure 5a shows that the circum-burst medium density (n) affects the peak time ( $t_{\rm peak}$ ) of receding jet dramatically. A higher number density usually leads to a smaller $t_{\rm peak}$ . The strength of the receding jet component is also obviously enhanced. It again hints that the receding jet component is most likely detectable in a dense environment. Similarly, the initial kinetic energy ( $E_{\rm0,iso}$ ) also affects $t_{\rm peak}$ significantly, with larger $E_{\rm0,iso}$ corresponding to a larger $t_{\rm peak}$ (Fig. 5b). The effect of the initial jet opening angle ( $\theta _{\rm j}$ ) on $t_{\rm peak}$ can also be clearly seen in Fig. 5c. It should be further noted that the receding jet component is more marked when the opening angle is smaller. In Fig. 5d, we can observe an obvious rebrightening when the radiation efficiency ( $\varepsilon$ ) is large. However, in a realistic case, $\varepsilon$ is unlikely to be so large. At such late stages, the external shock should be adiabatic, so that $\varepsilon$ should be nearly zero.

$\begin{figure} \par\includegraphics[width=6.7cm,clip]{11612f6a.eps}\hspace{0.8c... ...\hspace{0.8cm} \includegraphics[width=6.7cm,clip]{11612f6d.eps} \end{figure}$	Figure 6: The effects of various parameters ( $\xi _{\rm e}$ , $\xi _{\rm B}^2$ , p, and $\theta _{\rm obs}$ ) on the 8.46 GHz radio afterglow light curves of double-sided jets. In each panel, ``(s)'' corresponds to the ``standard'' condition as defined in Sect. 3, and other lines are drawn with only one certain parameter altered.
Open with DEXTER

In Fig. 5d, we also plot the radio afterglow light curves for double-sided jets under some special physical assumptions. The dash-dotted line is plotted by assuming that both the forward jet and the receding jet do not experience any lateral expansion. Since the deceleration of the jets is much slower in this case, we see that the receding jet component emerges much later and is also much less obvious compared to our ``standard'' case. The dotted line is plotted by assuming a much smaller initial Lorentz factor ( $\gamma_0 = 30$ ), which may correspond to the so-called failed GRBs (Huang et al. 2002). The receding jet component emerges slightly earlier compared to the solid line, but its role becomes correspondingly less significant.

Figure 6 illustrates the effects of the other four parameters ( $\xi _{\rm e}$ , $\xi _{\rm B}^2$ , p, and $\theta _{\rm obs}$ ) on the receding jet component. Generally speaking, a larger $\xi _{\rm e}$ and/or $\xi _{\rm B}^2$ can enhance the receding jet component markedly. On the other hand, although p has an important influence on the overall afterglow light curve, its impact on the relative strength of the receding jet component is not significant. Again, note that in all the cases, the contribution from the receding jet only emerges as a plateau, but not as any obvious rebrightening. In Fig. 6d, when the observing angle ( $\theta _{\rm obs}$ ) increases, the forward jet component becomes weaker, while the receding jet component becomes stronger. It is in accord with our expectation (also see Granot & Loeb 2003). However, the contribution from the receding jet still generally plays a minor role in the total afterglow light curve. Additionally, for off-axis twin jets, the GRB from the forward jet is un-observable, so that even the afterglow from the forward jet itself (i.e., the orphan afterglow) is difficult to observe. Note that in Fig. 6d, when $\theta_{\rm obs} = \pi / 2$ (i.e., the thick solid line), the contribution from the receding jet and the forward jet are equal.

Equation (14) tells us that the peak time of the receding component should be relevant to the 3 parameters of n, $E_{\rm0,iso}$ , $\theta _{\rm j}$ ; on the other hand, other parameters such as $\xi _{\rm e}$ , $\xi _{\rm B}^2$ , p do not affect the peak time. These tendencies can be clearly seen in Figs. 5 and 6.

$\begin{figure} \par\includegraphics[width=6.7cm,clip]{11612f7a.eps}\hspace*{0.8c... ...\hspace*{0.8cm} \includegraphics[width=6.7cm,clip]{11612f7d.eps} \end{figure}$

Figure 7:

8.46 GHz radio afterglow light curves of double-sided jets. In this figure, we assume that the parameters of the receding jet can be different from those of the forward jet. In each panel, the solid line is plotted under the ``standard'' condition, i.e., the parameters are the same for the twin jets (but note that we have evaluated $\xi _{\rm e}$ as 0.01 and $\xi _{\rm B}^2$ as 10^-4 here). For other light curves, one or two parameters are changed for the receding jet, to see their effect on the afterglows.

Open with DEXTER

In all the above calculations, we have assumed that the conditions and parameters of the twin jets are the same. However, this may not be the case for realistic GRBs. The circum-burst environment and the micro-physics parameters may actually be different for the twin jets, as may happen in the two component jet structure (Huang et al. 2004; Jin et al. 2007; Racusin et al. 2008). In Fig. 7, we have plotted the overall afterglow light curves by assuming different parameters for the forward jet and the receding jet. In each panel of Fig. 7, we first plot a common light curve (the solid line) by adopting the standard parameter set, but change $\xi _{\rm e}$ to 0.01 and change $\xi^2_{\rm B}$ to 10^-4. We then increase the values of $\xi _{\rm e}$ , $\xi _{\rm B}^2$ , and n for the receding jet to see their effects on the afterglow light curve. It is encouraging to see that the emission from the receding jet can be greatly enhanced, so that it can manifest as an obvious rebrightening in the overall light curve. In Figs. 7a, b and d, the peak flux of the rebrightening can be nearly 100 times larger than the ``background'' level in the best cases. It is imaginable that in the most favorable cases, when all $\xi _{\rm e}$ , $\xi _{\rm B}^2$ and n are larger for the receding jet at the same time, the rebrightening will be even more remarkable. However, note that the contrary condition may also exist in realistic GRBs, i.e., these parameters may also be smaller for the receding jet. Then the emission from the receding jet will be unnoticeable.

4 Conclusion and discussion

We have studied the emission of the receding jet numerically. The effect of the EATS is included in our calculations. Clearly, this effect plays an important role in the process. It is found that the contribution from the receding jet is generally quite weak. In most cases, it only manifests as a short plateau in the overall afterglow light curve, but not a marked rebrightening. The flux density of the plateau is usually much less than 100 $\mu$ Jy in radio bands even at a small redshift of z=0.1. If we place the GRB at a more typical redshift of z=1, then the flux density of the plateau will be less than 0.1 $\mu$ Jy at 8.46 GHz. We noticed that the observed radio afterglow emission is generally on the level of 0.1-1 mJy at about the peak time. After several months, the radio afterglow usually decreases to a very low level, and is submerged by the emission from the host galaxy, whose strength can be 40-70 $\mu$ Jy (Berger et al. 2001). Additionally, the error bar of radio observations is usually $\sim$ 30-50 $\mu$ Jy at very late stages (Frail et al. 2003). Thus the contribution from the receding jet, i.e. the plateau, is actually very difficult to detect, especially for those GRBs at $z \sim 1$ . Our results are consistent with a recent observational report by van der Horst et al. (2008), who failed to detect any clear clues of the receding jet emission.

However, as shown in our Fig. 7, if the micro-physics parameters of the receding jet were different from the forward jet, or if the receding jet were in a much denser environment, then it is still possible that the contribution from the receding jet can be greatly enhanced. For example, if $\xi _{\rm e}$ and/or $\xi _{\rm B}^2$ of the receding jet is much larger than that of the forward jet, then the receding jet can manifest as an obvious rebrightening.

Also, our Fig. 5a shows that a dense circum-burst environment can suppress the emission of the forward jet, and enhance the contribution from the receding jet. If the GRB occurs in a very dense molecular cloud with $n > 10^3 / {\rm cm}^{3}$ (Dai & Lu 1999), the contribution from the receding jet may be much easier to detect. Additionally, if the GRB is very near to us at the same time, then the possibility of successfully detecting the receding jet is very high (see the thin lines in Fig. 3a).

In short, we believe that the effort of trying to search for the afterglow contribution from the receding jet is still meaningful. If observed, it would provide useful clues to study the circum-burst environment and the micro-physics of external shocks. We suggest that nearby GRBs (with redshift $z \leq 0.1$ ) should be good candidates for such studies.

Acknowledgements

We would like to thank the anonymous referee for constructive suggestions that lead to an overall improvement of this study. We also thank Z. Li for stimulating discussion. This research was supported by the National Natural Science Foundation of China (grant 10625313), and by the National Basic Research Program of China (grant 2009CB824800). Xin Wang is also supported by 2008' National Undergraduate Innovation Program of China (grant 081028441).

References

Aloy, M. A., Müller, E., Ibáñez, J., Martí, J., & MacFadyen, A. 2000, ApJ, 531, L119 [NASA ADS] [CrossRef] (In the text)
Berger, E., Kulkarni, S. R., & Frail, D. A. 2001, ApJ, 560, 652 [NASA ADS] [CrossRef] (In the text)
Blandford, R. D., & McKee, C. F. 1976, Phys. Fluids, 19, 1130 [NASA ADS] [CrossRef] (In the text)
Chevalier, R. A., & Li, Z. Y. 2000, ApJ, 536, 195 [NASA ADS] [CrossRef] (In the text)
Costa, E., Frontera, F., Heise, J., et al. 1997, Nature, 387, 783 [NASA ADS] [CrossRef] (In the text)
Dai, Z. G., & Lu, T. 1999, ApJ, 519, L155 [NASA ADS] [CrossRef]
Frail, D. A., Kulkarni, S. R., Berger, E., & Wieringa, M. H. 2003, AJ, 125, 2299 [NASA ADS] [CrossRef] (In the text)
Frail, D. A., Kulkarni, S. R., Nicastro, S. R., Feroci, M., & Taylor, G. B. 1997, Nature, 389, 261 [NASA ADS] [CrossRef] (In the text)
Frail, D. A., Kulkarni, S. R., Sari, R., et al. 2001, ApJ, 562, L55 [NASA ADS] [CrossRef] (In the text)
Gou, L. J., Dai, Z. G., Huang, Y. F., & Lu, T. 2001, A&A, 368, 464 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Granot, J., & Loeb, A. 2003, ApJ, 593, L81 [NASA ADS] [CrossRef] (In the text)
Hjorth, J., Sollerman, J., Møller, P., et al. 2003, Nature, 423, 847 [NASA ADS] [CrossRef] (In the text)
Huang, Y. F., & Cheng, K. S. 2003, MNRAS, 341, 263 [NASA ADS] [CrossRef] (In the text)
Huang, Y. F., Dai, Z. G., & Lu, T. 1999, MNRAS, 309, 513 [NASA ADS] [CrossRef] (In the text)
Huang, Y. F., Dai, Z. G., & Lu, T. 2000a, A&A, 355, L43 [NASA ADS] (In the text)
Huang, Y. F., Dai, Z. G., & Lu, T. 2000b, MNRAS, 316, 943 [NASA ADS] [CrossRef] (In the text)
Huang, Y. F., Dai, Z. G., & Lu, T. 2002, MNRAS, 332, 735 [NASA ADS] [CrossRef] (In the text)
Huang, Y. F., Wu, X. F., Dai, Z. G., Ma, H. T., & Lu, T. 2004, ApJ, 605, 300 [NASA ADS] [CrossRef] (In the text)
Jin, Z. P., Yan, T., Fan, Y. Z., & Wei, D. M. 2007, ApJ, 656, L57 [NASA ADS] [CrossRef] (In the text)
Kumar, P., & Granot, J. 2003, ApJ, 591, 1075 [NASA ADS] [CrossRef] (In the text)
Lazzati, D. 2006, New J. Phys., 8, 131 [CrossRef] (In the text)
Li, Z., & Song, L. M. 2004, ApJ, 614, L17 [NASA ADS] [CrossRef] (In the text)
Liang, E. W., Racusin, J. L., Zhang, B., Zhang, B. B., & Burrows, D. N. 2008, ApJ, 675, 528 [NASA ADS] [CrossRef] (In the text)
Longair, M. S. 1992, High Energy Astrophysics (Cambridge: Cambridge University Press), 1 (In the text)
MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] (In the text)
Mészáros, P. 2002, ARA&A, 40, 137 [NASA ADS] [CrossRef] (In the text)
Mészáros, P. 2006, Rep. Prog. Phys., 69, 2259 [NASA ADS] [CrossRef] (In the text)
Mészáros, P., Rees, M. J., & Wijers, R. A. M. J. 1998, ApJ, 499, 301 [NASA ADS] [CrossRef] (In the text)
Piran, T. 2004, Rev. Mod. Phys., 76, 1143 [NASA ADS] [CrossRef] (In the text)
Racusin, J. L., Karpov, S. V., Sokolowski, M., et al. 2008, Nature, 455, 183 [NASA ADS] [CrossRef] (In the text)
Rhoads, J. E. 1997, ApJ, 487, L1 [NASA ADS] [CrossRef] (In the text)
Rhoads, J. E. 1999, ApJ, 525, 737 [NASA ADS] [CrossRef] (In the text)
Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley) (In the text)
Sari, R. 1998, ApJ, 494, L49 [NASA ADS] [CrossRef] (In the text)
Sari, R., Piran, T., & Halpern, J. P. 1999, ApJ, 519, L17 [NASA ADS] [CrossRef] (In the text)
Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef]
Sedov, L. 1969, Similarity and Dimensional Methods in Mechanics, Chap. 4 (New York: Academic) (In the text)
Shu, F. H. 1991, The Physics of Astrophysics (Mill Valley, California: University Science Books), 1 (In the text)
van der Horst, A. J., Kamble, A., Resmi, L., et al. 2008, A&A, 480, 35 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
van Paradijs, J., Groot, P. J., Galama, T., et al. 1997, Nature, 386, 686 [NASA ADS] [CrossRef] (In the text)
Waxman, E. 1997, ApJ, 491, L19 [NASA ADS] [CrossRef] (In the text)
Waxman, E., Kulkarni, S. R., & Frail, D. A. 1998, ApJ, 497, 288 [NASA ADS] [CrossRef] (In the text)
Woosley, S. E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] (In the text)
Wright, E. L. 2006, PASP, 118, 1711 [NASA ADS] [CrossRef] (In the text)
Wu, X. F., Dai, Z. G., Huang, Y. F., & Ma, H. T. 2004, ChJAA, 4, 455 [NASA ADS] (In the text)
Yost, S. A., Harrison, F. A., Sari, R., & Frail, D. A. 2003, ApJ, 597, 459 [NASA ADS] [CrossRef] (In the text)
Zhang, W. Q., & MacFadyen, A. 2009, ApJ, 698, 1261 [NASA ADS] [CrossRef] (In the text)

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{11612f1.eps} \end{figure}$	Figure 1: The evolution of the Lorentz factors of the twin jets. The solid line corresponds to the receding jet and the dashed line is plotted for the forward jet. The twin jets are in the ``standard'' condition as defined in Sect. 3. The observers' time has been corrected for the cosmological effect (z=0.1).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11612f2.eps} \end{figure}$	Figure 2: Schematic illustration of the EATSs at three moments, $t_1 \approx 114$ d, $t_2 \approx 286$ d and $t_3 \approx 572$ d. In this calculation, we have used the ``standard'' parameter set as defined in Sect. 3. ``O'' is the position of the central engine, and the observer is on the far right side with Y=0. The dotted lines indicate the jet boundary. For the receding jet, the EATSs are plotted in thick solid lines, while for the forward jet the surfaces are plotted in thin solid lines. Note that on the forward jet branches, the bulk Lorentz factors of the material at the peak of the EATSs are 1.17, 1.07, and 1.03 for t₁, t₂, and t₃, respectively. On the receding jet branches, the bulk Lorentz factors of the material at the peak of the EATSs are 56.07, 11.79, and 3.95 for t₁, t₂, and t₃, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7cm,clip]{11612f3a.eps}\hspace*{1cm} \includegraphics[width=7cm,clip]{11612f3b.eps} \end{figure}$	Figure 3: 8.46 GHz radio afterglow a) and R-band optical afterglow b) from the forward jet and the receding jet. The thick lines are plotted for a ``standard'' double-sided jet as defined in Sect. 3. The thin lines are plotted for the double-sided jet with only one parameter altered compared to the ``standard'' condition, i.e. $n=1000 / {\rm cm}^{3}$ . In each group, the dotted line reflects the emission from the forward jet, the dashed line reflects the contribution from the receding jet, and the solid line is the total light curve.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{11612f4a.eps}\hspace*{0.8cm} \includegraphics[width=7cm,clip]{11612f4b.eps} \end{figure}$	Figure 4: Multiwavelength afterglow light curves of a double-sided jet. Radio afterglows are illustrated in panel a), and optical/IR afterglows are plotted in panel b). In this calculation, we have used the ``standard'' parameter set as defined in Sect. 3.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.7cm,clip]{11612f5a.eps}\hspace{1cm}... ...s}\hspace{1cm} \includegraphics[width=6.7cm,clip]{11612f5d.eps} \end{figure}$	Figure 5: The effects of various parameters (n, $E_{\rm0,iso}$ , $\theta _{\rm j}$ , and $\varepsilon$ ) on the 8.46 GHz radio afterglow light curves of double-sided jets. In each panel, ``(s)'' corresponds to the ``standard'' condition as defined in Sect. 3, and other lines are drawn with only one certain parameter altered or one condition changed. In panel d), the dash-dotted line is plotted for a double-sided jet without lateral expansion; and the dotted line is plotted for a double-sided jet with a low initial Lorentz factor ( $\gamma _{\rm0} = 30$ ), which may correspond to the so-called failed GRBs.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.7cm,clip]{11612f6a.eps}\hspace{0.8c... ...\hspace{0.8cm} \includegraphics[width=6.7cm,clip]{11612f6d.eps} \end{figure}$	Figure 6: The effects of various parameters ( $\xi _{\rm e}$ , $\xi _{\rm B}^2$ , p, and $\theta _{\rm obs}$ ) on the 8.46 GHz radio afterglow light curves of double-sided jets. In each panel, ``(s)'' corresponds to the ``standard'' condition as defined in Sect. 3, and other lines are drawn with only one certain parameter altered.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.7cm,clip]{11612f7a.eps}\hspace{0.8c... ...\hspace{0.8cm} \includegraphics[width=6.7cm,clip]{11612f7d.eps} \end{figure}$	Figure 7: 8.46 GHz radio afterglow light curves of double-sided jets. In this figure, we assume that the parameters of the receding jet can be different from those of the forward jet. In each panel, the solid line is plotted under the ``standard'' condition, i.e., the parameters are the same for the twin jets (but note that we have evaluated $\xi _{\rm e}$ as 0.01 and $\xi _{\rm B}^2$ as 10^-4 here). For other light curves, one or two parameters are changed for the receding jet, to see their effect on the afterglows.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

On the afterglow from the receding jet of -ray bursts

1 Introduction

2 Model description

2.1 Hydrodynamic evolution

2.2 Radiation process

3 Numerical results

4 Conclusion and discussion

References

All Figures

On the afterglow from the receding jet of $\gamma$ -ray bursts