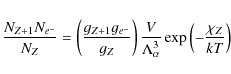| Issue |
A&A
Volume 505, Number 2, October II 2009
|
|
|---|---|---|
| Page(s) | 735 - 742 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/20077713 | |
| Published online | 28 July 2009 | |
The solar-interior equation of state with the path-integral formalism
I. Domain of validity
A. Perez1,2 - K. Mussack3,4 - W. Däppen3 - D. Mao3
1 - Laboratoire de Physique Théorique (UMR CNRS/ULP 7085),
Université Louis Pasteur de Strasbourg, 67084 Strasbourg Cedex,
France
2 - Department of Applied Physics, Jerusalem College of
Technology, 92221 Jerusalem, Israel
3 - Department of Physics and Astronomy, USC, Los Angeles,
CA 90089-1342, USA
4 - Institute of Astronomy, University of Cambridge, Cambridge CB3 0HA, UK
Received 25 April 2007 / Accepted 19 July 2009
Abstract
Aims. This is the first paper in a series that deals with solar-physics applications of the equation-of-state formalism based on the formulation of the so-called ``Feynman-Kac (FK) representation''. Here, the FK equation of state is presented and adapted for solar applications. Its domain of validity is assessed. The practical application to the Sun will be dealt with in Paper II. Paper III will extend the current FK formalism to a higher order.
Methods. A recent rigorous quantum-statistical formalism for Coulomb systems is used to compute the thermodynamical quantities for solar modeling, taking into account the necessary requirements on smoothness and accuracy. The FK formalism being a virial expansion, it suffers from the well-known deficiency that it is limited to nearly full ionization. This point is elaborated in detail, and the quantitative criterion for the domain of validity of the FK equation of state is established.
Results. Use of the FK equation of state is limited to physical conditions for which more than 90% of helium is ionized. This includes the inner region of the Sun out to about .98 of the solar radius. Despite this limitation, in the parts of the Sun where it is applicable, the FK equation of state has the power to be more accurate than the equations of state currently used in solar modeling. The FK approach is especially suited to study physical effects such as Coulomb screening, bound states, the onset of recombination of fully ionized species, as well as diffraction and exchange effects.
Conclusions. Despite technical difficulties in its application, there are unique features in the FK approach that promise to turn it into the most exact of the available formalisms, provided FK is restricted to the deeper layers of the Sun where more than 90% of helium is ionized. The localizing power of helioseismology allows a test of the FK equation of state. Such a test will be beneficial both for better solar models and for tighter solar constraints of the equation of state.
Key words: equation of state - stars: interiors - Sun: interior - Sun: helioseismology
1 Introduction
This paper is the first of a series of three devoted to the study
of the equation of state based on the formalism of the path
integral in the framework of the Feynman-Kac (hereinafter FK)
representation. This formalism leads to a virial expansion of the
thermodynamic functions in powers of the total density of a
Coulomb plasma (Alastuey & Perez 1992; Alastuey et al. 1995,1994; Alastuey & Perez 1996). The path-integral
approach is the latest in a series of attempts to improve the
equation of state for the solar interiors. However, so far there
has only been a very limited amount of astrophysical applications
of that formalism. One (Perez & Chabrier 2004) was an application to the
screening enhancement of nuclear fusion. Another one was a
precursor (Perez & Däppen 1995) of the present series of articles, which
addressed the possibility of using the FK formalism in solar and
stellar modeling. Here, we embark on a more systematic application
of the FK representation. It is well known that solar and stellar
modeling requires thermodynamic quantities that are smooth,
consistent, valid over a large range of temperatures and
densities, and incorporate the most important
astrophysically relevant chemical elements. Let us briefly review
the two major equation-of-state efforts of the last 20 years. Both
were made in the context of the two most recent opacity
recalculations.
One of them is the international Opacity Project (OP; see the books by Berrington 1997; Seaton 1995); it contains the so-called Mihalas-Hummer-Däppen equation of state (Nayfonov et al. 1999; Trampedach et al. 2006; Mihalas et al. 1988; Däppen et al. 1988; Hummer & Mihalas 1988, hereinafter MHD), dealing with heuristic concepts about the modification of atoms and ions in a plasma. Specifically, in MHD the destruction of atomic states is modeled, on the one hand by neutral species according to excluded volume, and on the other hand by Stark dissolution due to the surrounding microfield. From the included 15 astrophysically relevant elements (H, He, C, N, O, Ne, Na, Mg, Al, Si, S, Ar, K, Ca, Fe), users can select any subset. Although MHD in its current version does not contain free parameters, several of the physical quantities are, in principle, open to revision. Possible candidates for adjustment are i) the atomic and ionic radii (which can be chosen to match observations), ii) the strength of the assumed microfield distribution, and iii) the specific form of the interaction potential between species. Since MHD is basically a heuristic equation of state, such future improvements will be legitimate and they can be developed under the guidance of observations. For more details see Trampedach et al. (2006).
The other recent opacity effort is the OPAL project pursued at Livermore. In contrast to OP, its underlying equation of state has relied on the so-called physical picture, which is built on the notion of fundamental particles only, that is, electrons and nuclei. It provides a systematic method to include non-ideal effects. Its so-called ACTEX (``activity expansion'') equation of state (see Rogers et al. 1996; Rogers & Nayfonov 2002; Rogers 1986, and references therein) became part of the OPAL opacity project at Livermore (Iglesias & Rogers 1996; Iglesias et al. 1987; Iglesias & Rogers 1991,1995,1993). For this reason, the ACTEX equation of state is hereinafter referred to as the OPAL equation of state. As mentioned, OPAL is a physical-picture formalism, starting out from the grand-canonical ensemble of a system of the basic constituents (electrons and nuclei) interacting through the Coulomb potential. In the currently released version, the OPAL equation of state includes the following astrophysically relevant elements: H, He, C, N, O, Ne (but the OPAL opacity calculation includes other elements, such as Fe, as well). In OPAL, any effects of the plasma environment on the internal states are obtained directly from the statistical-mechanical analysis, rather than by assertion as in the chemical picture. Therefore, in contrast to the intuitive MHD, in OPAL there are no adjustable parameters. On the one hand, this is its strength, on the other hand, it means that one cannot easily upgrade OPAL even if observations were to suggest so. Thus in the current OPAL equation of state tables, any residual inaccuracy is either structural, a result of i) the finite truncation in the underlying activity expansion, and ii) the utilization of effective atomic and ionic potentials, or it could be due to the limited number of chemical elements in the current tables.
The equation of state for solar and stellar structure and
seismology has to be formally precise and consistent, even
before the question of the accuracy of the physical description is
asked. It has to satisfy four conditions: i) a large domain of
applicability (in ![]() ,
T), ii) a high precision of its
numerical realization, iii) consistency between the thermodynamic
quantities, and iv) the possibility to take into account
relatively complex mixtures with at least several of the more
abundant chemical elements. These requirement are generally easy
to satisfy with relatively simple formalisms, such as the popular,
widely used CEFF equation of state (Christensen-Dalsgaard & Däppen 1992), which is an
offspring of the widely used Eggleton-Faulkner-Flannery (EFF)
equation of state (Eggleton, Faulkner, & Flannery 1973), or the other offspring of EFF,
the SIREFF equation of state (Rogers et al. 1996).
,
T), ii) a high precision of its
numerical realization, iii) consistency between the thermodynamic
quantities, and iv) the possibility to take into account
relatively complex mixtures with at least several of the more
abundant chemical elements. These requirement are generally easy
to satisfy with relatively simple formalisms, such as the popular,
widely used CEFF equation of state (Christensen-Dalsgaard & Däppen 1992), which is an
offspring of the widely used Eggleton-Faulkner-Flannery (EFF)
equation of state (Eggleton, Faulkner, & Flannery 1973), or the other offspring of EFF,
the SIREFF equation of state (Rogers et al. 1996).
However, the demands from helioseismology are such that formal considerations are not sufficient. The equation of state has to be accurate, not just smooth. Even state-of-the-art equations of state such as OPAL and MHD are not completely sufficient (Däppen 2006), and improvements are still necessary. Improvements can be made either formally (phenomenologically) or rigorously. A formal option is to merge the good features of OPAL and MHD (Liang & Däppen 2003; Liang 2004; Däppen & Mao 2009; Starostin et al. 2003) to create an equation of state that matches reality as closely as possible. However, as a phenomenological effort, such a hybrid formalism would not be a scientific improvement but merely a better computational tool for solar and stellar modeling. As far as the development of a real theory is concerned, genuine improvements in the physical model must be made. The rigorous equation of state in the FK representation is such an improvement. In principle, it is a better theory than either MHD or OPAL. A case in point is the treatment of Coulomb screening. Here, the electrons are taken into account with the exact quantum-mechanical exchange and diffraction terms. These are corrections that deal, on the one hand, with the ``Pauli blocking'' of electrons (exchange terms) and, on the other hand, their finite thermal de Broglie wavelength (diffraction terms). For these terms, both MHD and OPAL use approximations. However, this better physics of FK comes with a price: the FK equation of state has a limited domain of validity unlike the more global MHD and OPAL. It only works for nearly fully ionized plasmas.
As a theory, FK is quite similar to OPAL, since it is realized in the physical picture and the grand-canonical ensemble. However, its net result is that of a virial (density) expansion (unlike OPAL, which is based on activity). The virial coefficients of the FK expansion are evaluated by the path-integral formalism, which in its essence uses the equivalence between a point-charge quantum system and a classical one made of extended filaments. In this spirit, the calculation of all non-ideal contributions to the equation of state becomes possible, systematically, exactly, and analytically. The fact that FK has the form of a virial expansion is the source of its limitation to near full ionization. In Sect. 2 we illustrate the well-known fact that in the case of reacting gases, virial expansions are inadequate to deal with recombination (unlike the activity expansions of OPAL). We discuss this deficiency quite in detail and develop a quantitative criterion for the validity of the FK equation of state. The adopted criterion is a limitation to physical conditions such that more than 90% of helium is ionized. The subsequent sections discuss the physical condition quantitatively, in terms of a solar model.
Despite the aforementioned limitation to nearly fully ionized matter, the FK approach can be applied to solar modeling. The reason for this is twofold. First, a large part of the solar interior (out to about .98 of the solar radius) lies inside its domain of validity, and second, helioseismology allows a localized analysis of thermodynamic properties despite the fact that there is no complete coverage of the Sun by the FK equation of state.
Here the FK equation of state is presented and its domain of
validity discussed. Paper II will then be dedicated to solar
applications. They will be based on ``mixed'' thermodynamic
tables, with FK in the highly ionized part, and a conventional
equation of state (OPAL or MHD) outside the domain of validity of
FK. We note in passing that once these tables exist they can be
used also for stellar modeling, but it is not clear if stellar
application would ever require such an accuracy of the equation of
state, in contrast to solar application for which this need has
been well established (see, e.g. Däppen 2006). In any case,
stellar applications are beyond the scope of this current series
of papers. Finally, paper III will be a natural extension of the
current level of the FK formalism. While the current level of FK
is based on an expansion of pressure in terms of the density with
up to order
![]() ,
the next (rather elaborate) step is the
extension to calculation of the thermodynamic functions up to
order
,
the next (rather elaborate) step is the
extension to calculation of the thermodynamic functions up to
order ![]() .
Then we will be able to take into account
three-body effects, allowing us to treat helium exactly, beyond
the hydrogenic approximation.
.
Then we will be able to take into account
three-body effects, allowing us to treat helium exactly, beyond
the hydrogenic approximation.
2 Illustration of the limitation of virial expansions for reacting systems
The principle can be understood by considering the exact equation of the ideal (non-relativistic) Fermi gas. One starts out from an implicit equation of state, obtained from the grand-canonical partition function (see, e.g. Huang 1963)
Here,
Expanding the Fermi integrals as a series in the high-temperature limit, and eliminating the fugacity
Alternatively, one can continue to work with fugacity expansion
With the introduction of the activity
These expressions above are exact for the partially degenerate ideal Fermi gas, they retain their formal structure for any real gas (this follows from their origin in the grand-canonical partition function). Therefore, all the physics lies in the value of the coefficients of the expansions. For the activity, one formally writes
and for density,
Inspection of Eqs. (4) and (7) reveals the relation
While we derived the relation for the ideal Fermi gas, Eq. (12) is a general result, valid for all real gases (see, e.g. Huang 1963). The second-virial coefficient is a function of temperature only; an explicit expression is obtained from classical statistical mechanics by the two-body configuration integral over the interaction potential U12
![\begin{figure}
\par\includegraphics[width=8.5cm]{07713f01.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg25.png) |
Figure 1:
Illustration of the behavior of activity (solid line) and density expansions
(dashed line) for reacting systems, here for the simple reaction of neutral hydrogen H
recombining to hydrogen molecules |
| Open with DEXTER | |
Of course, as infinite series, activity and density expansions would be strictly equivalent, but when dealing with recombination, a density expansion would have to go to a very high order to match the accuracy of even a second-order activity expansion. Indeed, for recombinations, the activity expansion (9,10) is vastly superior to the virial expansion (11). This is easily seen from Eq. (13), where for a (necessarily) attractive two-body potential and low temperatures B2 becomes large negative, which will cause inevitably a negative total pressure at some low temperature. In other words, the virial expansion breaks down. This breakdown is illustrated by the dashed line of Fig. 1 (from Ebeling et al. 1976). For simplicity, that figure is for hydrogen molecular dissociation, but qualitatively it would be the same for ionization. In contrast, the activity expansion can avoid this breakdown, as revealed by a more detailed discussion of Eqs. (9) and (10) that can be found elsewhere (e.g. Ebeling et al. 1976; Kremp et al. 2005). Importantly, already to lowest non-ideal order, the activity expansion can correctly describe complete low-temperature recombination (solid line in Fig. 1). This property of activity expansions is the principal reason for the remarkable success of the OPAL equation of state.
In contrast, as a virial expansion, the FK equation of state suffers from the pathology illustrated by Fig. 1, irrespective of the fact that its low-order virial coefficients are exact. Nevertheless there is a domain of applicability where we can use FK: Fig. 1 shows the overlap region of the virial and activity expansions. A natural quantitative limit for the application of a virial expansion becomes apparent: as long as the physical conditions are such that more than about 90% of the bound particles remain ionized, the resulting thermodynamic quantities still will be reliable. In the following we adopt this criterion for the FK approach.
3 The path-integral formalism in the framework of the Feynman-Kac representation
In many situations, stellar matter can be adequately described in terms of quantum plasmas made of electrons and nuclei. In this part, we summarize the main steps of the path-integral formalism in the FK representation. Details of the calculation can be found in Alastuey & Perez (1992) and Alastuey et al. (1995,1994). The general method can be divided in two steps. In a first step only Maxwell-Boltzmann (MB) statistic is considered and all exchange effects are omitted. Using the FK representation, an equivalent classical system made of closed filaments interacting via two-body forces is introduced. Applying traditional techniques of classical mechanics inspired by Abe-Meeron's method (Abe 1959; Meeron 1958), a formal diagrammatic representation of the MB quantities was obtained, which is term-by-term well-behaved.
In a second step of this approach, the exchange contribution was introduced, evaluated perturbatively via Slater sums. Use of the FK representation leads to the appearance of open filaments (impurities) immersed in a bath of closed filaments described by MB statistics. This problem can be dealt with using the method that is explained in the MB case to inhomogeneous situations.
Collecting all the contributions arising from both the MB and the
exchange treatment, a systematic virial expansion of the equation
of state was obtained, which includes screening, diffraction,
bound states, and exchange contributions to the ideal gas
(depending on the statistics of the particles). The expression of
the pressure was calculated up to and including order
![]() (with
(with ![]() being the overall density of the system). To this
order of density, the calculation of Alastuey & Perez (1992) and Alastuey et al. (1995,1994)
describes exactly all the effects pertaining to bound states,
diffusive and exchange processes of a system consisting of two
species of elementary particles.
being the overall density of the system). To this
order of density, the calculation of Alastuey & Perez (1992) and Alastuey et al. (1995,1994)
describes exactly all the effects pertaining to bound states,
diffusive and exchange processes of a system consisting of two
species of elementary particles.
3.1 Exact expression of the equation of state to the order of
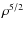
The virial expansion of the pressure to
order
![]() gives (Alastuey & Perez 1992)
gives (Alastuey & Perez 1992)
with
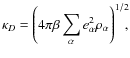
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and the Euler-Mascheroni
constant
C =0.577216.
,
and the Euler-Mascheroni
constant
C =0.577216.
In Eq. (14),
![]() refers to the
so-called quantum second-virial coefficient first introduced by
Ebeling and co-workers (Ebeling et al. 1976; Kraeft et al. 1986).
refers to the
so-called quantum second-virial coefficient first introduced by
Ebeling and co-workers (Ebeling et al. 1976; Kraeft et al. 1986).
while
![]() is defined as the two-body exchange integral,
is defined as the two-body exchange integral,
In Eqs. (15) and (16),
![]() is the
one-body Hamiltonian of the relative particle with mass
is the
one-body Hamiltonian of the relative particle with mass
![]() submitted to the Coulomb potential
submitted to the Coulomb potential
![]() .
The functions Q and E only depend on the temperature via the
single dimensionless parameter
.
The functions Q and E only depend on the temperature via the
single dimensionless parameter
![]() .
.
3.2 Deriving other thermodynamic variables
The expression for the pressure in Eq. (14) can be used to derive other thermodynamic variables. For example, the relationship between the pressure and the free energy is given bywhere f is the free energy per unit volume. The internal energy per unit volume u is then found as a derivative of the free energy
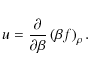 |
(18) |
Other quantities of interest can be derived in a similar way via the usual thermodynamic derivatives.
3.3 The general structure of 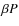
First, the classical
contributions of the long-range part of the interactions are
polynomials in the inverse temperature, the charges and the
densities, which do not involve Planck's constant. The involved
coefficients are evaluated analytically or, like C1 and C2,
by numerical computations of dimensionless integrals. The
lower-order contribution is nothing but the familiar
Debye-H
![]() ckel term in
ckel term in
![]() ,
and constitutes
the leading correction to the MB ideal pressure in
Eq. (17). It can be quoted, here, that the classical OCP
limit up to order
,
and constitutes
the leading correction to the MB ideal pressure in
Eq. (17). It can be quoted, here, that the classical OCP
limit up to order
![]() included does coincide with those
calculated by Cohen & Murphy (1969), as it should.
included does coincide with those
calculated by Cohen & Murphy (1969), as it should.
The contribution of quantum diffraction at large distances appears
only at the order
![]() and reduces to
and reduces to
![]() The occurrence of this term shows that the
long-range part of the interactions cannot be entirely treated at
a classical level. The diffraction correction is merely
proportional to
The occurrence of this term shows that the
long-range part of the interactions cannot be entirely treated at
a classical level. The diffraction correction is merely
proportional to ![]() ,
because it arises from large distances
where the quantum effects can be treated perturbatively ``à la-Wigner-Kirkwood''.
,
because it arises from large distances
where the quantum effects can be treated perturbatively ``à la-Wigner-Kirkwood''.
The term
![]() is the total contribution from both bound and
scattering states of two charges
is the total contribution from both bound and
scattering states of two charges ![]() and
and ![]() .
The
truncation of
.
The
truncation of
![]() in the integral defining Q
ensures that this contribution is finite. This regularization is
not an arbitrary mathematical artifact. It is directly related to
the truncated structure of the bond fT, and reflects the
screening of the Coulomb interaction at large distances. For
opposite charges such that
in the integral defining Q
ensures that this contribution is finite. This regularization is
not an arbitrary mathematical artifact. It is directly related to
the truncated structure of the bond fT, and reflects the
screening of the Coulomb interaction at large distances. For
opposite charges such that
![]() ,
one may extract
from Q a contribution of the bound states which reduces to the
familiar Planck-Larkin (PL) sum
,
one may extract
from Q a contribution of the bound states which reduces to the
familiar Planck-Larkin (PL) sum
where
![]() are the
energy levels of the hydrogenic atom with Hamiltonian
are the
energy levels of the hydrogenic atom with Hamiltonian
![]() .
However, other definitions of the bound states
contributions can be introduced from Eq. (15) by using the
basic properties of the trace. For instance, as shown by
Bollé (1987), there exists an infinite set of arbitrary
decompositions in terms of bound and scattering contributions of
the PL sum itself. So, as far as thermodynamic quantities are
concerned, only the total contribution of both bound and
scattering states is an unambiguous quantity. The
.
However, other definitions of the bound states
contributions can be introduced from Eq. (15) by using the
basic properties of the trace. For instance, as shown by
Bollé (1987), there exists an infinite set of arbitrary
decompositions in terms of bound and scattering contributions of
the PL sum itself. So, as far as thermodynamic quantities are
concerned, only the total contribution of both bound and
scattering states is an unambiguous quantity. The
![]() -contribution from bound and scattering states merely
reduces to its
-contribution from bound and scattering states merely
reduces to its ![]() counterpart multiplied by
counterpart multiplied by
![]() .
This multiplicative factor arises from
many-body effects which induce a constant shift
.
This multiplicative factor arises from
many-body effects which induce a constant shift
![]() on the energy levels of the two-particles
states.
on the energy levels of the two-particles
states.
Finally, the contribution
![]() arises from the
exchange of two charges
arises from the
exchange of two charges ![]() in the vacuum. It is finite,
independently of any screening effect, because the off-diagonal
matrix elements
in the vacuum. It is finite,
independently of any screening effect, because the off-diagonal
matrix elements
![]() are short ranged.
The magnitude of this contribution is smaller than the one
relative to free particles because the repulsive potential
are short ranged.
The magnitude of this contribution is smaller than the one
relative to free particles because the repulsive potential
![]() inhibits the exchange. Similarly to what happens
for the contributions of bound and scattering states, at the order
inhibits the exchange. Similarly to what happens
for the contributions of bound and scattering states, at the order
![]() ,
the many-body effects on the two-particle exchange
amounts to lowering the repulsive barrier
,
the many-body effects on the two-particle exchange
amounts to lowering the repulsive barrier
![]() by the
constant
by the
constant
![]() .
.
3.4 The nature of the non-ideal terms in the FK equation of state
As is usual for a weakly non-ideal plasma (see, e.g. Ebeling et al. 1976), the most important contributions beyond the ideal gas limit are the exchange terms, the Debye screening corrections, the short-range corrections and diffraction (in decreasing order of importance). Let us recall briefly the various conditions allowing us to check the nature of the short-range corrections for a given temperature and density.
Since the current level of our FK equation of state
is truncated at
the order
![]() ,
it can only include processes with two-body effects.
It comes naturally, from the structure of the equation of
state, that short-range quantum effects are virtually decoupled
from the other corrections. This means that in all orders of density,
the main impact of these short-range quantum
corrections merely pertains to the
recombination and ionization processes.
The magnitude of the neglected higher-order terms will
indicate the influence of three-body or higher interactions.
The comparison with solar data will allow us
a quantitative estimate of these neglected terms.
,
it can only include processes with two-body effects.
It comes naturally, from the structure of the equation of
state, that short-range quantum effects are virtually decoupled
from the other corrections. This means that in all orders of density,
the main impact of these short-range quantum
corrections merely pertains to the
recombination and ionization processes.
The magnitude of the neglected higher-order terms will
indicate the influence of three-body or higher interactions.
The comparison with solar data will allow us
a quantitative estimate of these neglected terms.
Similarly, one has to be aware of the higher Debye corrections
beyond the
![]() term. A careful
analysis of the virial expansion shows that the quantum short-range
correction that only involves the two-body virial coefficient
term. A careful
analysis of the virial expansion shows that the quantum short-range
correction that only involves the two-body virial coefficient
![]() results in an alternating series in
results in an alternating series in ![]() ,
which
is therefore convergent. Since the leading Debye correction to pressure
(included in our formalism) is negative, the following term must be
positive. Should at some physical conditions the neglected higher corrections
lead to a lowering of pressure, we will be able to interpret them as a
manifestation of a recombination process occurring under these
thermodynamical conditions.
,
which
is therefore convergent. Since the leading Debye correction to pressure
(included in our formalism) is negative, the following term must be
positive. Should at some physical conditions the neglected higher corrections
lead to a lowering of pressure, we will be able to interpret them as a
manifestation of a recombination process occurring under these
thermodynamical conditions.
4 Limits of validity of the FK equation of state
4.1 Dimensionless parameters
A detailed analysis of this equation of state suggests rewriting the truncated expression of the thermodynamic quantities (for example pressure) in terms of three characteristic lengths:
- mean interparticle distance
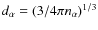 ;
;
- thermal de Broglie wavelength
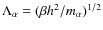 ;
;
- Landau length
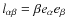 .
.
Here the notation is standard, and there should be no confusion
between ![]() being both a label and 1/(kT). Note that since we are now
dealing with quantitative applications, we denote number density by
the usual symbol n rather than the
being both a label and 1/(kT). Note that since we are now
dealing with quantitative applications, we denote number density by
the usual symbol n rather than the ![]() that was used in the
preceding theoretical sections of this paper.
that was used in the
preceding theoretical sections of this paper.
Before the FK equation of state can be applied to the Sun, we must
determine where the formalism is applicable. Here we evaluate the
relevant criteria throughout the Sun, based on a standard solar
model (Model S from Christensen-Dalsgaard, as described
in Christensen-Dalsgaard et al. 1996) First, we verify the well-known result that the plasma
in the solar interior is indeed not strongly coupled.
Fig. 2 shows the coupling parameter
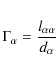
through the solar model. The index
Figs. 3-5 show the degeneracy parameter
![]() ,
again for electrons, protons, and
helium nuclei, respectively.
,
again for electrons, protons, and
helium nuclei, respectively.
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f02.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg82.png) |
Figure 2: Coupling parameters for electrons, protons, and helium nuclei from the surface to the center of the Sun. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f03.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg83.png) |
Figure 3: Degeneracy parameter for electrons from the surface to the center of the Sun. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f04.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg84.png) |
Figure 4: Degeneracy parameter for protons from the surface to the center of the Sun. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f05.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg85.png) |
Figure 5: Degeneracy parameter for helium nuclei from the surface to the center of the Sun. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f06.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg86.png) |
Figure 6: Ionization degree of hydrogen from the surface to the center of the Sun. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f07.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg87.png) |
Figure 7: First ionization degree of helium from the surface to the center of the Sun. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f08.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg88.png) |
Figure 8: Second ionization degree of helium from the surface to the center of the Sun. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f09.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg89.png) |
Figure 9: First and second ionization degree of oxygen (as a representative heavy element) from the surface to the center of the Sun. |
| Open with DEXTER | |
4.2 Qualitative discussion of ionization and recombination
As we discussed in detail in Sect. 2, avoiding too much recombination is the most restrictive criterion for the FK equation of state. Figures 6-9 show that it is certainly more restrictive than coupling and degeneracy. Obviously, our low-density virial expansion cannot be used in the cooler outer layers of the Sun, where the plasma is far from fully ionized. To obtain an estimate of limit of validity of FK, which we identified with 90% ionization, we have calculated the hydrogen and helium ionization fraction using the standard (ground-state-only) Saha equationthroughout the same solar model. As usual,
Figures 6-9 show the recombination fraction for hydrogen, helium, and the first two ionization stages of oxygen (as a typical representative heavy element). The 90%-ionization level is also shown. Clearly, at some point in the colder outside layers, our virial expansion must break down.
However, in the deeper layers of the Sun (and non-compact stars in general), we can verify that the weak-coupling and low-degeneracy criteria are fully satisfied and the limitation from the ``recombination criterion'' is totally negligible for the temperatures and densities of those regions.
4.3 The treatment of heavier elements
Adding heavier elements (other than hydrogen and helium) reduces the domain of validity of the FK equation of state to even higher temperatures. This is obvious because it is harder to ionize these elements. Figure 9 shows this quantitatively for oxygen. We therefore adopt the simplest solution which is to ignore the heavier elements altogether. Indeed, in the solar application of Paper II, we will merely add the pressure of the heavier elements to the FK expansion 14. Since in the Sun, the number abundance of all elements other than hydrogen and helium is only about 10-3, adding the heavier elements to FK with an equation of state such as MHD, which is at least as accurate as 1% (e.g. Däppen 2006) will limit the total error of such a simplified procedure to an acceptable order of magnitude of 10-5.
In addition, knowing the domain of validity also allows us to study selected recombination reactions in the framework of the FK equation of state. For instance, in the calculation of nuclear reaction cross sections, the ionization degree of the various nuclei plays a role, because the statistical presence of electrons around the nucleus modulates the reaction rate (enhancement factor). This has consequences for solar physics especially with respect to the neutrino problem, where the reactions involving Be and B have to be know very accurately (Perez & Chabrier 2004).
4.4 Solar models with a hybrid equation of state
Because of its limitations to nearly full ionization, it is impossible to use the FK formalism for the entire Sun. Therefore, for our applications in Paper II, we will have to use a hybrid two-zone equation of state, consisting of FK serving in the interior, and a more conventional one (OPAL or MHD) in the outer layers. Although such a hybrid equation of state will have discontinuities at the transition, these discontinuities will not preclude the solution of the usual stellar structure equations. Their main effect is expected to be a small jump in the gradient of the physical quantities, similar to that caused, for instance, by standard interpolation in equation-of-state and opacity tables. As detailed studies (Christensen-Dalsgaard & Däppen 1992) have shown, successful equation of state tests can still be made despite such small imperfections. The analysis of Paper II will reveal if the small discontinuities will cause problems. If so, they can be avoided by the introduction of suitable smooth ramp functions at the juncture line of the two-zone equation of state.
4.5 Distribution of FK equation of state
OPAL and MHD have been made available to solar and stellar modelers through the use of tables. Although this saves the modelers a bit of computing time, the tables have only been provided for a limited range of conditions. In order to make the FK equation of state more versatile, we plan to develop a computational routine for which users can define their own input parameters such as element abundances. This implementation of FK will be ideally suited for exploring issues such as He diffusion and the inconsistency between seismology and the new values of heavy element abundances (Grevesse et al. 2007; Asplund et al. 2005; Asplund 2005).
5 Conclusions
Despite the limitation to nearly fully ionized matter, the FK approach can be applied to large parts of the solar interior, more precisely to the part where helium is at least 90% ionized. In those regions the FK approach is applicable, and it is especially suited to study screening effects, bound states, recombination of fully ionized ions, and exchange effects.
Paper II will be dedicated to these observational tests. Since the
important relativistic correction for electrons (Elliott & Kosovichev 1998) is
not part of the original FK equation of state (14), we
will add it in Paper II. Paper III will go further, on a rigorous
theoretical level, to the calculation of the thermodynamic
functions up to order ![]() in density. The additional
higher-order terms will allow us to take into account the
three-body effects that occur in a moderately ionized plasma (for
example, in the case of the solar center, the possibility of a
recombination of
in density. The additional
higher-order terms will allow us to take into account the
three-body effects that occur in a moderately ionized plasma (for
example, in the case of the solar center, the possibility of a
recombination of
![]() is still an unsolved problem).
is still an unsolved problem).
Despite the severe technical difficulties involving the practical application of the FK equation of state for solar physics, there are unique features in the FK approach that promise to turn it into the most exact of the available formalisms, if they are limited to the layers of the Sun where more than 90% of helium is ionized. The localizing power of helioseismology allows us to test FK observationally, promising both better and tighter constraints on the equation of state. For instance, by virtue of its exactness, the FK equation of state becomes a promising tool for tweaking parameterizable equations of state such as MHD. More generally, the FK equation of state will lead to better solar models as well as tighter solar constraints of the equation of state.
Acknowledgements
We thank Jørgen Christensen-Dalsgaard for the solar model used in this study. This work was supported by the grant AST-0708568 of the National Science Foundation.
References
- Abe, R., 1959, Progr. Theor. Phys., 22, 213 [NASA ADS] [CrossRef]
- Alastuey, A., & Perez, A. 1992, Europhys. Lett., 20, 19 [NASA ADS] [CrossRef]
- Alastuey, A., & Perez, A. 1996, Phys. Rev. E, 53, 5714 [NASA ADS] [CrossRef]
- Alastuey, A., Cornu, F., & Perez, A. 1994, Phys. Rev. E, 49, 1077 [NASA ADS] [CrossRef]
- Alastuey, A., Cornu, F., & Perez, A. 1995, Phys. Rev. E, 51, 1725 [NASA ADS] [CrossRef]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef]
- Asplund, M. Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, San Francisco, California, ed. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25
- Berrington, K. A. 1997, The Opacity Project, Vol. II (Bristol: Institute of Physics Publishing)
- Bollé, D. 1987, Phys. Rev. A, 36, 3259 [NASA ADS] [CrossRef] (In the text)
- Christensen-Dalsgaard, J., & Däppen, W. 1992, A&A, 4, 267 (In the text)
- Christensen-Dalsgaard, J., Däppen, W., & the GONG Team 1996, Science, 272, 1286 [NASA ADS] [CrossRef] (In the text)
- Cohen, E. G. D., & Murphy, T. J. 1969, Phys. Fluids, 12, 1404 [NASA ADS] [CrossRef] (In the text)
- Däppen, W. 2006, J. Phys. A: Math. Gen., 39, 4441 [NASA ADS] [CrossRef] (In the text)
- Däppen, W., & Mao, D. 2009, J. Phys. A: Math. Theor., 42, 214006 [NASA ADS] [CrossRef]
- Däppen, W., Mihalas, D., Hummer, D. G., & Mihalas, B. W. 1988, ApJ, 332, 261 [NASA ADS] [CrossRef]
- Ebeling, W., Kraeft, W. D., Kremp, D., 1976, Theory of Bound States and Ionization Equilibrium in Plasmas and Solids (Berlin, DDR: Akademie Verlag) (In the text)
- Eggleton, P. P., Faulkner, J., & Flannery, B. P. 1973, A&A, 23, 325 [NASA ADS] (In the text)
- Elliott, J. R., & Kosovichev, A. G. 1998, ApJ, 500, L199 [NASA ADS] [CrossRef] (In the text)
- Grevesse, N., Asplund, M. & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [NASA ADS] [CrossRef]
- Huang K. 1963, Statistical Mechanics (New York: John Wiley), Chapt. 14 (In the text)
- Hummer, D. G., & Mihalas, D. 1988, ApJ, 331, 794 [NASA ADS] [CrossRef]
- Iglesias, C. A., Rogers, F. J., & Wilson, B. G. 1987, ApJ, 322, L45 [NASA ADS] [CrossRef]
- Iglesias, C. A., & Rogers, F. J., 1991, ApJ, 371, 408 [NASA ADS] [CrossRef]
- Iglesias, C. A., & Rogers, F. J. 1993, ApJ, 412, 752 [NASA ADS] [CrossRef]
- Iglesias, C. A., & Rogers, F. J. 1995, ApJ, 443, 460 [NASA ADS] [CrossRef]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef]
- Kraeft W. D., Kremp D., Ebeling W., Röpke G., 1986, Quantum Statistics of Charged Particle Systems (New York: Plenum)
- Kremp D., Schlanges, M., Kraeft, W.-D., 2005, Quantum Statistics of Nonideal Plasmas (Springer: Berlin and Heidelberg)
- Liang, A., 2004, in Equation-of-State and Phase-Transition Issues in Models of Ordinary Astrophysical Matter, ed. V. Celebonovic, W. Däppen, & D. Gough, (New York: Melville), AIP Conf. Proc., 731, 106
- Liang, A., & Däppen, W. 2003, in Proc. SOHO 12/GONG+ 2002 Workshop (Noordwijk, The Netherlands), ESA SP-517, 333
- Meeron, E., 1958, J. Chem. Phys., 28, 630 [NASA ADS] [CrossRef]
- Mihalas, D., Däppen W., & Hummer, D. G. 1988, ApJ, 331, 815 [NASA ADS] [CrossRef]
- Nayfonov, A., Däppen, W., Hummer, D. G., & Mihalas, D. M. 1999, ApJ, 526, 451 [NASA ADS] [CrossRef]
- Perez, A., & Chabrier, G. 2004, in Equation-of-State and Phase-Transition Issues in Models of Ordinary Astrophysical Matter, ed. V. Celebonovic, W. Däppen, & D. Gough, (New York: Melville), AIP Conf. Proc., 731, 208 (In the text)
- Perez, A., & Däppen, W. 1995, in Proc. of Fourth SOHO Workshop Helioseismology (June 1995), ESA-SP-376, 15 (In the text)
- Rogers, F.J. 1986, ApJ, 310, 723 [NASA ADS] [CrossRef]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [NASA ADS] [CrossRef]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef]
- Seaton, M. J. 1995, The Opacity Project, Vol. I (Bristol: Institute of Physics Publishing)
- Starostin A., Roerich, V. C., & More, R. M. 2003, Contrib. Plasma Phys., 43, 369 [NASA ADS] [CrossRef]
- Trampedach, R., Däppen, W., & Baturin, V. A., 2006, ApJ, 646, 560 [NASA ADS] [CrossRef]
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm]{07713f01.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg25.png) |
Figure 1:
Illustration of the behavior of activity (solid line) and density expansions
(dashed line) for reacting systems, here for the simple reaction of neutral hydrogen H
recombining to hydrogen molecules |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f02.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg82.png) |
Figure 2: Coupling parameters for electrons, protons, and helium nuclei from the surface to the center of the Sun. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f03.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg83.png) |
Figure 3: Degeneracy parameter for electrons from the surface to the center of the Sun. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f04.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg84.png) |
Figure 4: Degeneracy parameter for protons from the surface to the center of the Sun. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f05.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg85.png) |
Figure 5: Degeneracy parameter for helium nuclei from the surface to the center of the Sun. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f06.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg86.png) |
Figure 6: Ionization degree of hydrogen from the surface to the center of the Sun. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f07.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg87.png) |
Figure 7: First ionization degree of helium from the surface to the center of the Sun. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f08.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg88.png) |
Figure 8: Second ionization degree of helium from the surface to the center of the Sun. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8.5cm]{07713f09.eps} %
\end{figure}](/articles/aa/full_html/2009/38/aa7713-07/Timg89.png) |
Figure 9: First and second ionization degree of oxygen (as a representative heavy element) from the surface to the center of the Sun. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



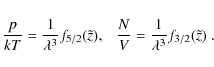
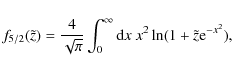
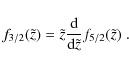
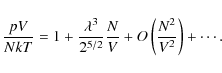
![\begin{displaymath}{p \over {kT}} = {1 \over {\lambda^3}}\left[{\tilde z} - {1 \over
{2^{5/2}}}{\tilde z}^2 + \cdots \right],
\end{displaymath}](/articles/aa/full_html/2009/38/aa7713-07/img16.png)
![\begin{displaymath}{N \over V} ={1 \over {\lambda^3}}\left[{\tilde z} - {1 \over
{2^{3/2}}}{\tilde z}^2 + \cdots \right].
\end{displaymath}](/articles/aa/full_html/2009/38/aa7713-07/img17.png)
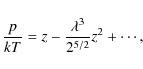
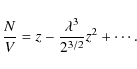
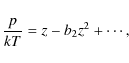
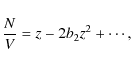
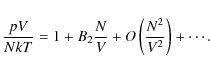
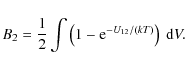
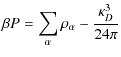
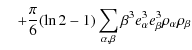


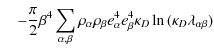
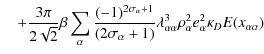

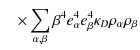
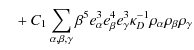
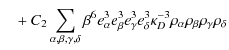
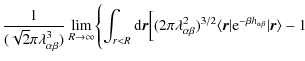
![$\displaystyle +{\beta e_{\alpha}e_{\beta} \over
r}-{\beta^{2}e_{\alpha}^{2}e_{\...
...ln \left({{3 \sqrt{2}R} \over {\lambda_{\alpha
\beta}}}\right)+C\right]\Biggr\}$](/articles/aa/full_html/2009/38/aa7713-07/img47.png)
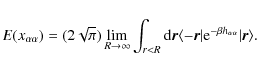
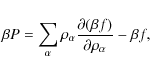
![\begin{displaymath}\sum_{n=1}^{\infty}n^2\Bigl[\exp(-\beta \epsilon_n^{\alpha
\beta})-1+\beta\epsilon_n^{\alpha \beta}\Bigr],
\end{displaymath}](/articles/aa/full_html/2009/38/aa7713-07/img65.png)