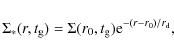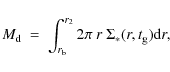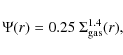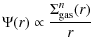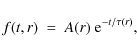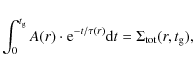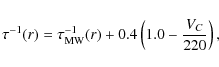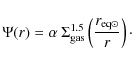| Issue |
A&A
Volume 505, Number 2, October II 2009
|
|
|---|---|---|
| Page(s) | 497 - 508 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912316 | |
| Published online | 03 August 2009 | |
Milky Way versus Andromeda: a tale of two disks
J. Yin1,5 - J. L. Hou1 - N. Prantzos2 - S. Boissier3 - R. X. Chang1 - S. Y. Shen1 - B. Zhang4
1 - Key Laboratory for Research in Galaxies and Cosmology,
Shanghai Astronomical Observatory, CAS, 80 Nandan Road, Shanghai,
200030, PR China
2 - CNRS, UMR7095, Institut d'Astrophysique de
Paris, 75014 Paris, France
3 - Laboratoire d'Astrophysique de
Marseille, BP8, Traverse du Siphon, 13376 Marseille Cedex 12,
France
4 - Department of Physics, Hebei Normal University, 113
Yuhua Dong Road, Shijiazhuang, 050016, PR China
5 -
Graduate School, the Chinese Academy of Sciences, Beijing,
100039, PR China
Received 10 April 2009 / Accepted 22 June 2009
Abstract
Aims. We study the chemical evolution of the disks of the Milky Way (MW) and of Andromeda (M 31), to identify the common properties and differences between the two major galaxies of the Local Group.
Methods. We use a large set of observational data for M 31, including observations of the star formation rate (SFR) and gas profiles, as well as stellar metallicity distributions along its disk. When expressed in terms of the corresponding disk scale lengths, we show that the observed radial profiles of MW and M 31 exhibit interesting similarities, suggesting the possibility of a description within a common framework.
Results. We find that the profiles of stars, gas fraction, and metallicity of the two galaxies, as well as most of their global properties, are well described by our model, provided that the star formation efficiency in M 31 disk is twice as high as in the MW. We show that the star formation rate profile of M 31 cannot be described by any form of the Kennicutt-Schmidt law (KS Law) for star formation. We propose that these discrepancies are caused by the fact that M 31 has an active star formation history in the recent past, consistent with the hypotheses of a ``head-on'' collision with the neighboring galaxy (most probably M 32) about 200 Myr ago.
Conclusions. The MW has most probably experienced quiescent secular evolution, making possible a fairly successful description with a simple model. If M 31 is more typical of spiral galaxies, more complex models, involving galaxy interactions, will be required for the description of spirals.
Key words: Galaxy: disk - Galaxy: formation - galaxies: evolution - Local Group - galaxies: individual: M 31 - galaxies: abundances
1 Introduction
Substantial progress has been made in understanding the evolution of disk galaxies in a cosmological context, both with analytical models (Mo et al. 1998; Efstathiou 2000) and with numerical simulations, by adopting much higher resolution and including more and more physical ingredients, such as dark matter profiles and assembly, baryon accretion histories, gas cooling and supernova feedback, and multi-phase interstellar medium (e.g., Cole et al. 2000; Samland & Gerhard 2003; Monaco 2004; Kang et al. 2005; Heller et al. 2007; Guo & White 2008; Roskar et al. 2008). However, the complexity of the relevant baryonic physics is not yet fully understood and no satisfactory disk model at present exists, although most recent simulations of high resolution and improved treatment about stellar feedback have succeeded in producing disks resembling observed ones (Governato et al. 2007; Mayer et al. 2008).
Because of those difficulties, the simple phenomenological models developed in the eighties and nineties may still be of considerable help. In those models, the complex processes related to disk formation through gas accretion (e.g., merging histories, gas cooling, stellar feedback) are simply described by an analytical infall law. These models do not construct the galaxy ``ab initio'' but rely on the observed present-day features of a galaxy to infer its past history, thus they have been characterized as ``backwards'' models (e.g., Ferreras & Silk 2001). They have been widely used in studies of the chemical evolution of the Milky Way (e.g., Matteucci & Francois 1989; Prantzos & Aubert 1995; Chiappini et al. 1997; Prantzos & Silk 1998; Boissier & Prantzos 1999; Chang et al. 1999, 2002; Cescutti et al. 2007 etc.) allowing important progress towards our understanding of our Galaxy's evolution. Some agreement has been reached among the various groups concerning e.g.,: i) the necessity of substantial infall on long timescales (to explain the local G-dwarf metallicity distribution and the small degree of astration of deuterium); ii) the necessity of radially varying timescales for the infall and the star formation rate (to obtain the observed profiles of metallicity, gas fraction, and colors); and iii) no need to vary IMF or strong galactic winds.
As one of the three disk galaxies in the Local Group, Andromeda (M 31 or NGC224) provides a unique opportunity for testing theories of galaxy formation and evolution (Klypin et al. 2002; Widrow et al. 2003; Widrow & Dubinski 2005; Geehan et al. 2006; Tamm et al. 2007; Tempel et al. 2007). The wealth of available data can be used to constrain models of the evolution of the disk, bulge and halo of M 31. However, because of its size, proximity and large bulge, most work has been completed on the stellar and kinematic properties of M 31 halo and globular clusters (Beasley et al. 2004; Burstein et al. 2004; Durrell et al. 2004; Chapman et al. 2006; Font et al. 2008; Koch et al. 2008; Lee et al. 2008), outer disk (Ibata et al. 2005; Irwin et al. 2005; Worthey et al. 2005; Brown et al. 2006, 2007, 2008; Richardson et al. 2008) and the central bulge (Jacoby & Ciardullo 1999; Salow & Statler 2004; Sarajedini & Jablonka 2005; Davidge et al. 2006; Olsen et al. 2006).
Star formation (SF) histories in various regions of the M 31 disk and
halo have also been measured with the Hubble Space Telescope (HST)
and ground-based large telescopes. For example, Williams (2003a,
b) has measured the star formation history in several regions of
the M 31 disk from the KPNO/CTIO Local Group survey and found that
the total mean star formation rate for the disk is about 1 ![]() yr-1. With deep HST photometry, Bellazzini et al. (2003) and
Worthey et al. (2005) studied the stellar abundance distributions
and star formation history in many locations of the disk (see also
Ferguson & Johnson 2001; Sarajedini & van Duyne 2001; Williams
2002; Brown et al. 2006; Olsen et al. 2006). Those observations
inferred that the M 31 disk has a mean disk age of around 6-8 Gyr and
mean metallicity of [Fe/H]
yr-1. With deep HST photometry, Bellazzini et al. (2003) and
Worthey et al. (2005) studied the stellar abundance distributions
and star formation history in many locations of the disk (see also
Ferguson & Johnson 2001; Sarajedini & van Duyne 2001; Williams
2002; Brown et al. 2006; Olsen et al. 2006). Those observations
inferred that the M 31 disk has a mean disk age of around 6-8 Gyr and
mean metallicity of [Fe/H] ![]() ,
albeit with substantial spread
in both cases.
,
albeit with substantial spread
in both cases.
Compared with the Milky Way, M 31 appears to have been more active in the past, although its current star formation rate is lower than that of our Galaxy. Based on a survey of spiral properties, Hammer et al. (2007) suggested that the Milky Way is a rather quiescent galaxy, atypical of its class, while the M 31 may be closer to a typical spiral. Using detailed two components (disk+halo) chemical evolution models, Renda et al. (2005) compared some chemical properties of the M 31 and MW disk/halo, and concluded that M 31 must have a higher star formation efficiency and/or shorter infall timescale. Deep photometry of the M 31 halo shows that it hosts populations of old and metal-poor stars, along with younger ones and of higher metallicity, pointing to a prolonged period of active merging (Brown 2009 and references therein). The two ring-like structures observed in M 31 (Block et al. 2006) are interpreted as the result of a recent (<200 Myr ago) collision with a companion galaxy (Block et al. 2006) and infer that M 31 has experienced recent merging.
In this paper, we attempt a comparative study of the chemical evolution of MW and M 31, by constraining our model with a more extended data set than in any previous work. Our data include global properties and radial profiles of gas, stars, gas fraction, star formation rate, and oxygen abundances, as well as stellar metallicity distributions along the disk of M 31 (Sect. 2). We find that, when the radial profiles are expressed in terms of the corresponding scalelengths of the stellar disks, the MW and M 31 present some interesting similarities (Sect. 2.4) encouraging us to adopt a single phenomenological model for the description of both galaxies (Sect. 3). The model describes fairly well all of the key properties of MW and most of M 31 (Sect. 4), provided the star formation efficiency is twice as large in the latter case. We discuss the successes and failures of the model, and we compare to previous work in Sect. 5. Section 6 summarizes our results.
2 Observational properties
2.1 Stellar disks: scalelengths and masses
The stellar disks of Milky Way and M 31 are well described by
exponential surface density profiles, given by
where
where
Observed disk scalelengths are obtained from measurements of
surface brightness profiles in various wavelength bands and are
wavelength dependent. A B band scalelength reflects mostly the SFR
profile in the past ![]() 1 Gyr, while K or R scalelengths
reflect the total stellar population, cumulated over the age of the
disk.
1 Gyr, while K or R scalelengths
reflect the total stellar population, cumulated over the age of the
disk.
For the Milky Way disk, we adopt the mean value of
![]() kpc (from measurements in the R or I bands), derived from the
compilation of Hammer et al. (2007). The total mass up to 15 kpc is then
kpc (from measurements in the R or I bands), derived from the
compilation of Hammer et al. (2007). The total mass up to 15 kpc is then ![]()
![]()
![]() .
.
By adding ![]()
![]()
![]() for the gaseous disk mass
(as estimated in the next section) one derives a total baryonic disk
mass of
for the gaseous disk mass
(as estimated in the next section) one derives a total baryonic disk
mass of ![]()
![]()
![]() ,
in good agreement with mass
models of the Milky Way (e.g., Dehnen & Binney 1998; Naab &
Ostriker 2006).
,
in good agreement with mass
models of the Milky Way (e.g., Dehnen & Binney 1998; Naab &
Ostriker 2006).
Based on the observed disk surface brightness of M 31, Walterbos &
Kennicutt (1987, 1988) measured the disk scalelength at different wavelengths. They obtained
![]() ,
5.8, 5.3, and 5.2 kpc in the U,B,V, and R bands, respectively. Worthey et al. (2005) obtained 5.6 kpc in the I band, while for K band Hiromoto et al. (1983) found
,
5.8, 5.3, and 5.2 kpc in the U,B,V, and R bands, respectively. Worthey et al. (2005) obtained 5.6 kpc in the I band, while for K band Hiromoto et al. (1983) found
![]() kpc. With IRAC onboard the SPITZER space telescope, Barmby et al. (2006) measured, for the first time, the mid-infrared surface brightness profile of M 31 and found a scalelength of 6.08 kpc in the L band. We note that different authors adopt different distance scales for M 31. In Table 1, we list all the available observed disk scalelengths and scale them to the
same distance of 785 kpc (McConnachie et al. 2005). Overall, the
values are consistent for different bands, except at shorter
wavelengths that are likely to be affected by dust extinction. In
this paper, we adopt an averaged value from four observed values
from three bands (R, I, K), which is
kpc. With IRAC onboard the SPITZER space telescope, Barmby et al. (2006) measured, for the first time, the mid-infrared surface brightness profile of M 31 and found a scalelength of 6.08 kpc in the L band. We note that different authors adopt different distance scales for M 31. In Table 1, we list all the available observed disk scalelengths and scale them to the
same distance of 785 kpc (McConnachie et al. 2005). Overall, the
values are consistent for different bands, except at shorter
wavelengths that are likely to be affected by dust extinction. In
this paper, we adopt an averaged value from four observed values
from three bands (R, I, K), which is
![]() kpc. This value is
within the range of
kpc. This value is
within the range of
![]() kpc found in Hammer et al.
(2007).
kpc found in Hammer et al.
(2007).
The total mass of M 31 disk is obtained from observational data and
mass models. In their disk-bulge-halo model, Widrow et al. (2003)
found that their best-fit model requires the M 31 disk mass (stars +
gas) to be about
![]()
![]() .
The mass model of Geehan
et al. (2006) also infers a similar disk mass of
.
The mass model of Geehan
et al. (2006) also infers a similar disk mass of ![]()
![]()
![]() ,
by adopting a disk mass-to-light ratio of 3.3. In
this paper, we adopt the M 31 total disk mass of
,
by adopting a disk mass-to-light ratio of 3.3. In
this paper, we adopt the M 31 total disk mass of
![]()
![]() .
By subtracting a gas mass of
.
By subtracting a gas mass of ![]()
![]()
![]() (see next section), we obtain a total disk stellar mass
of
(see next section), we obtain a total disk stellar mass
of
![]()
![]() for Andromeda.
for Andromeda.
In summary, the M 31 disk is about 2 times as massive and 2.4 times as large as the Milky Way disk.
Table 1: Observation of Milky Way and M 31 (re-scaled to 785 kpc).
2.2 Gas and SFR profiles
The present-day profiles of gas and star formation provide strong
constraints on models of the chemical evolution of a galactic disk.
In the case of the Milky Way, relevant observational data were
collected in Boissier & Prantzos (1999), and we adopt those data in this work (Fig. 1, left panels). The gaseous profile is
characterized by a broad peak at a galactocentric distance ![]() 4-5 kpc (caused by the ``molecular ring'' present at this distance) and
the SFR profile is also concentrated towards the inner disk. The
total gas mass is estimated to be
4-5 kpc (caused by the ``molecular ring'' present at this distance) and
the SFR profile is also concentrated towards the inner disk. The
total gas mass is estimated to be ![]()
![]()
![]() and the
total star formation rate is SFR
and the
total star formation rate is SFR ![]() 1-3
1-3 ![]() yr-1 (e.g., Boissier &
Prantzos 1999, and references therein).
yr-1 (e.g., Boissier &
Prantzos 1999, and references therein).
For M 31, the observed radial profiles for HI and H2 gas surface densities (Berkhuijsen 1977; Walterbos 1986; Koper et al. 1991; Loinard et al. 1999) allow us to establish the radial gas profile displayed in Fig. 1 (right top). It is also characterized by a broad peak, located at a galactocentric distance twice as large as in the case of the MW. The HI profile from these studies is also consistent with the one measured by Chemin et al. (2009).
The star formation rate in several regions of M 31 disk has been
carefully measured by both ground-based photometry and Hubble Space
Telescope (Bellazzini et al. 2003; Williams 2002, 2003a,b; Brown et al. 2006; Olsen et al. 2006). The current total SFR of the M 31 disk
is estimated to be
![]()
![]() yr-1 (Williams 2003a,b; Barmby et al. 2006), i.e., less than half of the value in the Milky Way disk; this shows that M 31 is currently a rather quiescent galaxy.
yr-1 (Williams 2003a,b; Barmby et al. 2006), i.e., less than half of the value in the Milky Way disk; this shows that M 31 is currently a rather quiescent galaxy.
By analyzing data from the GALEX UV satellite, it is now possible to
obtain SFR radial profiles for a number of local galaxies derived
not from H![]() data, but from the UV continuum (Boissier et al.
2007). In Fig. 1, we show the adopted gas
(upper panels) and SFR (lower panels) profiles of the Milky Way and
M 31 disks. From this figure, we see that the two spirals have quite
different properties in their gas and SFR profiles in the inner part
of the disk (between 3 and 7 kpc). The Milky Way has more gas in
this region, while M 31 has most of its gas outside that region.
data, but from the UV continuum (Boissier et al.
2007). In Fig. 1, we show the adopted gas
(upper panels) and SFR (lower panels) profiles of the Milky Way and
M 31 disks. From this figure, we see that the two spirals have quite
different properties in their gas and SFR profiles in the inner part
of the disk (between 3 and 7 kpc). The Milky Way has more gas in
this region, while M 31 has most of its gas outside that region.
The total gas mass of the disks is obtained by integrating the gas
profiles from Fig. 1 for both galaxies,
starting from the inner disk boundary (assumed to be at the bulge
radius
![]() kpc for the MW and
kpc for the MW and
![]() kpc for M 31)
outwards. We find
kpc for M 31)
outwards. We find
![]()
![]() and
and
![]()
![]() (average value, taking
uncertainties into account). Since the M 31 disk is twice as massive
as the Milky Way disk, its global gas fraction is about 1/2 that of
the Milky Way disk (0.09 versus 0.19, respectively). This implies
that the disk of M 31 had an overall higher star formation efficiency
than the Milky Way (assuming that they have similar ages).
(average value, taking
uncertainties into account). Since the M 31 disk is twice as massive
as the Milky Way disk, its global gas fraction is about 1/2 that of
the Milky Way disk (0.09 versus 0.19, respectively). This implies
that the disk of M 31 had an overall higher star formation efficiency
than the Milky Way (assuming that they have similar ages).
![\begin{figure}
\par\includegraphics[width=8.8cm]{12316fg1.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg55.png) |
Figure 1: Observed profiles of the gas and star formation rate for the Milky Way and M 31 disks. Upper panel: current surface density profiles of HI, molecular gas, and total gas in the Milky Way and M 31. Lower panel: observed estimations of SFR of the Milky Way (filled symbols, from Boissier & Prantzos 1999) and M 31 disks (open symbols from Boissier et al. 2007). The lines in the lower panels are the results calculated according to the star formation law given in the right panel. |
| Open with DEXTER | |
UV studies of star formation with GALEX have shown that, in general,
the correlation between SFR and gas surface density is compatible
with empirical Kennicutt (1998a,b) SFR laws, with some scatter at low surface densities. However, as Boissier et al. (2007) show, this correlation fails for some individual galaxies, and especially for
M 31 (see their Fig. 6). In the lower two panels of Fig. 1, we also show the expected behaviour
of two different SFR laws. The first depends only on gas surface
density, according to
on the basis of the observational data of Kennicutt (1998b, hereafter KS Law). The second depends on both gas surface density and radius and is motivated by the idea that star formation is induced by spiral waves moving around a rotating disk (e.g., Wyse & Silk 1989, see also Sect. 3.2):
For the MW disk, the observed gas and SFR profiles are found to be reproduced well by both SFR laws; as a result, the total SFR is also readily reproduced. However, for M 31, none of the SFR laws brings agreement between observed gas and SFR profiles: there is a great difference between theoretical expectations and observations in the inner part of the disk (with little gas but, curiously, high observed SFR). As a result, any attempt to fit the SFR of the inner disk with one of the aforementioned SFR laws will lead to an overestimate of the SFR in the outer disk.
![\begin{figure}
\par\includegraphics[width=8.8cm]{12316fg2.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg58.png) |
Figure 2: Relationship between observed gas surface density and star formation rate surface density for M 31 (filled circles) and Milky Way disks (filled triangles). Full line is the classical Kennicutt law (Eq. (3)). Regions between two dashed lines indicate the results for a number of local galaxies observed by GALEX (from Boissier et al. 2007). The M 31 shows an untypical path in its inner region, while the Milky Way shows a rather normal behaviour. |
| Open with DEXTER | |
To demonstrate further the different behaviour of local star formation rate in M 31 and Milky Way disks, we plot the relationship between the observed gas surface density and star formation rate surface density in Fig. 2. We also show the general trend of SFR with gas surface density (within dashed curves) for a number of nearby galaxies (from Boissier et al. 2007). It is clear that M 31 has a peculiar behaviour compared to both the Milky Way and other local galaxies, especially in its inner region, where high star formation rate corresponds to low amount of gas. In the range 7-11 kpc, the SFR decreases as the gas surface density increases, in contrast to the classical SFR law. Beyond 11 kpc, both SFR and amount of gas decrease with radius, roughly in agreement with the Kennicutt law.
If observations of SFR in M 31 are not heavily distorted by incorrect extinction corrections, then one may conclude that the current SFR in that galaxy does not obey one of the classical star formation laws (Schmidt, Kennicutt, or some modified form of them). Star formation in M 31 is maybe(or has been) perturbed by some external event, e.g., a major recent encounter with a galaxy of the Local Group. Observations of a two-ring-like structures by Block et al. (2006) are interpreted as evidence that a nearly central head-on encounter with a companion galaxy (probably M 32) occurred about 200 Myr ago. If this is indeed the case, then the present day SFR profile of M 31 cannot be used as a constraint on the chemical evolution model, since the perturbation induced in the gaseous disk by the collision most probably affected, for (at least) one orbital time, the SFR in M 31. Time-integrated observable, such as e.g., the total stellar profile or the abundance profile (and, to a lesser extent, the gaseous profile) certainly remain valid constraints.
2.3 Disk abundance gradients
Abundance gradients are an essential ingredient in an accurate
picture of galaxy formation and evolution (Boissier & Prantzos
1999; Hou et al. 2000; Chiappini et al. 2001; Hou et al. 2002;
Cescutti et al. 2007; Magrini et al. 2009; Fu et al. 2009). The
existence of abundance gradients along the MW disk has been
established using different tracers (Hou & Chang 2001). However,
the size of this gradient is still debated. Thus, oxygen or/and iron
abundance gradients of between about -0.06 and ![]() -0.07 dex kpc-1 are obtained by using tracers as HII regions and B stars
(Rudolph et al. 2006 and references therein), planetary nebulae
(Maciel et al. 2006; Maciel & Costa 2008), and open clusters (Chen et al. 2003, 2008). However, values about 40% smaller are obtained
by using those same tracers, e.g., Deharveng et al. (2000, with HII regions), Daflon & Cunha (2004, using several tracers), and Andrievsky et al. (2004, with Cepheids).
-0.07 dex kpc-1 are obtained by using tracers as HII regions and B stars
(Rudolph et al. 2006 and references therein), planetary nebulae
(Maciel et al. 2006; Maciel & Costa 2008), and open clusters (Chen et al. 2003, 2008). However, values about 40% smaller are obtained
by using those same tracers, e.g., Deharveng et al. (2000, with HII regions), Daflon & Cunha (2004, using several tracers), and Andrievsky et al. (2004, with Cepheids).
The situation for the abundance gradient in the disk of M 31 is also
far from clear. Early observations (Dennefeld & Kunth 1981; Blair et al. 1982) used HII regions and supernova remnants. A value of
dlog(O/H)/dr =
![]() dex kpc-1 was derived using nebular
emission line ratios by Galarza et al. (1999). The main uncertainty
originates in the empirical calibrations used to derive the
electronic temperatures in the nebular phase. By reanalysing earlier
data from various authors, Trundle et al. (2002) found smaller
values for the oxygen abundance gradient, ranging from -0.027 dex kpc-1 down to -0.013 dex kpc-1. Furthermore, their analysis of
five B-type supergiants covering the galactocentric distances of
5-12 kpc inferred to a negligible oxygen abundance gradient of
dex kpc-1 was derived using nebular
emission line ratios by Galarza et al. (1999). The main uncertainty
originates in the empirical calibrations used to derive the
electronic temperatures in the nebular phase. By reanalysing earlier
data from various authors, Trundle et al. (2002) found smaller
values for the oxygen abundance gradient, ranging from -0.027 dex kpc-1 down to -0.013 dex kpc-1. Furthermore, their analysis of
five B-type supergiants covering the galactocentric distances of
5-12 kpc inferred to a negligible oxygen abundance gradient of
![]() dex kpc-1; in contrast, they found a slightly more
significant gradient for Mg, of
dex kpc-1; in contrast, they found a slightly more
significant gradient for Mg, of
![]() dex kpc-1.
dex kpc-1.
In summary, the abundance gradient in M 31 is very poorly known at
present. We adopt here a value of -0.017 dex kpc-1, i.e., the mean
between the most extreme values of -0.027 dex kpc-1, and -0.006 dex kpc-1 found in the various analysis of Trundle et al. (2002). We
note that this value is substantially smaller (factor 3-4) than that
of the Milky Way disk (-0.07 dex kpc-1), but only by a factor of 2
if the value of -0.04 dex kpc-1 is adopted for our Galaxy.
Finally, if we express the abundance gradients in terms of
corresponding scalelengths (dex/![]() ), then the scaled gradient of
M 31 disk is found to be two times smaller (equal) than that of the
MW disk for the cases of -0.07 dex kpc-1 (-0.04 dex kpc-1).
), then the scaled gradient of
M 31 disk is found to be two times smaller (equal) than that of the
MW disk for the cases of -0.07 dex kpc-1 (-0.04 dex kpc-1).
![\begin{figure}
\par\includegraphics[height=9cm,width=9cm]{12316fg3.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg62.png) |
Figure 3: Observed oxygen abundance gradient in the Milky Way ( top, data from Rudolph et al. 2006; Deharveng et al. 2000) and M 31 ( bottom, data from Dennefeld & Kunth 1981; Blair 1982; Trundle et al. 2002). In the top panel, the two commonly referred values of -0.07 dex kpc-1and -0.04 dex kpc-1appear as dashed and solid line respectively. |
| Open with DEXTER | |
Figure 3 displays the observed oxygen abundance profiles in the Milky Way and M 31 disks. In the case of MW, two values of the gradient are shown, corresponding to -0.07 dex kpc-1 (circles) and -0.04 dex kpc-1 (solid line), respectively.
2.4 A unified description of the Milky Way and M 31
Table 1 summarizes the main observational features of the MW and M 31 disks. The different sizes of the two major galaxies of the Local Group ensure that a direct comparison between their radial profiles is difficult, thus giving no information about the physical ingredients required to describe successfully both disks. To obtain a coherent picture, we attempt here a more physical description, by expressing all distances in terms of the corresponding disk scalelengths.
![\begin{figure}
\par\includegraphics[height=14cm,width=18cm]{12316fg4.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg63.png) |
Figure 4:
Observed profiles for Milky Way and M 31 disks, with radius expressed in units of the corresponding scalelengths |
| Open with DEXTER | |
In Fig. 4, we plot the radial profiles of gas, star, SFR, gas fraction, and the oxygen abundance gradients for the two disks, using their scalelengths as distance units. It can be seen that:
- (1)
- the gaseous profiles (top left) are rather similar, in the sense
that they both display a broad peak at
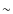 2 scalelengths from
their centers. The MW has a more extended gaseous profile (in terms
of scalelength);
2 scalelengths from
their centers. The MW has a more extended gaseous profile (in terms
of scalelength);
- (2)
- the Milky Way disk is more compact than M 31, since it has a
higher stellar surface density at a given
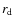 value (middle left).
value (middle left).
- (3)
- The profiles of scaled gas fractions (middle right) of the two
galaxies are quite similar in the inner disks. However, the overall
gas fractions of the two disks are quite different, the MW having a
gas fraction that is twice as high as that of M 31;
- (4)
- the scaled abundance gradients between the two disks are similar if we adopt the smaller reported value for the MW disk (bottom left).
3 The model
In the case of the Milky Way, models with radially dependent infall and star formation laws, forming the disk inside-out, are generically used (Prantzos & Aubert 1995; Boissier & Prantzos 1999; Hou et al. 2000; Chiappini et al. 2001; Magrini et al. 2009). These models reproduce several of the salient observational features of the MW disk (including the abundance gradients), albeit with different levels of success.
In this section, we present briefly our chemical evolution model that is similar to the one adopted successfully in the past for the Milky Way disk (see details in Boissier & Prantzos 1999, 2000; Hou et al. 2000).
3.1 IMF and stellar yields
The initial mass function (IMF) ![]() describes the mass
distribution of newborn stars and can be inferred from the observed
luminosity function on the basis of the mass-to-light ratio for
stars. Similar to our previous works, we adopt the IMF from the work
of Kroupa et al. (1993, KTG93), where some complex factors
(such as stellar binarity, ages, and metallicities, as well as
mass-luminosity and colour-magnitude relationships) are explicitly
taken into account (Boissier & Prantzos 1999, 2000; Hou et al. 2000).
describes the mass
distribution of newborn stars and can be inferred from the observed
luminosity function on the basis of the mass-to-light ratio for
stars. Similar to our previous works, we adopt the IMF from the work
of Kroupa et al. (1993, KTG93), where some complex factors
(such as stellar binarity, ages, and metallicities, as well as
mass-luminosity and colour-magnitude relationships) are explicitly
taken into account (Boissier & Prantzos 1999, 2000; Hou et al. 2000).
Stellar yields are taken from Woosley & Weaver (1995, WW95) for
massive stars, and from van den Hoek & Groenewegen (1997, vdHG97) for low and intermediate mass stars (mass from 0.8 to 8 ![]() ). They
are all metallicity dependent.
). They
are all metallicity dependent.
To account for the additional source of Fe-peak elements, required
to explain the observed decline in the O/Fe abundance ratio (with
increasing metallicity) in the Milky Way disk (Goswami & Prantzos
2000), we utilize the yields of SNIa from the exploding Chandrashekhar-mass CO white dwarf models W7 and W70 of Iwamoto et al. (1999). These are updated versions of the original W7 model of Thielemann et al. (1986), calculated for metallicities Z = ![]() (W7) and Z = 0 (W70), respectively.
(W7) and Z = 0 (W70), respectively.
3.2 Infall rate and timescale
We assume that the MW and M 31 disks are progressively built up by
the infall of cooling primordial gas from their dark haloes. The
form of the time dependence of the infall rate is unknown at present. In Prantzos & Silk (1998), an asymmetric Gaussian infall rate was assumed, on the basis of dynamical arguments. However, simpler parametrizations usually are adopted, i.e., the infall rate
decreases exponentially with time
where A(r) is a normalizing function and can be obtained by
where
The radial dependence of the infall timescale for the MW disk is
given by
![]() ,
where
,
where ![]() is the scalelength and
b is a free parameter. Positive values of b imply an inside-out
formation of the disk and we adopt here b = 2.5, which infers
formation timescales of
is the scalelength and
b is a free parameter. Positive values of b imply an inside-out
formation of the disk and we adopt here b = 2.5, which infers
formation timescales of ![]() 2 Gyr for the inner disk and
2 Gyr for the inner disk and ![]() 10 Gyr for the outer disk.
10 Gyr for the outer disk.
In the case of M 31, we adopt the prescription used in Boissier &
Prantzos (2000), according to which the infall timescale is assumed to be correlated with both surface density and galaxy mass
where VC (in km s-1) is the flat rotational velocity for the galaxy disk and
3.3 Star formation
The star formation rate remains the major unknown in chemical
evolution studies. Kennicutt (1998a,b) found that the global SFR of disks and circumnuclear starburst galaxies is correlated with the
local gas density over a wide range of surface density and SFR per
unit area, spanning 5 orders in magnitude. Over that range, the
empirical SFR versus gas surface density relation can be fitted by a
simple power law with index
![]() .
Kennicutt (1998a,b) also found that the data can be reproduced equally well as a function of
the local dynamical timescale
.
Kennicutt (1998a,b) also found that the data can be reproduced equally well as a function of
the local dynamical timescale
![]() by
by
![]() ,
where
,
where ![]() is the rotation speed of the gas. Since
is the rotation speed of the gas. Since
![]() ,
the SFR could be expressed as
,
the SFR could be expressed as
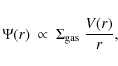 |
(8) |
where V(r) is the circular velocity at radius r. Since spiral galaxies follow the relation
Boissier & Prantzos (1999) adopted the index n of the M-KS SFR
law to be n=1.5 on an empirical basis, to derive the present day
profiles of the MW SFR (Fig. 1, bottom left). They also adopted this
M-KS law in subsequent models for external spirals, which can
successfully reproduce most of the chemical and photometric
properties of disk galaxies (Boissier & Prantzos 2000; Boissier et al. 2001) and in particular the observed abundance gradients (Prantzos & Boissier 2000). Fu et al. (2009) used both the KS law and M-KS law to predict the time evolution of the Galactic disk abundance gradient. By comparing the model predictions with the
observed results from open clusters and planetary nebulae with
different ages, they concluded that by adopting the M-KS law, model
results are more consistent with the observed evolution of abundance
gradient. Therefore, we adopt this M-KS law for Milky Way and M 31
disks:
The coefficient
Table 2: Model parameters.
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm]{12316fg5.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg87.png) |
Figure 5:
Current profiles of gas, stars, SFR, gas fraction, and oxygen abundance ( from top to bottom) for MW and M 31. In the left and middle panels, profiles for MW and M 31, respectively, are expressed in terms of physical radius r (in kpc); in the right panels, profiles for both disks are expressed in terms of normalised radius
|
| Open with DEXTER | |
4 Model results and comparison with both the Milky Way and M 31 disks
We run our simulations with the parameters of Table 2 for the MW and
M 31 disks. We note that we adopt the same model parameters for both
galaxies, hence attempt to describe them in a unified framework,
except for: (i) the small difference in their infall rate from Eq. (7), which infers that M 31 is slightly older than the MW;
and (ii) the star formation efficiency parameter ![]() ,
assumed
here to be twice as large for M 31 as for the MW, i.e.,
,
assumed
here to be twice as large for M 31 as for the MW, i.e.,
![]() and
and
![]() .
.
4.1 Radial profiles
In Fig. 5, we show the model predictions of the
radial profiles for gas, stars, SFR, gas fraction, and oxygen at
time t = 13.5 Gyr, and we compare them with observational data. The
first two columns display results for MW and M 31, respectively, as a
function of radius r expressed in kpc. The third column presents
the same results on a common scale of normalized radius
![]() for
both galaxies; this allows us to visualize the similarities and
differences between the two disks more clearly.
for
both galaxies; this allows us to visualize the similarities and
differences between the two disks more clearly.
The main results of the comparison with observations can be summarized as follows:
- 1)
- In both cases, exponential disk profiles are naturally obtained,
since most of the infalling gas (the radial profile of which is
normalised by means of Eq. (6)) is converted into stars.
- 2)
- The model gaseous profiles reach a broad maximum, attained at the
observed position, approximately at two scalelengths from the
galactic centers. This maximum is obtained in the models by means of
the radial dependence of the SF efficiency (being greater in the
inner disk, it produces a gas fraction profile
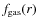 that
increases with radius, see next paragraph) and the total surface
density profile
that
increases with radius, see next paragraph) and the total surface
density profile
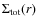 ,
which is constrained to decrease
with radius. The gaseous profile is the product of the two , i.e.,
,
which is constrained to decrease
with radius. The gaseous profile is the product of the two , i.e.,
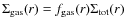 ,
so the resulting curve
goes through a maximum, and within our unified scheme this happens
at
,
so the resulting curve
goes through a maximum, and within our unified scheme this happens
at 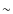 2
2 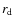 .
.
![\begin{figure}
\par\includegraphics[height=10cm,width=9cm]{12316fg6.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg93.png)
Figure 6: Time evolution of global gas, star, gas fraction, infall rate, and SFR in M 31 and Milky Way disks. The disk parameters are given in Table 2, and the coefficients
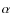 of SFR in Table 2 for the Milky Way and M 31 disks are
of SFR in Table 2 for the Milky Way and M 31 disks are
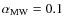 ,
,
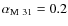 ,
respectively. Infall timescale is
,
respectively. Infall timescale is
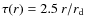 .
Bar in the right of each plot gives the observed estimations.
It can be seen that the model predicts too high a present value of SFR
for M 31 disk.
.
Bar in the right of each plot gives the observed estimations.
It can be seen that the model predicts too high a present value of SFR
for M 31 disk. Open with DEXTER - 3)
- The gas fraction profile decreases monotonically inwards, in
perfect agreement with observations for the MW and in fair agreement
for the inner disk of M 31. The model predicts slightly higher than
observed gas fractions only for the outer disk of M 31. We note that,
in terms of normalized radius
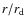 ,
the gas fraction profiles of
the two disks are very similar, which explains their successful
description by our unified model. We also note that, in terms of
physical radius, M 31 has a smaller gas fraction than the MW at
a given r, which explains the need for a higher SF efficiency in
that case. The situation is less satisfactory in the outer disk of
M 31, where the gas fraction is overestimated by our model.
,
the gas fraction profiles of
the two disks are very similar, which explains their successful
description by our unified model. We also note that, in terms of
physical radius, M 31 has a smaller gas fraction than the MW at
a given r, which explains the need for a higher SF efficiency in
that case. The situation is less satisfactory in the outer disk of
M 31, where the gas fraction is overestimated by our model.
- 4)
- Our model predicts correctly the present day SFR profile of MW,
but fails completely in the case of M 31, and in particular in the
outer disk of M 31. As already noticed (Sect. 2.2) the observed SFR
versus gas relationship in M 31 cannot be reproduced by any form of
the KS laws. Our result reflects just this impossibility. As already
argued (last paragraph of Sect. 2.2), we believe that the observed
SFR is affected by recent perturbations of the gaseous disk of M 31,
e.g., the collision with a nearby galaxy suggested by Block et al.
(2006).
![\begin{figure}
\par\includegraphics[height=10cm,width=9cm]{12316fg7.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg94.png)
Figure 7: The metallicity distribution functions of various regions in the Milky Way and M 31 disks. The observed data in the solar neighborhood of the Milky Way disk come from Holmberg et al. (2007) and Chang et al. (1999), and the data of M 31 come from Worthey et al. (2005). The model predictions are plotted as smooth curves, after convolution with a Gaussian error function with
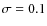 dex (full lines)
and 0.3 dex (dashed lines). For M 31, we construct metallicity distributions for the age-range of RGB stars observed by Worthey et al. (2005) (stellar ages between 6 and 12 Gyr).
dex (full lines)
and 0.3 dex (dashed lines). For M 31, we construct metallicity distributions for the age-range of RGB stars observed by Worthey et al. (2005) (stellar ages between 6 and 12 Gyr). Open with DEXTER - 5)
- The resulting abundance gradients are compatible with observations for both MW and M 31. The predicted abundance profile of MW is somewhat steeper than in the case of M 31, which is not a surprise because the two disks do not have the same scale. At the same distance from the galactic center, they have different amounts of gas and SFRs. As a result of its larger scalelength, the gas is presently more wide spread in M 31 than in the Milky Way, its a resulting gas fraction rising less steeply in Andromeda, producing correspondingly a flatter abundance gradient. When we express the model abundance gradient in terms of their scalelengths, we obtain similar value for the two disks. In any case, taking into account all the uncertainties mentioned in Sect. 2.3, we consider the overall agreement as satisfactory. Further observations will hopefully establish the true abundance profiles of MW and M 31 with greater accuracy, and perhaps allow us to develop different prescriptions for our unified model.
4.2 Infall and star formation history
In Fig. 6, we show the evolution of the total
amount of gas, stars, SFR, and infall rate, and of the gas fraction
for the disks of MW and M 31. Reasonable agreement with observations
is obtained for all those quantities in the case of MW disk; this
agreement results from the adopted normalization of the total disk
mass and the adopted star formation efficiency. In the case of M 31,
the model predicts a current global SFR![]() 2.0
2.0 ![]()
![]() ,
which is substantially higher than observational estimates
(Williams 2003a,b; Barmby et al. 2006). In view of the discussion in
Sect. 2.2, we do not consider this discrepancy as being significant:
star formation in M 31 may have been perturbed considerably by
external effects (i.e., collision with another galaxy), which are
unaccounted for in our model. We also note that the current infall
rate is poorly constrained for MW and virtually unconstrained for
M 31. In the case of M 31, Thilker et al. (2004) found that an
extensive population of HI clouds exists in the outskirts of the
galaxy. The values displayed in Fig. 6 are in the range of 0.2-2
,
which is substantially higher than observational estimates
(Williams 2003a,b; Barmby et al. 2006). In view of the discussion in
Sect. 2.2, we do not consider this discrepancy as being significant:
star formation in M 31 may have been perturbed considerably by
external effects (i.e., collision with another galaxy), which are
unaccounted for in our model. We also note that the current infall
rate is poorly constrained for MW and virtually unconstrained for
M 31. In the case of M 31, Thilker et al. (2004) found that an
extensive population of HI clouds exists in the outskirts of the
galaxy. The values displayed in Fig. 6 are in the range of 0.2-2 ![]()
![]() ,
the former being the typical value inferred from
observations of accreting cold gas in disks (Sancisi et al. 2008)
and the latter from a simple theoretical argument, namely that these
values are required to maintain a quasi-constant SFR over disk
history for MW-size disks.
,
the former being the typical value inferred from
observations of accreting cold gas in disks (Sancisi et al. 2008)
and the latter from a simple theoretical argument, namely that these
values are required to maintain a quasi-constant SFR over disk
history for MW-size disks.
4.3 Metallicity distributions
We now compare the model metallicity distribution functions (MDFs)
with available observations for various regions of the Milky Way and
M 31 disks. The model results correspond to main sequence stars with
lifetimes ![]() Gyr, and they have been convolved with Gaussian
error functions with
Gyr, and they have been convolved with Gaussian
error functions with
![]() dex (Fig. 7).
dex (Fig. 7).
For the Milky Way disk, the observed data in the solar neighborhood are from the GK survey (Holmberg et al. 2007, who revised estimates in Nordström et al. 2004), which includes ages, metallicity, and kinematic properties for about 14 000 F and G dwarfs. MDFs in other regions are unavailable at present, but future surveys, e.g., SDSS/SEGUE (Ivezic et al. 2008) and China's LAMOST project (Zhao et al. 2006), are also expected to provide information on those regions. As expected (from the adopted infall rate) our model fits rather well, albeit not perfectly, the local MDF. We note that we compare with the data of Holmberg et al. (2007) corrected for the scale height of stellar populations (dashed curve in their Fig. 22, right panel): indeed, our results concern the full extent of the so-called ``solar cylinder'' at 8 kpc from the Galactic center, while local surveys are complete only within a limited volume centered on the Sun. However, the corrections in Holmberg et al. (2007) are made after some assumptions about the star formation history of the local disk, which is not necessarily the same as the SF history in our model. Thus, it should not be surprising that the fit is not perfect.
In the case of M 31, data are available for the MDF in various places
along its disk (Bellazzini et al. 2003; Worthey et al. 2005; Chapman
et al. 2006). Right panel histograms are results from Worthey et al. (2005), who observed 11 regions from the inner regions to the outer
disk along the major axis of M 31. The median abundances in each
observed field increase steadily from the inner to the outer disk.
The mean stellar metallicity is ![]() 0.2 dex lower than the
gas-phase abundance (Fig. 3) in the same
location.
0.2 dex lower than the
gas-phase abundance (Fig. 3) in the same
location.
In the right panels of Fig. 7, we also present the model predictions for the MDFs in the same radial positions as the data available for M 31. Our results are in broad agreement with observations and they reproduce the decrease of mean stellar metallicity with radius, as a consequence of the star formation and infall schemes adopted for the disk. We conclude then that, to a first approximation, M 31 evolved inside-out, as expected for a normal spiral. Despite this, rather satisfactory agreement, between the data and our model, we would like to emphasize the need for more data on the MDFs of M 31 as a function of radial position in order to further constrain the evolution of its disk.
We note that when plotting the model-predicted MDFs for M 31 disk, we
have assumed an error about of 0.1 dex based on Worthey et al.
(2005). This assumption is self-consistent with observations since
we used the data from Worthey et al. (2005). However, this adopted
error in the photometric metallicity may be too small because we
know that even for the situation of the halo, where the age spread
should be smaller than in the disk (and associated uncertainties
lower) a comparison of spectroscopic and photometric metallicities
for RGB stars in M 31 should scatter about ![]() 0.3 dex (see Kalirai
et al. 2008). Therefore, we also indicate the model MDFs for the M 31
disk with photometric errors of 0.3 dex by dashed lines in
Fig. 7. As expected, the model-predicted MDFs are wider
than the observed distributions in this case, but the peak position
is roughly the same.
0.3 dex (see Kalirai
et al. 2008). Therefore, we also indicate the model MDFs for the M 31
disk with photometric errors of 0.3 dex by dashed lines in
Fig. 7. As expected, the model-predicted MDFs are wider
than the observed distributions in this case, but the peak position
is roughly the same.
We emphasize that while calculating the models, the results are for disk evolution with full star formation history, that is, includes all stars in the disk with all ages. Worthey et al. (2005) did not discuss the age spread in detail, but they claimed that the age spread for their RGB stars is about 6-12 Gyr (Sect. 2, last paragraph in Worthey et al.). Therefore, we construct the metallicity distributions for M 31 disk with the age range of RGB stars observed by Worthey et al. (stellar ages between 6 and 12 Gyr) and compare them to their observations in Fig. 7.
On the other hand, Koch et al. (2005) found that for the Carina dSph, there is a larger age spread (from 2 Gyr to more than 11 Gyr), while its colour-magnitude diagram shows a narrow RGB distribution. The large age spread implies that Carina dSph must have undergone various episodes of star formation process. This is different from the smaller age spread reported by Worthey et al. (2005). We understand that this uncertainty calls for a more work on the observational side about the metallicity distribution of M 31 disk.
5 Discussion
Early works on the parallel modeling of MW and M 31 (Diaz & Tosi 1984) found some similarities between the evolutionary properties of the two disks, but they were performed at an epoch when limited observational data provided little constraint on the models (for instance, Diaz & Tosi 1984 compared their model to M 31 data available only in the 5-11 kpc region). A more detailed comparison to observations was completed by Molla et al. (1996), who used a multi-parameter model and reproduced several features of the M 31 disk successfully.
Renda et al. (2005) focuses on MW and M 31, benefitting from a larger
data set and found some similarities to our work. The disks are
constructed inside-out by slow infall and the adopted SFR is
![]() ,
i.e., with an exponent n = 2 instead of
1.5 in our case. By adopting exactly the same SFR law for MW and
M 31, Renda et al. (2005) found that the gaseous profile is over
predicted in M 31 (their model M 31a), hence the need to increase
their SF efficiency
,
i.e., with an exponent n = 2 instead of
1.5 in our case. By adopting exactly the same SFR law for MW and
M 31, Renda et al. (2005) found that the gaseous profile is over
predicted in M 31 (their model M 31a), hence the need to increase
their SF efficiency ![]() by a factor of 2 to improve the fit to
the data (their model M 31b). If they had noticed the lower gas
fraction in M 31, they would have anticipated the problem (see our
discussion in Sect. 3.3). Our conclusion based on our models agree
both in terms of a higher SF efficiency in M 31 compared to the MW as
well as the resulting abundance gradients (smaller in the case of
M 31), when radius in all radially dependent terms is expressed in
e.g., kpc. For some unclear reason, our model reproduces the gaseous
profile of M 31 more successfully, perhaps because of our smaller
exponent n = 1.5 in the adopted SFR. Finally, both our model and
theirs fail to reproduce observational data for the outer disk of
M 31. It is difficult to continue the comparison further, because
Renda et al. (2005) do not provide SFR and stellar or gas fraction
profiles. The latter are mandatory in any work on chemical
evolution, since they constrain, more than anything else the
combined history of star formation and infall.
by a factor of 2 to improve the fit to
the data (their model M 31b). If they had noticed the lower gas
fraction in M 31, they would have anticipated the problem (see our
discussion in Sect. 3.3). Our conclusion based on our models agree
both in terms of a higher SF efficiency in M 31 compared to the MW as
well as the resulting abundance gradients (smaller in the case of
M 31), when radius in all radially dependent terms is expressed in
e.g., kpc. For some unclear reason, our model reproduces the gaseous
profile of M 31 more successfully, perhaps because of our smaller
exponent n = 1.5 in the adopted SFR. Finally, both our model and
theirs fail to reproduce observational data for the outer disk of
M 31. It is difficult to continue the comparison further, because
Renda et al. (2005) do not provide SFR and stellar or gas fraction
profiles. The latter are mandatory in any work on chemical
evolution, since they constrain, more than anything else the
combined history of star formation and infall.
Despite their simplicity (independently evolving rings, no cosmological framework), models such as that presented here can provide some interesting physical insights into the evolution of MW and M 31, based both on their successes and failures. The success in reproducing simultaneously the profiles of gas, SFR, and metallicity in the MW, as well as its global properties (gas fraction, total SFR, and colours, the latter being discussed in Boissier & Prantzos 1999) implies that the overall history of the Milky Way cannot have been very different from the one found here, i.e., a slow, inside-out disk formation. However, similar solutions may, perhaps, be obtained by some other combinations of SFR and infall rate, i.e., the problem may well be degenerate, thus no firm conclusions can be drawn on each one of those two key ingredients.
In the case of M 31, it is clear that a higher star formation
efficiency is required, as inferred from its gas fraction, lower by
a factor of ![]() 2 than in the MW. This was already found by Renda
et al. (2005), while Hammer et al. (2007) went one step further, to
suggest that the MW is a particularly ``quiescent'' disk galaxy (for
its mass) and M 31 may be closer to an average large spiral. This
``quiescence'' of the MW may be due to its relative isolation, while
M 31 may have undergone a larger number of (and/or more important)
interactions with neighboring galaxies. This picture is in line
with the finding of Block et al. (2006), namely that M 31 has
undergone a major interaction about 200 Myr ago; no such interaction
appears to have occurred in the case of the MW over the past few
billions of years.
2 than in the MW. This was already found by Renda
et al. (2005), while Hammer et al. (2007) went one step further, to
suggest that the MW is a particularly ``quiescent'' disk galaxy (for
its mass) and M 31 may be closer to an average large spiral. This
``quiescence'' of the MW may be due to its relative isolation, while
M 31 may have undergone a larger number of (and/or more important)
interactions with neighboring galaxies. This picture is in line
with the finding of Block et al. (2006), namely that M 31 has
undergone a major interaction about 200 Myr ago; no such interaction
appears to have occurred in the case of the MW over the past few
billions of years.
Our formalism allows us to describe in a unified framework the properties of both the MW and M 31, by using the same expression for the radial dependence of the SFR in both cases. This description is required because of the similarity between the radial profiles of the two disks, when they are expressed in terms of their respective scalelengths (Sect. 2.4). However, it is not clear whether the higher SF efficiency of M 31 is caused by an external factor (i.e., more frequent/important interactions of that galaxy) or to an internal one (e.g., its mass, as argued in Boissier & Prantzos 2000). Applying this formalism to other disk galaxies for which large data basis are available (work in progress) will help us to clarify the situation.
On the other hand, the failure of both this work and Renda et al. (2005) to reproduce satisfactorily the gaseous profile of M 31, and because we over-predict the global SFR of M 31, as well as its outer SFR profile, the properties are affected considerably by recent interactions. Thus, they cannot be predicted by such simple models (unless more parameters are introduced). If this is true, and if M 31 is really closer to a typical disk (as Hammer et al. 2007 suggest), then the cosmological framework will be mandatory for the description of galactic disks; simple models, such as this one, will be able to describe successfully only the most quiescent disks, such as the MW.
6 Summary
We have studied the chemical evolution of the disk of M 31, using a model that had already been applied to the study of the Milky Way (Boissier & Prantzos 1999; Hou et al. 2000). We used an extensive data set of M 31 properties, including radial profiles of gas surface density, gas fraction, star formation rate, oxygen abundances, as well as metallicity distribution functions at different regions of the disk. The star formation rate profile of M 31 was derived from GALEX UV data (Boissier et al. 2007). Our main aim was to determine whether a simple chemical evolution model can successfully describe the radial and global properties of both disks.
We first summarized and compared the observational data (Sect. 2) for the two galaxies. The disk of M 31 is about 2.4 times larger and 2 times more massive than the Milky Way disk, while its gas fraction is approximately half of the one of the MW. All other things being equal, this implies that there has been a higher average star formation efficiency in M 31 disk. We found that the SF radial profile of MW is well described by ``standard'' SF laws, but not that of M 31 (Sect. 2.2). We attributed the later findings to a major perturbation of M 31 by a nearby galaxy, in line with the findings of Block et al. (2006). We concluded that our model (which adopts ``standard'' SF laws) will fail to reproduce the observed SF profile of M 31, and perhaps also the gas profile.
We found that, when radii are expressed in terms of the corresponding scalelengths, the two disks display very interesting similarities in their radial profiles (Sect. 2.4). This concerns, in particular, the gas fraction, the profile of which is quasi-identical inside the innermost two scalelengths (Fig. 4). The scaled abundance gradients of the two disks are also quite similar if we adopt for the MW the lower range of reported values (e.g., Deharveng et al. 2000; Daflon & Cunha 2004; Andrievsky et al. 2004; Chen et al. 2008). This similarity was also found in a sample of external spirals that cover a much wider range of galaxy properties than the two disks studied here and successfully described by the models of Boissier & Prantzos (2001). We emphasize, however, that the status of the MW abundance gradient, especially in the outer part, is still very controversial: observations show that it may not be described by a simple exponential (see e.g., Yong et al. 2005 and Carraro et al. 2007 for open cluster abundances; and Andrievsky et al. 2004 and Lemasle et al. 2008 for Cepheids). Assuming that the scaled abundance gradients are similar in MW and M 31, we tried for a description of the radial properties of the two disks within the framework of a single model, which we presented in Sect. 3.
Detailed calculations illustrated that our unified model describes well all the main properties of the MW disk and most of those of M 31, provided that the SF efficiency of M 31 is adjusted to be twice as high in M 31 disk (as implied by the lower gas fraction of M 31). The radial profiles of both MW and M 31 were well described, albeit less successfully in the case of M 31. In particular, the model fails to match the present SFR in M 31, producing too high values in the outer disk and globally. We attributed this failure to M 31 having been perturbed recently by a major encounter, as is implied by the fact that the observed SFR profile of M 31 did not follow any form of the Kennicutt-Schmidt star formation law. On the other hand, the stellar metallicity distributions measured along the disk of M 31 reflect the disk integrated star formation during the entire history of the and should not be affected by recent events. Our model, where the bulk of Fe originates in SNIa, reproduces those distributions well, from 6 to 21 kpc.
The unified description that we have proposed here for MW and M 31, by expressing their radial profiles in terms of ``natural units'' (the corresponding disk scalelengths), offers valuable insights into the evolution of those two disk galaxies, and our results may also be applicable to other spirals as well (work in progress).
Acknowledgements
This work is supported by the National Science Foundation of China No. 10573028, the Key Project No. 10833005, the Group Innovation Project No. 10821302, and by 973 program No. 2007CB815402.
References
- Andrievsky, S. M., Luck, R. E., Martin, P., et al. 2004, A&A, 413, 159 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Barmby, P., Ashby, M. L. N., Bianchi, L., et al. 2006, ApJ, 650, L45 [NASA ADS] [CrossRef] (In the text)
- Beasley, M. A., Brodie, J. P., Strader, J., et al. 2004, AJ, 128, 1623 [NASA ADS] [CrossRef] (In the text)
- Bellazzini, M., Cacciari, C., Federici, L., et al. 2003, A&A, 405, 867 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Berkhuijsen, E. M. 1977, A&A, 57, 9 [NASA ADS] (In the text)
- Blair, W. P., Kirshner, R. P., & Chevalier, R. A. 1982, ApJ, 254, 50 [NASA ADS] [CrossRef] (In the text)
- Blitz, L., Spergel, D. N., Teuben, P. J., et al. 1999, ApJ, 514, 818 [NASA ADS] [CrossRef]
- Block, D. L., Bournaud, F., Combes, F., et al. 2006, Nature, 443, 832 [NASA ADS] [CrossRef] (In the text)
- Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] (In the text)
- Boissier, S., & Prantzos, N. 2000, MNRAS, 312, 398 [NASA ADS] [CrossRef] (In the text)
- Boissier, S., & Prantzos, N. 2001, MNRAS, 325, 321 [NASA ADS] [CrossRef]
- Boissier, S., Boselli, A., Prantzos, N., et al. 2001, MNRAS, 321, 733 [NASA ADS] [CrossRef] (In the text)
- Boissier, S., Gil de Paz, A., Boselli, A., et al. 2007, ApJS,173, 524 (In the text)
- Brown T. M. 2009 [arXiv:0901.2577], in proceedings of ``Galaxy Evolution: Emerging Insights and Future Challenges'', 11-14 November 2008, Austin, USA (In the text)
- Brown, T. M., Smith, E., Ferguson, H. C., et al. 2006, ApJ, 652, 323 [NASA ADS] [CrossRef] (In the text)
- Brown, T. M., Smith, E., Ferguson, H. C., et al. 2007, ApJ, 658, L95 [NASA ADS] [CrossRef] (In the text)
- Brown, T. M., Beaton, R., Chiba, M., et al. 2008, ApJ, 685, L121 [NASA ADS] [CrossRef] (In the text)
- Burstein, D., Li, Y., Freeman, K. C., et al. 2004, ApJ, 614, 158 [NASA ADS] [CrossRef] (In the text)
- Carignan, C., Chemin, L., Huchtmeier, W. K., et al. 2006, ApJ, 641, L109 [NASA ADS] [CrossRef]
- Carraro, G., Geisler, D., Villanova, S., et al. 2007, A&A, 476, 217 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Case, G. L., & Bhattacharya, D. 1998, ApJ, 504, 761 [NASA ADS] [CrossRef]
- Cescutti, G., Matteucci, F., Francois, P., et al. 2007, A&A, 462, 943 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chang, R. X., Hou, J. L., Shu, C. G., et al. 1999, A&A, 350, 38 [NASA ADS] (In the text)
- Chang, R. X., Shu, C. G., & Hou, J. L. 2002, ChJA&A, 2, 226 [NASA ADS] (In the text)
- Chapman, S. C., Ibata, R., Lewis, G. F., et al. 2006, ApJ, 653, 255 [NASA ADS] [CrossRef] (In the text)
- Chemin, L., Carignan, C., & Foster, T. 2009, ApJ, submitted [arXiv:0908.0326] (In the text)
- Chen, L., Hou, J. L., & Wang, J. J. 2003, AJ, 125, 1397 [NASA ADS] [CrossRef] (In the text)
- Chen, L., Hou, J. L., Zhao, J. L., et al. 2008, IAUS, 248, 433 [NASA ADS] (In the text)
- Chiappini, C., Matteucci, F., Gratton, R., et al. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] (In the text)
- Chiappini, C., Matteucci, F., Romano, D., et al. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] (In the text)
- Cole, S., Lacey, C. G., Baugh, C. M., et al. 2000, MNRAS, 319, 168 [NASA ADS] [CrossRef] (In the text)
- Daflon, S., & Cunha, K. 2004, ApJ, 617, 1115 [NASA ADS] [CrossRef] (In the text)
- Dame, T. M. 1993, AIP Conf., 278, 267 [NASA ADS]
- Dame, T. M., Koper, E., Israel, F. P., et al. 1993, ApJ, 418, 730 [NASA ADS] [CrossRef]
- Davidge, T. J., Jensen, J. B., & Olsen, K. A. G. 2006, AJ, 132, 521 [NASA ADS] [CrossRef] (In the text)
- Deharveng, L., Peña, M., Caplan, J., et al. 2000, MNRAS, 311, 329 [NASA ADS] [CrossRef] (In the text)
- Dehnen, W., & Binney, J. 1998, MNRAS, 294, 429 [NASA ADS] [CrossRef] (In the text)
- Dennefeld, M., & Kunth, D. 1981, AJ, 86, 989 [NASA ADS] [CrossRef] (In the text)
- Diaz, A., & Tosi, M. 1984, MNRAS, 208, 365 [NASA ADS] (In the text)
- Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef]
- Durrell, P. R., Harris, W. E., & Pritchet, C. J. 2004, AJ, 128, 260 [NASA ADS] [CrossRef] (In the text)
- Efstathiou, G. 2000, MNRAS, 317, 697 [NASA ADS] [CrossRef] (In the text)
- Ferguson, A. M. N., & Johnson, R. A. 2001, ApJ, 559, 13 [NASA ADS] [CrossRef] (In the text)
- Ferreras, I., & Silk, J. 2001, ApJ, 557, 165 [NASA ADS] [CrossRef] (In the text)
- Flynn, C., Holmberg, J., Portinari, L., et al. 2006, MNRAS, 372, 1149 [NASA ADS] [CrossRef] (In the text)
- Font, A. S., Johnston, K. V., Ferguson, A. M. N., et al. 2008, ApJ, 673, 215 [NASA ADS] [CrossRef] (In the text)
- Fraternali, F., & Binney, J. J. 2008, MNRAS, 386, 935 [NASA ADS] [CrossRef]
- Freudenreich, H. T. 1998, ApJ, 492, 495 [NASA ADS] [CrossRef]
- Fu, J., Hou, J. L., Yin, J., et al. 2009, ApJ, 696, 668 [NASA ADS] [CrossRef] (In the text)
- Geehan, J. J., Fardal, M. A., Babul, A., et al. 2006, MNRAS, 366, 996 [NASA ADS] (In the text)
- Galarza, V. C., Walterbos, R. A. M., & Braun, R. 1999, AJ, 118, 2775 [NASA ADS] [CrossRef] (In the text)
- Goswami, A., & Prantzos, N. 2000, A&A, 359, 191 [NASA ADS] (In the text)
- Governato, F., Willman, B., Mayer, L., et al. 2007, MNRAS, 374, 1479 [NASA ADS] [CrossRef] (In the text)
- Guibert, J., Lequeux, J., & Viallefond, F. 1978, A&A, 68, 1 [NASA ADS]
- Guo, Q., & White, S. D. M. 2008, MNRAS, 384, 2 [NASA ADS] [CrossRef] (In the text)
- Hammer, F., Puech, M., Chemin, L., et al. 2007, ApJ, 662, 322 [NASA ADS] [CrossRef] (In the text)
- Heller, C. H., Shlosman, I., & Athanassoula, E. 2007, ApJ, 671, 226 [NASA ADS] [CrossRef] (In the text)
- Hiromoto, N., Maihara, T., Oda, N., et al. 1983, PASJ, 35, 413 [NASA ADS] (In the text)
- Holmberg, J., & Flynn, C. 2004, MNRAS, 352, 440 [NASA ADS] [CrossRef]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hou, J. L., & Chang, R. X. 2001, Progr. Astron., 19(1), 68 (In the text)
- Hou, J. L., Prantzos, N., & Boissier, S. 2000, A&A, 362, 921 [NASA ADS] (In the text)
- Hou, J. L., Chang, R. X., & Chen, L. 2002, ChJAA, 2, 17 [NASA ADS] (In the text)
- Ibata, R., Chapman, S., Ferguson, A. M. N., et al. 2005, ApJ, 634, 287 [NASA ADS] [CrossRef] (In the text)
- Irwin, M. J., Ferguson, A. M. N., Ibata, R. A., et al. 2005, ApJ, 628, 105 [NASA ADS] [CrossRef] (In the text)
- Ivezic, Z., Sesar, B., Juric, M., et al. 2008, ApJ, 684, 287 [NASA ADS] [CrossRef] (In the text)
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] (In the text)
- Jacoby, G. H., & Ciardullo, R. 1999, ApJ, 515, 169 [NASA ADS] [CrossRef] (In the text)
- Kalirai, J. S., Gilbert, K. M., Guhathakurta, P., et al. 2008, ApJ, 648, 389 [NASA ADS] [CrossRef] (In the text)
- Kang, X., Jing, Y. P., Mo, H. J., et al. 2005, ApJ, 631, 21 [NASA ADS] [CrossRef] (In the text)
- Kennicutt, R. C. 1998a, ARA&A, 36, 189 [NASA ADS] [CrossRef] (In the text)
- Kennicutt, R. C. 1998b, ApJ, 498, 541 [NASA ADS] [CrossRef]
- Kent, S. M., Dame, T. M., Fazio, G., et al. 1991, ApJ, 378, 131 [NASA ADS] [CrossRef]
- Klypin, A., Zhao, H. S., & Somerville, R. S. 2002, ApJ, 573, 597 [NASA ADS] [CrossRef] (In the text)
- Koch, A., Wilkinson, M., Grebel, E. K., et al. 2005, Proc. IAU Colloq. 198, ed. H. Jerjen, & B. Binggeli (Cambridge: Cambridge University Press), 134
- Koch, A., Rich, R. M., Reitzel, D. B., et al. 2008, ApJ, 689, 958 [NASA ADS] [CrossRef] (In the text)
- Koper, E., Israel, F. P., Dame, T. M., et al. 1991, ApJ, 383, L11 [NASA ADS] [CrossRef] (In the text)
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] (In the text)
- Kulkarni, S., & Heiles, C. 1987, In Interstellar Processes, ed. D. Hollenbach, & H. Thronson (Dordrecht: Kluwer), 87
- Lacey, C. G., & Fall, S. M. 1985, ApJ, 290, 154 [NASA ADS] [CrossRef]
- Lee, M. G., Hwang, H. S., Kim, S. C., et al. 2008, ApJ, 674, 886 [NASA ADS] [CrossRef] (In the text)
- Lemasle, B., Francois, P., Piersimoni, A., et al. 2008, A&A, 490, 613 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Loinard, L., Dame, T. M., Heyer, M. H., et al. 1999, A&A, 351, 1087 [NASA ADS] (In the text)
- Lyne, A., Manchester, R., & Taylor, J. 1985, MNRAS, 213, 613 [NASA ADS]
- Maciel, W. J., & Costa, R. D. D. 2008 [arXiv:0806.3443] (In the text)
- Maciel, W. J., Lago, L. G., & Costa, R. D. D. 2006, A&A, 453, 587 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Magrini, L., Sestito, P., Randich, S., et al. 2009, A&A, 494, 95 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [NASA ADS] (In the text)
- Mayer, L., Governato, F., & Kaufmann, T. 2008, Adv. Sci. Lett., 1, 7 (In the text)
- McConnachie, A. W., Irwin, M. J., Ferguson, A. M. N., et al. 2005, MNRAS, 356, 979 [NASA ADS] [CrossRef] (In the text)
- Molla, M., Ferrini, F., & Diaz, A. 1996, ApJ, 466, 668 [NASA ADS] [CrossRef] (In the text)
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [NASA ADS] [CrossRef] (In the text)
- Monaco, P. 2004, MNRAS, 352, 181 [NASA ADS] [CrossRef] (In the text)
- Naab, T., & Ostriker, J. P. 2006, MNRAS, 366, 899 [NASA ADS] (In the text)
- Nieten, Ch., Neininger, N., Guélin, M., et al. 2006, A&A, 453, 459 [NASA ADS] [CrossRef] [EDP Sciences]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Olsen, K. A. G., Blum, R. D., Stephens, A. W., et al. 2006, AJ, 132, 271 [NASA ADS] [CrossRef] (In the text)
- Prantzos, N. 2008, A&A, 489, 525 [NASA ADS] [CrossRef] [EDP Sciences]
- Prantzos, N., & Aubert, O. 1995, A&A, 302, 69 [NASA ADS] (In the text)
- Prantzos, N., & Boissier, S. 2000, MNRAS, 313, 338 [NASA ADS] [CrossRef] (In the text)
- Prantzos, N., & Silk, J. 1998, ApJ, 507, 229 [NASA ADS] [CrossRef] (In the text)
- Renda, A., Kawata, D., Fenner, Y., et al. 2005, MNRAS, 356, 1071 [NASA ADS] [CrossRef] (In the text)
- Richardson, J. C., Ferguson, A. M. N., Johnson, R. A., et al. 2008, AJ, 135, 1998 [NASA ADS] [CrossRef] (In the text)
- Roskar, R., Debattista, V. P., Quinn, T. R., et al. 2008, ApJ, 684, L79 [NASA ADS] [CrossRef] (In the text)
- Rudolph, A. L., Fich, M., Bell, G. R., et al. 2006, ApJS, 162, 346 [NASA ADS] [CrossRef] (In the text)
- Sackett, P. D. 1997, ApJ, 483, 103 [NASA ADS] [CrossRef]
- Salow, R. M., & Statler, T. S. 2004, ApJ, 611, 245 [NASA ADS] [CrossRef] (In the text)
- Sakamoto, T., Chiba, M., & Beers T. C. 2003, A&A, 397, 899 [NASA ADS] [CrossRef] [EDP Sciences]
- Samland, M., & Gerhard, O. E. 2003, A&A, 399, 961 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sancisi, R., Fraternali, F., Oosterloo, T., et al. 2008, A&ARv, 15, 189 [NASA ADS] (In the text)
- Sarajedini, A., & Jablonka, P. 2005, AJ, 130, 1627 [NASA ADS] [CrossRef] (In the text)
- Sarajedini, A., & van Duyne, J. 2001, AJ, 122, 2444 [NASA ADS] [CrossRef] (In the text)
- Smartt, S. J., Crowther, P. A., Dufton, P. L., et al. 2001, MNRAS, 325, 257 [NASA ADS] [CrossRef]
- Tamm, A., Tempel, E., & Tenjes, P. 2007 [arXiv:0707.4375v1] (In the text)
- Tempel, E., Tamm, A., & Tenjes, P. 2007 [arXiv:0707.4374v1] (In the text)
- Thielemann, F. K., Nomoto, K., & Yokoi, K. 1986, A&A, 158, 17 [NASA ADS] (In the text)
- Thilker, D. A., Braun, R., Walterbos, R. A. M., et al. 2004, ApJ, 601, L39 [NASA ADS] [CrossRef] (In the text)
- Trundle, C., Dufton, P. L., Lennon, D. J., et al. 2002, A&A, 395, 519 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- van den Bergh, S. 1999, A&ARv, 9, 273 [NASA ADS]
- van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] (vdHG97) (In the text)
- van der Kruit, P. C. 1986, A&A, 157, 230 [NASA ADS]
- Walterbos, R. A. M. 1986, BAAS, 18, 915 [NASA ADS] (In the text)
- Walterbos, R. A. M., & Kennicutt, R. C. 1987, A&AS, 69, 311 [NASA ADS] (In the text)
- Walterbos, R. A. M., & Kennicutt, R. C. 1988, A&A, 198, 61 [NASA ADS] (In the text)
- Widrow, L. M., & Dubinski, J. 2005, ApJ, 631, 838 [NASA ADS] [CrossRef] (In the text)
- Widrow, L. M., Perrett, K. M., & Suyu, S. H. 2003, ApJ, 588, 311 [NASA ADS] [CrossRef] (In the text)
- Williams, B. F. 2002, MNRAS, 331, 293 [NASA ADS] [CrossRef] (In the text)
- Williams, B. F. 2003a, AJ, 126, 1312 [NASA ADS] [CrossRef] (In the text)
- Williams, B. F. 2003b, MNRAS, 340, 143 [NASA ADS] [CrossRef]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] (WW95) (In the text)
- Worthey, G., España, A., MacArthur, L. A., et al. 2005, ApJ, 631, 820 [NASA ADS] [CrossRef] (In the text)
- Wyse, R. F. G., & Silk, J. 1989, ApJ, 339, 700 [NASA ADS] [CrossRef] (In the text)
- Xue, X. X., Rix, H. W., Zhao, G., et al. 2008, ApJ, 684, 1143 [NASA ADS] [CrossRef]
- Yong, D., Carney, B. W., & Teixera de Almeida, M. L. 2005, AJ, 130, 597 [NASA ADS] [CrossRef] (In the text)
- Zhao, G., Chen, Y. Q., Shi, J. R., et al. 2006, ChJA&A, 6, 265 [NASA ADS] (In the text)
- Zheng, Z., Flynn, C., Gould, A., et al. 2001, ApJ, 555, 393 [NASA ADS] [CrossRef]
All Tables
Table 1: Observation of Milky Way and M 31 (re-scaled to 785 kpc).
Table 2: Model parameters.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm]{12316fg1.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg55.png) |
Figure 1: Observed profiles of the gas and star formation rate for the Milky Way and M 31 disks. Upper panel: current surface density profiles of HI, molecular gas, and total gas in the Milky Way and M 31. Lower panel: observed estimations of SFR of the Milky Way (filled symbols, from Boissier & Prantzos 1999) and M 31 disks (open symbols from Boissier et al. 2007). The lines in the lower panels are the results calculated according to the star formation law given in the right panel. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{12316fg2.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg58.png) |
Figure 2: Relationship between observed gas surface density and star formation rate surface density for M 31 (filled circles) and Milky Way disks (filled triangles). Full line is the classical Kennicutt law (Eq. (3)). Regions between two dashed lines indicate the results for a number of local galaxies observed by GALEX (from Boissier et al. 2007). The M 31 shows an untypical path in its inner region, while the Milky Way shows a rather normal behaviour. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=9cm,width=9cm]{12316fg3.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg62.png) |
Figure 3: Observed oxygen abundance gradient in the Milky Way ( top, data from Rudolph et al. 2006; Deharveng et al. 2000) and M 31 ( bottom, data from Dennefeld & Kunth 1981; Blair 1982; Trundle et al. 2002). In the top panel, the two commonly referred values of -0.07 dex kpc-1and -0.04 dex kpc-1appear as dashed and solid line respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm,width=18cm]{12316fg4.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg63.png) |
Figure 4:
Observed profiles for Milky Way and M 31 disks, with radius expressed in units of the corresponding scalelengths |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm]{12316fg5.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg87.png) |
Figure 5:
Current profiles of gas, stars, SFR, gas fraction, and oxygen abundance ( from top to bottom) for MW and M 31. In the left and middle panels, profiles for MW and M 31, respectively, are expressed in terms of physical radius r (in kpc); in the right panels, profiles for both disks are expressed in terms of normalised radius
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=10cm,width=9cm]{12316fg6.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg93.png) |
Figure 6:
Time evolution of global gas, star, gas fraction, infall rate, and SFR in M 31 and Milky Way disks. The disk parameters are given in Table 2, and the coefficients |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=10cm,width=9cm]{12316fg7.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12316-09/Timg94.png) |
Figure 7:
The metallicity distribution functions of various regions in the Milky Way and M 31 disks. The observed data in the solar neighborhood of the Milky Way disk come from Holmberg et al. (2007) and Chang et al.
(1999), and the data of M 31 come from Worthey et al. (2005). The model predictions are plotted as smooth curves, after convolution with a Gaussian error function with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.