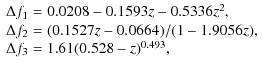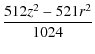| Issue |
A&A
Volume 505, Number 2, October II 2009
|
|
|---|---|---|
| Page(s) | 613 - 623 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200912220 | |
| Published online | 03 August 2009 | |
Novel explanation for the shape of the lenticular galaxy bulge and its implication for red spiral galaxy evolution
R. A. Schachar1 - G. G. Liao2 - R. D. Kirby2 - F. Kamangar3 - Z. E. Musielak1,4 - G. Rosensteel5
1 - Department of Physics, University of Texas
at Arlington, Arlington, TX 76019, USA
2 -
Department of Mathematics, University of Texas
at Arlington, Arlington, TX 76019, USA
3 -
Department of Computer Science and Engineering,
University of Texas at Arlington, Arlington,
TX 76019, USA
4 -
Kiepenheuer-Institut für Sonnenphysik,
Schöneckstr. 6, Freiburg, 79104 Germany
5 -
Department of Physics, Tulane University, New
Orleans, LA 70118, USA
Received 28 March 2009 / Accepted 28 July 2009
Abstract
Aims. According to Hubble's classification scheme, lenticular galaxies represent an intermediate evolutionary step between elliptical and spiral galaxies. This evolutionary path predicts that the aspect ratios of both lenticular and spiral galaxies should be smaller than the aspect ratios of their E6 or E7 elliptical predecessors. In contradiction to this prediction, observation has demonstrated that the aspect ratio of lenticular galaxies is larger than its immediate elliptical predecessor. In this paper, we suggest a novel explanation for this inconsistency.
Methods. The approach described in this paper is primarily based on analytical methods; however, some numerical methods are also used.
Results. Our idea comes from theoretical and experimental results, which show that a small increase in the equatorial diameter of an oblate spheroid with an aspect ratio ![]() 0.6 surprisingly causes its minor axis to also increase. We demonstrate that the same phenomenon occurs in the isodensity contours of elliptical galaxies given by Miyamoto & Nagai (Miyamoto M., & Nagai R., 1975, PASJ, 27, 533) and in a Maclaurin spheroidal mass in response to the gravitational force generated by a circumferential equatorial disk.
0.6 surprisingly causes its minor axis to also increase. We demonstrate that the same phenomenon occurs in the isodensity contours of elliptical galaxies given by Miyamoto & Nagai (Miyamoto M., & Nagai R., 1975, PASJ, 27, 533) and in a Maclaurin spheroidal mass in response to the gravitational force generated by a circumferential equatorial disk.
Conclusions. The result of this paper is our explanation for the transformation of a disky elliptical galaxy into a lenticular galaxy which in response to rotation and equatorial diameter expansion evolves into a red spiral galaxy. This evolutionary path is consistent with the common environmental location of disky ellipticals, lenticular and red spiral galaxies and explains why elliptical galaxies are generally ![]() E4. The proposed evolutionary path is opposite to the generally accepted formation of lenticular galaxies from the merger of spiral galaxies.
E4. The proposed evolutionary path is opposite to the generally accepted formation of lenticular galaxies from the merger of spiral galaxies.
Key words: galaxies: bulge - galaxies: elliptical, lenticular, cD - galaxies: evolution
1 Introduction
Lenticular galaxies, labeled S0 in Hubble's classification scheme, form a transition between elliptical and spiral galaxies (Hubble 1926, 1936). The fact that this transition is smooth, which means that some S0 galaxies might well be classified as ellipticals and others as spirals, has led to controversy as to whether lenticular galaxies are more closely linked to elliptical or spiral galaxies (van den Bergh 1980). Jeans (1928) postulated that lenticular galaxies evolve from elliptical galaxies as a consequence of rotation (Sandage 2005). Consistent with Jeans' postulate, Miyamoto & Nagai (1975) showed that a family of decreasing isodensity contours with declining aspect ratios can describe the morphological differences of elliptical and spiral galaxies (see also Satoh 1980; Zhenglu 2000; Baes 2008). However, there are two basic problems with this evolutionary path:
First, spiral galaxies are bluer in color, signifying that they are younger in age than the redder elliptical and lenticular galaxies. Recently, Bamford et al. (2009) studied the morphology, color, environment and stellar mass of galaxies using data from over 105 objects from Galaxy Zoo, the largest sample of visually classified morphologies yet compiled. Interestingly, they demonstrate the existence of red spiral galaxies located in the same environment as elliptical and lenticular galaxies and show that there is an environmental dependence for color beyond that for morphology. This finding implies that the evolution of spiral galaxies may depend on their environment. Young blue spiral galaxies are routinely observed in less dense environments where there are fewer lenticular galaxies. Red spirals are located in denser environments where there are many elliptical and lenticular galaxies. Does this imply different evolutionary paths for young and old spiral galaxies?
Second, it has been observed that the mean aspect ratio, minor
axis/major axis ratio, of lenticular galaxies is
0.5 ![]() 0.25(calculated from Table 2 of Michard & Marchal
1994), which is greater than E6 and E7 elliptical
galaxies, that have aspect ratios of 0.4 and 0.3,
respectively. According to the Hubble - Jean's scheme E6 and/or E7
galaxies should evolve by rotation into lenticular galaxies. But
how can this occur when the aspect ratio and therefore the minor
axis of lenticular galaxies is greater than their immediate
elliptical predecessors?
0.25(calculated from Table 2 of Michard & Marchal
1994), which is greater than E6 and E7 elliptical
galaxies, that have aspect ratios of 0.4 and 0.3,
respectively. According to the Hubble - Jean's scheme E6 and/or E7
galaxies should evolve by rotation into lenticular galaxies. But
how can this occur when the aspect ratio and therefore the minor
axis of lenticular galaxies is greater than their immediate
elliptical predecessors?
=.24em plus .1em minus .1em The latter question is addressed by the general belief that lenticular galaxies form as a consequence of the collision of spiral galaxies (Abraham & van den Bergh 2001; Bedregal et al. 2006); however, this hypothesis has not yet been confirmed by N-body simulations (Hernandez & Lee 2004; Maller et al. 2006). In addition, the complex relationship between morphology, color, stellar mass and the environmental location of galaxies implies a gentle evolutionary path, not violent major mergers (Bamford et al. 2009).
The purpose of this paper is to suggest, consistent with Bamford's
et al. (2009) data, that there may be separate
pathways for the development of blue (younger) and red (older)
spiral galaxies. This differentiation is based on our explanation
for the increase of the minor axis of an elliptical galaxy as it
transforms into a lenticular galaxy. The idea is based on the
change in shape that occurs when the major axis of an encapsulated
biconvex object with a long oval cross sectional profile is
increased ![]() 5%, counterintuitively, the length of its minor
axis also increases, its central surfaces steepen, and its
peripheral surfaces flatten; i.e., the object morphologically
obtains a ``steep profile''. It has been demonstrated that this
morphological ``steep profile'' occurs as a consequence of
minimization of surface curvature, a surrogate for bending energy
(Schachar et al. 2008). The morphological ``steep
profile'' has a remarkable resemblance to the edge-on isophotal
shape of a lenticular galaxy bulge as shown by the ``steep
profile'' induced in a floating oil film in response to equatorial
traction (Fig. 1). The floating oil film experiment is
shown as an example of the effect of minimization of energy on
object shape and not to imply that the hydrodynamics, molecular
forces and surface tension of the floating oil film are directly
applicable to a rotating body of stars controlled by gravity.
5%, counterintuitively, the length of its minor
axis also increases, its central surfaces steepen, and its
peripheral surfaces flatten; i.e., the object morphologically
obtains a ``steep profile''. It has been demonstrated that this
morphological ``steep profile'' occurs as a consequence of
minimization of surface curvature, a surrogate for bending energy
(Schachar et al. 2008). The morphological ``steep
profile'' has a remarkable resemblance to the edge-on isophotal
shape of a lenticular galaxy bulge as shown by the ``steep
profile'' induced in a floating oil film in response to equatorial
traction (Fig. 1). The floating oil film experiment is
shown as an example of the effect of minimization of energy on
object shape and not to imply that the hydrodynamics, molecular
forces and surface tension of the floating oil film are directly
applicable to a rotating body of stars controlled by gravity.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[width=17cm]{12220f1-new.eps}}\end{figure}](/articles/aa/full_html/2009/38/aa12220-09/Timg5.png) |
Figure 1: Photograph of a ``steep profile'' induced by applying traction in the 180 degree meridian to an oil film floating on water. The tractional pins extend into the oil film and not into the water below. |
| Open with DEXTER | |
To demonstrate that the same phenomenon can be important for galaxy evolution, we consider the shape changes that occur to isodensity contours of elliptical galaxies given by Miyamoto & Nagai (1975) and a Maclaurin spheroidal mass in response to the gravitational force of a circumferential equatorial disk. In both cases, similar morphological ``steep profiles'' are observed. The obtained results are used to justify our suggestion that disky elliptical galaxies transform into lenticular galaxies, which then evolve into red spiral galaxies as a consequence of an increase in the equatorial diameter of the lenticular galaxy (see Sects. 2 and 3). Our discussion and conclusions can be found in Sects. 4 and 5. Obviously, our goal is not to develop a detailed model of spiral galaxy evolution, but only to demonstrate that the phenomenon may be relevant.
2 Transformation of galaxies with Miyamoto & Nagai's isodensity contours into ``steep profiles''
When a circumferential equatorial disk is added to an elliptical galaxy, the disk applies a gravitational force that expands the galaxy in its equatorial plane. The redistribution of the galaxy's mass changes the overall shape of the galaxy so that it is in a minimal energy state. To determine the new shape of the galaxy, the minimal energy state of the mass distribution of the galaxy is simulated by minimizing the curvature of the galaxy's isodensity contour.
Using solutions of Poisson's equation, Miyamoto & Nagai (1975) calculated the isodensity contours of a rotating elliptical galaxy with declining density distribution. They show that the induced density change can account for the morphological differences between elliptical and spiral galaxies; however, their analysis does not predict the existence of a lenticular galaxy between an elliptical and spiral galaxy with an aspect ratio greater than both types of galaxies.
It has been well established that most elliptical galaxies have disks (Bender et al. 1989; Rix & White 1990; Jørgensen & Franx 1994; Magorrian 1999; Cappellari 2008; Krajnovic et al. 2008) and these disky elliptical galaxies are distinguishable from lenticular galaxies (Jaffe et al. 1994; Caon & Einasto 1995; Katsiyannis et al. 2001; Kormendy et al. 2009). We propose that the gravitational force generated by the circumferential equatorial disk increases the equatorial diameter (major axis) of the elliptical galaxy causing it to evolve into a lenticular galaxy. To assess this possibility, we evaluate the morphological changes that will occur to an elliptical galaxy when its major axis is increased.
We begin by calculating the shape of an elliptical galaxy using
cylindrical coordinates as given by Miyamoto & Nagai's
(1975)
where
where
Since the mean aspect ratio of lenticular galaxies is 0.5 and the Jeans-Hubble scheme predicts an E6 or E7 elliptical galaxy will convert into a lenticular galaxy, shape parameters are selected to cover this range of elliptical galaxies; i.e., E7 to E4 (0.3
The curvature of the isodensity contour is given by
To simulate the gravitational effect of a circumferential
equatorial disk, the major axis of the isodensity contour of the
elliptical galaxy is increased 1.5%. To ensure the new galaxy
shape is in the lowest energy state, the calculus of variation is
used to minimize the square of the difference of the curvatures
between the isodensity contour of the elliptical galaxy and the
new galaxy contour
The problem is solved numerically using standard optimization software with the following constraints:
Arc length
Area
Surface area
where 1.01
The boundary conditions are
where (Xo, 0) is the intercept of the isodensity contour with the major axis of the elliptical galaxy.
The obtained results are given in Figs. 2-5, which show that in each case the minor axis of the galaxy isodensity contour increases as a consequence of an increase in its major axis transforming the galaxy isodensity contour into a ``steep profile''.
 |
Figure 2: Simulation of the effect of a circumferential equatorial disc on the shape of galaxy isodensity contours (solid curve) with aspect ratios = 0.6 and densities P = 0.1-0.0001, which all change into ``steep profiles'' (dashed curves). |
| Open with DEXTER | |
 |
Figure 3: Simulation of the effect of a circumferential equatorial disc on the shape of galaxy isodensity contours (solid curve) with aspect ratios = 0.5 and densities P = 0.1-0.0001, which all change into ``steep profiles'' (dashed curves). |
| Open with DEXTER | |
 |
Figure 4: Simulation of the effect of a circumferential equatorial disc on the shape of galaxy isodensity contours (solid curve) with aspect ratios = 0.4 and densities P = 0.1-0.0001, which all change into ``steep profiles'' (dashed curves). |
| Open with DEXTER | |
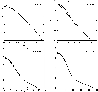 |
Figure 5: Simulation of the effect of a circumferential equatorial disc on the shape of galaxy isodensity contours (solid curve) with aspect ratios = 0.3 and densities P = 0.1-0.0001, which all change into ``steep profiles'' (dashed curves). |
| Open with DEXTER | |
3 Formation of a ``steep profile'' in a Maclaurin spheroid with a toroidal disk
The shape changes of a Maclaurin spheroidal mass in response to
increasing angular momentum have been used to predict the shapes
of galaxies (Sandage 2005). With increasing angular
momentum the Maclaurin spheroidal mass becomes more oblate until
it has an eccentricity of 0.8, which is equivalent to an aspect
ratio of 0.6. At this point, the Maclaurin spheroid is unstable
and with a decrease in angular momentum will become a Jacobi
ellipsoid (Eriguchi & Hachisu 1982; Dankova &
Rosensteel 1998). Alternatively, we propose that if
a Maclaurin spheroid mass has an aspect ratio ![]() 0.6 and has a
circumferential equatorial disk, the Maclaurin spheroid will
morphologically form a ``steep profile'' while angular momentum
remains constant.
0.6 and has a
circumferential equatorial disk, the Maclaurin spheroid will
morphologically form a ``steep profile'' while angular momentum
remains constant.
3.1 Configuration
Consider the symmetry axis of a surface of revolution aligned with
the z-axis. The surface bounds a connected region ![]() that
contains a total mass M in a volume V = vol(
that
contains a total mass M in a volume V = vol(![]() ). The
mass is distributed uniformly inside the surface. Using
cylindrical coordinates, the profile of the surface is defined by
a function r = f (z) for
- zm
). The
mass is distributed uniformly inside the surface. Using
cylindrical coordinates, the profile of the surface is defined by
a function r = f (z) for
- zm ![]() z
z ![]() zm. For each point
z along the symmetry axis inside the surface, the polar
coordinate ranges from r = 0, the symmetry axis, to r = f (z),
the boundary of the surface. The surface of revolution is
symmetrical:
f (- z) = f (z) for
- zm
zm. For each point
z along the symmetry axis inside the surface, the polar
coordinate ranges from r = 0, the symmetry axis, to r = f (z),
the boundary of the surface. The surface of revolution is
symmetrical:
f (- z) = f (z) for
- zm ![]() z
z ![]() zm.
zm.
Another mass Mext is distributed uniformly along the circumference of a circle of radius R in the z = 0 plane. This circle is centered at the origin, which is the geometrical center of the symmetrical surface. The radius R > > f (0) > zm > 0. The external mass models a toroidal galactic disk.
The total potential energy U is the sum of two terms: 1) the
gravitational interaction energy
Uext between the mass
M and the external mass
Mext and 2) the gravitational
self-energy
Uself of the mass. The total kinetic energy
is just the kinetic energy of the rigidly rotating mass M within
the region ![]() . The kinetic energy and self-energy of the
toroidal mass are considered constants.
. The kinetic energy and self-energy of the
toroidal mass are considered constants.
3.2 Volume of the Maclaurin spheroid
To determine the volume of the mass, imagine the mass is divided
into narrow cylindrical slices perpendicular to the symmetry axis.
The slice at position z along the axis has width dz and
radius r = f (z). The slice's volume is
![]() | f (z)|2 dzand the mass's volume is the integral
| f (z)|2 dzand the mass's volume is the integral
| V = |
(12) |
For an oblate spheroid, the profile is
fsph(z) = a![]() ,
where c = zm denotes the minor semi-axis length and a > c is the major
semi-axis length. The volume is
V = 4
,
where c = zm denotes the minor semi-axis length and a > c is the major
semi-axis length. The volume is
V = 4![]() a2c/3.
a2c/3.
3.3 Two-dimensional ``steep profile'' and volume corrections
Using a reference ellipse with a semimajor axis length a = 1(arbitrary units) and semiminor axis length c = 1/2 and the
``steep profile'' generated by increasing the major axis of the
reference ellipse 2%, the difference ![]() f between the
``steep profile's'' function, r = f (z), and the ellipse's
function,
r = fsph(z), are plotted in Fig. 6.
f between the
``steep profile's'' function, r = f (z), and the ellipse's
function,
r = fsph(z), are plotted in Fig. 6.
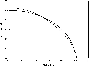 |
Figure 6: Reference ellipse (solid curve) and ``steep profile'' (dashed curve). |
| Open with DEXTER | |
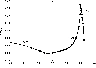 |
Figure 7:
Difference function
r - r |
| Open with DEXTER | |
The difference function is approximated by three segments
(Fig. 7).
where
The area of one quadrant of the ellipse is
![]() ac/4 =
ac/4 = ![]() /8 = 0.393. The difference between the single quadrant areas bounded
by the ``steep profile'' and ellipse is
/8 = 0.393. The difference between the single quadrant areas bounded
by the ``steep profile'' and ellipse is
| + |
(14) |
The fractional change in the quadrant's area is 0.02%, a negligible shift.
3.3.1 Three-dimensional surface of revolution
The difference between the volume of the ``steep profile'' and the
volume of the ellipsoid is
| (15) |
The difference ![]() g between the square of the ``steep
profile's'' function and the square of the ellipse's function is
approximated by three segments (Fig. 8)
g between the square of the ``steep
profile's'' function and the square of the ellipse's function is
approximated by three segments (Fig. 8)
| |
= | 0.0379 - 4.4286z2 + 72.7588z4 - 554.5930z6, | (16) |
| = | -0.0637 - 0.6697z2 + 6.8028z4 - 7.5373z6, | (17) | |
| = | 0.7366 - 2.6411z2, | (18) |
where z
 |
Figure 8:
Difference |
| Open with DEXTER | |
The function ![]() g is
g is
| (19) |
where the characteristic function is
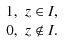
|
(20) |
The volume of the ellipsoid is
4![]() a2c/3 = 2
a2c/3 = 2![]() /3 = 2.094.
The difference between the volumes bounded by the ``steep
profile'' and ellipse is
/3 = 2.094.
The difference between the volumes bounded by the ``steep
profile'' and ellipse is
| +2 |
(21) |
The fractional change in the volume is -3.2%.
3.3.2 Volume correction
The volumes
V![]() of the surfaces of revolution, indexed by
of the surfaces of revolution, indexed by
![]() > 0 and defined by the cylindrical radial function
> 0 and defined by the cylindrical radial function
| r |
(22) |
where the ellipsoid's radial function is
| rsph2(z) = (1 - 4z2) |
(23) |
are less than the volume of the reference spheroid Vsph = 2
| (24) |
To reset the volumes equal to the ellipsoid's value, define the dilation
| r |
(25) |
for
| (26) |
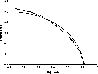 |
Figure 9: Ellipse (solid curve), ``steep profile'' (dashed curve) and volume-corrected ``steep profile'' (dotted curve). |
| Open with DEXTER | |
3.4 Kinetic energy of the Maclaurin spheroid and the ``steep profile''
When the surface of revolution rotates rigidly about its symmetry z-axis, the moment of inertia is| (27) |
where d = M/V is the uniform density. When the surface is a spheroid with semi-axis lengths, a = b and c, the moment of inertia is
| (28) |
where R3 = a2c and the eccentricity is e =
For the volume-corrected surface of revolution, the moment is
| |
= | ||
| = | |||
| (29) |
When
![]() = 0, the moment of inertia simplifies to the ellipsoidal
value
= 0, the moment of inertia simplifies to the ellipsoidal
value
| |
= | ||
| = | (30) |
The moment of inertia of the volume-corrected ``steep profile'' is
| (31) |
The kinetic energy is the square of the angular momentum Ldivided by twice the moment of inertia. Let U0 denote a
convenient energy unit (chosen below to give the gravitational
self-energy of a sphere of mass M and radius R) and define the
dimensionless angular momentum
![]() = L/
= L/![]() .
The kinetic energy, in units of U0, of a spheroid is
.
The kinetic energy, in units of U0, of a spheroid is
Tsph = 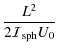 =
= |
(32) |
and for the ``steep profile''
| T |
(33) |
3.5 Self-energy of the ``steep profile''
The ``steep profile'' forms as a result of a small incompressible
deformation of the spheroid. The mass density
d (![]() ) equals
a constant d for a position vector
) equals
a constant d for a position vector ![]() inside the ``steep
profile'' and equals zero for
inside the ``steep
profile'' and equals zero for ![]() outside the region
outside the region
![]() . The mass density of the ellipsoid,
dsph(
. The mass density of the ellipsoid,
dsph(![]() ), equals d when
), equals d when ![]() is inside the ellipsoid
and equals zero for
is inside the ellipsoid
and equals zero for ![]() outside the ellipsoid. The
difference between these densities is a function
outside the ellipsoid. The
difference between these densities is a function
![]() d (
d (![]() ) = d (
) = d (![]() ) - dsph(
) - dsph(![]() ) which is zero
except for a narrow domain around the surface of the ellipsoid.
More generally, consider a family of ``steep profiles'' indexed by
a real number
) which is zero
except for a narrow domain around the surface of the ellipsoid.
More generally, consider a family of ``steep profiles'' indexed by
a real number ![]() with the densities
with the densities
| d |
(34) |
At
![]() = 0 the ``steep profile's'' density
d
= 0 the ``steep profile's'' density
d![]() equals the ellipsoid's density
dsph. The self-energy of a
``steep profile'' is
equals the ellipsoid's density
dsph. The self-energy of a
``steep profile'' is
Uself = - 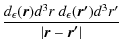 , , |
(35) |
where G is the universal gravitational constant and |
| Uself | - 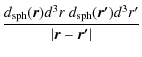 |
||
- 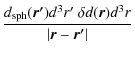 . . |
(36) |
The first term is the Maclaurin spheroid's self-energy
Usph and is a known quantity (Chandrasekhar
1969; Dankova & Rosensteel
1998),
| Usph = - U0 (1 - e2)1/6 |
(37) |
where the eccentricity e =
The second integral may be expressed in terms of the function
Usurf(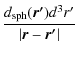 . . |
(38) |
Therefore, the ``steep profile's'' self-energy is, to order
| Uself = Usph+ |
(39) |
Since
![]() d (
d (![]() ) is zero outside of a narrow region near the ellipsoid's
surface, the potential energy
Usurf(
) is zero outside of a narrow region near the ellipsoid's
surface, the potential energy
Usurf(![]() ) due to the ellpsoidal mass
must be determined only for points
) due to the ellpsoidal mass
must be determined only for points ![]() near the ellipsoid's surface.
near the ellipsoid's surface.
For the ``steep profile's'' surface of revolution, the integral is
| Uself - Usph | = | d |
|
| (40) |
where, to obtain overall accuracy of order
Let us define
![]() U
U ![]() Uself - Usph and write
Uself - Usph and write
| |
= | ||
| = | - ( |
(41) |
The first term in this integral, to order
| |
= | ||
| = | |||
| + |
(42) |
since
| |
= | - ( |
|
| = | - ( |
||
| = | - (0.002095)U0 |
(43) |
where A1
3.6 Potential energy of the Maclaurin spheroid
The surface of the ellipsoid is defined by the equation, 1 = x12/a12 + x22/a22 + x32/a32. The gravitational potential energy for the interior and exterior of a homogeneous ellipsoid with semi-axis lengths a1, a2, a3 is defined by two quantities: the gravitational potential energy V and the gravitational self-energy W (Chandrasekhar 1969).
3.6.1 Interior points
At an interior point
![]() = (x1, x2, x3), the
potential energy (Chandrasekhar 1969) is
= (x1, x2, x3), the
potential energy (Chandrasekhar 1969) is
| V = |
(44) |
where I =
A1 = A2 = 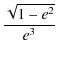 arcsin(e) - arcsin(e) - |
(45) |
A3 = 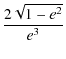 arcsin(e). arcsin(e). |
(46) |
For points interior to the ellipsoid's surface, Usurf = - V.
3.6.2 Surface points
The gravitational potential at an ellipsoid's surface is
3.6.3 Points exterior to the suface
At an exterior point
![]() = (x1, x2, x3), the potential
energy (Chandrasekhar 1969) is
= (x1, x2, x3), the potential
energy (Chandrasekhar 1969) is
| V = |
(48) |
where
| (49) |
For points exterior to the ellipsoid's surface, Usurf = - V.
For oblate spheroids, the above integrals may be evaluated as
follows:
| = | 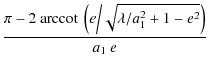 , , |
(50) | |
| = | 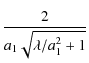 , , |
(51) | |
| = | 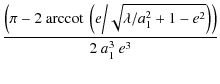 |
||
- 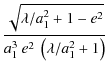 , , |
(52) | ||
| = |  , , |
(53) | |
| = | - 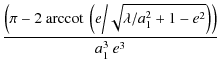 |
||
+ 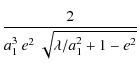 , , |
(54) | ||
| = |  . . |
(55) |
3.7 Potential energy due to the external toroidal mass
For a mass
Mext distributed uniformly along a circle of radius R0in the z = 0 plane external to the ellpsoid with linear mass density
Mext/2![]() R0, the gravitational potential energy at a point
R0, the gravitational potential energy at a point ![]() is
is
| Uext( |
(56) |
where the integration is over the circumference of a circle of radius R0, the points of which are denoted by
| (57) |
where
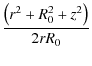 |
(58) |
and Qm - 1/2 is the half-integer Legendre function of the second kind (Cohl & Tohline 1999).
The integrals for every term in the summation except m = 0 are zero and the potential simplifies to
| Uext( |
(59) |
The m = 0 Legendre function of the second kind is
Q-1/2(![]() ) =
) = ![]() K(
K(![]() ),
where K is the complete elliptic integral of the first kind and
),
where K is the complete elliptic integral of the first kind and
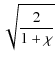 =
= 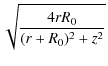 . . |
(60) |
Therefore the potential field due to the external mass is
| Uext(r, z) = - |
(61) |
A useful approximation to the complete elliptic integral of the first kind is
| K( |
|||
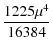 + ...
+ ... |
(62) |
For large R0 the potential field may be approximated by a Taylor series
in
1/![]() , we obtain
, we obtain
3.8 Interaction energy between the Maclaurin spheroid and the external toroidal mass
The gravitational interaction energy between a spheroid
and the toroidal mass is
| Usph - tor | = | (64) | |
| = | d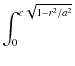 dz[F(r, z)] dz[F(r, z)] |
||
| = | - |
where
| F(r, z) = - |
(65) |
G(r, u) = sinh-1(u) + 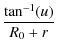 + ... ,
+ ... , |
(66) |
and u = c
When R0 is large compared to the dimensions of the ellipsoid,
the interaction energy
Ust ![]() Usph - tor/U0reduces to
Usph - tor/U0reduces to
| Ust | = | - |
|
| + |
|||
| = | - |
(67) |
where
| (68) |
3.9 Interaction energy between the ``steep profile'' and the external toroidal mass
Using the Taylor series for the gravitational potential, Eq. (63),
the interaction energy
Usph - tor between a ``steep
profile'' and the toroidal mass is
| Usph - tor | = | d |
|
| = | - |
||
| = | - |
||
| - |
|||
| x |
|||
| - |
|||
| x |
|||
| = | - |
||
| x (0.6243 - 0.02824 |
|||
| = | - |
||
| = | Us - t + (0.00921) |
(69) |
3.10 Equilibrium configurations of the rotating masses
By minimizing the total energy, we determine equilibrium configurations.
3.10.1 Total energy of the Maclaurin spheroid
The total energy E of an ellipsoid of eccentricity e is the sum of the kinetic energy of rigid rotation and the gravitational self-energy,| E = |
(70) |
where the energies are in units of U0 and the angular momentum
| (71) |
3.10.2 Total energy of the Maclaurin spheroid + external toroidal mass
The total energy is
| E = |
(72) |
Energy minimization determines the angular momentum of the equilibrium states
Note that the zero angular momentum equilibrium solution occurs at eccentricity e > 0.
3.10.3 Total energy of the ``steep profile'' + external toroidal mass
When the energy is minimized for an ellipsoid with eccentricity
e = ![]() /2 plus an external toroidal mass, Eq. (73) determines
the angular momentum. If the ellipsoid is deformed continuously
into the ``steep profile'' while the angular momentum is held
constant, the total energy changes from its spheroidal value
EMaclaurin to
/2 plus an external toroidal mass, Eq. (73) determines
the angular momentum. If the ellipsoid is deformed continuously
into the ``steep profile'' while the angular momentum is held
constant, the total energy changes from its spheroidal value
EMaclaurin to
| E``steep profile'' = EMaclaurin - (0.00005 - 0.0057 |
(74) |
This expression is a Taylor series which, for small ![]() ,
determines accurately the derivative of the energy of the ``steep
profile'' as a function of
,
determines accurately the derivative of the energy of the ``steep
profile'' as a function of ![]() . For large values of
. For large values of ![]() ,
which is a measure of the strength of the interaction between the
mass M and the external toroidal mass
Mext, terms
beyond the first two in the expansion of Eq. (63) must be included
in the derivation. The ``steep profile'' has a lower energy than
the spheroid when
,
which is a measure of the strength of the interaction between the
mass M and the external toroidal mass
Mext, terms
beyond the first two in the expansion of Eq. (63) must be included
in the derivation. The ``steep profile'' has a lower energy than
the spheroid when
![]() < 0.008 transforming the disky elliptical
galaxy into a lenticular galaxy. The negative change from the
spheroidal energy is the result of an increase in the kinetic
energy that is offset by a slightly greater decrease in the
gravitational
self-energy.
< 0.008 transforming the disky elliptical
galaxy into a lenticular galaxy. The negative change from the
spheroidal energy is the result of an increase in the kinetic
energy that is offset by a slightly greater decrease in the
gravitational
self-energy.
4 Discussion
Our results demonstrate that the minor axes of both the isodensity
surfaces of elliptical galaxies with aspect ratios ![]() 0.6 and
Maclaurin spheroidal masses will increase and morphologically form
``steep profiles'' when subjected to a small increase in their
major axes in response to the gravitational force of a
circumferential equatorial disk. The small displacement and
consequently minimal force required to make this change may
explain the transformation of a disky elliptical galaxy into a
lenticular galaxy.
0.6 and
Maclaurin spheroidal masses will increase and morphologically form
``steep profiles'' when subjected to a small increase in their
major axes in response to the gravitational force of a
circumferential equatorial disk. The small displacement and
consequently minimal force required to make this change may
explain the transformation of a disky elliptical galaxy into a
lenticular galaxy.
Disky elliptical galaxies can form as a consequence of the collapse of an elliptical galaxy. During the collapse sufficient outward transfer of angular momentum is generated to produce a circumferential equatorial disk (Larson 1975). Alternatively, disky elliptical galaxies may form from minor mergers (Bournaud et al. 2007; Naab et al. 1999) or rotation (Jeans 1928). Disky elliptical galaxies appear to represent a different track for galaxy evolution (Bender et al. 1989; Nieto & Bender, 1989; Kormendy et al. 2009).
Since such a disky elliptical galaxy rotates rapidly (Cappellari
et al. 2006, 2007), its
eccentricity will increase until it becomes an E4, aspect ratio =
0.6. At that point, a small gravitational force generated by the
circumferential equatorial disk will increase both the major and
minor axes of the elliptical galaxy transforming it into a
lenticular galaxy (Fig. 10). This process is more
efficient as the aspect ratio of the disky elliptical galaxy
declines below 0.6 (Schachar et al. 2008). This may
explain why elliptical galaxies are ![]() E7 and the majority are
E7 and the majority are
![]() E4 (Cresci et al. 2006; Hao et al.
2006).
E4 (Cresci et al. 2006; Hao et al.
2006).
 |
Figure 10: A nearly edge-on photograph of lenticular galaxy NGC 2549 (Courtesy of Sloan Digital Sky Survey) with superposition of an oil film's ``steep profile'' outline on the lenticular galaxy's bulge. |
| Open with DEXTER | |
According to the above discussion, the transformation of a disky elliptical galaxy into a lenticular galaxy seems to be a plausible process. Morphological high-resolution, multi-wavelength data from high-resolution Hubble Space Telescope (HST) Advanced Camera Surveys suggests lenticular galaxy formation is a slow process (Wilman et al. 2009). The Sloan Digital Sky Survey (SDSS) shows that disky elliptical and lenticular galaxies are mostly found in isolated high density environments (Bamford et al. 2009). Lenticular galaxies exist where the gas density and temperature are too low for them to form by ram pressure striping or evaporation of a spiral galaxy and the bulge-disc ratio of lenticular galaxies is systematically larger than those of spiral galaxies (Dressler 1980). The distance between lenticular, elliptical and red spiral galaxies (Bamford et al. 2009) is smaller than the distance between lenticular and bluer spiral galaxies (Dressler et al. 1997; Bamford et al. 2009).
The age of the bulge and the disc of lenticular galaxies (Fisher et al. 1996), kinematics, and properties of lenticular and elliptical galaxies are similar (Sandage & Visvanathan 1978; Fisher et al. 1996; Jørgensen et al. 1996; De Propris et al. 2005; Cappellari et al. 2006, 2007; Emsellem et al. 2007a; Helmboldt 2007; Naab & Ostriker 2009); however, it is important to appreciate and differentiate between slowly rotating elliptical galaxies, which have low ellipticities, are generally massive, metal-rich, and have shallow photometric profiles, and the rapidly rotating elliptical, disky elliptical and lenticular galaxies, which have high ellipticities, tend to be rotationally supported, are fainter objects, and tend to be metal-poor (Davies & Illingworth 1983; Jaffe et al. 1994; Kormendy & Bender 1996; Erwin et al. 2004; Bedregal et al. 2007; Cappellari et al. 2006, 2007). The distribution of fast and slow rotating galaxies and the evidence that boxy and disky ellipticals represent different evolutionary paths justifies separating fast and slow rotating galaxies (Bender et al. 1989; Nieto & Bender 1989; Emsellem et al. 2007a; Kormendy et al. 2009). Slowly rotating galaxies are more commonly classified as massive elliptical galaxies, while fast rotators are generally fainter and classified as elliptical or lenticular galaxies (Bender 1988; Emsellem et al. 2007b).
Francis & Anderson (2009) have proposed a new theory for the formation of galaxy spiral arms that does not require a significant increase in galaxy rotational velocity. According to this theory, spiral arms are formed as a consequence of an increase in galaxy equatorial diameter. Once the spiral arms form they enlarge and eventually form two enduring spiral arms. This theory fits with our postulation of the transformation of a lenticular galaxy into a red spiral galaxy.
A small equatorial diameter expansion of a disky E4 in response to the gravitational force of its circumferential equatorial disk transforms the disky E4 into a lenticular galaxy. If the mass of the circumferential equatorial disk increases by accretion or a minor merger, it will apply more gravitational force, which will further expand the equatorial diameter of the lenticular galaxy initiating the formation of spiral arms as proposed by Francis & Anderson (2009). In addition, lenticular galaxies have a range of rotational velocities (Emsellem et al. 2004, 2007a). Any increase in rotational velocity will enhance spiral arm formation (Jeans 1928) and the transformation of a lenticular galaxy into a red spiral galaxy.
The transition of a disky elliptical galaxy into a lenticular
galaxy and then into a red spiral galaxy is consistent with their
location with respect to the galaxies' group center. A greater
percentage of elliptical galaxies are located closer to the group
center than red spiral galaxies, which have a clear fractional
peak that is located further from the group center. Approximately
30% of red spiral galaxies are located at ![]() 0.4
0.4
The proposed evolutionary pathway is opposite to the generally accepted formation of lenticular and elliptical galaxies from the merger of spiral galaxies. Although it is documented that galaxy mergers occur, it is our contention that this is not the major evolutionary path for lenticular or red spiral galaxies. That disky elliptical galaxies transform into lenticular galaxies which convert into spiral galaxies implies that the etiology of Hubble's ``tuning fork'' scheme should be re-examined. Jeans (1928) theorized that the Hubble's ``tuning fork'' was a consequence of galaxy rotation. As the rotational velocity of an elliptical galaxy increased it would progressively flatten and eventually form spiral arms. According to Jeans (1928) hypothesis rotational velocity should predict galaxy type and lenticular galaxies should have a smaller aspect ratio than their immediate elliptical predecessors. Neither of these predictions is true. Jeans (1928) was not aware of the existence of disky elliptical galaxies. Therefore he did not consider the implications of the gravitational force of the circumferential equatorial disk on the shape of a galaxy and its ability to initiate the formation of spiral arms with a minimal change in rotational velocity.
Although we contend that blue spiral galaxies follow a different evolutionary path than red spiral galaxies, it is possible that they are part of Hubble's ``tuning fork'' scheme. An E4 disky elliptical transforms into a lenticular galaxy that develops spiral arms converting it into a red spiral galaxy. The formation of spiral arms causes greater turbulence and pockets of high density generating molecular gas clouds from which protostars form (Francis & Anderson 2009) transforming the red spiral galaxy into a blue spiral galaxy (Kannappan et al. 2009).
5 Conclusions
The main result of this paper is our novel explanation for the
observation that the aspect ratio of lenticular galaxies is
greater than their immediate elliptical predecessors. The idea is
that a small increase in the major axis of an oblate object with
an aspect ratio ![]() 0.6 causes its minor axis to increase
(Schachar et al. 2008). The circumferential
equatorial disk of an E4 elliptical galaxy supplies the
gravitational force required to increase its equatorial diameter.
This causes the E4 to transform into a lenticular galaxy. An
increase in mass of the disk of the lenticular galaxy causes the
equatorial diameter of the lenticular galaxy to expand initiating
the formation of spiral arms (Francis & Anderson
2009). This converts the lenticular galaxy into a
red spiral galaxy. The common environment of disky elliptical,
lenticular, and red spiral galaxies, and their fractional
groupocentric distances support this evolutionary process (Bamford
et al. 2009).
0.6 causes its minor axis to increase
(Schachar et al. 2008). The circumferential
equatorial disk of an E4 elliptical galaxy supplies the
gravitational force required to increase its equatorial diameter.
This causes the E4 to transform into a lenticular galaxy. An
increase in mass of the disk of the lenticular galaxy causes the
equatorial diameter of the lenticular galaxy to expand initiating
the formation of spiral arms (Francis & Anderson
2009). This converts the lenticular galaxy into a
red spiral galaxy. The common environment of disky elliptical,
lenticular, and red spiral galaxies, and their fractional
groupocentric distances support this evolutionary process (Bamford
et al. 2009).
Acknowledgements
We thank the anonymous referee for a careful reading of the manuscript and the invaluable, thoughtful suggestions that significantly improved and broadened the implications of our work.
References
- Abraham, R. G., & van den Bergh, S. 2001, Sci, 293, 1273 [NASA ADS] [CrossRef] (In the text)
- Baes, M. 2008, MNRAS, arxiv.org/pdf/0810.5483v1 (In the text)
- Bamford, S. P., Nichol, R. C., Baldry, I. K., et al. 2009, MNRAS, 393, 1324 [NASA ADS] [CrossRef] (In the text)
- Bedregal, A. G., Aragón-Salamanca, A. Merrifield, M. R., & Milvang-Jensen, B. 2006, MNRAS, 371, 1912 [NASA ADS] [CrossRef] (In the text)
- Bedregal, A. G., Aragón-Salamanca, A., Merrifield, M. R., & Cardiel, N. 2007, in Proc. IAU Symp., 241, 1 (In the text)
- Bender, R. 1988, A&A, 193, L7 [NASA ADS] (In the text)
- Bender, R., Surma, P., Döbereiner, S., et al. 1989, A&A 217, 35 (In the text)
- Bournaud, F., Jog, C. J., & Combes, F. 2007, A&A, 476, 1179 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Caon, N., & Einasto, M. 1995, MNRAS, 273, 913 [NASA ADS] (In the text)
- Cappellari, M. 2008, MNRAS, 390, 71 [NASA ADS] [CrossRef] (In the text)
- Cappellari, M. Bacon, R., Bureau, M., et al. 2006, MNRAS, 366, 1126 [NASA ADS] (In the text)
- Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418 [NASA ADS] [CrossRef] (In the text)
- Chandrasekhar, S. 1969, Ellipsoidal Figures of Equilibrium (New Haven: Yale Univ. Press) (In the text)
- Cohl, H. S., Tohline, & J. E. 1999, ApJ, 527, 86 [NASA ADS] [CrossRef] (In the text)
- Cresci, G., Davies, R. I., Baker, A. J., et al. 2006, A&A, 458, 385 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dankova, Ts., & Rosensteel, G. 1998, Am. J. Phys. 66, 1095 (In the text)
- Davies, R. L., & Illingworth, G. 1983, ApJ, 266, 516 [NASA ADS] [CrossRef] (In the text)
- De Propris, R., Colless, M., Driver, S. P., et al. 2005, MNRAS, 357, 590 [NASA ADS] [CrossRef] (In the text)
- Dressler A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] (In the text)
- Dressler, A., Oemler Jr., A., Couch, W. J., et al. 1997, ApJ, 490, 577 [NASA ADS] [CrossRef] (In the text)
- Emsellem, E., Cappellari, M., Peletier, R. F., et al. 2004, MNRAS, 352, 721 [NASA ADS] [CrossRef] (In the text)
- Emsellem, E., Cappellari, M., Krajnovic, D., et al. 2007a, MNRAS, 379, 401 [NASA ADS] [CrossRef] (In the text)
- Emsellem, E., Cappellari, M., Krajnovic, D., et al. 2007b, Proc. IAU Symp., 245, 1 (In the text)
- Eriguchi, Y., & Hachisu, I. 1982, Prog. Theor. Phys., 67, 844 [NASA ADS] [CrossRef] (In the text)
- Erwin, P., Beckman, J. E., & Beltrán, J. C. V. 2004, arxiv.org/pdf/0409103v1 (In the text)
- Fisher, D., Franx, M., & Illingworth, G. 1996, ApJ, 459, 110 [NASA ADS] [CrossRef] (In the text)
- Francis, C., & Anderson, E. 2009, arxiv.org/pdf/0901.3503v2 (In the text)
- Hao, C. N., Mao, S., Deng, Z. G., et al. 2006, MNRAS, 370, 1339 [NASA ADS] [CrossRef] (In the text)
- Helmboldt, J. F. 2007, MNRAS 379, 1227 (In the text)
- Hernandez, X., & Lee, W. H. 2004, MNRAS, 347, 1304 [NASA ADS] [CrossRef] (In the text)
- Hubble, E., 1926, AJ, 64, 321 [NASA ADS] [CrossRef] (In the text)
- Hubble, E. P. 1936, The Realm of the Nebulae (New Haven: Yale Univ. Press) (In the text)
- Jaffe, W., Ford, H. C., O'Connell, R. W., et al. 1994, AJ, 108, 1567 [NASA ADS] [CrossRef] (In the text)
- Jeans, J. H. 1928, Astronomy and Cosmogony (Cambridge: Cambridge Univ. Press) (In the text)
- Jørgensen, I., & Franx, M. 1994, ApJ, 433, 553 [NASA ADS] [CrossRef] (In the text)
- Jørgensen, I., Franx, M., & Kjærgaard P. 1996, MNRAS, 280, 167 [NASA ADS] (In the text)
- Kannappan, S. J., Guie, J. M., & Baker, A. J. 2009, AJ, 138, 579 [NASA ADS] [CrossRef]
- Katsiyannis, A. C., Boumis, P., & Meaburn, J. 2001, arxiv.org/pdf/0111443v1 (In the text)
- Kormendy, J., & Bender, R. 1996, ApJ, 464, L119 [NASA ADS] [CrossRef] (In the text)
- Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJ, Suppl. Ser., 182, 216 (In the text)
- Krajnovic, D., Bacon, R., Cappellari, M., et al. 2008, MNRAS, 390, 93 [NASA ADS] [CrossRef] (In the text)
- Larson, R. B. 1975, MNRAS, 173, 671 [NASA ADS] (In the text)
- Magorrian, J. 1999, MNRAS, 302, 530 [NASA ADS] [CrossRef] (In the text)
- Maller, A. H., Katz, N., Keres, D., et al. 2006, ApJ, 647, 763 [NASA ADS] [CrossRef] (In the text)
- Michard, R., & Marchal, J. 1994, Astron. Astrophys. Suppl. Ser. 105, 481 (In the text)
- Miyamoto, M., & Nagai, R. 1975, Publ. Astron. Soc. Japan, 27, 533 [NASA ADS] (In the text)
- Naab, T., & Ostriker J. P. 2009, ApJ 690, 1452 (In the text)
- Naab, T., & Burkert, A., & Hernquist, L. 1999, ApJ, 523, L133 [NASA ADS] [CrossRef] (In the text)
- Nieto, J.-L., & Bender, R. 1989, A&A, 215, 266 [NASA ADS] (In the text)
- Rix, H.-W., & White, S. D. M. 1990, ApJ, 362, 52 [NASA ADS] [CrossRef] (In the text)
- Sandage, A. 2005, ARA&A, 43, 581 [NASA ADS] [CrossRef] (In the text)
- Sandage, A., & Visvanathan, N. 1978, ApJ, 225, 742 [NASA ADS] [CrossRef] (In the text)
- Satoh, C. 1980, Publ. Astron. Soc. Japan, 32, 41 [NASA ADS] (In the text)
- Schachar, R. A., Liao, G. G., Kirby, R. D., et al. 2008, J. Phys. A: Math. Theor. 41, 495204 (In the text)
- Schawinski, K., Lintott, C., Thomas, D. et al. 2009, MNRAS, arxiv.org/pdf/0903.3415v1 (In the text)
- van den Bergh, S. 1980, Phil. Trans. R. Soc. Lond. A, 296, 319 [NASA ADS] [CrossRef] (In the text)
- Wilman, D. J., Oemler Jr., A., Mulchaey, J. S., et al. 2009, ApJ, 692, 298 [NASA ADS] [CrossRef] (In the text)
- Zhenglu, J. 2000, MNRAS, 319, 1067 [NASA ADS] [CrossRef] (In the text)
All Figures
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[width=17cm]{12220f1-new.eps}}\end{figure}](/articles/aa/full_html/2009/38/aa12220-09/Timg5.png) |
Figure 1: Photograph of a ``steep profile'' induced by applying traction in the 180 degree meridian to an oil film floating on water. The tractional pins extend into the oil film and not into the water below. |
| Open with DEXTER | |
| In the text | |
 |
Figure 2: Simulation of the effect of a circumferential equatorial disc on the shape of galaxy isodensity contours (solid curve) with aspect ratios = 0.6 and densities P = 0.1-0.0001, which all change into ``steep profiles'' (dashed curves). |
| Open with DEXTER | |
| In the text | |
 |
Figure 3: Simulation of the effect of a circumferential equatorial disc on the shape of galaxy isodensity contours (solid curve) with aspect ratios = 0.5 and densities P = 0.1-0.0001, which all change into ``steep profiles'' (dashed curves). |
| Open with DEXTER | |
| In the text | |
 |
Figure 4: Simulation of the effect of a circumferential equatorial disc on the shape of galaxy isodensity contours (solid curve) with aspect ratios = 0.4 and densities P = 0.1-0.0001, which all change into ``steep profiles'' (dashed curves). |
| Open with DEXTER | |
| In the text | |
 |
Figure 5: Simulation of the effect of a circumferential equatorial disc on the shape of galaxy isodensity contours (solid curve) with aspect ratios = 0.3 and densities P = 0.1-0.0001, which all change into ``steep profiles'' (dashed curves). |
| Open with DEXTER | |
| In the text | |
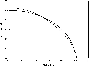 |
Figure 6: Reference ellipse (solid curve) and ``steep profile'' (dashed curve). |
| Open with DEXTER | |
| In the text | |
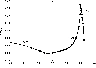 |
Figure 7:
Difference function
r - r |
| Open with DEXTER | |
| In the text | |
 |
Figure 8:
Difference |
| Open with DEXTER | |
| In the text | |
 |
Figure 9: Ellipse (solid curve), ``steep profile'' (dashed curve) and volume-corrected ``steep profile'' (dotted curve). |
| Open with DEXTER | |
| In the text | |
 |
Figure 10: A nearly edge-on photograph of lenticular galaxy NGC 2549 (Courtesy of Sloan Digital Sky Survey) with superposition of an oil film's ``steep profile'' outline on the lenticular galaxy's bulge. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\displaystyle {\frac{aR^2 +[q+3\sqrt{z^2 +
b^2}][a+\sqrt{z^2 + b^2}]}{\{ R^2 + [a + \sqrt{z^2 +
b^2}]^2\}^{\frac{5}{2}}(z^2+b^2)^{\frac{3}{2}}}}$](/articles/aa/full_html/2009/38/aa12220-09/img8.png) ,
,![$\displaystyle {\frac{X^2 +[1+3\sqrt{Z^2 +
q^2}][1+\sqrt{Z^2+q^2}]^2}{\{X^2 + [1+\sqrt{Z^2 +
q^2}]^2)\}^{\frac{5}{2}}(Z^2+q^2)^{\frac{3}{2}}}}$](/articles/aa/full_html/2009/38/aa12220-09/img14.png) ,
,![$\displaystyle {\frac{q^2\{X^2 +[1+3\sqrt{Z^2 +
q^2}][1+\sqrt{Z^2+q^2}]^2\}}{\{X^2 + [1+\sqrt{Z^2 +
q^2}]^2)\}^{\frac{5}{2}}(Z^2+q^2)^{\frac{3}{2}}}}$](/articles/aa/full_html/2009/38/aa12220-09/img17.png) .
.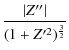 .
.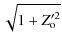 dX
dX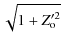 dX,
dX,