Study of star-forming galaxies in SDSS up to redshift 0.4

M. A. Lara-López; J. Cepa; A. Bongiovanni; A. M. Pérez García; H. Castañeda; M. Fernández Lorenzo; M. Pović; M. Sánchez-Portal

doi:10.1051/0004-6361/200912214

Free Access

Issue		A&A Volume 505, Number 2, October II 2009


Page(s)		529 - 539
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/200912214
Published online		11 August 2009

I. Metallicity evolution

M. A. Lara-López¹ - J. Cepa^1,2 - A. Bongiovanni¹ - A. M. Pérez García¹ - H. Castañeda^1,3 - M. Fernández Lorenzo¹ - M. Povic¹ - M. Sánchez-Portal⁴

1 - Instituto de Astrofísica de Canarias, 38200 La Laguna, Spain
2 - Departamento de Astrofísica, Universidad de la Laguna, Spain
3 - Departamento de Física, Escuela Superior de Física y Matemática, IPN, Mexico D.F., Mexico
4 - Herschel Science Center, INSA/ESAC, Madrid, Spain

Received 26 March 2009 / Accepted 2 July 2009

Abstract
Context. The chemical composition of the gas in galaxies over cosmic time provides a very important tool for understanding galaxy evolution. Although there are many studies at high redshift, they are rather scarce at lower redshifts. However, low redshift studies can provide important clues about the evolution of galaxies, furnishing the required link between the local and high redshift universe. In this work, we focus on the metallicity of the gas of star-forming galaxies at low redshift, looking for signs of chemical evolution.
Aims. We aim to analyze the metallicity contents star-forming galaxies of similar luminosities and masses at different redshifts. With this purpose, we present a study of the metallicity of relatively massive (log( $M_{\rm star}$ / $M_{\odot }$ ) $\gtrsim$ 10.5) star forming galaxies from SDSS-DR5 (Sloan Digital Sky Survey-data release 5), using different redshift intervals from 0.04 to 0.4.
Methods. We used data processed with the STARLIGHT spectral synthesis code, correcting the fluxes for dust extinction, estimating metallicities using the R₂₃ method, and segregating the samples with respect to the value of the [N II] $\lambda$ 6583/[O II] $\lambda$ 3727 line ratio in order to break the R₂₃ degeneracy selecting the upper branch. We analyze the luminosity and mass-metallicity relations, and the effect of the Sloan fiber diameter looking for possible biases.
Results. By dividing our redshift samples in intervals of similar magnitude and comparing them, significant signs of metallicity evolution are found. Metallicity correlates inversely with redshift: from redshift 0 to 0.4 a decrement of $\sim$ 0.1 dex in 12 + log(O/H) is found.

Key words: galaxies: abundances - galaxies: evolution - galaxies: starburst

1 Introduction

Determination of the chemical composition of the gas and stars in galaxies versus cosmic time provides a very important tool for understanding galaxy evolution, due to its important impact on fields such as stellar evolution and nucleosynthesis, gas enrichment processes, and the primary or secondary nature of the different chemical species. Historically, the main observational evidence suggestive of chemical evolution of galaxies has been provided by the observation of different chemical compositions of stars of different ages of the Milky Way and its environment (see the reviews by Audouze & Tinsley 1976; Wheelet et al. 1989; Wilson & Matteucci 1992; McWilliam 1997).

The study of the evolution of metal enrichment in galaxies is based mainly on two methods. One is based on the detection of absorption lines in QSO spectra produced by the neutral interstellar medium (ISM) of galaxies in the line-of-sight of the QSO (Prochaska et al. 2003), while the other uses emission lines of the warm ISM (H II regions) detected in the integrated galaxy spectra.

Optical emission lines in galaxies have been widely used to estimate abundances in extragalactic H II regions (e.g. Aller 1942; Searle 1971; Pagel 1986; Shields 1990, among others). Among the different methods developed to estimate metallicities, we can distinguish between theoretical models, empirical calibrations, or a combination of both (for a review see, e.g., Kewley & Dopita 2002; Kewley & Ellison 2008). The direct method to estimate metallicities in galaxies is known as the `` $T_{\rm e}$ method" (Pagel et al. 1992; Skillman & Kennicutt 1993), which consists of measuring the ratio of the [O III] $\lambda$ 4363 auroral line to a lower excitation line such as [O III] $\lambda$ 5007. Assuming a classical H II region model, this ratio provides an estimate of the electron temperature of the gas, which is then converted into metallicity (Osterbrock 1987). However, [O III] $\lambda$ 4363 is too weak to be easily observed, not only in metal rich, but even in metal poor galaxies, $Z < 0.5 \ Z_ \odot$ (log(O/H) + 12 < 8.6), and according to Kobulnicky et al. (1999), for low-metallicity galaxies, the [O III] $\lambda$ 4363 diagnostic systematically underestimates the global oxygen abundance. Also, the same authors show that for massive, metal-rich galaxies, empirical calibrations using strong emission-line ratios can be reliable indicators of the overall oxygen abundance in H II regions.

For these reasons, theoretical metallicity calibrations of strong-line ratios using photoionization models are used instead for determining abundances of high metallicity star-forming galaxies, such as: [N II] $\lambda$ 6584/[O II] $\lambda$ 3727 (Kewley & Dopita 2002) and the R₂₃ ratio, introduced by Pagel et al. (1979). The first one provides an excellent abundance diagnostic for $Z > 0.5 \ Z_ \odot$ (log(O/H) + 12 $\gtrsim$ 8.6), because $\rm {N}^{+}$ and $\rm {O}^{+}$ have similar ionization potentials, and this ratio is almost independent of ionization parameter. However it cannot be used at lower abundances ( $Z < 0.5 \ Z_ \odot$ ), where the metallicity dependence of the [N II] $\lambda$ 6584/[O II] $\lambda$ 3727 ratio is lost because nitrogen (like oxygen) is predominantly a primary nucleosynthesis element in this metallicity range (Kewley & Dopita 2002). The R₂₃ method is a widely used and well calibrated method (see for example Alloin et al. 1979; Edmunds & Pagel 1984; McCall et al. 1985; Dopita & Evans 1986; McGaugh 1991; Zaritsky et al. 1994; Kewley & Dopita 2002; Kobulnicky & Kewley 2004; Tremonti et al. 2004, hereafter T04; Liang et al. 2006, hereafter L06). However, it has the disadvantages of being double-valued as a function of 12+ log(O/H), and that it depends on the ionization parameter, particularly for $Z < 0.5 \ Z_ \odot$ , being less sensitive to metallicity in this range.

Alternatively, when the direct method cannot be used, empirical calibrations can be obtained by fitting the relationship between direct $T_{\rm e}$ metallicities and strong-line ratios as well. Typical empirical calibrations are: the R₂₃ ratio (Pilyugin 2001; Pilyugin & Thuan 2005; Liang et al. 2007), from which Pilyugin (2001) derived an empirical calibration based on $T_{\rm e}$ metallicities for a sample of H II regions, the [N II] $\lambda$ 6583/ H $\alpha$ ratio (Pettini & Pagel 2004, hereafter PP04), and the ([O III] $\lambda$ 5007/H $\beta$ )/([N II] $\lambda$ 6583/H $\alpha$ ) ratio (O3N2), (PP04). Although the latest method is of little use when O3N2 $\gtrsim$ 2, at lower values the relation is relatively tight and linear (PP04).

As an example of a combined calibration, we have the N2 = [N II] $\lambda$ 6583/ H $\alpha$ method (Denicoló et al. 2002), which follows a linear relation with log(O/H) that holds approximately from 1/50th to twice the Solar value. This method is based on a fit to the relationship between the $T_{\rm e}$ metallicities and the [N II] $\lambda$ 6583/H $\alpha$ ratio, of which some have metallicities derived using the $T_{\rm e}$ method, and the remaining metallicities were estimated using either the theoretical R₂₃ or an empirical method.

Nevertheless, comparisons among the metallicities estimated using different theoretical and empirical methods reveal large discrepancies (e.g., Pilyugin 2001; Bresolin et al. 2004; Garnett et al. 2004), with theoretical calibrations favouring higher metallicity values than those obtained using electron temperature estimations.

In the field of metallicity evolution versus cosmic time, there exist many studies, both theoretical and observational. Among the models we have, for example, that of Buat et al. (2008) and Kobayashi et al. (2007), who derived models of metallicity as a function of z, which show a progressive increase in metallicity with time, even at low redshift. Savaglio et al. (2005) developed an empirical model of metallicity evolution based on observations, in which the metallicity at z < 1 is an interpolation of that at higher redshifts. Also, Brooks et al. (2007) and Finlator & Davé (2008), among others, derived cosmological models of the mass-metallicity relation. The cosmic metal enrichment is attributed to a higher past volume-averaged star formation rate (see for example Madau et al. 1996; Lilli et al. 1996; Flores et al. 1999).

In addition, the metallicity and masses of galaxies are strongly correlated, with massive galaxies showing higher metallicities than less massive galaxies. This mass-metallicity (M-Z) relation has been intensively studied (Skillman et al. 1989; Brodie & Huchra 1991; Zaritsky et al. 1994; Richer & McCall 1995; Garnett et al. 1997; Pilyugin & Ferrini 2000, among others), and it is well established in the local universe ( $z \sim 0.1$ ) by the work of T04 using SDSS data. Regarding this evolution of the mass-metallicity relation of star-forming galaxies at high redshift, Erb et al. (2006) found that star-forming galaxies at redshift $\sim$ 2 have 0.3 dex fainter metallicities. Similarly, Maiolino et al. (2008) found evolution at $z \sim 3.5$ , which appears to be much stronger than the one observed at lower redshifts, suggesting that this redshift corresponds to an epoch of major activity in terms of star formation and metal enrichment. At intermediate redshifts (1 < z < 2), there are several important studies of the evolution of the chemical composition of the gas, such as the ones by Maier et al. (2006), Pérez-Montero et al. (2009), and Liu et al. (2008); the last one found that the zero point of the M-Z relation evolves with redshift, in the sense that galaxies at fixed stellar mass become more metal-rich at lower redshift.

Among the studies at z < 1, usually based on small samples, Savaglio et al. (2005) have investigated the mass-metallicity relations using galaxies at 0.4 < z < 1, finding that metallicity is lower at higher redshift by $\sim$ 0.15 dex, for the same stellar mass. Also, Maier at al. (2005), from a sample of 30 galaxies with 0.47 < z < 0.92, found that one-third have metallicities lower than those of local galaxies with similar luminosities and star formation rates. Consistently, Hammer et al. (2005) and Liang et al. (2006) found that at $z \sim 0.7$ , emission line galaxies were poorer in metals than present-day spirals by 0.3 dex. However, Kobulnicky & Kewley (2004) report a smaller variation of 0.14 dex for 0 < z < 1. This difference could be attributed to the fact that the last authors used equivalent widths and standard underlying stellar absorption, rather than high quality calibrated spectra to measure the Balmer absorption. Lilly et al. (2003), from a sample of 66 star forming galaxies with 0.47 < z < 0.92, found a smaller variation in metallicity of $\sim$ 0.08 dex compared with the metallicity observed locally, showing only modest evolutionary effects. On the contrary, Carollo & Lilly (2001), from emission-line ratios of 15 galaxies in a range of 0.5 < z < 1, found that their metallicities appear to be remarkably similar to those of local galaxies selected with the same criteria. A similar result, consistent with no significant evolution, was found for the luminosity-metallicity relation by Lamareille et al. (2006), comparing 131 intermediate redshift star-forming galaxies ( 0.2 < z < 1, split in 0.2 redshift bins). However, a recent study of Lamareille et al. (2009) focused on the evolution of the M-Z relation up to $z \sim 0.9$ , suggesting that the M-Z relation is flatter at higher redshifts. At $z \sim 0.77$ , galaxies of 10^9.4 solar mass have -0.18 dex lower metallicities than galaxies of similar mass in the local universe, while galaxies of 10^10.2 solar mass have -0.28 dex lower metallicities.

These discrepancies point to a need to study lower redshift galaxy samples, to ascertain whether or not at such low redshifts (i.e. an age of 8.4 Gyr for $z \sim 0.5$ , using a concordance $\Lambda$ -CDM cosmology, H₀=70, $\Omega_{\rm m}=0.3$ and $\Omega_\Lambda=0.7$ ; Spergel et al. 2003) there exists evidence for metallicity evolution, and also to serve as a calibrator of higher redshift studies. However, to be able to compare different redshift samples, it is advisable to use the same method for estimating metallicities, since, as explained above, theoretical and empirical calibrations generate discrepancies in the metallicity estimates depending on the used method.

The SDSS database provides an excellent opportunity to extend these studies down to $z \sim 0.4$ , in order to explore the possible evolution of metallicity at low redshift, but using large samples, thus deriving more statistically significant results. In this paper, we extend the study presented in our previous article (Lara-López et al. 2009, hereafter L09), from 207 to more than 12 000 galaxies, spanning more luminosity intervals in redshift bins of 0.1 from $\sim$ 0 to 0.4, and adding analyses of the mass and luminosity-metallicity relations, as well as of the origin of nitrogen in our galaxies.

This paper is structured as follows: in Sect. 2 we give a detailed description of the data used, in Sect. 3 we describe the metallicity estimates, the [N II] $\lambda$ 6583/[O II] $\lambda$ 3727 diagram and its metallicity distribution, in Sect 4 we investigate the origin of nitrogen in our galaxies, and in Sect. 5 we discuss our results taking into account the possible biases of our samples. Our conclusions are given in Sect. 6.

2 Sample selection

We analyzed the properties of a selected sample of emission lines galaxies from SDSS-DR5 (Adelman-McCarthy et al. 2007). Targets were observed using a 2.5 m telescope located at Apache Point Observatory (Gunn et al. 2006). The SDSS spectra were obtained through 3 arcsec diameter fibres, covering a wavelength range of 3800-9200 Å, and with a mean spectral resolution $\lambda$ / $\Delta\lambda$ $\sim$ 1800. The SDSS-DR5 spectroscopy database contains spectra for ${\sim}{10}^6$ objects over ${\sim}5700$ deg². Further technical details can be found in Stoughton et al. (2002).

We used the SDSS-DR5 spectra from the STARLIGHT database, which were processed through the STARLIGHT spectral synthesis code, developed by Cid Fernandes and colleagues (Cid Fernandes et al. 2005, 2007; Mateus et al. 2006; Asari et al. 2007). From them, we obtained the emission lines fluxes measurements of our samples from the contiuum subtracted spectra. For each emission line, STARLIGHT code returns the rest frame flux and its associated equivalent width, linewidth, velocity displacement relative to the rest-frame wavelength and the S/N of the fit. In the case of Balmer lines, the STARLIGHT code corrects for underlying stellar absorption using synthetic spectra obtained by fitting an observed spectrum with a combination of 150 simple stellar populations (SSPs) from the evolutionary synthesis models of Bruzual & Charlot (2003), computed using a Chabrier (2003) initial mass function, ``Padova 1994" evolutionary tracks (Alongi et al. 1993; Bressan et al. 1993; Fagotto et al. 1994a,b; Girardi et al. 1996), and STELIB library (Le Borgne et al. 2003). The 150 base elements span 25 ages between 1 Myr and 18 Gyr, and six metallicities, from Z=0.005 to 2.5 $Z_{\odot}$ ; for more details see Mateus et al. (2006).

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12214f1.ps} \end{figure}$

Figure 1:

Absolute Petrosian r-magnitude histograms. From top to bottom, histograms for the z₃, z₂, z₁, and z₀ sub-samples, respectively. The dot-dashed line represents the completeness for the z₃ sample, solid line shows the completeness for the z₂ sample, and dashed lines the completeness for the z₁ sample. All of them extend along the l-samples a, b and c, where N is the number of galaxies, respectively.

Open with DEXTER

Our objective is to study the chemical evolution of emission-line galaxies by comparing galaxies at different redshifts in small and equal ranges of luminosities. To this aim, our sample is divided in redshift intervals of 0.1 from $z \sim 0$ to 0.4. The purpose for selecting small ranges in luminosity is to alleviate the problem of the magnitude completeness, since the Sloan sample is only complete in the magnitude range 14.5 < m_r < 17.7 (e.g., Asari et al. 2007), and then becomes incomplete at redshift above z > 0.1 (e.g., Kewley et al. 2006). However, this procedure limits the study to the more luminous galaxies, since they are the ones detected at any redshift interval.

With this aim, our initial sample was divided in the following redshift intervals: z₀=(0.04-0.1), z₁=(0.1-0.2), z₂=(0.2-0.3) and z₃=(0.3-0.4). To ensure covering >20% of the light, we selected galaxies for the z₀ sub-sample with z > 0.04 , as recomended by Kewley et al. (2005). This preliminary selection give us 197 967 galaxies for z₀, 226012 for z₁, 42205 for z₂, and 38305 for the z₃ sub-samples. Absolute magnitudes were both K and Galactic extinction corrected, by using the code provided by Blanton et al. (2003), and the maps of Schlegel et al. (1998), respectively, as provided by the STARLIGHT team.

In order to determine the luminosity intervals at each redshift, we estimate the completeness of the absolute Petrosian r magnitude for each redshift-interval. We obtained our luminosity-complete samples selecting all galaxies brighter than the median for the larger redshift interval to be compared with, as shown in Fig. 1. According to that, we proceed constructing three luminosity-samples (hereafter l-samples): the l-sample a was constructed by taking the interval of the luminosity-completeness of z₁ ( -23.8 < M_r <-21.7); this allows comparison of redshift-intervals z₀, and z₁; in l-sample b we take the luminosity-completeness of z₂ (-24.8 < M_r <-22.9), to compare redshift-intervals z₂, and z₁; and in l-sample c we take the luminosity-completeness of z₃ (-24.8 < M_r <-23.1), to compare redshift-intervals z₃, z₂, and z₁, as shown in Table 1 and Fig. 1. As seen in this figure, it was not possible to introduce the z₀ redshift-sample for comparison with l-samples b and c, due to the small number of galaxies at their luminosity completeness.

Table 1: Luminosity-samples studied with their respective luminosity interval in absolute Petrosian r-magnitude, and the redshift samples that can be compared.

The resulting samples contain, for the l-sample b: 2352 galaxies for z₂ and 1386 for z₁; for l-sample a: 37777 for z₁ and 9288 for z₀. The l-sample c was already studied in L09.

From these samples we only consider galaxies whose spectra show the H $\alpha$ , H $\beta$ , [N II] $\lambda$ 6583, [O II] $\lambda$ 3727, [O III] $\lambda$ 4959 and [O III] $\lambda$ 5007 lines in emission, with H $\alpha$ , H $\beta$ , [N II] $\lambda$ 6583 and [O II] $\lambda$ 3727 signal-to-noise ratios higher than 3 $\sigma$ .

Finally, we selected star-forming galaxies following the criteria given by Kauffmann et al. (2003) in the Baldwin et al. (1981) diagram: log[O III] $\lambda$ 5007/H $\beta$ $\le$ 0.61/ $\{$ log([N II] $\lambda$ 6583/H $\alpha$ )-0.05 $\}$ + 1.3, used for example by Veilleux & Osterbrock (1987), Kewley et al. (2001, 2006), Stasinska et al. (2006), among others. After all these selections, the number of galaxies for each sample is, for the l-sample b: 335 galaxies for z₂, and 148 for z₁, and for the l-sample a: 10477 for z₁, and 1577 for z₀.

2.1 Dust extinction

Since Balmer lines are already corrected for underlying stellar absorption by the STARLIGHT code, it only remains to correct for dust extinction. Our extinction correction was derived using the Balmer decrements in order to obtain the reddening coefficient C(H $\beta$ ). Assuming case B recombination with a density of 100 cm^-3 and a temperature of 10⁴ K, the predicted ratio (unaffected by reddening or absorption) of H $\alpha$ /H $\beta$ is 2.86 (Osterbrock 1989), and the coefficient is given by:

$\begin{eqnarray*}{\rm C}({\rm H}\beta)=\frac{1}{f(\lambda)}\log \left[\frac{I({\... ...ta})}\bigg/ \frac{F({\rm {H}\alpha})}{F({\rm {H}\beta})}\right], \end{eqnarray*}$

where F( $\lambda$ ) and I( $\lambda$ ) are the observed and the theoretical fluxes, respectively, and f( $\lambda$ ) is the reddening curve normalized to H $\beta$ using the Cardelli et al (1989) law, with R_v = A_v/E(B - V)=3.1.

Once we have obtained the reddening coefficient for each galaxy of our samples, we proceed to estimate the corrected fluxes using $F_{\rm corr}$ ( $\lambda$ ) = $F_{\rm obs}(\lambda)10^{0.4 A_\lambda}$ , with

$\begin{eqnarray*}&&A_{\rm {H}\beta}=2.5{\;}C({\rm H}\beta)\\ &&A_{[{\rm {N~II}}... ...)\\ &&A_{[{\rm {O~II}}] \lambda3727}=3.303{\;} C({\rm H}\beta), \end{eqnarray*}$

as calculated from the prescription given by Cardelli et al. (1989).

3 Metallicity estimates and evolution

We estimate metallicities using the R₂₃ relation, introduced by Pagel et al. (1979),

$\begin{eqnarray*}R_{23}=([{{\rm O}~\textsc{ii}}] \lambda3727+[{{\rm O}~\textsc{iii}}] \lambda\lambda 4959, 5007)/{\rm H} \beta, \end{eqnarray*}$

adopting the calibration given by Tremonti et al. (2004),

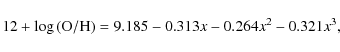$\begin{displaymath}12+\log {\rm (O/H)} = 9.185 - 0.313x - 0.264x^2 - 0.321x^3, \end{displaymath}$

(1)

where $x = \log R_{23}$ .

However, this calibration is valid only for the upper branch of the double-valued R₂₃ abundance relation, and additional line ratios, such as [N II] $\lambda$ 6583/[O II] $\lambda$ 3727, are required to break this degeneracy. Since the upper and lower branches of the R₂₃ calibration bifurcate at log([N II]/[O II]) $\sim$ -1.2 for the SDSS galaxies (Kewley & Ellison 2008), which corresponds to a metallicity of $12+\log {\rm (O/H)} \sim 8.4$ , we further select galaxies having $12+ \log{\rm (O/H)} > 8.4$ and log([N II]/[O II]) > -1.2, corresponding to the upper R₂₃ branch. Applying this final discrimination, we end for l-sample b with 331 galaxies for z₂ and 146 for z₁, and for l-sample a with 10434 galaxies for z₁ and 1576 for z₀. These are the samples that will be analyzed in this paper.

From these data, we derived the abundance-sensitive diagnostic diagram [N II] $\lambda$ 6583/[O II] $\lambda$ 3727 vs. $12+ \log {\rm (O/H)}$ , represented in Fig. 2. This diagram has also been used, for example, by Kewley & Dopita (2002), Nagao et al. (2006), and L06, among other metallicity-sensitive emission-line ratios, like log([N II] $\lambda$ 6583/H $\alpha$ ), log([O III] $\lambda$ 5007/H $\beta$ )/[N II] $\lambda$ 6583/H $\alpha$ ), and log([O III] $\lambda$ 4959, 5007/H $\beta$ ). We selected this specific diagram due to its low scatter and to the additional physical information that it provides. The advantages of using [N II] $\lambda$ 6583 and [O II] $\lambda$ 3727 lines are that they are not affected by underlying stellar population absorption, and because this ratio is almost independent of the ionization parameter, since $\rm {N}^{+}$ and $\rm {O}^{+}$ have similar ionization potentials. Of all the diagnostic diagrams cited before, this one presents the lowest scatter, and since both axes are sensitive to metallicity, possible signs of evolution could be easily identified in it.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12214f2.ps} \end{figure}$

Figure 2:

Calibration relation between 12+log(O/H) and log([N II] $\lambda$ 6583/[O II] $\lambda$ 3727). From top to bottom, l-sample a, b, and c. Circles, triangles, squares and asterisks represent galaxies for the redshift-sample z₀, z₁, z₂, and z₃, respectively. The solid line represents the best fit of the data using a linear fit, with the 2 $\sigma$ dispersion indicated by the short-dashed lines, while the dot-dash line shows the order-3 polynomial fit. (See the electronic edition of the Journal for a color version of this figure.)

Open with DEXTER

$\begin{figure} \includegraphics[width=8cm,clip]{12214f3.ps} \end{figure}$	Figure 3: Normalized metallicity histograms for our three l-samples. The dotted line represents the redshift sample interval z₀, dashed line the redshift sample z₁, solid line the redshift sample z₂ and dot-dash line the redshift-sample z₃. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER

For every l-sample of Fig. 2, we fit both a linear and an order three polynomial, obtaining the coefficients shown in Table 2.

Table 2: Coefficients for the l-samples.

To interpret our results, it is important to note that we are working with the integrated spectra, and it is well known that metallicity decreases with distance from the galaxy center (Garnett et al. 1997). As shown by Kewley et al. (2005), and L06 using the sample of Jansen et al. (2000), data points from nuclear spectra follow the SDSS galaxies nuclear spectra very well, but data points from the integrated spectra show lower $12~+~\log{\rm (O/H)}$ . Nuclear metallicities exceed metallicities derived from integrated spectra by $\sim$ 0.13 dex on average.

As shown in L09, for the l-sample c there is a clear decrement in the z₃ redshift-sample of $\sim$ 0.1 dex in $12+\log$ (O/H) with respect to the z₁ and z₂ redshift-samples. However, l-samples a and b, show only small decrements, indicating that the redshift 0.3 represents an important epoch in the evolution of galaxies. As argued by Kewley et al. (2008), using a single metallicity calibration, the difference in relative metallicities should be the same using any other metallicity calibration, although the absolute metallicities might differ from one calibration to another. Thus, our main result is a relative decrement in metallicity of $\sim$ 0.1 dex of z₃ with respect to the z₁ and z₂ redshift-samples of l-sample c.

Table 3: Mean and mode of the metallicity distributions, and the metallicity range that includes 66 $\%$ of the total metallicity distribution around the mode for the different luminosity samples.

In order to study the behaviour of the metallicities for the different l-samples, we proceed to generate a metallicity histogram for our three l-samples as shown in Fig. 3. In the histograms we can observe a shift to lower metallicities as redshift increases, which is more evident in l-sample c, as argued in L09. L-samples a and b do not show any important variation in metallicity, as can be seen in Table 3. As a measure of the dispersion of the histograms, we estimated the interval that encompasses 66 $\%$ of the galaxies around the mode of the distribution. With this criterion, we find for l-sample a, an interval of 0.16 dex in $12+\log$ (O/H) for z₀, and 0.17 dex for z₁; for l-sample b, 0.17 dex for z₁, and 0.16 for z₂, and for l-sample c, 0.26 dex for z₁, 0.18 for z₂, and 0.35 for z₃. As can be observed in Table 3, the dispersion of the metallicity histograms increases for the samples with the more limited number of galaxies, as can be seen in l-sample c for z₁ and z₃.

For the redshift samples, we observe a maximum metallicity for z₀, followed by a small decrement in metallicity for redshift z₁ which remains constant for z₂, and then a significant decrement for z₃. As indicated by Carollo et al. (2001), the redshift interval 0.5< z < 1 represents a transition between the high-redshift universe at z > 1 and that seen today. Then evolutionary effects should be more evident in the galaxy population at these redshifts. Nevertheless, in this work we find a significant metallicity evolution at redshift 0.3.

4 Nitrogen and oxygen abundances

The primary and secondary origin of nitrogen is of importance in understanding the processes inside stars, and the evolution of galaxies. Although this is not the aim of this paper, we are in a position to investigate the origin of nitrogen in our galaxy samples.

The nuclear mecanism producing nitrogen in stellar interiors result from the CN cycle of the CNO reactions, which takes place in the stellar hydrogen burning layer, with the net result that ¹⁴N is synthesized from ¹²C and ¹⁶O (Meynet & Maeder 2002; Pettini et al. 2008). Nitrogen can be of either primary or secondary origin. If the oxygen and carbon are produced in the star prior to the CNO cycling, then the amount of nitrogen produced is said to be primary. If initial amounts of oxygen and carbon are incorporated into a star at its formation, and a constant mass fraction is processed, then the amount of nitrogen produced is proportional to the initial heavy-element abundance, and the nitrogen is said to be of secondary origin (Vila-Costas & Edmunds 1993).

Several autors (Edmunds & Pagel 1978; Barbuy 1983; Tomkin & Lambert 1984; Matteucci 1986; Carbon et al. 1987; Henry et al. 2000) demonstrated that the ratio of nitrogen to oxygen remains constant at lower metallicities, Z < 0.5 $Z_{\odot}$ [log(O/H) + 12 $\lesssim$ 8.3, adopting 12 + log(O/H) $_{\odot}=8.66$ from Asplund et al. (2005)], with a plateau at log(N/O) $\sim$ -1.5 in the early evolution of the galaxy, thus implying a primary origin of nitrogen. When the oxygen abundance is greater than $Z \sim 0.5~Z_{\odot}$ , the N/O ratio rises steeply with increasing O/H. This is the regime where nitrogen is predominantly secondary (Alloin et al. 1979; Considère et al. 2000; Pettini et al. 2008). The fact that the N/O ratio is relatively flat at low metallicities indicates that production of nitrogen is dominated by primary processes at low metallicities, and by secondary processes at high metallicities (Garnett et al. 1997; Ferguson et al. 1998; Henry & Worthey 1999).

In order to determine the origin of nitrogen in our l-samples, we estimated the nitrogen abundances for these galaxies. To estimate the electron temperature in the [N II] emission region ( $T_{[{\rm {{N_{II}}}}]}$ ) from log R₂₃, we used the formula given by Thurston et al. (1996),

$\begin{eqnarray*}T_{[{\rm {{N_{II}}}}]} = 6065 + 1600(\log R_{23}) + 1878(\log R_{23}) + 2803(\log R_{23}), \end{eqnarray*}$

with $T_{[{\rm {{N_{II}}}}]}$ in units of K. The ionic abundance ratio is estimated from the $T_{[{\rm {{N_{II}}}}]}$ temperature and the emission-line ratio ([N II] $\lambda\lambda$ 6548, 6583)/([O II] $\lambda$ 3727) by assuming N/O = $\rm {N}^{+}/\rm {O}^{+}$ , and the flux of [N II] $\lambda$ 6548 = (1/3) [N II] $\lambda$ 6583. With these, we apply the formula given by Pagel et al. (1992), based upon a five-level atom calculation:

$\begin{eqnarray*}\log\left({\frac{\rm {N}^{+}}{\rm {O}^{+}}}\right)~&=&~\log \le... ...log t_{[{\rm {N}_{II}}]} - {\frac{0.726}{t_{[{\rm {N}_{II}}]}}}, \end{eqnarray*}$

where $t_{[{\rm {{N_{II}}}}]}$ = 10^-4 $T_{[{\rm {{N_{II}}}}]}$ .

$\begin{figure} \par\includegraphics[width=17cm,clip]{12214f4.ps} \end{figure}$

Figure 4:

Abundances of N and O ratios as a function of their $12+\log$ (O/H) abundances derived from the R₂₃ calibration for our three l-samples in redshift, following the same code of symbols used in Fig. 2. The dot-dashed line and the dashed line represent an aproximation of empirical limits of the primary and secondary levels, respectively, of N production, taken from Vila-Costas & Edmunds (1993). (See the electronic edition of the Journal for a color version of this figure.)

Open with DEXTER

$\begin{figure} \par\includegraphics[width=17cm,clip]{12214f5.ps} \end{figure}$	Figure 5: Absolute Petrosian r magnitude and $12+\log$ (O/H) for our l-sample of galaxies (L-Z relation). Symbols follow the same code used in Fig. 2. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER

In Fig. 4, the abundances of N and O are shown as a function of $12+\log$ (O/H). Because nitrogen is predominantly a secondary element above metallicities of about half solar, the galaxies of our samples mainly have nitrogen of secondary origin, as can be seen in Fig. 4. This is because we are working with both massive, log( $M_{\rm star}$ / $M_{\odot}) \gtrsim 10.5$ (see Fig. 6), and high metallicity galaxies. In spite of our high metallicities, we can observe signs of a horizontal population in l-sample a at log(N/O) $\sim$ -1.2, in a range of metallicities from 8.4 to $\sim$ 8.6, which is a little higher than the standard value [log(N/O) $\sim -1.5$ ], but comparable to the results obtained by Pettini et al. (2008) and Considère et al. (2002), who shown a population of galaxies in the same region. This result is not surprising, because, as argued above, the transition zone from primary to secondary production of nitrogen occurs at $12+\log$ (O/H) $\sim 8.3$ , which is close to our lower limit.

Because low metallicity galaxies ( $12+\log$ (O/H) < 8.3) are absent in our samples, nothing can be concluded for the primary production of nitrogen.

5 Discussion

To investigate whether the origin of the decrement in metallicity is due to instrumental effects, to an inherent property of the sample of galaxies, or a mixture of both, it is necessary to explore two important effects: the luminosity and mass-metallicity relations, and the effect of the 3 arcsec diameter of the Sloan fibers.

5.1 Effect of the mass and luminosity-metallicity relations

The luminosity-metallicity (L-Z) relation was first observed by McClure & van den Bergh (1968) in elliptical galaxies, and confirmed by Garnett & Shields (1987), while the mass-metallicity relation was first identified for irregular and blue compact galaxies by Lequeux et al. (1979), and Kinman & Davidson (1981), respectively, and confirmed by Skillman et al. (1989). Since then, as luminosities are easier to estimate than masses, many studies have focused on the L-Z relation (e.g., Skillman et al. 1989; Brodie & Huchra 1991; Zaritsky et al. 1994; Garnett et al. 1997; Lamareille et al. 2004, 2006; Maier et al. 2004), which correlates the absolute magnitude of galaxies with metallicity, the more metal rich being more luminous. The M-Z and L-Z relations have been studied at both low and high redshift (e.g. T04; Savaglio et al. 2005; Erb et al. 2006; Maiolino et al. 2008; Lamareille et al. 2009).

There are two main ways to explain the origin of the M-Z relation, one is attributed to metal and baryon loss due to gas outflow, where low-mass galaxies eject large amounts of metal-enriched gas by supernovae winds before high metallicities are reached, while massive galaxies have deeper gravitational potentials which helps to retain their gas, thus reaching higher metallicities (Larson 1974; Dekel & Silk 1986; MacLow & Ferrara 1999; Maier et. al. 2004; T04; De Lucia et al. 2004; Kobayashi et al. 2007; Finlantor & Dave 2008). A second scenario to explain the M-Z relation is by assuming low star formation efficiencies in low-mass galaxies (Efstathiou 2000; Brooks et al. 2007; Mouhcine et al. 2008; Tassis et al. 2008; Scannapieco et al. 2008).

As pointed out in the high-resolution simulations of Brooks et al. (2007), supernovae feedback plays a crucial role in lowering the star formation efficiency in low-mass galaxies. Without energy injection from supernovae to regulate the star formation, gas that remains in galaxies rapidly cools, forms stars, and increases its metallicity too early, producing a M-Z relation too flat compared to observations. However, Calura et al. (2009) reproduced the M-Z relation with chemical evolution models for ellipticals, spirals and irregular galaxies, by means of an increasing efficiency of star formation with mass in galaxies of all morphological types, without the need for outflows favoring the loss of metals in the less massive galaxies. A recent study that supports this result for massive galaxies is that of Vale Asari et al. (2009), modelling the time evolution of stellar metallicity using a closed-box chemical evolution model. They suggest that the M-Z relation for galaxies in the mass range from 10^9.8 to 10^11.65 $M_{\odot }$ is mainly driven by the star formation history and not by inflows or outflows.

$\begin{figure} \par\includegraphics[width=17.2cm,clip]{12214f6.ps} \end{figure}$	Figure 6: Relation between stellar mass, in units of solar masses, and $12+\log$ (O/H) for our l-sample of galaxies (M-Z relation). The dashed line represents the fit of Tremonti et al. (2004), and symbols follow the same code used in Fig. 2. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER

Table 4: Median Petrosian r magnitude (M_r), median of the logarithm-mass [log( $M_{\rm star}$ / $M_{\odot }$ )], and the logarithm-mass range that include 66 $\%$ of the total mass distribution around the median logarithm-mass value for l-samples a, b, and c.

As explained in Sect. 2, we selected small intervals of luminosity for all redshift samples. Such a selection was aimed to avoid possible biases since the SLOAN star-forming sample becomes incomplete at redshifts above z > 0.1 (e.g., Kewley et al. 2006). Then, this could introduce a bias, since our high-redshift sample is formed by the most luminous galaxies, resulting in higher metallicity estimates.

As can be seen from Fig. 5, the galaxies of our samples do not show a luminosity-metallicity dependence, since this relation can be clearly seen only when spanning ranges of more than $\sim$ 4 mag in luminosity (e.g. T04). The masses of our galaxies were estimated in order to check their behaviour in our luminosity intervals with the STARLIGHT code, using a Chabrier (2003) initial mass function between 0.1 and 100 $M_{\odot }$ ; for details on the mass estimates, see Mateus et al. (2006). The M-Z diagram for our l-samples do not show any correlation either, as can be seen in Fig. 6, since masses again correspond to a small interval in luminosity for each redshift bin.

For each l-sample, we overplot the polynomial fit of the local M-Z relation of Tremonti et al. (2004), which is valid over the range $8.5 < \log(M_{\rm star}{/}M_{\odot}$ ) < 11.5, with a steep M-Z relation for masses from 10^8.5 to 10^10.5 $M_{\odot }$ that flattens at higher masses. As can be seen in Fig. 6, galaxies of the l-sample a, b and c, correspond to this flat and massive zone [log( $M_{\rm star}$ / $M_{\odot }$ ) > 10.5] of the M-Z relation, for the reasons discussed above. The mass ranges where we can find two thirds ( $\sim$ 66 $\%$ ) of each l-sample are shown in Table 4, as well as the median Petrosian r magnitude, and the median mass in log( $M_{\rm star}$ / $M_{\odot }$ ).

5.2 Effects of the Sloan fiber diameter

With respect to the Sloan fiber diameter, and depending on the galaxy size, we expect that at higher redshift the projected size of the Sloan fibers will cover a larger fraction of the galaxy area than for nearby galaxies. This effect, as argued in Sect. 3, could introduce a bias in our samples since integrated metallicities are lower than nuclear ones. In order to quantify this contribution, we estimate the percentage of angular size of each galaxy inside the three arcsec diameter of the Sloan fiber using the Petrosian total radius in the r-band in arcsec. To this aim, we divide the fibre radius (1.5 arcsec) by the Petrosian total radius in the r-band (petrorad_r), as can be seen in the histograms of Fig. 7 for all our l-samples. Thus, this ratio can be taken as the fraction of the galaxy size that is actually covered by the fibre.

As expected, in all l-samples the distribution shifts to a maximum coverage of the galaxy size as redshift increases. This is an effect that must be taken into account, because it could change the metallicity estimation according to the fraction of galaxy diameter inside the Sloan fiber. As argued in L09, the decrement observed in metallicity for l-sample c cannot be atributed to the percentage of the galaxy inside the Sloan fiber, because fibers cover less than 50 $\%$ of galaxy sizes for $\sim$ 95 $\%$ of this sample. However, the effect could be noticeable at lower redshifts.

$\begin{figure} \par\includegraphics[width=5.5cm,clip]{12214f7.ps}\hspace{1mm} \... ...4f8.ps}\hspace{1mm} \includegraphics[width=5.5cm,clip]{12214f9.ps} \end{figure}$	Figure 7: Percentage of angular size of each galaxy inside the three arcsec diameter of the Sloan fiber for l-samples a, b, and c.
Open with DEXTER

To minimize systematic errors from this aperture bias, as explained in Sect. 2, we selected galaxies with z > 0.04 following the recommendations of Kewley et al. (2005), who investigate the effects of a fixed-size aperture on spectral properties for a large range of galaxy types and luminosities, concluding that a minimum flux covering fraction of 20 $\%$ , corresponding to a median redshift of $z \sim 0.04$ , is required for metallicities to approximate the global values. In Fig. 7 we plot the percentage of angular size of each galaxy inside the three arcsec diameter of the Sloan fiber, which is not the same as the flux covering fraction used by Kewley et al. (2005).

However, in spite of this redshift limit and in order to test how much the percentage of angular size inside the Sloan fiber diameter affect our metallicities, we compare in Fig. 8 our original metallicity estimates of redshift sample z₀ with that from galaxies with a percentage of angular size within the fiber >20 $\%$ , which corresponds to 45 $\%$ of the sample. We observe that the result is the same, with a quite small difference in the mean of the order of $\sim$ 0.001 in 12 + log(O/H) for galaxies with a percentage of angular size within the fiber >20 $\%$ .

If the redshift sample z₀, which contains a maximum fraction of galaxies with a percentage of angular size <20 $\%$ inside the Sloan fiber diameter, does not show variations in the mean metallicity, we can assume that none of our samples are significantly affected by aperture effects due to the Sloan fiber diameter.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12214f10.ps} \end{figure}$	Figure 8: Normalized metallicity histograms for redshift sample z₀. The dotted clear line is the same as in Fig. 3a, and the dotted dark line represents galaxies of the same redshift sample with covering fraction >20. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER

6 Conclusions

Although similar studies of metallicity using SDSS exists, they are either restricted to a redshift $\sim$ 0.1 (e.g. T04), or do not segregate their samples as a function of redshift (e.g. L06), thus making it not possible to detect metallicity evolution at low redshift. On the other hand, studies at high redshift are statistically limited.

We divided our sample in redshift intervals of $\Delta z \sim 0.1$ with the goal of identifying any evolution in metallicity, and each redshift in small intervals of luminosity in order to avoid biases due to the luminosity and mass-metallicity relations. Because we are comparing galaxies from redshift 0.04 to 0.4, we selected luminous and massive galaxies [ $\sim$ log( $M_{\rm\rm star}$ / $M_{\odot }$ ) > 10.5], which are present in all redshift intervals.

We conclude that the nitrogen production for our sample of galaxies is mainly secondary, because our sample is formed by massive, luminous and high metallicity galaxies. In this work we cannot conclude anything about the production of nitrogen in low mass galaxies.

We derived the M-Z and L-Z relations for our sample of galaxies, showing a flat L-Z relation, and an M-Z relation populated only in the massive zone $\sim$ log( $M_{\rm star}$ / $M_{\odot }$ ) > 10.5, which is due to the absence of dwarf galaxies. Both relations behave as expected since our sample is selected to cover the more luminous and hence massive galaxies.

Since we have metallicity estimates for redshifts up to 0.4 in bins of 0.1, we are able to represent redshift versus metallicity, as shown in Fig. 9. We plotted the mean metallicity for all l-samples a, b, and c. Error estimates of the mean metallicity were obtained from the line error fluxes provided by STARLIGHT, taking into account the number of galaxies of each sample.

As shown in Fig. 9, we can observe, for l-sample a, an initial metallicity of $\sim$ 9.02 for z₀, followed by a small decrease in metallicity for z₁. For l-sample b, the metallicity of z₁ and z₂ remains constant, a trend also observed for l-sample c in the same redshift samples, but with lower metallicity values, and finally a large decrement for z₃. We overplot the model of Buat et al. (2008) for galaxies with a rotational velocity of 360 km/s, which corresponds to a log( $M_{\rm star}$ / $M_{\odot }$ ) $\sim 11.2$ in their model.

Since the model of Buat et al. (2008) is calibrated in solar metallicities, with log( $Z{/}Z_{\odot}$ ) $\sim$ -0.03 at redshift zero, we assume a solar metallicity of 12 + log(O/H) =9.05 in order to match his fit to our metallicity values, finding a good correlation between their model and our metallicity dependence versus redshift. Finally, we fit a second order polynomial ( y=a₀+a₁x+a₂x²), with a₀=9.018, a₁=0.015, and a₃=-0.799, (see Fig. 9).

Our results are also in good agreement with those of Rodrigues et al. (2008), who find a linear evolution of metallicity as a function of the lookback time for galaxies at 0.5 < z < 3, by extrapolating their fit to redshifts lower than 0.4. This gives further support to the idea, demonstrated in the present paper, that the evolution of the gas phase in massive galaxies is still active down to z=0.4.

This result is valid for massive, luminous, and high metallicity galaxies. Lower metallicity and stellar mass galaxies are absent from our sample due to the selection criteria applied.

Although it is well known that metallicities decrease with redshift, it is the first time that a statistically significant sample of galaxies is analyzed looking for metallicity evolution at such a low redshift, detecting small decrements as redshift increases, with prima facie evidence of a significant decrement at the redshift interval 0.3-0.4, as already pointed out in L09.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12214f11.ps} \end{figure}$

Figure 9:

Metallicity evolution derived from our l-samples up to redshift 0.4, vertical lines show the error with respect to the mean metallicity for every redshift interval. Circles, triangles and asterisks, represent the mean metallicity of the l-samples a, b and c, with its respective redshift-samples. Solid line represents the model of Buat et al. (2008) for galaxies with a rotational velocity of 360 km s^-1, and dashed line represents a second-order polynomial fit. (See the electronic edition of the Journal for a color version of this figure.)

Open with DEXTER

Acknowledgements

This work was supported by the Spanish Plan Nacional de Astronomía y Astrofísica under grant AYA2008-06311-C02-01. The Sloan Digital Sky Survey (SDSS) is a joint project of The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, the Max-Planck-Institute for Astronomy, Princeton University, the United States Naval Observatory, and the University of Washington. Apache Point Observatory, site of the SDSS, is operated by the Astrophysical Research Consortium. Funding for the project has been provided by the Alfred P. Sloan Foundation, the SDSS member institutions, the National Aeronautics and Space Administration, the National Science Foundation, the US Department of Energy, and Monbusho. The official SDSS web site is www.sdss.org. We thank the STARLIGHT project team (UFSC, Brazil), specially William Schoenell, who helped us downloading the whole data set. We thank Veronique Buat and Samuel Boissier for providing the data of their metallicity evolution model. We also thank the anonymous referee for his/her meticulous revision of the manuscript and for the constructive comments. Maritza A. Lara-López is supported by a CONACyT and SEP mexican fellowships.

References

Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2007, ApJS, 172, 634 [NASA ADS] [CrossRef] (In the text)
Aller, L. H. 1942, ApJ, 95, 52 [NASA ADS] [CrossRef] (In the text)
Alloin, D., Collin-Souffrin, S., Joly, M., & Vigroux, L. 1979, A&A, 78, 200 [NASA ADS] (In the text)
Alongi, M., Bertelli, G., Bressan, A., et al. 1993, A&AS, 97, 851 [NASA ADS] (In the text)
Asari, N. V., Cid Fernandes R., Stasinska G., et al. 2007, MNRAS, 381, 263 [NASA ADS] [CrossRef] (In the text)
Audouze, J., & Tinsley, B. M. 1976, ARA&A, 14, 43 [NASA ADS] [CrossRef] (In the text)
Baldwin, J., Phillips, M., & Terlevich, R., 1981, PASP, 93, 5 [NASA ADS] [CrossRef]
Barbuy, B. 1983, A&A, 123, 1 [NASA ADS] (In the text)
Blanton, M. R., Brinkmann, J., Csabai, I., et al. 2003, AJ, 125, 2348 [NASA ADS] [CrossRef]
Bresan, A., Fagotto, F., Bertelli, G., & Chiosi, C. 1993, A&AS, 100, 647 [NASA ADS]
Bresolin, F. 2006, [arXiv:astro-ph/0608410]
Brodie, J. P., & Huchra, J. P. 1991, ApJ, 379, 157 [NASA ADS] [CrossRef] (In the text)
Brooks, A. M., Governato, F., Booth, C. M., et al. 2007, ApJ, 655, L17 [NASA ADS] [CrossRef] (In the text)
Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] (In the text)
Buat, V., Boissier, S., Burgarella, D., et al. 2008, A&A, 483, 107 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Calura, F., Pipino, A., Chiappini, C., Matteucci, F., & Maiolino, R. 2009, [arXiv:0904.2180] (In the text)
Carbon, D. F., Barbuy, B., Kraft, R. P., Friel, E. D., & Suntzeff, N. B. 1987, PASP, 99, 335 [NASA ADS] [CrossRef] (In the text)
Cardelli, J. A., Clayton G. C., & Mathis J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
Carollo, C. M., & Lilly, S. J. 2001, ApJ, 548, L153 [NASA ADS] [CrossRef] (In the text)
Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] (In the text)
Cid Fernandes, R., Mateus A., Sodré L., Stasinska G., & Gomes J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] (In the text)
Cid Fernandes, R., Asari, N. V., Sodré, L., et al. 2007, MNRAS, 375, L16 [NASA ADS] (In the text)
Considère, S., Coziol, R., Contini, T., & Davoust, E. 2000, A&A, 356, 89 [NASA ADS] (In the text)
Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] (In the text)
De Lucia, G., Kauffman, G., & White, S. D. M., 2004, MNRAS, 349, 1101 [NASA ADS] [CrossRef]
Denicoló, G., Terlecivh, R., & Terlevich, E. 2002, MNRAS, 330, 69 [NASA ADS] [CrossRef] (In the text)
Dopita, M. A., & Evans, I. N. 1986, ApJ, 307, 431 [NASA ADS] [CrossRef] (In the text)
Edmunds, M. G., & Pagel, B. E. J. 1978, MNRAS, 185, 77 [NASA ADS] (In the text)
Edmunds, M. G., & Pagel, B. E. J. 1984, MNRAS, 211, 507 [NASA ADS] (In the text)
Efstathiou, G. 2000, MNRAS, 317, 697 [NASA ADS] [CrossRef] (In the text)
Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] (In the text)
Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994a, A&AS, 104, 365 [NASA ADS] (In the text)
Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994b, A&AS, 105, 29 [NASA ADS]
Ferguson, A. M. N., Gallagher, J. S., & Wyse, R. F. G. 1998, AJ, 116, 673 [NASA ADS] [CrossRef] (In the text)
Finlator, K., & Davé, R. 2008, MNRAS, 385, 2181 [NASA ADS] [CrossRef] (In the text)
Flores, H., Hammer, F., Thuan, T. X., et al. 1999, ApJ, 517, 148 [NASA ADS] [CrossRef] (In the text)
Garnett, D. R., & Shields, G. A. 1987, ApJ, 317, 82 [NASA ADS] [CrossRef] (In the text)
Garnett, D. R., Shields, G. A., Skillman, E. D., Sagan, S. P., & Dufour, R. J. 1997, ApJ, 489, 36 [NASA ADS] [CrossRef] (In the text)
Garnett, D. R., Kennicutt, R. C., & Bresolin, F. 2004, ApJ, 607, L21 [NASA ADS] [CrossRef] (In the text)
Girardi, L., Bressan, A., Chiosi, C., Bertelli, G., & Nasi, E. 1996, A&AS, 117, 113 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] (In the text)
Hammer, F., Flores, H., Elbaz, D., et al. 2005, A&A, 430, 115 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Henry, R. B. C., & Prochaska Jason X. 2007, PASP, 119, 962 [NASA ADS] [CrossRef]
Henry, R. B. C., & Worthey, G. 1999, PASP, 111, 919 [NASA ADS] [CrossRef] (In the text)
Henry, R. B. C., Edmunds, M. G., & Köppen, J. 2000, ApJ, 541, 660 [NASA ADS] [CrossRef] (In the text)
Jansen, R. A., Fabricant, D., Franx, M., & Caldwell, N. 2000, ApJS, 126, 331 [NASA ADS] [CrossRef] (In the text)
Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [NASA ADS] [CrossRef] (In the text)
Kennicutt, R. C., Jr., Bresolin, F., & Garnett, D. R. 2003, ApJ, 591, 801 [NASA ADS] [CrossRef]
Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] (In the text)
Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] (In the text)
Kewley, L. J., Dopita M. A., Sutherland R. S., Heisler C. A., & Trevena J. 2001, ApJ, 556, 121 [NASA ADS] [CrossRef] (In the text)
Kewley, L. J., Jansen, R. A., & Geller, M. J. 2005, PASP, 117, 227 [NASA ADS] [CrossRef] (In the text)
Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [NASA ADS] [CrossRef] (In the text)
Kinman, T. D., & Davidson, K. 1981, ApJ, 243, 127 [NASA ADS] [CrossRef] (In the text)
Kobayashi, C., Springel, V., & White, S. D. M. 2007, MNRAS, 376, 1465 [NASA ADS] [CrossRef] (In the text)
Kobulnicky, H. A., & Kewley, L. J. 2004, ApJ, 617, 204 [NASA ADS] [CrossRef] (In the text)
Kobulnicky, H. A., Kennicutt , R. C., & Pizagno, J. L. 1999, ApJ, 514, 544 [NASA ADS] [CrossRef] (In the text)
Kobulnicky, H. A., Willmer, C. N. A., Phillips, A. C., et al. 2003, ApJ, 599, 1006 [NASA ADS] [CrossRef]
Lamareille, F., Mouhcine, M., Contini, T., Lewis, I., & Maddox, S. 2004, MNRAS, 350, 396 [NASA ADS] [CrossRef] (In the text)
Lamareille, F., Contini, T., Brinchmann, J., et al. 2006, A&A, 448, 907 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lamareille, F., Brinchmann, J., Contini, T., et al. 2009, A&A, 495, 53 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2008 A&A, 493, L5 (L09)
Larson, R. B. 1974, MNRAS, 169, 229 [NASA ADS] (In the text)
Le Borgne, J.-F., Bruzual, G., Pelló, R., et al. 2003, A&A, 402, 433 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lequeux, J., Rayo, J.-F., Serrano, A., Peimbert, M., & Torres-Peimbert, S. 1979, A&A, 80, 155 [NASA ADS] (In the text)
Liang, Y. C., Yin, S. Y., Hammer, F., et al. 2006, ApJ, 652, 257 [NASA ADS] [CrossRef] (L06) (In the text)
Liang, Y. C., Hammer, F., Yin, S. Y., et al. 2007, A&A, 473, 411 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lilly, S. J., Le Fèvre, O., Hammer, F., & Crampton, D. 1996, ApJ, 460, L1 [NASA ADS] [CrossRef]
Lilly, S. J., Carollo, C. M., & Stockton, A. 2003, ApJ, 597, 730 [NASA ADS] [CrossRef] (In the text)
Liu, X., Shapley, A. E., Coil, A. L., Brinchmann, J., & Ma, C.-P. 2008, ApJ, 678, 758 [NASA ADS] [CrossRef] (In the text)
MacLow, M., & Ferrara, A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef] (In the text)
Madau, P., Ferguson, H. C., Dickinson, M. E., et al. 1996, MNRAS, 283, 1388 [NASA ADS] (In the text)
Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Maier, C., Meisenheimer, K., & Hippelein, H. 2004, A&A, 418, 475 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Maier, C., Lilly, S., Carollo, C. M., Stockton, A., & Brodwin, M. 2005, ApJ, 634, 849 [NASA ADS] [CrossRef] (In the text)
Maier, C., Lilly, S., Carollo, C. M., et al. 2006, ApJ, 639, 858 [NASA ADS] [CrossRef] (In the text)
Matteucci, F. 1986, MNRAS, 221, 911 [NASA ADS] (In the text)
Mateus, A., Sodré L., Cid Fernandes R., et al. 2006, MNRAS, 370, 721 [NASA ADS] (In the text)
Meynet, G., & Maeder, A. 2002, A&A, 381, L25 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1 [NASA ADS] [CrossRef] (In the text)
McClure, R. D., & van den Bergh, S. 1968, AJ, 73, 1008 [NASA ADS] [CrossRef] (In the text)
McGaugh, S. S. 1991, ApJ, 380, 140 [NASA ADS] [CrossRef] (In the text)
McWilliam, A. 1997, ARA&A, 35, 503 [NASA ADS] [CrossRef] (In the text)
Melbourne, J., & Salzer, J. J. 2002, AJ, 123, 2302 [NASA ADS] [CrossRef]
Mouhcine, M., Gibson, B. K., Renda, A., & Kawata, D. 2008, A&A, 486, 711 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Nagao, T., Maiolino, R., & Marconi, A. 2006, A&A, 459, 85 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Osterbrock, D. R. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Mill Valley CA: University Science Books)
Pagel, B. E. J. 1986, PASP, 98, 1009 [NASA ADS] [CrossRef] (In the text)
Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] (In the text)
Pagel, B. E. J., Simonson, E. A., Terlevich, R. J., & Edmunds, M. G. 1992, MNRAS, 255, 325 [NASA ADS] (In the text)
Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] (In the text)
Pettini, M., Ellison, S. L., Bergeron, J., & Petitjean, P. 2002, A&A, 391, 21 [NASA ADS] [CrossRef] [EDP Sciences]
Pettini, M., Zych, B. J., Steidel, C. C., & Chaffee, F. H. 2008, MNRAS, 385, 2011 [NASA ADS] [CrossRef] (In the text)
Pilyugin, L. S. 2000, A&A, 362, 325 [NASA ADS] (In the text)
Pilyugin, L. S. 2001, A&A, 369, 594 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Pilyugin, L. S., & Ferrini, F. 2000, A&A, 358, 72 [NASA ADS]
Pilyugin, L. S., & Thuan, T. X. 2005, ApJ, 631, 231 [NASA ADS] [CrossRef] (In the text)
Prochaska, J. X., Gawiser, E., Wolfe, A. M., Castro, S., & Djorgovski, S. G. 2003, ApJ, 595, L9 [NASA ADS] [CrossRef] (In the text)
Richer, M. G., & McCall, M. L. 1995, ApJ, 445, 642 [NASA ADS] [CrossRef] (In the text)
Rodrigues, M., Hammer, F., Flores, H., et al. 2008, A&A, 492, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Savaglio, S., Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] (In the text)
Scannapieco, C., Tissera, P. B., White, S. D. M., & Springel, V. 2008, MNRAS, 389, 1137 [NASA ADS] [CrossRef] (In the text)
Schlegel, D. J., Finkbeiner D. P., & Davis M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] (In the text)
Searle, L. 1971, ApJ, 168, 327 [NASA ADS] [CrossRef] (In the text)
Shields, G. A. 1990, ARA&A, 28, 525 [NASA ADS] [CrossRef] (In the text)
Skillman, E. D., & Kennicutt, R. C., Jr. 1993, ApJ, 411, 655 [NASA ADS] [CrossRef] (In the text)
Skillman, E. D., Kennicutt, R. C., Jr., & Hodge, P. W. 1989, ApJ, 347, 875 [NASA ADS] [CrossRef] (In the text)
Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] (In the text)
Stasinska, G., Cid Fernandes, R., Mateus, A., Sodré, L., & Asari, N. V. 2006, MNRAS, 371, 972 [NASA ADS] [CrossRef] (In the text)
Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] (In the text)
Thurston, T. R., Edmunds, M. G., & Henry, R. B. C. 1996, MNRAS, 283, 990 [NASA ADS] (In the text)
Tomkin, J., & Lambert, D. L. 1984, ApJ, 279, 220 [NASA ADS] [CrossRef] (In the text)
Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] (T04) (In the text)
Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef]
Vila-Costas, M. B., & Edmunds, M. G. 1993, MNRAS, 256, 199 [NASA ADS] (In the text)
Vílchez, J. M., & Esteban, C. 1996, MNRAS, 280, 720 [NASA ADS]
Wheeler, J. C., Sneden, C., & Truran, J. W. 1989, ARA&A, 27, 279 [NASA ADS] [CrossRef] (In the text)
Wilson, T. L., & Matteucci, F. 1992, A&ARv, 4,1 (In the text)
Zaritsky, D., Kennicutt, R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] (In the text)

Footnotes

... database: http://www.starlight.ufsc.br

All Tables

Table 1: Luminosity-samples studied with their respective luminosity interval in absolute Petrosian r-magnitude, and the redshift samples that can be compared.

Table 2: Coefficients for the l-samples.

Table 3: Mean and mode of the metallicity distributions, and the metallicity range that includes 66 $\%$ of the total metallicity distribution around the mode for the different luminosity samples.

All Figures

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12214f1.ps} \end{figure}$	Figure 1: Absolute Petrosian r-magnitude histograms. From top to bottom, histograms for the z₃, z₂, z₁, and z₀ sub-samples, respectively. The dot-dashed line represents the completeness for the z₃ sample, solid line shows the completeness for the z₂ sample, and dashed lines the completeness for the z₁ sample. All of them extend along the l-samples a, b and c, where N is the number of galaxies, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12214f2.ps} \end{figure}$	Figure 2: Calibration relation between 12+log(O/H) and log([N II] $\lambda$ 6583/[O II] $\lambda$ 3727). From top to bottom, l-sample a, b, and c. Circles, triangles, squares and asterisks represent galaxies for the redshift-sample z₀, z₁, z₂, and z₃, respectively. The solid line represents the best fit of the data using a linear fit, with the 2 $\sigma$ dispersion indicated by the short-dashed lines, while the dot-dash line shows the order-3 polynomial fit. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER
In the text

$\begin{figure} \includegraphics[width=8cm,clip]{12214f3.ps} \end{figure}$	Figure 3: Normalized metallicity histograms for our three l-samples. The dotted line represents the redshift sample interval z₀, dashed line the redshift sample z₁, solid line the redshift sample z₂ and dot-dash line the redshift-sample z₃. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm,clip]{12214f4.ps} \end{figure}$	Figure 4: Abundances of N and O ratios as a function of their $12+\log$ (O/H) abundances derived from the R₂₃ calibration for our three l-samples in redshift, following the same code of symbols used in Fig. 2. The dot-dashed line and the dashed line represent an aproximation of empirical limits of the primary and secondary levels, respectively, of N production, taken from Vila-Costas & Edmunds (1993). (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm,clip]{12214f5.ps} \end{figure}$	Figure 5: Absolute Petrosian r magnitude and $12+\log$ (O/H) for our l-sample of galaxies (L-Z relation). Symbols follow the same code used in Fig. 2. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17.2cm,clip]{12214f6.ps} \end{figure}$	Figure 6: Relation between stellar mass, in units of solar masses, and $12+\log$ (O/H) for our l-sample of galaxies (M-Z relation). The dashed line represents the fit of Tremonti et al. (2004), and symbols follow the same code used in Fig. 2. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=5.5cm,clip]{12214f7.ps}\hspace{1mm} \... ...4f8.ps}\hspace{1mm} \includegraphics[width=5.5cm,clip]{12214f9.ps} \end{figure}$	Figure 7: Percentage of angular size of each galaxy inside the three arcsec diameter of the Sloan fiber for l-samples a, b, and c.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12214f10.ps} \end{figure}$	Figure 8: Normalized metallicity histograms for redshift sample z₀. The dotted clear line is the same as in Fig. 3a, and the dotted dark line represents galaxies of the same redshift sample with covering fraction >20. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12214f11.ps} \end{figure}$	Figure 9: Metallicity evolution derived from our l-samples up to redshift 0.4, vertical lines show the error with respect to the mean metallicity for every redshift interval. Circles, triangles and asterisks, represent the mean metallicity of the l-samples a, b and c, with its respective redshift-samples. Solid line represents the model of Buat et al. (2008) for galaxies with a rotational velocity of 360 km s^-1, and dashed line represents a second-order polynomial fit. (See the electronic edition of the Journal for a color version of this figure.)
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.